Đề khảo sát Toán 9 năm 2020 – 2021 trường THCS Nguyễn Trãi – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2020 – 2021 trường THCS Nguyễn Trãi – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
UBND QUẬN THANH XUÂN
ĐỀ KIỂM TRA KHẢO SÁT KHỐI 9
TRƯỜNG THCS NGUYỄN TRÃI
NĂM HỌC 2020 – 2021
Môn kiểm tra: TOÁN 9
Ngày kiểm tra: 23/5/2021 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề kiểm tra gồm 01 trang)
Bài I (2 điểm): Cho hai biểu thức: 2 + x x 1 1 A = và B = − +
với x > 0 và x ≠ 4. x x − 4 2 − x x + 2 1. Tính giá trị của 1 A khi x = . 4 2. Rút gọn B. A 3. Cho P =
. Tìm các giá trị nguyên của x để 3 Px ≤ ( x −1). B 2
Câu II(2 điểm): Giải các bài toán có ứng dụng thực tiễn
1. Một đội sản xuất phải làm 200 sản phẩm trong một thời gian qui định. Trong 4 ngày đầu họ đã
thực hiện theo đúng kế hoạch, những ngày còn lại họ đã làm vượt mức mỗi ngày 10 sản phẩm
nên đã hoàn thành công việc sớm hơn 2 ngày. Hỏi theo kế hoạch mỗi ngày đội phải làm bao nhiêu sản phẩm?
2. Một quả bóng đá hình cầu có đường kính bằng 24cm. Tính diện tích da dùng
để khâu thành quả bóng đó, biết tỉ lệ da sử dụng làm bóng bị hao hụt 3%. (hình minh họa) 24cm Câu III (2 điểm) 2x + y +1 = x − 7
1. Giải hệ phương trình: 1 3x − 2 y +1 = x − 0 1
2. Cho phương trình: x2 – (2m + 3)x – 2m – 4 = 0 (1)
a) Giải phương trình khi m = 2.
b) Tìm m để phương trình (1) có hai nghiệm x + = 1, x2 sao cho x x 5 1 2
Câu IV (3,0 điểm)
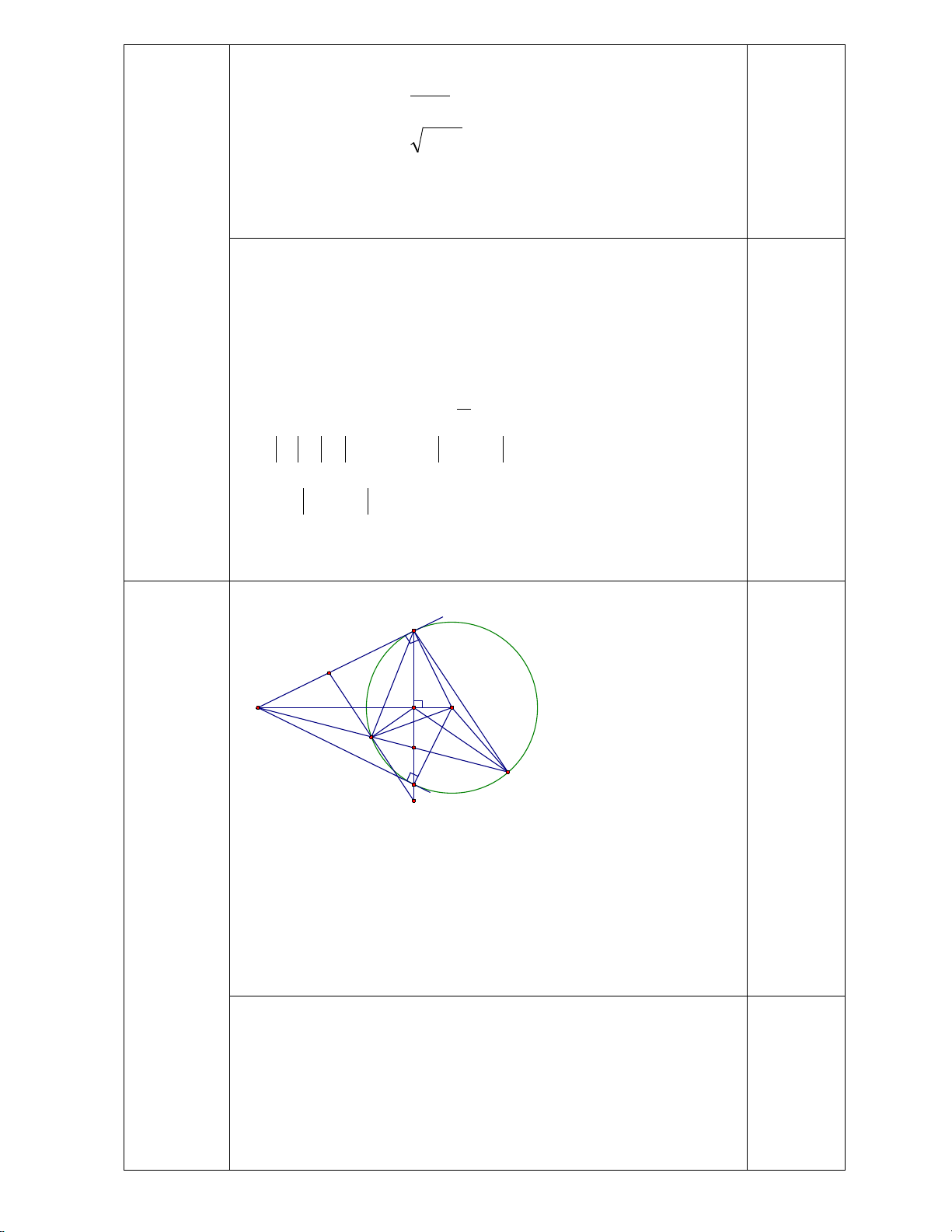
Từ điểm A ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC (B, C là các tiếp điểm) và cát
tuyến ADE thuộc nửa mặt phẳng bờ là đường thẳng OA không chứa điểm B của đường tròn (O). Gọi
H là giao điểm của OA và BC.
1. Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.
2. Chứng minh AO ⊥ BC tại H và AH.AO = AD.AE.
3. Đường thẳng đi qua điểm D và song song với đường thẳng BE cắt AB, BC lần lượt tại I, K.
Chứng minh tứ giác OHDE nội tiếp và D là trung điểm của IK.
Câu V (0,5 điểm) Cho 1 < x < 2. Tìm giá trị nhỏ nhất của biểu thức: 1 1 1 S = + + 2 2 (x −1) (2 − x) (x −1)(2 − x)
------------------------Giám thị không giải thích gì thêm------------------------
ĐÁP ÁN + BIỂU ĐIỂM ĐỀ THI THỬ VÀO LỚP 10 BÀI ĐÁP ÁN ĐIỂM 1 1) Thay x =
(TMĐK x > 0 và x ≠ 4) vào A, ta được 4 0,25 1 2 + 4 A = . = 5 1 0,25 4 KL:………………. x + x + + x − 2) Biến đổi ( 2) ( 2) B = 0,5
( x − 2)( x + 2) 1(2,0 đ) Tìm được x B = và kết luận. 0,5 x − 2 x − 3) Tìm được 4 P = . x Biến đổi 3 0,25 Px ≤
( x −1) ⇔ 2x − 3 x − 5 ≤ 0 2 Suy ra được 25 0 < x ≤ . 4
Kết luận hợp điều kiện thu được 0,25 x ∈{1; 2;3;5; } 6 .
1.Gọi số sản phẩm phải làm mỗi ngày theo kế hoạch là x (sp; 0,25 x ∈ N*; x< 200)
Thời gian dự định làm xong 200 sản phẩm: 200 (ngày) x 0,25
Số sản phẩm đã làm trong 4 ngày đầu là: 4x (sp)
Số sản phẩm cần làm tiếp là: 200 – 4x (sp)
Những ngày còn lại mỗi ngày làm được: x + 10 (sp) 0,25
Thời gian làm hết số sản phẩm còn lại: 200 − 4x (ngày) 0,25 x + 10
Vì đội sản suất đã hoàn thành công việc sớm hơn 2 ngày nên, 2 (2,5đ) ta có phương trình: 200 200 − 4x − 4 + = 2 0,25 x x + 10
Biến đổi phương trình về dạng: x2 + 30x – 1000 = 0 0,25
Giải pt tìm được: x1 = - 50 (KTM), x2 = 20 (TM) 0,25
KL: .................................... 0,25 2.
Tính được bán kính quả bóng: 24 : 2 = 12 (cm)
Diện tích bề mặt quả bóng: 4 πR2 = 4 π122 = 576π(cm2) 0,25
Diện tích da dùng dùng để khâu bóng:
576π + 3%.576π = 593,28π (cm2) 0,25 1.ĐKXĐ: x ≠ 1; y ≥ -1 0,25 x = Giải hpt, tìm được: 2 x −1 0,25 y +1 = 3 x = 2 …… ⇔ 0,25 (TM) y = 8 KL: .................. 0,25
2.a) Khi m = 2, ta được phương trình: x2 – 7x – 8 = 0 0,25
Do a – b + c = 0, nên x1 = - 1; x2 = 8 3(2đ) KL: ........................ 0,25
b) Do a – b + c = 0, nên x1 = - 1; x2 = 2m + 4
Để pt có 2 nghiệm phân biệt thì x ≠ 1 x2 5 ⇔ 2m + 4 ≠ 1 − ⇔ m ≠ − 0,25 2 x + x = 5 ⇔ 1 + 2m + 4 = 5 1 2 Từ: 2m + 4 = 4 m = 0 ⇔ 2m + 4 = 4 ⇔ ⇔ (TM) 0,25 2m + 4 = 4 − m = 4 − KL: .......................
(HS có thể giải theo cách khác đúng vẫn cho điểm tối đa) B 0,25 I A H O D M E C K
a) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau (B, C là các tiếp điểm) ⇒ = 0 0,5 ABO ACO = 90
⇒ B, C thuộc đường tròn đường kính OA 0,25 4(3,0đ)
⇒ Bốn điểm A, B, O, C cùng thuộc đường tròn đường kính OA.
b) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau 0,25
⇒ AB = AC ⇒ A thuộc trung trực của đoạn BC
Có OB = OC ( = R) ⇒ O thuộc trung trực của đoạn BC
Do đó OA là trung trực của đoạn BC ⇒ OA ⊥ BC tại H. 0,25 + Xét A ∆ BO có 0
ABO = 90 , BH ⊥ OA 2
⇒ AH.AO = AB (hệ thức lượng) (1) 0,25 + Xét (O) có = ABD
AEB (góc nội tiếp và góc tạo bởi tia tiếp
tuyến và dây cùng chắn BD ) ⇒ C/m được: A ∆ BD A
∆ EB (g-g) ⇒ AD. AE = AB2 (2)
Từ (1) và (2)⇒ AH. AO = AD. AE 0,25 AH AE +) Có AH. AO = AD. AE ⇒ = AD AO ⇒ C/m được: A ∆ DH A
∆ OE (c.g.c) ⇒ = ADH AOE 0,25
⇒ C/m được tg DHOE nội tiếp 0,25
+ ) Có tg DHOE nội tiếp (cmt)⇒ = AHD OED
- Xét (O) có OD = OE (=R) ⇒ ODE ∆ cân tại O ⇒ = OED ODE
Lại có tg DHOE nội tiếp (cmt)⇒ = ODE OHE ⇒ = AHD OHE
- Gọi M là giao điểm của BC và AE 0,25
C/m được HM là phân giác của DHE
Lại có HA ⊥ HM (vì OA ⊥ BC)
⇒ HA là phân giác của góc ngoài tại H của ∆ HDE MD AD DH ⇒ = = ME AE EH
Có IK // BE (gt) ⇒ DK // BE ⇒ DK DM = BE ME
Có IK // BE (gt) ⇒ DI // BE ⇒ DI AD = BE AE DK DI 0,25 ⇒ =
⇒ DK = DI hay D là trung điểm của IK BE BE
Đặt a = x – 1, b = 2 – x ⇒ a, b > 0, a + b = 1 2 1 1 1 1 1 3 M = + + = − + 2 2 a b ab a b ab
Áp dụng bắt đẳng thức Cosi ta có: a + b ≥ 2 ab ⇒ 1 ≥ 2 ab 1 3 0,25 ⇒1≥ 4ab ⇒ ≥ 4 ⇒ ≥12 5 (0,5đ) ab ab 2 1 1 Mà: − ≥ 0 nên M ≥ 12 a b
Dấu “=” xảy ra khi a = b = 1 2 Vậy MinA = 12 khi x 1 3 – 1 = 2 – x = ⇔ x = 0,25 2 2