
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 9 THẠCH THẤT
Năm học: 2021 – 2022
(Thời gian làm bài: 120 phút không kể thời gian giao đề) (Đề thi gồm 01 trang)
Bài I (1,5 điểm) Cho biểu thức x + 3 A − = , x 3 7 x 4 B = + −
với x ≥ 0, x ≠ 1 x −1 x −1
x + 2 x + x − 2
1) Tính giá trị của biểu thức A khi x = 25 2) Rút gọn B
3) Biết P = A⋅ B . Tìm giá trị lớn nhất của P
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một phân xưởng theo kế hoạch phải sản xuất 1000 bộ đồ bảo hộ y tế phục vụ công tác
phòng chống dịch bệnh trong một thời gian quy định. Nhưng do tình hình diễn biến dịch bệnh
phức tạp, để đáp ứng nhu cầu đồ bảo hộ y tế, mỗi ngày phân xưởng đã sản xuất vượt mức 20
bộ đồ bảo hộ y tế nên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định là 1
ngày và làm thêm được 80 bộ đồ bảo hộ y tế. Hỏi theo kế hoạch mỗi ngày phân xưởng phải
sản xuất bao nhiêu bộ đồ bảo hộ y tế?
2) Một hình cầu có thể tích bằng 288π (cm3). Tính diện tích của mặt cầu đó? (cho π = 3,14)
Bài III (2 điểm) 7 x − 3 − = 2 y
1) Giải hệ phương trình 7 5 x −3 + = 4 y 2) Cho phương trình 2
x + (2 − m) x + 3(m −5) = 0 với m là tham số.
a) Chứng minh rằng với mọi giá trị của m phương trình luôn có nghiệm x = 3.
b) Tìm giá trị của m để phương trình trên có nghiệm x = 3+ 2 .
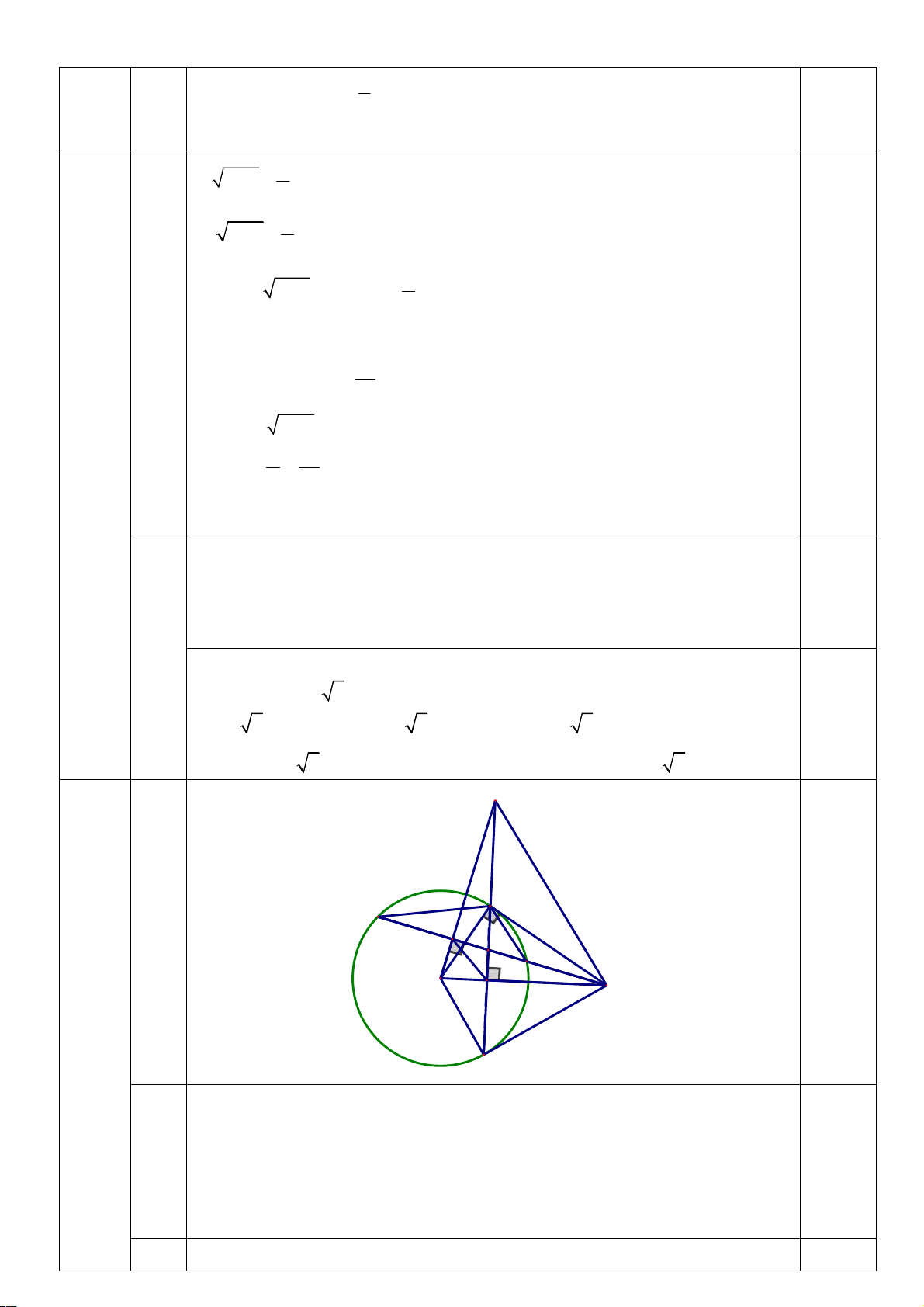
Bài IV (3.5 điểm) Cho đường tròn ( ;
O R) , dây CD cố định. Lấy H là trung điểm của CD. Trên tia
đối của tia DC lấy điểm M. Từ M kẻ các tiếp tuyến MA, MB với (O) (A, B là các tiếp điểm). Đường
thẳng AB cắt các đường thẳng MO, OH lần lượt tại K và N.
1) Chứng minh tứ giác MNHK nội tiếp.
2) Chứng minh OH.ON = OK.OM
3) Khi M di động trên tia đối của tia DC hãy chứng minh đường thẳng AB luôn đi qua một điểm cố định.
4) Gọi P là giao điểm của AB và CD. Chứng minh 2 1 1 = + MP MC MD 2 + − + Bài V 2020x 2021 1 x 2022
( 0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức A = 2 1− x -------- HẾT --------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN, BIỂU ĐIỂM CHẤM THẠCH THẤT
ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 9
Năm học: 2021 - 2022
(Đáp án gồm 03 trang) BÀI Ý HƯỚNG DẪN ĐIỂM 25 3 1
Khi x 25 (TMĐK) thì A 2 0,25đ 25 1
Với x 0; x 1 ta có: x 3 7 x 4 x 3 7 x 4 B x 1 x 2 x x 2 x 1 x 2
( x 1)( x 2) 0,25đ x ( x 2) 3( x 1) 7 x 4 B 2
( x 1)( x 2)
( x 1)( x 2)
( x 1)( x 2)
x 2 x 3 x 3 7 x 4 x 2 x 1 B 0,25đ 1
( x 1)( x 2)
( x 1)( x 2) 2 (1,5đ) ( x 1) x 1 B 0,25đ
( x 1)( x 2) x 2
Với x 0; x 1 ta có: x 3 x 1 x 3 1 P . A B . 1 x 1 x 2 x 2 x 2 0,25đ 3 1 1 1 3 Do x 0 x 2 2
max P 1 x 2 2 2 2 0,25đ
Dấu "=" xảy ra khi và chỉ khi x 0 3 Vậy GTLN của P khi x 0 2
Gọi số bộ đồ bảo hộ y tế mà phân xưởng sản xuất mỗi ngày theo kế 0,25đ hoạch là x ( * x , bộ)
Số bộ đồ bảo hộ y tế phân xưởng sản xuất thực tế mỗi ngày là 0,25đ x 20 (bộ) 1000 0,25đ
Thời gian phân xưởng sản xuất đồ bảo hộ y tế theo kế hoạch x (ngày)
Thời gian phân xưởng sản xuất đồ bảo hộ y tế thực tế là 0,25đ 2 1 1000 80 1080 (2,5đ) (ngày) x 20 x 20
Vì phân xưởng đã hoàn thành sớm hơn thời gian quy định là 1 ngày. Ta có phương trình: 0,75đ 1000 1080 1 x x 20
Giải phương trình tìm được x 100 (tmđk)
Vậy số bộ đồ bảo hộ y tế phân xưởng sản xuất mỗi ngày theo kế 0,25đ hoạch là 100 bộ. 4 0,25đ Theo đề bài ta có: 3
R 288 R 6 (cm) 2 3
Diện tích của mặt cầu đó là: 2 2 2
S 4 R 4.3,14.6 452,16 (cm ) . 0,25đ 7 x 3 2 y
ĐKXĐ: x 3; y 0. 7 5 x 3 4 y 1
Đặt a x 3 a 0 và b b 0 , ta có hệ phương trình 0,25đ y 1
a 1 t / m
a 7b 2 1 . 5a 7b 4 b 0,25đ t / m 7 x 3 1 x 4 3 Do đó 1 1 . Ta tìm được (thỏa mãn). 0,25đ y 7 (2đ) y 7
Vậy hệ phương trình đã cho có nghiệm ; x y 4; 7 . 0,25đ
a) Thay x 3 vào vế trái của phương trình ta được: 0,25đ 2
3 2 m.3 3m 5 9 6 3m 3m 15 0 đúng với mọi m
Vậy phương trình có nghiệm x 3 với mọi m . 0,25đ 2
b) Vì phương trình luôn có nghiệm x 3 nên để phương trình có
nghiệm x 3 2 thì theo định lý Vi-et ta có: 0,25đ
33 2 3m 5 3 2 m 5 m 8 2 .
Vậy m 8 2 thì phương trình trên có nghiệm x 3 2 0,25đ N A C H 0,25đ P D O K M 4 (3,5đ) B
Vì H là trung điểm CD nên OH vuông góc CD , suy ra 0,25đ o OHM=MHN=90 (1) 1
Vì OA = OB = R; MA = MB (tc 2 tt cắt nhau) nên OM là đường trung 0,25đ trực AB , suy ra o M N K = 90 (2).
Từ (1)(2) lập luận suy ra tứ giác MNHK nội tiếp. 0,25đ 2 ONK = OMH (cùng phụ KON ); o OHM = OKN = 90 0,5đ nên ΔOKN ΔOHM g.g ON OK 0,5đ Suy ra = ON.OH = OK.OM OM OH Ta có: 2 2 OK.OM = OA = R
Vì CD cố định nên H cố định suy ra OH không đổi. 0,25đ 3 2 OK.OM R Mà ON = =
không đổi nên N cố định. OH OH 0,5đ
Vậy AB luôn đi qua điểm cố định N . 2 1 1 = + MP MC MD
2MC.MD = MP MD+MC MC.MD = MP.MH (*) 0,25đ (Do MC + MD = 2MH ) ΔMDA 2 ΔMAC MC.MD = MA (1) 4 ΔMKP ΔM HO MP.MH = MK.MO (2) 0,25đ
Tam giác ΔOAM vuông tại A có đường cao AK 2 MK.MO = MA (3) 0,25đ
Từ (1), (2), (3) MC.MD = MP.MH (**) Từ (*) và (**) đpcm 2 2
ĐK: 1 x 0 x 1 x 1 1 x 1 2
2020x 2021 1 x 2022
20211 x 1 x Ta có: A 2021 2 2 1 x 1 x 0,25đ 5 2
2021 1 x1 x 2021 2021 2 2021 (0,5đ)
1 x1 x 2020
Dấu "=" xảy ra 20211 x 1 x 2021 2021x 1 x x 0,25đ 2022 2020
Vậy MinA 2021 2 2021 x 2022 Lưu ý:
- Học sinh có cách làm khác đúng cho điểm tương đương.
- Điểm toàn bài làm tròn đến 0,5 điểm./.
--------------------- Hết ------------------------




