Đề khảo sát Toán 9 năm 2021 – 2022 phòng GD&ĐT thành phố Thái Nguyên
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2021 – 2022 phòng GD&ĐT thành phố Thái Nguyên giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
trường
51
26 lượt tải
Tải xuống
UBND
TP THAI NGUYEN
KIEM TRA KHA9 sA1'
HQC
SINH
LoP 9
pHoNG_q4q
luc_yADAo
rao
Nim hsc 202t
_
2022
MON: TOAN
Thdi
gian
ldm
bdi:
120
philt,
kh6ng ke thdt
gion giao
di
pO
mem tra
gdm
c6 01 trang, L0 cffu,
m6i ceu 1,0 tli6m)
on
gA.r
Cflu
1. Kh6ng dirng
mdy
tinh
cdmtay,rut
ggn
bi6u
thric:
o:(# 4Jr*fi)
Jr-Ji
Ciu2.Khdng
dirng mdy tinhcAm tay,
hdy
giinhQ phuong
trinh:
{'*-^'= .'
lx+3Y
=
4
Cffu
3.
Cho
phucmg
trinh
2x2
-6x+2m-5
=
0 (1)
v6i
m ld
tham
s6.
a) Gi6i
phuong
trinh
(1)
v6i m:2.
t1
b)
Tim
gi|tactra
m
dO
phucmg
trinh
(1)
c6 hai nghiQm
phan
biQt
x,, xr
thohmdn
'
+
j-
=
6
xt x2
t- r-
Ciu
4.
Cho
bi6uthirc:
p
=
2^l*;9
-+!
*2tU
+1'
voi x) 0,x
*4,x+9
x-54x
+6 tlx
-2
...lx
-3
a) Rirt
ggn
bi6u thirc
P. b) Tim t?rt cit
gi|tri
oia
x
dC
p
> f .
C6u
5.
Cho ducmgthSng
(d):y
=(r-2k)x+3.
Tim
ei6tri
cirak
AC ducrngthing
(d)
cAt
tryc
hodnh
tpi mQt di6m
c6 hodnh dQ bing
-
2.
C6u
6. Hdng ngey bpn Lan di
hgc
bdng
xe dap,
queng
ducrng tu
nha d6n trudng ddi
4 km.
H6m nay, khi dA di du-o. c 1 km thi xe dap bi
h6ng, ngay lfp tuc Lan di nhd d6n
truong bdttg
xe m6y v6i van
t6c
lon hon
van
t6c khi di xe dpp
ld24 krnlh,
vi
th6 Lan ddd5n trudng s6m
hcvn 10
phirt.
Tinh vQn t6c cria bpn Lan
khi
<Ii
hgc
bing
xe dpp.
Ciu
7.
Cho
tam
gi6c
ABC vu6ng tai A dulng cao
AH,
c6
AB
:
9
cm, AC
:
12 cm.
Tinh dO dai cludng cao AH, dopn
HC
vd s,5 do
g6c
B
(ldm
trdn d6n d0).
,
Cffu 8. Cho tam
gi6c
ABC ngopi titip tlucrng trdn
(O;
r),
Gqi
I ld ti6p cli6m cta
cpnh BC
v6i
duong trdn
(O).
Ve
dudng kinh
IN,
tiiip
tuy6n cria dudrng trdn
(O)
tai N cit AB vd
AC
lAn luqt
tpi
D
vd
E.
Chimg
minh ring: DN .
BI
:
12.
Cffu
9.
Cho
hai ducrng tron
(O)
vd
(O')
c8t nhau tai A vd
B.
VC
hinh binh henh
OCO'B.
Chrmg
minh ring ACIIOO'.
C6u
L0.
Cho
tam
gi6c
nhqn ABC
nQi
ti6p
dudng tron
(O).
C6c
ducrng cao AD,
BE,
CF
.
(D e
BC, E
e
AC, F
e
AB)
cria
tam
gi6c
chtnhau
tpi H.
Chrmg
minh .irg'
a) Tir
gi6c
AEFtr'
nQi ti6p dugc
mQt dudng trdn.
b)
DE
+
DF', <
BC.
------ n6t
Hq vd ftn thi sinh;
.........Sd
bdo danh;
UBND
THANH PHO THAI NGUYEN
PHdNG
GrAo
DUC vA
DAo rAo
nuoxc nAN cHAnn KrEM
TRA xuAo sAr cnAr
LtIgI,{G HQC SINH
LOP 9
naON roAN
I. Hudng din
chung
-
Gi6m
kh6o cA, n6.n
vimg
y6u
cAu cria hu6ng
d6n ch6m
OC Aann
giq
dring
bdi
ldm cria thi sinh. Thi
sinh ldrm c6ch
kh6c dap
6nn6u dirng
vdn cho
di6m t6i
da.
-
Khi
vQn
dpng ddp
6nvd thang
di6m,
gi6m
kh6o cdn chir
dQng,
linh ho4t
v6i tinh th6n
tr6n trgng bdi
ldm ctra hgc sinh.
-
N6u c6 viQc
chi titit h6a di6m
cdc
y
cAn
phii
d6m b6o
kh6ng sai lQch v6i
t6ng di6m vd dugc
th6ng nh6t trong
todn hQi d6ng ch6m
thi.
-
Di0m todn bdi
ld t6ng di6m diua
cilc c6u
hoi trong dO thi, ch6m
di6m
16 d6n
0,25
vitkh6ng
ldm trdn.
II. Dfp rin vir
th eIi6mn
Ya
tha
Bni
N6i
dung
Di6m
1
o:(Jt
-3Jr.Jo)"0-J-s
=
(rJi
-3nry.
fi)
.",!-2
-
Ji
=(-.lr.Jo)
Jr-Ji
=
-Jr.J,
*
Jto
.Ji
-
J5
=
-(Jr)'
*
Jn
-
J5
T: I:
:-l+lV)-V)
., 17
--l,-r!J
chf
j:
IYdu thi sinh
ra luin bw6c
,rili cins,
khbng bi\n
d6t cho 0,5
ctiAm.
0,25
0,5
0,25
2
Vfly
he
phucrng
trinh co
nghiQm
(*;y)=
f+,+)''/
\7'7)
Chri
f:
.
+
Niiu
thf sinh
gidi
theo
phwong
phdp
thii itfing
vdn
cho iliiim t6i
ita;
+
Nila thi sinhiW
atug-MTCT,
ia nghiQm
itfing
cho 0.5
tti6m;
+
Nilu th{ sinh
sirti
ittiis
nhtng
khilng
*ih tuAn
cho di6m
fii cta.
lZ*-r=-3 lZ*-!:-3 lty--tt
<
<><
<f<
lx+3y=4 l2x+6y=8 lx+3y=4
t rt I
ll
lr'-- lt'--
^)'
t
^)"
7
e1
e1
_
l.r=+-3.11 l*=:l
lzlz
0,5
0,5
a
J
Phuong trinh:
2x2
-6x+2m-5
-
0
(1)
v6i m ld tham s6.
a) V6i m: 2 ta c6
phucrng
trinh:
2x2
-6x -
1
=
0
A'=11>0
Phucrng
trinh c6 hai nghiQm
phAn
biQt:
:+J1 3-d1
"r=
2
i
xz=
Z
;
chf
f:
+
Ndu
thi sinh tfnh theo
L itfing
vdn
cho itihm fii ita.
+
Nhu HS sfr d4ng MTCT, ra nghiQm drtng thi cho 0,25 iti6m.
0,25
0,25
b) Phucrng trinh
(1)
co
hai nghiCm
phdn
biet khi:
A'
>
0 <>3'
-212m-5)>
o
<>
*.*
4
[.. + r,
:3
Ap dung
dinh
li
Vi-et ta co:
]
^ ^'
z)
-s
l.'''t':
2
Theo
Ae Uai ta c6:
l*l
-
6 <+ xt+ x2
=
6xrx,
xt x2
e 3
-
U.2m-5
2
e2m-5=1
em-3(rlm)
Vfly m:3 thoa mdn
y6u
cAu cira AC Uai.
0,25
0,25
4
a) V6i
x) 0,x
+ 4,x +
9
ta co
,_
zJi-g
_..,[+g
*2Ji+l
x-s.'[+6
Ji-z J*-s
2.,[i
-g
(Ji
* 3XJ;
-
3)
,
e^[;
+ r;1Ji
-
zy
:Grxf=;-m-rxf5-@
_zJi
-g -d;
+sLd;
-zL+eJ;
+ttrJ;
-zt
(#
-
zt<Ji
-e)
_z^,li
-s
-(*-s)+(z*-sJ;
-z)
(#
-
2)(J;
-z)
0,25
x-J;-2
(J,-zltJi-sl
r,,!*
-zl(Ji -
gl
'[i
+t
r/x
-3
0,25
b)Voi x)0,x+4,x+9
r
p
>le
p_
1
>o
e
Vx
+1
_1
>
o e_J-ro
Jx
-3
Jx
-3
oJr-3>0<>r>9
K6t ho.
p
v6i di6u ki6n x
)
O,x
* 4,x *9
taduoc x
>9 .
0,25
0,25
5
Vi ducrng thdng
(d)
c6t trpc
hoirnh
tai di6m c6
hodnh d0 - 2, thay
x
=
-2
, !
=
0vdo
phuong
trinh dudng thEng ta dugc:
.l
(l-2k).(-2)+3:0
oO:;
_l
.l
Vav
k:-
thoa
man
veu
cau.
'J
4
'
0,25
0,5
0,25
6
Ggi
vfn t6c cria b4n Lan khi di hgc bdng xe dpp
lir
x
(km/h),
(
x
>
0)
Thdi
gian
hdng ngey Lan di
xe
dpp tt
nhd
d6n trucmg
ta:
1
1fr)
x
Thdi
gian
Lan di 1 km
bdng
xe dpp h:
l(ko/h)
x
Vpn tdc ctra
xe m6y
ld:
x+ 24
(ko/h)
Thdi
gian
Lan di nhd xe m6y i16n truong ld:
4
=-16<mltr)
a
x+24 x+24\
/
Vi
h6m nay Lan
d6n truong sorn
hon
trinh:
10
phrit:
I
SiO
n6n ta c6
phucrng
4
(t
3
)
l
--l -r-
l-
x
[r,
,+Z+)-O
331
rr x+24
6
e x2
+24x-432=O
[x
=
l2
(rh6a
min)
t\
,'-O I
lx=-36
(loai)
L
0,25
0,25
0,25
0,25
Vpy
hdng ngay
Lan di
hgc
bing
xe dpp
v6i vfn t6c
12 km/h
7
Ap
dung
h6
thuc
lugng trong tam
gi6c
vu6ng
ta c6:
1
1 1 1 r
(S)'
HA'
-
A#
*
Atr:
Cn
n':
t
;.,J
e AH
:7,2(cm)
X6t AAHC vu6ng tai H c6:
AC2
:
AH2
+
uC2
1or
Pytago)
e
HC
JAc'-AH'
<+ HC
,[r'
J J
:
e.6(cm
)
X6t AABC
vu6ng
tai A c6
AC124
tanll:
=0=530
AB93
0,25
0,25
0,25
0,25
8
Ke oH LAB.
X6t
(o)
c6:
(1)
Hai titip
tuy6n
DN
vd
DH cdt
nhau tai D
=
DN:
DH
(2)
Haitii5p tuy6n
BH vd
BI cit nhau
tpi B
=
BI
:
BH
Tir
(1)
vd
(2)
suy
ra: fdD
=90'
(g6c
tpo bdi
hai tia
ph6n
gi6c
cinhai
g6c
kC
bu).
Xdt LD)B vu6ng
tpi O c6
dulng cao OH,
6p dpng
hQ
!hit9
luqng trong
tarfl
gi6c
vu6ng
ta c6; OH2
=
DH.BH
=
DN.BI
=
12
0,25
0,25
0,25
0,25
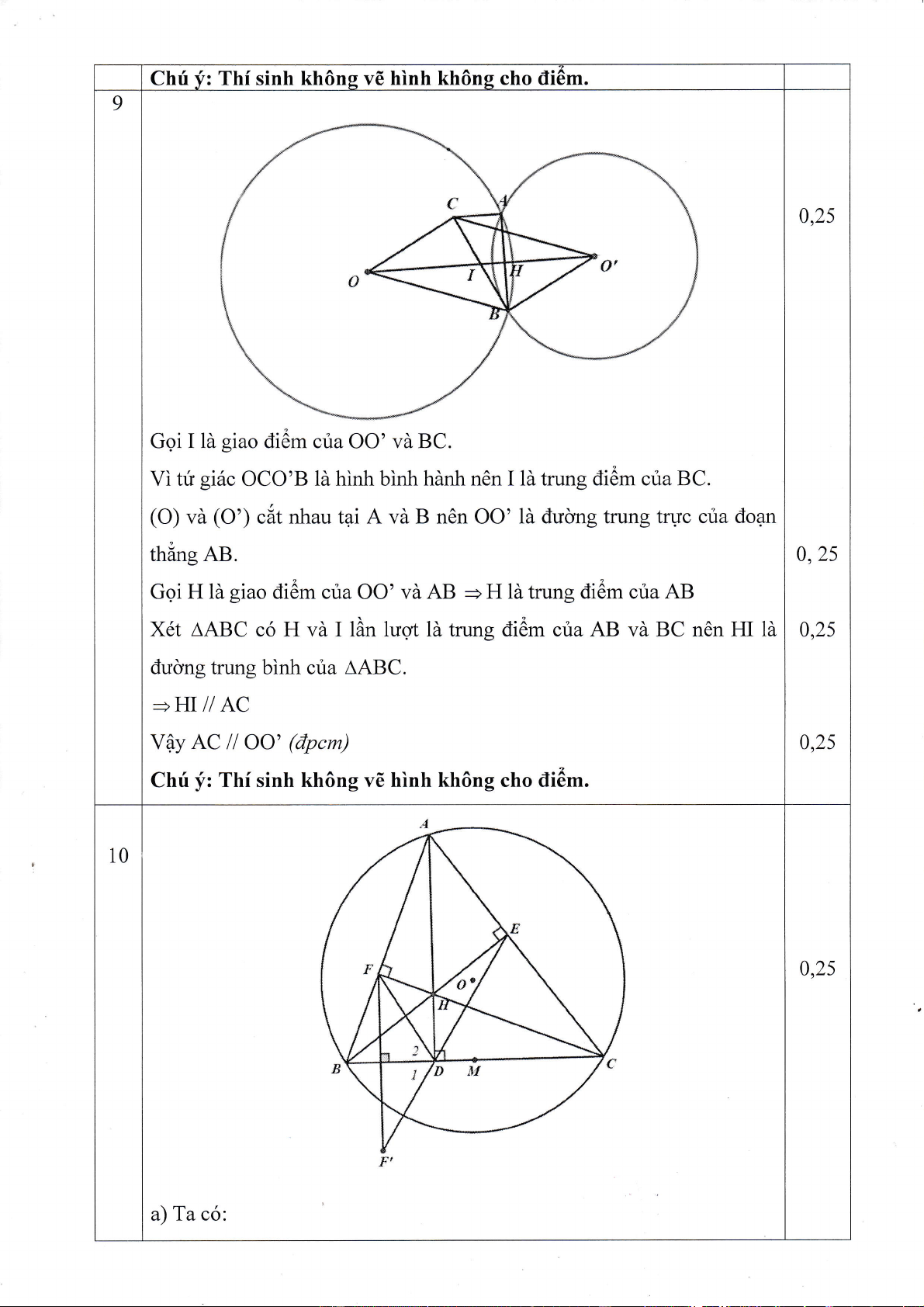
Chri
f:
Thf sinh kh6ns vE
hinh khdne cho cli6m.
9
Gqi I ld
giao
di6m cria
OO'
vd BC.
Vi
tf
gi6c
OCO'B
le hinh binh hdnh
n6n I ld
trung
di6m ctra BC.
(O)
va
(O')
clt nhau tai
A
vi
B n6n
OO'
ld dulng trung trgc cria
thdng
AB.
Gqi
H ld
giao
di6m cria OO'
vd AB
+
H ld trung diOm cria AB
X6t AABC
c6
H
vd
I lAn luqt ld
trung
di6m cria AB
vi
BC n6n
ducrng trung binh cta
AABC.
=HI
ll AC
Vfy
AC
ll OO'
(dpcm)
Chf
f
:
Thi
sinh
kh6ng
vE
hinh kh6ng cho tli6m.
do4n
HI 1e
0,25
0,25
0,25
0,25
10
a) Ta c6:
0,25
BEIAC=ffi=900
CFIAB=ffi:9OO
Tri
gi6c
AEHF
c6: frpL: trA: eo"
V4y
tir
gi5^
AEHF
n6i ti6p ducrng trdn
duhng kinh AH
(dpcm).
0,25
b) Gqi F' ld di6m doi xung
voi F
quaBC
=DF:DF';0
:fr
(f)
Vi ATa: ffia: eoo
=
AFDC
n6i
ti6p
=
fl
:6Ib
Vi
ffiE: ADB:900
=
AEDB n6i titlp
=
pDc:6IL
3 D,
:
EDC
(2)
Tir
(1)
vd
(2)
suy ra:
0
:
EDa
^
=
D, + BDE
=
EDC + BDE:1800
=
E, D, F' thing
hdng.
Do d6: DE
+
DF
:
DE
+
DF'
:
EF'
Vi
F
vdF'd6i
xirng
quaBC
n6n 6FB:BFC=900vd tu
giirc
BFEC n6i
,i
tiep
duong tron duong
kinh BC.
3
B, F,
E,
C,
F' cirng thuQc dudng trdn
dulng kinh BC.
Gqi
M ld
trung di6m cua canh
BC.
X6t ducmg trdn
(M)
duong kinh BC co:
EF' le dAy cung
BC ld duong kinh
Do do: EF'
<
BC eDE
+
DF <BC
(dpcm)
Ddu
":"
xiy
ra khi D
:M
=
AABC
cdn tai
A.
Chri
y:
- Thi sinh khdng vE
hinh khdng
cho
tli6m.
-
y
b):
Thf
sinh
kh6ng x6t d6u
$-D
xay ra
khi
D
=M
vin
cho
eli6m t6i Aa.
0,25
0,25
Lu'u
rt
: Hgc sinh lcim
cdch khtic ctfing vdn cho
ttiOm tili cta.t
Bấm Tải xuống để xem toàn bộ.