



Preview text:
PHÒNG GD – ĐT QUẬN CẦU GIẤY
ĐỀ KHẢO SÁT TOÁN 9 LẦN
TRƯỜNG THCS LÊ QUÝ ĐÔN Năm học 2021 - 2022 (Đề gồm 01 trang) Ngày kiểm tra: 31/5/2022
Thời gian làm bài: 90 phút(Không kể thời gian phát đề)
Bài I. (2,0 điểm) Cho các biểu thức 2 x x 8 x x 1 x 1 A và B
với x > 0, x ≠ 4 x x 4 x 2 2 x
1) Tính giá trị biểu thức A khi x = 16.
2) Rút gọn biểu thức B. 3
3) Cho P = A : B. Tìm tất cả các giá trị của x thỏa mãn: .
P x x 1 . 2
Bài II. (2,5 điểm)
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai vòi cùng chảy vào một bể không có nước thì sau 1 giờ 20 phút đầy bể. Nếu để vòi I
chảy một mình trong 10 phút rồi khóa lại và mở tiếp vòi II chảy trong 12 phút thì cả hai vòi chảy 2 được
bể. Tính thời gian mỗi vòi chảy một mình đầy bể? 15
2) Một chiếc nón có đường kính đáy bằng 40cm, độ dài đường sinh là 30cm. Người ta lát
mặt xung quanh hình nón bằng 3 lớp lá khô. Tính diện tích lá cần dùng để tạo nên một chiếc nón
như thế (lấy 3,14)
Bài III. (2,0 điểm) x
1 y 3 xy 22
1) Giải hệ phương trình: x 2 y 1 xy 8 2) Cho ph ương trình: 2 x mx m 3 0. a) Giải phương trình v ới m 3 .
b) Tìm m để phương trình có 2 nghiệm x , x là độ dài hai cạnh góc vuông của tam giác 1 2
vuông có cạnh huyền bằng 21.
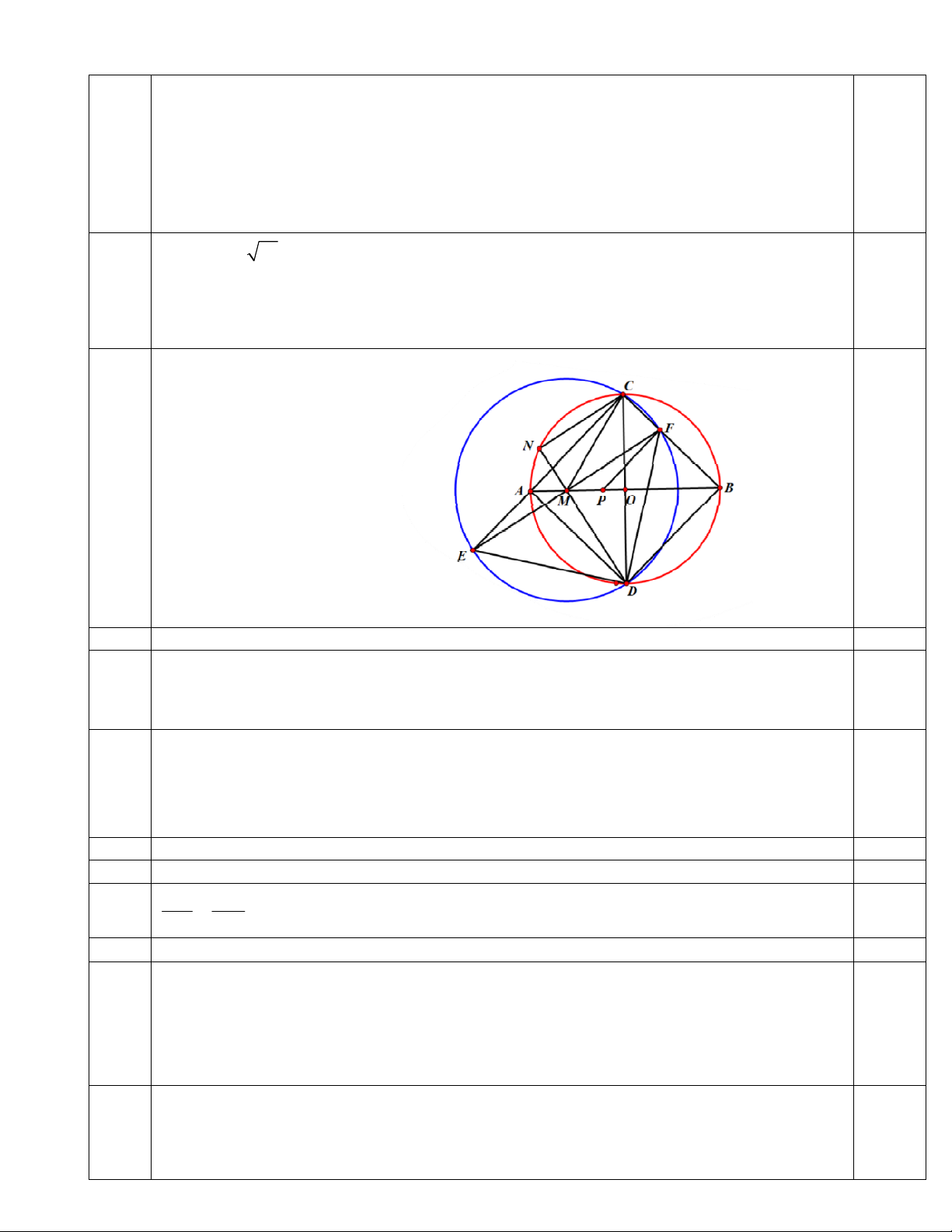
Bài IV. (3,0 điểm) Cho đường tròn tâm O bán kính R có hai đường kính AB, CD vuông góc với
nhau. Lấy điểm M bất kì thuộc đoạn thẳng OA (M khác O và A). Tia DM cắt đường tròn (O) tại N.
1) Chứng minh bốn điểm O, M, N, C cùng thuộc một đường tròn.
2) Chứng minh DM.DN = DO.DC = 2R2.
3) Đường tròn tâm M bán kính MC cắt AC, CB lần lượt tại E và F. Chứng minh ba điểm E, 4 1
M, F thẳng hàng. Tìm vị trí của điểm M trên đoạn thẳng OA để S
CE CF đạt giá trị nhỏ nhất.
Bài V. (0,5 điểm) Cho a, b, c là các số thực không âm thỏa mãn a + b + c = 2.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = ab + bc - 2ca.
--------- Hết ---------
PHÒNG GD – ĐT QUẬN CẦU GIẤY
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT TOÁN 9 LẦN
TRƯỜNG THCS LÊ QUÝ ĐÔN Năm học 2021 - 2022 Ngày kiểm tra: /5/2022 (Đề gồm 01 trang)
Thời gian làm bài: 90 phút(Không kể thời gian phát đề) Bài Nội dung Điểm I 2,0 2 x 1 A với x > 0 0,5 x
Thay x = 16 (tmđk): Ax 2 16 0,25 16 3 A 0,25 2 x 8 x x 1 x 1 2 B 1,0 x 4 x 2 2 x x 8 x x 1 x 1 B x 4 x 2 x 2 x x
x 1 x 2 x 1 x 2 8 0,5 B x 4
x 2 x 2 x 2 x 2 x x x x 2 2 x B 0,5
x 2 x 2 x 2 x 2 x 2 3 0,5 2 x x x 4
P A : B : x x 2 x 3 0,25
P x x 3 .
1 x 4 x
1 2x 3 x 5 0 2 2
x 12 x 5 0 2 x 5 0 ( x 1 0) 5 25 0,25
x x 2 4 (tmđk) II 2,5 1 2,0 4
Gọi thời gian vòi I, II lần lượt chảy một mình đầy bể là x, y (giờ), (x,y> ) 0,25 3 1 1
Trong 1 giờ, vòi I chảy được:
(bể), vòi I chảy được: (bể) x y 0,25 4 3
Cả hai vòi chảy được: 1: (bể) 3 4 4
Cả hai vòi cùng chảy sau 1 giờ 20 phút đầy bể, ta có PT: (1h20’ = (h) ) 3 1 1 3 0,25 x y 4 1 Sau 10 phút 1
h , vòi I chảy được: (bể) 6 6x 1 Sau 12 phút 1
h , vòi II chảy được: (bể) 0,5 5 5y 1 1 2
Hai vòi chảy được 2 bể, ta có PT: 15 6x 5y 15 1 1 3 x y 4 Ta có HPT: 0,25 1 1 2 6x 5y 15
Giải hệ PT được: x = 2(tmđk); y = 4 (tmđk) và KL 0,5 2 0,5 R = 20cm 0,25 Sxq = Rl = .20.30 (cm2)
Diện tích lá cần dùng là: 3..20.30 3,14.1800 = 5652 (cm2) 0,25
Vậy diện tích lá cần dung để tạo nên một chiếc nón khoảng 5652 (cm2) III 2,0 x
1 y 3 xy 22 1
Giải hệ phương trình: 1,0 x 2 y 1 xy 8 3
x y 25 Biến đổi thành 0,5
x 2y 10 x 8 Giải được: 0,5 y 1 và KL 2
Cho phương trình: x2 – mx + m – 3 = 0 1,0 a 0,5
Thay m = -3 ta được: x2 + 3x – 6 = 0 0,25 3 33 3 33
Giải PT được nghiệm: x ; x 0,25 1 2 2 2
Tìm m để phương trình có 2 nghiệm là độ dài hai cạnh góc vuông của tam giác vuông có b cạnh huyền bằng 21 0,5 ' 0 x 0 1 x 0 0,25 2 x x 212 2 2 1 2 m 2 ' 2 8 0 m
x x m 1 2
HT Vi-ét: x x m 3 1 2 x 0 x x 0 m 0 m 0 1 1 2 m 3 x 0 x x 0 m 3 0 m 3 2 1 2
x x 212 x x 2 2 2 2x x 21 1 2 1 2 1 2 2
m 2m 3 2
21 m 2m 15 0 0,25
Giải m = 5 (tm) và m = -3 (ko tm) Kết hợp… m = 5 IV 3,0
1 Chứng minh bốn điểm O, M, N, C cùng thuộc một đường tròn. 1,0
Vẽ hình đúng đến câu 1)
Ta có AB CD tại O (gt) 0 MOC 90 0,5 0
DNC 90 ( góc nội tiếp chắn nửa đường tròn (O)) 0 MNC 90 Tứ giác OMNC có 0 0 0
MNC MOC 90 90 180 MNC và
MOC là hai góc đối nhau 0,5
Suy ra tứ giác OMNC nội tiếp (dhnb)
Vậy 4 điểm O, M, N, C cùng thuộc một đường tròn
2 Chứng minh DM.DN = DO.DC = 2R2 1,0
Chứng minh: NDC ∽ ODM (g.g) 0,5 DN DC 2
DM.DN DO.DC .
R 2R 2R 0,5 DO DM 3 1,0
+) Chứng minh ba điểm E, M, F thẳng hàng
ACB là góc nội tiếp chắn nửa đường tròn (O) 0 ACB 90 hay 0 ECF 90 Mà
ECF là góc nội tiếp chắn cung EF của (M, MC) 0,5
Suy ra EF là đường kính của đường tròn tâm M.
Ba điểm E, M, F thẳng hàng.
+) Chứng minh CE+CF không đổi khi M di động trên đoạn thẳng OA.
C/m: ADE = BDF(g.c.g)(AD=BD;
ADE FDB (cùng phụ với góc ADF) 0,25
Suy ra AE BF
Mà CE+CF = (CA+AE)+(BC-BF) = CA+BC+AE-BF= 2AC
Tính được AC R 2 Suy ra CE+CF= 2R 2
Vậy CE+CF không đổi khi M di động trên đoạn thẳng OA. 4 1
+) Tìm vị trí của điểm M trên đoạn thẳng OA để S
đạt giá trị nhỏ nhất CE CF 4 1 9 9 Ta có S =
CE CF CE CF 2 2R 9 2 1 S nhỏ nhất CE 2CF 2 2R CE CF
CA AE 2BC 2BF BC 3.BF 0,25 BF BD 1 1 Kẻ FP//EC (P thuộc AB),
BP BA BC BA 3 3 Mà A EM PEM g c g 1 2
. . AM MP BP MP AM AB R 3 3 2
Vậy M thuộc AO sao cho AM= AO . 3
Cho a, b, c là các số thực không âm thỏa mãn a + b + c = 2. V 0,5
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = ab + bc - 2ca
Từ a b c 2 a c 2 b
a c 2 ac mà
0 2 ac 2 0 ac 1 2 b 2 do b 0 0,25
* P ab bc 2ca ba c 2ac 0.a c 2 P 2 P 2
a c 1, b 0 min b b
* P ab bc ca ba c ac b b 2 2 2 2 2 1 4 0,25
P 1 P 1 b 1, a 0, c 0 hoặc b 1, c 0, a 0 max




