


Preview text:
PHÒNG GD&ĐT QUẬN HOÀN KIẾM
ĐỀ KHẢO SÁT CHẤT LƯỢNG
TRƯỜNG THCS NGUYỄN DU
Môn: Toán học, Lớp 9
Ngày khảo sát: 18/2/2023 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
(Đề thi gồm 01 trang)
Bài I (2,0 điểm). Cho hai biểu thức x − 2 x A − = và x 1 3 x 2 B = + + với x + 2 x + 2 x − 2 x − 4
x ≥ 0; x ≠ 4
1) Tính giá trị của biểu thức A khi x = 9. 2) Chứng minh rằng x B = . x − 2
3) Cho biểu thức P = .
A B . Tìm x để P <1 .
Bài II (2,0 điểm). Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào một cái bể không có nước thì sau 5 giờ sẽ đầy bể. Nếu vòi thứ
nhất chảy một mình trong 3 giờ và vòi thứ 2 chảy một mình trong 4 giờ thì cả hai vòi chảy
được 2 bể. Hỏi nếu mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể. 3 Bài III (2 điểm): 3
x − 2 + y = 5
1) Giải hệ phương trình:
5 x − 2 − y = 3 2x + y =1 2) Cho hệ phương trình
. Tìm m∈ để hệ có nghiệm duy nhất ( ; x y) sao cho mx + 2y = 3
biểu thức P = 3x + y nhận giá trị là số nguyên.
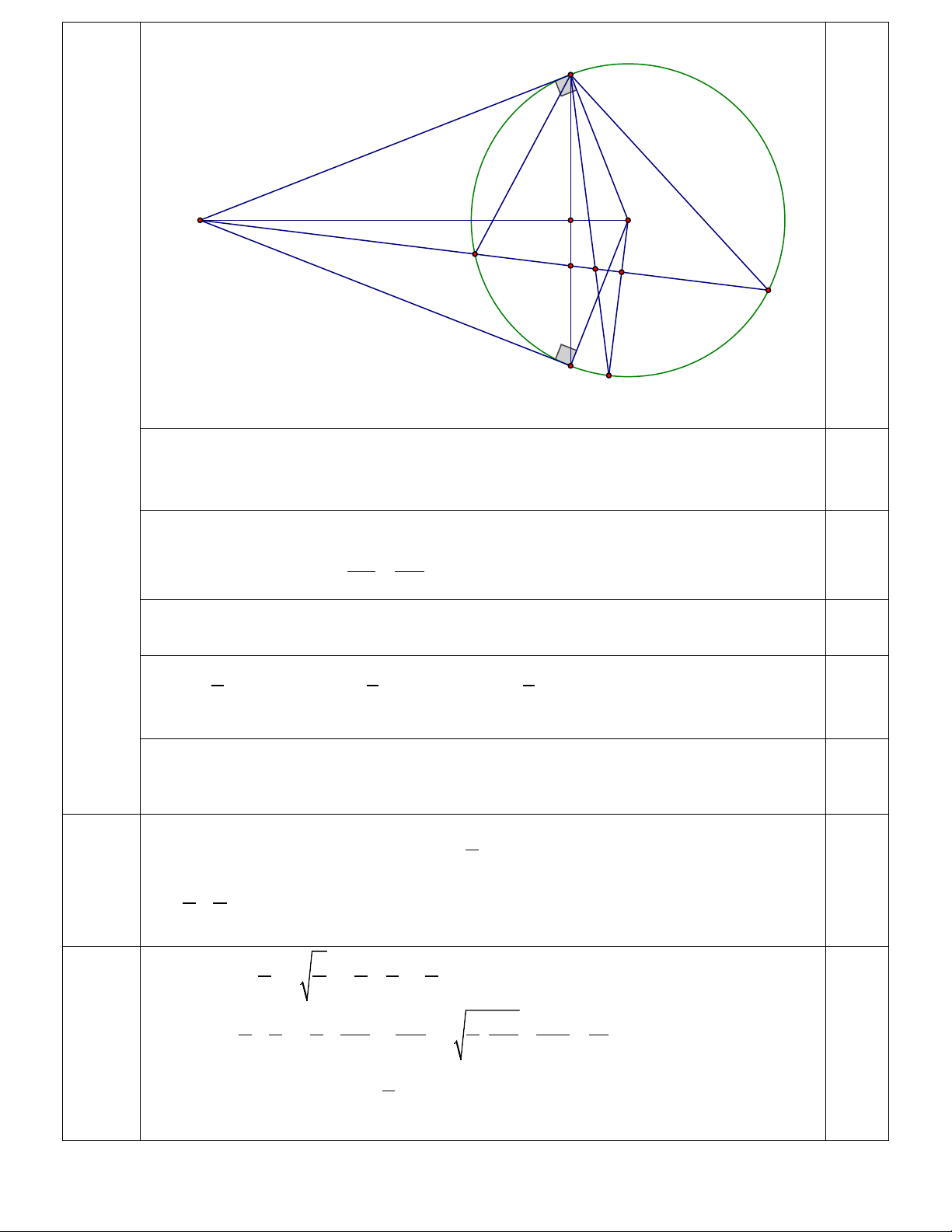
Bài IV (3,5 điểm): Từ một điểm A nằm ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC
với đường tròn (O)( B,C là hai tiếp điểm). Gọi H là giao điểm của hai đường thẳng AO và
BC . Qua A kẻ cát tuyến ADE với đường tròn (O) ( D,E ∈(O) ), sao cho tia AE nằm giữa
hai tia AO, AC và AD < AE.
a) Chứng minh đường thẳng AO vuông góc với đường thẳng BC ; b) Chứng minh 2 AB = A . D AE ;
c) Đường phân giác của
DBE cắt đường thẳng DE tại M và cắt đường tròn tại điểm thứ
hai N . Chứng minh ON ⊥ DE và AB = AM ;
d) Đường thẳng AE cắt đường thẳng BC và đường thẳng ON lần lượt tại K và I . Chứng minh 2
ID = IK.IA.
Bài V (0,5 điểm). Cho các số thực dương x, y thỏa mãn 1 x + ≤1. y
Tìm giá trị nhỏ nhất của biểu thức x y P = + . y x
…………..……. Hết …………………
PHÒNG GD&ĐT QUẬN HOÀN KIẾM HƯỚNG DẪN CHẤM
TRƯỜNG THCS NGUYỄN DU MÔN TOÁN LỚP 9
Ngày khảo sát: 18/2/2023 Bài Ý
Đáp án – Hướng dẫn chấm Điểm Bài I 1)
Tính giá trị của biểu thức A khi x = 9 0,5 đ (2,0 điểm)
Thay x = 9 (TMĐK) vào biểu thức A 0,25 9 2 9 3 A − = = 9 + 2 5 0.25 2) x 1 3 x − 2 B = + + x + 2 x − 2 ( x 0,25 − 2)( x + 2)
x ( x − 2)+ x + 2+3 x − 2 B = ( 0,25 x − 2)( x + 2) x + 2 x B = ( x + 2)( x − 2) 0,25 x ( x + 2) x B = ( = 0,25 x + 2)( x − 2) x − 2 3) Cho biểu thức P = .
A B . Tìm x để P <1. 0,5đ − − Ta có x x x x x 2 P = . A B = ; P <1 ⇔ <1 ⇔ −1< 0 ⇔ < 0 0,25 x + 2 x + 2 x + 2 x + 2
⇔ x − x − 2 < 0 ⇔ ( x − 2)( x + )
1 < 0 ⇔ x − 2 < 0 ⇔ x < 4
Kết hợp điều kiện suy ra 0 ≤ x < 4 0,25 Bài II
Giải bài toán bằng cách lập hệ phương trình: 2 (2,0
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là x(h) và y(h) , đk: điểm) 0,25
x > 5; y > 5 Trong 1 giờ:
Vòi 1 chảy được 1 (bể) x
Vòi 2 chảy được 1 (bể) y 0,25
Cả hai vòi chảy được 1 (bể) 5 Ta có pt: 1 1 1 + = x y 5
Trong 3 giờ vòi 1 chảy được 3 (bể) 0,25 x
Trong 4 giờ vòi 2 chảy được 4 (bể) y
Do cả hai vòi chảy được 2 (bể), nên ta có pt: 3 4 2 + = 3 x y 3 1 1 1 + = x y 5 Vậy ta có hệ: 3 4 2 0,25 + = x y 3
Giả hệ ta được: x = 7,5(tm); y =15(tm) 0,75
Vậy thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là 7,5(h)và 15(h) , 0,25 Bài III 1) 2 điểm Giải hệ phương trình 3
x − 2 + y = 5 1đ
5 x − 2 − y = 3
(điều kiện: x ≥ 2; y ≥ 0 ) 0,25
Giải hệ được x = 3; y = 4 0,5 Vậy hệ có nghiệm (3;4) 0,25 2 2x + y =1 Cho hệ phương trình
. Tìm m∈ để hệ có nghiệm duy nhất ( ; x y) mx + 2y = 3 1đ
sao cho biểu thức P = 3x + y nhận giá trị là số nguyên.
Hệ có nghiệm duy nhất khi m 2 ≠ ⇔ m ≠ 4 0,25 2 1 Tính được 1 m − 6 x = ; y = 0,25 m − 4 m − 4 m − 3 1
P = 3x + y = = 1+ m − 4 m − 4
P ∈ ⇔ m − 4∈U ( ) 1 ⇔ m∈{3; } 5 0,5 Bài IV 3.5 điểm B H A O 0,25 D K M I E C N AB = AC OB = OC 0,5
Suy ra AO là trung trực của BC , suy ra AO ⊥ BC 0,25 Chỉ ra = ABD AEB 0,5 A ∆ BD A
∆ EB(g − g) AB AD 2 ~ ⇒ = ⇒ AB = A . D AE 0,5 AE AB
Chỉ ra N là điểm chính giữa cung DE 0,25
Suy ra ON ⊥ DE 0,25 1 = + BMD (sdBD sdNE) 1 = + (sdBD sdND) 1 = = sd BN ABN 0,25 2 2 2 0,25
Suy ra tam giác ABM cân tại A nên AB = AM 2
AK AI = AH AO = AB = AD AE = ( AI − ID)( AI + IE) 2 2 . . . = AI − ID 0,25 Suy ra 2 2
ID = AI − AI.AK = AI ( AI − AK ) = AI.IK 0,25 Bài V 1
0,5điểm Cho các số thực dương x, y thỏa mãn x + ≤1. Tìm giá trị nhỏ nhất của biểu thức y x y 0,5 P = + . y x 1 x x 1 1≥ + ≥ 2 y x ⇒ ≤ ⇒ ≥ 4 . y y y 4 x x y x y 15y x y 15.4 17 A = + = + + ≥ 2 ⋅ + = .
y x y 16x 16x y 16x 16 4 1 0,5
Dấu “=” xảy ra khi x = ; y = 2. 2




