Đề khảo sát Toán 9 tháng 12 năm 2023 phòng GD&ĐT Tiên Yên – Quảng Ninh
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2023 – 2024 phòng GD&ĐT Tiên Yên – Quảng Ninh giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
trường
Preview text:
UBND HUYỆN TIÊN YÊN
ĐỀ KHẢO SÁT CHẤT LƯỢNG THÁNG 12
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN 9
Thời gian làm bài 120 phút ĐỀ CHÍNH THỨC
(Không kể thời gian giao đề)
Câu 1 (2,0 điểm) Giải các phương trình sau 1) 2 (2x − − 3) =1 2) 2 7 x = + 5 x + 3 x + 3 Câu 2 (2,0 điểm) +
1) Rút gọn biểu thức: P = 2 x x 1 x + 2 − :
với x ≥ 0;x ≠ 1 x x 1 x 1 − − x + x + 1
2) Hai lớp 9A và 9B được giao chỉ tiêu thu gom 130kg giấy vụn làm kế hoạch
nhỏ. Khi thực hiện, cả hai lớp đều rất tích cực nên lớp 9A thu gom vượt chỉ tiêu 30%,
lớp 9B thu gom vượt chỉ tiêu 20% nên tổng số giấy mà hai lớp thu gom được là 162 kg.
Hỏi theo kế hoạch, mỗi lớp được giao chỉ tiêu thu gom bao nhiêu kg giấy vụn? Câu 3 (2,0 điểm)
1. Tìm tham số m để đường hẳng = ( 2
y m − )1x + 3 song song với đường thẳng y = 3x + m+1.
2. Cho các hàm số y = 2x -3m và y = x – 2m + 1 có đồ thị cắt nhau tại điểm
A(x; y). Tìm m sao cho biểu thức P= -2x2 + 3y +1 đạt giá trị lớn nhất. Câu 4 (3,0 điểm)
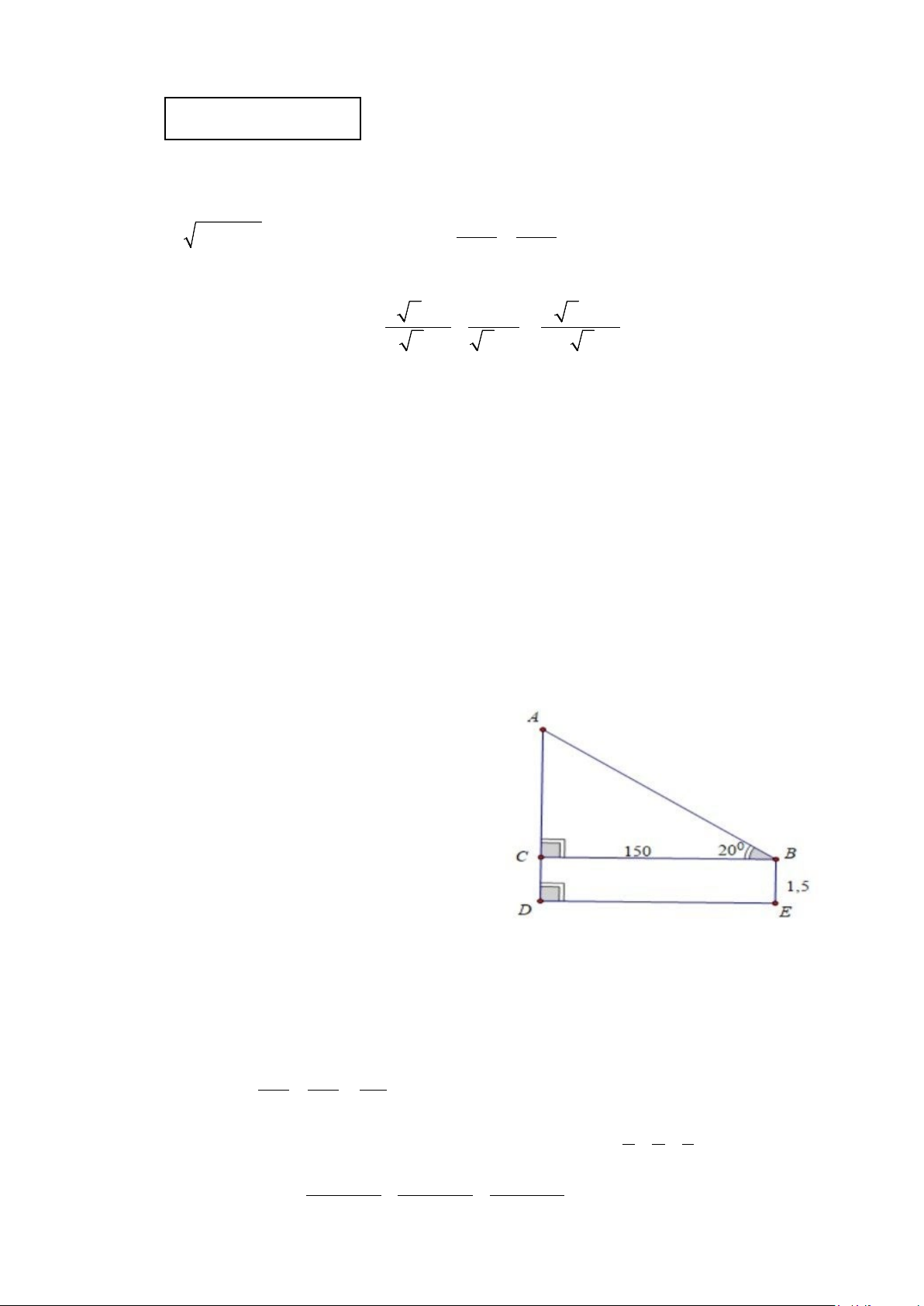
1) Một người đứng ở mặt đất cách tháp
150m. Biết rằng người đó nhìn thấy đỉnh tháp
ở góc 200 so với đường nằm ngang. Khoảng
cách từ mắt người đó đến mặt đất là 1,5m.
Hãy tính chiều cao của tháp (Làm tròn đến
chữ số thập phân thứ nhất)
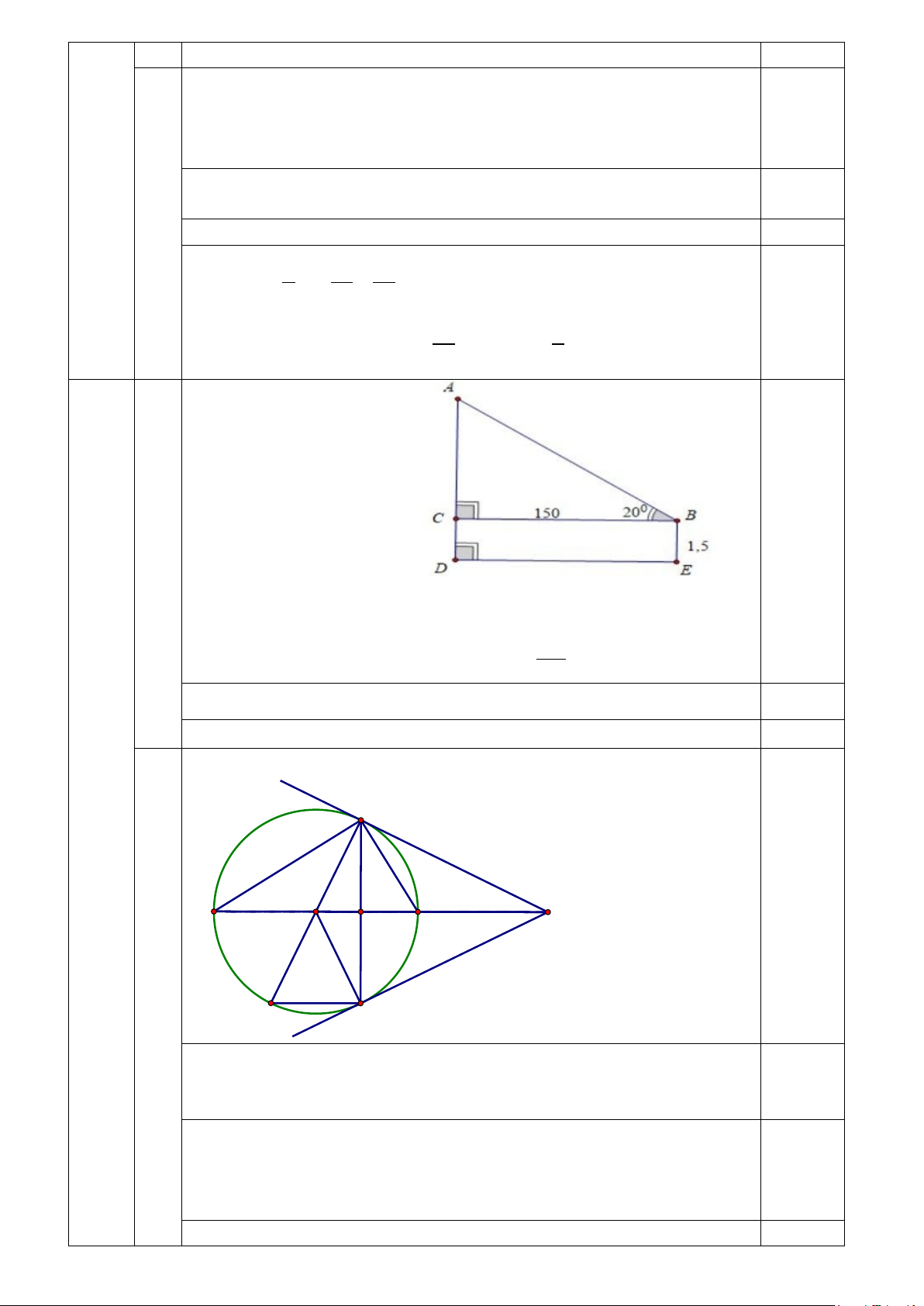
2) Cho đường tròn (O) điểm A nằm ngoài đường tròn, kẻ tiếp tuyến AB, AC với
đường trong (B,C là các tiếp điểm). Kẻ dây CD song song với AO. Gọi H là giao điểm của AO và BC.
a) Chứng minh bốn điểm A, B, O, C cùng nằm trên một đường tròn và CD ⊥ BC.
b) AO cắt đường tròn (O) tại hai điểm E và F (E nằm giữa A và O). 1 1 2 Chứng minh: − = EH EA FE
Câu 5 (1,0 điểm) Cho x, y, z là ba số thực dương thỏa mãn: 1 1 1 + + = 4 . x y z Chứng minh: 1 1 1 A = + + ≤ 1
2x + y + z x + 2y + z x + y + 2z
………………Hết…………….. UBND HUYỆN TIÊN YÊN HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN 9
Ngày tháng 12 năm 2023 Câu Ý Đáp án Biểu điểm 2
(2x − 3) =1 |2x-3| =1 0,25 1) TH1 : 2x-3 =1 x= 2 0,25 TH2 : 2x-3 = -1 x = 1 0,25
Vậy phương trình có nghiệm x 1 1= 1, x2 = 2 0,25 ĐKXĐ : x ≠ -3 0,25 (2đ) 2 7 − x − + = + 5 ⇔ 2 7 x 5(x 3) = + ⇒ 2 = 7 – x + 5(x+3) 0,25 2) x + 3 x + 3 x + 3 x + 3 x + 3
⇔ 2 = 7 – x + 5x + 15⇔ 4x = -20 ⇔ x = -5(TM) 0,25
Vậy phương trình có nghiệm là x = -5 0,25 P 2 x + x 1 x + 2 ( = − 0,25 x − ) 1 (x + x + ) : 1
x −1 x + x +1 2 x x x x 1 + + + x + x +1 ( = − 0,25 x − ) 1 (x + x + ) 1
( x − )1(x + x + ) . 1 x + 2 1)
2 x + x − x − x −1 x + x +1 x −1 x + x +1 = ( = x − ) 1 (x + x + ). 1 x +
( x − )1(x+ x + ). 2 1 x + 2 0,25 1 = . Vậy P 1 =
với x ≥ 0;x ≠ 1 0,25 2 x + 2 x + 2 (2đ)
Gọi theo kế hoạch lớp 9A được giao chỉ tiêu thu gom số giấy
vụn là x (kg); Điều kiện 0 < x < 130
Theo kế hoạch lớp 9B được giao chỉ tiêu thu gom số giấy vụn là 0,25 130-x (kg)
Trong thực tế: Số giấy vụn lớp 9A thu gom được là: 130%. x 2) (kg)
Số giấy vụn lớp 9B thu gom được là 120%. (130-x) (kg) 0,25
Ta có phương trình: 130%. x + 120%. (130-x) = 162
Giải pt tìm được x = 60 (TM) 0,25
Vậy theo kế hoạch, lớp 9A được giao chỉ tiêu thu gom 60 kg
giấy vụn. Lớp 9B được giao chỉ tiêu thu gom 70 kg giấy vụn. 0,25 Hai đường thẳng = ( 2 y m − ) 1 x + 3 và y = 3x + m+1 2
song song với nhau khi: m − 1 = 3 0,25 3 3 ≠ m +1 (2đ) 1) m = 2 ± 0,25 m ≠ 2 => m = -2 0,25
Vậy m = -2 thoả mãn đầu bài. 0,25
2) Ta có 2≠ 1 nên hai đường thẳng y = 2x -3m và y = x – 2m + 1
luôn cắt nhau. Hoành độ giao điểm của 2 đường thẳng trên là nghiệm của pt: 0,25
2x -3m = x – 2m + 1 x = m+1
Thay x = m+1 vào hàm số y = x – 2m + 1 ta được y = 2-m
Tọa độ điểm A(m+1; 2- m) 0,25
Ta có P = -2x2 + 3y +1 = -2m2-7m+5 0,25 P = -2(m+ 7 )2 + 89 89 ≤ với mọi m 4 8 8
Vậy giá trị lớn nhất của P= 89 khi m = - 7 . 0,25 8 4 1
Khoảng cách từ người đó đến tháp là DE = BC =150m
Khoảng cách từ mắt người đó đến mặt đất là BE = DC =1,5m 0,5
Tam giác ABC vuông tại C: tan ABC = AC BC => 0 0
AC = BC.tan 20 =150.tan 20 ≈ 54,6(m) 0,25
Độ cao của tháp là: AD = AC +CD ≈ 56,1(m) 0,25 Vẽ được hình câu a 4 B (3đ) 2a 0,25 F O A H E D C
Vì AB là tiếp tuyến của đường tròn (O) nên: OB ⊥ AB ⇒ O ∆ ABvuông tại B 0,25
=> Ba điểm A,B,O thuộc đường tròn đường kính OA. Tương tự có O ∆ AC vuông tại C
=> Ba điểm A,O,C thuộc đường tròn đường kính OA.
Do đó bốn điểm A, B, O, C cùng thuộc đường tròn đường kính 0,25 OA.
Ta có AB = AC (Theo tính chất hai tiếp tuyến cắt nhau)
=> ∆ABC cân tại A có AO là đường phân giác
=> AO đồng thời là đường cao 0,25 => AO ⊥ BC Mà AO // CD => CD⊥ BC 0,25 + 0 Ta có : + 0
ABE EBO = 90 (AB ⊥ OB) EBH BEO = 90 ( BH ∆ E vuông tại H) = EBO BEO ( O
∆ BE cân tại )⇒ = ABE EBH ⇒BE là tia phân giác của HBA 0,25 2b Mà BF ⊥ BE ( BF ∆
E nội tiếp (O) đường kính FE)
⇒ BE, BF lần lượt là các đường phân giác trong và ngoài tại B 0,25 của H ∆ BA , do đó: EH FH BH = = EA FA BA EH FH EF EF 1 2EA+EF 2 1 1 1 2 ⇒ = = = ⇒ = = + ⇒ - = 0,25 EA FA EA+FA 2EA+EF EH EA.EF EF EA EH EA EF
Do x, y, z là ba số thực dương nên ta có:
(x − y)2 ≥ 0 0,25 ( ⇒ x + y)2 1 1 4 1 1 1 1 ≥ 4xy ⇒ + ≥ ⇔ ≤ + x y x + y
x + y 4 x y 1 1 1 1 ≤ + 5
2x (y z) 4 2x y z + + + (1đ) 1 1 1 1 ≤ + 0,25
2y (x z) 4 2y x z + + + 1 1 1 1 ≤ +
2z (x y) 4 2z x y + + +
Cộng từng vế các bất đẳng thức trên ta được 1 1 1 1 1 1 1 1 1 A ≤ + + + + +
4 2x y z 4 2y x z 4 2z x y + + + 0,25 1 1 1 1 1 1 1 A ≤ + + + + +
4 2x y z 2y x z 2z x y + + +
1 1 1 1 1 1 1 1 1 1 1 1 1 1 A ≤ + + + + + + + +
4 2 x y z 4 y z 4 x z 4 x y 1 1 1 A .4 .2.4 ≤ + 4 2 4 A ≤1
Vậy khi x, y, zlà ba số thực dương thỏa mãn: 1 1 1 + + = 4 . Thì x y z 0,25 1 1 1 + + ≤ 1
2x + y + z x + 2y + z x + y + 2z
Ghi chú: Học sinh có thể làm nhiều cách khác nhau đúng GV vẫn cho điểm tối đa)
……………………………………