Đề khảo sát Toán 9 tháng 9 năm 2021 trường THCS Lê Ngọc Hân – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm 2021 trường THCS Lê Ngọc Hân – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
học
Preview text:
TRƯỜNG THCS LÊ NGỌC HÂN
ĐỀ KHẢO SÁT CHẤT LƯỢNG THÁNG 9
MÔN: TOÁN – LỚP 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút
Ngày kiểm tra: 30 tháng 9 năm 2021
Bài I(2 điểm). Cho hai biểu thức: x − 3 x 5 2 x +1 A = và B = − + .
với x ≥ 0; x ≠ 1; x ≠ 4. x − 2 x −1 x +1 1− x 2
1. Tính giá trị biểu thức A khi x = 16.
2. Rút gọn biểu thức B.
3. Cho biểu thức M = A.B Tìm giá trị của x để biểu thức M luôn nhận giá trị dương.
Bài II (2,5 điểm).
1. Giải bài toán bằng cách lập phương trình .
Một người đi xe máy từ nhà đến công ty với vận tốc 40km/h.Người đó ở lại làm
việc trong 3 giờ rồi đi xe máy quay về nhà với vận tốc 30km/h,tổng cộng hết
6 giờ 30 phút kể cả thời gian làm việc. Tính quãng đường từ nhà đến công ty của người đó.
2. Bài toán thực tế.
Để đo chiều cao của một ngọn tháp, không thể trèo lên đỉnh.
Người ta dùng thước dài, thước đo góc và đèn laser thực hiện
thao tác đo thu được kết quả như hình vẽ. Hãy tính chiều cao của tháp.
(kết quả làm tròn đến chữ số thập phân thứ nhất)
Bài III (1,5 điểm) 1) Tính: + − − − ( − )2 2 3 48 75 243 1 3 2) Giải phương trình:
x + x − 5 = 11
Bài IV (3,5 điểm).
Cho ΔABC có đường cao AH. Kẻ HD vuông góc AB tại D. Biết AH = 8cm; AB = 10cm. a) Tính HB, HD.
b) Biết góc ACB = 300. Giải ΔAHC.
c) Kẻ HE vuông góc với AC. Chứng minh rằng ΔAED đồng dạng với ΔABC
d) Tính diện tích tứ giác BDEC. (kết quả làm tròn đến chữ số thập phân thứ 3)
Bài V (0,5 điểm). Tìm giá trị lớn nhất của P = x + 4 − x .
Chúc em làm bài tốt!
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
MÔN TOÁN 9 (30/9/2021) Bài Câu Đáp án Điểm 1
Thay x = 16(t/m ) vào A, ta có: 0,25 16 − 3 4 − 3 1 A = = = 16 − 2 4 − 2 2 0,25 1
Vậy tại x = 16 thì A = 2 x 5 2 x +1 B = − − 0,25 x −1 x +1 ( x − )1( x + ) . 1 2 I 2 − + + = ( x 4 x 3 0,25 x − ) 1 ( x + ) x 1 . 1 2
( x − )1( x −3) x +1 = ( 0,25 x − ) 1 ( x + ) . 1 2 x − 3 = 0,25 2 3 − − ( x − x x )2 3 3 3 M = . A B = = x − 2 2 2( x − 2) ( x − )2 3 M > 0 ( x − ) 0 2 2 2 x − 3 0 2
Lập luận ( x −3) ( )
0 = M 0 0,25 2 ( x − 2) 0 x 9 x 4 0,25
KL: Vậy x > 4 và x 9 thì M > 0 1.
Gọi quãng đường từ nhà đến công ty của người đó dài là: x (km; x > 0) 0,25 x
Thời gian người đó đi từ nhà đến công ty với vận tốc 40km/h là : (h) 0,25 40 II x
Thời gian người đó đi từ công ty về nhà với vận tốc 30km/h là : (h) 0,25 30
Vì thời gian người đó đi và về tổng cộng hết 6 giờ 30 phút kể cả thời
gian làm việc ,ta có phương trình. 0,5 x x 1 + + 3 = 6 40 30 2
Giải phương trình tìm được: x = 60 (t/m) 0,5
Vậy quãng đường từ nhà đến công ty của người đó dài 60km 0,25 2.
( HS không phải vẽ lại hình)
* Trên hình vẽ, AB là chiều cao của tháp ;BC là bóng của tháp trên
mặt đất.Tháp vuông góc với mặt đất nên ABC vuông tại B 0,25
=> AB = 20 . tan400 16,8 (m)
Vậy chiều cao của tháp là khoảng 16,8m 0,25 1 + − − − ( − )2 2 3 48 75 243 1 3 0,25 III
= 2 3 + 16.3 − 25.3 − 81.3 − 1− 3 0,25
= 2 3 + 4 3 − 5 3 − 9 3 − ( 3 − ) 1 = 8 − 3 − 3 +1 0,25 =1− 9 3 2 ĐK: 5 x 11 0,25
x + x − 5 = 11
x − 5 = 11− x
x − 5 = (11− x)2 ... 2
x − 23x +126 = 0
(x −9)(x −14) = 0
x − 9 = 0 = x = 9(t / m)
x−14=0= x =14(kot /m) 0,25 0,25 KL: S = 9 Hình
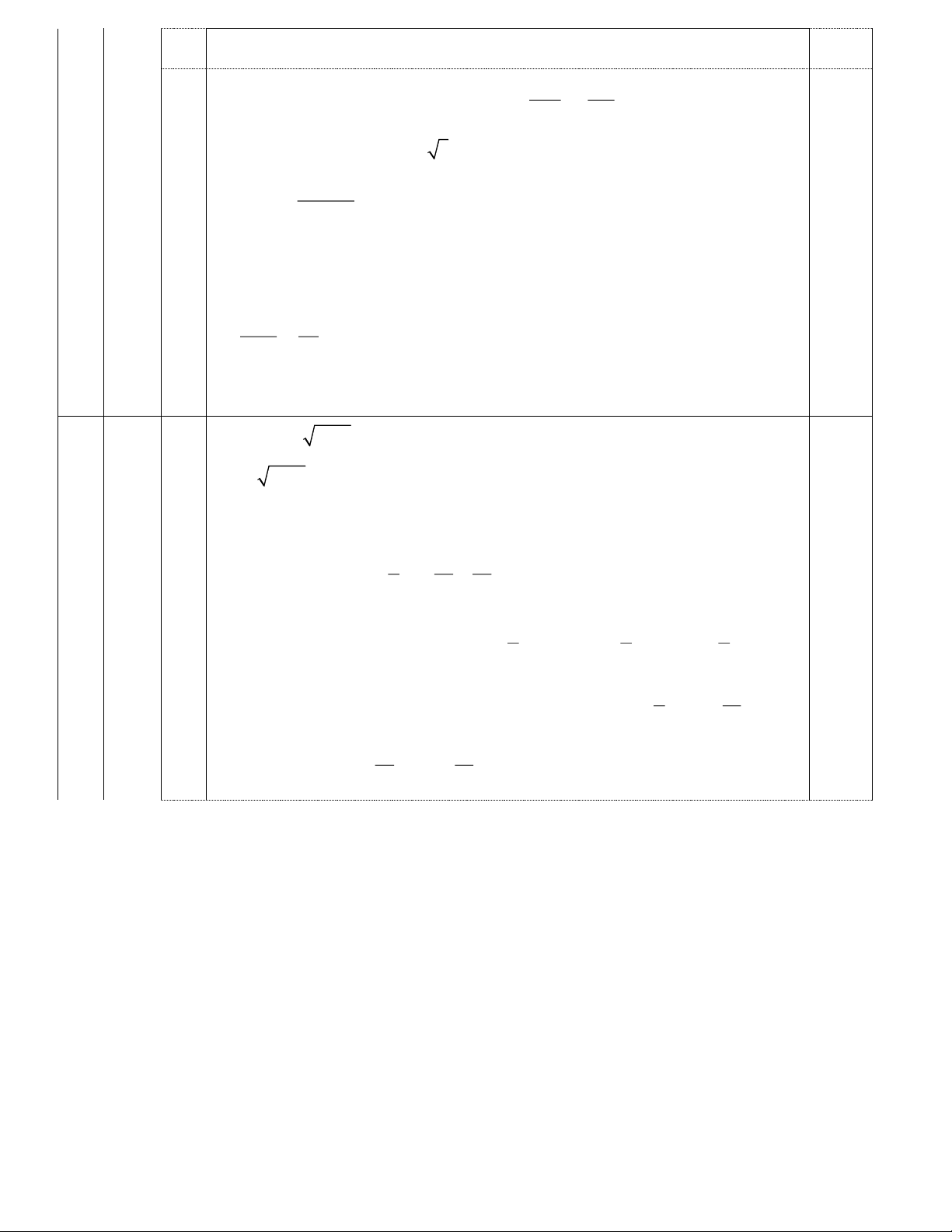
Vẽ hình đến câu a A E 0,25 D C B H 1
Xét ΔABH vuông tại H ( AH ⊥ BC) Có AB2 = AH2 + BH2 (Pitago) 0,25 Tính được BH = 6cm IV
Chỉ ra ΔABH vuông tại H, đường cao DH
AB . DH = AH . BH (Hệ thức lượng) 0,25 Tính được DH = 4,8cm 0,25 2
Vì ΔACH vuông tại H tính được góc ACH = 300 0,25
Có HC = AH. cotC =8.cot 300 = 8 3 (cm) 0,25
AC = AH : sinC = 8: sin300 = 16(cm) 0,5
ΔAHB vuông tại H có HD ⊥ AB => AH2 = AD.AB (HTL) 0,25
ΔAHC vuông tại H có HE ⊥ AC => AH2 = AE.AC (HTL) 0,25 AD AE => = AC AB 0,25
Chứng minh đc ΔADE đồng dạng ΔACB (c.g.c) 0,25 2
Vì ΔADE đồng dạng ΔACB(cmt) nên S AE ADE = S AB ABC
Có BC = BH + HC = 6 + 8 3 19,856 (cm) AH.BC => S = ABC 2 0,25 Tính được S 79, 424 ABC
Có AH2 = AE . AC => AE = 4(cm) S 4 => ADE = => S 12,708(cm2) 0,25 S 25 ADE ABC S = S -S 66,716 (cm2) BDEC ABC ADE V
Có P = x + 4 − x ĐK x 4 Đặ
t: 4 − x = y (đk: y 0 ) Suy ra 2 2
y = 4 − x x = 4 − y 2 1 17 17 2
P = 4 − y + y = − y − + 2 4 4 0,25 2 1 1 1
Dấu “ = “ xảy ra khi và chỉ khi y −
= 0 y − = 0 y = (t/m) 2 2 2 1 15 4 − x = x = (t/m) 4 4 0,25 17 15 Vậy P có GTLN là x = 4 4 Chú ý :
1) Học sinh phải lập luật đúng và chặt chẽ mới cho điểm tối đa.
2) Nếu học sinh có cách giải đúng mà khác với hướng dẫn chấm thì giáo viên thống nhất chia điểm
dựa vào hướng dẫn chấm dành cho câu hay ý đó.
3) Giáo viên có thể chia nhỏ các bước giải để chấm điểm cho học sinh
4) Phần hình học: nếu học sinh không vẽ hình tương ứng hoặc vẽ hình sai thì không cho điểm.
5) Điểm tổng toàn bài để lẻ đến 0,25.