UBND HUYỆN YÊN ĐỊNH
ĐỀ KHẢO SÁT VÀO LỚP 10 THPT LẦN 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM 2025 MÔN: TOÁN
Ngày khảo sát: 17/3/2025
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
Đề thi gồm có 02 trang
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm, gồm 08 câu, mỗi câu 0,25
điểm).
Chọn đáp án đúng và ghi vào phần bài làm cho mỗi câu sau:
Câu 1. Phương trình 4x −12 = 0 có nghiệm là:
A. x =12 B. x = -3 C. x = 4 D. x = 3
Câu 2. Kết quả rút gọn của biểu thức ( − )2 2 6 5 bằng
A. 2 6 − 5. B. 6 − 3.
C. 5 − 2 6. D. 6 + 3.
Câu 3. Đồ thị hàm số 2
y = ax đi qua điểm A( 1;
− 4). Khi đó a bằng A. 4. − B. 4. C. 1. D. 1 . 4
Câu 4. Bất phương trình 3x −5 > 4x + 2 có nghiệm là A. x > 7. B. x < 7. C. x < 7. − D. x > 7. −
Câu 5. Cho α và β là hai góc nhọn bất kỳ thoả mãn α + β = 900. Khẳng định nào sau đây là đúng?
𝐀𝐀. tanα = sinβ 𝐁𝐁. tanα = cotβ 𝐂𝐂. tanα = cosβ 𝐃𝐃. tanα = tanβ
Câu 6. Cho đường tròn (O;R) và đường thẳng d cắt nhau. Khoảng cách từ tâm O đến đường
thẳng d là 5cm. Khẳng định nào sau đây là đúng? A. R > 5 (cm) B. R < 5 ( cm ) C. R ≤ 5 (cm) D. R = 5 (c m)
Câu 7. Một lớp 9 thực hiện khảo sát về phương tiện đi lại của học sinh. Kết quả khảo sát
được trình bày như sau: Phương tiện
Xe đạp Xe máy điện Xe buýt Đi bộ Tần số (n) 20 10 8 2
Tần số tương đối f (%) 50 25 20 5
Tần số tương đối của phương tiện xe buýt là bao nhiêu ? A. 8% B. 20% C. 25% D. 50%
Câu 8. Một hộp đựng 36 tấm thẻ giống nhau được đánh số 1;2;3;4.. . ; 35;36 bạn Nam rút
ngẫu nhiên một tấm thẻ trong hộp. Xác suất của biến cố rút được tấm thẻ ghi số nguyên tố là: A. 13 B. 1 C. 1 D. 11 36 3 4 36
PHẦN II. TỰ LUẬN (8,0 điểm).
Câu 9. (1,5 điểm)
a) (0,75 điểm). Giải phương trình: 2
2x − 3x − 5 = 0 3x +  2y = 4
b) (0,75 điểm). Giải hệ phương trình:  4x - y = 9
Câu 10. (1,0 điểm) Rút gọn biểu thức 𝑃𝑃 = 2√𝑥𝑥 + √𝑥𝑥+1 + 3+7√𝑥𝑥 , với 𝑥𝑥 ≥ 0, 𝑥𝑥 ≠ 9. √𝑥𝑥+3 √𝑥𝑥−3 9−𝑥𝑥
Câu 11.(1,0 điểm) Cho phương trình: 2
x − 2(m − 2) x − 2m = 0 với m là tham số. Tìm các
giá trị của m để phương trình có 2 nghiệm phân biệt x , x
x − x = x 1 2 thỏa mãn hệ thức: 2 2 1 1 .
Câu 12. (1,0 điểm) Ông Tuấn có khoản tiết kiệm 600 triệu đồng. Ông Tuấn muốn dùng
một khoản gửi tiết kiệm ở ngân hàng với lãi suất 10%/năm và và một khoản mang đi đầu
tư khác với lãi suất 20%/năm. Tổng số lãi thu được là 85 triệu. Tính số tiền mà Ông Tuấn
mang đi gửi ngân hàng và mang đi đầu tư khác.
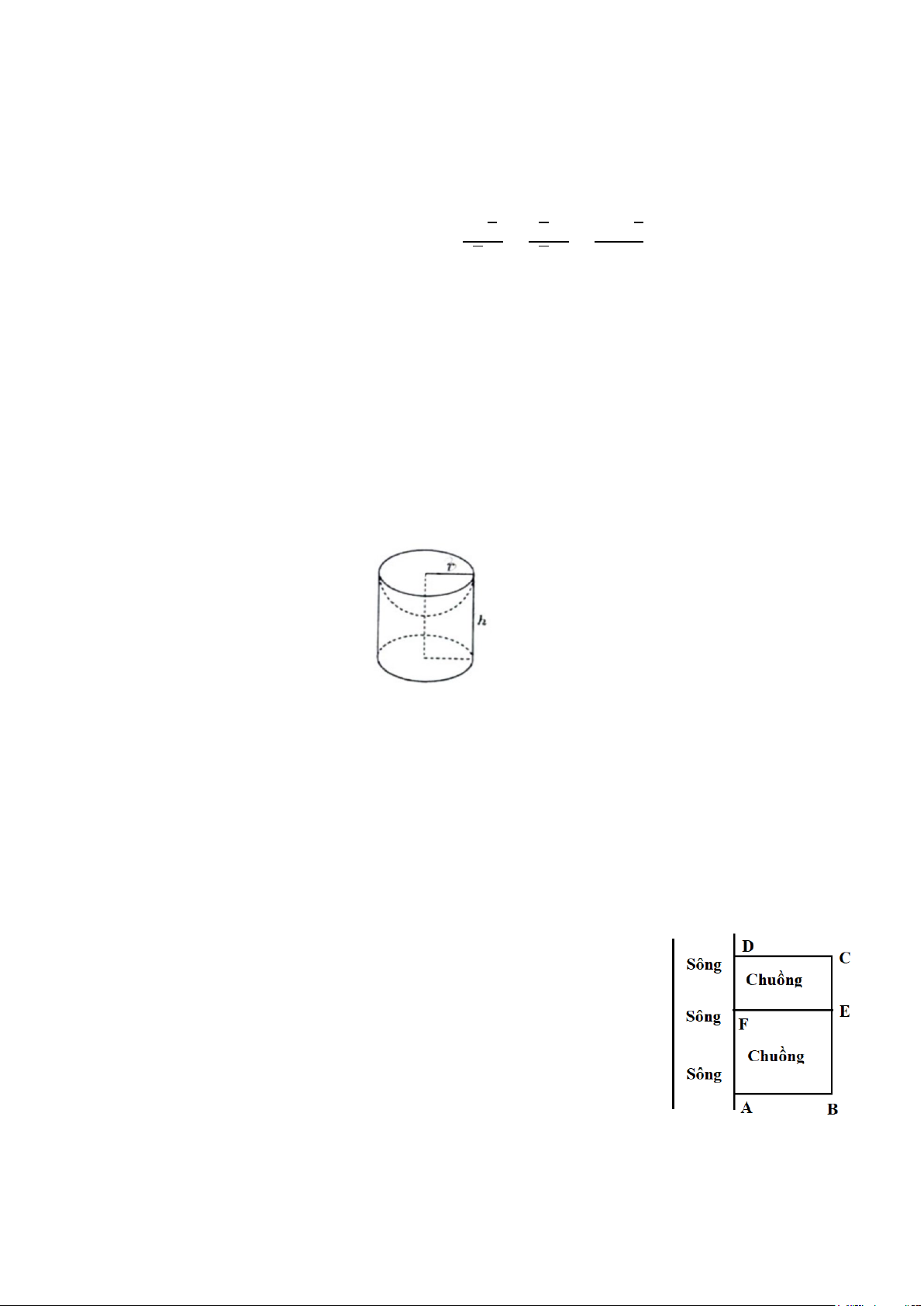
Câu 13. (1,0 điểm) Bác Vượng có một khối gỗ dạng hình trụ với bán kinh đường tròn đáy
r = 4 cm và chiều cao h = 9 cm . Bác Vượng khoét khối gỗ đó một nửa hình cầu có bán
kính bằng bán kính đáy của khối gỗ ( minh họa như hình bên dưới). Tính thể tích của phần khối gỗ còn lại
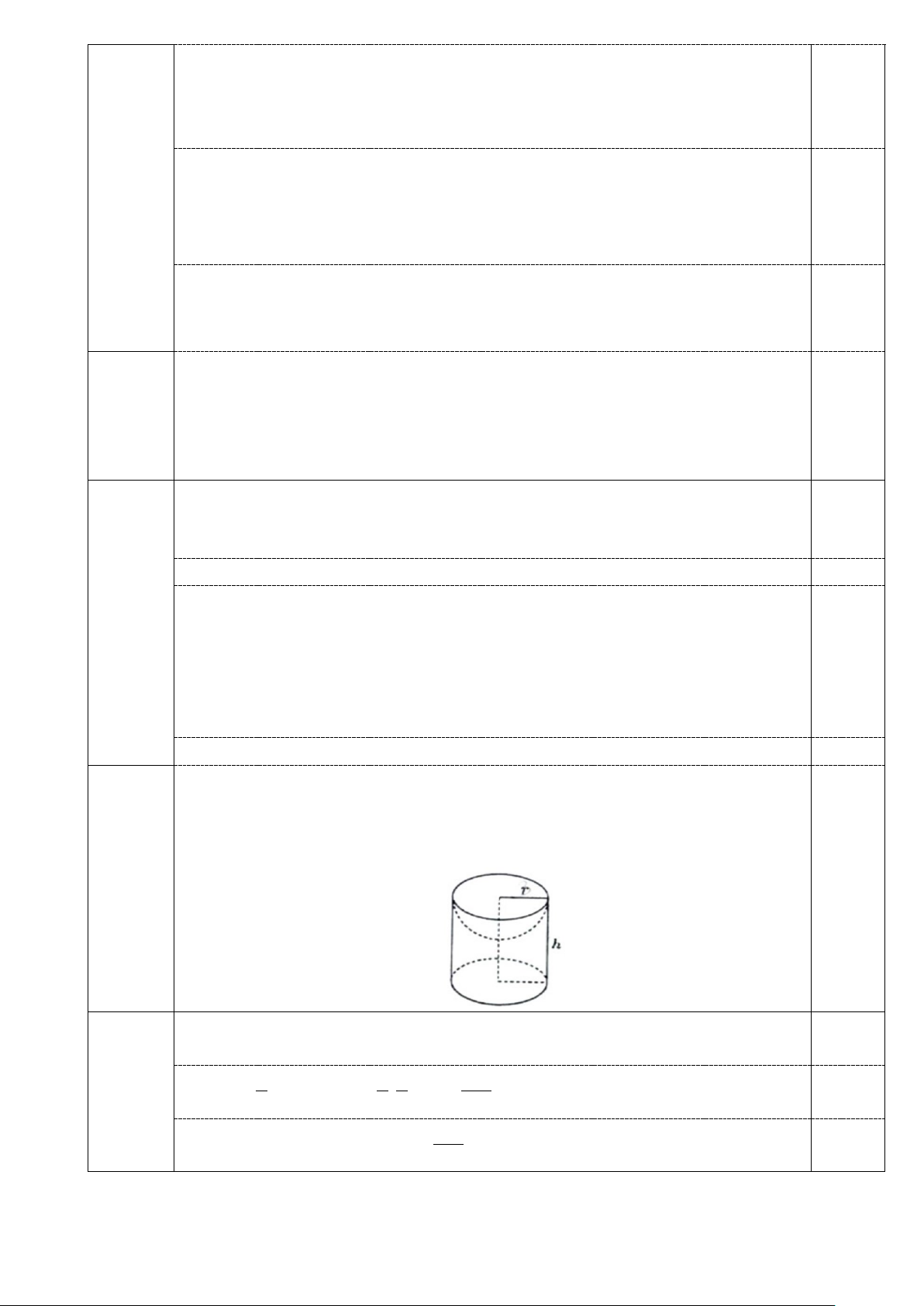
Câu 14.(2,0 điểm) Cho đường tròn (O) và dây cung BC cố định không đi qua O, lấy điểm
A trên cung lớn BC . Ba đường cao AD, BE,CF của tam giác ABC cắt nhau tại H
(D∈BC;E ∈ AC;F ∈ AB).
a) Chứng minh tứ giác AEHF nội tiếp. b) Chứng minh 2
BH.BE + CH.CF = BC . Tìm vị trí của điểm A trên cung lớn BC để diện tích tam giác AHE lớn nhất.
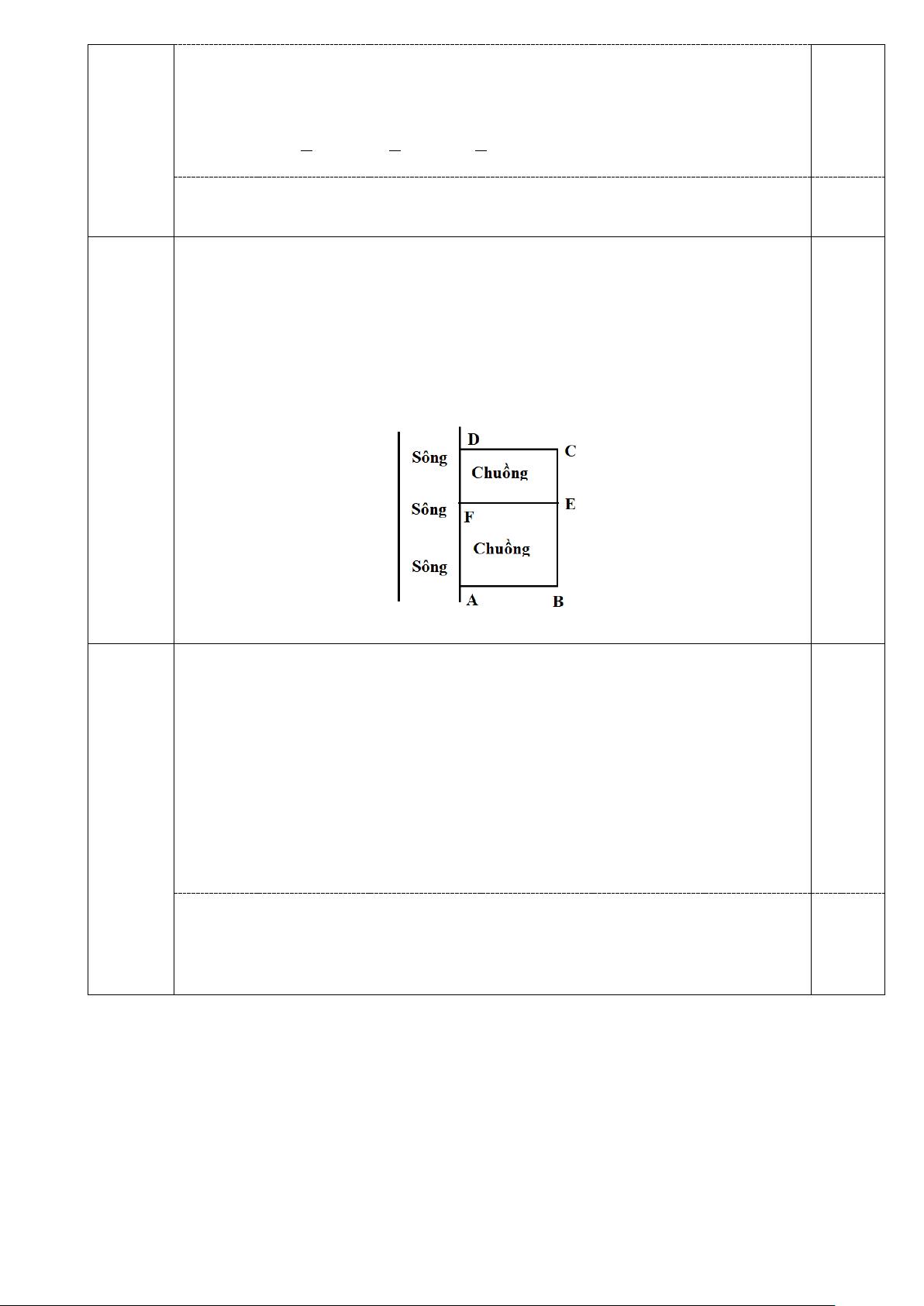
Câu 15. (0,5 điểm)
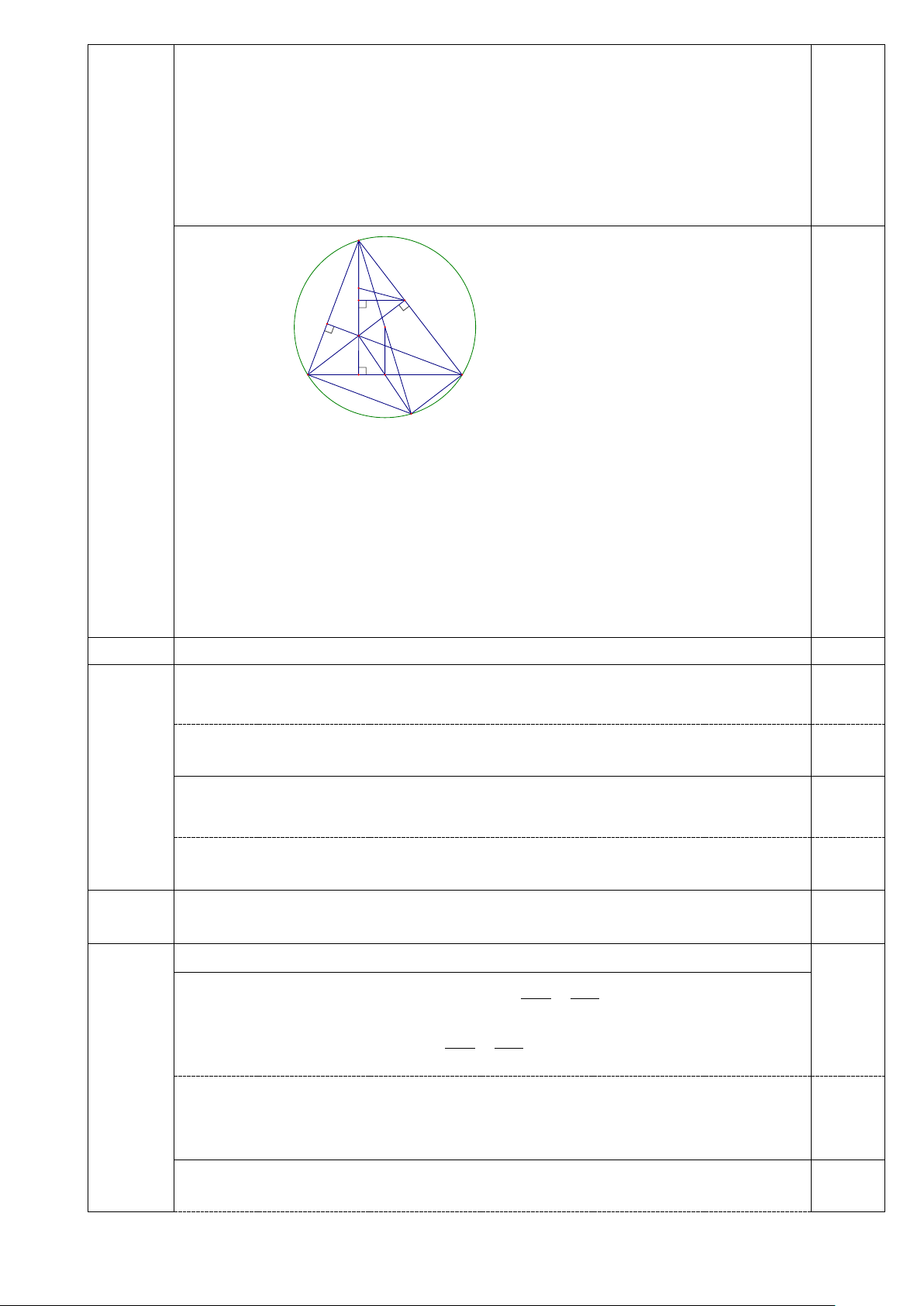
Một trang trại nhà bác Thành Minh nuôi gia cầm muốn
rào thành chuồng có dạng hình chữ nhật sát với nhau và sát
một con sông, một chuồng nuôi gà và một chuồng nuôi vịt
(Như hình vẽ). Biết rằng gia đình bác Thành Minh đã có
sẵn 240m hàng rào. Hỏi diện tích lớn nhất có thể bao
quanh chuồng là bao nhiêu?
( Biết rằng không rào bờ sông AD)
……………………….Hết………………… HƯỚNG DẪN CHẤM
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm, gồm 08 câu, mỗi câu 0,25 điểm). Câu 1 2 3 4 5 6 7 8 Đáp án D C B C B A B D
PHẦN II. TỰ LUẬN (8,0 điểm). Câu Nội dung Điểm
Câu 9a. a) Ta có: a = 2;b = 3 − ;c = 5
Vì a − b + c = 2 − ( 3 − ) + ( 5 − ) = 0 0,25
nên Phương trình có hai nghiệm: 5 x = 1; − x = 1 2 2 0,5
Vậy Phương trình có hai nghiệm: 5 x = 1; − x = 1 2 2
Câu 9b. Giải hệ phương trình: 3x +  2y = 4 3  x + 2y = 4 11  x = 22  ⇔  ⇔ 0,25 4x -y = 9 8  x 2y 18 3  − =  x + 2y = 4 x = 2 x = 2 ⇔  ⇔ 0,25 6 2y 4  + = y = 1 −
Vậy hệ phương trình có 1 nghiệm duy nhất: (x, y) = (2; -1) 0,25
Câu 10 Rút gọn biểu thức = 2√𝑥𝑥 + √𝑥𝑥+1 + 3+7√𝑥𝑥 , với 𝑥𝑥 ≥ 0,𝑥𝑥 ≠ 9. 1,0 √𝑥𝑥+3 √𝑥𝑥−3 9−𝑥𝑥
Với 𝑥𝑥 ≥ 0, 𝑥𝑥 ≠ 9 biểu thức P xác định. Ta có:
P = 2√𝑥𝑥 + √𝑥𝑥+1 + −7√𝑥𝑥−3 0,25 √𝑥𝑥+3 √𝑥𝑥−3
(√𝑥𝑥−3)(√𝑥𝑥+3)
2√𝑥𝑥(√𝑥𝑥 − 3) + (√𝑥𝑥 + 1)(√𝑥𝑥 + 3) − 7√𝑥𝑥 − 3 = 0,25
(√𝑥𝑥 − 3)(√𝑥𝑥 + 3)
2𝑥𝑥 − 6√𝑥𝑥 + 𝑥𝑥 + 4√𝑥𝑥 + 3 − 7√𝑥𝑥 − 3 = 0,25
(√𝑥𝑥 − 3)(√𝑥𝑥 + 3) = 3𝑥𝑥−9√𝑥𝑥
= 3√𝑥𝑥(√𝑥𝑥−3) = 3√𝑥𝑥
(√𝑥𝑥−3)(√𝑥𝑥+3)
(√𝑥𝑥−3)(√𝑥𝑥+3) √𝑥𝑥+3 0,25
Vậy P = 3√𝑥𝑥 với x≥ 0, x≠ 9. √𝑥𝑥+3
Câu 11 Cho phương trình: 2x − 2(m − 2) x − 2m = 0 với m là tham số. Tìm các
giá trị của m để phương trình có 2 nghiệm phân biệt x , x 1 2 thỏa mãn hệ 1,0 thức: 2
x − x = x 2 1 1 . Ta có: ∆ = −  (m − ) 2  −  (− m) 2 ' 2 1. 2
= m − 4m + 4 + 2m 0,25
= m − m + = (m − )2 2 2 4 1 + 3 > 0 với mọi m.
Suy ra phương trình luôn có hai nghiệm phân biệt với mọi m
x + x = 2 m − 2 1 2 ( )
Theo hệ thức Vi - ét ta có:  0,25 x x = 2 − m 1 2 Khi đó: 2 2
x − x = x ⇒ x = x + x 2 1 1 2 1
1 (1) với x > x 2 1
x + x = 2 m − 2
x + x = 2m − 4 1 2 ( ) Lại có: 1 2  ⇔ 
⇔ x + x + x x = 4 − 1 2 1 2 (2) x x = 2 − m x x = 2 − m 1 2 1 2
Thay (1) vào (2) ta được: 2
x + x + x + x ( 2x + x = 4 − 1 1 1 1 1 1 ) 3 2
⇒ x + 2x + 2x + 4 = 0 ⇒ (x + 2)( 2 x + 2 = 0 0,25 1 1 1 1 1 ) ⇒ x = 2 − 1 (do 2 x + 2 > 0 ) 1 Thay x = 2 − 1
vào (1) ta được: x = 2 2 Do 𝑥𝑥 0,25
1𝑥𝑥2 = −2𝑚𝑚 ⇒ −2𝑚𝑚 = −4 ⇔ m = 2
Vậy m = 2 là giá trị cần tìm.
Câu 12 Ông Tuấn có khoản tiết kiệm 600 triệu đồng. Ông Tuấn muốn dùng một
khoản gửi tiết kiệm ở ngân hàng với lãi suất 10% /năm và và một khoản
mang đi đầu tư khác với lãi suất 20% /năm. Tổng số lãi thu được là 85 1,0
triệu. Tính số tiền mà Ông Tuấn mang đi gửi ngân hàng và mang đi đầu tư khác.
Gọi a,b (triệu)lần lượt là số tiền mà Ông Tuấn mang đi gửi ngân hàng và
mang đi đầu tư khác (0 < a < 600, 0 < b < 600). 0,25
Vì Ông Tuấn có khoản tiết kiệm là 600 triệu đồng nên ta có: a + b = 600
Tổng lãi thu được khi gửi ngân hàng và đầu tư khác là:0,1a+0,2b=85 0,25 a + b = 600 a + b = 600
Ta có hệ phương trình  ⇔  0,1a + 0,2b = 85 a + 2b =   850 0,25 a + b = 600 a = 350 ⇔  ⇔  (TMĐK) b  = 250 b  = 250
Vậy tiền Ông Tuấn gửi ngân hàng là 350(triệu) và đầu tư khác là 250(triệu). 0,25
Câu 13 Bác Vượng có một khối gỗ dạng hình trụ với bán kinh đường tròn đáy r
= 4cm và chiều cao h = 9cm . Bác Vượng khoét khối gỗ đó một nửa hình
cầu có bán kính bằng bán kính đáy của khối gỗ ( minh họa như hình bên
dưới). Tính thể tích của phần khối gỗ còn lại 1,0
Thể tích khối gỗ còn lại là hiệu giữa thể tích hình trụ và nửa thể tích hình cầu 0,25 1 2 1 4 3 304
V = V − V = π − π = π (cm3) tru cau .4 .9 . .4 0,5 2 2 3 3
Vậy thể tích khối gỗ còn lại là 304π cm3 0,25 3
Câu 14 Cho đường tròn (O) và dây cung BC cố định không đi qua O , lấy điểm
A trên cung lớn BC . Ba đường cao AD, BE,CF của tam giác ABC cắt
nhau tại H (D∈ BC;E ∈ AC;F ∈ AB). 2,0
a) Chứng minh tứ giác AEHF nội tiếp. b) Chứng minh 2
BH.BE + CH.CF = BC . Tìm vị trí của điểm A trên cung
lớn BC để diện tích tam giác AHE lớn nhất. A I J E F O H B D K C M
a) Chứng minh tứ giác AEHF nội tiếp. 1,0
Ta có: BE;CE là đường cao A
∆ BC ⇒ BE ⊥ AC ⇒ 
AEB = 90°. Nên tam giác 0,25 AEH vuông tại E.
Gọi I là trung điểm của AH, khi đó IA=IH=IE. Suy ra A,E,H nằm trên đường tròn đường kính AH. 0,25
CF ⊥ AB ⇒ 
AFC = 90°, nên tam giác AFH vuông tại F, khi đó IA=IF=IH.
Suy ra A,F,H nằm trên đường tròn đường kính AH. 0,25
Suy ra 4 điểm A,E,H,F nằm trên đường tròn đường kính AH.
Suy ra tứ giác AEHF nội tiếp. 0,25 b)
b) Chứng minh 2
BH.BE + CH.CF = BC . Tìm vị trí của điểm A trên cung lớn 1,0
BC để diện tích tam giác AHE lớn nhất. * Chứng minh 2
BH.BE + CH.CF = BC
+ Chứng minh được BH BD B ∆ HD∽ B ∆ CE ⇒ =
⇒ BH.BE = BC.BD (1) 0,25 BC BE -Tương tự: CH CD CH ∆ D∽ CB ∆ F ⇒ =
⇒ CH.CF = BC.CD (2) BC CF Từ (1) và (2) suy ra
BH.BE + CH.CF = BC.BD + BC.CD = BC.(BD + CD) = BC.BC 0,25 ⇒ 2
BH.BE + CH.CF = BC (đpcm)
*Tìm vị trí của điểm A trên cung lớn BC để diện tích tam giác AHE lớn nhất. 0,25
Kẻ đường kính AM , chứng minh được tứ giác BHCM là hình bình hành. rồi
suy ra AH = 2.OK không đổi
Kẻ EJ vuông góc với AH tại J Ta có 1 1 1 2 S
= AH EJ ≤ AH EI = AH không đổi AHE . . 2 2 4
Dấu bằng xảy ra khi EJ = EI hay J trùng với I ⇒ J
∆ AS vuông cân tại E 0,25 ⇒  0
ACB = 45 ⇒ Điểm A nằm trên cung lớn BC sao cho  0 ACB = 45
Câu 15 Một trang trại nhà bác Thành Minh nuôi gia cầm muốn rào thành
chuồng có dạng hình chữ nhật sát với nhau và sát một con sông, một
chuồng nuôi gà và một chuồng nuôi vịt (Như hình vẽ). Biết rằng gia đình
bác Thành Minh đã có sẵn 240m hàng rào. Hỏi diện tích lớn nhất có thể
bao quanh chuồng là bao nhiêu?
( Biết rằng không rào bờ sông AD) 0,5
Xét hình chữ nhật ABCD như hình vẽ thì ta cần rào là các cạnh AB, BC,CD,EF. Theo bài ra ta có: AB + EF +CD + BC = 240 Nên: 3AB +BC= 240 0,25
Diện tích của 2 chuồng chính là diện tích của hình chữ nhất ABCD nên: S = AB BC ABC . D
Đặt AB= x (m). Điều kiện x> 0 Khi đó: BC= 240-3x (m) Nên 2 S = AB BC = x − = − ABC . .(240 3x) 240x 3x D 2 S = − x − + ≤ ABC 3( 40) 4800 4800 D 0,25
Vậy diện tích lớn nhất có thể bao quanh là 4800 (m2)
Chú ý: - Học sinh làm cách khác đúng vẫn cho điểm tối đa.
- Câu 14 (hình học) nếu không vẽ hình hoặc vẽ hình sai thì không tính điểm.
Xem thêm: ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN
https://thcs.toanmath.com/de-thi-tuyen-sinh-lop-10-mon-toan
Document Outline

• Đáp-án-Đề-thi-thử-Yên-ĐỊnh-Thanh-Hóa
• TS 10