Đề kiểm tra cuối học kỳ 2 Toán 8 năm 2023 – 2024 sở GD&ĐT Bắc Ninh
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề kiểm tra cuối học kỳ 2 môn Toán 8 năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Bắc Ninh; kỳ thi được diễn ra vào ngày 09 tháng 05 năm 2024; đề thi có đáp án trắc nghiệm và hướng dẫn chấm tự luận. Mời bạn đọc đón xem!
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II BẮC NINH NĂM HỌC 2023 - 2024 Môn: Toán 8 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Chọn phương án trả lời đúng trong các câu sau:
Câu 1. Bậc của đơn thức 3 2 M 3x y là A. 3 . B. 4 . C. 5 . D. 2 . 2 x 1
Câu 2. Điều kiện xác định của phân thức là x(x 5) A. x 0 hoặc x 5 . B. x 0 và x 5 . C. x 0 . D. x 5 .
Câu 3. Tập nghiệm của phương trình 7x 2 0 là 2 7 2 7 A. S . B. S . C. S . D. S . 7 2 7 2
Câu 4. Hệ số góc của đường thẳng y 3x 4 là A. 7 . B. 4 . C. 1. D. 3 .
Câu 5. Cho hàm số y 2x 3 . Giá trị của y khi x 0 là. A. 3 . B. 2 . C. 2 . D. 3 . 3xy 5 2 4xy
Câu 6. Kết quả của phép tính là 7 7 7 xy 7xy 3 A. . B. xy 1 . C. xy 1 . D. . 7 7
Câu 7. Cho ABC vuông tại A , đường cao AH . Khẳng định nào dưới đây sai? A. 2 AB BH BC . B. AH AB AC BC . C. 2 AH BH CH . D. AH BC AB AC . AM 1 A
Câu 8. Cho hình 1, biết MN / /BC và , BM 2
khẳng định nào sau đây là đúng? N M B C Hình 1 AN 1 AN 1 NC 1 NC 1 A. . B. . C. . D. . AC 3 NC 3 NA 3 AC 3 Câu 9. Cho A
BC đường phân giác AD (D BC). Khẳng định nào sau đây là sai? AB AC AB AC AB BD A. . B. . C. . D. BAD CAD . BD CD BC CD AC DC
Câu 10. Có 9 tấm thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên một tấm thẻ. Số kết quả
thuận lợi để rút được tấm thẻ đánh số chẵn là A. 2 . B. 3 . C. 4 . D. 5 .
Câu 11. Một đề thi trắc nghiệm 50 câu. Mỗi câu có bốn đáp án và chỉ có một đáp án đúng. Một
thí sinh làm bài thi, có hai câu thí sinh đó chọn ngẫu nhiên mỗi câu một đáp án. Xác suất để cả
hai câu đó đều đúng là 1 1 1 1 A. . B. . C. . D. . 2 4 25 16 1
Câu 12. Một hình chóp tam giác đều có thể tích bằng 3
12 3 cm , chiều cao bằng 4cm . Độ dài
cạnh đáy của hình chóp tam giác đều đó là A. 9cm . B. 2 9cm . C. 6cm . D. 2 6cm . II. TỰ LUẬN (7,0 điểm) Câu 1 (2,5 điểm) 1 3 2x
a) Rút gọn biểu thức A với x 1 2 x 1 x 1 1 x x 2x 1 x b) Giải phương trình x 3 2 6
c) Tìm a,b để phương trình đường thẳng y ax 2b 1 đi qua điểm M (1;3) và song
song với đường thẳng y 2x 1
Câu 2 (1,0 điểm) (Giải bài toán bằng cách lập phương trình)
Một phân xưởng theo kế hoạch cần sản xuất một số sản phẩm trong 5 ngày. Do tăng năng
suất nên so với kế hoạch mỗi ngày phân xưởng sản xuất thêm được 400 sản phẩm và hoàn thành
sớm 2 ngày. Hỏi theo kế hoạch phân xưởng cần sản xuất bao nhiêu sản phẩm? Câu 3 (3,0 điểm)
Cho tam giác ABC cân tại A đường cao AH , BK (H BC; K AC) . Kẻ HM AC (M AC). a) Chứng minh C HM ∽ C AH b) Chứng minh 2 BC 2CK CA
c) Gọi I là trung điểm của HM chứng minh AI BM và B MC∽ A IH Câu 4 (0,5 điểm)
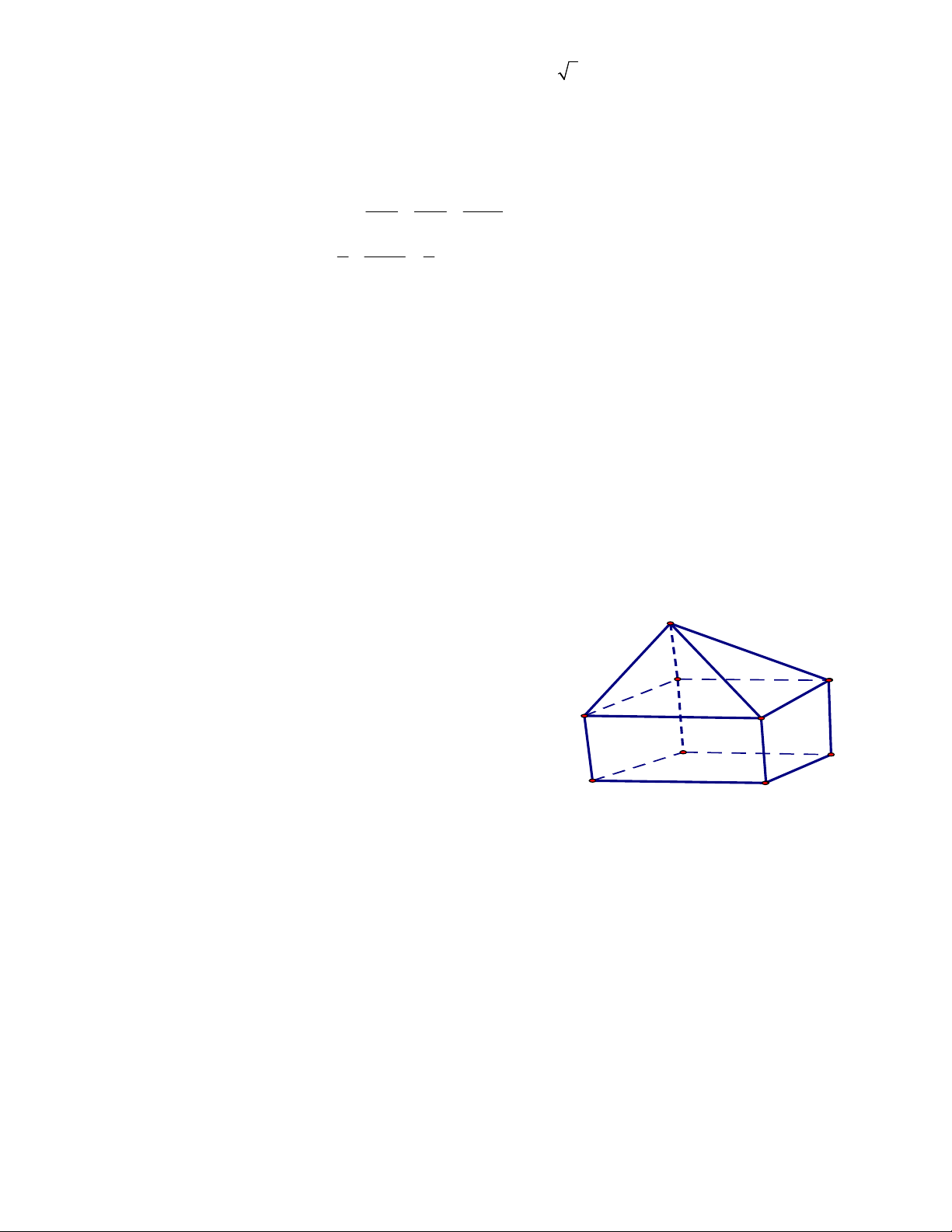
Người ta muốn lợp ngói cho mái nhà dạng hình chóp
tứ giác đều. Mặt trần nhà hình vuông cạnh 12m.
Khoảng cách từ đỉnh của hình chóp đến góc trần nhà
là 10m. Số tiền ít nhất mà người đó phải trả để mua 10m
ngói lợp là bao nhiêu? Biết giá mỗi viên ngói là
17000 (VNĐ) và cứ 10 viên ngói lợp được 1m2. 12m ====== HẾT ====== 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
ĐỀ KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2023 - 2024 Môn: Toán 8 I. TRẮC NGHIỆM (3,0 điểm)
Mỗi câu đúng 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B A D D B B A B C D C II. TỰ LUẬN (7,0 điểm) Câu Đáp án Điểm 1.a 0,75 1 3 2x A với x 1 2 x 1 x 1 1 x 0,5 x 1 3(x 1) 2x A
(x 1)(x 1) (x 1)(x 1) (x 1)(x 1) 2x 2 2 (x 1)(x 1) x 1 2 Vậy A với x 1 0,25 x 1 1.b 0,75 x 2x 1 x 2x 6x 3 x 6x x 0,5 3 2 6 6 6 6 6
2x 6x 3 x 6x x 3
Vậy phương trình có nghiệm duy nhất x 3 0,25 1.c 1,0
Vì đường thẳng y ax 2b 1 đi qua M (1;3) thay x 1; y 3 ta được 4 a 0,5
a 2b 1 3 b (1) 2
Vì đường thẳng y ax 2b 1 song song với đường thẳng y 2x 1 a 2 a 2
. Thay a 2 vào (1) b 3(thỏa mãn) 0,5 2b 1 1 b 0 Vậy a 2;b 3 2 1,0
Gọi số sản phẩm phân xưởng phải sản xuất theo kế hoạch là x ( sản phẩm) Điều kiện : * x 0,25 x
Số sản phẩm phải sản xuất một ngày theo kế hoạch là ( sản phẩm) 5 3 x 0,25
Thực tế số sản phẩm mà phân xưởng sản xuất trong một ngày là 400 (sản phẩm) 5 x
Vì hoàn thành sớm 2 ngày ta có phương trình 3( 400) x 5 x 3x 0,25 3( 400) x
1200 x 3x 6000 5x 2x 6000 5 5 x 3000 (thỏa mãn)
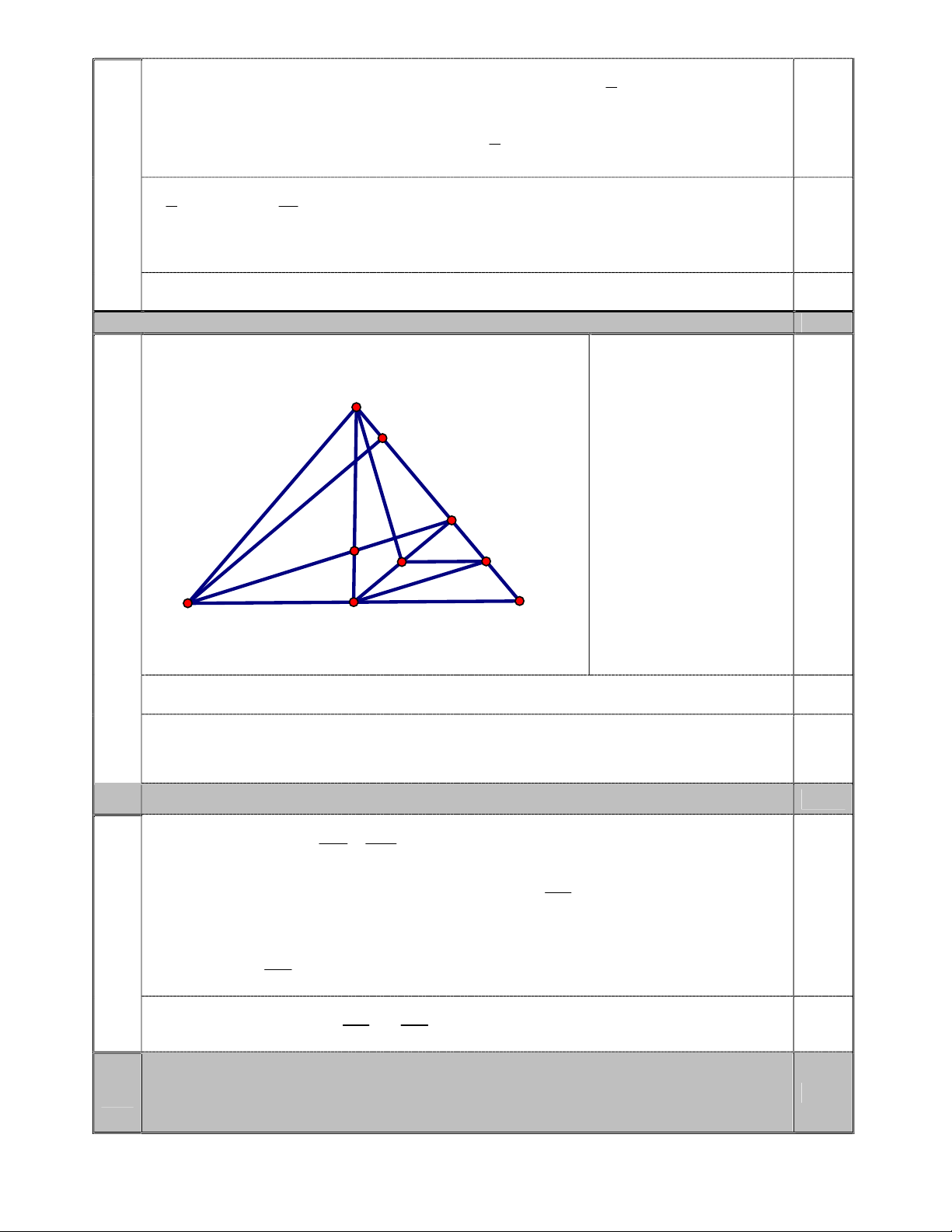
Vậy theo kế hoạch phân xưởng đó phải sản xuất 3000 sản phẩm. 0,25 3.a 1,25 A K GT,KL 0,5 M D O I B H C
Vì AH BC HM AC AHC 0 ; HMC 90 0,25 Xét CHM và CAH 0,5 có HMC 0 AHC 90 ; ACH (chung) C HM ∽ C AH(g g) (đpcm) 3b 0,75 CH CM Vì 2 CHM ∽CAH CH CM CA (1) CA CH BC
Mặt khác ABC cân tại A có AH BC BH HC (2) 2 0,5
Xét KBC có BH HC; HM / /BK (vì HM AC; BK AC) CK MK MC (3) . 2 BC CK Thay (2);(3) vào (1) Ta có 2 2 ( )
CA BC 2CK CA (đpcm) 0,25 2 2 3c 1.0 4
Gọi O là trung điểm của CM ; D là giao của BM và AH .
Xét CHM có IH IM ;OM OC OI / /HC OI AH 0,5
Lại có HI AC I là trực tâm A HO AI HO
Mặt khác xét BCM cóOM OC; HB HC HO / /BM AI BM (đpcm) C BM 0 HDB 90
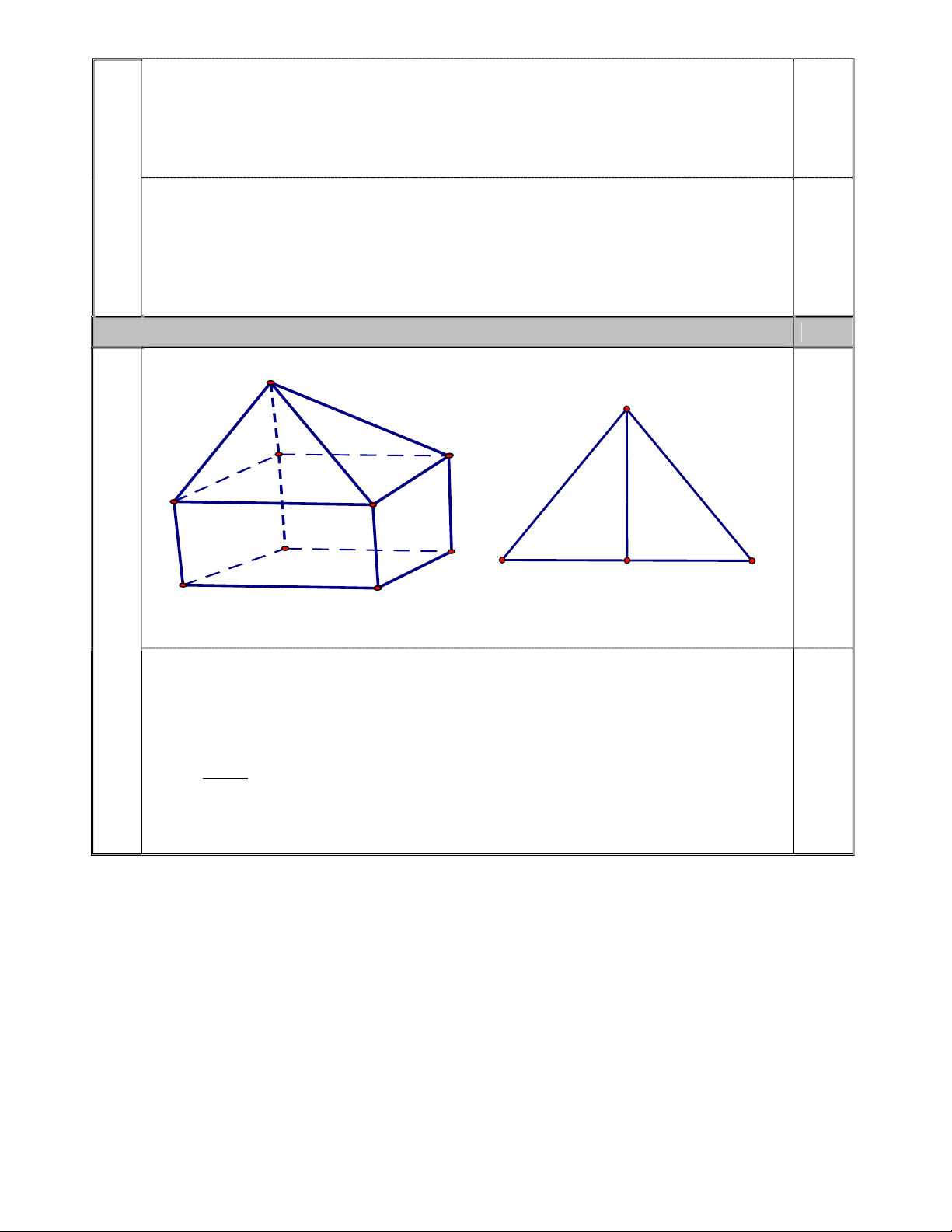
Vì AI BM ; AH BC HAI 0 ADM 90 0,5 Mà HDB ADM (đối đỉnh) CBM HAI Ta cũng có BCM AHM (cùng phụ MHC ) B MC∽ A IH (đpcm) 4 0,5 S 10m 12m A I B
Giả sử một mặt bên của hình chóp tứ giác đều là tam giác SAB cân tại S có AB 12 ;
m SA 10m . Gọi I là trung điểm của AB IA 6m và SI AB Xét S
IA vuông tại I theo Pythagore 2 2 2
SI IA SA SI 8m
Suy ra trung đoạn của hình chóp là 8m. Diện tích xung quanh của hình chóp là 0,5 8.4.12 2 S 192m . XQ 2
Số viên ngói phải dùng ít nhất là 192.10=1920 (viên)
Số tiền ít nhất phải trả là 1920.17000= 32 640 000 (VNĐ) 5