Đề Kiểm Tra Cuối Học Kỳ môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077
SỞ GIÁO DỤC & ĐO TẠO TP.HCM
KIỂM TRA CUỐI HỌC K I
TRƯỜNG THPT NGUYỄN CHÍ THANH
NĂM HỌC 2022 - 2023 Đề chính thức M N
TO`N Khối lớp 12
Thời gian lm b i : 90 phœt
(Đề thi có 04 trang)
(kh ng kể thời gian phát ề)
Họ v tŒn học sinh :..................................................... Số báo danh : ................... Mª ề 101
C u 4. Cho h nh trụ có bán kính áy r 3 và ộ dài ường sinh l 1. Diện t ch xung quanh của h nh trụ ª cho bằng A. 9 . B. 6 . C. 3 . D. 24
C u 5. Một người gửi số tiền 200 triệu ồng v o một ng n h ng với lªi suất 8%/năm. Biết rằng nếu kh ng rœt tiền ra khỏi ng n
h ng th cứ sau mỗi năm, số tiền sẽ ược nhập v o vốn ban ầu ( người ta gọi ó là lªi kØp). Để người ó lªnh ược số tiền 450
triệu th người ó cần gửi trong khoảng thời gian bao nhiêu năm? (nếu trong khoảng thời gian n y kh ng rœt tiền ra v lªi suất không thay ổi) A. 11 năm. B. 10 năm. C. 20 năm. D. 15 năm.
C u 6. Khối lập phương có bao nhiêu mặt phẳng ối xứng? A. 8. B. 6. C. 9. D. 4.
C u 7. Cho a l số thực dương, biểu thức a a3 viết dưới dạng lũy thừa với số mũ hữu tỷ l A. a . B. a . C. a . D. a .
C u 8. Cho h nh n n c ường sinh l 5,ường kính áy bằng 6 .Diện t ch to n phần của h nh n n ó là. A. S tp 15 . B. Stp 20 . C. Stp 24 . D. Stp 22 .
C u 9. Cho h m số y f x( ) xác ịnh trŒn R \
1;1 liŒn tục trŒn mỗi khoảng xác ịnh v c bảng biến thiŒn như sau:
Tổng số ường tiệm cận của ồ thị h m số l A. 1. B. 3. C. 2. D. 4.
C u 10. Nghiệm của bất phương trnh 9x 12.3x 27 0 l
A. 1 x 2.
B. x 3 x 9 .
C. 3 x 9.
D. x 1 x 2 .
C u 11. T nh thể t ch khối lăng trụ ứng ABCABC. ’
’ ’ c BB ’ a , ABC vu ng c n tại B, AC a 2 . lOMoAR cPSD| 22014077 3 a 3 a 3 a A. 3 V a B. V C. V D. V 6 2 3
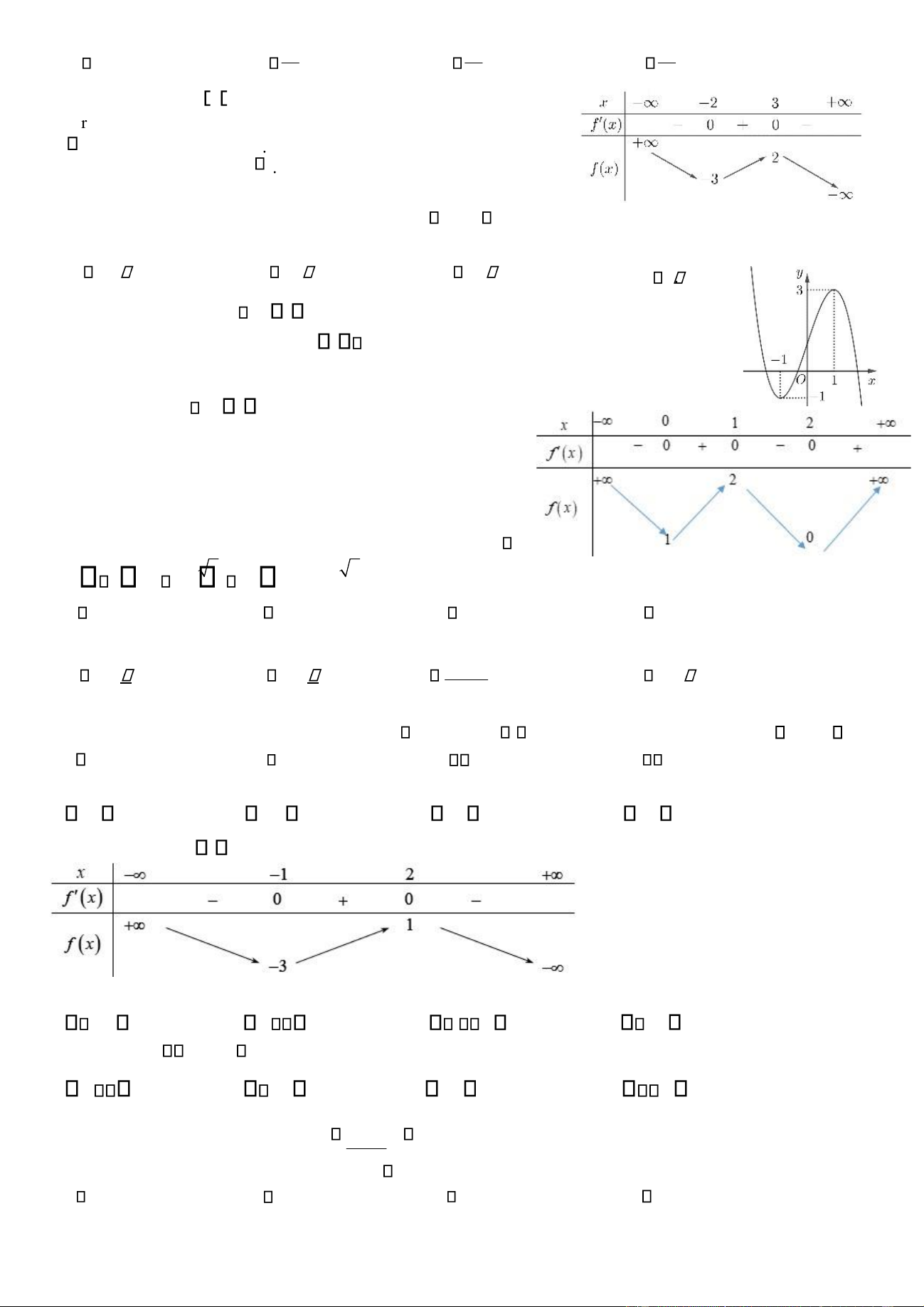
Cu 12. Cho hm s ố fx c b ả ng bi ến thiên như sau.
GiÆ trị c ực ạ i c ủ a hm s ố b ằ ng A. 3. B. 2 C. 3. D. 2
C u 13. Trong kh ng gian cho h nh chữ nhật ABCD c AB 1, AD 2. Gọi M N, lần lượt là trung iểm của AD v BC. Quay h
nh chữ nhật ó xung quanh trục MN ta ược một h nh trụ. T nh diện t ch to n phần Stp của h nh trụ ó. A. S tp 10 . B. Stp 6 . C. Stp 4 . D. S 2. tp
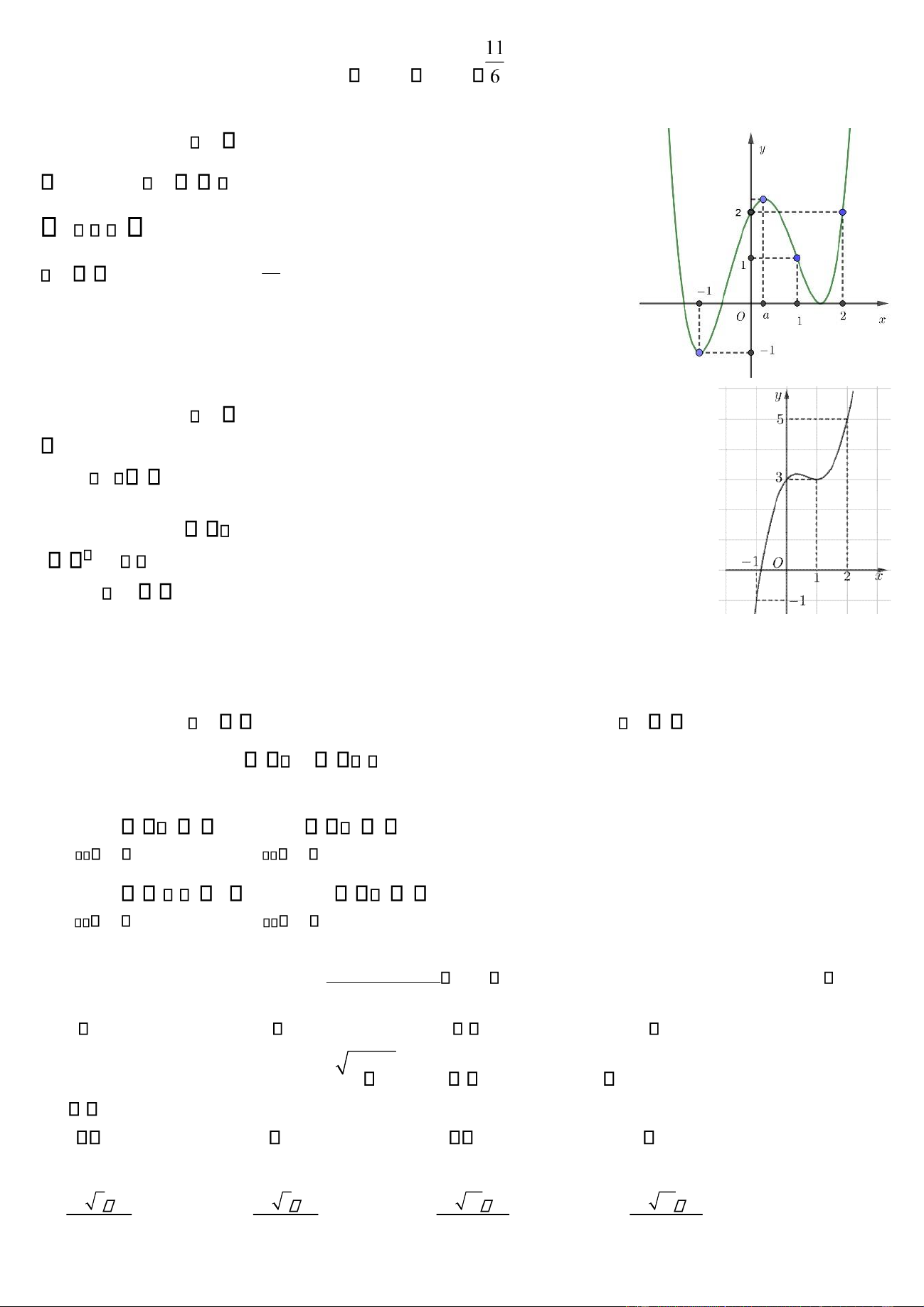
C u 14. Cho h m số bậc ba y f x có ồ thị là ường cong trong h
nh bŒn. Số nghiệm của phương tr nh f x 1 l D. 3. A. 1. B. 2. C. 0.
C u 15. Cho h m số y f x c bảng biến thiên như sau
Chọn khẳng ịnh úng trong các khẳng ịnh sau
A. Tổng giá trị lớn nhất v giÆ trị nhỏ nhất của hm số trŒn tập xác ịnh l 2.
B. GiÆ trị lớn nhất của hm số trŒn tập xác ịnh l 2 C. H m số không
có giá trị lớn nhất trŒn tập xác ịnh.
D. GiÆ trị nhỏ nhất của hm số trŒn tập xác ịnh l 1 C u 16. T nh S ln 2 2 3 2022 ln 3 2 2 2022
A. S 2022.
B. S 0 .
C. S 20222. D. S 1.
C u 17. T nh thể t ch của khối cầu c bÆn k nh bằng 5a?
A. V 500 a3 .
B. V 100 a3 . C. V 500a3 .
D. V 500 a3. 3 3 3 ,
C u 18. Gọi x x 1 2
l nghiệm của phương trnh log2 x log3 x.log27 4
0. T nh giÆ trị của biểu thức A logx1 log x2. A. A 3 B. A 4 C. A 3 D. A 2
C u 19. Khối hai mươi mặt ều l một khối a diện ều loại A. 3;5 . B. 3; 4 . C. 4;3 . D. 5;3 .
C u 20. Cho h m số f x c bảng biến thiên như sau
H m số ª cho ồng biến trŒn khoảng nào dưới ây? A. 1; 2 . B. 2; . C. 1; . D. 3;1 . C u 21. H m số y
x4+2x2 2022 ồng biến trŒn khoảng A. 0; . B. 1;0 . C. 0;1 . D. ;0 . 4x 1
C u 22. Tiệm cận ngang của ồ thị h m số y l x 1
A. y 4. B. y 1. C. x 4. D. x 1. 2/4 - Mª ề 101 lOMoAR cPSD| 22014077
C u 23. Cho h m số y
x3 3 2022x . Gọi M v m lần lượt l giÆ trị lớn nhất v nhỏ nhất của h m số ª cho trŒn oạn
0;2 th M m bằng A. 4044 . B. 4022 . C. 4040 . D. 4046 .
C u 24. Đồ thị sau ây là của h m số n o? y 1 x
A. y x 2 B. y x x 2
C. y x 2
D. y x 1 x x 1 1
C u 25. Biết rằng ường thẳng y 4x 5 cắt ồ thị h m số y x3 2x 1 tại iểm 1 x O 2 duy nhất, k hiệu x 2 2 0; y0
l tọa ộ của iểm ó. Khi ó x0 y0 bằng A. 298. B. 173. C. 13. D. 82.
C u 26. Thể t ch khối trụ có bán kính áy r a v chiều cao h a 2 bằng bao nhiŒu? a 2 A. 3 .
B. 4 a3 2 . C. 2 a3.
D. a3 2 . 3
C u 27. Thể t ch khối lăng trụ c diện tích áy B v c chiều cao h l
A. Bh. B. Bh. C. 3Bh.
C u 28. Trong cÆc h m số sau h m số n o nghịch biến trŒn ? D. Bh. e A. y x . B. y x . C. y log x3 . D. log3 x. 4 3
C u 29. T m tập xác ịnh của h m số y log2022 3x x2 .
A. D . B. D 0; . C. D ; 0 3; . D. D 0; 3 .
C u 30. Cho h nh ch p S ABCD. có áy ABCD l h nh vu ng cạnh bằng 2a, cạnh SA vu ng g c với áy và mặt phẳng SBC
tạo với áy một g c 60. Thể t ch của khối ch p S ABCD. bằng A. . B. . C. . D. .
C u 31. Cho khối n n c chiều cao bằng 2a v bÆn k nh bằng a 3 . Thể t ch của khối nón ª cho bằng 4 a
A. 4 a3. B. 6 a3. C. 2 a3. D. 3 . 3
C u 32. Cho h nh lập phương nội tiếp trong một mặt cầu bÆn k nh R a . Độ d i cạnh của h nh lập phương bằng 2a 3 a 3 a 3
A. a 3 . B. . C. . D. . 3 3 2
C u 33. Cho a l số thực dương khác 1. Mệnh ề nào dưới ây úng với mọi số dương x y, ? x A. log a
x loga x loga y. B. loga
loga x loga y. y y a x a x y . x x D. loga loga . C. log log y y loga y lOMoAR cPSD| 22014077
C u 34. T m nghiệm của phương trnh log x2 log x4 log x8 ? A. 3. B. 5. C. 4. D. 2.
C u 35. Cho h m số y f x
có ạo h m y f ’ x x2 x2 1
, x . H m số y
f x có bao nhiêu iểm cực trị? A. 3. B. 4. C. 1. D. 2.
C u 36. Cho h m số y f x
liŒn tục trŒn  và ồ thị h m số y f x cho bởi
h nh vẽ bŒn. Đặt g x f x
x2 , x . Hỏi ồ thị
h m số y g x c bao 2 nhiêu iểm cực trị? A. 4 . B. 2 . C. 3. D. 1.
C u 37. Cho h m số y f x có ạo h m v liŒn tục trŒn . Biết rằng ồ thị h m số y f ’ x
như dưới ây. XØt h m số g x f x
x2 x trŒn . Chọn khẳng ịnh úng trong cÆc khẳng ịnh sau? A. max g x
g 2 . B. max g x g 1 . x 1;2 x 1;2
C. max g x g 1 . D. max g x g 0 . x 1;2 x 1;2 log5 a
C u 38. Với hai số thực dương a b, tøy v
log6 b 2. Khẳng ịnh nào dưới ây là khẳng ịnh úng? (1 log 2)log3 53
A. a 36b .
B. a b log 36 .
C. 2a 3b 0.
D. a b log 26 . 0
C u 39. Tập nghiệm của bất phương trnh
4 2x.log2(x 1) c dạng S ab [ ; ].T nh giÆ trị của biểu thức
T a 2 b2. A. T 1. B. T 4. C. T 4 . D. T 1.
C u 40. Cho h nh ch p S. ABCD có áy ABCD là hnh chữ nhật, AB = a. AD = 3a, SA vuông góc áy. Góc tạo bởi SC v áy (
ABCD) bằng 600. Thể t ch của khối cầu ngoại tiếp h nh ch p S. ABCD bằng bao nhiŒu? 20 5 a3 40 3 a3 20 10 a3 40 10 a3 A. . B. . C. . D. . 4/4 - Mª ề 101 lOMoAR cPSD| 22014077 3 3 3 3
C u 41. Cho h nh n n c ường sinh bằng 2a v g c ở ỉnh bằng 900.Cắt h nh n n bằng mặt phẳng ( )P i qua ỉnh sao cho g c giữa (
)P v mặt áy hnh n n bằng 600.T nh diện t ch S của thiết diện tạo th nh.
A. S 4 23a2 .
B. S 8 23a2 .
C. 5a23 2 .
D. S 23a2 . 3x2 3x m 1 2
C u 42. C bao nhiŒu giÆ trị nguyŒn của tham số m ể phương trnh log 2 2
x 5x 2 m c hai nghiệm
2x x 1 ph n biệt lớn hơn 1. A. 4 . B. 3. C. V số. D. 2 .
C u 43. Cho h nh lăng trụ tam giÆc ABC ABC. có áy ABC l tam giÆc vu ng tại A v AB a 2 , AC a 6 . Biết A A
A B A C a 6 , thể t ch khối lăng trụ ABC ABC. bằng A. .
B. 2a3 3. C.
. D. a3 3.
C u 44. T m m ể ptr nh 9x 2 m 1 .3 x 3 m 9 0c 2 nghiệm x1, x2 sao cho x1 + x2 = 3. A. m .
B. Kh ng tồn tại m. C. m 12. D. m 12.
C u 45. Ch p SABC c ABC l tam giÆc ều cạnh a, mặt bŒn SAB vu ng c n tại S v nằm trong mặt phẳng vu ng g c với áy.
Tính thể t ch khối ch p SABC. a 3 a 3 a 3 a 3 A. V 3 B. V 3 C. V 3 D. V 3 6 12 8 24
C u 46. Gọi L, N lần lượt l giÆ trị lớn nhất v giÆ trị nhỏ nhất của h m số y x2 8 e x trên oạn 3;0 . T nh
S ln L ln N . A. S 9,47 B. S 11
C. S 5 ln 4 D. S 2ln 4 3
C u 47. Tìm m ể phương trình x3 3x2 2
m có 3 nghiệm phân biệt trong ó có úng một nghiệm lớn hơn 1. A. m 0; 2 B. m 0; 2 C. m 2; 2 D. m 0; 2
C u 48. Cho h nh ch p S ABCD.
có áy ABCD l h nh vu ng cạnh a ,SA vu ng g c với mặt phẳng ABCDv SM
SA a .Điểm M thuộc cạnh SA sao cho
k,0 k 1.Khi ó giá trị n o của k ể mặt phẳng (BMC) chia khối ch p SA
S ABCD. th nh hai phần c thể t ch bằng nhau? 1 5 1 5 1 2 1 5 A. . B. . C. . D. . 2 4 2 4
C u 49. Cho hàm số y
x3 mx2 (m2 m 1)x 1. Có bao nhiêu giá trị nguyên của tham số m ể hàm số ạt cực trị tại x x 2 2 1 2, thỏa mãn x1 x2 6 ? A. 0. B. 2. C. 1. D. 3.
C u 50. Một thùng ựng sơn dạng h nh trụ c thể t ch 1m3. Biết chi phí ể l m mặt xung quanh và áy thùng là
200.000 ồng/m2 , chi phí ể l m nắp ậy l 100.000 ồng/m2 . Để chi ph l m vỏ thùng sơn trên thấp nhất th chiều cao h của thøng bằng bao nhiŒu? 9 4 4 A. h 3 m B. h 3 m C. h 3 m D. h 3 m 4 9 4
------ HẾT ------ lOMoAR cPSD| 22014077
Phần áp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 50. 101 103 105 107 1 A C C D 2 A A B A 3 A D B D 4 B B D B 5 A B B B 6 C D C A 7 A D D A 8 C B D C 9 B D C D 10 D C A B 11 C D B B 12 B C B A 13 C B B C 14 D A A D 15 C D B A 16 B A D A 17 A C C C 18 C A B B 19 A B A B 20 A D D D 21 C B D D 22 A D D B 23 A A A B 24 C D B B 1 lOMoAR cPSD| 22014077 25 B B C C 26 D A A A 27 B C C B 28 A A D C 29 D A D D 30 B B A B 31 C A B C 32 B A A A 33 A D A A 34 D B C B 35 D A D B 36 B A B B 37 B B D C 38 A C A A 39 C C B D 40 D A A C 41 A A B D 42 D B C D 43 B B C C 44 C C D C 45 D D B D 46 C D D D 47 D C A B 48 A A B C 49 C D C B 50 A C D B 2 lOMoAR cPSD| 22014077
MA TRẬN ĐỀ KIỂM TRA CUỐI K I NĂM HỌC 2022−2023 M
N: TO`N 12 THỜI GIAN LM B I: 90 phœt
Mức ộ nhận thức Tổng % tổng Nội dung kiến Nhận biết Th ng hiểu Vận dụng Vận dụng cao Số CH iểm TT
Đơn vị kiến thức thức Thời Số Thời Số Thời Số Thời Số Thời gian gian gian gian gian TN TL (phœt) CH
(phœt) CH (phœt) CH (phœt) CH (phœt)
1.1. Sự ồng biến, nghịch biến của hm số 2 1 1 1 3 2 1. Ứng dụng
1.2. Cực trị của hm số 1 1 1 1 1 3 1 6 4 11 ạo hàm
1.3. GiÆ trị lớn nhất v giÆ trị nhỏ nhất của
ể khảo h m số 1 1 1 1 1 3 1 6 4 11
1 sát v vẽ ồ 34
1.4. Đường tiệm cận 1 1 1 1 2 2 thị của h
1.5. Bảng biến thiên và ồ thị của hm số 1 1 1 1 2 2 m số
1.6. CÆc vấn ề liên quan ến khảo sát hm số 1 1 1 3 2 4 2.1. Lũy thừa. 1 1 1 1 2.2. L garit. 2 1 1 1 1 3 4 5
2. H m số lũy 2.3. H m số lũy thừa. Hm số mũ. Hm số l thừa, hm số garit 2 1 1 1 3 2
2 mũ v h m số 28
2.4. Phương trnh mũ và phương tr nh l logarit 1 1 1 1 1 3 1 6 4 11 garit
2.5. Bất phương trnh mũ v bất phương tr nh l garit 1 1 1 3 2 4
3.1. KhÆi niệm về khối a diện. Khối a diện
lồi v khối a diện ều 3 3. Khối a diện 1 1 1 1 2 2 16
3.2. Thể tích của khối a diện 2 1 1 1 2 6 1 6 6 14 4. Mặt nón, 4.1. Mặt nón 2 1 1 1 1 3 4 5 4
Mặt trụ, Mặt 4.2. Mặt trụ 2 2 1 1 1 6 4 9 22 cầu 4.3. Mặt cầu 1 1 1 1 1 3 3 5 Tổng 20 15 15 15 10 30 5 30 50 90 100 1 lOMoAR cPSD| 22014077 Tỉ lệ (%) 40 30 20 10 Tỉ lệ chung (%) 70 3 0
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA CUỐI K I M
N: TO`N 12 THỜI GIAN LM B I: 90 PH T
Số câu hỏi theo mức ộ nhận thức Nội dung TT
Đơn vị kiến thức Tổng kiến thức
Mức ộ kiến thức, kĩ năng cần kiểm tra, ánh giá Vận Nhận
Th ng Vận dụng biết
hiểu dụng cao 1 Ứng dụng Nhận biết: ạo hàm -
Biết tính ơn iệu của hm số. ể khảo -
Biết mối liŒn hệ giữa tính ồng biến, nghịch biến của một sát v vẽ ồ thị
h m số v dấu ạo hm cấp một của nó. của h m số Th ng hiểu: -
Hiểu tính ơn iệu của hm số; mối liŒn hệ giữa tính ồng
biến, nghịch biến của một hm số v dấu ạo hm cấp một của n .
1.1. Sự ồng biến, Xác ịnh ược nghịch biến của hm
tính ơn iệu của một hm số trong một số t nh huống 2 1 17 số cụ thể, ơn giản. Vận dụng: -
Vận dụng ược tính ồng biến, nghịch biến của hm số xét
tính ồng biến, nghịch biến của một hm số; vận dụng sự biến
thiŒn của hm số giải các bi toÆn liŒn quan. Vận dụng cao: -
Vận dụng sáng tạo, linh hoạt tính ồng biến, nghịch biến
của hm số giải cÆc b i toÆn liŒn quan. 2 lOMoAR cPSD| 22014077 Nhận biết: -
Biết cÆc khÆi niệm iểm cực ại, iểm cực tiểu, iểm cực trị của hm số. -
Biết các iều kiện ủ ể có iểm cực trị của hm số. Th ng
1.2. Cực trị của hm số hiểu: 1 1 1 1 -
Hiểu cÆc khÆi niệm iểm cực ại, iểm cực tiểu, iểm cực
trị của hm số; các iều kiện ủ ể có iểm cực trị của hm số. Xác
ịnh ược iểm cực trị v cực trị của một hm số trong một số tnh
huống cụ thể, ơn giản. TT Nội dung
Số câu hỏi theo mức ộ nhận Tổng kiến thức thức
Đơn vị kiến thức
Mức ộ kiến thức, kĩ năng cần kiểm tra, ánh giá Vận Nhận
Th ng Vận dụng biết
hiểu dụng cao Vận dụng: -
Vận dụng l thuyết cực trị ể tm iểm cực trị v cực trị một
h m số; giải các bi toÆn liŒn quan: xác ịnh tham số ể hm số ạt
cực trị tại iểm xo, Vận dụng cao: -
Vận dụng sáng tạo, linh hoạt l thuyết cực trị ể tm iểm
cực trị v cực trị một hm số; giải các bi toÆn liŒn quan. 3 lOMoAR cPSD| 22014077 Nhận biết: -
Biết cÆc khÆi niệm giá trị lớn nhất, giá trị nhỏ nhất
của hm số trŒn một tập hợp. Th ng hiểu: -
Tính ược giÆ trị lớn nhất, giá trị nhỏ nhất của hm số
trŒn một oạn, một khoảng trong các tnh huống ơn giản. Vận dụng:
1.3. GiÆ trị lớn nhất -
T m ược giÆ trị lớn nhất, giá trị nhỏ nhất của hm số
v giÆ trị nhỏ nhất của trŒn một tập cho trước; ứng dụng vo một số bi toÆn thực tế ơn 1 1 1 1 hm số giản. Vận dụng cao: -
Vận dụng sáng tạo, linh hoạt l thuyết giá trị lớn nhất,
giá trị nhỏ nhất của hm số vo cÆc b i toÆn liŒn quan: t m iều
kiện ể phương trnh, bất phương trnh c nghiệm, ứng dụng vo một
số tnh huống thực tế Nhận biết: -
Biết các bước khảo sát v vẽ ồ thị hm số (tm tập xác ịnh,
1.4. Bảng biến thiŒn xØt chiều biến thiŒn, t m cực trị, tm tiệm cận, lập bảng biến và ồ thị của hm số 1 2 1
thiŒn, vẽ ồ thị . -
Nhớ ược dạng ược ồ thị của các hm số bậc ba, bậc bốn
trùng phương, bậc nhất / bậc nhất. TT Nội dung
Số câu hỏi theo mức ộ nhận Tổng kiến thức thức
Đơn vị kiến thức
Mức ộ kiến thức, kĩ năng cần kiểm tra, ánh giá Vận Nhận
Th ng Vận dụng biết
hiểu dụng cao 4 lOMoAR cPSD| 22014077 Th ng hiểu: -
Hiểu cÆch khảo sát v vẽ ồ thị của các hm số bậc ba,
bậc bốn trùng phương, bậc nhất / bậc nhất. -
Xác ịnh ược dạng ược ồ thị của các hm số bậc ba, bậc
bốn trùng phương, bậc nhất / bậc nhất; hiểu ược bảng biến thiŒn. Vận dụng: -
Ứng dụng ược bảng biến thiên, ồ thị của hm số vo cÆc
bài toán liên quan: dùng ồ thị hm số ể biện luận số nghiệm của
một phương trnh, viết phương trnh tiếp tuyến của ồ thị
h m số tại một iểm thuộc ồ thị hm số… Vận dụng cao:
- Vận dụng, liŒn kết kiến thức về bảng biến thiên, ồ thị của h
m số với các ơn vị kiến thức khác vo giải quyết các bi toÆn liŒn quan. Nhận biết: -
Biết cÆc khÆi niệm ường tiệm cận ứng, ường tiệm cận
ngang của ồ thị hm số.
1.5. Đường tiệm cận Th ng hiểu: 1 1 -
T m ược ường tiệm cận ứng, ường tiệm cận ngang của ồ thị hm số. 2 H m số lũy
2.1. Lũy thừa. Hm số Nhận biết: 1 14
thừa, hm số lũy thừa -
Biết cÆc khÆi niệm v t nh chất lũy thừa với số mũ mũ v h m
nguyŒn của một số thực; lũy thừa với số mũ hữu tỉ v lũy thừa số logarit
với số mũ thực của một số thực dương. -
Biết khÆi niệm, t nh chất, c ng thức tính ạo hm, dạng ồ
thị của hm số lũy thừa. Th ng hiểu: -
Tính ược giÆ trị các biểu thức lũy thừa ơn giản, thực hiện Nội dung
Số câu hỏi theo mức ộ nhận TT
Đơn vị kiến thức kiến thức
Mức ộ kiến thức, kĩ năng cần kiểm tra, ánh giá thức Tổng 5 lOMoAR cPSD| 22014077 Vận Nhận
Th ng Vận dụng biết
hiểu dụng cao
ược cÆc phØp biến ổi ơn giản: ơn giản biểu thức, so sÆnh
những biểu thức có chứa lũy thừa…
- Vẽ ược ồ thị các hm số lũy thừa; tính ược ạo hm của cÆc h m số lũy thừa. 2.2. L garit. H m số Nhận biết: 4 2 1 mũ. Hm số lôgarit -
Biết cÆc khÆi niệm v t nh chất của lôgarit. -
Biết khÆi niệm, tính chất, công thức tính ạo hm, dạng ồ
thị của hm số mũ v h m số lôgarit. Th ng hiểu: -
Tính ược giÆ trị các biểu thức ơn giản, thực hiện ược
cÆc phØp biến ổi ơn giản. -
Vẽ ược ồ thị các hm số mũ, hm số lôgarit; tính ược ạo h
m của các hm số mũ v h m số lôgarit. Vận dụng: -
`p dụng ược tính chất của l garit, h m số mũ, hm số l
garit v o cÆc b i toÆn liŒn quan: t nh giÆ trị biểu thức, so sánh
giÆ trị biểu thức, bi toÆn c m h nh thực tế (“lªi kØp , tăng
trưởng”, …), ... Vận dụng cao: -
Vận dụng, liŒn kết kiến thức về mũ v l garit với các ơn
vị kiến thức khác vo giải quyết các bi toÆn liŒn quan.
2.3. Phương trnh mũ Nhận biết: và phương trnh l -
Biết c ng thức nghiệm của phương trnh mũ, lôgarit cơ garit bản. Th ng hiểu: 1 1 1 1 -
T m ược tập nghiệm của một số phương trnh mũ,
lôgarit ơn giản. Vận dụng: -
Giải ược các phương trnh mũ v l garit bằng cách sử dụng 6 lOMoAR cPSD| 22014077 TT Nội dung
Số câu hỏi theo mức ộ nhận Tổng kiến thức thức
Đơn vị kiến thức
Mức ộ kiến thức, kĩ năng cần kiểm tra, ánh giá Vận Nhận
Th ng Vận dụng biết
hiểu dụng cao
cÆc c ng thức v quy tắc biến ổi. Vận dụng cao:
- Vận dụng sáng tạo, linh hoạt kiến thức giải phương trnh
mũ, l garit v liŒn kết với các ơn vị kiến thức khác vo giải
quyết các bi toÆn liŒn quan.
2.4. Bất phương trnh Nhận biết:
mũ v bất phương tr - Biết c ng thức nghiệm của bất phương trnh mũ, lôgarit cơ bản. 1 1 nh l garit 3 Khối a diện 3.1. KhÆi niệm về Nhận biết: khối a diện. Khối a 5. diện lồi v khối a
- Biết khÆi niệm khối a diện, khối a diện ều v nhận dạng ược diện ều
cÆc khối a diện, khối a diện ều. Biết khÆi niệm phép ối xứng 1 1
qua mặt phẳng v sự bằng nhau của hai khối a diện. Th ng hiểu: 3.3. Thể tích của Nhận biết: khối a diện -
Biết khÆi niệm về thể tích khối a diện; nhớ ược c ng
thức t nh thể tích của khối lăng trụ v khối chóp. Th ng hiểu: -
Tính ược thể tích của khối lăng trụ v khối chóp khi cho
chiều cao v diện tích áy. 8 Vận dụng: 2 1 2 1 -
Tính ược thể tích của khối lăng trụ v khối chóp khi xác
ịnh ược chiều cao v diện tích áy. Vận dụng cao: -
Tính ược thể tích của khối a diện gắn với việc phân chia
v lắp ghép các khối a diện; vận dụng, liŒn kết kiến thức về thể
t ch khối a diện với các ơn vị kiến thức khác vo giải quyết 7 lOMoAR cPSD| 22014077 TT Nội dung
Số câu hỏi theo mức ộ nhận Tổng kiến thức thức
Đơn vị kiến thức
Mức ộ kiến thức, kĩ năng cần kiểm tra, ánh giá Vận Nhận
Th ng Vận dụng biết
hiểu dụng cao cÆc b i toÆn liŒn quan. 4 Mặt
nón, 4.1. Mặt nón, Mặt trụ, Nhận biết:
Mặt trụ, Mặt mặt cầu -
Biết khÆi niệm mặt nón, mặt trụ, mặt cầu; nhớ ược c cầu
ng thức tính diện tích xung quanh của hnh n n, h nh trụ; nhớ
ược c ng thức tính diện tích mặt cầu; nhớ ược c ng thức t nh
thể tích khối nón, khối trụ v khối cầu. Th ng hiểu: -
Nắm ược khÆi niệm mặt nón, mặt trụ, mặt cầu; tính 5 3 2 1 11
ược cÆc yếu tố của mặt nón, mặt trụ, mặt cầu khi biết các yếu
tố khÆc liŒn quan; tính ược diện tích xung quanh của hnh n
n, h nh trụ; tính ược diện tích mặt cầu; tính ược thể tích khối n
n, khối trụ v khối cầu, khối nón, khối trụ. Tổng 20 15 10 5 50 8