Đề kiểm tra học kỳ 1 Toán 7 năm 2018 – 2019 trường THCS Mỹ Đình 1 – Hà Nội

Đề kiểm tra học kỳ 1 Toán 7 năm 2018 – 2019 trường THCS Mỹ Đình 1 – Hà Nội được biên soạn theo hình thức trắc nghiệm khách quan kết hợp với tự luận, phần trắc nghiệm gồm 4 câu, chiếm 1 điểm, phần tự luận gồm 5 câu, chiếm 9 điểm, học sinh làm bài trong 90 phút, đề thi có lời giải chi tiết, lời giải được trình bày bởi thầy Nguyễn Hữu Phúc.

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 7

Môn: Toán 7

Thông tin:

13 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
1/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
PHÒNG GD & ĐT NAM TỪ LIÊM
TRƯỜNG THCS MỸ ĐÌNH 1
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2018 − 2019
MÔN: TOÁN 7
Thời gian làm bài: 90 phút.
I. TRẮC NGHIỆM: (1,0 điểm)
Chọn chữ cái đứng trước đáp án đúng:
Câu 1. Cách viết nào sau đây là đúng:
A.
0,25 0,25− = −
B.
0,25 ( 0,25)− − = − −
C.
0,25 0,25− − =
D.
0,25 0,25− =
Câu 2. Điểm thuộc đồ thị hàm số
2y x= −
là:
A.
( 1; 2)− −
B.
1
; 4
2
−
C.
(0;2)
D.
−( 1;2)
Câu 3. Cho tam giác
ABC
vuông tại A, ta có:
A.
+ >
0
90B C
B.
+ <
0
90B C
C.
+ =
0
90B C
D.
+ =
0
180B C
Câu 4. Cho
ABC∆
có
0 0
60 ; 55A B
= =
. Số đo góc ngoài tại đỉnh
C
là:
A.
0
65
B.
0
130
C.
0
125
D.
0
115
2/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
II. TỰ LUẬN (9,0 điểm)
Bài 1. (3,0 điểm).
1) Thực hiện phép tính (tính hợp lý nếu được):
a)
− + + −
3 5 10 6
15
13 11 13 11
b)
−
+ ⋅ +
2
3 1
3 : 36 0,75
2 9
c)
⋅ + ⋅
1 2 18 2
2 15
19 3 19 3
2) Tìm
x
biết:
a)
2 5 7
:
3 8 12
x
− + = −
b)
1
2 1 0,5
3
x
+ − =
Bài 2 (1,0 điểm). Cho hàm số
( ) 2 6
y f x x
= = +
a) Tính
1
2
f
?
b) Điểm
( 2; 4)
A
− −
có thuộc đồ thị hàm số
2 6y x= +
không?
Bài 3. (1,0 điểm) Một mảnh vườn hình chữ nhật có chu vi 70 mét. Tỉ
số giữa hai cạnh của nó là
3
4
. Tìm diện tích mảnh vườn.
3/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 4. (3,5 điểm) Cho
ABC
∆
vuông tại A, cạnh AB bằng cạnh
AC
,
H
là trung điểm của
BC
.
a) Chứng minh
AHB AHC
∆ = ∆
b) Chứng minh AH vuông góc với
BC
c) Trên tia đối của tia AH lấy điểm
E
sao cho
AE BC
=
, trên tia đối
của tia
CA
lấy điểm
F
sao cho
CF AB
=
. Chứng minh
BE BF
=
d) Tính số đo góc
EBF
Bài 5. (0,5 điểm) Cho
, ,a b c
là 3 số thực dương thỏa mãn:
a b c b c a c a b
c a b
+ − + − + −
= =
Tính giá trị của biểu thức
1 1 1
b a c
M
a c b
= + + +
4/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
HƯỚNG DẪN GIẢI
I. TRẮC NGHIỆM: (1,0 điểm)
Chọn chữ cái đứng trước đáp án đúng:
Câu 1. Cách viết nào sau đây là đúng:
A.
0,25 0,25− = −
B.
0,25 ( 0,25)− − = − −
C.
0,25 0,25− − =
D.
0,25 0,25− =
Lời giải
Cách viết đúng là:
0,25 0,25− =
(Với
:x x x∈ = −ℚ
nếu 0x < )
Chọn D.
Câu 2. Điểm thuộc đồ thị hàm số
2y x= −
là:
A.
( 1; 2)− −
B.
1
; 4
2
−
C.
(0;2)
D.
−
( 1;2)
Lời giải
Thay 1x = − vào hàm số
2y x= −
, ta được:
2.( 1) 2y = − − =
Suy ra: Điểm
( 1; 2)− −
không thuộc đồ thị hàm số
2y x= −
Thay
1
2
x =
vào hàm số
2y x= −
, ta được:
1
2 1
2
y = − ⋅ = −
Suy ra: Điểm
1
; 4
2
−
không thuộc đồ thị hàm số
2y x= −
Thay 0x = vào hàm số
2y x= −
, ta được:
2 0 0y = − ⋅ =
Suy ra: Điểm
(0;2)
không thuộc đồ thị hàm số
2y x= −
5/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
Thay 1x = − vào hàm số
2y x= −
, ta được:
2.( 1) 2y = − − =
Suy ra: Điểm
−
( 1;2)
thuộc đồ thị hàm số
2y x= −
Chọn D.
Câu 3. Cho tam giác
ABC
vuông tại A, ta có:
A.
+ >
0
90
B C
B.
+ <
0
90
B C
C.
+ =
0
90
B C
D.
+ =
0
180
B C
Lời giải
Xét
ABC∆
vuông tại A có:
+ =
0
90
B C
(Trong một tam giác vuông,
hai góc nhọn phụ nhau)
Chọn C.
Câu 4. Cho
ABC∆
có
0 0
60 ; 55A B= =
. Số đo góc ngoài tại đỉnh
C
là:
A.
0
65
B.
0
130
C.
0
125
D.
0
115
Lời giải
Xét
ABC∆
có:
0
180A B C+ + =
(Định lý về tổng 3 góc của tam giác)
0 0 0
60 55 180C+ + =
0 0
115 180C+ =
0 0
0
180 115
65
C
C
= −
=
Số đo của góc ngoài tại đỉnh C là:
0 0 0
180 65 115− = (Góc ngoài của tam
giác là góc kề bù với một góc của tam giác ấy)
Chọn D.
6/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
II. TỰ LUẬN (9,0 điểm)
Bài 1. (3,0 điểm).
1) Thực hiện phép tính (tính hợp lý nếu được):
a) − + + −
3 5 10 6
15
13 11 13 11
= + + − − +
3 10 5 6
15
13 13 11 11
= + − +
13 11
15
13 11
= + − +1 ( 1) 15
= + =0 15 15
b)
−
+ ⋅ +
2
3 1
3 : 36 0,75
2 9
= + ⋅ +
9 1 3
3 : 6
4 9 4
= + +
4 2 3
3 3 4
= + =
3 3
2 2
4 4
c)
⋅ + ⋅
1 2 18 2
2 15
19 3 19 3
= ⋅ +
2 1 18
2 15
3 19 19
= ⋅ =
2
18 12
3
7/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
2) Tìm x biết:
a)
2 5 7
:
3 8 12
x
− + = −
2 7 5
:
3 12 8
x
− = − −
2 29
:
3 24
x
− = −
2 29
:
3 24
16
29
x
x
= − −
=
b)
1
2 1 0,5
3
x + − =
1 1
2 1
3 2
x + − =
1 1 5
2 1
2 3 6
x + = + =
5 5
1 : 2
6 12
x + = =
5
1
12
x⇒ + =
hoặc
5
1
12
x + = −
5
1
12
x⇒ = −
hoặc
5
1
12
x = − −
7
12
x
−
⇒ =
hoặc
17
12
x = −
Vậy
7
12
x
−
=
hoặc
17
12
x = −
8/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 2 (1,0 điểm). Cho hàm số
( ) 2 6y f x x= = +
a) Tính
1
2
f
?
b) Điểm
( 2; 4)A − −
có thuộc đồ thị hàm số
2 6y x= +
không?
Lời giải
a)
1 1
2 6 1 6 7
2 2
f
= ⋅ + = + =
b) Thay
2
A
x = −
vào hàm số
2 6y x= +
, ta được:
2.( 2) 6 ( 4) 6 2
A
y y= − + = − + = ≠
Vậy điểm
( 2; 4)
A − −
không thuộc đồ thị hàm số
2 6y x= +
9/1
3
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 3. (1,0 điểm) Một mảnh vườn hình chữ nhật có chu vi 70 mét. Tỉ
số giữa hai cạnh của nó là
3
4
. Tìm diện tích mảnh vườn.
Lời giải
Nửa chu vi mảnh vườn hình chữ nhật là:
70 : 2 35( )
m=
Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là
,
a b
( 0a b> > )
Tỉ số giữa hai cạnh của mảnh vườn hình chữ nhật là
3
4
nên ta có:
4 3
a b
=
Và nửa chu vi hình chữ nhật là 35m nên ta có: 35a b+ =
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
35
5
4 3 4 3 7
a b a b+
= = = =
+
5 4.5 20( )
4
a
a m= ⇒ = =
5 3.5 15( )
3
b
b m= ⇒ = =
Chiều dài của mảnh vườn hình chữ nhật là: 20m
Chiều rộng của mảnh vườn hình chữ nhật là: 20m
Diện tích mảnh vườn hình chữ nhật là:
2
20.15 300( )
m=
10/
13
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 4. (3,5 điểm) Cho
ABC∆
vuông tại A, cạnh AB bằng cạnh
AC
,
H
là trung điểm của
BC
.
a) Chứng minh
AHB AHC∆ = ∆
b) Chứng minh AH vuông góc với
BC
c) Trên tia đối của tia AH lấy điểm
E
sao cho
AE BC=
, trên tia đối
của tia
CA
lấy điểm
F
sao cho
CF AB=
. Chứng minh
BE BF=
d) Tính số đo góc
EBF
Lời giải
a) Chứng minh
AHB AHC∆ = ∆
Xét AHB∆ và
AHC∆
có:
( )
AB AC gt=
AH là cạnh chung
( )
HB HC gt=
Do đó:
( . . )
AHB AHC c c c∆ = ∆
b) Chứng minh AH vuông góc với
BC
Vì
( . . )
AHB AHC c c c∆ = ∆
nên
AHB AHC=
(Hai góc tương ứng)
Mà
0
180
AHB AHC+ =
(Hai góc kề bù)
0
90
AHB AHC AH BC⇒ = = ⇒ ⊥
H
C
B
A
11/
13
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
c) Trên tia đối của tia AH lấy điểm
E
sao cho
AE BC=
, trên tia đối
của tia
CA
lấy điểm
F
sao cho
CF AB=
. Chứng minh
BE BF=
Xét
ABC∆
vuông tại A có:
0
90
ABC ACB+ =
Mà
ABC ACB=
(vì
( . . )
AHB AHC c c c∆ = ∆
)
0
45
ABC ACB⇒ = =
Ta có:
0
180
FCB ACB+ =
(vì
FCB
là góc ngoài tại
C
của
ABC∆
)
0 0 0 0 0
45 180 180 45 135
FCB FCB+ = ⇒ = − =
0 0 0
90 45 135
EAB = + =
(vì
EAB
là góc ngoài tại A của ABH∆ )
Xét ABE∆ và
CFB∆
có:
( )
AB CF gt=
0
135
FCB EAB= =
( )
AE BC gt=
Do đó:
( . . )
ABE CFB c g c∆ = ∆
BE BF⇒ = (Hai cạnh tương ứng)
F
E
H
C
B
A
12/
13
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
d) Tính số đo góc
EBF
Xét EAB∆ có:
0
180
EAB AEB ABE+ + =
0 0
135 180
AEB ABE+ + =
0 0 0
180 135 45
AEB ABE+ = − =
(1)
Tương tự, xét
FCB∆
có:
0
180
FCB CFB CBF+ + =
0 0
135 180
CFB CBF+ + =
0 0 0
180 135 45
CFB CBF+ = − =
(2)
Từ (1) và (2) suy ra:
0 0 0
45 45 90
AEB ABE CFB CBF+ + + = + =
Mà
CFB ABE=
;
CBF AEB=
(vì
( . . )
ABE CFB c g c∆ = ∆
)
0
2. 2. 90
ABE CBF⇒ + =
0 0
90
2.( ) 90 45
2
ABE CBF ABE CBF⇒ + = ⇒ + = =
0 0 0
45 45 90
EBF ABC ABE CBF= + + = + =
Vậy
0
90
EBF =
F
E
H
C
B
A
13/
13
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 5. (0,5 điểm) Cho
, ,
a b c
là 3 số thực dương thỏa mãn:
a b c b c a c a b
c a b
+ − + − + −
= =
Tính giá trị của biểu thức
1 1 1
b a c
M
a c b
= + + +
Lời giải
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
1
a b c b c a c a b a b c b c a c a b a b c
c a b a b c a b c
+ − + − + − + − + + − + + − + +
= = = = =
+ + + +
1 2
a b c
a b c c a b c
c
+ −
= ⇒ + − = ⇒ + =
1 2
b c a
b c a a b c a
a
+ −
= ⇒ + − = ⇒ + =
1 2
c a b
c a b b c a b
b
+ −
= ⇒ + − = ⇒ + =
1 1 1
b a c
M
a c b
= + + +
a b c a b c
M
a c b
+ + +
=
2 2 2
c b a
M
a c b
= ⋅ ⋅
8
8
abc
M
abc
= =
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

1/1 3
Thầy Phúc Toán – GV dạy Toán Online
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2018 − 2019
PHÒNG GD & ĐT NAM TỪ LIÊM MÔN: TOÁN 7
TRƯỜNG THCS MỸ ĐÌNH 1
Thời gian làm bài: 90 phút.
I. TRẮC NGHIỆM: (1,0 điểm)
Chọn chữ cái đứng trước đáp án đúng:
Câu 1. Cách viết nào sau đây là đúng: A. 0 − ,25 = 0 − ,25 B. − 0 − ,25 = ( − 0 − ,25) C. − 0 − ,25 = 0,25 D. 0 − ,25 = 0,25
Câu 2. Điểm thuộc đồ thị hàm số y = 2 − x là:   A. ( 1 − ; 2 − ) B. 1; 4 −   C. (0;2) D. (−1;2)  2 
Câu 3. Cho tam giác ABC vuông tại A, ta có: A. B + C > 0 90 B. B + C < 0 90 C. B + C = 0 90 D. B + C = 0 180 Câu 4. Cho A ∆ BC có 0 0
A = 60 ; B = 55 . Số đo góc ngoài tại đỉnh C là: A. 0 65 B. 0 130 C. 0 125 D. 0 115
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 2/1 3
Thầy Phúc Toán – GV dạy Toán Online
II. TỰ LUẬN (9,0 điểm) Bài 1. (3,0 điểm).
1) Thực hiện phép tính (tính hợp lý nếu được): a) 3 − 5 + + 10 − 6 15 13 11 13 11  − 2 b) 3 + 1 3 : ⋅ 36 +   0, 75  2  9 c) 1 ⋅ 2 + 18 ⋅ 2 2 15 19 3 19 3 2) Tìm x biết: a) 2 5 7 − : x + = − 3 8 12 b) 1 2 x + 1 − = 0,5 3
Bài 2 (1,0 điểm). Cho hàm số y = f (x) = 2x + 6   a) Tính 1 f   ?  2  b) Điểm ( A 2 − ; 4
− ) có thuộc đồ thị hàm số y = 2x + 6 không?
Bài 3. (1,0 điểm) Một mảnh vườn hình chữ nhật có chu vi 70 mét. Tỉ
số giữa hai cạnh của nó là 3 . Tìm diện tích mảnh vườn. 4
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 3/1 3
Thầy Phúc Toán – GV dạy Toán Online
Bài 4. (3,5 điểm) Cho A
∆ BC vuông tại A, cạnh AB bằng cạnh AC ,
H là trung điểm của BC .
a) Chứng minh ∆AHB = A ∆ HC
b) Chứng minh AH vuông góc với BC
c) Trên tia đối của tia AH lấy điểm E sao cho AE = BC , trên tia đối
của tia CA lấy điểm F sao cho CF = AB . Chứng minh BE = BF
d) Tính số đo góc EBF
Bài 5. (0,5 điểm) Cho a, ,
b c là 3 số thực dương thỏa mãn:
a + b − c
b + c −a
c + a −b = = c a b    
Tính giá trị của biểu thức b a c M = 1 + 1 + 1 +      a  c  b
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 4/1 3
Thầy Phúc Toán – GV dạy Toán Online HƯỚNG DẪN GIẢI
I. TRẮC NGHIỆM: (1,0 điểm)
Chọn chữ cái đứng trước đáp án đúng:
Câu 1. Cách viết nào sau đây là đúng: A. 0 − ,25 = 0 − ,25 B. − 0 − ,25 = ( − 0 − ,25) C. − 0 − ,25 = 0,25 D. 0 − ,25 = 0,25 Lời giải Cách viết đúng là: 0
− ,25 = 0,25 (Với x ∈ℚ : x = x − nếu x < 0) Chọn D.
Câu 2. Điểm thuộc đồ thị hàm số y = 2 − x là:   A. ( 1 − ; 2 − ) B. 1; 4 −   C. (0;2) D. (−1;2)  2  Lời giải
Thay x = −1 vào hàm số y = 2
− x , ta được: y = 2 − .( 1 − ) = 2 Suy ra: Điểm ( 1 − ; 2
− ) không thuộc đồ thị hàm số y = 2 − x Thay 1 x = vào hàm số y = 2 − x , ta được: 1 y = 2 − ⋅ = 1 − 2 2   Suy ra: Điểm 1; 4 − 
 không thuộc đồ thị hàm số y = 2 − x  2 
Thay x = 0 vào hàm số y = 2
− x , ta được: y = 2 − ⋅ 0 = 0
Suy ra: Điểm (0;2) không thuộc đồ thị hàm số y = 2 − x
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 5/1 3
Thầy Phúc Toán – GV dạy Toán Online
Thay x = −1 vào hàm số y = 2
− x , ta được: y = 2 − .( 1 − ) = 2
Suy ra: Điểm (−1;2) thuộc đồ thị hàm số y = 2 − x Chọn D.
Câu 3. Cho tam giác ABC vuông tại A, ta có: A. B + C > 0 90 B. B + C < 0 90 C. B + C = 0 90 D. B + C = 0 180 Lời giải Xét A
∆ BC vuông tại A có: B + C = 0
90 (Trong một tam giác vuông, hai góc nhọn phụ nhau) Chọn C. Câu 4. Cho A ∆ BC có 0 0
A = 60 ; B = 55 . Số đo góc ngoài tại đỉnh C là: A. 0 65 B. 0 130 C. 0 125 D. 0 115 Lời giải Xét A ∆ BC có: 0
A + B +C = 180 (Định lý về tổng 3 góc của tam giác) 0 0 0 60 + 55 +C = 180 0 0 115 +C = 180 0 0 C = 180 − 115 0 C = 65
Số đo của góc ngoài tại đỉnh C là: 0 0 0
180 − 65 = 115 (Góc ngoài của tam
giác là góc kề bù với một góc của tam giác ấy) Chọn D.
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 6/1 3
Thầy Phúc Toán – GV dạy Toán Online
II. TỰ LUẬN (9,0 điểm) Bài 1. (3,0 điểm).
1) Thực hiện phép tính (tính hợp lý nếu được): a) 3 − 5 + + 10 − 6 15 13 11 13 11     = 3 + 10 + − 5 − 6 +     15  13 13   11 11    = 13 + − 11 +   15 13  11  = 1 + (−1) + 15 = 0 + 15 = 15  − 2 b) 3 + 1 3 : ⋅ 36 +   0, 75  2  9 = 9 + 1 ⋅ + 3 3 : 6 4 9 4 = 4 + 2 + 3 3 3 4 = + 3 = 3 2 2 4 4 c) 1 ⋅ 2 + 18 ⋅ 2 2 15 19 3 19 3   = 2 ⋅ 1 2 + 18  15  3  19 19  = 2 ⋅ 18 = 12 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 7/1 3
Thầy Phúc Toán – GV dạy Toán Online 2) Tìm x biết: a) 2 5 7 − : x + = − 3 8 12 2 7 5 − : x = − − 3 12 8 2 29 − : x = − 3 24 2  29  x = − : −   3  24  16 x = 29 b) 1 2 x + 1 − = 0,5 3 1 1 2 x + 1 − = 3 2 1 1 5 2 x + 1 = + = 2 3 6 5 5 x + 1 = : 2 = 6 12 5 ⇒ x + 1 = hoặc 5 x + 1 = − 12 12 5 ⇒ x = − 1 hoặc 5 x = − − 1 12 12 7 − ⇒ x = hoặc 17 x = − 12 12 − Vậy 7 x = hoặc 17 x = − 12 12
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 8/1 3
Thầy Phúc Toán – GV dạy Toán Online
Bài 2 (1,0 điểm). Cho hàm số y = f (x) = 2x + 6   a) Tính 1 f   ?  2  b) Điểm ( A 2 − ; 4
− ) có thuộc đồ thị hàm số y = 2x + 6 không? Lời giải   a) 1 1 f = 2 ⋅ + 6 = 1 + 6 =   7  2  2 b) Thay x = 2
− vào hàm số y = 2x + 6, ta được: A y = 2.( 2 − )+ 6 = ( 4 − )+ 6 = 2 ≠ y A Vậy điểm ( A 2 − ; 4
− ) không thuộc đồ thị hàm số y = 2x + 6
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 9/1 3
Thầy Phúc Toán – GV dạy Toán Online
Bài 3. (1,0 điểm) Một mảnh vườn hình chữ nhật có chu vi 70 mét. Tỉ
số giữa hai cạnh của nó là 3 . Tìm diện tích mảnh vườn. 4 Lời giải
Nửa chu vi mảnh vườn hình chữ nhật là: 70 : 2 = 35(m)
Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là a,b
(a > b > 0)
Tỉ số giữa hai cạnh của mảnh vườn hình chữ nhật là 3 nên ta có:a b = 4 4 3
Và nửa chu vi hình chữ nhật là 35m nên ta có: a +b = 35
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: a b a + b 35 = = = = 5 4 3 4 + 3 7
a = 5 ⇒a = 4.5 = 20(m) 4
b = 5 ⇒b = 3.5 =15(m) 3
Chiều dài của mảnh vườn hình chữ nhật là: 20m
Chiều rộng của mảnh vườn hình chữ nhật là: 20m
Diện tích mảnh vườn hình chữ nhật là: 2 20.15 = 300(m )
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 10/ 13
Thầy Phúc Toán – GV dạy Toán Online
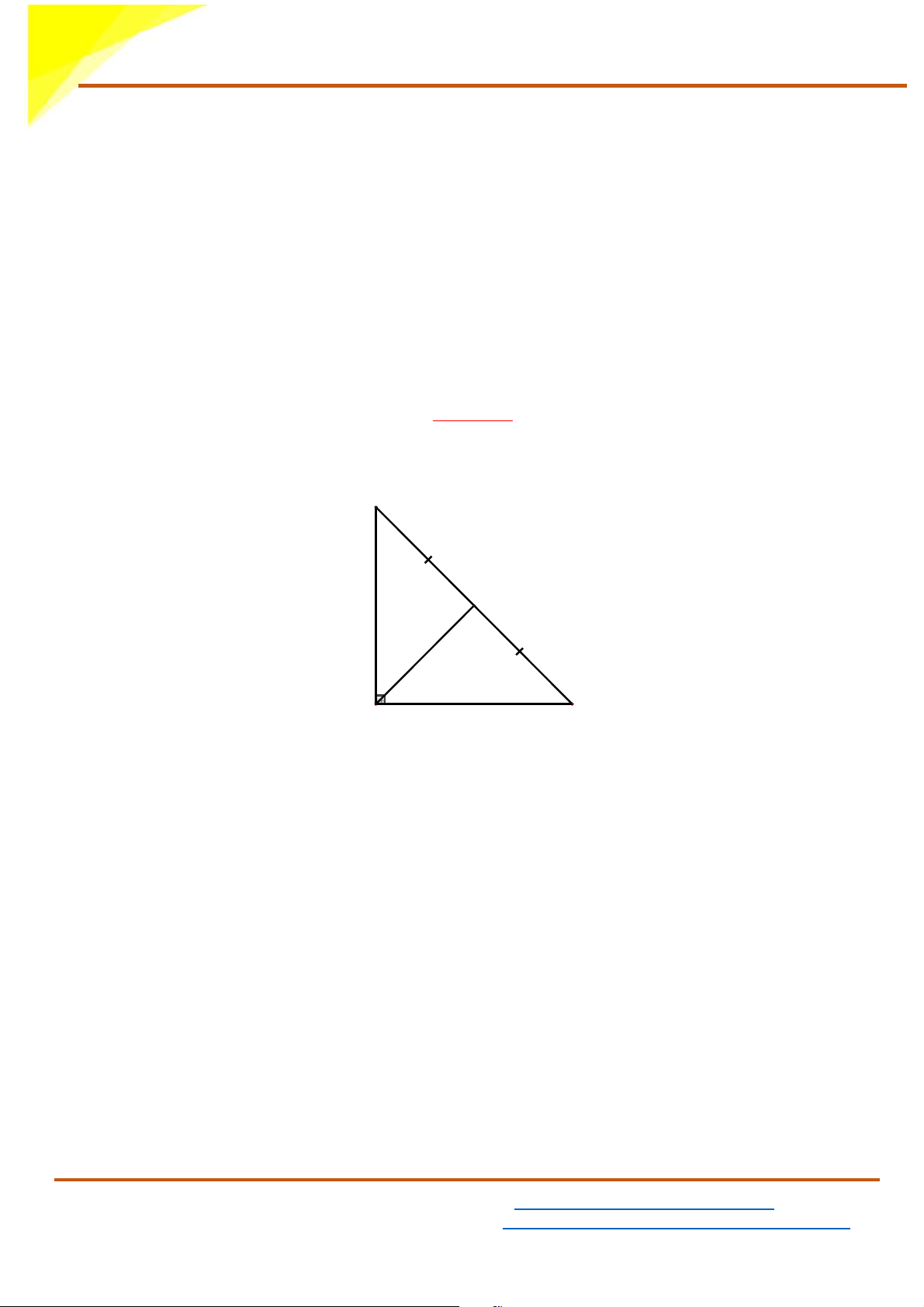
Bài 4. (3,5 điểm) Cho A
∆ BC vuông tại A, cạnh AB bằng cạnh AC ,
H là trung điểm của BC .
a) Chứng minh ∆AHB = A ∆ HC
b) Chứng minh AH vuông góc với BC
c) Trên tia đối của tia AH lấy điểm E sao cho AE = BC , trên tia đối
của tia CA lấy điểm F sao cho CF = AB . Chứng minh BE = BF
d) Tính số đo góc EBF Lời giải
a) Chứng minh ∆AHB = A ∆ HC C H A B
Xét ∆AHB và A ∆ HC có:
AB = AC(gt) AH là cạnh chung
HB = HC(gt)
Do đó: ∆AHB = ∆AHC(c.c.c)
b) Chứng minh AH vuông góc với BC
Vì ∆AHB = ∆AHC(c.c.c) nên AHB = AHC (Hai góc tương ứng) Mà 0
AHB + AHC = 180 (Hai góc kề bù) 0
⇒ AHB = AHC = 90 ⇒ AH ⊥ BC
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 11/ 13
Thầy Phúc Toán – GV dạy Toán Online
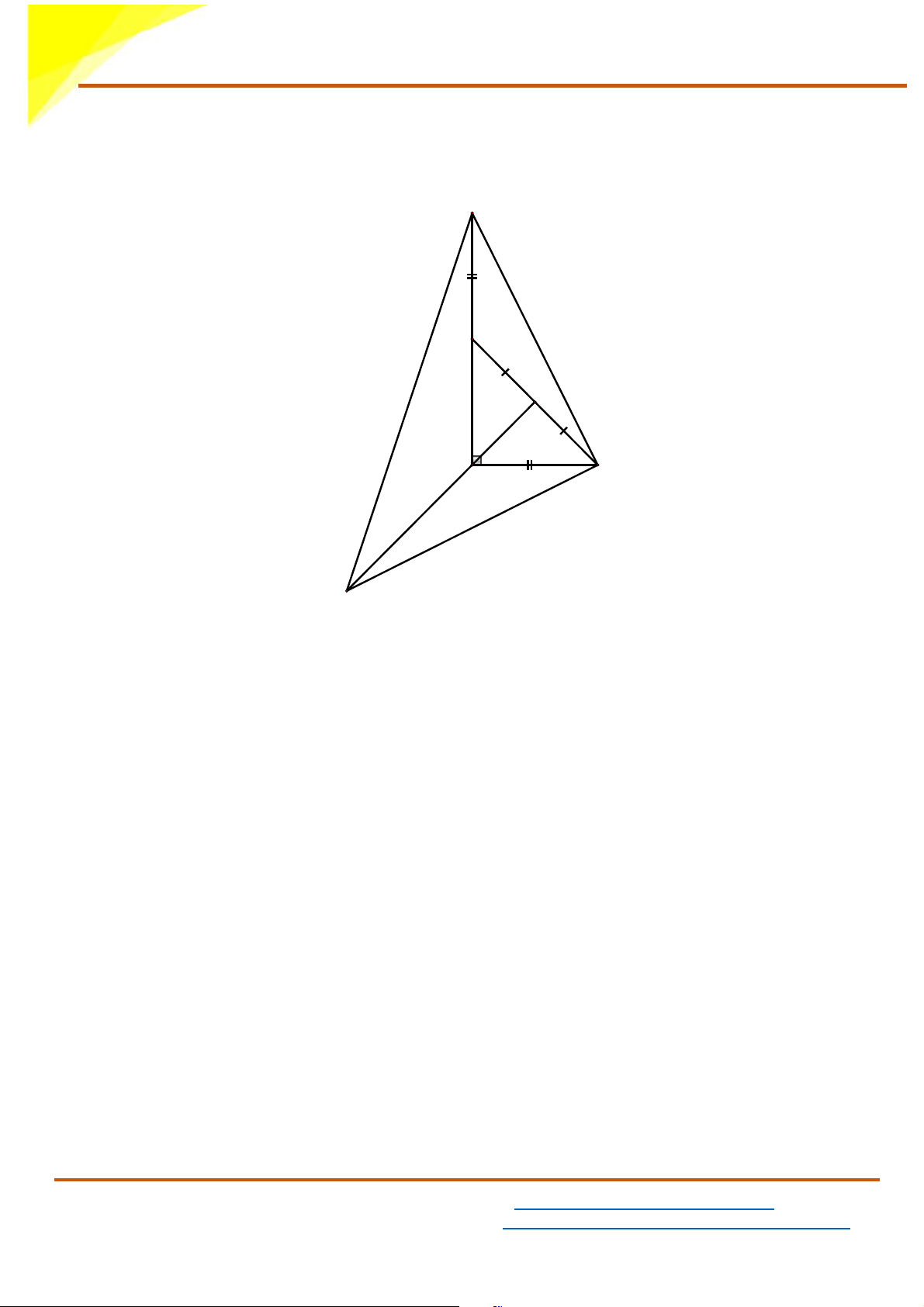
c) Trên tia đối của tia AH lấy điểm E sao cho AE = BC , trên tia đối
của tia CA lấy điểm F sao cho CF = AB . Chứng minh BE = BF F C H A B E Xét A
∆ BC vuông tại A có: 0 ABC + ACB = 90
Mà ABC = ACB (vì ∆AHB = ∆AHC(c.c.c)) 0
⇒ ABC = ACB = 45 Ta có: 0
FCB + ACB = 180 (vì FCB là góc ngoài tại C của A ∆ BC ) 0 0 0 0 0
FCB + 45 = 180 ⇒ FCB = 180 − 45 = 135 0 0 0
EAB = 90 + 45 = 135 (vì EAB là góc ngoài tại A của ∆ABH )
Xét ∆ABE và ∆CFB có:
AB = CF(gt) 0 FCB = EAB = 135
AE = BC(gt)
Do đó: ∆ABE = C
∆ FB(c.g.c)
⇒ BE = BF (Hai cạnh tương ứng)
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 12/ 13
Thầy Phúc Toán – GV dạy Toán Online
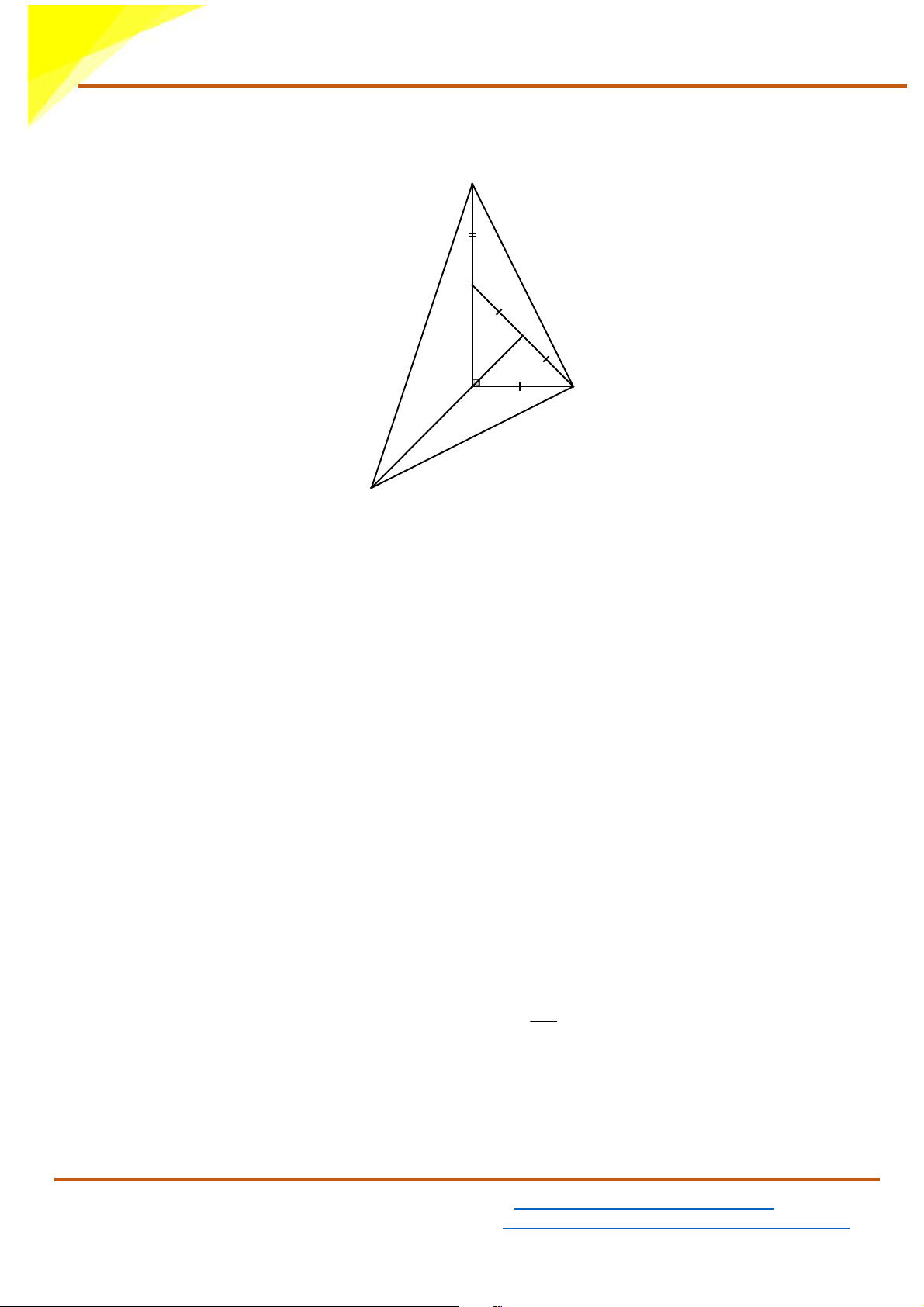
d) Tính số đo góc EBF F C H A B E Xét ∆EAB có: 0
EAB + AEB + ABE = 180 0 0
135 + AEB + ABE = 180 0 0 0
AEB + ABE = 180 − 135 = 45 (1)
Tương tự, xét ∆FCB có: 0
FCB +CFB +CBF = 180 0 0
135 +CFB +CBF = 180 0 0 0
CFB +CBF = 180 − 135 = 45 (2) Từ (1) và (2) suy ra: 0 0 0
AEB + ABE +CFB +CBF = 45 + 45 = 90
Mà CFB = ABE ; CBF = AEB (vì ∆ABE = C
∆ FB(c.g.c)) 0
⇒ 2.ABE + 2.CBF = 90 90 0 0
⇒ 2.(ABE +CBF) = 90 ⇒ ABE +CBF = = 45 2 0 0 0
EBF = ABC + ABE +CBF = 45 + 45 = 90 Vậy 0 EBF = 90
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 13/ 13
Thầy Phúc Toán – GV dạy Toán Online
Bài 5. (0,5 điểm) Cho a, ,
b c là 3 số thực dương thỏa mãn:
a + b − c
b + c −a
c + a −b = = c a b    
Tính giá trị của biểu thức b a c M = 1 + 1 + 1 +      a  c  b  Lời giải
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a + b − c
b + c −a
c + a − b
a + b −c + b + c − a + c + a − b a + b + c = = = = = 1 c a b a + b + c a + b + c
a + b − c = 1⇒a +b −c =c ⇒a +b = 2c c
b + c − a = 1 ⇒b +c −a =a ⇒b +c = 2a a
c + a −b = 1⇒c +a −b =b ⇒c +a = 2b bb  a  c M = 1 + 1 + 1 +      a  c  b
a +b  c +a  b +c M =    
a  c  b  2c 2b 2a M = ⋅ ⋅ a c b 8abc M = = 8 abc
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017