
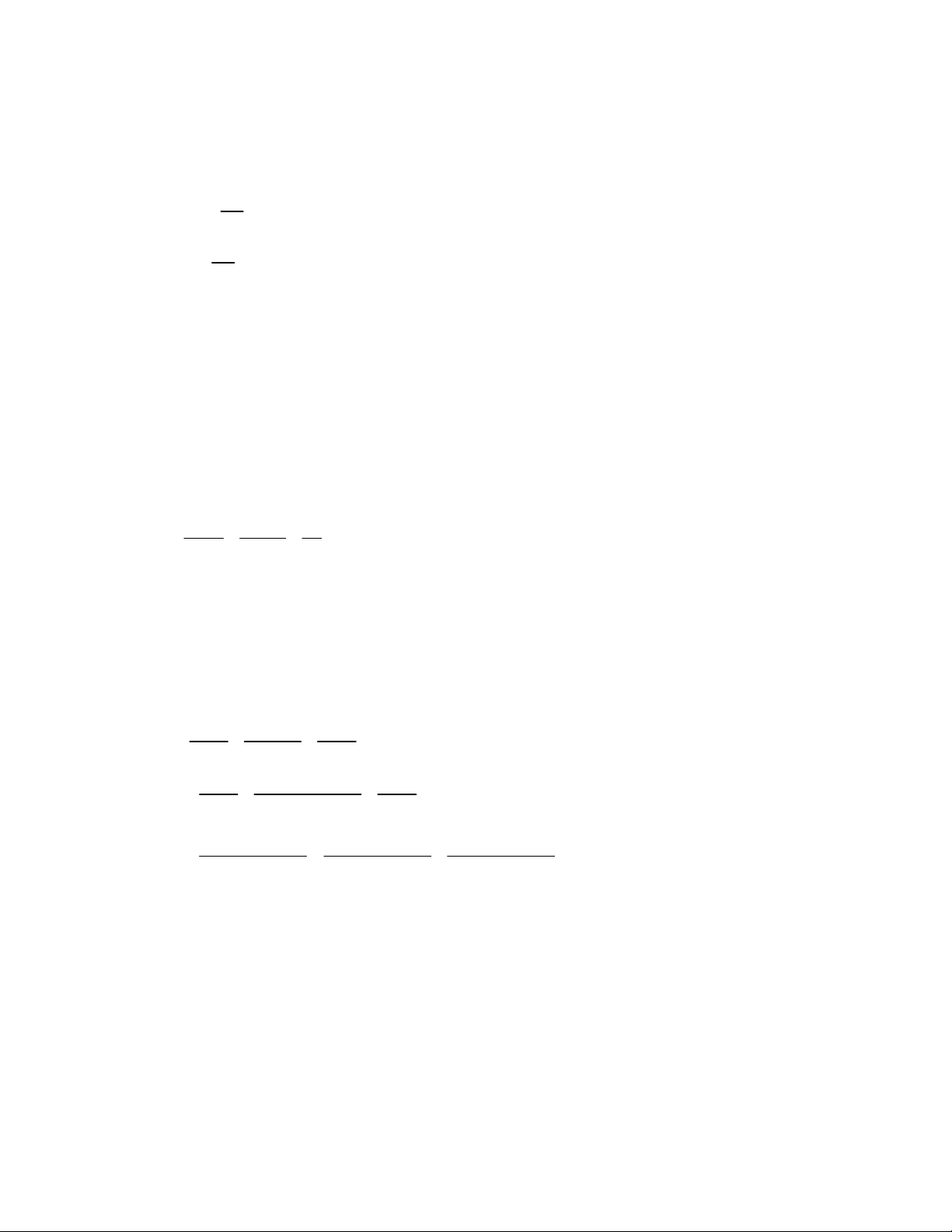



Preview text:
UỶ BAN NHÂN DÂN QUẬN 12
TRƯỜNG THCS NGUYỄN HIỀN
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2019-2020 Môn : Toán 8 Thời gian : 90 phút
(Không kể thời gian phát đề)
Câu 1 (3 điểm) : Giải phương trình : a) x 1 x
1 5x x x 3 8
b) 2x x 5 4x 20 0 x 7 2x 1 x c) 3 5 15 d) x 1 15 x 2 2 x 5 x 25 x 5
Câu 2 (1 điểm) : Giải các bất phương trình sau : a) x 2
2 5x x x 7 10 b) 2x 1 x 5 x 1 5 4 20
Câu 3 (1,5 điểm) : Một ô tô đi từ A đến B với vận tốc 50 km/h. Cùng lúc đó, một xe khách cũng đi
từ A đến B với vận tốc 60 km/h nhưng theo một con đường khác ngắn hơn 5km. Do đó xe khách đã
đến B trước ô tô 30 phút. Tính quãng đường AB mà ô tô đã đi.
Câu 4 (1 điểm) : Sau Tết An có 1 500 000 đồng tiền lì xì. Mỗi ngày An để dành được 25 000 đồng.
An muốn mua một chiếc xe đạp giá 3 280 000 đồng. Hỏi An phải để dành ít nhất bao nhiêu ngày ?
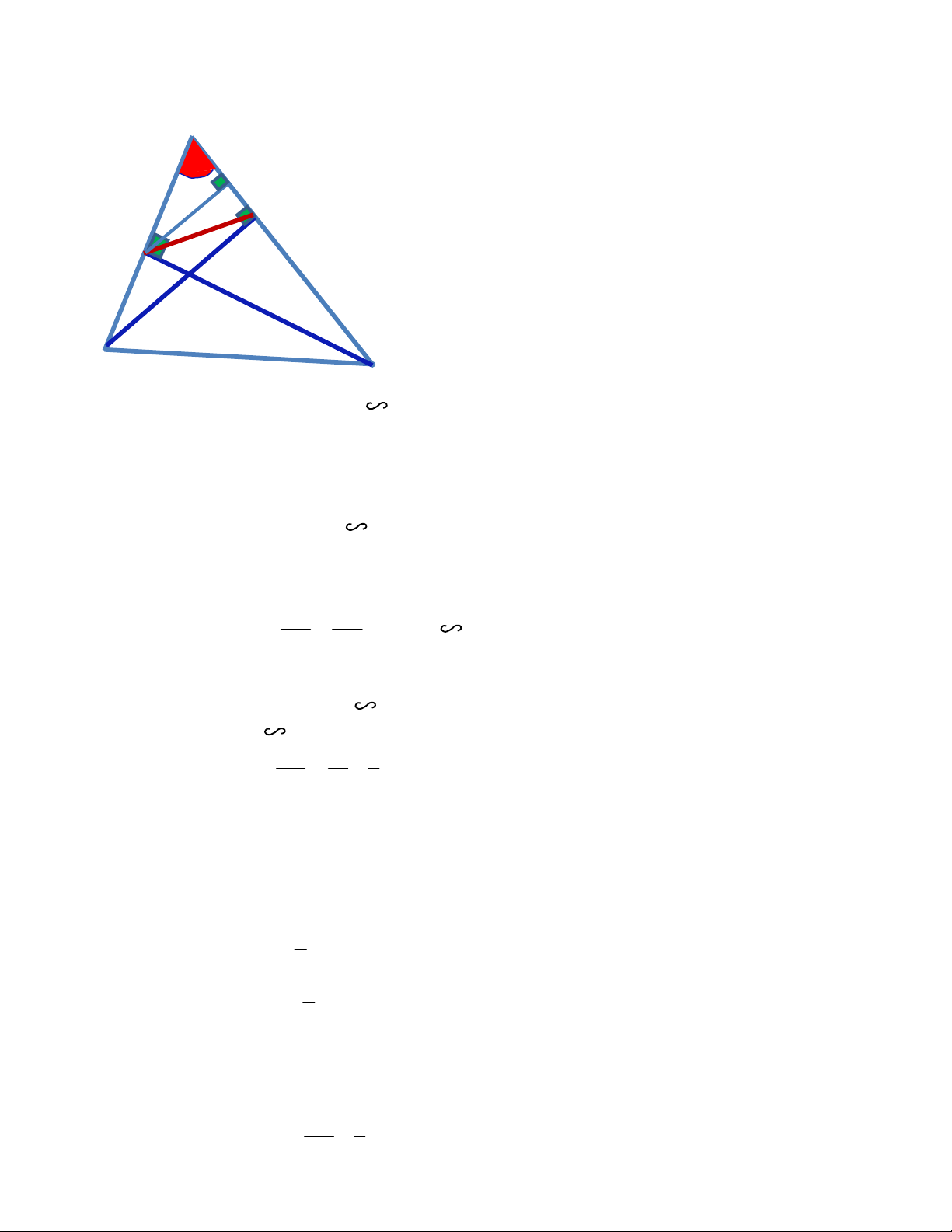
Câu 5 (0,5 điểm) : Một cột đèn cao 10m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột
đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét). D B 10m 2m 4,8m C M A
Câu 6 (3 điểm) : Cho ABC nhọn (ABa) Chứng minh : ABE ACF b) Chứng minh : ˆ ˆ AEF ABC
c) Cho AB = 12cm, AE = 4cm, SABC = 108cm2. Kẻ FD AE. Tính SAEF và FD. Hết ĐÁP ÁN VÀ BIỂU ĐIỂM Câu 1 : a) x 1 x
1 5x x x 3 8 2 2
x 1 5x x 3x 8 0,25 2x 9 0,25 9 x 0,25 2 9 S 2 b)
2x x 5 4x 20 0
2x x 54x 5 0 0,25
x 52x 4 0 0,25
x 50 hoac 2x 40 x 5 hoac x 2 0,25 S 2; 5 c) x 7 2x 1 x 3 5 15
5 x 7 32x 1 x 0,25
5x 35 6x 3 x 0 0,25 2x 38 x 19 0,25 S 1 9 d) x 1 15 x 2 x 5,x 5 2 ĐK: x 5 x 25 x 5 x 1 15 x 2
x 5 x 5 x 5 x 5 x 1x 5 15 x 2 x 5 0,25
x 5x 5 x 5x 5 x 5x 5 x
1 x 515 x 2x 5 2
x 5x x 5 15 x 2x 10 2 x 5x 0 0,25 xx 5 0 x 0 hoac x 50 x 0 hoac x 5 (nhận) (loại) 0,25 S 0
Câu 2 (1 điểm) : a) x 22 5x x x 7 10 2 2 0,25
x 4x 4 5x x 7x 10 6x 6 x 1 0,25 S x / x 1 b) 2 x 1 x 5 x 1 5 4 20
4 2 x 1 5 x 5 x 20 0,25
8x 4 5x 25 x 20 2 x 1 1 x 2 0,25 1 S x / x 2 Câu 3 (1,5 điểm) :
Gọi x là quãng đường ô tô đã đi (km) (x>0)
Quãng đường xe khách đã đi là : x–5 0,25 x
Thời gian ô tô đi từ A đến B : 0,25 50 x5
Thời gian xe khách đi từ A đến B : 0,25 60 Theo đề bài, ta có pt : x x 5 1 50 60 2 0,25
6x 5 x 5 150 0,25 x 1 25 (nhận)
Vậy : quãng đường ô tô đã đi là 125 km. 0,25
Câu 4 (1 điểm) : Gọi x là số ngày An để dành tiền (ngày) x N * Theo đề bài, ta có : 25000x 1500000 3280000 0,5 25000x1780000 x 71,2 0,25
Vậy : An phải để dành ít nhất là 72 ngày 0,25 Câu 5 (0,5 điểm): MC = MA+AC = 4,8+2 = 6,8 (m)
Xét DCM có AB // CD nên : AB MA
(Hệ quả của định lýTa-let ) 0,25 CD MC AB 4 8 , 10 6 8 , 0,25 AB 7 ( m ) Câu 6 (3 điểm) A D E F B C
a) Chứng minh : ABE ACF : Xét ABE và ACF có 0 ˆ ˆ
AE B AF C 90 ( gt ) 0,25 ˆ 0,25 Achung ABE ACF (g.g) 0,5 b) Chứng minh : ˆ ˆ AEF ABC Xét AEF và ABC có AE AB 0,5 (ABE ACF) AF AC ˆ Achun g 0,2 5 0,25 AEF ABC (c.g.c) c) AEF ABC (cmt) AE 4 1 0,25 k AB 12 3 2 S S 1 AEF 2 AEF k S 108 3 ABC 2 S 12 cm 0,25 AEF Tính FD : 1 S CF.AB ABC 2 1 108 .CF 1 . 2 2 CF 18 cm 0,25 FD Ta co' : k CF FD 1 18 3 0,25 FD 6 ( cm ) UBND QUẬN 12
TRƯỜNG THCS NGUYỄN HIỀN
ĐỀ KIỂM TRA HỌC KÌ II MÔN: TOÁN 8
THỜI GIAN LÀM BÀI: 90 PHÚT
( Không kể thời gian phát đề)
Bài 1: (3 điểm) Giải các phương trình sau:
Bài 2: (1điểm) Giải các bất phương trình : a/
Bài 3: (1,5 điểm) Giải bài toán bằng cách lập phương trình.
Một xe ô tô chạy trên quãng đường từ TPHCM đi Phan Thiết. Lúc đi, xe chạy với vận tốc 90 km/h.
Lúc về, xe chạy với vận tốc 60 km/h, do đó thời gian về nhiều hơn thời gian đi là 2 giờ. Tính quãng
đường TPHCM – Phan Thiết.
Bài 4: (1 điểm) Ba bạn Lan mới mua một miếng đất hình vuông có diện tích là 2500 m2. Ông muốn
làm hàng rào xung quanh miếng đất bằng dây kẽm gai hết tất cả 3 000 000 đồng (cả chi phí dây kẽm
và công làm của thợ). Hỏi Ba bạn Lan phải trả bao nhiêu tiền công cho thợ rào hết hàng rào? Biết
rằng giá mỗi mét dây kẽm là 12 000 đồng.
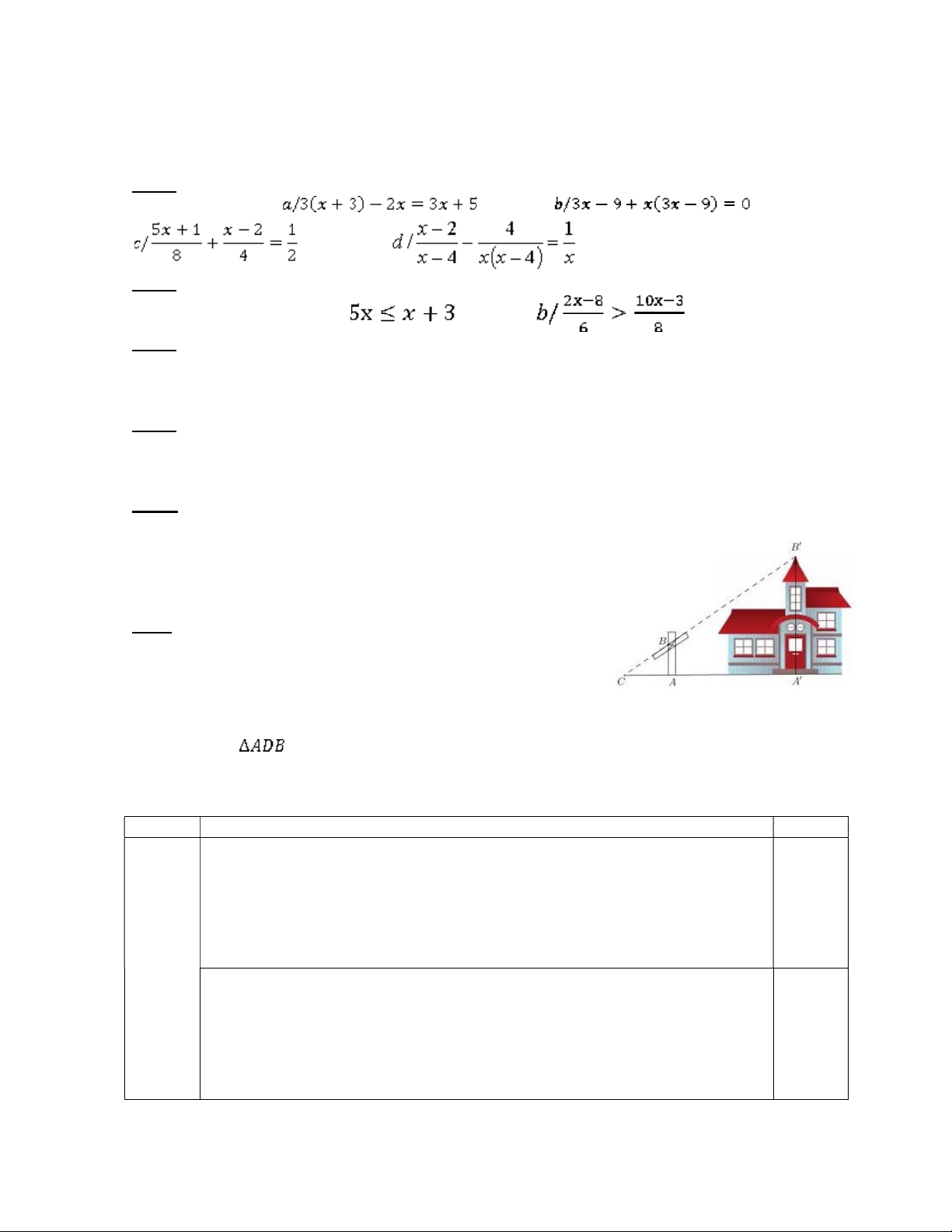
Bài 5: (0,5 điểm) Để gián tiếp đo chiều cao của một ngôi nhà người ta dùng dụng cụ đo như hình vẽ
bên dưới và đo các khoảng cách dưới mặt đất. Biết cột AB cao 1,5m; AC = 2m; AA’ = 14m. Tính chiều cao A’B’ của căn nhà.
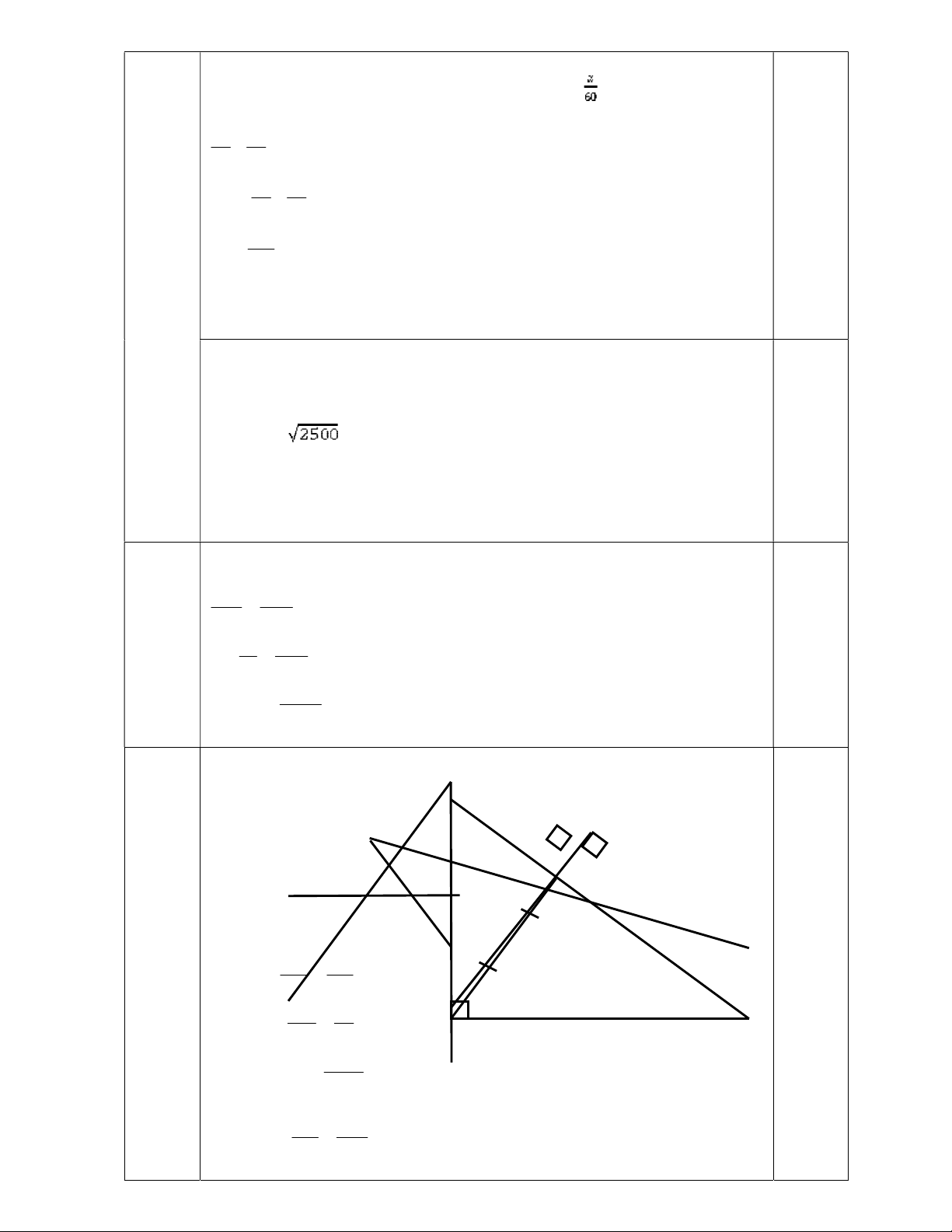
Bài 6: (3 điểm) Cho tam giác ABC vuông tại A (AB < AC) , AB
= 15 cm, BC = 25 cm, và có đường cao AH.
a/ Chứng minh BHA và BAC đồng dạng. Tính độ dài BH.
b/ Trên tia đối của tia AB lấy điểm E sao cho AE nhỏ hơn AB. Từ
E kẻ EM vuông góc BC. Chứng minh BE.BA=BM.BC
c) Gọi N là trung điểm của AH. Qua B kẻ đường thẳng vuông góc với BC lần lượt cắt CN, CA tại D, P. chứng minh cân. HẾT ĐÁP ÁN BÀI NỘI DUNG ĐIỂM Bài 1 a /
3 x 3 2x 3x 5 0,25
3x 9 2x 3x 5 0,25
3x 2x 3x 5 9 Vậy S = { 2 } 0,25 2x 4 x 2
b / 3x 9 x3x 9 0 0,25
3x 91 x 0 0,25 3x 9 0ha 1
y x 0 Vậy S = { 3 ; -1 } 0,25 3x 9hayx 1 x 3hayx 1 5x 1 x 2 1 c / 8 4 2 0,25 5x 1 2x 2 4 8 8 8 0,25 5x 1 2x 2 4 8 8 Vậy S = { 1 } 0,25 5x 1 2x 4 4 0,25 7x 3 4 7x 4 3 7x 7 x 1 x 2 4 1 d / x 4 xx 4 x xx 2 4 x 4
xx 4 xx 4 xx 4 xx 2 4 x 4 0,25 xx 4 xx 4
xx 2 4 x 4 ĐK: 0,25 2 x 2x 4 x 4 2
x 2x 4 x 4 0 2 x 3x 0 xx 3 0 x 0hayx 3 0 x 0(loai)hayx ( 3 nhân) Bài 2 a / 5x x 3 5x x 3 0,25 4x 3 0,25 3 x 4 Vậy S = { x } 0,25 0,25 Vậy S = { x } Bài 3
Gọi x(km) là quaõng ñöôøng TPHCM – Phan Thieát (x>0)
Vận tốc của ô tô lúc đi từ TPHCM – Phan Thieát là: 90 km/h.
Thời gian của ô tô lúc đi từ TPHCM – Phan Thieát là: h 0,25
Vận tốc của ô tô lúc về từ Phan Thieát- TPHCM là: 60 km/h.
Thời gian của ô tô lúc về từ Phan Thieát -TPHCM là: h 0,25 Vì th
ời gianveà nhieàu hôn thôøi gian ñi laø 2 giôø ta có phương trình: x x 2 0,25 60 90 1 1 x 2 60 90 0,5 Bài 4 1 . x 2 0,25 180 x 36 ( 0 nhâ ) n
Vậy quaõng ñöôøng TPHCM – Phan Thieát dài 360km.
Ta có miếng đất hình vuông có diện tích là 2500 m2
Gọi a(m) là độ dài cạnh miếng đất (a>0) 0,25 Ta có: a .a = 2500 a2 = 2500 a = a = 50 (m) 0,25
Chu vi miếng đất: a. 4 = 50 . 4 = 200 (m) 0,25
Số tiền mua kẽm là: 200 . 12 000 = 2 400 000 (đ)
Tiền công phải trả cho thợ là: 3 000 000 – 2 400 000 = 600 000 đồng 0,25 Bài 5
Xét tam giác A’CB’ có AB // A’B’
Theo hệ quả của đinh lí Talet ta có 0,25 CA AB CA' ' ' A B 0,25 2 5 , 1 hay 16 ' ' A B ' ' 16 5 , 1 . A B 12 2
Vậy chiều cao của căn nhà là 12m Bài 6 B H D M A P a) Chứng m inh BHA ~ BAC.(g.g) 0,5 BH AB N AB BC BH 15 hay 0,5 15 25 C 15 1 . 5 BH c 9 m 0,5 25 0,5
b) Chứng minh BAC ~ BME (g.g) 0,25 BE BM ⇒ ⇒ BE.BA=BM.BC BC BA 0,5 c) Chứng minh AH // BP,
sau đó sử dụng hệ quả của định lí Talet vào hai tam giác CBD và CPD suy ra: 0,25 mà N là trung điểm AH
nên suy ra D là trung điểm PB. Từ đó suy ra cân.




