





Preview text:
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC ƠNG I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC CHƯ
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC ĐỀ TEST SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
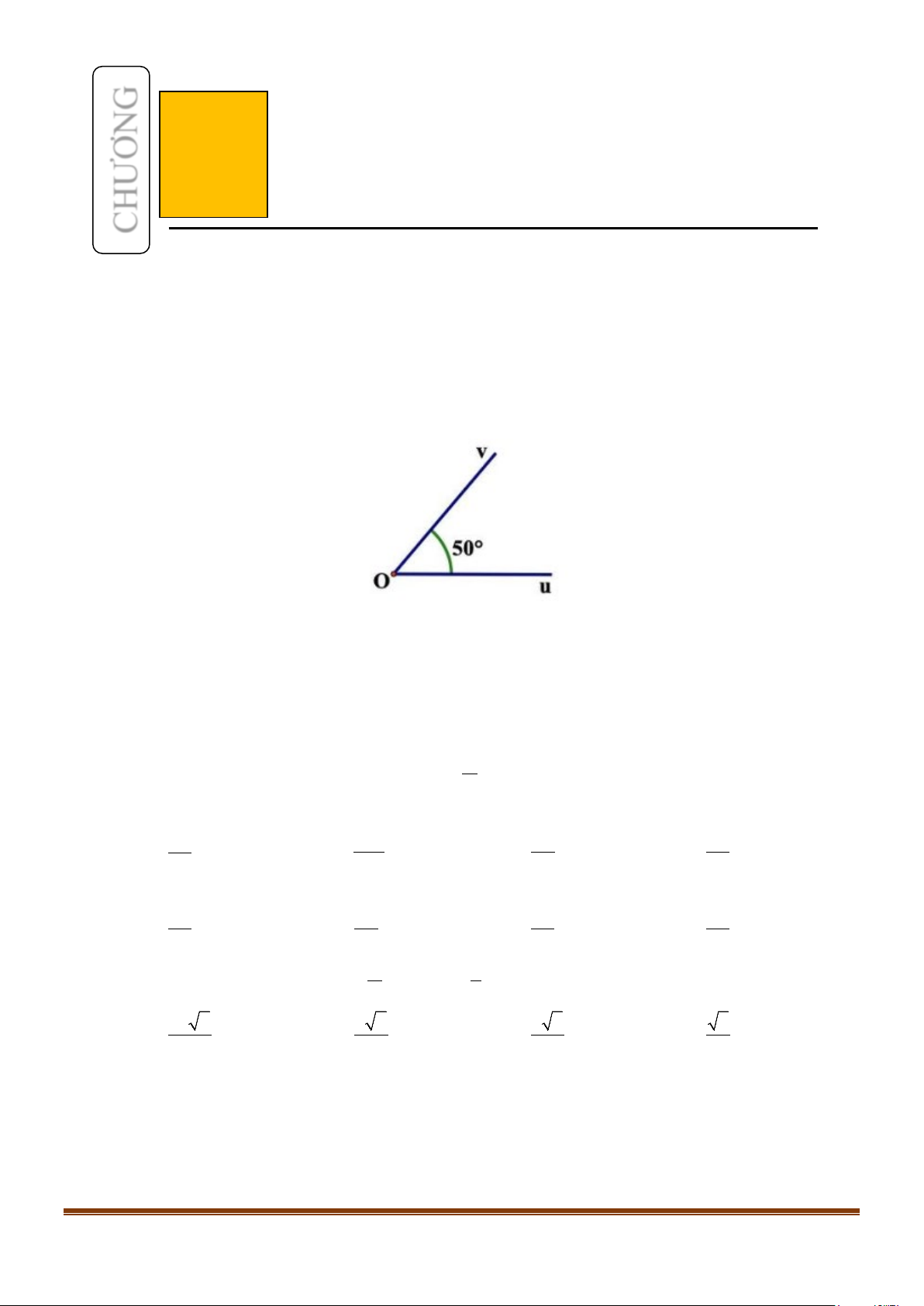
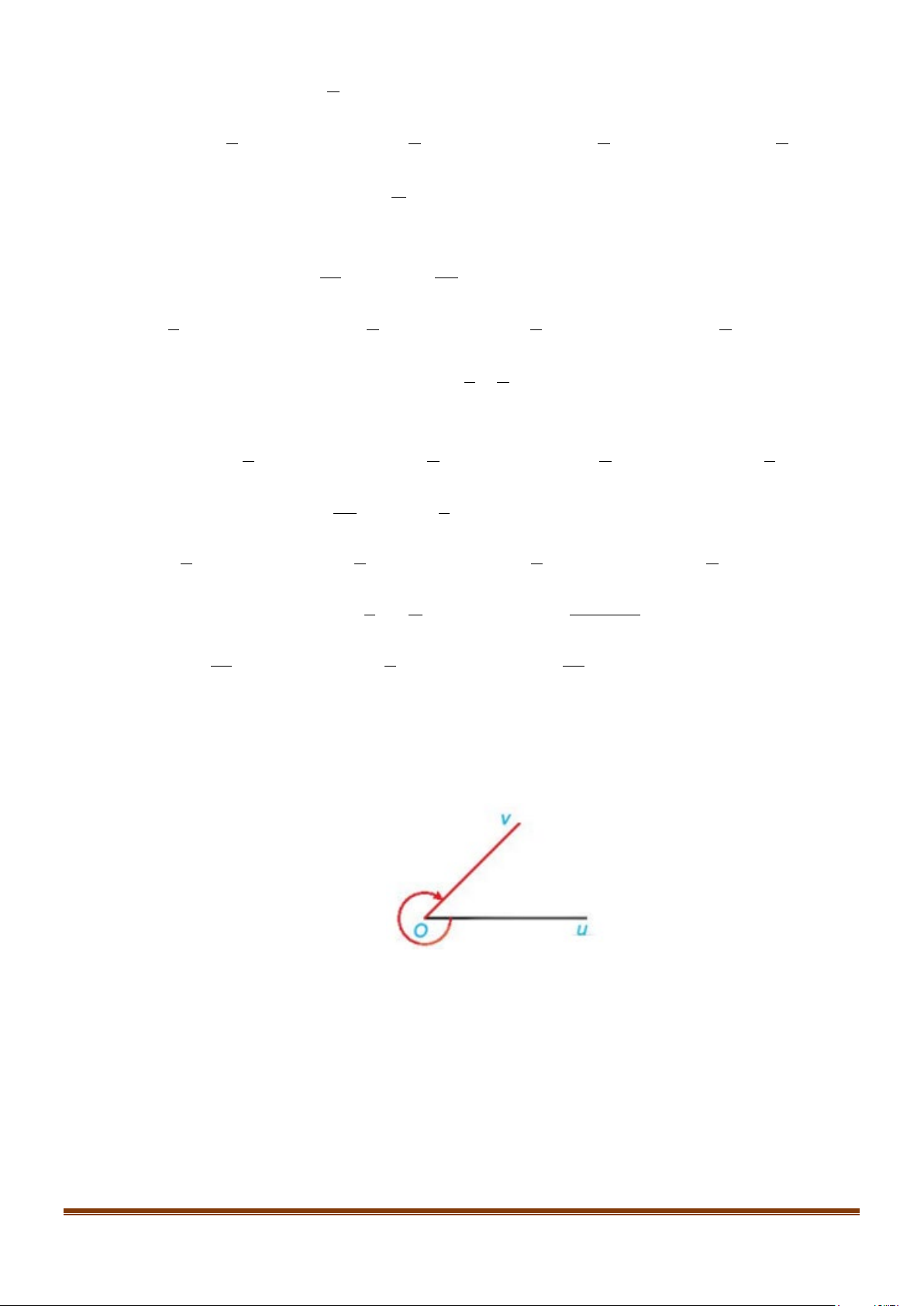
Câu 1: Cho góc hình học uOv có số đo 50° (hình vẽ). Xác định số đo của các góc lượng giác (Ou;Ov) .
A. sđ (Ou;Ov) = 50° + k360 ,°k ∈ .
B. sđ (Ou;Ov) = 50° + 180 k ,°k ∈ .
C. sđ (Ou;Ov) = 50
− ° + k360 ,°k ∈ .
D. sđ (Ou;Ov) = 50 − ° + 180 k ,°k ∈ .
Câu 2: Bánh xe của người đi xe đạp quay được 2 vòng trong 6 giây. Hỏi trong 1 giây, bánh xe quay được bao nhiêu độ: A. 60 . ° B. 72 . ° C. 240 . ° D. 120 . ° π
Câu 3: Cho góc lượng giác (Ou,Ov) có số đo là .Số đo của góc lượng giác nào sau đây có cùng tia 4
đầu là Ou và tia cuối là Ov? π π π A. 3π . B. 17 . C. 7 . D. 5 . 4 4 4 4
Câu 4: Đổi số đo góc 105° sang rađian, ta được A. 5π π π π rad.
B. 7 rad.
C. 9 rad.
D. 5 rad. 12 12 12 8 π
Câu 5: Cho góc α thỏa mãn 0 < α < và 1 cosα = . Tính sinα. 2 3 A. 2 − 2 . B. 2 2 . C. − 2 . D. 2 . 3 3 3 3
Câu 6: Bánh xe của người đi xe đạp quay được 13 vòng trong 4 giây. Tính độ dài quãng đường mà
người đi xe đạp đã đi được trong 2 phút, biết rằng đường kính của bánh xe đạp là 580mm , lấy π ≈ 3,14 .
A. 710,6283 (km).
B. 1421,2565 (m).
C. 710,6283 (m) .
D. 1421,2565(km). Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 7: Trên đường tròn lượng giác, số đo của các góc lượng
giác có tia đầu OA , tia cuối OB là π π
A. + kπ,k ∈ .
B. + k2π ,k ∈ . 2 4 π π
C. − + k2π ,k ∈ .
D. + 2kπ,k ∈ 2 2 Câu 8: Cho 4 π
sinα = và < α < π . Tính cosα . 5 2 3 1 3 A. . B. . C. 1 − . 5 5 − . D. 5 5
Câu 9: Cho một góc lượng giác (Ox,Ou) có số đo là 120 −
° và một góc lượng giác (Ox,Ov) có số đo
230 .° Số đo của các góc lượng giác (Ou,Ov) là:
A. sđ (Ou,Ov) = 350° + k.360° (k ∈).
B. sđ (Ou,Ov) =110° + k.360° (k ∈).
C. sđ (Ou,Ov) = 350 −
° + k.360° (k ∈).
D. sđ (Ou,Ov) = 110 −
° + k.360° (k ∈).
Câu 10: Trên đường tròn bán kính r =15 , độ dài của cung có số đo α = 50° là
A. l = 750. B. 180 π π l =15. . C. 15 l = . D. 25 l = . π 180 6 π Câu 11: Cho 2 cosα = và 3 α ;2π ∈ . Tính cotα . 3 2 A. 2 5 . B. 2 5 − . C. 5 . D. 5 − . 5 5 3 3 Câu 12: Cho 3 π
cosα = và 3 < α < 2π . Khi đó sinα bằng 7 2 4 4 2 10 A. . B. − . C. − . 7 7 7 . D. 2 10 7
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
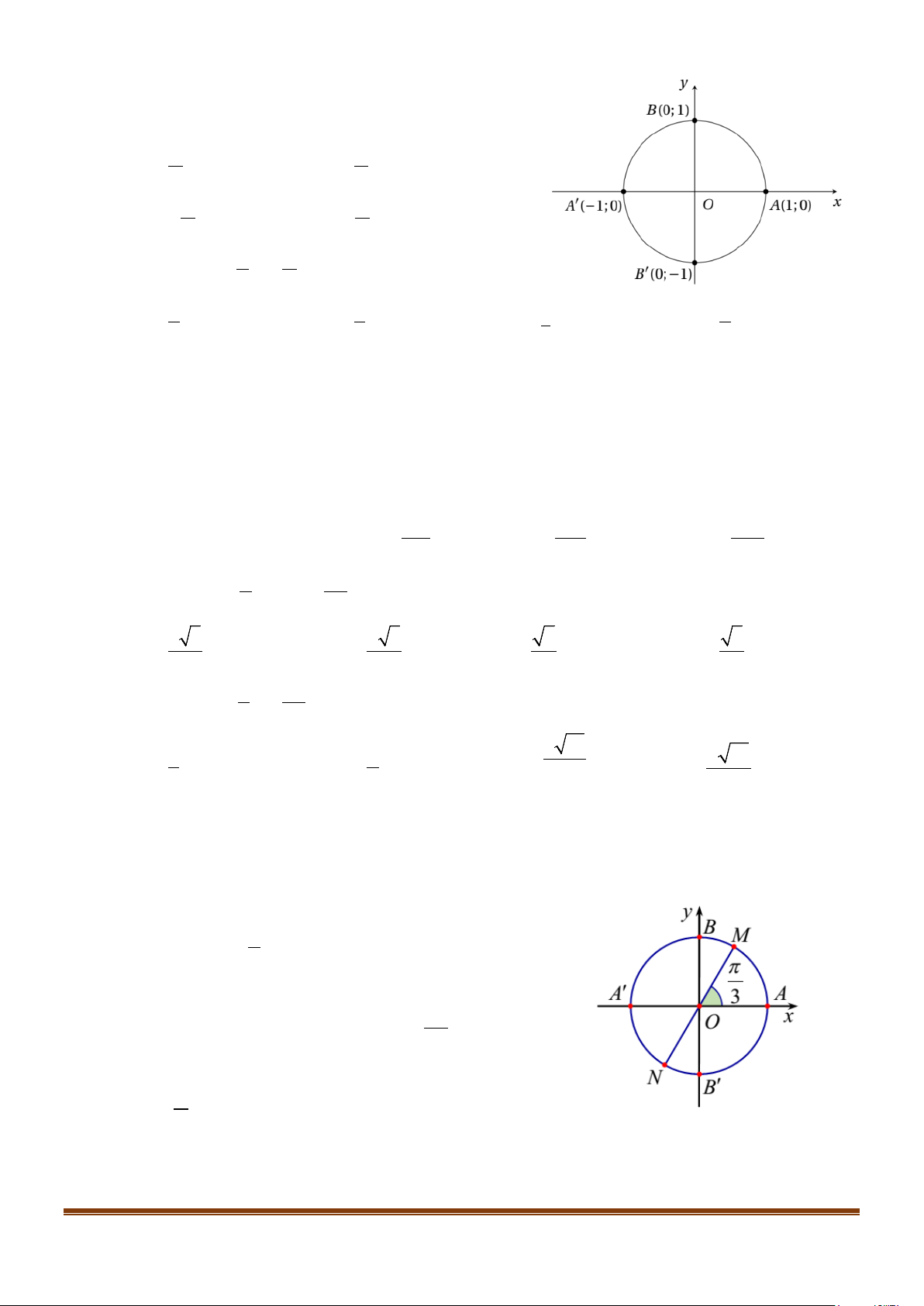
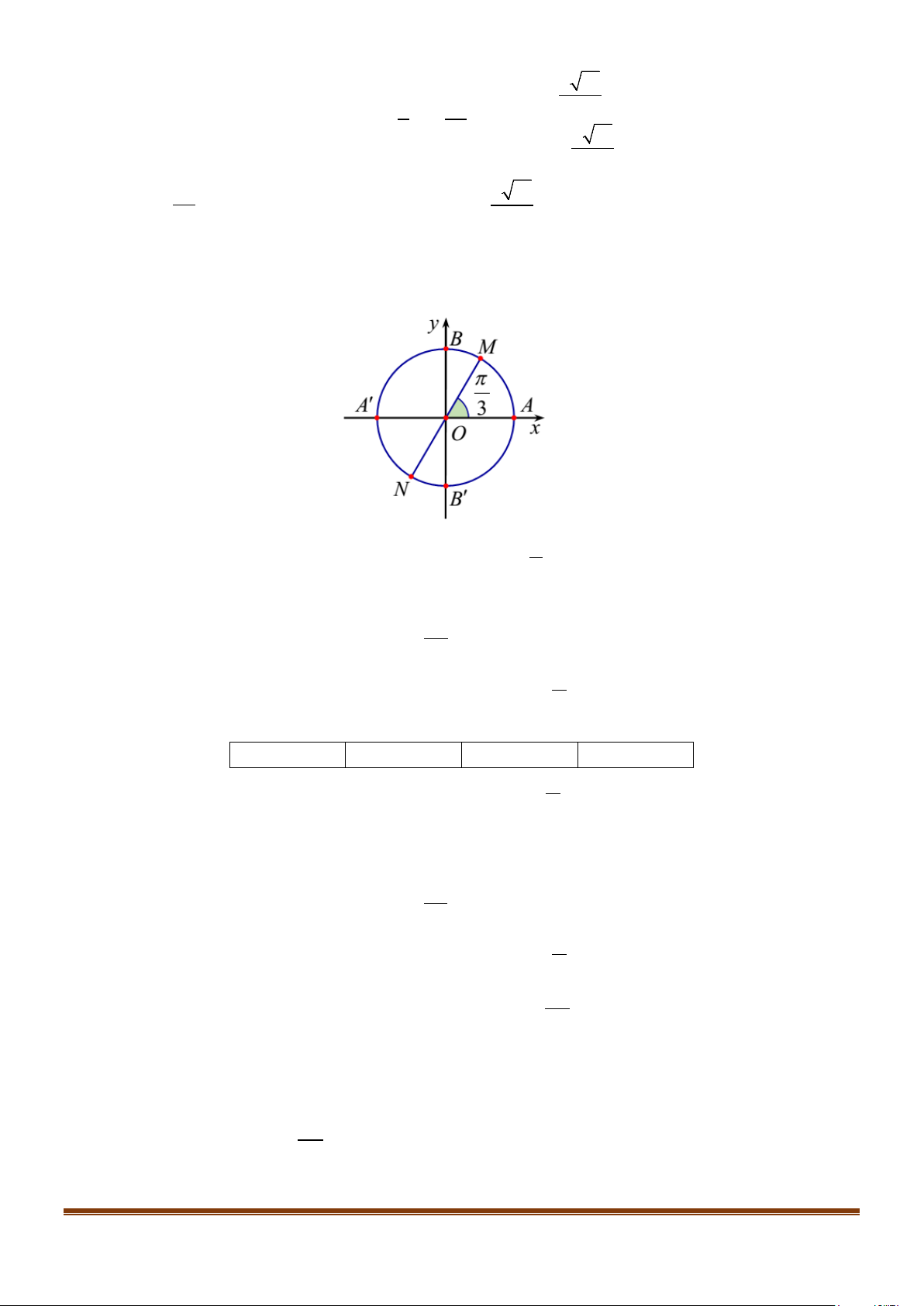
Câu 1: Cho hình vẽ sau:
a) Số đo góc lượng giác (OM , ) OA là π
sđ(OM,OA)= +k2π (k ∈) . 3
b)sđ(ON,OA) = sđ(ON,OM) - sđ(OA,OM) . π
c) Độ dài cung tròn AM lớn là: 2 l = . AM 3
d) Hai điểm M , N biểu diễn các cung có số đo là: π
x = + kπ (k ∈) . 3 Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 3π
Câu 2: Cho góc lượng giác α có số đo theo đơn vị rađian là . 4
a) Góc lượng giác α có số đo theo đơn vị độ là 155° .
b) Điểm biểu diễn góc lượng giác α là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I. 5π c) Góc lượng giác −
có cùng điểm biểu diễn trên đường tròn lượng giác với góc α . 4
d) Góc lượng giác 855° có cùng điểm biểu diễn trên đường tròn lượng giác với góc α .
Câu 3: Cho góc α thỏa mãn 3 π
cosα = và − < α < 0 . 5 2 a) sinα > 0. b) tanα < 0 . c) 4 sinα = − . 5 d) π α − − ( α − ) 7 sin sin = . 2 5
Câu 4: Cho góc α (0° < α <180°) thỏa mãn tanα = 3. a) 1 cotα = . 3 b) cosα > 0 . c) 3 10 sinα = . 10 α − α − d) 2sin 3cos 3 P = = . 3sinα + 2cosα 11
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1: Cho 1
cos x = . Tính giá trị biểu thức 2 2
P = 3sin x + 4cos x . (kết quả làm tròn đến hàng phần 3 mười) Câu 2: Cho tanα α α
2 , Giá trị biểu thức 4sin 5cos P là 2sinα 3cosα Câu 3: Cho biết 1
cot x = . Tính giá trị của biểu thức 2 A = . 2 2 2
sin x − sin .xcos x − cos x
Câu 4: Bánh xe đạp của người đi xe đạp quay được 2 vòng trong 5 giây. Hỏi trong 2 giây, bánh xe
quay được 1 góc bao nhiêu rad (kết quả làm tròn đến hàng phần mười)?
Câu 5: Một bánh xe đạp quay được 25 vòng trong 10 giây.
Tính độ dài quãng đường mà người đi xe thực hiện được trong 2,35 phút, biết rằng bán kính bánh
xe bằng 340 mm . (Tính theo đơn vị mét, kết quả được làm tròn đến hàng đơn vị). Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 6: Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m so với mặt đất, thời gian
thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất
của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét so với mặt đất?
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Cho góc hình học uOv có số đo 50° (hình vẽ). Xác định số đo của các góc lượng giác (Ou;Ov) .
A. sđ (Ou;Ov) = 50° + k360 ,°k ∈ .
B. sđ (Ou;Ov) = 50° + 180 k ,°k ∈ .
C. sđ (Ou;Ov) = 50
− ° + k360 ,°k ∈ .
D. sđ (Ou;Ov) = 50 − ° + 180 k ,°k ∈ . Lời giải
Câu 2: Bánh xe của người đi xe đạp quay được 2 vòng trong 6 giây. Hỏi trong 1 giây, bánh xe quay được bao nhiêu độ: A. 60 . ° B. 72 . ° C. 240 . ° D. 120 . ° Lời giải
Trong 6s bánh xe quay được: 2.360° = 720°
⇒ Trong 1s bánh xe quay được: 720° : 6 = 120° π
Câu 3: Cho góc lượng giác (Ou,Ov) có số đo là .Số đo của góc lượng giác nào sau đây có cùng tia 4
đầu là Ou và tia cuối là Ov? π π π A. 3π . B. 17 . C. 7 . D. 5 . 4 4 4 4 Lời giải π π π
Ta có 17 = 4π + nên suy ra góc lượng giác có số đo 17 có cùng tia đầu là Ou và tia cuối 4 4 4 π là Ov với góc . 4
Câu 4: Đổi số đo góc 105° sang rađian, ta được A. 5π π π π rad.
B. 7 rad.
C. 9 rad.
D. 5 rad. 12 12 12 8 Lời giải Cách 1: Ta có: π π 10 105 7 5° = rad = rad. 180 12
Cách 2: Sử dụng MTCT π
Câu 5: Cho góc α thỏa mãn 0 < α < và 1 cosα = . Tính sinα. 2 3 Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC A. 2 − 2 . B. 2 2 . C. − 2 . D. 2 . 3 3 3 3 Lời giải 2 2 2 sinα = Ta có: 2 2 1 8 = − = − = ⇔ 3 sin α 1 cos α 1 . 3 9 2 − 2 sinα = 3 π Do 0 < α < nên chọn 2 2 sinα = . 2 3
Câu 6: Bánh xe của người đi xe đạp quay được 13 vòng trong 4 giây. Tính độ dài quãng đường mà
người đi xe đạp đã đi được trong 2 phút, biết rằng đường kính của bánh xe đạp là 580mm , lấy π ≈ 3,14 .
A. 710,6283 (km).
B. 1421,2565 (m).
C. 710,6283 (m) .
D. 1421,2565(km). Lời giải Đổi 2 phút= 120 giây
Mỗi giây xe đi được số vòng là 13 4
Trong 2 phút bánh xe quay được 13 120. = 390 vòng 4
Quãng đường mà người đi xe đạp đã đi được trong hai phút là
390.580.π = 710628,2582(mm) = 710,628m
Câu 7: Trên đường tròn lượng giác, số đo của các góc lượng giác có tia đầu OA, tia cuối OB là π π π π
A. + kπ,k ∈ .
B. + k2π ,k ∈ .
C. − + k2π ,k ∈ . D. + 2kπ,k ∈ 2 4 2 2 Lời giải π Ta có ( ,
OA OB) = + k2π,k ∈ . 2 Câu 8: Cho 4 π
sinα = và < α < π . Tính cosα . 5 2 3 1 3 A. . B. . C. 1 − . 5 5 − . D. 5 5 Lời giải Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC Ta có 2 2 2 2 16 9
sin α + cos α =1 ⇔ cos α =1− sin α =1− =
. Mặt khác vì π < α < π nên 25 25 2 cosα < 0 . Vậy 3 cosα = − . 5
Câu 9: Cho một góc lượng giác (Ox,Ou) có số đo là 120 −
° và một góc lượng giác (Ox,Ov) có số đo
230 .° Số đo của các góc lượng giác (Ou,Ov) là:
A. sđ (Ou,Ov) = 350° + k.360° (k ∈).
B. sđ (Ou,Ov) =110° + k.360° (k ∈).
C. sđ (Ou,Ov) = 350 −
° + k.360° (k ∈).
D. sđ (Ou,Ov) = 110 −
° + k.360° (k ∈). Lời giải
Với ba tia Ou ,Ov ,Ox bất kì, ta có:
sđ(Ou,Ov) = sđ(Ox,Ov) − sđ(Ox,Ou) + k.360° (k ∈) . = 230° − ( 120 −
°) + k.360° = 350° + k.360 ,° (k ∈).
Câu 10: Trên đường tròn bán kính r =15 , độ dài của cung có số đo α = 50° là
A. l = 750. B. 180 π π l =15. . C. 15 l = . D. 25 l = . π 180 6 Lời giải Ta có: 0 5π π 50 = 25 ⇒ l = α r = . 18 6 π Câu 11: Cho 2 cosα = và 3 α ;2π ∈ . Tính cotα . 3 2 A. 2 5 . B. 2 5 − . C. 5 . D. 5 − . 5 5 3 3 Lời giải 5 sinα = Vì 2 2 2 5 3
sin α + cos α =1 ⇔ sin α = ⇔ . 9 5 sinα = − 3 π Do 3 α ;2π ∈ nên 5 sinα < 0 ⇒ sinα = − . 2 3 Khi đó 2 5 cotα = − . 5 Câu 12: Cho 3 π
cosα = và 3 < α < 2π . Khi đó sinα bằng 7 2 4 4 2 10 A. . B. − . C. − . 7 7 7 . D. 2 10 7 Lời giải Áp dụng công thức: Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 2 10 2 sinα = 2 2 2 3 40 7
sin α =1− cos α ⇔ sin α =1− = ⇔ 7 49 2 10 sinα = − 7 3π Do
< α < 2π nên sinα < 0 . Vậy 2 10 sinα = − . 2 7
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
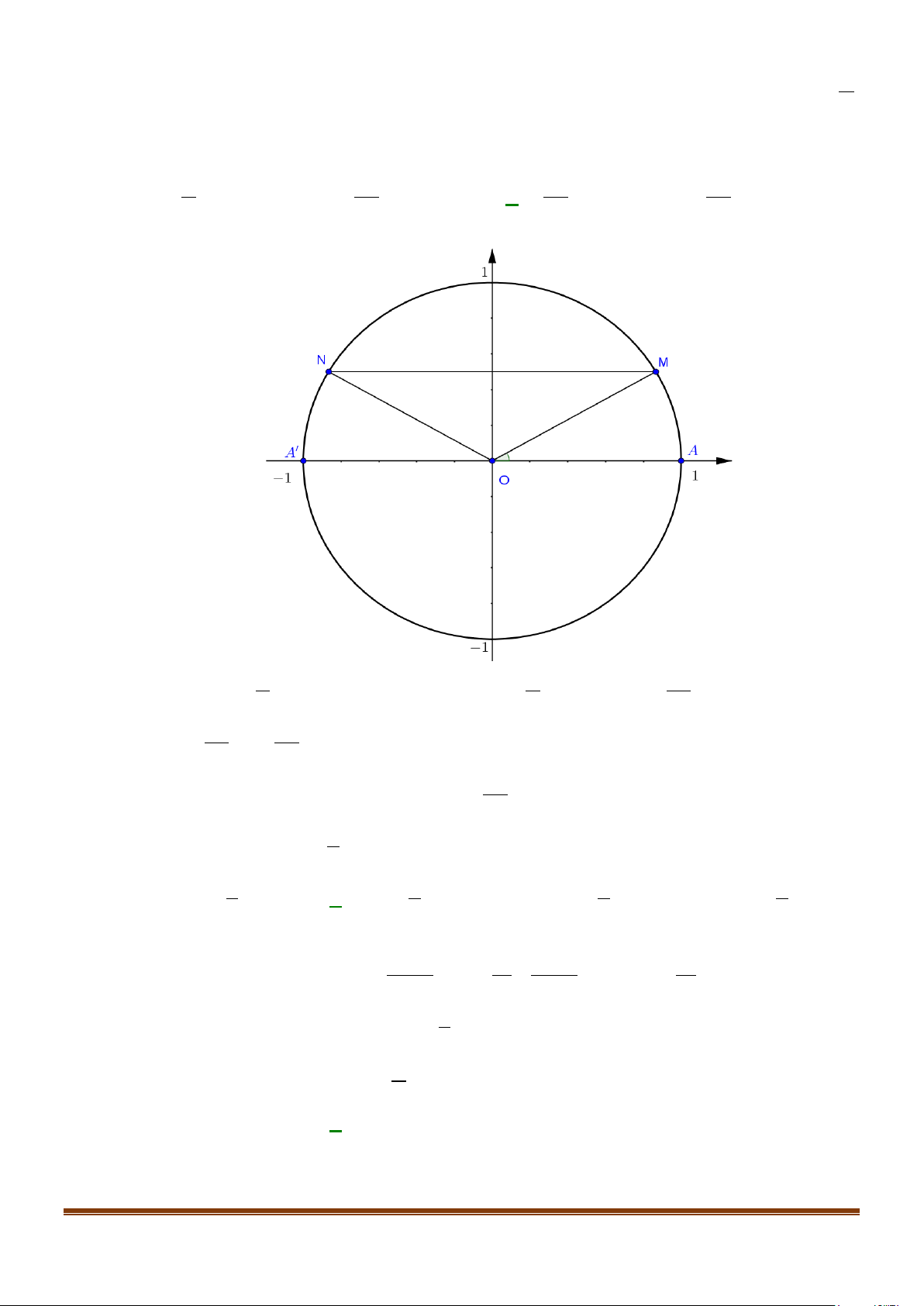
Câu 1: Cho hình vẽ sau:
a) Số đo góc lượng giác (OM , ) OA là π
sđ(OM,OA)= +k2π (k ∈) . 3
b)sđ(ON,OA) = sđ(ON,OM) - sđ(OA,OM) . π
c) Độ dài cung tròn AM lớn là: 2 l = . AM 3 π
d) Hai điểm M , N biểu diễn các cung có số đo là: x = + kπ (k ∈) . 3 Lời giải a) Sai b) Đúng c) Sai d) Đúng π
a) Số đo góc lượng giác (OM , ) OA làsđ(OM , )
OA = − + k2π (k ∈) nên mệnh đề sai. 3
b) Theo hệ thức Chales: sđ(ON, ) OA + sđ( ,
OA OM ) = sđ(ON,OM ) ⇒ sđ(ON, )
OA = sđ(ON,OM ) − sđ( ,
OA OM ) nên mệnh đề đúng.
c) Độ dài cung tròn AM lớn là: 5π l = nên mệnh đề sai. AM 3 π
d) Hai điểm M , N biểu diễn các cung có số đo là: x = + kπ (k ∈) nên mệnh đề đúng 3 3π
Câu 2: Cho góc lượng giác α có số đo theo đơn vị rađian là . 4
a) Góc lượng giác α có số đo theo đơn vị độ là 155° .
b) Điểm biểu diễn góc lượng giác α là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I. 5π c) Góc lượng giác −
có cùng điểm biểu diễn trên đường tròn lượng giác với góc α . 4
d) Góc lượng giác 855° có cùng điểm biểu diễn trên đường tròn lượng giác với góc α . Page 8
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC Lời giải a) Sai b) Sai c) Đúng d) Đúng 3π 3.180 ° a) rad = = 135° nên mệnh đề sai. 4 4
b) Điểm biểu diễn góc lượng giác α là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ II sao cho góc
AOM =135° nên mệnh đề sai. 5 − π 3π 5π c) Ta có = − 2π do đó −
cùng điểm biểu diễn trên đường tròn lượng giác với góc 4 4 4 α nên mệnh đề đúng.
d) Ta có 855° = 135° + 2.360° do đó 855° có cùng điểm biểu diễn trên đường tròn lượng
giác với góc α nên mệnh đề đúng.
Câu 3: Cho góc α thỏa mãn 3 π
cosα = và − < α < 0 . 5 2 a) sinα > 0. b) tanα < 0 . c) 4 sinα = − . 5 d) π α − − ( α − ) 7 sin sin = . 2 5 Lời giải a) Sai b) Đúng c) Đúng d) Sai π
a) Vì − < α < 0 nên sinα < 0 . Do đó sinα > 0 nên là sai. 2π
b) Vì − < α < 0 nên tanα < 0 . Do đó tanα < 0 là đúng. 2 π
c) Vì − < α < 0 nên 2 4
sinα = − 1− cos α = − . Do đó 4 sinα = − là đúng. 2 5 5 d) Vì π α π − − ( α − ) 1 sin sin = cosα + sinα = − . Do đó −α − ( α − ) 7 sin sin = là sai. 2 5 2 5
Câu 4: Cho góc α (0° < α <180°) thỏa mãn tanα = 3. a) 1 cotα = . 3 b) cosα > 0 . c) 3 10 sinα = . 10 α − α − d) 2sin 3cos 3 P = = . 3sinα + 2cosα 11 Lời giải a) Sai b) Đúng c) Đúng d) Sai a) 1
tanα.cotα =1⇒ cotα = nên mệnh đề sai. 3
b) 0° < α <180° ⇒ sinα > 0 , mà tanα > 0 ⇒ cosα > 0 nên mệnh đề đúng. Page 9
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
c) Ta có: 0° < α <180° ⇒ sinα > 0 . 2 1 1+ cot α = 2 sin α 1 1 10 ⇔ =1+ = 2 9 3 10 ⇔ sin α = ⇒ sinα = 2 sin α 9 9 10 10 Mệnh đề đúng.
d) Vì tanα = 3 nên cosα ≠ 0, chia cả tử và mẫu cho cosα ta được: 2sinα − 3cosα sin 2 α −3 cosα cosα 2tanα − 3 2.3− 3 3
P = 3sinα 2cosα = sinα = = = + . Mệnh đề sai. 3tanα + 2 3.3+ 2 11 3 + 2 cosα cosα
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1: Cho 1
cos x = . Tính giá trị biểu thức 2 2
P = 3sin x + 4cos x . (kết quả làm tròn đến hàng phần 3 mười) Lời giải Trả lời: 3,1 Khi đó: 2 2 P = x + x = ( 2 − x) 2 1 1 28 3sin 4cos 3 1 cos + 4cos x = 3 1− + 4. = ≈ 3,1. 9 9 9 Câu 2: Cho tanα α α
2 , Giá trị biểu thức 4sin 5cos P là 2sinα 3cosα Lời giải Trả lời: 13 4 tanα 5 4.25 P 13 2 tanα 3 2.23 Câu 3: Cho biết 1
cot x = . Tính giá trị của biểu thức 2 A = . 2 2 2
sin x − sin .xcos x − cos x Lời giải Trả lời: 10 2 1 + 2 2( 2 2 + 1 2 1 cot x) Ta có sin x 4 A = = = = = 10. 2 2 2 2
sin x − sin .xcos x − cos x 1− cot x − cot x 1− cot x − cot x 1 1 1− − 2 4
Câu 4: Bánh xe đạp của người đi xe đạp quay được 2 vòng trong 5 giây. Hỏi trong 2 giây, bánh xe
quay được 1 góc bao nhiêu rad (kết quả làm tròn đến hàng phần mười)? Lời giải Trả lời: 5,1
Trong 2 giây bánh xe đạp quay được 2.2 4
= vòng tức là quay được cung có độ dài là 5 5 4 8
l = .2π R = π R . 5 5 8 πR Ta có l 5 8
l = Rα ⇔ α = = = π ≈ 5,1. R R 5 Page 10
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 5: Một bánh xe đạp quay được 25 vòng trong 10 giây.
Tính độ dài quãng đường mà người đi xe thực hiện được trong 2,35 phút, biết rằng bán kính bánh
xe bằng 340 mm . (Tính theo đơn vị mét, kết quả được làm tròn đến hàng đơn vị). Lời giải Trả lời: 753
Sau 2,35 phút ( = 141 giây), số vòng mà bánh xe thực hiện được là: 141.25 = 352,5 vòng. 10
Bán kính bánh xe: R = 340 mm = 0,34 m .
Quãng đường mà người đi xe đạp thực hiện được sau 2,35 phút là: 2397
352,5⋅2π R = 352,5⋅2π ⋅0,34 = π ≈ 753( m). 10
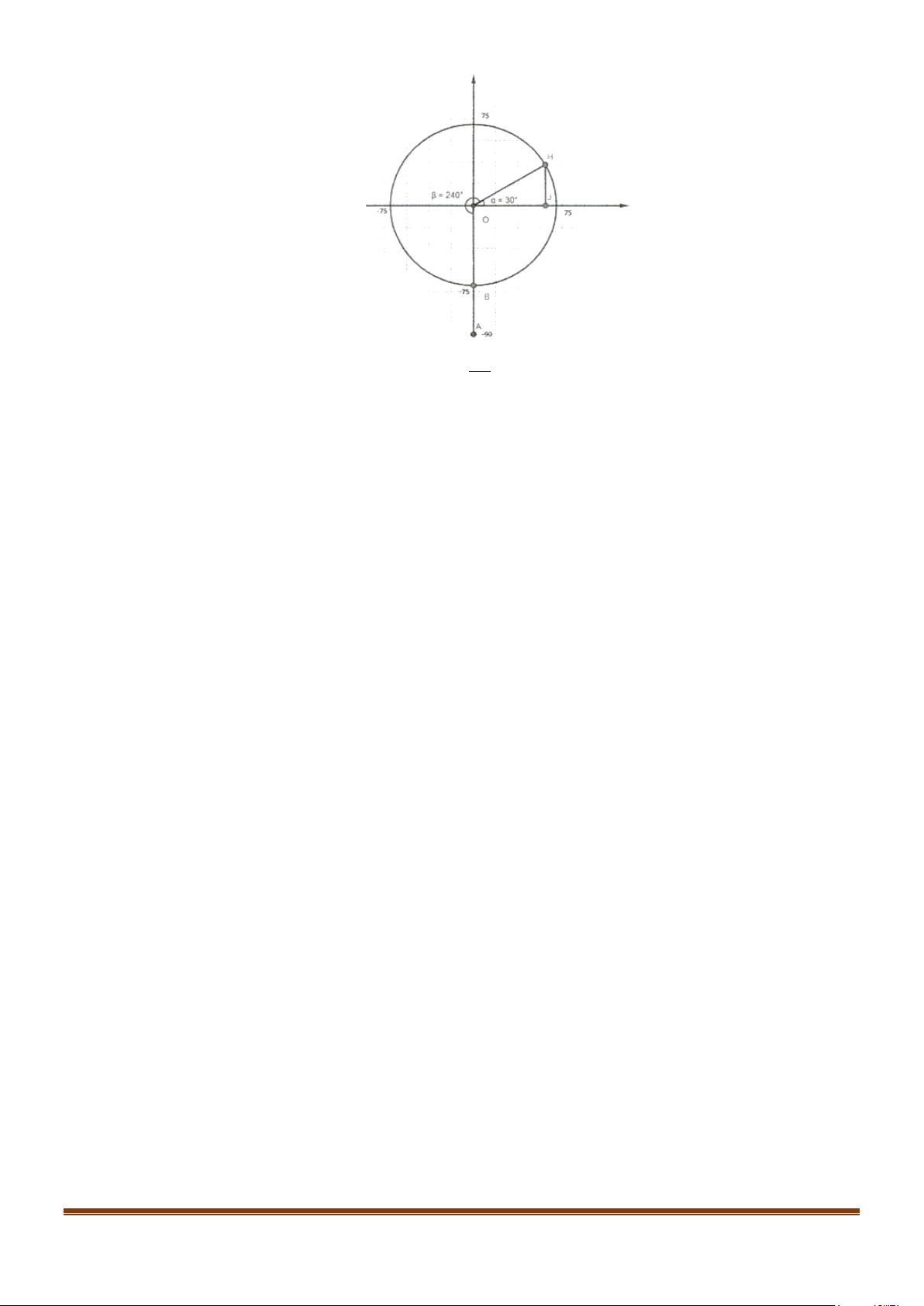
Câu 6: Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m so với mặt đất, thời gian
thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất
của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét so với mặt đất? Lời giải Trả lời: 127,5
Do tính đối xứng, dù đu quay chuyển động theo chiều kim đồng hồ hay ngược chiều kim đồng
hồ, ta đều thấy rằng độ cao của người đó là như nhau sau cùng một khoảng thời gian. Ở đây ta
xét đu quay chuyển động theo chiều kim đồng hồ.
Gắn đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m vào hệ trục tọa độ Oxy ta được hình bên: Page 11
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Sau 20 phút quay cabin đi được một góc là 20 ⋅360° = 240° tức là đến vị trí điểm H . 30 Khi đó góc
HOJ = 30° và HJ = OH.sin 30° = 37,5( m) .
Vậy sau 20 phút quay, người đó ở độ cao 37,5 + 90 =127,5( m) .
---------- HẾT ---------- Page 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC ƠNG I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC CHƯ
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC ĐỀ TEST SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Đổi số đo của góc π rad sang đơn vị độ ta được góc có số đo bằng bao nhiêu? 12 A. 15° . B. 10°. C. 6°. D. 5° . Câu 2: Cho
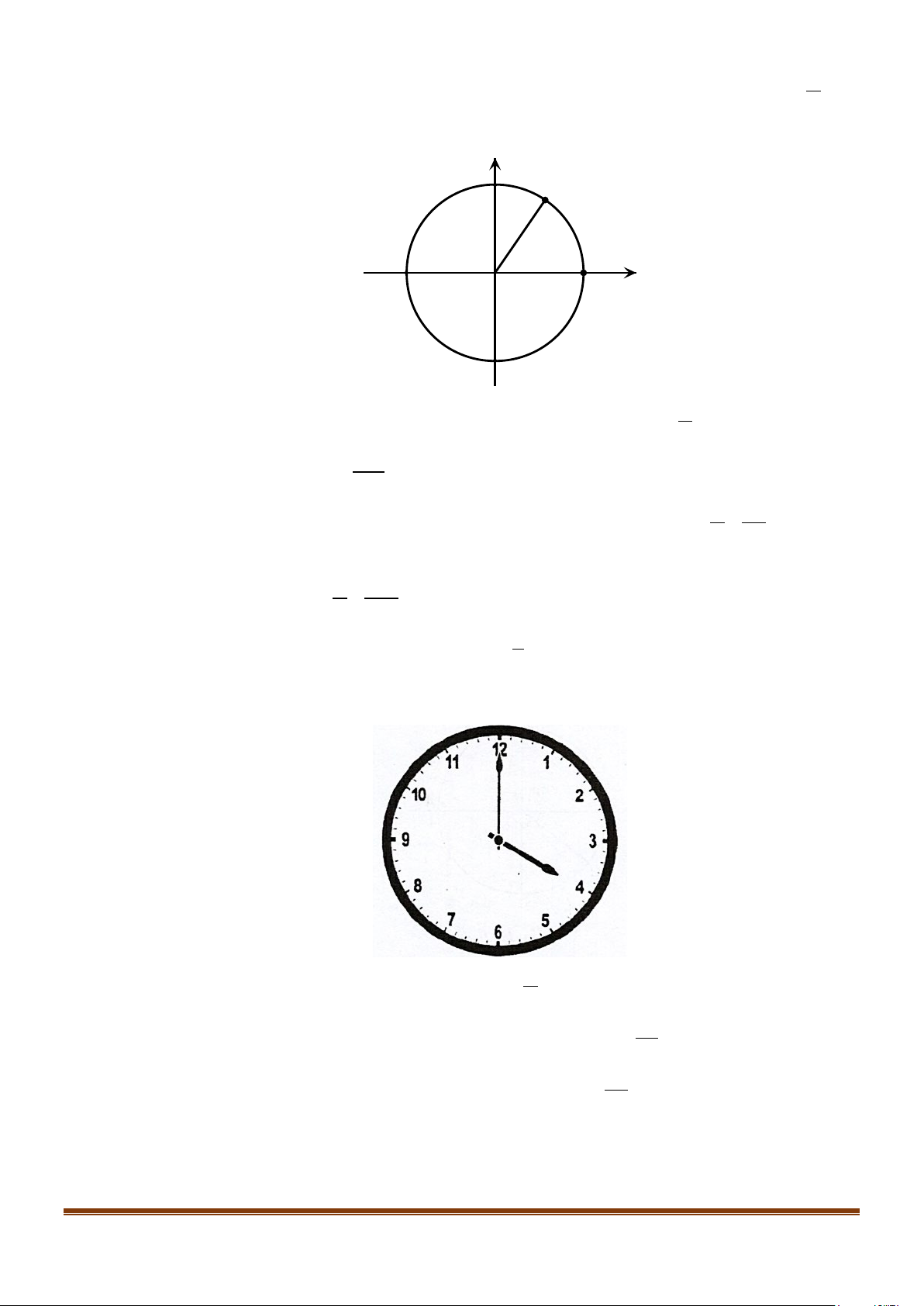
MON = 60°. Xác định số đo của góc lượng giác được biểu diễn trong hình vẽ. A. 420°. B. 60°. C. 780°. D. 780 − ° .
Câu 3: Nếu góc lượng giác có π
sđ (Ox,Oz) 63 = −
thì hai tia Ox và Oz. 2 A. Trùng nhau. B. Vuông góc.
C. Tạo với nhau một góc bằng 3π . D. Đối nhau. 4
Câu 4: Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là A. 60°. B. 30° . C. 40°. D. 50° .
Câu 5: Cho góc lượng giác (Ou,Ov) có số đo là 3π π −
, góc lượng giác (Ou,Ow) có số đo là 11 . Tìm 4 4
số đo của góc lượng giác (Ov,Ow) . π π
A. k2π (k 3 3 ∈ ).
B. 2π + k2π (k ∈ ) . C.
+ k2π (k ∈ ) . D. −
+ k2π (k ∈ ) 2 2 π
Câu 6: Trên đường tròn lượng giác với điểm gốc (
A 1;0), cho điểm M biểu diễn cho góc lượng giác 6
. Gọi N là điểm đối xứng với điểm M qua trục Oy , điểm N biểu diễn cho góc lượng giác nào dưới đây? π π π π A. − . B. 2 . C. 7 − . D. 7 . 6 3 6 6 Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 7: Cho góc α thỏa 3
cotα = và 0° < α < 90 .° Khẳng định nào sau đây đúng? 4 A. 4 cosα = . B. 4 sinα = . C. 4 sinα = − . D. 4 cosα = − . 5 5 5 5 π
Câu 8: Đơn giản biểu thức A cos α = − , ta được: 2 A. cosα . B. sinα . C. –cosα . D. −sinα . − π Câu 9: Cho (α + π ) 3 cos 2024 = và 3 π < α <
. Khi đó giá trị của tanα là 5 2 A. 3 . B. 3 − . C. 4 . D. 4 − . 4 4 3 3
Câu 10: Trên đường tròn lượng giác, biết điểm 3 4 M ; −
là điểm biểu diễn góc lượng giác có số đo α 5 5
. Khẳng định nào sau đây là sai? A. 3 cot . B. 3 tan . C. 4 sinα = − . D. 3 cosα = . 4 4 5 5 Câu 11: Cho góc π α thỏa 3 3 π < α <
, cosα = − . Tính giá trị lượng giác của tanα . 2 5 A. 4 − . B. 4 . C. 4 . D. 3 . 3 5 3 2
Câu 12: Cho góc α thỏa mãn 3 π α
sinα = và < α < π . Tính tan P = 5 2 2 1+ tan α A. 12 P = − . B. 3 P = . C. 12 P = . D. P = 3 − . 25 7 25
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho góc lượng giác (Ou,Ov) như hình vẽ sau, biết góc hình học uOv = 45°.
a) Trong hình vẽ, tia Om quay quanh gốc O từ tia Ou đến tia Ov theo chiều dương.
b) Trong hình vẽ, số đo của góc lượng giác (Ou,Ov) bằng 315 − ° .
c) Tia Om quay quanh gốc O từ Ou đến tia Ov lần đầu tiên theo chiều dương quét một góc
lượng giác có số đo 45°.
d) Tia Om quay quanh gốc O từ tia Ou đến tia Ov theo chiều dương chạm tia Ov năm lần
quét một góc lượng giác có số đo là 1485° . Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 2: Trên đường tròn lượng giác tâm O và hệ trục tọa độ π
Oxy cho điểm M sao cho AOM = như 3 hình vẽ bên dưới: y 1 M A x -1 O 1 -1
a) Số đo của các góc lượng giác có tia đầu là OA tia cuối là OM bằng π + k2π (k ∈) . 3
b) Góc lượng giác có số đo 16π có cùng tia đầu và tia cuối với góc lượng giác ( , OA OM ) 3
c) Trên đường tròn lượng giác, số điểm biểu diễn góc lượng giác có số đo π kπ +
,k ∈ là 6 3 2 điểm. d) Khi biểu diễn góc π k2π α = +
,k ∈ lên đường tròn lượng giác ta được tập hợp điểm là một 3 3
đa giác đều thì diện tích của đa giác đều đó bằng 3 . 4
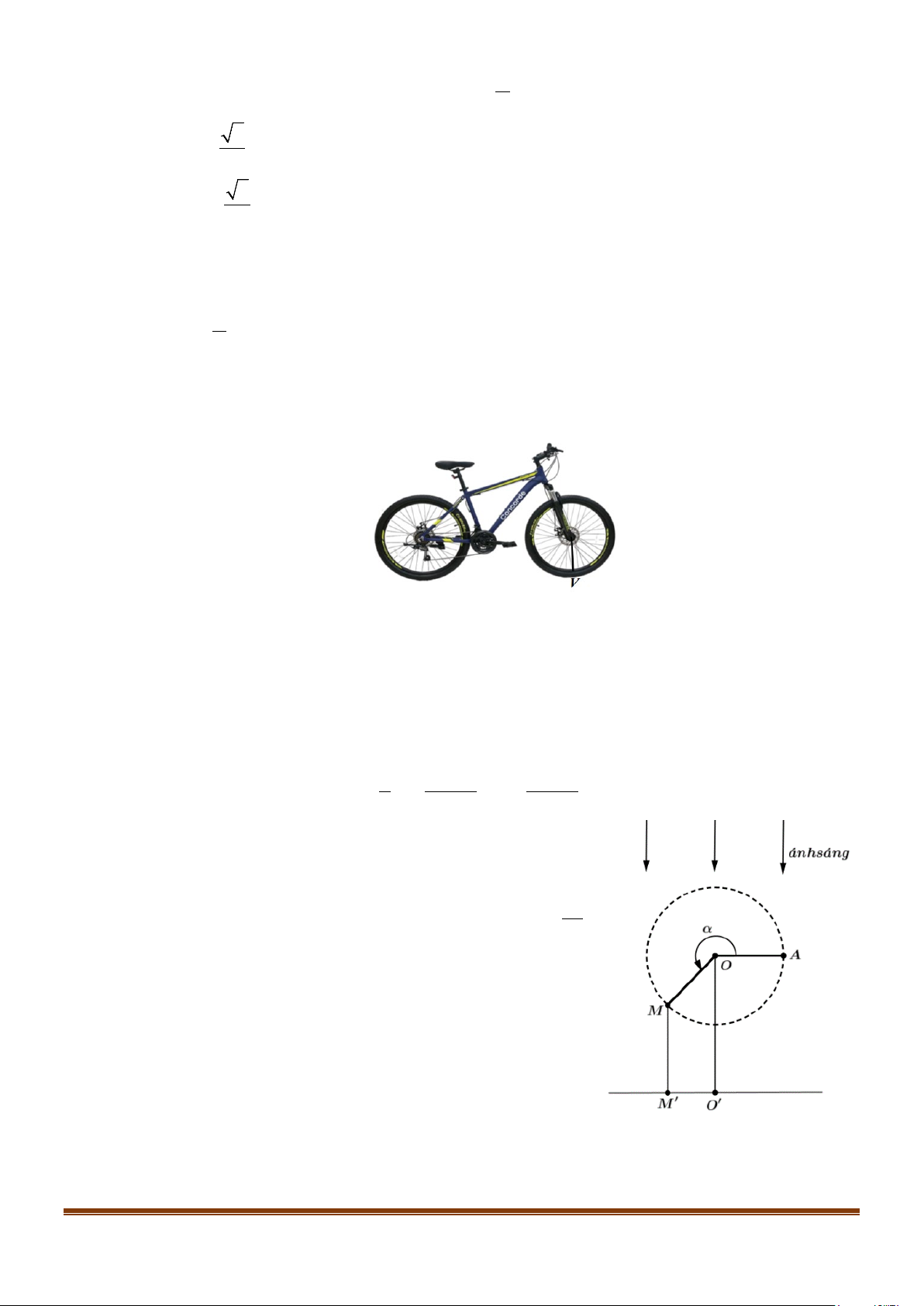
Câu 3: Một chiếc đồng hồ có kim giờ và kim phút được cho như trong hình vẽ sau. Chiều dài kim giờ,
kim phút lần lượt bằng 8cm và 10cm. π
a) Đồng hồ chỉ 6 giờ kim giờ quay được góc bằng . 3 π
b) Đồng hồ chỉ 6 giờ kim giờ quét được một cung có độ dài bằng 8 (cm) . 3 π
c). Đồng hồ chỉ 6 giờ 15 phút kim phút quay được góc bằng 9 2
d) Đồng hồ chỉ 6 giờ 15 phút kim phút quét được một cung có độ dài bằng 90π (cm) . Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC π
Câu 4: Tính được các giá trị lượng giác của góc α = − + (2k + )
1 π (biết k ∈ ). 4 a) 2 sinα = 2 b) 2 cosα = 2 c) tanα = 1 − d) cotα = 1 −
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1: Cho π
α = + k2π , k ∈ . Tìm được bao nhiêu giá trị của k để 10π < α <11π. 2
Câu 2: Bánh xe của người đi xe đạp quay được 12 vòng trong 5 giây. Giả sử tại thời điểm bắt đầu quay
van xe nằm ở vị trí V vuông góc với mặt đất. Hỏi trong một giây tia OV (O là trục bánh xe) quét
một góc lượng giác bao nhiêu độ?
Câu 3: Một người đi xe đạp đã đi được quãng đường 614,8m trong thời gian 3 phút. Biết rằng đường
kính bánh xe là 700mm . Tính góc lượng giác ( đơn vị Radian) mà bánh xe quay được trong 5
giây (giả sử bánh xe quay theo chiều dương, kết quả làm tròn đến một chữ số sau dấu phẩy)?
Câu 4: Một đồng hồ có kim giờ dài 5,5(cm); kim phút dài 11(cm) và chỉ thời gian lúc 12 giờ. Hỏi hai
kim trùng với nhau lần thứ 3 thì tổng độ dài cung của hai kim đã quay là bao nhiêu radian? (làm
tròn đến hàng đơn vị) π π
Câu 5: Cho góc α thỏa mãn 4 tanα = − và 2017 2019 < α < . Tính sinα. 3 2 2
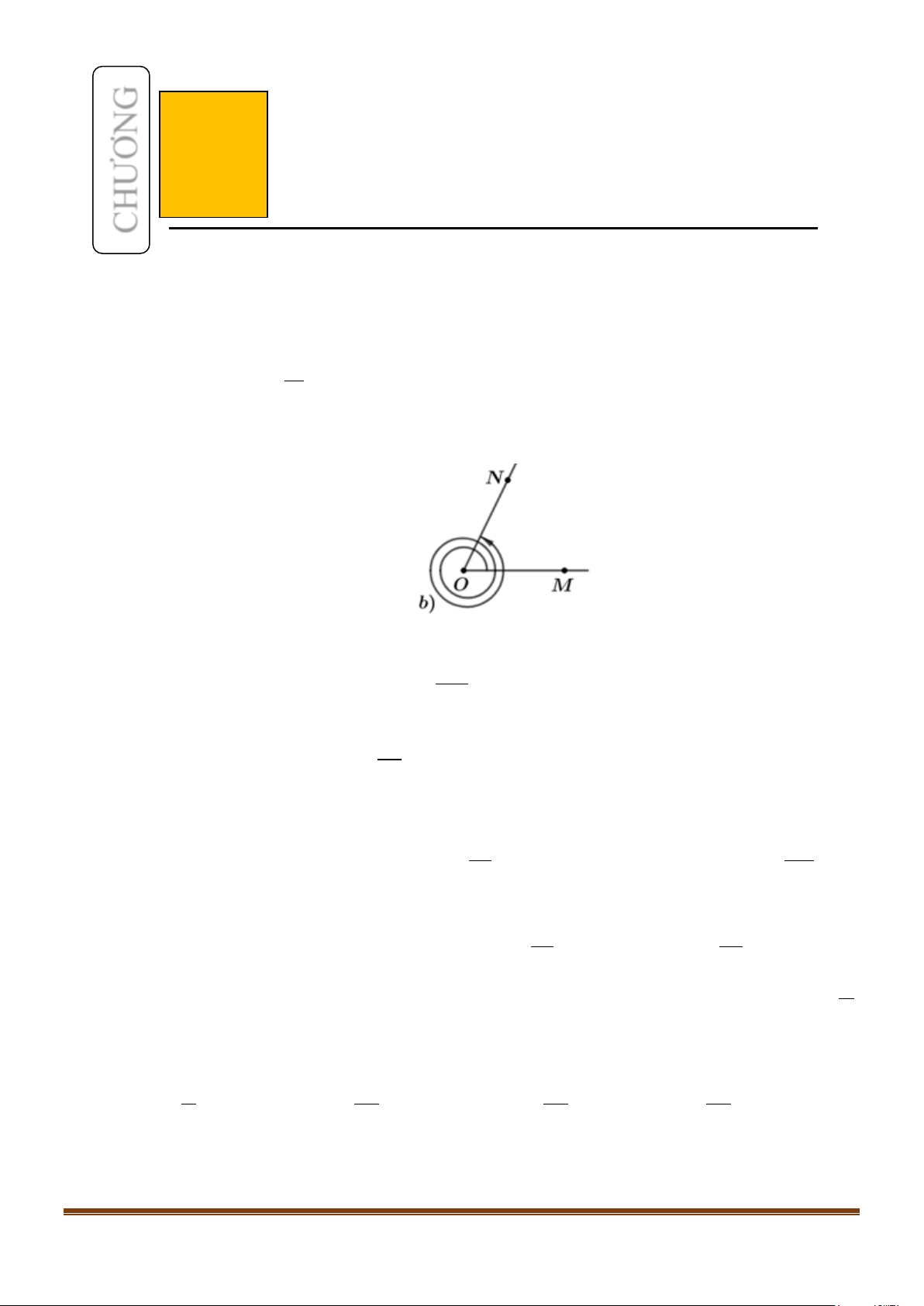
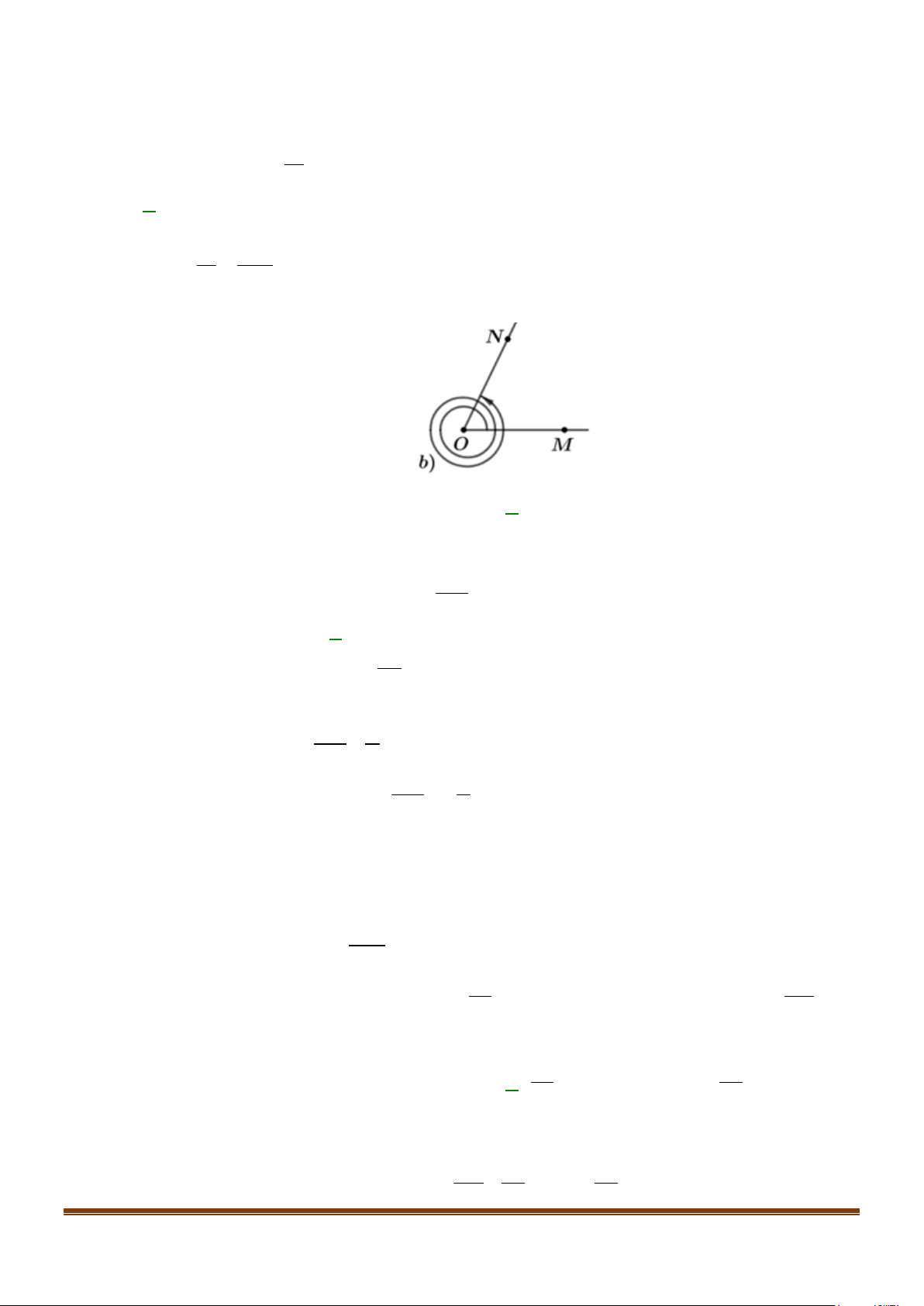
Câu 6: Thanh OM quay ngược chiều kim đồng hồ quanh gốc O
của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc
xuống mặt đất như hình bên. Vị trí ban đầu của thanh là OA
. Hỏi độ dài bóng O M
′ của OM khi thanh quay được 60 13
vòng là bao nhiêu, biết độ dài thanh OM là 10 cm ? (kết
quả làm tròn đến hàng phần mười).
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Đổi số đo của góc π rad sang đơn vị độ ta được góc có số đo bằng bao nhiêu? 12 A. 15° . B. 10°. C. 6°. D. 5° . Lời giải Ta có: π 180 = ° =15°. 12 12 Câu 2: Cho
MON = 60°. Xác định số đo của góc lượng giác được biểu diễn trong hình vẽ. A. 420°. B. 60°. C. 780°. D. 780 − ° . Lời giải
Số đo của góc lượng giác được biểu diễn trên hình đã cho là: 60° + 2.360° = 780° .
Câu 3: Nếu góc lượng giác có π
sđ (Ox,Oz) 63 = −
thì hai tia Ox và Oz. 2 A. Trùng nhau. B. Vuông góc.
C. Tạo với nhau một góc bằng 3π . D. Đối nhau. 4 Lời giải Ta có: π π
sđ (Ox,Oz) 63 = − = − 32π 2 2
Vì hai góc lượng giác có số đo 63π π −
và có cùng tia đầu và tia cuối nên hai tia Ox và Oz 2 2 vuông góc với nhau.
Câu 4: Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là A. 60°. B. 30° . C. 40°. D. 50° . Lời giải
1 bánh răng tương ứng với 360° = 5° ⇒10 bánh răng là 50° . 72
Câu 5: Cho góc lượng giác (Ou,Ov) có số đo là 3π π −
, góc lượng giác (Ou,Ow) có số đo là 11 . Tìm 4 4
số đo của góc lượng giác (Ov,Ow) . π π
A. k2π (k 3 3 ∈ ).
B. 2π + k2π (k ∈ ) . C.
+ k2π (k ∈ ) . D. −
+ k2π (k ∈ ) 2 2 Lời giải
Theo hệ thức Chasles, ta có: ( π π π
Ov Ow) = (Ou Ow) − (Ou Ov) 11 3 3 , , , + k2π = + + k2π =
+ 2π + k2π (k ∈ ) . 4 4 2 Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC π
Câu 6: Trên đường tròn lượng giác với điểm gốc (
A 1;0), cho điểm M biểu diễn cho góc lượng giác 6
. Gọi N là điểm đối xứng với điểm M qua trục Oy , điểm N biểu diễn cho góc lượng giác nào dưới đây? π π π π A. − . B. 2 . C. 7 − . D. 7 . 6 3 6 6 Lời giải π π π Ta có
AOM = và do tính đối xứng nên
A′ON = . Suy ra 5 AON = . 6 6 6 π π Do góc 5 và 7 −
hơn kém nhau 2π nên có cùng điểm biểu diễn 6 6 π
Vậy điểm N biểu diễn cho góc lượng giác 7 − . 6
Câu 7: Cho góc α thỏa 3
cotα = và 0° < α < 90 .° Khẳng định nào sau đây đúng? 4 A. 4 cosα = . B. 4 sinα = . C. 4 sinα = − . D. 4 cosα = − . 5 5 5 5 Lời giải Áp dụng công thức: 2 1 1 9 1 + cot α = ⇔ 1+ = 2 16 ⇔ sin α = 2 sin α 2 16 sin α 25 Do 4
0° < α < 90° ⇒ sinα > 0 ⇒ sinα = . 5 π
Câu 8: Đơn giản biểu thức A cos α = − , ta được: 2 A. cosα . B. sinα . C. –cosα . D. −sinα . Lời giải Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC π π Ta có: A cos α = − = cos −α = sinα . 2 2 − π Câu 9: Cho (α + π ) 3 cos 2024 = và 3 π < α <
. Khi đó giá trị của tanα là 5 2 A. 3 . B. 3 − . C. 4 . D. 4 − . 4 4 3 3 Lời giải Ta có: (α + π ) 3 cos 2024 =cosα ⇒ cosα = − . 5 π Vì 3 π < α < nên sinα < 0 . Do đó 2 9 4
sinα = − 1− cos α = − 1− = − . 2 25 5 α Vậy sin 4 tanα = = cosα 3
Câu 10: Trên đường tròn lượng giác, biết điểm 3 4 M ; −
là điểm biểu diễn góc lượng giác có số đo α 5 5
. Khẳng định nào sau đây là sai? A. 3 cot . B. 3 tan . C. 4 sinα = − . D. 3 cosα = . 4 4 5 5 Lời giải Điểm 3 4 M ; − nên ta có: 3 cosα = ; 4 sinα = − , suy ra 4 tanα = − và 3 cotα = − . 5 5 5 5 3 4 Câu 11: Cho góc π α thỏa 3 3 π < α <
, cosα = − . Tính giá trị lượng giác của tanα . 2 5 A. 4 − . B. 4 . C. 4 . D. 3 . 3 5 3 2 Lời giải Ta có 3π π < α < ⇒ sinα < 0 . 2 2 Mà 2 2 2 3 4 sin α cos α 1 sinα 1 cos α + = ⇒ = − − = − 1− − = − . 5 5 4 sinα − 5 4 Vậy tanα = = = . cosα 3 3 − 5
Câu 12: Cho góc α thỏa mãn 3 π α
sinα = và < α < π . Tính tan P = 5 2 2 1+ tan α A. 12 P = − . B. 3 P = . C. 12 P = . D. P = 3 − . 25 7 25 Lời giải 2 Ta có 2 2 2 2 3 16
sin α + cos α =1⇒ cos α =1−sin α =1− = . 5 25 Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC Vì π 4
< α < π ⇒ cosα = − 2 5 sinα tanα cosα 3 4 12 P = = = sinα.cosα = . − = − . 2 1 tan α 1 5 5 + 25 2 cos α
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho góc lượng giác (Ou,Ov) như hình vẽ sau, biết góc hình học uOv = 45°.
a) Trong hình vẽ, tia Om quay quanh gốc O từ tia Ou đến tia Ov theo chiều dương.
b) Trong hình vẽ, số đo của góc lượng giác (Ou,Ov) bằng 315 − ° .
c) Tia Om quay quanh gốc O từ Ou đến tia Ov lần đầu tiên theo chiều dương quét một góc
lượng giác có số đo 45°.
d) Tia Om quay quanh gốc O từ tia Ou đến tia Ov theo chiều dương chạm tia Ov năm lần
quét một góc lượng giác có số đo là 1485° . Lời giải a) Sai b) Đúng c) Đúng d) Đúng
a) Tia Om quay quanh gốc O từ tia Ou đến tia Ov theo chiều kim đồng hồ nên đó là chiều âm
suy ra mệnh đề sai. b) Ta có:
uOv = 45° ⇒ (Ou ,Ov) = 315 −
° suy ra mệnh đề đúng. c) Ta có:
uOv = 45°. Tia Om quay quanh gốc O từ Ou đến tia Ov lần đầu tiên theo chiều dương
có (Ou,Ov) = 45° suy ra mệnh đề đúng.
d) Tia Om quay quanh gốc O từ Ou đến tia Ov theo chiều dương chạm tia Ov năm lần nên ta
có (Ou,Ov) = 45° + 4.360° =1485° suy ra mệnh đề đúng.
Câu 2: Trên đường tròn lượng giác tâm O và hệ trục tọa độ π
Oxy cho điểm M sao cho AOM = như 3 hình vẽ bên dưới: y 1 M A x -1 O 1 -1 Page 8
Sưu tầm và biên soạn




