















Preview text:
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP NG I MỆNH ĐỀ ƯƠ VÀ TẬP HỢP CH BÀI 1: MỆNH ĐỀ ĐẾ TEST SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Phát biểu nào sau đây là một mệnh đề?
A. Mùa thu Hà Nội đẹp quá!
B. Bạn có đi học không?
C. Đề thi môn Toán khó quá!
D. Hà Nội là thủ đô của Việt Nam.
Câu 2: Phát biểu nào sau đây không phải là mệnh đề?
A. Số 3 là một số nguyên tố.
B. 24 chia hết cho 7 .
C. “Chí Phèo” là một tác phẩm của Nam Cao. D. Nóng quá!
Câu 3: Trong các câu sau câu nào là mệnh đề chứa biến?
A. 9 là số nguyên tố. B. 18 là số chẵn. C. ( 2
x + x)3 , x∈ . D. Hình chữ nhật có hai đường chéo bằng nhau.
Câu 4: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau.
B. Nếu hai tam giác có các cạnh bằng nhau thì chúng có các góc bằng nhau.
C. Nếu hai tam giác có diện tích bằng nhau thì bằng nhau.
D. Một tam giác cân có một góc bằng 60 thì tam giác đó đều.
Câu 5: Trong các câu dưới đây, câu nào là mệnh đề toán học?
A. Hôm nay trời nóng quá!
B. Bạn có thích học toán không?
C. Bài tập này khó quá!
D. 2 là số nguyên tố nhỏ nhất.
Câu 6: Cho mệnh đề đúng: A⇒ B . Phát biểu nào sau đây không thể dùng để phát biểu mệnh đề A⇒ B ?
A. Nếu A thì B .
B. A kéo theo B .
C. A là điều kiện đủ để có B .
D. A là điều kiện cần để có B .
Câu 7: Cho mệnh đề: "Nếu hai tam giác bằng nhau thì diện tích hai tam giác đó bằng nhau". Trong các
mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
A. "Nếu hai tam giác có diện tích không bằng nhau thì hai tam giác đó không bằng nhau".
B. "Nếu hai tam giác bằng nhau thì hai tam giác đó có chu vi bằng nhau."
C. "Nếu hai tam giác không bằng nhau thì diện tích hai tam giác đó không bằng nhau".
D. "Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau."
Câu 8: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu a và b cùng chia hết cho c thì a + b chia hết cho c .
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
C. Nếu a chia hết cho 3 thì a chia hết cho 9.
D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5. Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 9: Mệnh đề phủ định của mệnh đề “21 là số nguyên tố” là mệnh đề:
A. 21 là số nguyên tố. B. 21 chia hết cho 2.
C. 21 không phải là số nguyên tố.
D. 21 chia hết cho 7.
Câu 10: Mệnh đề phủ định của mệnh đề 2 " x
∀ ∈ : x > x + 7" là A. 2 " x
∀ ∈ : x ≤ x + 7". B. 2 " x
∃ ∈ : x < x + 7". C. 2 " x
∃ ∈ : x > x + 7". D. 2 " x
∃ ∈ : x ≤ x + 7".
Câu 11: Cho tứ giác ABCD . Xét mệnh đề P : “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau”
và mệnh đề Q : “Tứ giác ABCD là hình bình hành”. Lập mệnh đề P ⇔ Q .
A. Mệnh đề P ⇔ Q là: “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau suy ra tứ giác
ABCD là hình bình hành”.
B. Mệnh đề P ⇔ Q là: “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau là điều kiện
cần để tứ giác ABCD là hình bình hành”.
C. Mệnh đề P ⇔ Q là:“ Tứ giác ABCD có cặp cạnh đối song song và bằng nhau là điều kiện
cần và đủ để tứ giác ABCD là hình bình hành”.
D. Mệnh đề P ⇔ Q là: “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau là điều kiện
đủ để tứ giác ABCD là hình bình hành”.
Câu 12: Cho định lý “ Nếu tứ giác là hình vuông thì tứ giác đó có bốn cạnh bằng nhau”. Sử dụng điều
kiện cần hoặc điều kiện đủ hoặc điều kiện cần và đủ phát biểu lại định lý trên.
A. “Tứ giác có bốn cạnh bằng nhau là điều kiện cần để tứ giác đó là hình vuông”.
B. “Tứ giác có bốn cạnh bằng nhau là điều kiện cần để tứ giác đó là hình thoi”.
C. “Tứ giác là hình vuông là điều kiện cần và đủ để tứ giác đó có bốn cạnh bằng nhau.”.
D. “Tứ giác có bốn cạnh bằng nhau là điều kiện đủ để tứ giác đó là hình vuông”.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho các phát biểu sau: x∈,2x < 3( ) 1 ; 4 2
x∈, x − x < 0 (2). Khi đó:
a) (1) là 1 mệnh đề chứa biến.
b) Khi x =1 thì (1) trở thành mệnh đề đúng. c) Khi x = 2
− thì (2) trở thành mệnh đề đúng.
d) Không có số nguyên x nào để cả (1) và (2) trở thành các mệnh đề đúng.
Câu 2: Cho P(n) 2
= n − 6n +10 với n là số tự nhiên. Xét tính đúng sai của các mệnh đề sau a) P( ) 1 chia hết cho 3 .
b) P(2) là số lẻ.
c) P(2n) > P(n) −1 với n =1. 2P(n) −1
d) Tồn tại số tự nhiên n thỏa mãn điều kiện là số nguyên. n − 3
Câu 3: Một số nguyên dương n được gọi là “số hoàn hảo” nếu số đó bằng tổng các ước nguyên dương
thực sự của nó. Ví dụ số 6 là một số hoàn hảo vì các ước nguyên dương thực sự của 6 là 1; 2; 3 và 6 =1+ 2 + 3 .
a) Không có số hoàn hảo nào nhỏ hơn 10.
b) Số 10 là một số không hoàn hảo.
c) Tất cả các số nguyên tố đều là các số không hoàn hảo.
d) Số 2020 không phải là một số hoàn hảo. Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 4: Cho các mệnh đề: 2 P :" x
∃ ∈ : x > x " và 2 Q :" x
∀ ∈ : x > 0" . Khi đó:
a) P là mệnh đề đúng.
b) Q là mệnh đề sai.
c) P Q là mệnh đề đúng.
d) P QP Q là mệnh đề đúng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề chứa biến?
1 "2x +1 là số lẻ" ( x là số tự nhiên). 2) "x +1 = 0".
3) "x − 2y > 0" 4) ( + )2
" x y là số chính phương" ( x, y là số tự nhiên). 5) 2
"x − 3x + 2 = 0".
6) "2x là số chẵn"( x là số tự nhiên). 7) "2x −1≤ 7".
Câu 2: Cho mệnh đề:
A: “Tổng hai cạnh của môt tam giác lớn hơn cạnh còn lại”. B: “ 2 x
∃ ∈ : x + 5x − 6 = 0 ”.
C: “ 125 là số nguyên”. D: “ Phương trình: 4 2
x + 2x + 3 = 0 có nghiệm”.
Mệnh đề phủ định của các mệnh đề trên có bao nhiêu mệnh đề đúng? Lời giải
Câu 3: Trong các câu sau, có bao nhiêu câu là mệnh đề toán học? 1) Ăn phở rất ngon!
2) Hà Nội là thủ đô của Việt Nam. 3) Số 18 chia hết cho 6 . 4) 2 + 8 = 6. 5) x ≤1. 6) 3−1 = 2 . 7) 3 >1. 8) 3+ 4 ≠ 7
Câu 4: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?
1) Bình phương của một số thực bất kì là số âm.
2) Số π là một số hữu tỉ hay số vô tỉ?
3) 2x +1 là số lẻ. 4) 2 là số nguyên tố.
5) Hôm nay, cả lớp đều học bài.
6) Có bạn nào chưa làm bài tập không? 7) 3+ 5 = 9 .
8) Thời tiết hôm nay nóng quá!
9) Chu vi hình chữ nhật bằng tích của chiều dài và chiều rộng của nó.
10) Nếu một số tự nhiên có tận cùng bằng 0 thì số đó chia hết cho 10. Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 5: Trong các mệnh đề sau đây, có bao nhiêu mệnh đề đúng? 1. 2
∃x ∈ : x ≤ x 2. 2 x
∃ ∈ : x + 8x + 7 = 0 3. x ∀ ∈ : x > 0 4. 2
∃x ∈ : −x > 0 5. 2 x
∃ ∈ : x +1 = 0 . 6. 2 x
∃ ∈ : x < 0 . 7. 2 x
∃ ∈ : 2x −1< 0 . 8. 2 x
∃ ∈ N : x − 2 = 0 . 9. 2 " x
∀ ∈ , x + 2x + 3 > 0". 10. 2 " x
∃ ∈ , x + 5x + 6 = 0". 11. 1 " x ∃ ∈ , x < ". x
Câu 6: Trong các mệnh đề sau đây, có bao nhiêu mệnh đề sai? 1. 3 " x ∀ ∈ ,
x < 3x" . 2. 2
"∃x ∈, x ≠17" . 3. 2
"∃x ∈, x + 4 < 4x" . 4. 2
"∃x ∈,3x − 2x − 5 = 0". 5. 2
∀x∈, x > 0. 6. 2
∃x∈, x + 4x + 3 = 0 . 7. 2
∃x∈, x + 2x + 4 < 0. 8. 2 x ∃ ∈ , x ≤ 0.
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Phát biểu nào sau đây là một mệnh đề?
A. Mùa thu Hà Nội đẹp quá!
B. Bạn có đi học không?
C. Đề thi môn Toán khó quá!
D. Hà Nội là thủ đô của Việt Nam. Lời giải
Phát biểu ở A, B, C là câu cảm thán và câu hỏi nên không phải là mệnh đề
Phát biểu ở D là mệnh đề vì là câu khẳng định.
Câu 2: Phát biểu nào sau đây không phải là mệnh đề?
A. Số 3 là một số nguyên tố.
B. 24 chia hết cho 7 .
C. “Chí Phèo” là một tác phẩm của Nam Cao. D. Nóng quá! Lời giải
“Nóng quá!” là câu cảm thán nên nó không phải là một mệnh đề.
Câu 3: Trong các câu sau câu nào là mệnh đề chứa biến?
A. 9 là số nguyên tố. B. 18 là số chẵn. C. ( 2
x + x)3 , x∈ . D. Hình chữ nhật có hai đường chéo bằng nhau. Lời giải
Ta có mệnh đề C là một mệnh đề chứa biến. Tính đúng sai còn phụ thuộc giá trị của biến.
Câu 4: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau.
B. Nếu hai tam giác có các cạnh bằng nhau thì chúng có các góc bằng nhau.
C. Nếu hai tam giác có diện tích bằng nhau thì bằng nhau.
D. Một tam giác cân có một góc bằng 60 thì tam giác đó đều. Lời giải
Loại phương án C vì hai tam giác có diện tích bằng nhau chưa đủ điều kiện để hai tam giác đó bằng nhau.
Câu 5: Trong các câu dưới đây, câu nào là mệnh đề toán học?
A. Hôm nay trời nóng quá!
B. Bạn có thích học toán không?
C. Bài tập này khó quá! D. 2 là số nguyên tố nhỏ nhất. Lời giải
Các câu A,C là câu cảm thán, câu B là câu hỏi nên không phải là mệnh đề. Câu D là câu khẳng
định đúng nên câu D là mệnh đề đúng.
Câu 6: Cho mệnh đề đúng: A ⇒ B . Phát biểu nào sau đây không thể dùng để phát biểu mệnh đề A ⇒ B ?
A. Nếu A thì B .
B. A kéo theo B .
C. A là điều kiện đủ để có B .
D. A là điều kiện cần để có B . Lời giải
Câu 7: Cho mệnh đề: "Nếu hai tam giác bằng nhau thì diện tích hai tam giác đó bằng nhau". Trong các
mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
A. "Nếu hai tam giác có diện tích không bằng nhau thì hai tam giác đó không bằng nhau".
B. "Nếu hai tam giác bằng nhau thì hai tam giác đó có chu vi bằng nhau."
C. "Nếu hai tam giác không bằng nhau thì diện tích hai tam giác đó không bằng nhau".
D. "Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau." Lời giải Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Mệnh đề đảo của mệnh đề trên là: "Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau."
Câu 8: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu a và b cùng chia hết cho c thì a + b chia hết cho c .
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
C. Nếu a chia hết cho 3 thì a chia hết cho 9.
D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5. Lời giải
Nếu a chia hết cho 9 thì a chia hết cho 3 là mệnh đề đúng.
Câu 9: Mệnh đề phủ định của mệnh đề “21 là số nguyên tố” là mệnh đề:
A. 21 là số nguyên tố. B. 21 chia hết cho 2.
C. 21 không phải là số nguyên tố.
D. 21 chia hết cho 7. Lời giải
Thêm từ “không phải” vào trước vị ngữ của mệnh đề.
Câu 10: Mệnh đề phủ định của mệnh đề 2 " x
∀ ∈ : x > x + 7" là A. 2 " x
∀ ∈ : x ≤ x + 7". B. 2 " x
∃ ∈ : x < x + 7". C. 2 " x
∃ ∈ : x > x + 7". D. 2 " x
∃ ∈ : x ≤ x + 7". Lời giải
Mệnh đề phủ định của mệnh đề 2 " x
∀ ∈ : x > x + 7" là 2 " x
∃ ∈ : x ≤ x + 7"
Câu 11: Cho tứ giác ABCD . Xét mệnh đề P : “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau”
và mệnh đề Q : “Tứ giác ABCD là hình bình hành”. Lập mệnh đề P ⇔ Q .
A. Mệnh đề P ⇔ Q là: “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau suy ra tứ giác
ABCD là hình bình hành”.
B. Mệnh đề P ⇔ Q là: “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau là điều kiện
cần để tứ giác ABCD là hình bình hành”.
C. Mệnh đề P ⇔ Q là:“ Tứ giác ABCD có cặp cạnh đối song song và bằng nhau là điều kiện
cần và đủ để tứ giác ABCD là hình bình hành”.
D. Mệnh đề P ⇔ Q là: “Tứ giác ABCD có cặp cạnh đối song song và bằng nhau là điều kiện
đủ để tứ giác ABCD là hình bình hành”. Lời giải
Mệnh đề P ⇔ Q có thể phát biểu ở những dạng sau:
1. P tương đương Q .
2. P là điều kiện cần và đủ để có Q .
3. P khi và chỉ khi Q .
4. P nếu và chỉ nếu Q .
Vậy cách phát biểu C dùng để phát biểu mệnh đề P ⇔ Q .
Câu 12: Cho định lý “ Nếu tứ giác là hình vuông thì tứ giác đó có bốn cạnh bằng nhau”. Sử dụng điều
kiện cần hoặc điều kiện đủ hoặc điều kiện cần và đủ phát biểu lại định lý trên.
A. “Tứ giác có bốn cạnh bằng nhau là điều kiện cần để tứ giác đó là hình vuông”.
B. “Tứ giác có bốn cạnh bằng nhau là điều kiện cần để tứ giác đó là hình thoi”.
C. “Tứ giác là hình vuông là điều kiện cần và đủ để tứ giác đó có bốn cạnh bằng nhau.”.
D. “Tứ giác có bốn cạnh bằng nhau là điều kiện đủ để tứ giác đó là hình vuông”. Lời giải Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Cách phát biểu đúng khi sử dụng điều kiện cần hoặc điều kiện đủ hoặc điều kiện cần và đủ phát
biểu lại định lý trên là:
“Tứ giác có bốn cạnh bằng nhau là điều kiện cần để tứ giác đó là hình vuông”
Hoặc “Tứ giác là hình vuông là điều kiện đủ để tứ giác đó có bốn cạnh bằng nhau”
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho các phát biểu sau: x∈,2x < 3( ) 1 ; 4 2
x∈, x − x < 0 (2). Khi đó:
a) (1) là 1 mệnh đề chứa biến.
b) Khi x =1 thì (1) trở thành mệnh đề đúng. c) Khi x = 2
− thì (2) trở thành mệnh đề đúng.
d) Không có số nguyên x nào để cả (1) và (2) trở thành các mệnh đề đúng. Lời giải a) Đúng b) Đúng c) Sai d) Đúng + Xét a): Đ
+ Xét b): Khi x =1 thì (1) trở thành: 2.1< 3 là mệnh đề Đúng ⇒ Đ + Xét c): Khi x = 2
− thì (2) trở thành: (− )4 −(− )2 2
2 < 0 là mệnh đề sai ⇒ S x ≠ 0 x ≠ 0 + Xét d): Ta có: 4 2 2
x − x < 0 ⇔ x ( 2 x − ) 1 < 0 ⇔ ⇔ 2 x <1 1 − < x <1
Mà x ∈ nên không có giá trị nào của x làm cho (2) đúng ⇒Không có số nguyên x nào để
cả (1) và (2) trở thành các mệnh đề đúng⇒ Đ
Câu 2: Cho P(n) 2
= n − 6n +10 với n là số tự nhiên. Xét tính đúng sai của các mệnh đề sau a) P( ) 1 chia hết cho 3 .
b) P(2) là số lẻ.
c) P(2n) > P(n) −1 với n =1. 2P(n) −1
d) Tồn tại số tự nhiên n thỏa mãn điều kiện là số nguyên. n − 3 Lời giải a) Sai b) Sai c) Sai d) Đúng
a) Mệnh đề sai vì: P( )
1 = 5 không chia hết cho 3 .
b) Mệnh đề sai vì: P(2) = 2 là số chẵn.
c) Mệnh đề sai vì:
P(2n) > P(n) 2 2 2
−1 ⇔ 4n −12n +10 > n − 6n +10 −1 ⇔ 3n − 6n +1 > 0 2
Khi : n =1⇒ VT = 3.1 − 6.1+1 = 2 − < 0
d) Mệnh đề đúng vì: 2P(n) −1 ( 2
2 n − 6n +10) −1 2(n −3)2 +1 Ta có: = = = (n − ) 1 2 3 + n − 3 n − 3 n − 3 n − 3 2P(n) −1 Suy ra: ∈ ⇔
(n − 3) là ước của 1 n − 3
⇔ n − 3 =1 ⇔ n = 4 Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 3: Một số nguyên dương n được gọi là “số hoàn hảo” nếu số đó bằng tổng các ước nguyên dương
thực sự của nó. Ví dụ số 6 là một số hoàn hảo vì các ước nguyên dương thực sự của 6 là 1; 2; 3 và 6 =1+ 2 + 3 .
a) Không có số hoàn hảo nào nhỏ hơn 10.
b) Số 10 là một số không hoàn hảo.
c) Tất cả các số nguyên tố đều là các số không hoàn hảo.
d) Số 2020 không phải là một số hoàn hảo. Lời giải a) Sai b) Đúng c) Đúng d) Đúng
Ta có số 6 là một số hoàn hảo nên mệnh đề a) sai.
Ta có ước nguyên dương thực sự của số 10 là 1; 2; 5 và 1+2 + 5 = 8 < 10 nên số 10 không phải
là số hoàn hảo nên mệnh đề b) là mệnh đề đúng.
Ta có ước nguyên dương thực sự của các số nguyên tố là số 1 và 1 < p với mọi số nguyên tố p.
Nên số nguyên tố không phải là số hoàn hảo mệnh đề c) là mệnh đề đúng.
Ta thấy các ước nguyên dương thực sự của số 2
2020 = 2 .5.101 là 1; 2; 4; 5; 10; 20; 101; 202;
404; 505; 1010 và đồng thời 1+ 2+ 4+ 5+ 10+ 20+ 101+ 202+ 404+ 505+ 1010 > 2020 nên số
2020 không phải là số hoàn hảo. Vậy mệnh đề d) là mệnh đề đúng.
Câu 4: Cho các mệnh đề: 2 P :" x
∃ ∈ : x > x " và 2 Q :" x
∀ ∈ : x > 0" . Khi đó:
a) P là mệnh đề đúng.
b) Q là mệnh đề sai.
c) P Q là mệnh đề đúng.
d) P QP Q là mệnh đề đúng. Lời giải a) Đúng b) Sai c) Sai d) Đúng a) 2 P :" x ∃ ∈ 1 1
: x > x " là mệnh đề đúng vì 2
x = ⇒ x = mà 1 1 > . 2 4 2 4 Vậy a) đúng b) 2 Q :" x
∀ ∈ : x > 0" là mệnh đề sai vì 2
x = 0 ⇒ x = 0 mà 0 = 0. Suy ra Q là mệnh đề đúng. Vậy b) Sai
c) P là mệnh đề đúng, Q là mệnh đề sai. Suy ra P Q là mệnh đề sai. Vậy c) Sai
d) P là mệnh đề đúng nên P là mệnh đề sai, Q là mệnh đề sai.
Suy ra P Q là mệnh đề đúng. (1).
P là mệnh đề đúng, Q là mệnh đề đúng nên P Q là mệnh đề đúng. (2)
Từ (1) và (2) suy ra P QP Q là mệnh đề đúng. Vậy d) Đúng
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề chứa biến?
1 "2x +1 là số lẻ" ( x là số tự nhiên). 2) "x +1 = 0".
3) "x − 2y > 0" 4) ( + )2
" x y là số chính phương" ( x, y là số tự nhiên). Page 8
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP 5) 2
"x − 3x + 2 = 0".
6) "2x là số chẵn"( x là số tự nhiên). 7) "2x −1≤ 7". Lời giải Trả lời : 4
Câu 1), 4) và 6) là các mệnh đề đúng.
Vậy có bốn mệnh đề chứa biến là câu 2), 3), 5) và 7).
Câu 2: Cho mệnh đề:
A: “Tổng hai cạnh của môt tam giác lớn hơn cạnh còn lại”. B: “ 2 x
∃ ∈ : x + 5x − 6 = 0 ”.
C: “ 125 là số nguyên”. D: “ Phương trình: 4 2
x + 2x + 3 = 0 có nghiệm”.
Mệnh đề phủ định của các mệnh đề trên có bao nhiêu mệnh đề đúng? Lời giải Trả lời: 2 __
A : Tổng hai cạnh của một tam giác không lớn hơn cạnh còn lại. (sai). __ x =1 B : “ 2 x
∀ ∈ : x + 5x − 6 ≠ 0 ” (sai vì 2
x + 5x − 6 = 0 ⇔ ). x = 6 − __
C : “ 125 không là số nguyên” ( đúng vì 125 = 5 5 là số vô tỉ) __
D : “ Phương trình: 4 2
x + 2x + 3 = 0 vô nghiệm” ( đúng vì x + x + = (x + )2 4 2 2 2 3 1 + 2 > 0, x ∀ ).
Câu 3: Trong các câu sau, có bao nhiêu câu là mệnh đề toán học? 1) Ăn phở rất ngon!
2) Hà Nội là thủ đô của Việt Nam. 3) Số 18 chia hết cho 6 . 4) 2 + 8 = 6. 5) x ≤1. 6) 3−1 = 2 . 7) 3 >1. 8) 3+ 4 ≠ 7 Lời giải Trả lời: 5
Các câu 3), 4), 6), 7), 8) là mệnh đề toán học.
Câu 4: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?
1) Bình phương của một số thực bất kì là số âm.
2) Số π là một số hữu tỉ hay số vô tỉ?
3) 2x +1 là số lẻ. 4) 2 là số nguyên tố.
5) Hôm nay, cả lớp đều học bài.
6) Có bạn nào chưa làm bài tập không? 7) 3+ 5 = 9 .
8) Thời tiết hôm nay nóng quá!
9) Chu vi hình chữ nhật bằng tích của chiều dài và chiều rộng của nó.
10) Nếu một số tự nhiên có tận cùng bằng 0 thì số đó chia hết cho 10. Page 9
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP Lời giải Trả lời: 5
Các phát biểu sau là mệnh đề:
1) Bình phương của một số thực bất kì là số âm. 4) 2 là số nguyên tố. 7) 3+ 5 = 9 .
9) Chu vi hình chữ nhật bằng tích của chiều dài và chiều rộng của nó.
10) Nếu một số tự nhiên có tận cùng bằng 0 thì số đó chia hết cho 10.
Vậy các phát biểu 1), 4), 7), 9) và 10 là các mệnh đề.
Phát biểu 2) và 6) là một câu hỏi, 8) là câu cảm tháng và 5) chưa xác định được tính đúng sai nên
2), 5), 6) và 8) không phải mệnh đề.
Phát biểu 3) là một mệnh đề chứa biến nên không phải mệnh đề.
Vậy trong các phát biểu đã cho có 5 mệnh đề.
Câu 5: Trong các mệnh đề sau đây, có bao nhiêu mệnh đề đúng? 1. 2
∃x ∈ : x ≤ x 2. 2 x
∃ ∈ : x + 8x + 7 = 0 3. x ∀ ∈ : x > 0 4. 2
∃x ∈ : −x > 0 5. 2 x
∃ ∈ : x +1 = 0 . 6. 2 x
∃ ∈ : x < 0 . 7. 2 x
∃ ∈ : 2x −1< 0 . 8. 2 x
∃ ∈ N : x − 2 = 0 . 9. 2 " x
∀ ∈ , x + 2x + 3 > 0". 10. 2 " x
∃ ∈ , x + 5x + 6 = 0". 11. 1 " x ∃ ∈ , x < ". x Lời giải Trả lời: 5
+ Với x = 0 thì 2 x ≤ x nên 2
∃x ∈ : x ≤ x đúng với x = 0 . + Ta có 2 2 1
2x −1< 0 ⇔ x < . Do x ∈ nên ta chọn x = 0 . 2 + Mệnh đề “ 2 x
∀ ∈ , x + 2x + 3 > 0 ” đúng vì 2
x + 2x + 3 = (x + )2 1 + 2 > 0 x ∀ ∈ . x = 2 − + Mệnh đề “ 2 x
∃ ∈ , x + 5x + 6 = 0” đúng vì 2
x + 5x + 6 = 0 ⇔ ∈ . x = 3 − + Mệnh đề “ 1 x
∃ ∈ , x < ” đúng vì thay 1
x = ta được mệnh đề đúng. x 2
Câu 6: Trong các mệnh đề sau đây, có bao nhiêu mệnh đề sai? 1. 3 " x ∀ ∈ ,
x < 3x" . 2. 2
"∃x ∈, x ≠17" . 3. 2
"∃x ∈, x + 4 < 4x" . 4. 2
"∃x ∈,3x − 2x − 5 = 0". Page 10
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP 5. 2
∀x∈, x > 0. 6. 2
∃x∈, x + 4x + 3 = 0 . 7. 2
∃x∈, x + 2x + 4 < 0. 8. 2 x ∃ ∈ , x ≤ 0. Lời giải Trả lời : 6 x < − 3 Ta có 3 3
x < 3x ⇔ x − 3x < 0 ⇔ nên mệnh đề sai. 0 < x < 3 Với x = 2 , ta có 2
2 ≠17 nên mệnh đề đúng. Ta có 2 2
x + 4 < 4x ⇔ x − 4x + 4 < 0 ⇔ (x − 2)2 < 0 , vô nghiệm nên mệnh đề sai. x = −1∉ Ta có 2 3x 2x 5 0 − − = ⇔ 5 nên mệnh đề sai. x = ∉ 3 + Mệnh đề 2
∀x∈, x > 0 sai khi x = 0 . x = 1 − + 2
x + 4x + 3 = 0 ⇔ và 1 − ∉ ; 3
− ∉ nên mệnh đề sai. x = 3 − + 2
x + 2x + 4 = ( x + )2
1 + 3 > 0,∀x ∈ nên mệnh đề sai. + Mệnh đề 2 x
∃ ∈ , x ≤ 0đúng khi x = 0 . Page 11
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP NG I MỆNH ĐỀ ƯƠ VÀ TẬP HỢP CH BÀI 1: MỆNH ĐỀ ĐẾ TEST SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Phát biểu nào sau đây là một mệnh đề?
A. Trời hôm nay đẹp quá!
B. New York là thủ đô của Việt Nam.
C. Con đang làm gì đó?
D. Số 3 có phải là số tự nhiên không?
Câu 2: Trong các câu sau, câu nào không là một mệnh đề chứa biến? A. 2 + 5 = 6 . B. 2
4x − 7x − 9 = 0 .
C. 4x − y = 1.
D. 2x +1chia hết cho 5.
Câu 3: Cho mệnh đề chứa biến P(n) 2
:"n +1 chia hết cho 5". Trong các mệnh đề sau, mệnh đề nào sai? A. P(4). B. P(2). C. P(3) . D. P(7).
Câu 4: Cho mệnh đề: ”Có một học sinh trong lớp 10B không thích học môn Toán ”. Mệnh đề phủ định
của mệnh đề này là
A. ”Có một học sinh trong lớp 10B không thích học môn Toán ”.
B. ”Mọi học sinh trong lớp 10B đều thích học môn Toán ”.
C. ”Mọi học sinh trong lớp 10B đều không thích học môn Toán ”.
D. ”Có ít nhất một học sinh trong lớp 10B thích học môn Toán ”.
Câu 5: Cho mệnh đề P : “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Một phát
biểu khác của mệnh đề P là
A. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.
C. Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau.
D. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.
Câu 6: Phát biểu nào sau đây có cùng nội dung với mệnh đề “Nếu a và b chia hết cho c thì a + b chia
hết cho c .”
A. Nếu a + b chia hết cho c thì a và b chia hết cho c .
B. a và b chia hết cho c là điều kiện đủ để a + b chia hết cho c .
C. a và b chia hết cho c là điều kiện cần để a + b chia hết cho c .
D. a + b chia hết cho c là điều kiện đủ để a và b chia hết cho c .
Câu 7: Viết mệnh đề sau bằng kí hiệu ∀ hoặc ∃ : “Có một số nguyên bằng bình phương của chính nó” A. 2 x
∃ ∈ , x − x = 0. B. 2 x
∃ ∈ , x = x . C. 2 x
∀ ∈, x = x . D. 2 x
∃ ∈, x = x .
Câu 8: Cho mệnh đề P :" x
∀ ∈ , 3x − 5 = 0". Mệnh đề phủ định của P là A. P :" x
∀ ∈ , 3x − 5 ≠ 0" . B. P :" x
∃ ∈ , 3x − 5 ≠ 0". C. P :" x
∃ ∈ , 3x − 5 = 0". D. P :" x
∀ ∈ , 3x − 5 = 0". Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 9: Phát biểu định lý đảo của định lý “ Nếu một tam giác có một góc bằng o 90 thì tam giác đó là tam giác vuông”.
A. Một tam giác là tam giác vuông là điều kiện cần và đủ để tam giác đó có một góc bằng o 90 .
B. Một tam giác có có một góc bằng o
90 khi và chỉ khi tam giác đó là tam giác vuông.
C. Một tam giác có có một góc bằng o
90 là điều kiện đủ để tam giác đó là tam giác vuông.
D. Một tam giác là tam giác vuông là điều kiện đủ để tam giác đó có một góc bằng o 90 .
Câu 10: Cho P ⇔ Q là mệnh đề đúng. Khẳng định nào sau đây là sai?
A. P ⇔ Q sai.
B. P ⇔ Q đúng.
C. P ⇔ Q sai.
D. Q ⇔ P sai
Câu 11: Cho tứ giác ABCD. Xét hai mệnh đề:
P: “ Tứ giác ABCD là hình thoi”
Q: “ Tứ giác ABCD có hai đường chéo vuông góc”.
Phát biểu mệnh đề P Q .
A. Tứ giác ABCD có hai đường chéo vuông góc thì nó là hình thoi.
B. Tứ giác ABCD là hình thoi thì nó có hai đường chéo vuông góc.
C. Tứ giác ABCD là hình thoi là điều kiện cần và đủ để tứ giác đó có hai đường chéo vuông góc.
D. Tứ giác ABCD là hình thoi nếu nó có hai đường chéo vuông góc.
Câu 12: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
A. Nếu tổng hai số a + b > 2 thì có ít nhất một số lớn hơn 1.
B. Trong một tam giác cân hai đường cao bằng nhau.
C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.
D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho các mệnh đề: A:" x
∀ ∈ : x −3 > 0"; B : " : 2n n ∃ ∈ +1" là số nguyên; 2 C :" n
∃ ∈ ,n 9 ⇒ n9"Trong các câu khẳng định sau câu nào đúng?
a) Mệnh đề A đúng.
b) Mệnh đề phủ định của A là: A: x
∃ ∈ : x − 3 < 0 . c) Mệnh đề B sai.
d) Mệnh đề C đúng.
Câu 2: Cho hai mệnh đề sau:
P : “ Hình bình hành có một góc vuông là hình chữ nhật”.
Q : “ Số 7 là hợp số”.
a) Mệnh đề P là mệnh đề đúng.
b) Mệnh đề Q là mệnh đề đúng.
c) Mệnh đề P ⇒ Q là mệnh đề đúng.
d) Mệnh đề Q ⇒ P là mệnh đề sai.
Câu 3: Cho hai mệnh đề sau: A: “ 2 n ∀ ∈ ,n > . n ” và B: “ 2 n
∃ ∈ : n + 3n chia hết cho 3”.
a) Mệnh đề A sai.
b) Mệnh đề phủ định của mệnh đề A là A : “ 2 n
∀ ∈ , n ≤ n ”.
c) Mệnh đề phủ định của mệnh đề B là B : “ 2 n
∀ ∈ : n + 3n không chia hết cho 3”.
d) Mệnh đề B là mệnh đề đúng. Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 4: Cho các mệnh đề: A : “ 2 n
∃ ∈, n −8 = 0”, B : “ x ∀ ∈ (x − )2 , 2 ≠ x − 2 ”, C :“ 2 n
∃ ∈, n +11n + 2 chia hết cho 11”. Khi đó:
a) Mệnh đề A sai.
b) Mệnh B đúng.
c) Mệnh đề phủ định của mệnh đề C là: C :“ 2 n
∃ ∈ , n +11n + 2 không chia hết cho 11”.
d) Mệnh đề C đúng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?
1. 2x −1< 0 .
2. 2024 là số nguyên tố.
3. 3+π > 5 .
4. Cầu Trường Tiền bắc qua sông Hương.
5. Số 17 chia hết cho 3.
6. Hình thoi có hai đường chéo vuông góc.
7. London là thủ đô của Pháp.
8. Hôm nay thời tiết mát!
Câu 2: Trong các câu sau, có bao nhiêu câu là mệnh đề toán học?
a) Huế là một thành phố của Việt Nam.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Hãy trả lời câu hỏi này ! d) 5 +19 = 24 . e) 6 + 81 = 25 .
f) Bạn có rỗi tối nay không ? g) x + 2 =11. h) 10 2 −1chia hết cho 11. k) 19là hợp số.
Câu 3: Cho các mệnh đề sau:
(1) Mọi số tự nhiên chia hết cho 2 và 3 thì chia hết cho 6 .
(2) Với a∈ : a3 ⇔ a9 .
(3) Trong tam giác vuông bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. (4) : 2n n ∃ ∈ +1 là số nguyên. (5) 2 n
∀ ∈ : n > 0.
(6) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Câu 4: Cho các mệnh đề sau:
(1) “ là số hữu tỉ”.
(2) “ 8 không chia hết cho 3”.
(3) “ Tứ giác có tổng số đo các góc bằng 3600 ”.
(4) “ Hình bình hành có hai đường chéo luôn luôn bằng nhau”. (5) 2 P :" x
∀ ∈ , x ≥ x" (6) 2 Q :" x
∀ ∈ ,2x − 3x +1 ≠ 0"
Số mệnh đề có mệnh đề phủ định đúng là Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
Câu 5: Trong các mệnh đề sau có bao nhiêu mệnh đề sai?
Nếu n là một số nguyên tố lớn hơn 3 thì 2
n + 20 là một hợp số. Năm 2100 là năm nhuận.
Có đúng 2 cặp số hữu tỉ dương x, y thỏa mãn x + y và 1 1 + là số nguyên. x y * 2
∀n∈ ,n + n +1 là số nguyên tố. Q: “ n ∃ ∈ ( 2 , n + ) 1 chia hết cho 4 ”.
Câu 6: Cho các mệnh đề P : “Số 4 là số chẵn”, Q : “Số 4 chia hết cho 2”, R : “Số 4 là số nguyên tố”.
Xét các mệnh đề sau, hỏi có bao nhiêu mệnh đề đúng?
(1) “ P ⇒ Q ”;
(2) “Q ⇔ R ”;
(3) “(P ⇒ Q) ⇒ R ”; (4) “(P ⇒ Q) ⇔ Q ”.
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Phát biểu nào sau đây là một mệnh đề?
A. Trời hôm nay đẹp quá!
B. New York là thủ đô của Việt Nam.
C. Con đang làm gì đó?
D. Số 3 có phải là số tự nhiên không? Lời giải
New York là thủ đô của Việt Nam là một mệnh đề sai.
Câu 2: Trong các câu sau, câu nào không là một mệnh đề chứa biến? A. 2 + 5 = 6 . B. 2
4x − 7x − 9 = 0 .
C. 4x − y = 1.
D. 2x +1chia hết cho 5. Lời giải
"2 + 5 = 6" là một mệnh đề, không phải là mệnh đề chứa biến.
Câu 3: Cho mệnh đề chứa biến P(n) 2
:"n +1 chia hết cho 5". Trong các mệnh đề sau, mệnh đề nào sai? A. P(4). B. P(2). C. P(3) . D. P(7). Lời giải
Ta có: P(4) =17, P(2) = 5 , P(3) =10, P(7) = 50 .
Câu 4: Cho mệnh đề: ”Có một học sinh trong lớp 10B không thích học môn Toán ”. Mệnh đề phủ định
của mệnh đề này là
A. ”Có một học sinh trong lớp 10B không thích học môn Toán ”.
B. ”Mọi học sinh trong lớp 10B đều thích học môn Toán ”.
C. ”Mọi học sinh trong lớp 10B đều không thích học môn Toán ”.
D. ”Có ít nhất một học sinh trong lớp 10B thích học môn Toán ”. Lời giải
Mệnh đề phủ định của mệnh đề này là ”Mọi học sinh trong lớp 10B đều thích học môn Toán ”.
Câu 5: Cho mệnh đề P : “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Một phát
biểu khác của mệnh đề P là
A. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.
C. Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau.
D. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau. Lời giải
Cách phát biểu khác của P : “Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau”.
Câu 6: Phát biểu nào sau đây có cùng nội dung với mệnh đề “Nếu a và b chia hết cho c thì a + b chia
hết cho c .”
A. Nếu a + b chia hết cho c thì a và b chia hết cho c .
B. a và b chia hết cho c là điều kiện đủ để a + b chia hết cho c .
C. a và b chia hết cho c là điều kiện cần để a + b chia hết cho c .
D. a + b chia hết cho c là điều kiện đủ để a và b chia hết cho c . Lời giải
Mệnh đề “Nếu P thì Q ” có thể phát biểu là: “ P là điều kiện đủ để có Q ” hoặc “Q là điều
kiện cần để có P ”.
Câu 7: Viết mệnh đề sau bằng kí hiệu ∀ hoặc ∃ : “Có một số nguyên bằng bình phương của chính nó” Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP A. 2 x
∃ ∈ , x − x = 0. B. 2 x
∃ ∈ , x = x . C. 2 x
∀ ∈, x = x . D. 2 x
∃ ∈, x = x . Lời giải
Dựa vào mệnh đề: “Có một số nguyên bằng bình phương của chính nó”.
Câu 8: Cho mệnh đề P :" x
∀ ∈ , 3x − 5 = 0". Mệnh đề phủ định của P là A. P :" x
∀ ∈ , 3x − 5 ≠ 0" . B. P :" x
∃ ∈ , 3x − 5 ≠ 0". C. P :" x
∃ ∈ , 3x − 5 = 0". D. P :" x
∀ ∈ , 3x − 5 = 0". Lời giải
Mệnh đề phủ định của P là: P :" x
∃ ∈ , 3x − 5 ≠ 0"
Câu 9: Phát biểu định lý đảo của định lý “ Nếu một tam giác có một góc bằng o 90 thì tam giác đó là tam giác vuông”.
A. Một tam giác là tam giác vuông là điều kiện cần và đủ để tam giác đó có một góc bằng o 90 .
B. Một tam giác có có một góc bằng o
90 khi và chỉ khi tam giác đó là tam giác vuông.
C. Một tam giác có có một góc bằng o
90 là điều kiện đủ để tam giác đó là tam giác vuông.
D. Một tam giác là tam giác vuông là điều kiện đủ để tam giác đó có một góc bằng o 90 . Lời giải
Định lý đảo của định lý “ Nếu một tam giác có một góc bằng o
90 thì tam giác đó là tam
giác vuông” là: “ Nếu một tam giác là tam giác vuông thì tam giác đó có một góc bằng o 90 ”.
Mệnh đề P ⇒ Q , ta có:
P là điều kiện đủ để có Q
Q là điều kiện cần để có P .
Câu 10: Cho P ⇔ Q là mệnh đề đúng. Khẳng định nào sau đây là sai?
A. P ⇔ Q sai.
B. P ⇔ Q đúng.
C. P ⇔ Q sai.
D. Q ⇔ P sai Lời giải
P ⇒ Q =1 P ⇒ Q =1
Ta có: P ⇔ Q =1 ⇔ ⇔
⇔ P ⇔ Q =1 Q ⇒ P =1 Q ⇒ P =1
Câu 11: Cho tứ giác ABCD. Xét hai mệnh đề:
P: “ Tứ giác ABCD là hình thoi”
Q: “ Tứ giác ABCD có hai đường chéo vuông góc”.
Phát biểu mệnh đề P Q .
A. Tứ giác ABCD có hai đường chéo vuông góc thì nó là hình thoi.
B. Tứ giác ABCD là hình thoi thì nó có hai đường chéo vuông góc.
C. Tứ giác ABCD là hình thoi là điều kiện cần và đủ để tứ giác đó có hai đường chéo vuông góc.
D. Tứ giác ABCD là hình thoi nếu nó có hai đường chéo vuông góc. Lời giải Xét hai mệnh đề:
P: “ Tứ giác ABCD là hình thoi” và Q: “ Tứ giác ABCD có hai đường chéo vuông góc”.
Mệnh đề P Q là:
“Tứ giác ABCD là hình thoi là điều kiện cần và đủ để tứ giác đó có hai đường chéo vuông góc”.
Câu 12: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
A. Nếu tổng hai số a + b > 2 thì có ít nhất một số lớn hơn 1.
B. Trong một tam giác cân hai đường cao bằng nhau.
C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.
D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3. Lời giải
Xét mệnh đề “Trong một tam giác cân hai đường cao bằng nhau ”. Mệnh đề này có mệnh đề đảo
là “Nếu tam giác có hai đường cao bằng nhau thì tam giác đó là tam giác cân”.
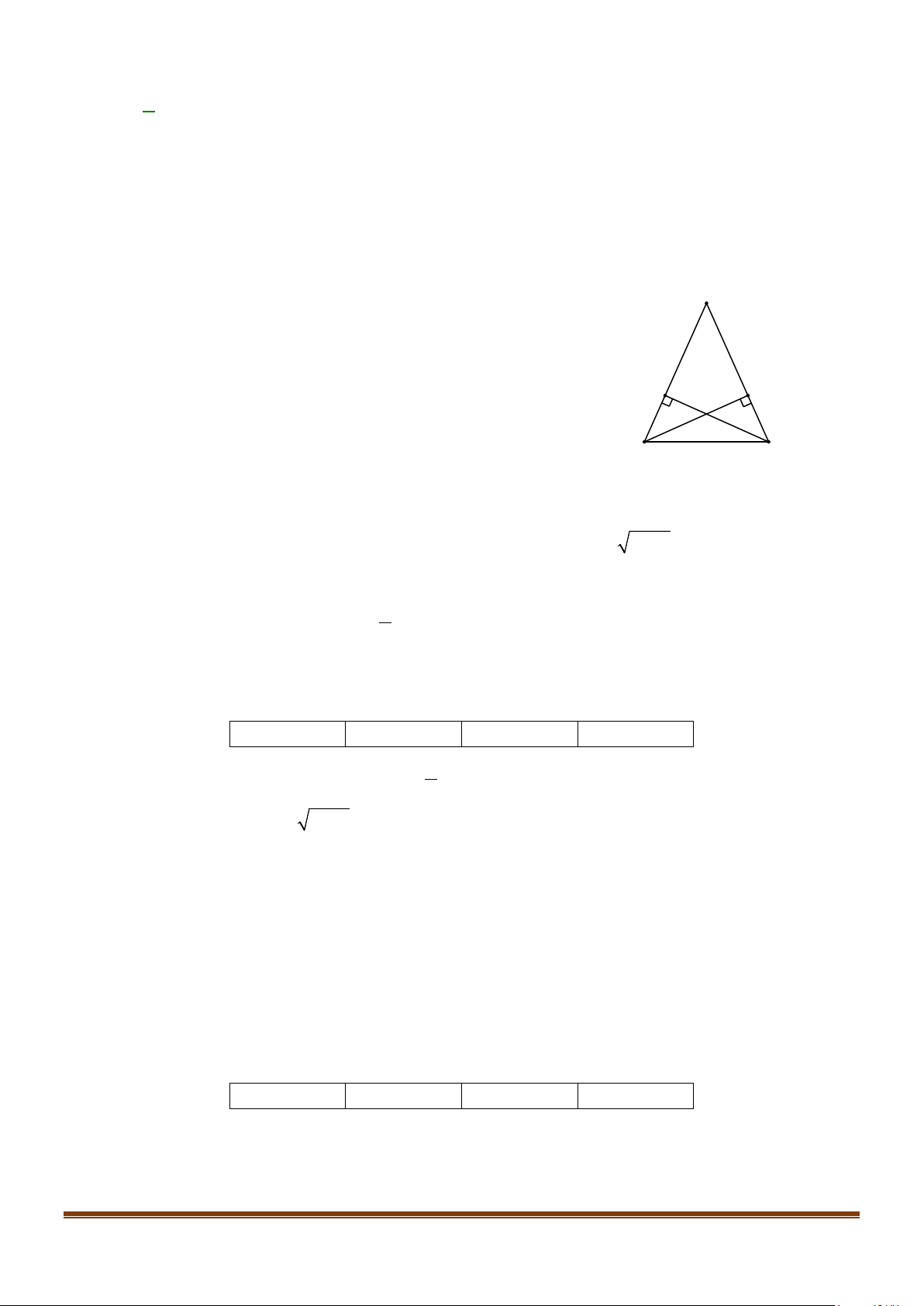
Ta chứng minh mệnh đề đảo này là mệnh đề đúng. A
Giả sử tam giác ABC có hai đường cao BE và CF bằng nhau.
Xét hai tam giác vuông B ∆ CE và B ∆ CF có
BC là cạnh chung; F E
BE = CF (giả thiết). Suy ra ∆ = ∆ ⇒ = BCE BCF FBC ECB hay tam giác
ABC cân tại A. B C
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho các mệnh đề: A:" x
∀ ∈ : x −3 > 0"; B : " : 2n n ∃ ∈ +1" là số nguyên; 2 C :" n
∃ ∈ ,n 9 ⇒ n9"Trong các câu khẳng định sau câu nào đúng?
a) Mệnh đề A đúng.
b) Mệnh đề phủ định của A là: A: x
∃ ∈ : x − 3 < 0 . c) Mệnh đề B sai.
d) Mệnh đề C đúng. Lời giải a) Sai b) Sai c) Đúng d) Đúng
a) Sai vì x =1 thì 1− 3 < 0 .
b) Sai vì mệnh đề phủ định của A là: A: x
∃ ∈ : x − 3 ≤ 0 c) Đúng vì 3
n = 3 thì 2 +1 = 3∈ . d) Đúng vì 2
n = 3 thì 3 9 nhưng 3 không chia hết cho 9.
Câu 2: Cho hai mệnh đề sau:
P : “ Hình bình hành có một góc vuông là hình chữ nhật”.
Q : “ Số 7 là hợp số”.
a) Mệnh đề P là mệnh đề đúng.
b) Mệnh đề Q là mệnh đề đúng.
c) Mệnh đề P ⇒ Q là mệnh đề đúng.
d) Mệnh đề Q ⇒ P là mệnh đề sai. Lời giải a) Đúng b) Đúng c) Sai d) Sai
a) Mệnh đề P là mệnh đề đúng. (Đúng)
b) Mệnh đề Q là mệnh đề đúng. (Sai vì 7 là số nguyên tố)
Mệnh đề A ⇒ B chỉ sai khi A đúng và B sai, nên ta có: Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP
c) Mệnh đề P ⇒ Q là mệnh đề đúng. (Sai)
d) Mệnh đề Q ⇒ P là mệnh đề sai. (Sai)
Câu 3: Cho hai mệnh đề sau: A: “ 2 n ∀ ∈ ,n > . n ” và B: “ 2 n
∃ ∈ : n + 3n chia hết cho 3”.
a) Mệnh đề A sai.
b) Mệnh đề phủ định của mệnh đề A là A : “ 2 n
∀ ∈ , n ≤ n ”.
c) Mệnh đề phủ định của mệnh đề B là B : “ 2 n
∀ ∈ : n + 3n không chia hết cho 3”.
d) Mệnh đề B là mệnh đề đúng. Lời giải a) Đúng b) Sai c) Đúng d) Sai a) Đúng. Vì 2 n = 0 ⇒ 0 = 0.
b) Sai. Mệnh đề phủ định của mệnh đề A là A : “ 2 n
∃ ∈ , n ≤ n ”. c) Đúng. d) Sai. Ta có: B: “ 2 n
∃ ∈ : n + 3n chia hết cho 3” ⇒ B : “ 2 n
∀ ∈ : n + 3n không chia hết cho 3”.
Xét n = 3k + r,(k ∈,r ∈{0;1; } 2 ) 2 ⇒ n + n = ( 2
k + kr + k ) + ( 2 3 9 6 3 r + r)
Với r = 0 hoặc r = 2 thì 2
n + 3n chia hết cho 3 nên B sai.
Câu 4: Cho các mệnh đề: A : “ 2 n
∃ ∈, n −8 = 0”, B : “ x ∀ ∈ (x − )2 , 2 ≠ x − 2 ”, C :“ 2 n
∃ ∈, n +11n + 2 chia hết cho 11”. Khi đó:
a) Mệnh đề A sai.
b) Mệnh B đúng.
c) Mệnh đề phủ định của mệnh đề C là: C :“ 2 n
∃ ∈ , n +11n + 2 không chia hết cho 11”.
d) Mệnh đề C đúng. Lời giải a) Đúng b) Sai c) Sai d) Sai a) Đúng vì 2 2
n −8 = 0 ⇔ n = 8 ⇔ n = 2 ± 2 ∉ . b) Sai vì x ∃ = (x − )2 2: 2 = x − 2 .
c) Sai vì mệnh đề phủ định của mệnh đề C là: C :“ 2 n
∀ ∈ , n +11n + 2 không chia hết cho 11”.
d) Sai vì khi n = 3 thì giá trị của ( 2
n +11n + 2) bằng 44 11
, nên C đúng ⇒ C sai.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?
1. 2x −1< 0 .
2. 2024 là số nguyên tố.
3. 3+π > 5 .
4. Cầu Trường Tiền bắc qua sông Hương.
5. Số 17 chia hết cho 3.
6. Hình thoi có hai đường chéo vuông góc.
7. London là thủ đô của Pháp.
8. Hôm nay thời tiết mát! Lời giải Page 8
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – CHƯƠNG I – MỆNH ĐỀ – TẬP HỢP Trả lời: 6
Phát biểu 1. là mệnh đề chứa biến.
Phát biểu 8. không phải là mệnh đề.
Các phát biểu 2. 3. 4. 5. 6. 7. là mệnh đề.
Câu 2: Trong các câu sau, có bao nhiêu câu là mệnh đề toán học?
a) Huế là một thành phố của Việt Nam.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Hãy trả lời câu hỏi này ! d) 5 +19 = 24 . e) 6 + 81 = 25 .
f) Bạn có rỗi tối nay không ? g) x + 2 =11. h) 10 2 −1chia hết cho 11. k) 19là hợp số. Lời giải Trả lời: 4
Theo định nghĩa, trong các câu đã cho chỉ có mệnh đề 5 +19 = 24 ; 6 + 81 = 25 ; 10 2 −1chia hết
cho 11; 19là hợp số là mệnh đề toán học.
Câu 3: Cho các mệnh đề sau:
(1) Mọi số tự nhiên chia hết cho 2 và 3 thì chia hết cho 6 .
(2) Với a∈ : a3 ⇔ a9 .
(3) Trong tam giác vuông bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. (4) : 2n n ∃ ∈ +1 là số nguyên. (5) 2 n
∀ ∈ : n > 0.
(6) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? Lời giải Trả lời: 4
Mệnh đề: đúng vì 2 và 3 nguyên tố cùng nhau nên số chia hết cho 2 và 3 sẽ chia hết cho 6 .
Mệnh đề: sai vì 63 nhưng 6/9. Mệnh đề: đúng.
Mệnh đề: đúng vì với n = 3 thì 3 2 +1 = 3 là số nguyên.
Mệnh đề: sai vì n = 0 thì 0 = 0 . Mệnh đề: đúng.
Câu 4: Cho các mệnh đề sau:
(1) “ là số hữu tỉ”.
(2) “ 8 không chia hết cho 3”.
(3) “ Tứ giác có tổng số đo các góc bằng 3600 ”.
(4) “ Hình bình hành có hai đường chéo luôn luôn bằng nhau”. (5) 2 P :" x
∀ ∈ , x ≥ x" (6) 2 Q :" x
∀ ∈ ,2x − 3x +1 ≠ 0"
Số mệnh đề có mệnh đề phủ định đúng là Lời giải Page 9
Sưu tầm và biên soạn




