Đề KSCL mũi nhọn Toán 7 năm 2023 – 2024 phòng GD&ĐT Nông Cống – Thanh Hóa

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KHẢO SÁT CHẤT LƯỢNG MŨI NHỌN CẤP HUYỆN HUYỆN NÔNG CỐNG NĂM HỌC 2023 - 2024 MÔN: TOÁN 7 Đề chí nh thức
Thời gian: 150 phút, không kể thời gian phát đề Ngày thi: 03/4/2024
(Đề có 01 trang, gồm 05 câu)
Câu I. (4,0 điểm) Tính giá trị của các biểu thức sau: 15 9 20 9 1. 5.4 .9 − 4.3 .8 A = 10 19 29 6 5.2 .6 − 7.2 .27 2. 1  1   1   1   1 B .1 .1 .1 .....1  = + + + + 2 1.3 2.4 3.5 2022.2024         
Câu II. (4,0 điểm)
1. Tìm số nguyên dương x biết: 1 + ( + ) 1 + ( + + ) 1 + ( + + + ) 1 1 1 2 1 2 3
1 2 3 4 +......+ (1+ 2 + 3+....+ x) =115 2 3 4 x
2. Cho x, y, z là các số thực khác 0, thỏa mãn y + z +1 x + z + 2 x + y − = = 3 = 1 x y z x + y + z
Tính giá trị của biểu thức: A = 4048.x + y2023 + z2023.
3. Cho ba hình chữ nhật, biết diện tích hình thứ nhất và hình thứ hai tỉ lệ với 4 và 5,
diện tích hình thứ hai và hình thứ ba tỉ lệ với 7 và 8. Hình thứ nhất và hình thứ hai có cùng
chiều dài và tổng các chiều rộng của chúng là 27cm, Hình thứ hai và hình thứ ba có cùng
chiều rộng và chiều dài của hình thứ ba là 24cm. Tính diện tích mỗi hình chữ nhật đó.
Câu III. (4,0 điểm)
1. Tìm 𝑥𝑥, 𝑦𝑦 biết: |𝑥𝑥2 − 1| + 2 = 6 (𝑦𝑦+1)2+3
2. Chứng minh không tồn tại 4 số nguyên tố a, b, c, d khác nhau thỏa mãn: 2 2 2 2 a = b + c + d .
Câu IV. (6,0 điểm)
Cho tam giác ABC có AB < AC. Từ trung điểm D của BC vẽ đường vuông góc với tia
phân giác của góc A tại H. Đường thẳng này cắt các tia AB tại E và AC tại F. Vẽ tia BM song song với EF (M∈AC). a) Chứng minh ∆ABM cân.
b) Chứng minh: MF = BE = CF.
c) Qua D vẽ đường thẳng vuông góc với BC cắt tia AH tại I. Tính  IFC
Câu V. (2,0 điểm)
Trong một bảng ô vuông gồm 5x5 ô vuông, người ta viết vào mỗi ô vuông chỉ một
trong ba số 1; 0 hoặc -1. Chứng minh rằng trong các tổng của 5 số theo mỗi cột, mỗi
hàng, mỗi đường chéo phải có ít nhất hai tổng bằng nhau.
------------------ Hết -----------------
Họ tên thí sinh:…… ……........................………… Số báo danh: ……………......................
Giám thị số 1:……………………….......…… Giám thị số 2: …...........……………………
Giám thị không giải thích gì thêm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT CHẤT LƯỢNG HUYỆN NÔNG CỐNG
MŨI NHỌN CẤP HUYỆN NĂM HỌC 2023 - 2024 MÔN: TOÁN 7 Câu NỘI DUNG Điểm 15 9 20 9 5.4 .9 − 4.3 .8 1.A = 10 19 29 6 − 5.2 .6 7.2 .27 2 15 . 2 9 . 2 20 9 . 3 = 2. 5 3 . − 2 3 . 2 . 0,5đ 10 19 19 29 6 . 3 2 . 5 2 . 3 . − . 7 2 .3 2 . 29 318(5 2 . − 32 ) 1,0đ = 229 3 . 18( 3 . 5 − 7) − 0,5đ =10 9 1 = 15 − 7 8 I 2. 4,0 điểm 1  1   1   1   1 B .1 .1 .1 .....1  = + + + + 2 1.3 2.4 3.5 2022.2024         
1 1.3+1  2.4 +1  3.5 +1  2022.2024 +1 . . . .....  = 2 1.3 2.4 3.5  2022.2024  0,5đ        
1  2 2   3 3   4 4   2023 20 = . 23 
 . . . . . . . . . 0,5đ 2 
 1 3   2 4   3 5   2022 2024 
1.2.3.4.....2022.2023 2.3.4.....2022.2023 = . 0,5đ 1.2.3.4.....2022 2.3.4......2023.2024 2023 0,5đ = 2024 II 1. 4,0 1 1 1 1
điểm 1+ (1+ 2) + (1+ 2 + 3) + (1+ 2 + 3+ 4) +......+ (1+ 2 + 3+....+ x) =115 2 3 4 x
1  2.3  1  3.4  1  4.5  1  x(x + ) 1  1+ + +     . +   .......+ . =   115
2  2  3  2  4  2  x  2  0,25đ 3 4 x +1 1 1+ + +.....+
= .[2 + 3+ 4 +......+ (x +1)] =115 2 2 2 2 0,5đ 1  x(x + 3) .  =115 0,5đ 2  2    x(x + 3) = 460
Mà x là số nguyên dương nên x và x+3 là ước dương của 460 nên x = 20 0,25đ Vậy x=20
Từ đề bài ta có x, y, z và x + y + z khác 0 0,25đ
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
y + z +1 x + z + 2 x + y − 3 1 = = = = 2 x y z x + y + z 5 , 0 0,5đ − x +1 5 , 0 − y + 2 5 , 0 − z − 3
⇒ x + y + z = 5 , 0 ⇒ = = = 2 x y z 1 5 5
⇒ x = ; y = ; z = − 0,5đ 2 6 6
Khi đó ta có 4048.x + y2023 + z2023 = 4048. 1 + 0 = 2024 2
Vậy với x, y, z là các số thực thỏa mãn
y + z +1 x + z + 2 x + y − = =
3 = 1 thì giá trị của biểu thức A= 4046.x x y z x + y + z 0,25đ + y2023 + z2023 là 2023
3.Gọi diện tích các hình chữ nhật thứ nhất, thứ hai, thứ ba lần lượt là S ,S ,S ; 1 2 3
các chiều dài và chiều rộng tương ứng lần lượt là
d ,r ;d ,r ;d ,r S ,S ,S ,d ,r ;d ,r ;d ,r > 0 . Theo đề bài ta có: 1 1 2 2 3 3 ( 1 2 3 1 1 2 2 3 3 ) 0,25đ S 4 S 7 1 2 = ;
= và d = d ;r + r = 27;r = r ; d = 24 S 5 S 8 1 2 1 2 2 3 3 2 3 Từ S 4 d .r r r r r + r 27 1 1 1 1 1 2 1 2 = = = ⇒ = = = = 3 (Do d = d ) 0,25đ 1 2 S 5 d .r r 4 5 4 + 5 9 2 2 2 2
⇒ r =12cm; r =15cm ⇒ r =15cm 1 2 3 0,25đ Từ S 7 d .r d 7 7 2 2 2 2 = = =
(Do r = r ) ⇒ d = .d = .24 = 21cm ⇒ d = 21cm 2 3 2 3 S 8 d .r d 8 8 1 3 3 3 3 Từ đó tính được 2 2 2
S = 252cm ; S = 315cm ; S = 360cm 1 2 3
Vậy diện tích các hình chữ nhật thứ nhất, thứ hai, thứ ba lần lượt là 0,25đ 252 cm2; 315cm2; 360cm2.
III Ta có: |𝑥𝑥2 − 1| ≥ 0 => |𝑥𝑥2 − 1| + 2 ≥ 0 + 2 = 2 (1) 0,5 4,0
điểm Mà (𝑦𝑦 + 1)2 ≥ 0 => (𝑦𝑦 + 1)2 + 3 ≥ 3 => 6 ≤ 2 (2) 0,5 (𝑦𝑦+1)2+3
Từ (1) và (2) => |𝑥𝑥2 − 1| + 2 = 6 (𝑦𝑦+1)2+3 Khi �𝑥𝑥2 − 1 = 0 0,5
𝑦𝑦 + 1 = 0 => �𝑥𝑥 = 1 ℎ𝑜𝑜ặ𝑐𝑐 𝑥𝑥 = −1 𝑦𝑦 = −1 0,5
Vậy 𝑥𝑥 = −1, 𝑦𝑦 = 1 ℎoặc 𝑥𝑥 = 1, 𝑦𝑦 = 1
2. Giả sử cả 4 số a, b, c, d đều là số lẻ thì a2, b2, c2, d2 đều chia 4 dư 1. 0,5 Mà : 2 2 2 2
a = b + c + d nên a2 chia 4 dư 3 ( vô lí). Suy ra trong 4 số a, b,
c, d phải có ít nhất một số chẵn. 0,5 Vì 2 2 2 2
a = b + c + d và a, b, c, d khác nhau nên a > b, c, d; a > 2 0,25
Không mất tính tổng quát, giả sử b = 2 thì a2 = 4 + c2 + d2. 0,25
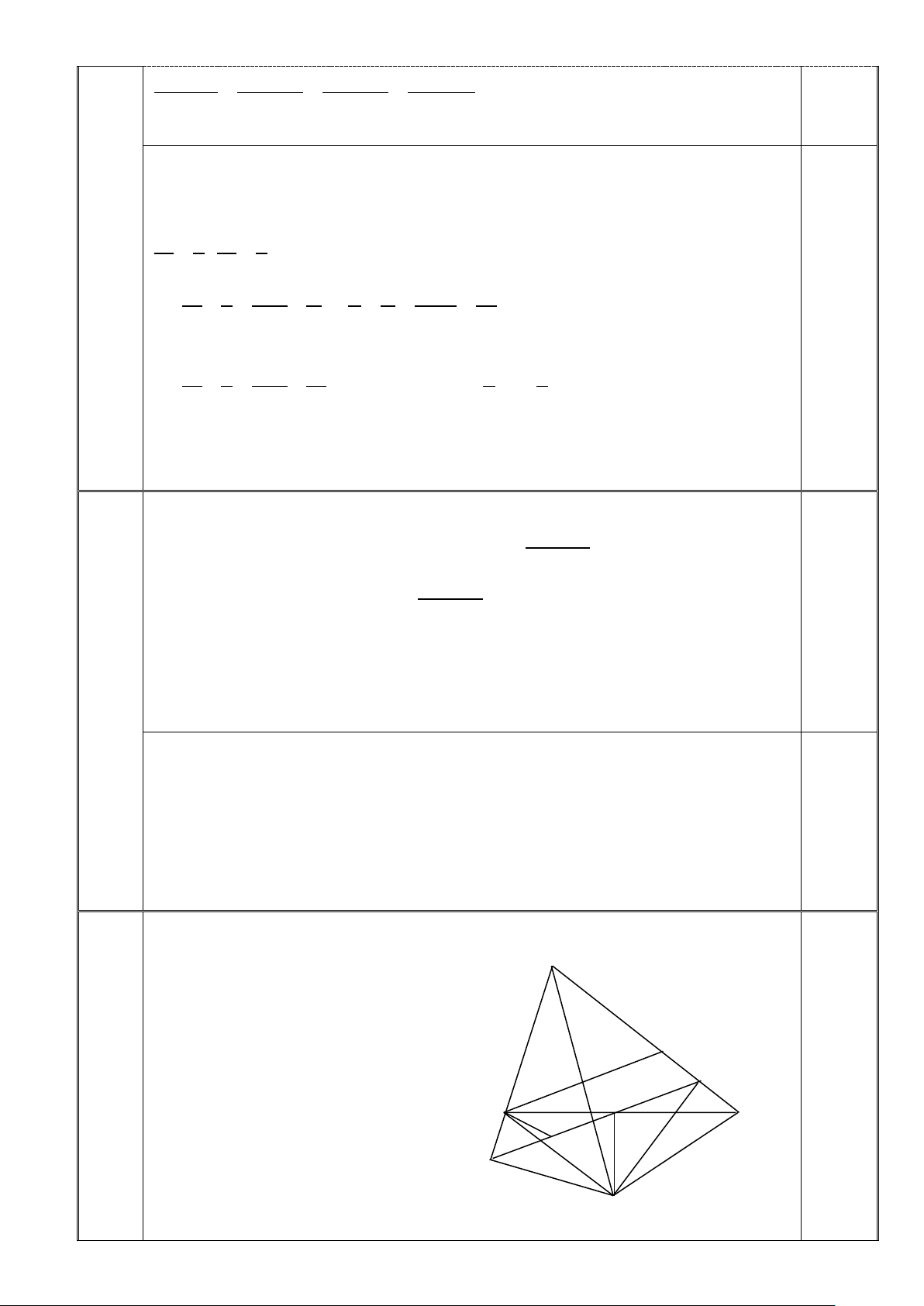
Vì a2 chia 4 dư 1, 4 + c2 + d2 chia 4 dư 2 (vô lí) 0, 5 Suy ra ĐPCM IV 6,0 A điểm M N F B D C K H E I 1.
Gọi giao điểm của AH và BM là N 0,5đ Ta có BM // EF (gt) HA 0,5 đ ⊥ EF (gt) ⇒ AH ⊥ BM hay AN ⊥ BM 0,5đ
Chứng minh được ∆ABN = ∆AMN (g.c.g)
⇒ AB = AM (hai cạnh tương ứng) 0,5đ ⇒ ∆ABM cân tại A 2.Kẻ BK//AC ( K ∈EF)
Chứng minh được ∆AEH = ∆AFH (g.c.g) ⇒ AE = AF
Mà AB = AM ⇒ AE – AB = AF – AM ⇒ BE = MF (1) 0,5đ
Chứng minh ∆BDK = ∆CDF (g.c.g) ⇒ BK = CF (2) Ta có  = 
BKE AFE (hai góc đồng vị của BK // AC) 0,5đ và  = 
AEF AFE (vì ∆AEF cân tại A) 0,5đ ⇒  = 
BKE BEF ⇒ ∆EBK cân tại B ⇒ BE = BK (3)
Từ (1); (2) và (3) ta có MF = BE = CF 0,5đ
Nối IB, IC và chứng minh được IB = IC ( Tính chất đường trung trực)
Chứng minh ∆AIE = ∆AIF (c.g.c) ⇒ IE = IF và  =  AEI AFI (4) 0,5đ 0,5đ
Chứng minh ∆IEB = ∆IFC (c.c.c)  =  BEI IFC hay  =  AEI IFC (5) Từ (4) và (5)  =  AFI IFC mà  +  0
AFI IFC =180 (hai góc kề bù) 0,5đ  =  0 AFI IFC = 90 0,5đ Vậy  0 IFC = 90 V
Ta có 5 cột, 5 dòng , 2 đường chéo nên được 12 tổng . Mỗi ô vuông nhận một
2,0 trong ba giá trị 1; 0 hoặc -1 nên mỗi tổng nhận được một trong các giá trị từ -5 điểm đến 5. 1,0đ
Ta có 11 số nguyên từ -5 đến 5 là -5; -4; -3; ….; 3; 4; 5.
Vậy theo nguyên tắc Dirichlet phải có ít nhất hai tổng bằng nhau 1,0đ Chú ý:
- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám khảo tự phân
chia trên cơ sở tham khảo điểm thành phần của đáp án.
- Các trường hợp khác tổ chấm thống nhất phương án chấm.