Đề KSCL Toán 12 thi TN THPT 2025 lần 1 trường THPT Sầm Sơn – Thanh Hóa có đáp án

SỞ GD&ĐT THANH HÓA
KÌ THI CHẤT LƯỢNG TN NĂM 2025 - LẦN THỨ 1
TRƯỜNG THPT SẦM SƠN NĂM HỌC 2024 - 2025 Môn: Toán, Lớp 12
(Đề thi có 05 trang)
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:…………………………………………………..........SBD:……………...... 201
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
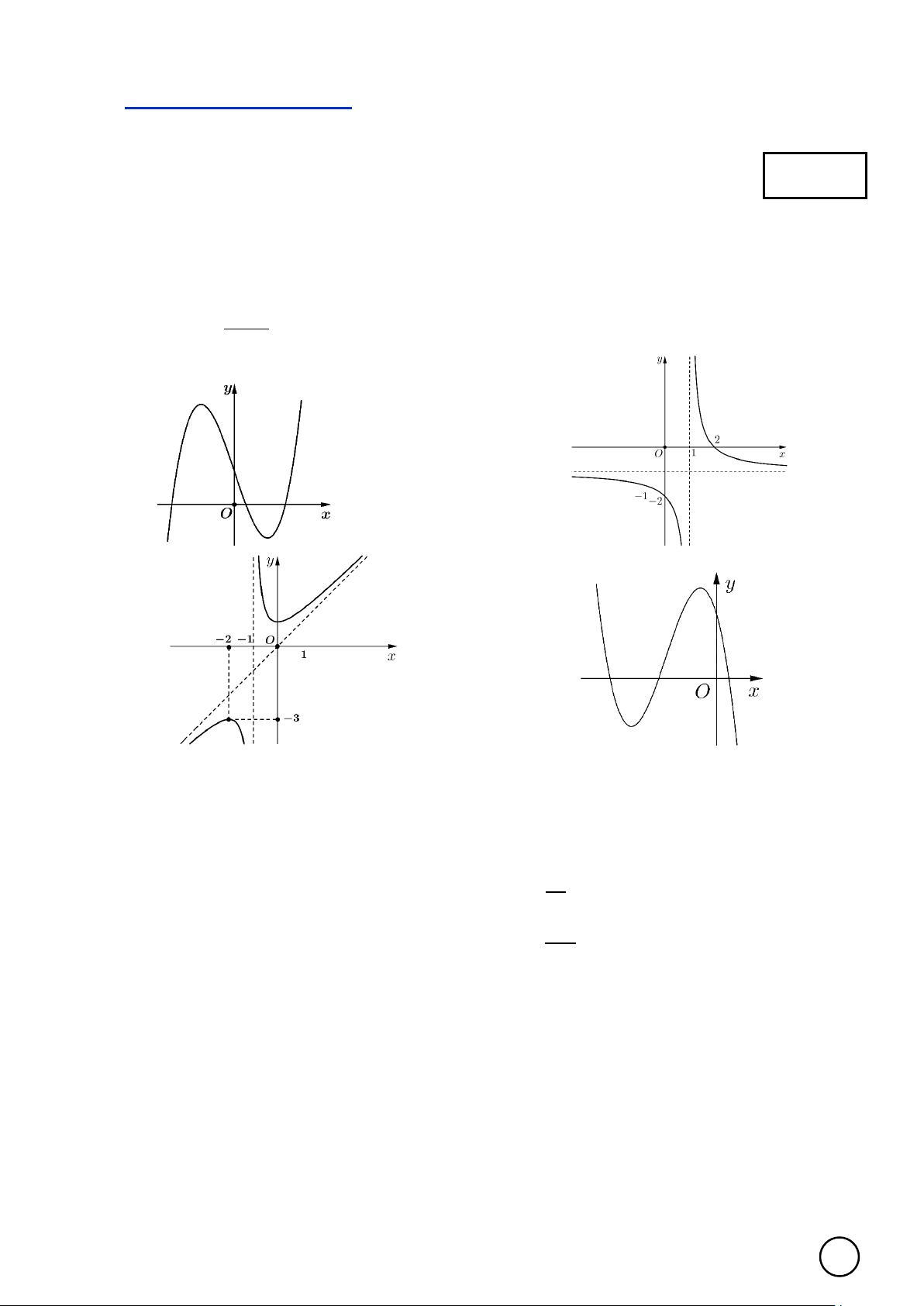
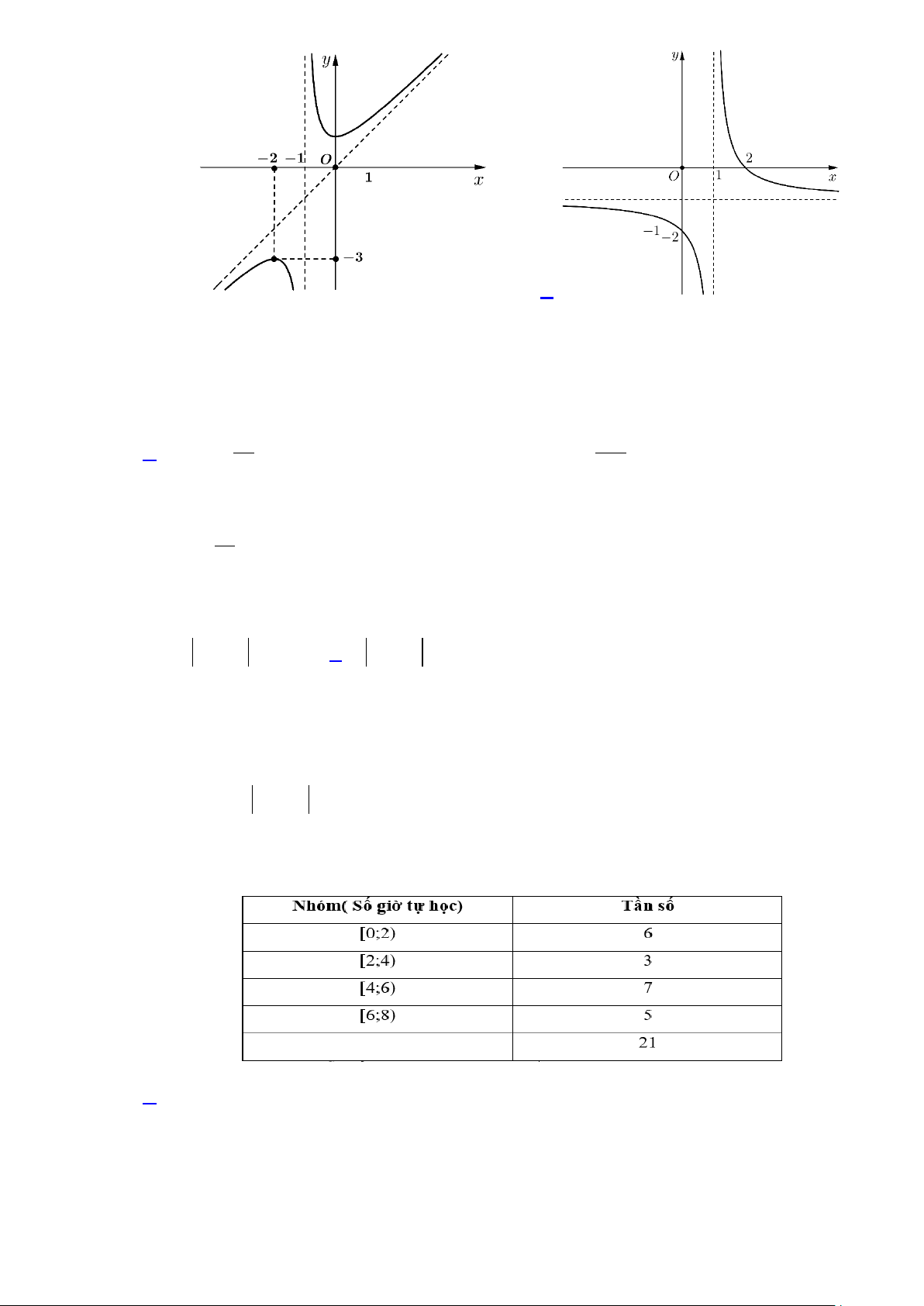
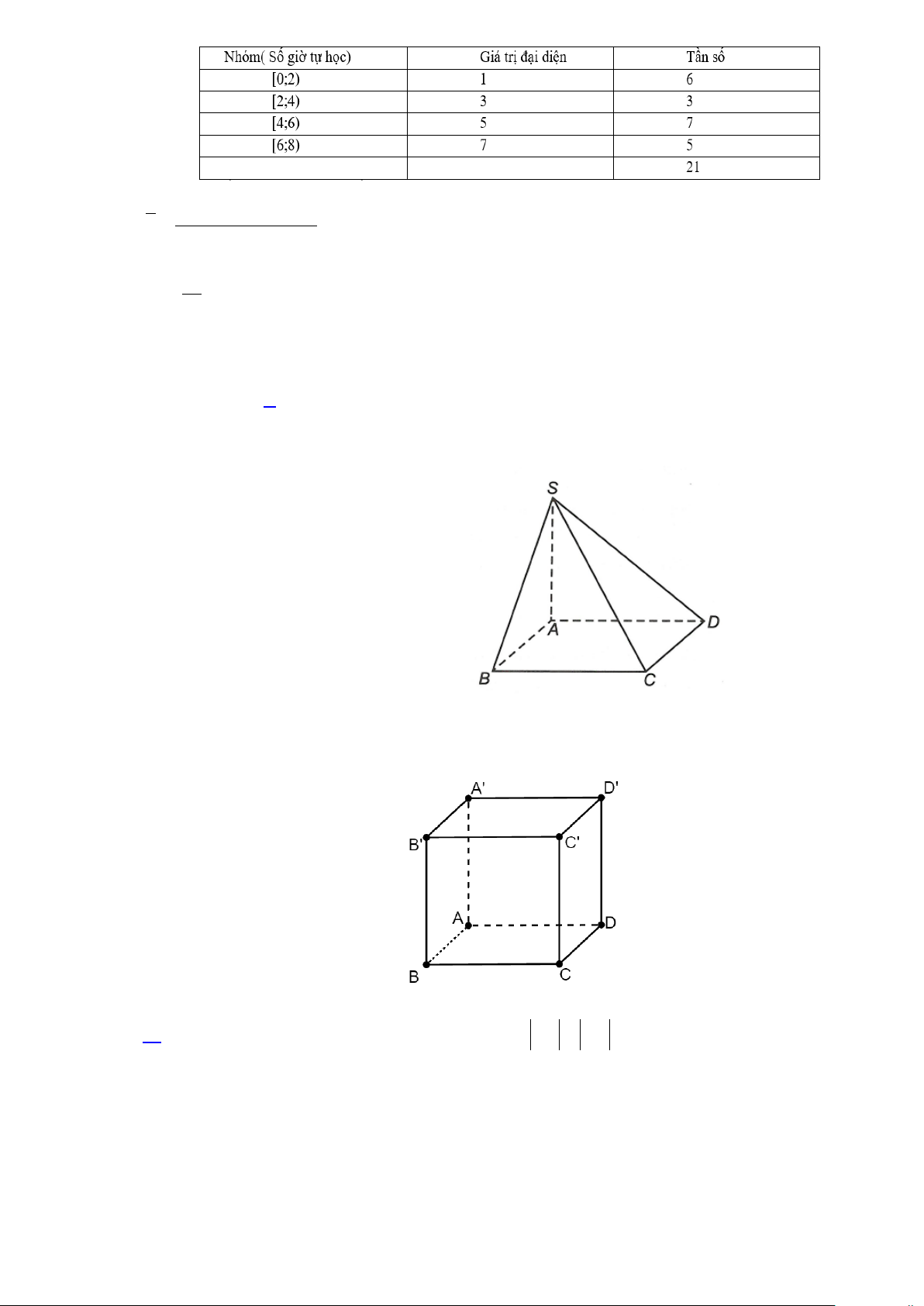
sinh chỉ chọn một phương án. Câu 1. Cho hàm số −x + 2 y =
, đồ thị của hàm số đã cho là đồ thị nào sau đây x −1 A. . B. . C. . D. .
Câu 2. Tính đạo hàm của hàm số 𝑦𝑦 = 2sin𝑥𝑥 + 1
A. 𝑦𝑦′ = 2cos𝑥𝑥 + 1.
B. 𝑦𝑦′ = −2cos𝑥𝑥.
C. 𝑦𝑦′ = −2cos𝑥𝑥 + 1.
D. 𝑦𝑦′ = 2cos𝑥𝑥.
Câu 3. Nghiệm của phương trình x+2 3 = 27 là A. x = 2 − . B. x = 1 − . C. x =1.
D. x = 2 .
Câu 4. Khẳng định nào dưới đây đúng? 6
A. x dx = x + ∫ 5 4 5 C . B. 5 x x dx = + ∫ C . 65 C. = + ∫ 5 6 x dx x C . D. 5 x x dx = + ∫ C . ln 5
Câu 5. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho điểm 𝐴𝐴(1; −2; 3). Hình chiếu vuông góc của điểm 𝐴𝐴 trên mặt phẳng
(𝑂𝑂𝑥𝑥𝑦𝑦) là điểm 𝑀𝑀 có tọa độ là
A. 𝑀𝑀(1; −2; 0).
B. 𝑀𝑀(0; −2; 3).
C. 𝑀𝑀(1; 0; 3).
D. 𝑀𝑀(2; −1; 0).
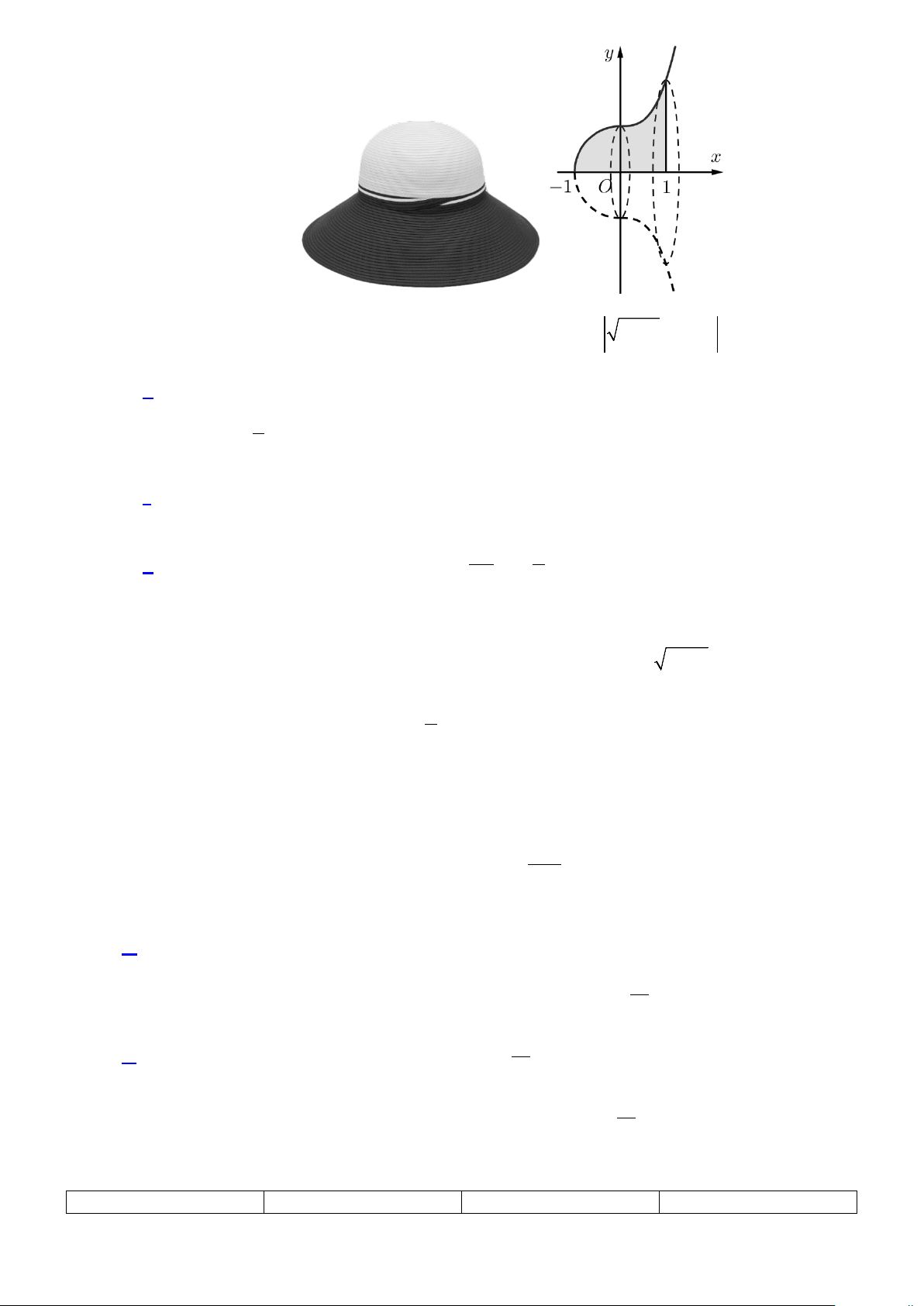
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy.
Khẳng định nào sau đây sai?
A. BC ⊥ (SAB).
B. CD ⊥ (SAD).
C. BD ⊥ (SAC).
D. AC ⊥ (SBD).
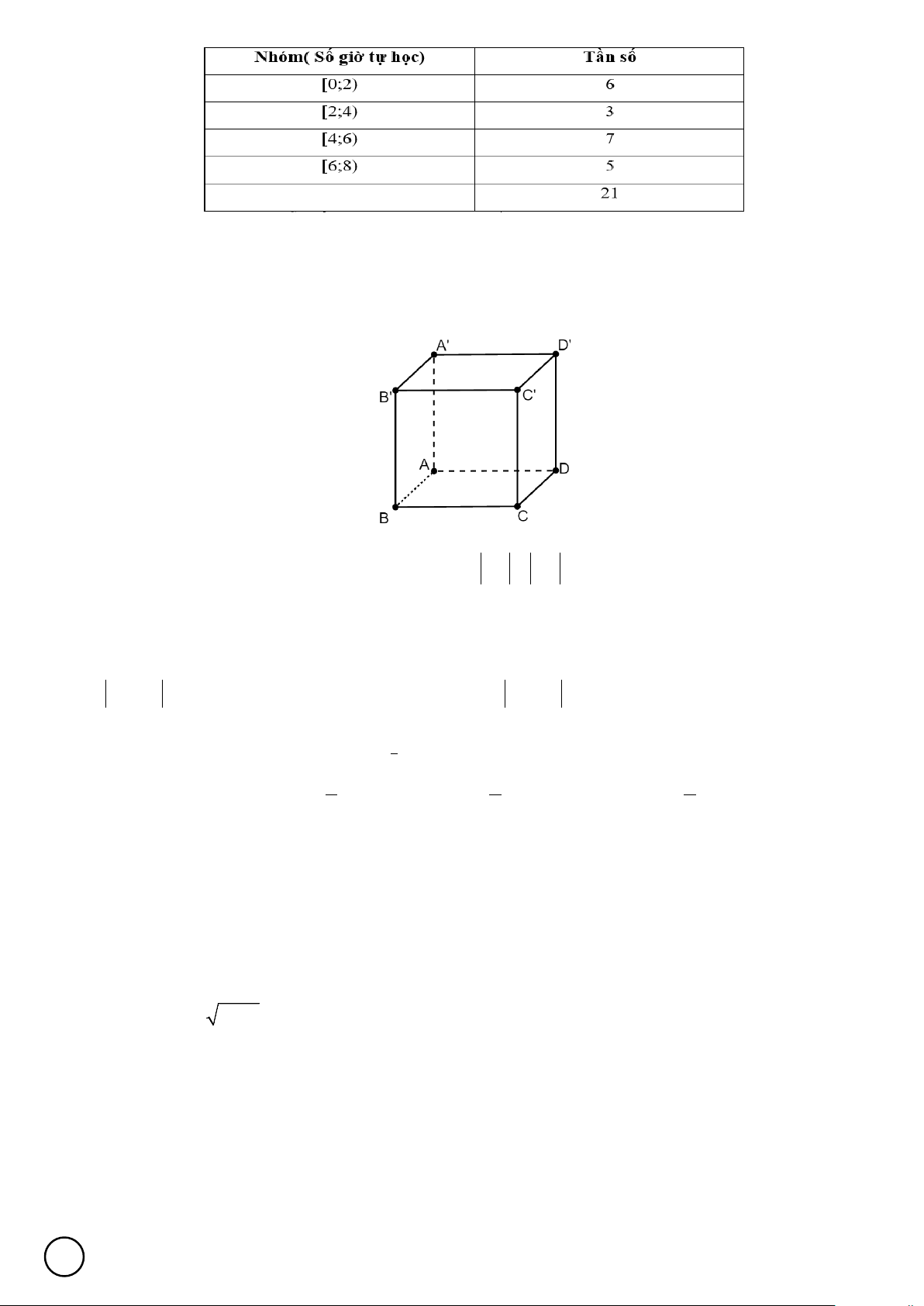
Câu 7. Bảng dưới đây thống kê số giờ tự học ở nhà của 21 học sinh lớp 12 được hỏi ngẫu nhiên tại một trường
THPT của Thành phố Sầm Sơn. Mã đề 201 1/5
Khi đó phương sai của mẫu số liệu ghép nhóm trên là A. 5,19 . B. 2,28 . C. 4,05 . D. 5,29.
Câu 8. Cho cấp số cộng (u , biết và . Giá trị của n ) u = 3 u = 7 u bằng 2 4 15 A. 27 . B. 35. C. 31. D. 29 .
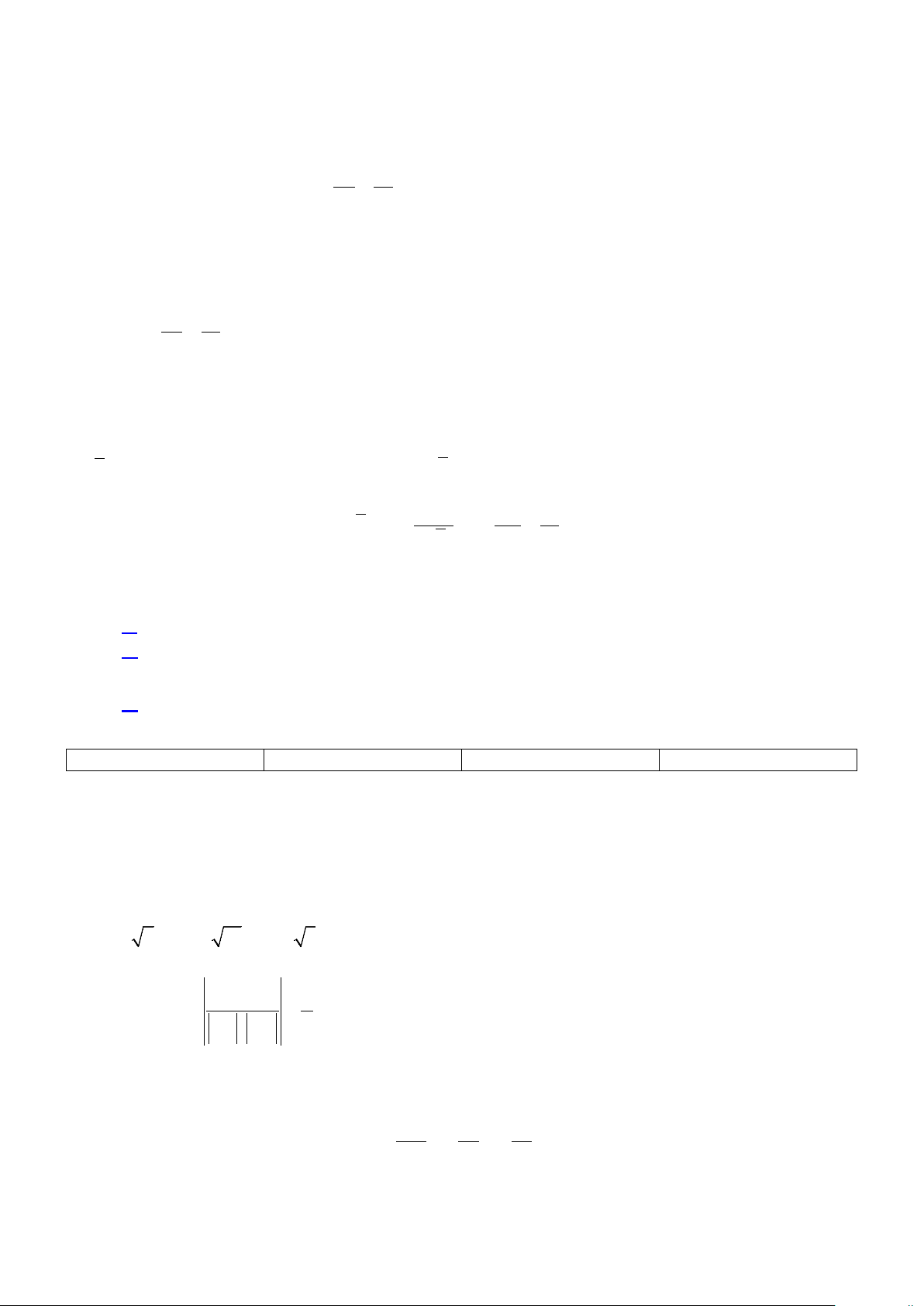
Câu 9. Cho hình lập phương ABC . D A′B C ′ D ′ ′ .
Đẳng thức nào sau đây sai?
     
A. BA + BC + BB′ = BD′ .
B. AB = BC .  
  
C. AB = AD .
D. CB + CD = CA.
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − 4x , trục hoành và hai đường thẳng x = 0 ; x = 3 bằng 3 3 3 3 A. 3
x − 4xdx ∫ .
B. ∫( 3x −4x)dx. C. 3
π x − 4xdx ∫ .
D. π ∫(x −4x)2 3 dx . 0 0 0 0
Câu 11. Tập nghiệm của bất phương trình log x − 3 ≤1 1 ( ) 2 A. ( ; −∞ log 7 . B.  7      ;  −∞ . C. 7 ;+ ∞ . D. 7  ;+ ∞ . 2 ) 2       2   2 
Câu 12. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho hai vectơ 𝑎𝑎⃗ = (−3 ; 1 ; 0), 𝑏𝑏�⃗ = (0 ; −1 ; 2). Vectơ 𝑎𝑎⃗ + 𝑏𝑏�⃗ có tọa độ là
A. (−3 ; 0 ; 2).
B. (−3 ; 2 ; −2).
C. (−1 ; 0 ; 0).
D. (−3 ; 2 ; 2).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.
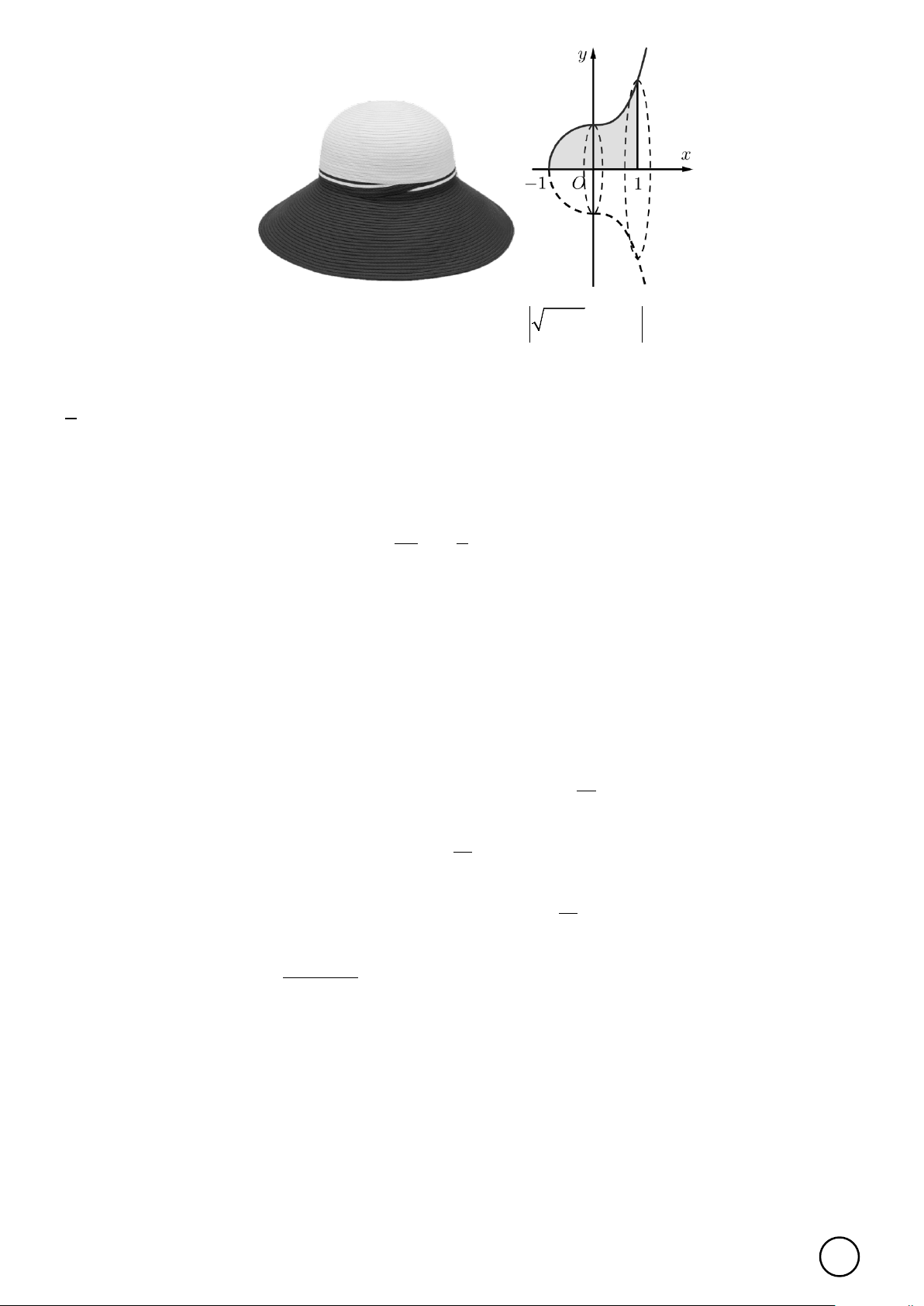
Câu 1. Giả sử chiếc nón rộng vành sau có thể mô hình hóa bằng cách cho hình phẳng (H ) giới hạn bởi đồ thị 3 x +1 khi 0 < x ≤  1
hàm số y = f (x) = 
, trục Ox và các đường thẳng x = 1
− và x =1 quay quanh trục 2
 1− x khi −1≤ x ≤ 0
Ox (đơn vị trên trục là dm). Xét tính đúng sai của các khẳng định sau: 2/5 Mã đề 201 1
a) Diện tích hình phẳng (H ) được tính theo công thức 2 3 S =
1− x + x +1 dx ∫ . 1 −
b) Diện tích hình phẳng giới hạn bới đồ thị hàm số y = f (x) với trục hoành và hai đường thẳng x = 0; x =1 là 5 dm2. 4 1 − 1
c) Công thức tính thể tích khối tròn xoay trên là V = π ( 2 x − ) 1 dx +π ( 6 3 x + 2x + ∫ ∫ )1dx. 0 0 aπ a
d) Nếu thể tích của khối tròn xoay có dạng
với là phân số tối giản thì a + b =139. b b
Câu 2. Trong không gian Oxyz, cho các điểm (
A 0;1;1), B(1;2;−1), C( 1 − ;2;2), D( 3 − ;3;3).   
a) Nếu vectơ u(a; ;
b c) vuông góc với cả hai vectơ AB và CD thì a = b = . c
b) Hình chiếu của A lên mặt phẳng (Oxy) có toạ độ là (0; 1; 0). c) ,
A B, C là ba đỉnh của một tam giác cân.
d) Góc giữa hai đường thẳng AB và CD bằng 0 60 .
Câu 3. Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Khi đó:
a) Số phần tử của không gian mẫu là 45 .
b) Xác suất để trong hai người được chọn không có nữ nào cả bằng 11 . 15
c) Xác suất cả hai người được chọn đều là nữ bằng 1 . 15
d) Xác suất để trong hai người được chọn có ít nhất một nữ bằng 14 . 15 2 Câu 4. Cho hàm số x − x + 2
y = f (x) =
có đồ thị (C). x − 2
a) Tập xác định của hàm số là D =  \{ } 2 .
b) Hàm số đồng biến trên (0;2) .
c) Đường thẳng y = x +1 là tiệm cận xiên của đồ thị (C).
d) Có 2024 giá trị nguyên của m∈[0;2025] để đường thẳng y = m cắt đồ thị (C) tại hai điểm phân biệt.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Mã đề 201 3/5
Câu 1. Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau t (giây) (0 ≤ t ≤ 20) từ lúc bắt đầu được
cho bởi công thức h(t) 4 3 49 2 98 = − t + t −
t + 20. Trong khoảng thời gian ( ;
a b) (đơn vị tính là giây) tàu 255 85 17
lượn đi lên. Tính a + 2b .
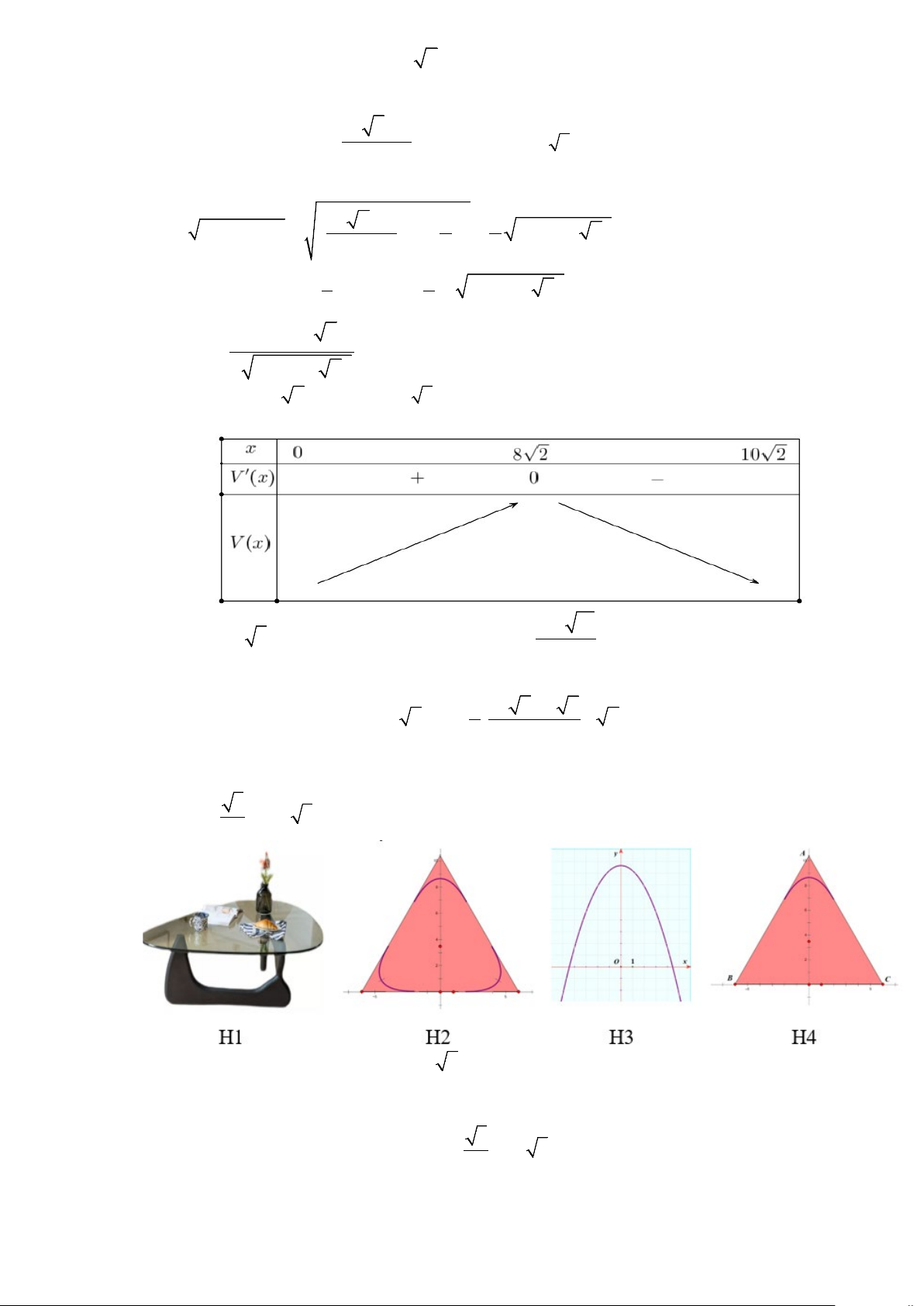
Câu 2. Một tấm bạt hình vuông cạnh 20m như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm bạt
rồi gập và may lại (các đường may không đáng kể), nhằm mục đích phủ lên tháp đèn trang trí (tháp dạng hình
chóp tứ giác đều) để tránh hư hại tháp khi trời mưa.
Biết khối chóp hình thành sau khi gập và may lại cần thể tích lớn nhất thì mới phủ kín tháp đèn. Hỏi phần
diện tích tấm bạt bị cắt là bao nhiêu 2
m để đảm bảo yêu cầu trên.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh  a, ABC 60° =
. Gọi O là giao điểm của AC và a BD . Biết rằng 3
SO ⊥ (ABCD), SO =
. Khoảng cách từ O đến mặt phẳng (SCD) bằng ma với m là 4 n n
phân số tối giản, m > 0,n > 0 . Giá trị 2m + n bằng bao nhiêu?
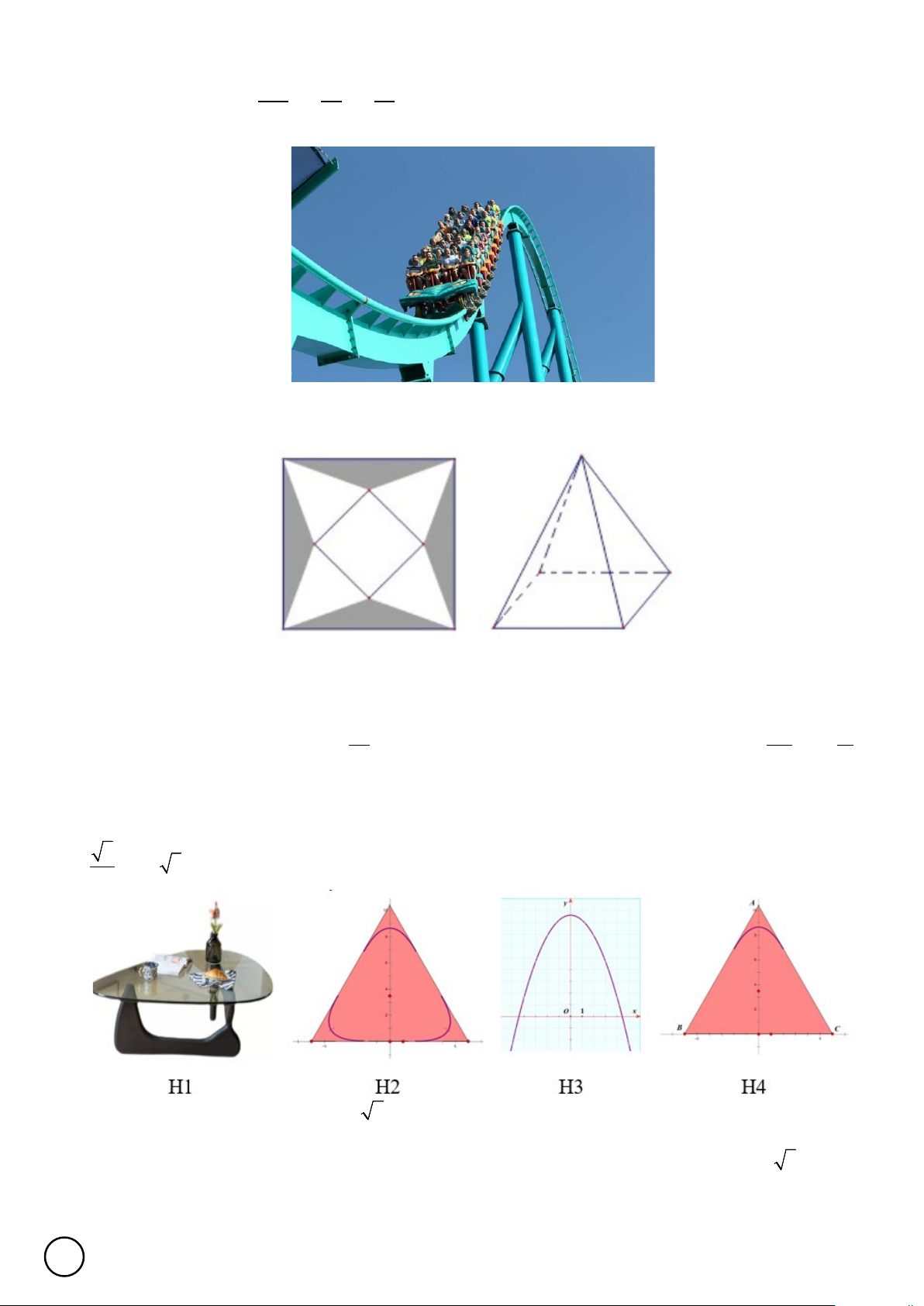
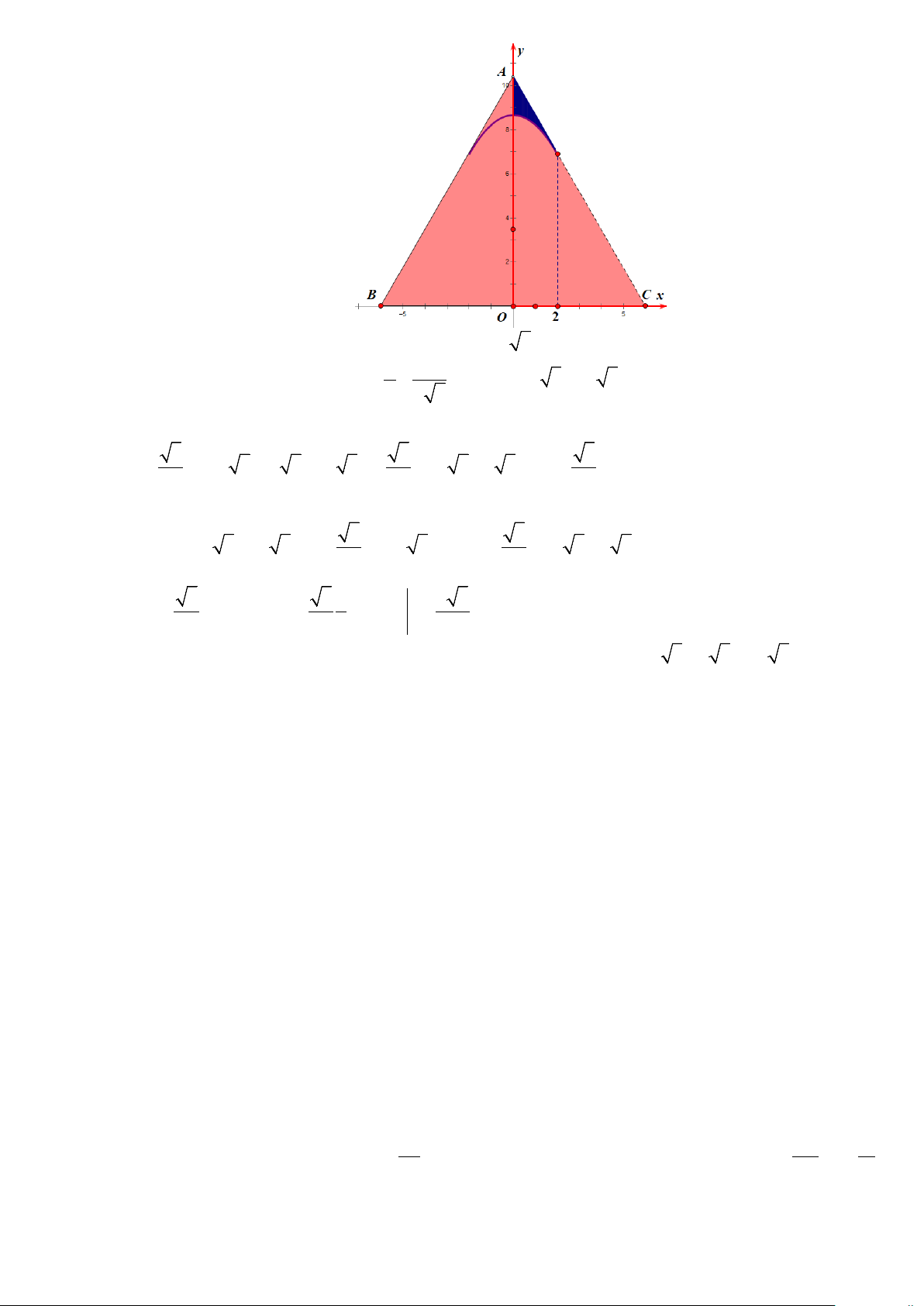
Câu 4. Một tấm kính làm mặt bàn (H1) có hình dáng tam giác đều với 3 đỉnh được làm cong (H2). Biết cạnh
tấm kính tam giác ban đầu bằng 12 (dm). Để cắt góc được đẹp thì người ta dùng đường Parabol (P): 3 2 y = −
x + 5 3 (H3) có hai nhánh tiếp giáp với hai cạnh của tam giác (H4) 4
Diện tích mặt kính là một số có dạng a b . Tính tổng a + b .
Câu 5. Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ 
Oxyz như hình vẽ với độ dài đơn vị trên mỗi trục tọa độ là 1. Biết AB = ( ; a ;
b c) . Tính T = 2a + 2b 3 + c . 4/5 Mã đề 201
Câu 6. An và Bình thi đấu với nhau một trận bóng bàn. Người nào thắng trước 3 séc sẽ giành chiến thắng
chung cuộc. Xác suất An thắng mỗi séc là 0,4 (không có hoà). Xác suất để An thắng chung cuộc bằng bao
nhiêu (Kết quả làm tròn đến hàng phần trăm)?
-------------- HẾT -------------- Mã đề 201 5/5
TRƯỜNG THPT SẦM SƠN TỔ TOÁN BẢNG ĐÁP ÁN
KÌ THI CHẤT LƯỢNG TN NĂM 2025 - LẦN THỨ 1 NĂM HỌC 2024 - 2025
PHẦN I: Trắc nghiệm nhiều lựa chọn
- Mỗi câu đúng được 0,25 điểm. Mã đề 1 2 3 4 5 6 7 8 9 10 11 12 201 B D C B A D A D C A C A
PHẦN II: Trắc nghiệm đúng sai
- Điểm tối đa mỗi câu là 1 điểm.
- Đúng 1 ý được 0,1 điểm; đúng 2 ý được 0,25 điểm; đúng 3 ý được 0,5 điểm; đúng 4 ý được 1 điểm. Mã đề Câu 1 Câu 2 Câu 3 Câu 4 201
a)S - b)Đ - c)Đ - d)Đ a)Đ - b)Đ - c)S - d)Đ a)Đ - b)S - c)Đ - d)S a)Đ - b)S - c)Đ - d)S
PHẦN III: Trắc nghiệm trả lời ngắn - tự luận
- Mỗi câu đúng được 0,5 điểm. Mã đề Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 201 42 80 14 35 50 0,32 SỞ GD-ĐT THANH HOÁ
KÌ THI CHẤT LƯỢNG TN NĂM 2025 - LẦN THỨ 1
TRƯỜNG THPT SẦM SƠN MÔN TOÁN LỚP 12
(Đề thi có 11 trang, gồm 3 phần)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ, tên thí sinh:................................................... Số báo danh:................................................. ĐỀ GỐC SỐ 1
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 26. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Cho cấp số cộng (u , biết u = 3 và u = 7. Giá trị của u bằng n ) 2 4 15 A. 27 . B. 31. C. 35. D. 29 . Lời giải Chọn D u  + d = 3 u  =1
Từ giả thiết u = 3 và u = 7 suy ra hệ phương trình: 1 1 ⇒ . 2 4 u  +3d =   7 d = 2 1
Vậy u = u +14d = 29 . 15 1
Câu 2. Nghiệm của phương trình x+2 3 = 27 là A. x = 2 − . B. x = 1 − .
C. x = 2 . D. x =1. Lời giải Chọn D Ta có: x+2 3 = 27 x+2 3
⇔ 3 = 3 ⇔ x + 2 = 3 ⇔ x =1.
Câu 3. Tập nghiệm của bất phương trình log x − 3 ≤1 1 ( ) 2 A.  7 ;  −∞      . B. 7  ;+ ∞ . C. 7 ;+ ∞ . D. ( ; −∞ log 7 . 2 ) 2        2  2  Lời giải Chọn C  x − 3 > 0 Ta có:  7
log x − 3 ≤1 ⇔  ⇔ x ≥ . 1 ( ) 1 x − 3 ≥ 2 2  2
Câu 4. Tính đạo hàm của hàm số 𝑦𝑦 = 2sin𝑥𝑥 + 1
A. 𝑦𝑦′ = 2cos𝑥𝑥 + 1.
B. 𝑦𝑦′ = −2cos𝑥𝑥 + 1.
C. 𝑦𝑦′ = 2cos𝑥𝑥.
D. 𝑦𝑦′ = −2cos𝑥𝑥. Lời giải Chọn C
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng ( 1; − ) 1 . Câu 5. Cho hàm số −x + 2 y =
, đồ thị của hàm số đã cho là đồ thị nào sau đây x −1 A. . B. . 1 C. . D. . Lời giải Chọn D
Đồ thị của hàm số đó có một đường tiệm cận đứng, một đường tiệm cận ngang, nên ta Chọn D
Câu 6. Khẳng định nào dưới đây đúng?
A. x dx = x + ∫ 5 4 5 C . B. = + ∫ 5 6 x dx x C . 6 5 C. 5 x x dx x = + ∫ C . D. 5 x dx = + C . 6 ∫ ln 5 Lời giải Chọn C 6 5 . x x dx = + C ∫ 6
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − 4x , trục hoành và hai đường thẳng x = 0 ; x = 3 bằng 3 3 3 3 A. 3
π x − 4xdx ∫ . B. 3
x − 4xdx ∫ .
C. π ∫(x −4x)2 3
dx . D. ∫( 3x −4x)dx. 0 0 0 0 Lời giải Chọn B
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − 4x , trục hoành và hai đường thẳng x = 0 , 3 x = 3 là 3
S = x − 4xdx ∫ . 0
Câu 8. Bảng dưới đây thống kê số giờ tự học ở nhà của 21 học sinh lớp 12 được hỏi ngẫu nhiên tại một
trường THPT của Thành phố Sầm Sơn.
Khi đó phương sai của mẫu số liệu ghép nhóm trên là A. 5,19 . B. 5,29. C. 4,05 . D. 2,28 . Lời giải Chọn A Ta có: 2
Số trung bình của mẫu số liệu ghép nhóm là: 6.1 3.3 7.5 5.7 x + + + = = 4,05 21
Phương sai của mẫu số liệu ghép nhóm là: S =  ( − )2 + ( − )2 + ( − )2 + ( − )2 2
1 6. 1 4,05 3. 3 4,05 7. 5 4,05 5. 7 4,05  ≈ 5,19 21  
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy.
Khẳng định nào sau đây sai?
A. BC ⊥ (SAB).
B. AC ⊥ (SBD).
C. BD ⊥ (SAC).
D. CD ⊥ (SAD). Lời giải Chọn B Ta có: BC ⊥ AB +) 
⇒ BC ⊥ (SAB) (A đúng). BC ⊥ SA C  D ⊥ AD +) 
⇒ CD ⊥ (SAD) (D đúng) C  D ⊥ SA BD ⊥ AC +) 
⇒ BD ⊥ (SAC) (C đúng) BD ⊥ SA
Suy ra đáp án B sai.
Câu 10: Cho hình lập phương ABC . D A′B C ′ D ′ ′ .
Đẳng thức nào sau đây sai?    
A. AB = AD .
B. AB = BC .
  
   
C. CB + CD = CA.
D. BA + BC + BB′ = BD′ . Lời giải
Chọn A  
Hai vec tơ AB và AD là 2 vectơ không cùng phương nên chúng không bằng nhau.
Câu 11: Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho điểm 𝐴𝐴(1; −2; 3). Hình chiếu vuông góc của điểm 𝐴𝐴 trên mặt phẳng
(𝑂𝑂𝑥𝑥𝑦𝑦) là điểm 𝑀𝑀 có tọa độ là 3
A. 𝑀𝑀(1; −2; 0).
B. 𝑀𝑀(0; −2; 3).
C. 𝑀𝑀(1; 0; 3).
D. 𝑀𝑀(2; −1; 0). Lời giải: Chọn A
Câu 12: Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho hai vectơ 𝑎𝑎⃗ = (−3 ; 1 ; 0), 𝑏𝑏�⃗ = (0 ; −1 ; 2). Vectơ 𝑎𝑎⃗ + 𝑏𝑏�⃗ có tọa độ là
A. (−3 ; 0 ; 2).
B. (−3 ; 2 ; −2).
C. (−1 ; 0 ; 0).
D. (−3 ; 2 ; 2). Lời giải Chọn A
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a),b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. 2 Câu 13. Cho hàm số x − x + 2
y = f (x) =
có đồ thị (C). x − 2
a) Tập xác định của hàm số là D =  \{ } 2 .
b) Hàm số đồng biến trên (0;2) .
c) Đường thẳng y = x +1 là tiệm cận xiên của đồ thị (C).
d) Có 2024 giá trị nguyên của m∈[0;2025] để đường thẳng y = m cắt đồ thị (C) tại hai điểm phân biệt. Lời giải a) Đúng. b) Sai.
Hàm số đồng biến trên ( ; −∞ 0);(4;+∞) .
Hàm số nghịch biến trên (0;2);(2;4) c) Đúng. Ta có 4
y = f (x) = x +1+ x − 2 (y (x ))  4  (y (x ))  4 lim 1 lim 0; lim 1 lim  − + = = − + = =     0 x→+∞
x→+∞  x − 2 x→−∞ x→−∞   x − 2 
⇒ Tiệm cận xiên của (C) là đường thẳng y = x +1. d) Sai.
Phương trình hoành độ giao điểm của (C) và đường thẳng y = m là: 2 x − x + 2 = m (x ≠ 2) x − 2 2
⇔ x − (m +1)x + 2m + 2 = 0 (1)
Đường thẳng y = m cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai 2
∆ = m − 6m − 7 > 0 m < 1 − nghiệm phân biệt khác 2 (1) ⇔  ⇔  . 2
2 − (m +1).2 + 2m + 2 ≠ 0 m > 7
Do m nguyên và m∈[0;2025] nên có 2025− 7 = 2018 giá trị
Câu 14. Giả sử chiếc nón rộng vành sau có thể mô hình hóa bằng cách cho hình phẳng (H ) giới hạn bởi đồ 3 x +1 khi 0 < x ≤  1
thị hàm số y = f (x) = 
, trục Ox và các đường thẳng x = 1 − và x =1 quay 2
 1− x khi −1≤ x ≤ 0
quanh trục Ox (đơn vị trên trục là dm). Xét tính đúng sai của các khẳng định sau: 4 1
a) Diện tích hình phẳng (H ) được tính theo công thức 2 3 S =
1− x + x +1 dx ∫ . 1 −
b) Diện tích hình phẳng giới hạn bới đồ thị hàm số y = f (x) với trục hoành và hai đường thẳng
x = 0; x =1 là 5 dm2. 4 1 − 1
c) Công thức tính thể tích khối tròn xoay trên là V = π ( 2 x − ) 1 dx +π ( 6 3 x + 2x + ∫ ∫ )1dx. 0 0 π d) a a
Nếu thể tích của khối tròn xoay có dạng
với là phân số tối giản thì a + b =139. b b Lời giải 0 1
a) Sai: Diện tích hình phẳng (H ) được tính bằng công thức: S = ( 2
1− x )dx + ( 3x + ∫ ∫ )1dx 1 − 0 1
b) Đúng: Diện tích S = ( 3 x + ) 5 1 dx = ∫ dm2. 4 0 1 − 1
c) Đúng: Công thức tính thể tích khối tròn xoay trên là V = π ( 2 x − ) 1 dx +π ( 6 3 x + 2x + ∫ ∫ )1dx 0 0 1 − 1 π
d) Đúng: V = π ( 2
x − )dx + π ( 6 3 x + x + ) 97 1 2 1 dx = ∫ ∫
nên a = 97 và b = 42 ⇒ a + b =139 . 42 0 0
Câu 15: Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Khi đó:
a) Số phần tử của không gian mẫu là 45 .
b) Xác suất để trong hai người được chọn không có nữ nào cả bằng 11 . 15
c) Xác suất cả hai người được chọn đều là nữ bằng 1 . 15
d) Xác suất để trong hai người được chọn có ít nhất một nữ bằng 14 . 15 Lời giải a) Đúng b) Sai c) Đúng d) Sai 5
a) Ta có số phần tử của không gian mẫu là 2
n(Ω) = C = 45 . 10
b) Gọi A : "2 người được chọn không có nữ" thì A : "2 người được chọn đều là nam". Ta có 2 n( )
A = C = 21. Vậy 21 7 7 P( ) A = = . 45 15
c) Gọi B : "2 người được chọn là nữ". Ta có 2
n(B) = C = 3. 3 Vậy 3 1 P(B) = = . 45 15
d) Số phần tử của không gian mẫu là: 2 n(Ω) = C . 10
Gọi biến cố D : "Hai người được chọn có ít nhất một người nữ".
⇒ D : "Hai người được chọn không có nữ" 2
⇒ n(D) = C . 7 2 n(Ω) C 8
Vậy xác suất cần tìm là: 7
P(D) =1− P(D) =1− =1− = . 2 n(D) C 15 10
Câu 16: Trong không gian Oxyz, cho các điểm (
A 0;1;1), B(1;2;−1), C( 1 − ;2;2), D( 3 − ;3;3).   
a) Nếu vectơ u(a; ;
b c) vuông góc với cả hai vectơ AB và CD thì a = b = .c
b) Hình chiếu của A lên mặt phẳng (Oxy) có toạ độ là (0; 1; 0). c) ,
A B, C là ba đỉnh của một tam giác cân.
d) Góc giữa hai đường thẳng AB và CD bằng 0 60 . Lời giải a) Đúng b) Đúng c) Sai d) Đúng  
a) Ta có: AB = (1;1; 2 − ) và CD = ( 2 − ;1;1) .      ⊥ 
Do đó u AB  .uAB = 0  a +b − 2c = 0
  ⇔   ⇔ 
⇔ a = b = c u  ⊥ CD  . u CD = 0  2a − + b + c = 0
b) Hình chiếu của A lên mặt phẳng (Oxy) có toạ độ là (0;1; 0).
c) AB = 6, BC = 13, AC = 3 nên ,
A B, C không phải là ba đỉnh của một tam giác cân.   d) A . B CD 1 cos(A ;
B CD) =   = Vậy nên góc giữa hai đường thẳng AB và CD bằng 0 60 . AB . CD 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 17 đến câu 22.
Câu 17. Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau t (giây) (0 ≤ t ≤ 20) từ lúc bắt đầu
được cho bởi công thức h(t) 4 3 49 2 98 = − t + t −
t + 20. Trong khoảng thời gian (a;b) (đơn vị 255 85 17
tính là giây) tàu lượn đi lên. Tính a + 2b . 6 Lời giải Trả lời: 42
Ta có: h (t) 4 2 98 98 ' = − t + t − . 85 85 17 t = h'(t) 4 98 98 17,5 2 = 0 ⇔ − t + t − = 0 ⇔ . 85 85 17  t = 7 Lập Bảng biến thiên
Dựa vào bảng biến thiên ta thấy tàu lượn chuyển động đi lên ( h(t) tăng) trong khoảng(7;17,5)
Khi đó a = 7;b =17,5 . Vậy a + 2b = 7 +17,5.2 = 42.
Câu 18. Một tấm bạt hình vuông cạnh 20m như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm
bạt rồi gập và may lại (các đường may không đáng kể), nhằm mục đích phủ lên tháp đèn trang trí
(tháp dạng hình chóp tứ giác đều) để tránh hư hại tháp khi trời mưa.
Biết khối chóp hình thành sau khi gập và may lại cần thể tích lớn nhất thì mới phủ kín tháp đèn. Hỏi
phần diện tích tấm bạt bị cắt là bao nhiêu 2
m để đảm bảo yêu cầu trên. Lời giải Trả lời: 80
Gọi cạnh đáy hình vuông của tháp là x(m). 7
Độ dài đường chéo tấm bạt bằng 20 2 (m).
Gọi hình chóp tứ giác đều là S.ABCD , Gọi M , N lần lượt là trung điểm AB,CD . 20 2 −
Khi đó MN = x(m) , = x SN (m) với . 2 0 < x <10 2
Gọi O là tâm của hình vuông, ta có 2 2  − x  2 2 20 2  x  1
SO = SN − ON =   − =     800 − 40 2x . 2    2  2 Thể tích khối chóp 1 1 2 V = S .SO = x 800 − x . ABCD 40 2 3 6 20x(80 −5 2x) Ta có V ' = 6 800 − 40 2x
⇒ V ' = 0 ⇔ x = 8 2 với 0 < x <10 2 . Xét bảng biến thiên: 256 10
Vậy khi x = 8 2 thì thể tích khối chóp lớn nhất V = ( 3m). 3
Diện tích phần bị cắt của tấm bạt: −
S = S − S − S = − − = m . hv ABCD ∆SAB ( )2 2 1 20 2 8 2 4. 20 8 2 4. . .8 2 80( 2 ) 2 2
Câu 19. Một tấm kính làm mặt bàn (H1) có hình dáng tam giác đều với 3 đỉnh được làm cong (H2). Biết
cạnh tấm kính tam giác ban đầu bằng 12 (dm). Để cắt góc được đẹp thì người ta dùng đường Parabol (P): 3 2 y = −
x + 5 3 (H3) có hai nhánh tiếp giáp với hai cạnh của tam giác (H4) 4
Diện tích mặt kính là một số có dạng a b . Tính tổng a + b . Lời giải. Trả lời: 35
Diện tích tam giác ABC bằng 2 3 S = = ABC ∆ 12 . 36 3 4
Dựng hệ trục như hình vẽ 8
Vì tam giác ABC đều cạnh bằng 12 nên AO = 6 3 .
Phương trình đường thẳng : x y AC +
=1 ⇔ y = − 3x + 6 3 6 6 3
Ta có phương trình hoành độ giao điểm của (P) và đường thẳng AC 3 2 3 2 3 −
x + 5 3 = − 3x + 6 3 ⇔
x − 3x + 3 = 0 ⇔
(x − 2)2 = 0 ⇔ x = 2 4 4 4
Diện tích phần tô đậm giới hạn bởi (P) , (AC) và trục Oy trong hình bằng 2     
S = ∫ (− 3x +6 3) 2 3 2 3 2 − − x + 5 3  dx  = ∫
x − 3x + 3 dx  4    4      0  0   2 2 3 = ∫(x− )2 3 1 dx = (x − )3 2 3 2 2 = 4 4 3 3 0 0
Vì mặt bàn đối xứng nên diện tích kính cần tính bằng S − = − = 2 (dm ) ∆ S ABC 6 36 3 4 3 32 3
Vậy a + b = 35 .
Câu 20: An và Bình thi đấu với nhau một trận bóng bàn. Người nào thắng trước 3 séc sẽ giành chiến thắng
chung cuộc. Xác suất An thắng mỗi séc là 0,4 (không có hoà). Xác suất để An thắng chung cuộc
bằng bao nhiêu (Kết quả làm tròn đến hàng phần trăm)? Lời giải Trả lời: 0,32
Giả sử số séc trong trận đấu giữa An và Bình là x . Dễ dàng nhận thấy 3 ≤ x ≤ 5. Ta xét các trường hợp:
TH1: Trận đấu có 3 séc ⇒ An thắng cả 3 séc.
Xác suất thắng trong trường hợp này là: P = 0,4.0,4.0,4 = 0,064 . 1
TH2: Trận đấu có 4 séc ⇒ An thua một trong 3 séc đầu và thắng ở séc thứ 4.
Số cách chọn 1 séc để An thua là: 1
C (chú ý xác suất để An thua trong một séc là: 3 0,6 ) 1 3
⇒ P = C .0,4 .0,6 = 0,1152 2 3
TH3: Trận đấu có 5 séc ⇒ An thua hai trong 4 séc đầu và thắng ở séc thứ 5.
Số cách chọn 2 séc để An thua là: 2
C (chú ý xác suất để An thua trong một séc là: 4 0,6 ) 2 3 2
⇒ P = C .0,4 .0,6 = 0,13824 3 4
Như vậy xác suất để An thắng chung cuộc là: P = P + P + P = 0,31744 ≈ 0,32 . 1 2 3
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh  a, ABC 60° =
. Gọi O là giao điểm của AC và a BD . Biết rằng 3
SO ⊥ (ABCD), SO =
. Khoảng cách từ O đến mặt phẳng (SCD) bằng ma với m 4 n n
là phân số tối giản, m > 0,n > 0 . Giá trị 2m + n bằng bao nhiêu? 9 Lời giải Trả lời: 14
Gọi I là hình chiếu của O trên CD, H là hình chiếu của O trên SI .
Thấy rằng CD ⊥ (SOI) nên CD ⊥ OH . Mà OH ⊥ SI nên OH ⊥ (SCD) . Suy ra
d(O,(SCD)) = OH . Vì  AB BC, ABC 60° = =
nên tam giác ABC đều. Suy ra a 3 = = , a OB OD OA = OC = . 2 2 a 3 a ⋅
Xét tam giác vuông DOC có 2 2 a 3 OI = = a 4 3a a 3 2 2 ⋅    
Xét tam giác vuông SOI có 3a a 3 a 3 4 4 3 = +     = và a SI OH = = . 4  4    2   a 3 8 2 Suy ra m 3
= . Vậy 2m + n = 2.3+ 8 =14 . n 8
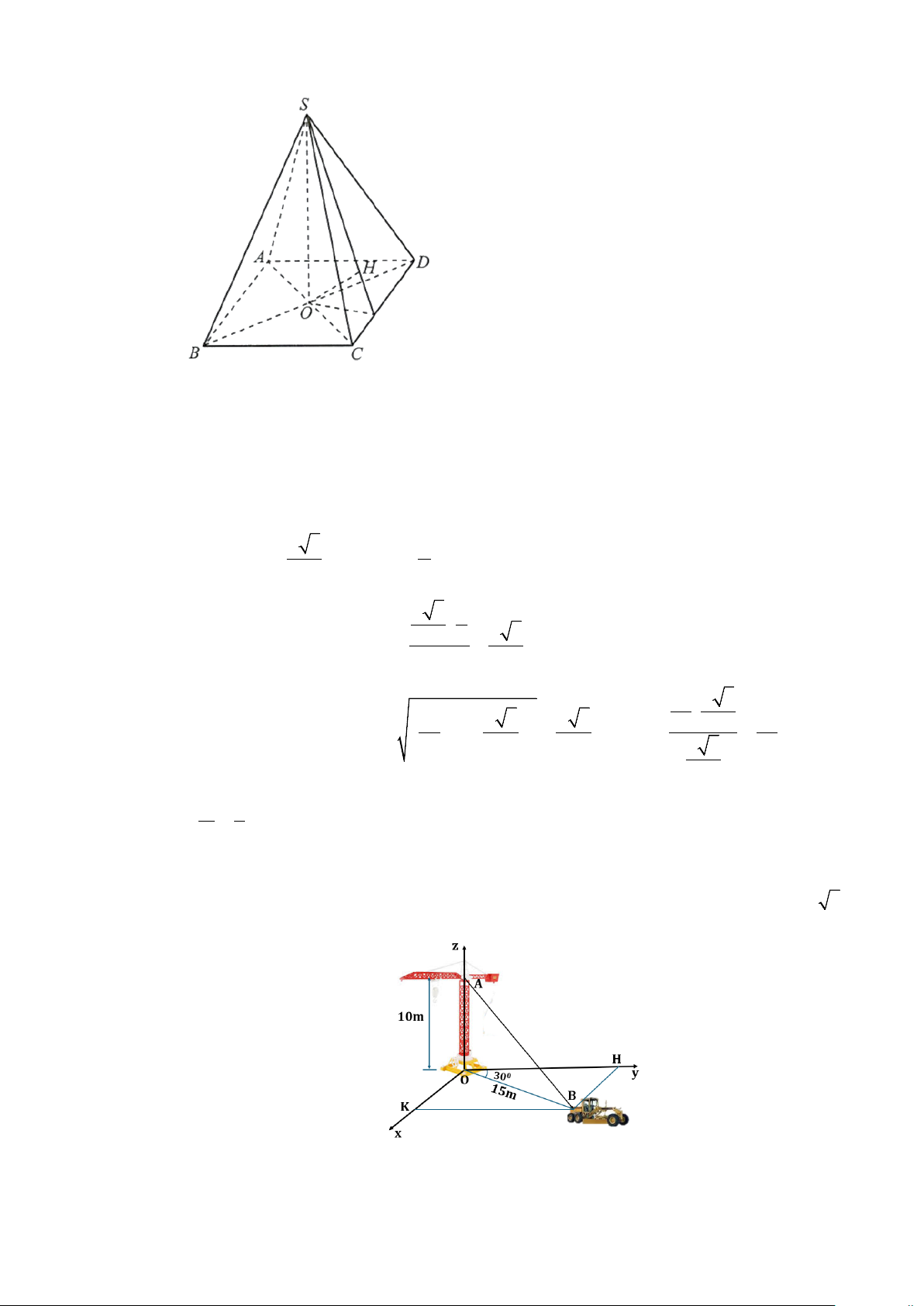
Câu 22. Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa 
độ Oxyz như hình vẽ với độ dài đơn vị trên mỗi trục tọa độ là 1. Biết AB = ( ; a ;
b c) . Tính T = 2a + 2b 3 + c . Lời giải Trả lời: 50 10
Xét tam giác OBH vuông tại H có 0 OK = BH = . OB sin 30 = 7,5 , 0 15 3 OH = . OB cos30 = . Vì tứ giác 2
OHBK là hình chữ nhật nên x = x = , 15 3 y = y = . B K 7,5 B H 2  
Do B nằm trên mặt phẳng (Oxy)nên 15 3 B7,5; ;0 . 2     
Điểm A nằm trên trục Oz và có cao độ bằng 10 nên A(0;0;10).    Vậy 15 3 AB = 7,5; ;−10 và 15 3
T = 2a + 2b 3 + c = 2.7,5 + 2. . 3 + ( 10) − = 50 . 2      2
………………………………..HẾT……………………………
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. 11
Xem thêm: ĐỀ THI THỬ THPT MÔN TOÁN
https://toanmath.com/de-thi-thu-thpt-mon-toan
Document Outline