Đề KSCL Toán 9 năm 2020 – 2021 phòng GD&ĐT quận Hai Bà Trưng – Hà Nội

PHÒNG GIÁO DỤC & ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 9 QUẬN HAI BÀ TRƯNG NĂM HỌC 2020-2021
MÔN: TOÁN; Ngày khảo sát 24/5/2021 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
Bài 1 (2,0 điểm) x −1 1 2 − x Cho 2 biểu thức A = và B = −
với x ≥ 0; x ≠ 4 x − 2 x +1 x x +1 1
a) Tính giá trị của biểu thức A khi x = 4
b) Rút gọn biểu thức B
c) Cho P = ( A − )
1 .B . Tìm các giá trị của x để P ≥ 2 .
Bài 2 (2,0 điểm)
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai tổ công nhân may một số khẩu trang để phục vụ cho vùng dịch Covid-19. Nếu hai tổ cùng làm sau
12 giờ sẽ xong. Họ làm chung với nhau trong 4 giờ thì tổ thứ nhất được
điều đi làm việc khác, tổ thứ hai làm nốt công việc còn lại trong 10 giờ.
Hỏi nếu mỗi tổ làm một mình thì sau bao lâu sẽ hoàn thành công việc.
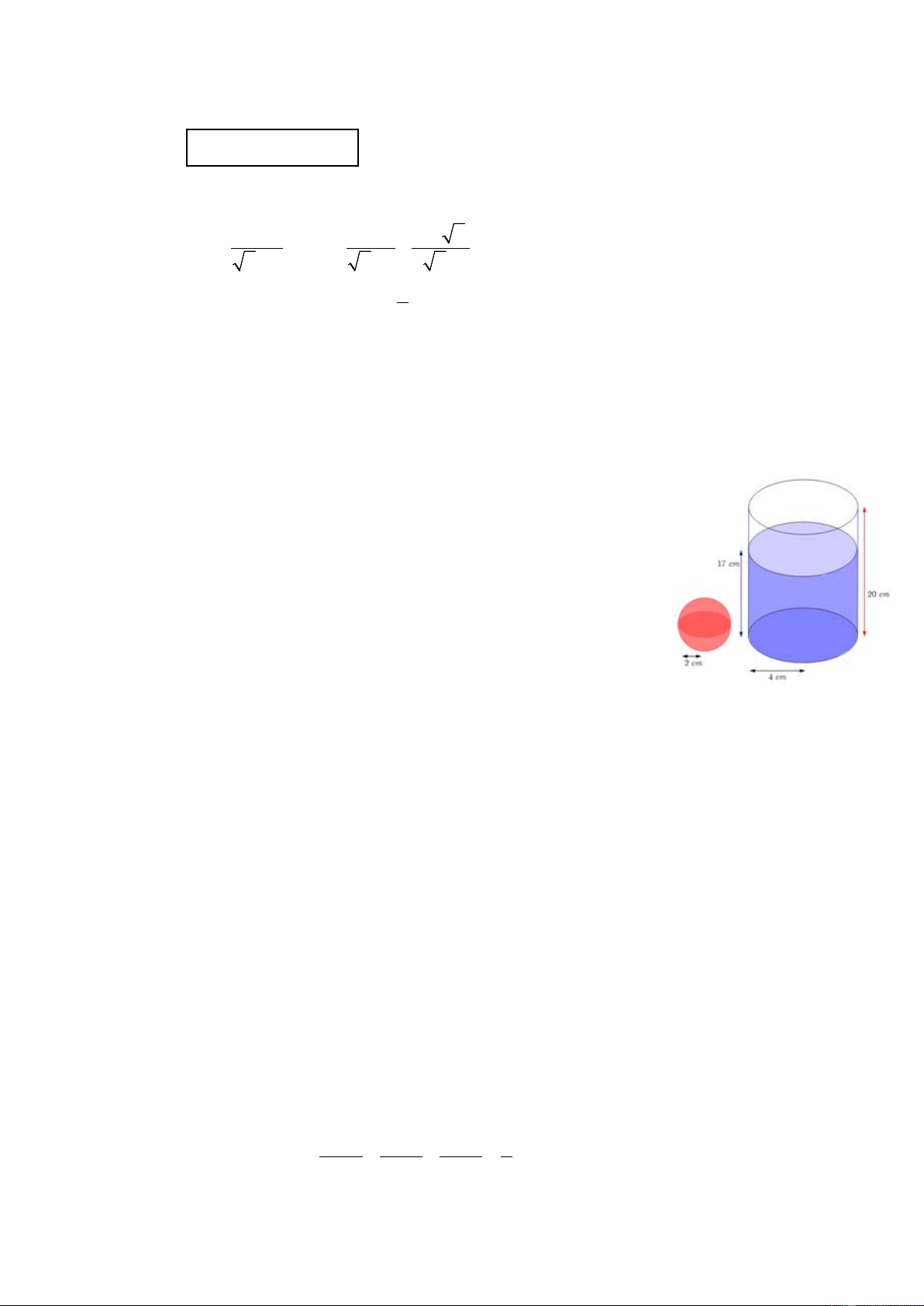
2) Một ly nước hình trụ có chiều cao 20 cm và bán kính đáy bằng 4
cm. Bạn Nam đổ nước vào ly cho đến khi mực nước cách đáy ly 17 cm thì
dừng lại. Sau đó, Nam lấy các viên đá lạnh hình cầu có cùng bán kính 2
cm thả vào ly nước. Bạn Nam dự định bỏ 6 viên đá hình cầu vào cốc nước.
Hỏi nước có bị trào ra ngoài ly không?
Bài 3 (2,5 điểm) 1) Giải phương trình ( 2 x − x)( 2 x − x + ) 1 = 6 2) Cho parabol 2
y = x (P) và đường thẳng y = mx + 2 (d ) ( m là tham số)
a) Chứng minh (P) và (d ) luôn cắt nhau tại hai điểm phân biệt A và B nằm về hai phía của trục tung.
b) Tìm m để diện tích tam giác OAB bằng 3 ( O là gốc tọa độ).
Bài 4 (3,5 điểm)
Cho đường tròn (O, R) đường kính AB . Lấy điểm C thuộc đường tròn sao cho AC = R ; điểm D
thuộc cung nhỏ BC ( D khác B,C ) . Kéo dài AC và BD cắt nhau tại E ; kẻ EH vuông góc với AB tại
H ( H thuộc AB ) , EH cắt AD tại I .
a) Chứng minh : tứ giác AHDE là tứ giác nội tiếp.
b) Kéo dài DH cắt (O, R) tại điểm thứ hai là F . Chứng minh CF song song với EH và tam giác
BCF là tam giác đều.
c) Giả sử điểm D thay đổi trên cung nhỏ BC nhưng vẫn thỏa mãn điều kiện của đề bài. Xác định
vị trí của D để chu vi tứ giác ABDC đạt giá trị lớn nhất . Bài 5 (0,5 điểm)
Cho ba số thực dương a,b,c có tổng thỏa mãn điều kiện a + b + c = 3. Chứng minh bất đẳng 1 1 1 3 thức sau: + + ≥ . 1+ ab 1+ bc 1+ ca 2 ------Hết------
ĐÁP ÁN ĐỀ KIỂM TRA KHẢO SÁT CHẤT LƯỢNG
NĂM HỌC: 2020 -2021. MÔN TOÁN 9 Bài 1. (2,0 điểm) x −1 1 2 − x
Cho hai biểu thức A = và B = −
với x ≥ 0; x ≠ 4 x − 2 x +1 x x +1 1
a) Tính giá trị của biểu thức A khi x = 4
b) Rút gọn biểu thức B
c) Cho P = ( A − )
1 .B . Tìm các giá trị của x để P ≥ 2 . Lời giải 1 1) Thay x =
(TMDK) vào biểu thức A ta có: 4 1 −3 −3 −1 1 4 4 4 A = = = = 1 3 1 − 2 − − 2 2 2 2 4 1 1 Vậy với x = thì A = . 4 2 1 2 − x b) B = − x +1 x x +1
x − x +1− 2 + = x B ( x + ) 1 ( x − x + ) 1 x ( x + )1( x − − )1 1 B = ( x ) = +1 (x − x + ) 1
( x + )1(x− x + )1 x −1 B = x − x +1 x −1
Vậy với x ≥ 0; x ≠ 4 thì B = x − x +1  x −  x −
c) Ta có P = ( A − ) 1 1 1 .B = −1 .    x − 2  x − x +1
 x −1− x + 2  x −1 P =  .   x − 2 x − x +1   x − x +1 x −1 P = . x − 2 x − x +1 x −1 P = x − 2 Để x −1 P ≥ 2 ⇔ ≥ 2 x − 2 x −1 ⇔ − 2 ≥ 0 x − 2
x −1− 2 x + 4 ⇔ ≥ 0 x − 2 3 − ⇔ x ≥ 0 x − 2  3  − x ≥ 0
 x ≤ 3 x ≤ 9   
 x − 2 > 0  x > 2 x > 4 ⇔  ⇔  ⇔ ⇔ 4 < x ≤ 9   − x ≤  x ≥ x ≥ 9 3 0 3     (l)   x − <  x < x < 4 2 0 2
Kết hợp với điều kiện x ≥ 0; x ≠ 4 thì 4 < x ≤ 9 thỏa mãn đề bài. Bài 2. (2 điểm)
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai tổ công nhân may một số khẩu trang để phục vụ để phục vụ cho vùng dịch Covid-19.
Nếu hai tổ cùng làm sau 12giờ sẽ xong. Họ làm chung với nhau trong 4 giờ thì tổ thứ nhất
được điều đi làm việc khác, tổ thứ hai làm nốt công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ
làm một mình thì sau bao lâu sẽ hoàn thành công việc. Lời giải
Gọi x là số giờ để tổ một làm một mình xong việc (Đơn vị: giờ; Điều kiện: x >12 )
Khi đó, trong một giờ tổ một làm được 1 (công việc) x
Vì hai tổ cùng làm sau 12giờ sẽ xong nên trong một giờ hai tổ làm được 1 (công việc) 12
Nên suy ra trong một giờ tổ hai làm được 1 1 − (công việc) 12 x
Trong 4 giờ cả hai tổ làm được 4 1 = (công việc) 12 3  
Trong 10 giờ tổ hai làm được 1 1 5 10 10 − = −   (công việc) 12 x  6 x
Từ đó ta có phương trình: 1 5 10 + − = 1 3 6 x 10 1 5 2 5 6 1 ⇔ = + −1 = + − = x 3 6 6 6 6 6
⇒ x = 60 (thỏa mãn)
Khi đó, trong một giờ tổ hai làm được 1 1 5 1 4 1 − = − = = (công việc) 12 60 60 60 60 15
Nên thời gian để tổ hai làm một mình xong công việc là 15 giờ.
Vậy, thời gian để tổ một và tổ hai làm một mình xong công việc
lần lượt là 60 giờ và 15 giờ.
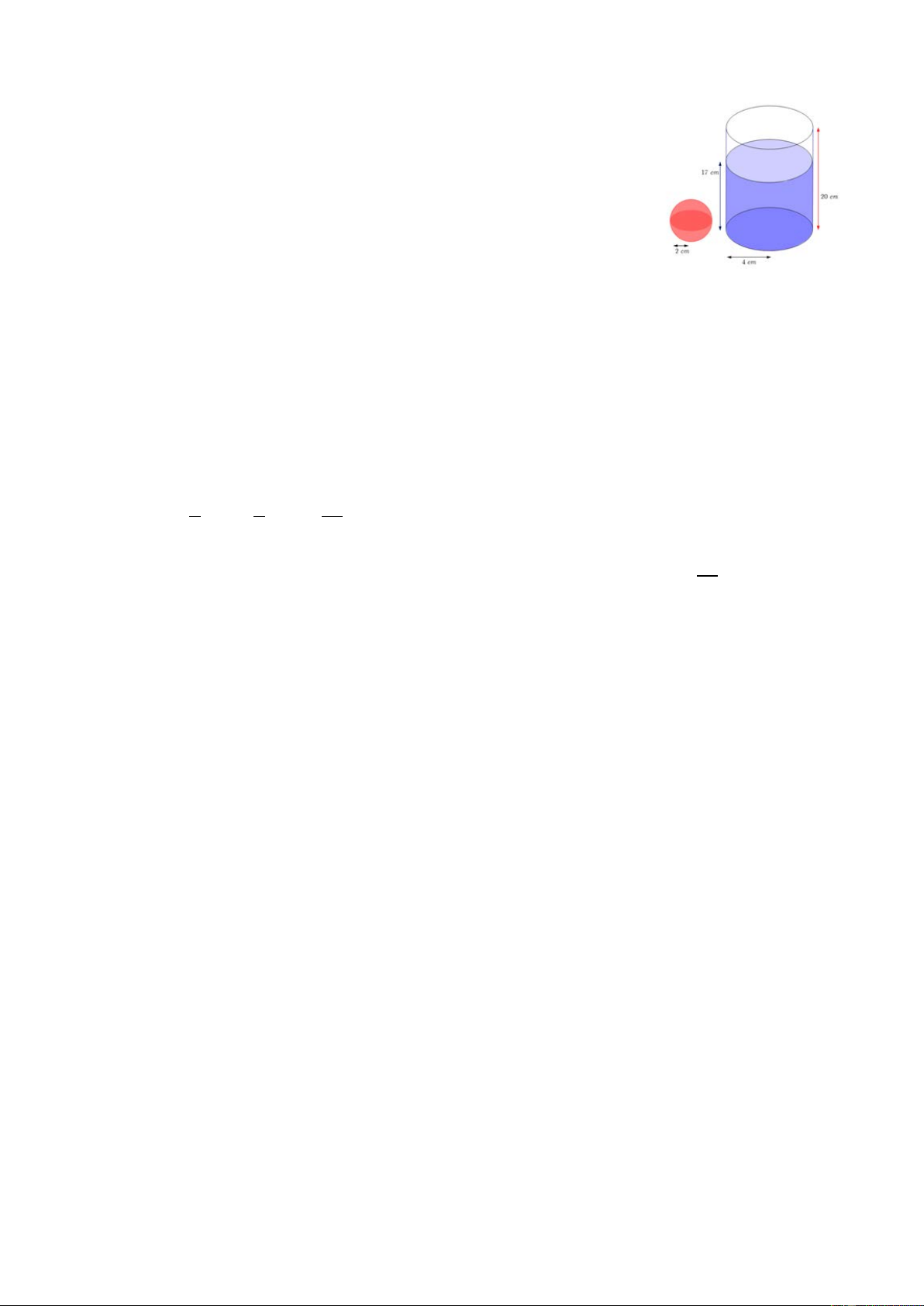
2) Một ly nước hình trụ có chiều cao 20 cm và bán kính đáy
bằng 4 cm. Bạn Nam đổ nước vào ly cho đến khi mực nước
cách đáy ly 17 cm thì dừng lại. Sau đó, Nam lấy các viên đá
lạnh hình cầu có cùng bán kính 2 cm thả vào ly nước. Bạn Nam
dự định bỏ 6 viên đá hình cầu vào cốc nước. Hỏi nước có bị trào ra ngoài ly không? Lời giải
Thể tích ly nước khi đầy ly là: 2 2 V = π h R = π = π ( 3 20. .4 320 cm )
Sau khi đổ nước vào ly thì thể tích nước trong ly là: 2 2 V = π h R = π = π ( 3 17. .4 272 cm )
Thể tích 6 viên đá hình cầu bán kính 2 cm là: 4 4 32 3 3 V = π R = .π.2 = π ( 3 cm ) 3 3 3
Thể tích nước trong ly sau khi thả 6 viên đá hình cầu trên là:  32  V = 272 + π ≈ 282,7π   ( 3 cm )  3 
Vì 320π > 282, 7π nên khi Nam bỏ 6 viên đá hình cầu vào cốc nước thì nước không bị trào ra ngoài ly. Bài 3. (2,5 điểm) 1) Giải phương trình ( 2 x − x)( 2 x − x + ) 1 = 6 2) Cho parabol 2
y = x (P) và đường thẳng y = mx + 2 (d ) ( m là tham số)
a) Chứng minh (P) và (d ) luôn cắt nhau tại hai điểm phân biệt A và B nằm về hai phía của trục tung.
b) Tìm m để diện tích tam giác OAB bằng 3 ( O là gốc tọa độ). Lời giải 1) Giải phương trình ( 2 x − x)( 2 x − x + ) 1 = 6 (1) Đặt 2
t = x − x , khi đó: (1) ⇔ t (t + ) 1 = 6 2
⇔ t + t − 6 = 0 2
⇔ t + 3t − 2t − 6 = 0
⇔ t (t + 3) − 2(t + 3) = 0
⇔ (t + 3)(t − 2) = 0 t + 3 = 0 ⇔  t − 2 = 0 t = 3 − ⇔  t = 2 Trả ẩn: 1 11 Với t = 3 − 2 ⇔ x − x = 3 − 2
⇔ x − x + 3 = 0 2 ⇔ x − x + + = 0 4 4 2  1  11 ⇔ x − + = 0  
(vô lý) ⇒ x ∉ ∅  2  4 Với t = 2 2 ⇔ x − x = 2 2
⇔ x − x − 2 = 0 2
⇔ x + x − 2x − 2 = 0 ⇔ x(x + ) 1 − 2 ( x + ) 1 = 0 x + = x = − ⇔ ( 1 0 1 x + )
1 ( x − 2) = 0 ⇔  ⇔  x − 2 = 0 x = 2 Vậy x ∈{ 1 − ; } 2 2) Cho parabol 2
y = x (P) và đường thẳng y = mx + 2 (d ) ( m là tham số)
a) Chứng minh (P) và (d ) luôn cắt nhau tại hai điểm phân biệt A và B nằm về hai phía của trục tung.
b) Tìm m để diện tích tam giác OAB bằng 3 ( O là gốc tọa độ). Lời giải
a) Xét phương trình hoành độ giao điểm của (P) và (d) : 2 x = mx + 2 2
⇔ x − mx − 2 = 0 (1)
a = 1, b = − , m c = 2 − 2
có ∆ = (−m) − (− ) 2 4.
2 = m + 8 > 0, ∀m nên phương trình luôn có hai nghiệm phân biệt x , x 1 2 với mọi m . x + x = Theo đị m (2) nh lý Viet, ta có: 1 2  . x x = 2 − (3)  1 2 Vì x x = 2
− < 0 nên x , x trái dấu. 1 2 1 2
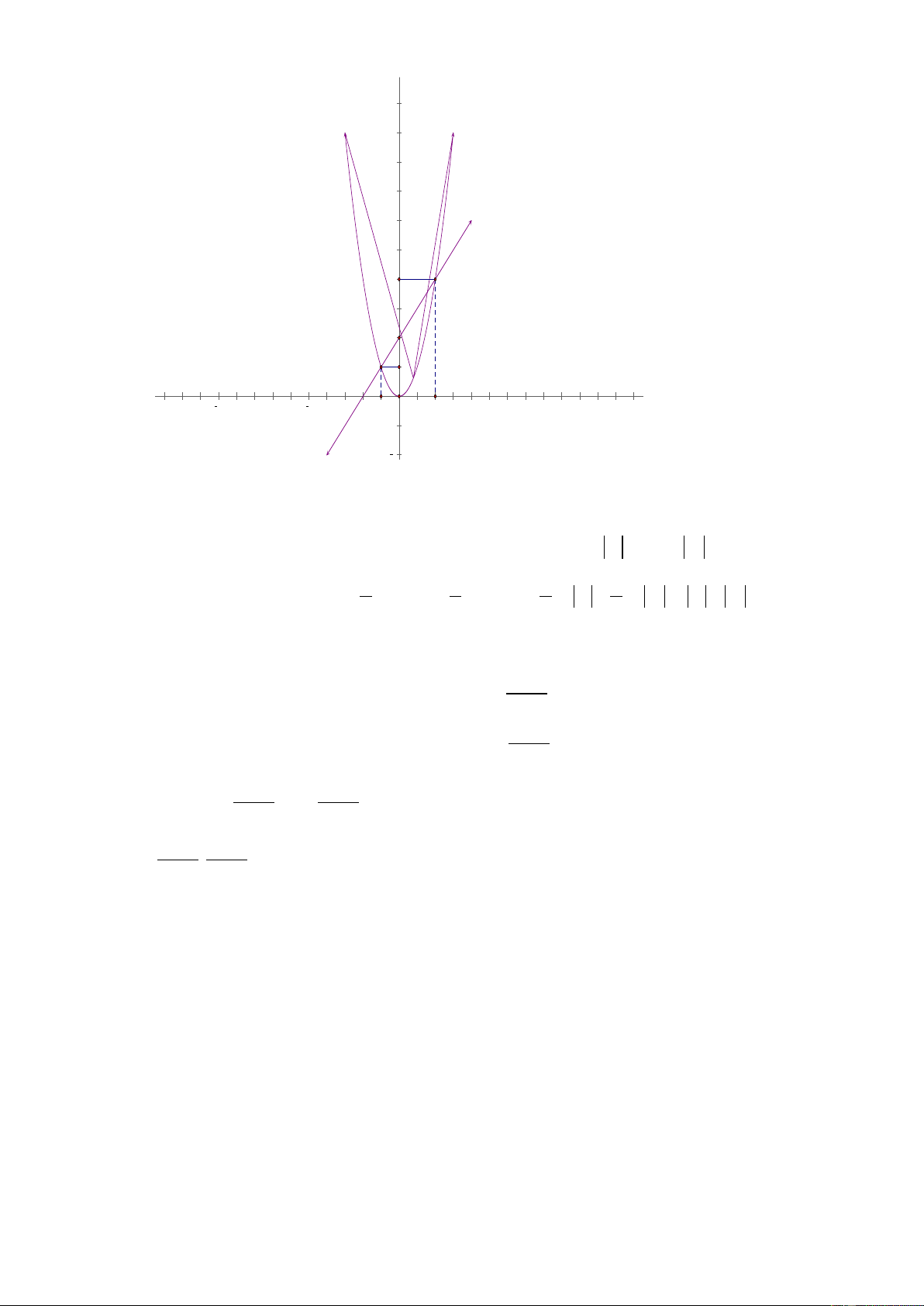
Vậy (P) và (d ) luôn cắt nhau tại hai điểm phân biệt A và B nằm về hai phía của trục tung. b) 10 8 6 4 K B C 2 A H 10 5 5 10 x1 O x2 2
Gọi A( x ; y , B x ; y và H , K lần lượt là hình chiếu của ,
A B lên trục tung; (d ) cắt trục 1 1 ) ( 2 2 ) tung tại điểm C .
Ta có C (0; 2) , H (0; y , K (0; y . Suy ra OC = 2 , AH = x , BK = x 2 ) 1 ) 1 2 1 1 1 1 Có S = S + = AH OC + = x + = x + ∆ S . BK.OC .2. .2. x x OAB ∆OAC ∆OBC 2 2 1 2 2 2 1 2
Coi x < 0 < x , mà S
= 3 nên −x + x = 3 (4) 1 2 ∆OAB 1 2  m − 3  x = x + x = m  1  2 Từ (2) và (4) ta có hệ: 1 2  ⇔ −  . x + x = 3  m + 3 1 2 x = 2  2 m − 3 m + 3 Thay x = , x = vào (3) , ta được : 1 2 2 2 m − 3 m + 3 . = 2
− ⇔ (m − 3)(m + 3) = 8 − 2 ⇔ m − 9 = 8 − 2
⇔ m = 1 ⇔ m = 1 ± 2 2 Vậy m = 1
± là giá trị cần tìm. Bài 4. (3,5 điểm)
Cho đường tròn (O, R) đường kính AB . Lấy điểm C thuộc đường tròn sao cho AC = R ;
điểm D thuộc cung nhỏ BC ( D khác B,C ) . Kéo dài AC và BD cắt nhau tại E ; kẻ
EH vuông góc với AB tại H ( H thuộc AB ) , EH cắt AD tại I .
a) Chứng minh : tứ giác AHDE là tứ giác nội tiếp.
b) Kéo dài DH cắt (O, R) tại điểm thứ hai là F . Chứng minh CF song song với EH và tam
giác BCF là tam giác đều.
c) Giả sử điểm D thay đổi trên cung nhỏ BC nhưng vẫn thỏa mãn điều kiện của đề bài. Xác
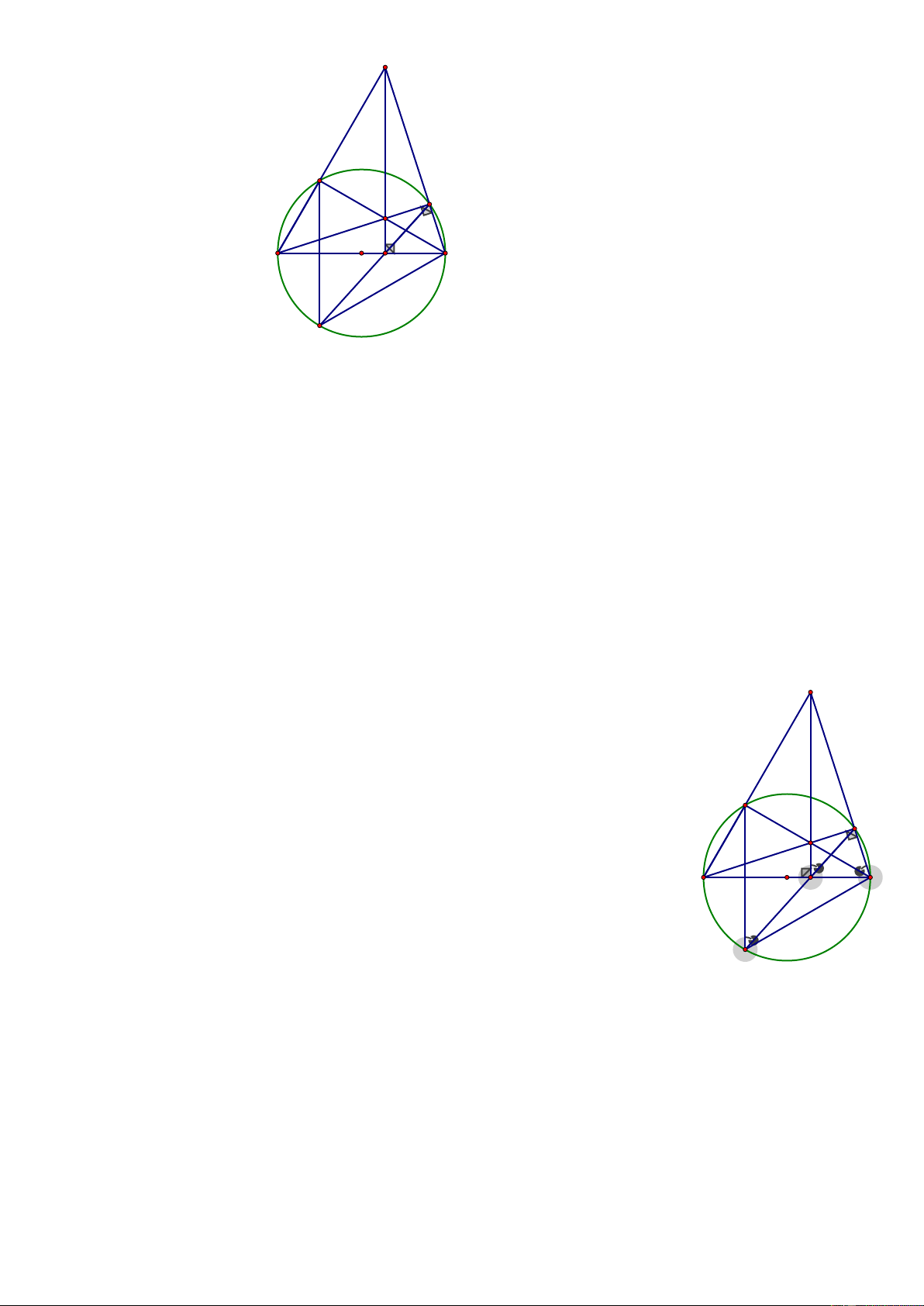
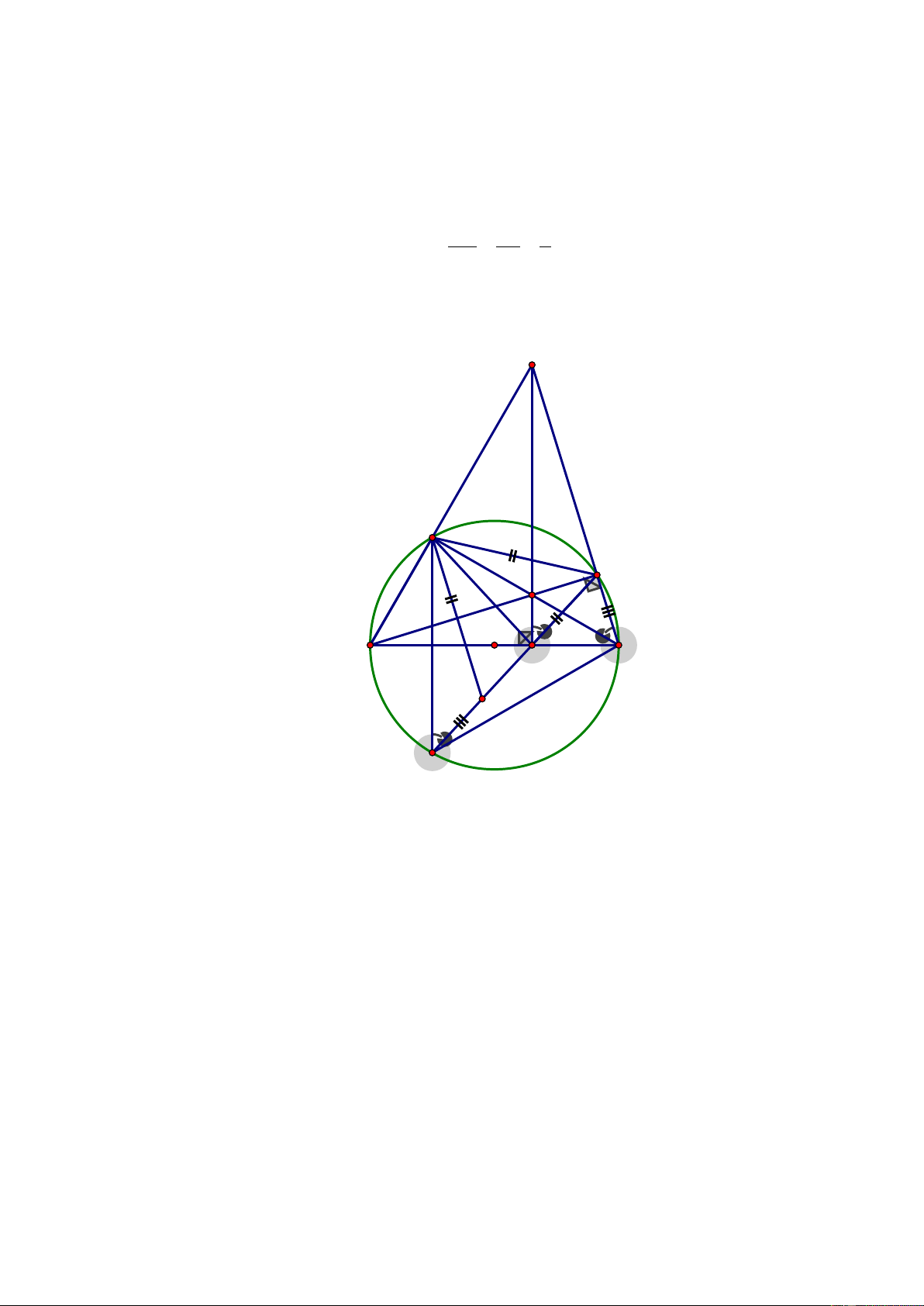
định vị trí của D để chu vi tứ giác ABDC đạt giá trị lớn nhất . Lời giải E C D I A B O H F
a) Chứng minh: Tứ giác AHDE là tứ giác nội tiếp.
Xét đường tròn (O) có:
EH ⊥ AB = {H} ⇒  EHA =  EHB = 90° .
Mặt khác: AB là đường kính của (O) . D ∈(O) . ⇒ 
ADB = 90° (góc nội tiếp chắn nửa đường tròn) mà  ADB + 
ADE = 180° ( kề bù ) ⇒  ADE = 90° .
Xét tứ giác AHDE có:  ADE =  AHE = 90° .
⇒ tứ giác AHDE nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh AE góc 90° ) .
b) Chứng minh : CF song song với EH và tam giác BCF là tam giác đều. E Ta có :  ADB = ° ⇒  90
IDB = 90° ( I ∈ AD)  EHB = 90° ⇒ 
IHB = 90° ( I ∈ EH ) . C
Xét tứ giác BHID có:  IDB + 
IHB = 90° + 90° = 180° . D ⇒ tứ giác I
BHID nội tiếp (tứ giác có tổng 2 góc đối bằng 180° ). 1 1 ⇒  H =  B A B 1
1 ( hai góc nội tiếp cùng chắn cung  ID ) ( ) 1 O H
Xét đường tròn (O) có: 1  F =  B 2 F 1
1 ( hai góc nội tiếp cùng chắn cung  CD ) ( ) Từ (1) và (2) ⇒  H = 
F mà hai góc này ở vị trí đồng vị 1 1
⇒ CF / / EH (đpcm) . Lại có : CF / / EH   ⇒ CF ⊥ ⊥
AB (quan hệ từ vuông góc đến song song) EH AB 
Xét đường tròn (O) có: CF ⊥ AB ,
CF là dây cung ; AB là đường kính
⇒ AB là trung trực của CF (quan hệ đường kính vuông góc với dây cung)
⇒ BC = BF ( tính chất các điểm thuộc đường trung trực của đoạn thẳng )
⇒ ∆BCF cân tại B . (3)  +) ACB 90° =
(góc nội tiếp chắn nửa đường tròn) ⇒ ∆ACB vuông tại C . AC R 1
Xét ∆ACB vuông tại C có :  CAB = = = ⇒  0 cos CAB = 60 . AB 2R 2 Lại có :  CAB =  0
CFB = 60 ( hai góc nội tiếp cùng chắn cung  CB ) (4)
Từ (3),(4) ⇒ ∆BCF là tam giác đều ( đpcm ). E C D I 1 1 A B O H P 1 F
c) Xác định vị trí của D để chu vi tứ giác ABDC đạt giá trị lớn nhất .
Ta có : AB là trung trực của CF mà AB cố định , C cố định ⇒ F cố định .
Trên cạnh DF lấy điểm P sao cho DC = DP ⇒ ∆DCP cân tại P . (5) Lại có :  CDF =  0
CBF = 60 ( hai góc nội tiếp cùng chắn cung  CF ) ⇒  0 CDP = 60 (5)
Từ (5)(6) ⇒ ∆DCP là tam giác đều ⇒ DC = CP .
+) Do ∆BCF là tam giác đều ⇒ CB = CF .
Xét ∆CPF và ∆CDB có: CD = CP    PCF =  0 DCB = − 
( 60 PCB)⇒∆CPF = ∆CDB( .cgc)⇒ PF = BD  CF = CB 
Chu vi tứ giác ABDC bằng :
AB + BD + DC + CA = 3R + BD + DC = 3R + PF + DP = 3R + DF
Chu vi tứ giác ABDC lớn nhất khi DF lớn nhất ⇒ DF là đường kính của đường tròn
(O;R) ⇒ D là điểm chính giữa của cung nhỏ BC . Bài 5. (0,5 điểm)
Cho ba số thực dương a,b,c có tổng thỏa mãn điều kiện a + b + c = 3.
Chứng minh bất đẳng thức sau: 1 1 1 3 + + ≥ . 1+ ab 1+ bc 1+ ca 2 Lời giải 2
*Chứng minh bất đẳng thức: (a + b + c) ≥ 3(ab + bc + ca) (1) (Đẳng thức xảy ra khi
a = b = c ) 2 2 2
Thật vậy: (1) ⇔ a + b + c + 2ab + 2bc + 2ca − 3ab − 3bc − 3ca ≥ 0 2 2 2
⇔ a + b + c − ab − bc − ca ≥ 0 2 2 2
⇔ 2a + 2b + 2c − 2ab − 2bc − 2ca ≥ 0 ⇔ ( 2 2
a − ab + b ) + ( 2 2
b − bc + c ) + ( 2 2 2 2
c − 2ac + a ) ≥ 0
⇔ (a − b)2 + (b − c)2 + (c − a)2 ≥ 0 (luôn đúng)
Dấu “=” xảy ra khi a = b = c . 1 1 1 9
*Chứng minh bất đẳng thức: + + ≥
(2) (Đẳng thức xảy ra khi a = b = c ) a b c a + b + c  
Thật ậy: (1) ⇔ (a + b + c) 1 1 1 + + ≥ 9   v  a b c    a b a c b c
Xét (a + b + c) 1 1 1 + + = 3 + + + + + +    a b c  b a c a c b a b a c b c Mà
+ ≥ 2; + ≥ 2; + ≥ 2 (bđt Cô Si) b a c a c b  
Suy ra: (a + b + c) 1 1 1 + + ≥ 3 + 2 + 2 + 2 = 9   (đpcm)  a b c  Dấ “=” ả
x y ra khi a = b = c . u 2
Áp dụng bất đẳng thức (1) ta có: 9 = (a + b + c) ≥ 3(ab + bc + ca)
⇒ ab + bc + ca ≤ 3 1 1 1 9 9 3
Áp dụng bất đẳng thức (2) ta có: + + ≥ ≥ = 1+ ab 1+ bc 1+ ca
3 + ab + bc + ca 3 + 3 2
a = b = c Dấu “=” xảy ra khi 
⇔ a = b = c = 1
a + b + c = 3 1 1 1 3 Vậy + +
≥ . Dấu “=” xảy ra khi a = b = c =1. 1+ ab 1+ bc 1+ ca 2
Document Outline

• Lại có : ( hai góc nội tiếp cùng chắn cung )
• Xét và có:
• Chu vi tứ giác ABDC bằng :