


Preview text:
PHÒNG GD&ĐT QUẬN CẦU GIẤY
ĐỀ KHẢO SÁT CHẤT LƯỢNG MÔN TOÁN 9 TRƯỜNG THCS CẦU GIẤY NĂM HỌC 2021 – 2022 Ngày thi: 13/05/2022 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút x 2 x 1 2x x 3
Bài I. (2,0 điểm) Cho biểu thức A = 2 x 1 và B = với x 0, x 9 x x 3 x 3 x 9
1) Tính giá trị của biểu thức A khi x 25 ;
2) Rút gọn biểu thức B;
3) Tìm x N để biểu thức P = A.B đạt giá trị lớn nhất. Bài II. (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một đoàn xe cần vận chuyển hàng hóa thiết yếu tới các vùng có dịch. Nếu xếp mỗi xe 15 tấn
thì còn thừa lại 5 tấn, còn nếu xếp mỗi xe 16 tấn thì chở được thêm 3 tấn nữa. Hỏi đoàn xe phải
chở bao nhiêu tấn hàng và có mấy xe?
2) Môn bi sắt (tên gọi quốc tế là pétanque) là một trong 40 môn thi đấu tại SEA Games 31
được tổ chức tại Việt Nam. Một viên bi sắt hình cầu có đường kính 8 cm thì thể tích của viên bi đó là bao nhiêu 3
cm ? (Kết quả làm tròn đến 2 chữ số thập phân) (Lấy 3,14 ). Bài III. (2,0 điểm) 3 2 x 2y 1
1) Giải hệ phương trình: 2x 1 1 3 x 2y 7 2x 1
2) Trong mặt phẳng tọa độ Oxy , cho parabol (P) : 2
y x và đường thẳng (d ) : y 5x m 1 .
Tìm tất cả các giá trị của m để (d ) cắt (P) tại hai điểm phân biệt có hoành độ x ; x sao cho 1 2 2x x . 1 2 Bài IV. (3,0 điểm)
Cho đường tròn (O; R) và dây BC cố định không đi qua O. Trên cung lớn BC lấy điểm A
sao cho ABtrên AK và M là trung điểm của BC.
1) Chứng minh 4 điểm C, E,O, M cùng thuộc một đường tròn;
2) Kẻ AD BC tại D . Chứng minh A . B AC A . D 2R và DE BK ;
3) Chứng minh MDE cân và tâm đường tròn ngoại tiếp DEF là một điểm cố định khi A di động trên cung lớn BC.
Bài V. (0,5 điểm) Cho các số thực a,b, c không âm thỏa mãn: không có hai số nào đồng thời bằng 2ab 2bc 2ac 0 và 2 2 2
a b c 2ab bc ca . Chứng minh: 1 2 2 2 2 2 2 a b b c a c ---------- Hết ----------
ĐÁP ÁN ĐỀ KHẢO SÁT CHẤT LƯỢNG MÔN TOÁN 9 NĂM HỌC 2021 – 2022 Ngày thi: 13/05/2022 Bài Ý Đáp án Điểm Bài I I.1
1) Thay x 25 (tmđk) vào A ta có: A = 2 25 1 0,25 25 (2,0 0,5đ điểm) 9 A 0,25 5 I.2
x x 3 2 x
1 x 3 2x x 3 0,25 2) B 1,0đ x 3 x 3
x 3 x 2x 6 x x 3 2x x 3 B 0,25 x 3 x 3 x 3 x B 0,25 x 3 x 3 x x 3 0,25 x B x 3 x 3 x 3 I.3 2 x 1 5 c) P . A B 2 0,25 0,5đ x 3 x 3
- Trong 2 trường hợp x 3 0 và x 3 0 để P lớn nhất thì 0,25
x 3 0 . Mà x N x 10 x 3 10 3 0 2 10 1 P
17 5 10 x 10(tmdk) max 10 3 Bài II II.1
1) - Gọi số xe của đoàn là x (xe) ( x N ) ; 0,5 (2,5
2,0đ số tấn hàng cần vận chuyển là y (tấn) y 5 điểm) - Theo đề bài:
Xếp mỗi xe 15 tấn thì còn thừa lại 5 tấn 15x y 5 0,5
Xếp mỗi xe 16 tấn thì chở được thêm 3 tấn nữa 16x y 3 1 5x y 5 0,25 - Ta có hệ pt: 1 6x y 3 x 8 0,5 - Giải hệ pt: y 125
- Kiểm tra ĐK và KL : 8 xe và 125 tấn hàng 0,25 II.2
2) Bán kính viên bi sắt hình cầu: 4cm 0,5đ 0,25 4 Thể tích viên bi sắt: 3 V R 3 Với 3,14 0,25 4 V 3,14 3 .4 267, 95 3 cm 3 Bài III III.1 3 2 x 2 y 1 2x 1 1 (2,0 1,0đ 1) ĐKXĐ: x 2y; x 0,25 1 2 điểm) 3 x 2y 7 2x 1 x 1 0,5 Giải hpt được: 3 y 2 3 0,25
Kiểm tra ĐK và KL nghiệm của hệ pt: 1; 2
III.2 2) Phương trình hoành độ giao điểm của (d ) và (P) là: 0,25 1,0đ 2 x 5x m 1 0 (*)
(d ) cắt (P) tại hai điểm phân biệt PT (*) có 2 nghiệm phân biệt 0,25 21 0 m 4 x x 5 1 1 2
Theo hệ thức Vi ét ta có: x x m 1 2 1 2 0,25 2
2x x x 4x x 0; x 0 1 2 2 1 1 2 x 1 tm 1 Thế vào (1) ta có: 2 4x +x 5 0 1 1 5 x ko tm 0,25 1 4 21
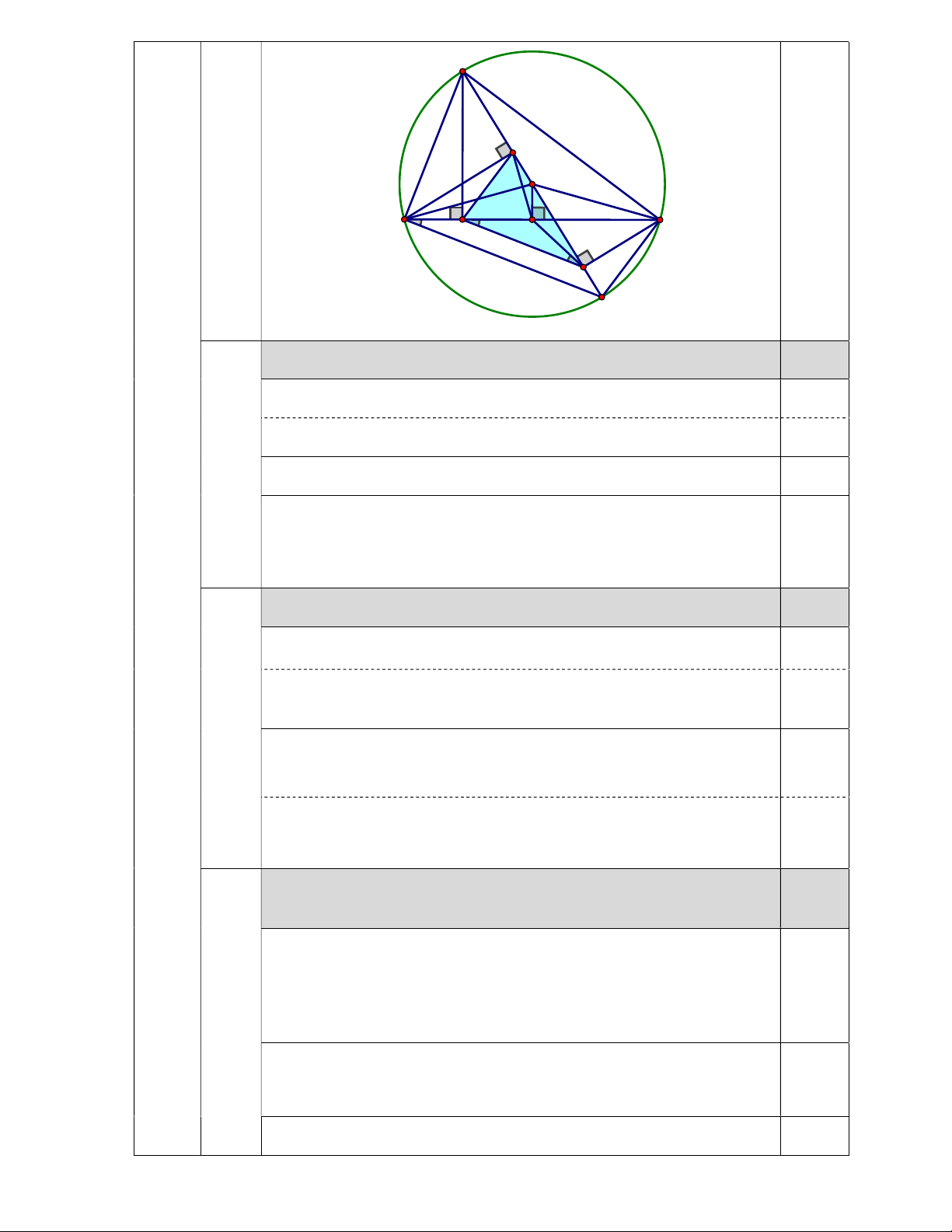
Khi đó: x 4 tm . Thay vào (2): m 3tm m 2 4 Bài IV IV.1 A (3,0 1,0đ điểm) F O B D M C E K
1) Chứng minh 4 điểm C, E,O, M cùng thuộc một đường tròn;
Vẽ hình đúng đủ để giải câu 1) 0,25 Chứng minh: 0 OMC 90 0,25 Chỉ ra 0 OEC 90 0,25
Từ đó suy ra C, E,O, M cùng thuộc một đường tròn đường kính OC 0,25
(Hoặc chứng minh tứ giác OMEC nội tiếp theo dhnb đúng cho điểm tối đa) IV.2 2) Chứng minh A . B AC A . D 2R và DE BK ; 1,0đ
Chứng minh: ABD AKC gg 0,25 A . B AC AD.AK 0,25 A . B AC AD.2R
Chứng minh: Tứ giác ADEC nội tiếp 0,25 CDE CAE Mà CBK CAE 0,25
CDE CBK DE BK IV.3
Chứng minh MDE cân và tâm đường tròn ngoại tiếp DEF là 1,0đ
một điểm cố định khi A di động trên cung lớn BC
+) Xét (O): CME COE 2.CAE 0,25
+) Xét đường tròn ngoại tiếp tứ giác ADEC: CAE MDE
Mà CME MDE MED MDE MED 0,25 MDE cân tại M (1) +) Chứng minh MEF cân: MFO MBO MCO MCO MEO 0,25 MFO MEO MEF cân tại M (2)
+) Từ (1) và (2) MD ME MF
Mà M là trung điểm BC cố định 0,25
Tâm đường tròn ngoại tiếp DEF là điểm M cố định khi A di động trên cung lớn BC Bài V
0,5đ Với mọi x, y, z 0 ta luôn có: (0,5 x y z2 2 2 2 2 2 2
x y z x y z x y z điểm) - Áp dụng ta có: 2ab 2bc 2ac 2ab 2bc 2ac 2 2 2 2 2 2 2 2 2 2 2 2 a b b c a c a b b c a c Mà a,b,c 0 0,5 2ab 2bc 2ac 2 2 2 2 2 2 a b b c a c 2ab 2bc 2ac 2 2 2 2 2 2 2 2 2 a b c a b c a b c 2ab bc ca 2 2 2 a b c 1 2 2 2 2 2 2 a b c a b c
Dấu “=” xảy ra a b 0; c 0 và các hoán vị của chúng.




