Đề minh họa học kì 2 Toán 12 năm 2022 – 2023 trường THPT Triệu Phong – Quảng Trị

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2022 – 2023 .Mời bạn đọc đón xem.

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

9 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1
Trường THPT Triệu Phong
Tổ Toán
ĐỀ MINH HỌA
KIỂM TRA HỌC KÌ 2 LỚP 12 - THPT
Năm học 2022 – 2023
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề có 4 trang)
Họ tên: ............................................................... Số báo danh: ...................
Câu 1. Số phức
43zi
= −
có môđun bằng
A.
8.
B.
2 2.
C.
5.
D.
Câu 2. Trong mặt phẳng
Oxy
, điểm nào sau đây biểu diễn số phức
2
zi
= +
?
A.
(2;0).M
B.
(2;1).N
C.
(2; 1).P −
D.
(1; 2).
Q
Câu 3. Trong không gian
,Oxyz
cho đường thẳng
∆
có phương trình chính tắc
31
2 31
x yz−+
= =
−
. Tìm
phương trình tham số của đường thẳng
∆
.
A.
32
1 3.
xt
yt
zt
= +
=−−
=
B.
23
3.
xt
yt
zt
= +
=−−
=
C.
32
13 .
xt
yt
zt
=−+
= −
=
D.
32
13 .
xt
yt
zt
=−−
= +
=
Câu 4. Cho hai số phức
1
2zi= +
và
2
23
zi
=−+
. Số phức
12
zz−
bằng
A.
4 2.
i−
B.
4.i
C.
4 2.i
−+
D.
2.i−
Câu 5. Trong không gian
Oxyz
, cho đường thẳng
12
:
212
xy z
d
−−
= =
−
. Điểm nào dưới đây thuộc đường
thẳng
d
?
A.
( )
1; 2; 0 .M −−
B.
(
)
1; 2; 0 .
M
C.
(
)
2;1; 2 .M −
D.
( )
3; 3; 2 .M
Câu 6. Tìm các số thực
,xy
thỏa mãn
2 34.x i yi+=+
A.
1
3, .
2
xy= =
B.
1
3, .
2
xy= = −
C.
1
3, .
2
xy=−=
D.
3, 2.xy= =
Câu 7. Tìm phần ảo của số phức
1
32
z
i
=
+
.
A.
2
.
13
−
B.
2
.
13
C.
2
.
13
i−
D.
3
.
13
Câu 8. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
3; 5; 7 , 1;1; 1 .AB−
Tìm tọa độ trung điểm
I
của đoạn
thẳng
.AB
A.
( )
2; 4;6 .I −−
B.
( )
4;6; 8 .I −
C.
( )
1; 2; 3 .I −−
D.
( )
2;3;3 .I
Câu 9. Tích phân
1
3
2
x dx
∫
bằng
A.
l7
3
.
B.
7
3
.
C.
26
3
.
D.
5
.
3
Câu 10. Trong không gian
Oxyz
, mặt phẳng
( )
:2 3 1 0P x yz− −−=
có một vectơ pháp tuyến là
A.
( )
3
3; 4; 1 .n =−−

B.
( )
1
2; 3;1 .n =

C.
( )
2
2;3;1.n = −−

D.
( )
4
1; 2; 3 .n =−−

Câu 11. Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
fx
trên
. Giá trị của
( )
[ ]
2
0
1 f x dx+
∫
bằng
A.
8.
B.
7.
C.
6.
D.
20.
Câu 12. Trong không gian cho
( )
1; 2 ; 3A
và
( )
2 ; 1; 2B −
. Đường thẳng đi qua hai điểm
AB
có phương
trình là.
A.
212
.
131
x yz− +−
= =
B.
123
.
1 31
xy z−−−
= =
−−
C.
123
.
13 1
xy z−−−
= =
−−
D.
123
.
1 31
xy z−−−
= =
−
Câu 13. Số phức liên hợp của số phức
53i−
là
A.
5 3.i−+
B.
5 3.i+
C.
3 5.i−+
D.
5 3.i−−
Trang 2
Câu 14. Phươngtrình mặt phẳng
( )
P
đi qua 3 điểm
(
) (
) (
)
3; 0; 0 , 0;1; 0 , 0; 0; 2
A BC
là
A.
1
312
xyz
++=
. B.
1
213
xyz
−+=
. C.
1
312
xyz
++=−
. D.
0
312
xyz
++=
.
Câu 15. Cho hàm số
( )
y fx=
có đạo hàm trên đoạn
[ ]
1;1−
thỏa
( )
1
1
d5fxx
−
′
=
∫
và
( )
14f =
. Tính
(
)
1
f
−
.
A.
( )
11
f −=
. B.
( )
19f −=
. C.
( )
19f −=−
. D.
( )
11f
−=−
.
Câu 16. Cho hai số phức
1
12
zi= +
và
2
3zi
=−+
. Trong mặt phẳng tọa độ, điểm biểu diễn số phức
12
.z zz=
có tọa độ là
A.
( )
5; 5 .−−
B.
( )
1; 6 .−−
C.
( )
2;3 .−
D.
( )
1; 5 .
−
Câu 17. Cho
( )
2
1
3f x dx =
∫
và
( )
1
2
4g x dx =
∫
. Tính
( ) ( )
2
1
I f x g x dx
= −


∫
.
A.
1.I =
B.
1.I = −
C.
12.I =
D.
7.I =
Câu 18. Trong không gian
Oxyz
, tính bán kính
R
của mặt cầu (S) có phương trình
2 22
2 4 4 30xyz xyz++ + − − +=
.
A.
3R =
. B.
6R =
. C.
33R =
. D.
6R =
.
Câu 19. Trong không gian Oxyz, cho vectơ
23x ij k
= −+

. Tìm tọa độ của vectơ
x
A.
(1; 2;3).x =
B.
(2;1;3).x =
C.
(
)
.
2; 1; 3
x =
−
D.
(3;2;1).x =
Câu 20. Cho sốphức
z
thỏa mãn
2( 1 2 ) 9 5zi i+− = −
. Môđun của
z
bằng
A.
52
.
2
B.
5 2.
C.
2.
D.
5.
Câu 21. Họ tất cả các nguyên hàm hàm số
( )
2
1
cos
fx
x
=
là
A.
cot .xC
+
B.
tan .xC−+
C.
cot .xC−+
D.
tan .xC+
Câu 22. Gọi
D
là hình phẳng giới hạn bởi các đường
, 0, 0
x
y ey x= = =
và
2x =
. Thể tích khối tròn xoay
tạo thành khi quay
D
quanh
Ox
bằng
A.
2
0
d
x
ex
π
∫
. B.
2
2
0
d
x
ex
∫
. C.
2
2
0
d
x
ex
π
∫
. D.
2
0
d
x
ex
∫
.
Câu 23. Họ tất cả các nguyên hàm hàm số
( )
sin 2fx x=
là
A.
1
cos 2 .
2
xC+
B.
1
cos 2 .
2
xC−+
C.
2cos 2 .xC−+
D.
2cos 2 .xC+
Câu 24. Gọi
1
z
và
2
z
là hai nghiệm của phương trình
2
2 10 0zz−+=
. Tính
22
12
Pz z= +
.
A.
20P =
. B.
40P =
. C.
0P =
. D.
2 10P =
.
Câu 25. Cho hàm số
2
() 3 1fx x= +
. Trong các khẳng định sau, khẳng định nào đúng?
A.
3
()f x dx x x C= −+
∫
. B.
3
()f x dx x x C= ++
∫
. C.
3
() 3f x dx x x C= −+
∫
. D.
3
()f x dx x C= +
∫
.
Câu 26. Cho hai số phức
1
12zi= +
và
2
1zi= −
. Tìm mô đun của số phức
1
2
z
z
.
A.
10
.
2
B.
5
.
2
C.
5
.
2
D.
10.
Câu 27. Tìm nguyên hàm của hàm số
( )
3
x
fx=
.
A.
3 3 ln 3 .
xx
dx C= +
∫
B.
3 3.
x
x
dx C= +
∫
C.
3
3.
ln 3
x
x
dx C= +
∫
D.
1
33 .
xx
dx C
+
= +
∫
Câu 28. Cho
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 50zz+ +=
, trong đó
1
z
có phần ảo dương. Số
phức liên hợp của số phức
12
2zz+
là
A.
3 2i−
. B.
2i+
. C.
2i−
. D.
3 2i−+
.
Trang 3
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
( ) ( )
,f x y gxy ==
liên tục trên đoạn
[ ]
;
ab
và
hai đường thẳng
;x ax b= =
có công thức tính là
A.
(
)
( )
( )
b
a
S f x g x dx= −
∫
.B.
( ) ( )
2
.
b
a
S f x g x dx
π
= −


∫
C.
( ) ( )
b
a
S f x g x dx= +
∫
.D.
(
)
( )
b
a
S f x g x dx
= −
∫
.
Câu 30. Họ tất cả các nguyên hàm của hàm số
( )
cosfx x x=
là
A.
sinx xC−+
. B.
cos sinx x xC++
. C.
sin cosx x xC−+
. D.
sin cosx x xC++
.
Câu 31. Tính tổng phần thực và phần ảo của số phức
z
thỏa
( )
13iz i+=+
.
A.
3
. B.
1−
. C.
32
. D.
1
.
Câu 32. Cho hàm số
( )
fx
liên tục trên
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( )
, 0, 1y fx y x= = = −
và
4x =
(như hình vẽ bên). Mệnh đề nào dưới đây là đúng?
A.
( ) ( )
14
11
S f x dx f x dx.
−
=−+
∫∫
B.
( ) ( )
14
11
S f x dx f x dx.
−
= −
∫∫
C.
( ) ( )
14
11
S f x dx f x dx.
−
= +
∫∫
D.
( )
4
1
S f x dx.
−
=
∫
Câu 33. Gọi
( )
H
là hình phẳng giới hạn bởi các đường
2
,0y x xy=+=
. Tính thể tích khối tròn xoay
được tạo thành khi quay hình
( )
H
quanh trục hoành.
A.
1
.
6
B.
.
30
π
C.
1
.
30
D.
.
6
π
Câu 34. Trong không gian
Oxyz
, cho hai điểm
( ) (
)
1;0; 1 , 3; 2;1
AB−
. Phương trình mặt phẳng trung trực
của đoạn thẳng
AB
là
A.
10xyz+ ++=
. B.
20xyz++=
. C.
30
xyz++−=
. D.
2 10x yz+ +−=
.
Câu 35. Trong không gian
Oxyz
, cho điểm
(
)
2;1; 3M −
và mặt phẳng
( )
:3 2 1 0P x yz− ++=
. Phương
trình mặt phẳng đi qua
M
và song song với
( )
P
là
A.
3 2 10x yz− ++=
. B.
3 2 50x yz+ +−=
. C.
2 3 14 0xy z−+ + =
. D.
3 2 50x yz− ++=
.
Câu 36. Cho số phức
z
thỏa mãn
2 6 2.+=+
zz i
Điểm biểu diễn số phức
z
có tọa độ là
A.
( )
2; 2−
. B.
( )
2; 2−−
. C.
( )
2; 2
. D.
( )
2; 2−
.
Câu 37. Trong không gian
Oxyz
, cho các vectơ
( ) ( ) ( )
1; 2;3 , 2; 4;1 , 1; 2;1ab c= =−=−

. Tìm tọa độ vectơ
23
u a bc=−+

.
A.
( )
9; 10; 4 .u = −
B.
( )
9;10;4 .u =
C.
( )
0; 4;5 .u =
D.
( )
4; 9;10 .u = −
Câu 38. Diện tích
S
của hình phẳng giới hạn bởi các đường
3
1, 1yx yx=−=−
bằng
A.
1
4
S
π
=
. B.
1
2
S
π
=
. C.
1
2
S
=
. D.
1
.
4
S =
Câu 39. Cho
( )
H
là hình phẳng giới hạn bởi đường cong
( )
2
:4Cy x x=−+
và đường thẳng
:.dy x=
Tính thể tích
V
của vật thể tròn xoay do hình phẳng
( )
H
quay xung quanh trục hoành.
A.
81
.
10
V
π
=
B.
81
.
5
V
π
=
C.
108
.
5
V
π
=
D.
108
.
10
V
π
=
Câu 40. Họ tất cả các nguyên hàm của hàm số
( )
( )
2
31
2
x
fx
x
−
=
+
là
A.
7
3ln 2
2
xC
x
++ +
+
. B.
7
ln 2
2
xC
x
+− +
+
.C.
3 7ln 2x xC− ++
. D.
( )
2
7
3ln 2
2
xC
x
+− +
+
.
Câu 41. Cho tích phân
( )
( )
1
0
2 ln 1 ln 2
b
I x x dx a
c
=+ += −
∫
trong đó
,,abc
là các số nguyên và
b
c
là phân
số tối giản. Tổng
222
Sabc=++
bằng
Trang 4
A.
81.
B.
16.
C.
49.
D.
100.
Câu 42. Cho hàm số
(
)
y fx=
liên tục trên
và
( ) ( )
2
f x fx x−+ =
. Tính
(
)
1
1
I f x dx
−
=
∫
.
A.
2
.
3
I
B.
1
.
3
I
C.
4
.
3
I
D.
1
.
2
I
Câu 43. Trongkhông gian
Oxyz
, mặt phẳng đi qua 2 điểm
(1; 1; 2 )A
,
( )
1; 2; 1B −
và song song với trục
Ox
có phương trình là
A.
10yz−+=
. B.
20
xz
−+=
. C.
3 10
yz
−−=
. D.
30yz+−=
.
Câu 44. Tính tổng phần thực và phần ảo của số phức
z
thỏa mãn
25
86zi
z
+=−
.
A.
1.−
B.
7.
C.
1.
D.
4.
Câu 45. Trong không gian
Oxyz
, cho các điểm
( ) ( ) ( )
1;0;2 , 1;2;1 , 3;2;0A BC
và
( )
1;1;3D
. Đường
thẳng đi qua
A
và vuông góc với mặt phẳng
( )
BCD
có phương trình là
A.
1
3.
22
xt
yt
zt
= −
=
= −
B.
1
4.
22
xt
yt
zt
= +
=
= +
C.
1
4.
22
xt
y
zt
= +
=
= +
D.
1
3.
22
xt
yt
zt
= +
=
= +
Câu 46. Có bao nhiêu giá trị nguyên của tham số
( )
0; 20m∈
để phương trình
2
60z zm− +=
có hai
nghiệm phân biệt
12
,zz
thỏa mãn
11 2 2
zz zz=
.
A.
13.
B.
11.
C.
12.
D.
10.
Câu 47. Trong không gian
Oxyz
, cho đường thẳng
113
:
12 2
xyz
d
+−−
= =
−
và mp
( )
:2 2 3 0
P x yz− +−=
,
phương trình đường thẳng
∆
nằm trong mặt phẳng
( )
P
, cắt
d
và vuông góc với
d
là
A.
215
.
256
x yz− −+
= =
B.
215
.
25 6
x yz+ +−
= =
−
C.
215
.
256
x yz+ +−
= =
D.
215
.
25 6
x yz+ −−
= =
−
Câu 48. Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
thỏa mãn
( )
11f = −
và
( )
( )
37
1 2,xf x f x x x x
′
− + = +− ∈
. Tính tích phân
( )
1
0
dI fx x=
∫
.
A.
2
.
3
B.
5
.
9
−
C.
5
.
9
D.
2
.
3
−
Câu 49. Trong không gian tọa độ
Oxyz
cho 3 điểm
( ) ( ) (
)
0; 2;1 , 1; 0; 2 , 2;1; 3ABC−
. Tập hợp các điểm
M
thỏa mãn
22 2
20MA MB MC++ =
là một mặt cầu. Lập phương trình mặt cầu đó.
A.
( ) ( )
22
2
4
11 .
9
x yz− ++ +=
B.
( ) ( )
( )
2 22
2
1 1 1.
3
xyz−+−+−=
C.
( ) ( )
22
2
2
11 .
3
x yz−+−+=
D.
( ) ( )
22
2
2
11 .
3
x yz+ +−+=
Câu 50. Bác Việt có một bồn hoa hình tròn tâm
O
. Bác dự định chia bồn hoa
thành bốn phần bởi hai đường parabol có chung đỉnh
O
và đối xứng với nhau qua
O
. Hai đường này cắt đường tròn tại bốn điểm
,,,
ABC D
tạo thành một hình vuông có
cạnh bằng
4m
(như hình vẽ). Phần diện tích
34
,SS
được dùng để trồng cỏ, và
12
,
SS
được dùng để trồng hoa. Biết kinh phí trồng cỏ là
100000
đồng
2
/m
, trồng hoa là
250000
đồng. Hỏi chi phí để bác Việt trồng bồn hoa là bao nhiêu? (Số tiền làm tròn
đến hàng nghìn)
A.
3270 000
đồng. B.
4897 000
đồng. C.
4798000
đồng. D.
3702 000
đồng.
----Hết---
Trang 5
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Đáp
án
C B A A B A A D C C C B B A D A D D C A D C B A B
Câu
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Đáp
án
A C A D D A B B C D A A C C A A B D B B D C D C C
HƯỚNG DẪN GIẢI
Câu 36.Cho số phức
z
thỏa mãn
2 6 2.+=+zz i
Điểm biểu diễn số phức
z
có tọa độ là
A.
( )
2; 2−
. B.
(
)
2; 2
−−
. C.
( )
2; 2
. D.
( )
2; 2−
.
Lời giải
Chọn A.
Gọi
,,z a bi a b=+∈
Ta có:
( )
36 2
2 62 2 62
22
aa
z z i a bi a bi i
bb
= =

+ =+⇔++ − =+⇔ ⇔

−= =−

Vậy
22
zi
= −
suy ra điểm biểu diễnsố phức
z
có tọa độ là
(
)
2; 2−
Câu 37.Trong không gian
Oxyz
, cho các vectơ
( ) ( ) ( )
1; 2;3 , 2; 4;1 , 1; 2;1ab c
= =−=−

. Tìm tọa độ vectơ
23u a bc=−+

.
A.
( )
9; 10; 4 .u = −
B.
( )
9;10;4 .u =
C.
( )
0; 4;5 .
u =
D.
( )
4; 9;10 .u = −
Lời giải
Chọn A.
Ta có:
( )
( )
( )
( )
2 2; 4; 6
3 6;12;3 2 3 9; 10; 4
1; 2; 1
a
b a bc
c
=
=− ⇒ − += −
= −


Câu 38.Diện tích
S
của hình phẳng giới hạn bởi các đường
3
1, 1yx yx=−=−
bằng
A.
1
4
S
π
=
. B.
1
2
S
π
=
. C.
1
2
S =
. D.
1
.
4
S =
Lời giải
Chọn C.
Ta có:
33
1
11 0
0
x
x x xx
x
= ±
−= −⇔ − = ⇔
=
Khi đó diện tích
1
3
1
1
2
S x x dx
−
=−=
∫
Câu 39.Cho
( )
H
là hình phẳng giới hạn bởi đường cong
( )
2
:4Cy x x=−+
và đường thẳng
:.dy x=
Tính
thể tích
V
của vật thể tròn xoay do hình phẳng
( )
H
quay xung quanh trục hoành.
A.
81
.
10
V
π
=
B.
81
.
5
V
π
=
C.
108
.
5
V
π
=
D.
108
.
10
V
π
=
Lời giải
Chọn C.
Ta có:
22
3
4 30
0
x
x xx x x
x
=
−+ =⇔ − =⇔
=
Khi đó thể tích
( )
3
2
22
0
108
4
5
V x x x dx
ππ
= −+ − =
∫
Câu 40.Họ tất cả các nguyên hàm của hàm số
( )
( )
2
31
2
x
fx
x
−
=
+
là
Trang 6
A.
7
3ln 2
2
xC
x
++ +
+
. B.
7
ln 2
2
xC
x
+− +
+
.
C.
3 7ln 2x xC− ++
. D.
( )
2
7
3ln 2
2
xC
x
+− +
+
.
Lời giải
Chọn A.
Ta có:
(
)
( ) ( )
22
31 3 7 7
3ln 2
22
22
x
f x dx dx dx x C
xx
xx

−
= = − = ++ +

++
++


∫∫ ∫
Câu 41.Cho tích phân
( )
(
)
1
0
2 ln 1 ln 2
b
I x x dx a
c
=+ += −
∫
trong đó
,,abc
là các số nguyên và
b
c
là phân số
tối giản. Tổng
222
Sabc
=++
bằng
A.
81.
B.
16.
C.
49.
D.
100.
Lời giải
Chọn A.
Đặt
(
)
( )
2
1
ln 1
1
1
2
2
2
du dx
ux
x
dv x dx
vxx
=
= +

+
⇒

= +
= +
Ta có:
(
) (
)
( )
1
11
2
2
00
0
1 14
2 ln 1 2 ln 1
2 21
xx
I x x dx x x x dx
x
+

= + + = + +−

+

∫∫
( )
( )
( )
1
1
1
2
22
0
0
0
1 1 31 1 7
2 ln 1 3 2 ln 1 3 3ln 1 4ln 2
2 2 1 2 22 4
x
xxx x dx xxx x x
x


 
=++−+−=++−+−+=−


 
+
 


∫
Câu 42.Cho hàm số
(
)
y fx
=
liên tục trên
và
( )
( )
2
f x fx x−+ =
. Tính
(
)
1
1
I f x dx
−
=
∫
.
A.
2
.
3
I
B.
1
.
3
I
C.
4
.
3
I
D.
1
.
2
I
Lời giải
Chọn B.
Ta có:
( ) ( ) ( ) ( )
1 11
22
1 11
21
2
33
f x f x x f x dx f x dx x dx I I
− −−
−+ = ⇒ − + = ⇔ = ⇔=
∫ ∫∫
Câu 43.Trongkhông gian
Oxyz
, mặt phẳng đi qua 2 điểm
(1; 1; 2 )A
,
( )
1; 2; 1B −
và song song với trục
Ox
có
phương trình là
A.
10yz−+=
. B.
20xz−+=
. C.
3 10yz−−=
. D.
30yz+−=
.
Lời giải
Chọn D.
Ta có:
( ) ( ) ( )
2;1; 1 , 1; 0; 0 , 0; 1; 1AB i n AB i

=− − = ⇒ = = −−

 

Khi đó, Phương trình mặt phẳng đi qua
(1; 1; 2 )A
:
30yz+−=
.
Câu 44.Tính tổng phần thực và phần ảo của số phức
z
thỏa mãn
25
86zi
z
+=−
.
A.
1.−
B.
7.
C.
1.
D.
4.
Lời giải
Chọn B.
Trang 7
Ta có:
( ) ( )
25
86 . 25 86 *z i zz z i
z
+ =−⇔ + = −
2
25 .10
zz⇒ +=
Đặt
,0t zt= ≥
ta có:
2
25 10 5
t tt+ = ⇔=
Thay vào (*) có
( )
25 15 8 6 4 3z iz i+ = − ⇔=+
Câu 45.Trong không gian
Oxyz
, cho các điểm
( ) ( ) ( )
1;0;2 , 1;2;1 , 3;2;0A BC
và
( )
1;1;3
D
. Đường thẳng
đi qua
A
và vuông góc với mặt phẳng
( )
BCD
có phương trình là
A.
1
3.
22
xt
yt
zt
= −
=
= −
B.
1
4.
22
xt
yt
zt
= +
=
= +
C.
1
4.
22
xt
y
zt
= +
=
= +
D.
1
3.
22
xt
yt
zt
= +
=
= +
Lời giải
Chọn B.
Ta có:
(
) ( )
( )
( )
2; 0; 1 , 0; 1; 2 , 1; 4; 2
BCD
BC BD n BC BD

= − = − ⇒ = =−−−

   
Khi đó, đường thẳng đi qua
( )
1; 0; 2A
vuông góc
( )
BCD
với nhận
(
)
1;4;2
a
=
làm VTCP có pt:
1
4.
22
xt
yt
zt
= +
=
= +
Câu 46.Có bao nhiêu giá trị nguyên của tham số
( )
0; 20
m
∈
để phương trình
2
60z zm− +=
có hai nghiệm
phân biệt
12
,zz
thỏa mãn
11 2 2
zz zz=
.
A. 13 B. 11 C. 12 D.10
Lời giải
Chọn D.
Phương trình đã cho
( )
2
39zm⇔− =−
+) Nếu
93mz=⇒=
(loại vì phương trình chỉ có một nghiệm).
+) Nếu
9
m <
thì phương trình đã cho có hai nghiệm thực
12
39 ; 39z mz m=−− =+−
.
Ta có
( ) ( )
22
11 2 2 1 2
39 39zz zz z z m m= ⇔ = ⇔− − =+ −
(
)
39 39
90 9
39 39
mm
mm
m m VN
− −=+ −
⇔ ⇔ −=⇔=
−−=−−−
(loại).
+) Nếu
9m >
thì phương trình đã cho có hai nghiệm phức
12
3 9, 3 9.z im z im=−−=+−
Ta có
2
11 2 2 0
39zz zz m==+−
(luôn đúng).
9m⇒>
thỏa mãn yêu cầu bài toán.
Vì
;
)0 20(
m
m
∈
∈
nên
{ }
10;11;12;...;19 .m∈
Vậy có 10 giá trị thỏa mãn yêu cầu bài toán.
Câu 47.Trong không gian
Oxyz
, cho đường thẳng
113
:
12 2
xyz
d
+−−
= =
−
và mp
( )
:2 2 3 0
P x yz− +−=
,
phương trình đường thẳng
∆
nằm trong mặt phẳng
( )
P
, cắt
d
và vuông góc với
d
là
A.
215
.
256
x yz− −+
= =
B.
215
.
25 6
x yz+ +−
= =
−
C.
215
.
256
x yz+ +−
= =
D.
215
.
25 6
x yz+ −−
= =
−
Lời giải
Chọn C.
Trang 8
Gọi
( )
(
) (
)
2; 1; 5
Md
Md P M
P
=∆∩
⇒ = ∩ ⇒ −−
∆⊂
Ta có:
( )
[ ]
( )
, 2; 5; 6
Pd
d
a na
P
∆
∆⊥
⇒= =
∆⊂

Khi đó phương trình đường thẳng
∆
đi qua
M
và có VTCP
( )
2; 5; 6a
∆
=
:
215
.
256
x yz+ +−
= =
Câu 48: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
thỏa mãn
( )
11f = −
và
( )
( )
37
1 2,xf x f x x x x
′
− + = +− ∈
. Tính tích phân
(
)
1
0
dI fx x=
∫
.
A.
2
3
. B.
5
9
−
. C.
5
9
. D.
2
3
−
.
Lời giải
Chọn D.
Từ
( )
(
)
37
1 2,
xf x f x x x x
′
− + = +− ∈
. Suy ra
( )
( )
2 3 82
1 2,x f x xf x x x x x
′
− + =+− ∈
Do đó
( )
( )
( )
1 11
2 3 82
0 00
1 2dx f x dx xf x dx x x x x
′
− + = +−
∫ ∫∫
(1).
+ Xét
( )
1
23
0
1dA xf x x= −
∫
:
Đặt
32
1 d 3dt x t xx
=−⇒=−
. Khi đó:
( )
( ) ( )
011
100
111
dd d
333
A ft t ft t fx x=−==
∫∫∫
(2).
+ Xét
( )
1
0
d:B xf x x
′
=
∫
Sử dụng tích phân từng phần ta được:
( ) ( )
(
)
11
1
0
00
1B xfx fxdx fxdx= − =−−
∫∫
(3)
Thay (2) và (3) vào (1) ta được:
( ) ( )
11
00
15
1
39
f x dx f x dx
−
−− =
∫∫
( )
1
0
24
39
f x dx
−
⇔=
∫
( )
1
0
2
d
3
fxx
−
⇔=
∫
.
Câu 49: Trong không gian tọa độ
Oxyz
cho 3 điểm
( ) ( ) ( )
0; 2;1 , 1; 0; 2 , 2;1; 3ABC−
. Tập hợp các điểm
M
thỏa mãn
22 2
20MA MB MC
++ =
là một mặt cầu. Lập phương trình mặt cầu đó.
A.
( )
(
)
22
2
4
11
9
x yz
− ++ +=
. B.
( ) ( ) ( )
2 22
2
111
3
xyz
−+−+−=
.
C.
( ) ( )
22
2
2
11
3
x yz−+−+=
. D.
(
) ( )
22
2
2
11
3
x yz+ +−+=
Lời giải
Chọn C.
Gọi
G
là trọng tâm tam giác
ABC
ta có
( )
1;1; 0G
, ta có:
0GA GB GC++=
  
,
3GA =
,
5GB =
,
10GC =
.
( )
( ) ( )
22 2
22 2
20 20MA MB MC MG GA MG GB MG GC++=⇔+++ ++ =
     
222 2
6
3 20 .
3
MG GA GB GC MG⇔ +++ =⇔=
   
Vậy tập hợp điểm
M
là mặt cầu tâm
G
, bán kính
6
3
R =
nên phương trình là:
( )
( )
22
2
2
11
3
x yz−+−+=
Trang 9
Câu 50:Bác Việt có một bồn hoa hình tròn tâm
O
. Bác dự định chia bồn hoa thành
bốn phần bởi hai đường parabol có chung đỉnh
O
và đối xứng với nhau qua
O
. Hai
đường này cắt đường tròn tại bốn điểm
,,,ABC D
tạo thành một hình vuông có cạnh
bằng
4m
(như hình vẽ). Phần diện tích
34
,SS
được dùng để trồng cỏ, và
12
,SS
được
dùng để trồng hoa. Biết kinh phí trồng cỏ là
100000
đồng
2
/m
, trồng hoa là
250000
đồng. Hỏi chi phí để bác Việt trồng bồn hoa là bao nhiêu? (Số tiền làm tròn đến hàng
nghìn)
A.
3270 000
đồng. B.
4897 000
đồng.
C.
4798000
đồng. D.
3702 000
đồng.
Lời giải
Chọn C.
Chọn hệ tọa độ
Oxy
như hình vẽ
Parabol có hàm số dạng có đỉnh là gốc tọa độ và đi qua điểm
( )
2; 2B
nên có phương trình
2
1
2
yx=
Đường tròn tâm
O
có bán kính
1
22
2
OB BD= =
có phương trình:
22
8xy+=
Khi đó,
2
22
12
2
1 88
2 8 24 2 4
2 33
S S x x dx
ππ
−

+= −− = + −=+


∫
34
88
8 44
33
SS
π ππ

+=−+ = −


Suy ra chi phí trồng bồn hoa là:
88
250000. 4 100000. 4
33
ππ
 
+ + −≈
 
 
4798230 đồng.
Vậy chi phí để bác Việt trồng bồn hoa là 4.798.000 đồng (Số tiền làm tròn đến hàng nghìn)
| 1/9
| | Tải xuống

Có thể bạn quan tâm:

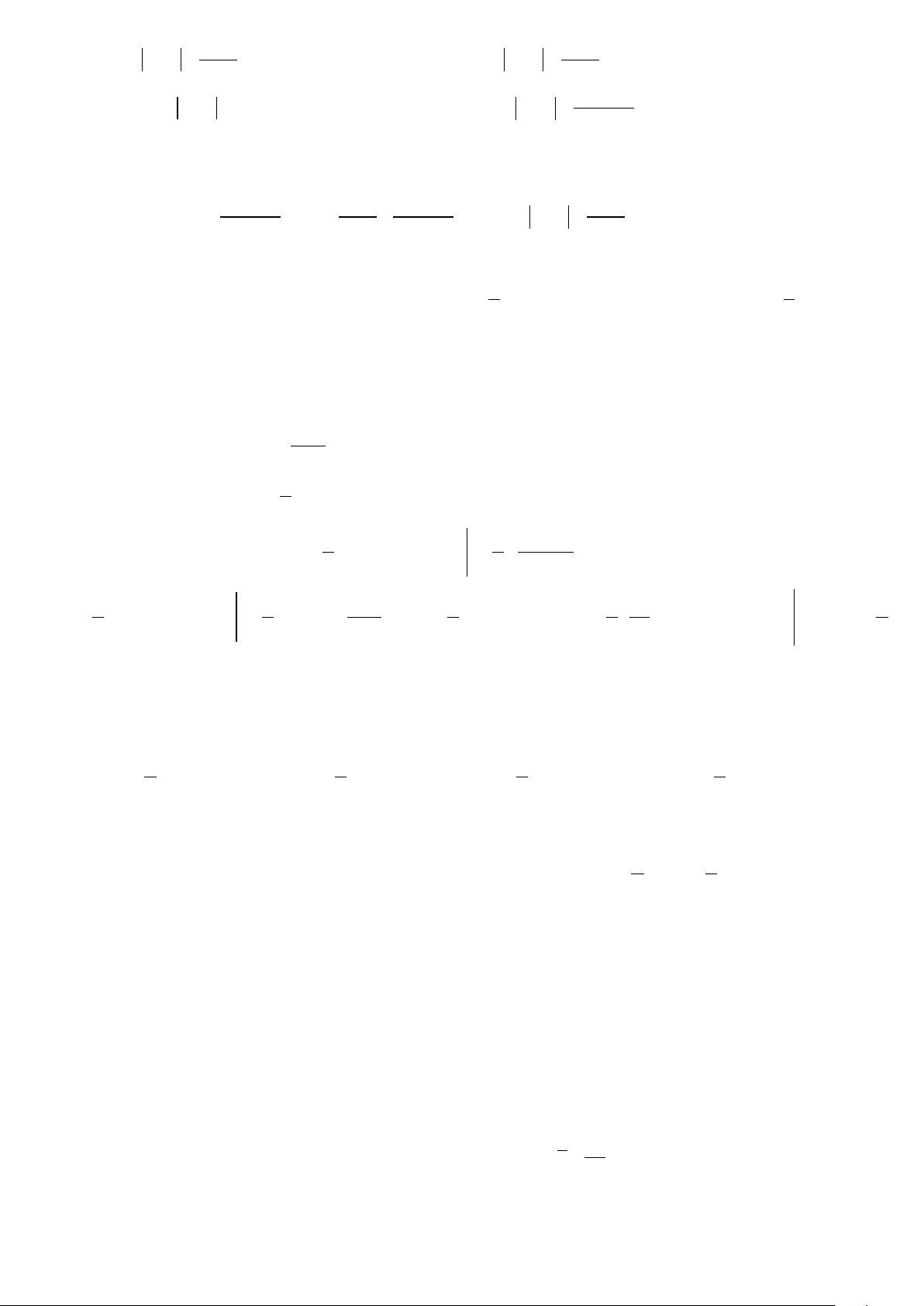
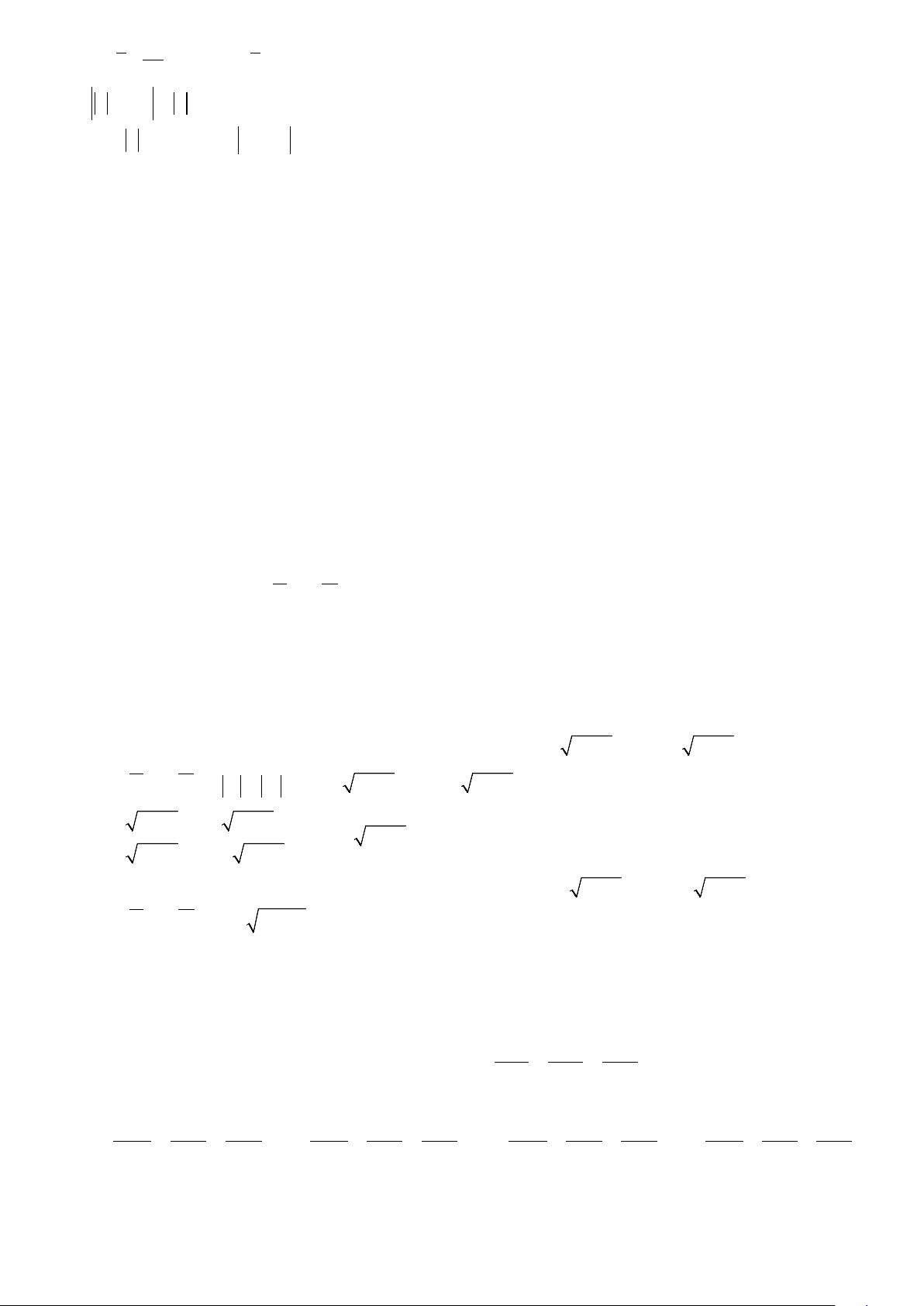
Preview text:

Trường THPT Triệu Phong
KIỂM TRA HỌC KÌ 2 LỚP 12 - THPT Tổ Toán
Năm học 2022 – 2023 ĐỀ MINH HỌA Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề có 4 trang)
Họ tên: ............................................................... Số báo danh: ...................
Câu 1. Số phức z = 4 −3i có môđun bằng A. 8. B. 2 2. C. 5. D. 25.
Câu 2. Trong mặt phẳng Oxy , điểm nào sau đây biểu diễn số phức z = 2 + i ?
A. M (2;0).
B. N(2;1). C. P(2; 1) − .
D. Q(1;2).
Câu 3. Trong không gian Oxyz, cho đường thẳng x − y + z
∆ có phương trình chính tắc 3 1 = = . Tìm 2 3 − 1
phương trình tham số của đường thẳng ∆ . x = 3 + 2tx = 2 + 3tx = 3 − + 2tx = 3 − − 2t A.      y = 1 − − 3t. B. y = 3 − − t.
C. y =1− 3t .
D. y =1+ 3t . z =     t z =  t z =  t z =  t
Câu 4. Cho hai số phức z = 2 + i z = 2 − + 3i z − z 1 và 2 . Số phức 1 2 bằng A. 4 − 2 .i B. 4 .i C. 4 − + 2 .i D. 2 − .i Câu 5. − − Trong không gian x y z
Oxyz , cho đường thẳng 1 2 d : = =
. Điểm nào dưới đây thuộc đường 2 1 2 − thẳng d ? A. M ( 1; − 2 − ;0).
B. M (1;2;0). C. M (2;1; 2 − ). D. M (3;3;2).
Câu 6. Tìm các số thực x, y thỏa mãn x + 2i = 3+ 4y .i A. 1
x = 3, y = . B. 1
x = 3, y = − . C. 1 x = 3, − y = .
D. x = 3, y = 2. 2 2 2 1
Câu 7. Tìm phần ảo của số phức z = . 3+ 2i A. 2 − . B. 2 . C. 2 − .i D. 3 . 13 13 13 13
Câu 8. Trong không gian Oxyz , cho hai điểm A(3;5;7),B(1;1;− )
1 . Tìm tọa độ trung điểm I của đoạn thẳng A . B A. I ( 2; − 4; − 6). B. I (4;6; 8 − ). C. I ( 1; − 2 − ;3). D. I (2;3;3). 3 Câu 9. Tích phân 2 x dx ∫ bằng 1 A. l7 . B. 7 . C. 26 . D. 5. 3 3 3 3
Câu 10. Trong không gian Oxyz , mặt phẳng (P) : 2x −3y − z −1= 0 có một vectơ pháp tuyến là     A. n = 3 − ;4; 1 − .
B. n = 2;3;1 . C. n = 2; 3 − ; 1 − . D. n = 1; − 2; 3 − . 4 ( ) 2 ( ) 1 ( ) 3 ( ) 2 Câu 11. Biết ( ) 2
F x = x là một nguyên hàm của hàm số f (x) trên  . Giá trị của ∫[1+ f (x)]dx bằng 0 A. 8. B. 7. C. 6. D. 20.
Câu 12. Trong không gian cho A(1;2;3) và B(2; 1;
− 2) . Đường thẳng đi qua hai điểm AB có phương trình là. − + − − − − − − − − − −
A. x 2 y 1 z 2 = =
. B. x 1 y 2 z 3 = =
. C. x 1 y 2 z 3 = =
. D. x 1 y 2 z 3 = = . 1 3 1 1 3 − 1 − 1 − 3 1 − 1 3 − 1
Câu 13. Số phức liên hợp của số phức 5−3i là A. 5 − + 3 .i
B. 5 + 3 .i C. 3 − + 5 .i D. 5 − − 3 .i Trang 1
Câu 14. Phươngtrình mặt phẳng (P) đi qua 3 điểm A(3;0;0), B(0;1;0),C (0;0;2) là A. x y z + + =1. B. x y z − + =1. C. x y z + + = 1 − . D. x y z + + = 0 . 3 1 2 2 1 3 3 1 2 3 1 2 1
Câu 15. Cho hàm số y = f (x) có đạo hàm trên đoạn[ 1; − ] 1 thỏa f ′
∫ (x)dx = 5 và f ( )1 = 4 . Tính f (− )1. 1 − A. f (− ) 1 =1. B. f (− ) 1 = 9 . C. f (− ) 1 = 9 − . D. f (− ) 1 = 1 − .
Câu 16. Cho hai số phức z =1+ 2i z = 3 − + i 1 và 2
. Trong mặt phẳng tọa độ, điểm biểu diễn số phức z = z .z
1 2 có tọa độ là A. ( 5; − 5 − ). B. ( 1; − 6 − ). C. ( 2; − 3). D.(1; 5 − ). 2 1 2 Câu 17. Cho f
∫ (x)dx = 3 và g
∫ (x)dx = 4. Tính I =  f
∫ (x)− g(x)dx  . 1 2 1
A. I =1. B. I = 1. −
C. I =12. D. I = 7.
Câu 18. Trong không gian Oxyz , tính bán kính R của mặt cầu (S) có phương trình 2 2 2
x + y + z + 2x − 4y − 4z + 3 = 0 .
A. R = 3.
B. R = 6 .
C. R = 33 . D. R = 6 .    
Câu 19. Trong không gian Oxyz, cho vectơ x = 2i − j + 3k . Tìm tọa độ của vectơ x
A. x = (1;2;3).
B. x = (2;1;3). C. x = (2; 1; − 3).
D. x = (3;2;1).
Câu 20. Cho sốphức z thỏa mãn 2(z +1− 2i) = 9 −5i . Môđun của z bằng A. 5 2 . B. 5 2. C. 2. D. 5. 2
Câu 21. Họ tất cả các nguyên hàm hàm số f (x) 1 = là 2 cos x
A. cot x + C.
B. − tan x + C.
C. −cot x + C.
D. tan x + C.
Câu 22. Gọi D là hình phẳng giới hạn bởi các đường x
y = e , y = 0, x = 0 và x = 2 . Thể tích khối tròn xoay
tạo thành khi quay D quanh Ox bằng A. 2 x π e dx ∫ . B. 2 2x e dx ∫ . C. 2 2x π e dx ∫ . D. 2 x e dx ∫ . 0 0 0 0
Câu 23. Họ tất cả các nguyên hàm hàm số f (x) = sin 2x là
A. 1 cos 2x + C. B. 1
− cos 2x + C. C. 2
− cos 2x + C.
D. 2cos 2x + C. 2 2
Câu 24. Gọi z và z là hai nghiệm của phương trình 2
z − 2z +10 = 0. Tính 2 2 = + . 1 2 P z z 1 2
A. P = 20 .
B. P = 40 .
C. P = 0 . D. P = 2 10 . Câu 25. Cho hàm số 2
f (x) = 3x +1. Trong các khẳng định sau, khẳng định nào đúng? A. 3
f (x)dx = x − x + C ∫ . B. 3
f (x)dx = x + x + C ∫ . C. 3
f (x)dx = 3x − x + C ∫ . D. 3
f (x)dx = x + C ∫ .
Câu 26. Cho hai số phức z =1+ 2i z =1−i z 1 và 2
. Tìm mô đun của số phức 1 . z2
A. 10 . B. 5 .C. 5 . D. 10. 2 2 2
Câu 27. Tìm nguyên hàm của hàm số ( ) 3x f x = . x
A. 3x = 3x dx ln 3+ C. ∫
B. 3x dx = 3x + C. ∫ C. x 3 3 dx = + C. ∫ D. x x 1 3 dx 3 + = + C. ln 3 ∫
Câu 28. Cho z , z là hai nghiệm phức của phương trình 2
z + 2z + 5 = 0 , trong đó z có phần ảo dương. Số 1 2 1
phức liên hợp của số phức z + 2z là 1 2 A. 3− 2i . B. 2 + i . C. 2 −i . D. 3 − + 2i . Trang 2
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), y = g (x) liên tục trên đoạn [ ; a b] và
hai đường thẳng x = ;
a x = b có công thức tính là b b b b
A. S = ∫( f (x)− g(x))dx .B.S =π  f
∫ (x)− g(x) 2 . dxC. S = f
∫ (x)+ g(x) dx.D.S = f
∫ (x)− g(x) dx. a a a a
Câu 30. Họ tất cả các nguyên hàm của hàm số f (x) = xcos x là
A. x − sin x + C .
B. xcos x + sin x + C . C. xsin x − cos x + C .
D. xsin x + cos x + C .
Câu 31. Tính tổng phần thực và phần ảo của số phức z thỏa (1+ i) z = 3+ i . A. 3. B. 1 − . C. 3 2 . D. 1.
Câu 32. Cho hàm số f (x) liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f ( x), y = 0, x = 1
− và x = 4 (như hình vẽ bên). Mệnh đề nào dưới đây là đúng? 1 4 1 4
A. S = − f
∫ (x)dx+ f
∫ (x)dx. B. S = f
∫ (x)dx− f
∫ (x)dx. 1 − 1 1 − 1 1 4 4 C. S = f
∫ (x)dx+ f
∫ (x)dx. D. S = f
∫ (x)dx. 1 − 1 1 −
Câu 33. Gọi (H ) là hình phẳng giới hạn bởi các đường 2
y = x + x, y = 0 . Tính thể tích khối tròn xoay
được tạo thành khi quay hình (H ) quanh trục hoành. π π A. 1 . B. . C. 1 . D. . 6 30 30 6
Câu 34. Trong không gian Oxyz , cho hai điểm A(1;0;− ) 1 , B(3;2; )
1 . Phương trình mặt phẳng trung trực
của đoạn thẳng AB là
A. x + y + z +1 = 0.
B. 2x + y + z = 0 .
C. x + y + z − 3 = 0 .
D. x + 2y + z −1 = 0.
Câu 35. Trong không gian Oxyz , cho điểm M ( 2
− ;1;3) và mặt phẳng (P) :3x − 2y + z +1 = 0 . Phương
trình mặt phẳng đi qua M và song song với (P) là
A. 3x − 2y + z +1 = 0 .
B. 3x + 2y + z − 5 = 0. C. 2x − y + 3z +14 = 0 . D. 3x − 2y + z + 5 = 0.
Câu 36. Cho số phức z thỏa mãn z + 2z = 6 + 2 .i Điểm biểu diễn số phức z có tọa độ là A.(2; 2 − ) . B. ( 2; − 2 − ). C. (2;2) . D. ( 2; − 2) .  
Câu 37. Trong không gian Oxyz , cho các vectơ a = (1;2;3),b = ( 2; − 4; ) 1 ,c = (1; 2; − ) 1 . Tìm tọa độ vectơ   
u = 2a − 3b + c . A. u = (9; 1 − 0;4).
B. u = (9;10;4).
C. u = (0;4;5). D. u = (4; 9; − 10).
Câu 38. Diện tích S của hình phẳng giới hạn bởi các đường 3
y = x −1, y = x −1 bằng A. 1 S = π . B. 1 S = π . C. 1 S = . D. 1 S = . 4 2 2 4
Câu 39. Cho (H ) là hình phẳng giới hạn bởi đường cong (C) 2
: y = −x + 4x và đường thẳng d : y = .x
Tính thể tích V của vật thể tròn xoay do hình phẳng (H ) quay xung quanh trục hoành. π π π π A. 81 V = . B. 81 V = . C. 108 V = . D. 108 V = . 10 5 5 10 3x −1
Câu 40. Họ tất cả các nguyên hàm của hàm số f (x) = ( là x + 2)2 A. 7 3ln x + 2 + + C . B. 7 ln x + 2 −
+ C .C. 3x − 7ln x + 2 + C . D. 7 3ln x + 2 − + C . x + 2 x + 2 (x + 2)2 1
Câu 41. Cho tích phân = ( + 2)ln( + ) 1 = ln 2 b I x x dx a − ∫
trong đó a,b,c là các số nguyên và b là phân c c 0 số tối giản. Tổng 2 2 2
S = a + b + c bằng Trang 3 A. 81. B. 16. C. 49. D. 100. 1
Câu 42. Cho hàm số y = f (x) liên tục trên  và (− ) + ( ) 2 f x
f x = x . Tính I = f ∫ (x)dx. 1 − A. 2 I  . B. 1 I  . C. 4 I  . D. 1 I  . 3 3 3 2
Câu 43. Trongkhông gian Oxyz , mặt phẳng đi qua 2 điểm ( A 1;1;2), B( 1; − 2; )
1 và song song với trục Ox có phương trình là
A. y − z +1 = 0 .
B. x − z + 2 = 0 .
C. 3y − z −1= 0.
D. y + z −3 = 0 .
Câu 44. Tính tổng phần thực và phần ảo của số phức z thỏa mãn 25 z + = 8 − 6i . z A. 1. − B. 7. C. 1. D. 4.
Câu 45. Trong không gian Oxyz , cho các điểm A(1;0;2), B(1;2; )
1 ,C (3;2;0) và D(1;1;3) . Đường
thẳng đi qua A và vuông góc với mặt phẳng (BCD) có phương trình là  x =1− tx =1+ tx =1+ tx =1+ t A.      y = 3t .
B. y = 4t . C. y = 4 .
D. y = 3t . z = 2−     2t z = 2 +  2t z = 2 +  2t z = 2 +  2t
Câu 46. Có bao nhiêu giá trị nguyên của tham số m∈(0;20) để phương trình 2
z − 6z + m = 0 có hai
nghiệm phân biệt z , z thỏa mãn z z = z z . 1 2 1 1 2 2 A. 13. B. 11. C. 12. D. 10. Câu 47. + − − Trong không gian x y z
Oxyz , cho đường thẳng 1 1 3 d : = =
và mp(P) : 2x − 2y + z −3 = 0 , 1 2 2 −
phương trình đường thẳng ∆ nằm trong mặt phẳng (P) , cắt d và vuông góc với d là
A. x − 2 y −1 z + 5 + + − + + − + − − = =
. B. x 2 y 1 z 5 = =
. C. x 2 y 1 z 5 = =
. D. x 2 y 1 z 5 = = . 2 5 6 2 5 6 − 2 5 6 2 5 6 −
Câu 48. Cho hàm số y = f (x) có đạo hàm liên tục trên  thỏa mãn f ( ) 1 = 1 − và 1 xf ( 3
− x ) + f ′(x) 7 1
= x + x − 2, x ∈  . Tính tích phân I = f ∫ (x)dx . 0 A. 2 . B. 5 − . C. 5. D. 2 − . 3 9 9 3
Câu 49. Trong không gian tọa độ Oxyz cho 3 điểm A(0;2; )
1 , B(1;0;2),C (2;1; 3
− ) . Tập hợp các điểm M thỏa mãn 2 2 2
MA + MB + MC = 20 là một mặt cầu. Lập phương trình mặt cầu đó.
A. (x − )2 + ( y + )2 2 4 1 1 + z = .
B. (x − )2 + ( y − )2 + (z − )2 2 1 1 1 = . 9 3
C. (x − )2 + ( y − )2 2 2 1 1 + z = .
D. (x + )2 + ( y − )2 2 2 1 1 + z = . 3 3
Câu 50. Bác Việt có một bồn hoa hình tròn tâm O . Bác dự định chia bồn hoa
thành bốn phần bởi hai đường parabol có chung đỉnh O và đối xứng với nhau qua O
. Hai đường này cắt đường tròn tại bốn điểm ,
A B,C, D tạo thành một hình vuông có
cạnh bằng 4m (như hình vẽ). Phần diện tích S , S được dùng để trồng cỏ, và S , S 3 4 1 2
được dùng để trồng hoa. Biết kinh phí trồng cỏ là 100000 đồng 2 /m , trồng hoa là
250000 đồng. Hỏi chi phí để bác Việt trồng bồn hoa là bao nhiêu? (Số tiền làm tròn đến hàng nghìn)
A. 3270000 đồng.
B. 4897000 đồng.
C. 4798000 đồng. D. 3702000 đồng. ----Hết--- Trang 4
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI Câu 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Đáp án
C B A A B A A D C C C B B A D A D D C A D C B A B
Câu 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 Đáp án
A C A D D A B B C D A A C C A A B D B B D C D C C HƯỚNG DẪN GIẢI
Câu 36.Cho số phức z thỏa mãn z + 2z = 6 + 2 .i Điểm biểu diễn số phức z có tọa độ là A.(2; 2 − ) . B.( 2; − 2 − ). C.(2;2) . D.( 2; − 2) . Lời giải Chọn A.
Gọi z = a + bi,a,b∈  a = a =
Ta có: z + z = + i ⇔ a + bi + (a −bi) 3 6 2 2 6 2 2 = 6 + 2i ⇔  ⇔  b 2 b  − =  = 2 −
Vậy z = 2 − 2i suy ra điểm biểu diễnsố phức z có tọa độ là(2; 2 − )  
Câu 37.Trong không gian Oxyz , cho các vectơ a = (1;2;3),b = ( 2; − 4; ) 1 ,c = (1; 2; − ) 1 . Tìm tọa độ vectơ   
u = 2a − 3b + c . A. u = (9; 1 − 0;4).
B. u = (9;10;4).
C. u = (0;4;5). D. u = (4; 9; − 10). Lời giải Chọn A. 2a = (2;4;6)      Ta có: 3b ( 6;12;3) = − 
 ⇒ 2a − 3b + c = (9; 1 − 0;4) c (1; 2; ) 1  = − 
Câu 38.Diện tích S của hình phẳng giới hạn bởi các đường 3
y = x −1, y = x −1 bằng A. 1 S = π . B. 1 S = π . C. 1 S = . D. 1 S = . 4 2 2 4 Lời giải Chọn C. x = 1 ± Ta có: 3 3
x −1 = x −1 ⇔ x − x = 0 ⇔  x = 0 1 Khi đó diện tích 3 1
S = x − x dx = ∫ − 2 1
Câu 39.Cho (H ) là hình phẳng giới hạn bởi đường cong (C) 2
: y = −x + 4x và đường thẳng d : y = .x Tính
thể tích V của vật thể tròn xoay do hình phẳng (H ) quay xung quanh trục hoành. π π π π A. 81 V = . B. 81 V = . C. 108 V = . D. 108 V = . 10 5 5 10 Lời giải Chọn C. x = 3 Ta có: 2 2
−x + 4x = x ⇔ x − 3x = 0 ⇔  x = 0 3
Khi đó thể tích V = π ∫ (−x + x)2 2 2 108 4 − x dx = π 5 0 3x −1
Câu 40.Họ tất cả các nguyên hàm của hàm số f (x) = ( là x + 2)2 Trang 5 A. 7 3ln x + 2 + + C . B. 7 ln x + 2 − + C . x + 2 x + 2
C. 3x − 7ln x + 2 + C . D. 7 3ln x + 2 − + C . (x + 2)2 Lời giải Chọn A. 3x 1  3 7  − 7 Ta có: f ∫ (x)dx = dx =  −
dx = 3ln x + 2 + + C ∫ ( ∫ x + 2)2  x + 2  (x + 2)2  x + 2  1
Câu 41.Cho tích phân = ( + 2)ln( + ) 1 = ln 2 b I x x dx a − ∫
trong đó a,b,c là các số nguyên và b là phân số c c 0 tối giản. Tổng 2 2 2
S = a + b + c bằng A. 81. B. 16. C. 49. D. 100. Lời giải Chọn A.  1  =  ln ( + ) 1 du = dx u x  Đặt  x +1  ⇒  dv =  (x + 2)dx 1  2
v = x + 2x  2 1 1 1 2 Ta có: ∫( ) ( )  1 2  = + + = + ( + ) 1 x + 4 2 ln 1 2 ln 1 x I x x dx x x x −   dx ∫  2  2 x +1 0 0 0 1 1 1 2  1        2 = +   ( + ) 1 3 1 2 − + − = ∫   +   ( + ) 1 x x x x x dx x x x −  + x − (x + ) 7 2 ln 1 3 2 ln 1 3 3ln 1  = 4ln 2 −  2  2  x +1  2  2  2  4 0 0 0 1
Câu 42.Cho hàm số y = f (x) liên tục trên  và (− ) + ( ) 2 f x
f x = x . Tính I = f ∫ (x)dx. 1 − A. 2 I  . B. 1 I  . C. 4 I  . D. 1 I  . 3 3 3 2 Lời giải Chọn B. 1 1 1 2 1
Ta có: f (−x) + f (x) 2
= x ⇒ f (−x)dx + f (x) 2
dx = x dx ⇔ 2I = ⇔ I = ∫ ∫ ∫ − − − 3 3 1 1 1
Câu 43.Trongkhông gian Oxyz , mặt phẳng đi qua 2 điểm ( A 1;1;2), B( 1; − 2; )
1 và song song với trục Ox có phương trình là
A. y − z +1 = 0 .
B. x − z + 2 = 0 .
C. 3y − z −1= 0.
D. y + z −3 = 0 . Lời giải Chọn D.      Ta có: AB = ( 2 − ;1;− )
1 ,i = (1;0;0) ⇒ n = AB,i  = (0; 1; − − ) 1  
Khi đó, Phương trình mặt phẳng đi qua (
A 1;1;2): y + z −3 = 0 .
Câu 44.Tính tổng phần thực và phần ảo của số phức z thỏa mãn 25 z + = 8 − 6i . z A. 1. − B. 7. C. 1. D. 4. Lời giải Chọn B. Trang 6 Ta có: 25 z +
= 8 − 6i ⇔ z.z + 25 = z (8 − 6i) (*) z 2
⇒ z + 25 = z .10
Đặt t = z ,t ≥ 0 ta có: 2t + 25 =10t ⇔ t = 5
Thay vào (*) có 25 +15 = z (8 − 6i) ⇔ z = 4 + 3i
Câu 45.Trong không gian Oxyz , cho các điểm A(1;0;2), B(1;2; )
1 ,C (3;2;0) và D(1;1;3) . Đường thẳng
đi qua A và vuông góc với mặt phẳng (BCD) có phương trình là  x =1− tx =1+ tx = 1+ tx =1+ t A.      y = 3t .
B. y = 4t . C. y = 4 .
D. y = 3t . z = 2−     2t z = 2 +  2t z = 2 +  2t z = 2 +  2t Lời giải Chọn B.      Ta có: BC = (2;0;− ) 1 , BD = (0; 1 − ;2) ⇒ n
= BC, BD = ( 1 − ; 4; − 2 − BCD ) ( )    x =1+ t
Khi đó, đường thẳng đi qua 
A(1;0;2) vuông góc (BCD) với nhận a = (1;4;2) làm VTCP có pt: y = 4t . z = 2+  2t
Câu 46.Có bao nhiêu giá trị nguyên của tham số m∈(0;20) để phương trình 2
z − 6z + m = 0 có hai nghiệm
phân biệt z , z thỏa mãn z z = z z . 1 2 1 1 2 2 A. 13 B. 11 C. 12 D.10 Lời giải Chọn D.
Phương trình đã cho ⇔ (z − )2 3 = 9 − m
+) Nếu m = 9 ⇒ z = 3 (loại vì phương trình chỉ có một nghiệm).
+) Nếu m < 9 thì phương trình đã cho có hai nghiệm thực z = 3− 9 − m; z = 3+ 9 − m . 1 2
Ta có z z = z z ⇔ z = z ⇔ (3− 9− m)2 = (3+ 9− m)2 1 1 2 2 1 2
3− 9 − m = 3+ 9 − m ⇔ 
⇔ 9 − m = 0 ⇔ m = 9 (loại). 3− 9 − m = 3 − − 9 − m  (VN )
+) Nếu m > 9 thì phương trình đã cho có hai nghiệm phức z = 3− i m − 9, z = 3+ i m − 9. 1 2 Ta có 2
z z = z z = 3 + m − 9 (luôn đúng).⇒ m > 9 thỏa mãn yêu cầu bài toán. 1 1 2 2 0 m∈ Vì 
nên m∈{10;11;12;...; } 19 . m∈( ; 0 ) 20
Vậy có 10 giá trị thỏa mãn yêu cầu bài toán.
Câu 47.Trong không gian x + y − z −
Oxyz , cho đường thẳng 1 1 3 d : = =
và mp(P) : 2x − 2y + z −3 = 0 , 1 2 2 −
phương trình đường thẳng ∆ nằm trong mặt phẳng (P) , cắt d và vuông góc với d là
A. x − 2 y −1 z + 5 + + − + + − + − − = =
. B. x 2 y 1 z 5 = =
. C. x 2 y 1 z 5 = =
. D. x 2 y 1 z 5 = = . 2 5 6 2 5 6 − 2 5 6 2 5 6 − Lời giải Chọn C. Trang 7
M = ∆ ∩ d  Gọi  ∆ ⊂ (  ⇒ = ∩ ⇒ − − P) M d (P) M ( 2; 1;5)  ∆ ⊥ d  Ta có:     ∆ ⊂ (  ⇒ = = P) a∆ [n a P , d ] (2;5;6)  + + −
Khi đó phương trình đường thẳng ∆ đi qua M và có VTCP ax y z = : 2 1 5 = = . ∆ (2;5;6) 2 5 6
Câu 48: Cho hàm số y = f (x) có đạo hàm liên tục trên  thỏa mãn f ( ) 1 = 1 − và 1 xf ( 3
− x ) + f ′(x) 7 1
= x + x − 2, x ∈  . Tính tích phân I = f ∫ (x)dx . 0 A. 2 − − . B. 5 . C. 5 . D. 2 . 3 9 9 3 Lời giải Chọn D. Từ xf ( 3
− x ) + f ′(x) 7 1
= x + x − 2, x ∈  . Suy ra 2 x f ( 3
− x ) + xf ′(x) 8 2 1
= x + x − 2x, x ∈  1 1 1 Do đó 2 x f ∫ ( 3
1− x )dx + xf ′
∫ (x)dx = ∫( 8 2
x + x − 2x)dx (1). 0 0 0 1 + Xét 2 A = x f ∫ ( 3 1− x )dx : 0 0 1 1 Đặt 1 1 1 3 2
t =1− x ⇒ dt = 3
− x dx . Khi đó: A = − f
∫ (t)dt = f
∫ (t)dt = f ∫ (x)dx (2). 3 3 3 1 0 0 1
+ Xét B = xf ′ ∫ (x)dx: 0 1 1
Sử dụng tích phân từng phần ta được: B = xf (x)1 − f ∫ (x)dx = 1 − − f ∫ (x)dx (3) 0 0 0 1 1 1 − 1
Thay (2) và (3) vào (1) ta được: 1 2 4 2 f ∫ (x)dx f ∫ (x) 5 1 dx − − − = ⇔ f ∫ (x)dx = f ∫ (x)dx − ⇔ = . 3 9 3 9 3 0 0 0 0
Câu 49: Trong không gian tọa độ Oxyz cho 3 điểm A(0;2; )
1 , B(1;0;2),C (2;1; 3
− ) . Tập hợp các điểm M thỏa mãn 2 2 2
MA + MB + MC = 20 là một mặt cầu. Lập phương trình mặt cầu đó.
A. (x − )2 + ( y + )2 2 4 1 1 + z = .
B. (x − )2 + ( y − )2 + (z − )2 2 1 1 1 = . 9 3
C.(x − )2 + ( y − )2 2 2 1 1 + z = .
D. (x + )2 + ( y − )2 2 2 1 1 + z = 3 3 Lời giải Chọn C.
Gọi G là trọng tâm tam giác ABC ta có G (1;1;0) , ta có:
   
GA + GB + GC = 0 , GA = 3 , GB = 5 , GC = 10 .      
MA + MB + MC =
⇔ (MG +GA)2 +(MG +GB)2 + (MG +GC)2 2 2 2 20 = 20
2 2 2 2 6
⇔ 3MG + GA + GB + GC = 20 ⇔ MG = . 3
Vậy tập hợp điểm M là mặt cầu tâm G , bán kính 6 R = nên phương trình là: 3
(x − )2 +( y − )2 2 2 1 1 + z = 3 Trang 8
Câu 50:Bác Việt có một bồn hoa hình tròn tâm O . Bác dự định chia bồn hoa thành
bốn phần bởi hai đường parabol có chung đỉnh O và đối xứng với nhau qua O . Hai
đường này cắt đường tròn tại bốn điểm ,
A B,C, D tạo thành một hình vuông có cạnh
bằng 4m (như hình vẽ). Phần diện tích S , S được dùng để trồng cỏ, và S , S được 3 4 1 2
dùng để trồng hoa. Biết kinh phí trồng cỏ là 100000 đồng 2
/m , trồng hoa là 250000
đồng. Hỏi chi phí để bác Việt trồng bồn hoa là bao nhiêu? (Số tiền làm tròn đến hàng nghìn)
A.3270000 đồng.
B. 4897000 đồng.
C. 4798000 đồng.
D. 3702000 đồng. Lời giải Chọn C.
Chọn hệ tọa độ Oxy như hình vẽ
Parabol có hàm số dạng có đỉnh là gốc tọa độ và đi qua điểm B(2;2) nên có phương trình 1 2 y = x 2
Đường tròn tâm O có bán kính 1
OB = BD = 2 2 có phương trình: 2 2 x + y = 8 2 Khi đó, 2  2 1 2  8  8 S + S = 2
8 − x − x dx = 2 4 + 2π − = + ∫     4π 1 2 −  2   3  3 2  8  8 S + S = 8π − +  4π =  4π − 3 4  3  3
Suy ra chi phí trồng bồn hoa là:  8   8 250000. 4π  100000.4π  + + − ≈  4798230 đồng. 3 3     
Vậy chi phí để bác Việt trồng bồn hoa là 4.798.000 đồng (Số tiền làm tròn đến hàng nghìn) Trang 9