








Preview text:
Trang 6
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn KHÓA HỌC IMOE
ĐỀ MINH HỌA CHINH PHỤC KÌ THI TỐT NGHIỆP
THẦY ĐỖ VĂN ĐỨC
NĂM HỌC 2024 - 2025; MÔN TOÁN ĐỀ SỐ 01
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
1. Giả sử mẫu số liệu ghép nhóm được cho dưới dạng bảng tần số ghép nhóm: Nhóm Nhóm 1 Nhóm 2 … Nhóm 𝑘𝑘 Giá trị đại diện 𝑐𝑐1 𝑐𝑐2 … 𝑐𝑐𝑘𝑘 Tần số 𝑛𝑛1 𝑛𝑛2 … 𝑛𝑛𝑘𝑘
Đặt 𝑛𝑛 = 𝑛𝑛1 + 𝑛𝑛2 + ⋯ + 𝑛𝑛𝑘𝑘.
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu 𝑥𝑥̅, được tính theo công thức nào?
n c + n c +...+ n c
n c + n c +...+ n c A. 1 1 2 2 k k x = . B. 1 1 2 2 k k x = . n n
n c + n c +...+ n c 2 2 2
n c + n c +...+ n c C. 1 1 2 2 k k x = . 1 1 2 2 k k x = . 2 D. n n
2. Khối hộp 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴. 𝐴𝐴′𝐴𝐴′𝐴𝐴′𝐴𝐴′ có thể tích bằng 27 thì thể tích khối tứ diện 𝐴𝐴𝐴𝐴𝐴𝐴′𝐴𝐴′ bằng 27 A. 9. B. . 2 C. 18. D. 3.
3. Tập nghiệm của bất phương trình log2(20 − 2𝑥𝑥) ≤ 2𝑥𝑥 có chứa bao nhiêu phần tử nguyên? A. 7. B. 8. C. 9. D. 10.
4. Trong không gian 𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂, cho hai điểm 𝐴𝐴(−3; 4; 0) và 𝐴𝐴(5; 0; 12). Côsin của góc giữa 𝑂𝑂��𝐴𝐴 �⃗ và 𝑂𝑂�𝐴𝐴 ��⃗ bằng: 3 5 5 3 A. . . − . − . 13 B. 6 C. 6 D. 13
5. Họ nguyên hàm của hàm số 𝑓𝑓(𝑥𝑥) = √𝑥𝑥 + 1 là
A. F (x) = x x + x + C. B. F (x) 1 = x x + C. 2 1 C. F (x) 2
= x x + x + C. + C. 3 D. x
6. Hàm số 𝑂𝑂 = log5(𝑥𝑥3 − 3𝑥𝑥2 + 4) có bao nhiêu điểm cực trị? A. 2. B. 1. C. 3. D. 0.
7. Có 5 bạn, trong đó có 1 bạn tên là Đức. Có bao nhiêu cách xếp 5 bạn này thành 1 hàng ngang,
sao cho Đức luôn đứng giữa 2 bạn khác? A. 72. B. 96. C. 48. D. 100.
Thực chiến luyện đề môn Toán | Đề số 01 Trang 7
8. Cho hàm số 𝑓𝑓(𝑥𝑥) xác định, liên tục trên đoạn [−2; 2] và có bảng biến thiên 𝑥𝑥 −2 0 1 2
𝑓𝑓′(𝑥𝑥) + || − 0 + 4 2 𝑓𝑓(𝑥𝑥) −3 1
Gọi 𝑀𝑀 và 𝑚𝑚 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 𝑓𝑓(𝑥𝑥) trên đoạn [−2; 2].
Giá trị của 𝑀𝑀 + 𝑚𝑚 bằng A. 5. B. 1. C. 2. − D. 1. −
9. Trong không gian 𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂, đường thẳng song song với trục 𝑂𝑂𝑂𝑂 và đi qua điểm 𝑀𝑀(1; 1; 1) có phương trình là x =1+ t x = 1+ t x = t x =1 A. y =1+ t. B. y =1+ t. C. y = t. D. y =1. z = t z = 1 z = 1 z = t
10. Một khối chóp có đáy là tam giác vuông với một góc nhọn bằng 60° và độ dài cạnh huyền
bằng 2𝑎𝑎, đồng thời chiều cao của khối chóp là 3𝑎𝑎. Thể tích của khối chóp bằng 3 3 3 3 A. 3 a . B. 3 2a . C. 3 a . D. 3 a . 2 2 2
11. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 𝑂𝑂 = 2𝑥𝑥2 − 2 và trục hoành? 10 8 2 4 A. . . . . 3 B. 3 C. 3 D. 3
12. Trong không gian 𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂, cho mặt phẳng (𝑃𝑃): 𝑥𝑥 + 𝑂𝑂 + 𝑂𝑂 + 𝑚𝑚 = 0 và mặt cầu (𝑆𝑆) có phương
trình (𝑥𝑥 − 2)2 + (𝑂𝑂 + 1)2 + 𝑂𝑂2 = 16. Tìm các giá trị của 𝑚𝑚 để (𝑃𝑃) cắt (𝑆𝑆) theo giao tuyến là
đường tròn có bán kính lớn nhất? A. m = 0. B. m ≠ 0. C. m =1. D. m = 1. − Trang 8
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b),
c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
1. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑥𝑥) = 𝑎𝑎𝑥𝑥 + 𝑏𝑏 + 1 có đồ thị như hình vẽ. x − c
a) Đồ thị hàm số nhận 𝑂𝑂 = 𝑥𝑥 làm tiệm cận xiên.
b) Tâm đối xứng của đồ thị hàm số là 𝐼𝐼(1; 1)
c) 𝑎𝑎 + 𝑏𝑏 + 𝑐𝑐 = 0.
d) Gọi 𝐴𝐴, 𝐴𝐴 là các điểm cực trị của đồ thị hàm số; 𝑀𝑀 là điểm di
động trên trục 𝑂𝑂𝑥𝑥 sao cho góc 𝐴𝐴𝑀𝑀𝐴𝐴
� không tù, giá trị nhỏ
nhất của hoành độ điểm 𝑀𝑀 là 3
2. Một chất điểm 𝐴𝐴 xuất phát từ 𝑂𝑂, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật v(t) 1 2 13 = t +
t (m / s), trong đó 𝑡𝑡 (giây) là khoảng thời gian tính từ lúc 𝐴𝐴 bắt đầu 100 30
chuyển động. Từ trạng thái nghỉ, một chất điểm 𝐴𝐴 cũng xuất phát từ 𝑂𝑂, chuyển động thẳng
cùng hướng với 𝐴𝐴 nhưng chậm hơn 10 giây so với 𝐴𝐴 và có gia tốc bằng 𝑎𝑎 (m/s2) (𝑎𝑎 là hằng
số). Biết sau khi 𝐴𝐴 xuất phát 15 giây thì đuổi kịp 𝐴𝐴.
a) Vận tốc của chất điểm 𝐴𝐴 được tính theo công thức 𝑣𝑣𝐵𝐵(𝑡𝑡) = 𝑎𝑎𝑡𝑡 (với mốc thời gian tính từ
lúc 𝐴𝐴 bắt đầu chuyển động).
b) Quãng đường mà chất điểm 𝐴𝐴 đi được trong 25 giây là 375 m. 2
c) Quãng đường 𝑆𝑆𝐵𝐵(𝑡𝑡) mà chất điểm 𝐴𝐴 đi được trong thời gian 𝑡𝑡 giây (𝑡𝑡 > 0) kể từ khi xuất t
phát được tính theo công thức S t = v t t B ( ) ∫ ( )d . 0
d) Vận tốc của chất điểm 𝐴𝐴 tại thời điểm đuổi kịp chất điểm 𝐴𝐴 là 25 (m/s).
3. Tổ I có 8 học sinh nam và 7 học sinh nữ. Tổ II có 6 học sinh nam và 9 học sinh nữ. Chọn ngẫu
nhiên 6 học sinh từ 30 học sinh của hai tổ.
Thực chiến luyện đề môn Toán | Đề số 01 Trang 9
a) Xác suất để chọn được toàn bộ 6 học sinh đều là nam hoặc đều là nữ là nhỏ hơn 5%.
b) Xác suất để chọn được chính xác 3 học sinh từ tổ I và 3 học sinh từ tổ II thuộc khoảng (0,34; 0,35).
c) Nếu biết rằng đã chọn được toàn bộ 6 học sinh đều là nam hoặc đều là nữ, thì xác suất để
chọn được 3 học sinh từ tổ I và 3 học sinh từ tổ II bằng 116 . 5915
d) Xác suất để chọn được 6 học sinh trong đó có đúng 3 học sinh nam và 3 học sinh nữ là 1. 3
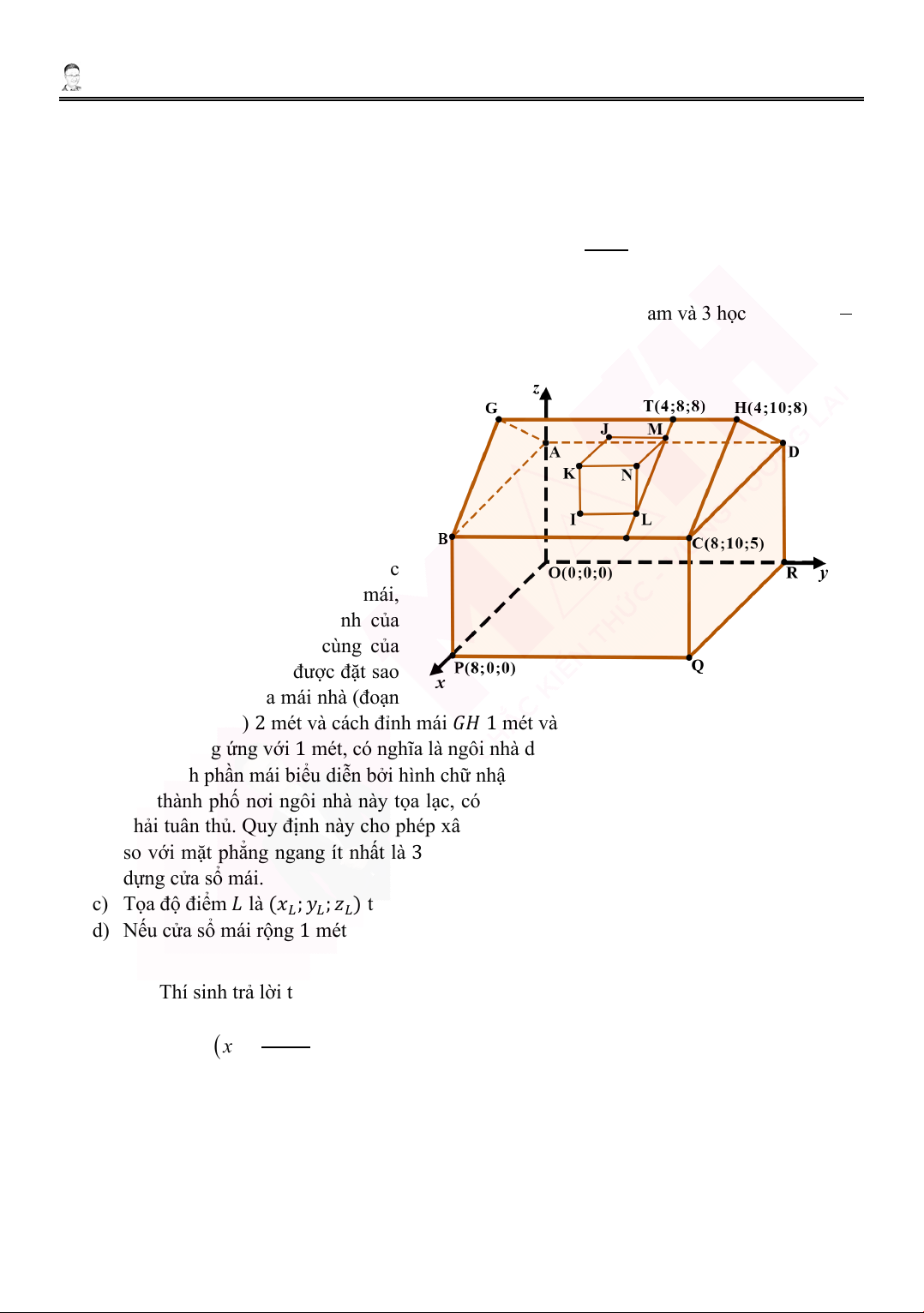
4. Hình vẽ mô tả một ngôi nhà một tầng
đơn giản đặt trên một mặt phẳng nằm
ngang. Trên một trong hai mái nhà
hình chữ nhật, người ta muốn xây
thêm một cửa sổ mái. Các điểm
𝐴𝐴, 𝐴𝐴, 𝐴𝐴, 𝐴𝐴, 𝑂𝑂, 𝑃𝑃, 𝑄𝑄 và 𝑅𝑅 là các đỉnh của
một hình hộp chữ nhật. Hình lăng trụ
đứng 𝐿𝐿𝑀𝑀𝐿𝐿𝐼𝐼𝐿𝐿𝐿𝐿, mặt 𝐿𝐿𝐿𝐿𝑀𝑀𝐿𝐿 song song
với mặt đất và mặt 𝐿𝐿𝐿𝐿𝐿𝐿𝐼𝐼 vuông góc
với mặt đất, biểu diễn cửa sổ mái,
đoạn thẳng 𝐺𝐺𝐺𝐺 biểu diễn đỉnh của
mái nhà, tức là cạnh trên cùng của
mái nhà. Cửa sổ mái sẽ được đặt sao
cho cách mép bên của mái nhà (đoạn
𝐺𝐺𝐴𝐴 trong mô hình) 2 mét và cách đỉnh mái 𝐺𝐺𝐺𝐺 1 mét và cách 𝐴𝐴𝐴𝐴 1 mét. Một đơn vị đo trong
hệ tọa độ tương ứng với 1 mét, có nghĩa là ngôi nhà dài 10 mét.
a) Diện tích phần mái biểu diễn bởi hình chữ nhật 𝐴𝐴𝐴𝐴𝐺𝐺𝐺𝐺 là 50 m2.
b) Tại thành phố nơi ngôi nhà này tọa lạc, có một quy định xây dựng mà mọi chủ nhà đều
phải tuân thủ. Quy định này cho phép xây dựng cửa sổ mái nếu góc nghiêng của mái nhà
so với mặt phẳng ngang ít nhất là 35° thì ngôi nhà không đáp ứng được yêu cầu để xây dựng cửa sổ mái.
c) Tọa độ điểm 𝐿𝐿 là (𝑥𝑥 2 2 2
𝐿𝐿; 𝑂𝑂𝐿𝐿; 𝑂𝑂𝐿𝐿) thì 𝑥𝑥𝐿𝐿 − 𝑂𝑂𝐿𝐿 + 𝑂𝑂𝐿𝐿 = 12,9.
d) Nếu cửa sổ mái rộng 1 mét (𝐼𝐼𝐿𝐿 = 1), tọa độ điểm 𝐿𝐿 là (𝑥𝑥𝐾𝐾 ; 𝑂𝑂𝐾𝐾 ; 𝑂𝑂𝐾𝐾) thì 𝑥𝑥2 2 2
𝐾𝐾 + 𝑂𝑂𝐾𝐾 − 𝑂𝑂𝐾𝐾 > 50.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6. 1. + Cho hàm số ( ) x a f x =
. Đặt M = max f (x) và m = min f (x). Gọi 𝑆𝑆 là tập hợp tất cả các 2x +1 [0;2] [0;2]
giá trị của 𝑎𝑎 để 𝑀𝑀 = 6𝑚𝑚. Nếu tổng các phần tử của 𝑆𝑆 bằng 𝑘𝑘 thì 29𝑘𝑘 bằng bao nhiêu? Đáp số: ………. Trang 10
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
2. Cho hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴 có Δ𝐴𝐴𝐴𝐴𝐴𝐴 vuông cân tại 𝐴𝐴, 𝐴𝐴𝐴𝐴 = 1. Biết 𝑆𝑆𝐴𝐴 ⊥ 𝐴𝐴𝐴𝐴,
𝑆𝑆𝐴𝐴 = 𝑆𝑆𝐴𝐴 và góc giữa 𝑆𝑆𝐴𝐴 và mặt phẳng (𝐴𝐴𝐴𝐴𝐴𝐴) bằng 60°. Tính thể tích
khối chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴 (kết quả làm tròn đến hàng phần trăm). Đáp số: ……….
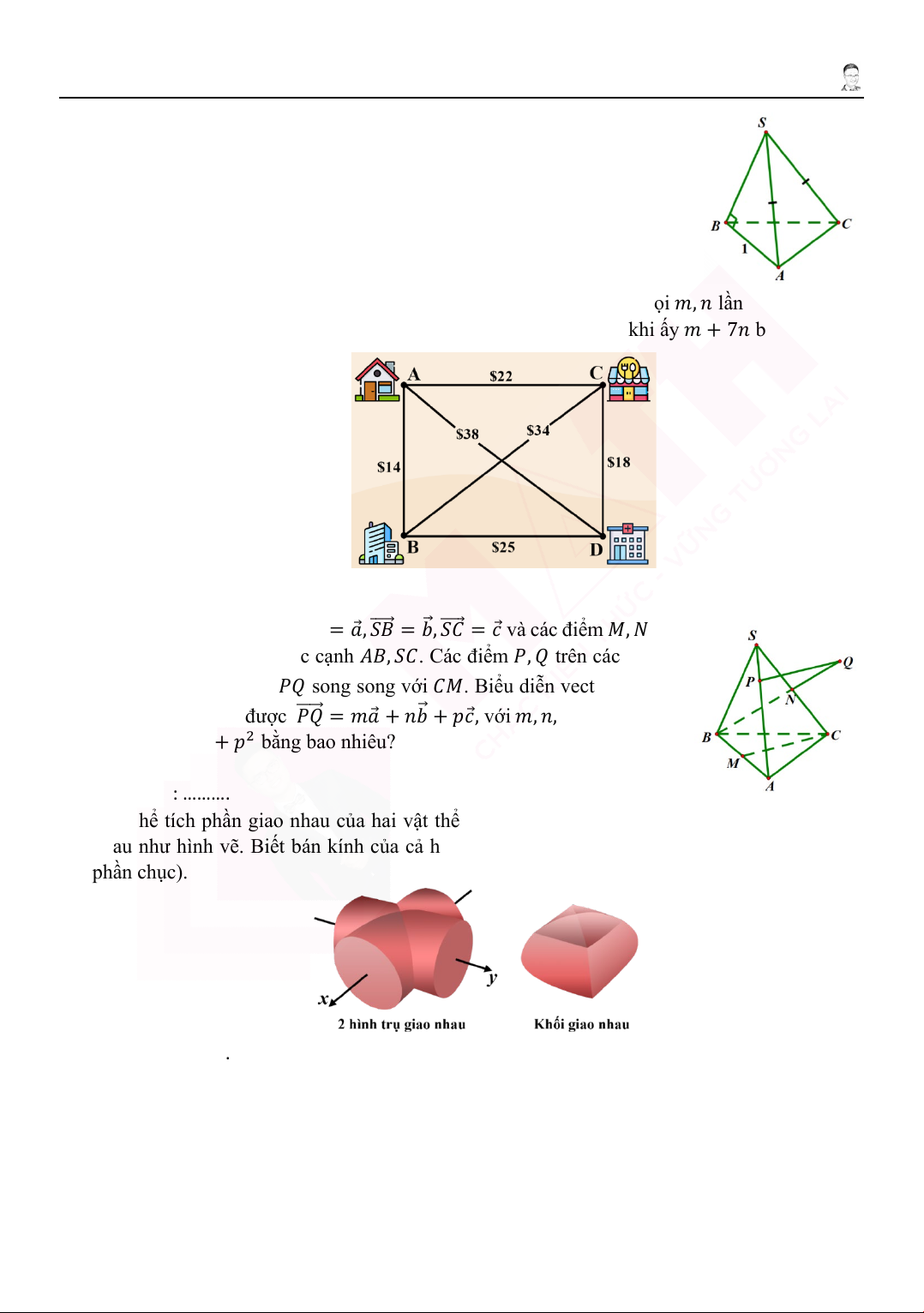
3. Anh Bình cần đi qua các địa điểm 𝐴𝐴, 𝐴𝐴, 𝐴𝐴, 𝐴𝐴, mỗi địa điểm có mặt đúng
1 lần, nhưng không may xe anh Bình bị hư nên phải dùng dịch vụ chạy
Grab để đi qua các địa điểm ấy. Biết rằng trọng số của từng cạnh nối giữa
các điểm chỉ giá tiền khi anh Bình đặt Grab chạy các địa điểm ấy. Gọi 𝑚𝑚, 𝑛𝑛 lần lượt là số tiền
nhỏ nhất và số tiền lớn nhất mà anh Bình cần phải trả (đơn vị $), khi ấy 𝑚𝑚 + 7𝑛𝑛 bằng Đáp số: ……….
4. Cho hình chóp S. ABC có 𝑆𝑆�𝐴𝐴
��⃗ = 𝑎𝑎⃗, 𝑆𝑆�𝐴𝐴
��⃗ = 𝑏𝑏�⃗, 𝑆𝑆�𝐴𝐴�⃗ = 𝑐𝑐⃗ và các điểm 𝑀𝑀, 𝐿𝐿 lần
lượt là trung điểm của các cạnh 𝐴𝐴𝐴𝐴, 𝑆𝑆𝐴𝐴. Các điểm 𝑃𝑃, 𝑄𝑄 trên các đường
thẳng 𝑆𝑆𝐴𝐴, 𝐴𝐴𝐿𝐿 sao cho 𝑃𝑃𝑄𝑄 song song với 𝐴𝐴𝑀𝑀. Biểu diễn vecto 𝑃𝑃�𝑄𝑄 ��⃗ theo
ba vectơ 𝑎𝑎⃗, 𝑏𝑏�⃗, 𝑐𝑐⃗, ta được 𝑃𝑃�𝑄𝑄
��⃗ = 𝑚𝑚𝑎𝑎⃗ + 𝑛𝑛𝑏𝑏�⃗ + 𝑝𝑝𝑐𝑐⃗, với 𝑚𝑚, 𝑛𝑛, 𝑝𝑝 ∈ ℝ. Giá trị
của 4𝑚𝑚2 + 𝑛𝑛2 + 𝑝𝑝2 bằng bao nhiêu? Đáp số: ……….
5. Tìm thể tích phần giao nhau của hai vật thể hình trụ có trục đối xứng cắt và vuông góc với
nhau như hình vẽ. Biết bán kính của cả hai hình trụ đều bằng 1 (kết quả làm tròn đến hàng phần chục). Đáp số: ……….
6. Trong một kho rượu có số lượng rượu loại A và loại B như nhau. Người ta chọn ngẫu nhiên
một chai rượu trong kho và đưa cho 5 người nếm thử để xác định xem đó là loại rượu nào. Giả
sử mỗi người đều có xác suất đoán đúng là 75%. Có 4 người kết luận đó là chai rượu loại A
Thực chiến luyện đề môn Toán | Đề số 01 Trang 11
và 1 người kết luận đó là chai rượu loại B. Hỏi xác suất để chai rượu đó thuộc loại A là bao
nhiêu? (kết quả làm tròn đến hàng phần trăm). Đáp số: ……….
--- Hết --- PHẦN GHI CHÉP RIÊNG
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………... Trang 12
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
Thực chiến luyện đề môn Toán | Đề số 2 Trang 13 KHÓA HỌC IMOE
ĐỀ MINH HỌA KÌ THI TỐT NGHIỆP THPT 2025
THẦY ĐỖ VĂN ĐỨC MÔN TOÁN ĐỀ SỐ 02
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
1. Cho 3 học sinh nam và 4 học sinh nữ. Có bao nhiêu cách chọn ra 1 cặp nam nữ để tham gia khiêu vũ? A. 7. B. 36. C. 24. D. 12.
2. Giá trị lớn nhất của hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) = 𝑥𝑥4 − 8𝑥𝑥2 + 16 trên đoạn [−1; 3] bằng A. 0. B. 25. C. 19. D. 9.
3. Cho hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) có bảng biến thiên như sau: 𝑥𝑥 −∞ −2 0 +∞ 𝑦𝑦′ − + − +∞ +∞ +∞ 𝑦𝑦 1 −∞ 2
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng A. 3. B. 0. C. 2. D. 1.
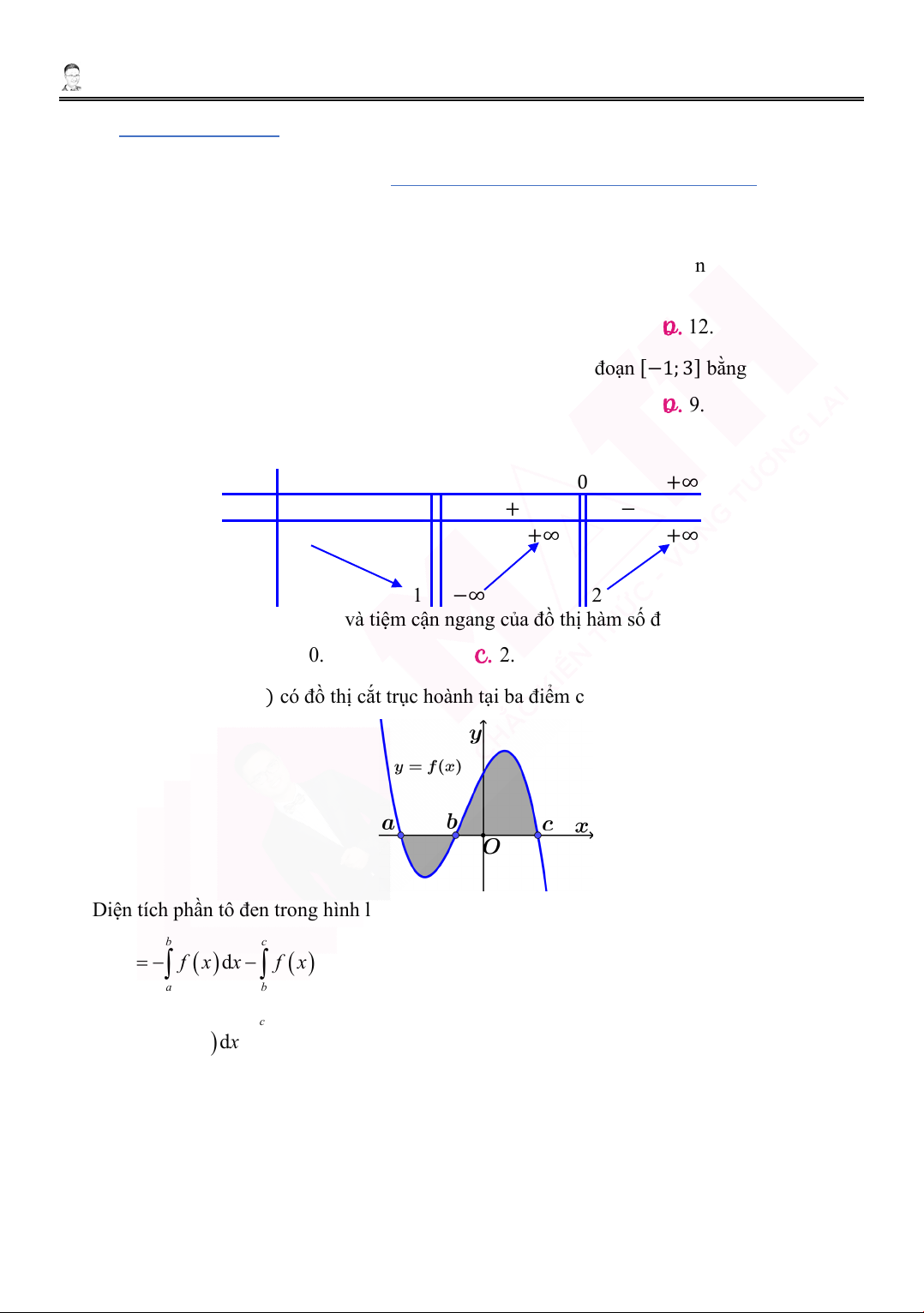
4. Cho hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) có đồ thị cắt trục hoành tại ba điểm có hoành độ 𝑎𝑎, 𝑏𝑏, 𝑐𝑐 (như hình vẽ).
Diện tích phần tô đen trong hình là: b c b c A. S = − f
∫ (x)dx− f ∫ (x)d .x B. S = f
∫ (x)dx+ f ∫ (x)d .x a b a b b c b c C. S = − f
∫ (x)dx+ f ∫ (x)d .x D. S = f
∫ (x)dx− f ∫ (x)d .x a b a b
5. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho điểm 𝐴𝐴(−1; 2; −4). Điểm đối xứng với 𝐴𝐴 qua mặt phẳng (𝑂𝑂𝑦𝑦𝑂𝑂) có tọa độ là A. ( 1 − ;− 2;− 4). B. ( 1; − − 2;4). C. (1;2;− 4). D. (1;− 2;4). Trang 14
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
6. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho tam giác 𝐴𝐴𝐴𝐴𝐴𝐴 có 𝐴𝐴(0; 1; 2), 𝐴𝐴(2; 1; 4), 𝐴𝐴(−1; 2; 2). Gọi
𝐻𝐻(𝑥𝑥; 𝑦𝑦; 𝑂𝑂) là trực tâm tam giác 𝐴𝐴𝐴𝐴𝐴𝐴. Giá trị của biểu thức 𝑇𝑇 = 𝑥𝑥 + 𝑦𝑦 + 𝑂𝑂 bằng A. 2 . B. 1. C. 1. D. 2. 3 3
7. Trong một hộp có 10 viên bi đánh số từ 1 đến 10, lấy ngẫu nhiên ra hai viên bi. Tính xác suất
để tích hai số trên chúng là một số chẵn. 2 1 4 7 A. . B. . C. . D. . 9 2 9 9
8. Tập nghiệm của phương trình log5(2𝑥𝑥 + 1) + 2 log25(3𝑥𝑥 − 1) = 2 là 13 13 A. S = {− } 2 . B. S = { } 2 . C. S = . D. S = 3; − . 6 6
9. Hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có đáy là hình vuông cạnh 𝑎𝑎, cạnh bên 𝑆𝑆𝐴𝐴 vuông góc với đáy, đường thẳng
𝑆𝑆𝐴𝐴 tạo với mặt phẳng (𝑆𝑆𝐴𝐴𝐴𝐴) góc 30°. Thể tích của khối chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 là 3 a 2 2 2 A. . B. 3 a . C. 3 2a . D. 3 a . 3 2 4
10. Trong không gian với hệ tọa độ 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho đường thẳng
𝑥𝑥 − 13 𝑦𝑦 − 1 𝑂𝑂 − 4 𝑑𝑑: 8 = 2 = 3
và mặt phẳng (𝛼𝛼): 𝑥𝑥 + 2𝑦𝑦 − 3𝑂𝑂 + 1 = 0. Gọi 𝑀𝑀(𝑎𝑎; 𝑏𝑏; 𝑐𝑐) là giao điểm của đường thẳng 𝑑𝑑 và
mặt phẳng (𝛼𝛼). Giá trị của 𝑎𝑎 + 𝑏𝑏 + 𝑐𝑐 bằng 2 1 A. . B. 0. C. . D. 2. − 3 2
11. Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ bên? x + 2 A. y = . B. 3
y = −x − 2x +1. C. 3
y = x − 2x −1. D. 4 y = −x +1. x +1
12. Cho 𝐹𝐹(𝑥𝑥) là một nguyên hàm của hàm số 𝑓𝑓(𝑥𝑥) = |1 + 𝑥𝑥| − |1 − 𝑥𝑥| trên ℝ và thỏa mãn
𝐹𝐹(1) = 3. Tính tổng 𝐹𝐹(0) + 𝐹𝐹(2). A. 3. B. 2. C. 7. D. 5.
Thực chiến luyện đề môn Toán | Đề số 2 Trang 15
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
1. Một nhà máy có ba phân xưởng I, II, III cùng sản xuất một loại
sản phẩm với tỉ lệ phế phẩm tương ứng là 1%; 0,5%; 0,2%. Các
phân xưởng này lần lượt sản xuất 35%; 45%; 20% số sản phẩm
của nhà máy. Kiểm tra ngẫu nhiên một sản phẩm của nhà máy.
a) Xác suất để sản phẩm được kiểm tra là phế phẩm là 0,615%.
b) Biết rằng sản phẩm được kiểm tra là phế phẩm, thì xác suất
sản phẩm đó đến từ phân xưởng I cao hơn xác suất đến từ phân xưởng III.
c) Xác suất sản phẩm được kiểm tra là phế phẩm của phân xưởng II là cao nhất.
d) Xác suất để sản phẩm không phải là phế phẩm của nhà máy lớn hơn 99%.
2. Cho hình vuông có cạnh bằng 2 cm như hình vẽ. Bên trong hình
vuông kẻ bốn góc phần tư của một đường tròn có tâm là các đỉnh
của hình vuông và bán kính bằng 2 cm như hình vẽ. Đặt hệ tọa độ
gốc 𝐴𝐴, trục 𝑂𝑂𝑥𝑥 trùng với 𝐴𝐴𝐴𝐴, trục 𝑂𝑂𝑦𝑦 trùng với 𝐴𝐴𝐴𝐴, mỗi đơn vị trên
trục tọa độ 𝑂𝑂𝑥𝑥𝑦𝑦 dài 1 cm.
a) Phương trình đường tròn chứa cung tròn tâm 𝐴𝐴 là
𝑦𝑦 = 2 − �−𝑥𝑥2 + 4𝑥𝑥.
b) Cung tròn tâm 𝐴𝐴 và cung tròn tâm 𝐴𝐴 cắt nhau tại điểm có hoành độ bằng 2 − √3.
c) Diện tích hình phẳng giới hạn bởi cung tròn tâm 𝐴𝐴 và cung tròn tâm 𝐴𝐴 là 𝜋𝜋 − 2 cm2.
d) Diện tích của phần tô đậm là 1,2 cm2 (làm tròn đến hàng phần chục).
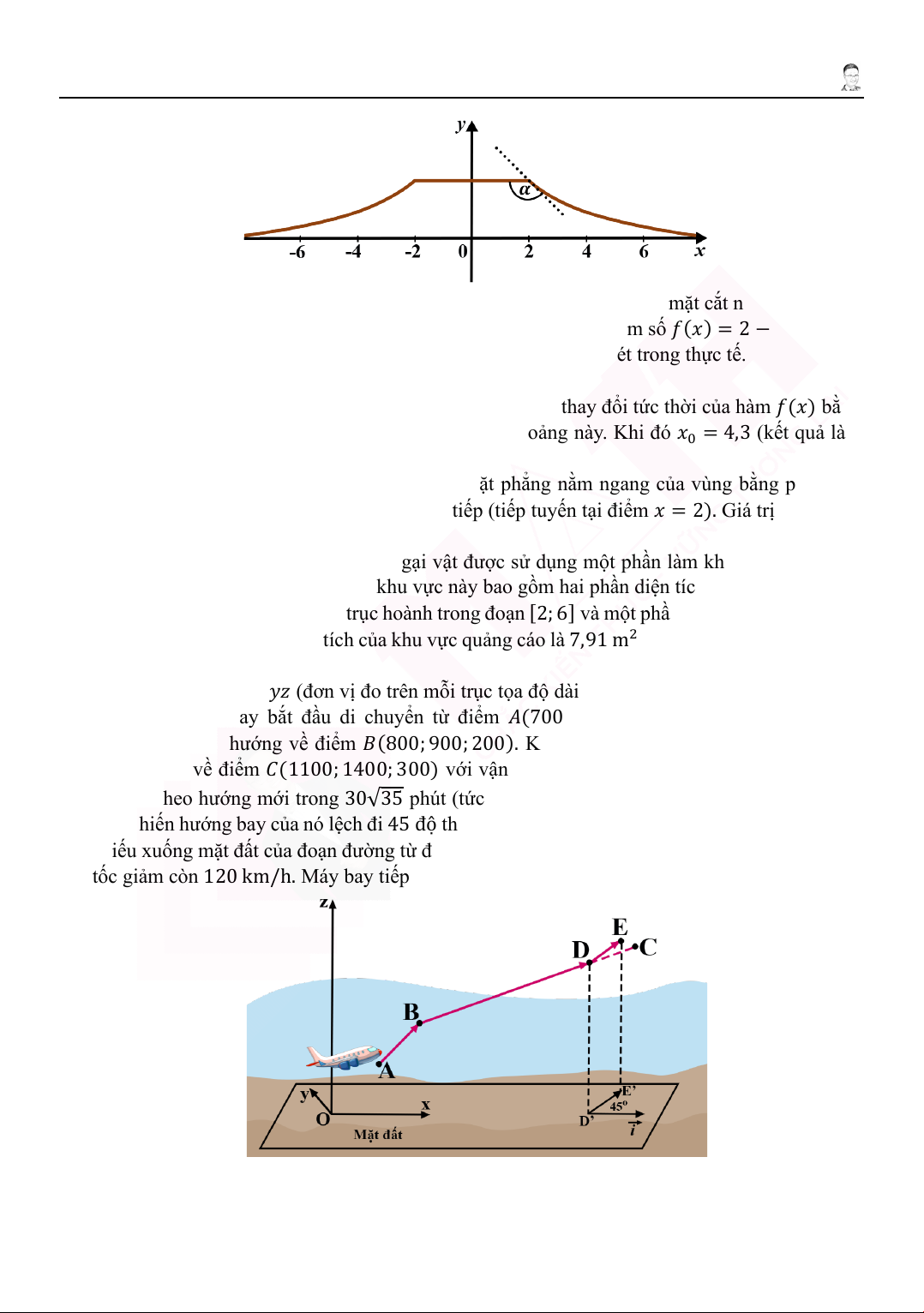
3. Hình vẽ bên dưới minh họa một phần khu vực thiết kế dành cho các hoạt động trượt ván, patin.
Đường lên của khu vực này dẫn đến một bề mặt nằm ngang (gọi là vùng bằng phẳng), tiếp
theo là đoạn dốc xuống, hai đường đối xứng nhau hai bên. Mặt trước và mặt sau của chướng
ngại vật vuông góc với mặt đất ngang. Để mô tả mặt bên phía trước một cách toán học, ta xét
mặt phẳng 𝑂𝑂𝑥𝑥𝑦𝑦 với trục 𝑂𝑂𝑥𝑥 là phần bên dưới, trục 𝑂𝑂𝑦𝑦 là trục đối xứng của bề mặt đang xét. Trang 16
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
Vùng bằng phẳng trải dài trong mô hình từ −2 ≤ 𝑥𝑥 ≤ 2. Đường cong mặt cắt ngang của đoạn
dốc xuống trong khoảng 2 ≤ 𝑥𝑥 ≤ 8 được mô tả bởi đồ thị của hàm số 𝑓𝑓(𝑥𝑥) = 2 − ln(𝑥𝑥 − 1).
Trong hệ tọa độ này, một đơn vị chiều dài tương ứng với một mét trong thực tế.
a) Chiều cao của vùng bằng phẳng là 2 m.
b) Trên khoảng (2; 8) có một điểm 𝑥𝑥0 mà tại đó, tốc độ thay đổi tức thời của hàm 𝑓𝑓(𝑥𝑥) bằng
tốc độ thay đổi trung bình của hàm 𝑓𝑓(𝑥𝑥) trên khoảng này. Khi đó 𝑥𝑥0 = 4,3 (kết quả làm
tròn đến hàng phần chục).
c) Trên mô hình, góc 𝛼𝛼 được xác định bởi mặt phẳng nằm ngang của vùng bằng phẳng và
đoạn đường dốc xuống tại cạnh chuyển tiếp (tiếp tuyến tại điểm 𝑥𝑥 = 2). Giá trị của góc 𝛼𝛼 bằng 135°.
d) Mặt bên phía trước của chướng ngại vật được sử dụng một phần làm khu vực quảng cáo
(xem Hình 1). Trong mô hình, khu vực này bao gồm hai phần diện tích, cụ thể là diện tích
giữa đồ thị hàm số 𝑓𝑓(𝑥𝑥) và trục hoành trong đoạn [2; 6] và một phần đối xứng với nó trong
góc phần tư thứ II. Diện tích của khu vực quảng cáo là 7,91 m2 (kết quả làm tròn đến hàng phần trăm).
4. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂 (đơn vị đo trên mỗi trục tọa độ dài 1 km, mặt đất là mặt phẳng 𝑂𝑂𝑥𝑥𝑦𝑦)
một chiếc máy bay bắt đầu di chuyển từ điểm 𝐴𝐴(700; 850; 100) với vận tốc không đổi
150 km/h theo hướng về điểm 𝐴𝐴(800; 900; 200). Khi tới 𝐴𝐴, máy bay thay đổi hướng bay
theo hướng về điểm 𝐴𝐴(1100; 1400; 300) với vận tốc giữ nguyên là 150 km/h. Máy bay di
chuyển theo hướng mới trong 30√35 phút (tức là mới tới điểm 𝐴𝐴 ∈ 𝐴𝐴𝐴𝐴) thì bất ngờ gặp gió
lớn, khiến hướng bay của nó lệch đi 45 độ theo phương nằm ngang (tức là nếu 𝑢𝑢�⃗ là vectơ hình
chiếu xuống mặt đất của đoạn đường từ điểm 𝐴𝐴 trở đi thì góc lượng giác (𝚤𝚤⃗, 𝑢𝑢�⃗) = 45°), và vận
tốc giảm còn 120 km/h. Máy bay tiếp tục bay theo hướng lệch trong 30 phút.
Thực chiến luyện đề môn Toán | Đề số 2 Trang 17
a) Tổng thời gian bay thực tế của máy bay trong cả hành trình này là 142 phút (kết quả làm
tròn đến hàng đơn vị)
b) Khi bắt đầu gặp gió lớn, máy bay cách mặt đất 275 km.
c) Gọi 𝐸𝐸(𝑎𝑎; 𝑏𝑏; 𝑐𝑐) là vị trí cuối cùng của máy bay trong hành trình này, khi đó 𝑎𝑎 + 𝑏𝑏 + 𝑐𝑐 =
2670 (làm tròn đến hàng đơn vị).
d) Tổng quãng đường cả hành trình dài hơn 650 km.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
1. Cho hình chóp đều 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có cạnh đáy bằng 2 cm. Gọi 𝑀𝑀 là trung
điểm của 𝐴𝐴𝐴𝐴. Biết rằng góc giữa đường thẳng 𝐴𝐴𝑀𝑀 với mặt bên (𝑆𝑆𝐴𝐴𝐴𝐴) là góc 𝛼𝛼 thỏa mãn 1 tanα =
. Tính thể tích khối chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 (đơn 5
vị cm3, kết quả làm tròn đến hàng phần chục). Đáp số: ……….
2. Hệ thống dây diện trong thành phố khá chằng chịt như hình vẽ. Xét hệ trục tọa độ 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, có 2
dây trung tâm có phương trình:
x −1 y +1 z x y −1 : = = , : z d d = = . 1 2 1 1 − 2 1 2 1
Người ta cần nối 1 đoạn đây thẳng kết nối 2 dây trung tâm này, thì độ dài đoạn dây thẳng đó
bằng bao nhiêu, biết đoạn dây đó phải đi qua điểm 𝑀𝑀(5; −3; 5) (kết quả làm tròn đến hàng phần chục) Đáp số: ……….
3. Một tấm bìa cứng hình chữ nhật có kích thước 3𝑚𝑚 × 8𝑚𝑚. Người ta cắt mỗi góc của tấm bìa
một hình vuông có cạnh 𝑥𝑥(𝑚𝑚) để tạo ra hình hộp chữ nhật không nắp (như hình vẽ). Thể tích
của khối hộp đó lớn nhất khi 𝑥𝑥 = a (m), với a là phân số tối giản. Tính 𝑎𝑎 + 𝑏𝑏. b b Đáp số: ………. Trang 18
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
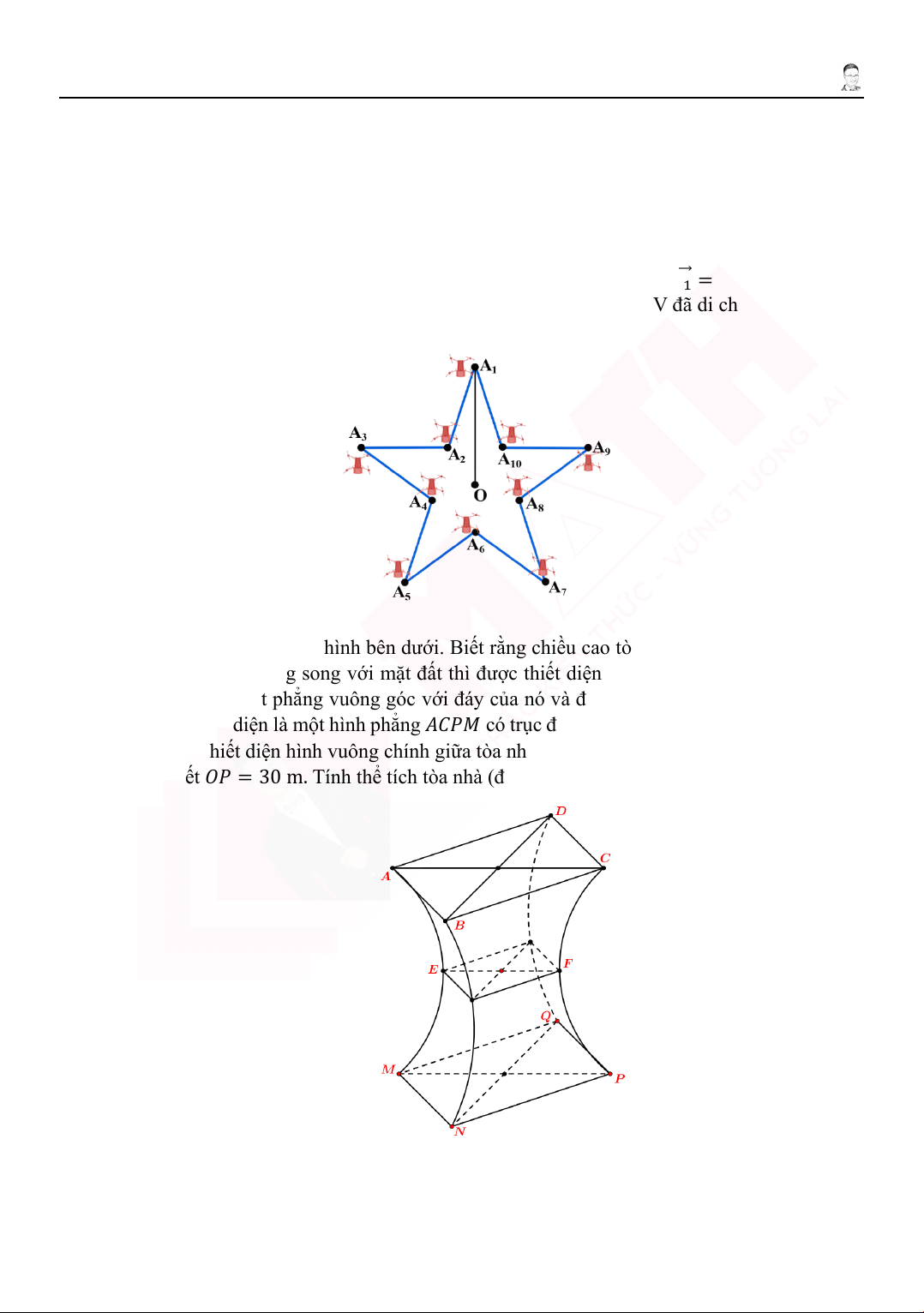
4. Nhân dịp kỷ niệm 80 năm ngày thành lập Quân đội Nhân dân Việt Nam (22/12/1944 −
22/12/2024) có một màn trình diễn máy bay không người lái UAV trên bầu trời thường được
gọi là "drone light show". Các UAV bay theo sự điều khiển chính xác, tạo thành hình ngôi sao
5 cánh cân đối trên bầu trời, biểu trưng cho sự đoàn kết và sức mạnh của Quân đội Nhân dân
Việt Nam. Khi trình diễn các chiếc UAV sẽ di chuyển theo các đoạn thẳng từ đỉnh
𝐴𝐴1 → 𝐴𝐴2 → 𝐴𝐴3 → 𝐴𝐴4 → 𝐴𝐴5 → 𝐴𝐴6 → 𝐴𝐴7 → 𝐴𝐴8 → 𝐴𝐴9 → 𝐴𝐴10 → 𝐴𝐴1
Biết rằng khi gắn hệ tọa độ 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂 (với 𝑂𝑂 là tâm của hình ngôi sao) thì 𝑂𝑂��𝐴𝐴
�� 1�⃗ = (100; 200; 200),
đơn vị trên các trục tọa độ là 1 mét. Quãng đường mà một chiếc UAV đã di chuyển một vòng
như trên là bao nhiêu mét? (kết quả làm tròn đến hàng đơn vị). Đáp số: ……….
5. Một tòa nhà có kết cấu như hình bên dưới. Biết rằng chiều cao tòa nhà là 48 m. Cắt ngôi nhà
bởi một mặt phẳng song song với mặt đất thì được thiết diện là các hình vuông. Khi cắt mô
hình này bởi các mặt phẳng vuông góc với đáy của nó và đi qua đường chéo hình vuông hai
đáy ta được thiết diện là một hình phẳng 𝐴𝐴𝐴𝐴𝐴𝐴𝑀𝑀 có trục đối xứng, với 𝐴𝐴𝑀𝑀, 𝐴𝐴𝐴𝐴 là hai cung tròn.
Gọi 𝑂𝑂 là tâm thiết diện hình vuông chính giữa tòa nhà như hình vẽ, 𝑂𝑂𝐴𝐴 là tiếp tuyến của cung
tròn 𝐴𝐴𝐴𝐴. Biết 𝑂𝑂𝐴𝐴 = 30 m. Tính thể tích tòa nhà (đơn vị dam3), làm tròn đến hàng phần chục. Đáp số: ……….
Thực chiến luyện đề môn Toán | Đề số 2 Trang 19
6. Cho lưới ô vuông gồm 6 × 8 hình vuông đơn vị. Gọi 𝑀𝑀 là điểm nẳm ở góc trái dưới và 𝑁𝑁 là
điểm nằm ở góc phải trên của lưới ô vuông. Ngoài ra ta lấy hai điểm 𝐴𝐴, 𝐴𝐴 như hình vẽ. Để đi
từ điểm 𝑀𝑀 đến điểm 𝑁𝑁 trên lưới ô vuông, một con kiến di chuyển ngẫu nhiên sang phải hoặc
lên trên theo các đoạn thẳng là các cạnh của các hình vuông đơn vị. Xét hai biến cố:
• 𝐴𝐴: “Con kiến đi từ 𝑀𝑀 qua 𝐴𝐴 và đến 𝑁𝑁”
• 𝐴𝐴: “Con kiến đi từ 𝑀𝑀 qua 𝐴𝐴 và đến 𝑁𝑁”
Gọi 𝑎𝑎 = 𝐴𝐴(𝐴𝐴|𝐴𝐴) và 𝑏𝑏 = 𝐴𝐴(𝐴𝐴|𝐴𝐴). Tính 𝑎𝑎 + 𝑏𝑏 (kết quả làm tròn đến hàng phần trăm). Đáp số: ………. PHẦN GHI CHÉP RIÊNG
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………... Trang 20
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
……………………………………………………………………………………………………...
Thực chiến luyện đề môn Toán | Đề số 03 Trang 21 KHÓA HỌC IMOE
ĐỀ MINH HỌA CHINH PHỤC KÌ THI TỐT NGHIỆP
THẦY ĐỖ VĂN ĐỨC
NĂM HỌC 2024-2025; MÔN TOÁN ĐỀ SỐ 03
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
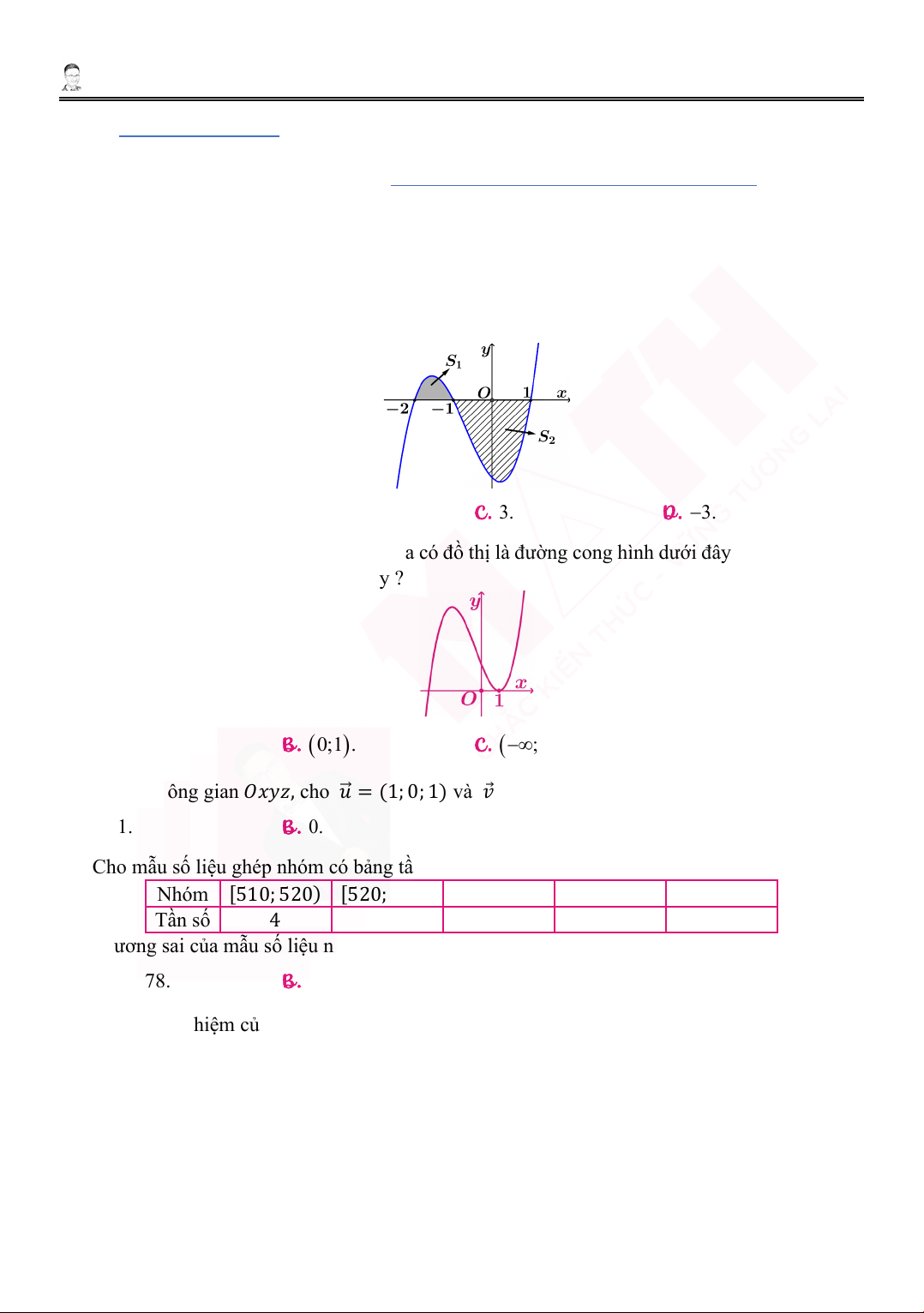
1. Cho hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) có đồ thị như hình vẽ. Biết diện tích phần tô đậm là 𝑆𝑆1 = 2 và diện tích 1
phần gạch chéo 𝑆𝑆2 = 5. Giá trị f
∫ (x)dx bằng 2 − A. 5. B. 7. C. 3. D. 3. −
2. Cho hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) là hàm số bậc ba có đồ thị là đường cong hình dưới đây. Hàm số đã cho
đồng biến trên khoảng nào dưới đây ? A. (1;+∞). B. (0; ) 1 . C. ( ;2 −∞ ). D. ( ;0 −∞ ).
3. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho 𝑢𝑢�⃗ = (1; 0; 1) và 𝑣𝑣⃗ = (0; 1; 0). Giá trị 𝑢𝑢�⃗. 𝑣𝑣⃗ bằng A. 1. B. 0. C. 2. D. 3.
4. Cho mẫu số liệu ghép nhóm có bảng tần số ghép nhóm như sau:
Nhóm [510; 520) [520; 530) [530; 540) [540; 550) [550; 560) Tần số 4 3 6 3 4
Phương sai của mẫu số liệu này bằng: A. 13,78. B. 190. C. 187,3. D. 14,1.
5. Tổng các nghiệm của phương trình log2 𝑥𝑥 + log8(𝑥𝑥 − 3)3 = 2 bằng? A. 3. B. 2. C. 4. D. 0.
6. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho (𝑃𝑃): 2𝑥𝑥 + 𝑂𝑂 + 1 = 0. Một vectơ pháp tuyến của (𝑃𝑃) là A. (2;1 ) ;1 . B. (2;1;0). C. (1;2;0). D. (2;0; ) 1 . Trang 22
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
7. Một khối lăng trụ đứng có cạnh bên bằng 4, đáy là hình vuông có cạnh bằng 2 thì thể tích của khối lăng trụ bằng 16 32 A. . B. 16. C. 32. D. . 3 3 x 8. Cho hàm số 1 y
= . Khẳng định nào sau đây là sai? 2
A. Hàm số nghịch biến trên ℝ.
B. Đồ thị hàm số nhận 𝑂𝑂𝑦𝑦 làm tiệm cận đứng.
C. Đồ thị hàm số luôn nằm trên 𝑂𝑂𝑥𝑥.
D. Đồ thị hàm số nhận 𝑂𝑂𝑥𝑥 làm tiệm cận ngang. 2 9. − − +
Tiệm cận xiên của đồ thị hàm số x 3x 4 y =
là đường thẳng có phương trình x + 2
A. y = −x −1. B. y = x −1. C. y = −x +1. D. y = x +1.
10. Cho hàm số 𝑓𝑓(𝑥𝑥) liên tục trên ℝ. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 𝑦𝑦 = 𝑓𝑓(𝑥𝑥),
trục hoành và hai đường thẳng 𝑥𝑥 = 𝑎𝑎, 𝑥𝑥 = 𝑏𝑏 (𝑎𝑎 < 𝑏𝑏) là: b b a b A. f (x) d . x ∫
B. f (x)dx ∫ C. − f ∫ (x)d .x D. π f ∫ (x) d .x a a b a 11. Trong không gian x y z
𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, cho đường thẳng d : = =
. Mặt phẳng nào sau đây song song 2 2 1 − với 𝑑𝑑?
A. x − y = 0.
B. x + y − z −1 = 0.
C. x + 2z −1 = 0.
D. x + 2y + 3z + 4 = 0.
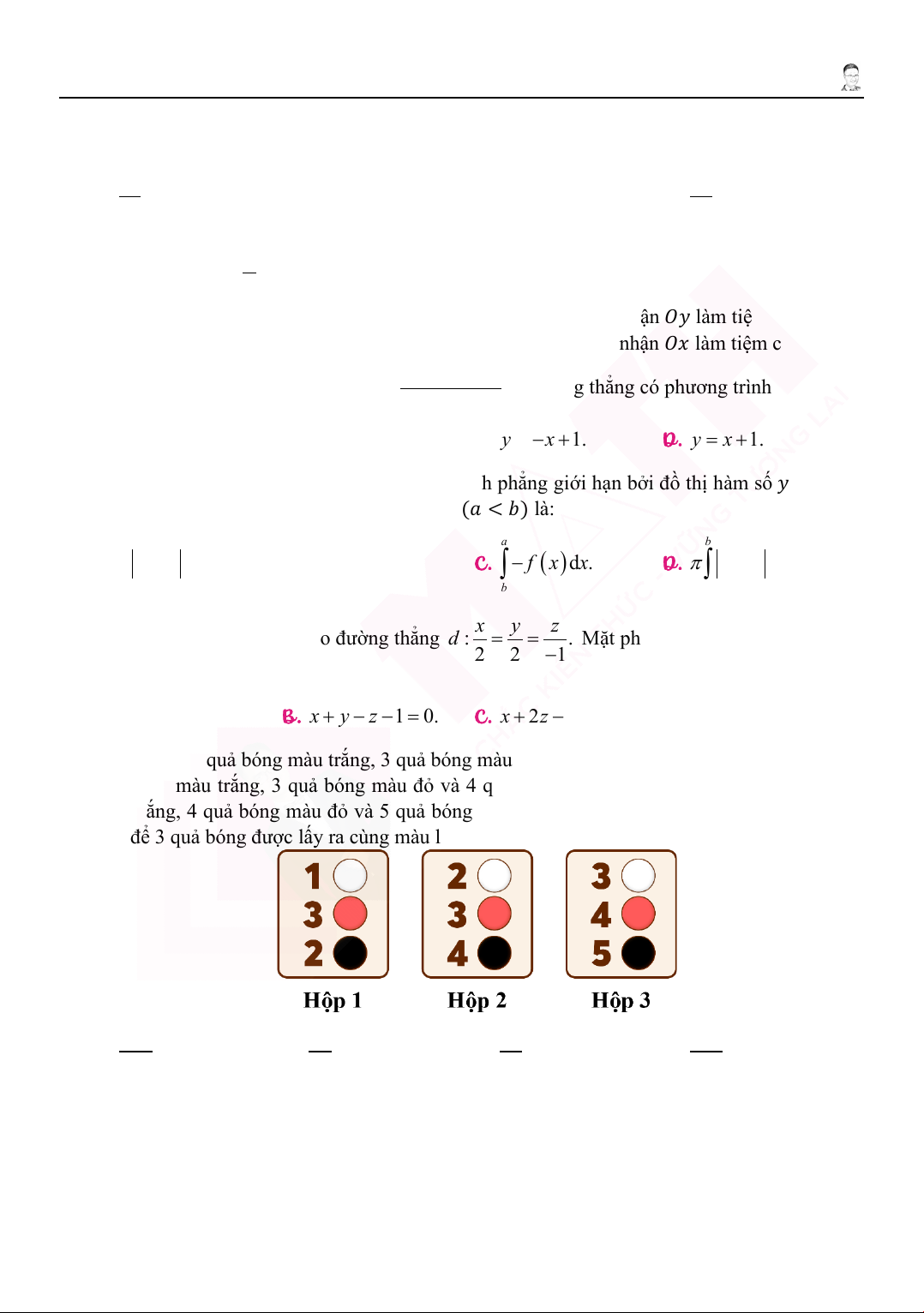
12. Hộp 𝐼𝐼 chứa 1 quả bóng màu trắng, 3 quả bóng màu đỏ và 2 quả bóng màu đen. Hộp 𝐼𝐼𝐼𝐼 chứa 2
quả bóng màu trắng, 3 quả bóng màu đỏ và 4 quả bóng màu đen. Hộp 𝐼𝐼𝐼𝐼𝐼𝐼 chứa 3 quả bóng
màu trắng, 4 quả bóng màu đỏ và 5 quả bóng màu đen. Nếu mỗi hộp lấy ra 1 quả bóng, xác
suất để 3 quả bóng được lấy ra cùng màu là: 41 5 31 283 A. . B. . C. . D. . 324 36 36 324
Thực chiến luyện đề môn Toán | Đề số 03 Trang 23
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
1. Giả sử chi phí tiền xăng 𝐶𝐶 (nghìn đồng) khi xe đi được 100 km phụ thuộc vào tốc độ trung
bình 𝑣𝑣 (km/h) trên cả đoạn đường theo công thức: 16000 5 𝐶𝐶(𝑣𝑣) =
𝑣𝑣 + 2 𝑣𝑣 (0 < 𝑣𝑣 ≤ 120)
a) Nếu tài xế lái xe với tốc độ trung bình là 40 km/h thì chi phí tiền xăng là 500 nghìn đồng.
b) C′(v) 16000 5 =
+ (với 0 < 𝑣𝑣 < 120). 2 v 2
c) Tài xế càng đi nhanh thì chi phí tiền xăng càng giảm.
d) Xe đi trên đường có biển báo như hình vẽ
Biết đây là biển báo tốc độ tối đa cho phép 50 km/h. Nếu tài xế tuân thủ luật giao thông,
chi phí tiền xăng tối thiểu của tài xế khi đi 100 km trên đoạn đường này là 445 nghìn đồng
2. Vào một buổi sáng, bạn Bảo đi xe đạp từ nhà tới trường với vận tốc 𝑣𝑣(𝑡𝑡) = 2𝑡𝑡2 + 1 (mét/phút)
(với 𝑡𝑡 là thời gian tính bằng phút, kết từ lúc bắt đầu đi).
a) Vận tốc của Bảo tại thời điểm 𝑡𝑡 = 10 phút là 12,06 km/h.
b) Quãng đường Bảo đi được sau 5 phút là 51 m.
c) Biết quãng đường từ nhà tới trường của Bảo là 2265 mét. Thời gian cần đề di chuyển tới
trường của Bảo là 15 phút.
d) Sau khi di chuyển được 9 phút, Bảo nhìn thấy phía trước có công trường, nên đã thay đổi
tốc độ và di chuyển chậm dần đều với gia tốc không đổi. Đi được thêm 30 giây thì Bảo tới
công trường. Biết công trường cách nhà Bảo 545 mét. Vận tốc tức thời của Bảo khi tới
công trường là 37 mét/phút.
3. Trong một cuộc trưng cầu dân ý ở một khu vực, đối với các hộ gia đình sống ở một vùng ngoại
ô (mỗi hộ gia đình có một cặp vợ chồng và các con), xác suất để người chồng sẽ đi bỏ phiếu
là 0,2, xác suất để người vợ sẽ đi bỏ phiếu là 0,35 và xác suất để cả hai vợ chồng sẽ đi bỏ phiếu là 0,11. Trang 24
► Đỗ Văn Đức | Khóa học Online môn Toán | thayduc.vn
a) Xác suất để có ít nhất một trong hai vợ chồng sẽ đi bỏ phiếu là 0,44.
b) Xác suất để người chồng sẽ đi bỏ phiếu, biết rằng người vợ đã đi bỏ phiếu là 0,31 (làm
tròn kết quả tới hàng phần trăm).
c) Giả sử khảo sát 13 hộ gia đình, khi đó xác suất để có đúng 2 hộ gia đình mà cả vợ và chồng
đều tham gia bỏ phiếu là 0,26 (làm tròn kết quả tới hàng phần trăm).
d) Bên cạnh đó, người ta cũng nhận thấy rằng nếu cả hai vợ chồng đều tham gia bỏ phiếu thì
xác suất ít nhất một người con của họ cũng tham gia bỏ phiếu là 0,99. Ngược lại, nếu vợ
hoặc chồng hoặc cả hai không tham gia bỏ phiếu thì xác suất không có người con nào của
họ tham gia bỏ phiếu là 0,79.
Xác suất để chọn ngẫu nhiên một hộ gia đình thì có ít nhất một người con tham gia bỏ
phiếu là 0,29 (làm tròn kết quả tới hàng phần trăm).
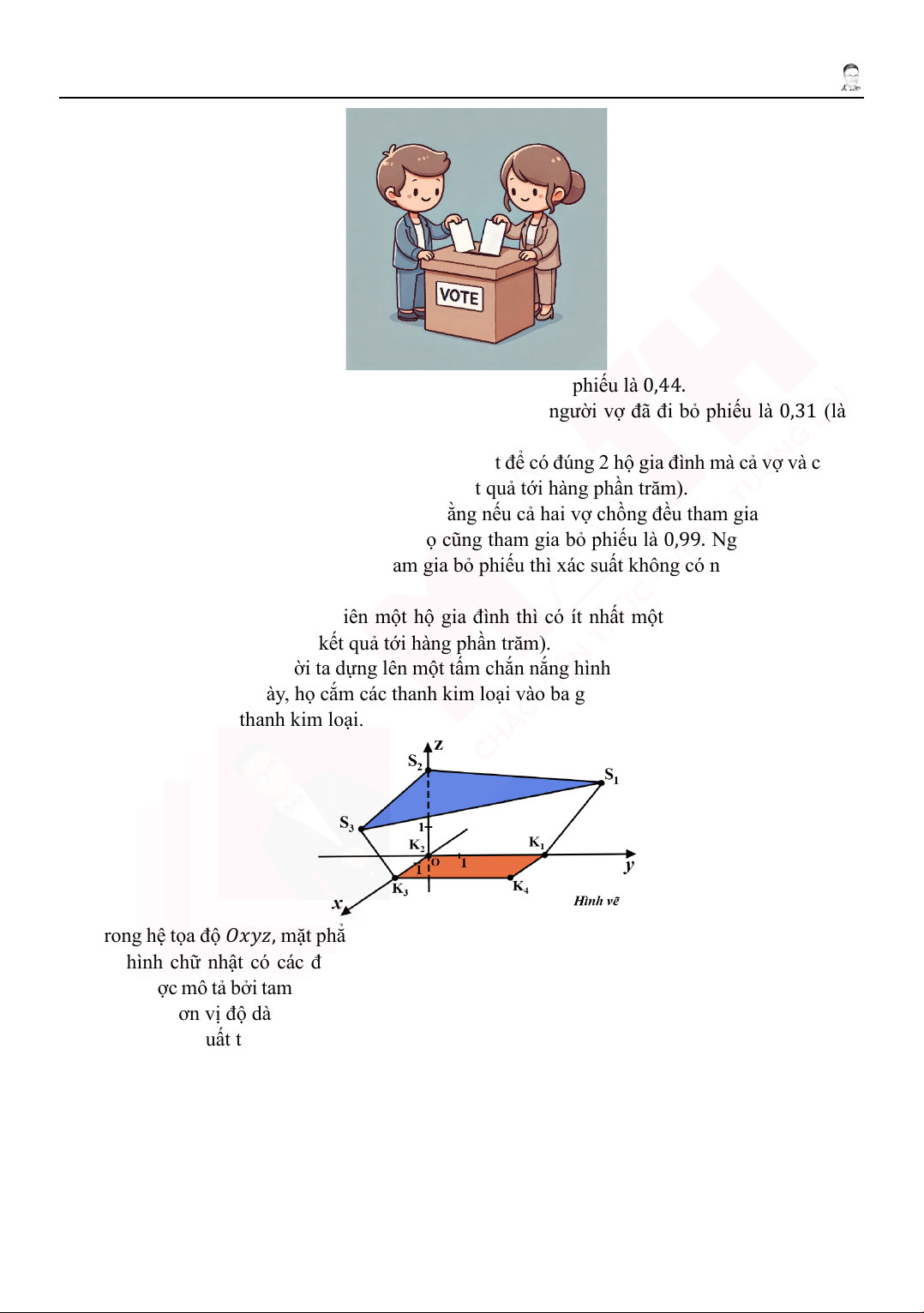
4. Trong một sân chơi, người ta dựng lên một tấm chắn nắng hình tam giác để che bóng cho một
bể cát. Để làm điều này, họ cắm các thanh kim loại vào ba góc của bể cát và cố định tấm chắn
nắng vào các đầu thanh kim loại.
Trong hệ tọa độ 𝑂𝑂𝑥𝑥𝑦𝑦𝑂𝑂, mặt phẳng 𝑂𝑂𝑥𝑥𝑦𝑦 biểu diễn mặt đất nằm ngang. Bể cát được mô hình hóa
bởi hình chữ nhật có các đỉnh 𝐾𝐾1(0; 4; 0), 𝐾𝐾2(0; 0; 0), 𝐾𝐾3(3; 0; 0) và 𝐾𝐾4(3; 4; 0). Tấm chắn
nắng được mô tả bởi tam giác phẳng có các đỉnh 𝑆𝑆1(0; 6; 2,5), 𝑆𝑆2(0; 0; 3) và 𝑆𝑆3(6; 0; 2,5) (hình
vẽ). Một đơn vị độ dài trong hệ tọa độ tương ứng với một mét trong thực tế.
a) Nhà sản xuất tấm chắn nắng khuyến cáo rằng, đối với tấm chắn nắng có diện tích lớn hơn
20 m2, nên sử dụng thêm dây cáp để cố định giữa các thanh kim loại nhằm tăng cường độ
ổn định. Trong tình huống này không cần thiết phải thêm dây cáp để bảo vệ.
b) Để đảm bảo cho nước mưa có thể thoát đi, tấm chắn nắng phải có góc nghiêng ít nhất là
8° so với mặt đất nằm ngang. Trong trường hợp này, việc thoát nước mưa chưa được đảm bảo.
Thực chiến luyện đề môn Toán | Đề số 03 Trang 25
c) Ánh sáng mặt trời chiếu vào tấm chắn nắng được biểu diễn bằng các đường thẳng song
song có vectơ chỉ phương là 𝑆𝑆�1�𝐾𝐾
�� 1�⃗. Tấm chắn nắng tạo ra bóng hình tam giác trên mặt đất.
Bóng của các đỉnh 𝑆𝑆 ′ ′ ′
2 và 𝑆𝑆3 của tấm chắn nắng lần lượt được kí hiệu là 𝑆𝑆2 và 𝑆𝑆3. Khi đó 𝑆𝑆2
nằm trên trục 𝑂𝑂𝑦𝑦 và 𝑆𝑆′3(6; −2; 0).
d) Có hơn một nửa bể cát được che nắng.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
1. Cho hình hộp chữ nhật 𝐴𝐴𝐴𝐴𝐶𝐶𝐴𝐴. 𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸 có 𝐴𝐴𝐴𝐴 = 𝐴𝐴𝐸𝐸 = 2 (m), 𝐴𝐴𝐴𝐴 = 3 (m). Lấy hai điểm
𝑀𝑀, 𝑁𝑁 thỏa mãn 1 2
AM = AD, EN = EC. Độ dài đoạn 𝑀𝑀𝑁𝑁 bằng bao nhiêu mét? (làm tròn kết 5 5
quả đến hàng phần trăm) Đáp số: ……….
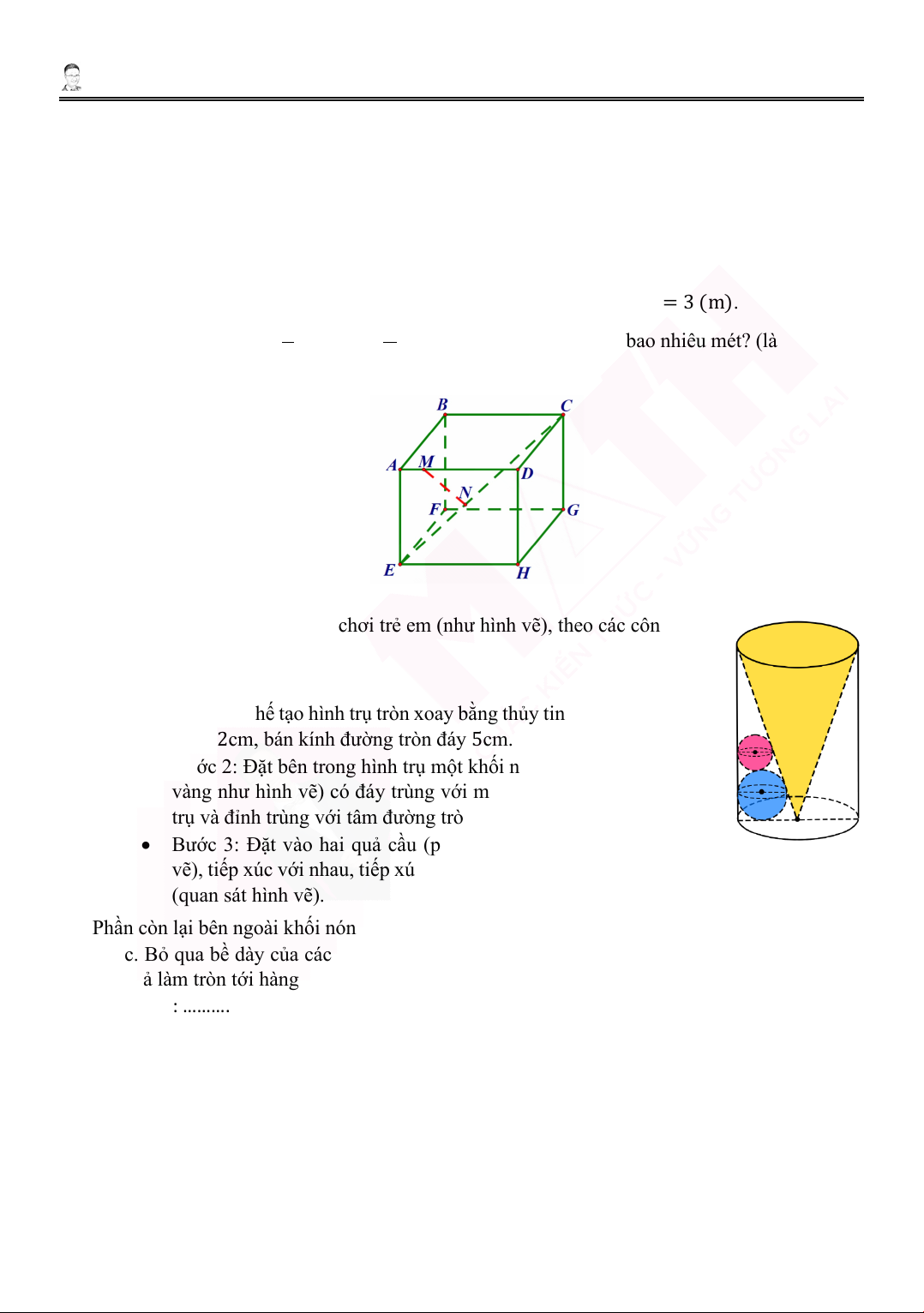
2. Người ta chế tạo một món đồ chơi trẻ em (như hình vẽ), theo các công đoạn như sau:
• Bước 1: Chế tạo hình trụ tròn xoay bằng thủy tinh trong suốt, chiều
cao 12cm, bán kính đường tròn đáy 5cm.
• Bước 2: Đặt bên trong hình trụ một khối nốn tròn xoay (phần màu
vàng như hình vẽ) có đáy trùng với một đường tròn đáy của hình
trụ và đỉnh trùng với tâm đường tròn đáy còn lại của hình trụ.
• Bước 3: Đặt vào hai quả cầu (phần màu xanh và hồng như hình
vẽ), tiếp xúc với nhau, tiếp xúc với các đường sinh, mặt đáy của hình trụ và hình nón (quan sát hình vẽ).
Phần còn lại bên ngoài khối nón, bên ngoài hai khối cầu và bên trong hình trụ người ta đổ đầy
nước. Bỏ qua bề dày của các lớp vỏ. Hỏi thể tích nước cần đổ bằng bao nhiêu? (đơn vị cm3,
kết quả làm tròn tới hàng đơn vị) Đáp số: ……….




