Đề minh họa số 48 môn Toán C1 - Đáp án chi tiết và phân tích | Đại Học Nội Vụ Hà Nội

lOMoARcP SD| 59062 190 Kh a học PIMAX PLUS Sưu tầm v biŒn soạn aøp aøn chi tieÆt Phạm Minh Tuấn ĐỀ CH˝NH THỨC
phaøt trien æe minh hoa cau 48
Thời gian: 90 phœt (kh ng kể thời gian phát đề)
Đề thi gồm c 13 trang, 50 c u C u 1.
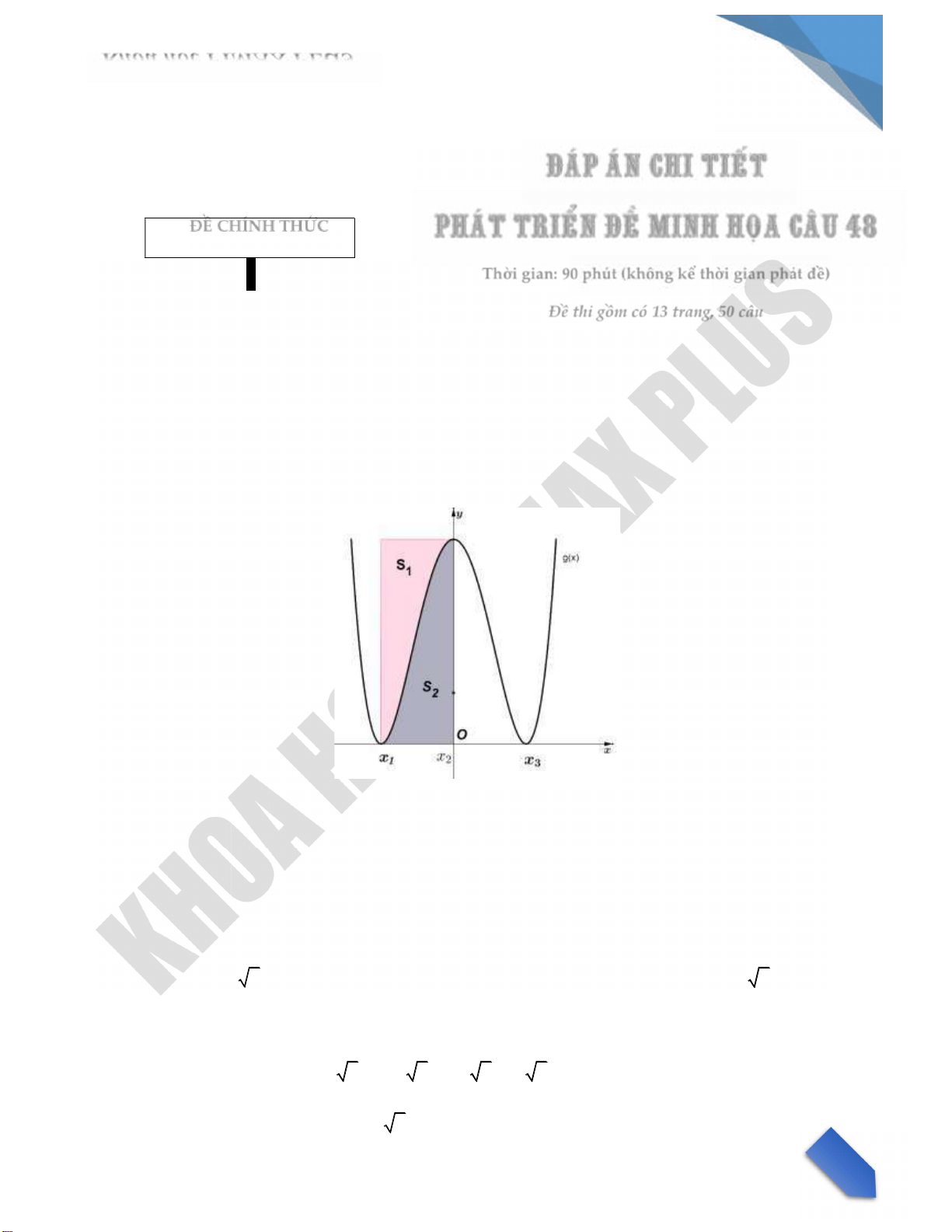
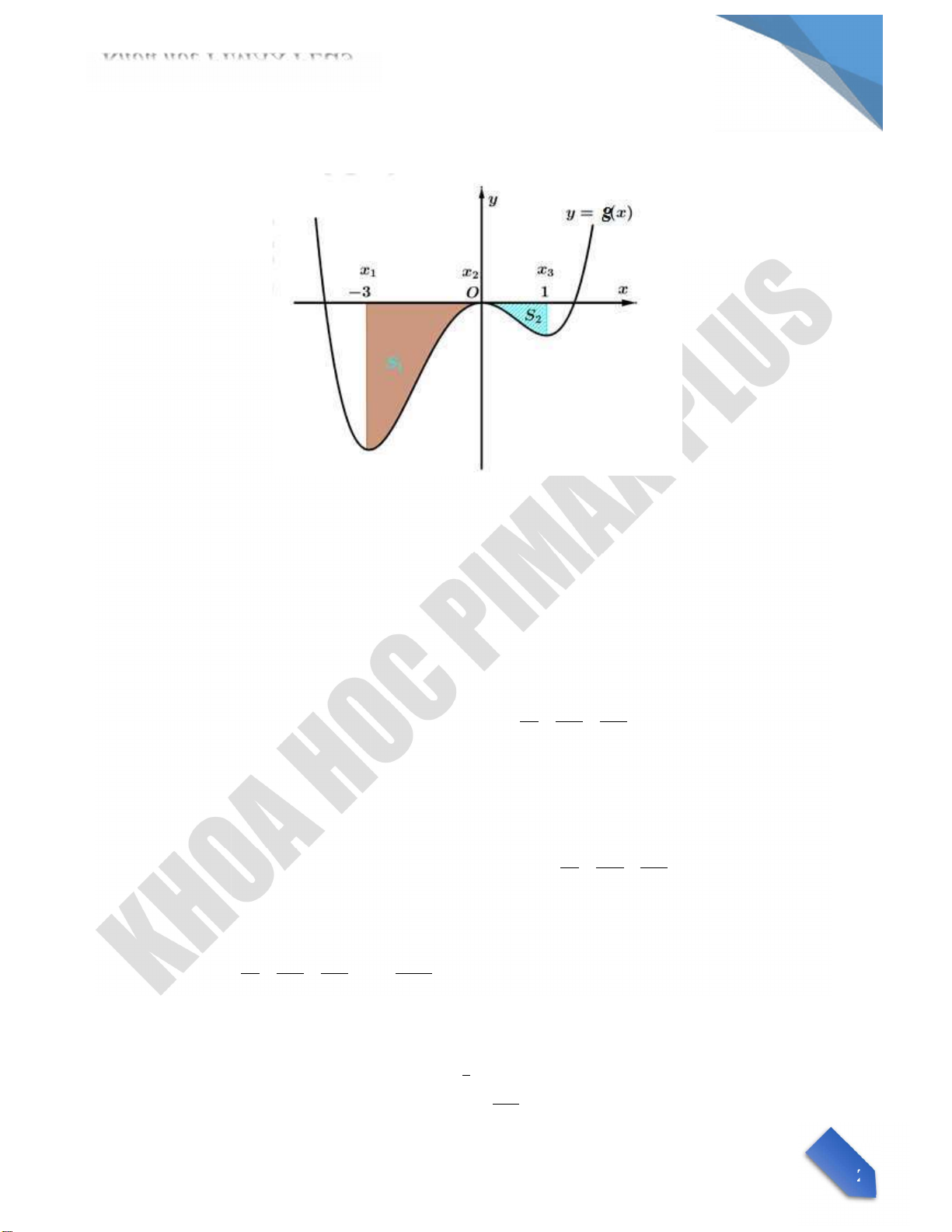
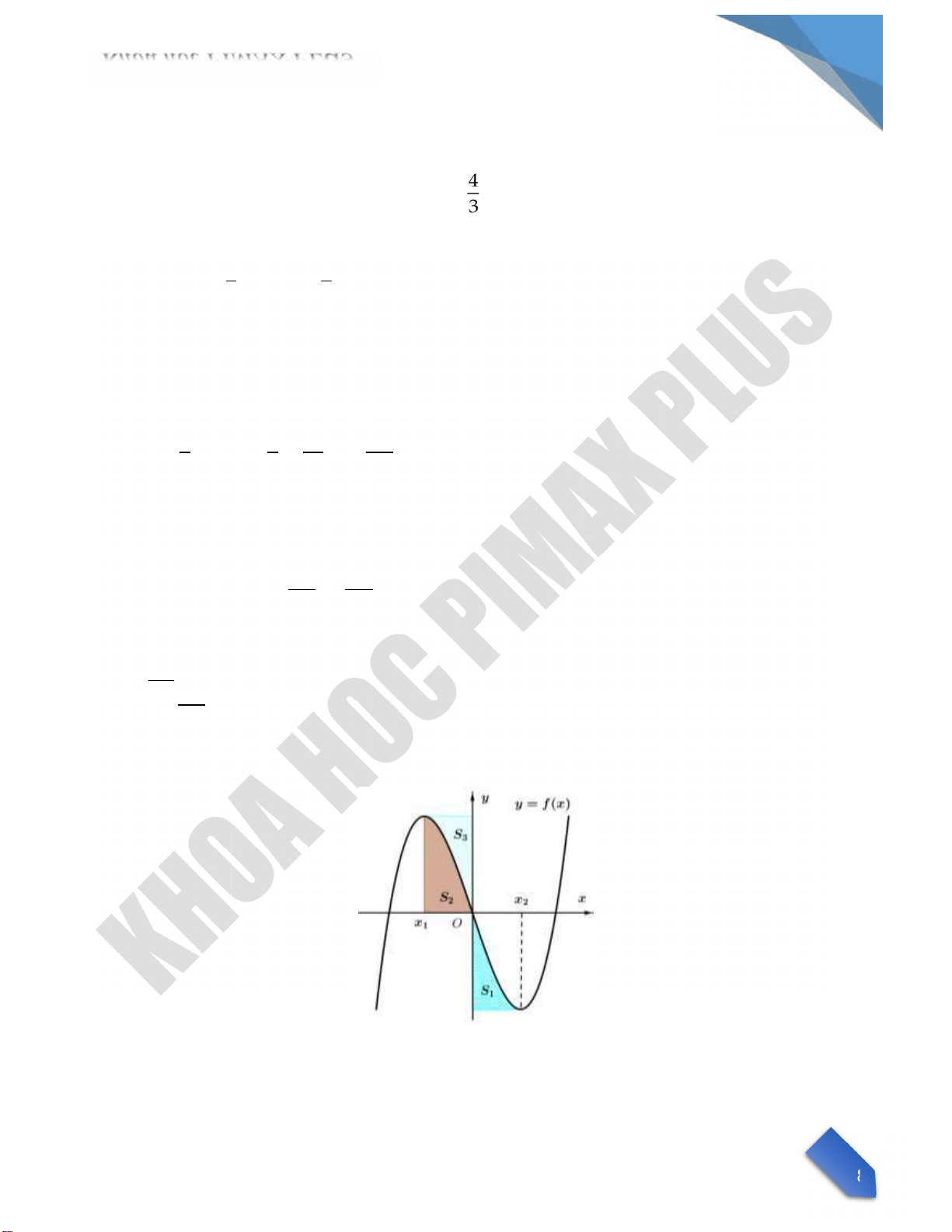
Ta tịnh tiến đồ thị sang trÆi sao cho trục đối xứng trøng với Oy , ta được h m số y  g x , rı r ng diện
t ch S S1; 2 là không đổi.
Theo đề b i f x( 1)  f x( 2)  f x( 3)  4 m f x( 1)  f x( 3)  0  f x( 2)  4
M x1  x2  x3  2 2 , nŒn h m số g x  đạt cực trị tại điểm x x1; 2; x3 v x1 0x3  2 2 1 
Mặt khÆc lœc n y h m g x  c dạng y  g x( )  ax4 bx2 4 (a  0)  g x( )  4ax3 2bx. M lOMoARcP SD| 59062 190 Kh a học PIMAX PLUS
x1  x3 kết hợp  1  x3  2  g 2  8a 2  2b 2  0  b  4a  g x(
)  ax4 4ax2 4, do g(x3)  f  2  0  a  1.
Vậy ta c h m số g( )x  x4 4x2 4 .   1 2
0 (x4  4x2  4)dx  32 2 .
Gọi S l diện t ch h nh chữ nhật được ghØp từ S S; suy ra S2 2 15
S  4 2 S1  S S 2  4 2  32 2  28 2  S1  7 . 15 15 S2 8 C u 2.
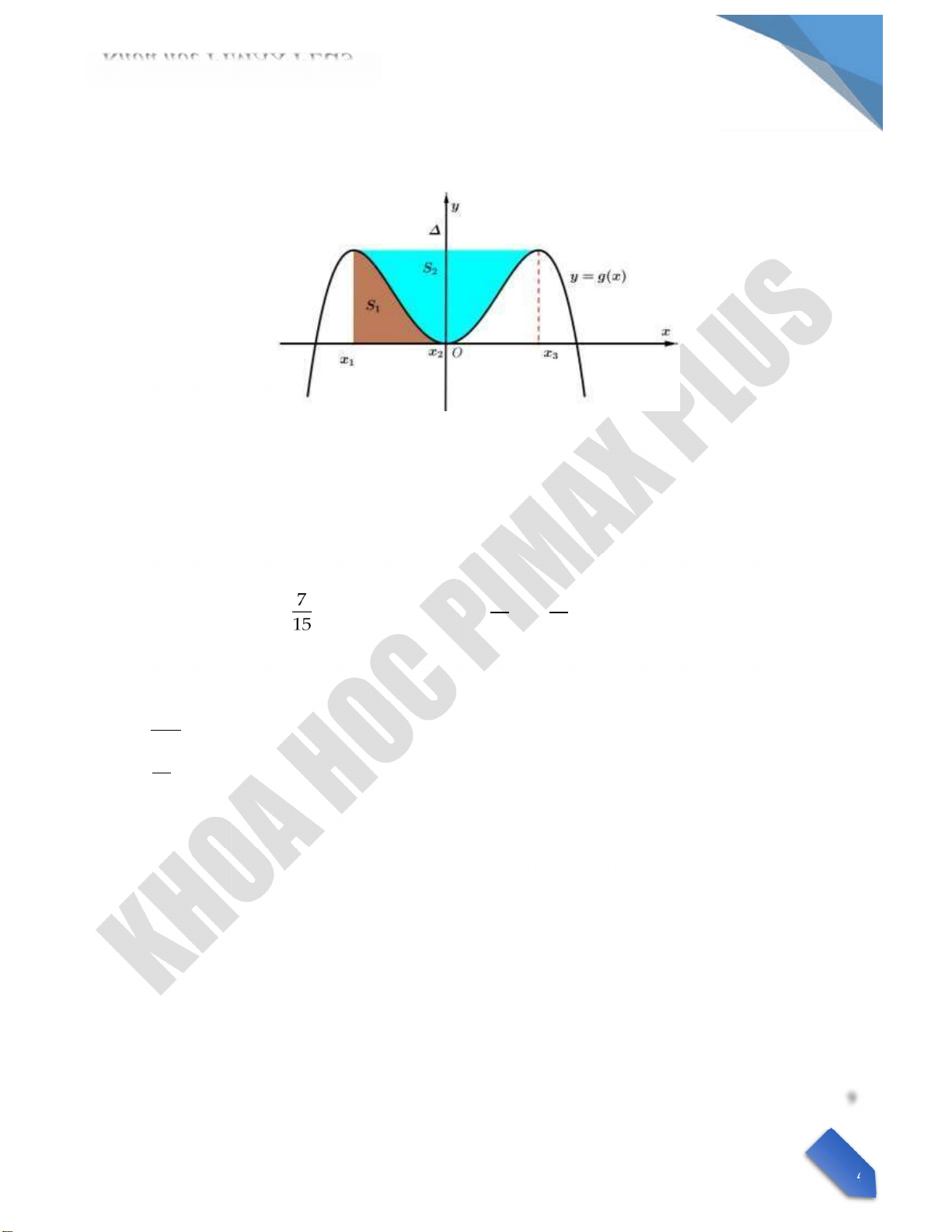
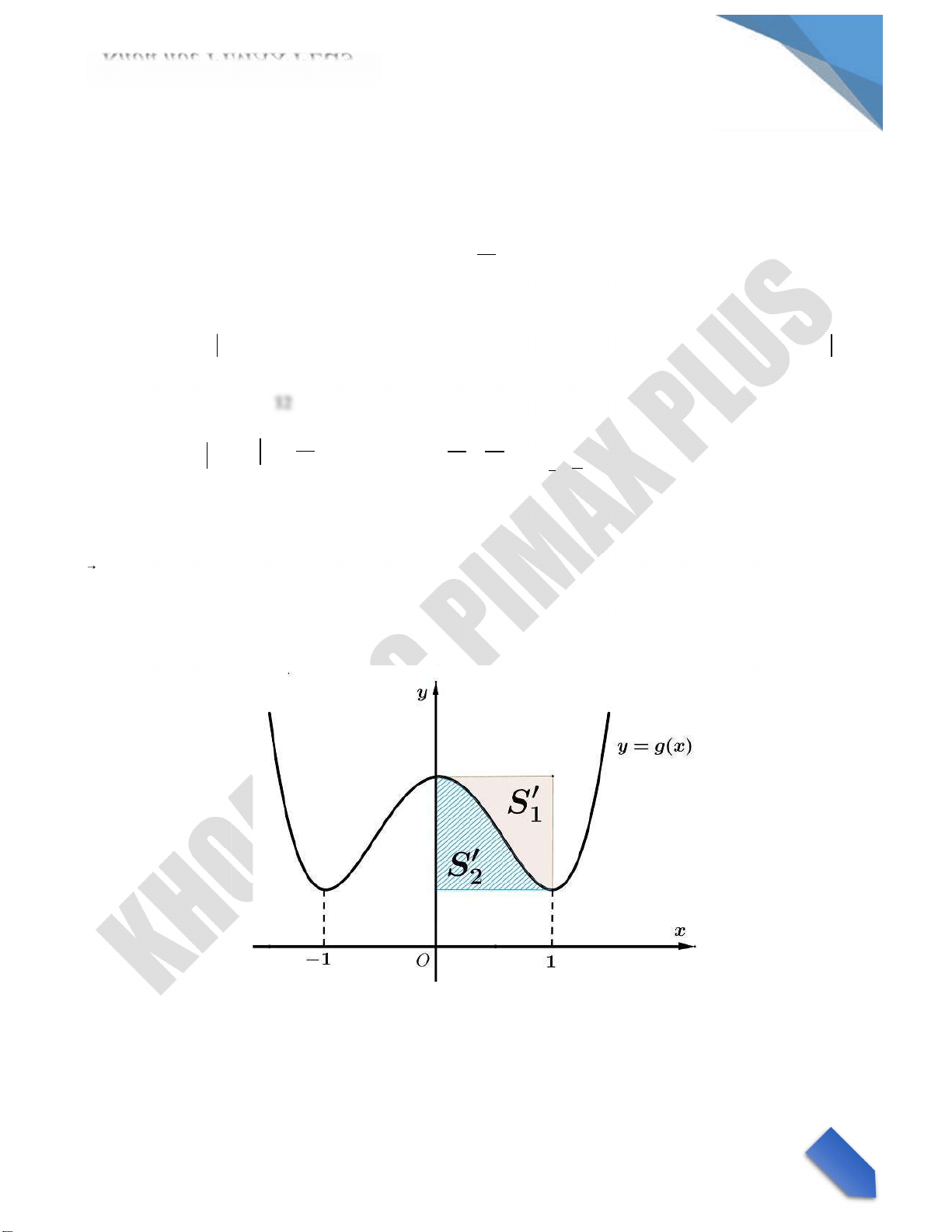
Kết quả bài toán không đổi nếu ta tịnh tiến đồ thị sang phải cho điểm uốn trùng với gốc tọa độ O. Gọi g
x   ax3 bx2 cxd là hàm số, khi đó ta dễ thấy g x  lẻ nên b d 0 v g x   ax3 cx có 2
điểm cực trị tương ứng là 2; 2 cũng là nghiệm của 3ax2 c  0 g x’   k x 2x 2  k
x 2 4 g x( )  k x3 4x với k0  3 32
Xét diện tích hình chữ nhật S1 S2   3 2.g2  k
S2  0 g x dx( ) k0 x3  4x dx  20 k 2 2 3 3
 32 k 20 k  4k v S1  3 NŒn S 1 3 3 S2 5 C u 3.
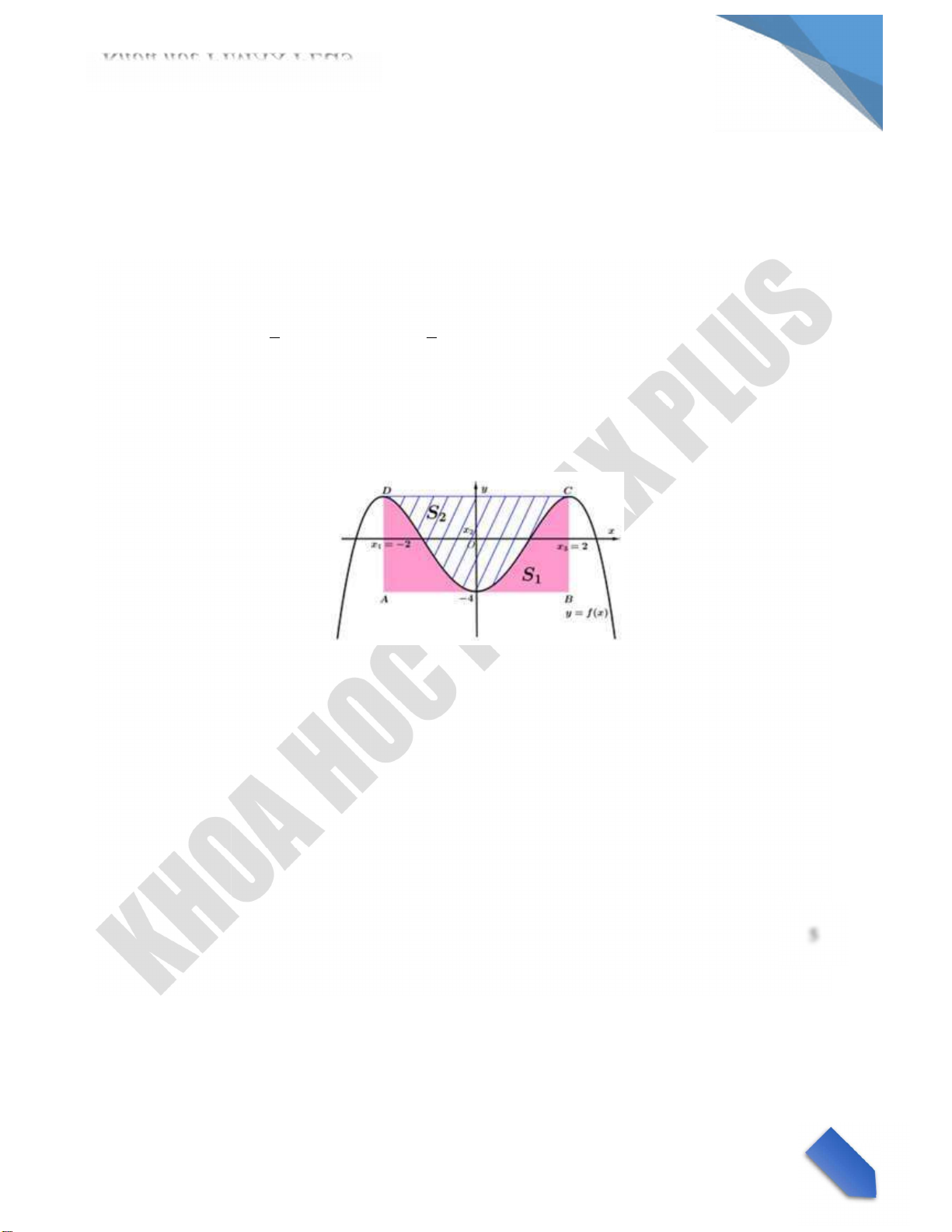
Từ đồ thị  C nhận thấy a  0;b  0;c  0
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 2 lOMoARcP SD| 59062 190 Kh a học PIMAX PLUS
Ta c : f( 1)  0 suy ra: a b c   0 (1); Gọi A1;0
Phương trình tiếp tuyến tại A1;0l  d : y  y’ 1 x1   4a 2bx1
Phương trình hoành độ giao điểm của tiếp tuyến  d và đồ thị  C : 4a 2bx 1  ax4 bx2 c * 4a 2b  c 
M x  0,x  2 l nghiệm của (*) suy ra 12a6b  16a 4bc (2).
{Hệ tạo bởi (1) v (2) v số nghiệm}  c   a b    c a b  c  2a
Từ (1) v (2) ta c : 4a2b   a b  b  3a b  3a Ta c : S 
1  0 ax4 bx2    c  4a2bx1dx  0 ax4  3ax2  2a 2a x 1dx 1 1  a  0 x4  3x2  2x dx  a 1 5
S2  24a2bx1ax4 bx2 c dx  a2x4  3x2  2x dx  28a 0 0 5 S1 1  Vậy: S2 28 lOMoARcP SD| 59062 190 Kh a học PIMAX PLUS C u 4.
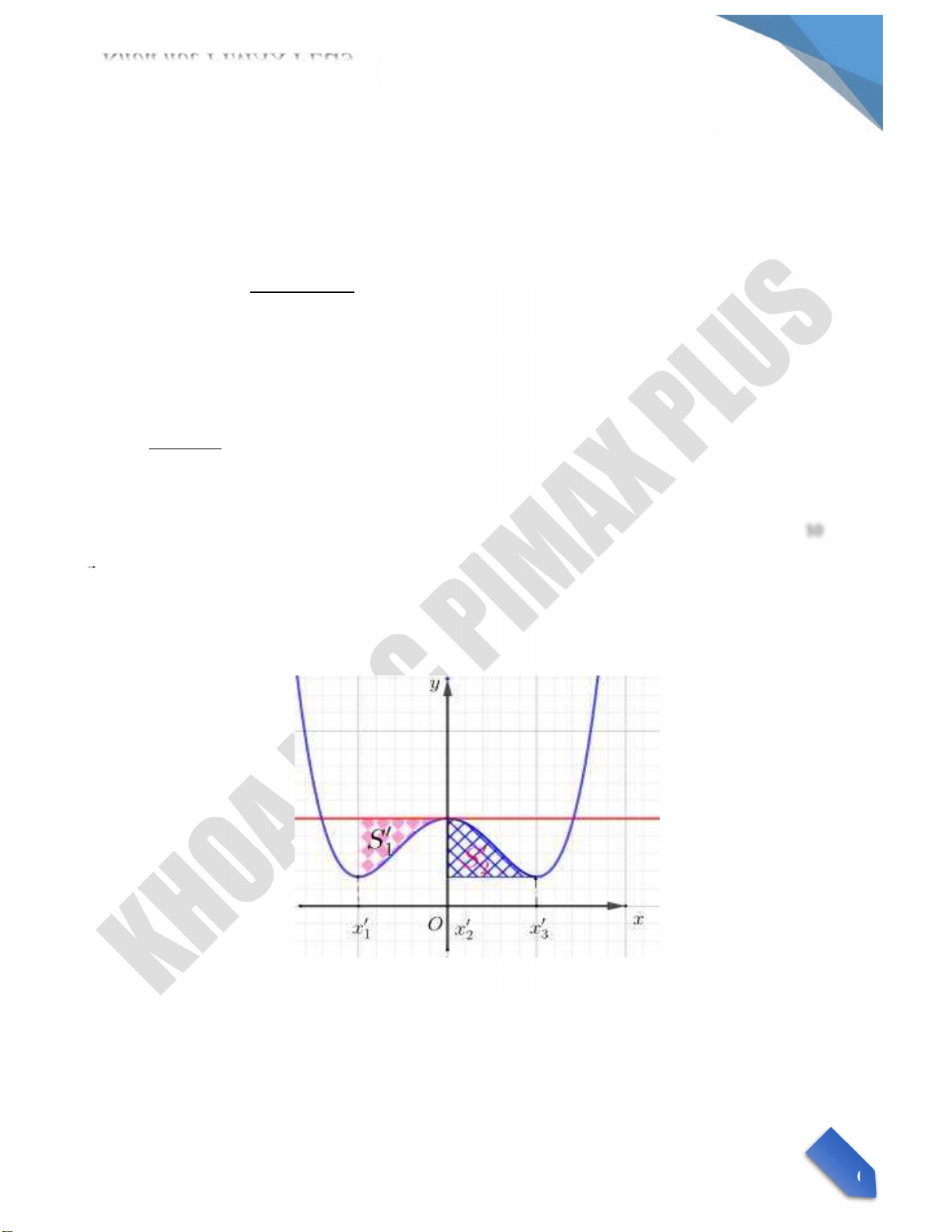
Dựa vào đồ thị h m số g x’( ) ta c g x’( )  2x 4.
Khi đó g x( )  x2 4x C . Do g(0)  2 nŒn g x( )  x2 4x2 .
Khi đó, ta có đồ thị như hình bên. Từ giao
điểm của y  f x( ) v y  g x( ) ta c
f x( ) g x( ) kx x( 2)(x3)
 g x( ) f x( )kx x( 2)(x3).  
Ta c 23 g x  f x dx  125 k x x 23   2x 3dx  125  k 1.
Khi đó, diện t ch h nh phẳng giới hạn bởi hai đồ thị y  f x( ) v y  g x( ) l 3
S  x x  2x 3dx  . 0 C u 5.
Tỉ số không thay đổi với cÆc h m số thỏa mªn
Chọn x1  1; x2  2  f ’ x  a x 1x 2  a x( 2  x 2)  g x   k x 2 x 2 
       x3 x2  2xC
 f x  a x1 x 2 dx  a
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 4 lOMoARcP SD| 59062 190 Kh a học PIMAX PLUS  3 2 
Chọn a  2  f x   x3 x2 4x C
Mặt khÆc: f 1 f  2   13 2C  0 C  13  f x   2 x3 x2 4x 13 3 6 3 6  13  2k  13  k 13 M tọa độ 0;
 là giao điểm của hai h m số.  6  6 12
  13 2 x2  g x  x 12 Gọi
I 1 ;0là giao điểm của f x  với trục Ox(x <1 1  2  2  2  16
1 2 39  13 x2 x 2dx  39 S   16 12  32 2 13 2
x2 2 x3 x2 4x 13  179 S   x 0  12  3 6  288 S1  351  1,96 S2 179 lOMoARcP SD| 59062 190 Kh a học PIMAX PLUS C u 6.
H m số đã cho có dạng f x( )  ax4 bx3 cx2 d x1  e
f x’( )  4ax3 3bx2 2cx d 1.   
Từ giả thiết ta c x x
13x3  1  2xx23 2 xx12 1dd  xxx123   1221 . d 2  
Do vậy ta thấy đồ thị h m số có ba điểm cực trị l (1;0),
1 ; y2 v ( 2 ;0) v cắt trục tung tại điểm c  2 
tung độ bằng 1 nŒn ta c hệ:  f(0)  1  e      f( 2) 0  16a 8b 4c  2d  1  1 
 f ’   0   1 a 3 b c d   2    2 4 1  f ’( 2) 0 32a12b 4c d1   f ’(1)   3b 2c d 0  4a 1
 1 x4  1 x3  3 x2  x 1. Do đó f x( ) 4 2 4 2  Diện t ch h nh phẳng S  2 S3 f x dx   0     
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 6 lOMoARcP SD| 59062190 Kh a học PIMAX PLUS 1 1  4    b 1 . e 0   2  0  c  43 1 0  1 d1  1   a .  S1  8 85  4. Vậy : S2 S3 C u 7.
Phương trình hoành độ giao điểm của (P) v ( )d : x2   ax b 0  
SP xx x11 2. x2  ab V x 
1  x2  3  x1  x2  3  x1 x2 2  9  S2  4P 9  a2  4b  9(1)
Mặt khÆc do f x( 1)  f x( 2)  5  ax1 b ax2 b  5  ax1 b ax2 b  5  a x  1  x2
 2b 5  a2 2b  5(2)
Giải hệ (1) v (2) v từ h nh dạng đồ thị nŒn a  0 ta được nghiệm a 1;b 2. lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS x  x  a  Do đó  1
2  x1 xx22   31  xx12   12. x1 x2  3 x1 0 1
S1   x dx2 8 ; S2  x dx2  1 2 3 0 3 Vậy S1 S2  3 . C u 8.
Tịnh tiến đồ thị h m số sao cho trục Oy đi qua điểm cực trị x2 , th diện t ch của h nh phẳng kh ng thay đổi.
Khi đó ta có y  f x l h m số bậc bốn trùng phương .
Gọi f x   ax4 bx2 c với a  0. Biết f x  2
 f  0   4c  4 , vậy f x   ax4 bx2  4 .
Lại c theo b i ra x3  x1  4 nŒn khi tịnh tiến đồ thị ta có 3 điểm cực trị l x1  2,x2  0,x3  2 .
M f x  4ax3  2bx  f 2  32a 4b  0  b  8a .
Vậy f x   ax4  8ax2  4 .
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 8 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS Theo h nh vẽ ta c S 
2  22 f x    4 dx  22ax4 8ax dx2  2 ax5  8ax3  2  448a . 0 0  5 3 0 15
Lại c f  2  16a 4 nên độ dài các đoạn AB  4,BC  16a .
Suy ra S1 SABCD S2  ABBC. 
448a 64a 448a  512a . 15 15 15 S1 512  8 . Vậy  S2 448 7 C u 9 .
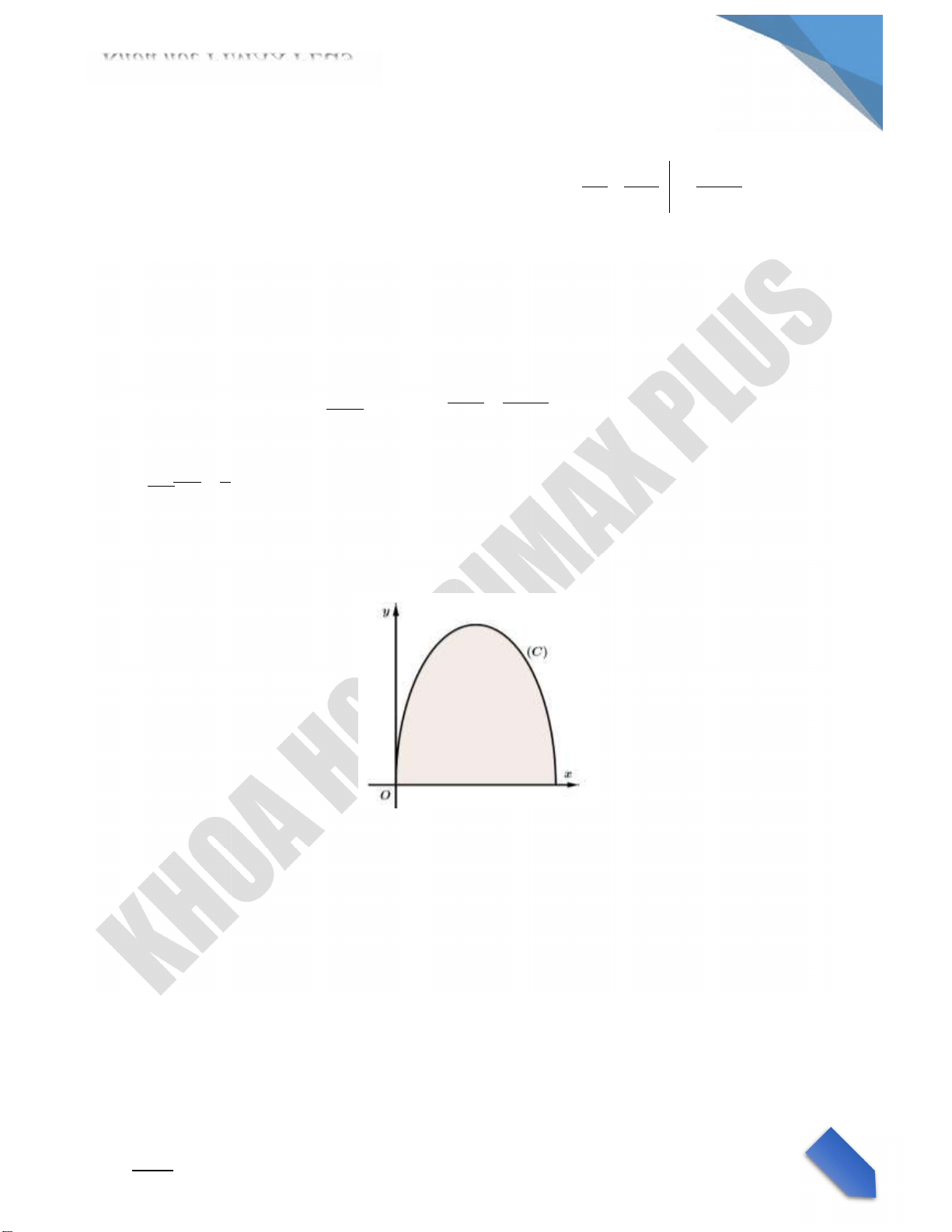
Ta c :  f x 2  f x .f x 4  0 .
 f x 2  f   x f x.
  4  f   x f x.   4.
  f   x .f x  dx  4dx  f x . f x   4x C .
  f x . f x dx  4x C dx   f x df x     2x2 Cx C1. f2 x 2 2   2 1 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS   2x Cx C 1  f x  4x  2Cx 2C 2 M f  0  0, f
 1   3 .  2 
NŒn ta c hệ phương trình
2C1  0 C1  0   2 2 x  0   2C1  4  C  4 . f x  4x
 8x ;4x  8x  0  x  2 . C 2
S   4x2 8xdx  22x2 x dx . 0 0 Đặt x 2sin2t dx 2sin2tdt .  Đổi cận:x   0 t 0,x   2 t . 2   22 2
2 x2  x dx 4sin2 2tdt  21cos4tdt  2t  sin4t  2 . 0 0 0  4  0 Vậy: S. C u 10.
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 10 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS
Kết quả bài toán không thay đổi nếu ta tịnh tiến đồ thị sang trÆi sao cho I O . Khi đó chọn đồ thị h m
số g x   ax3 bx2 cxd . Khi đó dễ thấy g x  lẻ nŒn b d 0 v g x   ax3 cx có hai điểm
cực trị tương ứng l 1;1 , cũng là nghiệm của 3ax2  c 0 . Do đó g x   a x 3  3x,a  0 .
S1 S2 2g1  4a .
S1  a0 x3  3x dx  5 aS2  11 a . 1 4 4 S1 5  Vậy . S2 11 C u 11.
Tịnh tiến đồ thị y  f x( )sang trái sao cho điểm cực trị x2 trøng với gốc tọa độ. Ta thấy diện t ch S1 ; S2
không thay đổi. Đồ thị y  f x( )chuyển thành đồ thị y  g x( ) lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS  x2  0
Dựa vào đồ thị ta c x1  3 là ba điểm cực trị của h m số y  g x( ) nŒn suy ra  x3  1
g’( )x  a x  3 . . x x 1, (a  0)  
     3 2   x4 2x3 3x2 C  g x( )  a
x 3 . .x x1 dx a x  2x  3x dx a  4 3 2 
Vì đồ thị h m số đi qua điểm 0;0 nŒn C 0. Suy ra g x( ) a x4  2x3  3x2   4 3 2  
S1 0 x4  2x3  3x2 dx  297a   a  3  4 3 2  20  S1  891. Khi đó  1 4 3 2
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 12 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS 
 S2   a x  2x  3x dx  17a S2 17  0  4 3 2  60 C u 12.
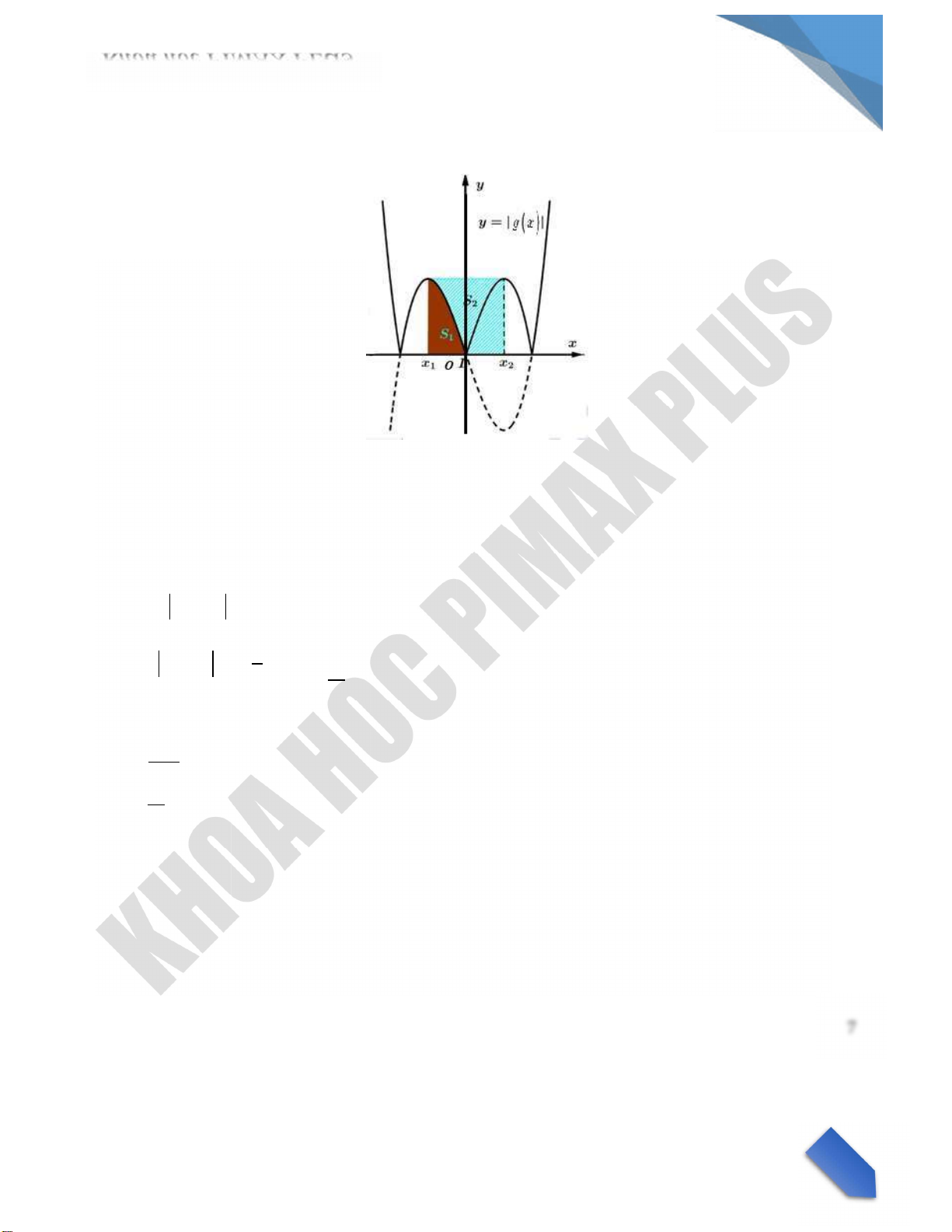
Ta tịnh tiến hệ tọa độ Oxy theo vectơ u x 2;0 .Khi đó, x2  0; x1  2; x3  2
Suy ra f ’ x  kx x  2x  2  f x   ax4  8ax2 c , với k  4a . Dựa và đồ thị của f x   a  0. f x   2
 f  0  c f x;  3  f  2  16ac . Do 9 f x   2
 7 f x 3  0  c  7a . Vậy f x   ax4  8ax2  7a 4 2 x  1
Ta c f x   0  ax 8ax 7a  0   . x   7
 S1 S2  1. f  0  7a . s 
1  1 f x dx  1 ax4 8ax2 7a dx 68a S2  37a . Vậy S1  68 . 0 0 15 15 S2 37 C u 13.
Tịnh tiến đồ thị y  f x  sang phải sao cho đường thẳng Oy ( vu ng g c với Ox tại x2 ) ta được h m số y  g x .
Khi đó ta thấy đồ thị h m số y  g x  đối xứng nhau qua trục Oy  y  g x  l h m số chẵn và đồ thị
h m số đi qua điểm O0;0 . lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS
M y  g x  l h m số bậc bốn suy ra g x   ax4 bx2 a  0.
Từ giả thiết ta c g x   4ax3  2bx  0 c cÆc nghiệm tương ứng 1;0;1
b  2a  g x   ax4  2ax2 .  S1 0 ax4 
2ax2dx a; S2 Shcn 2S1  2a 14 a  16 a. 115 15 S1 7  Vậy . S2 16 C u 14 .
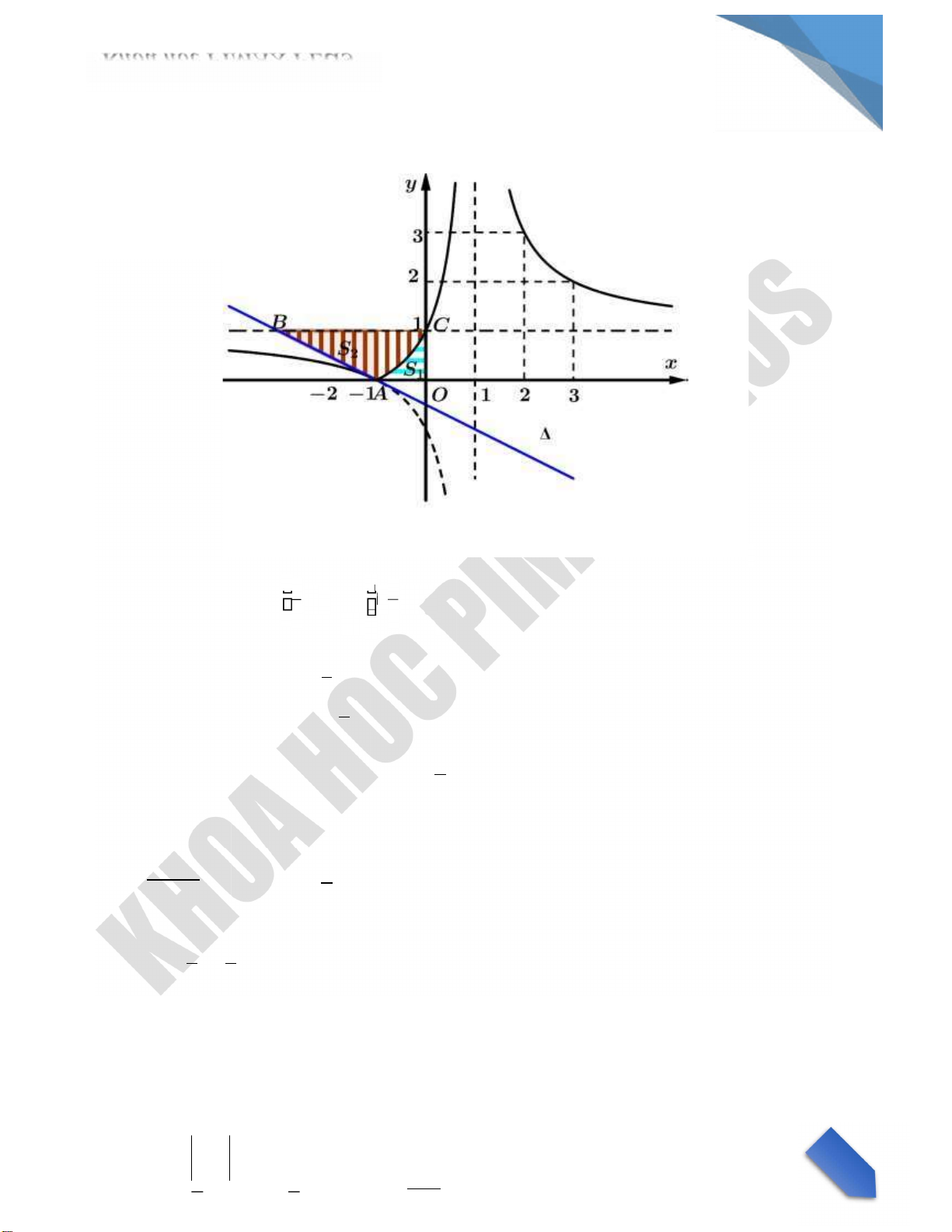
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 14 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS  a   b     1  1 Căn cứ vào đồ th c v  a ị ta c   d  1  db  1 c
Suy ra a b c  d, chọn a1 ( ):C y  x1 x1  y 
2 2  y( 1)  1 (x1) 2
 : y  1 x 1 ,  cắt y  1 tại B( 3 ;1) 2 2
Từ đồ thị ( )C ta suy ra đồ thị (C ’)bằng cÆch giữ nguyên đồ thị ( )C nằm ph a trŒn trục ho nh, bỏ phần
đồ thị ( )C nằm phía dưới trục hoành nhưng lấy đối xứng của phần n y qua truc ho nh ( h nh vẽ). Gọi các điểm A B C, , như trên hình vẽ.
Ta c S1  0 x1dx = 0 x1dx 0 (1 2)dx ( xØt dấu) lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS 1 x1 1 x1 1 x1  1 2ln2 Lại c SOABC  (OABC OC)  2 2
Suy ra S2  SOABC S1  3  2ln 2  k  32ln2  4,2  1 2ln2 C u 15.
Tịnh tiến đồ thị h m số y  f x  theo vectơ v   x2;0 ta thu được đồ thị h m số y  g x đối
xứng qua trục Oy nŒn h m số y  g x là hàm trùng phương . Ta thấy S S  
1, 2 trở th nh S1 ,S2 tương ứng không thay đổi giÆ trị.
V y  g x  là hàm trùng phương nên có dạng y  ax4 bx2 c a  0 có ba điểm cực trị lần lượt l x    
1 ,x2 ,x3 thỏa mªn x2  0;x3  x1 v x3  x1  4 .
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 16 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS
Khi đó ta được x1  2, x3  2 .
Ta c g x   4ax3  2bx c ba nghiệm x1  2,x2 0, x3  2.
Suy ra g2  0  8ab  0  b  8a.
Mặt khÆc, g 0  1  c  1.
Do đó, g x   ax4  8ax2 1.
Tại x  2 th g 2  16a1. Khi đó S  1  0
1ax4  8ax2 1dx  ax5  8ax3 0  224 a . 2  5 3  2 15 V S  2  2
ax4 8ax2  116a1dx   ax5  8ax3 16ax 2  256 a . 0  5 3 0 15 224
Vậy 24S1  24S1  24. 15 a  21. S2 S2 C u 16.
Theo giả thiết v từ h nh vẽ ta suy ra x1  2, x2  0, x3  2.
V f x( )  kx x( 2 4), (k  0).
Suy ra f x( )  k(x3  4 )x dx  k 1 x4  2x2 c.  4  lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS
Do f( 2)  f(2)  2 (0)f  k c( 4)  2kc  c  . 
Vậy f x( )  k 1 x4  2x2 4 .  4 3 
Gọi S  S1 S2, suy ra Sl phần diện t ch h nh chữ nhật như hình vẽ.
Suy ra S 4.4k 16k, 2 2   1 4 2x2  4  8kdx  128 k . S  k x 2  4 3  3  15
Suy ra S 1 S S2 16k 128 k  112 k . 15 15 S1 112 Vậy  S2 118 C u 17.
Kết quả của bài toán không thay đổi khi ta tịnh tiến đồ thị sang trÆi v xuống dưới 1 đơn vị sao cho điểm
uốn trøng với gốc tọa độ O.
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 18 lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS
Gọi g x( )  ax3 bx2 cx d
l h m số khi đó thì gx( ) lẻ nŒn ta c b d  0 v g x( )  ax3 cx c hai 
điểm cực trị l 1 v 1. Suy ra g x’( )  3ax2 c c x2 c 1  c 3a. 3a
Do đó g x( )  ax3 3ax (với a 0). Do tính đối xứng của đồ thị h m số nŒn S3  S1. Ta c
S1 S2  S2 S3  ( 1). ( 1) g   2a .
Lại c S2  a0 x3  3xdx  5a . Suy ra S1  2a 5a  3a . Vậy S1  3 . 1 4 4 4 S2 5 C u 18.
Tịnh tiến ĐTHS y  f x  theo vectơ v x 2;0 ,ta thu được ĐTHS y  g x  l h m chẵn đối xứng qua Oy .  
Ta thấy S1 v S2 trở th nh S1 v S2 tương ứng không thay đổi giÆ trị.
Ta thấy y  g x  l h m chẵn  y  g x   ax4 bx2  4 a  0 có ba điểm cực trị x1, x0 v x 1 (v x3  x2  1). 
Ta c g x    4ax3  2bx c ba nghiệm nghiệm x0, x1 v x1. lOMoAR cPSD|59 062 19 0 Kh a học PIMAX PLUS
 g 1  0  4a 2b  0  b  2a. Do đó g x   ax4  2ax2  4 .
Tại x 1 th g 1   a4 . Khi đó
S2  01 g x  g 1 dx  01 ax4  2ax2  4    a
4dx   ax55 
23 ax3 ax10  5a  23a a  158a S  
1  01 4  g x dx  01 4 ax4  2ax2  4dx  01 ax4  2ax dx2  
ax55  23 ax3 10  157a . S1  S1  7 . Vậy S2 S2 8 C u 19.  
Ta c : y’  3 x2  2bx  3 x x 4 b  0  x 4 2 b 2 2  3  3
Ta c x2   b l nghiệm của phương trình hoành độ giao điểm giữa đồ thị  C và đường thẳng y  1 nŒn:
1  4 b3 b 4 b2  3  1  b   3 2  3   3  2
Đồ thị  C có phương trình: y  1 x3  3 x2 3 2 2
Ever tried. Ever failed. No ma er. Try Again. Fail again. Fail be er 20