Đề minh họa thi hết học phần đại số môn Toán cao cấp 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58800262
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
ĐỀ MINH HỌA THI HẾT HỌC PHẦN KHOA CƠ BẢN 1 Môn: Đại số BỘ MÔN TOÁN
Số lượng câu hỏi: 40 câu ————
Thời gian làm bài: 80 phút
——————————–
Họ và tên sinh viên:....................................... Số báo danh: ......... Lưu ý: Sinh viên không được Mã đề thi 101 sử dụng tài liệu
Câu 1. Cho ánh xạ tuyến tính f : P2 → P2 xác định bởi
f(a0 + a1x + a2x2) = (a0 + a1 + ma2) + (a0 + ma1 + a2)x + (ma0 + a1 + a2)x2.
Tìm m để dim(Imf) = 2. A. m = 1.
B. m ̸= 1 và m ̸= −2. C. m = −2.
D. m = 1 hoặc m = −2.
Câu 2. Cho các tập con của không gian véc tơ R3:
A = {(x,y,z)| xz ≥ 0};B = {(x,y,z)| x = 2z}.
Khẳng định nào dưới đây đúng?
A. A và B là các không gian véc tơ con của R3.
B. Chỉ có B là không gian véc tơ con của R3.
C. A và B không là các không gian véc tơ con của R3.
D. Chỉ có A là không gian véc tơ con của R3.
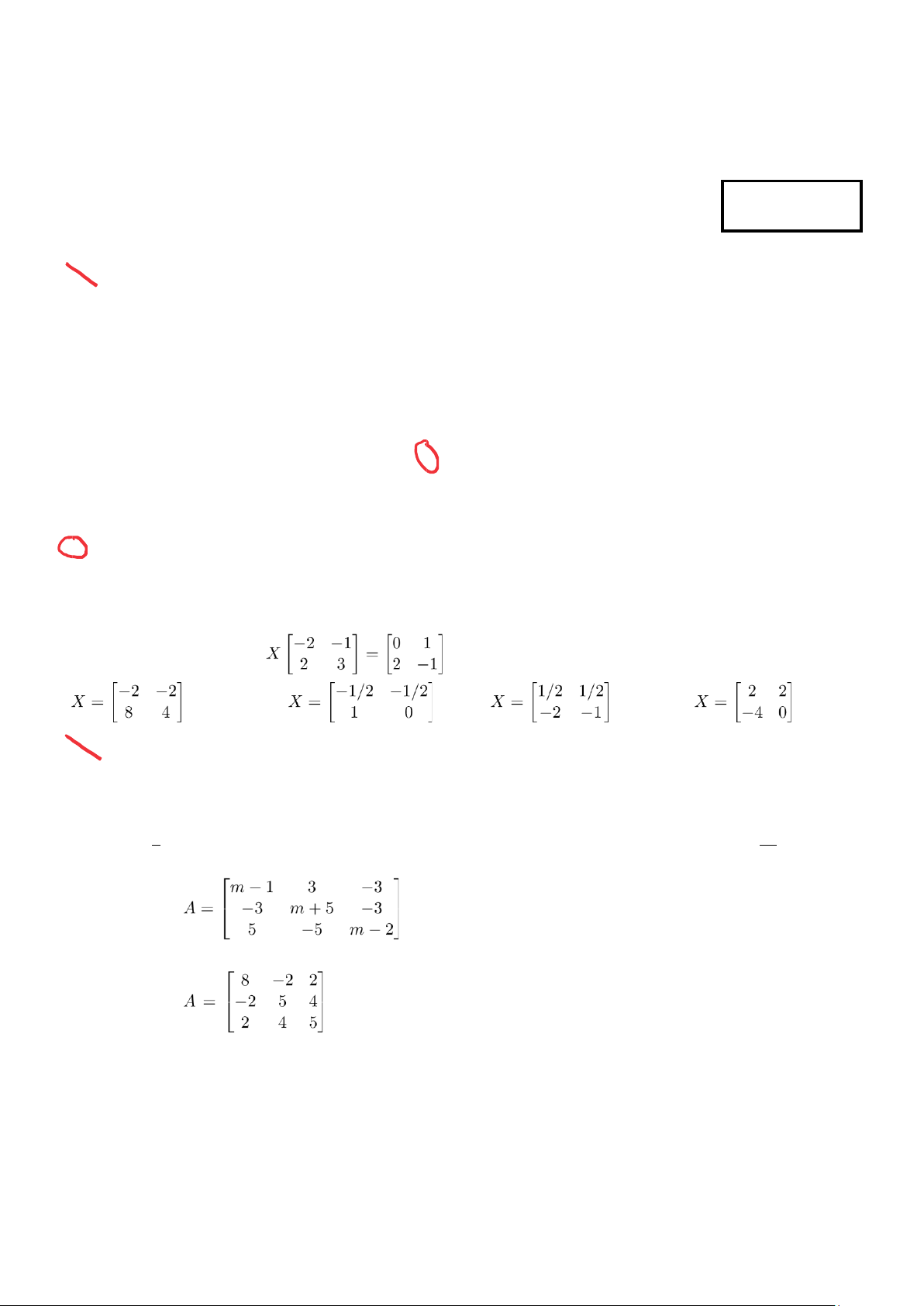
Câu 3. Tìm ma trận X thỏa mãn . A. . B. . C. . D. .
Câu 4. Cho tích vô hướng trên không gian véc tơ R2 xác định bởi
η(u,v) = x1y1 − 2x1y2 − 2x2y1 + 5x2y2, trong đó u =
(√ x1,x2),v = (y1,y2) ∈ R2. Xét véc tơ v = (1,2). Khẳng định nào dưới đây đúng√? A. ∥v∥ = 5. B. ∥v∥ = 1. C. ∥v∥ = 13. D. ∥v∥ = 13. Câu 5. Cho ma trận
. Điều kiện cần và đủ để A có ma trận nghịch đảo là
A. m ̸= −2 và m ̸= 1.
B. m ̸= 2 và m ≠ −2.
C. m = 2 hoặc m = −2.
D. m = −2 hoặc m = 1. Câu 6. Cho ma trận
. Biết λ = 9 là một giá trị riêng của A. Khẳng định nào dưới đây không đúng?
A. (−2,1,0) là một véc tơ riêng ứng với giá trị riêng λ = 9.
B. (3,2,3) là một véc tơ riêng ứng với giá trị riêng λ = 9. C. (2,1,2) là một véc tơ riêng ứng
với giá trị riêng λ = 9.
D. Không gian riêng ứng với giá trị riêng λ = 9 có số chiều là 2.
Câu 7. Cho A,B,C là các tập con của tập hợp E. Khẳng định nào dưới đây không đúng?
A. A ∩ (B \ A) = ∅.
B. Nếu A ∪ C = B ∪ C thì A = B.
C. (A ∩ B ∩ C) ⊂ (B ∩ C).
D. (A \ C) ∩ (C \ B) = ∅. lOMoAR cPSD| 58800262
Câu 8. Cho ma trận trực giao A. Khẳng định nào dưới đây đúng?
A. A khả nghịch và A−1 = At. B. detA = −1.
C. Các véc tơ hàng của A không tạo thành hệ trực chuẩn.
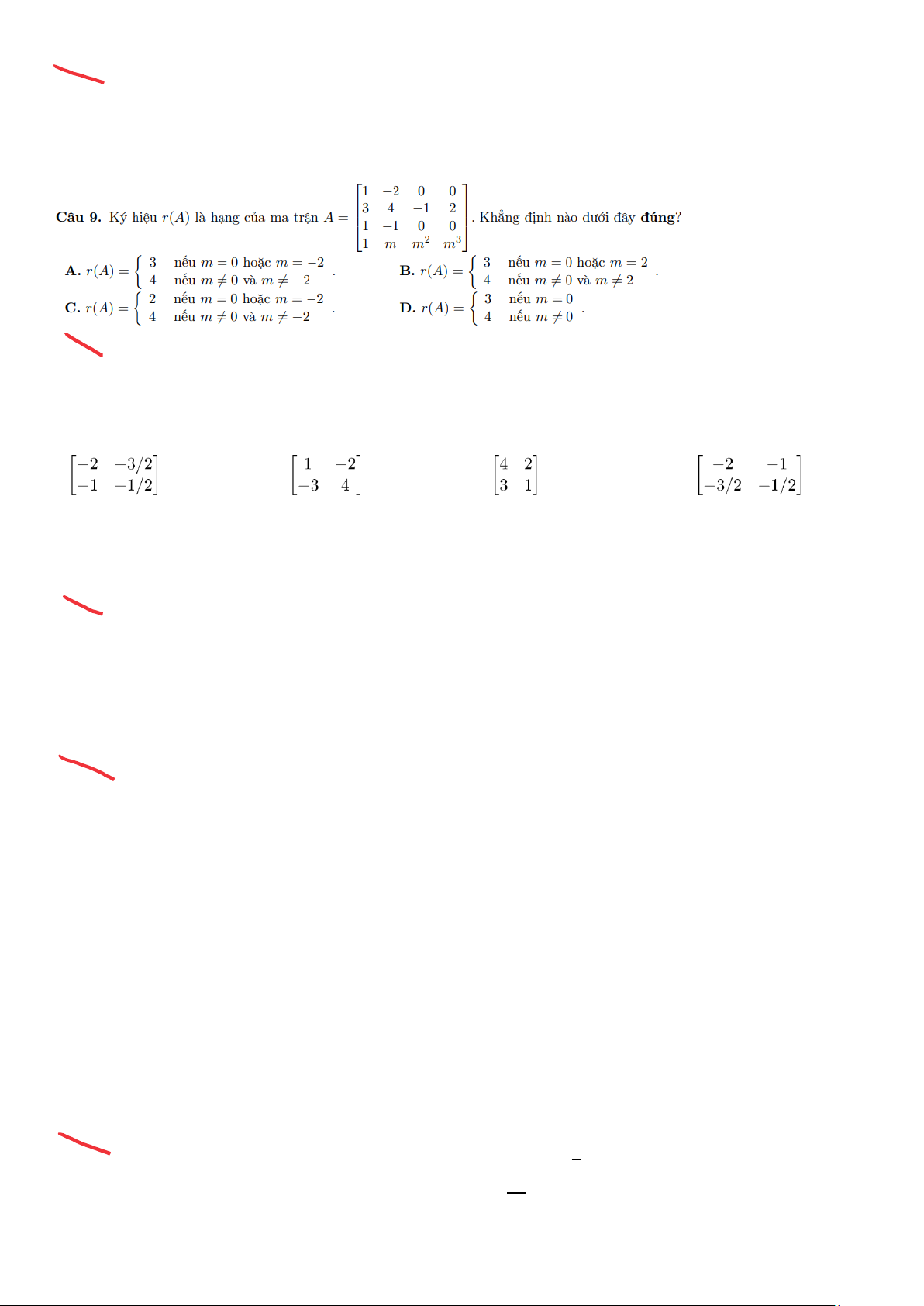
Câu 10. Đối ngẫu của công thức Boole (x′ ∨ 0) ∧ (y′ ∧ z) là
A. (x′ ∧ 1) ∨ (y′ ∨ z).
B. (x′ ∨ 1) ∧ (y′ ∧ z).
C. (x′ ∧ 0) ∨ (y′ ∨ z).
D. (x ∧ 1) ∨ (y ∨ z′).
Câu 11. Cho B = {(1,−3);(−2,4)} là một cơ sở của không gian véc tơ R2. Ma trận chuyển từ cơ sở B sang cơ sở chính tắc của R2 là A. . B. . C. . D. .
Câu 12. Ánh xạ f : R2 → R2 nào dưới đây không là một đẳng cấu?
A. f(x,y) = (x + 4y,−x + 2y).
B. f(x,y) = (2x + y,−3x + 2y).
C. f(x,y) = (x − 2y,−2x + 4y).
D. f(x,y) = (x + y,−3x + y).
Câu 13. Cho W1,W2 là các không gian véc tơ con của R3. Khẳng định nào dưới đây không đúng? A. W1 + W2 là tổng
trực tiếp khi và chỉ khi dim(W1 ∩ W2) = 0.
B. Nếu W1 = {(x,y,0)| x,y ∈ R};W2 = {(x,y,z)| x − y + 2z = 0} thì R3 = W1 ⊕ W2.
C. Nếu W1 = {(x,y,0)| x,y ∈ R};W2 = {(0,y,y)| y ∈ R} thì R3 = W1 ⊕ W2.
D. Nếu R3 = W1 ⊕ W2 thì dimW1 + dimW2 = 3.
Câu 14. Cho dạng toàn phương Q : R3 → R xác định bởi
Q(x,y,z) = x2 + 2y2 − z2 + 2xy + 2yz.
Ký hiệu (p,q) là cặp chỉ số quán tính dương và âm của Q. Khẳng định nào dưới đây đúng? A. p = 1,q = 2.
B. p = 2,q = 1. C. p = 0,q = 3. D. p = 1,q = 1.
Câu 15. Cho A là một ma trận vuông cấp 3. Khẳng định nào dưới đây đúng? A. Nếu A ̸= 0 thì A2 ̸= 0.
B. Nếu A có tổng các phần tử ở mỗi hàng đều bằng 0 thì A khả nghịch.
C. Nếu A2 = A và A ̸= 0 thì A = I.
D. Nếu A2 khả nghịch thì A khả nghịch.
Câu 16. Cho ánh xạ f : N → N,f(n) = n2 + n. Khẳng định nào dưới đây đúng?
A. f là toàn ánh nhưng không là đơn ánh.
B. f không là đơn ánh cũng không là toàn ánh. C. f là song ánh.
D. f là đơn ánh nhưng không là toàn ánh.
Câu 17. Cho các mệnh đề p,q,r. Mệnh đề nào dưới đây không đúng?
A. ((p ⇒ q) ∧ (p ⇒ r)) ≡ (p ⇒ (q ∧ r)).
B. (p ∨ q) ≡ (p ⇒ q).
C. ((p ⇒ r) ∧ (q ⇒ r)) ≡ ((p ∧ q) ⇒ r).
D. p ⇒ q ≡ (p ∧ q). lOMoAR cPSD| 58800262 Câu 18. Cho
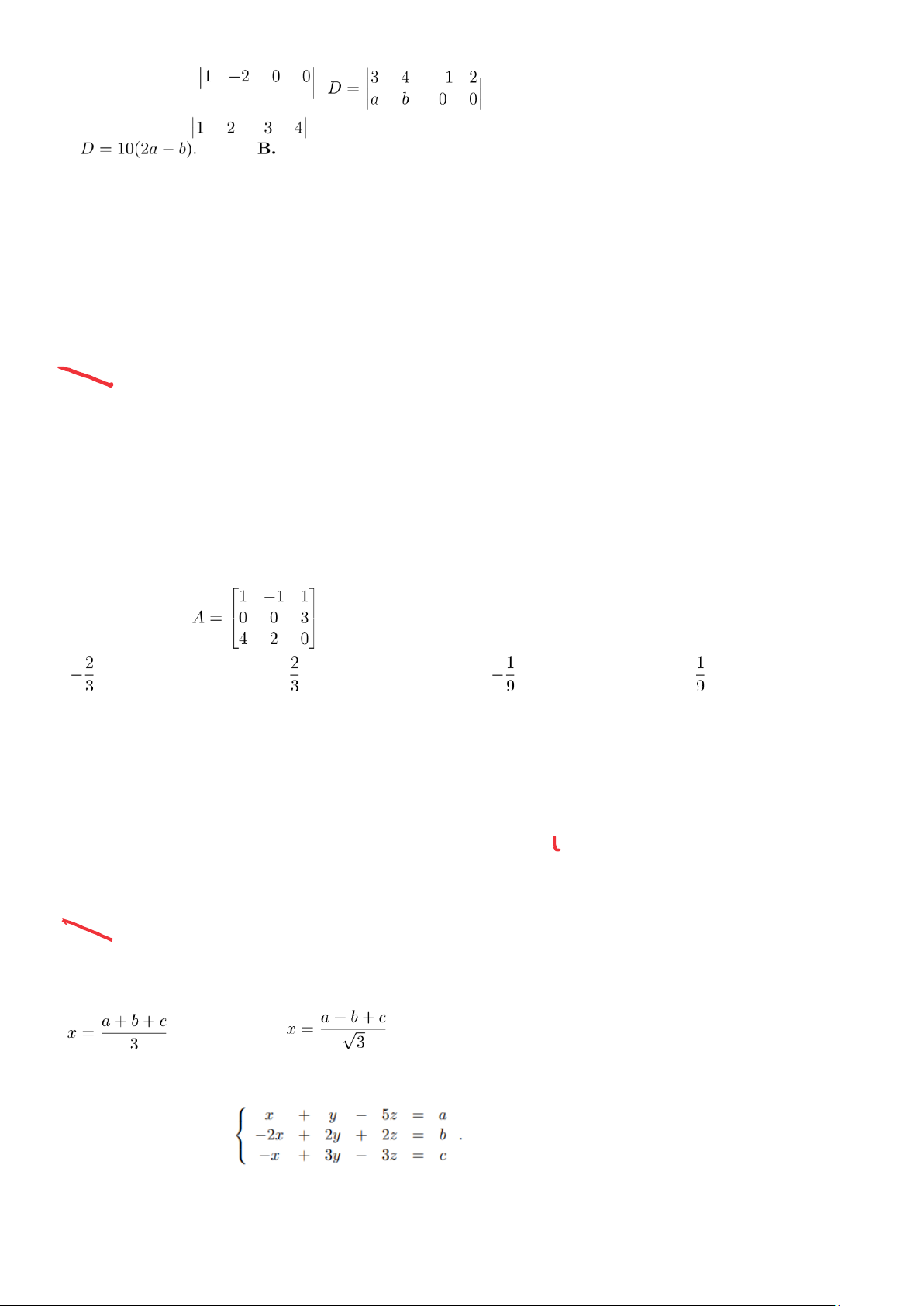
. Khẳng định nào dưới đây đúng? A.
D = 10(2a + b).
C. D = 10(b − 2a).
D. D = −10(2a + b).
Câu 19. Cho ánh xạ tuyến tính f : R4 → R3 xác định bởi
f(x,y,z,t) = (x − 2y − z − t,y + 2z + 3t,x − y + 3z).
Số chiều của Kerf là A. 4. B. 2. C. 3. D. 1.
Câu 20. Với giá trị nào của a thì x = (1,2,a) thuộc vào không gian con sinh bởi các véc tơ (3,1,2),(−1,1,−2),(2,−1,3) của R3? A. a ̸= −1. B. a ̸= 1. C. a = −1. D. a = 1.
Câu 21. Cho dạng song tuyến tính η : R2 × R2 → R xác định bởi
η(u,v) = x1y1 − 3x1y2 + x2y1 + 4x2y2,
trong đó u = (x1,x2),v = (y1,y2) ∈ R2. Khẳng định nào dưới đây đúng?
A. η xác định dương nhưng không đối xứng.
B. η không đối xứng cũng không xác định dương.
C. η đối xứng và xác định dương.
D. η đối xứng nhưng không xác định dương.
Câu 22. Khẳng định nào dưới đây không đúng? A. ∅ ∈ {x}.
B. ∅ ∈ {∅,{∅}}.
C. {x} ∈ {{x}}. D. x ∈ {x}. Câu 23. Cho ma trận
. Phần tử ở vị trí hàng 2, cột 1 của ma trận A−1 là A. . B. . C. . D. .
Câu 24. Cho ánh xạ tuyến tính f : R2 → R2,f(x,y) = (3x + 2y,4x + y). Một cơ sở gồm các véc tơ riêng của f là
A. {v1 = (1,−2);v2 = (1,1)}.
B. {v1 = (1,−2);v2 = (1,−1)}.
C. {v1 = (−2,1);v2 = (1,−1)}.
D. {v1 = (−2,1);v2 = (1,1)}.
Câu 25. Cho không gian véc tơ con của R4:
U = {(x,y,z,t)| x + 2y + z − 3z= 0}.
Khẳng định nào dưới đây đúng? A. dimU = 4. B. dimU = 1. C. dimU = 3. D. dimU = 2.
Câu 26. Trong R3, xét cơ sở trực giao
B = {u1 = (1,1,1),u2 = (1,−1,0),u3 = (1,1,−2)}.
Giả sử tọa độ của véc tơ u = (a,b,c) trong cơ sở B là (x,y,z). Khẳng định nào dưới đây đúng? A. . B. . C. x = a.
D. x = a + b + c.
Câu 27. Cho hệ phương trình
Điều kiện cần và đủ để hệ phương trình đã cho có nghiệm là
A. a + b − c ̸= 0.
B. 3a − b + c = 0.
C. a + b − c = 0.
D. 3a − b + c ̸= 0. lOMoAR cPSD| 58800262
Câu 28. Cho dạng toàn phương Q : R3 → R xác định bởi
Q(x,y,z) = x2 + 2y2 − z2 + 2xy + 2yz.
Câu 29. Với giá trị nào của a thì hệ phương trình dưới đây có nghiệm không tầm thường? A. a = 1. B. a = −1. C. a ̸= −1. D. a ̸= 1.
Câu 30. Ánh xạ nào dưới đây là toàn ánh? A. .
B. f : R → R,f(x) = x3 + 5.
C. f : R → R,f(x) = x2 + 2x.
D. f : N → N,f(n) = 2n.
Câu 31. Cho một hệ phương trình tuyến tính có ma trận hệ số và ma trận bổ sung lần lượt là A,A˜. Giả sử A là ma trận
cỡ 5 × 7 và r(A) = r(A˜) = 4 . Khẳng định nào dưới đây đúng? A. Hệ phương trình đã cho có vô số nghiệm phụ thuộc 4 tham số.
B. Hệ phương trình đã cho có nghiệm duy nhất.
C. Hệ phương trình đã cho có vô số nghiệm phụ thuộc 3 tham số.
D. Hệ phương trình đã cho có vô số nghiệm phụ thuộc 1 tham số.
Câu 32. Cho hệ phương trình
Khẳng định nào dưới đây đúng?
A. Hệ phương trình đã cho vô nghiệm.
B. Hệ phương trình đã cho có vô số nghiệm phụ thuộc 1 tham số. C. Hệ phương trình đã cho có
vô số nghiệm phụ thuộc 2 tham số.
D. Hệ phương trình đã cho có nghiệm duy nhất.
Câu 33. Hệ véc tơ nào dưới đây sinh ra không gian véc tơ P2 (không gian véc tơ các đa thức có bậc không vượt quá 2)?
A. {1 − 3t + 5t2,−3 + 8t − 2t2}.
B. {1 + t2,2 − t + t2,4 − 3t + t2}.
C. {2 − t + 3t2,4 − 2t + 6t2,1 − 3t + 5t2}. D. {3 + t + 2t2,−1 + t − 2t2,−1 + 5t + 3t2}. Câu 34. Cho ánh xạ tuyến tính
f : R3 → R2 xác định bởi
f(x,y,z) = (x − y − z,x + y − z).
Ma trận của f trong các cơ sở B1 = {(0,1,1);(1,1,1);(1,1,0)} của R3 và B2 = {(1,1);(1,2)} của R2 là lOMoAR cPSD| 58800262
Câu 35. Cho ánh xạ tuyến tính f : R2 → R2 có ma trận chính tắc
. Véc tơ nào dưới đây thuộc Imf? A. (6,−3). B. (3,−6). C. (3,6). D. (4,−2).
Câu 36. Cho một hệ phương trình tuyến tính thuần nhất gồm 3 phương trình, 6 ẩn. Khẳng định nào dưới đây đúng?
A. Hệ phương trình đã cho vô nghiệm.
B. Hệ phương trình đã cho có nghiệm duy nhất.
C. Không có đủ thông tin để kết luận về số nghiệm của hệ phương trình đã cho.
D. Hệ phương trình đã cho có vô số nghiệm.
Câu 37. Ánh xạ nào dưới đây là ánh xạ tuyến tính? A. f : R3 →
R,f(x,y,z) = 2x + 3y − z2.
B. f : P2 → P2,f(a0 + a1x + a2x2) = a1 − 2a0x + (a1 + a2)x2.
C. f : R3 → R3,f(x,y,z) = (xy,2y − z,x + y − 3z).
D. f : P2 → P2,f(a0 + a1x + a2x2) = a0 + a1 − (2a0 + 1)x + (a1 + a2)x2.
Câu 38. Cho hệ phương trình
Khẳng định nào dưới đây đúng?
A. Nếu m ̸= 2 và m ̸= −3 thì hệ phương trình đã cho có ngiệm duy nhất.
B. Nếu m = 3 thì hệ phương trình đã cho có vô số nghiệm.
C. Nếu m ̸= 2 và m ̸= 3 thì hệ phương trình đã cho có ngiệm duy nhất.
D. Nếu m = 2 thì hệ phương trình đã cho vô nghiệm.
Câu 39. Cho A là ma trận vuông cấp 3. Khẳng định nào dưới đây không đúng? A. det(AtA) = det(A2).
B. det(3A) = 3detA.
C. det(−A) = −detA.
D. Nếu A là ma trận tam giác và có một phần tử trên đường chéo chính bằng 0 thì detA = 0. Câu 40. Cho các ma trận
Phần tử ở vị trí hàng 1, cột 2 của ma trận AB − BA là A. 3. B. −4. C. 1. D. 4.
- - - - - - - - - - HẾT- - - - - - - - - - ĐÁPÁN
BẢNG ĐÁP ÁN CÁC MÃ ĐỀ Mã đề thi 101 1. C 2. B 3. C 4. D 5. B 6. B 7. B 8. A 9. A 10. A 11. D 12. C 13. B 14. B 15. D 16. D 17. C 18. B 19. D 20. C 21. A 22. A 23. A 24. A 25. C 26. A 27. C 28. A 29. B 30. B 31. C 32. B 33. D 34. B 35. B 36. D 37. B 38. A 39. B 40. B