










Preview text:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH – NĂM HỌC 2024 – 2025
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ ĐỀ MINH HOẠ Môn: Toán 12
Thời gian: 90 phút (không kể thời gian phát đề)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 20. NH
Mỗi câu hỏi thí sinh chỉ chọn một phương án. ÓM
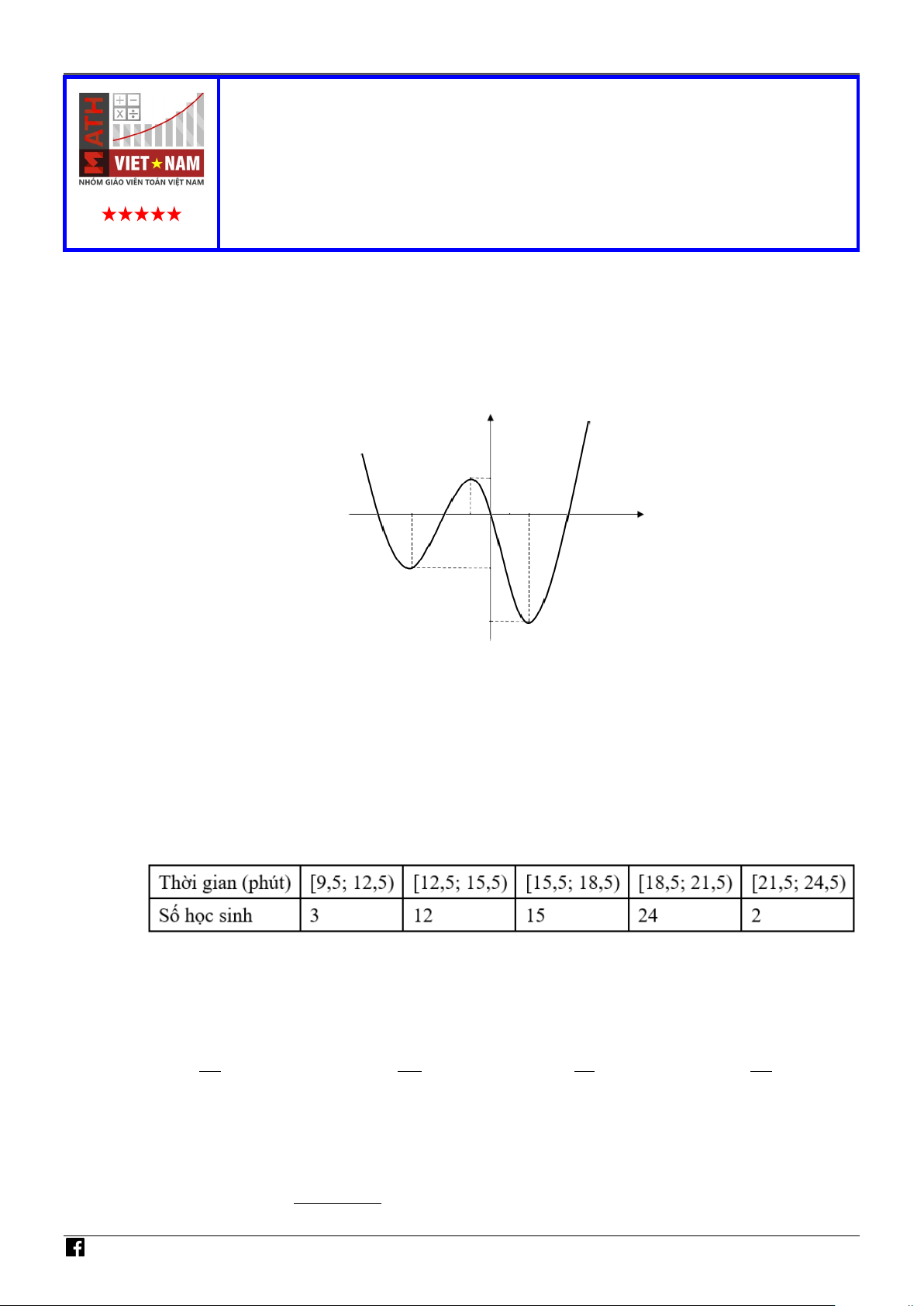
Câu 1. Cho hàm đa thức bậc năm y = f (x) có đồ thị của hàm số y = f ′(x) như hình vẽ bên. G y IÁO V I 2 ÊN T O x OÁ N V -3 IỆT N -6 AM
Số điểm cực đại của hàm số y = f (x) là A. 1. B. 4 . C. 2 . D. 3.
Câu 2. Cho hình hộp ABC . D A′B C ′ D
′ ′ có tâm O . Khi đó, AB + AD + AA′ + AC′ bằng A. BD . B. 2OC′ . C. 4AO . D. 2AC .
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho các vectơ a = (1; 1; − 2),b = (2;1; 3 − ),c = (0;3; 2 − ) . Điểm M ( ;
x y; z) thỏa mãn OM + a = 2b − c , tổng x + y + z bằng A. 3. B. 3 − . C. 4 . D. 2 − . NH
Câu 4. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau: ÓM GIÁ O V
Khoảng tứ phân vị của mẫu số liệu trên là A. 10,75. B. 4,75 . C. 4,63. D. 4,38. IÊ
Câu 5. Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ đúng số 3, kim phút OP chỉ đúng số 12. N T
Số đo góc lượng giác mà kim giờ quét được từ lúc xét đến khi kim phút và kim giờ gặp nhau lần OÁ đầu tiên bằng N V A. π α π π π = . B. 2 α = − . C. α = − . D. α = − . 22 45 21 22 IỆ u = 5 T
Câu 6. Cho dãy số (u được cho bởi hệ thức truy hồi 1
. Giá trị của u là n ) u = u + ∈ ≥ 3 − n n n n n , , 2 1 A. 10. B. 14. C. 7. D. 9. 2
Câu 7. Cho hàm số ( ) ax + bx + c f x =
có bảng biến thiên dưới đây mx + n
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25
Đường tiệm cận xiên của đồ thị hàm số là
A. y = 2x +1.
B. y = x −1.
C. y = 2x − 3 .
D. y = x + 3 .
Câu 8. Cho tứ diện đều ABCD có cạnh bằng 1. Giá trị của biểu thức S |
= AB + AD + AC | bằng A. 6 . B. 3 . C. y = 2 3 . D. 6 . NH 2
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho các điểm A(2;1; )
1 , B(1;2;3),C ( 1; − 2;0). Điểm ÓM M ( ;
x y; z) thỏa mãn cos( , MA MB)+ cos( ,
MA MC) = 0 và tồn tại số thực k sao cho G IÁ
AM = k AB + k (3k + )
1 AC . Tổng x + 2y + 3z − k bằng O V A. 19 . B. 5. C. 7 . D. 6 . IÊ 3 N T
Câu 10. Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị OÁ
đó trong một ngày. Số liệu được ghi lại trong bảng sau: N V IỆT N AM
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị chục nghìn đồng) là NH A. 6,8. B. 7,3. C. 3,3 . D. 46,1. ÓM
Câu 11. Số điểm biểu diễn tất cả các nghiệm của phương trình sin x(cos 2x + cos x) = 0 trên đường tr òn lượng giác là G I A. 2 . B. 3. C. 4 . D. 5. ÁO V
Câu 12. Cho các số thực dương a,b sao cho phương trình (a )x (b ) 2x 1 1 . 1 − + +
= 1 có hai nghiệm phân biệt I 2 Ê x x N T
x , x thỏa mãn 1 2 3
− 4x − 4x ≤ 3 4 . Giá trị x + x thuộc khoảng nào sau đây? 1 2 1 2 x + x 1 2 1 2 OÁ A. ( 1; − 0) . B. ( 2; − − ) 1 . C. (0; ) 1 . D. (1;2) . N V 2
ax + 4x + b I
Câu 13. Cho các số thực a,b,c thoả mãn lim = c . Tính 2 3
S = a + b + 6 . c Ệ 3 x→ 1 − x − 3x − 2 T A. 6. B. 10. C. 8. D. 12.
Câu 14. Gọi S là tập hợp các số có 4 chữ số được lấy từ các chữ số 2;3;4;5;6;7;8. Lấy ngẫu nhiên một
số từ tập S, tính xác suất để lấy được số chẵn có dạng abcd mà a ≤ b < c ≤ d.
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 A. 2 . B. 8 . C. 80 . D. 76 . 21 343 2401 2401 2 Câu 15. Gọi ,
A B là hai điểm phân biệt thuộc đồ thị hàm số x y =
và đối xứng với nhau qua đường x −1
thẳng y = x −1. Độ dài đoạn thẳng AB bằng A. 4 . B. 2 . C. 2 . D. 2 2 .
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AD = 2AB = 2 2 , đường thẳng SA
vuông góc với mặt phẳng ( ABCD) và SA = 4 . Gọi M , N là các điểm thỏa mãn BM = xBD ,
SN = ySC và độ dài đoạn MN nhỏ nhất. Tổng 2x + 3y bằng NH A. 4 . B. 11. C. 3. D. 22 . 7 7 ÓM
Câu 17. Trong không gian với hệ tọa độ Oxyz , cho tứ diện đều KABC có các điểm ,
A B,C lần lượt
thuộc các tia Ox,Oy,Oz sao cho OA = OB = OC = a . Biết điểm K có tọa độ là các số dương và GI
OK = 6. Giá trị a thuộc khoảng nào trong các khoảng sau đây? ÁO V A. 3 ;2 . B. 5 7 ; . C. 5 2; . D. 3 0; . I 2 2 2 2 2 ÊN T
Câu 18. Có bao nhiêu cặp số nguyên dương ( ; x y) thỏa mãn OÁ 10( 2 2
x + y − xy) 2
− log (x + y − ) 3 3
1 ≥ x + y − 4? 3 N V A. 25. B. 30. C. 40. D. 45. ′ ′ ′ I
Câu 19. Cho hình lăng trụ ABC.A B C có đáy ABC là tam giác đều cạnh .
a Hình chiếu của A′ lên mặt ỆT N
phẳng (ABC) là trung điểm cạnh BC. Tính khoảng cách giữa hai đường thẳng B C ′ ′ và AA′ ,
biết góc giữa hai mặt phẳng ( ABB A
′ ′) và ( A′B C ′ ′) bằng 60°. AM a a a a A. 3 7 . B. 21 . C. 3 . D. 3 . 14 14 4 4
Câu 20. Có bao nhiêu cách lấy ra 3 quả cầu từ một hộp chứa 50 quả cầu được đánh số từ 1 đến 50 sao
cho tích 3 số ghi trên 3 quả cầu lấy được là một số chia hết cho 8. A. 9930. B. 11950. C. 9650. D. 9950.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 6. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. NH ÓM
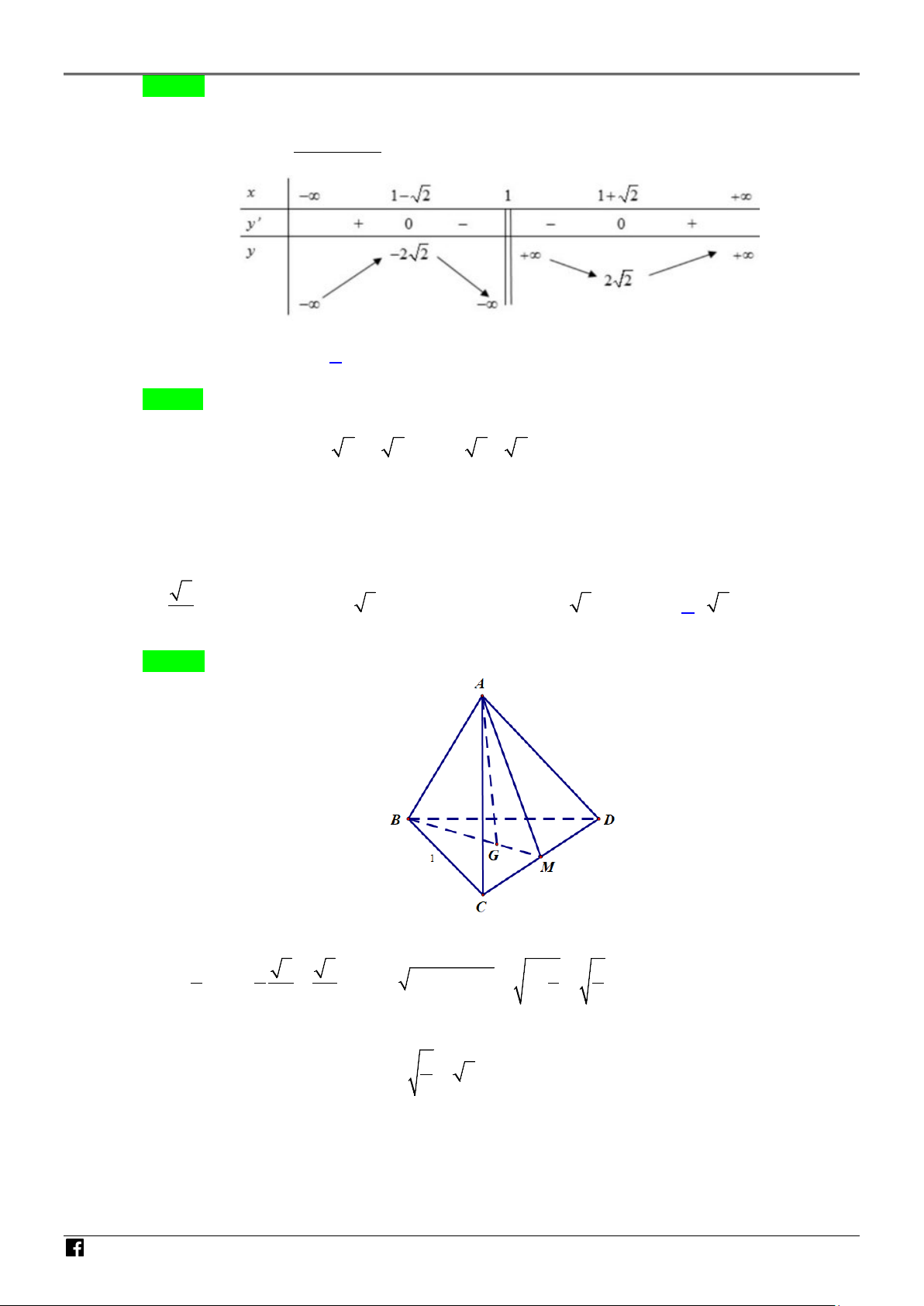
Câu 1. Cho hàm số y = f (x) xác định và liên tục trên \{ }
0 , có bảng biến thiên như sau: x −∞ 0 3 +∞ G ′ + I f (x) − 0 − 0 ÁO V 2 +∞ +∞ f (x) IÊN T −∞ 2 OÁ
a) Hàm số f (x) có cực tiểu bằng 3. N V
b) Trên đoạn [1;2], hàm số y = 2 + f (x) − 2 có giá trị nhỏ nhất bằng 2. IỆ
c) Đồ thị hàm số f (x) có hai đường tiệm cận vuông góc với nhau. T d) Trên khoảng ( 3 − ;− )
1 , hàm số y = 3− 2 f (2 − f (x)) nghịch biến.
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho các điểm A(1;2; 4
− ), B(1;2;0),C (0;2;0) .
a) B là hình chiếu vuông góc của A lên mặt phẳng (Oxy).
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25
b) Không tồn tại điểm M thuộc mặt phẳng (Oyz) thỏa mãn MA = MB = MC .
c) Gọi (H ) là khối hộp nhận các điểm O, ,
A B,C làm đỉnh và có một đỉnh thuộc trục Ox khác
O . Thể tích khối hộp (H ) bằng 4 . d) Nếu điểm D( ;
x y; z) thỏa mãn AD = BD = CD và OD song song với mặt phẳng ( ABC) thì
tổng 2x + y − 3z bằng 6 .
Câu 3. Bảng sau thống kê lại tổng số giờ nắng trong tháng 6 của các năm từ 2002 đến 2021 tại hai trạm
quan trắc đặt ở Nha Trang và Quy Nhơn. NH ÓM
a) Xét số liệu ở Nha Trang thì khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 32,64. GI
b) Nếu so sánh theo khoảng tứ phân vị thì số giờ nắng trong tháng 6 của Quy Nhơn đồng đều ÁO V hơn. I
c) Xét số liệu của Quy Nhơn ta có độ lệch chuẩn của mẫu số liệu ghép nhóm (làm tròn kết quả ÊN T
đến hàng phần trăm) là: 30,59. OÁ
d) Nếu so sánh theo độ lệch chuẩn thì số giờ nắng trong tháng 6 của Nha Trang đồng đều hơn. N V
Câu 4. Giả sử số miligam của các chất ô nhiễm trong một mét khối không khí trong một tháng tại một IỆ π T N
thành phố công nghiệp được xác định bởi công thức P(t) 2 37 = a + bsin t −
, (a,b > 0) 7 12 AM
trong đó t là số ngày kể từ ngày thứ Bảy của tuần đầu tiên của tháng đó.
a) Số miligam của các chất ô nhiễm trong một mét khối không khí trong một ngày của tháng
không vượt quá a + . b
b) Trong một tháng số miligam của các chất ô nhiễm trong một mét khối không khí bằng nhau sau ít nhất 7 ngày.
c) Giả sử ngày thứ bảy của tuần đầu tiên cũng là ngày đầu tiên của tháng Một và trong tháng Một
hệ số a = 30,b =15. Khi đó có 2 ngày trong một tháng Một số miligam của các chất ô nhiễm NH
trong một mét khối không khí bằng 37,5 (miligam). ÓM
d) Biết chất ô nhiễm trong một mét khối không khí cao nhất là 50 miligam và thấp nhất là 20
miligam. Trong các ngày: ngày thứ Hai của tuần thứ 2 , ngày thứ Tư của tuần thứ 3 và ngày thứ GI
Ba của tuần thứ 4 và ngày thứ Sáu của tuần thứ 4 của tháng thì số miligam chất ô nhiễm nhiều ÁO V
nhất là M , ít nhất là m . Khi đó M − m nhỏ hơn 23. IÊ
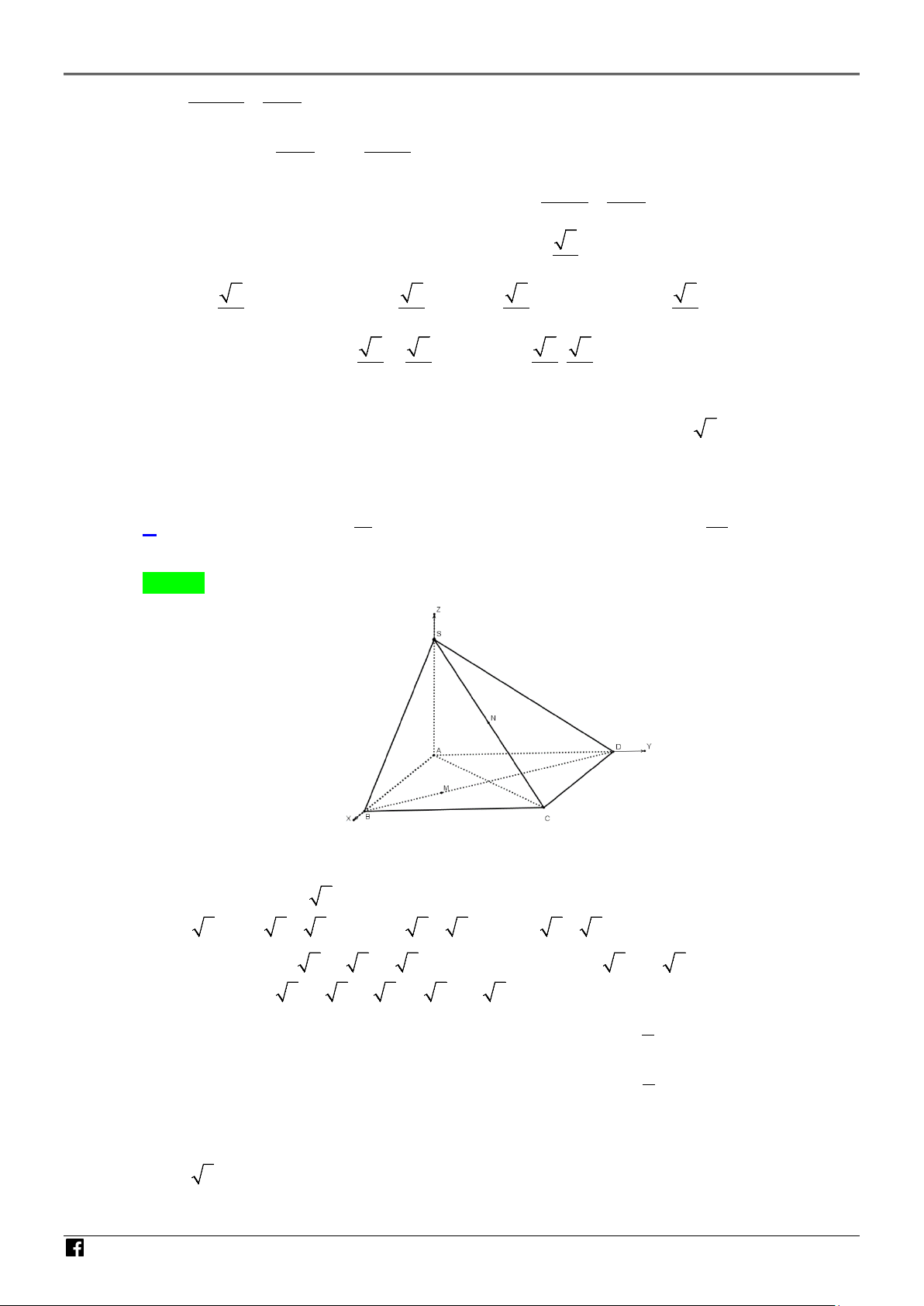
Câu 5. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a , góc giữa đường thẳng SA và N T
mặt phẳng ( ABCD) bằng 0
60 . Gọi E là điểm đối xứng với D qua trung điểm P của SA và OÁ
M là trung điểm của AE . N V
a) Đường thẳng PM vuông góc với đường thẳng . CD
b) Gọi J là điểm thoả mãn JD + 3JS = 0. Khi đó, đường thẳng JC cắt mặt phẳng (MAB). IỆT
c) Số đo của góc nhị diện [M , BC, A] bằng α mà 15 cosα = . 5
d) Khoảng cách từ điểm M đến mặt phẳng (SBC) bằng 31 . a 14
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25
Câu 6. Trong một trò chơi, người dẫn chương trình yêu cầu 18 thành viên đứng ngẫu nhiên, cách đều
nhau và tạo thành một vòng tròn. Sau đó, người dẫn chương trình gọi ngẫu nhiên 4 thành viên để
bốc thăm câu hỏi, các thành viên được chọn sẽ bốc câu hỏi từ một hộp đựng 8 câu hỏi khác nhau,
mỗi người bốc đúng một câu hỏi và không bỏ lại vào hộp. Để hoàn thành trò chơi, mỗi người
phải thực hiện yêu cầu của thăm mà người đó bốc được.
a) Số cách xếp các thành viên đứng thành vòng tròn là 18!.
b) Số cách chọn ra 4 thành viên sao cho có đúng 2 người đứng cạnh nhau là 1404.
c) Số cách chọn ra 4 thành viên và đều thực hiện bốc câu hỏi là 12533760.
d) Xác suất để chọn được 4 thành viên không có 2 thành viên nào đứng cạnh nhau và đều thực
hiện bốc câu hỏi bằng 91 . 170 NH
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 ÓM
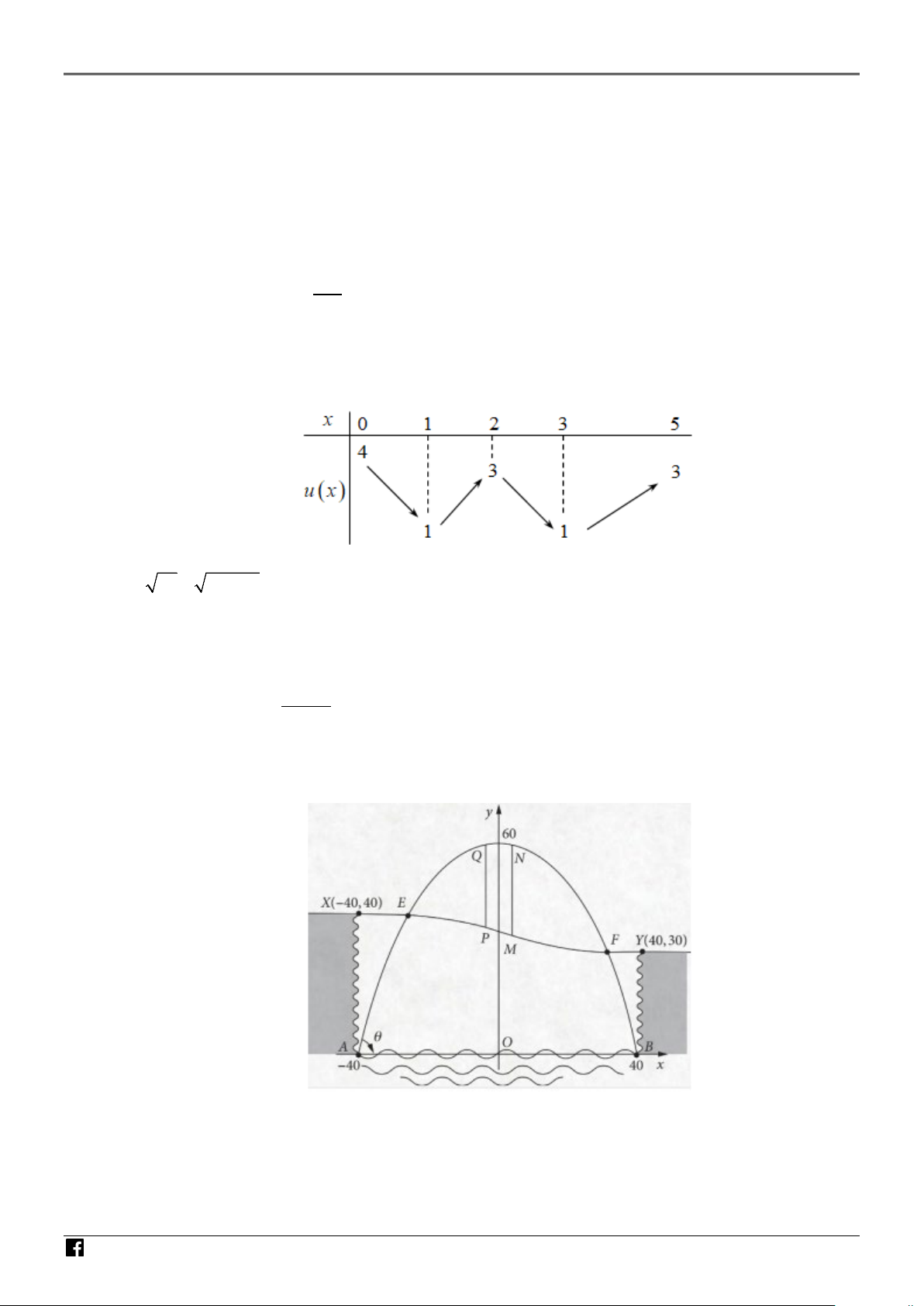
Câu 1. Cho hàm số u (x) liên tục trên đoạn [0;5] và có bảng biến thiên như hình vẽ sau: GIÁO V IÊN T OÁ N V
Có bao nhiêu giá trị nguyên của tham số m bé hơn 205 để bất phương trình
3x + 10 − 2x < .
m u (x) nghiệm đúng với mọi giá trị của x thuộc khoảng (0;5)? IỆT N
Câu 2. Thành phố A dự định xây một cây cầu bắc qua một con sông chảy qua hẻm núi. Hẻm có chiều AM
ngang 80 m, một bên cao 40 m và một bên cao 30 m. Mô hình thiết kế của cây cầu được gắn hệ
trục tọa độ Oxy như hình vẽ bên dưới. Cây cầu XY xuyên qua hẻm núi được mô hình hóa bằng phương trình: 1 3 y =
x + ax + b với a,b là các số thực. Hai cáp treo MN và PQ (cùng song 25600
song với trục Oy) là đoạn nối giữa khung của parabol và cầu XY. Tổng độ dài hai đoạn cáp treo
dài bao nhiêu mét (làm tròn kết quả đến hàng phần chục của đơn vị mét)? Biết rằng N và Q là
hai điểm đối xứng qua trục Oy và MN là đoạn có độ dài lớn nhất. NH ÓM GIÁO V IÊN T OÁ N V IỆT
Câu 3. Trong không gian Oxyz , cho bốn điểm A(3;4;4), B(1; 1
− ;0),C (3;2;4), D(2;0;2). Điểm M (a; ;
b c) di động trên mặt phẳng (Oxy) .
Khi biểu thức T = (MA MB)2 2 2 2 .
+ 2MB + 3MC − 4MD đạt giá trị nhỏ nhất thì tổng a + b + c bằng bao nhiêu?
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25
Câu 4. Gọi x là số thực dương sao cho tồn tại số thực y không bé hơn 1 thỏa mãn ( 2 + − − ) 2 − + 3 2 1 log = log y x xy x y y
. Có bao nhiêu số nguyên trong tập các giá trị của biểu x π π π π thức 6 sin x 3 2 sin x P = − − + ? 5 4 5 4
Câu 5. Một loại đá quý có dạng khối lập phương, cạnh bằng 2cm . Để làm đồ mỹ nghệ, với mỗi đỉnh
của khối lập phương người ta cắt khối lập phương bởi một mặt phẳng vuông góc với đường chèo
của hình lập phương xuất phát từ đình đ để tạo thành một khối mới có 14 mặt mà diện tích của
tất cả các mặt bằng nhau. Thể tích của khối thu được sau khi cất bằng bao nhiêu cm (làm tròn kết
quả đến háng phần trăm của đơn vị 3 cm ). NH
Câu 6. Một hộp đựng 8 thẻ được đánh số từ 2 đến 9. Bạn Lê lấy ngẫu nhiên một thẻ, ghi lại số trên ÓM
thẻ rồi bỏ thẻ vào hộp. Lần thứ hai, bạn Lê cũng lấy ngẫu nhiên một thẻ, ghi lại số trên thẻ rồi bỏ
thẻ vào hộp. Tiếp tục như vậy, sau năm lần bạn Lê đã ghi lại được 5 chữ số. Xác suất để trong GI
5 số ghi được có đúng 2 chữ số chia hết cho 4 là a với a là phân số tối giản. Giá trị của biểu Á b b O V
thức 5a − 2b bằng bao nhiêu? IÊ N T HẾT OÁ N V IỆT N AM NH ÓM GIÁO V IÊN T OÁ N V IỆT
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
C C B B D A B D A A C A C C B A D D A C HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 20.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
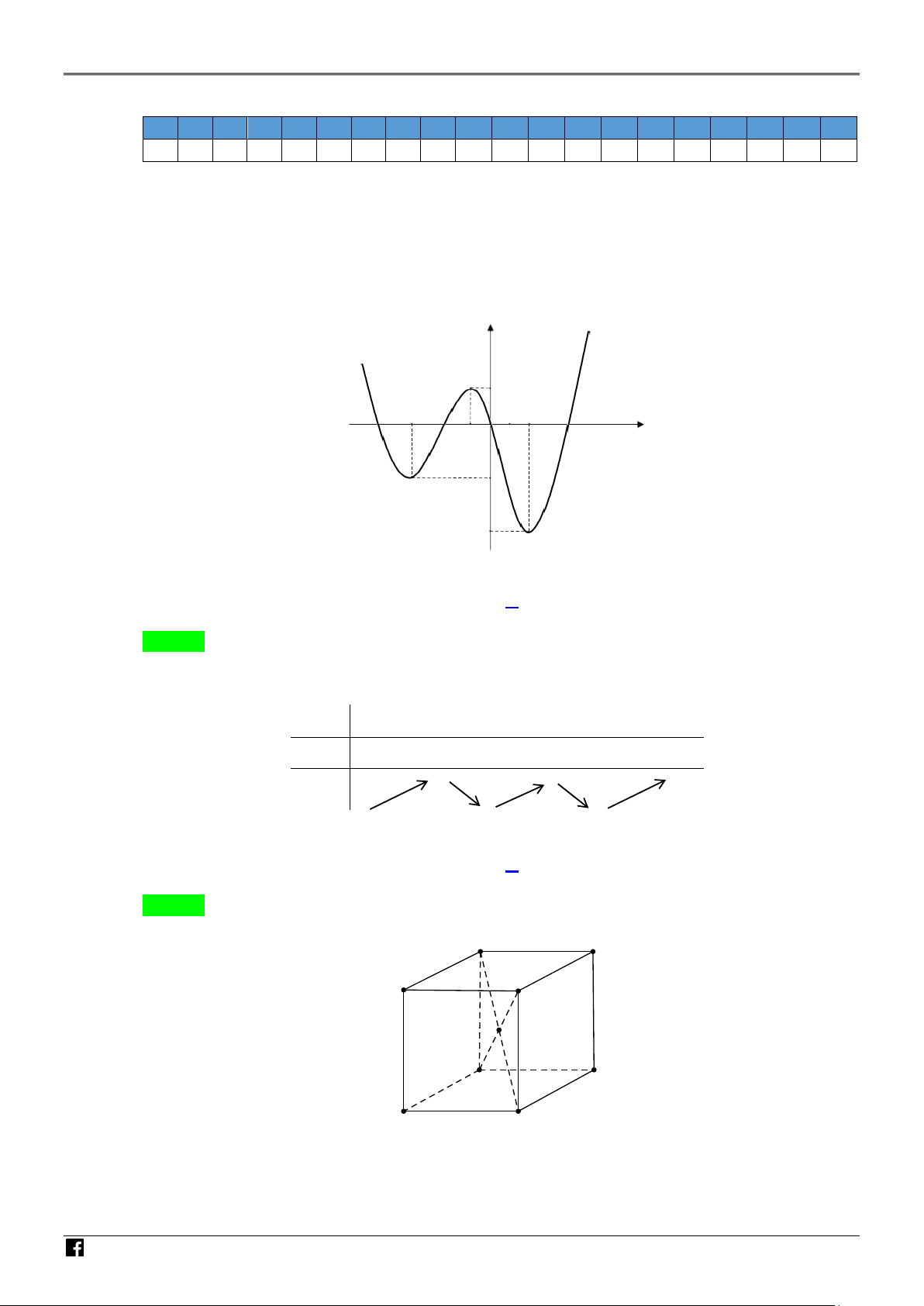
Câu 1. Cho hàm đa thức bậc năm y = f (x) có đồ thị của hàm số y = f ′(x) như hình vẽ bên. y NH ÓM 2 GI O x ÁO V I -3 ÊN T -6 OÁ N V
Số điểm cực đại của hàm số y = f (x) là IỆT N A. 1. B. 4 . C. 2 . D. 3. Lời giải Chọn C AM
Gọi giao điểm của đồ thị hàm số y = f ′(x) với trục hoành là a,b,c,d sao cho a < b < c < d .
Từ đồ thị ta có bảng biến thiên x −∞ a b c d +∞
f ′(x) + 0 − 0 + 0 − 0 + f ( x) .
NH
Câu 2. Cho hình hộp ABC . D A′B C ′ D
′ ′ có tâm O . Khi đó, AB + AD + AA′ + AC′ bằng A. BD . B. 2OC′ . C. 4AO . D. 2AC . ÓM Lời giải G Chọn C IÁ A' O V D' I C' Ê B' N T OÁ O N V A D IỆT B C
Áp dụng quy tắc hình hộp AB + AD + AA′ = AC′ .
Suy ra AB + AD + AA′ + AC′ = AC′ + AC′ = 2AC′ = 4AO .
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho các vectơ a = (1; 1; − 2),b = (2;1; 3 − ),c = (0;3; 2 − ) . Điểm M ( ;
x y; z) thỏa mãn OM + a = 2b − c , tổng x + y + z bằng A. 3. B. 3 − . C. 4 . D. 2 − . Lời giải
Chọn B
Ta có: OM + a = 2b − c ⇔ OM = −a + 2b − c = (3;0; 6 − ) .
Vậy x + y + z = 3+ 0 − 6 = 3 − .
Câu 4. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau: NH ÓM
Khoảng tứ phân vị của mẫu số liệu trên là A. 10,75. B. 4,75 . C. 4,63. D. 4,38. G Lời giải IÁ Chọn B O V
Cỡ mẫu là n = 3+12 +15 + 24 + 2 = 56. I … Ê Gọi x ; x ; ; x
là thời gian vào internet của 56 học sinh và giả sử dãy này được sắp xếp theo 1 2 56 N T thứ tự tăng dần. OÁ
n =14 nên nhóm chứa Q là [12,5;15,5) 1 N V 4 14 − 3 I Q =12,5 + . 15,5 −12,5 =15,25. 1 ( ) Ệ 12 T N
3n = 42 nên nhóm chứa Q là [18,5;21,5) 3 AM 4 42 − (3+12 +15) Q =18,5 + . 21,5 −18,5 = 20 . 3 ( ) 24
Khoảng tứ phân vị ∆ = Q − Q = − = . Q 20 15,25 4,75 3 1
Câu 5. Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ đúng số 3, kim phút OP chỉ đúng số 12.
Số đo góc lượng giác mà kim giờ quét được từ lúc xét đến khi kim phút và kim giờ gặp nhau lần đầu tiên bằng A. π α π π π = . B. 2 α = − . C. α = − . D. α = − . NH 22 45 21 22 ÓM Lời giải Chọn D G
Một giờ kim phút quay một góc 2 − π IÁ π π O V
Một giờ kim giờ quay một góc 2 − = − . 12 6 IÊ
Giá sử sau thời gian t giờ, kim phút và kim giờ gặp nhau lần đầu tiên. Ta có N T π π t (− π ) 11t 1 3 . 2 = − + t. − ⇔ = ⇔ t = (h) . OÁ 2 6 6 2 11 N V
Số đo góc lượng giác mà kim giờ quét được từ lúc xét đến khi kim phút và kim giờ gặp nhau lần π π I đầu tiên bằng 3 . − = − . Ệ 11 6 22 T u = 5
Câu 6. Cho dãy số (u được cho bởi hệ thức truy hồi 1
. Giá trị của u là n ) u = u + ∈ ≥ 3 − n n n n n , , 2 1 A. 10. B. 14. C. 7. D. 9. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 Chọn A
u = u + 2 = 7; u = u + 3 =10 . 2 1 3 2 2
Câu 7. Cho hàm số ( ) ax + bx + c f x =
có bảng biến thiên dưới đây mx + n
Đường tiệm cận xiên của đồ thị hàm số là NH
A. y = 2x +1.
B. y = x −1.
C. y = 2x − 3 .
D. y = x + 3 . ÓM Lời giải Chọn B G
Ta có tiệm cận đứng của đồ thị là x =1 IÁO V
Hai điểm cực trị là A(1− 2; 2
− 2); A(1+ 2;2 2) suy ra trung điểm của AB là I (1;0) chính I
là tâm đối xứng của đồ thị. Vì giao điểm hai tiệm cận là tâm đối xứng của độ thị và là giao điểm ÊN T
hai tiệm cận nên ta có I (1;0) thuộc tiệm cận xiên. Thử từng đáp án ta có đường tiệm cận xiên là OÁ y = x −1.
N V
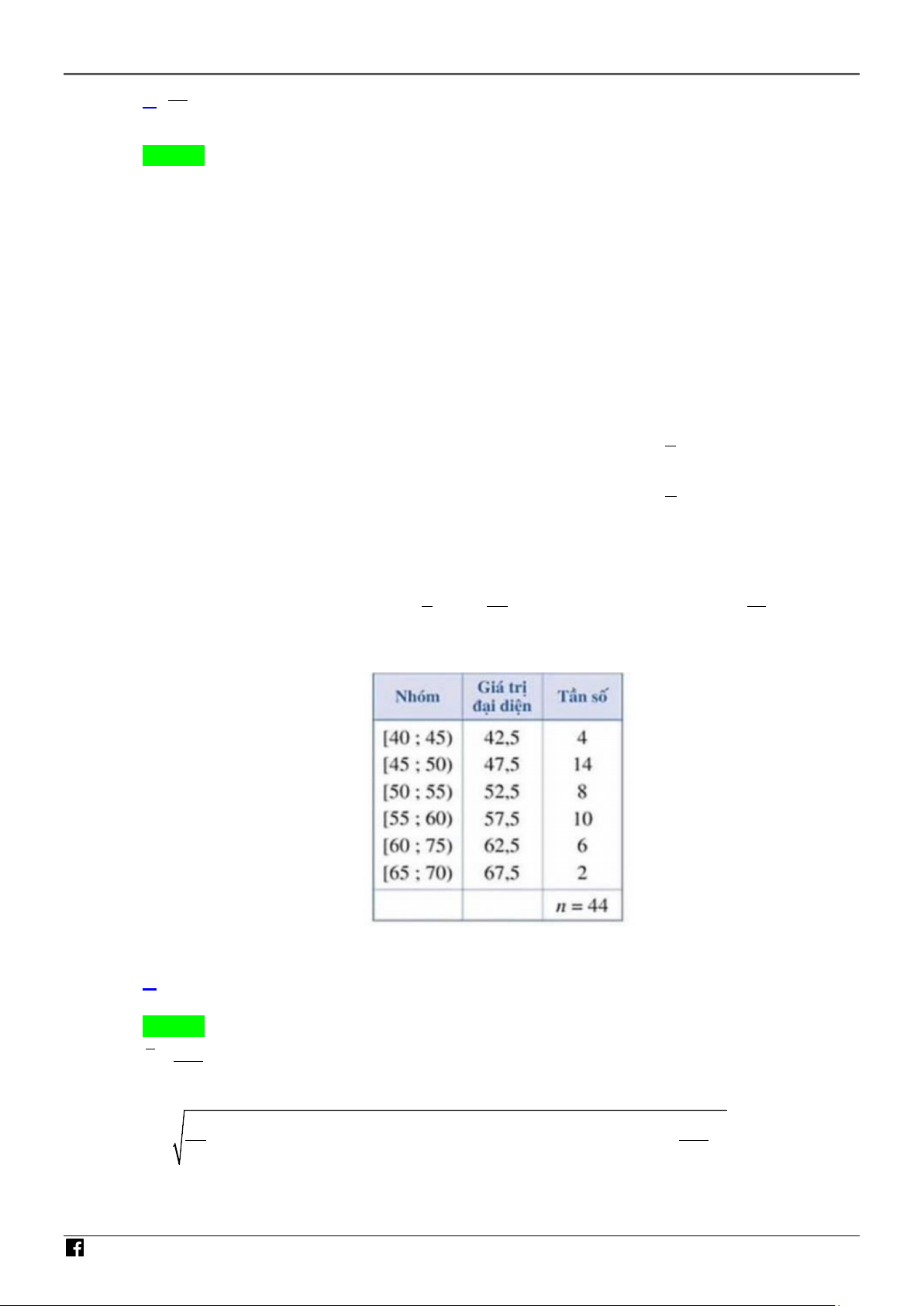
Câu 8. Cho tứ diện đều ABCD có cạnh bằng 1. Giá trị của biểu thức S |
= AB + AD + AC | bằng IỆ A. 6 . B. 3 . C. y = 2 3 . D. 6 . T N 2 Lời giải AM Chọn D NH ÓM G IÁ
Gọi G là trọng tâm tam giác BCD ta có AG ⊥ (BCD) O V 2 2 3 3 I = = = = − = − = Ê BG BM ; 2 2 1 2 AG AB BG 1 N T 3 3 2 3 3 3
Có AB + AD + AC = 3AG + (GB +GC +GD) = 3AG OÁ N V
Vậy S | 2
= AB + AD + AC |= 3AG = 3 = 6 . 3 IỆT
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho các điểm A(2;1; )
1 , B(1;2;3),C ( 1; − 2;0). Điểm M ( ;
x y; z) thỏa mãn cos( , MA MB)+ cos( ,
MA MC) = 0 và tồn tại số thực k sao cho
AM = k AB + k (3k + )
1 AC . Tổng x + 2y + 3z − k bằng
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 A. 19 . B. 5. C. 7 . D. 6 . 3 Lời giải Chọn A
AM = k AB + k (3k + ) 1 AC ⇒ ,
A B,C, M đồng phẳng.
AM (x − 2; y −1; z − ) 1 , AB( 1; − 1;2), AC ( 3 − ;1;− ) 1 2 x = 9 − k − 4k + 2
AM = k AB + k (3k + ) 2
1 AC ⇔ y = 3k + 2k +1 2 z = 3 − k + k +1 NH
(MA MB)+ (MA MC) = ⇒(MA MB)+(MA MC) 0 cos , cos , 0 , , = 180 ÓM
Do đó B, M ,C thẳng hàng theo thứ tự đó. BM ( 2 2 2 9
− k − 4k +1;3k + 2k −1; 3
− k + k − 2);BC ( 2 − ;0; 3 − ) GIÁ 1 O V k = 2 3 9
− k − 4k +1 = 2 − n IÊ 2 2
⇔ BM = nBC ⇔ k + k − = ⇔ n = N T
B, M ,C thẳng hàng 3 2 1 0 3 2 3
− k + k − 2 = 3 − n OÁ k = 1 − N V n = 2 I − Ệ
Mà M nằm trong đoạn BC nên 1 1 19 k = ⇒ x =
; y = 2; z =1⇒ x + 2y + 3z − k = . T N 3 3 3
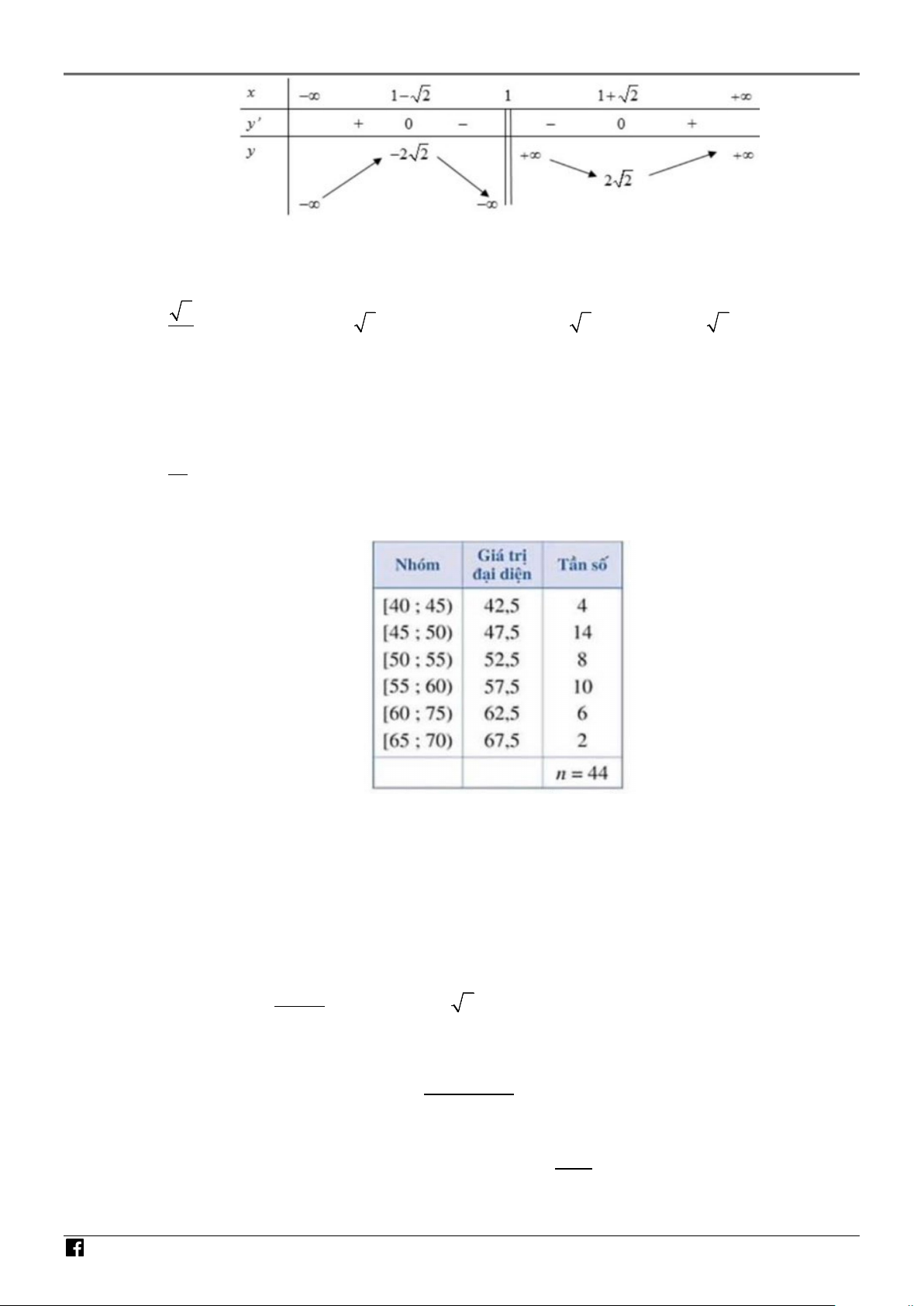
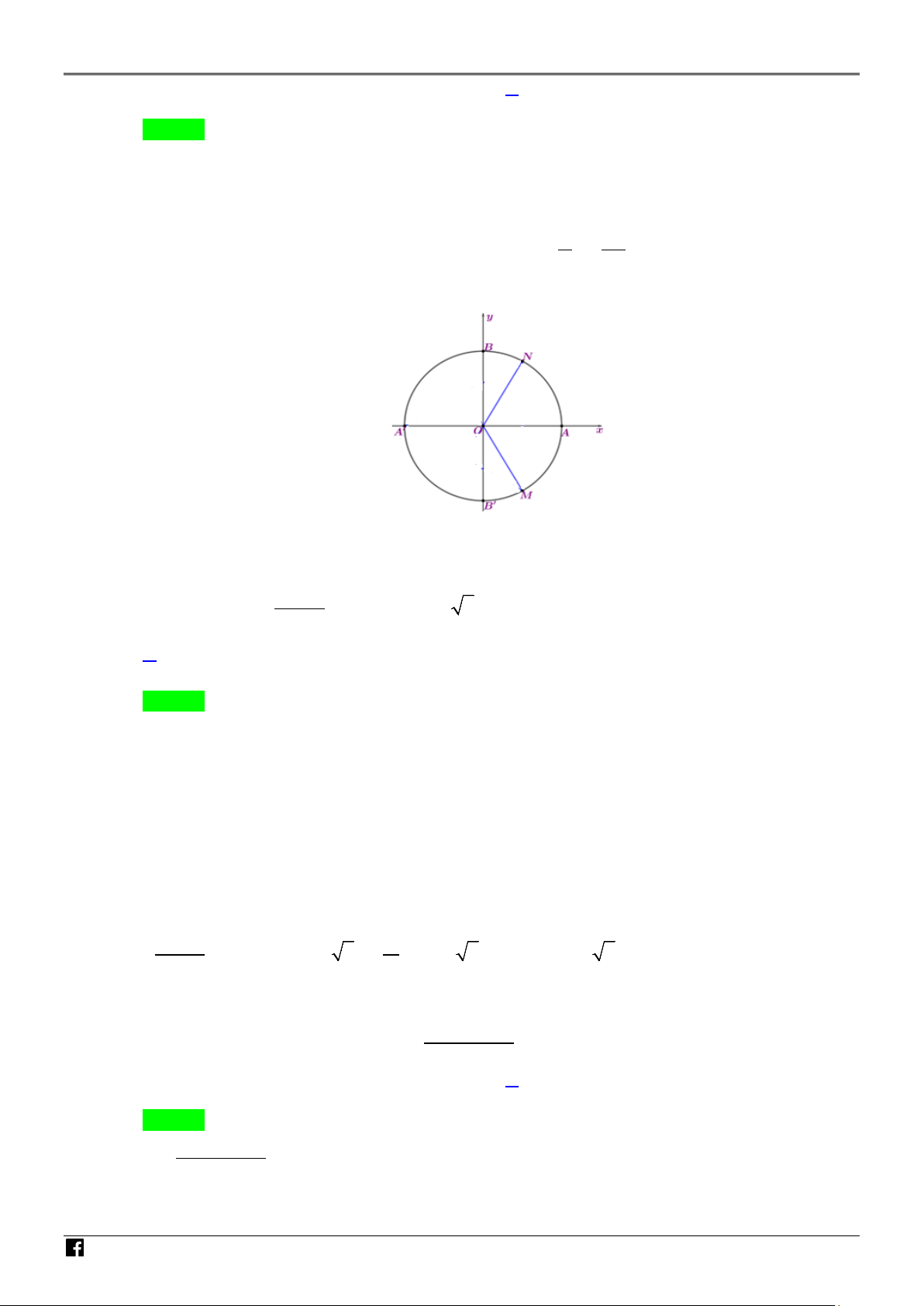
Câu 10. Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị AM
đó trong một ngày. Số liệu được ghi lại trong bảng sau: NH ÓM G IÁ
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị chục nghìn O V đồng) là I A. 6,8. B. 7,3. C. 3,3 . D. 46,1. ÊN T Lời giải Chọn A OÁ 585 N V x = 11 IỆ Áp dụng công thức: T 1 s ( ) 2 2 2 2 2 2 2 585
4.42,5 14.47,5 8.52,5 10.57,5 6.62,5 2.67,5 = + + + + + − ≈ 6,8. 44 11
Câu 11. Số điểm biểu diễn tất cả các nghiệm của phương trình sin x(cos 2x + cos x) = 0 trên đường tròn lượng giác là
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 A. 2 . B. 3. C. 4 . D. 5. Lời giải Chọn C x = x = Ta có x( x + x) sin 0 sin 0 sin cos 2 cos = 0 ⇔ ⇔
cos 2x cos x 0 + =
cos 2x = − cos x x = kπ x = kπ x kπ = π 2π ⇔ ⇔
x = π − x + k π ⇔ x = + k k ∈ cos 2x cos(π x) 2 2 ( ) = − 3 3 2x = π − + x + k2π x = π − + k2π NH ÓM GIÁO V IÊN T
Điểm biểu diễn tất cả các nghiệm của phương trình là các điểm ,
A A ,′ M , N . OÁ x x − N V
Câu 12. Cho các số thực dương a,b sao cho phương trình (a + ) (b + ) 2 1 1 . 1
= 1 có hai nghiệm phân biệt 2 I x x Ệ
x , x thỏa mãn 1 2 3
− 4x − 4x ≤ 3 4 . Giá trị x + x thuộc khoảng nào sau đây? T N 1 2 1 2 x + x 1 2 1 2 AM A. ( 1; − 0) . B. ( 2; − − ) 1 . C. (0; ) 1 . D. (1;2) . Lời giải Chọn A Ta có (a + )
1 x .(b + ) 2x 1 1 − =1 ⇔ xlog + + − = ⇔ + + − = . + a x x x + a b ( ) 2 2 1 1 0 logb 1 1 0 1 1 1 ( ) ( ) Ta có 2 ∆ = log + + > ∀ > . + a a b b 1 4 0, , 0 1 ( )
Suy ra, phương trình (1) luôn có 2 nghiệm phân biệt x , x . 1 2
x + x = −log + + a b 1 1 2 1 ( ) NH Định lý Viet có . x .x = 1 − 1 2 ÓM
Đặt t = x + x = −log + < − = ⇒ < . + a + t b 1 logb 1 0 0 1 2 1 ( ) 1 G Ta có I 2 Á ≈ − O V x x 1 t 0,794 1 2 3 3 3 3 2
− 4x − 4x ≤ 3 4 ⇔
− 4t − 3 4 ≤ 0 ⇔ 4
− t − 3 4t +1≤ 0 ⇔ 1 2 2 x + x t t ≥ 0,397 1 2 IÊN T
Vì t < 0 ⇒ t ≈ 0 − ,794∈( 1 − ;0) . 2 OÁ
Câu 13. Cho các số thực a,b,c thoả mãn ax + 4 lim
x + b = c . Tính 2 3
S = a + b + 6 . c 3 x→ 1 − − − N V x 3x 2 A. 6. B. 10. C. 8. D. 12. IỆ Lời giải T Chọn C 2 ax + 4 lim
x + b = c , 3x −3x−2 = 0 nhận x = 1
− là nghiệm, suy ra phương trình 3 x→ 1 − x − 3x − 2 2
ax + 4x + b = 0 nhận x = 1
− là nghiệm suy ra a + b − 4 = 0 hay b = 4 − a .
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 2 Thay b + + = 4 − a vào ax 4 lim
x b = c suy ra: 3 x→ 1 − x − 3x − 2 2 ax + 4x + 4 ( 2
ax − a) + (4x + 4) (x + ) 1 (ax + 4 − a) lim
− a = c ⇔ lim = c ⇔ lim = c 3 x→ 1 − x − 3x − 2 3 x→ 1 − x − 3x − 2 x→− ( x + ) 1 ( 2 1 x − x − 2) ax + 4 ⇔ lim − a = c 2 x→ 1
− x − x − 2 Do 2
x − x − 2 = 0 nhận x = 1
− là 1 nghiệm nên ax + 4 − a = 0 cũng có nghiệm là x = 1 − suy ra a = 2 . Suy ra 2x + 2 2 lim
= c ⇔ c = − . 2 x→ 1
− x − x − 2 3 NH Vậy 2 3 2 S = 2 + 2 − 6. = 8 . ÓM 3
Câu 14. Gọi S là tập hợp các số có 4 chữ số được lấy từ các chữ số 2;3;4;5;6;7;8. Lấy ngẫu nhiên một GI
số từ tập S, tính xác suất để lấy được số chẵn có dạng abcd mà a ≤ b < c ≤ d. ÁO V A. 2 . B. 8 . C. 80 . D. 76 . I 21 343 2401 2401 ÊN T Lời giải Chọn C OÁ
Số phần tử của không gian mẫu là: n(Ω) 4 = 7 . N V
Gọi A là biến cố lấy được một số chẵn có dạng abcd mà a ≤ b < c ≤ d. I
TH1: Nếu d = 8 thì 2 ≤ a ≤ b ≤ c ≤ 8 ⇔ 2 ≤ a < b +1< c +1≤ 9. Khi đó ứng với mỗi bộ số ỆT N
a,b +1,c +1 chọn từ các chữ số từ 2 đến 9 ta chỉ có một cách sắp xếp thỏa mãn. Suy ra số các số AM tạo ra là: 3 C . 8
TH2: Nếu d = 6 thì 2 ≤ a ≤ b ≤ c ≤ 6 ⇔ 2 ≤ a < b +1< c +1≤ 7 . Tương tự như TH1 số các số tạo ra là: 3 C . 6
TH3: Nếu d = 4 thì 2 ≤ a ≤ b ≤ c ≤ 4 ⇔ 2 ≤ a < b +1< c +1≤ 5 . Tương tự như TH1 số các số tạo ra là: 3 C . 4 Vậy n( A) 3 3 3
= C + C + C = 80 . P( A) 80 80 = = . 8 6 4 4 7 2401 2 x NH Câu 15. Gọi ,
A B là hai điểm phân biệt thuộc đồ thị hàm số y =
và đối xứng với nhau qua đường x −1 ÓM
thẳng y = x −1. Độ dài đoạn thẳng AB bằng G A. 4 . B. 2 . C. 2 . D. 2 2 . I Lời giải ÁO V Chọn B Ta phải tìm hai điểm ,
A B thuộc đồ thị sao cho đường thẳng AB vuông góc với đường thẳng IÊ = − = − N T
y x 1 và trung điểm I của AB phải thuộc đường thẳng y x 1.
Đường thẳng vuông góc với đường y = x −1 có dạng: y = −x + m OÁ 2 x N V Hoành độ các điểm ,
A B là các nghiệm của phương trình: = −x + m x −1 I 2 Ệ
⇔ 2x − (m +1)x + m = 0 (*) T 2
∆ = m − 6m +1> 0 m < 3− 2 2 ,
A B tồn tại ⇔ (*) có hai nghiệm phân biệt khác 1 ⇔ ⇔ 2 − (m + ) 1 + m ≠ 0 m > 3+ 2 2
Khi đó tọa độ trung diểm I của đoạn AB là:
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 x + x m + A B 1 x = = 1 2 4 m +1 3m −1
y = −x + m = − + m = 1 1 4 4
Điểm I thuộc đường thẳng y − +
= x −1 ⇔ y = x −1 3m 1 m 1 ⇔ = −1 ⇔ m = 1 − 1 1 4 4
Khi đó phương trình (*) trở thành: 2 2
2x −1 = 0 ⇔ x = ± 2 Nếu 2 x = thì 2 2
y = −x − = − − x = − thì 2 y = −x − = − B B 1 1 A A 1 1, A 2 2 B 2 2 NH
Vậy hai điểm cần tìm là: 2 2 A ;− −1 và 2 2 B− ; −1 . ÓM 2 2 2 2
Độ dài đoạn thẳng AB là: 2. G I = = Á
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AD 2AB 2 2 , đường thẳng SA O V
vuông góc với mặt phẳng ( ABCD) và SA = 4 . Gọi M , N là các điểm thỏa mãn BM = xBD , IÊ
SN = ySC và độ dài đoạn MN nhỏ nhất. Tổng 2x + 3y bằng N T A. 4 . B. 11. C. 3. D. 22 . OÁ 7 7 N V Lời giải Chọn A IỆT N AM NH
MN nhỏ nhất thì MN là đoạn vuông góc chung giữa BD và SC . Chọn hệ trục tọa độ như hình ÓM
vẽ. Khi đó tọa độ các điểm sẽ là: (
A 0;0;0), S(0;0;4), B( 2;0;0) , G I − − Á
D(0;2 2;0),C( 2;2 2;0); BD( 2;2 2;0); SC ( 2;2 2; 4) O V
BM = xBD ⇒ M (− 2x + 2;2x 2;0) và SN = ySC ⇒ N( 2y;2y 2; 4 − y + ) 4 I Ê
Suy ra ⇒ MN = ( 2y + 2x − 2;2y 2 − 2x 2; 4 − y + 4) N T 5 OÁ x = MN.BD = 0 2
− y − 2x + 2 + 8y −8x = 0 7 N V
Có ⇔ ⇔
⇒ 2x + 3y = 4 . MN.SC = 0
2y + 2x − 2 + 8y − 8x +16y −16 = 0 6 y = I Ệ 7 T
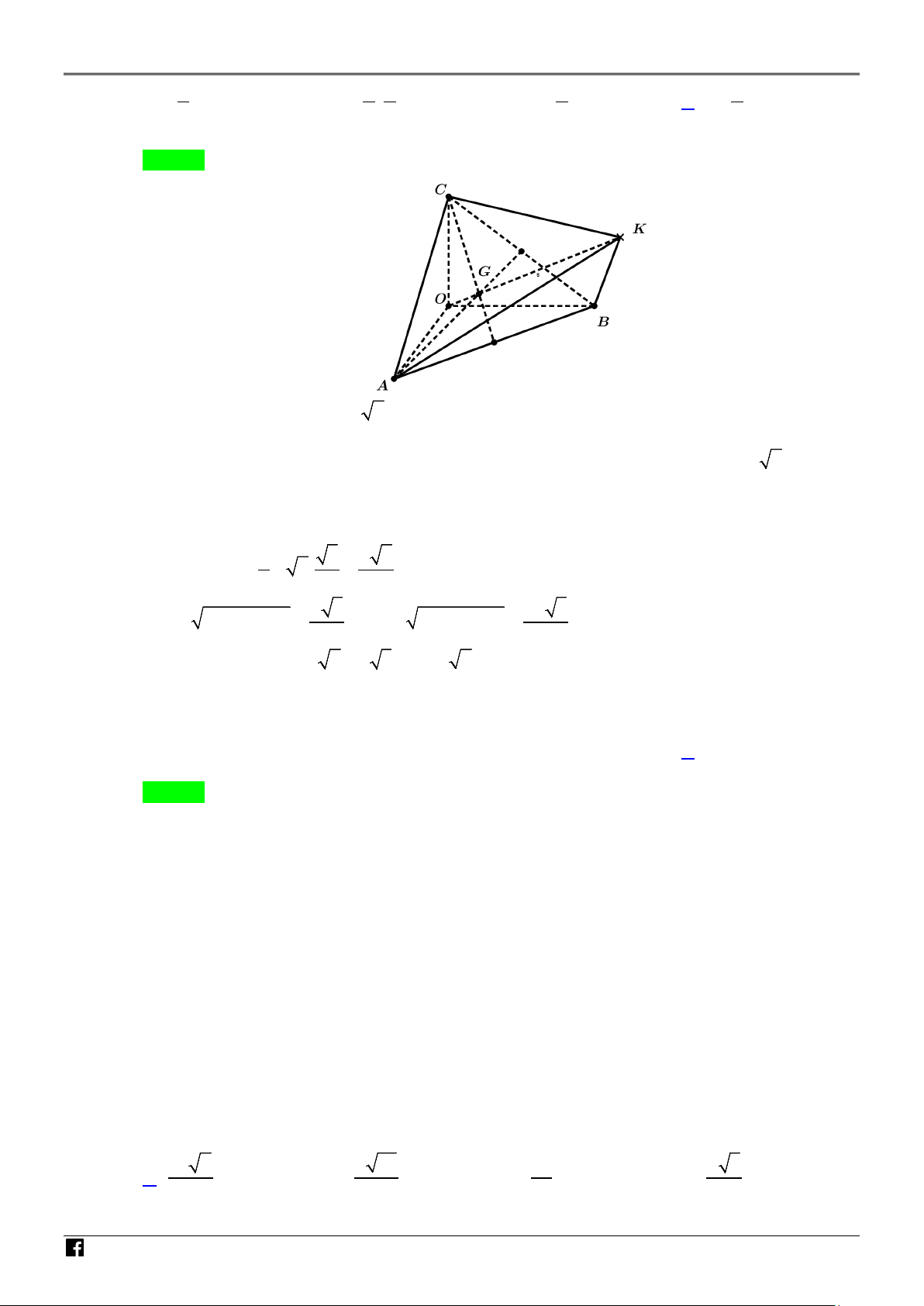
Câu 17. Trong không gian với hệ tọa độ Oxyz , cho tứ diện đều KABC có các điểm ,
A B,C lần lượt
thuộc các tia Ox,Oy,Oz sao cho OA = OB = OC = a . Biết điểm K có tọa độ là các số dương và
OK = 6. Giá trị a thuộc khoảng nào trong các khoảng sau đây?
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM - 24-25 A. 3 ;2 . B. 5 7 ; . C. 5 2; . D. 3 0; . 2 2 2 2 2 Lời giải Chọn D NH ÓM G
+) Ta có: AB = AC = BC = a 2 suy ra A ∆ BC đều. IÁ +) Hình chóp .
O ABC có OA = OB = OC = a , A ∆ BC đều nên .
O ABC là hình chóp đều. O V
+) Tứ diện KABC là tứ diện đều nên các cạnh của tứ diện đều KABC có độ dài a 2 . I ∆ Ê
+) Gọi G là trọng tâm của ABC suy ra OG, KG cùng vuông góc với (ABC) suy ra O,G, K N T thẳng hàng.
Mặt khác : OA < KA, điểm K có tọa độ là các số dương suy ra G nằm giữa K và O . OÁ a N V +) Ta có 2 3 6 CG = .a 2. = . 3 2 3 IỆ a a T N 2 2 3
OG = OC − OG = ; 2 2 2 3
KG = KC − CG = 3 3 AM
Do OK = OG + GK ⇔ 6 = a 3 ⇔ a = 2 .
Câu 18. Có bao nhiêu cặp số nguyên dương ( ; x y) thỏa mãn 10( 2 2
x + y − xy) 2
− log (x + y − ) 3 3
1 ≥ x + y − 4? 3 A. 25. B. 30. C. 40. D. 45. Lời giải Chọn D Ta có 10( 2 2
x + y − xy) 2
− log (x + y − ) 3 3
1 ≥ x + y − 4 3 NH ⇔ 10( 2 2
x + y − xy) −( 3 3 x + y ) 2
≥ log x + y −1 − 4 3 ( ) ÓM 2 2
⇔ (x + y − xy)[10 − (x + y)] ≥ log x + y −1 − 2 log x + y −1 + 2 3 ( ) 3 ( ) , (*) G
Do x, y là các số nguyên dương nên 2 2
x + y − xy > 0, log x + y −1 + 2 > 0 3 ( ) IÁO V
+) Nếu x + y >10 , VT (*) < 0, VP(*) > 0 suy ra (*) vô nghiệm I + ≤ ≥ ≤ Ê
+) Nếu x y 10 , VT (*) 0, VP(*) 0 suy ra (*) luôn đúng N T
Khi đó ta nhận được x + y ≤10 . OÁ Các cặp số dương ( ;
x y) thỏa mãn: (1;1);(1;2);...;(1;9);(2;1);(2;2);...(2;8);...;(9;1) . N V
Vậy có 9 + 8 + 7 +...+1 = 45 cặp thỏa mãn.
Câu 19. Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh .
a Hình chiếu của A′ lên mặt IỆ
phẳng (ABC) là trung điểm cạnh BC. Tính khoảng cách giữa hai đường thẳng B C ′ ′ và AA′ , T
biết góc giữa hai mặt phẳng ( ABB A
′ ′) và ( A′B C ′ ′) bằng 60°. A. 3a 7 . B. a 21 . C. 3a . D. a 3 . 14 14 4 4 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 14