Đề ôn tập Tính đơn điệu và cực trị của hàm số môn Toán 12
Đề ôn tập Tính đơn điệu và cực trị của hàm số môn Toán 12. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.
Chủ đề: Đề cương Toán 12 56 tài liệu
Môn: Toán 12 4.5 K tài liệu
Tác giả:
Preview text:
Ch¬ng 1. Hµm sè
D. 04 ĐỀ RÈN LUYỆN ĐƠN ĐIỆU & CỰC TRỊ ¶¶¶
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
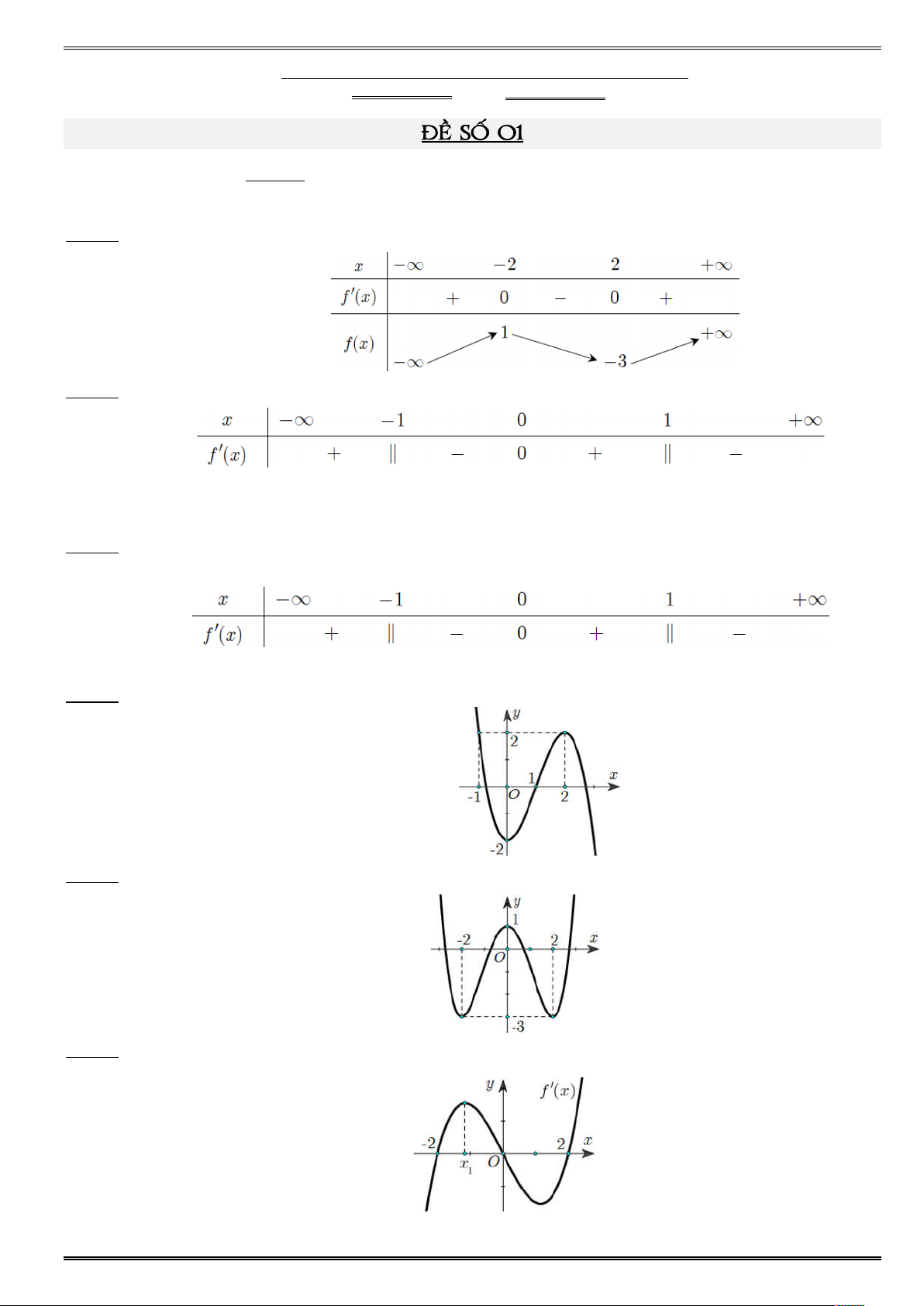
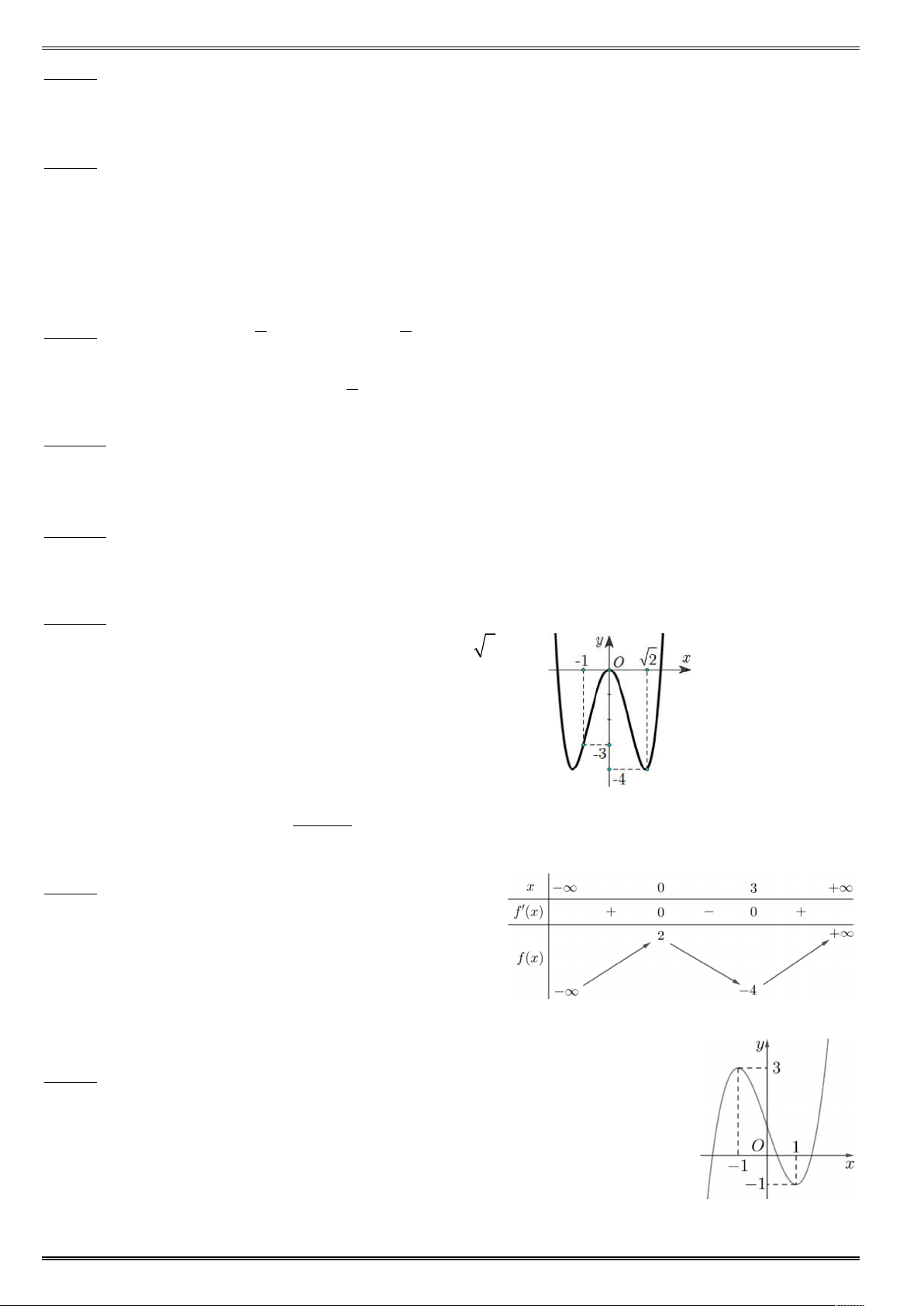
sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án) Câu 1. ố X có bả ến thiên bên dướ ố đã cho nghị ến trên khoả - - +¥ -¥ - Câu 2. ố = X xác đị ụ ¡ và có bả ấ ¢ X như ố điể ự ị ủa đồ ị ố = X Câu 3.
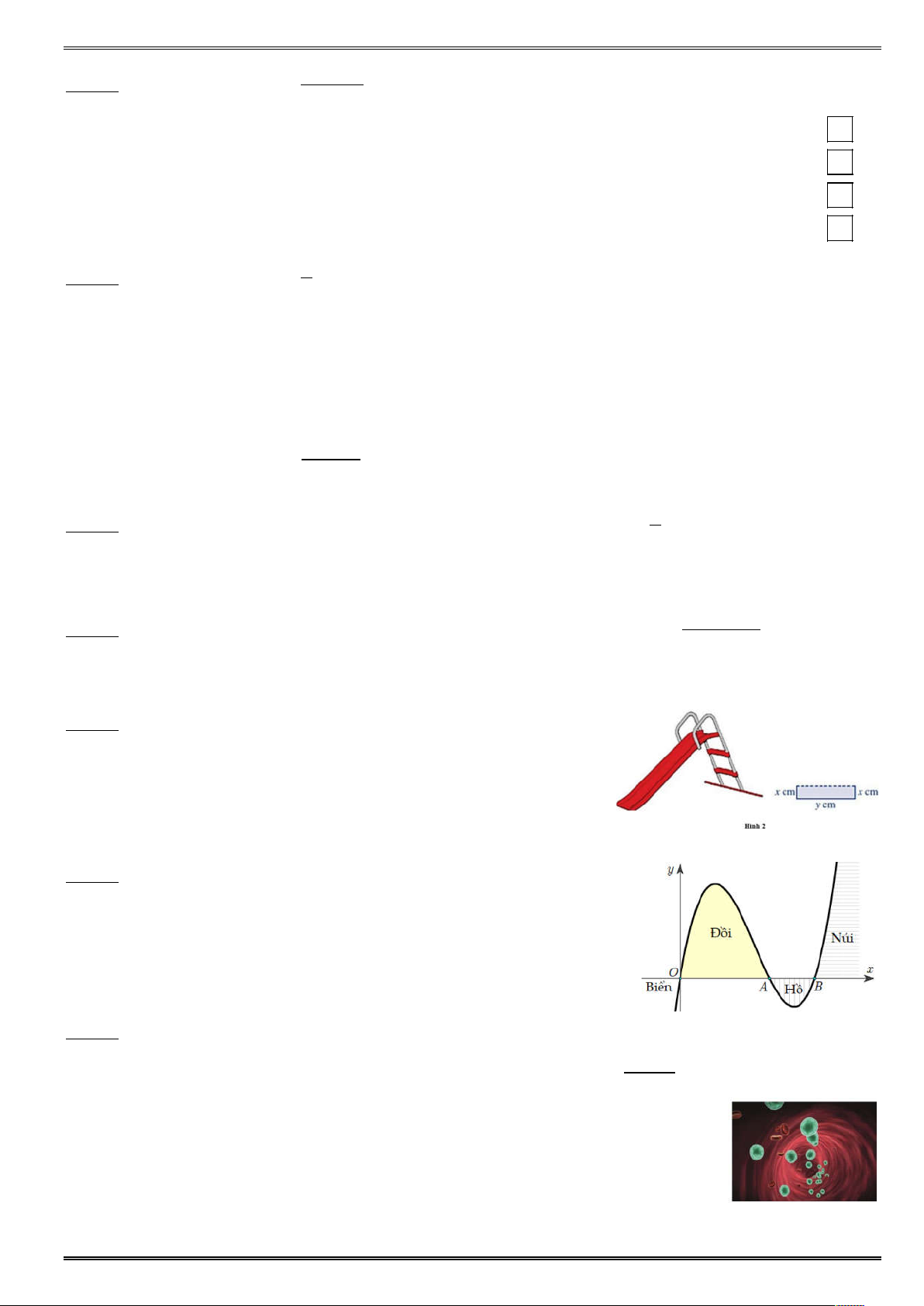
ố X xác định trên các khoả -¥ - - +¥ và có bả ấ ¢ X như sau: Câu 4. Cho đồ ị ố ậ
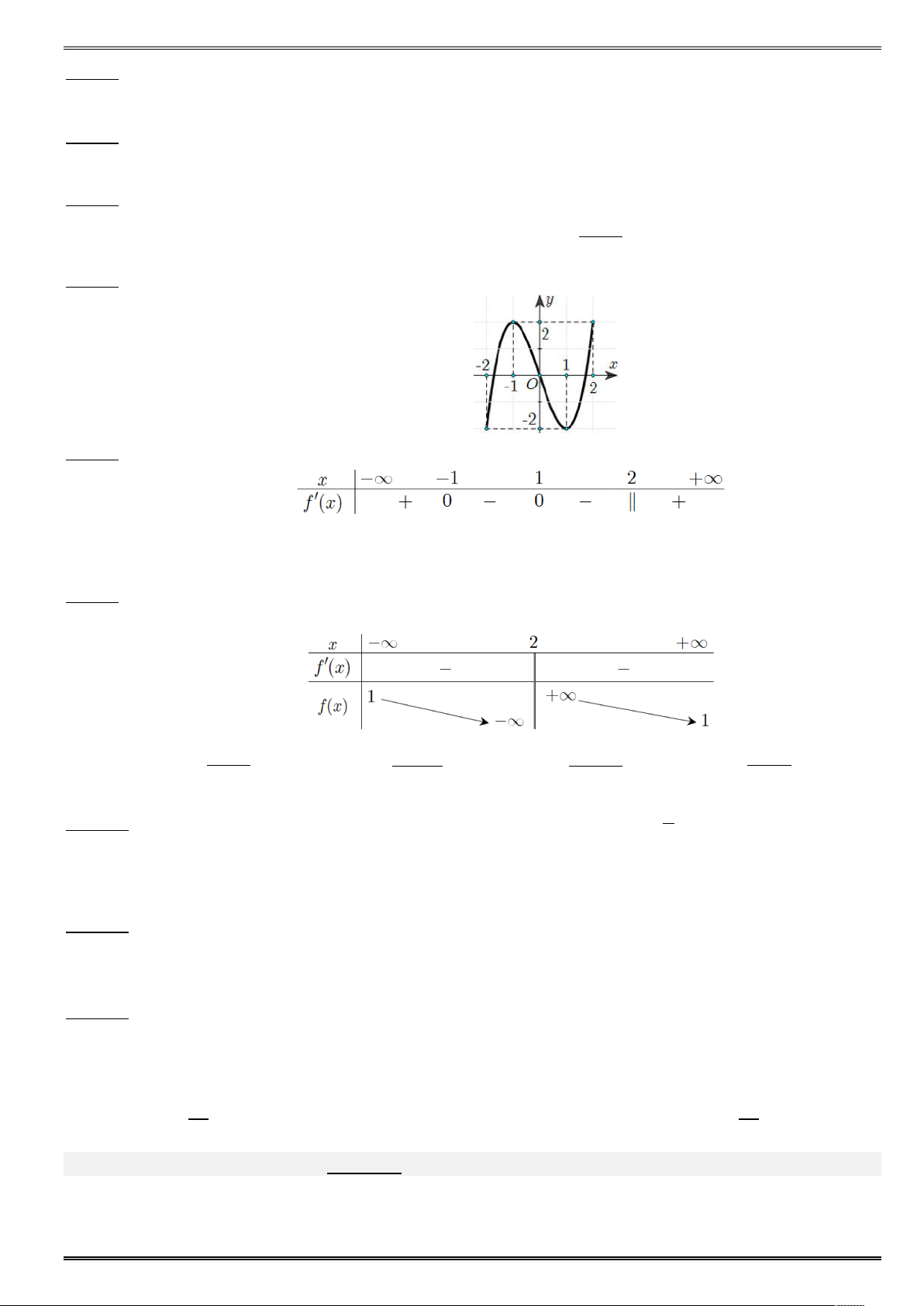
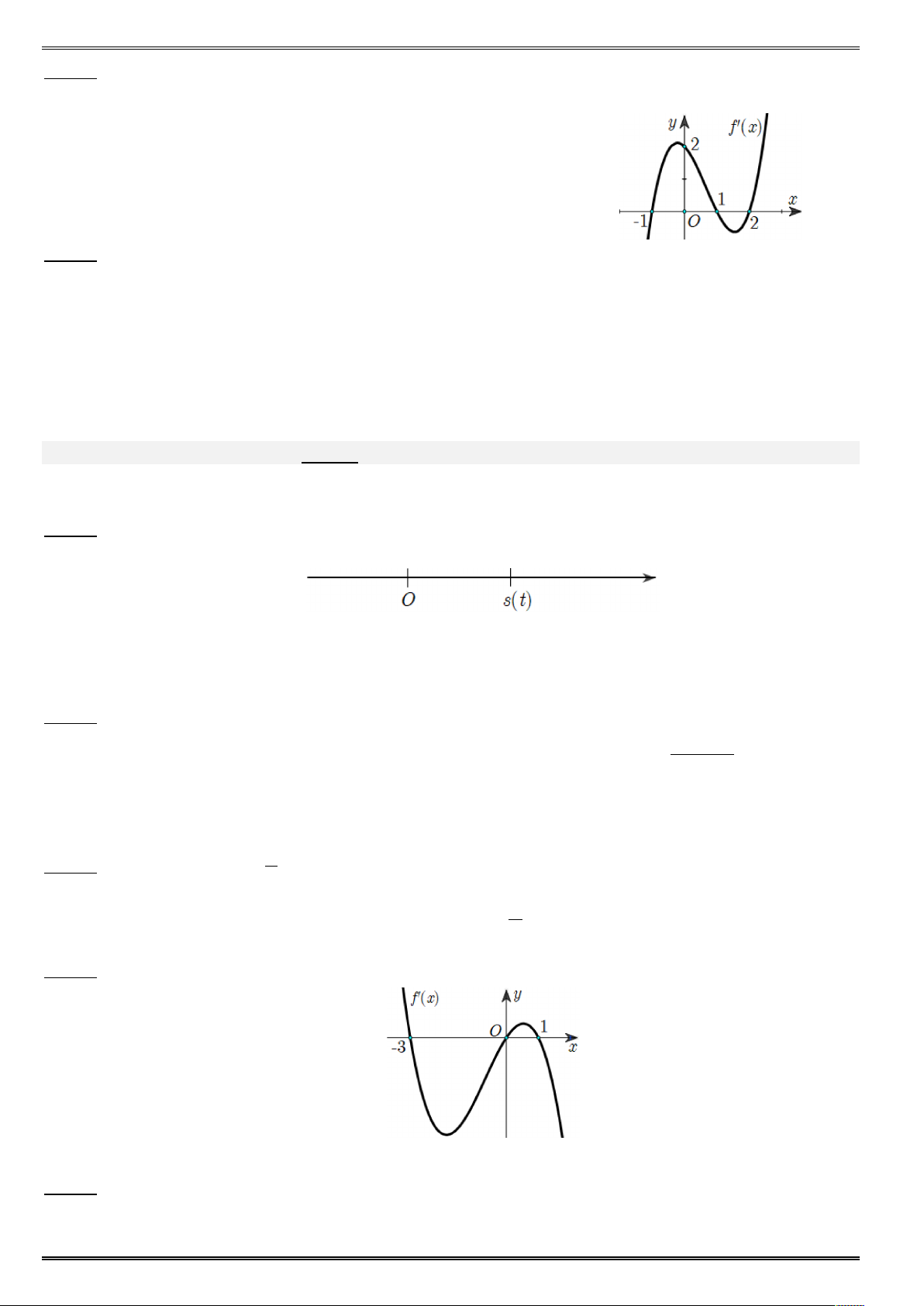
= X có đồ ị như hình vẽ bên dướ ố đã cho đồ ế
trên khoảng nào sau đây ? -¥ +¥ - Câu 5.
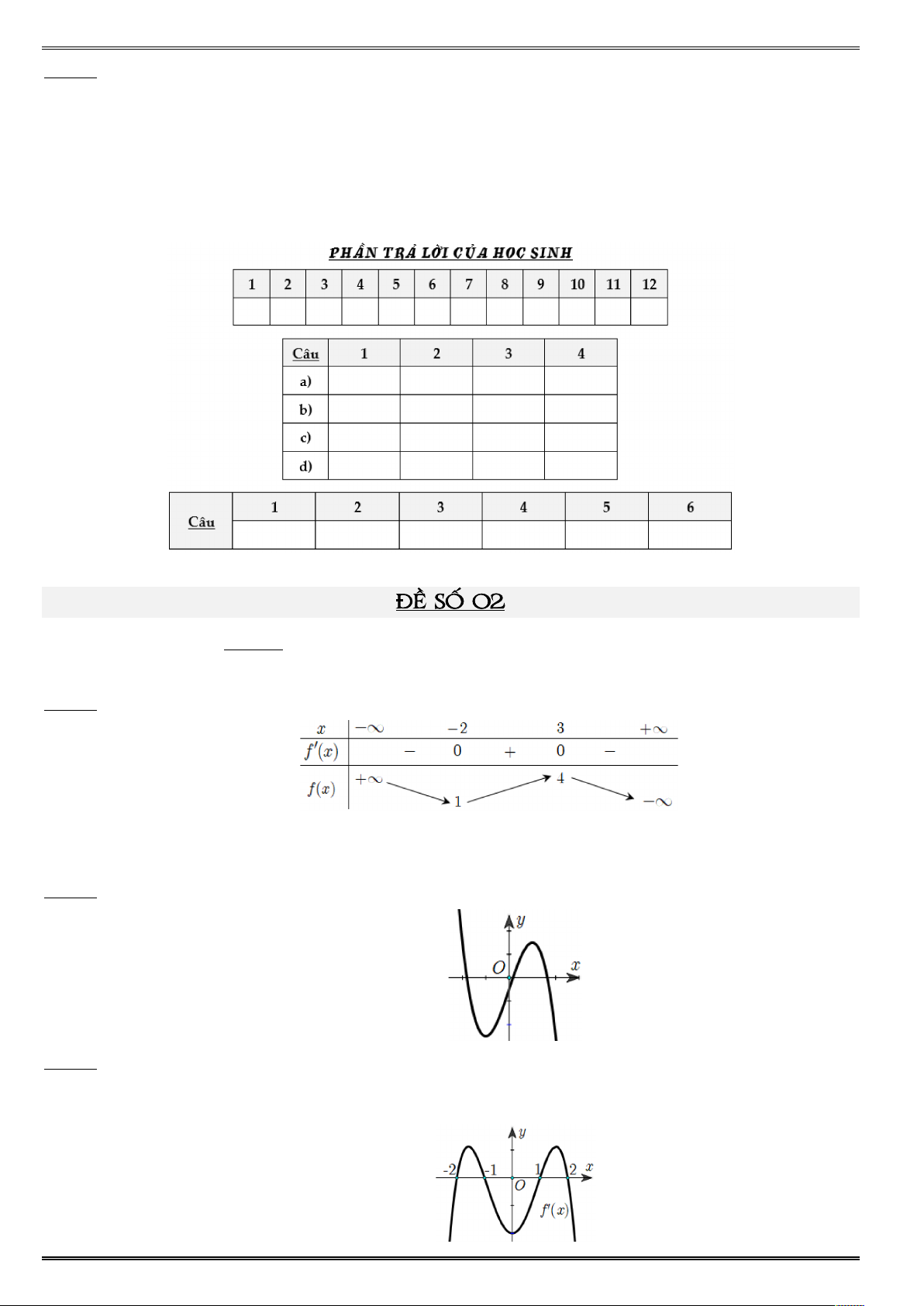
ố ậ ốn trùng phương = X có đồ ị là đường cong trong hình vẽ Điể ực đạ ủa đồ ị ố X = X = - Câu 6. ố X có đạ ¡ và đồ ị ố = ¢ X ¡ như hình vẽ ố
X đạ ực đạ ại điểm nào sau đây ? X = X X = X = - X =
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang Ch¬ng 1. Hµm sè Câu 7. ố = X ụ ¡ và có đạ ¢ X = X - X - X + X " Î ¡ ố X có bao nhiêu điể ự ể Câu 8. ố = X + X +
ệnh đề nào dưới đây là đúng ố đã cho đồ ến trên khoả -¥ +¥ ố đã cho nghị ến trên khoả -¥ +¥ ố đã cho nghị ến trên khoả -¥ và đồ ến trên khoả +¥ ố đã cho đồ ến trên khoả -¥ và nghị ến trên khoả +¥ Câu 9. ố = X - X + X + × ạ độ điể ực đạ ủa đồ ị ố æ ö - ç ÷ ç ÷ ç ÷ - çè ÷ø Câu 10.
ố = X xác định và liên tụ ¡ có ¢ X < X " Î ¡ Có tấ ả giá trị ủ X để X < X â ố Câu 11. ết đồ ị ố = X + X - X - có hai cự ị và
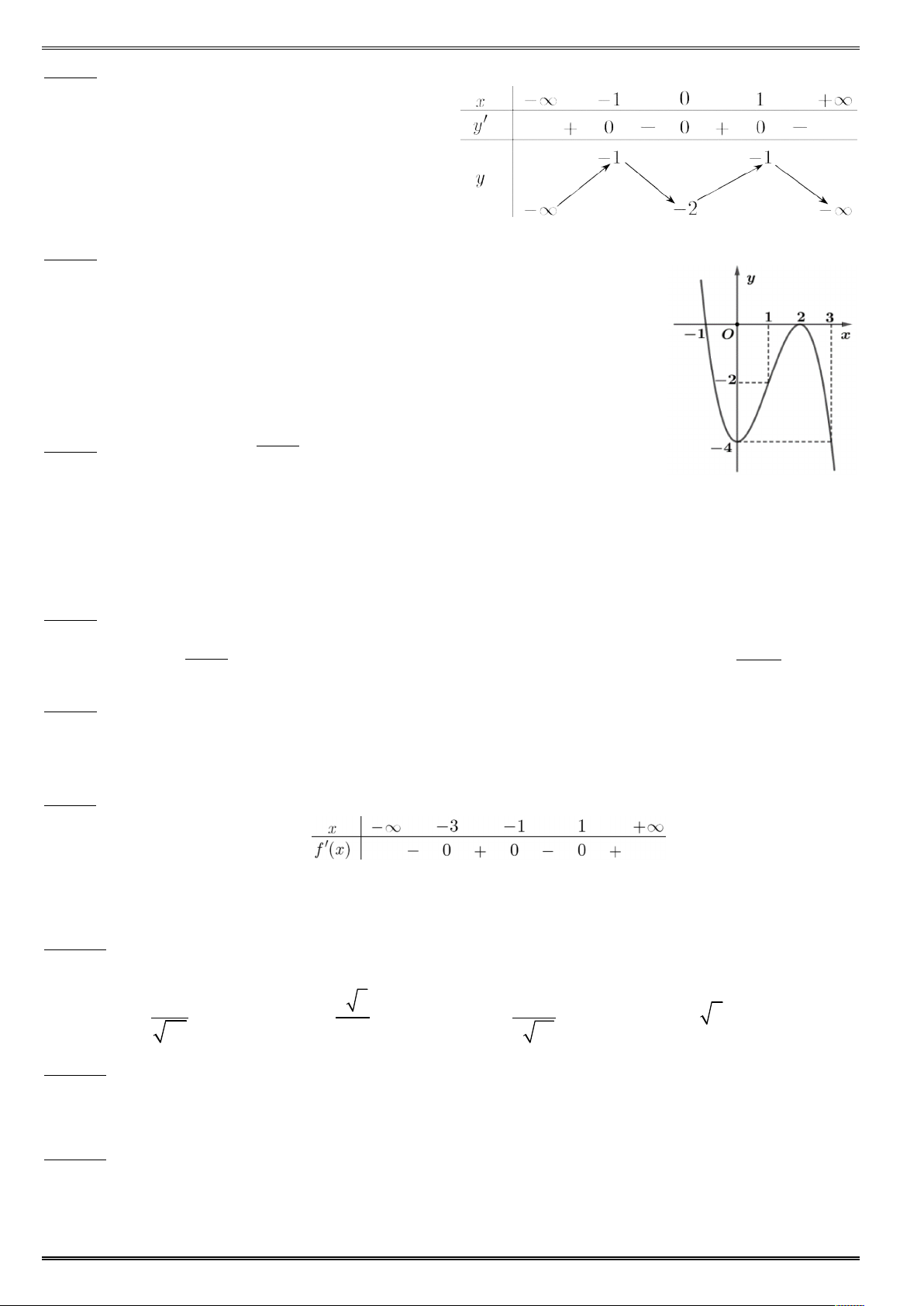
Điểm nào dưới đây thuộ đườ ẳ - - - - Câu 12. Đạ ¢ X ủ
ố X có đồ ị như hình vẽ bên dướ ố X = X + X + có bao nhiêu điể ự ị trong khoả -
Phần 2. Câu hỏi trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc chọn sai) Câu 1.
Cho hàm số = X có bảng biến thiên
ỗi khẳng định sau đây đúng hay sai ố X đồ ến trên khoả -¥ ố X ị ến trên khoả
ố X đạ ực đạ ạ điể X = Giá trị ự ể ủ ố = X = - Câu 2. ố ậ
= X có đồ ị như hình vẽ
ỗi khẳng định sau đây đúng hay sai ố = X đồ ến trên khoả -¥
ổng giá trị ực đại và giá trị ự ể ủ ố ố = X có hai cự ị trái dấ Phương trình đườ ẳng qua điể ự ị ủa đồ ị ố = X D = - X
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 56 Ch¬ng 1. Hµm sè Câu 3. ố X + X X = × X - ố X đồ ến trên khoả -¥ ực đạ ủ ố X ố X có đúng ba điể ự ị Đườ ẳ ối hai điể ự ị ủa đồ ị ố đã cho là D = X - Câu 4.
ố X = X + M + X + M + M X - vớ M ố ớ ọ M
ố đã cho luôn có hai điể ự ị ố đã cho â ị ế trên khoảng có độ ằ â ồ ại giá trị ủ ố M để ố đã cho đồ ế ¡ ố đã cho ị ế khoả - khi và chỉ khi M ³ -
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
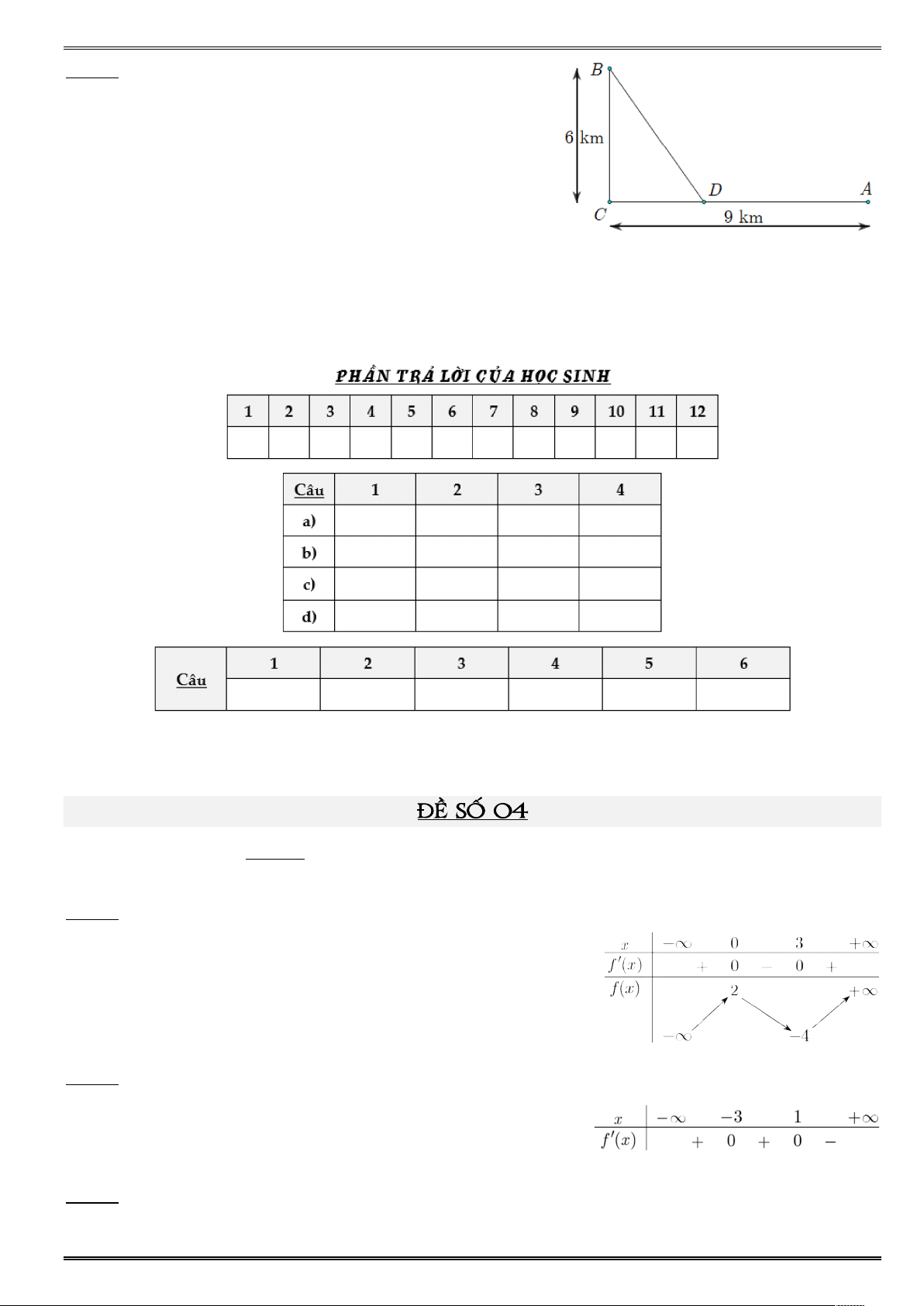
sinh trả lời từ câu 1 đến câu 6) Câu 1. ộ ển độ ẳng được xác đị ởi phươ T = T - T + T + vớ T > T ằng giây và ằng mét. Trong khoả ờ giây đầ vậ ố ủ vật tăng Câu 2. ự tăng trưở ủ ộ
ại virút được xác đị ở ố T = trong đó T - T + ời gian đượ Ở ứ ốc độ tăng trưở ủa loài virú ớ ấ Câu 3. Máng trượ ủ ộ ầu trượ ẻ em (hình a) đượ ố
ừ ộ ấm kim loại có bề ộ C ặ ắt đượ â ả ở ết kế khuyến cáo, diệ ặ ắ ớn thì càng đả ả ẻ ệ ủ
ặ ắt tăng dần, thì khoảng tăng này chứ ố X Câu 4. Lát ắ ủ
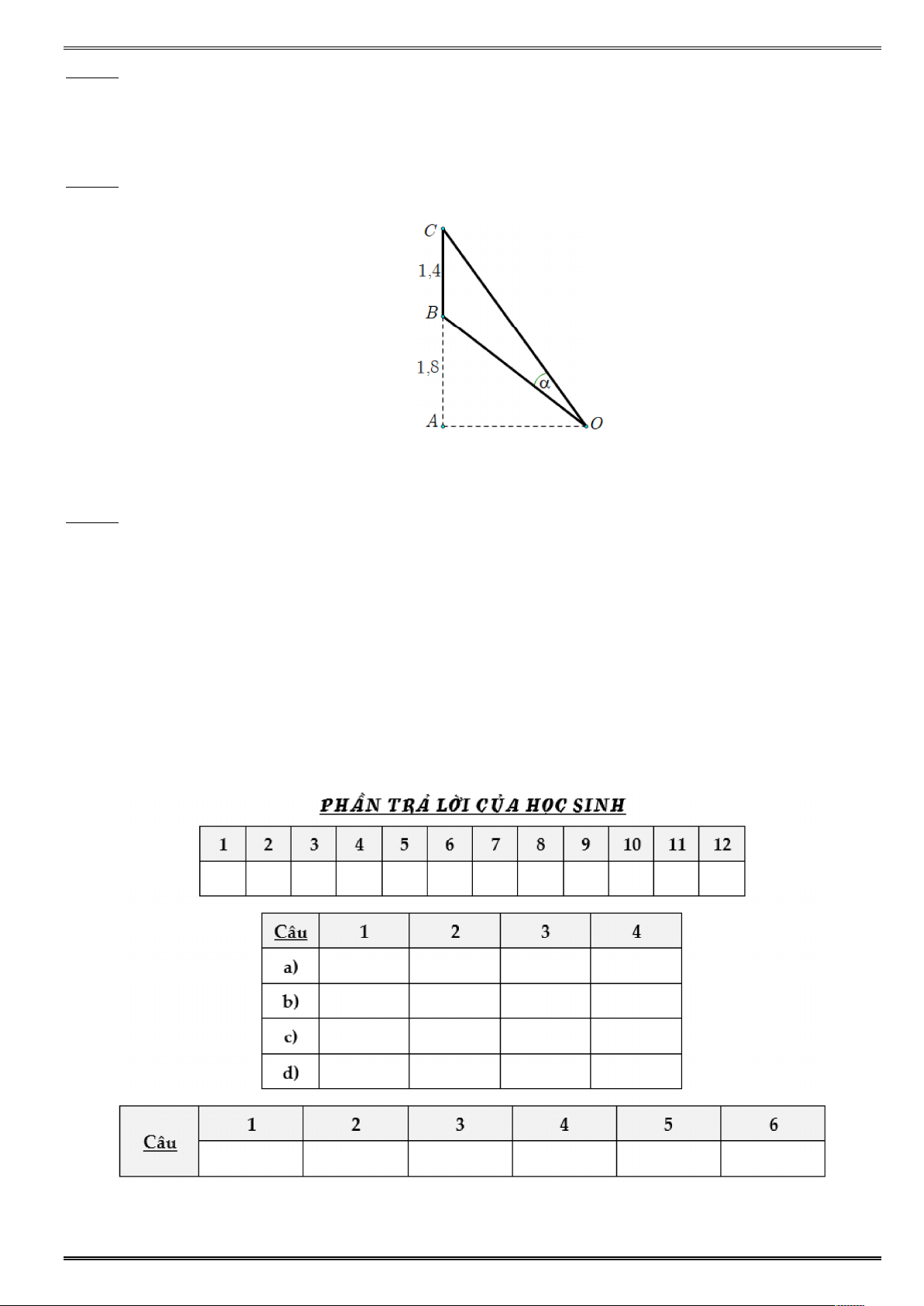
ột vùng đất quen biểu được mô hình hóa ộ ố ậ
= X có độ ị như hình vẽ (đơn
vị độ dài trên các trụ
ết khoảng cách hai bên chân đồ = độ ộ ủ ồ = và độ ủ ồ Tìm độ ủa đồ ằ ại điể
ấ (làm tròn đến hàng đơn vị) ? Câu 5. ạ
ốc A được tiêm vào bệ ồng độ l ủ ốc trong máu sau X ể ừ ắt đầ được xác đị ở â ứ X X = × Để X + đưa ra nhữ ời khuyên và cách xử ù ợ ệ ầ khoả ờ ồng độ ủ
ốc trong máu đang tăng. Em hãy ế ồng độ ốc trong máu
X đạt giá trị cực đại là bao nhiêu trong khoảng thời
phút sau khi tiêm (kết quả làm tròn đến hàng phần mười) ?
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 57 Ch¬ng 1. Hµm sè Câu 6.
ộ ửa hàng trung bình bán được 100 cái Tivi mỗi tháng với giá 14 triệu đồ ột cái. Chủ ử ậ ấ ế
ảm giá mỗi cái 500 ngàn đồ
ố lượng tivi bá ẽ tăng thêm 10
cái mỗi tháng. Hỏ ửa hàng nên bán với giá bao nhiêu để ử ớ ấ (đơn vị
ệu đồng, làm tròn đến một chữ ố ập phân sau đấu phẩy). Ế
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
(Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án) Câu 1. ố = X có bả ến thiên như sau: ố đã cho đồ
ến trên khoảng nào dưới đây ? - +¥ - +¥ -¥ - Câu 2.
ố = AX +BX +CX +D A B C D Î ¡ có đồ ị như hình vẽ ố điể ự ị ủ ố Câu 3.
ố X xác định và liên tụ ¡ ết đồ ị ủa đạ = ¢ X ỉ ắ ụ
ạ ốn điểm có hoành độ ần lượ
X = ± và X = ± như hình vẽ bên dưới. Khi đó ố = X đồ
ến trên khoảng nào sau đây ? -¥ - - -
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang Ch¬ng 1. Hµm sè Câu 4. Điể ực đạ ủa đồ ị ố = X - + X + - - - Câu 5. ố X có ¢ X = X X - X " Î ¡ ố X ị ến trên khoả +¥ -¥ +¥ Câu 6. ố nào dưới đây đồ ế ¡ - = X - X = X - X X = × = X + X X + Câu 7.
ố = X xác định trên đoạ ;-
và có đồ ị như hình vẽ bên dướ ố
X đạ ực đạ ại điểm nào dưới đây ? X = - X = - X = X = Câu 8. ố X có đạ ụ ¡ và dấ ủa đạ ở ả Giá trị ự ể ủ ố X ằ - â ồ ạ Câu 9. ế ằ ả ế ả ế ủ ộ
ố trong các hàm số đượ ệt kê
ở các phương án A, B, C, D dưới đây. ỏ ố đó là hàm số X + X - = × X - X + = × = × = × X - X + X + X - Câu 10. ậ
ợ ấ ả các giá trị ủ ố ự M để ố = X + MX + X - M đồ ến trên khoả -¥ +¥ -¥ - ; +¥ ;- -¥ Câu 11. ố = X
- - X + X - có giá trị ực đại và giá trị ự ể ần lượ M Khi đó kết quả đây đúng - M = - M = + M = - + M = Câu 12. ố ậ X = AX + A - X + CX + D A ¹ có đồ ị ọ ¢ là đồ ị ủ ố = ¢ X ế ằ và ¢ ắ
ại ba điểm có hoành độ X = X = và X = ổng các giá trị ự ị ủ ố X ằ - × - ×
ẦN 2. Câu trắc nghiệm đúng sai
ọc sinh trả lờ ừ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chỉ chọn đúng hoặc sai)
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang Ch¬ng 1. Hµm sè Câu 1. ố ậ
= X có đồ ị là đường cong trong hình dưới đây: ố = X ị ến trên các khoả -¥ - và +¥ b) Đồ ị ố = X có điể ự ể - -
ọ X và X ần lượt là hoành độ ủa điể ự ểu và điể ực đạ ủ
ố đã cho, khi đó ta luôn có có X + X = d) Phương trình đườ ẳng đi qua hai điể ự ị ủa đồ ị ố D X - + = Câu 2. ố = X ụ ¡ và có đạ ¢ X = X X + X - "X Î ¡ ố = X đạ ự ị ạ các điể X = - X = X = ố = X ị ế khoả - ố = X đồ ế -¥ - È ; +¥ æ ö ố = X ị ế khoả ç ÷ - ç ÷ ç ÷ çè ÷ø Câu 3. ố X có bả ế Giá trị ực đạ ủ ố X ằ ố X đồ ến trên khoả - > - Đồ ị ố X có ba điể ự
ị là ba đỉnh tam giác có diệ ằ Câu 4. ố = X có bả ến thiên như sau ố = X đồ ến trên các khoả và +¥ ố đồ ến trên khoả +¥ Đườ ẳ qua hai điể ự ị ủa đồ ị
ố với hoành độ không âm là X + = Ba điể ự ị ủa đồ ị ố ạ ột tam giác có ệ ằ
ẦN 3. Câu trắc nghiệm trả ời ngắn ả ờ ừ câu 1 đế Câu 1.
ột vật rơi tự do với phương ển độ S T = T trong đó = T ờ ằ S
ằng mét. Tính vậ ố ủa vậ ạ ời điể T = S Câu 2. Sau khi phát hiệ ệ
ịch, các chuyên gia y tế ướ ố ngườ ễ ệnh kể ừ ấ ệ ệnh nhân đầu tiên đế ứ T T = T -T ế ¢ T ốc độ ề ệnh (ngườ ạ ời điể T ỏi đế ứ ốc độ ề ệ (ngườ Câu 3. ộ ển động theo quy luậ S = T - + T + T + vớ T giây là khoả ờ ừ khi vậ ắt đầ
ển động và S (mét) là quãng đường vậ ển được trong khoả
ờ gian đó. Tính quãng đường vật đi đượ ắt đầ ừ lúc vậ ển độ ớ ời điểm vậ đạt được vậ ố ớ ấ
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 60 Ch¬ng 1. Hµm sè Câu 4. ộ ệ ả ất hàng hóa. Biế ổ ả ấ X đơn vị ả ẩ X = X - X + X + n đồ ổ
ố ền thu được khi bán X đơn vị ả ẩm đó là X = X - X (nghìn đồ ối ưu củ ệp đó.
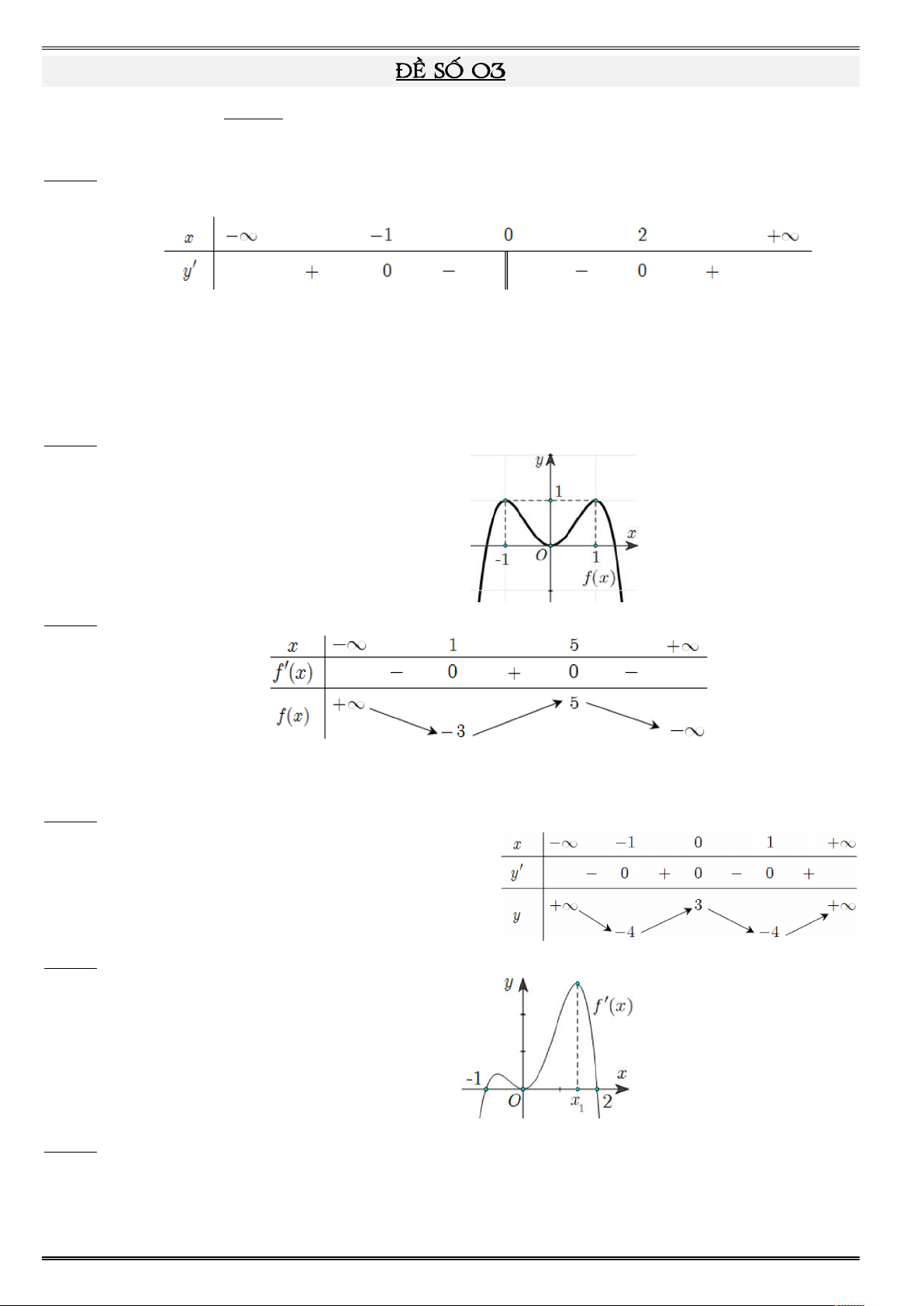
(đơn vị doanh thu tối ưu tính bằng triệu đồng). Câu 5. ộ ả ữ ậ được đặ ở độ so vớ ầ ắ ừ đầ
dướ ủa màn hình như hình vẽ Để ấ
ải xác định vị trí đứ sao cho góc nhìn lớ ất. Hãy xác định độ để ấ · ọi là góc nhìn). Câu 6.
Có tấ ả bao nhiêu giá trị ủ ố ự M để ứng vớ ỗi giá trị ủ M
ố X = MX + M - X + MX + không có điể ự ể Ế
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 61 Ch¬ng 1. Hµm sè
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
(Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án) Câu 1. ố = X có tập xác đị D = ¡ [ ] và có bả ấu đạ ¢ = ¢ X bên dướ
ệnh đề nào sau đây đúng ố đã cho đồ ến trên khoả - - ố đã cho đồ ến trên khoả ố đã cho nghị ến trên khoả - ố đã cho đồ ến trên khoả Câu 2.
ố = AX +BX + C có đồ ị như hình bên dướ ố đã cho nghị ế
trên khoảng nào dưới đây ? +¥ - -¥ - Câu 3. ố = X có bả ến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng - - Câu 4. ố = X có bả ến thiên bên dướ
ệnh đề nào sau đây đúng
ố đạt đã cho cực đạ ại điể X = ố đã cho có điể ực đạ ố đã cho có điể ự ị
ố đã cho đạ ự ể ại điể X = Câu 5. ố X có đạ ¡ và đồ ị ố = ¢ X ¡ như hình vẽ ố
X đạ ực đạ ại điểm nào sau đây ? X = X X = - X = X = Câu 6.
ố X xác định và có ¢ X = X X + X - "X Î ¡ ố điể ự ể ủ ố đã cho là
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 62 Ch¬ng 1. Hµm sè Câu 7. Đồ ị
ố = ¢ X có đồ ị như hình vẽ dưới đây. Hàm số = X + X + có bao nhiêu điể ự ị trong khoả - Câu 8. ố X = X +AX +BX - có bả
ến thiên bên dưới. Khi đó A + B ằ Câu 9.
ố X = AX +BX +C có đồ ị như hình vẽ bên dướ ố điể ự ị ủ ố = X Câu 10. ảng cách giữa hai điể ự ị ủa đồ ị ố X - X + = ằ X + Câu 11. ọ là ba điể ự ị ủa đồ ị ố = X - X + D ệ D ằ Câu 12. ố = MX + M + X - M + X + Có bao nhiêu giá trị ủ ố M để ố đồ ến trên khoả +¥
ần 2. Câu trắc nghiệm đúng sai
ọc sinh trả lờ ừ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chỉ chọn đúng hoặc sai) Câu 1. ố X = X - X ố X luôn đồ ế ¡ ố X ị ến trên khoả -
ố X đạ ự ể ại điể X = - Đồ ị ố X có hai cự ị và Điể - ộc đườ ẳ Câu 2. ố = X xác đị ¡ và có bả ến thiên như sau: ố X đồ ến trên khoả - ố X ị ến trên khoả +¥ "X X Î +¥ X < X Þ X < X "X X Î -¥ +¥ X = X Þ X = X
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 63 Ch¬ng 1. Hµm sè Câu 3. ố = X xác đị ¡ và có đạ ¢ X Đồ ị ủ ố ¢ X như hình vẽ bên dướ ố = X đồ ến trên khoả -¥ ố = X đồ ến trên khoả - ố = X có đúng điể ự ị ố X = - X có đúng điể ự ị Câu 4. ố X = X X " Î +¥ ố đã cho luôn đồ ế
ững khoảng mà nó xác đị
ố X = X - X có tập xác đị D = -¥ È +¥
ố X = X - X có đúng ột điể ự ị Có
giá trị nguyên dương củ ố M để ố X = X - MX luôn đồ ế trên khoả +¥
ần 3. Câu trắc nghiệm trả ời ngắn ả ờ ừ câu 1 đế Câu 1. ộ ất điể ển độ ộ ụ ố ằ
ều dương từ trái sang phải như hình vẽ ả ử vị S T ủa chât điể ụ ố đã chọ ạ ời điể T (giây) đượ ở â ứ S T = T - T + T T ³ ất điể ển độ ải trong khoả ờ ộ ậ ợ A B khi đó tậ ợ ứ ố Câu 2. ả ử ố ẳ ố ả ẩ ủ ộ ả ẩ
ới (trong vòng mộ ố năm nhấ
định) tuân theo quy luật logistic được mô hình hóa bằ ố T = T ³ T - + đó thờ T đượ
ằng năm, kể ừ khi phát hành sả ẩ ới. Khi đó, đạ ¢ T ẽ ể ị ốc độ bán hàng.
khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớ ấ Câu 3. ố X = X - X + - M X + Có bao nhiêu giá trị ủ ố M ộ æ ö để ố = C X ị ế p ç ÷ ç ÷ ç ÷ çè ÷ø Câu 4.
hàm số X = AX +BX + CX A B C Î ¡ Hàm số = ¢ X có đồ thị như hình vẽ
ố điểm cực trị của hàm số X = X + Câu 5. ộ ộ ữ lít có dạ ộ ữ
ật với đáy là hình vuông cạ ằ X C và chiề C
Tìm giá trị ủ X để ệ ầ ủ ộ ỏ ấ
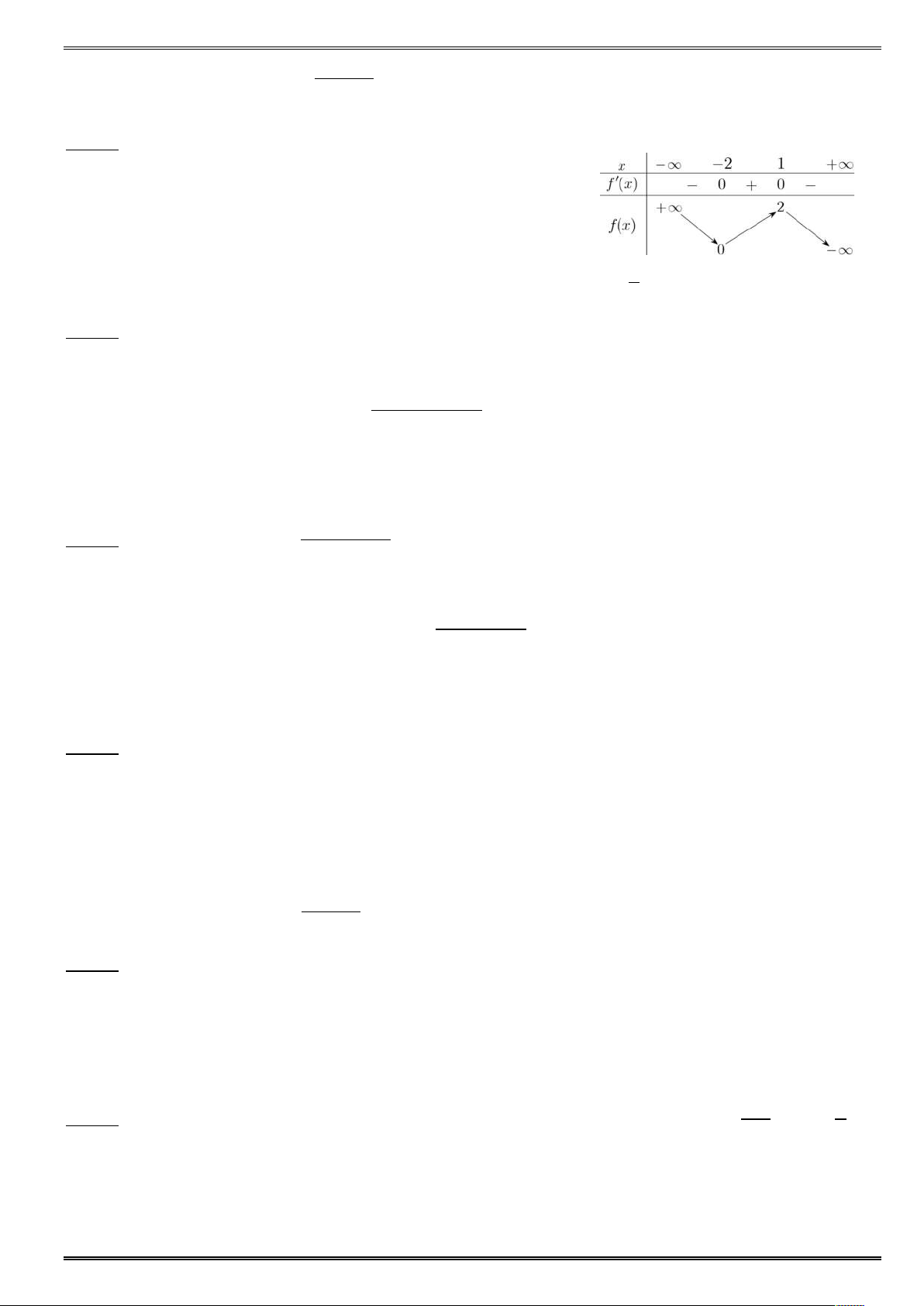
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 64 Ch¬ng 1. Hµm sè Câu 6. ộ â ố ự ệ ống dây cáp từ ạ ở ờ ển đế ột vị ộ
đảo. Hòn đảo cách bờ ể ọ là điể ờ vuông góc vớ ờ ể ảng cách ừ đế Giá để ắp đặ ỗi km ệ ố ờ
ệu đồng và dưới nướ ệ đồng. Ngườ ần xác đị ột vị
để ắp đặ ệ ống dây theo đườ ấp khúc ố ề ấ
ất. Khi đó chi phí lắp đặ ấ ấ ệu đồ Ế
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
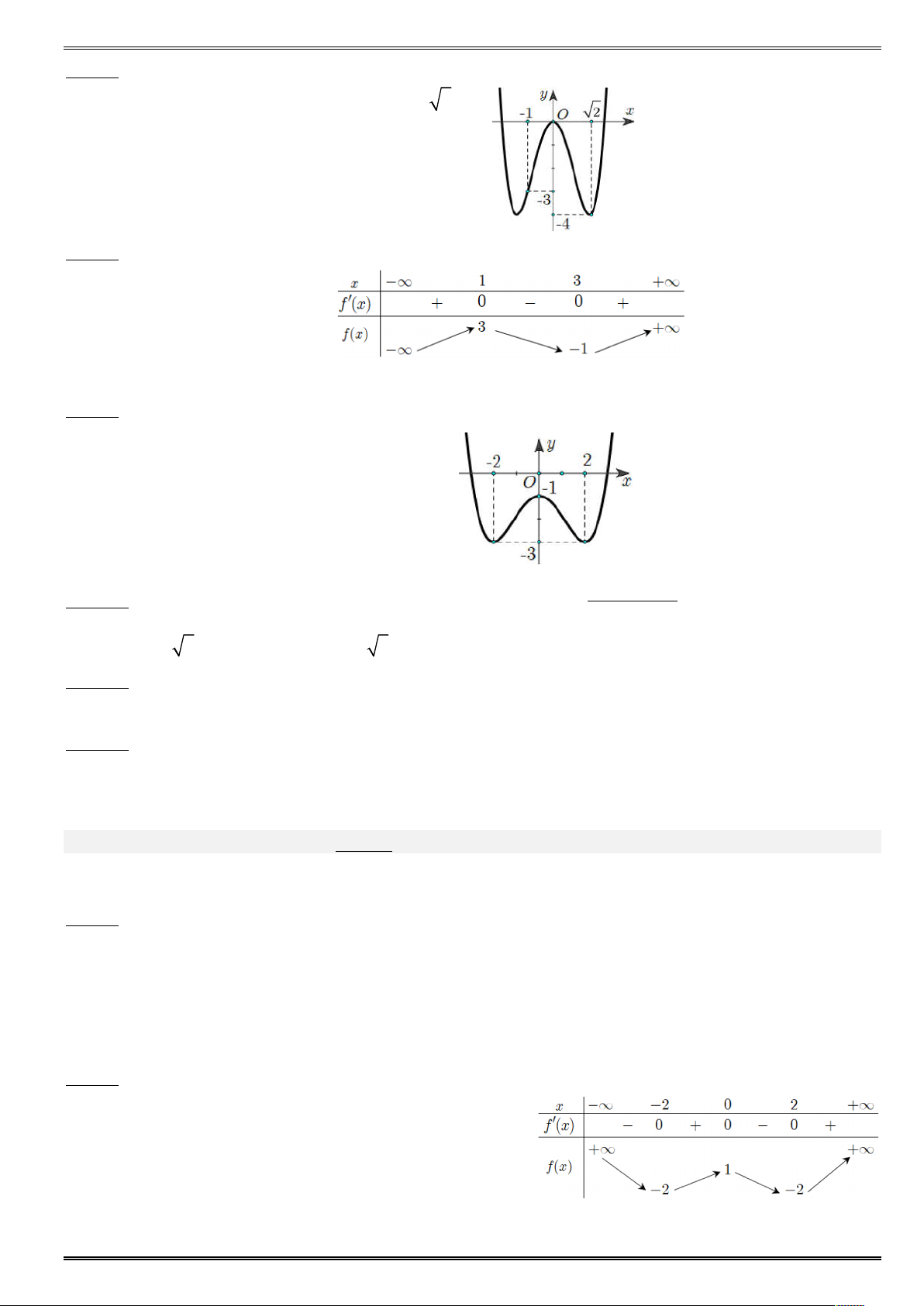
(Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án) Câu 1. ố = X có bả
ến thiên bên dưới. Đồ ị ố X có điể ự ể - X = 4 = - 4 Câu 2. ố X có bả ấ ủa đạ bên dướ ố đã cho nghị ế khoảng nào dưới đây +¥ -¥ - - +¥ - Câu 3.
Cho hàm số = X có ¢ X = X + X -
"X Î ¡ Điểm cực tiểu hàm số đã cho là X = X = X = - X = -
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 65 Ch¬ng 1. Hµm sè Câu 4.
Cho hàm số = X có bảng biến thiên bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây ? +¥ -¥ - Câu 5.
ố X = AX +BX +CX +D có đồ ị như hình vẽ dưới đây. Hàm số = X + đồ ến trên khoả +¥ -¥ - - Câu 6. ố X - =
ệnh đề nào dưới đây đúng X + ố đã cho ị ến trên khoả -¥ +¥ ố đã cho ị ến trên khoả - +¥ ố đã cho ị ến trên khoả -¥ - ố đã cho đồ ến trên khoả -¥ - Câu 7.
Hàm số nào dưới đây đồng biến trên khoảng -¥ +¥ X - = × + = X + X = X - - X X = × X - X + Câu 8.
Cho hàm số = X có ¢ X = X + X - - X
"X Î ¡ Mệnh đề nào đúng > > - > > - < - < - < < Câu 9.
Cho hàm số X bảng xét dấu của ¢ X như sau: Hàm số =
- X đồng biến trên khoảng nào dưới đây ? -¥ - Câu 10. Đồ ị
ố = X - X - X + có hai điể ự ị và Khi đó, khoảng cách từ ố ọa độ đến đườ ẳ × × ×
Câu 11. Có bao nhiêu giá trị ủ ố M để
ố = X - X + M - X có đúng ba điể ự ị
Câu 12. Có bao nhiêu giá trị ủ ố ự M Î ;- để ứng vớ ỗi giá trị M ố = X + MX - M X ị ến trên khoả
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 66 Ch¬ng 1. Hµm sè
Phần 2. Câu hỏi trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc chọn sai) Câu 1. ố X = AX +BX +CX +D A ¹ có bả ế bên dướ ố X đồ ến trên khoả ố X ị ến trên khoả +¥ ố X đồ ến trên khoả - æ ö ố X = X - ị ế khoả ç ÷ -¥ ç - ÷× ç ÷ çè ÷ø Câu 2. ố = X = X + X ập xác đị ủ ố D = -¥ - È +¥ ố đạ X + ¢ X = × X + X ố = X ị ế khoả +¥ ố X = đồ ế ¡ Câu 3. ố X - X + X = × X + ố X có tập xác đị ¡ ố + - X có đạ X X ¢ X = × X +
ố X có giá trị ực đạ ằ ố X = X - có đúng điể ự ị Câu 4. ố X X X X - - - = ập xác đị ủ ố D = ¡ X X X X X X - - - ¢ = - -
ố = X đạ ực đạ ạ điể X = ố X = đạ ự ể ạ điể X =
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
sinh trả lời từ câu 1 đến câu 6) Câu 1. ể ủ nướ ở ệt độ ° £ £
° đượ mô hình hóa ở â ứ = - + -
(Theo: J Stewart, Calculus, Seventh ọ A° B° là khoả ệt độ mà trong khoả đó khi nhiệt độ tăng ể ủ
nước cũng tăng Tính giá trị ể ứ = B - A
A B làm tròn đến hàng đơn vị) æ ö Câu 2.
ể tích nướ ủ ể bơi sau T phút bơm đượ â ứ T ç = ç T - T ÷÷ ç ÷ çè ÷ø vớ £ T £
Lưu lượng nướ ủa máy bơm tạ
ời điể T được xác đị ở V T = ¢ T ọ A B là khoả ờ mà lưu lượ
ủa máy bơm tăng. Hỏi trong khoả A B ứ ố
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 67 Ch¬ng 1. Hµm sè Câu 3. Sau khi phát hiệ ộ ệ
ịch, các chuyên gia y tế ướ ố ngườ ễ ệnh kể ừ ấ
ệ ệnh nhân đầu tiên đế ứ T T = T -T T Î [ ] ế T
ố xác định trên đoạ ; thì đạ ¢ T đượ ốc độ ề ệnh (ngườ ạ ời điể T ả ờ ốc độ ề ệ ả A B khi đó giá trị A - B Câu 4.
ộ ợp tác xã nuôi cá thí nghiệ ồ. Ngườ ấ ằ ế ỗi đơn vị ệ ủ ặ
ồ có N con cá thì trung bình mỗi con cá sau một vụ ặ N N N * = - Î ¥ ố cá nhiề
ất có thể ả vào hồ để ặ ủa vụ tăng Câu 5. ộ ộ cá nhân ỗ ả ất đượ X đôi giày £ X £ ổ ả ấ X đôi giày ìn đồ ở X = X - X - X - ả ộ cá này bán hế ả ẩ ỗi ngày với giá nghìn đồng/đôi ọ X ố ền bán được và X ợ
ận thu được khi bán X đôi giày. Hãy tính lợ ậ ối đa củ ộ cá ộ
(đơn vị ệu đồng, làm tròn đến một chữ ố ập phân sau dấu phẩy). Câu 6. ố X có đạ ¢ X = X - X - "X Î ¡ ế ố X = X - X có các khoảng đồ ế -¥ A và B C A + B + C
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn 0933.755.607 Trang 68
Tài liệu liên quan:
-
Tổng hợp bài toán thực tế ôn tập kì thi tốt nghiệp THPT năm 2025 môn Toán 12
14 7 -
Đề cương cuối kì 1 Toán 12 năm 2025 – 2026 trường THPT Bắc Thăng Long – Hà Nội
27 14 -
Đề cương cuối kỳ 1 Toán 12 năm 2025 – 2026 trường THPT Thanh Khê – Đà Nẵng
23 12 -
Đề cương cuối học kỳ 1 Toán 12 năm 2025 – 2026 trường THPT Sơn Động 3 – Bắc Ninh
26 13