Đề ôn tập toán TNTHPTQG năm 2024 - 2025

Đỗ Văn Đức – Đề tạm biệt 2K7 số 02 môn Toán Trang 1 KHÓA HỌC TENS
ĐỀ TẠM BIỆT 2K7 SỐ 02 | MÔN TOÁN
THẦY ĐỖ VĂN ĐỨC
THẦY ĐỖ VĂN ĐỨC Mã đề thi: 002 NĂM HỌC 2024-2025
Thời gian làm bài 90 phút, không kể thời gian phát đề
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
1. Ba bạn Đỗ, Đại, Học cùng viết ngẫu nhiên lên bảng một số tự nhiên có 1 chữ số. Xác suất để
3 bạn đó viết cùng 1 số là 1 3 1 1 A. . B. . C. . D. . 81 28 90 100
2. Giao điểm hai đường tiệm cận của đồ thị hàm số x − 5 y = là điểm có tọa độ 2x + 3  1   2   3 1  A. (5;0). B. 0; . C. −  ;0. D. −  ; .  2   3   2 2 
3. Tập nghiệm của bất phương trình log0,5(2𝑥𝑥 + 1) ≥ log0,5(3𝑥𝑥 − 4) là 4  4  4 A. ;  + ∞    . B. ;+ ∞  . C.  ;5 . D. [5;+ ∞). 3   3  3   
4. Anh Hưng gửi tiết kiệm khoản tiền 700 triệu đồng vào ngân hàng với lãi suất 7%/năm theo
hình thức lãi kép, kì hạn 1 năm. Sau ít nhất bao nhiêu năm, anh Hưng thu được số tiền nhiều
hơn 1 tỉ đồng (tính cả vốn lẫn lãi). A. 7. B. 5. C. 6. D. 8.
5. Thời gian luyện tập thể thao mỗi ngày của bác Hưng trong 20 ngày gần đây được cho bởi mẫu số liệu sau:
Thời gian (phút) [20; 25) [25; 30) [30; 35) [35; 40) [40; 45) Số ngày 6 6 4 3 1
Phương sai của mẫu số liệu trên là (kết quả làm tròn đến hàng phần trăm). A. 35,69. B. 5,97. C. 37,57. D. 6,13.
6. Nước chảy từ đáy bể chứa với tốc độ 𝑟𝑟(𝑡𝑡) = 200 − 4𝑡𝑡 (lít/phút), trong đó 0 ≤ 𝑡𝑡 ≤ 50. Tìm
lượng nước chảy ra khỏi bể trong 10 phút đầu tiên. A. 3 1800dm . B. 3 1,8dm . C. 3 2700dm . D. 3 2,7dm . 2 1 1  
7. Cho hàm số 𝑓𝑓(𝑥𝑥) = 3𝑥𝑥 − 1. Biết rằng 𝑎𝑎 là số thỏa mãn 2 f
∫ (x)dx = a f
∫ (x)dx . Giá trị 0 0  của 𝑎𝑎 là 1 1 A. 2. B. . C. 4. D. . 4 2 Trang 2
► Đỗ Văn Đức | Khóa học TENS 2025 môn Toán | tenschool.vn
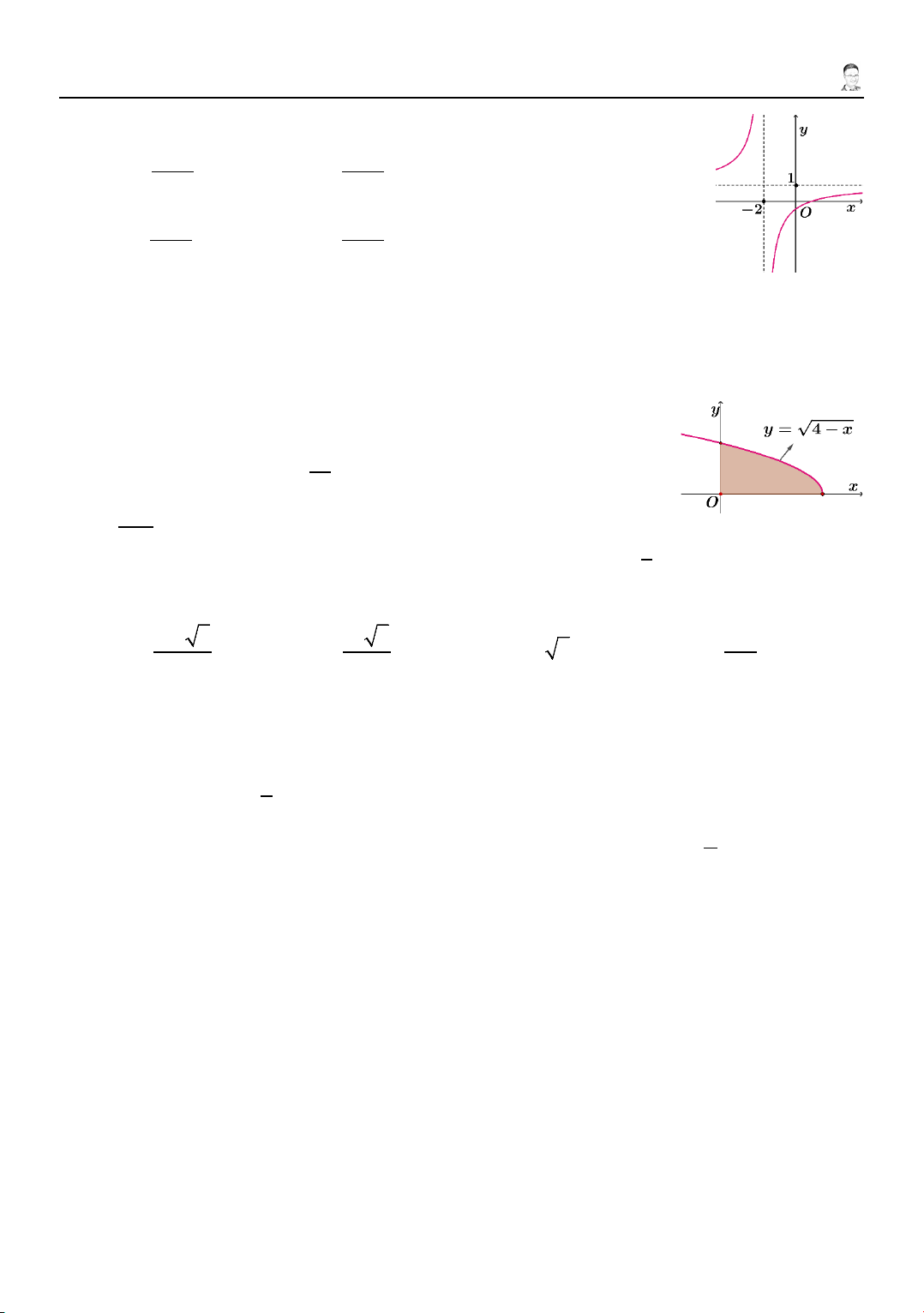
8. Đồ thị trong hình bên là của một trong 4 hàm số sau. Đó là hàm số nào? x − 2 x −1 A. y = . B. y = . x +1 x + 2 x +1 x + 2 C. y = . D. y = . x + 2 x −1
9. Trong không gian 𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂, cho 𝐴𝐴(−1; 2; 1), 𝐵𝐵(1; 3; 0) và 𝐶𝐶(0; −1; 2). Mặt phẳng (𝐴𝐴𝐵𝐵𝐶𝐶) có một vectơ pháp tuyến là: A. ( 2 − ;3;− 7). B. (2;3;7). C. (2;3; 7 − ). D. (2;3;− ) 11 .
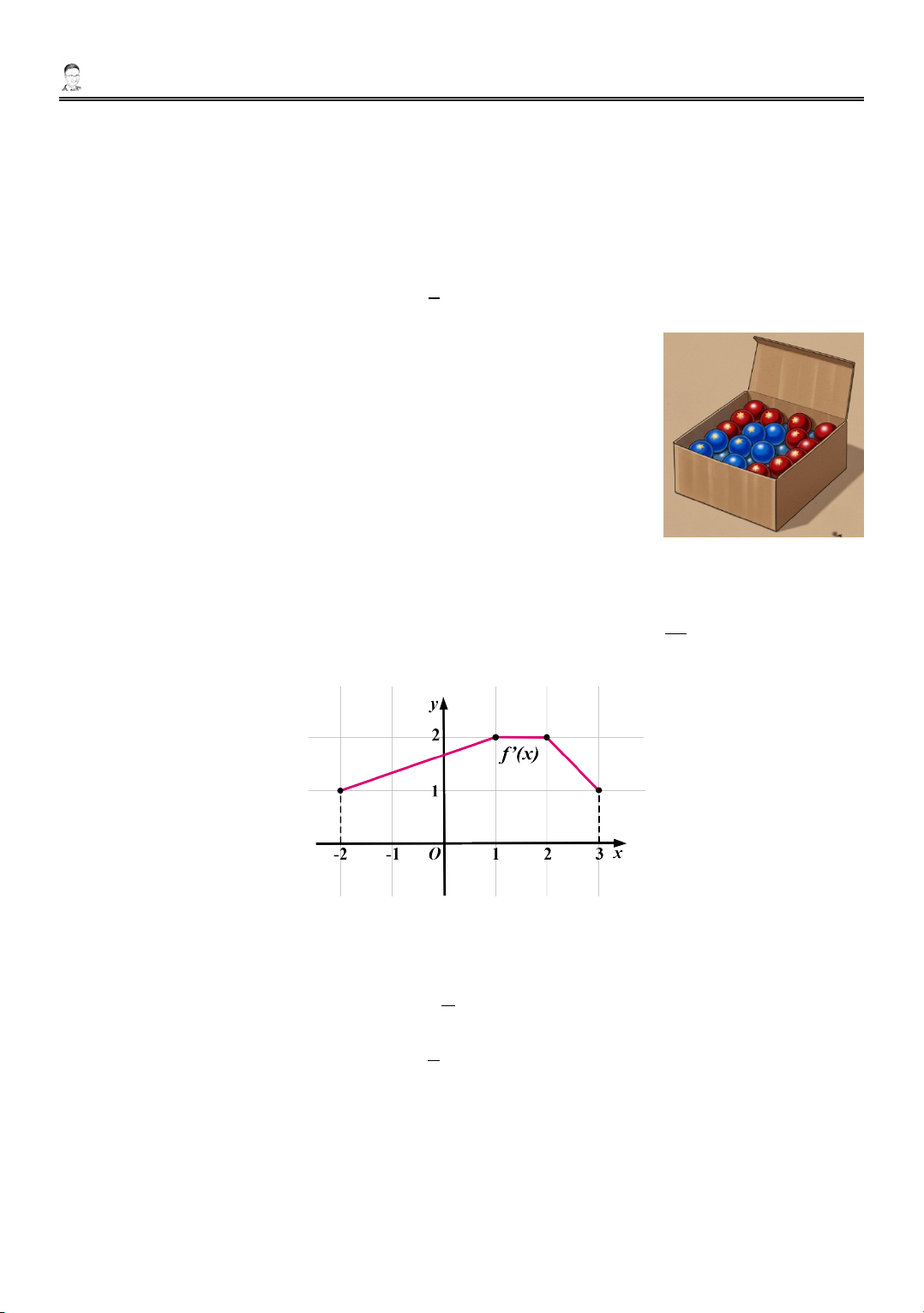
10. Thể tích vật thể tròn xoay khi quay hình phẳng tô đậm trong hình vẽ quanh trục hoành là A. 8. B. 16 . 3 π C. 16 . D. 8𝜋𝜋. 3
11. Cho khối chóp 𝑆𝑆. 𝐴𝐴𝐵𝐵𝐶𝐶𝐴𝐴 có đáy là hình chữ nhật 𝐴𝐴𝐵𝐵 = 𝑎𝑎, 𝐴𝐴𝐴𝐴 = 𝑎𝑎√3, 𝑆𝑆𝐴𝐴 ⊥ (𝐴𝐴𝐵𝐵𝐶𝐶𝐴𝐴) và 𝑆𝑆𝐶𝐶 tạo
với mặt phẳng (𝑆𝑆𝐴𝐴𝐵𝐵) một góc 30°. Tính thể tích 𝑉𝑉 của khối chóp đã cho 3 2a 6 3 a 6 3 4a A. V = . B. V = . C. 3 V = 2 6a . D. V = . 3 3 3 x = 2 − + t 12. Trong không gian 
𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂, cho đường thẳng ∆ : y = 2t
. Điểm 𝐼𝐼 thuộc Δ, có cao độ dương z =1−  3t
và thỏa mãn 𝑂𝑂𝐼𝐼 = √5. Hoành độ điểm 𝐼𝐼 bằng 9 A. 2. − B. 0. C. 1. D. − . 7
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
1. Nhà máy 𝐴𝐴 chuyên sản xuất một loại sản phẩm cho nhà máy 𝐵𝐵. Hai nhà máy thỏa thuận rằng,
hằng tháng 𝐴𝐴 cung cấp cho 𝐵𝐵 số lượng sản phẩm theo đơn đặt hàng của nhà máy 𝐵𝐵 (tối đa 100
tấn sản phẩm). Nếu số lượng đặt hàng là 𝑥𝑥 tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là
𝑃𝑃(𝑥𝑥) = 45 − 0,001𝑥𝑥2 (triệu đồng). Cho phí để 𝐴𝐴 sản xuất 𝑥𝑥 tấn sản phẩm trong một tháng là
𝐶𝐶(𝑥𝑥) = 100 + 30𝑥𝑥 triệu đồng (gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm).
a) Chi phí để 𝐴𝐴 sản xuất 10 tấn sản phẩm trong một tháng là 400 triệu đồng.
b) Số tiền 𝐴𝐴 thu được khi bán 10 tấn sản phẩm cho 𝐵𝐵 là 600 triệu đồng.
c) Lợi nhuận mà 𝐴𝐴 thu được khi bán 𝑥𝑥 tấn sản phẩm (0 ≤ 𝑥𝑥 ≤ 100) cho 𝐵𝐵 là
Đỗ Văn Đức – Đề tạm biệt 2K7 số 02 môn Toán Trang 3
𝐻𝐻(𝑥𝑥) = −0,001𝑥𝑥3 + 15𝑥𝑥 − 100.
d) 𝐴𝐴 bán cho 𝐵𝐵 khoảng 70,7 tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất.
2. Trong không gian 𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂, cho mặt phẳng (𝑃𝑃): 𝑥𝑥 − 𝑂𝑂 − 𝑂𝑂 − 3 = 0 và hai điểm 𝐴𝐴(1; 2; 1) và
𝐵𝐵(1; −3; −4). Một điểm 𝑀𝑀 di động trên mặt phẳng (𝑃𝑃).
a) Một vectơ pháp tuyến của (𝑃𝑃) là (1; −1; −1). b) 𝐴𝐴�𝐵𝐵 ��⃗ = (0; 5; 5).
c) Giá trị nhỏ nhất của 4𝑀𝑀𝐴𝐴2 + 𝑀𝑀𝐵𝐵2 bằng 56.
d) Giá trị nhỏ nhất của 𝑀𝑀𝐴𝐴 + 𝑀𝑀𝐵𝐵 là 5√2.
3. [ĐVĐ] Một chiếc hộp có 50 viên bi, trong đó có 30 viên bi màu xanh
và 20 viên bi màu đỏ, các viên bi có kích thước và khối lượng giống
nhau. Sau khi kiểm tra, người ta thấy có 70% số viên bi màu xanh
được đánh số và 60% số viên bi màu đỏ được đánh số, những viên
bi còn lại không đánh số.
Lấy ngẫu nhiên một viên bi từ hộp đó. Gọi các biến cố:
𝐴𝐴: “Viên bi lấy ra màu xanh”
𝐵𝐵: “Viên bi lấy ra được đánh số”. a) 𝑃𝑃(𝐴𝐴) = 0,6. b) 𝑃𝑃(𝐵𝐵) = 0,33.
c) Trong số các viên bi được đánh số, có 12 viên bi màu đỏ.
d) Viên bi lấy ra không được đánh số, xác suất viên bi đó màu đỏ là 8 . 17
4. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑥𝑥) có đồ thị hàm số 𝑂𝑂 = 𝑓𝑓′(𝑥𝑥) trên đoạn [−2; 3] cho bởi hình vẽ bên.
a) Hàm số 𝑓𝑓(𝑥𝑥) nghịch biến trên (2; 3). b) 𝑓𝑓(2) = 𝑓𝑓(1).
c) 𝑓𝑓(3) − 𝑓𝑓(−2) = 8.  1 − x khi 0 x <  d) Xét hàm số 
𝑔𝑔(𝑥𝑥) thỏa mãn g′(x) 2 =  Khi đó 2 ≤ −5. 1
∫ (𝑔𝑔′(𝑥𝑥) − 𝑓𝑓′(𝑥𝑥))d𝑥𝑥  −2 x khi 0. x ≥ 3 Trang 4
► Đỗ Văn Đức | Khóa học TENS 2025 môn Toán | tenschool.vn
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
1. [ĐVĐ] Cho hình lăng trụ đứng 𝐴𝐴𝐵𝐵𝐶𝐶. 𝐴𝐴′𝐵𝐵′𝐶𝐶′ có 𝐴𝐴𝐵𝐵 = 3, 𝐴𝐴𝐶𝐶 = 4. Biết góc nhị diện [𝐵𝐵, 𝐴𝐴𝐴𝐴′, 𝐶𝐶′]
bằng 60°. Tính khoảng cách giữa hai đường thẳng 𝐴𝐴𝐴𝐴′ và 𝐵𝐵𝐶𝐶. (Kết quả làm tròn đến hàng phần trăm).  Đáp số: ……….
2. Cho hàm số 𝑂𝑂 = 𝑓𝑓(𝑥𝑥) có 𝑓𝑓′(𝑥𝑥) = 𝑥𝑥(𝑥𝑥 + 𝑎𝑎)∀𝑎𝑎 ∈ ℝ. Số tự nhiên 𝑎𝑎 nhỏ nhất để hàm số 𝑓𝑓(𝑥𝑥)
nghịch biến trên (−2222; −100) là bao nhiêu?  Đáp số: ……….
3. Người ta dùng thuốc để khử khuẩn cho một thùng nước. Biết rằng nếu lúc đầu mỗi mililít nước
chứa 𝑃𝑃0 vi khuẩn thì sau 𝑡𝑡 giờ (kể từ khi cho thuốc vào thùng), số lượng vi khuẩn trong mỗi
mililít nước là 𝑃𝑃 = 𝑃𝑃0. 10−𝛼𝛼𝛼𝛼, với 𝛼𝛼 là một hằng số dương nào đó. Biết rằng ban đầu mỗi mililít
nước có 9 000 vi khuẩn và sau 2 giờ, số lượng vi khuẩn trong mỗi mililít nước là 6 000. Sau
thời gian bao lâu thì số lượng vi khuẩn trong mỗi mililít nước trong thùng ít hơn hoặc bằng
1 000? (Kết quả tính theo giờ và làm tròn đến hàng phần chục).  Đáp số: ……….
4. Một cái lu có đường xung quanh thân được xem là một phần của đồ thị hàm số
𝑂𝑂 = −0,01𝑥𝑥3 − 0,1𝑥𝑥2 + 2,48
quay quanh trục 𝑂𝑂𝑥𝑥 như hình vẽ. Biết miệng lu là đường tròn có đường kính bằng 4 dm và
chiều cao của lu bằng 6 dm. Mỗi đơn vị trên trục tọa độ bằng 1 dm. Hỏi cái lu có thể chứa tối
đa bao nhiêu lít nước? (kết quả làm tròn đến hàng đơn vị)  Đáp số: ……….
Đỗ Văn Đức – Đề tạm biệt 2K7 số 02 môn Toán Trang 5
5. [ĐVĐ] Một quả bóng hình cầu có bán kính bằng 2 m được treo lơ lửng trên một mặt đất phẳng.
Tâm quả bóng cách mặt đất 10 m. Chọn hệ trục tọa độ 𝑂𝑂𝑥𝑥𝑂𝑂𝑂𝑂 có gốc tọa độ 𝑂𝑂 là hình chiếu
vuông góc của tâm quả cầu trên mặt đất, tia 𝑂𝑂𝑂𝑂 chứa tâm của quả cầu, các trục 𝑂𝑂𝑥𝑥, 𝑂𝑂𝑂𝑂 thuộc mặt đất như hình vẽ.
Một nguồn sáng 𝑆𝑆(2; −1; 15) chiếu xuống quả cầu, bóng của quả cầu xuống mặt đất là vùng
hình phẳng 𝐻𝐻. Diện tích của 𝐻𝐻 bằng bao nhiêu m2? (Kết quả làm tròn đến hàng đơn vị).  Đáp số: ……….
6. [ĐVĐ] Bốn bạn Công, Thành, Danh, Toại cùng viết ngẫu nhiên lên bảng 1 số tự nhiên có 2 chữ
số khác nhau. Biết số viết ra của cả 4 bạn đôi một khác nhau. Tính xác suất để tất cả các chữ
số viết ra của cả 4 bạn đều khác nhau (Kết quả làm tròn đến hàng phần trăm).  Đáp số: ………. --- Hết ---
LỊCH LIVE CHỮA ĐỀ TẠM BIỆT 2K7 | THẦY ĐỖ VĂN ĐỨC Phát đề Live Công bố chữa BXH Tại Đề số 1 14h30-16h Thứ 2, ngày 23/06 16h 19h Page Tiktok Đề số 2 14h30-16h Thứ 3, ngày 24/06 16h 19h Page Tiktok Đề số 3 17h00-18h30 Thứ 4, ngày 25/06 18h30 20h Page Tiktok