Đề ôn tập toán vào 10 - Đề số 1

TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 01 Môn: Toán
Họ tên học sinh:……………………………………… Câu 1: (1,0 điểm).
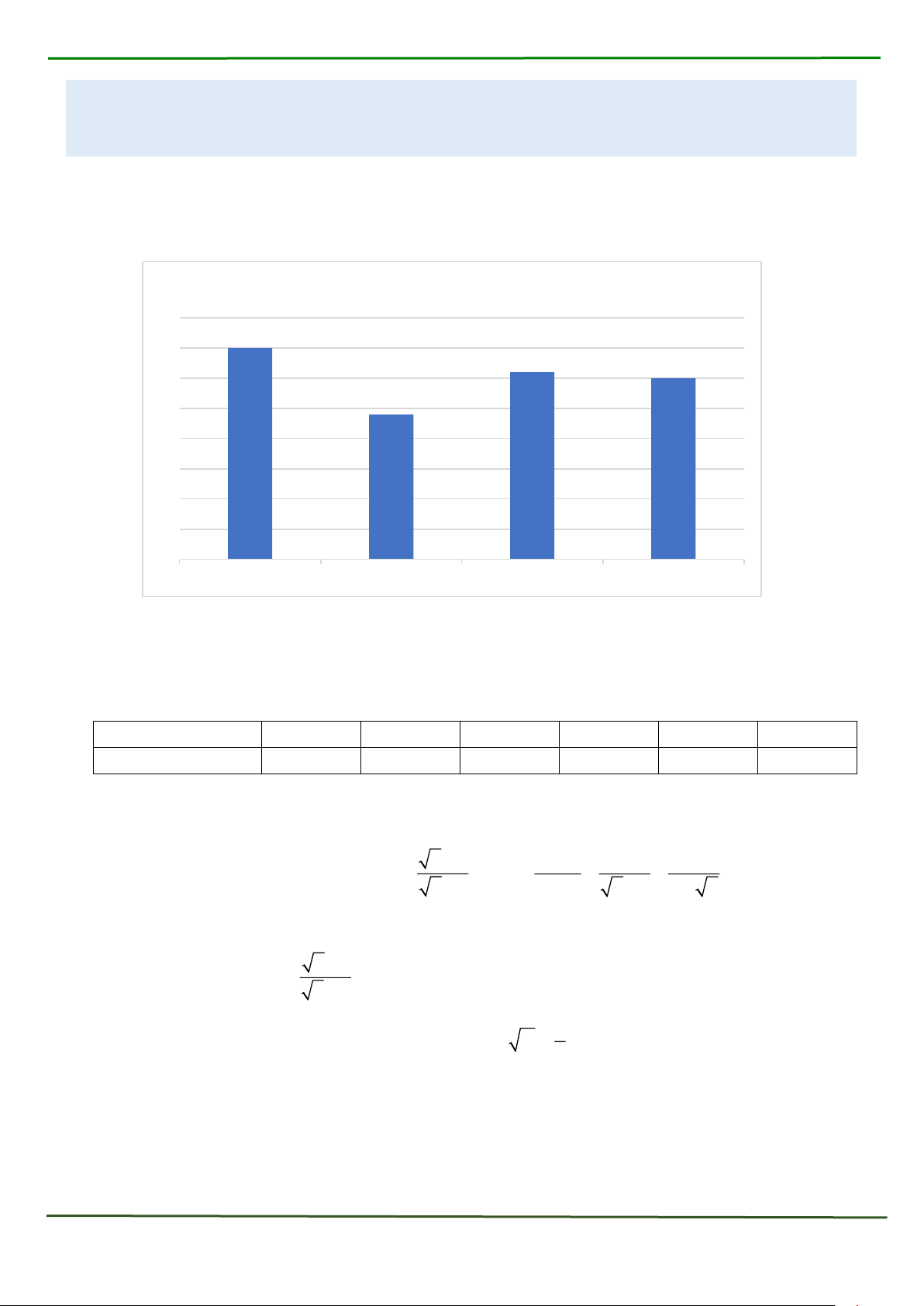
1) Số sách quyên góp cho đợt ủng hộ các em nghèo ở vùng cao của khối 8 thuộc 1 trường
THCS được ghi lại như sau.
Số lượng sách quyên góp (quyển) 80 70 70 62 60 60 48 50 40 30 20 10 0 8A 8B 8C 8D
Tính tỷ số phần trăm số sách quyên góp được của lớp 8D so với số sách quyên góp của cả khối.
2) Bạn Lan gieo một con xúc xăc 6 mặt cân đối 60 lần liên tiếp và thống kê được kết quả như sau: Mặt 1 chấm 2 chấm 3 chấm 4 chấm 5 chấm 6 chấm Số lần xuất hiện 14 18 9 7 6 6
Tính xác suất thực nghiệm của biến số. “Mặt xuất hiện của xúc xắc là mặt có số chấm không chia hết cho 3”. x + 2 x + 20 1 6
Câu 2: (2,0 điểm). Cho hai biểu thức A = và B = + +
( x  0; x  4 ) x + 5 x − 4 x + 2 2 − x
1) Tính giá trị của biểu thức A khi x =16 . x − 3 2) Chứng minh B = . x + 2 1
3) Đặt Q = AB . Tìm số nguyên x nhỏ nhất để Q  . 2 Câu 3: (2,5 điểm).
1) Một mảnh vườn hình chữ nhật. Nếu tăng mỗi kích thước của mảnh vườn lên thêm 4 m
thì diện tích tăng thêm 80 2
m . Nếu giảm chiều rộng đi 2 m và tăng chiều dài thêm 5 m
thì diện tích mảnh vườn không thay đổi. Tính diện tích mảnh vườn hình chữ nhật ban đầu.
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 1
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
2) Một tàu thuỷ chạy xuôi dòng một khúc sông dài 72 km , sau đó chạy ngược dòng khúc
sông ấy 54 km hết tất cả 6 giờ. Tính vận tốc riêng của tàu thuỷ biết vận tốc của dòng
nước là 3 km/h .
3) Giải phương trình Giải các phương trình: a) 2
x − 4x − 5 = 0; b) 2
x − 2 3x + 3 = 0; c) 2
3x − 2x + 2 = 0. Câu 4: (4,0 điểm). 1)
Bánh xe đạp bơm căng có đường kính là 73 cm .
a) Hỏi xe đạp đi được bao nhiêu km nếu bánh xe quay được 1000 vòng?
b) Hỏi bánh xe quay được bao nhiêu vòng khi xe đi được 4 km ?
(Làm tròn kết quả đến hàng đơn vị, lấy   3,14 ).
2) Cho đường tròn (O) đường kính AB = 2R . Gọi C là trung điểm OA. Dây MN vuông
góc với AB tại C . Trên cung nhỏ MB lấy điểm K bất kỳ ( K khác M , B ). Nối AK cắt MN tại H .
a) Chứng minh B,C, H , K cùng thuộc một đường tròn.
b) Chứng minh AH.AK = A .
B AC và tam giác BMN đều.
c) Tìm vị trí của K trên cung nhỏ MB để tổng KM + KN + KB lớn nhất. Câu 5: (0,5 điểm).
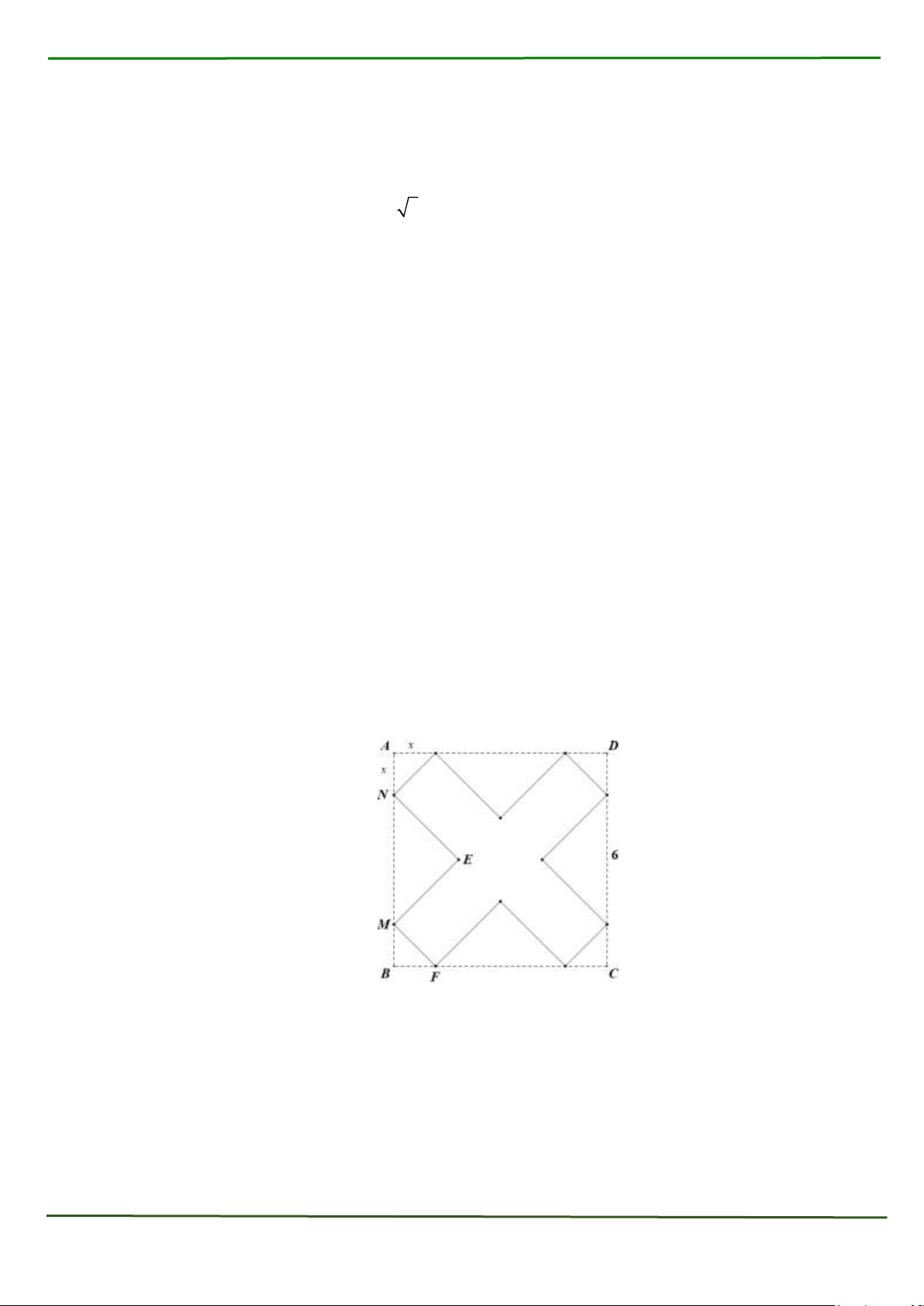
Từ hình vuông có cạnh bằng 6 bạn An cắt bỏ các tam giác vuông cân tạo thành hình chữ
thập như hình. Sau đó bạn An gập thành hộp quà có dạng hình hộp chữ nhật không nắp.
Tìm x để thể tích của khối hộp lớn nhất.
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 2
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 02 Môn: Toán
Họ tên học sinh:………………………………………. Câu I. (1,5 điểm)
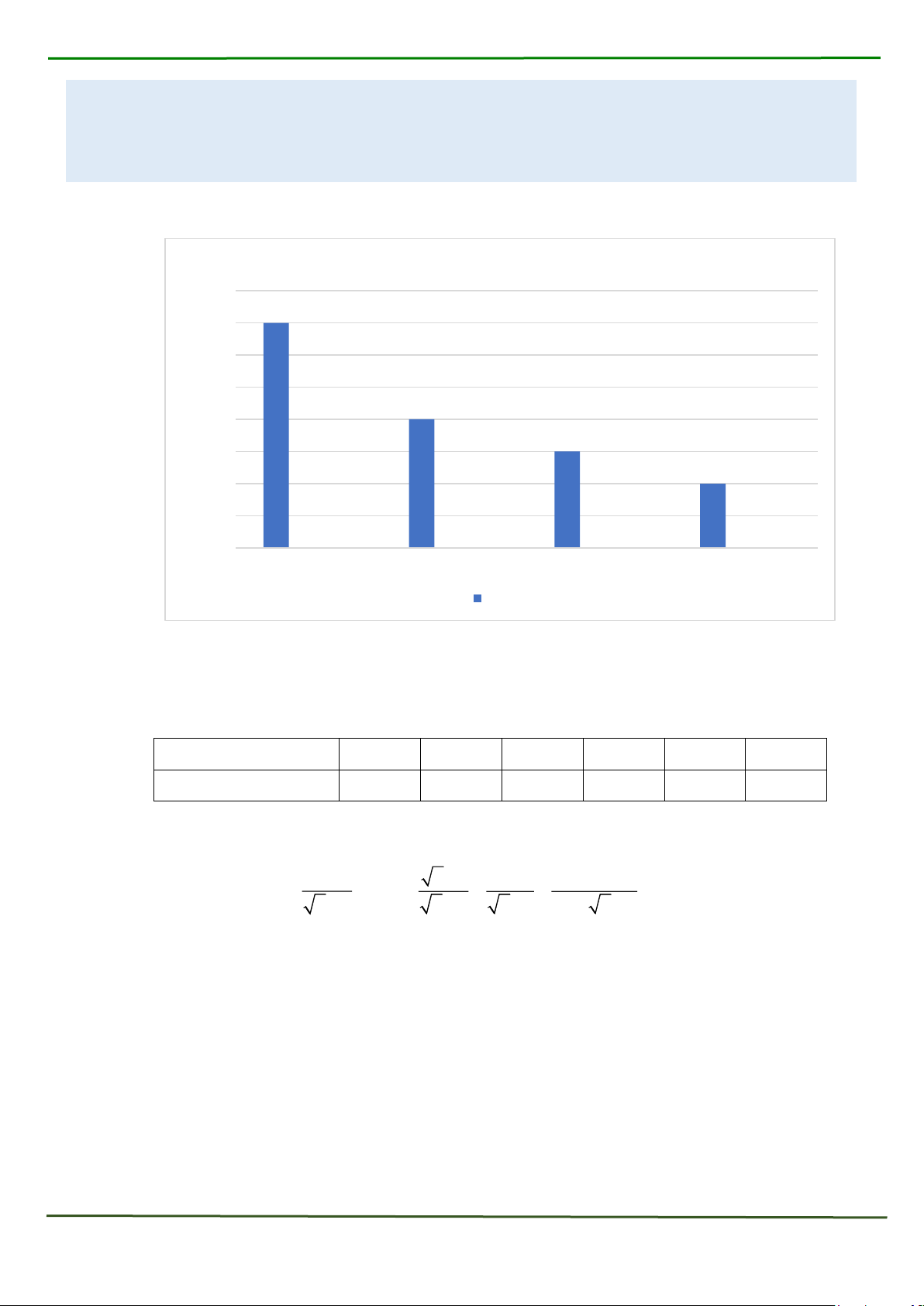
1. Biểu đồ sau cho biết số lượng các loại ô tô một cửa hàng bán được trong năm 2023 :
Số lượng xe các loại bán được năm 2023 40 35 30 25 ốs 20 ần T 15 10 5 0 Xe 4 chỗ ngồi Xe 7 chỗ ngồi Xe 16 chỗ ngồi Xe trên 16 chỗ ngồi Loại xe
a) Lập bảng tần số cho dữ liệu được biểu diễn trên biểu đồ.
b) Giả sử tỉ lệ các loại xe bán được không đổi và cửa hàng bán được tổng số 240 ô tô các
loại trong năm 2023. Hãy ước lượng số ô tô 4 chỗ cửa hàng bán được.
2. Gieo một con xúc xắc đồng chất 100 lần và ghi lại kết quả trong bảng sau: Số chấm xuất hiện 1 2 3 4 5 6 Tần số 20 15 x 30 12 10
Xét biến cố A: “Số chấm xuất hiện trên mặt xúc xắc là số lẻ chia hết cho 3 ”. Tính xác suất của biến cố A. 4 x −1 1 2
Câu II. (1,5 điểm) Cho A = và B = + − với x  0. x + 3 x + 3
x +1 x + 4 x + 3
a) Tính giá trị của biểu thức khi x = 4 .
b) Rút gọn biểu thức B .
c) Tìm giá trị của x để biểu thức P = .
A B đạt giá trị lớn nhất.
Câu III. (2,5 điểm)
1. Trong kỳ thi môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh
đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị
coi thi đếm được tổng số tờ là 42 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh
làm bài 1 tờ giấy thi, bao nhiêu thí sinh làm bài 2 tờ giấy thi? Biết rằng có 3 thí sinh làm 3 tờ giấy thi.
2. Theo kế hoạch, một xưởng may phải may xong 360 bộ quần áo trong một thời gian quy
định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 3
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
quần áo phải may trong một ngày theo kế hoạch. Vì thế xưởng đã hoàn thành kế hoạch trước
1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu bộ quần áo?
3. Tìm m để các phương trình bậc hai sau có hai nghiệm phân biệt. a) 2 2
x − 2mx + m − 2m − 2 = 0 b) 2 x − (m + ) 2 2
3 x + m − 5 = 0 Câu IV. (4,0 điểm)
1. Cho tam giác ABC đều có cạnh AB = 3cm nội tiếp đường tròn tâm O bán kính R . Hạ
AH vuông góc với BC . Tính diện tích phần nằm trong hình tròn ( ;
O R) và nằm ngoài tam
giác ABC (phần tô đậm trong hình bên).
2. Cho đường tròn (O) đường kính AB = 2R . Lấy điểm C trên đường tròn (O) và lấy điểm
M bất kì trên cung nhỏ BC ( M không trùng với B,C ). Gọi H là giao điểm của AM và
BC . Đường thẳng AC cắt đường thẳng BM tại D . DH cắt AB tại K .
1) Chứng minh rằng bốn điểm C, D, M , H cùng thuộc một đường tròn.
2) Chứng minh rằng D
 CM đồng dạng với D  BA.
3) Chứng minh rằng CKM = COM . MP
4) Kẻ phân giác góc AMB cắt AB tại P . Tìm vị trí của M thỏa mãn đề bài để MA + MB
đạt giá trị lớn nhất.
Câu IV. (0,5 điểm) Trong một xưởng cơ khí đang có sẵn những thanh thép dài 7, 4 m . Một công trình
xây dựng đang cần có 1000 đoạn thép dài 0,7 m và 2000 đoạn thép dài 0,5m (Cùng kích
cỡ với thép 7, 4 m ). Em hãy tìm xem cần dùng bao nhiêu thanh thép 7, 4 m để thoả mãn yêu
cần trên với chi phí tiết kiệm nhất.  HẾT 
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 4
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 03 Môn: Toán
Họ tên học sinh:…………………………………………. Câu 1 ( 1.5 điểm) Tần số
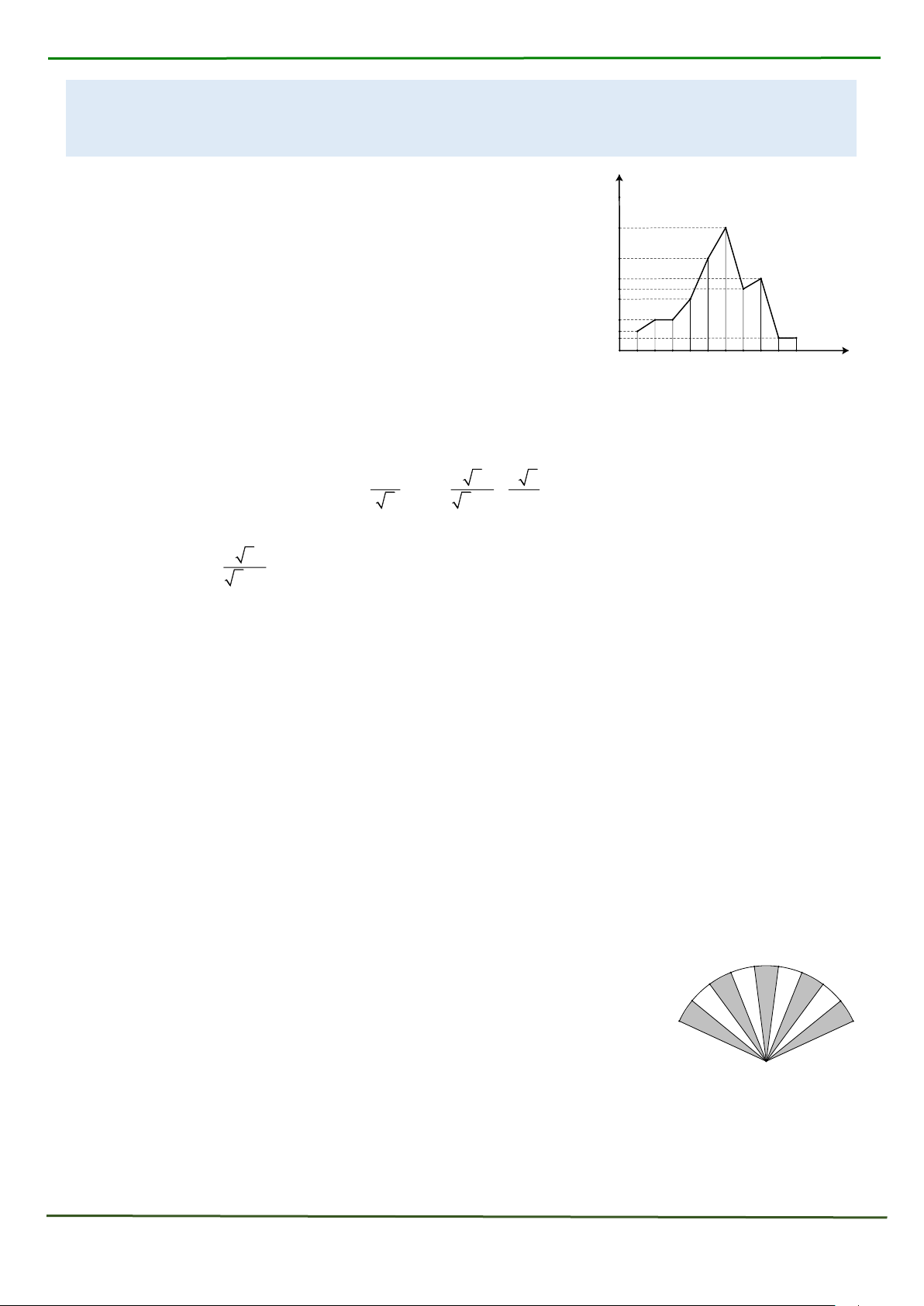
1) Một khu vui chơi dành cho trẻ em thống kê lại độ tuổi của trẻ 25
em đến chơi trong một ngày và lập được biểu đồ đoạn thẳng như 20 sau: 15
Quan sát biểu đồ cho biết: Trong các trẻ em đến khu vui chơi, trẻ
em ở độ tuổi nào là nhiều nhất và có bao nhiêu em trong độ tuổi 10 đó đến khu vui chơi? 5
2) Viết ngẫu nhiên một số tự nhiên có hai chữ số. 0 1 2 3 4 5 6 7 8 9 10 Tuổi
a) Viết tập hợp  tất cả các kết quả có thể xảy ra đối với số tự
nhiên được viết ra và tính số phần tử của tập hợp 
b) Xác định kết quả thuận lợi cho biến cố B : "Số tự nhiên được viết ra chia hết cho 11"; tính xác suất của biến cố B .
Câu 2 (2 điểm) Cho hai biểu thức: x − 3 x 4 x A = và B = −
với x  0,x  4 x x + 2 4 − x
1) Tính giá trị của biểu thức A biết x =16 2) Chứng minh: x B = x − 2
3) Cho P = A B . Tìm các giá trị nguyên của x để P  6 . Câu 3 (2.5 điểm):
1) Một trường THCS tổ chức cho 250 người bao gồm giáo viên và học sinh đi tham quan khu du lịch
Đảo Ngọc Xanh. Biết giá vé vào cổng của một giáo viên là 80000 đồng, vé vào cổng của một học sinh
là 60000 đồng. Nhà trường tổ chức đi vào đúng dịp Khai trương nên được giảm 5% cho mỗi vé vào
cổng, vì vậy nhà trường chỉ phải trả tổng số tiền là 14535000 đồng. Hỏi có bao nhiêu giáo viên và học
sinh của trường đi tham quan?
2) Một tổ sản xuất theo kế hoạch phải làm 575 chi tiết máy trong một thời gian quy định, mỗi ngày làm
được số chi tiết máy như nhau. Do cải tiến kĩ thuật thực tế mỗi ngày tổ làm thêm được 4 chi tiết máy
cùng loại so với kế hoạch. Vì vậy tổ đã hoàn thành công việc sớm hơn một ngày so với quy định. Tính
số chi tiết máy mà tổ sản xuất dự định làm trong một ngày.
3) Tìm m để các phương trình bậc hai sau có hai nghiệm phân biệt. a) 2
2x − 6x + 2m − 5 = 0 b) 2
x − 2x + m = 0 Câu 4 ( 3.5 điểm)
1) Một cây quạt giấy có bán kính 25 cm , biết góc lớn nhất khi cây quạt xòe
hết ra là 130 . Tính diện giấy của chiếc quạt, biết giấy được dán ở 2 mặt của
cây quạt giấy sao cho không nhìn thấy nan tre (lấy  = 3,14 và kết quả làm 25
tròn đến hàng phần mười).
2) Từ điểm A nằm ngoài ( ;
O R) vẽ hai tiếp tuyến A ,
B AC với đường tròn (B,C là các tiếp điểm). Kẻ
đường kính CD của (O) . a) Chứng minh: , A , B ,
O C cùng thuộc 1 đường tròn và BD / / AO .
b) AD cắt (O) tại E ( ,
A E, D theo thứ tự). Chứng minh rằng 2
AB = AE  AD .
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 5
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
c) Vẽ BH ⊥ DC tại H . Gọi I là trung điểm của BH . Chứng minh ba điểm ,
A I, D thẳng hàng. Câu 5 ( 0.5 điểm)
Một rạp chiếu phim có 120 ghế, giá vé hiện tại là 100 nghìn đồng mỗi vé. Với giá vé này, tất cả các
ghế đều được bán hết cho mỗi suât chiếu. Ban quản lý rạp phim đang xem xét việc tăng giá vé để tối
ưu hóa doanh thu. Sau khi thử nghiệm, rạp phim nhận thấy cứ mỗi lần tăng giá thêm 5 nghìn đồng, số
ghế bị bỏ trống sẽ tăng thêm 4 ghế. Hỏi mức giá vé mới là bao nhiêu để rạp phim đạt doanh thu lớn nhất ?
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 6
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 04 Môn: Toán
Họ tên học sinh:…………………………………………. Bài 1:
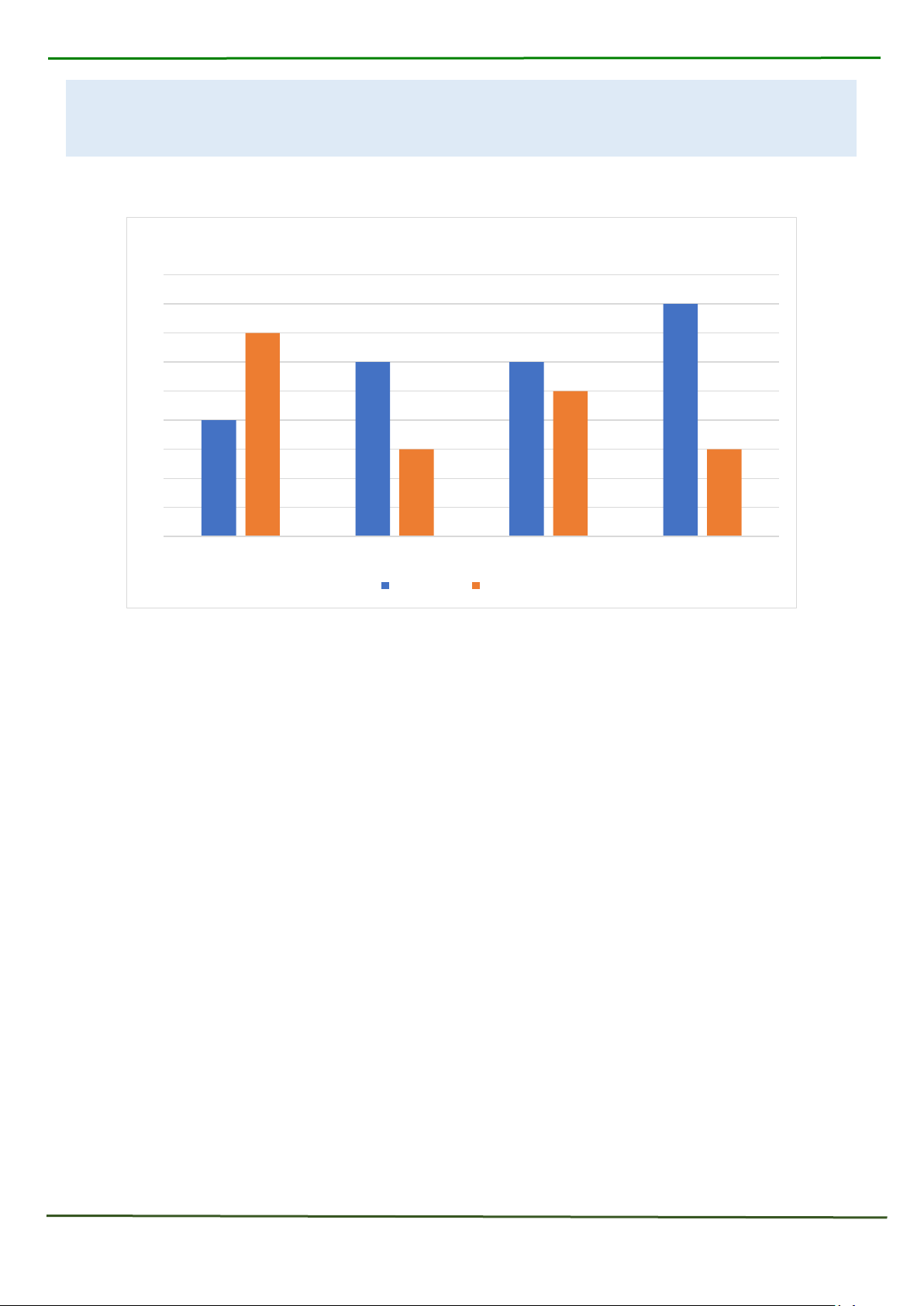
1) Biểu đồ cột kép dưới đây thể hiện số lượng xe đạp bán được của hai cửa hàng trong bốn tháng đầu năm.
Số lượng xe bán được của hai của hàng 45 44 44 43 43 42 42 42 41 41 40 40 39 39 39 38 37 36 Tháng 1 Tháng 2 Tháng 3 Tháng 4 Cửa hàng A Cửa hàng B
a) Xác định số xe cửa hàng A bán được trong tháng 2
b) Sau bốn tháng đầu năm, cửa hàng nào bán được nhiều xe hơn và bán được nhiều hơn bao nhiêu xe?
2) Một cỗ máy gieo một xúc xắc cân đối, đồng chất 30 lần liên tiếp, 5 lần xuất hiện mặt 4 chấm.
a) Tính xác suất thực hiện biến cố A:”Mặt xuất hiện của xúc xắc là mặt 4 chấm”
b) Giả sử cỗ máy gieo xúc xắc 12000 lần liên tiếp. Dự đoán số lần xuất hiện mặt 4 chấm.
Bài 2: 1) Tại một giải vô địch bóng đá, mỗi đội thi đấu tổng cộng 38 trận. Đội M đã vô địch giải
đấu với 5 trận thua và đạt được 89 điểm. Biết mỗi trận thắng được 3 điểm, mỗi trận hòa
được 1 điểm, mỗi trận thua được 0 điểm. Hỏi đội M có bao nhiêu trận thắng và bao trận hòa?
2) Hai thành phố A và B cách nhau 120km . Một xe máy khởi hành từ A và B , cùng lúc
đó một ô tô cũng khởi hành từ B đến A trên cùng con đường với vận tốc lớn hơn vận tốc
của xe máy là 10km / h . Khi ô tô đến A được 36 phút thì xe máy cũng đến B . tính vận tốc của xe máy. 3) Cho phương trình: ( 2 m − ) 2 1 x + 2(m + )
1 x +1 = 0 . Tìm m để phương trình có một nghiệm duy nhất.
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 7
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI x − 2 x + x 1 1
Bài 3: Cho hai biểu thức A = và B = + +
(x  0; x  9) . x − 3 x − 9 x + 3 3 − x 1
a) Tính giá trị của A khi x = . 4
b) Chứng minh A = B .
c) Tìm số nguyên x nhỏ nhất để B  2 − x . Bài 4: Cho đường tròn ( ;
O R) và một điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến AB
, và AC với đường tròn (O) ( B , C là các tiếp điểm).
1) Chứng minh bốn điểm A , B , O , C cùng thuộc một đường tròn.
2) Kẻ đường kính BD của đường tròn (O) . Gọi H là giao điểm của AO và BC .
Chứng minh HO // CD .
3) Kẻ CK vuông góc với BD tại K . Gọi I là giao điểm của AD và CK . Chứng minh
CK.OC = A .
C KD và HI ⊥ AB Bài 5:
Từ một miếng tôn hình bán nguyệt có bán kính R = 3cm , người ta muốn cắt ra một hình chữ
nhật MNPQ (hình vẽ). Tính độ dài NP sao cho hình chữ nhật MNPQ có diện tích lớn nhất. HẾT
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 8
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 05 Môn: Toán
Họ tên học sinh:………………………………………….
Câu 1: (1,5 điểm)
1. Tại một trại hè thanh thiếu niên quốc tế, người ta tìm hiểu xem mỗi đại biểu tham dự có
thể sử dụng được bao nhiêu ngoại ngữ. Kết quả được như bảng sau: Số ngoại ngữ 1 2 3 4  5 Số đại biểu 84 64 24 16 12
a. Tính tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ.
b. Tại trại hè thanh thiếu niên quốc tế tổ chức 1 năm trước đó, có 54 trong tổng số 220 đại
biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Có ý kiến cho rằng “Tỉ lệ đại biểu
sử dụng được 3 ngoại ngữ trở lên có tăng giữa hai năm đó”. Ý kiến đó đúng hay sai? Giải thích.
2. Trong hộp gỗ có 6 thẻ gỗ cùng loại, được đánh số tương ứng 12,13,14,15,16,17. Bình rút
ngẫu nhiên một thể xem số ghi trên thẻ rồi bỏ lại hộp gỗ. Tính xác suất biến cố.
a. A: “thẻ rút được có số ghi trên thẻ là ước của 24”.
b. B: “thẻ rút được có số ghi trên thẻ chia cho 3 dư 2”.
Nếu lặp lại hành động “rút ngẫu nhiên một thẻ xem số ghi trên thẻ rồi bỏ lại hộp gỗ”.
120 lần thì có bao nhiêu lần rút được thẻ có số chia cho 3 dư 2.
Câu 2: (1,5 điểm) x − 2 x 6 x 3
Cho hai biểu thức A = và B = + −
với x  0; x  9 . x − 3 x − 3 9 − x x + 3
1. Tính giá trị của biểu thức A khi x =16 .
2. Rút gọn biểu thức B .
3. Tìm các giá trị của x để biểu thức P = .
A B nhận giá trị nguyên.
Câu 3: (3,0 điểm)
1. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Cô Lan dự định mua một lò vi sóng và một máy rửa bát với tổng số tiền theo giá niêm yết là
8 610 000 đồng. Nhân dịp đón tết Ất Tỵ cửa hàng có chương trình khuyến mãi giảm 5% cho
lò vi sóng và 6% cho máy rửa bát nên cô Lan đã mua thêm một máy rửa bát nữa để tặng mẹ.
Tổng số tiền cô Lan trả cho cửa hàng là 13 527 000 đồng. Hỏi giá niêm yết của một lò vi
sóng và một máy rửa bát là bao nhiêu?
2. Một ô tô phải đi quãng đường AB dài 120 km trong một thời gian nhất định. ˆ O tô đi nửa
quãng đường đầu với vận tốc lớn hơn vận tốc dự định là 5 km / h và đi nửa quãng đường sau
với vận tốc kém vận tốc dự định là 4 km / h . Biết ô tô đến B đúng dự định. Tính thời gian ô
tô dự định đi quãng đường . AB
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 9
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
3. Cho phương trình bậc hai 2
x + 2mx + 4m − 3 = 0 . Tìm m để phương trình có nghiệm kép. Tìm nghiệm kép đó. Câu 4: (3,5 điểm)
1. Bạn An đi xe đạp từ A đến địa điểm B phải leo lên một con dốc AC và xuống một con dốc
CB (như hình vẽ dưới đây). Cho biết chiều dài con dốc AC là 440 m,  0 A = 6 ;B = 4 .
a) Tính chiều cao CH của con dốc theo đơn vị mét (làm tròn đến hàng đơn vị).
b) Biết vận tốc trung bình khi An đi xuống đoạn dốc CB là 18 km / h . Tính thời gian An đi
xe đạp xuống dốc từ C đến B (làm tròn đến giây).
2. Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến AB
và AC với đường tròn (O)(B,C là các tiếp điểm).
a) Chứng minh bốn điểm A, B,O,C cùng thuộc một đường tròn.
b) Kẻ đường kính BD của đường tròn (O) . Gọi H là giao điểm của AO và BC. Chứng minh HO / /CD .
c) Kẻ CK vuông góc với BD tại K. Gọi I là giao điểm của AD và CK. Chứng minh CK.OC = AC.KD và HI ⊥ AB.
Câu 5: (0,5 điểm) Nhà trường dự định dành ra một thửa đất có dạng hình chữ nhật trong mảnh đất
lớn của của trường để làm hồ cá sinh thái. Nhà trường dự định để phần đất ở giữa dạng hình
chữ nhật để xây hồ cá, phần còn lại làm lối đi (như hình bên). Biết tổng diện tích thửa đất
hình chữ nhật cần dùng là 2
864 m . Nhà trường nên chọn các kích thước của thửa đất hình chữ
nhật là bao nhiêu để diện tích phần cho hồ cá là lớn nhất và tính giá trị lớn nhất đó.
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 10
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 06 Môn: Toán
Họ tên học sinh:…………………………………………. Bài I (1,5 điểm).
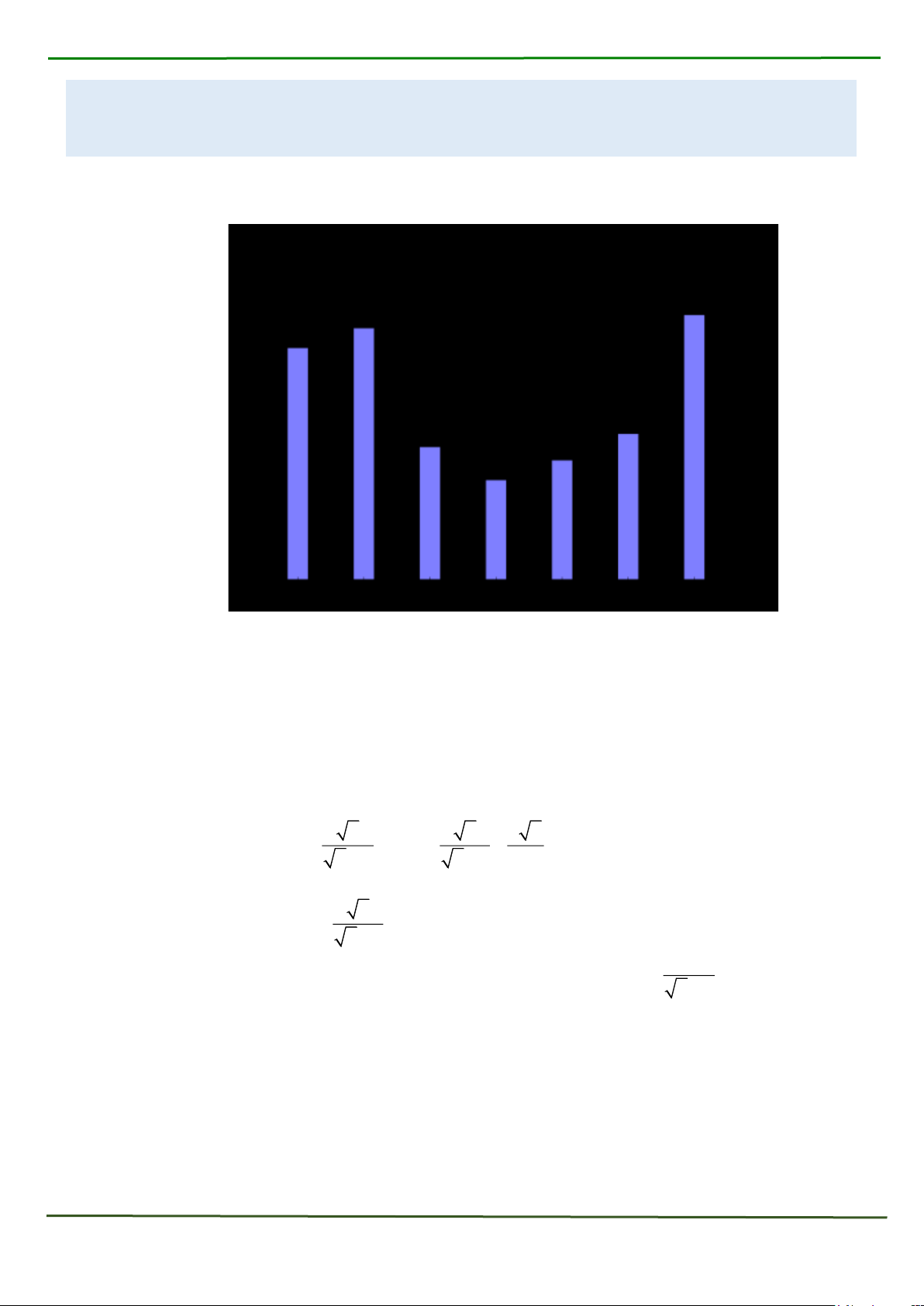
1) Biểu đồ dưới đây cho biết số lượng ti vi cửa hàng bác Quân bán được trong 6 tháng cuối năm 2024 .
a) Dựa vào biểu đồ, em hãy cho biết tháng nào cửa hàng bán được nhiều ti vi nhất?
Tháng nào cửa hàng bản được ít ti vi nhất?
b) Tính tỉ lệ phần trăm số ti vi cửa hàng bán được trong tháng 12 so với tổng số ti vi bán
được trong 6 tháng cuối năm? (Kết quả làm tròn đến chữ số thập phân thứ hai).
2) Một hộp có 25 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1;2;3;4;...;25 ; hai
thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp”
và biến cố M : “Sổ xuất hiện trên thẻ được rút ra là một số chia hết cho 3 ”. Tính xác
suất của biến cố M . Bài II (1,5 điểm). x x 6 x
Cho hai biểu thức A = và B = −
với x  0 ; x  4 ; x  9 . x − 2 x − 3 x − 9
1) Tính giá trị của biểu thức A khi x = 25 . x 2) Chứng minh B = . x + 3 4x + 3
3) Xét biểu thức P = A: B . Tìm tất cả các giá trị của x để P = x − 2
Bài III (2,5 điểm).
1) Giải bài toản sau bằng cách lập phương trình hoặc hệ phương trình:
Trong một chuyến đi trải nghiệm, học sinh lớp 9A trường THCS Bình Minh đã quyên
góp tiền mua 90 quyển vở gồm hai loại để tặng các em làng Nguyên Thủy (Chiềng Hắc
- Mộc Châu - Sơn La). Giá mỗi quyển vở loại thứ nhất là 8 nghìn đồng, giá mỗi quyển
vở loại thứ hai là 10 nghìn đồng. Hỏi lớp 9A đã mua bao nhiêu quyển vở mỗi loại? Biết
rằng tổng số tiền lớp 9A đã quyên góp được là 840 nghìn đồng.
2) Trong Hội chợ Tết, bạn Dương đề xuất với bố mẹ cho bán thêm mặt hàng bánh chưng
trong gian hàng của gia đình. Mỗi chiếc bánh chưng có giá mua vào là 40 nghìn đồng
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 11
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
và giá bán ra là 50 nghìn đồng. Để nhận được 500 nghìn đồng tiền lãi trở lên thì bạn
Dương phải bán được ít nhất bao nhiêu chiếc bánh chưng?
3) Giải phương trình: x + 2 + 16x + 32 =15. Bài IV (4,0 điểm).
1) Trong buổi diễn tập chào mừng 70 năm chiến thắng
Điện Biên Phủ (07 / 5 /1954 − 07 / 05 / 2024) , một chiếc
máy bay trực thăng của Trung đoàn Không quân 916
(Quân chủng Phòng không - Không quân, Bộ Quốc
phòng) làm nhiệm vụ bay biểu diễn kéo cờ Tổ quốc.
Giả sử máy bay bay với vận tốc là 600 m/phút.
a) Tính quãng đường máy bay bay được trong thời
gian 2 phút sau khi cất cánh.
b) Sau 2 phút, muốn đạt độ cao 450 mét thì máy bay
cần phải bay tạo mặt đất một góc bao nhiêu độ so A
với mặt đất (làm tròn kết quả đến độ)?
2) Cho tam giác ABC vuông tại A (với AB  AC ), đường cao AH (H  BC) . Đường
tròn (B) bán kính BA cắt AH tại E .
a) Chứng minh CA và CE là các tiếp tuyến của đường tròn (B) .
b) Kẻ AK ⊥ CE tại K . Đường thẳng qua B vuông góc với AK tại I cắt AC tại Q .
Chứng minh tứ giác BIKE là hình chữ nhật và 2
AB = BI  BQ .
c) Gọi F là giao điểm của EQ với BK . Chứng minh K  EB E  ∽
BQ và AF ⊥ FC . Bài V (0,5 điểm).
Hưởng ứng chương trình “Tình nguyện mùa đông 2024 ”, một đoàn tình nguyện cần thuê
xe để chờ 28 người và 9 tấn hàng để giúp đồng bào hai tỉnh Yên Bái và Lào Cai bị ảnh
hưởng bởi thiên tai. Nơi thuê xe có hai loại xe A và B , trong đó loại xe A có 10 chiếc
và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc
xe loại B cho thuê với giá 3 triệu. Biết rằng mỗi xe loại A có thể chở tối đa 4 người và
0, 6 tấn hàng; mỗi xe loại B có thể chở tối đa 2 người và 1,5 tấn hàng. Hỏi đoàn tình
nguyện phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là ít nhất?
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 12
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
LỚP TOÁN THẦY HẢI
ĐỀ ÔN TẬP VÀO 10 THPT ĐỀ ÔN SỐ: 07 Môn: Toán
Họ tên học sinh:………………………………………….
Bài I: (2 điểm)
1) Thống kê thời gian của 80 chương trình quảng cáo trên đài truyền hình tỉnh C cho kết quả như sau: Thời gian quảng cáo
Số chương trình quảng cáo Từ 0 −19 giây 12 Từ 20 − 39 giây 40 Từ 40 − 59 giây 24 Trên 60 giây 4
Tính xác suất thực nghiệm của các biến cố sau
a) A : “Chương trình quảng cáo của đài truyền hình tỉnh C kéo dài trên 1 phút”
b) B : “Chương trình quảng cáo của đài truyền hình tỉnh C kéo dài trong khoảng từ 20 đến 59 giây”
2) Giải các phương trình và bất phương trình sau − + a) ( x x x − )2 1 + 4x − 4 = 0 b) 2 5 4  2 11
Bài II. (1,5 điểm) 7 Cho hai biểu thức x A = và 2 18 B = + −
với x  0, x  9 . x + 8 x − 3 x + 3 x − 9
1) Tính giá trị của A khi x = 16. + 2) Chứng minh x 8 B = x + 3
3) Tìm các số hữu tỉ x để biểu thức P = A. B có giá trị là số nguyên
Bài III. (2 điểm)
1) Nước muối sinh lý NaCl 0,9% thường được dùng để làm sạch mũi, họng và mắt mà không
gây kích ứng khi tiếp xúc với niêm mạc, vì vậy nước muối sinh lý thường được dùng trong
mỗi gia đình. Để pha được 200g dung dịch NaCl 0,9% từ hai loại dung dịch NaCl 0,5% và
dung dịch NaCl 1% cần dùng bao nhiêu gam NaCl trong mỗi loại dung dịch?
2) Một khu vườn hình chữ nhật có chu vi bằng 48m . Nếu tăng chiều rộng lên bốn lần và
chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162m . Tìm diện tích của khu vườn ban đầu?
Bài IV. (4 điểm)
1) Một chiếc long đen bằng sắt có bề mặt là một hình vành khuyên.
Tính diện tích bề mặt (một mặt) của chiếc long đen này biết rằng
đường kính của hai đường tròn đồng tâm lần lượt là 3,6cm và 6cm (cho   3,14 )
(làm tròn kết quả đến hàng phần mười)
2) Cho (O;R) và điểm H cố định nằm ngoài đường tròn. Qua H kẻ một đường thẳng d
vuông góc với OH. Từ điểm M nằm trên đường thẳng d,
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 13
TUYỂN TẬP ĐỀ ÔN THI VÀO 10 THEO CT 2018 GV: BÙI CÔNG HẢI
kẻ tiếp tuyến MA, MB với (O) (A, B là tiếp điểm). Gọi I, K lần lượt là
giao điểm của AB với OM, OH.
a) Chứng minh: 4 điểm M, H, O, A cùng thuộc một đường tròn.
b) Chứng minh: OM vuông góc với AB và 2
OH.OK = R .
c) Vẽ đường thẳng đi qua điểm O, vuông góc với OM, cắt MA, MB lần lượt tại P, Q.
Tìm vị trí điểm M để diện tích tam giác MPQ nhỏ nhất?
Bài V (0,5 điểm). Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê
mỗi căn hộ với giá 2 000 000 đồng/tháng thì mọi căn hộ đều có người thuê và cứ tăng thêm
giá cho thuê mỗi căn hộ 50 000 đồng/tháng thì sẽ có 1 căn hộ bị bỏ trống. Hỏi hàng tháng
công ty muốn thu được số tiền cho thuê nhà nhiều nhất thì công ty đó phải cho thuê mỗi căn
hộ với giá bao nhiêu tiền? --- Hết---
Hơn cả học toán,đó là học cách làm người,không lười biếng và hèn nhát 14