Đề Ôn Thi HK 2 Môn Toán 12 Có Lời Giải Chi Tiết Năm 2022-Đề 4

Đề ôn thi HK2 môn Toán 12 được biên soạn dưới dạng file PDF gồm 20 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 4
ĐỀ ÔN THI HỌC KỲ II – NĂM HỌC 2021-2022
Môn: Toán lớp 12
Câu 1: Trong không gian
Oxyz
cho mặt cầu có phương trình:
2 2 2
2 6 1 0x y z x y
. Xác định tâm
I
và tính bán kính
R
của mặt cầu đã cho.
A.
1; 3;0 , 3IR
. B.
2; 6;0 , 40IR
.C.
1;3;0 , 3IR
. D.
Câu 2: Viết phương trình tham số của đường thẳng
d
đi qua điểm
1;2;3M
và có vectơ chỉ phương
1; 4;5a
.
A.
1
42
53
xt
yt
zt

. B.
1
24
35
xt
yt
zt



. C.
1
24
35
xt
yt
zt



. D.
1
42
53
xt
yt
zt

.
Câu 3: Tìm một vectơ pháp tuyến của mặt phẳng
:2 3 2 0P x y z
.
A.
2;1;3n
. B.
2; 1;3n
. C.
2; 1;3n 
. D.
2; 1; 3n 
.
Câu 4: Tính
1
0
1.
x
I x e dx
.
A.
e
. B.
2e
. C.
2 e
. D.
2e
.
Câu 5: Xác định tọa độ điểm biểu diễn cho số phức
23zi
.
A.
2;3
. B.
2;3
. C.
2; 3
. D.
2; 3
.
Câu 6: Trong không gian với hệ trục
Oxyz
, cho
3;2;1a
,
3;2;5b
. Xác định tọa độ vecto tích có
hướng
,ab



của hai vecto đã cho?
A.
0;8; 12
. B.
8; 12;5
. C.
0;8;12
. D.
8; 12;0
.
Câu 7: Cho hình phẳng giới hạn bởi các đường
3
1yx
,
0y
,
0x
,
1x
quay xung quanh trục
Ox
.
Tính thể tích của khối tròn xoay tạo thành?
A.
79
63
. B.
5
4
. C.
23
14
. D.
9
.
Câu 8: Với giá trị nào của tham số
m
thì đường thẳng
1 2 3
:
22
x y z
d
m

song song với đường thẳng
1
:2
22
xt
y t t
zt


?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 9: Gọi
12
;zz
là nghiệm của phương trình
2
2 3 0zz
. Tính giá trị của biểu thức
22
12
zz
?
A.
23
. B.
3
. C.
2
. D.
6
.
Câu 10: Xác định mặt phẳng song song với trục
Oz
trong các mặt phẳng sau?
A.
1x
. B.
0x y z
. C.
1z
. D.
1xz
.
Câu 11: Cho hàm số
fx
thỏa mãn
3
1
d5f x x
và
3
1
d1f x x
. Tính tích phân
1
1
dI f x x
?
A.
4I
. B.
6I 
. C.
6I
. D.
4I 
.
Câu 12: Tính khoảng cách từ điểm
3;0 ;0M
đến mặt phẳng
Oxy
?
A.
0
. B.
2
. C.
1
. D.
2
.
Trang2
Câu 13: Tính tích phân
6
3
0
sin .cos d
x x x
.
A.
5
. B.
6
. C.
1
64
. D.
4
.
Câu 14: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 3 0
x y z
và
:3 4 5 0
x y z
. Xác định góc tạo bởi hai mặt phẳng
và
?
A.
0
45
. B.
0
90
. C.
0
30
. D.
0
60
.
Câu 15: Tìm họ nguyên hàm của hàm số
3
32f x x x
?
A.
42
2
42
xx
F x x C
. B.
4
2
32
3
x
F x x x C
.
C.
2
33F x x x C
. D.
42
3
2
42
xx
F x x C
.
Câu 16: Xác định số phức
34
4
i
z
i
?
A.
16 11
15 15
i
. B.
9 23
25 25
i
. C.
94
25 25
i
. D.
16 13
17 17
i
.
Câu 17: Tính phần ảo của số phức
2 3 . 2 3z i i
.
A.
13
. B.
0
. C.
9i
. D.
13i
.
Câu 18: Ký hiệu
S
là diện tích hình thang cong giới hạn bởi đồ thị hàm số liên tục
y f x
, trục hoành
và hai đường thằng
,x a x b
như trong hình vẽ (Phần chấm đen). Tìm khẳng định sai?
A.
d
b
a
S f x x
. B.
d
b
a
S f x x
. C.
d
b
a
S f x x
. D.
d
b
a
S f x x
.
Câu 19: Trong không gian
Oxyz
, cho mặt cầu
2
22
: 2 1S x y z
và mặt phẳng
:3 4 12 0xz
. Khi đó khẳng định nào sau đây đúng?
A. Mặt phẳng
tiếp xúc mặt cầu
S
.
B. Mặt phẳng
cắt mặt cầu
S
theo một đường tròn.
C. Mặt phẳng
đi qua tâm của mặt cầu
S
.
D. Mặt phẳng
không cắt mặt cầu
S
.
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, cho hình hộp
.
ABCD A B C D
biết
2; 1;2A
,
1;2;1
B
,
2;3;2C
,
3;0;1
D
. Tìm tọa độ điểm
B
.
A.
1;2;2B
. B.
2; 2;1B
. C.
1; 2; 2B
. D.
2; 1;2B
.
Trang3
Câu 21: Cho hàm số
y f x
liên tục trên đoạn
;ac
và
abc
. Biết
10, 5

ba
ac
f x dx f x dx
.
Tính
?
b
c
f x dx
A.
15
. B.
15
. C.
5
. D.
5
.
Câu 22: Giả sử
Fx
là một nguyên hàm của
x
e
fx
x
trên
0;
và
3
3
1
x
e
I dx
x
. Khẳng định nào sau
đây đúng?
A.
42I F F
. B.
63I F F
. C.
93I F F
. D.
31I F F
.
Câu 23: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
P
song song với hai đường thẳng giả
sử
12
2
21
: , : 3 2
2 3 4
1
xt
x y z
yt
xt



. Tìm một vectơ pháp tuyến của mặt phẳng
P
?
A.
5; 6;7
P
n
. B.
5;6; 7
P
n
. C.
5; 6;7
P
n 
. D.
5;6;7
P
n 
.
Câu 24: Trong mặt phẳng phức (hình dưới), số phức
34zi
được biểu diễn bởi điểm nào trong các điểm
trên hình vẽ?
A. Điểm
A
. B. Điểm
D
. C. Điểm
C
. D. Điểm
B
.
Câu 25: Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
, trục hoành, trục tung, đường thẳng
1.x
Tính thể tích
V
hình tròn xoay sinh bởi
H
khi
H
quay quanh trục
?Ox
A.
7
8
V
. B.
8
15
V
. C.
15
8
V
. D.
4
3
V
.
Câu 26: Tìm một họ nguyên hàm của hàm số
42
?
x
f x e
A.
21
1
d.
2

x
f x x e C
. B.
21
1
d.
2

x
f x x e C
.
C.
21
d

x
f x x e C
. D.
42
1
d.
2

x
f x x e C
.
Câu 27: Cho số phức
, ; 0z a bi a b a
. Xác định kết quả của phép toán
zz
?
A.
0.
B. Số thuần ảo. C. Số thực. D.
2.
Câu 28: Trong không gian
Oxyz
, viết phương trình mặt phẳng
P
đi qua điểm
3;2; 5A
và vuông góc
với đường thẳng
32
:1
6
xt
d y t t
z

?
A.
2 3 0x y z
. B.
2 8 0xy
. C.
2 5 0xy
. D.
2 8 0xy
.
Trang4
Câu 29: Trong không gian
Oxyz
, cho hai đường thẳng
2 4 1
:
2 3 2
x y z
d

và
4
: 1 6 ;
14
xt
d y t t
zt
. Xác định vị trí tương đối giữa hai đường thẳng
d
và
?d
A.
d
và
d
cắt nhau. B.
d
và
d
song song với nhau.
C.
d
và
d
trùng nhau. D.
d
và
d
chéo nhau.
Câu 30:
Cho biết
5
1
d 15f x x
. Tính giá trị của
2
0
5 3 7 dP f x x


?
A.
27P
. B.
15P
. C.
37P
. D.
19P
.
Câu 31: Trong không gian với hệ trục tọa độ
Oxyz
, cho
1;2;3 , 3;0;1AB
. Viết phương trình mặt cầu
đường kính
AB
?
A.
2 2 2
1 2 3 3x y z
. B.
2 2 2
2 1 2 3x y z
.
C.
2 2 2
2 1 2 3x y z
. D.
2 2 2
2 1 2 12x y z
.
Câu 32: Cho số phức
0z a bi
. Xác định phần ảo của số phức
1
z
?
A.
ab
. B.
22
b
ab
. C.
22
a
ab
. D.
22
ab
.
Câu 33: Trong không gian
Oxyz
cho mặt phẳng
: 1 0P x y z
.Trong các đường thẳng sau, đường
thẳng nào cắt mặt phẳng
P
?
A.
3
1
:2
3
x
d y t
zt


. B.
4
1
:2
3
xt
d y t
z


.
C.
1
1 1 2
:
2 1 2
x y z
d

. D.
2
1 1 2
:
1 2 1
x y z
d

.
Câu 34: Trong không gian tọa độ
Oxyz
, cho mặt cầu có phương trình
2 2 2
2 2 6 2 0x y z x y z
cắt mặt phẳng
Oxz
theo một đường tròn, xác định bán kính của đường tròn giao tuyến đó?
A.
32
. B.
42
. C.
5
. D.
22
.
Câu 35: Cho hai số phức
12
,zz
là nghiệm của phương trình
2
4 13 0zz
. Tính môđun của số phức
1 2 1 2
w z z i z z
?
A.
185w
. B.
3w
. C.
17w
. D.
153w
.
Câu 36: Hình phẳng
H
được giới hạn bởi đồ thị hai hàm số
2
2, 2y x x y x
và hai đường thẳng
2, 3xx
. Tính diện tích của
H
.
A.
10
. B.
13
. C.
12
. D.
11
.
Câu 37: Trong mặt phẳng
Oxy
, gọi
A
là điểm biểu diễn của số phức
25zi
và
B
là điểm biểu diễn của
số phức
25zi
. Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hai điểm
A
và
B
đối xứng với nhau qua trục hoành.
B. Hai điểm
A
và
B
đối xứng với nhau qua trục tung.
C. Hai điểm
A
và
B
đối xứng với nhau qua đường thẳng
yx
.
D. Hai điểm
A
và
B
đối xứng với nhau qua gốc tọa độ
O
.
Câu 38: Cho số phức
z a bi
. Tìm mệnh đề đúng trong các mệnh đề sau?
Trang5
A.
2
2
zz
. B.
22
.z z a b
. C.
2z z a
. D.
2z z bi
.
Câu 39: Biết tích phân
3
2
0
3
ln2; ,
cos
x
dx b a b
xa
. Tính giá trị của biểu thức
ab
?
A.
1
B.
0
. C.
2
. D.
1
.
Câu 40: Biết
5
1
2 2 1
4 ln2 ln5; ;

x
I dx a b a b
x
. Tính
S a b
?
A.
11S
. B.
5S
. C.
9S
. D.
3S 
.
Câu 41: Biết
( ) 6 1F x x
là một nguyên hàm của
()
1
a
fx
x
. Tính giá trị của
a
?
A.
3
. B.
1
6
. C.
3
. D.
6
.
Câu 42: Cho hình phẳng giới hạn bởi các đường
ln , 0,y x x y x e
quay quanh trục
Ox
. Tính thể tích
khối tròn xoay tạo thành?
A.
3
41
9
e
. B.
3
41
9
e
. C.
3
21
9
e
. D.
3
21
9
e
.
Câu 43: Tìm số phức z biết rằng
2
1 1 1
?
1 2 (1 2 )

z i i
A.
10 35
13 26
zi
. B.
10 14
13 25
zi
. C.
8 14
25 25
zi
. D.
8 14
25 25
zi
.
Câu 44: Cho hàm số
()fx
liên tục trên
và thỏa mãn
8
2
3
2
01
()
tan (cos ) 6.
fx
xf x dx dx
x


Tính tích phân
0
2
2
()fx
dx
x
?
A.
10
. B.
6
. C.
7
. D.
4
.
Câu 45: Cho
2
1
ln
d
ln 2
e
x
Ix
xx
có kết quả dạng
lnI a b
với
,ab
. Tìm khẳng định đúng?
A.
1
1b
a

. B.
22
4 9 11ab
. C.
2 3 3ab
. D.
21ab
.
Câu 46: Trong mặt phẳng
Oxy
cho điểm
A
biểu diễn số phức
1
12zi
.
B
là điểm thuộc đường thẳng
2y
sao cho tam giác
OAB
cân tại
O
. Điểm
B
biểu diễn số phức nào sau đây?
A.
12zi
. B.
22zi
. C.
12
12
zi
zi

. D.
12zi
.
Câu 47: Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu
S
có phương trình
2 2 2
2 4 2 2 0x y z a b x a b c y b c z d
, tâm
I
nằm trên mặt phẳng
cố
định. Biết rằng
4 2 4a b c
, tìm khoảng cách từ điểm
1;2; 2D
đến mặt phẳng
?
A.
9
15
. B.
1
314
. C.
1
915
. D.
15
23
.
Câu 48: Trong không gian với hệ trục tọa độ
Oxyz
, cho
2 3 5OA i j k
. Điểm
M
thuộc mặt phẳng
Oxy
thỏa mãn độ dài
AM
nhỏ nhất. Xác định tọa độ của điểm
M
A.
0;3;0
. B.
2;3;5
. C.
3;5;0
. D.
2;3;0
.
Trang6
Câu 49. Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu
S
có phương trình
2 2 2
2 4 2 2 0x y z a b x a b c y b c z d
, tâm
I
nằm trên mặt phẳng
cố
định. Biết rằng
4 2 4a b c
, tìm khoảng cách từ điểm
1;2; 2D
đến mặt phẳng
?
A.
9
15
. B.
1
314
. C.
1
915
. D.
15
23
.
Câu 50. Trong không gian với hệ trục tọa độ
Oxyz
, cho
2 3 5OA i j k
. Điểm
M
thuộc mặt phẳng
Oxy
thỏa mãn độ dài
AM
nhỏ nhất. Xác định tọa độ của điểm
M
A.
0;3;0
. B.
2;3;5
. C.
3;5;0
. D.
2;3;0
.
BẢNG ĐÁP ÁN
1.A
2.B
3.B
4.B
5.C
6.D
7.C
8.A
9.D
10.A
11.D
12.A
13.C
14.C
15.D
16.D
17.A
18.B
19.D
20.A
21.B
22.B
23.D
24.B
25.B
26.A
27.C
28.D
29.B
30.D
31.C
32.B
33.C
34.D
35.A
36.B
37.B
38.A
39.C
40.B
41.A
42.D
43.A
44.C
45.A
46.C
47.C
48.D
49.C
50.D
ĐÁP ÁN CHI TIẾT
Câu 1. Trong không gian
Oxyz
cho mặt cầu có phương trình:
2 2 2
2 6 1 0x y z x y
. Xác định tâm
I
và tính bán kính
R
của mặt cầu đã cho.
A.
1; 3;0 , 3IR
. B.
2; 6;0 , 40IR
.
C.
1;3;0 , 3IR
. D.
1; 3;0 , 11IR
.
Lời giải
Chọn A
Từ phương trình
2 2 2
2 6 1 0x y z x y
suy ra:
1; 3; 0; 1a b c d
.
Vì
2 2 2
1 9 0 1 9 0a b c d
nên phương trình đã cho là phương trình mặt cầu tâm
1; 3;0I
, bán kính
3R
.
Câu 2. Viết phương trình tham số của đường thẳng
d
đi qua điểm
1;2;3M
và có vectơ chỉ phương
1; 4;5a
.
A.
1
42
53
xt
yt
zt

. B.
1
24
35
xt
yt
zt



. C.
1
24
35
xt
yt
zt



. D.
1
42
53
xt
yt
zt

.
Lời giải
Chọn B
Đường thẳng
d
đi qua điểm
1;2;3M
và có vectơ chỉ phương
1; 4;5a
nên có phương trình
tham số:
1
24
35
xt
yt
zt



.
Câu 3. Tìm một vectơ pháp tuyến của mặt phẳng
:2 3 2 0P x y z
.
A.
2;1;3n
. B.
2; 1;3n
. C.
2; 1;3n 
. D.
2; 1; 3n 
.
Lời giải
Trang7
Chọn B
Mặt phẳng
P
có phương trình
:2 3 2 0x y z
nên có một vectơ pháp tuyến
2; 1;3n
.
Câu 4. Tính
1
0
1.
x
I x e dx
.
A.
e
. B.
2e
. C.
2 e
. D.
2e
.
Lời giải
Chọn B
Đặt
1ux
và
x
dv e dx
, ta có
du dx
và
x
ve
. Do đó
11
1 1 1
0 0 0
00
1 . 1 . 1 0 1 1 2
x x x x x
x e dx x e e dx x e e e e

.
Vậy
2Ie
.
Câu 5. Xác định tọa độ điểm biểu diễn cho số phức
23zi
.
A.
2;3
. B.
2;3
. C.
2; 3
. D.
2; 3
.
Lời giải
Chọn C
Số phức
23zi
nên điểm biểu diễn
z
có tọa độ là
2; 3
.
Câu 6. Trong không gian với hệ trục
Oxyz
, cho
3;2;1a
,
3;2;5b
. Xác định tọa độ vecto tích có
hướng
,ab



của hai vecto đã cho?
A.
0;8; 12
. B.
8; 12;5
. C.
0;8;12
. D.
8; 12;0
.
Lời giải
Chọn D
Có vecto tích có hướng
2 1 1 3 3 2
, ; ; 8; 12;0
2 5 5 3 3 2
ab






.
Câu 7. Cho hình phẳng giới hạn bởi các đường
3
1yx
,
0y
,
0x
,
1x
quay xung quanh trục
Ox
.
Tính thể tích của khối tròn xoay tạo thành?
A.
79
63
. B.
5
4
. C.
23
14
. D.
9
.
Lời giải
Chọn C
Thể tích của khối tròn xoay tạo thành :
1
11
74
2
3 6 3
00
0
23
1 d 2 1 d 2
7 4 14
xx
V x x x x x x




.
Câu 8. Với giá trị nào của tham số
m
thì đường thẳng
1 2 3
:
22
x y z
d
m

song song với đường thẳng
1
:2
22
xt
y t t
zt


?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn A
Trang8
Đường thẳng
1 2 3
:
22
x y z
d
m

có vecto chỉ phương
1
2;2;um

. và đi qua điểm
1; 2;3M
.
Đường thẳng
1
:2
22
xt
y t t
zt


có vecto chỉ phương
2
1;1;2u
.
Dễ thấy
M 
do đó
//d
khi
12
;uu
cùng phương hay
22
4
1 1 2
m
m
.
Câu 9. Gọi
12
;zz
là nghiệm của phương trình
2
2 3 0zz
. Tính giá trị của biểu thức
22
12
zz
?
A.
23
. B.
3
. C.
2
. D.
6
.
Lời giải
Chọn D
Phương trình
2
2 3 0zz
có nghiệm
12
1 2 ; 1 2z i z i
.
Vậy
22
22
12
1 2 1 2 1 2 1 2 6z z i i
.
Câu 10. Xác định mặt phẳng song song với trục
Oz
trong các mặt phẳng sau?
A.
1x
. B.
0x y z
. C.
1z
. D.
1xz
.
Lời giải
Chọn A
Trục
Oz
có vecto chỉ phương
0;0;1k
và đi qua
0;0;0O
. Mặt phẳng song song với trục
Oz
phải có vecto pháp tuyến
n
thỏa mãn
.0nk

và không đi qua
0;0;0O
.
Xét đáp án A có vecto pháp tuyến
1;0;0n
. Vì
.0nk

và mặt phẳng
1x
không đi qua
0;0;0O
suy ra mặt phẳng song song với trục
Oz
nên chọn.
Xét đáp án B có
0 0 0 0
suy ra mặt phẳng
0x y z
đi qua
0;0;0O
nên loại.
Xét đáp án C có vecto pháp tuyến
0;0;1n
. Vì
. 1 0nk

nên loại.
Xét đáp án D có vecto pháp tuyến
1;0;1n
. Vì
. 1 0nk

nên loại.
Câu 11. Cho hàm số
fx
thỏa mãn
3
1
d5f x x
và
3
1
d1f x x
. Tính tích phân
1
1
dI f x x
?
A.
4I
. B.
6I 
. C.
6I
. D.
4I 
.
Lời giải
Chọn D
Ta có
3 1 3 1
1 1 1 1
d 1 d d 1 d 1 5 4f x x f x x f x x f x x
.
Câu 12. Tính khoảng cách từ điểm
3;0;0M
đến mặt phẳng
Oxy
?
A.
0
. B.
2
. C.
1
. D.
2
.
Lời giải
Chọn A
Ta có
;0
M
d M Oxy z
.
Trang9
Câu 13. Tính tích phân
6
3
0
sin .cos dx x x
.
A.
5
. B.
6
. C.
1
64
. D.
4
.
Lời giải
Chọn C
Cách 1:
Đặt
sin d dt x t cosx x
.
Đổi cận :
Khi đó
1
1
4
6
2
2
33
00
0
t1
sin .cos d t dt
4 64
x x x

.
Cách 2: Sử dụng caiso bấm ra kết quả.
Câu 14. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 3 0x y z
và
:3 4 5 0x y z
. Xác định góc tạo bởi hai mặt phẳng
và
?
A.
0
45
. B.
0
90
. C.
0
30
. D.
0
60
.
Lời giải
Chọn C
Gọi
là góc tạo bởi hai mặt phẳng
và
.
Ta có
2; 1;1 , 3; 4;5nn

.
22
2 2 2 2
.
6 4 5
3
cos
2
.
2 1 1 . 3 4 5
nn
nn



.
0
30

.
Câu 15. Tìm họ nguyên hàm của hàm số
3
32f x x x
?
A.
42
2
42
xx
F x x C
. B.
4
2
32
3
x
F x x x C
.
C.
2
33F x x x C
. D.
42
3
2
42
xx
F x x C
.
Lời giải
Chọn D
Câu 16. Xác định số phức
34
4
i
z
i
?
A.
16 11
15 15
i
. B.
9 23
25 25
i
. C.
94
25 25
i
. D.
16 13
17 17
i
.
Lời giải
Chọn D
Trang10
Ta co
2
2
3 4 . 4
3 4 12 3 16 4 16 13
4 17 17 17
41
ii
i i i i
zi
i

.
Câu 17. Tính phần ảo của số phức
2 3 . 2 3z i i
.
A.
13
. B.
0
. C.
9i
. D.
13i
.
Lời giải
Chọn A
Ta co
:
2
2 3 . 2 3 4 6 6 9 13z i i i i i
.
Câu 18. Ký hiệu
S
là diện tích hình thang cong giới hạn bởi đồ thị hàm số liên tục
y f x
, trục hoành
và hai đường thằng
,x a x b
như trong hình vẽ (Phần chấm đen). Tìm khẳng định sai?
A.
d
b
a
S f x x
. B.
d
b
a
S f x x
. C.
d
b
a
S f x x
. D.
d
b
a
S f x x
.
Lời giải
Chọn B
Dựa vào đồ thị hàm số
y f x
, ta có
d
b
a
S f x x
d
b
a
f x x
hoặc
d
b
a
S f x x
d
b
a
f x x
.
Vậy
d
b
a
S f x x
là khẳng định sai.
Câu 19. Trong không gian
Oxyz
, cho mặt cầu
2
22
: 2 1S x y z
và mặt phẳng
:3 4 12 0xz
. Khi đó khẳng định nào sau đây đúng?
A. Mặt phẳng
tiếp xúc mặt cầu
S
.
B.Mặt phẳng
cắt mặt cầu
S
theo một đường tròn.
C.Mặt phẳng
đi qua tâm của mặt cầu
S
.
D.Mặt phẳng
không cắt mặt cầu
S
.
Lời giải
Chọn D
Mặt cầu
2
22
: 2 1S x y z
có tâm
0;0;2I
và bán kính
1R
.
Ta có
2 2 2
4.2 12
,4
3 0 4
d I R

.
Trang11
Vậy Mặt phẳng
không cắt mặt cầu
S
.
Câu 20. Trong không gian với hệ tọa độ
Oxyz
, cho hình hộp
.ABCD A B C D
biết
2; 1;2A
,
1;2;1B
,
2;3;2C
,
3;0;1D
. Tìm tọa độ điểm
B
.
A.
1;2;2B
. B.
2; 2;1B
. C.
1; 2; 2B 
. D.
2; 1;2B
.
Lời giải
Chọn A
Gọi
;;B x y z
;
,IH
lần lượt là trung điểm của
,AC B D

. Suy ra
,0;1;2 2;1;1IH
.
Vì
.ABCD A B C D
là hình hộp nên
BB IH
1 2 0 1
2 1 1 2
1 1 2 2
xx
yy
zz





.
Câu 21. Cho hàm số
y f x
liên tục trên đoạn
;ac
và
abc
. Biết
10, 5
ba
ac
f x dx f x dx

.
Tính
?
b
c
f x dx
A.
15
. B.
15
. C.
5
. D.
5
.
Lời giải
Chọn B
5 10 15
b a b
c c a
f x dx f x dx f x dx
Câu 22. Giả sử
Fx
là một nguyên hàm của
x
e
fx
x
trên
0;
và
3
3
1
x
e
I dx
x
. Khẳng định nào sau
đây đúng?
A.
42I F F
. B.
63I F F
. C.
93I F F
. D.
31I F F
.
Lời giải
Chọn B
Đặt
1
3 d 3d d d ;
33
t
t x t x t x x
.
Đổi cận
Trang12
2 6 6
3
6
3
1 3 3
13
d d d ( ) (6) (3)
3
x t t
e e e
I x t t F t F F
x t t
.
Câu 23. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
P
song song với hai đường thẳng giả
sử
12
2
21
: , : 3 2
2 3 4
1
xt
x y z
yt
xt



. Tìm một vectơ pháp tuyến của mặt phẳng
P
?
A.
5; 6;7
P
n
. B.
5;6; 7
P
n
. C.
5; 6;7
P
n 
. D.
5;6;7
P
n 
.
Lời giải
Chọn D
Gọi
1
có vectơ chỉ phương
1
2; 3;4u 

2
có vectơ chỉ phương
2
1;2; 1u 
Do mặt phẳng
P
song song với hai đường thẳng
12
;
nên
P
có vectơ pháp tuyến
12
, 5;6;7 .
P
n u u


Câu 24. Trong mặt phẳng phức (hình dưới), số phức
34zi
được biểu diễn bởi điểm nào trong các điểm
trên hình vẽ?
A. Điểm
A
. B. Điểm
D
. C.Điểm
C
. D.Điểm
B
.
Lời giải
Chọn B
Điểm biểu diễn số phức
34zi
trong mặt phẳng tọa độ là điểm
3; 4 .D
Câu 25. Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
, trục hoành, trục tung, đường thẳng
1.x
Tính thể tích
V
hình tròn xoay sinh bởi
H
khi
H
quay quanh trục
?Ox
A.
7
8
V
. B.
8
15
V
. C.
15
8
V
. D.
4
3
V
.
Lời giải
Chọn B
Thể tích của khối tròn xoay cần tìm là
11
53
2
2 4 3 2 4
00
1
48
2 d 4 4 d .
0
5 3 15




xx
V x x x x x x x x
Trang13
Câu 26. Tìm một họ nguyên hàm của hàm số
42
?
x
f x e
A.
21
1
d.
2

x
f x x e C
. B.
21
1
d.
2

x
f x x e C
.
C.
21
d

x
f x x e C
. D.
42
1
d.
2

x
f x x e C
.
Lời giải
Chọn A
Ta có
2 1 2 1
1
d d . .
2


xx
f x x e x e C
Câu 27. Cho số phức
, ; 0z a bi a b a
. Xác định kết quả của phép toán
zz
?
A.
0.
B. Số thuần ảo. C. Số thực. D.
2.
Lời giải
Chọn C
Ta có
.z a bi z a bi
Suy ra
2z z a
, nên chọn đáp án C.
Câu 28. Trong không gian
Oxyz
, viết phương trình mặt phẳng
P
đi qua điểm
3;2; 5A
và vuông góc
với đường thẳng
32
:1
6
xt
d y t t
z

?
A.
2 3 0x y z
. B.
2 8 0xy
. C.
2 5 0xy
. D.
2 8 0xy
.
Lời giải
Chọn D
Đường thẳng
d
có vectơ chỉ phương
2;1;0
d
u
.
Mặt phẳng
P
vuông góc với đường thẳng
d
nên
P
có một vectơ pháp tuyến là
2;1;0
Pd
nu

.
Khi đó phương trình mặt phẳng
P
đi qua điểm
3;2; 5A
và có vectơ pháp tuyến là
2;1;0
P
n
:
2 3 2 0 2 8 0.x y x y
Câu 29. Trong không gian
Oxyz
, cho hai đường thẳng
2 4 1
:
2 3 2
x y z
d

và
4
: 1 6 ;
14
xt
d y t t
zt
. Xác định vị trí tương đối giữa hai đường thẳng
d
và
?d
A.
d
và
d
cắt nhau. B.
d
và
d
song song với nhau.
C.
d
và
d
trùng nhau. D.
d
và
d
chéo nhau.
Lời giải
Chọn B
Đường thẳng
d
có vectơ chỉ phương
2;3;2
d
u
và đi qua điềm
2; 4;1M
Đường thẳng
d
có vectơ chỉ phương
4;6;4
d
u
và đi qua điềm
0;1; 1M
Suy ra
, 0;0;0 0
dd
uu


Trang14
Ta có
.Md
Vậy
d
và
d
song song nhau.
Câu 30. Cho biết
5
1
d 15f x x
. Tính giá trị của
2
0
5 3 7 dP f x x


?
A.
27P
. B.
15P
. C.
37P
. D.
19P
.
Lời giải
Chọn D
Ta có
2 2 2
0 0 0
5 3 7 d 5 3 d 7 dP f x x f x x x


2 1 5
2
0
0 5 1
1 1 1
5 3 d 5 3 7 d 14 d 14 5 14 19.
3 3 3
f x x x f t t f t t
Câu 31. Trong không gian với hệ trục tọa độ
Oxyz
, cho
1;2;3 , 3;0;1AB
. Viết phương trình mặt cầu
đường kính
AB
?
A.
2 2 2
1 2 3 3x y z
. B.
2 2 2
2 1 2 3x y z
.
C.
2 2 2
2 1 2 3x y z
. D.
2 2 2
2 1 2 12x y z
.
Lời giải
Chọn C
Mặt cầu đường kính
AB
có tâm
2;1;2I
và bán kính
2 2 2
11
3 1 0 2 1 3 3
22
R AB
.
Nên phương trình của mặt cầu là:
2 2 2
2 1 2 3x y z
.
Câu 32. Cho số phức
0z a bi
. Xác định phần ảo của số phức
1
z
?
A.
ab
. B.
22
b
ab
. C.
22
a
ab
. D.
22
ab
.
Lời giải
Chọn B
Ta có
1
2 2 2 2 2 2
11 a bi a b
zi
z a bi a b a b a b

.
Vậy phần ảo của số phức
1
z
là:
22
b
ab
.
Câu 33. Trong không gian
Oxyz
cho mặt phẳng
: 1 0P x y z
.Trong các đường thẳng sau, đường
thẳng nào cắt mặt phẳng
P
?
A.
3
1
:2
3
x
d y t
zt


. B.
4
1
:2
3
xt
d y t
z


.
C.
1
1 1 2
:
2 1 2
x y z
d

. D.
2
1 1 2
:
1 2 1
x y z
d

.
Lời giải
Chọn C
Trang15
Mặt phẳng
P
có vec tơ pháp tuyến
(1; 1;1)n
+ Đáp án A: đường thẳng
3
d
đi qua điểm
3
(1;2;3)M
và có véc tơ chỉ phương
3
(0;1;1)u
3
. 1.0 1.( 1) 1.1 0un

đường thẳng
3
d
song song hoặc nằm trên
P
.
+ Đáp án B: đường thẳng
4
d
đi qua điểm
4
(1;2;3)M
và có véc tơ chỉ phương
4
(1;1;0)u
4
. 1.1 1.( 1) 0.1 0un

đường thẳng
4
d
song song hoặc nằm trên
P
.
+ Đáp án C: đường thẳng
1
d
đi qua điểm
4
(1; 1; 2)M 
và có véc tơ chỉ phương
1
(2;1;2)u
1
. 2.1 1.( 1) 2.1 3un

đường thẳng
1
d
cắt mặt phẳng
P
.
+ Đáp án D: đường thẳng
2
d
đi qua điểm
2
(1; 1; 2)M 
và có véc tơ chỉ phương
2
(1;2;1)u
2
. 1.1 2.( 1) 1.1 0un

đường thẳng
2
d
song song hoặc nằm trên
P
.
Câu 34. Trong không gian tọa độ
Oxyz
, cho mặt cầu có phương trình
2 2 2
2 2 6 2 0x y z x y z
cắt mặt phẳng
Oxz
theo một đường tròn, xác định bán kính của đường tròn giao tuyến đó?
A.
32
. B.
42
. C.
5
. D.
22
.
Lời giải
Chọn D
Mặt cầu có tâm
(1; 1;3)I
bán kính
3R
Mặt phẳng
Oxz
có phương trình
0y
Gọi
1;0;3H
là hình chiếu của
I
lên mặt phẳng
Oxz
IH Oxz
H là tâm đường tròn giao tuyến
Ta có :
( ; ) 1d I Oxz IH d
Bán kính đường tròn giao tuyến:
22
9 1 2 2r R d
.
Câu 35. Cho hai số phức
12
,zz
là nghiệm của phương trình
2
4 13 0zz
. Tính môđun của số phức
1 2 1 2
w z z i z z
?
A.
185w
. B.
3w
. C.
17w
. D.
153w
.
Lời giải
Chọn A
Theo định lí Vi-ét ta có:
12
12
4
. 13
zz
zz
.
Suy ra
2
2
13 4 13 4 185w i w
.
d
Trang16
Câu 36. Hình phẳng
H
được giới hạn bởi đồ thị hai hàm số
2
2, 2y x x y x
và hai đường thẳng
2, 3xx
. Tính diện tích của
H
.
A.
10
. B.
13
. C.
12
. D.
11
.
Lời giải
Chọn B
Diện tích hình phẳng
H
là:
3
2
2
3
2
2
23
22
22
23
33
22
22
4
44
4 4 13 .
33
H
S x x x dx
x dx
x dx x dx
xx
xx


Câu 37. Gọi
o
z
là nghiệm phức có phần ảo âm của phương trình
2
2 6 5 0zz- + =
. Điểm nào sau đây biểu
diễn số phức
o
iz
?
A.
1
13
;
22
M



. B.
2
31
;
22
M



. C.
3
31
;
22
M



. D.
4
13
;
22
M



.
Lời giải
Chọn A
Ta có
1
2
2
3
2
2 6 5 0
3
2
i
z
zz
i
z
é
+
ê
=
ê
- + = Û
ê
-
ê
=
ê
ê
ë
.
Khi đó
0 0 1
3 1 3 1 3
;
2 2 2 2 2
i
z iz i M
æö
-
÷
ç
= Þ = + Þ
÷
ç
÷
ç
èø
.
Câu 38. Cho hàm số
( )
2
2
7 4 0 1
41
x khi x
fx
x khi x
í
ï
- £ £
ï
=
ì
ï
->
ï
î
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
( )
fx
và các đường thẳng
0, 3, 0xxy= = =
?
A.
20
3
. B.
9
. C.
10
. D.
29
3
.
Lời giải
Chọn D
Diện tich hình phẳng cần tìm là:
( ) ( ) ( )
3 1 3
0 0 1
d d dS f x x f x x f x x= = +
ò ò ò
13
22
01
7 4 d 4 dx x x x= - + -
òò
Trang17
( ) ( ) ( )
1 2 3
2 2 2
0 1 2
7 4 d 4 d 4 dx x x x x x= - + - + - +
ò ò ò
29
3
=
.
Câu 39. Trong mặt phẳng
Oxy
, gọi
A
là điểm biểu diễn của số phức
25zi
và
B
là điểm biểu diễn
của số phức
25zi
. Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hai điểm
A
và
B
đối xứng với nhau qua trục hoành.
B. Hai điểm
A
và
B
đối xứng với nhau qua trục tung.
C.Hai điểm
A
và
B
đối xứng với nhau qua đường thẳng
yx
.
D.Hai điểm
A
và
B
đối xứng với nhau qua gốc tọa độ
O
.
Lời giải
Chọn B
A
là điểm biểu diễn của số phức
2 5 2;5z i A
.
B
là điểm biểu diễn của số phức
2 5 2;5z i B
.
Suy ra: hai điểm
A
và
B
đối xứng với nhau qua trục tung.
Câu 40. Cho số phức
z a bi
. Tìm mệnh đề đúng trong các mệnh đề sau?
A.
2
2
zz
. B.
22
.z z a b
. C.
2z z a
. D.
2z z bi
.
Lời giải
Chọn A
2
2 2 2
2z a bi z a bi a b abi
.
22
2
2
2 2 2 2 2 2 2
2z a b ab a b a b z
.
Câu 41. Biết tích phân
3
2
0
3
ln2; ,
cos
x
dx b a b
xa
. Tính giá trị của biểu thức
ab
?
A.
1
B.
0
. C.
2
. D.
1
.
Lời giải
Chọn C
Đặt:
2
tan
cos
ux
du dx
dx
vx
dv
x

Ta có:
3 3 3
2
0 0 0
3
0
sinx
tan tan tan
33
cos cos
00
cos
33
. 3 . 3 ln cos ln2 ln2
3
3 cos 3 3
0
x
dx x x xdx x x dx
xx
dx
xb
xa

Suy ra:
3; 1 2a b a b
.
Câu 42. Biết
5
1
2 2 1
4 ln2 ln5; ;
x
I dx a b a b
x

. Tính
S a b
?
A.
11S
. B.
5S
. C.
9S
. D.
3S 
.
Trang18
Lời giải
Chọn B
Ta có:
2 5 2 5
1 2 1 2
25
12
2 2 1 2 2 1
2 2 1 2 2 1
2 2 5 5
5 2 2 3
5ln 2 2 3ln
1 1 2 2
4 8ln 2 3ln5 4 ln2 ln5
8; 3 5 .
xx
xx
I dx dx dx dx
x x x x
xx
dx dx x x x x
xx
ab
a b S a b


Câu 43. Biết
( ) 6 1F x x
là một nguyên hàm của
()
1
a
fx
x
. Tính giá trị của
a
?
A.
3
. B.
1
6
. C.
3
. D.
6
.
Lời giải
Chọn A
Ta có:
d 2 1 6 1 3
1
a
x a x x a
x
.
Câu 44. Cho hình phẳng giới hạn bởi các đường
ln , 0,y x x y x e
quay quanh trục
Ox
. Tính thể tích
khối tròn xoay tạo thành?
A.
3
41
9
e
. B.
3
41
9
e
. C.
3
21
9
e
. D.
3
21
9
e
.
Lời giải
Chọn D
Ta có:
ln 0 1x x x
3
2
1
21
ln d
9
e
e
V x x x


(Bấm casio)
Câu 45. Tìm số phức z biết rằng
2
1 1 1
?
1 2 (1 2 )z i i


A.
10 35
13 26
zi
. B.
10 14
13 25
zi
. C.
8 14
25 25
zi
. D.
8 14
25 25
zi
.
Lời giải
Chọn A
Ta có:
2
8 14 25 10 35 10 35
.
1 1 1 1
1 2 (1 2 ) 25 8 14 13 26 13 26
i
z i z
ii iz
i
z


Câu 46. Cho hàm số
()fx
liên tục trên
và thỏa mãn
8
2
3
2
01
()
tan (cos ) 6.
fx
xf x dx dx
x


Tính
tích phân
0
2
2
()fx
dx
x
?
A.
10
. B.
6
. C.
7
. D.
4
.
Lời giải
Chọn C
Trang19
Xét
2
2
0
tan (cos ) 6.xf x dx
Đặt
22
cos 2sin .cos 2cos tan 2 tan tan .
2
dt
x t dt x xdx x xdx t xdx xdx
t
Đổi cận:
01
0
2
xt
xt
suy ra
0 1 1
1 0 0
( ) ( ) ( )
6 6 12
22
f t dt f t dt f t dt
t t t
Xét
8
3
1
()
6.
fx
dx
x
Đặt
32
3
3x u x u dx u du
Đổi cận
11
82
xu
xu
suy ra
2 2 2 2
2
3
1 1 1 1
( ) ( ) ( ) ( )
6 3 3 2 2.
f u f u f u f t
u du du du dt
u u u t
Tính
2
0
2
()fx
I dx
x
Đặt
2
2x t dt xdx
,
Đổi cận
00
22
xt
xt
suy ra :
2 2 1 2
0 0 0
2
1
( ) ( ) 1 ( ) ( ) 1
(12 2) 7.
2 22
f x f t f t f t
I dx dt dt
t t t
dt
x



Câu 47. Cho
2
1
ln
d
ln 2
e
x
Ix
xx
có kết quả dạng
lnI a b
với
,ab
. Tìm khẳng định đúng?
A.
1
1b
a

. B.
22
4 9 11ab
. C.
2 3 3ab
. D.
21ab
.
Lời giải
Chọn A
Đặt
1
ln 2t x dt dx
x
.
Khi đó
3
2
2
12
ln 2
d
ln 2
e
xt
I x dt
t
xx


3
2
2
12
I dt
tt



3
2
2
ln | |t
t




31
ln
23

.
Suy ra
31
;.
23
ab

Do đó
1
1b
a

.
Câu 48. Trong mặt phẳng
Oxy
cho điểm
A
biểu diễn số phức
1
12zi
.
B
là điểm thuộc đường thẳng
2y
sao cho tam giác
OAB
cân tại
O
. Điểm
B
biểu diễn số phức nào sau đây?
A.
12zi
. B.
22zi
. C.
12
12
zi
zi

. D.
12zi
.
Lời giải
Chọn C
Điểm
A
biểu diễn số phức
1
1 2 1; 2z i A
.
Vì
2 ; 2B y B x
.
Trang20
Tam giác
OAB
cân tại
O
2 2 2 2
1 2 2 1OA OB x x
.
Vậy
1; 2B
hoặc
1; 2B
. Do đó
B
biểu diễn số phức
12zi
hoặc
12zi
.
Câu 49. Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu
S
có phương trình
2 2 2
2 4 2 2 0x y z a b x a b c y b c z d
, tâm
I
nằm trên mặt phẳng
cố
định. Biết rằng
4 2 4a b c
, tìm khoảng cách từ điểm
1;2; 2D
đến mặt phẳng
?
A.
9
15
. B.
1
314
. C.
1
915
. D.
15
23
.
Lời giải
Chọn C
Ta có
4 ; ;I a b a b c b c
.
Giả sử
:0Ax By Cz D
, vì
I
nên ta có:
40A a b B a b c C b c D
40A B a A B C b B C c D
.
Theo bài ra
4 2 4a b c
, nên đồng nhất hệ số ta được:
1
4
4
17
41
4
2
25
4
4
4
A
AB
A B C
B
BC
C
D
D










.
Suy ra
1 17 25
: 4 0
4 4 4
x y z
hay
: 17 25 16 0x y z
.
Vậy
2 2 2
1 17.2 25 2 16
1
,
915
1 17 25
dD


.
Câu 50. Trong không gian với hệ trục tọa độ
Oxyz
, cho
2 3 5OA i j k
. Điểm
M
thuộc mặt phẳng
Oxy
thỏa mãn độ dài
AM
nhỏ nhất. Xác định tọa độ của điểm
M
A.
0;3;0
. B.
2;3;5
. C.
3;5;0
. D.
2;3;0
.
Lời giải
Chọn D
Ta có
2;3;5A
. Gọi
A
là hình chiếu của
A
trên mặt phẳng
Oxy
, suy ra
AA AM
.
Như vậy độ dài
AM
nhỏ nhất khi và chỉ khi
2;3;0M A M

.
HẾT
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 4
ĐỀ ÔN THI HỌC KỲ II – NĂM HỌC 2021-2022 Môn: Toán lớp 12 Câu 1:
Trong không gian Oxyz cho mặt cầu có phương trình: 2 2 2
x y z  2x  6 y 1  0 . Xác định tâm
I và tính bán kính R của mặt cầu đã cho. A. I 1; 3
 ;0, R  3 . B. I 2; 6
 ;0, R  40 .C. I  1
 ;3;0, R  3. D. I 1; 3  ;0, R  11 Câu 2:
Viết phương trình tham số của đường thẳng d đi qua điểm M 1;2;3 và có vectơ chỉ phương a1; 4  ;5 . x 1 tx 1 tx 1 tx 1 t     A. y  4   2t .
B. y  2  4t .
C. y  2  4t . D. y  4   2t .     z  5   3tz  3  5tz  3  5tz  5   3tCâu 3:
Tìm một vectơ pháp tuyến của mặt phẳng P : 2x y  3z  2  0 .    
A. n 2;1;3 .
B. n 2; 1;3 .
C. n 2; 1;3 .
D. n 2; 1; 3 . 1 Câu 4: Tính  1  . x I x e dx . 0 A. e . B. e  2. C. 2  e . D. e  2 . Câu 5:
Xác định tọa độ điểm biểu diễn cho số phức z  2 3i . A.  2  ;3 . B. 2;3 . C. 2; 3  . D.  2  ; 3   .   Câu 6:
Trong không gian với hệ trục Oxyz , cho a 3;2; 
1 , b 3; 2;5 . Xác định tọa độ vecto tích có  
hướng a ,b   của hai vecto đã cho? A. 0;8; 12 . B. 8; 12;5 . C. 0;8;12 . D. 8; 12;0 . Câu 7:
Cho hình phẳng giới hạn bởi các đường 3
y x 1 , y  0 , x  0 , x 1 quay xung quanh trục Ox .
Tính thể tích của khối tròn xoay tạo thành? 79 5 23 A. . B. . C. . D. 9 . 63 4 14 x y z Câu 8:
Với giá trị nào của tham số m thì đường thẳng 1 2 3 d :  
song song với đường thẳng 2 2 mx 1 t
 :y  2  t t   ? z  2 2tA. 4 . B. 2 . C. 3 . D. 1. Câu 9:
Gọi z ; z là nghiệm của phương trình 2
z  2z  3  0 . Tính giá trị của biểu thức 2 2 zz ? 1 2 1 2 A. 2 3 . B. 3 . C. 2 . D. 6 .
Câu 10: Xác định mặt phẳng song song với trục Oz trong các mặt phẳng sau? A. x 1.
B. x y z  0 . C. z  1.
D. x z 1. 3 3 1
Câu 11: Cho hàm số f x thỏa mãn f
 xdx  5 và f
 xdx 1. Tính tích phân I f  xdx? 1 1  1  A. I  4 . B. I  6  . C. I  6. D. I  4 .
Câu 12: Tính khoảng cách từ điểm M 3;0;0 đến mặt phẳng Oxy ? A. 0 . B. 2 . C. 1. D. 2 . Trang1  6
Câu 13: Tính tích phân 3 s in .cos d  x x x . 0 1 A. 5 . B. 6 . C. . D. 4 . 64
Câu 14: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  :2x y z  3  0 và
 :3x 4y 5z  0. Xác định góc tạo bởi hai mặt phẳng  và  ? A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 .
Câu 15: Tìm họ nguyên hàm của hàm số f x 3
x  3x  2 ? x x x
A. F x 4 2    2x C .
B. F x 4 2 
 3x  2x C . 4 2 3 x x
C. F x 2
 3x  3x C .
D. F x 4 2 3    2x C . 4 2  i
Câu 16: Xác định số phức 3 4 z  ? 4  i 16 11 9 23 9 4 16 13 A. i . B. i . C. i . D. i . 15 15 25 25 25 25 17 17
Câu 17: Tính phần ảo của số phức z  2  3i.2  3i . A. 13 . B. 0 . C. 9  i . D. 13i .
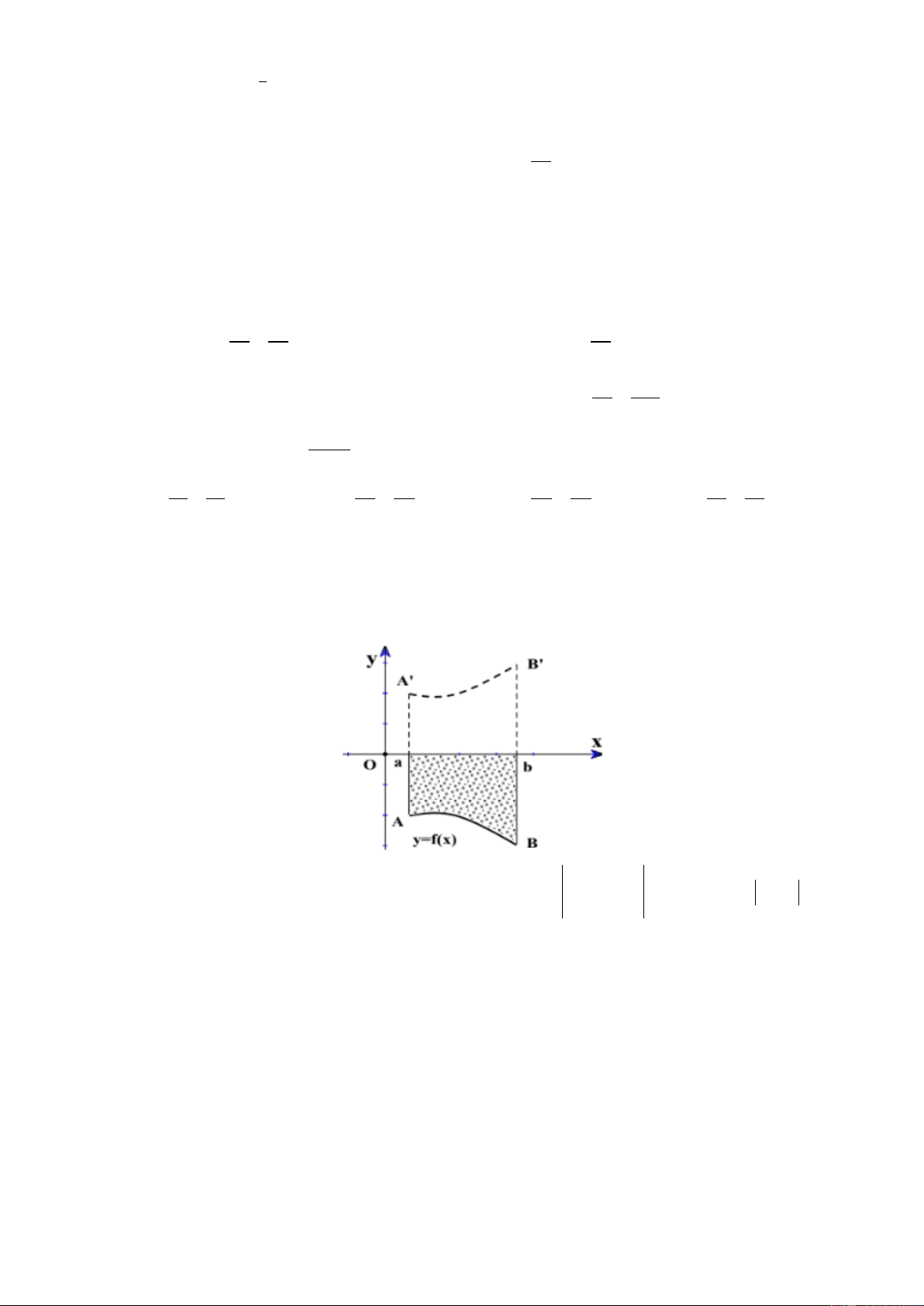
Câu 18: Ký hiệu S là diện tích hình thang cong giới hạn bởi đồ thị hàm số liên tục y f x , trục hoành
và hai đường thằng x a, x b như trong hình vẽ (Phần chấm đen). Tìm khẳng định sai? b b b b
A. S   f xdx . B. S f
 xdx. C. S f
 xdx . D. S f
 x dx . a a a a
Câu 19: Trong không gian Oxyz , cho mặt cầu
Sx y z  2 2 2 : 2 1 và mặt phẳng
:3x4z 12  0. Khi đó khẳng định nào sau đây đúng?
A. Mặt phẳng   tiếp xúc mặt cầu  S  .
B. Mặt phẳng   cắt mặt cầu  S  theo một đường tròn.
C. Mặt phẳng   đi qua tâm của mặt cầu  S  .
D. Mặt phẳng   không cắt mặt cầu  S  .
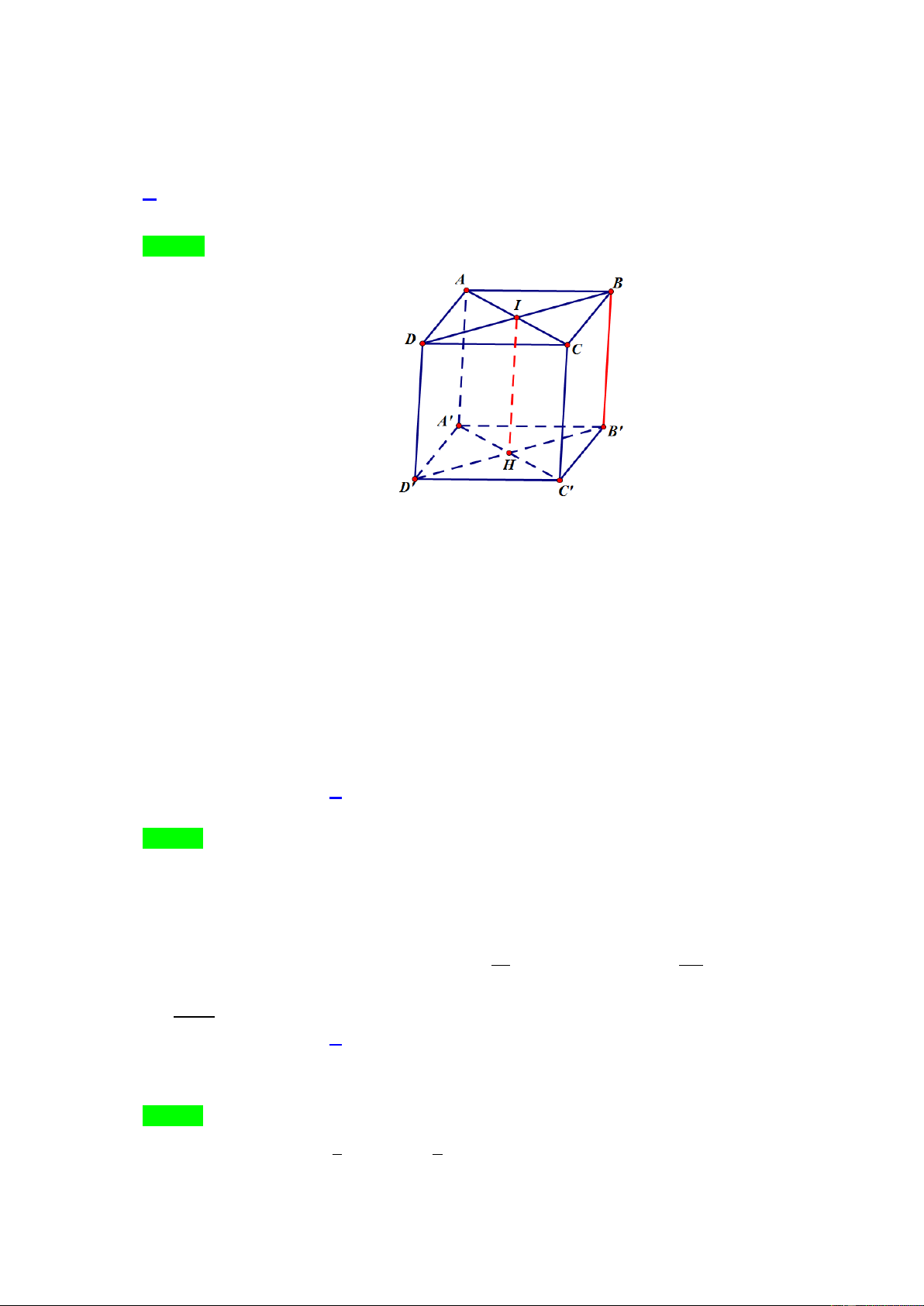
Câu 20: Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A B C 
D biết A2; 1; 2 , B1; 2  ;1 , C  2
 ;3;2 , D3;0 
;1 . Tìm tọa độ điểm B . A. B  1  ;2;2.
B. B 2;  2;  1 .
C. B 1;  2;  2 .
D. B 2; 1; 2 . Trang2 b a
Câu 21: Cho hàm số y f x liên tục trên đoạna;c và a b c . Biết f xdx  1
 0, f xdx  5    . a c b Tính
f xdx ?  c A. 15 . B. 15  . C. 5  . D. 5 . 3 3x e
Câu 22: Giả sử F x là một nguyên hàm của   x e f x
trên 0;  và I dx  . Khẳng định nào sau x x 1 đây đúng?
A. I F 4  F 2 .
B. I F 6  F 3. C. I F 9  F 3 . D. I F 3  F   1 .
Câu 23: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P song song với hai đường thẳng giả x  2  t    sử x 2 y 1 z  : 
 ,  : y  3 2t . Tìm một vectơ pháp tuyến của mặt phẳngP ? 1 2 2 3  4 x 1t      A. n   5  ; 6  ;7 . B. n   5  ;6; 7  .
C. n  5; 6;7 .
D. n  5;6;7 . PPPP
Câu 24: Trong mặt phẳng phức (hình dưới), số phức z  3  4i được biểu diễn bởi điểm nào trong các điểm trên hình vẽ? A. Điểm A . B. Điểm D . C. Điểm C . D. Điểm B .
Câu 25: Cho hình phẳng  H  giới hạn bởi các đường 2
y x  2x , trục hoành, trục tung, đường thẳng
x  1. Tính thể tích V hình tròn xoay sinh bởi  H khi  H quay quanh trục Ox ? 7 8 15 4 A. V  . B. V  . C. V  . D. V  . 8 15 8 3 
Câu 26: Tìm một họ nguyên hàm của hàm số   4 2  x f x e ? 1  1  A.   2 1 d  .   x f x x e C . B.   2 1 d  .   x f x x e C . 2 2 1  C.   2 1 d     x f x x e C . D.   4 2 d  .   x f x x e C . 2
Câu 27: Cho số phức z a bi a,b   ; a  0 . Xác định kết quả của phép toán z z ? A. 0. B. Số thuần ảo. C. Số thực. D. 2.
Câu 28: Trong không gian Oxyz , viết phương trình mặt phẳng  P đi qua điểm A3; 2; 5   và vuông góc x  3 2t
với đường thẳng d : y  1
  t t  ? z  6 
A. 2x y z  3  0 .
B. 2x y  8  0 .
C. 2x y  5  0 .
D. 2x y  8  0 . Trang3 x y   z Câu 29: Trong không gian Oxyz , cho hai đường thẳng d  2 4 1 :   2 3 2  và x  4t  
d : y  1 6t ;t    . Xác định vị trí tương đối giữa hai đường thẳng d  và d? z  1   4t
A. d  và d cắt nhau. B. d  và d song song với nhau.
C. d  và d trùng nhau.
D. d  và d chéo nhau. 5 2 Cho biết f
 x  . Tính giá trị của P   f
 53x7dx Câu 30: dx 15  ? 1  0 A. P  27 . B. P  15. C. P  37 . D. P  19.
Câu 31: Trong không gian với hệ trục tọa độ Oxyz , cho A1; 2;3, B 3;0; 
1 . Viết phương trình mặt cầu
đường kính AB ? 2 2 2 2 2 2 A. x  
1   y  2   z  3  3 .
B. x  2   y  
1   z  2  3 . 2 2 2 2 2 2
C. x  2   y  
1   z  2  3 .
D. x  2   y  
1   z  2  12 .
Câu 32: Cho số phức z a bi  0 . Xác định phần ảo của số phức 1 z ? b a
A. a b . B.  . 2 2 a  . C. b 2 2 a  . D. 2 2 a b b
Câu 33: Trong không gian Oxyz cho mặt phẳng  P : x y z 1 0 .Trong các đường thẳng sau, đường
thẳng nào cắt mặt phẳng P ? x 1 x 1 t  
A. d :  y  2  t .
B. d :  y  2  t . 3  4  z  3  tz  3  x 1 y 1 z  2 x 1 y 1 z  2 C. d :   . D. d :   . 1 2 1 2 2 1 2 1
Câu 34: Trong không gian tọa độ Oxyz , cho mặt cầu có phương trình 2 2 2
x y z  2x  2 y  6z  2  0
cắt mặt phẳng Oxz theo một đường tròn, xác định bán kính của đường tròn giao tuyến đó? A. 3 2 . B. 4 2 . C. 5 . D. 2 2 .
Câu 35: Cho hai số phức z , z là nghiệm của phương trình 2
z  4z 13  0 . Tính môđun của số phức 1 2
w   z z i z z ? 1 2  1 2 A. w  185 . B. w  3 . C. w  17 . D. w  153 .
Câu 36: Hình phẳng  H  được giới hạn bởi đồ thị hai hàm số 2
y x x  2, y x  2 và hai đường thẳng
x  2, x  3. Tính diện tích của  H  . A. 10 . B. 13 . C. 12 . D. 11.
Câu 37: Trong mặt phẳng Oxy , gọi A là điểm biểu diễn của số phức z  2  5i và B là điểm biểu diễn của số phức z  2
 5i . Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua đường thẳng y x .
D. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O .
Câu 38: Cho số phức z a bi . Tìm mệnh đề đúng trong các mệnh đề sau? Trang4 2 A. 2 z z . B. 2 2 .
z z a b .
C. z z  2a .
D. z z  2bi .  3 x 3
Câu 39: Biết tích phân dx
bln 2; a,b 
 . Tính giá trị của biểu thức a b ? 2   cos x a 0 A. 1 B. 0 . C. 2 . D. 1. 5 2 x  2 1
Câu 40: Biết I
dx  4  a ln 2  b ln 5;  ; a b  
  . Tính S a b ? x 1 A. S 11. B. S  5. C. S  9 . D. S  3  . a
Câu 41: Biết F( )
x  6 1 x là một nguyên hàm của f (x) 
. Tính giá trị của a ? 1 x 1 A. 3  . B. . C. 3 . D. 6 . 6
Câu 42: Cho hình phẳng giới hạn bởi các đường y x ln x, y  0, x e quay quanh trục Ox . Tính thể tích
khối tròn xoay tạo thành? 3 4e 1 3 4e 1 3 2e 1 3 2e 1 A.   . B.   . C.   . D.   . 9 9 9 9 1 1 1
Câu 43: Tìm số phức z biết rằng   ? 2 z 1 2i (1 2i) 10 35 10 14 8 14 8 14 A. z   i . B. z   i . C. z   i . D. z   i . 13 26 13 25 25 25 25 25  2 8 3 f ( x )
Câu 44: Cho hàm số f (x) liên tục trên  và thỏa mãn 2
tan xf (cos x)dx dx  6.   Tính tích phân x 0 1 2 2 f (x )dx  ? x 0 A. 10 . B. 6 . C. 7 . D. 4 . e ln x
Câu 45: Cho I   
x có kết quả dạng I  ln a b với a , b   . Tìm khẳng định đúng?
x ln x  2 d 2 1 1 A. b  1. B. 2 2
4a  9b  11 .
C. 2a  3b  3. D. 2ab 1. a
Câu 46: Trong mặt phẳng Oxy cho điểm A biểu diễn số phức z  1 2i . B là điểm thuộc đường thẳng 1
y  2 sao cho tam giác OAB cân tại O . Điểm B biểu diễn số phức nào sau đây? z 1 2i A. z  1  2i .
B. z  2  2i . C.  .
D. z 1 2i . z  1   2i
Câu 47: Trong không gian với hệ tọa độ Oxyz cho mặt cầu
S có phương trình 2 2 2
x y z  2a  4bx  2a b cy  2b cz d  0 , tâm I nằm trên mặt phẳng   cố
định. Biết rằng 4a b  2c  4 , tìm khoảng cách từ điểm D 1;2; 2 đến mặt phẳng   ? 9 1 1 15 A. . B. . C. . D. . 15 314 915 23    
Câu 48: Trong không gian với hệ trục tọa độ Oxyz , cho OA  2i  3 j  5k . Điểm M thuộc mặt phẳng
Oxy thỏa mãn độ dài AM nhỏ nhất. Xác định tọa độ của điểm M A. 0;3;0 . B. 2;3;5 . C. 3;5;0 . D. 2;3;0 . Trang5
Câu 49. Trong không gian với hệ tọa độ Oxyz cho mặt cầu S  có phương trình 2 2 2
x y z  2a  4bx  2a b cy  2b cz d  0 , tâm I nằm trên mặt phẳng   cố
định. Biết rằng 4a b  2c  4 , tìm khoảng cách từ điểm D 1;2; 2 đến mặt phẳng   ? 9 1 1 15 A. . B. . C. . D. . 15 314 915 23    
Câu 50. Trong không gian với hệ trục tọa độ Oxyz , cho OA  2i  3 j  5k . Điểm M thuộc mặt phẳng
Oxy thỏa mãn độ dài AM nhỏ nhất. Xác định tọa độ của điểm M A. 0;3;0 . B. 2;3;5 . C. 3;5;0 . D. 2;3;0 . BẢNG ĐÁP ÁN 1.A 2.B 3.B 4.B 5.C 6.D 7.C 8.A 9.D 10.A 11.D 12.A 13.C 14.C 15.D 16.D 17.A 18.B 19.D 20.A 21.B 22.B 23.D 24.B 25.B 26.A 27.C 28.D 29.B 30.D 31.C 32.B 33.C 34.D 35.A 36.B 37.B 38.A 39.C 40.B 41.A 42.D 43.A 44.C 45.A 46.C 47.C 48.D 49.C 50.D ĐÁP ÁN CHI TIẾT Câu 1.
Trong không gian Oxyz cho mặt cầu có phương trình: 2 2 2
x y z  2x  6 y 1  0 . Xác định tâm
I và tính bán kính R của mặt cầu đã cho. A. I 1; 3  ;0, R  3 . B. I 2; 6  ;0, R  40 . C. I  1  ;3;0, R  3. D. I 1; 3  ;0, R  11 . Lời giải Chọn A Từ phương trình 2 2 2
x y z  2x  6 y 1  0 suy ra: a  1;b  3
 ;c  0;d  1 . Vì 2 2 2
a b c d  1 9  0 1  9  0 nên phương trình đã cho là phương trình mặt cầu tâm I 1; 3
 ;0 , bán kính R  3. Câu 2.
Viết phương trình tham số của đường thẳng d đi qua điểm M 1;2;3 và có vectơ chỉ phương a1; 4  ;5 . x 1 tx 1 tx 1 tx 1 t     A. y  4   2t .
B. y  2  4t .
C. y  2  4t . D. y  4   2t .     z  5   3tz  3  5tz  3  5tz  5   3tLời giải Chọn B
Đường thẳng d đi qua điểm M 1;2;3 và có vectơ chỉ phương a1; 4
 ;5 nên có phương trình x 1 t
tham số:  y  2  4t . z  35tCâu 3.
Tìm một vectơ pháp tuyến của mặt phẳng P : 2x y  3z  2  0 .    
A. n 2;1;3 .
B. n 2; 1;3 .
C. n 2; 1;3 .
D. n 2; 1; 3   . Lời giải Trang6 Chọn B
Mặt phẳng  P có phương trình: 2x y  3z  2  0 nên có một vectơ pháp tuyến n 2; 1;3 . 1 Câu 4. Tính  1  . x I x e dx . 0 A. e . B. e  2. C. 2  e . D. e  2 . Lời giải Chọn B
Đặt u 1 x và x
dv e dx , ta có du dx và x
v e . Do đó 1 1
1 x. xedx  1 xx 1 x ee .
 dx  1 xx 1 x 1 ee
 0 1 e 1  e  2 . 0 0 0 0 0
Vậy I e  2 . Câu 5.
Xác định tọa độ điểm biểu diễn cho số phức z  2 3i . A.  2  ;3 . B. 2;3 . C. 2; 3  . D.  2  ; 3   . Lời giải Chọn C
Số phức z  2  3i nên điểm biểu diễn z có tọa độ là 2; 3   .   Câu 6.
Trong không gian với hệ trục Oxyz , cho a 3;2; 
1 , b 3; 2;5 . Xác định tọa độ vecto tích có  
hướng a ,b   của hai vecto đã cho? A. 0;8; 12 . B. 8; 12;5 . C. 0;8;12 . D. 8; 12;0 . Lời giải Chọn D    2 1 1 3 3 2 
Có vecto tích có hướng a ,b   ; ;   8;12;0   . 2 5 5 3 3 2   Câu 7.
Cho hình phẳng giới hạn bởi các đường 3
y x 1 , y  0 , x  0 , x 1 quay xung quanh trục Ox .
Tính thể tích của khối tròn xoay tạo thành? 79 5 23 A. . B. . C. . D. 9 . 63 4 14 Lời giải Chọn C
Thể tích của khối tròn xoay tạo thành : 1 1        1 x xV x
1 dx   x  2x   7 4 2 23 3 6 3 1 dx     2  x  .  7 4  14 0 0 0 x y z Câu 8.
Với giá trị nào của tham số m thì đường thẳng 1 2 3 d :  
song song với đường thẳng 2 2 mx 1 t
 :y  2  t t   ? z  2 2tA. 4 . B. 2 . C. 3 . D.1. Lời giải Chọn A Trang7     Đườ x 1 y 2 z 3 ng thẳng d :  
có vecto chỉ phương u  2; 2; m . và đi qua điểm 1   2 2 m M 1; 2;3 . x 1 t  
Đường thẳng  :y  2  t t   có vecto chỉ phương u  1;1;2 . 2   z  2 2t    m
Dễ thấy M  do đó d / /  khi u ;u cùng phương hay 2 2    m  4 . 1 2 1 1 2 Câu 9.
Gọi z ; z là nghiệm của phương trình 2
z  2z  3  0 . Tính giá trị của biểu thức 2 2 zz ? 1 2 1 2 A. 2 3 . B. 3 . C. 2 . D. 6 . Lời giải Chọn D Phương trình 2
z  2z  3  0 có nghiệm z  1 2i ; z  1 2i . 1 2 2 2 2 2 Vậy z
z  1 2i  1 2i  1 2  1 2  6 . 1 2    
Câu 10. Xác định mặt phẳng song song với trục Oz trong các mặt phẳng sau? A. x 1.
B. x y z  0 . C. z  1.
D. x z 1. Lời giải Chọn A
Trục Oz có vecto chỉ phương k 0; 0; 
1 và đi qua O 0;0;0 . Mặt phẳng song song với trục Oz   
phải có vecto pháp tuyến n thỏa mãn .
n k  0 và không đi qua O 0;0;0 .   
Xét đáp án A có vecto pháp tuyến n 1;0;0 . Vì .
n k  0 và mặt phẳng x 1 không đi qua
O 0;0;0 suy ra mặt phẳng song song với trục Oz nên chọn.
Xét đáp án B có 0  0  0  0 suy ra mặt phẳng x y z  0 đi qua O 0;0;0 nên loại.   
Xét đáp án C có vecto pháp tuyến n 0;0;  1 . Vì .
n k  1  0 nên loại.   
Xét đáp án D có vecto pháp tuyến n 1;0;  1 . Vì .
n k  1  0 nên loại. 3 3 1
Câu 11. Cho hàm số f x thỏa mãn f
 xdx 5 và f
 xdx 1. Tính tích phân I f  xdx? 1 1  1  A. I  4 . B. I  6  . C. I  6 . D. I  4 . Lời giải Chọn D 3 1 3 1 Ta có
f xdx 1
f xdx f xdx 1
f xdx 1 5  4      . 1  1  1 1 
Câu 12. Tính khoảng cách từ điểm M 3;0;0 đến mặt phẳng Oxy ? A. 0 . B. 2 . C. 1. D. 2 . Lời giải Chọn A
Ta có d M ;Oxy  z  0 . M Trang8  6
Câu 13. Tính tích phân 3
s in x.cos x dx  . 0 1 A. 5 . B. 6 . C. . D. 4 . 64 Lời giải Chọn C Cách 1:
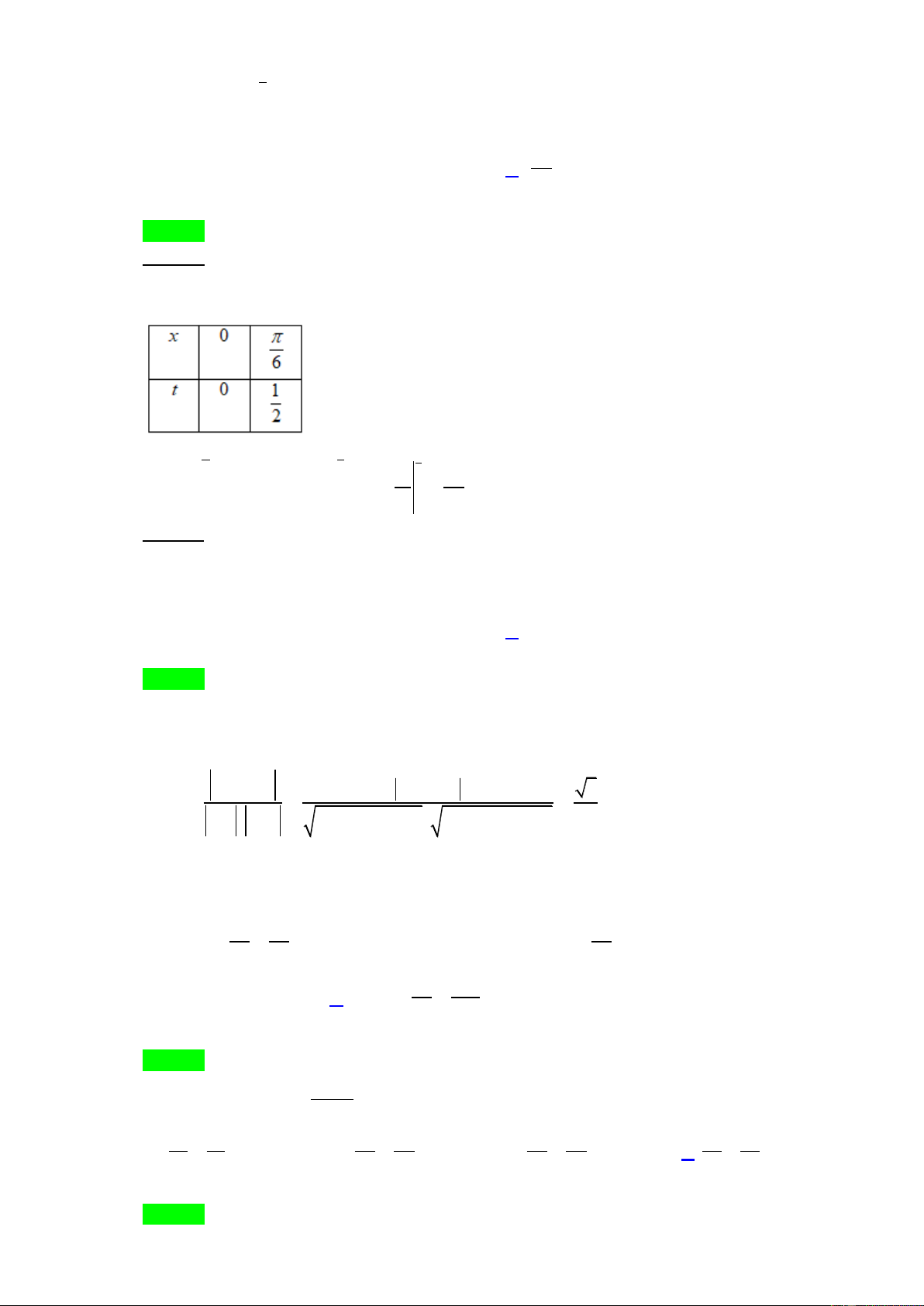
Đặt t  sin x  dt cos d x x . Đổi cận :  1 1 6 2 4 2 t 1 Khi đó 3 3
s in x.cos x dx  t dt     . 4 64 0 0 0
Cách 2: Sử dụng caiso bấm ra kết quả. Câu 14.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  :2x y z 3  0 và
 :3x 4y 5z  0. Xác định góc tạo bởi hai mặt phẳng   và  ? A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . Lời giải Chọn C
Gọi  là góc tạo bởi hai mặt phẳng   và   .   Ta có n  2;1;  1 , n     3; 4;5     .    n  .  n  6  4  5 3
cos      . 2 2  n  .  n  2 2    2 2 1 1 . 3   4   2 2  5 0    30 .
Câu 15. Tìm họ nguyên hàm của hàm số f x 3
x  3x  2 ? x x x
A. F x 4 2    2x C .
B. F x 4 2 
 3x  2x C . 4 2 3 x x
C. F x 2
 3x  3x C . D. F x 4 2 3    2x C . 4 2 Lời giải Chọn D 3  4i
Câu 16. Xác định số phức z  4  ? i 16 11 9 23 9 4 16 13 A. i . B. i . C.i . D.i . 15 15 25 25 25 25 17 17 Lời giải Chọn D Trang9 3  4i
3 4i.4  i 2    Ta co 12 3i 16i 4i 16 13 ́ z      i . 2 4  i 4 1 17 17 17
Câu 17. Tính phần ảo của số phức z  2  3i.2  3i . A. 13 . B. 0 . C. 9  i . D.13i . Lời giải Chọn A
Ta có : z    i   i 2
2 3 . 2 3  4  6i  6i  9i  13 .
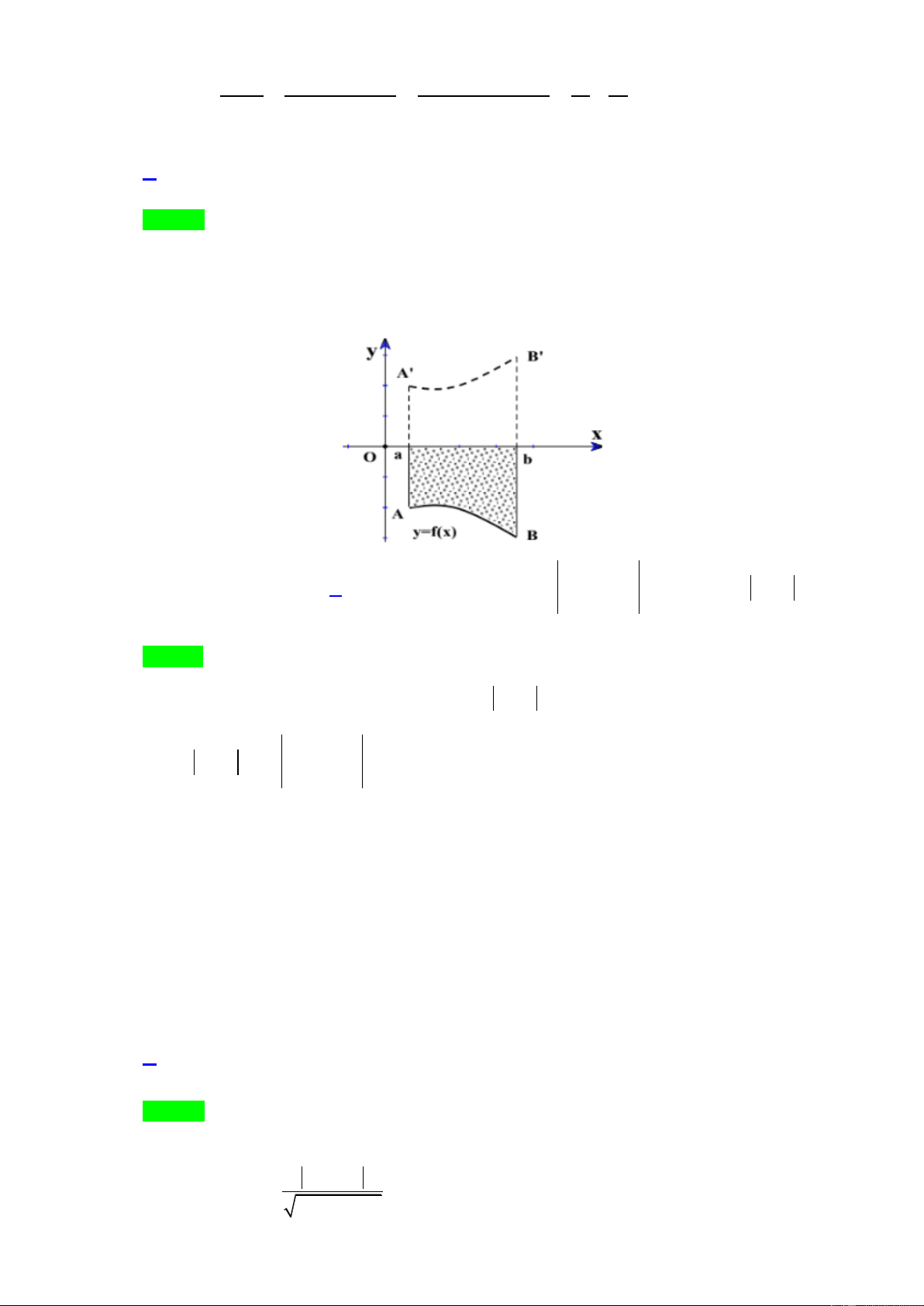
Câu 18. Ký hiệu S là diện tích hình thang cong giới hạn bởi đồ thị hàm số liên tục y f x , trục hoành
và hai đường thằng x a, x b như trong hình vẽ (Phần chấm đen). Tìm khẳng định sai? b b b b
A. S   f xdx . B. S f
 xdx. C.S f
 xdx . D.S f
 x dx . a a a a Lời giải Chọn B b b
Dựa vào đồ thị hàm số y f x , ta có S f
 x dx   f xdx hoặc a a b b S f
 x dx f  xdx . a a b Vậy S f
 xdx là khẳng định sai. a
Câu 19. Trong không gian Oxyz , cho mặt cầu S x y   z  2 2 2 : 2 1 và mặt phẳng
:3x4z 12  0. Khi đó khẳng định nào sau đây đúng?
A. Mặt phẳng   tiếp xúc mặt cầu  S  .
B.Mặt phẳng   cắt mặt cầu  S  theo một đường tròn.
C.Mặt phẳng   đi qua tâm của mặt cầu  S  .
D.Mặt phẳng   không cắt mặt cầu  S  . Lời giải Chọn D
Mặt cầu S x y   z  2 2 2 : 2
1 có tâm I 0;0;2 và bán kính R 1. 4.2 12
Ta có d I,    4  R . 2 2 2 3  0  4 Trang10
Vậy Mặt phẳng   không cắt mặt cầu  S  .
Câu 20. Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A BCD
  biết A2;1;2 , B1;2  ;1 , C  2
 ;3;2 , D3;0 
;1 . Tìm tọa độ điểm B . A. B  1  ;2;2.
B. B 2;  2;  1 .
C. B 1;  2;  2 .
D. B 2; 1; 2 . Lời giải Chọn A
Gọi B x; y ; z ; I , H lần lượt là trung điểm của AC, B D
  . Suy ra I 0;1;2, H 2;1  ;1 . 1   x  2  0 x  1      Vì ABC . D A BCD
  là hình hộp nên BB  IH  2  y 11  y  2 .   1 z  1 2 z  2   b a
Câu 21. Cho hàm số y f x liên tục trên đoạn ;
a c và a b c . Biết f xdx  1
 0, f xdx  5    . a c b Tính f  xdx? c A. 15 . B. 15  . C. 5  . D. 5 . Lời giải Chọn B b a b f
 xdx f
 xdxf
 xdx  5    1  0  1  5 c c a 3 3x e
Câu 22. Giả sử F x là một nguyên hàm của   x e f x
trên 0;  và I dx  . Khẳng định nào sau x x 1 đây đúng?
A. I F 4  F 2 .
B. I F 6  F 3. C. I F 9  F 3 .
D. I F 3  F   1 . Lời giải Chọn B 1 t
Đặt t  3x  dt  3dx  dt  dx; x  . 3 3 Đổi cận Trang11 2 3x 6 t 6 1 3 t e e e 6 I  dx  dt
dt F (t)  F (6)  F (3)    . 3 x 3 t t 1 3 3
Câu 23. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P song song với hai đường thẳng giả x  2  t    sử x 2 y 1 z  : 
 ,  : y  3 2t . Tìm một vectơ pháp tuyến của mặt phẳngP ? 1 2 2 3  4 x 1t      A. n   5  ; 6  ;7 . B. n   5  ;6; 7  .
C. n  5; 6;7 .
D. n  5;6;7 . PPPPLời giải Chọn D 
Gọi  có vectơ chỉ phương u  2; 3; 4 1   1 
 có vectơ chỉ phương u  1;2; 1  2   2
Do mặt phẳng P song song với hai đường thẳng  ; nên P có vectơ pháp tuyến 1 2     n u  ,u   5  ;6;7 . P 1 2    
Câu 24. Trong mặt phẳng phức (hình dưới), số phức z  3  4i được biểu diễn bởi điểm nào trong các điểm trên hình vẽ? A. Điểm A . B. Điểm D . C.Điểm C . D.Điểm B . Lời giải Chọn B
Điểm biểu diễn số phức z  3  4i trong mặt phẳng tọa độ là điểm D3; 4  .
Câu 25. Cho hình phẳng  H  giới hạn bởi các đường 2
y x  2x , trục hoành, trục tung, đường thẳng
x  1. Tính thể tích V hình tròn xoay sinh bởi  H khi  H quay quanh trục Ox ? 7 8 15 4 A. V  . B. V  . C.V  . D.V  . 8 15 8 3 Lời giải Chọn B
Thể tích của khối tròn xoay cần tìm là 1 V    x x    x  2x 1
dx   x  4x  4x  5 3 2 4 1 8 2 4 3 2 4 dx     x    .  5 3 0  15 0 0 Trang12
Câu 26. Tìm một họ nguyên hàm của hàm số   4 2  x f x e ? 1  1  A.   2 1 d  .   x f x x e C . B.   2 1 d  .   x f x x e C . 2 2 1  C.   2 1 d     x f x x e C . D.   4 2 d  .   x f x x e C . 2 Lời giải Chọn A  1  Ta có    2 1 2 1 d  d  .  .  x x f x x e x e C 2
Câu 27. Cho số phức z a bi a,b   ;a  0 . Xác định kết quả của phép toán z z ? A. 0. B. Số thuần ảo. C. Số thực. D. 2. Lời giải Chọn C
Ta có z a bi z a b . i
Suy ra z z  2a , nên chọn đáp án C.
Câu 28. Trong không gian Oxyz , viết phương trình mặt phẳng  P đi qua điểm A3; 2; 5   và vuông góc x  3 2t
với đường thẳng d : y  1
  t t  ? z  6 
A. 2x y z  3  0 .
B. 2x y  8  0 .
C. 2x y  5  0 .
D. 2x y  8  0 . Lời giải Chọn D Đườ 
ng thẳng d có vectơ chỉ phương u  2;1;0 . d
Mặt phẳng  P vuông góc với đường thẳng d nên  P có một vectơ pháp tuyến là  
n u  2;1;0 . P d
Khi đó phương trình mặt phẳng P đi qua điểm A3;2; 5
  và có vectơ pháp tuyến là 
n  2;1;0 : 2 x  3  y  2  0  2x y 8  0. Px y   z
Câu 29. Trong không gian Oxyz , cho hai đường thẳng d  2 4 1 :   2 3 2  và x  4t  
d : y  1 6t ;t    . Xác định vị trí tương đối giữa hai đường thẳng d  và d? z  1   4t
A. d  và d cắt nhau. B. d  và d song song với nhau.
C. d  và d trùng nhau.
D. d  và d chéo nhau. Lời giải Chọn B
Đường thẳng d  có vectơ chỉ phương u  2;3;2 và đi qua điềm M 2; 4  ;  1 d  
Đường thẳng d có vectơ chỉ phương u   
4;6;4 và đi qua điềm M0;1;  1 d     Suy ra u ,u     0;0;0 0 d d Trang13
Ta có M   d .
Vậy d  và d song song nhau. 5 2 Câu 30. Cho biết f
 xdx 15. Tính giá trị của P   f
 53x7dx  ? 1  0 A. P  27 . B. P  15. C. P  37 . D. P  19. Lời giải Chọn D 2 2 2
Ta có P   f
 53x7dx f
 53xdx7 dx  0 0 0 2 1  5 1   f
   x   x 2 1  x   f  t 1 5 3 d 5 3 7 dt 14  f
 tdt 14  514 19. 0 3 3 3 0 5 1 
Câu 31. Trong không gian với hệ trục tọa độ Oxyz , cho A1; 2;3, B 3;0; 
1 . Viết phương trình mặt cầu
đường kính AB ? 2 2 2 2 2 2 A. x  
1   y  2   z  3  3 .
B. x  2   y  
1   z  2  3 . 2 2 2 2 2 2
C. x  2   y  
1   z  2  3 .
D. x  2   y  
1   z  2  12 . Lời giải Chọn C
Mặt cầu đường kính AB có tâm I 2;1; 2 và bán kính 1 1 R AB  3 2 1
 0  22  1 32  3 . 2 2
Nên phương trình của mặt cầu là: x  2   y  2  z  2 2 1 2  3.
Câu 32. Cho số phức z a bi  0 . Xác định phần ảo của số phức 1 z ? b a
A. a b . B.  . 2 2 a  . C. b 2 2 a  . D. 2 2 a b b Lời giải Chọn B  1 1 a bi a b  Ta có 1 z      i 2 2 2 2 2 2 z a bi a b a b a  . bb
Vậy phần ảo của số phức 1 z là: 2 2 a  . b
Câu 33. Trong không gian Oxyz cho mặt phẳng  P : x y z 1 0 .Trong các đường thẳng sau, đường
thẳng nào cắt mặt phẳng P ? x 1 x 1 t  
A. d :  y  2  t .
B. d :  y  2  t . 3  4  z  3  tz  3  x 1 y 1 z  2 x 1 y 1 z  2 C. d :   . D. d :   . 1 2 1 2 2 1 2 1 Lời giải Chọn C Trang14
Mặt phẳng P có vec tơ pháp tuyến n(1;1;1) 
+ Đáp án A: đường thẳng d đi qua điểm M (1; 2;3) và có véc tơ chỉ phương u (0;1;1) 3 3 3  
u .n  1.0 1.( 1
 ) 1.1  0  đường thẳng d song song hoặc nằm trên P . 3 3 
+ Đáp án B: đường thẳng d đi qua điểm M (1; 2;3) và có véc tơ chỉ phương u (1;1;0) 4 4 4  
u .n  1.11.( 1
 )  0.1  0  đường thẳng d song song hoặc nằm trên P . 4 4 
+ Đáp án C: đường thẳng d đi qua điểm M (1; 1  ; 2
 ) và có véc tơ chỉ phương u (2;1;2) 1 4 1  
u .n  2.11.( 1
 )  2.1  3  đường thẳng d cắt mặt phẳng P . 1 1 
+ Đáp án D: đường thẳng d đi qua điểm M (1; 1  ; 2
 ) và có véc tơ chỉ phương u (1;2;1) 2 2 2  
u .n  1.1 2.( 1
 ) 1.1  0  đường thẳng d song song hoặc nằm trên P . 2 2
Câu 34. Trong không gian tọa độ Oxyz , cho mặt cầu có phương trình 2 2 2
x y z  2x  2 y  6z  2  0
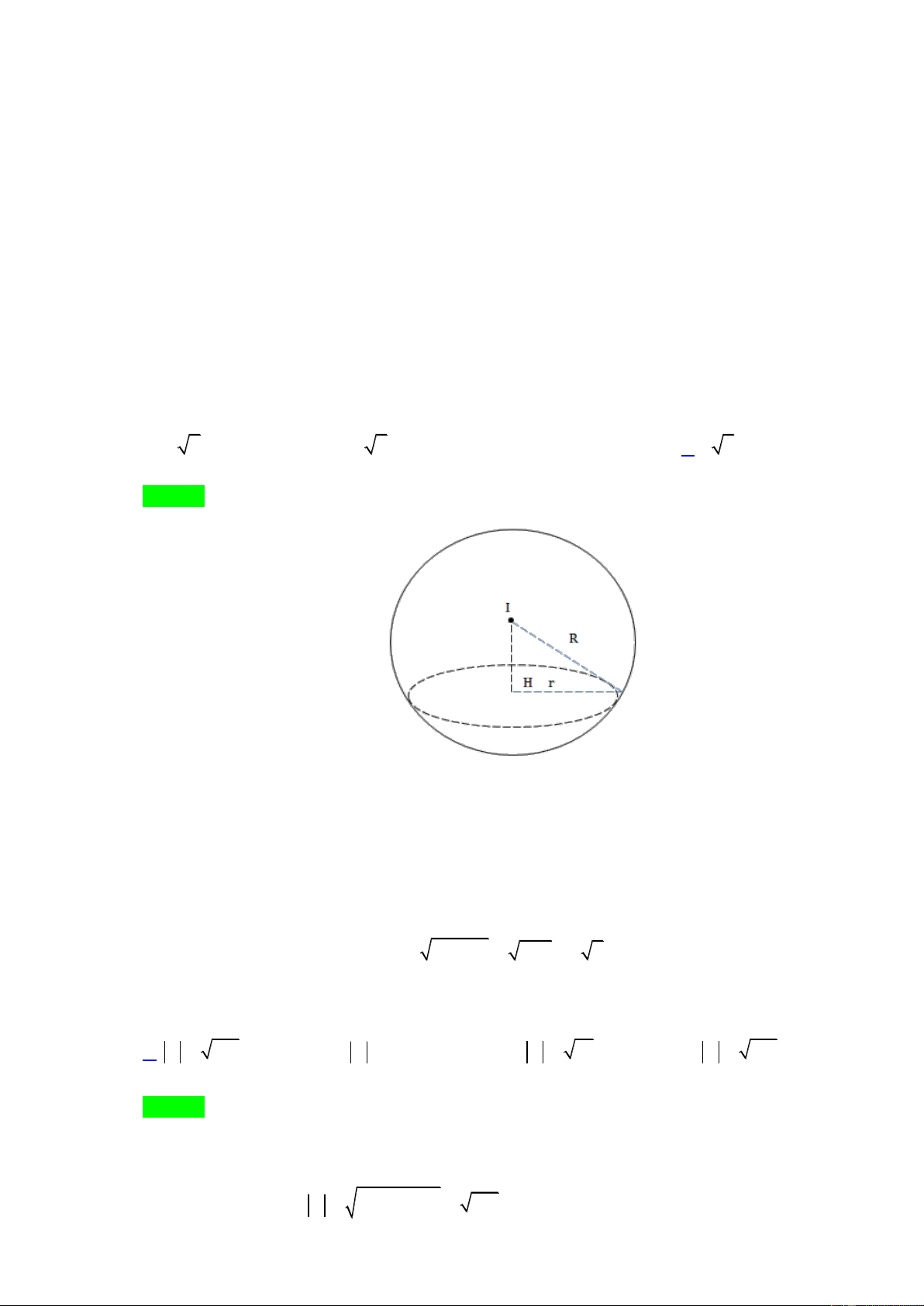
cắt mặt phẳng Oxz theo một đường tròn, xác định bán kính của đường tròn giao tuyến đó? A. 3 2 . B. 4 2 . C. 5 . D. 2 2 . Lời giải Chọn D d
Mặt cầu có tâm I (1; 1;3) bán kính R  3
Mặt phẳng Oxz có phương trình y  0
Gọi H 1;0;3 là hình chiếu của I lên mặt phẳng Oxz  IH  Oxz
H là tâm đường tròn giao tuyến
Ta có : d (I;Oxz)  IH  1  d
Bán kính đường tròn giao tuyến: 2 2 r
R d  9 1  2 2 .
Câu 35. Cho hai số phức z , z là nghiệm của phương trình 2
z  4z 13  0 . Tính môđun của số phức 1 2
w   z z i z z ? 1 2  1 2 A. w  185 . B. w  3 . C. w  17 . D. w  153 . Lời giải Chọn A
z z  4
Theo định lí Vi-ét ta có: 1 2  . z .z  13  1 2 Suy ra w   i w    2 2 13 4 13 4  185 . Trang15
Câu 36. Hình phẳng  H  được giới hạn bởi đồ thị hai hàm số 2
y x x  2, y x  2 và hai đường thẳng
x  2, x  3. Tính diện tích của  H  . A.10 . B. 13 . C.12 . D.11. Lời giải Chọn B
Diện tích hình phẳng  H  là: 3 2 S
x x  2  x dxH  2   2  3 2  x  4 dx 2 2
   x  4 3 2 dx   2 x  4 dx 2  2 2 3 3 3  x   x
   4x    4x 13 .  3   3  2  2
Câu 37. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
2z - 6z + 5 = 0 . Điểm nào sau đây biểu o
diễn số phức iz ? o  1 3   3 1   3 1   1 3  A. M ; . B. M ; . C. M ;  . D. M  ; . 1          2 2  2  2 2  3  2 2  4  2 2  Lời giải Chọn A é 3+ i z ê = 1 ê 2 Ta có 2
2z - 6z + 5 = 0 Û ê . ê 3- i z ê = 2 êë 2 - æ ö Khi đó 3 i 1 3 1 3 z = Þ iz = + i Þ M ç ; ÷ ç ÷. 0 0 1 2 2 2 çè2 2÷ø 2 íï 7- 4x khi 0 £ x £ 1 ï
Câu 38. Cho hàm số f (x)= ì
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 ïï 4- x khi x > 1 î
f (x) và các đường thẳng x = 0, x = 3, y = 0 ? 20 29 A. . B. 9 . C. 10 . D. . 3 3 Lời giải Chọn D
Diện tich hình phẳng cần tìm là: 3 1 3 S =
f (x) dx =
f (x) dx + f (x) dx ò ò ò 0 0 1 1 3 2 2 = 7 - 4x dx + 4 - x dx ò ò 0 1 Trang16 1 2 3 = ò ( 2
7 - 4x )dx + ò ( 2 4 - x )dx + ò ( 2 - 4 + x )dx 0 1 2 29 = . 3
Câu 39. Trong mặt phẳng Oxy , gọi A là điểm biểu diễn của số phức z  2  5i và B là điểm biểu diễn
của số phức z  2
 5i . Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C.Hai điểm A và B đối xứng với nhau qua đường thẳng y x .
D.Hai điểm A và B đối xứng với nhau qua gốc tọa độ O . Lời giải Chọn B
A là điểm biểu diễn của số phức z  2  5i A2;5 .
B là điểm biểu diễn của số phức z  2
  5i B 2  ;5.
Suy ra: hai điểm A và B đối xứng với nhau qua trục tung.
Câu 40. Cho số phức z a bi . Tìm mệnh đề đúng trong các mệnh đề sau? 2 A. 2 z z . B. 2 2 .
z z a b .
C. z z  2a .
D. z z  2bi . Lời giải Chọn A
z a bi z  a bi2 2 2 2
a b  2abi .
z  a b 2  ab2 2 2 2   2 2 a b 2 2 2 2 2
a b z .  3 x 3
Câu 41. Biết tích phân dx
bln 2; a,b 
 . Tính giá trị của biểu thức a b ? 2   cos x a 0 A. 1B. 0 . C. 2 . D.1. Lời giải Chọn C u x   du dx Đặt:  dx   dv   v  tan x 2  cos x Ta có:      3 3 3 x s inx
dx x tan x 3  tan xdx x tan x 3  dx    2 cos x cos x 0 0 0 0 0   3  d cos x  3 3  . 3 
 . 3  ln cos x 3    ln 2   bln 2  3 cos x 3 3 a 0 0
Suy ra: a  3;b  1  a b  2 . 5 2 x  2 1
Câu 42. Biết I
dx  4  a ln 2  b ln 5;  ; a b  
  . Tính S a b ? x 1 A. S 11. B. S  5. C. S  9 . D. S  3  . Trang17 Lời giải Chọn B Ta có: 2 5 2 2 x  2 1 2 x  2 1 2 2  x 5 1 2  x  2 1 I dx dx dx dx     x x x x 1 2 1 2 2 5 5  2x 2x  3 2 2 5 5  dx dx  5 ln x
 2x  2x  3ln x    x x 1 1 2 2 1 2
 4  8ln 2  3ln 5  4  a ln 2  bln 5
a  8;b  3
  S a b  5 . a
Câu 43. Biết F( )
x  6 1 x là một nguyên hàm của f (x) 
. Tính giá trị của a ? 1 x 1 A. 3  . B. . C. 3 . D. 6 . 6 Lời giải Chọn A a Ta có: dx  2
a 1 x  6 1 x a  3   . 1 x
Câu 44. Cho hình phẳng giới hạn bởi các đường y x ln x, y  0, x e quay quanh trục Ox . Tính thể tích
khối tròn xoay tạo thành? 3 4e 1 3 4e 1 3 2e 1 3 2e 1 A.   . B.   . C.  . D.  . 9 9 9 9 Lời giải Chọn D
Ta có: x ln x  0  x  1 e V  x x  3 2 2e 1 ln dx      (Bấm casio) 9 1 1 1 1
Câu 45. Tìm số phức z biết rằng   ? 2 z 1 2i (1 2i) 10 35 10 14 8 14 8 14 A. z   i . B. z   i . C. z   i . D. z   i . 13 26 13 25 25 25 25 25 Lời giải Chọn A Ta có: 1 1 1 1 8 14i 25 10 35 10 35      z    i z   . i 2 z 1 2i (1 2i) z 25 8 14i 13 26 13 26  2 8 3 f ( x ) Câu 46.
Cho hàm số f ( x) liên tục trên  và thỏa mãn 2
tan xf (cos x)dx dx  6.   Tính x 0 1 2 2 f (x ) tích phân dx  ? x 0 A. 10 . B. 6 . C. 7 . D. 4 . Lời giải Chọn C Trang18  2 Xét 2
tan xf (cos x)dx  6.  0  Đặ dt t 2 2
cos x t dt  2  sin .
x cos xdx  2 cos x tan xdx  2t tan xdx  tan xdx  . 2t
x  0  t 1  0 1 1 Đổ f (t)dt f (t)dt f (t)dt i cận:   suy ra 6   6    12    x   t  0  2  t 2t t  2 1 0 0 8 3 f ( x ) Xét dx  6.  x 1 Đặt 3 3 2
x u x u dx  3u du
x 1 u 1 2 2 2 2 Đổ f (u) f (u) f (u) f (t) i cận  suy ra 2 6  3u du  3 du du  2  dt  2.    
x  8  u  2 3 u u u t 1 1 1 1 2 2 f (x ) Tính I dxx 0 Đặt 2
x t dt  2xdx ,
x  0  t  0  Đổi cận  suy ra :
x  2  t  2 2 2 2 1 2 f (x ) f (t) 1  f (t) f (t)  1 I dx dt     dt dt     (12  2)  7. x 2t 2 t t 2 0 0  0 1  e ln x
Câu 47. Cho I   
x có kết quả dạng I  ln a b với a , b   . Tìm khẳng định đúng?
x ln x  2 d 2 1 1 A. b  1. B. 2 2
4a  9b  11 .
C. 2a  3b  3. D. 2ab 1. a Lời giải Chọn A Đặ 1
t t  ln x  2  dt dx . x e 3 3 ln x t  2 3     3 1 Khi đó 1 2 2 I      I   dt    ln | t |     ln  . x x dt ln x  2 d 2 2 t 2  t t   t  2 3 1 2 2 2 3 1 1 Suy ra a  ; b  . Do đó  b  1 . 2 3 a
Câu 48. Trong mặt phẳng Oxy cho điểm A biểu diễn số phức z  1 2i . B là điểm thuộc đường thẳng 1
y  2 sao cho tam giác OAB cân tại O . Điểm B biểu diễn số phức nào sau đây? z 1 2i A. z  1  2i .
B. z  2  2i . C.  .
D. z 1 2i . z  1   2i Lời giải Chọn C
Điểm A biểu diễn số phức z 1 2i A 1; 2 . 1  
Vì B y  2  B x ; 2 . Trang19
Tam giác OAB cân tại O 2 2 2 2
OA OB  1  2  x  2  x  1  .
Vậy B 1; 2 hoặc B  1
 ; 2 . Do đó B biểu diễn số phức z 12i hoặc z  1   2i .
Câu 49. Trong không gian với hệ tọa độ Oxyz cho mặt cầu S  có phương trình 2 2 2
x y z  2a  4bx  2a b cy  2b cz d  0 , tâm I nằm trên mặt phẳng   cố
định. Biết rằng 4a b  2c  4 , tìm khoảng cách từ điểm D 1;2; 2 đến mặt phẳng   ? 9 1 1 15 A. . B. . C. . D. . 15 314 915 23 Lời giải Chọn C
Ta có I a  4b;  a b c; b c .
Giả sử   : Ax By Cz D  0, vì I   nên ta có:
Aa  4b  B a b c  C b
  c  D  0   ABa  4AB Cb  B Cc D  0.  1 A    4 A B  4   17 
4A B C  1 B  
Theo bài ra 4a b  2c  4 , nên đồng nhất hệ số ta được:    4  . B C  2    25   4 C D     4  D  4  Suy ra   1 17 25 :  x y
z  4  0 hay   : x 17 y  25z 16  0 . 4 4 4 117.2 25 2  1  6 1
Vậy d D ,      . 2 2 2 1 17  25 915   
Câu 50. Trong không gian với hệ trục tọa độ Oxyz , cho OA  2i  3 j  5k . Điểm M thuộc mặt phẳng
Oxy thỏa mãn độ dài AM nhỏ nhất. Xác định tọa độ của điểm M A. 0;3;0 . B. 2;3;5 . C. 3;5;0 . D. 2;3;0 . Lời giải Chọn D
Ta có A2;3;5 . Gọi A là hình chiếu của A trên mặt phẳng Oxy , suy ra AA  AM .
Như vậy độ dài AM nhỏ nhất khi và chỉ khi M A  M 2;3;0 . HẾT Trang20