








Preview text:
Đề ôn thi học kỳ 2_ Đề 1
Phần 1 : Trắc nghiệm 4 phương án 2 2 2
Câu 1: Trong kgOxyz, cho điểm A (3, 2, 2) thuộc mặt cầu (S) : (x − ) 1 + (y − 2) + (z + ) 1 = 13 . Phương
trình mặt phẳng tiếp xúc với (S) tại A là
A. x + 2y + z − 9 = 0 . B. 2x + 3z −12 = 0.
C. x − 2y − z + 3 = 0 . D. 2x − 3z = 0 .
Câu 2: Trong kgOxyz, cho hai mặt phẳng (P) : mx − ( 2
m + 2)y + (2 − m)z +1= 0 và (Q) :
x −3y + z + 3 = 0 . Tìm m để (P) song song với (Q) A. m =1. B. m =1 m = 2 . C. m = 1 − m = 2 − . D. m = 2 . x y z x y −1 z +1
Câu 3: Trong kgOxyz, cho hai đường thẳng d : = = và d : = = . Đường thẳng d qua 1 1 1 1 2 2 1 1 − 3 A (2,1, 2
− ) và vuông góc với cả hai đường thẳng d và d có phương trình: 1 2 x − 2 y −1 z + 2 x − 2 y −1 z + 2 A. = = . B. = = . 2 −3 1 − 2 3 1 x + 2 y − 3 z +1 x + 2 y − 3 z +1 C. = = . D. = = . 2 − 1 − 2 2 1 − 2
Câu 4: Trong kgOxyz cho hai điểm A (− 2,1,3), B(4, 2, − )
1 . Gọi mp(P) qua A sao cho khoảng cách từ B
đến mp(P) là lớn nhất. Phương trình mặt phẳng (P) là
A. 6x + y − 4z + 23 = 0 . B. 6x + y − 4z − 23 = 0 .C. 6x − y − 4z + 23 = 0 . D. 6x − y − 4z − 23 = 0 2x + 3 , x 1
Câu 5: Cho hàm số f (x) =
. Biết F ( x ) là nguyên hàm của f ( x ) trên thỏa mãn 2 3 x + 2 , x 1
F (0) = 2 . Giá trị của F (− ) 1 + 2F (2) bằng A. 10 . B. 21. C. 11. D. 23.
Câu 6: Gọi (H) là hình phẳng giới hạn bởi các đường: x y =
xe , y = 0 , x = 0 , x = 1 . Cho (H) quay quanh
trục Ox, ta được vật thể tròn xoay có thể tích V bằng A. 2 . B. . C. e . D. 2 e .
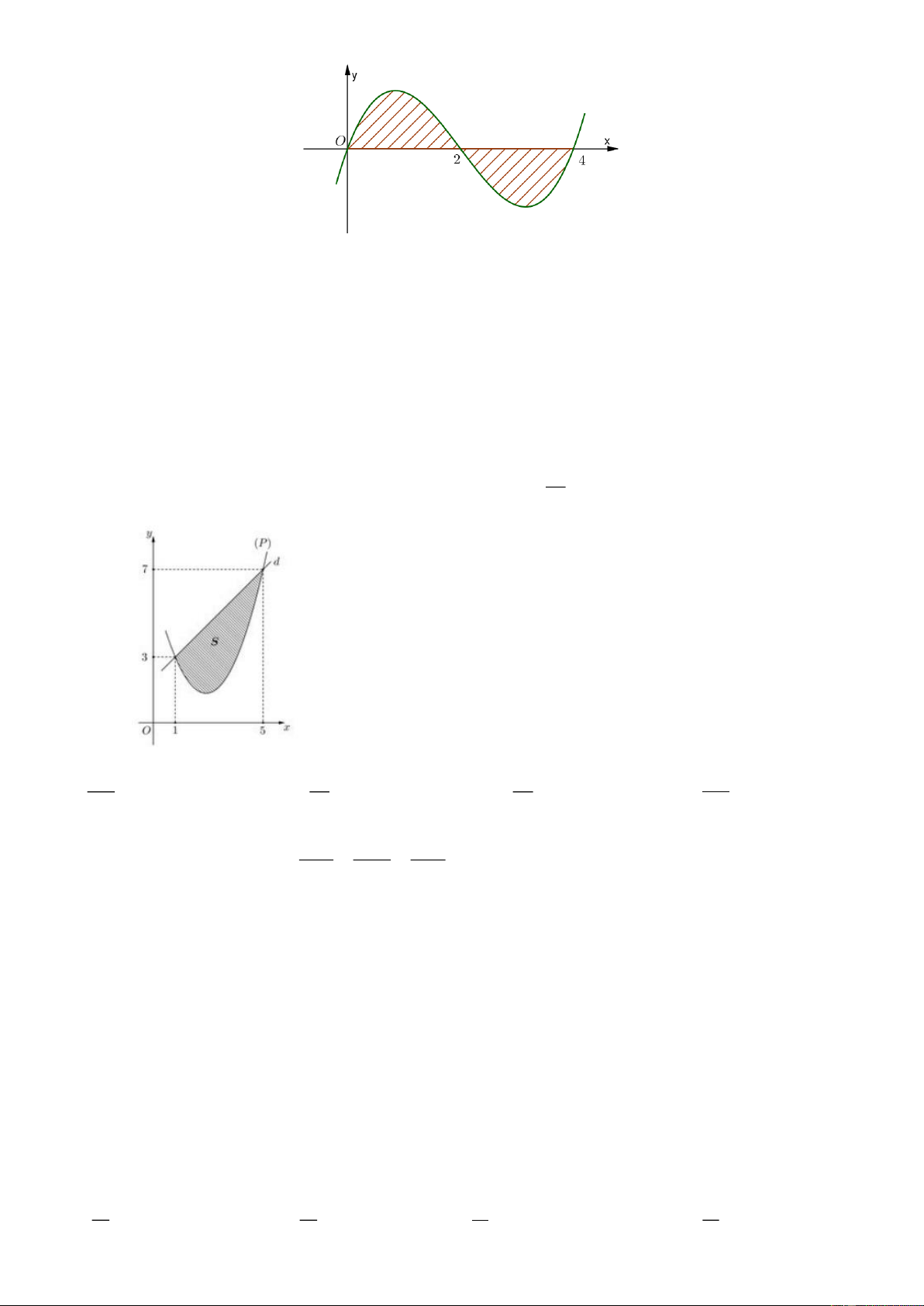
Câu 7: Diện tích S của hình phẳng được gạch chéo trong hình bên được tính theo công thức nào sau đây? 1 4 2 4 A. S = f (x)dx .
B. S = − f (x)dx + f (x)dx . 0 0 2 2 4 2 4 C. S =
f (x)dx − f (x)dx .
D. S = − f (x)dx + f (x)dx . 0 2 0 2
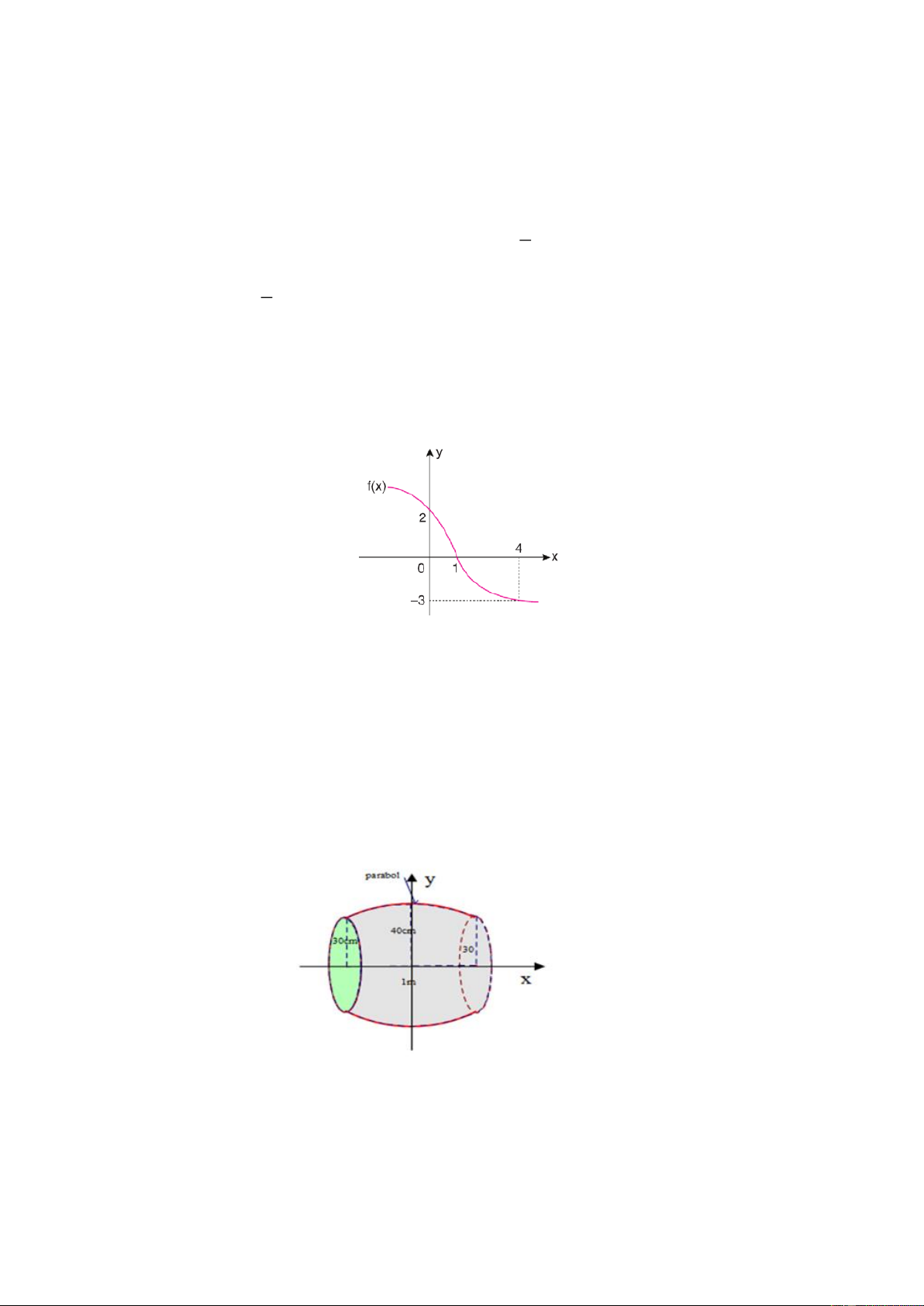
Câu 8: Cho hàm số f (x) có đồ thị (P) và đường thẳng d cắt (P) tại hai điểm như trong hình vẽ. Biết 32 5
diện tích hình phẳng giới hạn bởi (P) và d là S =
. Tích phân (2x −5) /f (x)dx bằng 3 1 104 76 22 188 A. . B. . C. . D. . 3 3 3 3 x −1 y − 2 z − 3
Câu 9: Trong kgOxyz cho d: = =
. Gọi (S) là mặt cầu có tâm I (4,3, 4) và tiếp xúc với d. 2 −1 1
Phương trình mặt cầu (S) là 2 2 2 2 2 2
A. (x − 4) + (y − 3) + (z − 4) = 25 .
B. (x + 4) + (y + 3) + (z + 4) = 5 . 2 2 2 2 2 2
C. (x − 4) + (y − 3) + (z − 4) = 5 .
D. (x + 4) + (y + 3) + (z + 4) = 25 .
Câu 10: Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 5 bi đỏ và 5 bi
xanh, hộp thứ hai chứa 6 bi đỏ và 4 bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển
sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai (giả sử viên bi được lấy ra
từ hộp thứ hai là bi đỏ). Tính xác suất viên bi đỏ đó là của hộp thứ nhất. 7 1 1 7 A. . B. . C. . D. . 13 13 11 11 2
Câu 11: Một hộp chứa 7 quả bóng được đánh số từ 1 đến 7. An lấy ngẫu nhiên một quả bóng, bỏ ra ngoài,
rồi lấy tiếp một quả bóng nữa. Xét các biến cố : A "Quả bóng lấy ra lần đầu có số chẵn" B: "Quả
bóng lấy ra lần hai có số lẻ". Tính P (B | A) . 2 2 3 1 A. . B. . C. . D. . 7 3 7 3
Câu 12: Cho hai biến cố A và B , với P ( B) = 0,8 , P( A | B) = 0,7 , P ( A | B) = 0, 45. Tính P(B | A) . 56 A. . B. 0,25. C. 0,65. D. 0,5. 65 Phần 2 : Đúng/Sai
Câu 1. Trong kgOxyz cho hai điểm A (1, −1, 2), B(3,1, 4) . Điểm M tùy ý thỏa M . A MB = 5 x − y + z −
a) Phương trình đường thẳng AB : 1 1 2 = = 2 2 1
b) Điểm M thuộc mặt cầu có phương trình (x − )2 + y + (z − )2 2 2 3 = 8 .
c) Diện tích lớn nhất của tam giác MAB là 4 6
d) Tổng giá trị lớn nhất và nhỏ nhất của đoạn OM bằng 2 13 3 2
Câu 2. Cho hàm số f (x) xác định trên 1
\ thỏa mãn f ( x) =
, f (0) = 1 và f = 2 3 3x −1 3 2 2 3 3 a)
f ( x) dx = 1 − . b) f
( x) − 4 dx 2 = − . 0 0 c) f (− ) 1 = ln 4 +1 . d) f (− )
1 + f (3) = 3 + 5ln 2 .
Câu 3. Một ô tô đang chạy thẳng đều với vận tốc 20 m/s thì người lái xe phát hiện có hàng rào chắn
ngang đường ở phía trước cách xe 45 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ
thời điểm đó, xe chuyển động chậm dần đều với vận tốc v (t ) = −2t + 20 (m/s) , trong đó t là thời
gian được tính từ lúc người lái đạp phanh.
a) Thời gian kể từ lúc đạp phanh đến khi ô tô dừng hẳn là 10s.
b) Quãng đường ô tô chạy được từ lúc đạp phanh đến khi ô tô dừng hẳn là 2000 . 3
c) Quãng đường ô tô chạy được trong 2s trước khi đạp phanh là 40m.
d) Quãng đường ô tô chạy được trong 12s cuối là 140m. 3
Câu 4. Số khán giả đến xem buổi biểu diễn ca nhạc ngoài trời phụ thuộc vào thời tiết. Giả sử nếu trời
không mưa thì xác suất để bán hết vé là 90%, nếu trời mưa xác suất để bán hết vé giảm xuống còn
35%. Dự báo thời tiết cho thấy khả năng có mưa vào buổi biểu diễn là 40% . Nhà tố chức sư kiện muốn biết khả năng để bán hết vé là bao nhiêu?
Xét hai biến cố sau: A: "Biến cố trời mưa"; B: "Biến cố bán hết vé".
a) P ( A) = 0, 4 .
b) P (B | A) = 0,9, P (B | A) = 0,35 .
c) P ( B) P ( A B) + P ( A B) .
d) P ( B) = 0, 68 .
Phần 3 : Điền đáp số
Câu 1. Cho hàm số y = f ( x) có đồ thị như hình bên. 4
Giá trị của 2 f
(x)dx bằng bao nhiêu? ĐS : 10 − 0
Câu 2. Một cái trống trường có bán kính các mặt trống là 30cm, thiết diện vuông góc với trục và cách đều
hai mặt trống có diện tích là 1600π(cm2), chiều dài của trống là 1m. Biết rằng mặt phẳng chứa
trục, cắt mặt xung quanh của trống là các đường Parabol. Biết thể tích của cái trống bằng a 3 dm .
Tìm a ( kết quả làm tròn đến hàng phần mười) ` ĐS : 425,2
Câu 3. Cho hàm số f ( x ) thỏa / f (x).f (x ) = 2x , x
R và f (0) =1. Gọi (H) là hình phẳng giới hạn
bởi đồ thị hàm số y = f (x), trục Ox, trục Oy, đường thẳng x = 3 . Tính thể tích V của vật thể tròn
xoay sinh ra khi cho (H) quay quanh Ox (làm tròn đến hàng phần trăm) ĐS : 65,97 4 x − y − z −
Câu 4. Trong kgOxyz cho hai điểm A (1,5, 0), B(4, 2, 6) và đường thẳng 2 1 1 d : = = . Gọi (S) 1 −1 − 2
là mặt cầu có tâm I (a,b,c) thuộc đường thẳng d và qua hai điểm A và B. Tính a + b + c . ĐS : 6
Câu 5.Một nhà máy có hai phân xưởng I và II. Phân xưởng I sản xuất 40% số sản phẩm và phân xưởng II
sản xuất 60% số sản phẩm. Tỉ lệ sản phẩm bị lỗi của phân xưởng I là 2% và của phân xưởng II là
1%.Kiểm tra ngẫu nhiên 1 sản phẩm của nhà máy.Tính xác suất để sản phẩm được kiểm tra do
phân xưởng I sản xuất, biết rằng sản phẩm đó bị lỗi ( kết quả làm tròn đến hàng phần nghìn) ĐS : 0,571
Câu 6. Trong kgOxyz với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng
điện thoại có dạng một hình cầu (S) (tập hợp những điểm nằm trong và nằm trên mặt cầu tương
ứng). Biết mặt cầu (S) có phương trình: 2 2 2
x + y + z − 2x − 4y − 6z + 5 = 0 . Một người đang ở vị trí 3 1, 2,
. Điểm xa nhất mà người đó thu được sóng là M(a, ,
b c) Tính a + b + c . ĐS : 9 2 ĐÁP ÁN Phần 1 : 1B 2A 3A 4A 5B 6B 7C 8B 9C 10B 11B 12A
Phần 2 : Câu 1 : Đ, Đ, Đ, Đ Câu 2 : S, S, Đ, Đ Câu 3 : Đ, S, Đ, Đ Câu 4 : Đ, Đ, S, Đ 5
Đề ôn thi học kỳ 2_Đề 2
Phần 1 : Trắc nghiệm 4 phương án
Câu 1. Họ nguyên hàm của hàm số ( ) 2025x f x = là 1 x + 2025 A. x 1 2025 + C + . C. 2025 .
x ln 2025 + C . D. + C . x + . B. 2025 2026x C 1 ln 2025
Câu 2. Cho hai biến cố ,
A B thỏa P ( B) = 0, 4 , P ( A | B) = 0, 04 , P ( A | B) = 0,03 . Khi đó, P ( B | A) bằng 8 1 9 A. . B. 0,48. C. . D. . 17 3 17
Câu 3. Trong không gian Oxyz , phương trình nào dưới đây là phương trình mặt phẳng ( P) đi qua điểm
M (1; 2; − 3) và có một vectơ pháp tuyến n = (1; − 2;3) ?
A. x − 2y + 3z −12 = 0 .
B. x − 2y − 3z + 6 = 0 .
C. x − 2y + 3z +12 = 0 .
D. x − 2y − 3z − 6 = 0 .
Câu 4. Trong kg Oxyz , mặt phẳng ( P) chứa hai điểm A(1;0;3) , B ( 1 − ;2;2) và song song với x = 3+ t d : y = 2
có phương trình là z = 0
A. 3x − y + z = 1.
B. y + 2z −1 = 0 .
C. x − 2y + z −1 = 0 .
D. y + 2z − 6 = 0 .
Câu 5. Trong không gian với hệ tọa độ Oxyz , đường thẳng đi qua điểm A(4;0; − ) 1 và vuông góc với mặt
phẳng (P) : −x + y − 3z + 2 = 0 có phương trình tham số là x = 4 + t x = 1+ 4t x = 4t x = 4 + t
A. y = −t . B. y = 1 − .
C. y = t − .
D. y = t − . z = −1 + 3t z = 3 − t z = 3 + 2t z = 1 − 3t
Câu 6. Cho hình phẳng D giới hạn bởi đường cong 2 y =
x +1 , trục hoành và các đường thẳng x = 0 ,
x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng 1 4 1
A. V = ( 2
x +1)dx . B. V = . C. V = ( 2 x + )1dx . D. V = 2 . 3 0 0
Câu 7. Cho hai biến cố ,
A B độc lập thỏa mãn P ( A) = 0, 4 , P ( B | A) = 0,12 . Khi đó P ( AB) bằng A. 0,352 . B. 0,48. C. 0,88 . D. 0, 072 . x + y − z +
Câu 8. Trong không gian tọa độ Oxyz , cho điểm A(0;0; −2) và đường thẳng 2 2 3 : = = . 2 3 2
Phương trình mặt cầu tâm A , cắt tại hai điểm B và C sao cho BC = 8 là ?
A. (S ) x + y + ( z + )2 2 2 : 2 =16 .
B. (S ) x + y + ( z + )2 2 2 : 2 = 25. 2 2 2
C. (S ) : ( x + 2) + ( y − 3) + ( z + ) 1 = 16 .
D. (S ) ( x + )2 2 2 : 2 + y + z = 25.
Câu 9. Trong kg Oxyz cho mặt phẳng (P) : x − 2y + 2z − 5 = 0 . Xét mặt phẳng (Q) : x + (2m − ) 1 z + 7 = 0 ,
với m 2 là tham số thực. Tìm tất cả các giá của m để mặt phẳng (P) tạo với mặt phẳng (Q) một góc . 4 A. m = 2 − 2 .
B. m = 4 .
C. m = 1. D. m = − 2 .
Câu 10. Gọi ( H ) là phần giao của hai khối 1 hình trụ có bán kính 2 , hai trục hình trụ vuông góc với 4
nhau như hình vẽ sau, thiết diện mặt cắt luôn là hình vuông. Tính thể tích của khối (H ) . 6 16 A. ( V ) = 4 . B. V = . C. V = . D. V = . H ( ) 6 H (H ) (H ) 2 3
Câu 11. Trước khi đưa sản phẩm ra thị trường, người ta đã phỏng vấn ngẫu nhiên 200 khách hàng về sản
phẩm đó và thấy có 50 người trả lời “sẽ mua”, 90 người trả lời “có thể sẽ mua” và 60 người trả lời “không
mua”. Kinh nghiệm cho thấy tỷ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng với những cách trả lời
trên tương ứng là 60%, 40% và 1%. Trong số khách hàng thực sự mua sản phẩm thì xác suất khách hàng a
trả lời “sẽ mua” là . Tính giá trị của biểu thức 1 T = a + . b b 5 A. 13 . B. 14,5 . C. 15 . D. 10 .
Câu 12. Trong không gian Oxyz , cho ba điểm B (2;1;0) , C (2;0; 2) , A(1;1; )
1 . Gọi ( P) là mặt phẳng
chứa BC và cách A một khoảng lớn nhất. Hỏi mặt cầu tâm A và tiếp xúc mặt phẳng (P) có bán kính là? 30 6 30 6 5 30 A. . B. . C. . D. . 30 5 30 6 Phần 2 : Đúng/Sai
Câu 1. Trong không gian ba chiều Oxyz , tọa độ các khu vực được xác định như sau:
Khu vực A(30;20;0) nằm trên mặt đất, cách trung tâm thành phố 3km.
Khu vực B (70;50;40) nằm trên tòa nhà cao tầng và ở độ cao 40m.
Khu vực C (50;80;70) nằm trên một đỉnh đồi ở độ cao 70m.
Gọi vị trí lắp đặt trạm phát sóng là D ( ; a ;
b c) sao cho khoảng cách từ D đến ba khu vực kể trên là bằng nhau.
a) Một vectơ pháp tuyến của ( ABC ) là n(3;20; 18 − )
b) Phương trình mặt phẳng ( ABC ) là 3x + 20y −18z + 490 = 0
c) D nằm trên đường thẳng đi qua trọng tâm tam giác ABC .
d) Nếu tổng khoảng cách từ D đến các điểm , A ,
B C là nhỏ nhất thì T = a + b + c 101
Câu 2. Một đội bắn súng gồm có 6 nam và 4 nữ. Xác suất bắn trúng của các xạ thủ nam là 0,85 còn của
các xạ thủ nữ là 0,8. Chọn ngẫu nhiên hai xạ thủ bắn một viên đạn và cả hai xạ thủ đó đã bắn trúng.
Gọi A là biến cố “Ít nhất một xạ thủ là nữ”, suy ra A là biến cố “cả 2 xạ thủ được chọn là nam”
Gọi B là biến cố “cả hai xạ thủ được chọn bắn trúng” a) P ( A) 1 =
b) P (B | A) = 0,7225
c) P ( B) = 0, 6 d) P ( A B) 4 | = 2 5
Câu 3. Trong không gian với hệ trục tọa độ Oxyz , cho điểm M (−3;3; 3 − ) thuộc mặt phẳng
(P):2x – 2y + z +15 = 0 và mặt cầu (S) 2 2 2
: (x− 2) + (y− 3) + (z− 5) = 100 .
a) Mặt cầu (S ) có tâm I (2;3;5) , bán kính R =10.
b) ( P) cắt mặt cầu (S ) theo giao tuyến là đường tròn (C ) có bán kính là 8.
c) H (2;7;3) là hình chiếu của I lên ( ) P x + 3 y − 3 z + 3 d) Đường thẳng : = =
M nằm trên mặt phẳng ( ) cắt (S) tại A , B thì độ dài 1 4 − qua , 6 AB lớn nhất. 7
Câu 4. Hình phẳng ( H ) được giới hạn bởi đồ thị (C ) : y = f ( x) của hàm đa thức bậc ba và parabol
(P): y = g (x) có trục đối xứng vuông góc với trục hoành. a) (C ) 3 2
: y = x − 3x + 2 b) ( P) 2
: y = −x − x
c) Phần tô đậm như hình vẽ có diện tích 37 . 12
d) Thể tích của khối (H) khi quay phần tô đậm xung quanh trục hoành là 261 70
Phần 3 : Điền đáp số Câu 1. Cho ( ) = ( 2 + + ) x F x ax bx
c e một nguyên hàm của hàm số f ( ) = ( 2 + 3 + ) 1 . x x x x e . Tính tổng
a + b + c . ĐS: 2 3
Câu 2. Cho các đồ thị hàm số 3 y =
x (C , cung tròn có phương trình 2 y =
4 − x (C và hình phẳng 2 ) 1 ) 9
(H ) được tô màu như hình vẽ
Biết thể tích của khối tròn xoay tạo thành khi quay a c
(H ) quanh trục hoành là V = − 3 + , b d trong đó a c *
a, b, c, d và ,
là các phân số tối giản. Tính a + b + c + d . ĐS: 46 b d x = 1+ 3t x −1 y + 1 z − 3
Câu 3. Trong kg Oxyz , cho hai đường thẳng d : = = d : y = 4 − . 1 1 1 2
− và đường thẳng 2 z = 4+t
Đường thẳng d đi qua điểm A(1;2;− )
1 và cắt d tại M , cắt d tại N . Tính 2 2
AM + AN . ĐS: 90 1 2 Câu 4. Cho 2 2 2
(S) : x + y + z − 2x − 2y + 6z + 2 = 0 và A(1;1; )
1 , B (2;1;0) . Điểm $D$ thuộc S sao cho 2 2
P = DA − 3DB đạt giá trị nhỏ nhất. Tính P . (làm tròn đến hàng đơn vị) ĐS: 65 −
Câu 5. Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các
viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp
thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai. Biết rằng 2 viên bi lấy ra từ hộp 8
thứ hai là bi đỏ, tính xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi xanh. (làm tròn kết quả đến hàng phần trăm) ĐS: 0,27
Câu 6. Cho đồ thị (C ) của hàm số 3 2
y = x − 3x +1. Gọi (d ) là tiếp tuyến của (C ) tại điểm A có hoành độ 27
x = a 0 . Biết diện tích hình phẳng giới hạn bởi (d ) và (C ) bằng
, giá trị của a là bao nhiêu? A 4 ĐS: 2 Đáp án Phần 1 : 1D 2A 3C 4D 5A 6B 7A 8B 9C 10C 11A 12C
Phần 2 : Câu 1 : Đ, S, S, Đ Câu 2 : S, Đ, S, S Câu 3 : Đ, Đ, S, S Câu 4 : Đ, S, Đ, S 9
Đề ôn thi học kỳ 2 _ Đề 3
Phần 1 : Trắc nghiệm 4 phương án 2
Câu 1. Biết F ( x) là một nguyên hàm của hàm f ( x) = cos3x và F = . Tính F . 2 3 9 3 + 2 3 − 2 3 + 6 3 − 6 A. F = B. F = C. F = D. F = 9 6 9 6 9 6 9 6
Câu 2. Trong không gian Oxyz , mặt phẳng (Oxy) đi qua điểm nào sau đây:
A. M (1; 2; 0) . B. N (3; 2; − )
1 . C. P (1; 0; 3
− ) . D. Q(0;2; 5 − ) .
Câu 3. Trong không gian Oxyz , một thiết bị phát sóng đặt tại vị trí A (3; 0; 0) . Vùng phủ sóng của thiết
bị có bán kính bằng 5. Hỏi vị trí của điểm nào sau đây không thuộc vùng phủ sóng của thiết bị nói trên?
A. M (5; 0; 0) . B. N (3; 2; )1 − . C. P( 1 − ;3; ) 1 . D. Q (0; 2 − ;0) .
Câu 4. Cho hai biến cố A và B độc lập với nhau, trong đó 0 P ( B) 1. Khẳng định nào sau đây đúng?
A. P ( A | B) = P ( A | B ) = P ( A) . B. P ( A | B) = 1− P ( A | B) .
C. P ( AB) = P( A) + P(B) .
D. P ( A) = 1− P ( B) .
Câu 5. Trong không gian Oxyz , cho mặt phẳng ( P) : 2x + 3y + z −11 = 0 . Mặt cầu (S ) có tâm I (1; 2
− ;1) và tiếp xúc với mặt phẳng (P) tại điểm H , khi đó H có tọa độ là: A. H ( 3 − ; 1 − ; 2 − ) . B. H ( 1 − ; 5
− ;0) . C. M (0;2; 1
− ) . D. H (3;1;2) . 1
Câu 6.Cho hàm số f ( x) thõa mãn f (0) = 4 và ( ) = + ex f x x , x
. Khi đó f (x)dx bằng 0 6e+13 6e+25 6e+25 6e+19 A. . B. . C. . D. . 6 6 3 6
Câu 7. Cho hình chóp .
S ABCDcó đáy là hình thang vuông tại A và B , thỏa mãn điều kiện,
AB = BC = a , AD = 2a , SA vuông góc với mặt đáy ( ABCD) , SA = a . Gọi M, N lần lượt là trung điểm
của SB,CD .Tính cosin của góc giữa MN và (SAC). 35 55 55 35 A. B. C. D. 10 2 10 3
Câu 8. Tại một nút giao thông có 2 con đường khác mức. Trên thiết kế, trong không gian Oxyz hai con x − 2 y − 2 x − 2 y +1
đường đó thuộc hai đường thẳng z z d : = = ; d : = =
. Người ta muốn tạo một 1 1 1 1 − 2 1 2 3 − con đường
cắt d ,d lần lượt tại A và B sao cho AB nhỏ nhất. Tính độ dài AB , kết quả làm tròn 1 2 đến hàng phần trăm.
A. 2, 45 B. 2,46 C. 2, 5 D. 3
Câu 9. Cho hai mặt cầu (S , S có cùng bán kính R = 3 thỏa mãn tính chất tâm 1 ) ( 2 )
của (S thuộc (S và ngược lại. Tính thể tích V phần chung của hai khối cầu tạo 2 ) 1 )
bởi (S , S . 1 ) ( 2 ) 45 45 45 45 A. V = . B. V = . C. V = . D. V = . 8 4 4 8
Câu 10. Một hộp chưa 9 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 9. Bạn An lấy ra ngẫu nhiên 1
thẻ từ hộp, xem số rồi bỏ ra ngoài. Nếu thẻ đó được đánh số chẵn, An cho thêm vào hộp thẻ số 10, 11;
ngược lại, An cho thêm vào hộp thẻ số 12, 13, 14. Sau đó, Bạn Việt lấy ra ngẫu nhiên đồng thời 3 thẻ từ 10
hộp. Gọi X là tích các số trên thẻ Việt lấy ra. Tính xác suất của biến cố An lấy được thẻ ghi số chẵn biết
rằng X chia hết cho 2.( Làm tròn kết quả đến hàng phần trăm.)
A. 0, 43 B. 0,41 C. 0, 4 D. 0, 42
Câu 11. Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật v (t) 1 13 2 = t +
t (m/s) , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển 100 30
động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng cùng hướng với A
nhưng chậm hơn 10 giây so với A và có gia tốc bằng a ( 2
m/s ) ( a là hằng số). Sau khi B xuất phát được
15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng A. 15 (m/s)
B. 9 (m/s) C. 42 (m/s) D. 25 (m/s)
Câu 12. Trong không gian Oxyz , cho điểm A(0;1; 2
− ), mặt phẳng (P): x + y + z +1= 0 và mặt cầu (S) 2 2 2
: x + y + z − 2x − 4y − 7 = 0 . Gọi là đường thẳng đi qua A và nằm trong mặt phẳng ( P) và
cắt mặt cầu (S ) tại hai điểm B ,C sao cho tam giác IBC có diện tích lớn nhất, với I là tâm của mặt cầu
(S). Phương trình của đường thẳng là x = t x = t x = t x = t A. y = 1
. B. y = 1+ t . C. y = 1− t . D. y = 1+ t . z = −2 − t z = 2 − + t z = 2 − z = 2 − Phần 2 : Đúng/Sai
Câu 1. Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia
tốc phụ thuộc vào thời gian t (s) là a(t) = t − ( 2 2
7 m/s ). Biết vận tốc đầu bằng 6 (m/s)
a) Vận tốc tức thời của chất điểm tại thời điểm t (s) xác định bởi v(t) 2
= t − 7t +10 .
b) Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
c) Độ dịch chuyển của vật trong khoảng thời gian 1 t 7 là 18 m.
d) Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s).
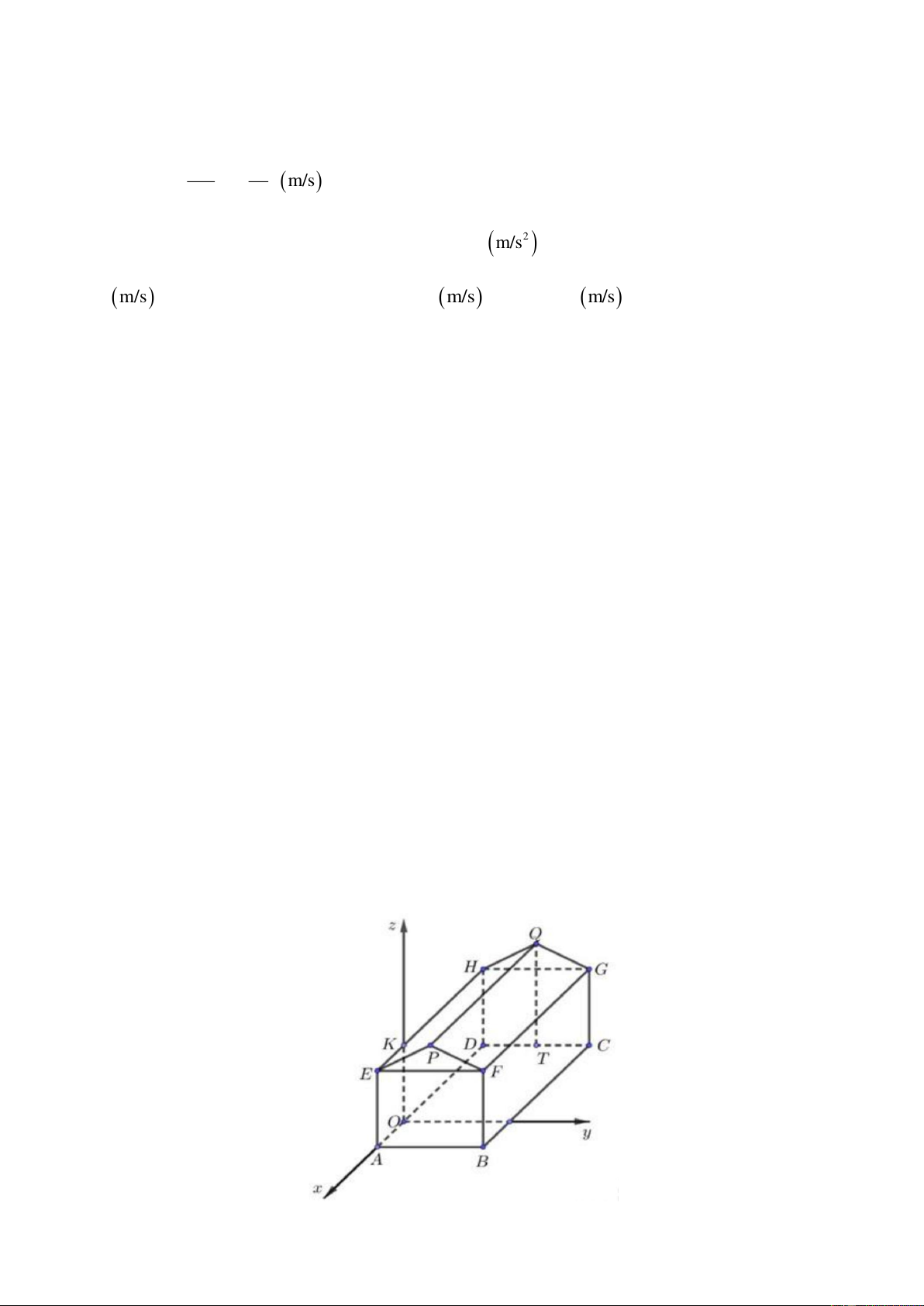
Câu 2. Một kho chứa hàng có dạng hình lăng trụ đứng ABFPE.DCGQH với ABFE là hình chữ nhật và
EFP là tam giác cân tại P . Gọi T là trung điểm của DC . Các kích thước của kho chứa lần lượt là
AB = 6 m; AE = 5 m; AD = 8 m;QT = 7 m . Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ
có gốc toạ độ là điểm O thuộc đoạn AD sao cho OA = 2 m và các trục toạ độ tương ứng như hình vẽ dưới đây. Khi đó: 11 x = t
a) Toạ độ điểm Q là ( 6 − ;3;5) .
b) Phương trình tham số của đường thẳng OC: y = t z = 0
c) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm của FG và đầu thu dữ liệu đặt tại
vị trí O . Người ta thiết kế đường dây cáp nối từ O đến K sau đó nối thẳng đến camera. Độ dài đoạn cáp
nối tối thiểu bằng 5 + 2 10 m .
d) Mái nhà được lợp bằng tôn Hoa Sen, giá tiền mỗi mét vuông tôn là 130.000 đồng. Số tiền cần bỏ ra để
mua tôn lợp mái nhà là 3.750.000 đồng (không kể hao phí do việc cắt và ghép các miếng tôn, làm tròn kết
quả đến hàng nghìn).
Câu 3. Trong không gian Oxyz , cho các điểm A(6;1;0), B( 1 − ;3;2) và C (1; 1 − ) ;1 và mặt cầu (S) 2 2 2
: x + y + z = 3
a) Biết rằng C là trọng tâm của tam giác ABE . Toạ độ của điểm E là ( 2 − ; 7 − ) ;1 .
b) Khoảng cách từ điểm A đến mặt phẳng (Oyz) bằng 37 .
c) Phương trình mặt phẳng cách đều hai điểm A, C là 5x − 2y + z +18 = 0 .
d) Một mặt phẳng ( ) tiếp xúc với mặt cầu ( S ) và cắt các tia Ox , Oy , Oz lần lượt tại M, N, P thỏa mãn 2 2 2
OM + ON + OP = 27 . Phương trình mặt phẳng ( ) là: x + y + z − 3 = 0 .
Câu 4. Để nghiên cứu sự phát triển của một loại cây, người ta trồng hạt giống của loại cây đó trên hai lô
đất thí nghiệm M, N khác nhau. Xác suất phát triển bình thường của cây đó trên các lô đất M và N lần lượt
là 0,56 và 0,62. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xét các biến cố:
A: “Cây phát triển bình thường trên lô đất M”;
B: “Cây phát triển bình thường trên lô đất N”.
a) Các cặp biến cố A và B, A và B là độc lập.
b) Hai biến cố C = A B và D = A B không là hai biến cố xung khắc.
c) P( A ) = 0,56; P( B ) = 0,62.
d) Xác suất để cây chỉ phát triển bình thường trên một lô đất là 0,4856.
Phần 3 : Điền đáp số
Câu 1.Trong không gian Oxyz (đơn vị của các trục tọa độ là ki – lô - mét), đài kiểm soát không lưu sân bay có tọa độ ( 6
− 4;128;64) . Máy bay bay trong phạm vi cách đài kiểm soát không quá 500 km thì sẽ
hiển thị trên màn hình ra đa. Một máy bay N xuất hiện trên màn hình ra đa và một máy bay M nằm
trong mặt phẳng (P) : x − 2y + 2z −1458 = 0 sao cho hai máy bay M , N thuộc đường thẳng có vectơ
chỉ phương là u = (1;1; )
1 . Khoảng cách nhỏ nhất giữa hai máy bay M , N là bao nhiêu km? (kết quả
làm tròn đến hàng đơn vị). ĐS : 260.
Câu 2. Xét hàm số y = f ( x) 4 2
= ax + bx + c (a 0) sao cho đồ thị hàm số có ba điểm cực trị là , A B,C (1; )
1 . Gọi y = g ( x) là hàm số bậc hai có đồ thị đi qua ba điểm ,
A B, C và (H ) là hình phẳng
giới hạn bởi đồ thị hàm số y = f ( x), y = g ( x) và hai đường thẳng Oy; x =1. Khi hình này có diện tích 2
bằng , hãy tính thể tích khối tròn xoay được tạo thành khi cho (H ) quay quanh trục hoành (làm tròn 5
kết quả đến hàng phần trăm). ĐS : 1,24. 12
Câu 3. Trong không gian Oxyz , cho các điểm
A(2; 2;0), B (2;0; − 2) và mặt phẳng
(P): x + 2y − z −1= 0. Xét điểm M (a;b;c) thuộc mặt phẳng (P) sao cho MA = MB và số đo góc
AMB lớn nhất. Khi đó giá trị A + b + c ( làm tròn đến hàng phần trăm) bằng bao nhiêu? ĐS: 1,27.
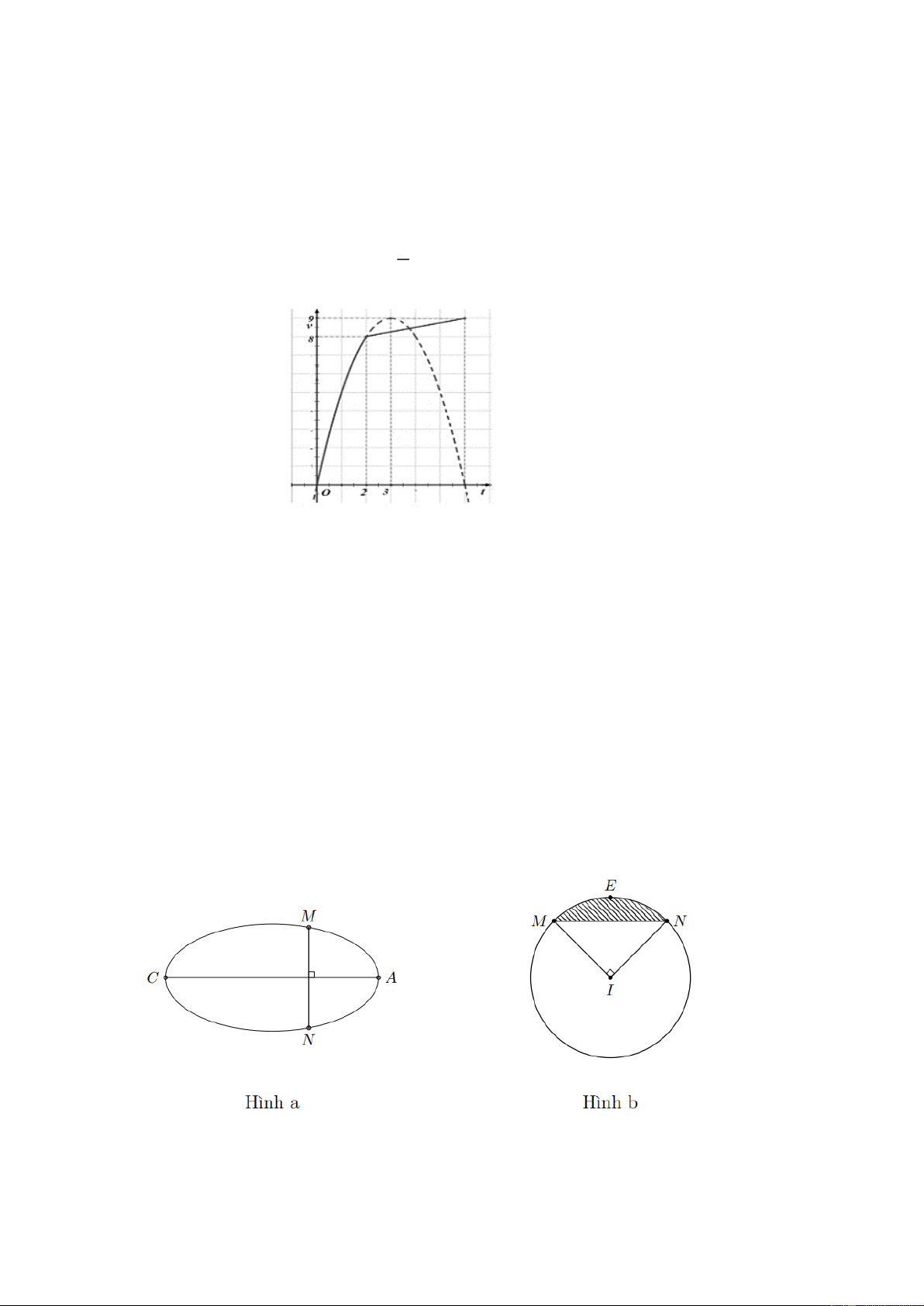
Câu 4. Một vật chuyển động trong 6 giờ với vận tốc v (km / h) phụ thuộc vào thời gian t (h) có đồ thị
như hình bên dưới. Trong khoảng thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường
Parabol có đỉnh I (3;9) và có trục đối xứng song song với trục tung. Khoảng thời gian còn lại, đồ thị vận 1
tốc là một đường thẳng có hệ số góc bằng . Tính quảng đường s(k )
m mà vật di chuyển được trong 8 4
giờ? (Kết quả làm tròn đến hàng phần mười) ĐS : 61,8
Câu 5. Có hai lô hàng. Lô 1: Có 7 chính phẩm và 3 phế phẩm. Lô 2: Có 8 chính phẩm và 2 phế phẩm.
Từ lô thứ nhất lấy ra 2 sản phẩm, từ lô thứ hai lấy ra 3 sản phẩm rồi trong số sản phẩm lấy được lấy ra lại
lấy tiếp ngẫu nhiên 2 sản phẩm. Tính xác suất để trong 2 sản phẩm đó có ít nhất một chính phẩm. (viết
kết quả dưới dạng số thập phân và làm tròn đến hàng phần nghìn)
Câu 6.Sân vận động Sports Hub (Singapore) là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á
được tổ chức ở Singapore năm 2015. Nền sân là một elip (E) có trục lớn dài 150 ,
m trục bé dài 90 m
(Hình 3). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của (E) và cắt elip (E) ở
M , N (Hình a) thì ta được thiết diện luôn là một phần của hình tròn có tâm I (phần tô đậm trong Hình b) với MN
là một dây cung và góc MIN = 90 . Để lắp máy điều hòa không khí cho sân vận động thì các kỹ
sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt
phẳng và thể tích vật liệu làm mái không đáng kể. Hỏi thể tích đó xấp xỉ bao nhiêu?( đơn vị dm3 , làm
tròn dến hàng đơn vị). ĐS: 116 dm3 13
Đề ôn thi học kỳ 2_Đề 4
Phần 1 : Trắc nghiệm 4 phương án Câu 1:
Tìm nguyên hàm của hàm số 2 f ( )
x = 3x + 8sin x A.
f (x)dx = 6x − 8 cos x + C B.
f (x)dx = 6x + 8 cos x + C C. 3
f (x)dx = x − 8 cos x + C D. 3
f (x)dx = x + 8 cos x + C Câu 2:
Cho đồ thị hàm số y = f (x) . Diện tích S của hình phẳng (phần tô đậm trong hình vẽ bên) là: 3 A. S = f (x)dx . 2 − 0 3 B. S = f (x)dx + f (x)dx . 2 − 0 3 0 C. S =
f (x)dx − f (x)dx . 0 2 − 0 0 D. S = f (x)dx + f (x)dx . 2 − 3 Câu 3:
Cho hàm số y = f (x) liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ
thị hàm số đã cho và trục Ox. Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể
tích V được xác định theo công thức 3 3 1 A. 2
V = [ f (x)] dx B. 2 V =
[ f (x)] dx 3 1 1 3 3 C. 2 2 V =
[ f (x)] dx D. 2
V = [ f (x)] dx 1 1 x y z Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : + + = 1. Vecto nào sau đây là 3 2 1
vectơ pháp tuyến của mặt phẳng ( ) P ? 1 1
A. n = (2;3;6) .
B. n = (3; 2;1) .
C. n = (6;3; 2) .
D. n = (1; ; ) . 2 3 Câu 5:
Phương trình nào dưới đây là phương trình của đường thẳng đi qua điểm ( A 2;3;0) và vuông góc với mặt phẳng ( )
P : x + 3y − z + 5 = 0? x =1+ 3t x = 1+ t x =1+ t x =1+ 3t
A. y = 3t .
B. y = 3t .
C. y = 1+ 3t .
D. y = 3t . z = 1− t z = 1− t z = 1− t z = 1+ t Câu 6:
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M (3; 2 − ;5) , N( 1 − ;6; 3 − ) . Phương
trình nào sau đây là phương trình của mặt cầu có đường kính là MN? A. 2 2 2
(S ) : (x +1) + ( y + 2) + (z +1) = 36 . B. 2 2 2
(S ) : (x −1) + ( y − 2) + (z −1) = 6 . C. 2 2 2
(S) : (x +1) + ( y + 2) + (z +1) = 6 . D. 2 2 2
(S) : (x −1) + ( y − 2) + (z −1) = 36 . 1 4x +15 Câu 7: Biết
dx = a ln 2 + b ln 3 với , a b . Mệnh đề nào đúng? 2 0 2 − x − x + 6 b 1 a 1 A. = − . B. = − .
C. b − a = 5 − .
D. b + a = 5 . a 4 b 4 Câu 8:
Cho hai biến cố A và B là hai biến cố độc lập, với P( A) = 0,2024 , P(B) = 0,2025. Khi đó P(A B ) bằng; A. 0, 7976 B. 0, 7975. C. 0, 2025 . D. 0, 2024 . Câu 9:
Cho hai biến cố A và B , với ( P )
B = 0,8 , P(A | )
B = 0, 7 , P(A | B) = 0, 45 . Tính P(B | ) A . 14 56 A. 0,25. B. . C. 0,65. D. 0,5. 65
Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị 2
y = x − 2x + 2 , 2
y = x + 4x + 5, y = 1 9 9 9 A. . B. . C. . D. 9. 4 8 2
Câu 11: Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y =
x , cung tròn có phương trình 2 y =
6 − x ( − 6 x 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V
của vật thể tròn xoay sinh ra khi quay hình phẳng D quanh Ox 22
A. V = 8 6 − 2 B. V = 8 6 + 3 22 22
C. V = 8 6 − D. V = 4 6 + . 3 3
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu 2 2 2
(S) : x + y + z − 2x − 4y − 6z − 2 = 0 . Viết phương trình mặt phẳng () chứa trục Oy và cắt
mặt cầu (S) theo thiết diện là một đường tròn có chu vi bằng 8 .
A. 3x + z = 0 .
B. 3x + z + 2 = 0 .
C. 3x − z = 0 .
D. x − 3z = 0 . Phần 2 : Đúng/Sai Câu 1:
Một máy bơm nước vào bể chứa nước. Gọi (
h t) là thể tích nước bơm được sau t giây. Cho 2 3 h (
t) = 6at + 2bt (m / s) và ban đầu bể không có nước. Các mệnh đề sau đúng hay sai? 3
a)Sau 3 giây thì thể tích nước trong bể là 2
(6at + 2bt)dt . 0
b)Sau 6 giây thể tích nước trong bể là 3
504m khi đó 432a + 36b = 504 .
c)Thể tích nước trong bể là 3
90m sau 3 giây và sau 6 giây thì thể tích nước trong bể là 3 504m .
Khi đó trong khoảng thời gian từ giây thứ 2 đến giây thứ 5 thể tích nước bơm được vào bể là 3 180m .
d)Thể tích nước trong bể là 3
90m sau 3 giây và sau 6 giây thì thể tích nước trong bể là 3 504m .
Khi đó thể tích nước trong bể sau khi bơm được 9 giây là 3 594m .
Câu 2: Hộp thứ nhất có 1 viên bi xanh và 5 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 5 viên bi đỏ.
Các viên bi cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ
nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 2 viên bi từ hộp thứ hai.
a) Xác suất để hai viên bi lấy ra từ hộp hai là bi đỏ bằng 19 . 45
b) Xác suất để hai viên bi lấy ra từ hộp hai có 1 bi đỏ và 1 bi xanh bằng 1 . 9
c) Biết rằng hai viên bi lấy ra từ hộp thứ hai là bi đỏ. Xác suất để 2 viên bi lấy ra từ hộp thứ
nhất cũng là bi đỏ bằng 14 . 19
d) Biết rằng hai viên bi lấy ra từ hộp thứ hai có 1 bi đỏ và 1 bi xanh. Xác suất để 2 viên bi lấy
ra từ hộp thứ nhất cũng có 1 bi đỏ và 1 bi xanh bằng 5 . 19 1 Câu 3: Trong không gian Oxyz, cho (0
A ;0; 2) , B(1;1;0) và mặt cầu 2 2 2
(S) : x + y + (z −1) = . 4
a)Mặt cầu (S) có tâm I (0;0;1) . 15
b)Điểm A nằm trong mặt cầu (S) .
c)Mặt cầu tâm A và đi qua B có bán kính bằng 6 .
d)Điểm M thay đổi thuộc (S) , giá trị nhỏ nhất của biểu thức 2 2
MA + 2MB bằng 5. Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho điểm (
A 3;1;1) và đường thẳng x = 3+ 2t d : y = 2
− − t ,t . Một mặt phẳng ( )
P thay đổi chứa d . z = 2 − − 2t
a) d nhận véc tơ u = ( 2
− ;1;2) làm một véc tơ chỉ phương.
b)Mặt phẳng qua A và vuông góc với d có phương trình là 2x − y − 2z − 3 = 0 .
c)Điểm H (1; 1
− ;0) là hình chiếu vuông góc của A lên đường thẳng d .
d)Khi khoảng cách từ điểm A đến mặt phẳng ( )
P đạt giá trị lớn nhất thì ( ) P đi qua O.
Phần 3 : Điền đáp số Câu 1:
Cho hàm số f (x) xác định trên \{ } 1 thỏa mãn 1 f ( x) = f = , f (2) = 2019 . x − , (0) 2018 1
Tính S = f (3) − f ( 1 − ) . ĐS : 1 Câu 2:
Một ô tô đang chạy đều với vận tốc a (m/s) thì người lái đạp phanh. Từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc v(t) = 5
− t + a(m / s) , trong đó t là thời gian tính bằng
giây kể từ lúc đạp phanh. Hỏi vận tốc ban đầu a của ô tô là bao nhiêu, biết từ lúc đạp phanh
đến khi dừng hẳn ô tô di chuyển được 40m? ĐS : 20 Câu 3:
Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh được
trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học.
Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có phương
trình trong hệ tọa độ Oxy là 2 2 2
16y = x (25 − x ) như hình vẽ.
Tính diện tích mảnh đất đó(Kết quả làm tròn đến hàng phần chục). ĐS : 41,7 Câu 4:
Bạn Bảo có lịch học theo hai môn: Toán và Văn. Nếu hôm nay bạn Bảo học Toán, xác suất để
ngày mai bạn học Văn là 0,4. Nếu hôm nay bạn Bảo học Văn, xác suất để ngày mai bạn học
Toán là 0,3. Biết rằng vào thứ Hai bạn Bảo học Văn. Tính xác suất để ngày thứ Tư và thứ Năm
bạn Bảo đều học Văn? (kết quả làm tròn đến hàng phần trăm) ĐS : 0,43 Câu 5:
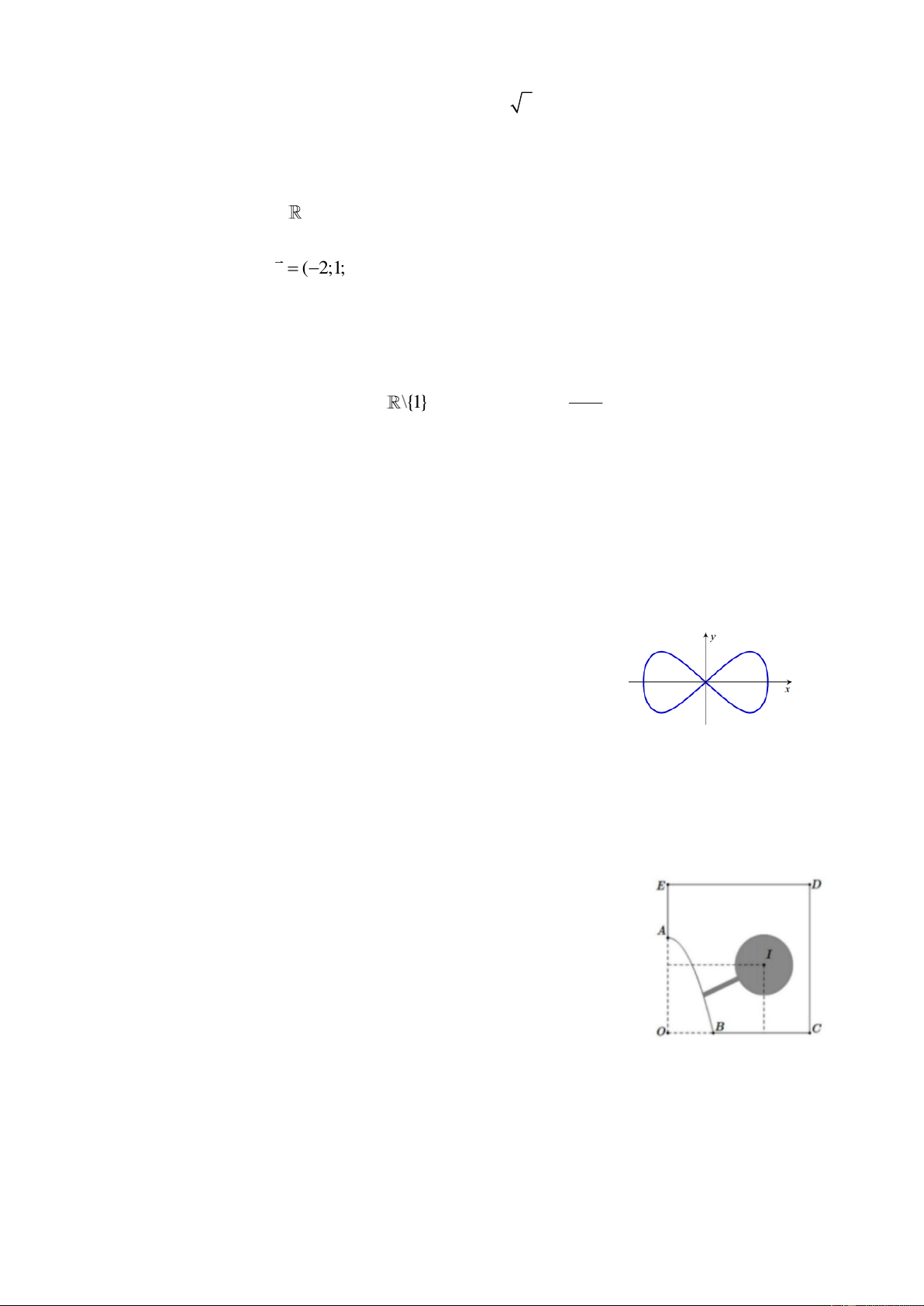
Một cái ao có hình ABCDE tham khảo hình vẽ dưới đây, ở giữa ao có một mảnh vườn trồng
hoa hình tròn bán kính 9 m người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hai bờ
AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai
đường thẳng này cắt nhau tại điểm O. Bờ AB là một phần của
parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng
OA. Độ dài đoạn OA và OB lần lượt là 48 m và 20 m, tâm I của
mảnh vườn cách đường thẳng AE và BC lần lượt là 48 m và 30
m. Độ dài ngắn nhất có thể của cây cầu là bao nhiêu mét (kết quả
làm tròn đến hàng phần chục)? ĐS : 25,2 Câu 6:
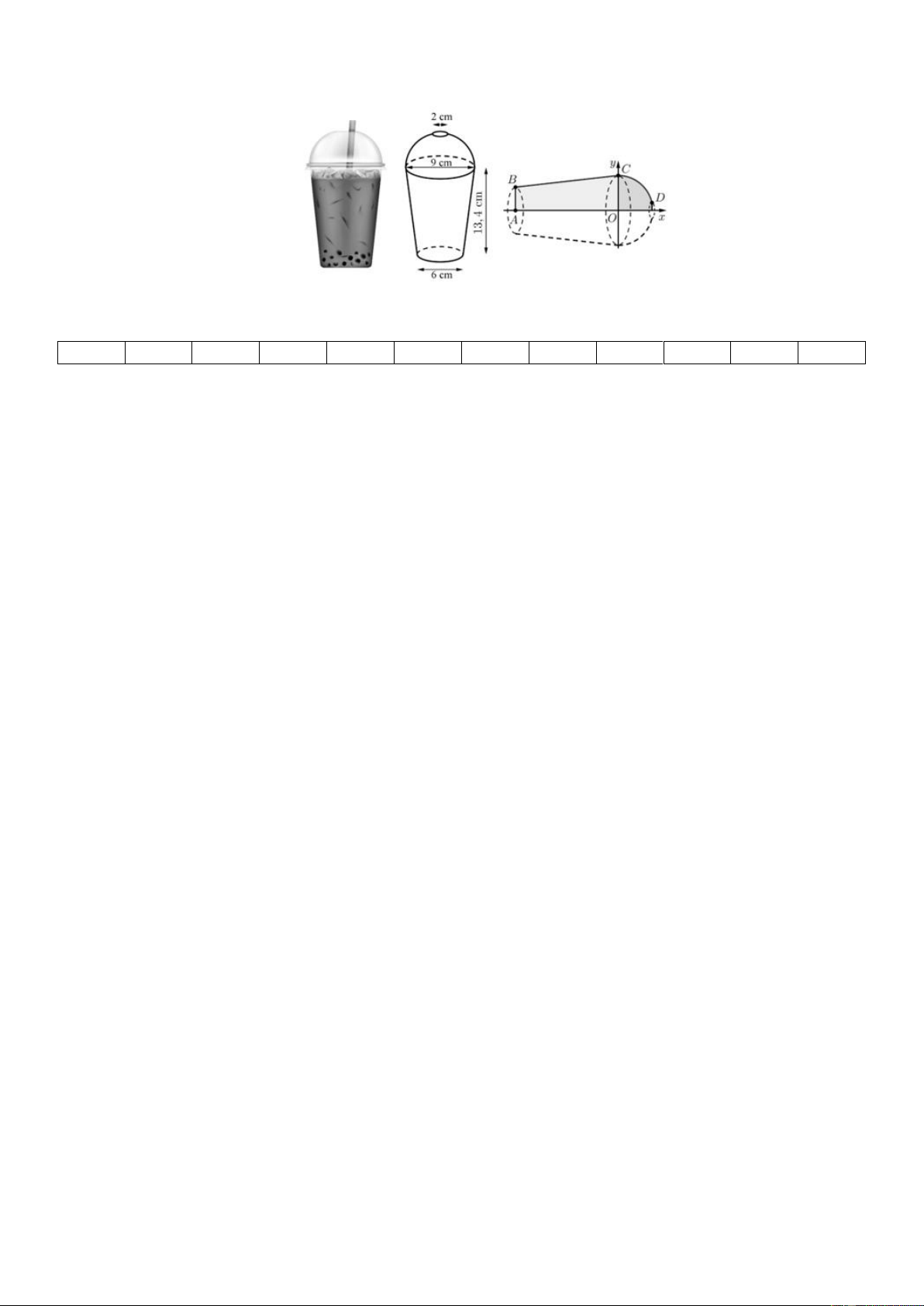
Một ly trà sữa dạng hình nón cụt, có đường kính đáy ly 6 cm, đường kính miệng ly 9 cm, chiều
cao 13,4 cm, ở miệng ly có sử dụng một nắp đậy có hình dạng nửa mặt cầu và ở đỉnh của nửa
mặt cầu này có một hình tròn có đường kính 2 cm để cắm ống hút, mặt phẳng chứa hình tròn
này song song với mặt phẳng chứa miệng ly (tham khảo hình vẽ sau). Chọn hệ trục Oxy ( đơn
vị trên trục là centimet) với trục Ox đi qua tâm của 2 đáy hình nón cụt và gốc tọa độ O trùng 16
với tâm của đáy lớn như hình vẽ trên. Thể tích bên trong của ly bao gồm cả thể tích của nắp là
bao nhiêu? (làm tròn kết quả đến hàng đơn vị) ĐS : 791 Đáp án Phần 1 : 1C 2C 3A 4A 5B 6D 7B 8D 9B 10A 11D 12C
Phần 2 : Câu 1 : Đ, Đ, S, S Câu 2 : Đ, S, Đ, S Câu 3 : Đ, S, Đ, S
Câu 4 : Đ, Đ, Đ, Đ. 17
Đề ôn thi học kỳ 2_Đề 5
Phần 1 : Trắc nghiệm 4 phương án
Câu 1. Cho hai biến cố A, B độc lập nhau có P ( A) = 0,3 , P ( AB ) = 0, 2 . Xác suất biến cố A B bằng 2 1 19 8 A. . B. . C. . D. . 3 3 30 15
Câu 2. Trong không gian Oxyz, mặt phẳng tiếp xúc mặt cầu (S ) 2 2 2
: x + y + z − 2x + 4 y = 0 tại O sẽ có phương trình là
A. x − 2y = 0 .
B. 2x − y = 0 .
C. x + 2y = 0 .
D. 2x + y = 0 .
Câu 3. Cho A, B lần lượt là 2 biến cố của cùng một phép thử. Khẳng định nào sau đây đúng?
A. P ( AB) = P ( A).P ( B)
B. P ( A B) = P ( A) + P ( B)
C. P ( B) = P ( A).P (B | A) + P ( A).P (B | A)
D. P ( A).P ( A | B) = P ( AB) x y − z
Câu 4. Trong không gian với hệ tọa độ Oxyz, đường thẳng 2 d : = = Oxz tại 1 2 3 − cắt mặt phẳng ( )
điểm có tọa độ là
A. (1; 0; − 3) .
B. (0; − 2; 0) .
C. (−1; 0; 3) . D. (0; 2; 0) 1
Câu 5. Một vật chuyển động theo quy luật 3 2
s = − t + 6t với t (giây) là khoảng thời gian tính từ khi vật 3
bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Khi vật
dừng lại lần đầu tiên kể từ khi bắt đầu chuyển động, vật đi được quảng đường là bao nhiêu?
A. 144 (m) .
B. 288(m) .
C. 72 (m) .
D. 360 (n) . x − y − z −
Câu 6. Trong không gian Oxyz, cho đường thẳng 1 2 3 d : = = và mặt phẳng 1 2 3
(P): x + y + z −1= 0. Viết phương trình mặt phẳng (Q) chứa d và tạo với mặt phẳng (P) góc lớn nhất.
A. (Q) : x − 2y + z = 0 .
B. (Q) : x + z − 4 = 0.
C. (Q) : 4x + y − 2z = 0 . D.
(Q): x +2y +3z −14 = 0
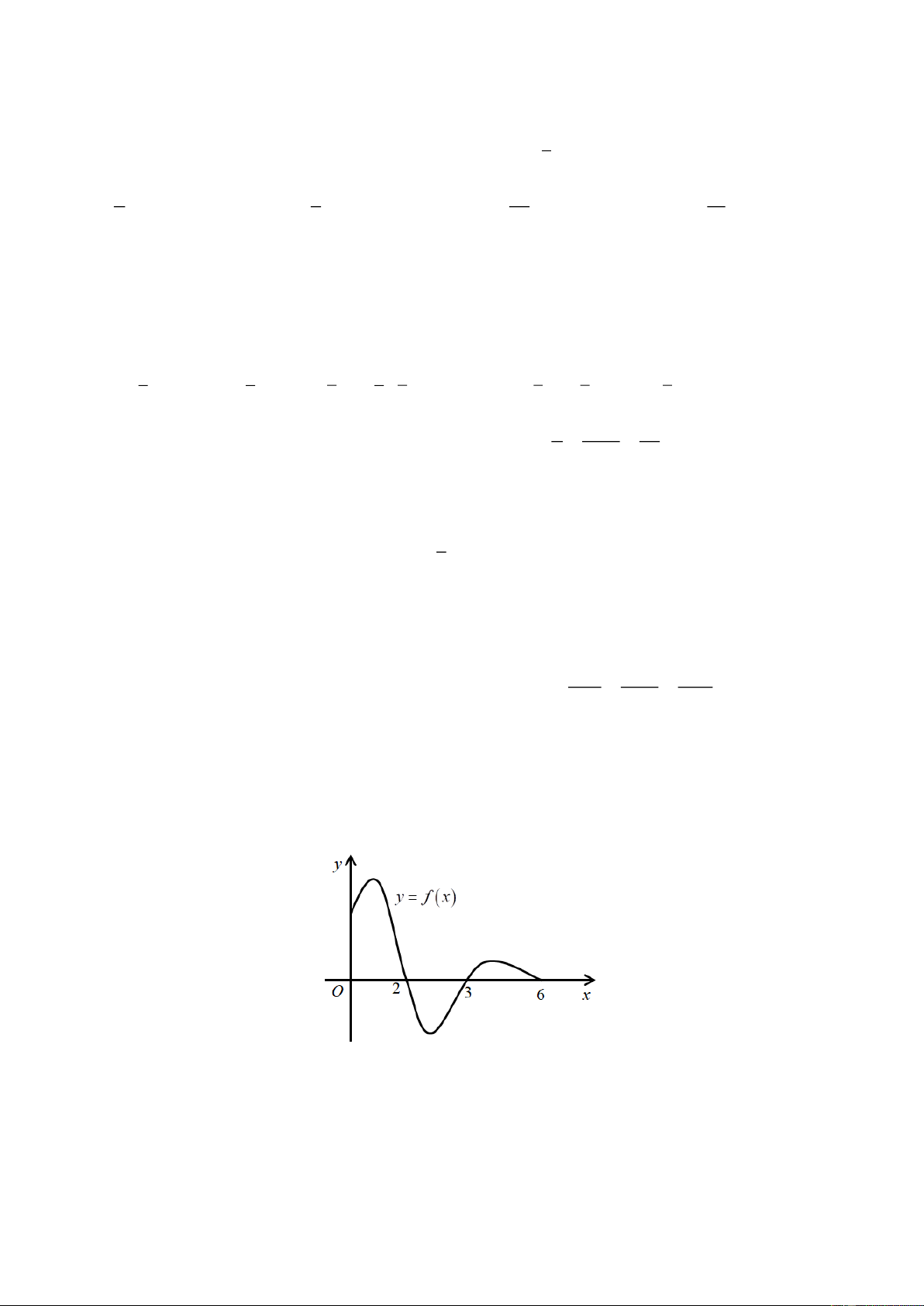
Câu 7. Cho đồ thị hàm số y = f ( x) trên đoạn 0; 6 như hình vẽ.
Hàm số F ( x) là một nguyên hàm của hàm số f (x) , cũng xác định và lien tục trên đoạn 0; 6 . Khi đó,
giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = F ( x) trên đoạn 0; 6 là
A. max F ( x) = F (6), min F ( x) = F (0)
B. max F ( x) = F (6), min F ( x) = F (3) 0; 6 0; 6 0; 6 0; 6
C. max F ( x) = F (2), min F ( x) = F (0)
D. max F ( x) = F (2), min F ( x) = F (3) 0; 6 0; 6 0; 6 0; 6 18 x + y − z
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 1 1 d : = = . Gọi d là hình 1 2 3 −
chiếu vuông góc của d trên mặt phẳng tọa độ (Oyz) . Một vectơ chỉ phương của d có tọa độ là
A. (0; − 2; 3)
B. (0; − 4; 3)
C. (1; − 3; 3) D. ( 1 − ; − 3; 3) Câu 9. Hàm số ( ) 1 2x f x e − =
là một nguyên hàm của hàm số nào sau đây? 1 1 − A. ( ) 1 2 2 x g x e − = . B. ( ) 1 2 2 x g x e − = − . C. ( ) 1 2 x g x e − = . D. ( ) 1 2 x g x = e − . 2 2
Câu 10. Trong không gian với hệ trục toạ độ Oxyz, cho hai mặt phẳng ( P) : x − y + z − 4 = 0 và
(Q): 2 x + y + z + 4 = 0 cắt nhau theo giao tuyến . Phương trình đường thẳng d đi qua điểm
A(3; 1; − 5) và song song giao tuyến có phương trình là x − 3 y −1 z + 5 x − 3 y −1 z + 5 A. d : = = d : = = 2 − 1 − . B. 3 2 1 3 − . x + 3 y +1 z − 5 x − 3 y −1 z + 5 C. d : = = d : = = 2 1 − 3 − . D. 2 1 − 3 − .
Câu 11. Biết diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − mx (với m là tham số thực) và trục
hoành bằng 2. Tích tất cả các giá trị m thỏa yêu cầu trên, gần bằng với giá trị nào sau đây? A. 2,29 B. 5 − ,24 C. 2 − ,29 D. 5,24
Câu 12. Trong không gian Oxyz, cho A(2; 2; 0) , B (0; 4; 4) và mặt phẳng ( P):x + y + z − 2 = 0 . Trong
tất cả các mặt cầu có tâm thuộc mặt phẳng (P) và đi qua điểm ,
A B , mặt cầu có bán kính nhỏ nhất bằng 336 3 70 12 5 A. . B. . C. . D. 6 . 7 7 7 Phần 2 : Đúng/Sai
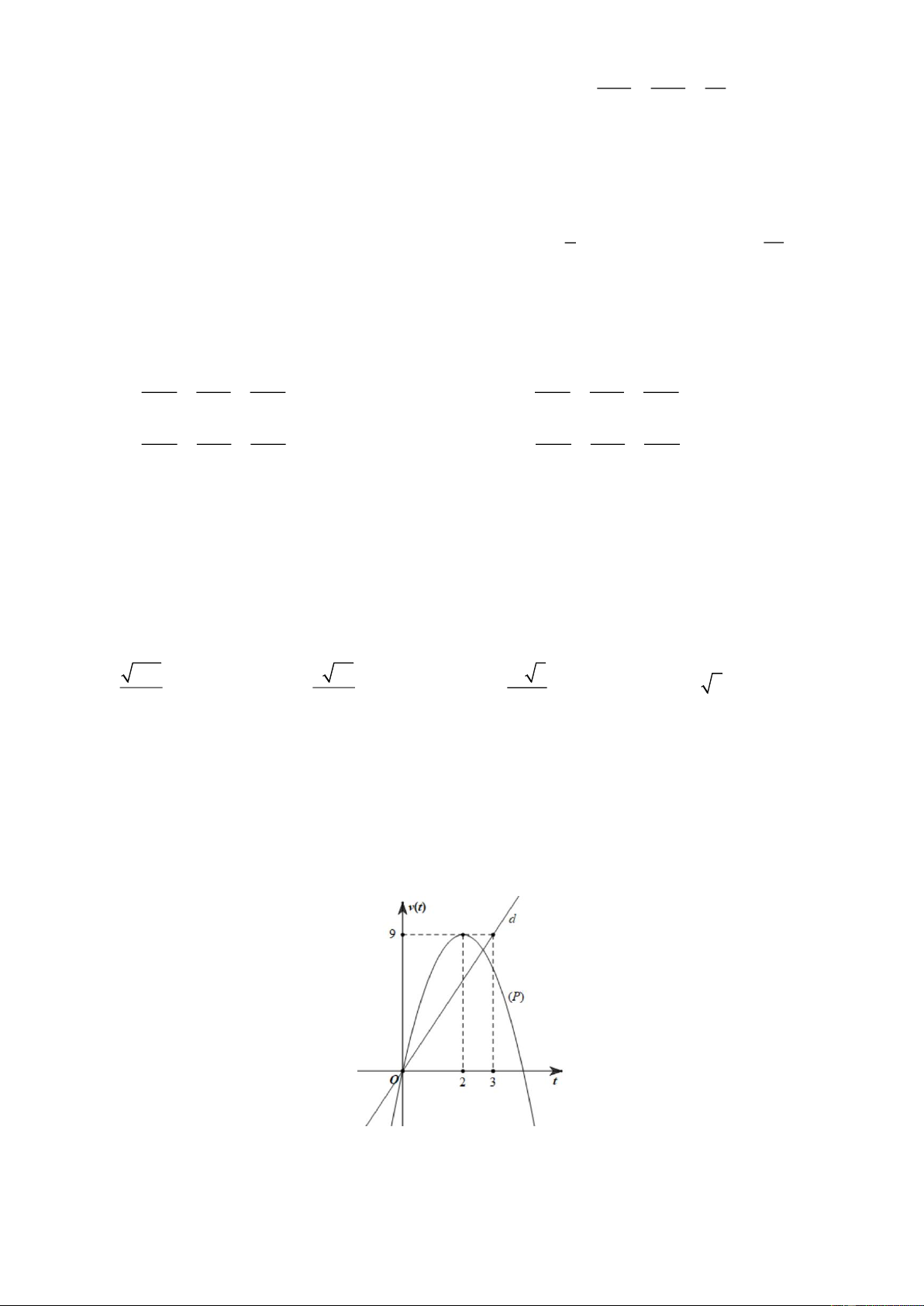
Câu 1. Có hai vật A, B di chuyển cùng một thời điểm, tại cùng vị trí xuất phát, trên cùng một đường
thẳng và theo hai hướng ngược nhau. Vật A có biểu thức vận tốc v t (m / s) phụ thuộc thời gian t (s) , 1 ( )
có đồ thị là một phần của đường parabol (P) như hình vẽ. Vật B có biểu thức vận tốc v t (m / s) phụ 2 ( )
thuộc thời gian t (s), có đồ thị là một phần của đường thẳng d như hình vẽ.
a) Vận tốc của vật B tại thời điểm t = 2 là 6(m / s) .
b) Sau 3 giây, vật B di chuyển được quảng đường là 9 mét. 19 −
c) Biểu thức vận tốc của vật A là v (t) 9 2 = t + 9t . 1 4
d) Khi hai vật đạt vận tốc bằng nhau (kể từ khi bắt đầu di chuyển) thì hai vật cách nhau 256 mét. 9 Câu 2.
Trong không gian Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z + 2x − 4 y − 2z + 3 = 0 có tâm I và đường x =1− t
thẳng d : y = t . z = 4
a) Mặt cầu có tâm I (1; − 2; − ) 1 .
b) Đường thẳng d và mặt cầu (S ) không có điểm chung.
c) Biết rằng, có hai mặt phẳng chứa d và lần lượt tiếp xúc mặt cầu ( S ) tại A, B . Khi đó, độ dài
đoạn thẳng AB bằng 2 2 .
d) Đường thẳng AB có một vectơ chỉ phương là u = (1; 1; 0) . Câu 3.
Cho hai biến cố A, B của cùng phép thử có P ( A) = 0,8 , P (B) = 0,3 và P ( AB) = 0,6 .
a) P (B A) 3 | =
b) P ( AB) = 0, 2 . c) P ( A B) 1 | = .
d) P ( A B) = 0,86 4 3 Câu 4.
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là kilomét), một trạm phát sóng điện
thoại đặt tại vị trí A(1; − 2; 0) (ta gọi là trạm phát A) và có bán kính phủ sóng là 4 (km). Nhà bạn Vy
đặt tại vị trí B (0; − 4; 2) , nhà bạn Vỹ đặt tại vị trí C (1; 2; 3) . Hôm nay, Vỹ có hẹn qua nhà chở Vy
đi học và đường đi từ nhà Vỹ đến nhà Vy được xem là một đường thẳng.
a) Để đi từ nhà Vỹ đến nhà Vy, ta cần di chuyển cùng hướng với vectơ u = (1; 6; ) 1 .
b) Điện thoại Vy có thể bắt được sóng của trạm A, còn điện thoại của Vỹ thì không.
c) Trước khi đi học, trạm phát sóng điện thoại gần nhà Vỹ bị hư, không thể phát sóng được. Đang
trên đường chạy đến nhà Vy thì điện thoại của Vỹ bắt được sóng của trạm phát A. Khi đó, Vỹ đã
chạy được đoạn đường 1,19 (km).
d) Ngay thời điểm điện thoại Vỹ bắt được sóng trạm A thì Vỹ nhận được tin nhắn của Vy đã gửi 2
phút trước đó với nội dung “Bạn chỉ còn đúng 10 phút để đón tôi”. Để kịp đón Vy, Vỹ phải chạy
đoạn đường còn lại với vận tốc trung bình tối thiểu là 37,32 (km / h) .
Phần 3 : Điền đáp số
Câu 1. Một vật đang chuyển động với vận tốc 6 (m / s) thì tăng tốc với gia tốc a (t ) = t ( 2
2 m / s ) . Tính
quãng đường vật đi được sau 6 giây kể từ lúc bắt đầu tăng tốc là ĐS: 108
Câu 2. Trong không gian với hệ trục toạ độ Oxyz , cho điểm M (1; 4; 2) và mặt phẳng
( ): x + 2y − z −1= 0. Gọi (S) là mặt cầu tâm M và cắt mặt phẳng ( ) theo giao tuyến là đường tròn có tâm H (a; ;
b c) . Tính T = a + b + c ĐS: 5
Câu 3. Biết (3 + 2). x = ( + ). x x e dx
ax b e + C với , a ,
b c R . Tính tổng a + b . ĐS. 2 x y −1 z +1 x −1 y −1 z
Câu 4. Trong không gian Oxyz , cho d : = = ; d : = = . Tính khoảng cách 1 2 1 − 2 2 1 2 − 2 −
giữa hai đường thẳng d , d (làm tròn đến hàng phần trăm). ĐS: 1,37 1 2 20




