Đề ôn thi toán 12 học kỳ 2 có đáp án và lời giải chi tiết

TÓM TẮT KIẾN THỨC ÔN TẬP HỌC KỲ I MÔN TOÁN 12
Kiến thức 1: CÁC VẤN ĐỀLIÊN QUAN ĐẾN PHƢƠNG TRÌNH BẬC HAI
1. Định lí Viet thuận
2. Định lí Viet đảo
Phƣơng trình bậc hai ( 2
ax  bx  c  0 )      S
Nếu  ,  là hai số có:   b    
Tổng 2 nghiệm: S  x  x  . P 1 2 a
thì chúng là 2 nghiệm phương trình:  c 2
Tích 2 nghiệm: P  x .x 
x  Sx  P  0 1 2 a
3. Điều kiện nghiệm của phƣơng trình
4. Phƣơng trình bậc hai chứa tham số thỏa bậc hai
điều kiện cho trƣớc
 Có 2 nghiệm trái dấu  . a c  0
 x < a < x 1 2    0 x  a   
Có 2 nghiệm cùng dấu   0 0 1    P  0  x  a  0
(x  a)(x  a)  0   2 1 2   0
 x < x < a   1 2
Có 2 nghiệm cùng dương  S  0    0 P  0  x  a  0  1  
 (x  a)  (x  a)  0 1 2   x  a  0 0  2
(x a)(x a)  0    1 2
Có 2 nghiệm cùng âm  S  0  
a < x < x 1 2 P  0    0 x  a  0  1  
 (x  a)  (x  a)  0 1 2 x  a  0  2
(x a)(x a)  0  1 2
Kiến thức 2: ĐẠO HÀM 1. Hàm sơ cấp 2. Hàm hợp 3. Quy tắc tính
1. Hàm thường gặp 1. Hàm thường gặp * Quy tắc:   
u v   C   0    ' u ' v ' u  1    u .u  
 .uv'  u'.v v'.u x  1   u u       u
u '.v v '.u  n  2 u   x  n 1  . n x 2   v  v     1 u '    
* CT Tính nhanh: x  1  2  u  u  2 x  ax  b  ad  bc 1.       cx  d  1  1  cxd2    2  x  x 2  2
 ax  bx  c  adx  aex be 
2. Hàm lượng giác 2 dc
2. Hàm lượng giác 2.      dx   e  dx e2 Trang 1    
sin x  cos x
sinu  .ucosu 2 2
 ax  bx  c  (ab  a b)x  2(ac a c)x  (bc  b c) 1 1 1 1 1 1 3.      2 2 2    
cos x  sin x cosu  u  .sinu a x b x c (a x b x c )   1 1 1 1 1 1   u  x 1 tan  tanu  2
4. Ứng dụng cos x 2 cos u   u 
1. Phương trình tiếp tuyến x 1 cot   cotu   2 sin x 2 sin u
y  f ' x . x  x  y 0   0  0
3. Hàm mũ-logarit
3. Hàm mũ-logarit 
+  x ; y là tọa độ tiếp điểm 0 0  x ' x a  a .ln a
 u' . u a u a .ln a 
+ f ' x là hệ số góc 0  x ' x e  e
 u' '. u e u e
2. Ứng dụng trong vật lí  u
Một chuyển động với quãng đường s t  có: x   u  a ' ' log a ' 1 log . x ln a . u ln a
+ Vận tốc: v(t)  s 't   u x 1 ln '   u ' ln ' 
+ Gia tốc: a(t)  v '(t)  s ' t  x u
Kiến thức 3: CÁC VẤN ĐỀ VỀ HÀM SỐ
1. Khảo sát sự biến thiên 2. Tìm cực trị
 Các bước khảo sát
 Cách 1: Dùng BBT
Bước 1: Tìm tập xác định
(Tương tự các bước như mục 1)
Bước 2: Tính y’
 Cách 2: Dùng y’’
Bước 3: Tìm nghiệm của y’ và những điểm y’ Bước 1: Tìm tập xác định không xác định
Bước 2: Tính y’
Bước 4: Lập bảng biến thiên
Bước 3: Tìm các nghiệm x của y’ i
Bước 5: Kết luận khoảng đồng biến, nghịch
Bước 4: Tính y '' biến Bướ 
c 5:Tính y ' (x )
Áp dụng giải phương trình i
Bước 6: Kết luận
+ Nếu f tăng(giảm) và f (x )  a thì phương 0
y ' (x )  0  x là điểm cực đại
trình f (x)  a có nghiệm duy nhất là x  x i i 0
y ' (x )  0  x là điểm cực tiểu
+ Nếu f tăng và g giảm và f (x )  g(x ) thì i i 0 0
phương trình f (x)  g(x) có nghiệm duy nhất là x  x0
+ Nếu f tăng (giảm) trên tập xác định
D thì: f (u)  f (v)  u  v (víi u,v  D) 3. Tìm max, min 4. Tìm tiệm cận
 Max, min trên đoạn [a;b]  Tiệm cận ngang
Bước 1: Tìm tập xác định
Bước 1:Tính lim y  y 1 Bướ x c 2: Tính y’   Bướ y
y là tiệm cận ngang
c 3: Tìm các điểm x 1 i là nghiệm của y’
hoặc là điểm mà y’ không xác định trên
Bước 2:Tính lim y  y2 x khoảng (a,b)
 y  y là tiệm cận ngang Bướ 2
c 4:Tính các giá trị f(xi), f(a), f(b)
Chú ý: Nếu hai giới hạn bằng nhau thì đths có Trang 2
Bước 5:So sánh và kết luận Max, min. một TCN
 Max, min trên khoảng hoặc nửa
 Tiệm cận đứng khoảng
Bước 1:Tìm những điểm x là những điểm Bướ 0
c 1: Tìm tập xác định không xác đị Bướ
nh của hàm số( với hàm phân thức c 2: Tính y’ thườ Bướ ng là nghiệm của mẫu)
c 3: Tìm nghiệm của y’ và những điểm y’   không xác đị
Bước 2:Kiểm tra điều kiện: lim x  hoặc nh trên khoảng (a,b)  x 0 x
Bước 4: Lập bảng biến thiên lim x    Bướ 
c 5: Kết luận Max, min x 0 x
 x  x là tiệm cận đứng. 0
Kiến thức 4: CÁC DẠNG ĐỒ THỊ Số nghiệm y ' 1. Hàm số bậc ba 3 2
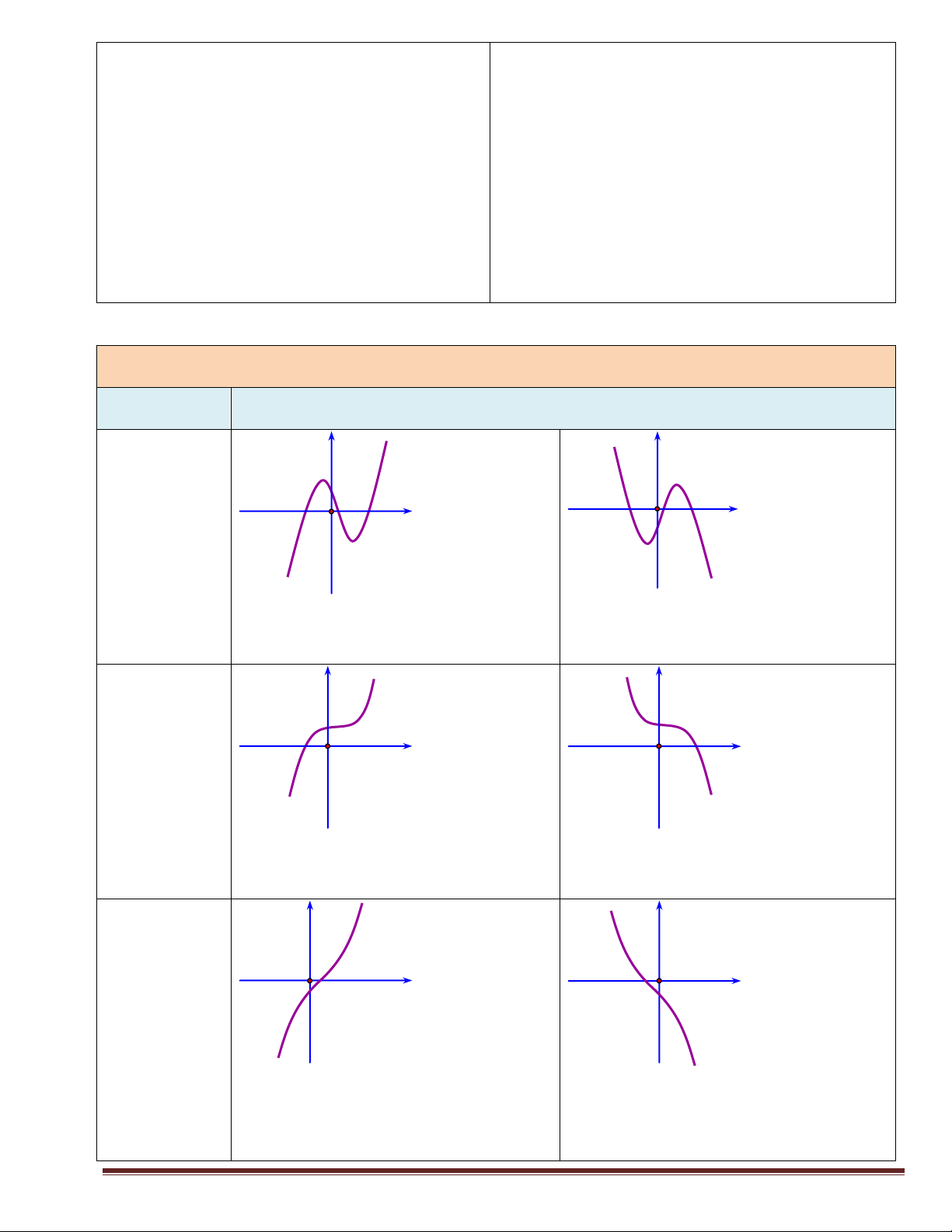
y  ax  bx  cx  d a  0 y y O x O x 2 nghiệm (2 cực trị) a  0 a  0 y y O x O x 1 nghiệm (0 cực trị) a  0 a  0 y y O O x x Vô nghiệm (0 cực trị) a  0 a  0 Trang 3 Số nghiệm y '
2. Hàm số bậc bốn trùng phƣơng 4 2
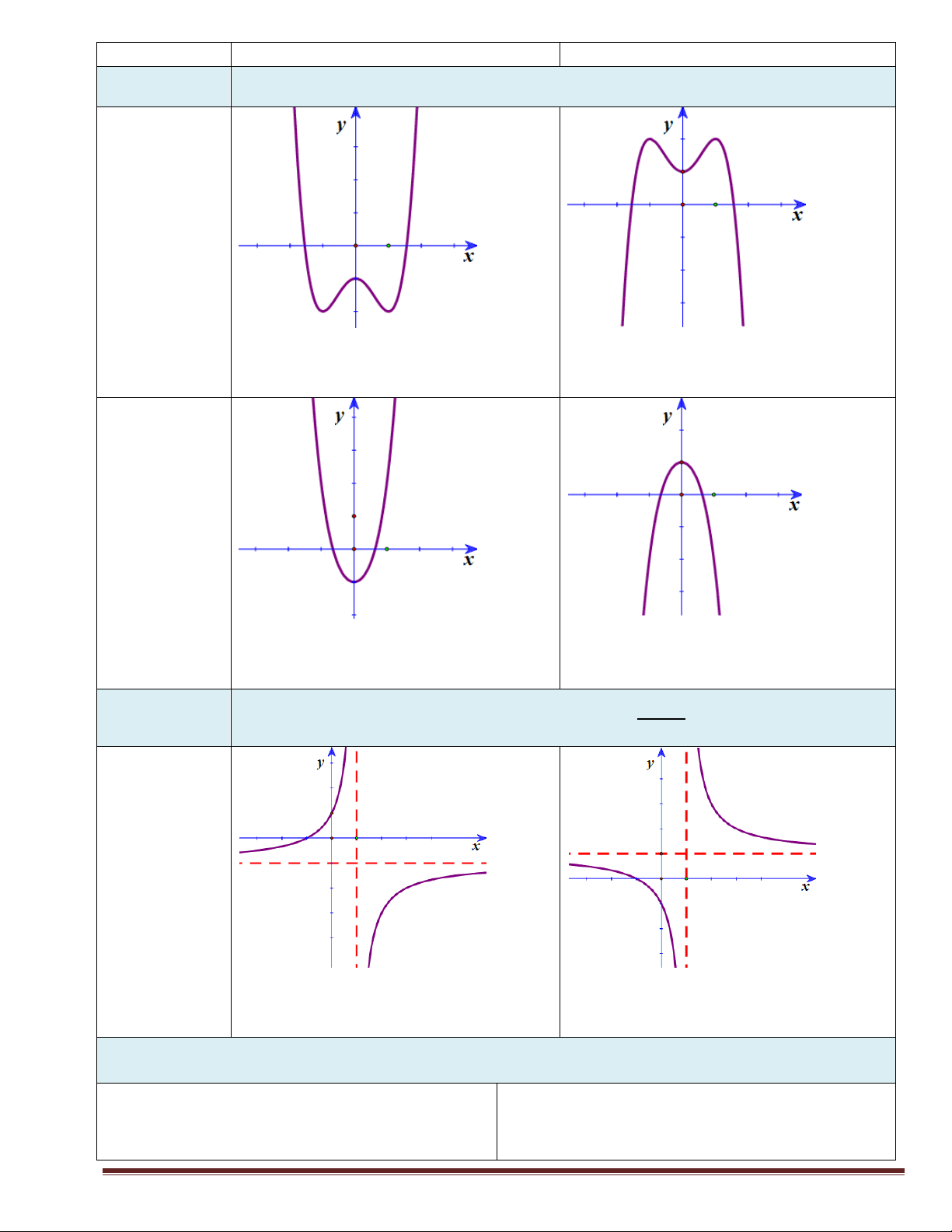
y  ax  bx  c a  0 3 nghiệm (3 cực trị) a  0 a  0 1 nghiệm (1 cực trị) a  0 a  0
ax  b
3. Hàm phân thức bậc nhất y 
, ab  bc  0
cx  d + Đồ thị không có cực trị + Có tâm đối xứng là giao điểm 2 tiệm cận
ad  bc  0 ad  bc  0
4. Các dạng toán liên quan đến đồ thị
 Tƣơng giao hai đồ thị (tìm giao điểm)
 Phƣơng trình tiếp tuyến
y  f (x); y  g(x)
Công thức: y  y  f '(x )(x  x ) 0 0 0 Trang 4
Bước 1: Tìm nghiệm x của phương trình (x ; y ) 0 0 0
là tọa độ tiếp điểm
hoành độ giao điểm f (x)  g(x) f '(x ) 0 Là hệ số góc
Bước 2: Thay vào công thức f (x) hoặc g(x) .
Được tung độ y  f (x )  g(x )
* Các trường hợp đặc biệt: 0 0 0
Giao điểm M (x ; y )
+ Tiếp tuyến song song với đường thẳng: 0 0
d : y  ax  b
 f '(x )  a
* Các trường hợp đặc biệt: 0
+ Giao với trục hoành (trục Ox): y  0
+ Tiếp tuyến vuông góc với đường thẳng:
d : y  ax  b
+ Giao với trục tung (trục Oy): x  0    f '(x ).a 1 0
Kiến thức 5: CÁC PHÉP BIẾN ĐỔI ĐỒ THỊ
1. Tịnh tiến đồ thị hàm số
2. Suy biến đồ thị
Hàm số y  f  x  có đồ thị là đường cong C
Hàm số y  f  x  có đồ thị là đường cong C
 Đồ thị hs y = f  x+ a :Tịnh tiếnC lên
 Đồ thị hs y = -f  x: Lấy đối xứng (C) qua trên a đơn vị. Ox
 Đồ thị hs y = f  x - a : Tịnh tiếnC
 Đồ thị hs y = f -x : Lấy đối xứng (C) qua
xuống dưới a đơn vị. Oy
 Đồ thị hs y = f  x + a : Tịnh tiếnC sang  Đồ thị hs y = f  x  : trái a đơn vị.
+ Giữ nguyên phần đồ thị C bên phải Oy, bỏ
 Đồ thị hs y = f  x - a: Tịnh tiếnC sang phần bên trái phải a đơn vị.
+ Lấy đối xứng phần đồ thị C được giữ lại qua Oy.
 Đồ thị hs y = f  x :
+ Giữ nguyên phần đồ thị C nằm trên Ox , bỏ
phần đồ thị C phía dưới Ox .
+ Lấy đối xứng phần đồ thị C bị bỏ qua Ox
 f x   0
Đồ thị hs y  f  x  
 y   f  x
+ Giữ nguyên phần đồ thị C nằm trên Ox , bỏ
phần đồ thị nằm phía dưới Ox
+ Lấy đối xứng phần đồ thị C được giữ lại qua Ox . Trang 5
Kiến thức 6: LŨY THỪA – MŨ - LOGARIT 1. Lũy thừa  Định nghĩa  Tính chất
Lũy thừa mũ nguyên dương: n a
( a )    
a  a  a
Lũy thừa mũ nguyên âm: n 1 a 
( a  0 )  n a a    a 
Lũy thừa mũ 0: 0 a a  1
( a  0 ) m   .
Lũy thừa mũ hữu tỉ:  n m (a )  a n a a
( a  0 )
Lũy thừa mũ vô tỉ:  a ( a  0 )   
(ab)  a b    a   a     b  b 2. Căn bậc n
 Định nghĩa
 Tính chất
Số a là căn bậc n của b nếu n a  b
Với a, b là các số dương:  Chú ý: n n n a. b  ab
+ Số dương b có 2 căn bậc chẵn:  n b
+ Số thực b bất kì có 1 căn bậc lẻ: n b n a a n  (b  0) + n n
0  0 (n  *, n  2) b b n a m n m
 a (a  0) m n mn a  a  a nÕu n lÎ n n a   a nÕu n ch½n  3. Logarit
 Định nghĩa
 Quy tắc tính
Với 2 số dương a, b và 
a  0 :   log b  a  b a
Lôgarit của tích: log (b .b )  log b  log b a 1 2 a 1 a 2
Logarit thập phân: log b  log b  lg b 10 b
Logarit tự nhiên: log b  ln b
Lôgarit của thương: 1 log
 log b  log b e a a 1 a 2 b  2 Tính chất  log a  1
Lôgarit của lũy thừa: log b  log b a a a log 1  0
Đổi cơ số: a loga b a  b log b c     log b log . a log b log b
log a   a c a c log a a c Đặ 1 1
c biệt: log b  ; log  b  log b a a log a a  b Trang 6
4. So sánh hai lũy thừa và logarit
 So sánh hai lũy thừa cùng cơ số
 So sánh hai logarit cùng cơ số
+ Nếu a  1:  
a  a    
+ Nếu a  1: log b  log b  b  b a 1 a 2 1 2
+ Nếu 0  a  1:  
a  a    
+ Nếu 0  a  1: log b  log b  b b a 1 a 2 1 2
 So sánh hai lũy thừa cùng số mũ(cơ số dương)
+ Nếu m  0 : m m
a  b  a  b
+ Nếu m  0 : m m
a  b  a  b
Kiến thức 7: HÀM SỐ LŨY THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT
1. Hàm số lũy thừa 2. Hàm số mũ 3. Hàm số logarit
 Dạng tổng quát
 Dạng tổng quát
 Dạng tổng quát 
y  x với   x
y  a , (a  0, a  1).
y  log x, (a  0, a  1) a TXĐ: TXĐ: D   
TXĐ: D  0; 
+  nguyên dương: D   
+  nguyên âm hoặc bằng 0: Đạo hàm  Đạo hàm x x   D   \   0 (a ) a .ln a   x  a  1 log
Đặc biệt: ( x) x e   e . x ln a
+  không nguyên: D  0;   Đạo hàm 1 Đố
Đặc biệt: (ln x)   
i với hàm hợp: 1 (x ) .x    . x ( u )  . u a
u a .ln a
Đối với hàm hợp: Đố u u   
i với hàm hợp:   Đặ e e u 1 c biệt: ( ) . (u ) .u    .u ' u  log u  a u.ln a  Đặ u
c biệt: (ln u)  u
Kiến thức 8: PHƢƠNG TRÌNH MŨ – PHƢƠNG TRÌNH LOGARIT 1. Phƣơng trình mũ
2. Phƣơng trình logarit
 Phƣơng trình mũ cơ bản
 Phƣơng trình logarit cơ bản Dạng TQ: x
a  b với 0  a  1.
Dạng TQ: log x  b với 0  a  1. a Nghiệm:
Điều kiện: x  0
+ Nếu b  0 thì phương trình vô nghiệm. Nghiệm: log b
x  b  x  a a
+ Nếu b  0 thì x
a  b  x  log b a .
 Một số phƣơng pháp giải
 Một số phƣơng pháp giải
- Đưa về cùng cơ số (chú ý trường hợp cơ số
(Chú ý đặt điều kiện phương trình)
là ẩn cần xét thêm trường hợp cơ số bằng 1) - Đưa về cùng cơ số. Trang 7
- Đặt ẩn phụ (chú ý điều kiện ẩn phụ) - Đặt ẩn phụ. - Logarit hóa. - Mũ hóa.
Kiến thức 9: BẤT PHƢƠNG TRÌNH MŨ – BẤT PHƢƠNG TRÌNH LOGARIT
1. Bất phƣơng trình mũ
2. Bất phƣơng trình logarit
 Bất phƣơng trình mũ cơ bản
 Bất phƣơng trình logarit cơ bản Dạng TQ: x a  b    (với 0  a  1)
Dạng TQ: log x b (với 0 a 1) a (hoặc x a  b x x   
; a  b ; a  b ) (hoặc log x ; b log x ; b log x b ) a a a Nghiệm:
Điều kiện: x  0 + Nếu b<0: BPT x a < b vô nghiệm Nghiệm: BPT x a > b vô số nghiệm log x > b log x < b + Nếu b>0: a a x a > 1 x  b a > b x a < b a  b x a a > 1
0 < a < 1 x  log b x  log b  b x a  b x a a a
Cơ số lớn hơn 1 giữ chiều, bé hơn 1 đảo
0 < a < 1 x  log b x  log b a a chiều
Cơ số lớn hơn 1 giữ chiều, bé hơn 1 đảo chiều  
Một số phƣơng pháp giải
Một số phƣơng pháp giải
(Chú ý đặt điều kiện bất phương trình) - Đưa về cùng cơ số. - Đưa về cùng cơ số.
- Đặt ẩn phụ (chú ý điều kiện ẩn phụ) - Đặt ẩn phụ. - Logarit hóa. - Mũ hóa.
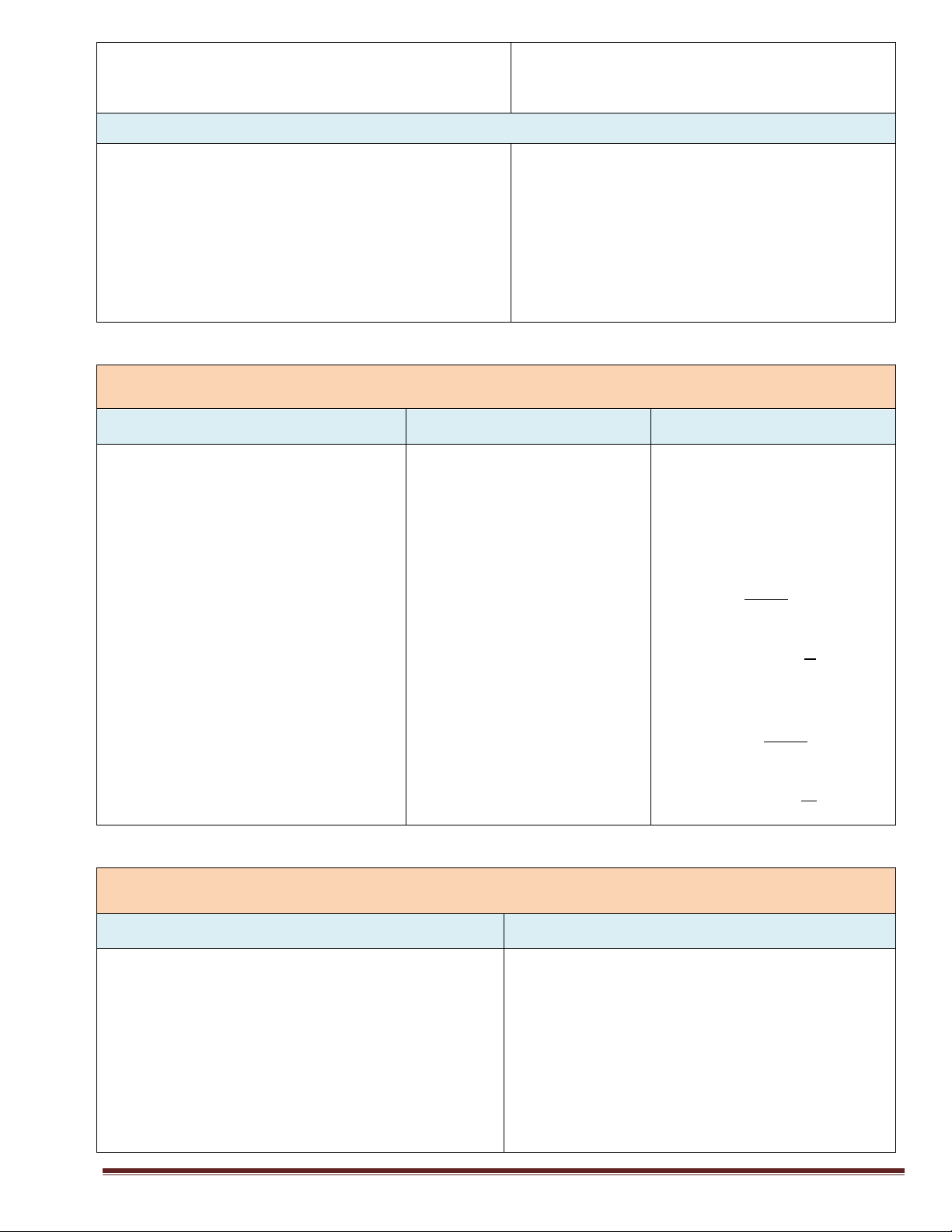
Kiến thức 10: HỆ THỨC LƢỢNG TRONG TAM GIÁC 1. Tam giác vuông 2. Tam giác thƣờng
Định lí cosin: 2 2 2
a  b  c (Pitagpo) 2 2 2
b  c  a 2 b  ab ' 2 2 2
a  b  c  2 .
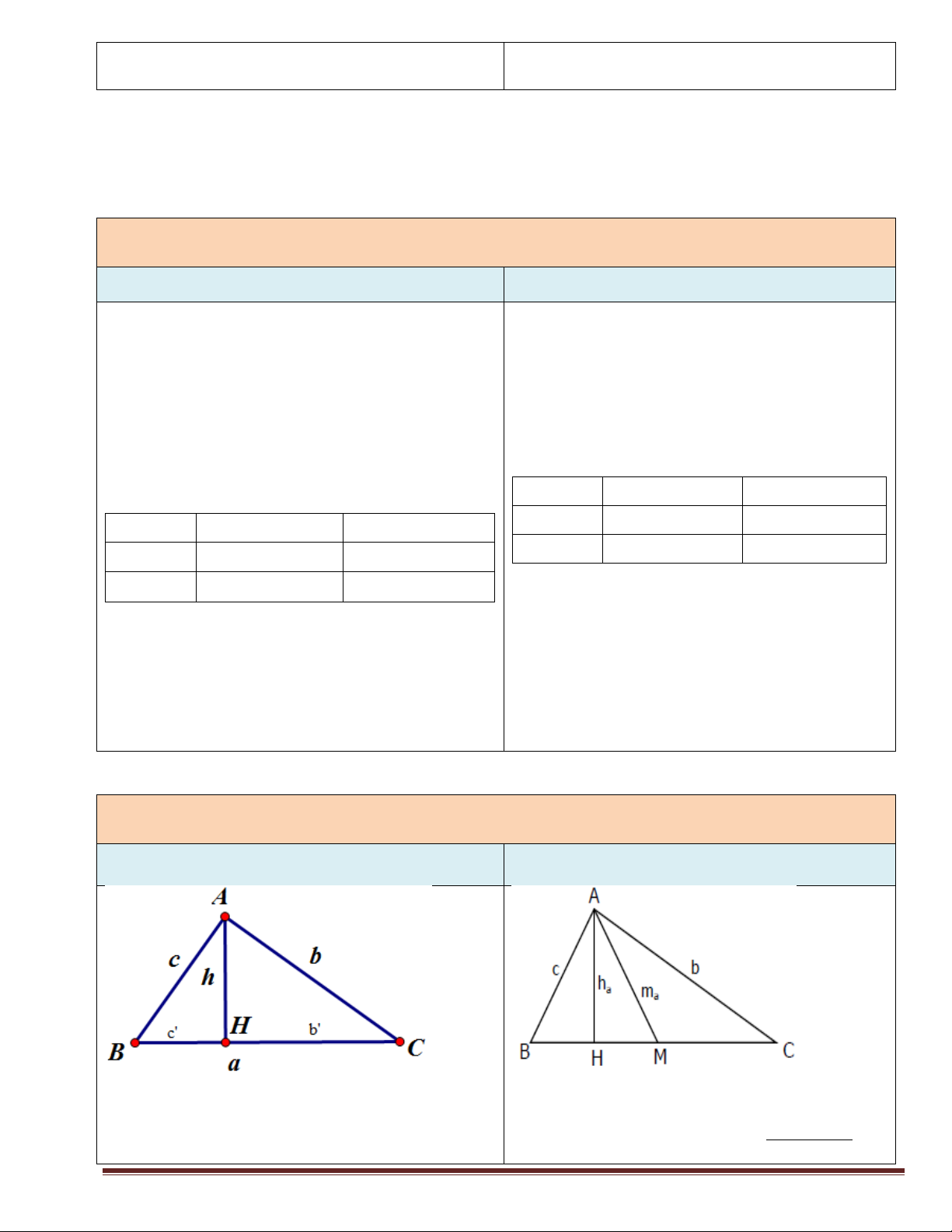
bc cosA  cosA  2bc Trang 8 2 c  ac ' Đị a b c nh lí sin:    2R 2
h  b 'c ' sinA sinB sinC 1 1 1 2 2 2     Độ 2 ( 2 b c ) a
dài trung tuyến: m  2 2 2 a h b c 4 ah  bc
Diện tích tam giác: b 1 1 1
sin B  cosC  S  ah  bh  ch a b c a 2 2 2 1 1 1 c S  bcSinA  acSinB  abSinC
cos B  sin C  2 2 2 a S  pr
(r là bán kính đường tròn nội tiếp) b tan B  cotC  abc c  S
(R là bán kính đường tròn ngoại 4R c
cot B  tan C  tiếp tam giác) b S 
p( p  a)( p  b)( p  c)
a  b  c (với p  ) 2
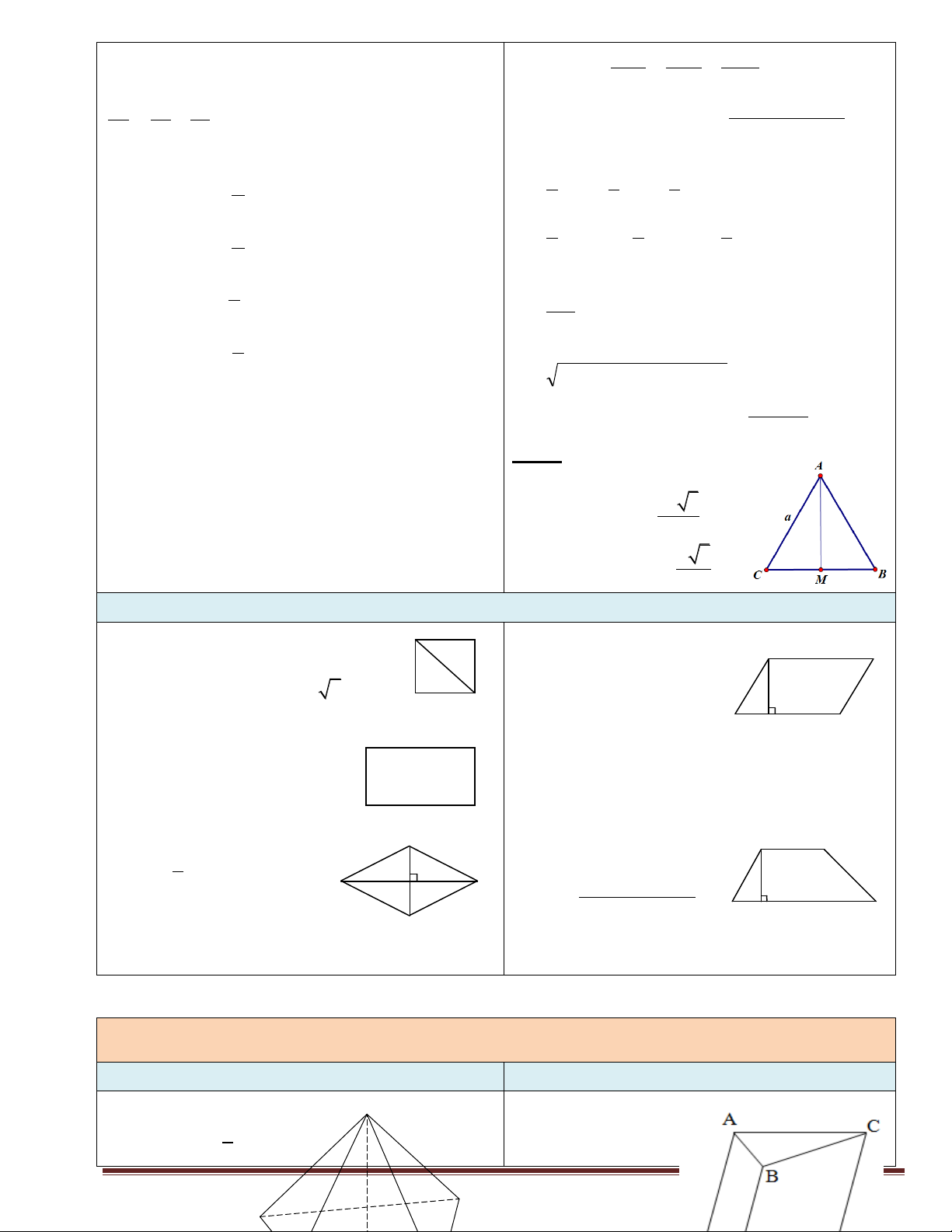
Chú ý:Với tam giác đều cạnh a 2 a 3 Diện tích: S  ABC  4 a 3
Trung tuyến: AM  2
3. Diện tích các hình
Hình vuông cạnh a A D
Hình bình hành Diện tích: 2 A D S  a S  B . C AH ABCD ABCD
Đường chéo: AC  BD  a 2  A . B A . D sin A B C B H C
Hình chữ nhật cạnh a, b A D S  . a b ABCD B C Hình thoi A Hình thang A D 1 S  AC.BD ABCD 2 B D
( AD  BC).AH   S . AB . AD sin A ABCD 2 B H C  C . AB . AD sin B
Kiến thức 11: KHỐI ĐA DIỆN 1. Khối chóp 2. Khối lăng trụ S 1
Thể tích:V = B.h Thể tích:V = B .h 3 Trang 9 D O
Khối chóp tam giác đều S.ABC
Lăng trụ đều: + Đáy là tam giác đều + Là lăng trụ đứng
+ Hình chiếu của đỉnh là trọng tâm của đáy + Đáy là đa giác đều
+ Các cạnh bên bằng nhau. + Các cạnh bên bằng nhau
Khối chóp tứ giác đều S.ABCD
Khối hộp chữ nhật: V = a. . b c + Đáy là hình vuông.
+ Hình chiếu của đỉnh là giao điểm AC và BD.
+ Các cạnh bên bằng nhau. S
Tỉ số thể tích V ¢ ¢ ¢ A’ B’ ¢ ¢ ¢ SA SB SC S .A B C = . . V SA SB SC S .A BC C’ A
B Khối lập phương: 3 V = a C
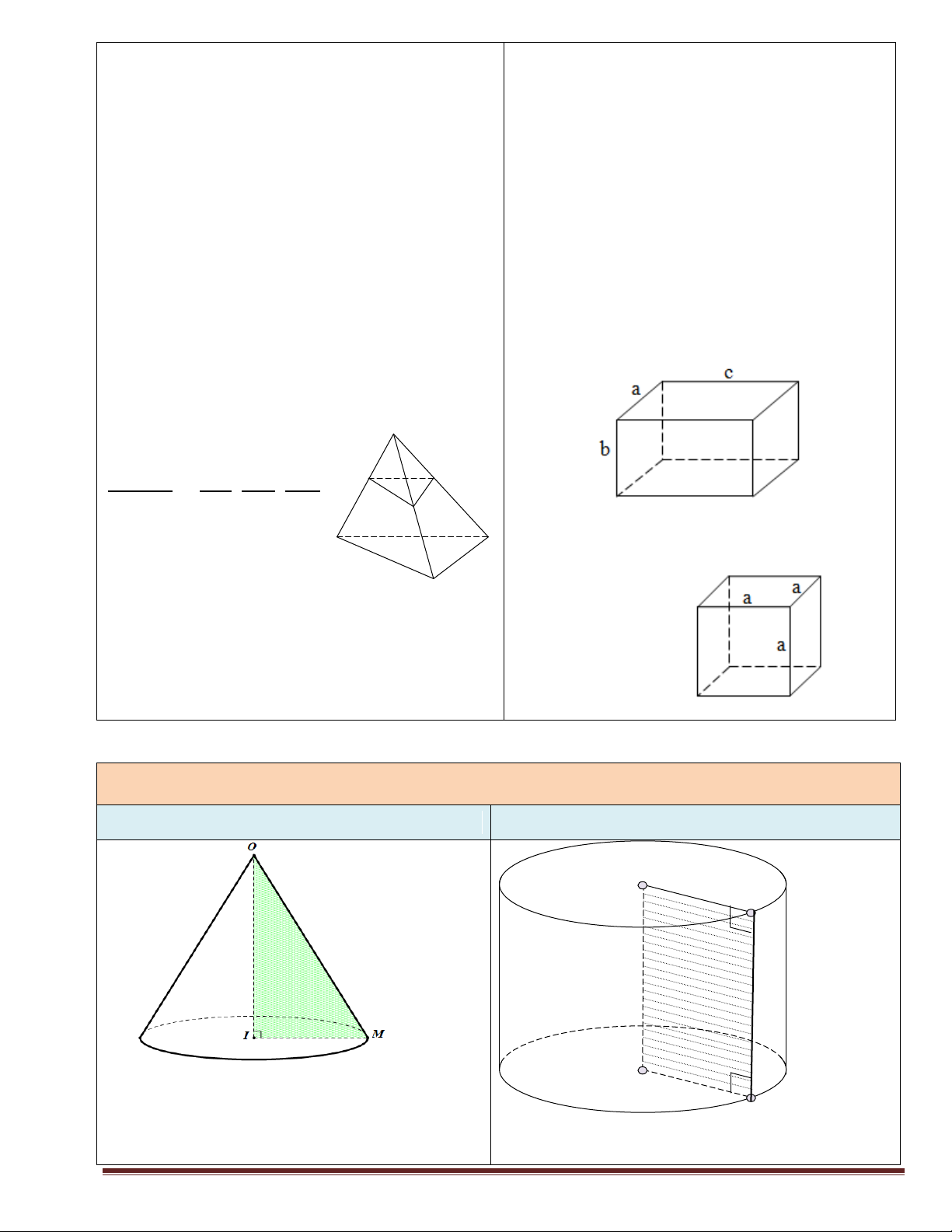
Kiến thức 12: MẶT TRÒN XOAY 1. Mặt nón 2. Mặt trụ A r D h l B Đườ r
ng sinh: l  OM C
Đường cao: h  OI
Bán kính đáy: r  IM
Đường sinh: l  DC Trang 10
Diện tích xung quanh: S   rl
Đường cao: h  AB  l xq
Bán kính đáy: r  AD 
Diện tích đáy: 2 S   BC đ r
Diện tích xung quanh: S  2 rl
Diện tích toàn phần: 2
S  S  S
 r rl xq tp đ xq
Diện tích toàn phần: 1 Thể tích: 2 V   r h 2 S  S
 S  2r  2rl  2r(r  l) 3 tp 2đ xq Thể tích: 2 V   r h 3. Mặt cầu
Diện tích mặt cầu: 2
S  4 R 4
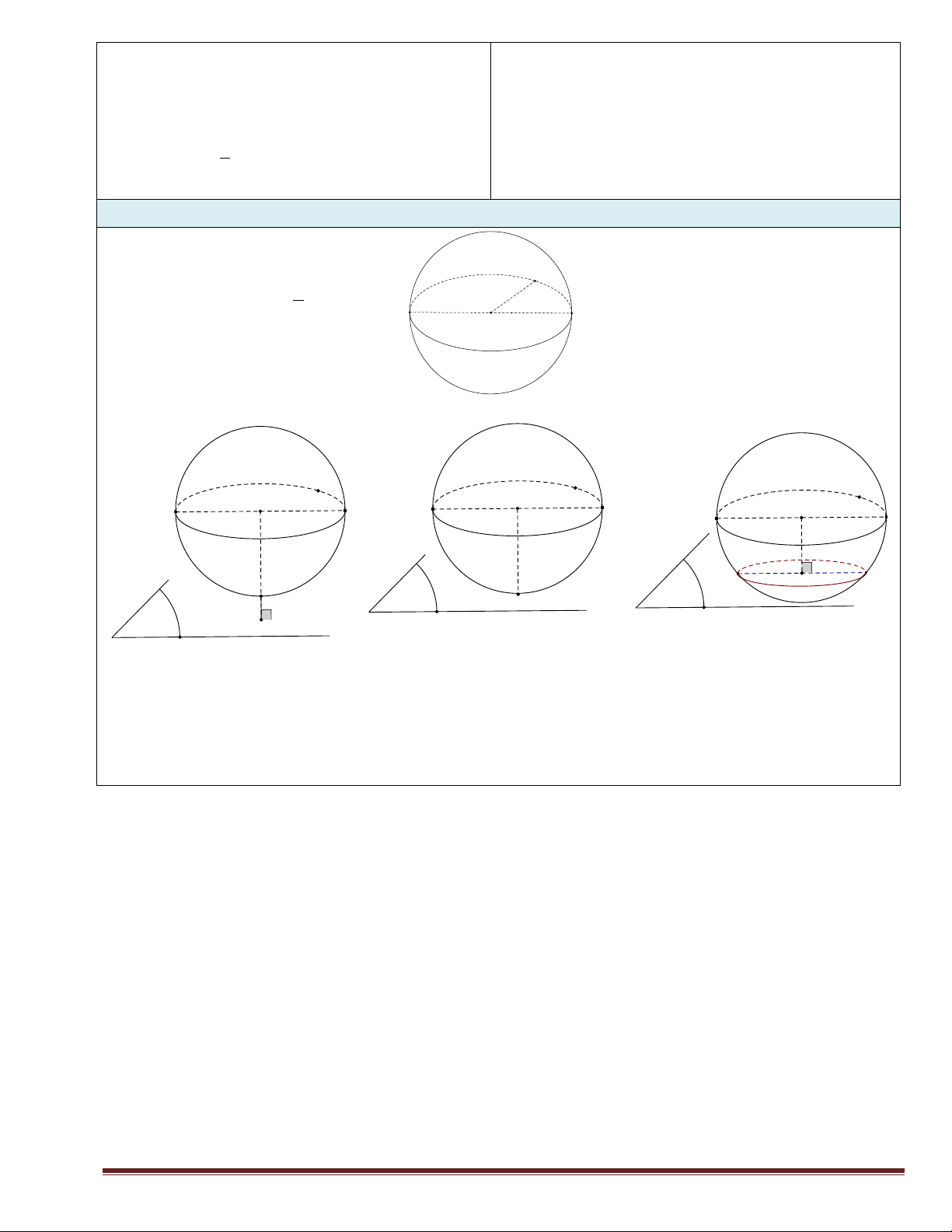
Thể tích khối cầu: 3 V   R R 3 O
Giao của mặt cầu và mặt phẳng O O O P H P H P H OHOH>R OH=R
(P) và mặt cầu S(O; R) không có điểm chung
(P) tiếp xúc với mặt cầu S(O; R) tại H (P) cắt mặt cầu S(O; R) Chú ý: OH  1. d (O, (P))
2. Trường hợp mặt phẳng cắt mặt cầu theo giao tuyến là đường tròn bán kính r , ta có: 2 2 2
OH  R  r Trang 11