Đề ôn thi toán 12 học kỳ 2 có đáp án và lời giải chi tiết

ĐỀ THI THỬ HỌC KÌ II Năm Học 2020-2021 MÔN: TOÁN LỚP 12
Câu 1: Cho hàm số f (x) xác định trên R và có 1 nguyên hàm là F(x) . Cho các mệnh đề sau :
1) Nếu f (x)dx  F(x)  C 
thì f (t)dx  F(t)  C  /
2)  f (x)dx  f (x)   3) /
f (x)dx  f (x)  C 
Trong số các mệnh đề trên , số mệnh đề là mệnh đề SAI là : A.0 B. 1 C. 2 D. 3 3
Câu 2 . Nguyên hàm của hàm số f (x) = 2 x   2 x là : x 3 x 4 3 x 4 A. 3  3ln x 
x  C B. 3  3ln x  x 3 3 3 3 3 x 4 3 x 4 C. 3  3lnx
x  C D. 3  3ln x  x  C 3 3 3 3
Câu 3.Hàm số F(x) = lnx là nguyên hàm của hàm số nào sau đây trên ( 0 ; +∞) ? 1 1 1 A.f(x) = B. f(x) = 
C. f(x) = x ln x  x  C D. f(x) =  x x 2 x
Câu 4 .Giá trị tham số m để hàm số F (x) = mx3 + (3m + 2 )x2 – 4x + 3 là 1 nguyên hàm của hàm
số f (x) = 3x2 + 10 x – 4 là :
A.Không có giá trị m B. m = 0 C. m = 1 D. m = 2
Câu 5. Biết F (x) là một nguyên hàm của f(x) =(2x -3 )lnx và F(1) =0 . Khi đó phương trình
2F(x) + x2 -6x + 5 =0 có bao nhiêu nghiệm ? A. 1 B. 4 C. 3 D. 2 x
Câu 6. Cho F (x) là một nguyên hàm của f(x) =
thỏa F (0) = 0 . Tính F ( ). 2 cos x 1 A. F    1 
B. F ( )  1 C. F( )  0 D. F(  ) = 2  π  a 29
Câu 7: Cho a  0;   . Tính J  dx  theo a .  2  2 cos x 0 1 A. J  tan a .
B. J  29cot a .
C. J=29 tana D. J  2  9tana . 29 1 Câu 8: Tính 2  d  x I e x . 0 1 2 e 1 A. e  . B. e 1. C. 2 e 1. D. 2 2 2 2 x  4x
Câu 9: Tính tích phân I  dx  . x 1 29 29 11  11 A. I  . B. I  . C. I  . D. 2 2 2 2 Trang 1  2 Câu 10: Tính 6
I  sin x cos d x . x  . 0 11 1 1 1 A. B. I   . C. I   . D. I  . 7 7 6 6 e 2ln x Câu 11: Biết 1 dx a . b e    
, với a,b   . Chọn khẳng định đúng trong các khẳng định sau: 2 x 1
A. a  b  3.
B. a  b  6.
C. a+b=-7 D. a  b  6  . 5 5 4 1 4 Câu 12: Cho f (x) dx  5  , f (t) dt  2   và g(u) du  
. Tính ( f (x)  g(x)) dx  bằng. 3 1  4 1  1  8 10 22 20 A. . B. . C. D . . 3 3 3 3 5 dx
Câu 13:Tính tích phân: I  
được kết quả I  a ln 3 bln 5. Tổng a  b là. x 3x 1 1 A. 1. B. 1 C. 3 . D. 2 .
Câu 14: Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f(x) ( liên tục trên
 ;ab ) , trục hoành Ox và hai đường thẳng x = a , x = b (a < b ) . Khi đó S được tính theo công thức nào sau đây ? b b b b
A. S = f (x)dx  B. S = f (x)dx  C. S = f (x)dx  D. S = 2
 f (x)dx  a a a a
Câu 15: Cho hình ( D) giới hạn bởi các đường y = f(x) , y = 0 , x = , x = e . Quay (D) quanh
trục Ox ta được khối tròn xoay có thể tích V. Khi đó V được xác định bằng công thức nào sau đây ?  e   A.V =  f (x)dx  B. V = 2  f (x)dx  C.V  f (x) dx  D. 2 V   f (x)dx  e  e e
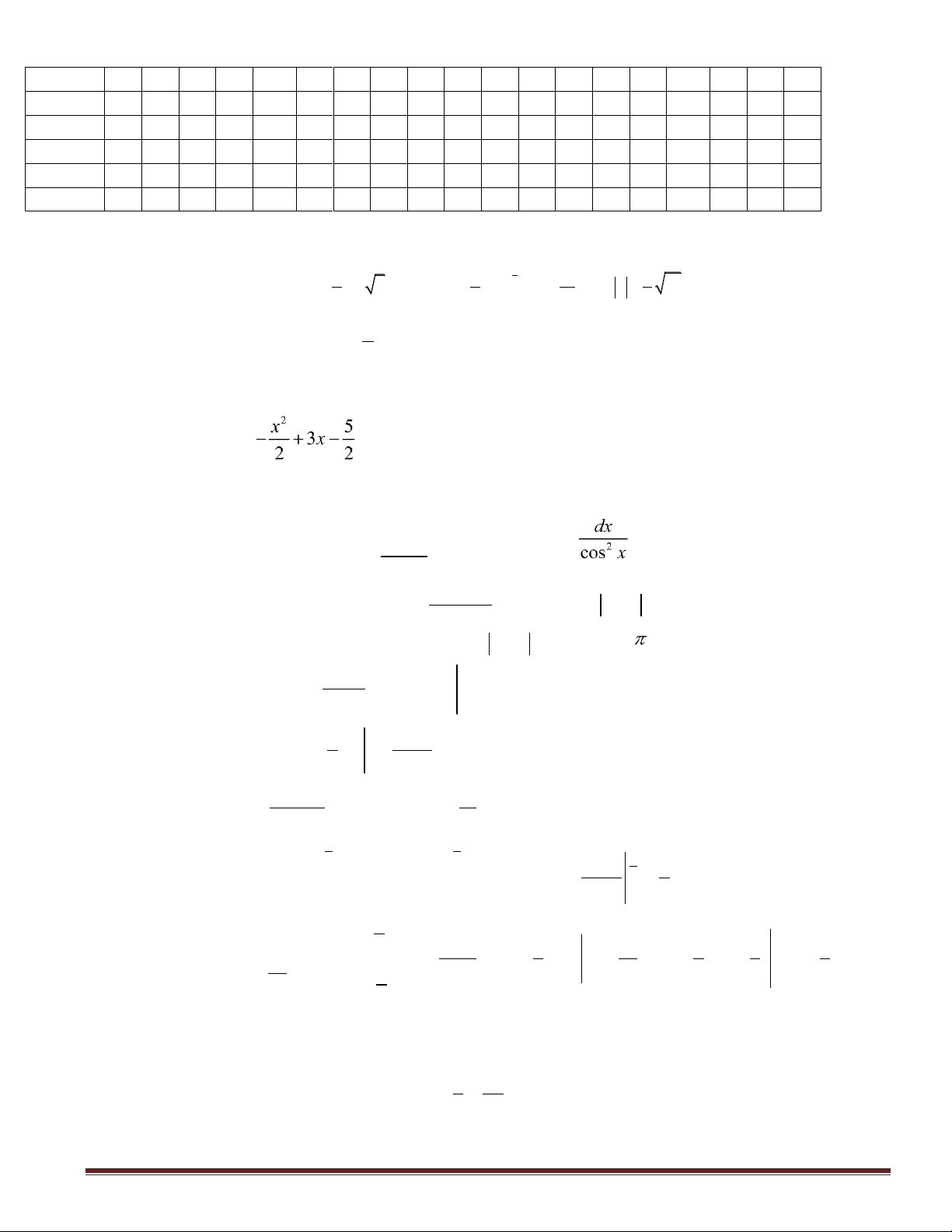
Câu 16: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = -2x3 + x2 + x + 5 và y = x2 –x + 5 bằng : 1
A.S =0 B.S = 1 C.S = D.S = 2
Câu 17: Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y =
4 , trục hoành , đường thẳng x =1 , x = 4 quanh Ox . x
A.V = ln256 B. V = 12  C. S = 12 D. S = 6
Câu 18: Một chất điểm chuyển động trên trục Ox với vận tốc thay đổi theo thời gian v (t) = 3t2 –
6t ( m/s). Tính quãng đường chất điểm đó đi được từ thời điểm t1 = 0 đến t2 = 4 (s) . 1536 A. 16 m B. m C. 96 m D. 24m 5
Câu 19: Số phức liên hợp của số phức z = -1 + 2i là số phức :
A. A. z = 2-i B.z = -2 + i C. z = 1-2i D. z = -1-2i
Câu 20: Cho hai số phức z1= 6 + 8i , z2 = 4 + 3i . Khi đó giá trị | z1 – z2| là: A.5 B. 29 C.10 D.2
Câu 21: Điểm biểu diễn của số phức z = m + mi với m nằm trên đường thẳng có phương trình là : A. y= 2x B.y = 3x C.y =4 x D.y= x Trang 2
Câu 22: Thu gọn z= ( 2-3i)(2 +3i) ta được: A.z=4 B.z=13 C.z= --9i D.z=4 –9i
Câu 23:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện | z –i|= 1 là :
A.Một đường thẳng B.Một đường tròn C. Một đoạn thẳng D.Một hình vuông
Câu 24 : Tìm số phức z biết |z| = 20 và phần thực gấp đôi phần ảo A.z1=4+3i,z2=3+4i
B. z1 = 2—i,z2= -2 +i
C.z1= -2+i ,z2= -2 –i D.z1=4+2i,z2= -4 –2i
Câu 25:Cho x,y là các số thực. Hai số phức z =3+i và z =( x +2y ) –yi bằng nhau khi: A.x=5,y= -1 B.x=1,y=1 C.x=3 ,y=0 D.x=2,y=-1
Câu 26 :Cho x,y là các số thực.Số phức z= 1 + xi +y +2i bằng 0 khi : A.x=2 ,y=1
B.x=-2,y=-1 C. x= 0,y=0 D.x=-2,y= -2
Câu 27: Có bao nhiêu số phức z thỏa : 2 z  z  0 A.0 B.1 C. 2 D. 3
Câu 28:Tập hợp điểm M biểu diễn số phức z thỏa điều kiện : |z +1-i|=|z+3-2i| là: A. Đường thẳng B.Elip C.Đoạn thẳng D.Đường tròn
Câu 29 : Trên mặt phẳng phức ,gọi A,B lần lượt là các điểm biểu diễn 2 nghiệm phương trình:z2-
4z +13 =0.Diện tích tam giác OAB là: A.16 B.8 C.6 D.2
Câu 30 :Phần thực của số phức (1+i)30 bằng : A. 0 B.1 C.215 D.-215
Câu 31: Trong không gian với hệ tọa độ Oxyz , cho điểm M 0;0; 2   và đường thẳng x  3 y 1 z  2  :  
. Viết phương trình mặt phẳng P đi qua điểm M và vuông góc với đường 4 3 1 thẳng  .
A. 4x  3y  z  7  0 .
B. 4x  3y  z  2  0 .
C. 3x  y  2z 13  0 .
D. 3x  y  2z  4  0 .
Câu 32: Trong không gian với hệ tọa độ Oxyz , mặt phẳng P song song với hai đường thẳng x  2  t x  2 y 1 z   : 
 ,  : y  3 2t . Vectơ nào sau đây là vectơ pháp tuyến của P ? 1 2 3  4 2 z 1t      A. n   5  ;6; 7
  . B. n   5  ; 6
 ;7 . C. n  5;6;7 . D. n  5;6;7 .
Câu 33: Mặt phẳng P đi qua ba điểm A0;1;0, B  2
 ;0;0,C 0;0;3 . Phương trình của mặt phẳng P là: A. P : 3  x 6 y 2z  0 .
B. P : 6x  3y  2z  0 . C. P : 3
 x  6y  2z  6 .
D. P : 6x  3y  2z  6 . x  y  z 
Câu 34: Trong không gian Oxyz cho đường thẳng 1 1 3 d :   . Trong các vectơ sau 2 1  2
vectơ nào là vectơ chỉ phương của đường thẳng d .    
A. u 2;1; 2 . B. u 1; 1; 3 . C. u  2  ; 1  ; 2   . D. u  2  ;1; 2   . Trang 3
Câu 35: Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A 1
 ;3;2, B2;0;5, C 0; 2  
;1 . Viết phương trình đường trung tuyến AM của tam giác ABC . x 1 y  3 z  2 x  2 y  4 z 1 A. AM :   . B. AM :   . 2 4 1 1 1 3 x 1 y  3 z  2 x 1 y  3 z  2 C. AM :   . D. AM :   . 2 4 1 2 4 1
Câu 36: Trong không gian với hệ tọa độ Oxyz cho d là đường thẳng đi qua A1; 2;3 và vuông
góc với mặt phẳng P :3x  4y 5z 1 0. Viết phương trình chính tắc của đường thẳng d . x 1 y  2 z  3 x 1 y  2 z  3 x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . C.   . D.   . 3  4 5  3 4 5 3 4  5  3 4  5 
Câu 37:Trong không gian với hệ tọa độ Oxyz, cho điểm A1; 1
 ;3 và hai đường thẳng. x  4 y  2 z 1 x  2 y 1 z 1 d :   , d :  
. Viết phương trình đường thẳng d đi qua điểm , A 1 2 1 4 2  1 1  1
vuông góc với đường thẳng d và cắt đường thẳng d . 1 2 x 1 y 1 z  3 x 1 y 1 z  3 A. d :   . B. d :   . 2 1 3 2  2 3 x 1 y 1 z  3 x 1 y 1 z  3 C. d :   . D. d :   . 4 1 4 2 1  1 
Câu 38: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 2  ;1;  1 và B0;1;  1 . Viết
phương trình mặt cầu đường kính . AB . A.  2 2
x  2  y   z  2 2 1 1  2. B.  x   2
1  y   z   1  8 . C.  2 2
x  2  y   z  2 2 1 1  2. D.  x   2
1  y   z   1  8 .
Câu 39: Trong không gian với hệ toạ độ Oxyz , cho mặt cầu 2 2 2
(S) : x  y  z  4x  2 y  6z  2  0 .
Mặt cầu (S ) có tâm I và bán kính R là. A. I ( 2  ;1;3), R  2 3 . B. I (2; 1  ; 3  ), R  12 .
C. I (2; 1; 3), R  4 .
D. I (2;1;3), R  4 .
Câu 40: Mặt cầu S  có tâm I  1  ;2 
;1 và tiếp xúc với mặt phẳng  P : x  2y  2z  2  0 . A.  2 2 2
x  2   y  2   z  2 1 2 1
 3 . B. x  
1   y  2   z   1  9 . C.  2 2 2
x  2   y  2   z  2 1 2 1
 3. D. x  
1   y  2   z   1  9 .
Câu 41: Cho ba điểm A2; 1  ;  5 , B 5;5;  7 và M  ; x y; 
1 . Với giá trị nào của x, y thì A, B , M thẳng hàng?
A. x  4; y  7 .
B. x  4; y  7 . C. x  4  ; y  7
 . D. x  4; y  7 .
Câu 42:Cho bốn điểm A ;
a 1; 6 , B 3
 ; 1;  4 ,C5; 1; 0và D1; 2; 
1 thể tích của tứ diện
ABCD bằng 30.Giá trị của a là. A. 2 hoặc 32. B. 32 . C.1 . D. 2 .   Câu 43:Tìm m
v  3;log 3;4 là góc nhọn. 5 
để góc giữa hai vectơ u  1;log 5;log 2 , 3 m  1 1 A. 0  m  . B. m  1hoặc 1 0  m  . C. m 
, m  1. D. m  1. 2 2 2 Trang 4
Câu 44:Trong không gian với hệ tọa độ Oxyz ,cho hai đường thẳng
x  2  3t  x  4 y 1 z d :  y  3
  t và d ':  
.Phương trình nào dưới đây là phương trình đường thẳng  3 1 2  z  4  2t 
thuộc mặt phẳng chứa d và d ' ,đồng thời cách đều hai đường thẳng đó. x  3 y  2 z  2 x  3 y  2 z  2 A.   . B.   . 3 1 2  3 1 2  x  3 y  2 z  2 x  3 y  2 z  2 C.   . D.   . 3 1 2  3 1 2 
Câu 45:Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x 1 kt x 1 y  2 z  3  d :  
và d :  y  t
.Tìm giá trị của k để d cắt d . . 1 1 2  1 2 1 2 z  1   2t  1 A. k  1. B. k  1  . C. k   . D. k  0 . 2
Câu 46:Trong không gian với hệ trục tọa độ Oxyz, gọi
d là giao tuyến của hai mặt phẳng có
phương trình lần lượt là 2x  y  z  2021  0 và x  y  z  5  0. Tính số đo độ góc giữa đường thẳng d và trục . Oz . A. O 45 . B. O 0 . C. O 30 . D. O 60 .
Câu 47:Trong không gian với hệ tọa độ Oxyz ,cho mặt phẳng  P : 3x  4y  2z  4  0 và hai điểm
A1;  2; 3, B1;1; 2 .Gọi d , d lần lượt là khoảng cách từ điểm A và B 1 2 đến mặt phẳng
P.Trong các khẳng định sau khẳng định nào đúng?
A. d  2d .
B. d  3d .
C. d  d .
D. d  4d . 2 1 2 1 2 1 2 1
Câu 48:Trong không gian với hệ tọa độ Oxyz ,cho mặt cầu S 2 2 2
: x  y  z  2x  4 y  6z  2  0 .Viết phương trình mặt phẳng   chứa Oy cắt mặt cầuS 
theo thiết diện là đường tròn có chu vi bằng 8 .
A.   : x  3z  0 .
B.   : 3x  z  2  0 .
C.   : 3x  z  0 .
D.   : 3x  z  0 .
Câu 49: Trong không gian với hệ trục tọa độ Oxyz ,cho mặt phẳng      ( ) : 2x 2y z 4 0 và    đường thẳng x 2 y 2 z 2 d :   . Tam giác ABC có ( A 1
 ;2;1) , các điểm B ,C nằm trên  1 2 1 
và trọng tâm G nằm trên đường thẳng d . Tọa độ trung điểm M của BC là. A. M (0;1; 2
 ). B. M (2;1;2) . C. M (1; 1  ; 4  ). D. M(2; 1  ; 2  ) .
Câu 50: Trong không gian với hệ toạ độ Oxyz , cho đường thẳng  nằm trong mặt
phẳng   : x  y  z 3  0 đồng thời đi qua điểm M 1;2;0 và cắt đường thẳng x  2 y  2 z  3 d :  
. Một vectơ chỉ phương của  là. 2 1 1    
A. u  1; 1;  2 B. u  1;0;  
1 C. u  1;  2; 
1 D. u  1;1;  2
…………………………………….HẾT………………………………………… Trang 5 ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Đáp án C A A C D C C D D A C C B C D B B A D Câu 20 21 22 23 24
25 26 27 28 29 30 31 32 33 34 35 36 37 38 Đáp án B D B B D A B D A C A D B C D A D D C Câu 39 40 41 42 43 44 45 46 47 48 49 50 Đáp án C D D A B A D A B D D D Hướng dẫn giải
Câu 1 Đáp án : C ( 1 và 3 sai ) 1 3 3  3  x 4
Câu 2 : Đáp án : A Vì 2 2 3 2
(x   2 x)dx  
x  2x dx  3ln x  x C x x 3 3   1
Câu 3 : Đáp án : A . Vì ( lnx)/ = x
Câu 4 Đáp án : C Ta có F/(x) = f (x)nên ta có 3m = 3 và 2 (3m + 2) = 10 .Suy ra m = 1 .
Câu 5. Đáp án : D Dùng phương pháp nguyên hàm từng phần ta tính được : F (x) = ( x2 -3x) lnx
Phương trình đã cho trở thành ( x2 -3x )lnx =0 nên có nghiệm x = 1, x= 3 ( do x = 0 không thỏa mãn ) . xdx
Câu 6. Đáp án C .Lời giải: F(x) =  ;Đặt u = x , dv =
, ta có du = dx , v = tanx 2 cos x d (cos x)
Suy ra F (x) = xtanx  tan xdx  x tan x   
= x tan x  ln cos x  C cos x
Từ F (0)= 0 , ta có C = 0 . Vây F (x) = xtanx + ln cos x . Do đó F( ) = 0 . a 29 a
Câu 7: Chọn C. Ta có J  x d = 29tanx  29 tan a  . 2 cos x 0 0 1 1 2 1 e 1 Câu 8: Chọn D. 2 2
I  e dx  e   x x . 2 2 0 0 2 2 2 x  4x 11
Câu 9: Chọn D. I 
dx  (x  4)dx    . x 2 1 1   2 2  sin x 1
Câu 10: Chọn A. Ta có: 6 6
I  sin x cos d x x  sin d x sinx 7 2     . 0 7 7 0 0  1 u   ln x du  d e x e e    x 2 ln x  1 e  1  1 1  2 Câu 11:Chọn C  1    dx   ln x 
dx   ln x  1       2 2 dv  dx 1 x    x  x  x x  e 2 1 1 1  v   1 x  x 4 5 5 4 5 5 Câu 12: Chọn C.
f (x) dx f (x) dx  f (x) dx  f (x) dx  f (x) dx f (x) dx  7       . 1  4 1  1  1  4 4 4 4 1 22
 ( f (x)  g(x))dx  f (x)dx g(x)dx  7      . 3 3 1  1  1  Trang 6 2 u 1
Câu 13: Chọn B. Đặt u  3x 1  x 
. Đổi cận : x 1 u  2 x  5  u  4. 3 4 4 2
u 1 u   4  Vậ 1 u 1 3 1 y I  du  du  ln
 ln  ln  2ln 3 ln 5   . 2 u 1 u   1 u   1 u 1 5 3 2 2 2
Do đó a  2; b  1
  a b 1.
Câu 14 .( Mức độ 1 ). Đáp án : C b Công thức S = f (x)dx 
chỉ đúng khi phương trình f(x) = 0 không có nghiệm thuộc khoảng (a ; b) a
hoặc nghiệm thuộc khoảng (a ;b ) là nghiệm bội chẵn . Hay nói cách khác , chỉ áp dụng công thức
này khi f(x) chỉ mang một dấu trên đoạn . 
Câu 15 . ( Mức độ 1 ), Đáp án D . Vì e < nên ta có 2 V   f (x)dx  e
Câu 16. Đáp án : B. Phương trình hoành độ giao điểm : -2x3 +x2 + x + 5 = x2 – x + 5 1
Có các nghiệm x = -1 , x =0 , x =1 . S = 3 2
 x  2xdx 1  0 4 16dx
Câu 17 ( Mức độ 2 ). Đáp án : B. Vì V   12  2 x 1 t2 4
Câu 18 Đáp án : A . Lời giải : Áp dụng công thức S = 2
v(t)dt  (3t  6t)dt  16   1 t 0
Câu 19:( NB) . Phương án đúng là D . Giải: số phức z =a + bi=> số phức liên hợp là a-- bi
Câu 20: (NB) .Phương án đúng là B.HD: Tính hiệu và sử dụng công thức tính mô đun
Câu 21: (NB) .Phương án D. HD: vì số phức z được biểu diễn là điểm có tọa độ (m;m)
Câu 22: (NB).Phương án đúng là B. HD :áp dụng công thức tìm tích 2 số phức
Câu 23. Phương án B. HD: số phức z =a + bi ,thay vào vế trái và sử dụng công thức mô đun
Câu 24 : (TH) .Phương án đúng là D. HD:Ap dụng công thức tính mô đun của z
Câu 25(TH):Phương án đúng là A . HD :Sử dụng tính chất 2 số phức bằng nhau
Câu 26(TH) : Phương án B. HD: số phức=0 khi phần thực bằng 0 và phần ảo bằng 0
Câu 27(VD):Phương án đúng là D.
Câu 28(VD):Phương án A. HD:Thay z= a+bi vào 2 vế và sử dụng công thức tính độ dài
Câu 29 (VD). Phương án đúng là C. HD:Tìm nghiệm pt và biểu diễ n hệ trục tọa độ
Câu 30(VD):Phương án đúng là A. HD:tách (1+i)30=[(1+i)2]15    
Câu 31.Chọn D.Bán kính mặt cầu là R  d  A P 1 4 2 2 ,   3. 3
Phương trình của mặt cầu  2 2 2 S  là x  
1  y  2  z   1  9 . 
Câu 32.Chọn B.Đường thẳng  có vectơ chỉ phương là u  4;3;  1 . 
Mặt phẳng P đi qua điểm M 0;0; 2
  và vuông góc với  nên nhận u  4;3;  1 làm
vectơ pháp tuyến có phương trình: 4x 03 y 01z  2  0  4x 3y  z  2  0 .
Câu 33.Chọn C.Phương trình theo đoạn chắn:   x y z P :
   1  P : 3x  6y  2z  6 . 2 1 3 Câu 34.Chọn D
Câu 35.Chọn A.Ta có M là trung điểm của BC nên M 1; 1  ;3 . Trang 7  AM  2; 4  
;1 .Đường thẳng AM đi qua A 1
 ;3;2, và có một vectơ chỉ phương là  x  y  z  AM  2; 4  
;1 .Vậy phương trình đường 1 3 2 AM :   . 2  . 4 1     Câu 36.Chọn D. x 1 y 2 z 3 d  ( ) P VTCP u       d (3; 4; 5) PTCT d : . . 3 4  5 
Câu 37.Chọn D.Giả sử d  d  M  M 2  t;1t;1 t . 2  
AM  1 t;  t;t  2 . d có VTCP u  1; 4;  2 . 1   1   
d  d  AM .u  0  1 t  4t  2 t  2  0  5
 t  5  0  t 1  AM  2;1;  1 . 1 1   
Đường thẳng d đi qua A1; 1
 ;3 có VTCP AM  2;1;  1 có phương trình là: x 1 y 1 z  3 d :   .. 2 1 1
Câu 38.Chọn C.Theo đề ta có mă ̣t cầu đường kính AB có tâm là trung điểm I  1  ;0;  1 của AB và bán kính AB 2 2 R 
 2 .Nên phương trình mă ̣t cầu là: x   2
1  y   z   1  2. 2
Câu 39. Chọn C.Mặt cầu 2 2 2
(S) : x  y  z  2ax  2by  2cz  d  0 (với a  2;b  1; c  3, d  2 ).có tâm I  ( ; a  ;
b c)  (2; 1  ; 3  ) , bán kính 2 2 2
R  a  b  c  d  4 .    
Câu 40.Chọn D.Bán kính mặt cầu là R  d  A P 1 4 2 2 ,   3. 3
Phương trình của mặt cầu  2 2 2 S  là x  
1  y  2  z   1  9  
Câu 41: Chọn D.Tacó: AB  3; 4
 ;2, AM  x  2; y 1; 4   . 1
 6  2y  2  0     x  4  , A ,
B M thẳnghàng   A ;
B AM   0  2x  4 12  0     .  y  7
3y  3  4x  8  0    
Câu 42: Chọn A.Tacó BA  a  3; 0;10, BC  8; 0; 4 , BD  4; 3; 5 .  
  
Suy ra BC, BD   1  2;  24; 24   .Do đó 1 V
 30  BC, BD.BA  30 . ABCD   6    a 1
 2a  3  24.0  24.10 180  a 17  32 15  .  . a  2     o 
Câu 43: Chọn B.Để u,v  90  cosu,v  0.    m  1 m 1 .
u v  0  3  log 5.log 3  4log 2  0 3 5 m  
.Kết hợp điều kiện m 0    1 .  1
4  4log 2  0  log 2  1  m  0  m  m m  2  2
Câu 44: Chọn A.Ta nhận thấy đường thẳng  cần tìm và d , d ' cùng thuộc mặt phẳng..
Tacó:  cách đều d, d 'nên  nằm giữa d, d '.Do đó: Gọi ( A 2; 3  ;4)d; ( B 4; 1  ;0)d ' .
Trung điểm AB là I(3; 2
 ;2) sẽ thuộc đường thẳng  cầntìm. Ta thế I (3; 2
 ;2) lần lượt vào các đáp án nhận thấy đáp án A thỏa.
Câu 45: Chọn D.Giảsử Trang 8 1
  m 1 kt    1
M  d  M 1 ; m 2  2 ; m 3  m    1    m 0
M  d  d    *
2 2m  t 2 2,3  1   k  0 . 1 2 M d *  t   2 2  
3m  12t  3
Câu 46: Chọn A. Hai mặt phẳng vuông góc với d lần lượt có các vectơ pháp tuyến là      n  2; 1  ;1 và n  1;1; 1 
nên đường thẳng d
u  n , n  0;3;3 . 2   1  
có vectơ chỉ phương là:  1 2   
Trục Oz có vectơ chỉ phương là k  0;0;  1 ..        u k  u.k 3 1 cos ,       u k  O ,  45 .. 2 2 u . k 3  3 . 1 2
Đây là góc nhọn nên góc giữa d và trục Oz cũng bằng O 45 . 3.1 4. 2    2.3 4 3.1 4.1 2.2  4 Câu 47: Chọn 5 15 B. d   , d   . 1 2 2 2 3  4  2 2 29 2 2 2 3  4  2 29
Câu 48: Chọn D. S  có tâm I 1;2;3 ,bán kính R  4 .Đường tròn thiết diện có bán kính
r  4 mặt phẳng   qua tâm I .   chứa Oy    : ax  cz  0 .
I    a  3c  0  a  3
 c .Chọn c  1
  a  3    :3x  z  0.
Câu 49: Chọn D.Vì G  d  G2  t;2  2t; 2
  t .Giả sử Bx ; y ;z ,Cx ; y ;z . 2 2 2  1 1 1   x  x 1 1 2  2  t  3 
x  x  3t  7 1 2
Vì G là trọng tâm ABC nên ta có:  y  y  2  . 1 2 
 2  2t  y  y  6t  4 1 2 3  z  z  3  t  7  1 2  z  z 1 1 2  2   t  3      
Vậy trung điểm của đoạn 3t 7 6t 4 3t 7 BC là M ; ;   .  2 2 2 
Do B , C nằm trên   nên M    t  1   M 2; 1  ; 2  . Câu 50: Chọn D.
Cách1: Gọi A2  2t; 2  t; 3  t d là giao điểm của  và d .  
MA  1 2t; t; 3  t  ,VTPTcủa   là n  1;1;  1 .    
Tacó:      MA  n  MA.n  0  1 2t  t  3  t  0  t  1  .    MA 1  ; 1; 2  1
 1; 1;  2.Vậyu  1; 1;  2 . d 
Cách2:Gọi B  d   . B  d  B 2  2t; 2  t; 3  t  .  
B    2  2t  2  t  3  t  3  0  t  1
  B0;1;2. BM 1;1; 2  u 1;1; 2 . d  Trang 9