ĐỀ SỐ 1-ĐỀ THI THỬ TN THPT QG 2025

ĐỀ SỐ
ĐỀ THI THỬ KÌ THI TỐT NGHIỆP 1 THPT QUỐC GIA 2025 Môn: Toán; khối: 12
Thời gian làm bài: 90 phút
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN Câu 1.
Cho hàm số y  f  x liên tục trên  và có bảng xét dấu của f  x như sau:
Hàm số y  f  x có bao nhiêu điểm cực trị? A. 4 . B. 3 . C. 2 . D. 1. Hướng dẫn giải: Chọn C.
Vì đạo hàm f  x của hàm số có hai nghiệm đơn x  2
 ; x  0 nên hàm số y  f  x có hai điểm cực trị x  2  ; x  0 . 3 3 Câu 2. Biết f
 xdx  3. Giá trị của 2 f xdx  bằng 1 1 3 A. 5 . B. 6 . C. 9 . D. . 2 Hướng dẫn giải: Chọn B. 3 3 Ta có 2 f  xdx  2 f
 xdx  23  6 . 1 1 Câu 3.
Trong không gian Oxyz , cho mặt phẳng  P đi qua điểm M 2; 2; 
1 và có một vectơ pháp tuyến
n 5; 2; 3. Phương trình mặt phẳng Plà
A. 5x  2y  3z 17  0 .
B. 2x  2 y  z 11  0 .
C. 5x  2 y  3z 11  0 .
D. 2x  2 y  z 17  0 . Hướng dẫn giải: Chọn C. 
Mặt phẳng  P qua điểm M 2; 2; 
1 , có một vectơ pháp tuyến n  5; 2; 3 nên có phương
trình 5 x  2  2 y  2 3 z  
1  0  5x  2y  3z 11  0 . Câu 4.
Nếu cấp số nhân u có số hạng đầu u  3 và công bội q  3 thì số hạng tổng quát u của cấp số n  1 n nhân đó bằng A. 3n . B. 1 3n . C. 1 3n  D. 3  n   1 .3 . Hướng dẫn giải: Chọn A. Ta có n 1  n 1  n * u  u  q  33  3 , n    . n 1 Câu 5.
Tập nghiệm của bất phương trình 2x  4 là A. ; 2. B. 0; 2 . C. ; 2 . D. 0; 2 . Hướng dẫn giải: Chọn A.
Ta có 2x  4  x  log 4  x  2 . 2
Tập nghiệm bất phương trình là S  ; 2 . Câu 6.
Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy bằng nhau và ABCD là hình vuông tâm
O . Khẳng định nào sau đây là khẳng định đúng? A. SA   ABCD . B. SO   ABCD . C. AB  SBC . D. AC  SBC . Hướng dẫn giải: Chọn B.
Vì SA  SC và O là trung điểm AC nên SO  AC ; Vì SB  SD và O là trung điểm BD nên SO  BD . Do đó SO   ABCD . Câu 7.
Phát biểu nào sau đây là đúng? 1 1 A. dx  x  C  . B. dx  ln x  C  . C. ln d x x  x  C  . D. ln x dx  lnx  C  . x x Hướng dẫn giải: Chọn B. 1 Ta có dx  ln x  C  . x Câu 8.
Cho hàm số y  f  x có đồ thị như hình dưới đây.
Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng A. y  x 1. B. y  x 1. C. y  x 1. D. y  x 1. Hướng dẫn giải: Chọn B.
Tiệm cận xiên của đồ thị hàm số đi qua hai điểm  1  ; 0, 0;   1 nên có phương trình x y 
 1  x  y 1  0  y  x 1. 1  1  Câu 9.
Cho hàm số f  x có đồ thị như hình vẽ bên. Giá trị nhỏ nhất của
hàm số f  x trên đoạn  2  ;2 bằng A. 2  . B. 1. C. 0 . D. 1. Hướng dẫn giải: Chọn C. Trên đoạn  2
 ;2 , giá trị nhỏ nhất hàm số bằng f   1  0 .
Câu 10. Bạn An rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày của bạn An được thống kê lại ở bảng sau:
Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây? A. 31, 25 . B. 31, 26 . C. 5, 4 . D. 5,6 . Hướng dẫn giải: Chọn D.
22,56  27,5 6  ...  42,51 85
Giá trị trung bình của mẫu số liệu ghép nhóm là x   . 18 3
Độ lệch chuẩn mẫu số liệu ghép nhóm là 2 2 2          2
(22,5 x ) 6 (27,5 x ) 6 ... (42,5 x) 1 125 s  s    5,6 . 18 4 x  1 t 
Câu 11. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :  y  5  t ? z  2  3t  A. Q 1  ;1; 3 . B. P 1; 2; 5 . C. M 1;1; 3 . D. N 1; 5; 2 . Hướng dẫn giải: Chọn D. 1   1 t 
Thay tọa độ N vào phương trình đường thẳng d, ta có: 5   5  t  t  0 . 2  2 3t 
Do đó điểm N  d . Dễ dàng chứng minh được các điểm còn lại không thuộc d.
Câu 12. Cho hình lập phương ABC . D A B  C  D
  (tham khảo hình bên). Giá trị sin của góc giữa đường thẳng
AC và mặt phẳng  ABCD bằng 3 A. . 3 2 B. . 2 3 C. . 2 6 D. . 3 Hướng dẫn giải Chọn A.
Ta có: AC là đường chéo hình lập phương ABC . D A B  C  D    AC  A . B 3 .  CC  (ABCD) Vì 
; suy ra góc  AC ,(ABCD)   AC, AC    C A
 C (góc nhọn); trong đó AC  (ABCD)  A  CC 1 3 sin C A  C    . Vậy  AC ABCD  3 sin , ( )  . AC 3 3 3
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Câu 13. Công thức log x  11,8 1, 5M cho biết mối liên hệ giữa năng lượng x
tạo ra (tính theo erg, 1 erg tương đương 7
10 jun) với độ lớn M theo thang
Richter của một trận động đất.
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Nếu năng lượng được tạo ra là 14
6,3.10 erg thì trận động đất phải có độ lớn  
bằng 2 độ Richter (làm tròn kết quả đến hàng đơn vị).
b) Trận động đất có độ lớn 3 độ Richter tạo ra năng lượng bằng  163 10 10 10  erg.  
c) Trận động đất có độ lớn 5 độ Richter tạo ra năng lượng gấp 1000 lần so với  
trận động đất có độ lớn 3 độ Richter.
d) Người ta ước lượng rằng một trận động đất có độ lớn khoảng từ 4 đến 6 độ
Richter thì năng lượng do trận động đất đó tạo ra nằm trong khoảng từ 17,8 10 erg   đến 20,8 10 erg. Hướng dẫn giải a) Mệnh đề đúng.  14 log 6,3.10  11,8 Ta có 14 x  6,3.10  M   2 độ Richter. 1,5 b) Mệnh đề sai. Ta có M  3 16,3
 log x  11,8 1,53  x  10 erg. c) Mệnh đề đúng.
Gọi x , x lần lượt là năng lượng tạo ra bởi các trận động đất có độ lớn 3 và 5 độ Richter. 3 5
log x  11,8 1,53 (1) Ta có hệ phương trình 3  . log x  11,8 1,55 (2)  5 x x 1 Lấy   1  2 ta được 3 log x  log x  3   log  3  3    x  1000x . 3 5 x 5 3 x 1000 5 5
Vậy trận động đất có độ lớn 5 độ Richter tạo ra năng lượng gấp 1000 lần so với trận động đất có độ lớn 3 độ Richter. d) Mệnh đề đúng.
Gọi x , x lần lượt là năng lượng tạo ra bởi các trận động đất có độ lớn 4 và 6 độ Richter. 4 6 17,8 log x  11,8 1,5 4 log x  17,8 x 10 Ta có 4 4 4      . 20,8 log x  11,8 1,56 log x  20,8   x  6 6 10  6
Vậy một trận động đất có độ lớn khoảng từ 4 đến 6 độ Richter thì năng lượng mà nó tạo ra nằm trong khoảng từ 17,8 10 erg đến 20,8 10 erg.
Câu 14. Tại một thành phố du lịch vào những ngày tháng 6, người ta luôn chứng kiến trời nắng hoặc trời mưa
(mỗi ngày có thể trời nắng xong đến mưa và ngược lại). 2
Người ta biết được có số ngày trong tháng là có nắng, 3 5
có số ngày trong tháng là có mưa. Nếu hôm nào bầu 6
trời tại thành phố chỉ có mưa thì khả năng kẹt xe gấp đôi
khả năng không kẹt xe; nếu hôm nào bầu trời chỉ có nắng
thì chắc chắn thành phố không xảy ra kẹt xe; những ngày
trời vừa có nắng vừa có mưa thì khả năng kẹt xe là 30%.
Xét tính đúng sai các mệnh đề sau: Đúng Sai 2
a) Nếu du khách đến thành phố vào ngày chỉ có mưa thì khả năng kẹt xe bằng .   3
b) Trong tháng 6, có 10 ngày mà thành phố vừa có mưa vừa có nắng.  
c) Một du khách đang cân nhắc sẽ đến thành phố vào một ngày tháng 6, xác suất
du khách gặp cảnh kẹt xe bằng 0,32 (làm tròn đến hàng phần trăm).  
d) Sau khi du khách đến nơi thì hôm ấy xảy ra kẹt xe thật, xác suất để thành phố  
vừa có nắng, vừa có mưa bằng 0,3 (làm tròn đến hàng phần chục). Hướng dẫn giải a) Mệnh đề đúng.
Vào ngày chỉ có mưa, khả năng kẹt xe gấp đôi khả năng không kẹt xe nên khả năng kẹt xe tại thành 2 1
phố là và khả năng không kẹt xe là . 3 3 b) Mệnh đề sai. 2 5 1 2 1 1
Trong tháng sẽ có  1  số ngày vừa có nắng vừa có mưa, có   số ngày chỉ có nắng 3 6 2 3 2 6 5 1 1
và có   số ngày chỉ có mưa. 6 2 3  2 5 
Số ngày trong tháng vừa có mưa vừa có nắng tại thành phố là:  1 30  15   (ngày).  3 6  c) Mệnh đề sai.
Gọi A là biến cố: “Ngày có nắng tại thành phố”, B là biến cố: “Ngày có mưa tại thành phố” và C là biến
cố “Ngày có sự cố kẹt xe xảy ra tại thành phố”. Ta tham khảo sơ đồ bên cạnh.
Xác suất kẹt xe xảy ra là: P C  1 1 3 1 2 67  0       0,37 6 2 10 3 3 180 d) Mệnh đề sai. 1 3  P ABC 27 Ta có: P  AB C    2 10 |  . P C     0,4 67 67 180
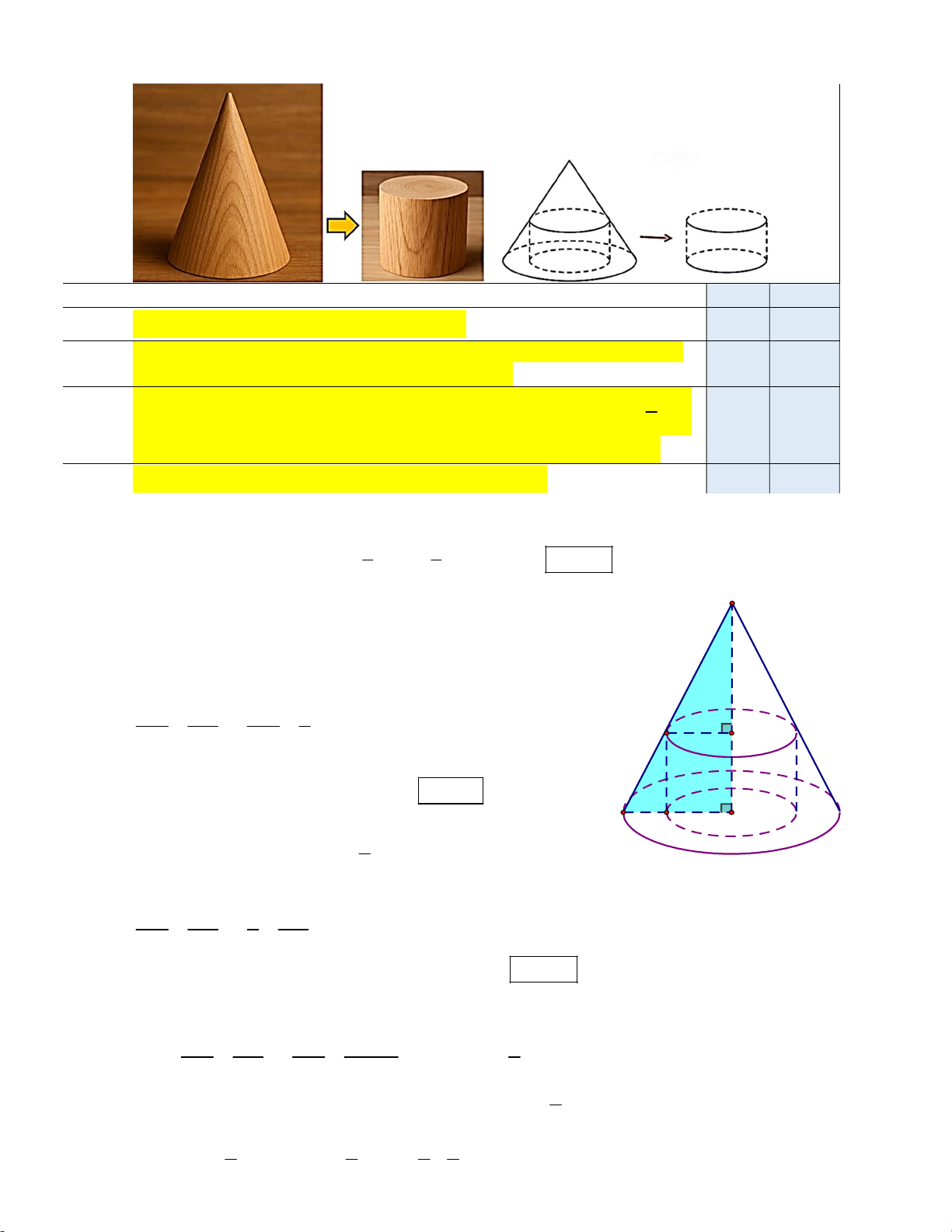
Câu 15. Một khối gỗ có dạng khối nón có bán kính đáy r  30 cm , chiều cao h  120 cm . Người thợ mộc tìm
cách chế tác khối gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ.
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Thể tích khối gỗ ban đầu bằng 3 36000 cm .  
b) Nếu người thợ mộc muốn tạo ra khối gỗ hình trụ có chiều cao bằng nửa khối
gỗ ban đầu thì khối gỗ mới tạo ra có thể tích 13500 .   2
c) Nếu người thợ mộc muốn tạo ra khối gỗ hình trụ có bán kính đáy bằng bán 3  
kính khối gỗ hình nón thì phần gỗ phải bỏ đi có thể tích bằng 3 20000 cm .
d) Thể tích lớn nhất của khối gỗ hình trụ bằng 3 0,016 m .   Hướng dẫn giải a) Mệnh đề đúng. 1 1
Thể tích khối gỗ hình nón là 2 2 3
V   r h   30 120  36 000 cm . 3 3 b) Mệnh đề đúng. S
Xét một nửa thiết diện qua trục của hình nón là tam giác SAB (tham khảo hình vẽ).
Các tam giác SMN và SAB đồng dạng (có S chung,  SMN   0 SAB  90 ), ta có: h=120 MN SM MN 1     MN 15 cm . AB SA 30 2 N M
Khối gỗ hình trụ mới được tạo thành có bán kính đáy 15 cm , chiều x
cao 60 cm nên có thể tích 2 3
 15 60  13500 cm . r = 30 c) Mệnh đề đúng. B A 2
Bán kính đáy khối gỗ hình trụ là 30  20 cm . 3
Các tam giác SMN và SAB đồng dạng (có S chung,  SMN   0 SAB  90 ), ta có: MN SM 2 
  SM  SM  80 cm  AM  40 cm . AB SA 3 120
Thể tích khối gỗ phải bỏ đi là 2 3
36 000   20  40  20000 cm . d) Mệnh đề đúng.
Đặt AM  x (cm) (0  x  120) . MN SM MN 120  x x Ta có:     MN  30  . AB SA 30 120 4
Vậy khối trụ mới được tạo thành có bán kính  30  x MN
, đường cao AM  x nên có thể tích: 4 2  x   x   x   x V  30  x  . 30  . 30  . .2       .  4   4   4  2 2  x   1  Xét hàm số 2 3 V (x)   30  x   900x 15x     x  với 0  x 120 .  4   16  2  3x  x  120 (loaïi) Ta có V (
 x)   900 30x    0   .  16  x  40 (nhaän) Bảng biến thiên: x 0 40 120 V (  x)  0  V (x) 16 000 1 5 Dễ thấy 3 3 V
 16 000 cm  0,016 m . max
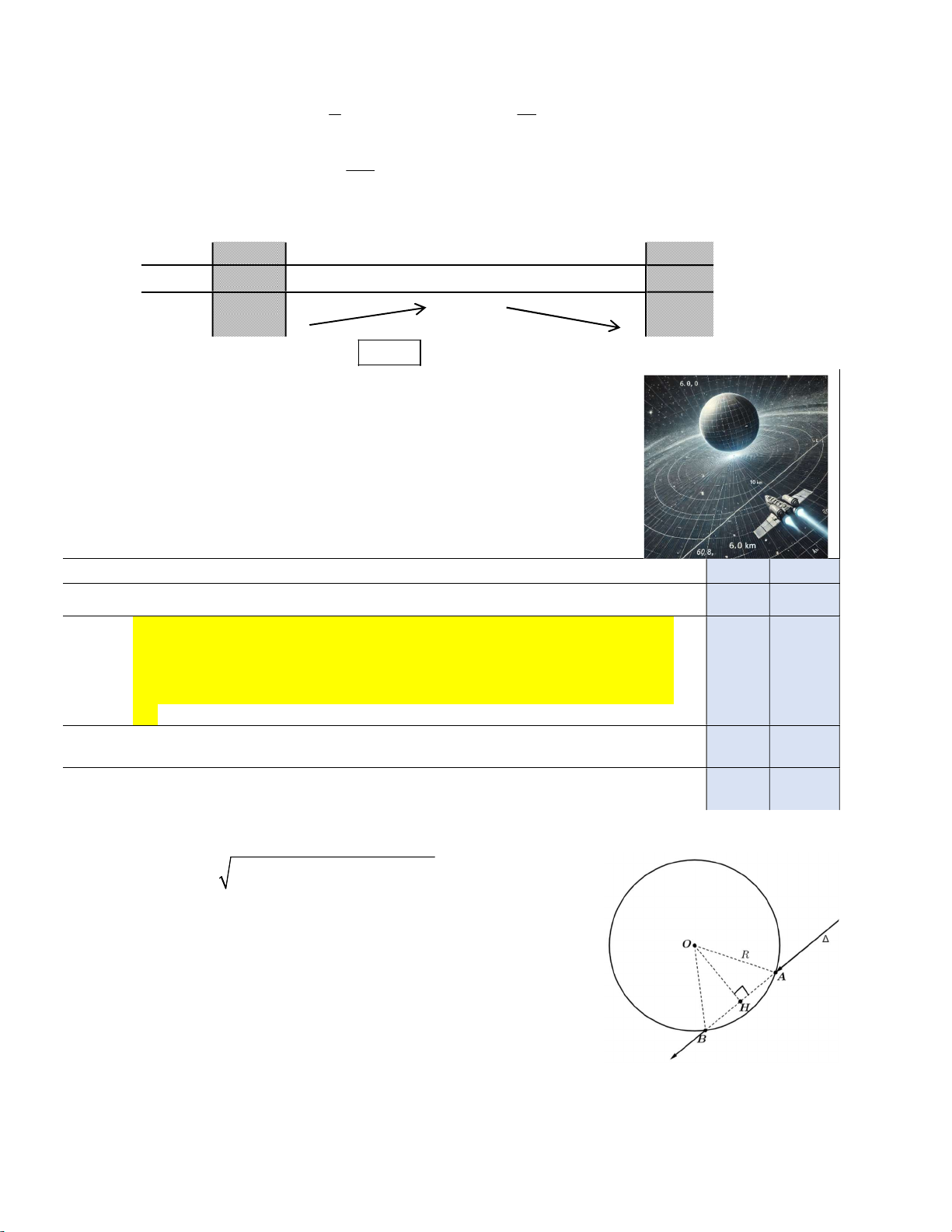
Câu 16. Trong không gian với hệ tọa độ Oxyz, đơn vị trên mỗi trục tọa độ là km,
NASA đang thiết kế một trạm vũ trụ hình cầu có tâm đặt tại điểm
O 0;0;0 và bán kính R 10 km. Một con tàu vũ trụ di chuyển với tốc
độ 27 000 km / h theo quỹ đạo là một đường thẳng qua điểm 
A6;8;0 và có vectơ chỉ phương u  2; 2;   1 .
Xét tính đúng sai các mệnh đề sau: Đúng Sai
a) Điểm A6; 8; 0 nằm bên trong trạm vũ trụ hình cầu.   x  6  2t 
b) Phương trình quỹ đạo di chuyển của tàu vũ trụ là  :  y  8  2t (t là tham    z  t  số).
c) Khoảng cách từ tâm của trạm vũ trụ đến đường thẳng quỹ đạo tàu vũ trụ là 3,8
km (làm tròn đến hàng phần chục, đơn vị km).  
d) Tàu vũ trụ sẽ tốn 2,3 giây (làm tròn đến hàng phần chục của giây) để vượt qua
phạm vi hình cầu của trạm vũ trụ.   Hướng dẫn giải a) Mệnh đề sai.
Ta có OA    2    2    2 6 0 8 0 0 0  10  R .
Do vậy điểm A nằm trên bề mặt hình cầu. b) Mệnh đề đúng.
Đường thẳng  qua A6;8;0 , có vectơ chỉ phương x  6  2t   u  2; 2;  
1 nên có phương trình tham số là  : y  8  2t z  t  (t là tham số). c) Mệnh đề sai.
Khoảng cách từ tâm O đến đường thẳng quỹ đạo là 4 km.  O  A  6; 8; 0   Ta có:    A O , u   8  ; 6;  4  . u     2; 2;   1   2 2   2 OA, u 8  6  4   2 29 Ta có: d O ,          3,6 km  . u    2 2 2 3 2 2 1 d) Mệnh đề sai.
Vì d O ,   R nên tàu vũ trụ sẽ đi qua phạm vi hình cầu của trạm vũ trụ, nó cắt mặt cầu tại hai
điểm A và B; gọi H là trung điểm AB. 2   Ta có 2 2 2 2 29 56
AB  2AH  2 OA  OH  2 10      km. 3  3    56 
Thời gian khi tàu vũ trụ đi qua phạm vi hình cầu là : 27 000 3600  2,5   (giây).  3 
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
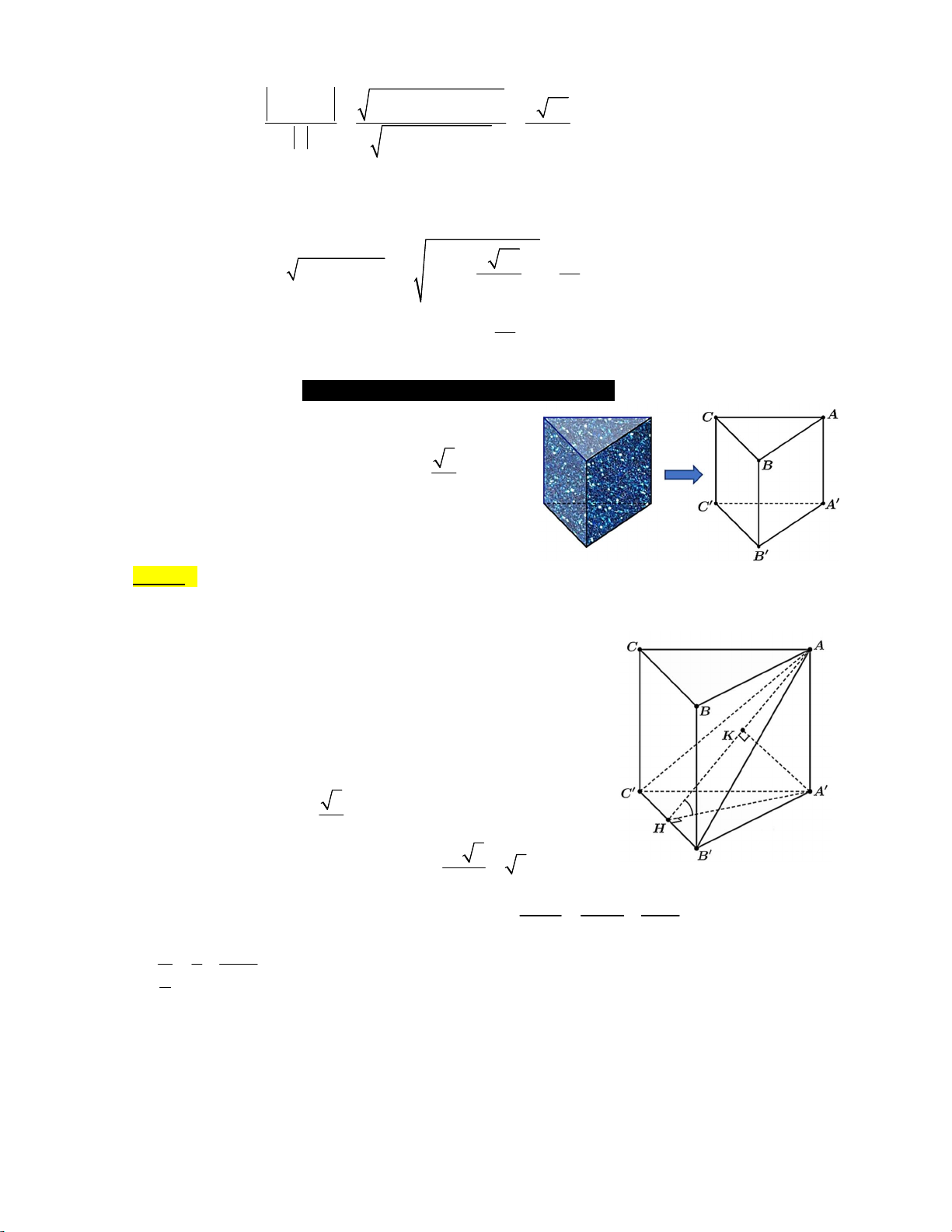
Câu 17. Một khối đá có dạng hình lăng trụ tam giác đều ABC.AB C
  với cạnh đáy bằng 2 dm, khoảng cách tứ 3
điểm A đến mặt phẳng  AB C   bằng dm . Tìm 2
khoảng cách giữa hai mặt phẳng đáy của khối đá hình
lăng trụ đã cho theo đơn vị dm. Trả lời:  Đáp số: 1 Hướng dẫn giải Trong mặt phẳng ( A B  C   ), kẻ A H   B C   tại H. Trong mặt
phẳng  AAH  , kẻ AK  AH tại K (1).   B C    A H Ta có:  BC A   A do A  A    A  B C  BC   A  A H    A K  BC 2 . Từ (1) và (2) suy ra A K    AB C   hay d   A  ABC 3 ,   A K  dm. 2 2  3 Tam giác A B  C
  đều có đường cao  A H   3 dm. 2 1 1 1
Tam giác AAH vuông tại A có đường cao AK nên   2 2 2 AK AH A A  1 1 1      A A  1 dm. 2 3 3  A A 4
Hai mặt đáy song song với nhau và có khoảng cách là d  ABC,   A BC  A  A  1 dm.
Câu 18. Giá bán P (đồng) của một sản phẩm y tế thay đổi theo số lượng Q (sản
phẩm) với 0  Q  1500 , được cung cấp ra thị trường theo công thức
P  1500  Q. Tính số lượng sản phẩm y tế đó nên được cung cấp ra thị
trường để doanh thu của công ty lớn nhất. Trả lời:  Đáp số: 1000 Hướng dẫn giải
Doanh thu của sản phẩm được tính theo công thức R  PQ  Q 1500  Q . 3Q 3000 Ta có R    ; R  0  Q  1000. 2 1500  Q
So sánh R 0, R1000 và R 1500 ta có R lớn nhất khi Q  1000 .
Câu 19. Một tấm đề can hình chữ nhật được cuộn tròn lại theo chiều dài tạo thành một
khối trụ có đường kính 50 (cm) . Người ta trải ra 250 vòng để cắt chữ và in
tranh cổ động, phần còn lại là một khối trụ có đường kính 45 (cm) . Hỏi phần
đã trải ra dài bao nhiêu mét (làm tròn đến hàng đơn vị)? Trả lời:  Đáp số: 373 Hướng dẫn giải
 Cách giải 1: Gọi a là bề dày của tấm đề can, sau mỗi vòng được quấn thì đường kính của vòng mới 50  45
sẽ được tăng lên 2a. Vì vậy: 2a  250  50  45  a   0,01 cm . 2 250
Gọi l là chiều dài đã trải ra và h là chiều rộng của tấm đề can (tức chiều cao hình trụ). 2 2  50   45    2 2 50  45  Khi đó ta có: lha   h  h      l   37306 cm  373 m .  2   2  4a
 Cách giải 2: Gọi a là bề dày của tấm đề can, sau mỗi vòng được quấn thì đường kính của vòng mới 50  45
sẽ được tăng lên 2a. Vì vậy: 2a  250  50  45  a   0,01 cm . 2 250
Chiều dài của phần trải ra là tổng chu vi của 250 đường tròn có bán kính là một cấp số cộng có số
hạng đầu bằng r  25 , công sai là d  0,01 (do khi trải ra thì bán kính các vòng tròn ngày càng 1
giảm với độ giảm bằng bề dày của tấm đề can).  
Do đó chiều dài của phần đề can đã trải ra là: l  2  r  r  ... r  1 2 250     S  250 (2  249 )  250 1  2  r d  250
 2 (2 25  2490,01)  37314 cm  373 m . 2 2
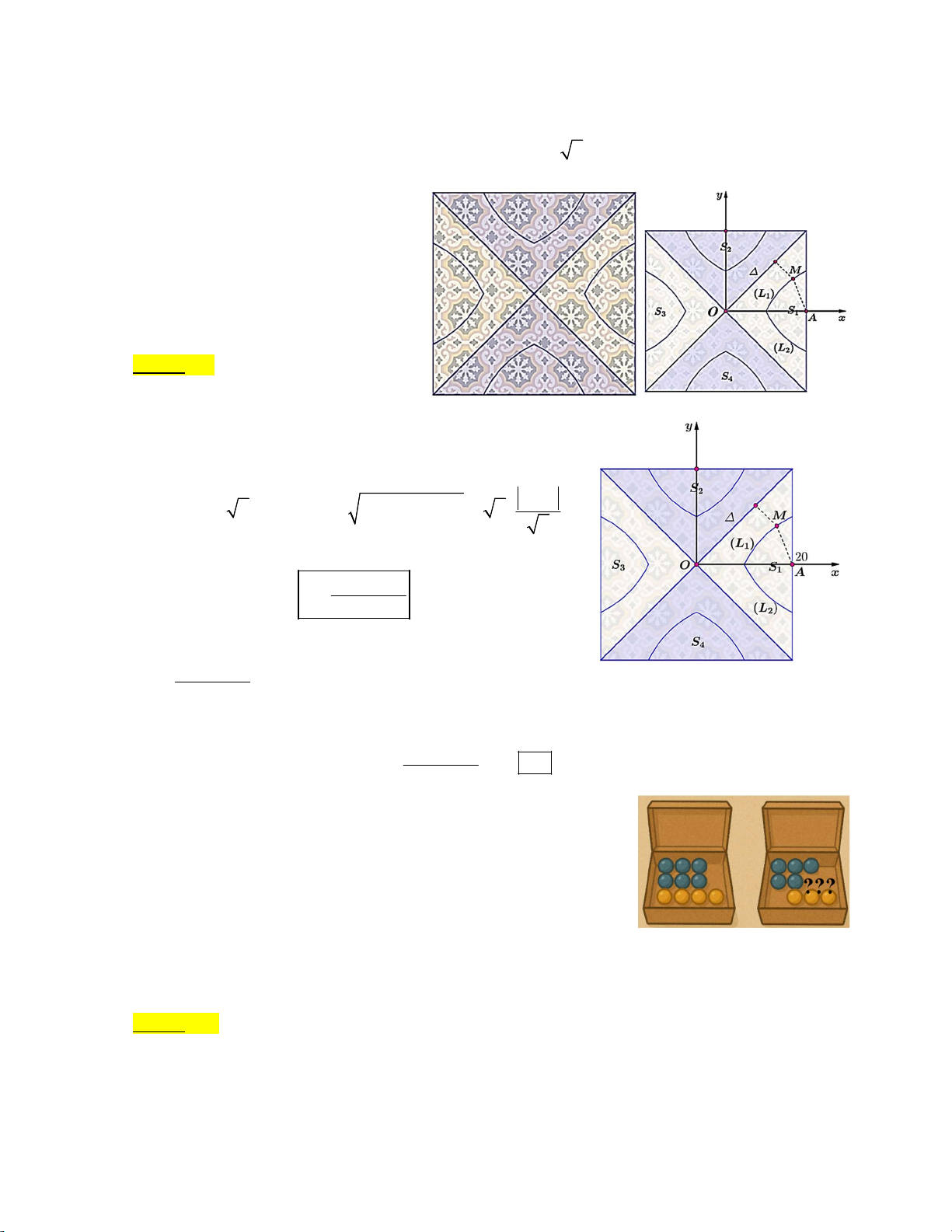
Câu 20. Một viên gạch lát nền nhà có dạng hình vuông với hoa văn được thiết kế bởi một học sinh lớp 12. Xét
hình phẳng có diện tích S được tạo thành bởi các đường cong L , L và một cạnh viên gạch, 1   2  1
trong đó đường L là tập hợp các điểm M thỏa mãn MA  2d M ,  (A là trung điểm một cạnh 1 
viên gạch;  là đường phân giác góc
phần tư thứ nhất theo hình vẽ); L đối 2 
xứng với L qua trục Ox. Biết viên gạch 1 
này có kích thước cạnh bằng 40 cm, tính
tổng diện tích S  S  S  S và làm 1 2 3 4
tròn đến hàng đơn vị của 2 cm . Trả lời:  Đáp số: 491 Hướng dẫn giải
Tọa độ A20; 0 và phương trình  : x  y  0 .
Gọi M  x; y là tập hợp các điểm thuộc đường cong L . 1  x  y Ta có: MA 
d M    x  2 2 2 , 20  y  2  2 2 2 2 2
 x  y  40x  400  x  y  2xy 20  200   20  200   x xy x y . x
Giao điểm giữa L với Ox thỏa hệ phương trình 1   20x  200  y   x  x  10 . y  0 20 20  200 Ta có: 2     4  42 d  491 . 1 2 3 4 1  x S S S S S x cm x 10
Câu 21. Hộp thứ nhất đựng 6 viên bi xanh và 4 viên bi vàng, hộp thứ hai đựng 5
viên bi xanh và một số bi vàng. Người ta thực hiện ngẫu nhiên ba hành động sau:
 Lấy ngẫu nhiên 2 viên bi từ hộp thứ nhất bỏ sang hộp thứ hai.
 Chọn ngẫu nhiên 1 viên bi từ hộp thứ hai rồi hoàn lại hộp này.
 Chọn ngẫu nhiên 1 viên bi từ hộp thứ hai lần nữa.
Biết hai lần lấy bi từ hộp thứ hai đều được bi xanh, tính xác suất để hai
lần lấy chọn trúng 1 viên bi, và đó cũng là viên bi từ hộp thứ nhất chuyển sang hộp thứ hai (làm tròn
kết quả đến hàng phần trăm). Trả lời:  Đáp số: 0,03 Hướng dẫn giải
Gọi A là biến cố: “Hai lần lấy bi từ hộp thứ hai đều được bi có màu xanh” và B là biến cố: “Hai lần lấy
đúng 1 bi và cũng là bi từ hộp thứ nhất chuyển qua”.
Giả sử ban đầu hộp thứ hai có 5 viên bi xanh và x viên bi vàng  * x    .
Xác suất để lấy được 2 bi xanh từ hộp thứ nhất chuyển 2 C 1
sang hộp thứ hai là 6  . 2 C 3 10
Xác suất để lấy được 1 bi xanh, 1 bi vàng từ hộp thứ 1 1 C C 8
nhất chuyển sang hộp thứ hai là 6 4  . 2 C 15 10
Xác suất để lấy được 2 bi vàng từ hộp thứ nhất chuyển 2 C 2 sang hộp thứ hai là 4  . 2 C 15 10
Ta biểu diễn bài toán bằng sơ đồ sau: 2 2 2 1  7  8  6  2  5  Ta có: P  A             . 3  x  7  15  x  7  15  x  7  1  2 8 1 2 1 8 1 1   2        x7  3 15     18 Do đó: PB|  3 x 7 x 7 15 x 7 x 7   A    0,03. 2 2 2 2 2 2 1  7  8  6  2  5  1  7 86 25  583               
3  x7 15  x7 15  x7 x 2 7  3 15 15 
Câu 22. Trong không gian với hệ trục tọa độ Oxyz thích hợp, đơn vị trên mỗi trục là mét. Một nhà sinh vật học
muốn theo dõi hai tổ chim ở các vị trí A2; 2; 0, B 2; 0;  2 , anh ta đã leo lên mái nhà thuộc mặt
phẳng P : x  2y  z 1  0 . Nhà sinh vật học muốn đặt một thiết bị
theo dõi ở vị trí M a;b;c thuộc mái nhà cách đều các tổ chim, đồng thời
vị trí đó cho anh một góc quan sát là lớn nhất đối với hai tổ chim nói trên (góc 
AMB lớn nhất). Khi đó tổng a  b  c bằng bao nhiêu (làm tròn đến hàng phần trăm)? Trả lời:  Đáp số: 1,27 Hướng dẫn giải
Ta có M thuộc mặt phẳng P và MA  MB nên M thuộc giao tuyến của hai mặt phẳng P và
Q , trong đó Q là mặt phẳng trung trực của đoạn thẳng AB . 
Mặt phẳng (Q) qua trung điểm I 2; 1;  
1 của AB, vectơ pháp tuyến AB  0;  2;  2 nên có
phương trình 0 x  2  2 y   1  2 z   1  0 hay y  z  0 . x  2y  z 1  0
Gọi d   P Q ; từ hệ phương trình 
, đặt z  t ta có phương trình tham số y  z  0 x 1 3t 
đường thẳng d là y  t . z   t  
Gọi với M 1 3t ;  t ; t d ; suy ra AM  3t 1;  t  2; t , BM  3t 1;  t ; t  2 . 2 2 2
  3t 1  2 t  2t 11t  2t 1 4 Ta có: cos 
AMB  cos  AM , BM         1  . 3t  2 1  t  t  22 2 2 2 11t  2t  5 11t  2t  5 4 Ta thấy  AMB lớn nhất khi cos  AMB bé nhất; suy ra 1 bé nhất. 2 11t  2t  5 4 2   1 Khi đó lớn nhất nên 2 1 54 11t  2t  5  11 t   bé nhất; suy ra t  . 2   11t  2t  5  11 11 11 14 1 1  14 1 1 14 Ta tìm được điểm M ;  ;   với a  ; b   ; c   S  a  b  c   1,27 .  11 11 11 11 11 11 11
_________________HẾT_________________