19 trang 30 lượt tải

Đề tập huấn thi tốt nghiệp THPT 2025 môn Toán sở GD&ĐT Bắc Ninh

60

Một đường dây điện được nối từ một nhà máy điện ở A (nằm tại bờ biển là đường thẳng AB) đến một hòn đảo C, khoảng cách ngắn nhất từ đảo về bờ biển là đoạn  BC dài 1 km, khoảng cách từ B đến A là 4 km được minh họa bằng hình vẽ dưới  đây. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Chủ đề: Đề thi THPTQG môn Toán năm 2025 190 tài liệu

Môn: Toán 2 K tài liệu

Tác giả:

Profile

Mỹ Châu

1 ngày trước
Danh sách Quiz
/19
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC NINH
(Đề có 4 trang)
BẮC NINH
ĐỀ TẬP HUẤN
KỲ THI TỐT NGHIỆP THPT NĂM 2025
MÔN: TOÁN
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề 0101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Tất cả các nghiệm của phương trình sin x = 0 là
A. x =
π
2
+ kπ, k ∈ Z. B. x = k2π, k ∈ Z.
C. x = π + k2π, k ∈ Z. D. x = kπ, k ∈ Z.
Câu 2. Trong không gian Oxyz, cho hai điểm A (1; 2; 3), B (−2; 4; 0). Trung điểm của đoạn thẳng
AB có tung độ bằng
A. 1. B. 3. C. 2. D. −1.
Câu 3. Giá trị của lim
n→+∞
2n − 3
n + 1
bằng
A. 2. B. −3. C. 1. D. +∞.
Câu 4. Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường
cao tốc trong một khoảng thời gian ở bảng sau:
Tốc độ (km/h) [75 ; 80) [80 ; 85) [85 ; 90) [90 ; 95) [95 ; 100)
Số xe 15 22 28 34 19
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng
A. 100 km/h. B. 25 km/h. C. 5 km/h. D. 75 km/h.
Câu 5. Trong không gian Oxyz, điểm M(1; −3; 2) thuộc mặt phẳng có phương trình nào sau
đây?
A. 2x + y − z + 3 = 0. B. 3x − y + z − 2 = 0. C. 2x + y − z + 4 = 0. D. x − 2y − z + 1 = 0.
Câu 6. Trong không gian Oxyz, cho hai véctơ
−→
u = (2; 0; −2) ,
−→
v = (−1; −1; 6). Tích vô hướng
−→
u ·
−→
v bằng
A. −14. B. 1. C. 0. D. 4.
Câu 7. Hàm số nào sau đây đồng biến trên R?
A. y = x
3
+ 3x. B. y = x
3
− 3x. C. y =
x − 1
x + 1
. D. y = x
4
− 3x
2
+ 1.
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [a; b] và f(a) = −2, f(b) = −4. Giá trị
của
b
Z
a
f
′
(x) dx bằng
A. 2. B. −2. C. −6. D. 6.
Câu 9. Họ nguyên hàm của hàm số f(x) = sin x + 2 là
A. −cos x + 2x + C. B. cos x + 2x + C. C. sin x + 2x + C. D. cos x + C.
Câu 10. Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy trong một số ngày gần đây của
bạn Chi được thống kê lại ở bảng sau:
Trang 1/4 − Mã đề 0101
Thời gian (phút) [20; 25) [25; 30) [30; 35) [35; 40) [40; 45)
Số ngày 6 6 4 1 1
Phương sai của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào dưới đây?
A. 33. B. 34,77. C. 32. D. 31,24.
Câu 11. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
y
′
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
00
33
00
+∞+∞
Hàm số có bảng biến thiên như trên là
A. y = −x
4
+ 2x
2
. B. y = 3x
4
− 6x
2
+ 3. C. y = x
3
− x. D. y = x
3
− x + 3.
Câu 12. Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số y =
5x − 1
x + 2
?
A. x = 5. B. y = 5. C. x = 2. D. x = −2.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Khảo sát một nhóm 50 học sinh ở một trường trung học người ta thấy rằng: có 20 học
sinh giỏi Ngoại ngữ, 15 học sinh giỏi Tin học, 10 học sinh giỏi cả Ngoại ngữ và Tin học. Chọn
ngẫu nhiên một học sinh từ nhóm đó.
a) Xác suất để chọn được học sinh giỏi Ngoại ngữ hoặc Tin học bằng 0,7.
b) Xác suất để chọn được học sinh giỏi Tin học bằng 0,3.
c) Xác suất để chọn được học sinh giỏi Ngoại ngữ bằng 0,4.
d) Xác suất để chọn được học sinh không giỏi Ngoại ngữ hoặc Tin học bằng 0,3.
Câu 2. Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình dưới đây:
x
y
′
y
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−3−3
55
−∞−∞
a) Hàm số y = f(x) có 2 điểm cực trị.
b) Hàm số y = f(x) đồng biến trên (−3; 5).
c) Đồ thị hàm số g(x) =
x − 4
f(x) − 5
có 3 đường tiệm cận.
d) Giá trị lớn nhất của hàm số g(x) = f (4x − x
2
) +
1
3
x
3
− 3x
2
+ 8x +
1
3
trên đoạn [1; 3] bằng
12.
Trang 2/4 − Mã đề 0101
Câu 3. Cho khối chóp cụt tứ giác đều ABCD.A
′
B
′
C
′
D
′
có chiều cao bằng 3 cm, diện tích hai đáy lần lượt bằng
72 cm
2
và 18 cm
2
. Gọi I, O tương ứng là tâm của hai
đáy ABCD và A
′
B
′
C
′
D
′
. Chọn hệ trục toạ độ Oxyz, với
đơn vị trên mỗi trục là cm sao cho tia Ox cùng hướng
với vectơ
−−→
OD
′
, tia Oy cùng hướng với vectơ
−−→
OC
′
, tia Oz
cùng hướng với vectơ
−→
OI (như hình vẽ).
x
y
z
D
′
C
′
B
′
A
′
O
D
C
BA
I
a) Tọa độ của điểm B
′
là (−6; 0; 0).
b) Khoảng cách từ O đến mặt phẳng (BCC
′
B
′
) bằng
√
3 cm.
c) Phương trình mặt phẳng (ABCD) là z = 3.
d) Hai mặt phẳng (BCC
′
B
′
) và (DCC
′
D
′
) tạo với nhau một góc lớn hơn 70 độ.
Câu 4. Một ô tô đang chuyển động thẳng đều với vận tốc v
0
m/s thì người lái xe đạp phanh. Từ
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = −5t + 20
m/s, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.
a) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5 giây.
b) v
0
= 20 m/s.
c)
Z
(−5t + 20)dt =
−5t
2
2
+ 20t + C.
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 400 m.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Một đường dây điện được nối từ một nhà máy điện ở A (nằm tại bờ biển là đường thẳng
AB) đến một hòn đảo C, khoảng cách ngắn nhất từ đảo về bờ biển là đoạn BC dài 1 km, khoảng
cách từ B đến A là 4 km được minh họa bằng hình vẽ dưới đây.
AB
C
S
Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất
3000 USD. Hỏi điểm S trên bờ cách B bao nhiêu km để khi mắc dây điện từ A qua S rồi đến C
có chi phí là ít nhất?
Câu 2. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5%/tháng theo hình
thức lãi kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi
suất 6%/năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 4 năm 3 tháng kể
từ lúc bắt đầu gửi tiết kiệm là bao nhiêu triệu đồng (kết quả được làm tròn đến hàng đơn vị)?
Câu 3. Cho hàm số f(x) =
√
ax
2
+ 1 − bx − 2
−x
3
+ 3x − 2
(với a, b là các hằng số). Biết rằng f(x) liên tục
tại điểm x = 1. Giá trị của f(1) bằng bao nhiêu?
Trang 3/4 − Mã đề 0101
Câu 4. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ
(đơn vị: mg/l) của thuốc trong máu sau x phút (kể từ khi bắt
đầu tiêm) được xác định bởi công thức C(x) =
30x
x
2
+ 2
. Để đưa
ra lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm
khoảng thời gian mà nồng độ của thuốc trong máu đang tăng.
Trong khoảng thời gian 6 phút sau khi tiêm, nồng độ thuốc
trong máu đạt giá trị lớn nhất bằng bao nhiêu mg/l (kết quả
được làm tròn đến hàng phần mười)?
Câu 5. Một hộp quà có dạng khối hộp chữ nhật ABCD.A
′
B
′
C
′
D
′
có đáy
là hình vuông, BD = 2 dm, số đo của góc phẳng nhị diện của góc nhị diện
[A
′
, BD, A] bằng 30
◦
. Nếu các mặt của vỏ hộp quà có độ dày bằng nhau và
bằng 0,6 cm thì phần bên trong của hộp quà đó có thể tích bằng bao nhiêu cm
3
(kết quả được làm tròn đến hàng đơn vị)?
Câu 6. Trong không gian Oxyz (đơn vị đo lấy theo km), radar
phát hiện một chiếc máy bay di chuyển với tốc độ và hướng
không đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong
10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay
thì toạ độ của máy bay sau 10 phút tiếp theo là D(x; y; z). Khi
đó, x − y + z bằng bao nhiêu?
Ø
A
B
D
HẾT
Trang 4/4 − Mã đề 0101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC NINH
(Đề có 4 trang)
BẮC NINH
ĐỀ TẬP HUẤN
KỲ THI TỐT NGHIỆP THPT NĂM 2025
MÔN: TOÁN
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề 0102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường
cao tốc trong một khoảng thời gian ở bảng sau:
Tốc độ (km/h) [75; 80) [80; 85) [85; 90) [90; 95) [95; 100)
Số xe 16 21 27 36 18
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng
A. 5 km/h. B. 25 km/h. C. 75 km/h. D. 100 km/h.
Câu 2. Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy trong một số ngày gần đây của bạn
Chi được thống kê lại ở bảng sau:
Thời gian (phút) [20; 25) [25; 30) [30; 35) [35; 40) [40; 45)
Số ngày 6 6 3 2 1
Phương sai của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào dưới đây?
A. 31,24. B. 32. C. 34,77. D. 33.
Câu 3. Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số y =
5x − 1
x − 2
?
A. x = −2. B. y = 5. C. x = 5. D. x = 2.
Câu 4. Tất cả các nghiệm của phương trình cos x = 0 là
A. x = k2π, k ∈ Z. B. x = π + k2π, k ∈ Z.
C. x =
π
2
+ kπ, k ∈ Z. D. x = kπ, k ∈ Z.
Câu 5. Hàm số nào sau đây đồng biến trên R?
A. y =
x − 3
x + 1
. B. y = x
3
− 2x. C. y = x
3
+ 2x. D. y = x
4
− 2x
2
+ 4.
Câu 6. Trong không gian Oxyz, điểm M(1; 3; 2) thuộc mặt phẳng có phương trình nào sau
đây?
A. x − 2y − z + 1 = 0. B. 2x + y − z + 3 = 0. C. 2x + y − z + 4 = 0. D. 3x − y + z − 2 = 0.
Câu 7. Họ nguyên hàm của hàm số f(x) = cos x + 2 là
A. −cos x + 2x + C. B. cos x + 2x + C. C. cos x + C. D. sin x + 2x + C.
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [a; b] và f(a) = 2, f(b) = 4. Giá trị
của
b
Z
a
f
′
(x)dx bằng
A. 6. B. 2. C. −2. D. −6.
Trang 1/4 − Mã đề 0102
Câu 9. Trong không gian Oxyz, cho hai điểm A (1; 2; 4), B (−2; 4; 0). Trung điểm của đoạn thẳng
AB có cao độ bằng
A. 3. B. 1. C. 2. D. −1.
Câu 10. Trong không gian Oxyz, cho hai véctơ
−→
u = (2; 0; −2) ,
−→
v = (8; −1; 6). Tích vô hướng
−→
u ·
−→
v bằng
A. 0. B. 1. C. 4. D. −14.
Câu 11. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
y
′
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
11
−2−2
+∞+∞
Hàm số có bảng biến thiên như trên là
A. y = x
3
− x − 2. B. y = −x
4
+ 2x
2
+ 1. C. y = 3x
4
− 6x
2
+ 1. D. y = x
3
− x + 1.
Câu 12. Giá trị của lim
n→+∞
−3n + 2
n + 1
bằng
A. 1. B. 2. C. −3. D. +∞.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Khảo sát một nhóm 50 học sinh ở một trường trung học người ta thấy rằng: có 20 học
sinh giỏi Ngoại ngữ, 15 học sinh giỏi Tin học, 10 học sinh giỏi cả Ngoại ngữ và Tin học. Chọn
ngẫu nhiên một học sinh từ nhóm đó.
a) Xác suất để chọn được học sinh giỏi Ngoại ngữ bằng 0,3.
b) Xác suất để chọn được học sinh giỏi Tin học bằng 0,4.
c) Xác suất để chọn được học sinh giỏi Ngoại ngữ hoặc Tin học bằng 0,6.
d) Xác suất để chọn được học sinh không giỏi Ngoại ngữ hoặc Tin học bằng 0,5.
Câu 2. Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình dưới đây:
x
y
′
y
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−3−3
55
−∞−∞
a) Hàm số y = f(x) nghịch biến trên khoảng (3; 5).
b) Hàm số y = f(x) có đúng 1 điểm cực đại.
c) Đồ thị hàm số g(x) =
x − 4
f(x) − 5
có đúng 2 đường tiệm cận đứng.
d) Giá trị nhỏ nhất của hàm số g(x) = f (4x − x
2
) +
1
3
x
3
− 3x
2
+ 8x +
1
3
trên đoạn [1; 3] bằng
12.
Trang 2/4 − Mã đề 0102
Câu 3. Một ô tô đang chuyển động thẳng đều với vận tốc v
0
m/s thì người lái xe đạp phanh. Từ
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = −5t + 20
m/s, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.
a)
Z
(−5t + 20)dt = −5t
2
+ 20t + C.
b) v
0
= 15 m/s.
c) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 4 giây.
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 50 m.
Câu 4. Cho khối chóp cụt tứ giác đều ABCD.A
′
B
′
C
′
D
′
có chiều cao bằng 3 cm, diện tích hai đáy lần lượt bằng
72 cm
2
và 18 cm
2
. Gọi I, O tương ứng là tâm của hai
đáy ABCD và A
′
B
′
C
′
D
′
. Chọn hệ trục toạ độ Oxyz, với
đơn vị trên mỗi trục là cm sao cho tia Ox cùng hướng
với vectơ
−−→
OD
′
, tia Oy cùng hướng với vectơ
−−→
OC
′
, tia Oz
cùng hướng với vectơ
−→
OI (như hình vẽ).
x
y
z
D
′
C
′
B
′
A
′
O
D
C
BA
I
a) Tọa độ của điểm D
′
là (6; 0; 0).
b) Phương trình mặt phẳng (ABCD) là z = 3.
c) Khoảng cách từ O đến mặt phẳng (BCC
′
B
′
) bằng 3
√
3 cm.
d) Hai mặt phẳng (BCC
′
B
′
) và (DCC
′
D
′
) tạo với nhau một góc lớn hơn 71 độ.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Một đường dây điện được nối từ một nhà máy điện ở A (nằm tại bờ biển là đường thẳng
AB) đến một hòn đảo C, khoảng cách ngắn nhất từ đảo về bờ biển là đoạn BC dài 1 km, khoảng
cách từ B đến A là 4 km được minh họa bằng hình vẽ dưới đây.
AB
C
S
Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất
3000 USD. Hỏi điểm S trên bờ cách A bao nhiêu km để khi mắc dây điện từ A qua S rồi đến C
có chi phí là ít nhất?
Câu 2. Một hộp quà có dạng khối hộp chữ nhật ABCD.A
′
B
′
C
′
D
′
có đáy
là hình vuông, BD = 2 dm, số đo của góc phẳng nhị diện của góc nhị diện
[A
′
, BD, A] bằng 30
◦
. Nếu các mặt của vỏ hộp quà có độ dày bằng nhau và
bằng 0,5 cm thì phần bên trong của hộp quà đó có thể tích bằng bao nhiêu cm
3
(kết quả được làm tròn đến hàng đơn vị)?
Trang 3/4 − Mã đề 0102
Câu 3. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5%/tháng theo hình
thức lãi kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi
suất 6%/năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 2 năm 3 tháng kể
từ lúc bắt đầu gửi tiết kiệm là bao nhiêu triệu đồng (kết quả được làm tròn đến hàng đơn vị)?
Câu 4. Cho hàm số f(x) =
√
ax
2
+ 1 − bx − 2
x
3
− 3x + 2
(với a, b là các hằng số). Biết rằng f(x) liên tục
tại điểm x = 1. Giá trị của f(1) bằng bao nhiêu?
Câu 5. Trong không gian Oxyz (đơn vị đo lấy theo km), radar
phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không
đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong 10 phút.
Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ
của máy bay sau 10 phút tiếp theo là D(x; y; z). Khi đó, x +y + z
bằng bao nhiêu?
Ø
A
B
D
Câu 6. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ
(đơn vị: mg/l) của thuốc trong máu sau x phút (kể từ khi bắt
đầu tiêm) được xác định bởi công thức C(x) =
30x
x
2
+ 3
. Để đưa
ra lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm
khoảng thời gian mà nồng độ của thuốc trong máu đang tăng.
Trong khoảng thời gian 6 phút sau khi tiêm, nồng độ thuốc
trong máu đạt giá trị lớn nhất bằng bao nhiêu mg/l (kết quả
được làm tròn đến hàng phần mười)?
HẾT
Trang 4/4 − Mã đề 0102
101 103 105 107 109 111 113 115 117 119 121 123 102 104 106 108 110 112 114 116 118 120 122 124
1
DCAACDBCDBBCBCBCCDBCADBA
2
BBBACABDBCBCCBBCCCDBCDCA
3
ADAADCDBCDBDDBCADDBBDABB
4
BACBADCBACBACAAABCDADDCA
5
ACDBCABAABDCCDDCCDBBAAAA
6
ABBBBCCDBADADCABCBBADCDC
7
ACAACDBACDDADBBABBDDDCDD
8
BDBADDBCBAABBCDADDDACDAA
9
ADBACBDDCADDCCBDDBBBADAD
10
DBBBACCCACBBCCBBADBCDDBD
11
BDBCBBAABABBCADDDCDBBDAC
12
DDAADDCAABBACBCCCBAACDAB
1
SĐĐSSĐĐĐ ĐSĐĐ SĐĐĐ ĐĐSĐ SĐĐĐ ĐSĐS ĐĐSS ĐĐSS ĐSĐĐ ĐSĐSSĐĐĐ SSSĐ SĐSS SSĐS SSSĐ SSSĐ SSSĐ SSSĐ SSSĐ SSĐSSĐĐS ĐSSS SSSĐ
2
ĐSĐĐ ĐĐSĐĐĐSS ĐĐSS ĐSĐSSĐĐS ĐSĐS ĐSĐS ĐS
ĐS ĐĐSS SĐĐS ĐĐSĐ SĐĐSSĐĐS ĐĐSS SĐĐSSSĐSSĐĐSSĐĐS ĐĐSS SĐĐSSĐĐS ĐĐSS ĐĐSS
3
ĐSĐĐ ĐSĐS ĐĐSĐ SĐĐĐ SĐĐĐ ĐSĐĐ ĐĐSĐĐĐSĐĐSĐĐ SĐĐS ĐĐSĐĐSĐSSSĐS ĐĐSS ĐSĐSSĐĐS ĐĐSS SĐĐSSĐĐSSĐSS SSSĐ SSSĐ SĐĐS ĐSĐS
4
SĐĐS ĐSĐS
ĐSĐS ĐĐSS ĐSĐS ĐĐSS ĐSĐĐ SĐĐĐ SĐĐĐ ĐSĐĐ S ĐĐĐ SĐĐS ĐĐSS SSSĐ SSSĐĐSSS SĐĐS ĐSSS SSĐSSĐĐSSĐĐSSĐSS SSSĐ SĐSS
1
0,75 10,6 1 64 489 10,6 766 489 10,6 10,6 1 489 3,25 8,7 1689 1689 824 57 -1 3,25 57 57 3,25 3,25
2
64 489 10,6 10,6 64 1 489 10,6 64 489 64 766 824 -1 8,7 -1 57 -1 1689 57 824 3,25 -1 8,7
3
1 766 64 489 10,6 489 0,75 64 1 1 10,6 0,75 57 3,25 824 824 8,7 8,7 8,7 824 1689 824 824 57
4
10,6 64 489 0,75 1 0,75 64 0,75 766 766 0,75 10,6 -1 1689 -1 3,25 1689 1689 824 -1 3,25 1689 1689 -1
5
766 0,75 766 766 0,75 766 1 766 489 64 489 64 1689 824 57 8,7 -1 3,25 57 1689 -1 8,7 57 824
6
489 1 0,75 1 766 64 10,6 1 0,75 0,75 766 1 8,7 57 3,25 57 3,25 824 3,25 8,7 8,7 -1 8,7 1689
ĐÁP ÁN TOÁN 12
Mã đề
Câu
HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Tất cả các nghiệm của phương trình
sin 0x =
là
A.
2
xk
π
π
= +
,
k ∈
. B.
2xk
π
=
,
k ∈
.
C.
2xk
ππ
= +
,
. D.
xk
π
=
,
.
Lời giải
Chọn D
Phương trình
xk
π
⇔=
,
k ∈
.
Vậy nghiệm phương trình là
xk
π
=
,
k ∈
.
Câu 2. Trong không gian
Oxyz
, cho hai điểm
( )
1; 2; 3A
,
( )
2; 4;0B −
. Trung điểm của đoạn thẳng
AB
có tung độ là
A.
1
. B.
3
. C.
2
. D.
1−
.
Lời giải
Chọn B
Gọi
I
là trung điểm của đoạn thẳng
AB
. Khi đó
2
AB
I
yy
y
+
=
24
2
+
=
3=
.
Câu 3. Giá trị của
23
lim
1
n
n
n
→+∞
−
+
bằng
A.
2
. B.
3−
. C.
1
. D.
+∞
.
Lời giải
Chọn A
Ta có
23
lim
1
n
n
n
→+∞
−
+
3
2
lim
1
1
x
n
n
→+∞
−
=
+
2
1
=
2=
.
Câu 4. Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường cao tốc
trong một khoảng thời gian ở bảng sau:
Tốc độ (km/h)
[
)
75;80
[
)
80;85
[
)
85;90
[
)
90;95
[
)
95;100
Số xe
15
22
28
34
19
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng?
A. 100 km/h. B. 25 km/h. C. 5 km/h. D. 75 km/h.
Lời giải
Chọn B
Khoảng biến thiên của mẫu số liệu ghép nhóm trên:
100 75 25R = −=
.
Câu 5. Trong không gian
Oxyz
, điểm
( )
1; 3; 2M −
thuộc mặt phẳng có phương trình nào sau đây?
A.
2 30xyz+−+=
. B.
3 20xyz−+−=
.
C.
2 40xyz+−+=
. D.
2 10x yz− −+=
.
Lời giải
Chọn A
Điểm
M
thuộc mặt phẳng
2 30xyz+−+=
.
Câu 6. Trong không gian
Oxyz
, cho hai vectơ
( )
( )
2; 0; 2 , 1; 1; 6uv= − =−−

. Tích vô hướng
.uv

bằng
A.
14−
. B.
1
. C.
0
. D.
4
.
Lời giải
Chọn A
Ta có
(
)
( ) ( )
. 2. 1 0. 1 2 .6 14uv
= −+ −+− =−

.
Câu 7. Hàm số nào sau đây đồng biến trên
.?
A.
3
3yx x= +
. B.
3
3yx x= −
.
C.
1
1
x
y
x
−
=
+
. D.
42
31yx x=−+
.
Lời giải.
Chọn A
Ta có với
3
3yx x= +
thì
2
3 3 0,yx x
′
= +> ∀
.
Câu 8. Cho hàm só
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
;
ab
và
(
) ( )
2, 4fa fb
=−=−
. Giá trị của
( )
d
b
a
fxx∫
′
bằng
A. 2. B. -2. C. -6. D. 6.
Lời giải.
Chọn B
Ta có
( )
( ) (
) ( )
d2
b
b
a
a
f x x fx fb fa
∫ = =−=−
′
.
Câu 9. Họ nguyên hìm của hàm số
( )
sin 2fx x= +
là
A.
cos 2x xC− ++
. B.
cos 2x xC++
.
C.
sin 2x xC++
. D.
cosxC+
.
Lời giải.
Chọn A
Câu 10. Bạn Chi rất thích nhảy hiện đại. Thời gian tâp nhảy trong môt sô ngày gần đây của bạn Chi được
thống kê lại bằng bảng sau:
Thời gian (phút)
(20;25)
( )
25;30
( )
30;35
( )
35;40
( )
40;45
Số ngày
6
6
4
1
1
Phương sai của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào dưới đây?
A. 33. B. 34,77. C. 32. D. 31,24.
Lời giải.
Chọn B
Cỡ mẫu
6 6 4 1 1 18n = + + ++=
.
Giá trị trung bình
45 55 65 75 85
.6 .6 .4 .1 .1
85
22222
18 3
x
++++
= =
.
Phương sai
2 2 222
2
45 85 55 85 65 85 75 85 85 85
6 6 411
23 23 23 23 23
35,156
18
x
s
 
−+ −+ −+−+−
 
 
=
Câu 11. Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Hàm số có bảng biến thiên như trên là
A.
42
2
yx x=−+
. B.
42
363yx x=−+
.
C.
3
yx x= −
. D.
3
3yx x= −+
.
Lời giải.
Chọn B
Đồ thị hàm số đã cho là đồ thị hàm bậc 4, ta kiểm tra được đồ thị ở câu B thỏa mãn yêu cầu bài
toán.
Câu 12. Đường thẳng nào là đường tiệm cận đứng của đồ thị hàm số
51
2
x
y
x
−
=
+
?
A.
5x =
. B.
5y
=
. C.
2x =
. D.
2
x = −
.
Lời giải.
Chọn D
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 01 đến câu 04. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Khảo sát một nhóm
50
học sinh ở một trường trung học người ta thấy rằng: có
20
học sinh giỏi
Ngoại ngữ,
15
học sinh giỏi Tin học,
10
học sinh giỏi cả Ngoại ngữ và Tin học. Chọn ngẫu nhiên
một học sinh từ nhóm đó.
a) Xác suất để chọn được học sinh giỏi Ngoại ngữ hoặc Tin học bằng
0,7
.
b) Xác suất để chọn được học sinh giỏi Tin học bằng
0,3
.
c) Xác suất để chọn được học sinh giỏi Ngoại ngữ bằng
0, 4
.
d) Xác suất để chọn được học sinh không giỏi Ngoại ngữ hoặc Tin học bằng
0,3
.
Lời giải
SAI – ĐÚNG – ĐÚNG – SAI.
(a) Để tính xác suất của biến cố "học sinh giỏi Ngoại ngữ hoặc Tin học" (tức là
AB∪
), ta sử
dụng công thức:
( ) () () ( ).PA B PA PB PA B∪= + − ∩
Với:
- Xác suất chọn được học sinh giỏi Ngoại ngữ:
( )
( )
20
0, 4.
50
nA
PA
N
= = =
- Xác suất chọn được học sinh giỏi Tin học:
( )
( )
15
0,3.
50
nB
PB
N
= = =
- Xác suất chọn được học sinh giỏi cả Ngoại ngữ và Tin học:
( )
( )
10
0, 2.
50
nA B
PA B
N
∩
∩= = =
Vậy
( ) 0, 4 0,3 0,2 0,5.PA B∪= + − =
Chọn Sai.
(b) Như đã tính ở trên, xác suất chọn được học sinh giỏi Tin học là
( ) 0,3.PB =
Chọn Đúng.
(c) Tương tự, xác suất chọn được học sinh giỏi Ngoại ngữ là
( ) 0, 4.PA=
Chọn Đúng
(d) Biến cố "học sinh không giỏi Ngoại ngữ hoặc Tin học" là biến cố đối của biến cố "học sinh
giỏi Ngoại ngữ hoặc Tin học". Tức là, ta cần tính xác suất của biến cố
AB∪
.
Ta có
( )
1 ( ) 1 0,5 0,5.PAB PAB∪=− ∪=− =
Chọn Sai.
Câu 2. Cho hàm số bậc ba
( )
y fx=
có bảng biến thiên như hình dưới đây
a) Hàm số
( )
y fx=
có 2 điểm cực trị.
b) Hàm số
( )
y fx=
đồng biến trên
( )
3; 5−
.
c) Đồ thị hàm số
( )
( )
4
5
x
gx
fx
−
=
−
có
3
đường tiệm cận.
d) Giá trị lớn nhất của hàm số
( )
( )
2 32
11
4 38
33
gx f x x x x x= − + − ++
trên đoạn
[ ]
1; 3
bằng
12.
Lời giải
ĐÚNG – SAI –– ĐÚNG – ĐÚNG.
(a) Hàm số đã cho có hai điểm cự trị tại
0x
=
và
Chọn Đúng.
(b) Dựa vào bẳng biến thiên ta thấy, hàm số đã cho đồng biến trên khoảng
( )
0; 4
.
Chọn Sai.
(c) Xét hàm số
( )
( )
4
5
x
gx
fx
−
=
−
Từ bảng biến thiên, ta thấy phương trình
(
)
5
fx
=
có một nghiệm
5x =
và một nghiệm
0.
xa= <
Nhận thấy rằng
( )
4
lim
5
xa
x
fx
+
→
−
= +∞
−
và
( )
5
4
lim
5
x
x
fx
+
→
−
= +∞
−
. Vậy đồ thị hàm số đã cho
có hai tiệm cận đứng.
Ta cũng có
( )
4
lim 0
5
x
x
fx
→±∞
−
=
−
, do tử số là đa thức bậc nhất trong khi mẫu số là đa thức bậc ba.
Vậy đồ thị hàm số đã cho có một đường tiệm cận ngang.
Tóm lại, đồ thị hàm số đã cho có ba đường tiệm cận.
Chọn Đúng.
(d) Xét hàm số
( )
( )
2 32
11
4 38
33
gx f x x x x x= − + − ++
trên đoạn
[
]
1; 3
.
Ta có
(
) ( )
( )
( )
( )
( )( )
( )
( )
( )
2
2
2
2
42 4 6 8
22 4 4 2
22 4 4
gx xf x x x x
xf x x x x
x f xx x
′′
=− − +−+
′
= − − +− −

′
= − − −−

Xét hàm số
( )
2
4ux x x= −
, trên đoạn
[ ]
1; 3
có
( )
34ux≤≤
suy ra
( )
( )
0f ux
′
≥
, hơn nữa
40x −<
với
[ ]
1; 3x ∈
. Vậy nên
( )
( )
[ ]
2
4 4 0, 1; 3f xx x x
′
− − − ≥ ∀∈
, dấu
""
=
xảy ra khi
4.x =
Trên
[ ]
1; 3
, phương trình
( )
0gx
′
=
có một nghiệm
2.
x =
Có
( ) ( )
( ) ( )
( ) ( )
17
13
3
19
33
3
2 4 7 12
gf
gf
gf
= +
= +
= +=
Do
( ) ( )
34ff<
và
17 19
7
33
<<
nên giá trị lớn nhất của hàm số
( )
gx
trên đoạn
[ ]
1; 3
bằng 12.
Chọn Đúng.
Câu 3. Cho khối chóp cụt tứ giác đều
D' ' ' 'ABC A B C D
có chiều cao bằng 3 cm, diện tích hai đáy lần
lượt bằng 72 cm
2
và 18 cm
2
. Gọi I, O tương ứng là tâm của hai đáy
DABC
và
''''ABCD
. Chọn
hệ trục toạ độ
Oxyz
, với đơn vị trên mỗi trục là cm sao cho tia Ox cùng hường với véc tơ
D'O

,
tia Oy cùng hướng với véc tơ
'OC

, tia Oz cùng hướng với véc tơ
OI

a) Toạ độ của điểm
'B
là
(
)
6;0; 0−
b) Khoảng cách từ O đến mặt phẳng
( )
''BCC B
bằng
3
cm
c) Phương trình mặt phẳng
( )
D
ABC
là
3x =
d) Hai mặt phẳng
( )
''BCC B
và
(
)
''DCC D
tạo với nhau một góc lớn hơn 70 độ.
Lời giải
a) Đúng
b) Sai
c) Sai
d) Đúng
a)Đúng
Diện tích hình vuông
''''ABCD
bằng 72 cm
2
suy ra cạnh hình vuông bằng
( )
6 2 ' ' ' ' 12 ' 6; 0;0AC BD B
⇒ = =⇒−
(b)Sai
( )
' 0; 6;0C
Diện tích hình vuông
ABCD
bằng 18 cm
2
suy ra cạnh hình vuông bằng
( )
3 2 6 0;3;3AC BD C⇒==⇒
Véc tơ pháp tuyến của mặt phẳng là
( )
1
' ', ' 18; 18; 0n BC BC

= = −

 
Phương trình mặt phẳng
(
)
''
BCC B
là
60xy−+=
Khoảng cách từ O đến mặt phẳng
( )
''BCC B
bằng
( )
( )
6
, ' ' 32
2
d O BCC B = =
(c)Đúng
(d)Đúng
( )
3; 0; 3D
Véc tơ pháp tuyến của mặt phẳng là
( )
2
D, ' 9; 9; 9n C CC

= =−−−

 
Ta có
( ) ( ) ( )
12
. 18. 9 18 . 9 0 0nn = −+− −+=⇒

góc giữa hai mặt phẳng bằng 90
0
.
Câu 4. Một ô tô đang chuyển động thẳng đều với vận tốc
0
/vms
thì người lái xe đạp phanh. Từ thời
điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số
( )
5 20 ( / )vt t m s=−+
, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh
a) Thời gian từ lúc người lái xe đạp phanh cho đến khi dừng hẳn là 5 giây.
b)
0
20 /v ms=
c)
(
)
2
5
5 20 20
2
t
t dt t C
−
−+ = + +
∫
d) Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là 400m.
Lời giải
a) Sai
b) Đúng
c)Đúng
d) Sai
a)Sai
Thời gian từ lúc người lái xe đạp phanh cho đến khi dừng hẳn
(
)
5 20 0 4
vt t t=− + =⇔=
b)Đúng
0
(0) 20 /v v ms= =
c)Đúng
( )
2
5
5 20 20
2
t
t dt t C
−
−+ = + +
∫
d)Đúng
Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là
( )
4
4
2
0
0
5
5 20 20 40
2
t
s t dt t m

−
= −+ = + =


∫
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Câu 1. Một đường dây điện được nối từ một nhà máy điện ở
A
(nằm tại bờ biển là đường thẳng
AB
) đến một hòn đảo
C
, khoảng cách ngắn nhất từ đảo về bờ biển là đoạn
BC
dài 1 km, khoảng
cách từ
B
đến
A
là 4 km được minh họa bằng hình vẽ dưới đây.
Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất
3000 USD. Hỏi điểm
S
trên bờ cách
A
bao nhiêu để khi mắc dây điện từ
A
qua
S
rồi đến
C
có
chi phí là ít nhất?
Lời giải
Trả lời: 3,25
Đặt
AS x
với
04x
, khi đó
4BS x
và
2
22
14CS BC BS x 
.
Chi phí lắp đặt dây điện từ
A
đến
S
là
1
3000Px
.
Chi phí lắp đặt dây diện từ
C
đến
S
là
2
2
5000 1 4Px 
.
Tổng chi phí lắp đặt dây điện là
2
12
3000 5000 1 4PPP x x 
.
Xét hàm
2
3000 5000 1 4
fx x x 
trên khoảng
0; 4
.
Ta có
2
5000 4
3000
8 17
x
fx
xx


.
Khi đó
2
13
0 5 4 3 8 17
4
fx x x x x

.
Bảng biến thiên của hàm số
fx
như sau
Vậy để chi phí mắc dây diện là ít nhất thì điểm
S
cách
A
một khoảng là
13
3, 25
4
km.
Câu 2. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất
/tháng theo hình thức lãi
kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi suất
6%
/năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 4 năm 3 tháng kể từ lúc bắt
đầu tiết kiệm là bao nhiêu triệu đồng (kết quả làm tròn đến hàng đơn vị)?
Lời giải
Trả lời: 64
Số tiền ông An thu được sau 3 tháng gửi với lãi suất
0,5%
/tháng là
3
50 1 0,5%
(triệu đồng).
Số tiền ông An thu được sau 4 năm 3 tháng kể từ lúc bắt đầu tiết kiệm là
34
50 1 0,5% 1 6% 64 
(triệu đồng).
Câu 3. Cho hàm số
( )
2
3
12
32
ax bx
fx
xx
+− −
=
−+ −
(với
a
,
b
là các hằng số). Biết rằng
( )
fx
liên tục tại
điểm
1
x =
. Giá trị của
( )
1f
bằng bao nhiêu?
Lời giải
Trả lời: 1
Ta có
(
)
(
) ( )
( ) ( )
(
)
( )
( ) (
)
(
)
( ) ( )
(
)
2
22
3
2
2
2
2
22
22
22
12 12
32
12 12
4
31
43
33
.
12 12 12 12
ax bx ax bx
fx
xx
x x ax bx
ba b
xx
a b x bx
x x ax bx x x ax bx
+−+ +−+
= =
−+ −
− − + ++ +

−
− ++

− −−

= =
− − + ++ + − − + ++ +
Hàm số
( )
fx
liên tục tại điểm
1x =
( ) ( )
1
lim 1
x
fx f
→
⇔=
(hữu hạn), suy ra
( )
2
2
2
2
3
1
4
4
3
11
3
33
4
.
2
2
3
ba
a
ba b
xxx
b
b
−
= −
=
−

+ += − ⇔ ⇔


= −
= −
Khi đó
( )
( )
11
2
3
lim lim 1
33
2 12
42
xx
fx
x xx
→→
= =

+ − +− +


.
Giá trị của
(
)
11f =
.
Cách 2: Đặt
( )
2
12g x ax bx= +− −
( )
2
1
ax
gx b
ax
′
⇒= −
+
.
Hàm số
( )
fx
liên tục tại điểm
1
x =
( ) ( )
1
lim 1
x
fx f
→
⇔=
(hữu hạn).
Do
1x =
là nghiệm kép của mẫu nên
( )
( )
0
0
gx
gx
=
′
=
1 20
0
1
ab
a
b
a
+−− =
⇔
−=
+
. Giải được
33
,
42
ab=−=−
.
Câu 4. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ (đơn vị: mg/l) của thuốc trong máu sau
x
phút (kể từ khi bắt đầu tiêm) được xác định bởi công thức
( )
2
30
2
x
Cx
x
=
+
. Để đưa ra lời khuyên
và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong
máu đang tăng. Trong khoảng thời gian
6
phút sau khi tiêm, nồng độ thuốc trong máu đạt giá trị
lớn nhất bằng bao nhiêu mg/l (kết quả được làm tròn đến hàng phần mười)?
Lời giải
Trả lời: 10,6
Ta có
( )
( )
2
2
2
30 60
2
x
Cx
x
−+
′
=
+
nên
( )
02Cx x
′
=⇔=
.
Suy ra
( )
( )
( )
0;6
15 2
max 2 10,6
2
Cx C= = ≈
.
Câu 5. Một hộp quà có dạng khối hộp chữ nhật
.ABCD A B C D
′′′′
có đáy là hình vuông,
2dmBD =
, số
đo của góc nhị diện
[
]
,,A BD A
′
bằng
30°
. Nếu các mặt của vỏ hộp quà đó có độ dày bằng nhau
và bằng
0,6cm
thì phần viền bên trong của hộp quà đó có thể tích bằng bao nhiêu
3
cm
(kết quả
làm tròn đến hàng đơn vị) ?
Lời giải
Trả lời: 766.
Ta có:
2dm = 20cm 10 2 cm
2
BD
BD AB= ⇒= =
.
Góc nhị diện
[ ]
,,A BD A
′
bằng
10
30 30 .tan 30
3
AOA AA AO
′′
°⇒ = °⇒ = °=
.
Gọi
.MNPQ EFGH
là khối hộp chữ nhật ruột của hộp quà có đáy là hình vuông, cạnh
6
2.0,6 10 2
5
EF AB=−=−
và chiều cao
10
2.0,6 1,2
3
h AA
′
=−=−
.
Phần viền bên trong của hộp quà đó có thể tích bằng:
2
.
10
1, 2 .
3
0
6
12
5
MNPQ EFGH
V

−≈

= −


766
3
cm
.
Câu 6. Trong không gian
Oxyz
( đơn vị lấy theo
km
), radar phát hiện một chiếc máy bay di chuyển với
tốc độ và hướng không đổi từ điểm
( )
800;500;7A
đến điểm
( )
940;550;8
B
trong
10
phút. Nếu
máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau
10
phút tiếp theo là
(
)
;;D xyz
. Khi đó,
xyz
−+
bằng bao nhiêu ?
Lời giải
Trả lời: 489.
Từ giả thiết
B⇒
là trung điểm của
AD
.
Suy ra
( )
1080;600;9 1080 600 9D xyz⇒−+= − +=
489
.

Tài liệu khác của Toán

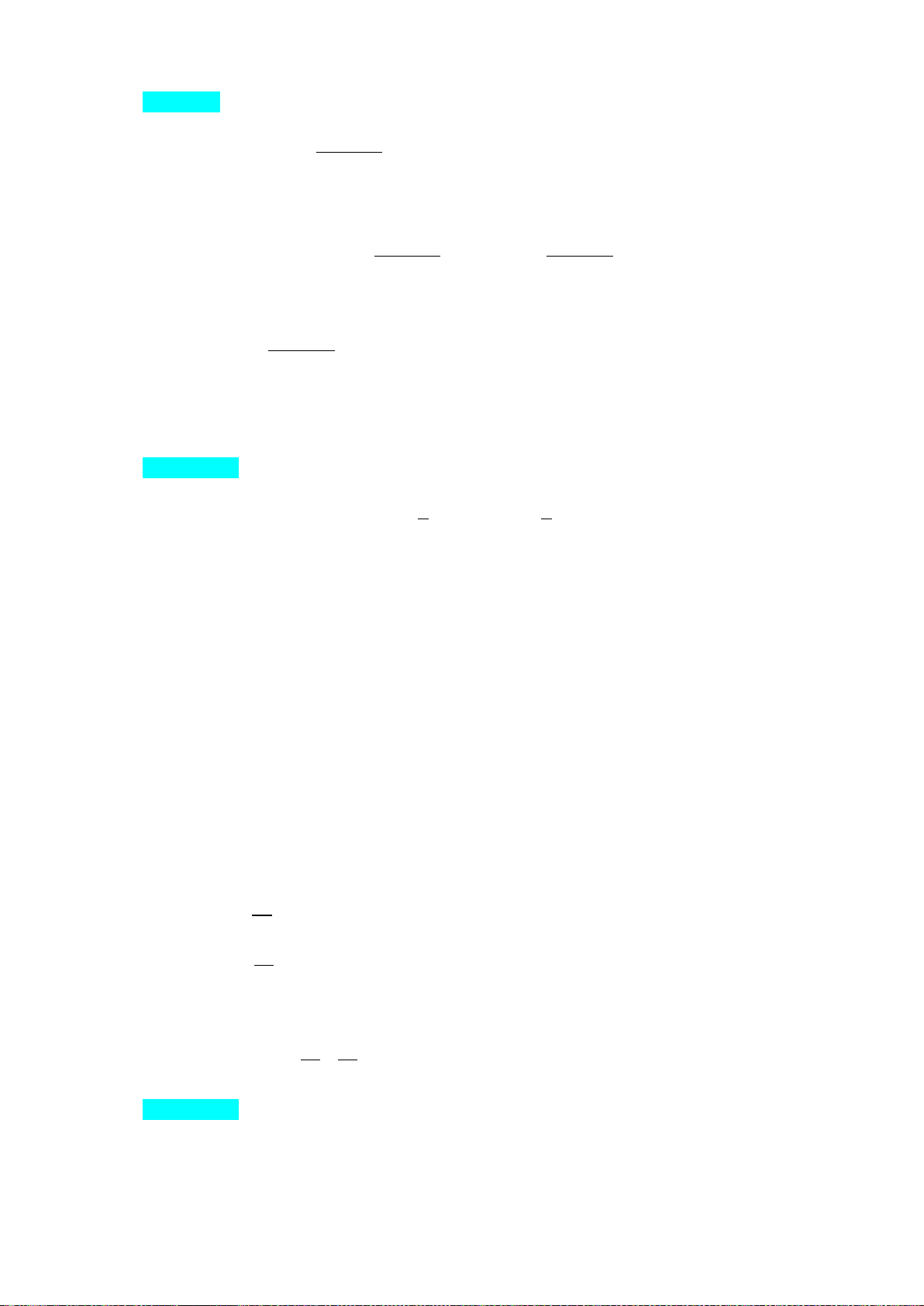
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ TẬP HUẤN BẮC NINH
KỲ THI TỐT NGHIỆP THPT NĂM 2025 (Đề có 4 trang) MÔN: TOÁN BẮC NINH
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề 0101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Tất cả các nghiệm của phương trình sin x = 0 là π A. x = + kπ, k ∈ Z. B. x = k2π, k ∈ Z. 2 C. x = π + k2π, k ∈ Z. D. x = kπ, k ∈ Z.
Câu 2. Trong không gian Oxyz, cho hai điểm A (1; 2; 3), B (−2; 4; 0). Trung điểm của đoạn thẳng AB có tung độ bằng A. 1. B. 3. C. 2. D. −1. 2n − 3 Câu 3. Giá trị của lim bằng n→+∞ n + 1 A. 2. B. −3. C. 1. D. +∞.
Câu 4. Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường
cao tốc trong một khoảng thời gian ở bảng sau:
Tốc độ (km/h) [75 ; 80) [80 ; 85) [85 ; 90) [90 ; 95) [95 ; 100) Số xe 15 22 28 34 19
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng A. 100 km/h. B. 25 km/h. C. 5 km/h. D. 75 km/h.
Câu 5. Trong không gian Oxyz, điểm M (1; −3; 2) thuộc mặt phẳng có phương trình nào sau đây?
A. 2x + y − z + 3 = 0. B. 3x − y + z − 2 = 0. C. 2x + y − z + 4 = 0. D. x − 2y − z + 1 = 0. − → − →
Câu 6. Trong không gian Oxyz, cho hai véctơ u = (2; 0; −2) , v = (−1; −1; 6). Tích vô hướng − → u · − → v bằng A. −14. B. 1. C. 0. D. 4.
Câu 7. Hàm số nào sau đây đồng biến trên R? x − 1 A. y = x3 + 3x. B. y = x3 − 3x. C. y = . D. y = x4 − 3x2 + 1. x + 1
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [a; b] và f (a) = −2, f (b) = −4. Giá trị b Z của f ′(x) dx bằng a A. 2. B. −2. C. −6. D. 6.
Câu 9. Họ nguyên hàm của hàm số f (x) = sin x + 2 là A. − cos x + 2x + C. B. cos x + 2x + C. C. sin x + 2x + C. D. cos x + C.
Câu 10. Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy trong một số ngày gần đây của
bạn Chi được thống kê lại ở bảng sau: Trang 1/4 − Mã đề 0101
Thời gian (phút) [20; 25) [25; 30) [30; 35) [35; 40) [40; 45) Số ngày 6 6 4 1 1
Phương sai của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào dưới đây? A. 33. B. 34,77. C. 32. D. 31,24.
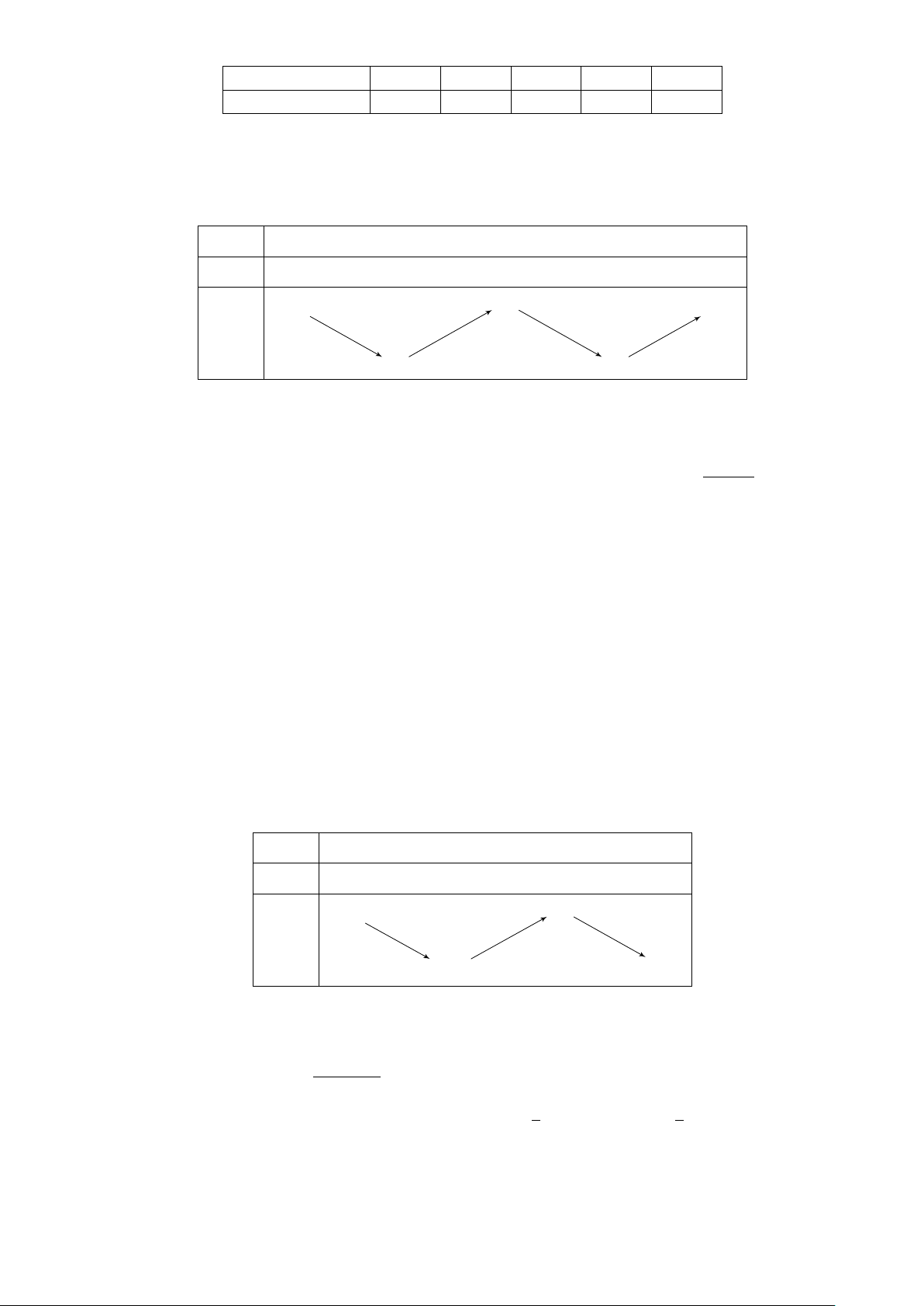
Câu 11. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 0 1 +∞ y′ − 0 + 0 − 0 + +∞ + 3 +∞ + y 0 0
Hàm số có bảng biến thiên như trên là A. y = −x4 + 2x2. B. y = 3x4 − 6x2 + 3. C. y = x3 − x. D. y = x3 − x + 3. 5x − 1
Câu 12. Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số y = ? x + 2 A. x = 5. B. y = 5. C. x = 2. D. x = −2.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Khảo sát một nhóm 50 học sinh ở một trường trung học người ta thấy rằng: có 20 học
sinh giỏi Ngoại ngữ, 15 học sinh giỏi Tin học, 10 học sinh giỏi cả Ngoại ngữ và Tin học. Chọn
ngẫu nhiên một học sinh từ nhóm đó.
a) Xác suất để chọn được học sinh giỏi Ngoại ngữ hoặc Tin học bằng 0,7.
b) Xác suất để chọn được học sinh giỏi Tin học bằng 0,3.
c) Xác suất để chọn được học sinh giỏi Ngoại ngữ bằng 0,4.
d) Xác suất để chọn được học sinh không giỏi Ngoại ngữ hoặc Tin học bằng 0,3.
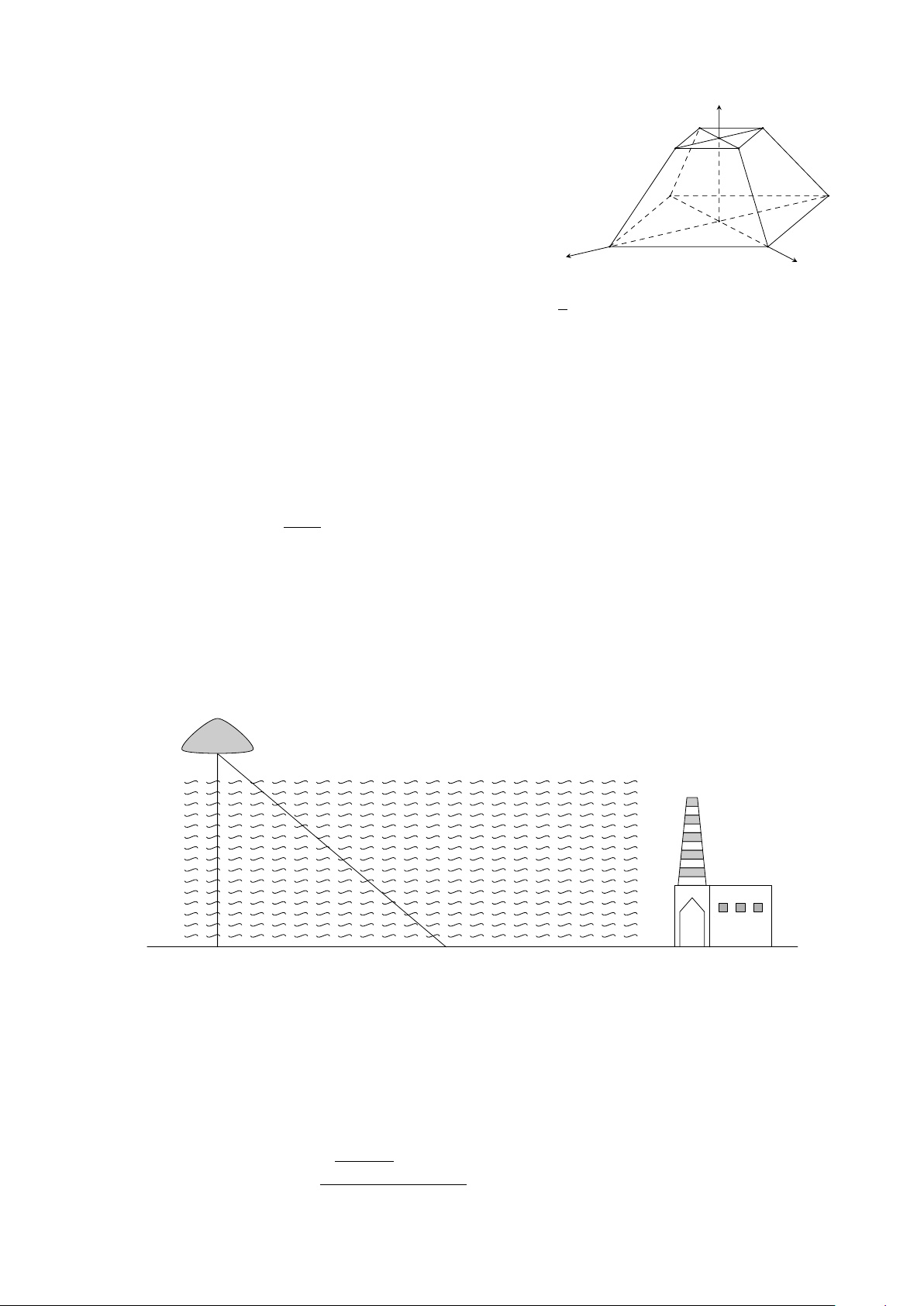
Câu 2. Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình dưới đây: x −∞ 0 4 +∞ y′ − 0 + 0 − +∞ + 5 y −3 −∞
a) Hàm số y = f (x) có 2 điểm cực trị.
b) Hàm số y = f (x) đồng biến trên (−3; 5). x − 4
c) Đồ thị hàm số g(x) = có 3 đường tiệm cận. f (x) − 5 1 1
d) Giá trị lớn nhất của hàm số g(x) = f (4x − x2) + x3 − 3x2 + 8x + trên đoạn [1; 3] bằng 3 3 12. Trang 2/4 − Mã đề 0101
Câu 3. Cho khối chóp cụt tứ giác đều ABCD.A′B′C′D′ z
có chiều cao bằng 3 cm, diện tích hai đáy lần lượt bằng A B
72 cm2 và 18 cm2. Gọi I, O tương ứng là tâm của hai D I C
đáy ABCD và A′B′C′D′. Chọn hệ trục toạ độ Oxyz, với
đơn vị trên mỗi trục là cm sao cho tia Ox cùng hướng −−→ −−→ B′ A′
với vectơ OD′, tia Oy cùng hướng với vectơ OC′, tia Oz − → O
cùng hướng với vectơ OI (như hình vẽ). D′ C′ x y
a) Tọa độ của điểm B′ là (−6; 0; 0). √
b) Khoảng cách từ O đến mặt phẳng (BCC′B′) bằng 3 cm.
c) Phương trình mặt phẳng (ABCD) là z = 3.
d) Hai mặt phẳng (BCC′B′) và (DCC′D′) tạo với nhau một góc lớn hơn 70 độ.
Câu 4. Một ô tô đang chuyển động thẳng đều với vận tốc v0 m/s thì người lái xe đạp phanh. Từ
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = −5t + 20
m/s, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.
a) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5 giây. b) v0 = 20 m/s. Z −5t2 c) (−5t + 20)dt = + 20t + C. 2
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 400 m.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
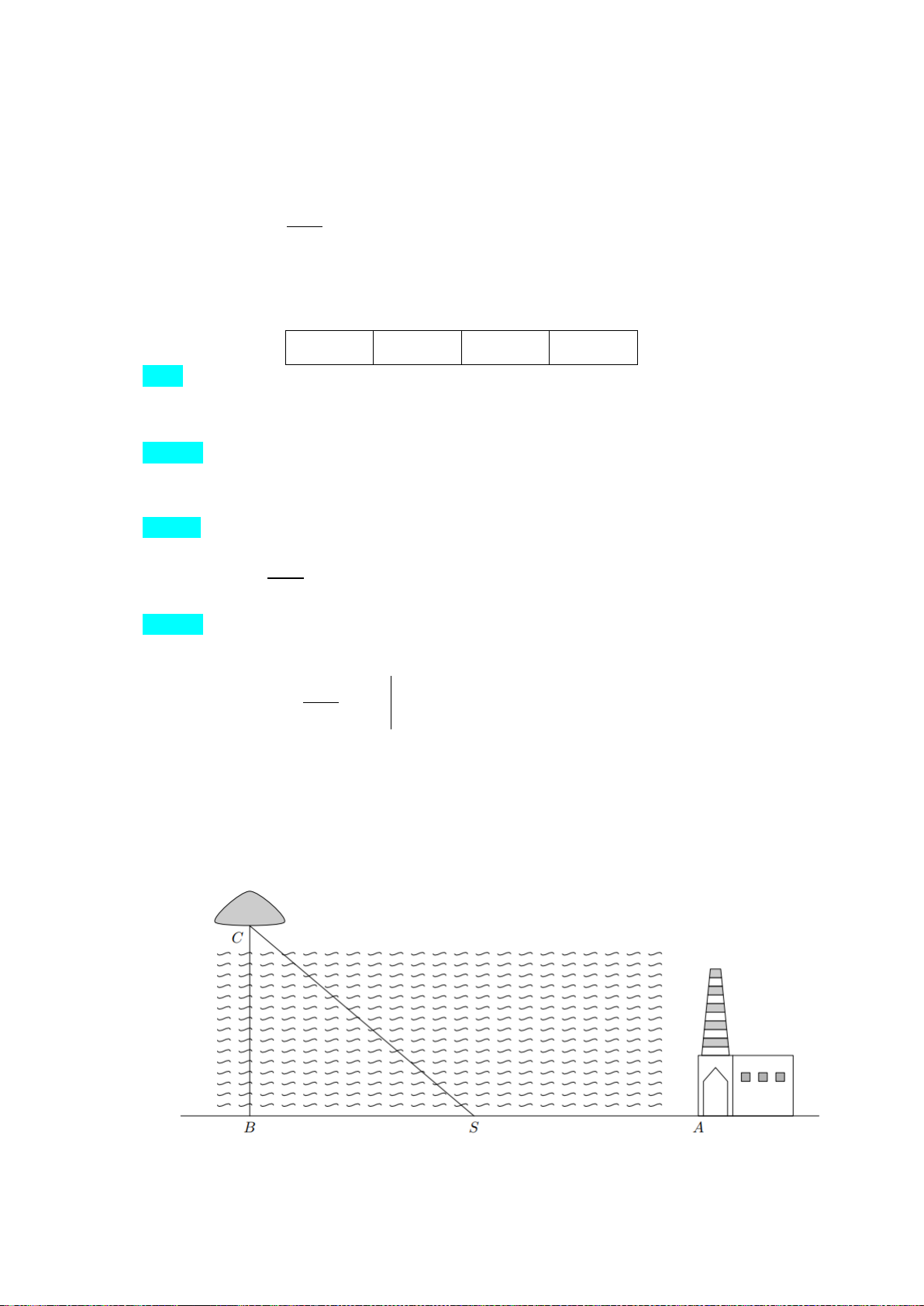
Câu 1. Một đường dây điện được nối từ một nhà máy điện ở A (nằm tại bờ biển là đường thẳng
AB) đến một hòn đảo C, khoảng cách ngắn nhất từ đảo về bờ biển là đoạn BC dài 1 km, khoảng
cách từ B đến A là 4 km được minh họa bằng hình vẽ dưới đây. C B S A
Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất
3000 USD. Hỏi điểm S trên bờ cách B bao nhiêu km để khi mắc dây điện từ A qua S rồi đến C có chi phí là ít nhất?
Câu 2. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5%/tháng theo hình
thức lãi kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi
suất 6%/năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 4 năm 3 tháng kể
từ lúc bắt đầu gửi tiết kiệm là bao nhiêu triệu đồng (kết quả được làm tròn đến hàng đơn vị)? √ax2 + 1 − bx − 2 Câu 3. Cho hàm số f (x) =
(với a, b là các hằng số). Biết rằng f (x) liên tục −x3 + 3x − 2
tại điểm x = 1. Giá trị của f (1) bằng bao nhiêu? Trang 3/4 − Mã đề 0101
Câu 4. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ
(đơn vị: mg/l) của thuốc trong máu sau x phút (kể từ khi bắt 30x
đầu tiêm) được xác định bởi công thức C(x) = . Để đưa x2 + 2
ra lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm
khoảng thời gian mà nồng độ của thuốc trong máu đang tăng.
Trong khoảng thời gian 6 phút sau khi tiêm, nồng độ thuốc
trong máu đạt giá trị lớn nhất bằng bao nhiêu mg/l (kết quả
được làm tròn đến hàng phần mười)? Câu 5.
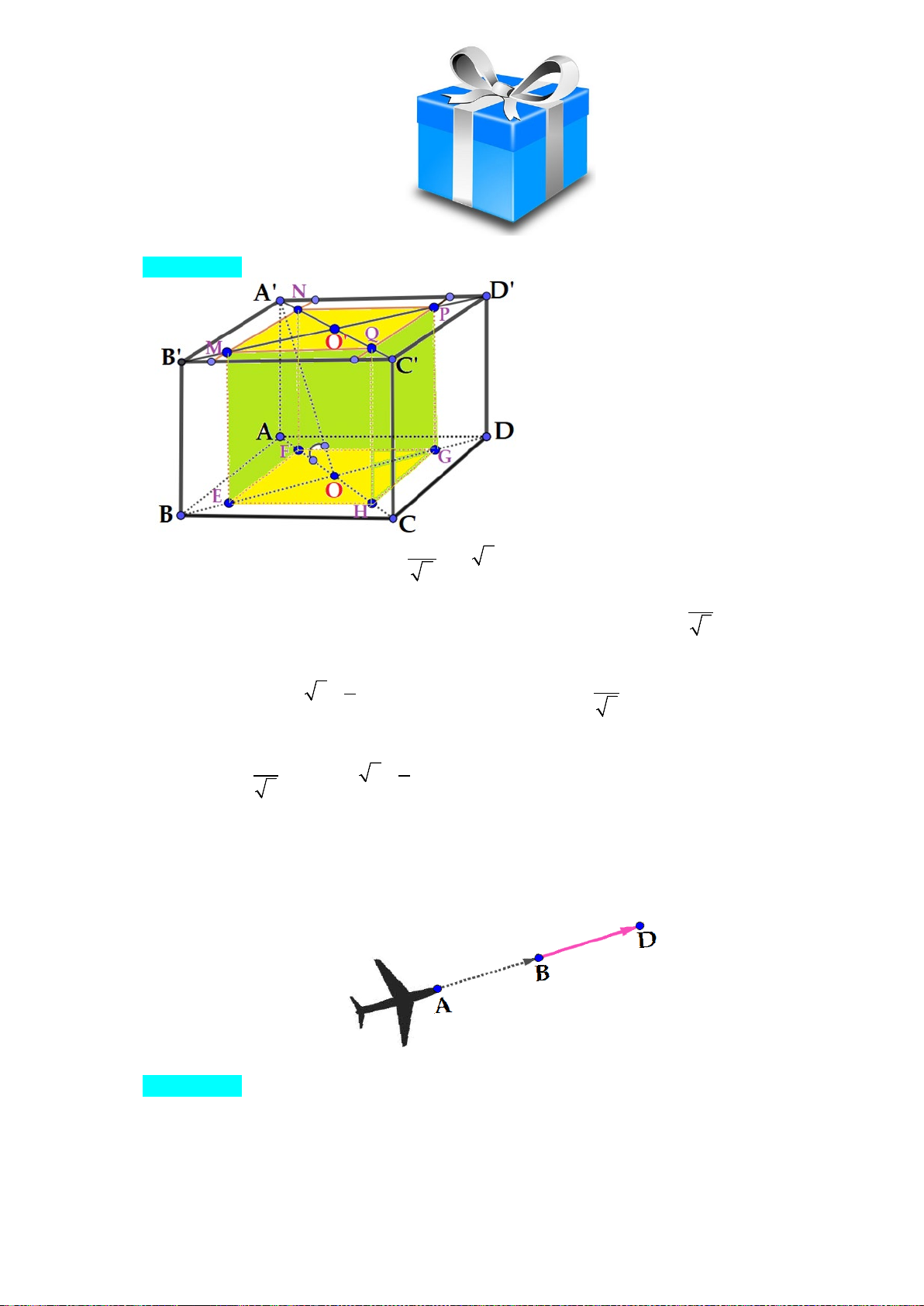
Một hộp quà có dạng khối hộp chữ nhật ABCD.A′B′C′D′ có đáy
là hình vuông, BD = 2 dm, số đo của góc phẳng nhị diện của góc nhị diện
[A′, BD, A] bằng 30◦. Nếu các mặt của vỏ hộp quà có độ dày bằng nhau và
bằng 0,6 cm thì phần bên trong của hộp quà đó có thể tích bằng bao nhiêu cm3
(kết quả được làm tròn đến hàng đơn vị)?
Câu 6. Trong không gian Oxyz (đơn vị đo lấy theo km), radar D
phát hiện một chiếc máy bay di chuyển với tốc độ và hướng
không đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong B
10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay
thì toạ độ của máy bay sau 10 phút tiếp theo là D(x; y; z). Khi Ø A
đó, x − y + z bằng bao nhiêu? HẾT Trang 4/4 − Mã đề 0101
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ TẬP HUẤN BẮC NINH
KỲ THI TỐT NGHIỆP THPT NĂM 2025 (Đề có 4 trang) MÔN: TOÁN BẮC NINH
Thời gian làm bài 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề 0102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường
cao tốc trong một khoảng thời gian ở bảng sau:
Tốc độ (km/h) [75; 80) [80; 85) [85; 90) [90; 95) [95; 100) Số xe 16 21 27 36 18
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng A. 5 km/h. B. 25 km/h. C. 75 km/h. D. 100 km/h.
Câu 2. Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy trong một số ngày gần đây của bạn
Chi được thống kê lại ở bảng sau:
Thời gian (phút) [20; 25) [25; 30) [30; 35) [35; 40) [40; 45) Số ngày 6 6 3 2 1
Phương sai của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào dưới đây? A. 31,24. B. 32. C. 34,77. D. 33. 5x − 1
Câu 3. Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số y = ? x − 2 A. x = −2. B. y = 5. C. x = 5. D. x = 2.
Câu 4. Tất cả các nghiệm của phương trình cos x = 0 là A. x = k2π, k ∈ Z. B. x = π + k2π, k ∈ Z. π C. x = + kπ, k ∈ Z. D. x = kπ, k ∈ Z. 2
Câu 5. Hàm số nào sau đây đồng biến trên R? x − 3 A. y = . B. y = x3 − 2x. C. y = x3 + 2x. D. y = x4 − 2x2 + 4. x + 1
Câu 6. Trong không gian Oxyz, điểm M (1; 3; 2) thuộc mặt phẳng có phương trình nào sau đây?
A. x − 2y − z + 1 = 0. B. 2x + y − z + 3 = 0. C. 2x + y − z + 4 = 0. D. 3x − y + z − 2 = 0.
Câu 7. Họ nguyên hàm của hàm số f (x) = cos x + 2 là A. − cos x + 2x + C. B. cos x + 2x + C. C. cos x + C. D. sin x + 2x + C.
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [a; b] và f (a) = 2, f (b) = 4. Giá trị b Z của f ′(x)dx bằng a A. 6. B. 2. C. −2. D. −6. Trang 1/4 − Mã đề 0102
Câu 9. Trong không gian Oxyz, cho hai điểm A (1; 2; 4), B (−2; 4; 0). Trung điểm của đoạn thẳng AB có cao độ bằng A. 3. B. 1. C. 2. D. −1. − → − →
Câu 10. Trong không gian Oxyz, cho hai véctơ u = (2; 0; −2) , v = (8; −1; 6). Tích vô hướng − → u · − → v bằng A. 0. B. 1. C. 4. D. −14.
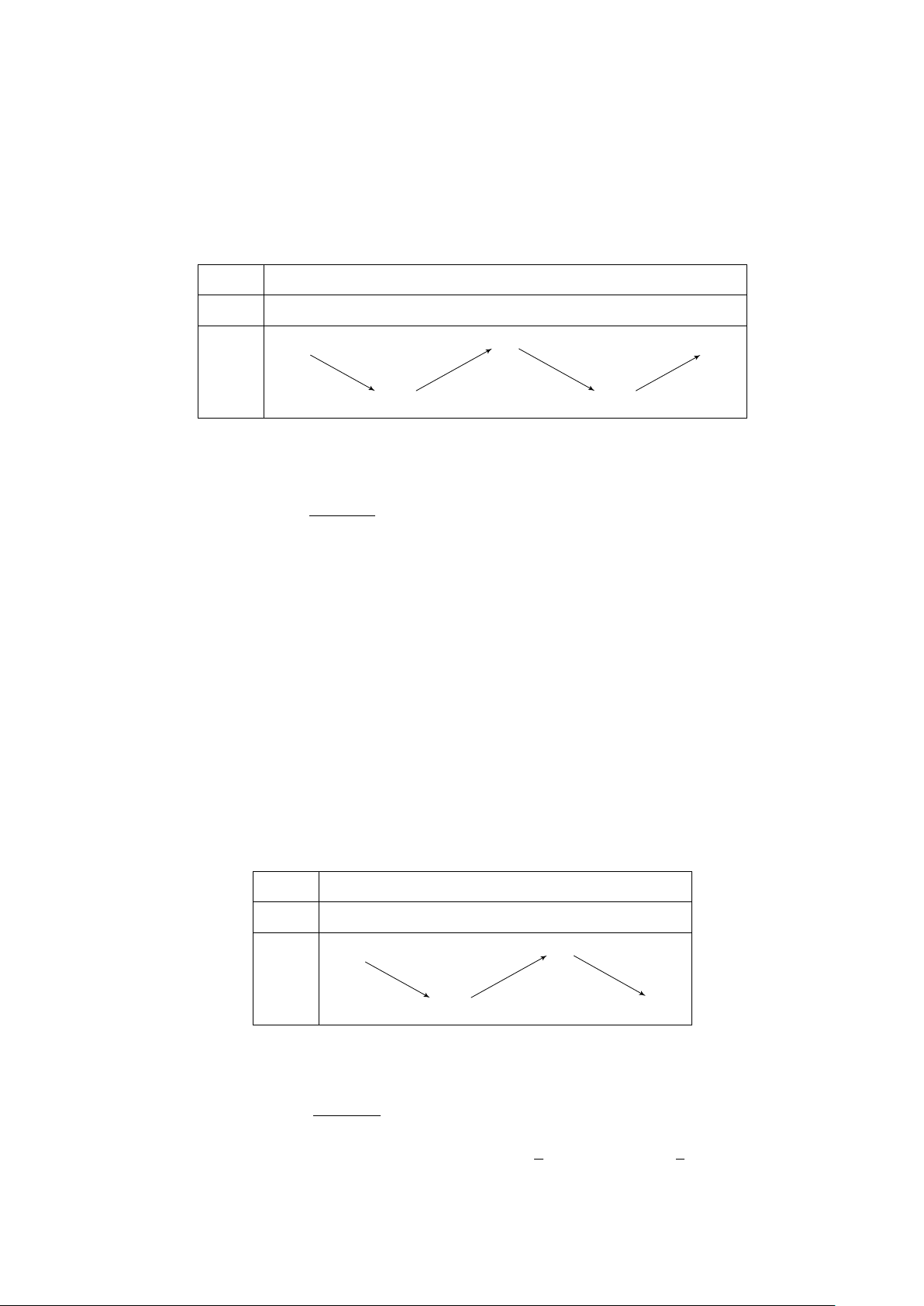
Câu 11. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 0 1 +∞ y′ − 0 + 0 − 0 + +∞ + 1 +∞ + y −2 −2
Hàm số có bảng biến thiên như trên là A. y = x3 − x − 2.
B. y = −x4 + 2x2 + 1. C. y = 3x4 − 6x2 + 1. D. y = x3 − x + 1. −3n + 2 Câu 12. Giá trị của lim bằng n→+∞ n + 1 A. 1. B. 2. C. −3. D. +∞.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Khảo sát một nhóm 50 học sinh ở một trường trung học người ta thấy rằng: có 20 học
sinh giỏi Ngoại ngữ, 15 học sinh giỏi Tin học, 10 học sinh giỏi cả Ngoại ngữ và Tin học. Chọn
ngẫu nhiên một học sinh từ nhóm đó.
a) Xác suất để chọn được học sinh giỏi Ngoại ngữ bằng 0,3.
b) Xác suất để chọn được học sinh giỏi Tin học bằng 0,4.
c) Xác suất để chọn được học sinh giỏi Ngoại ngữ hoặc Tin học bằng 0,6.
d) Xác suất để chọn được học sinh không giỏi Ngoại ngữ hoặc Tin học bằng 0,5.
Câu 2. Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình dưới đây: x −∞ 0 4 +∞ y′ − 0 + 0 − +∞ + 5 y −3 −∞
a) Hàm số y = f (x) nghịch biến trên khoảng (3; 5).
b) Hàm số y = f (x) có đúng 1 điểm cực đại. x − 4
c) Đồ thị hàm số g(x) =
có đúng 2 đường tiệm cận đứng. f (x) − 5 1 1
d) Giá trị nhỏ nhất của hàm số g(x) = f (4x − x2) + x3 − 3x2 + 8x + trên đoạn [1; 3] bằng 3 3 12. Trang 2/4 − Mã đề 0102
Câu 3. Một ô tô đang chuyển động thẳng đều với vận tốc v0 m/s thì người lái xe đạp phanh. Từ
thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = −5t + 20
m/s, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Z a)
(−5t + 20)dt = −5t2 + 20t + C. b) v0 = 15 m/s.
c) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 4 giây.
d) Quãng đường từ lúc đạp phanh cho đến khi xe dừng hẳn là 50 m.
Câu 4. Cho khối chóp cụt tứ giác đều ABCD.A′B′C′D′ z
có chiều cao bằng 3 cm, diện tích hai đáy lần lượt bằng A B
72 cm2 và 18 cm2. Gọi I, O tương ứng là tâm của hai D I C
đáy ABCD và A′B′C′D′. Chọn hệ trục toạ độ Oxyz, với
đơn vị trên mỗi trục là cm sao cho tia Ox cùng hướng −−→ −−→ B′ A′
với vectơ OD′, tia Oy cùng hướng với vectơ OC′, tia Oz − → O
cùng hướng với vectơ OI (như hình vẽ). D′ C′ x y
a) Tọa độ của điểm D′ là (6; 0; 0).
b) Phương trình mặt phẳng (ABCD) là z = 3. √
c) Khoảng cách từ O đến mặt phẳng (BCC′B′) bằng 3 3 cm.
d) Hai mặt phẳng (BCC′B′) và (DCC′D′) tạo với nhau một góc lớn hơn 71 độ.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Một đường dây điện được nối từ một nhà máy điện ở A (nằm tại bờ biển là đường thẳng
AB) đến một hòn đảo C, khoảng cách ngắn nhất từ đảo về bờ biển là đoạn BC dài 1 km, khoảng
cách từ B đến A là 4 km được minh họa bằng hình vẽ dưới đây. C B S A
Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất
3000 USD. Hỏi điểm S trên bờ cách A bao nhiêu km để khi mắc dây điện từ A qua S rồi đến C có chi phí là ít nhất? Câu 2.
Một hộp quà có dạng khối hộp chữ nhật ABCD.A′B′C′D′ có đáy
là hình vuông, BD = 2 dm, số đo của góc phẳng nhị diện của góc nhị diện
[A′, BD, A] bằng 30◦. Nếu các mặt của vỏ hộp quà có độ dày bằng nhau và
bằng 0,5 cm thì phần bên trong của hộp quà đó có thể tích bằng bao nhiêu cm3
(kết quả được làm tròn đến hàng đơn vị)? Trang 3/4 − Mã đề 0102
Câu 3. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5%/tháng theo hình
thức lãi kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi
suất 6%/năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 2 năm 3 tháng kể
từ lúc bắt đầu gửi tiết kiệm là bao nhiêu triệu đồng (kết quả được làm tròn đến hàng đơn vị)? √ax2 + 1 − bx − 2 Câu 4. Cho hàm số f (x) =
(với a, b là các hằng số). Biết rằng f (x) liên tục x3 − 3x + 2
tại điểm x = 1. Giá trị của f (1) bằng bao nhiêu?
Câu 5. Trong không gian Oxyz (đơn vị đo lấy theo km), radar D
phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không
đổi từ điểm A(800; 500; 7) đến điểm B(940; 550; 8) trong 10 phút. B
Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ
của máy bay sau 10 phút tiếp theo là D(x; y; z). Khi đó, x + y + z Ø A bằng bao nhiêu?
Câu 6. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ
(đơn vị: mg/l) của thuốc trong máu sau x phút (kể từ khi bắt 30x
đầu tiêm) được xác định bởi công thức C(x) = . Để đưa x2 + 3
ra lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm
khoảng thời gian mà nồng độ của thuốc trong máu đang tăng.
Trong khoảng thời gian 6 phút sau khi tiêm, nồng độ thuốc
trong máu đạt giá trị lớn nhất bằng bao nhiêu mg/l (kết quả
được làm tròn đến hàng phần mười)? HẾT Trang 4/4 − Mã đề 0102 Đ S SS Đ SS 124 A A B C D A D D C B S Đ 57 -1 SSS 8,7 ĐĐ Đ S 3,25 824 1689 S SS Đ 122 B C B CA D A B A A SSS -1 57 Đ ĐĐ 8,7 ĐĐ S SSS 3,25 824 1689 S S Đ SS 120 D D A D C CD D D D D ĐĐ ĐĐ Đ 57 -1 SSS 3,25 824 1689 8,7 SS SS Đ SS Đ 118 A C D D AAAA D D A D C 57 -1 SS ĐĐ ĐĐ 8,7 S SSS 824 1689 3,25 Đ SS SS SS 116 C B B A B A D BB A Đ 57 -1 SSS ĐĐ 8,7 ĐĐ 3,25 824 1689 Đ S SS SS Đ 114 B D B D B D DACDA BC D A -1 57 SSS ĐĐ ĐĐ SS 1689 8,7 824 3,25 Đ SS SS 112 D D C D B D BBB D C SSS 57 -1 SSS ĐĐ ĐĐ 8,7 S Đ 1689 3,25 824 Đ SS S Đ SS 110 D B C B D D A D S 57 -1 SSS ĐĐ 8,7 ĐĐ S 824 1689 3,25 Đ SS S 108 A C BCBB A D D SSS -1 57 SSS ĐĐ ĐĐ 8,7 S 1689 824 3,25 S SS ĐĐ Đ SS Đ 106 CA A D A B DA D S -1 57 SS 8,7 ĐĐ Đ SSS 1689 824 3,25 S SS SS Đ 104 D C B C A Đ -1 57 S ĐĐ 8,7 ĐĐ SSS 3,25 1689 824 Đ SS S Đ SS 102 DB CA C D D B CCB CBCCCB S 57 -1 SSS ĐĐ 8,7 S ĐĐ 3,25 824 1689 đề Mã Đ SS S S Đ 123 D C A B D A ĐĐĐ S ĐĐ 489 766 64 1 ĐĐ S 0,75 10,6 ÁP ÁN TOÁN 12 SS S ĐĐ Đ Đ S 121 B BA D D DA A D BBC B S ĐĐ 1 64 Đ S ĐĐĐ 489 766 ĐĐ S 10,6 0,75 S ĐĐ SS ĐĐ 119 BBCBCBCC D C B A A A CBBCCBB A B S ĐĐ S 489 1 766 64 Đ ĐĐ S Đ 10,6 0,75 S SS Đ ĐĐ 117 D BCBCCBBCCC C A A B CD B C A B A S S 64 1 ĐĐ Đ ĐĐĐ 766 489 S 10,6 0,75 S SS ĐĐ Đ S 115 D B A D A C D A A S Đ 64 1 ĐĐ Đ ĐĐĐ 489 766 S 10,6 0,75 S S ĐĐ Đ Đ S ĐĐ 113 BC B DB C B B B D A C S S S 64 1 Đ Đ 766 489 ĐĐ Đ 0,75 10,6 S ĐĐ SS 111 D A D A D CCC D ĐĐĐ ĐĐ S 1 489 766 64 S Đ ĐĐ 10,6 0,75 Đ SS S S Đ Đ 109 C C DC A C CD D CB A D S ĐĐĐ S 489 64 1 766 ĐĐ Đ S Đ 10,6 0,75 SS SS 107 A A A B B A A A A ĐĐĐ ĐĐĐ 64 489 766 1 S ĐĐ S ĐĐ 10,6 0,75 Đ S ĐĐ SS S Đ 105 A A C D A B B BCBB A S Đ S 1 64 489 766 Đ ĐĐ Đ 10,6 0,75 ĐĐ S S S Đ Đ 103 C D C BBBBCC D BBB D D ĐĐĐ S S 489 766 64 1 ĐĐ Đ Đ 10,6 0,75 SS S ĐĐ ĐĐ 101 D BBB A BA A A AC BD A D B D ĐĐ S S ĐĐ 64 1 S 766 489 Đ Đ S 0,75 10,6 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 1 2 3 4 5 6 Câu HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Tất cả các nghiệm của phương trình sin x = 0là A. π
x = + kπ , k ∈ .
B. x = k2π , k ∈ . 2
C. x = π + k2π , k ∈ .
D. x = kπ , k ∈ . Lời giải Chọn D
Phương trình ⇔ x = kπ , k ∈ .
Vậy nghiệm phương trình là x = kπ , k ∈ .
Câu 2. Trong không gian Oxyz , cho hai điểm A(1;2;3) , B( 2;
− 4;0). Trung điểm của đoạn thẳng AB có tung độ là A. 1. B. 3. C. 2 . D. 1 − . Lời giải Chọn B G y + y +
ọi I là trung điểm của đoạn thẳng AB . Khi đó A B y = 2 4 = = 3. I 2 2 Câu 3. Giá tr n − ị của 2 3 lim bằng n→+∞ n +1 A. 2 . B. 3 − . C. 1. D. +∞ . Lời giải Chọn A 3 2 − Ta có 2n − 3 lim = lim n 2 = = 2 . n→+∞ n +1 x→+∞ 1 1+ 1 n
Câu 4. Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường cao tốc
trong một khoảng thời gian ở bảng sau:
Tốc độ (km/h) [75;80) [80;85) [85;90) [90;95) [95;100) Số xe 15 22 28 34 19
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng? A. 100 km/h. B. 25 km/h. C. 5 km/h. D. 75 km/h. Lời giải Chọn B
Khoảng biến thiên của mẫu số liệu ghép nhóm trên: R =100 − 75 = 25.
Câu 5. Trong không gian Oxyz , điểm M (1; 3
− ;2) thuộc mặt phẳng có phương trình nào sau đây?
A. 2x + y − z + 3 = 0 .
B. 3x − y + z − 2 = 0 .
C. 2x + y − z + 4 = 0 .
D. x − 2y − z +1 = 0 . Lời giải Chọn A
Điểm M thuộc mặt phẳng 2x + y − z + 3 = 0 .   
Câu 6. Trong không gian Oxyz , cho hai vectơ u = (2;0; 2 − ), v = ( 1; − 1; − 6) . Tích vô hướng . u v bằng A. 14 − . B. 1. C. 0 . D. 4 . Lời giải Chọn A  Ta có . u v = 2.(− ) 1 + 0.(− ) 1 + ( 2 − ).6 = 14 − .
Câu 7. Hàm số nào sau đây đồng biến trên  .? A. 3
y = x + 3x . B. 3
y = x − 3x . C. x −1 y = . D. 4 2
y = x − 3x +1. x +1 Lời giải. Chọn A Ta có với 3
y = x + 3x thì 2
y′ = 3x + 3 > 0, x ∀ .
Câu 8. Cho hàm só f (x) có đạo hàm liên tục trên đoạn [a;b] và f (a) = 2, − f (b) = 4 − . Giá trị của b
∫ f ′ x x bằng a ( )d A. 2. B. -2. C. -6. D. 6. Lời giải. Chọn B
Ta có ∫ f ′(x)dx = f (x) b b
= f b − f a = − . a ( ) ( ) 2 a
Câu 9. Họ nguyên hìm của hàm số f (x) = sinx + 2 là
A. −cosx + 2x + C .
B. cosx + 2x + C .
C. sinx + 2x + C .
D. cosx + C . Lời giải. Chọn A
Câu 10. Bạn Chi rất thích nhảy hiện đại. Thời gian tâp nhảy trong môt sô ngày gần đây của bạn Chi được
thống kê lại bằng bảng sau:
Thời gian (phút) (20;25) (25;30) (30;35) (35;40) (40;45) Số ngày 6 6 4 1 1
Phương sai của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào dưới đây? A. 33. B. 34,77. C. 32. D. 31,24. Lời giải. Chọn B
Cỡ mẫu n = 6 + 6 + 4 +1+1 =18. 45 55 65 75 85 .6 + .6 + .4 + .1+ .1 Giá tr 2 2 2 2 2 85 ị trung bình x = = . 18 3 Phương sai 2 2 2 2 2  45 85   55 85   65 85   75 85   85 85 6 6 4 1 1  − + − + − + − + −           2  2 3   2 3   2 3   2 3   2 3 s  = x  35,156 18
Câu 11. Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số có bảng biến thiên như trên là A. 4 2
y = −x + 2x . B. 4 2
y = 3x − 6x + 3. C. 3
y = x − x . D. 3
y = x − x + 3. Lời giải. Chọn B
Đồ thị hàm số đã cho là đồ thị hàm bậc 4, ta kiểm tra được đồ thị ở câu B thỏa mãn yêu cầu bài toán. Câu 12. x −
Đường thẳng nào là đường tiệm cận đứng của đồ thị hàm số 5 1 y = ? x + 2
A. x = 5.
B. y = 5.
C. x = 2 . D. x = 2 − . Lời giải. Chọn D
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 01 đến câu 04. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Khảo sát một nhóm 50 học sinh ở một trường trung học người ta thấy rằng: có 20 học sinh giỏi
Ngoại ngữ, 15 học sinh giỏi Tin học, 10 học sinh giỏi cả Ngoại ngữ và Tin học. Chọn ngẫu nhiên
một học sinh từ nhóm đó.
a) Xác suất để chọn được học sinh giỏi Ngoại ngữ hoặc Tin học bằng 0,7 .
b) Xác suất để chọn được học sinh giỏi Tin học bằng 0,3.
c) Xác suất để chọn được học sinh giỏi Ngoại ngữ bằng 0,4 .
d) Xác suất để chọn được học sinh không giỏi Ngoại ngữ hoặc Tin học bằng 0,3. Lời giải
SAI – ĐÚNG – ĐÚNG – SAI.
(a) Để tính xác suất của biến cố "học sinh giỏi Ngoại ngữ hoặc Tin học" (tức là A∪ B ), ta sử
dụng công thức: P(A∪ B) = P( )
A + P(B) − P(A∩ B). Với: n A
- Xác suất chọn được học sinh giỏi Ngoại ngữ: P( A) ( ) 20 = = = 0,4. N 50 n B
- Xác suất chọn được học sinh giỏi Tin học: P(B) ( ) 15 = = = 0,3. N 50 n A∩ B
- Xác suất chọn được học sinh giỏi cả Ngoại ngữ và Tin học: P( A∩ B) ( ) 10 = = = 0,2. N 50
Vậy P(A∪ B) = 0,4 + 0,3− 0,2 = 0,5. Chọn Sai.
(b) Như đã tính ở trên, xác suất chọn được học sinh giỏi Tin học là P(B) = 0,3. Chọn Đúng.
(c) Tương tự, xác suất chọn được học sinh giỏi Ngoại ngữ là P( ) A = 0,4. Chọn Đúng
(d) Biến cố "học sinh không giỏi Ngoại ngữ hoặc Tin học" là biến cố đối của biến cố "học sinh
giỏi Ngoại ngữ hoặc Tin học". Tức là, ta cần tính xác suất của biến cố A∪ B .
Ta có P( A∪ B) =1− P(A∪ B) =1−0,5 = 0,5. Chọn Sai.
Câu 2. Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình dưới đây
a) Hàm số y = f (x) có 2 điểm cực trị.
b) Hàm số y = f (x) đồng biến trên ( 3 − ;5) . c) x − 4
Đồ thị hàm số g ( x) =
có 3 đường tiệm cận. f (x) −5 d) Giá tr 1 1
ị lớn nhất của hàm số g ( x) = f ( 2 4x − x ) 3 2
+ x − 3x + 8x + trên đoạn [1; ] 3 bằng12. 3 3 Lời giải
ĐÚNG – SAI –– ĐÚNG – ĐÚNG.
(a) Hàm số đã cho có hai điểm cự trị tại x = 0 và x = 4. Chọn Đúng.
(b) Dựa vào bẳng biến thiên ta thấy, hàm số đã cho đồng biến trên khoảng(0;4) . Chọn Sai. (c) Xét hàm s x − 4 ố g ( x) = f (x) − 5
Từ bảng biến thiên, ta thấy phương trình f (x) = 5 có một nghiệm x = 5 và một nghiệm − − x = a < 0. Nh x 4 x 4 ận thấy rằng lim = +∞ và lim
= +∞ . Vậy đồ thị hàm số đã cho x a+ → f (x) −5 x 5+ → f (x) −5 có hai tiệm cận đứng. x − 4 Ta cũng có lim
= , do tử số là đa thức bậc nhất trong khi mẫu số là đa thức bậc ba.
x→±∞ f ( x) 0 − 5
Vậy đồ thị hàm số đã cho có một đường tiệm cận ngang.
Tóm lại, đồ thị hàm số đã cho có ba đường tiệm cận. Chọn Đúng. (d) Xét hàm s 1 1
ố g ( x) = f ( 2 4x − x ) 3 2
+ x − 3x + 8x + trên đoạn [1; ] 3 . 3 3 Ta có
g′(x) = (4 − 2x) f ′( 2 4x − x ) 2 + x − 6x + 8
= 2(2 − x) f ′( 2
4x − x ) + (x − 4)(x − 2)
= 2(2 − x)  f ′  ( 2
4x − x ) −(x − 4)
Xét hàm số u (x) 2
= 4x − x , trên đoạn [1; ]
3 có 3 ≤ u (x) ≤ 4 suy ra f ′(u(x)) ≥ 0 , hơn nữa
x − 4 < 0 với x ∈[1; ] 3 . Vậy nên f ′( 2
4x − x ) −(x − 4) ≥ 0, x ∀ ∈[1; ]
3 , dấu " = " xảy ra khi x = 4. Trên [1; ]
3 , phương trình g′(x) = 0 có một nghiệm x = 2. Có g ( ) = f ( ) 17 1 3 + 3 g ( ) = f ( ) 19 3 3 + 3
g (2) = f (4) + 7 =12
Do f (3) < f (4) và 17 19 <
< 7 nên giá trị lớn nhất của hàm số g (x) trên đoạn [1; ] 3 bằng 12. 3 3 Chọn Đúng.
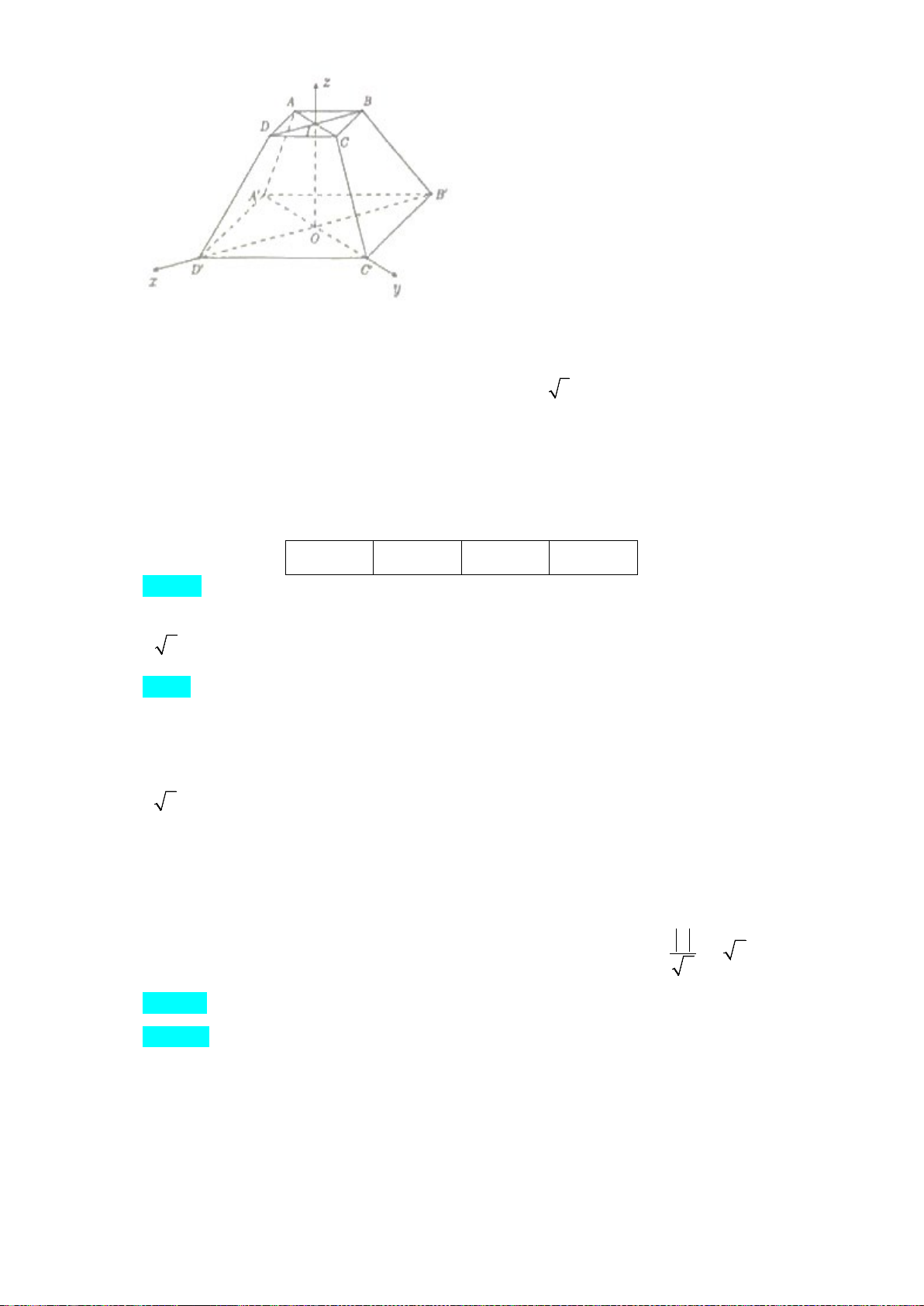
Câu 3. Cho khối chóp cụt tứ giác đều ABCDA'B 'C 'D' có chiều cao bằng 3 cm, diện tích hai đáy lần
lượt bằng 72 cm2 và 18 cm2. Gọi I, O tương ứng là tâm của hai đáy ABCD và A' B 'C ' D ' . Chọn 
hệ trục toạ độ Oxyz , với đơn vị trên mỗi trục là cm sao cho tia Ox cùng hường với véc tơ D' O ,  
tia Oy cùng hướng với véc tơ OC ' , tia Oz cùng hướng với véc tơ OI
a) Toạ độ của điểm B ' là ( 6; − 0;0)
b) Khoảng cách từ O đến mặt phẳng (BCC 'B') bằng 3cm
c) Phương trình mặt phẳng ( ABCD) là x = 3
d) Hai mặt phẳng (BCC 'B') và (DCC 'D') tạo với nhau một góc lớn hơn 70 độ. Lời giải a) Đúng b) Sai c) Sai d) Đúng a)Đúng
Diện tích hình vuông A'B 'C 'D ' bằng 72 cm2 suy ra cạnh hình vuông bằng
6 2 ⇒ A'C ' = B 'D ' =12 ⇒ B '( 6; − 0;0) (b)Sai C '(0;6;0)
Diện tích hình vuông ABCD bằng 18 cm2 suy ra cạnh hình vuông bằng
3 2 ⇒ AC = BD = 6 ⇒ C (0;3;3) 
 
Véc tơ pháp tuyến của mặt phẳng là n = B 'C ', B 'C = 18; 1 − 8;0 1 ( )  
Phương trình mặt phẳng (BCC ' B ') là x − y + 6 = 0
Khoảng cách từ O đến mặt phẳng (BCC ' B ') bằng d (O (BCC B )) 6 , ' ' = = 3 2 2 (c)Đúng (d)Đúng D(3;0;3)   
Véc tơ pháp tuyến của mặt phẳng là n2 = CD,CC ' = ( 9; − 9; − 9 − )   Ta có   n .n =18. 9 − + 18 − . 9
− + 0 = 0 ⇒ góc giữa hai mặt phẳng bằng 900. 1 2 ( ) ( ) ( )
Câu 4. Một ô tô đang chuyển động thẳng đều với vận tốc v m / s 0
thì người lái xe đạp phanh. Từ thời
điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = 5
− t + 20 (m / s)
, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh
a) Thời gian từ lúc người lái xe đạp phanh cho đến khi dừng hẳn là 5 giây.
b) v = 20m / s 0 2 c) ∫(− + ) 5 5 20 − t t dt =
+ 20t + C 2
d) Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là 400m. Lời giải a) Sai
b) Đúng c)Đúng d) Sai a)Sai
Thời gian từ lúc người lái xe đạp phanh cho đến khi dừng hẳn v(t) = 5
− t + 20 = 0 ⇔ t = 4 b)Đúng
v = v(0) = 20m / s 0 c)Đúng 2 ∫(− + ) 5 5 20 − t t dt =
+ 20t + C 2 d)Đúng Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là 4 4 2 = ∫(− + )  5 −  5 20 t s t dt = 
+ 20t  = 40m  2 0  0
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Câu 1. Một đường dây điện được nối từ một nhà máy điện ở A (nằm tại bờ biển là đường thẳng
AB ) đến một hòn đảo C , khoảng cách ngắn nhất từ đảo về bờ biển là đoạn BC dài 1 km, khoảng
cách từ B đến A là 4 km được minh họa bằng hình vẽ dưới đây.
Biết rằng mỗi km dây điện đặt dưới nước chi phí mất 5000 USD, còn đặt dưới đất chi phí mất
3000 USD. Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc dây điện từ A qua S rồi đến C có chi phí là ít nhất? Lời giải Trả lời: 3,25
Đặt AS x với 0  x  4 , khi đó BS  4 x và 2 2
CS BC BS  14 x2 .
Chi phí lắp đặt dây điện từ A đến S là P  3000x . 1
Chi phí lắp đặt dây diện từ C đến S là P  5000 14 x2 . 2
Tổng chi phí lắp đặt dây điện là
P P P  3000x 5000 14 x2 . 1 2
Xét hàm f x x    x2 3000 5000 1 4
trên khoảng 0;4. 50004 x
Ta có f x 3000 . 2 x 8x 17
Khi đó f x    x 2 13 0 5 4
 3 x 8x 17  x  . 4
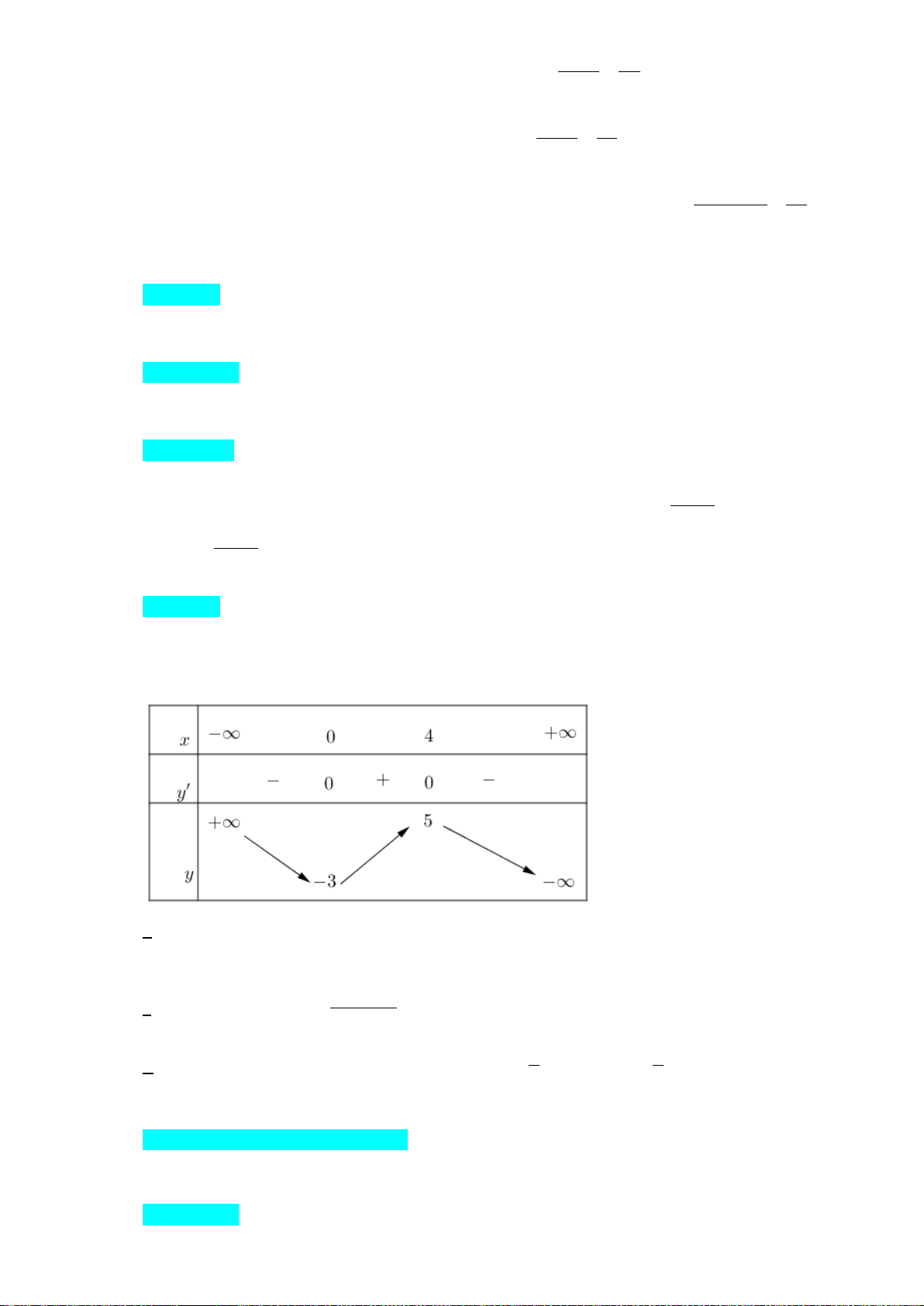
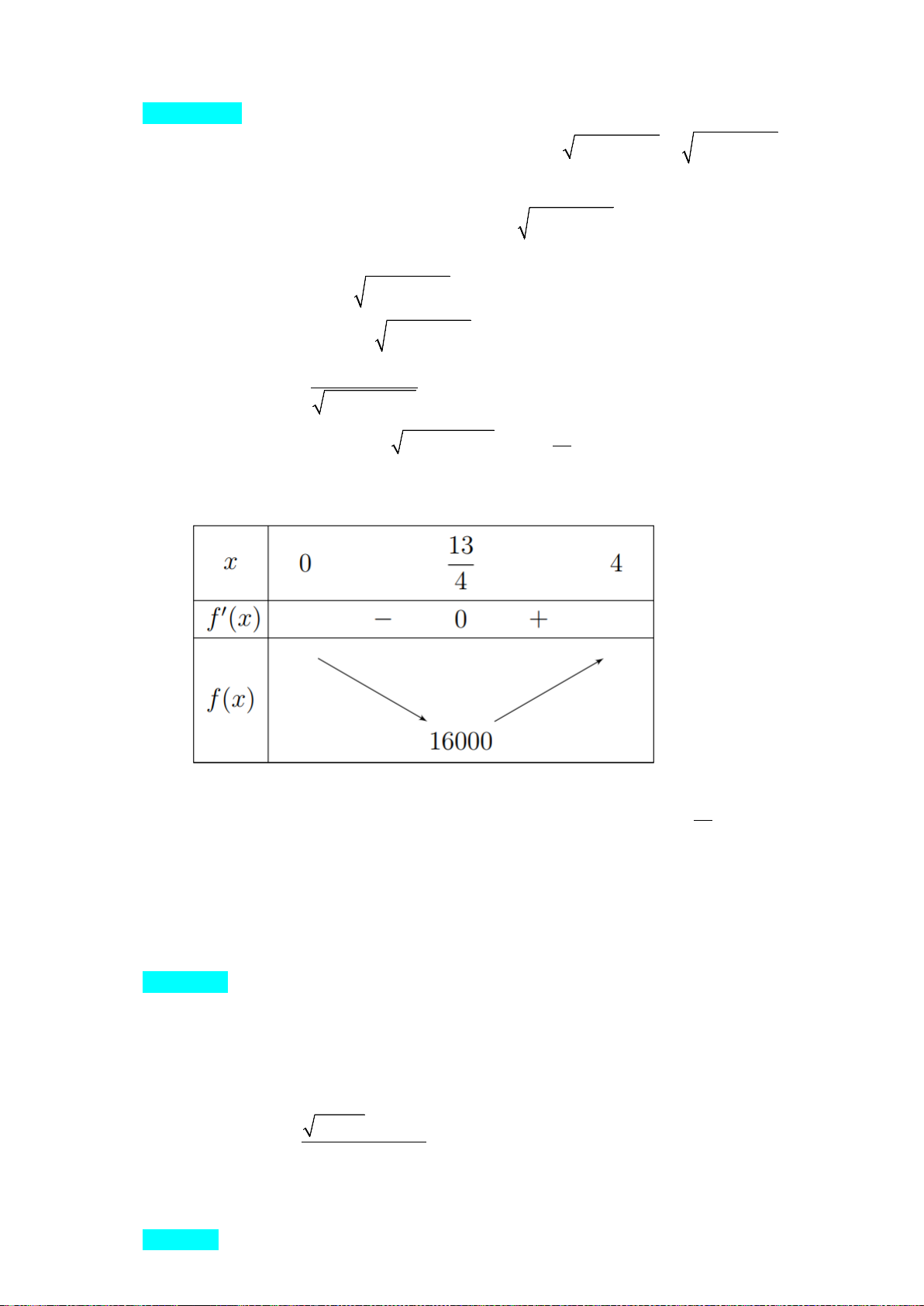
Bảng biến thiên của hàm số f x như sau 13
Vậy để chi phí mắc dây diện là ít nhất thì điểm S cách A một khoảng là  3,25 km. 4
Câu 2. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5% /tháng theo hình thức lãi
kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi suất 6%
/năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 4 năm 3 tháng kể từ lúc bắt
đầu tiết kiệm là bao nhiêu triệu đồng (kết quả làm tròn đến hàng đơn vị)? Lời giải Trả lời: 64
Số tiền ông An thu được sau 3 tháng gửi với lãi suất 0,5% /tháng là   3 50 1 0,5% (triệu đồng).
Số tiền ông An thu được sau 4 năm 3 tháng kể từ lúc bắt đầu tiết kiệm là   3   4 50 1 0,5%
1 6%  64 (triệu đồng). 2 Câu 3.
ax +1 − bx − 2
Cho hàm số f ( x) =
(với a , b là các hằng số). Biết rằng f (x) liên tục tại 3 −x + 3x − 2
điểm x = 1. Giá trị của f ( ) 1 bằng bao nhiêu? Lời giải Trả lời: 1 Ta có 2 2 2 + − + + − + f (x) ax 1 (bx 2) ax 1 (bx 2) = = 3 −x + 3x − 2 −(x − )2 1 (x + 2)( 2 ax +1 + bx + 2) 2 b − a 4b  (a b ) 2 2 2 3 − x + x +  1 x 4bx 3 3 3  − − −   = = . −(x − )2 1 (x + 2)( 2
ax +1 + bx + 2) −(x − )2 1 (x + 2)( 2 ax +1 + bx + 2)
Hàm số f ( x) liên tục tại điểm x =1 ⇔ lim f ( x) = f ( ) 1 (hữu hạn), suy ra x 1 → 2 b − a  3 2 =  1 a = − b − a  2 4b x + x +1 = (x − )2  3  4 1 ⇔  ⇔ 3 3  4b 3 = 2 − b  = − .  3  2 3
Khi đó lim f ( x) = lim = 1. x 1 → x 1 → (   x + ) 3 2 3
2  − x +1 − x + 2 4 2    Giá trị của f ( ) 1 =1. ax
Cách 2: Đặt g (x) 2
= ax +1 − bx − 2 ⇒ g′( x) = − b . 2 ax +1
Hàm số f ( x) liên tục tại điểm x =1 ⇔ lim f ( x) = f ( ) 1 (hữu hạn). x 1 → 
a +1 −b − 2 = 0 g ( x) = 0 Do 
x =1 là nghiệm kép của mẫu nên  ⇔  a . Giải được g′  ( x) = 0 − b =  0  a +1 3 3
a = − ,b = − . 4 2
Câu 4. Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ (đơn vị: mg/l) của thuốc trong máu sau x phút (k 30x
ể từ khi bắt đầu tiêm) được xác định bởi công thức C ( x) =
. Để đưa ra lời khuyên 2 x + 2
và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong
máu đang tăng. Trong khoảng thời gian 6 phút sau khi tiêm, nồng độ thuốc trong máu đạt giá trị
lớn nhất bằng bao nhiêu mg/l (kết quả được làm tròn đến hàng phần mười)? Lời giải Trả lời: 10,6 2 Ta có C′(x) 30 − x + 60 = ′ (
nên C (x) = 0 ⇔ x = 2 . x + 2)2 2 Suy ra
C (x) = C ( ) 15 2 max 2 = ≈ 10,6 . (0;6) 2
Câu 5. Một hộp quà có dạng khối hộp chữ nhật ABC . D A′B C ′ D
′ ′ có đáy là hình vuông, BD = 2dm , số
đo của góc nhị diện [ A ,′ BD, A] bằng 30° . Nếu các mặt của vỏ hộp quà đó có độ dày bằng nhau
và bằng 0,6cm thì phần viền bên trong của hộp quà đó có thể tích bằng bao nhiêu 3 cm (kết quả
làm tròn đến hàng đơn vị) ? Lời giải Trả lời: 766. Ta có: = 2dm = 20cm BD BD ⇒ AB = = 10 2 cm . 2
Góc nhị diện [A ,′ BD, A] bằng ° ⇒  10 30
AOA′ = 30° ⇒ AA′ = A . O tan 30° = . 3 Gọi MNP .
Q EFGH là khối hộp chữ nhật ruột của hộp quà có đáy là hình vuông, cạnh 6 10
EF = AB − 2.0,6 =10 2 − và chiều cao h = AA′ − 2.0,6 = −1,2. 5 3
Phần viền bên trong của hộp quà đó có thể tích bằng: 2  10 V    = − − ≈ 766 3 cm . MNPQ EFGH  1,2. 0 6 1 2 .   3   5 
Câu 6. Trong không gian Oxyz ( đơn vị lấy theo km ), radar phát hiện một chiếc máy bay di chuyển với
tốc độ và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;8) trong 10phút. Nếu
máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau 10phút tiếp theo là D( ;
x y; z). Khi đó, x − y + z bằng bao nhiêu ? Lời giải Trả lời: 489.
Từ giả thiết ⇒ B là trung điểm của AD .
Suy ra D(1080;600;9) ⇒ x − y + z =1080 −600 + 9 = 489 .
Document Outline

  • de-tap-huan-thi-tot-nghiep-thpt-2025-mon-toan-so-gddt-bac-ninh
    • 24_DE_IN_b0f66
    • DAP_AN_TOAN_1c020
  • 32. SỞ BẮC NINH - L3 - (Thi thử TN THPT 2025 môn Toán)

Tài liệu liên quan: