Đề tham khảo đánh giá tuyển sinh Đại học Công An Nhân Dân năm 2023 môn Toán

BỘ CÔNG AN BÀI THI ĐÁNH GIÁ MÃ BÀI THI CA1
TUYỂN SINH ĐẠI HỌC CÔNG AN NHÂN DÂN NĂM 2023 ĐỀ THI THAM KHẢO
Phần tự luận: TOÁN
(Đề thi có 01 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ tên thí sinh:…………………………………...
Số báo danh:……………………………………..
Câu I. (2 điểm)
1) Tìm giá trị nhỏ nhất của hàm số 3 2
y = x − 6x + 5 trên đoạn [ 1 − ;2]. 4 − x +12
2) Cho hàm số y =
có đồ thị là (C ) , đường thẳng d : y = 2x + m . Chứng x +1
minh rằng d cắt (C ) tại hai điểm phân biệt với mọi giá trị của tham số . m
Câu II. (2 điểm)
1) Tìm số phức z thỏa mãn z − 2z = 2 +15 . i 3x + 2
2) Tìm nguyên hàm của hàm số f ( x) = 2 x + 3x + . 2 Câu III. (2 điểm)
1) Trong mặt phẳng tọa độ Oxy , cho điểm I (1;2) và đường thẳng d : 3x − 4 y +10 = 0.
Viết phương trình đường tròn (C ) có tâm I và tiếp xúc với đường thẳng d. x y −1 z − 3
2) Trong không gian Oxyz , cho đường thẳng d : = = và mặt cầu 1 1 2 − (S) 2 2 2
: x + y + z − 2x + 6z − 6 = 0 . Viết phương trình mặt phẳng ( P) chứa đường thẳng d
sao cho giao tuyến của ( P) và (S ) là đường tròn có bán kính nhỏ nhất. Câu IV. (2 điểm)
1) Cho tập hợp A = {1, 2,, 2 }
0 gồm 20 số nguyên dương đầu tiên. Lấy ngẫu nhiên
hai số phân biệt từ tập .
A Tìm xác suất để tích hai số được chọn là một số chia hết cho 6.
2) Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, 𝐵𝐴𝐶 � = 120o, AB = AC= .
a Tam giác SAB vuông tại B , tam giác SAC vuông tại C , góc giữa hai mặt
phẳng (SAB) và ( ABC ) bằng o
60 . Gọi H là hình chiếu vuông góc của điểm S lên mặt phẳng
( ABC). Chứng minh rằng HB vuông góc AB và tính thể tích khối chóp S.ABC theo . a Câu V. (2 điểm) π 2 2 x sin x
1) Tính tích phân I = d . x ∫
x sin x + cos x 0 x x y
2) Cho các số thực dương x, y thay đổi thỏa mãn: log ( x + y) 2 2 + = log + x . 2 2 y 2 1 1
Tìm giá trị nhỏ nhất của biểu thức P = + . 2 2 x y
--------------------------HẾT--------------------------
Cán bộ coi thi không giải thích gì thêm Trang 1
HƯỚNG DẪN GIẢI VÀ ĐÁP ÁN
ĐỀ THAM KHẢO ĐÁNH GIÁ TUYỂN SINH ĐẠI HỌC CAND NĂM 2023
GIÁO VIÊN: TRƯƠNG VĂN TÂM Câu I. ( 2 điểm)
1. Tìm giá trị nhỏ nhất của hàm số 3 2
y  x  6x  5 trên đoạn  1  ;2. Lời giải Ta có 2
y  3x 12x . x  0  1  ;2   Khi đó 2
y  0  3x 12x  0   . x  4    1  ;2 
Hàm số đã cho liên tục trên đoạn  1
 ;2 và y 
1  2, y0 5 , y2 11  nên suy ra
min y  y2  11  . 1;2 4  x 12
2. Cho hàm số y 
có đồ thị C và đường thẳng d : y  2x  m . Chứng minh rằng d cắt x 1
C tại hai điểm phân biệt với mọi giá trị của tham số m . Lời giải 4x 12
Phương trình hoành độ giao điểm của d và C là
 2x  m . x    1   1 x 1
 4x 12  2x  mx   1 2
 2x m  6x  m 12  0 . 2
Xét phương trình 2 ta có 2 2
  m    m  2 6 4.2.
12  m  4m 132  m  2 128  0 , m  
Suy ra phương trình 2 luôn có hai nghiệm phân biệt với mọi m   . 2 Lại có 2 
1 m  6 
1  m 12  16  0 , m
   nên phương trình 2 có hai nghiệm phân biệt, khác 1
 với mọi m   .
Do đó phương trình  
1 luôn có hai nghiệm phân biệt với mọi m , tức là đường thẳng d luôn cắt
đồ thị C tại hai điểm phân biệt với mọi m   . Câu II. ( 2 điểm)
1. Tìm số phức z thoả mãn z  2z  2 15i . Lời giải
Giả sử số phức cần tìm là z  a  bi , với a , b   . Suy ra z  a  bi .
Theo đề ta có z  2z  2 15i  a  bi  2a  bi  2 15i  a
  3bi  2 15i Trang 2  a   2 a  2        . 3  b 15 b   5  
Vậy số phức cần tìm là z  2  5i . 3x  2
2. Tìm nguyên hàm của hàm số f x  . 2 x  3x  2 Lời giải 3x  2 4x   1 x  2 4 1
Ta có f x      . x   1 x  2 x   1 x  2 x  2 x 1   Suy ra f  x 4 1 4 1 dx       dx  dx  dx   x   x   C .    4ln 2 ln 1 x  2 x 1 x  2 x 1
Lưu ý: Ta có thể dùng “đồng nhất thức” như sau: 3x  2 A B Ax  
2  Bx   1
A Bx 2A B
Giả sử f x       x   1 x  2 x 1 x  2 x   1 x  2 x   1 x   2
A B  3 A  1     Khi đó ta có      
. Suy ra f x 1 4 . 2 A  B  2 B  4   x 1 x  2 Câu III. ( 2 điểm)
1. Trong mặt phẳng toạ độ Oxy , cho điểm I 1;2 và đường thẳng d : 3x  4 y 10  0 . Viết phương
trình đường tròn C có tâm I và tiếp xúc với đường thẳng d . Lời giải 3.1 4.2 10
Khoảng cách từ điểm I đến đường thẳng d là d I , d   1. 3 42 2
Đường tròn C tâm I và tiếp xúc với đường thẳng d có bán kính R  d I , d  1 nên có 2 2
phương trình là x  
1  y  2 1. x y 1  z 3
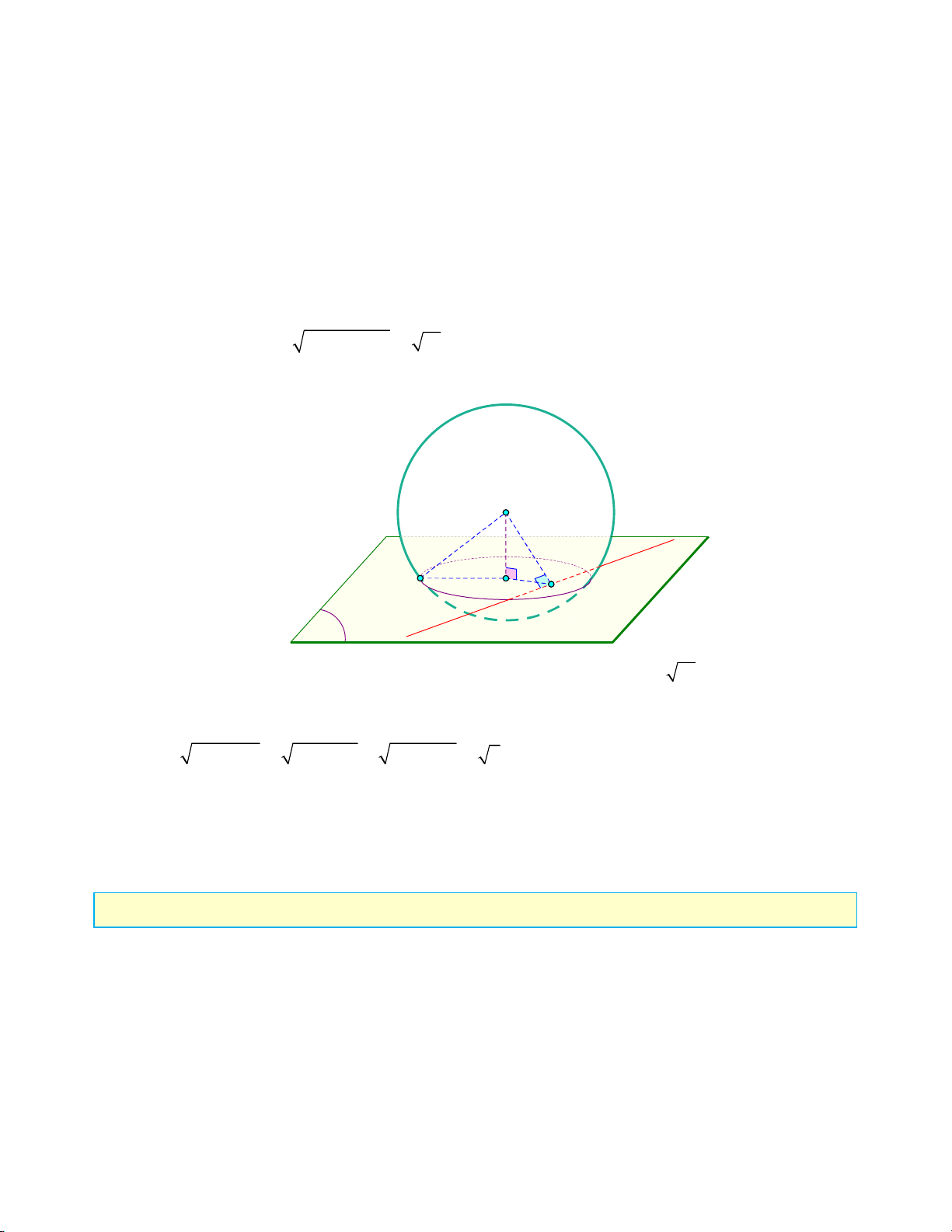
2. Trong không gian với hệ trục toạ độ Oxyz , cho đường thẳng d :   và mặt cầu 1 1 2  S 2 2 2
: x  y  z  2x  6z  6  0 . Viết phương trình mặt phẳng P chứa đường thẳng d sao cho
giao tuyến của P và S  là đường tròn có bán kính nhỏ nhất. Lời giải 2 2 Ta có 2 2 2
x  y  z  x  z    x   2 2 6 6 0
1  y z  
3 16 , suy ra mặt cầu S  có tâm I 1;0; 
3 và bán kính R  16  4 . Trang 3 
Đường thẳng d đi qua điểm A0;1; 
3 và nhận u  1;1; 2 làm vectơ chỉ phương nên có d x  t 
phương trình tham số là y 1 t  .
z  32t 
Gọi H là hình chiếu vuông góc của I lên đường thẳng d  H  d  H t ; 1 t ; 3 2t 
 IH t 1;1 t;6 2t.    
Ta có IH  u  IH . u  0   1 t   1  
1 1 t 26  2t  0  t  2 . Suy ra H 2;3;  1 . d d Ta tính được 2 2 2
IH  1  3  2  14  R nên H nằm trong mặt cầu S  . Do đó d cắt S 
tại hai điểm phân biệt (xem hình vẽ minh hoạ).
(S ) I R d r H K P
Gọi K là hình chiếu vuông góc của I lên P. Khi đó ta có IK  IH  14 .
Do đó, bán kính đường tròn giao tuyến của P và S  là 2 2 2 2 2 2 r 
R  IK  4  IK  4  IH  2
Dấu "  " xảy ra  K  H . 
Khi đó, mặt phẳng P đi qua điểm H 2;3; 
1 và nhận IH  1;3;2 làm vectơ pháp tuyến nên có phương trình là  1 x  2  3 y   3  2z  
1  0  x  3y  2z  9  0 . Câu IV. (2 điểm)
1. Cho tập hợp A  1;2;3;...; 
20 gồm 20 số nguyên dương đầu tiên. Lấy ngẫu nhiên hai số phân biệt từ
tập hợp A . Tính xác suất để tích 2 số được chọn là một số chia hết cho 6 . Lời giải
Chọn hai số phân biệt từ tập hợp A có 2 C 190 cách. 20
Suy ra số phần tử của không gian mẫu là n   190 .
Gọi X là biến cố: "Tích 2 số được chọn là một số chia hết cho 6 " . Trang 4
Nhận thấy rằng trong tập hợp A có
+ 3 số chia hết cho 6 là 6 ; 12; 18 và 17 số không chia hết cho 6 là các số còn lại.
+ 7 số chia hết cho 2 và không chia hết cho 6 là 2; 4;8;10;14;16; 20 .
+ 3 số chia hết cho 3 và không chia hết cho 6 là 3;9;15 .
TH1: Chọn cả hai số đều chia hết cho 6 có 2 C  3 cách. 3
TH2: Chọn một số chia hết cho 6 và một số không chia hết cho 6 có 1 1
C .C  51 cách. 3 17
TH3: Chọn hai số không chia hết cho 6, trong đó có một số chia hết cho 2 và một số chia hết cho 3 có 1 1 C .C  21. 7 3 Suy ra n 
A  3  51 21 75 . Vậy ta có P  75 15 A   . 190 38
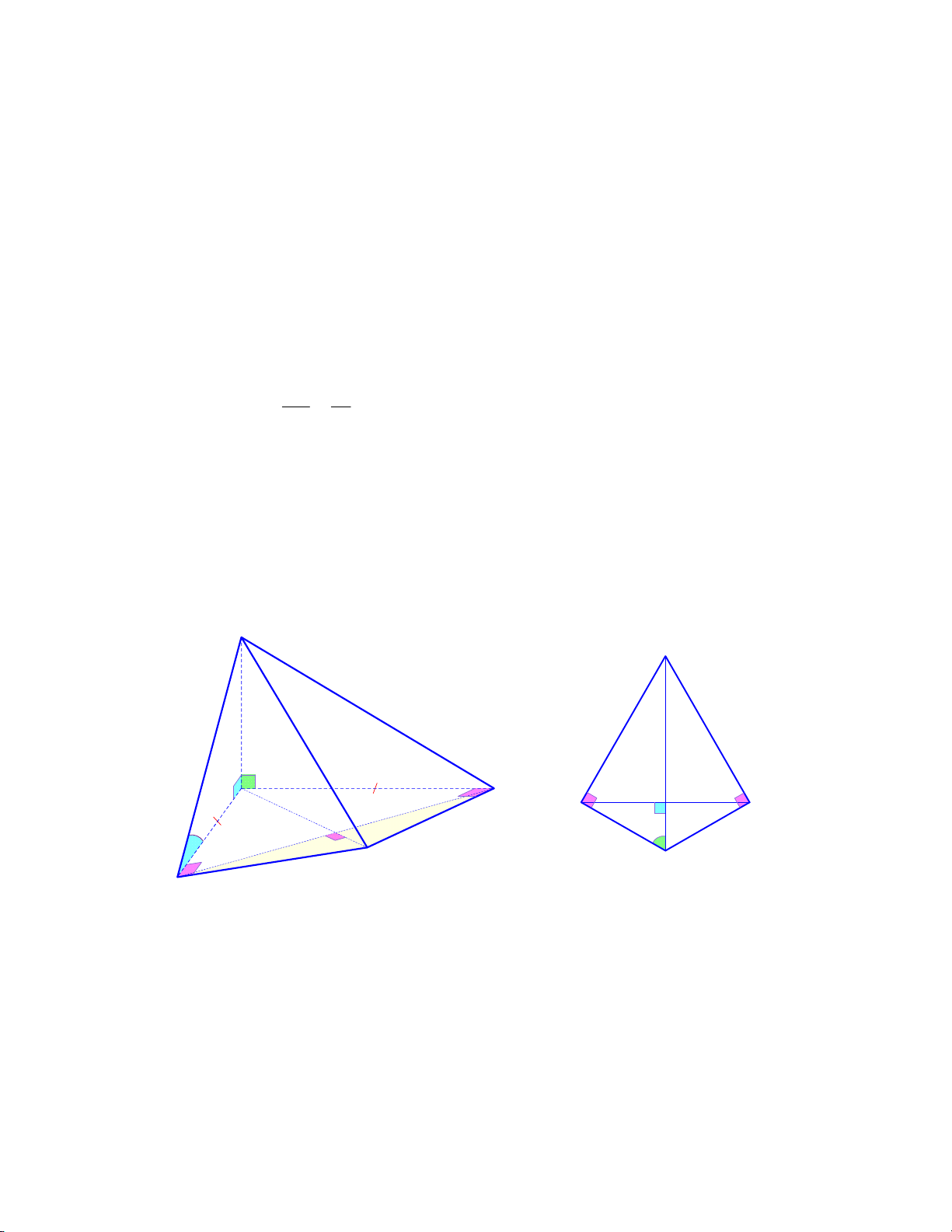
2. Cho hình chóp S.ABCD có đáy ABC là tam giác cân tại A , 
BAC  120 và AB  AC  a . Tam
giác SAB vuông tại B , tam giác SAC vuông tại C , góc giữa hai mặt phẳng SAB và  ABC bằng 60 .
Gọi H là hình chiếu vuông góc của điểm S lên  ABC. Chứng minh rằng HB vuông góc với AB và
tính thể tích khối chóp S.ABC theo a . Lời giải S H H C B K C K a a 60° a A A a B
Ta có H là hình chiếu của S lên  ABC nên SH   ABC  SH  AB .
AB  SB gt  Lúc đó ta có 
 AB  SHB    , mà HB
SHB nên AB HB . (đpcm) AB   SH cmt 
Chứng minh tương tự ta có AC  HC . (xem hình vẽ minh hoạ) 
 SABABCD AB
SHB AB  Ta có   
 SAB ABCD  SB HB   , ,  SBH  60.   SHB 
SAB SB SHB 
ABC HB  Trang 5  2 1 1 a 3
Diện tích tam giác ABC là S  .A .
B AC.sin BAC  . . a . a sin120  . ABC  2 2 4
Xét tam giác ABH vuông tại B ta có  BH  . AB tan BAH  .
a tan 60  a 3 .
Xét tam giác SHB vuông tại H ta có 
SH  BH.tan SBH  a 3.tan 60  3a . 2 3 1 1 a 3 3 a
Vậy thể tích khối chóp S.ABC là V  .S .SH  . .3a  . S . ABC  3 ABC 3 4 4 Câu V. (2 điểm)  2 2 x sin x 1. Tính tích phân dx  .
x sin x  cos x 0 Lời giải   2 2 2 2 x sin x
x sin x  x cos x  x cos x Ta có dx  dx  
x sin x  cos x
x sin x  cos x 0 0    2
xxsin x  cos x 2 2  x cos x x cos x  dx  x dx  dx    .
x sin x  cos x
x sin x  cos x 0 0 0
  I J   2 2 2 2 x  Trong đó I  x dx    . 2 8 0 0    2 2 x cos x
d x sin x  cos x 2 Xét tích phân J  dx 
 ln xsin x  cos x  
x sin x  cos x
x sin x  cos x 0 0 0     
 ln sin  cos ln 0sin 0  cos0  ln ln1 ln . 2 2 2 2 2  2 2 2 x sin x   Vậy ta có
dx  I  J  ln  .
x sin x  cos x 8 2 0   
Lưu ý: Ta có x sin x  cos x  x .sin x  x 
. sin x cos x  sin x  x cos x sin x  x cos x . 2 x x y
2. Cho hai số thực dương x , y thay đổi thỏa mãn log x  y 2   log
 x . Tìm giá trị nhỏ nhất 2 2 y 2 1 1
của biểu thức P   . 2 2 x y Lời giải 2 x x y x
Ta có log x  y 2   log
 x  log x  y 2 2
  log x  log y log 2  x 2 2 2 2 2 2 y 2 y Trang 6 x    x y x y
log x  y 2 2
log y  1 log x  x 2 2  log 
 log x  x .   1 2 2 2 y 2 2 y y
Xét hàm số f t  t  log t , ta có f t 1 1
 0 với mọi t  0 . Do đó hàm số f t đồng 2 t ln 2
biến trên 0;  . 2 x  y x Từ   1 và 2 suy ra 2 2
 x  x  y  x y  y 2 x  
1  x  y  . 2 y x 1 x  2 2 1 1 1 1 2 2 Lúc đó ta có 2 2 P      x  2  2 x .  2  2 2 2 . 2 2 2 2 2 2 x y x x x x 4 2 2 Dấu "  " xảy ra khi 2 4 4 x 
 x  2  x  2 do x   0  y  . 2 x 2 1
-----------------------------------------------------
CHÚC CÁC EM ÔN TẬP VÀ THI TỐT ! Trang 7
Document Outline

• de-tham-khao-danh-gia-tuyen-sinh-dai-hoc-cong-an-nhan-dan-nam-2023-mon-toan
• 2023_Đề tham khảo đánh giá TSCAND 2023