Đề tham khảo tuyển sinh 10 môn Toán 2025 – 2026 phòng GD&ĐT Quận 7 – TP HCM
Một công ty thương mại cần tuyển 2 nhân viên. Có 6 người nộp hồ sơ gồm 4 nam và 2 nữ. Giả sử rằng khả năng ứng xử của 6 người là như nhau. Hỏi công ty có bao nhiêu cách chọn ra 2 người từ 6 người nộp hồ sơ trên? Tính xác suất để hai người trúng tuyển là 1 nam và 1 nữ. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2025-2026 110 tài liệu
Môn: Môn Toán 1.4 K tài liệu
Tác giả:
Preview text:
ĐỀ THAM KHẢO TUYỂN SINH 10
NĂM HỌC 2025 – 2026
Môn: Toán – 120 phút
Bài 1. (1,5 điểm): Cho hàm số: y = x2 có đồ thị là (P). a. Vẽ đồ thị (P).
b. Tìm các điểm M thuộc (P) sao cho tung độ gấp 4 lần hoành độ.
Bài 2. (1,0 điểm) Cho phương trình: 2
3x − 6x − 2 = 0.
a. Chứng minh phương trình có hai nghiệm phân biệt x1, x2. + +
b. Tính giá trị của biểu thức 2x 1 2x 1 1 2 A = + . x x 2 1
Bài 3. (1,5 điểm) Một công ty thương mại cần tuyển 2 nhân viên. Có 6 người nộp hồ sơ gồm 4 nam
và 2 nữ. Giả sử rằng khả năng ứng xử của 6 người là như nhau.
a. Hỏi công ty có bao nhiêu cách chọn ra 2 người từ 6 người nộp hồ sơ trên?
b. Tính xác suất để hai người trúng tuyển là 1 nam và 1 nữ.
Bài 4. (1,0 điểm) Mỗi nơi trên thế giới có một múi giờ. Giờ trong ngày tại mỗi nơi được tính theo
công thức T = GMT + H, trong đó T là giờ tại nơi đó, GMT là giờ gốc, giờ ở múi giờ là 0, H được
xác định bởi bảng sau: Múi giờ 0 1 2 3 4 5 6 7 H 0 1 2 3 4 5 6 7 Múi giờ 8 9 10 11 12 13 14 15 H 8 9 10 11 12 –11 –10 –9 Múi giờ 16 17 18 19 20 21 22 23 H –8 –7 –6 –5 –4 –3 –2 –1
Như vậy, khi biết giờ ở một nơi có múi giờ này, ta có thể tính giờ ở nơi có múi giờ khác.
Múi giờ của một số thành phố được cho bởi bảng sau: Thành phố
Hồ Chí Minh New York Moscow Los Angeles Múi giờ 7 19 3 16
Dựa vào cách tính trên, em hãy tính xem:
a. Lúc 11 giờ ngày 3/6 ở New York thì ở Moscow là mấy giờ, ngày nào? 1
b/ Quỳnh đi chuyến bay từ Thành phố Hồ Chí Minh đến Moscow, xuất phát lúc 14 giờ 30 phút ngày
1/9 theo giờ tại Việt Nam và hạ cánh ở sân bay quốc tế Sheremetyevo của Moscow lúc 21 giờ ngày
1/9. Em hãy tính xem chuyến bay kéo dài bao lâu?
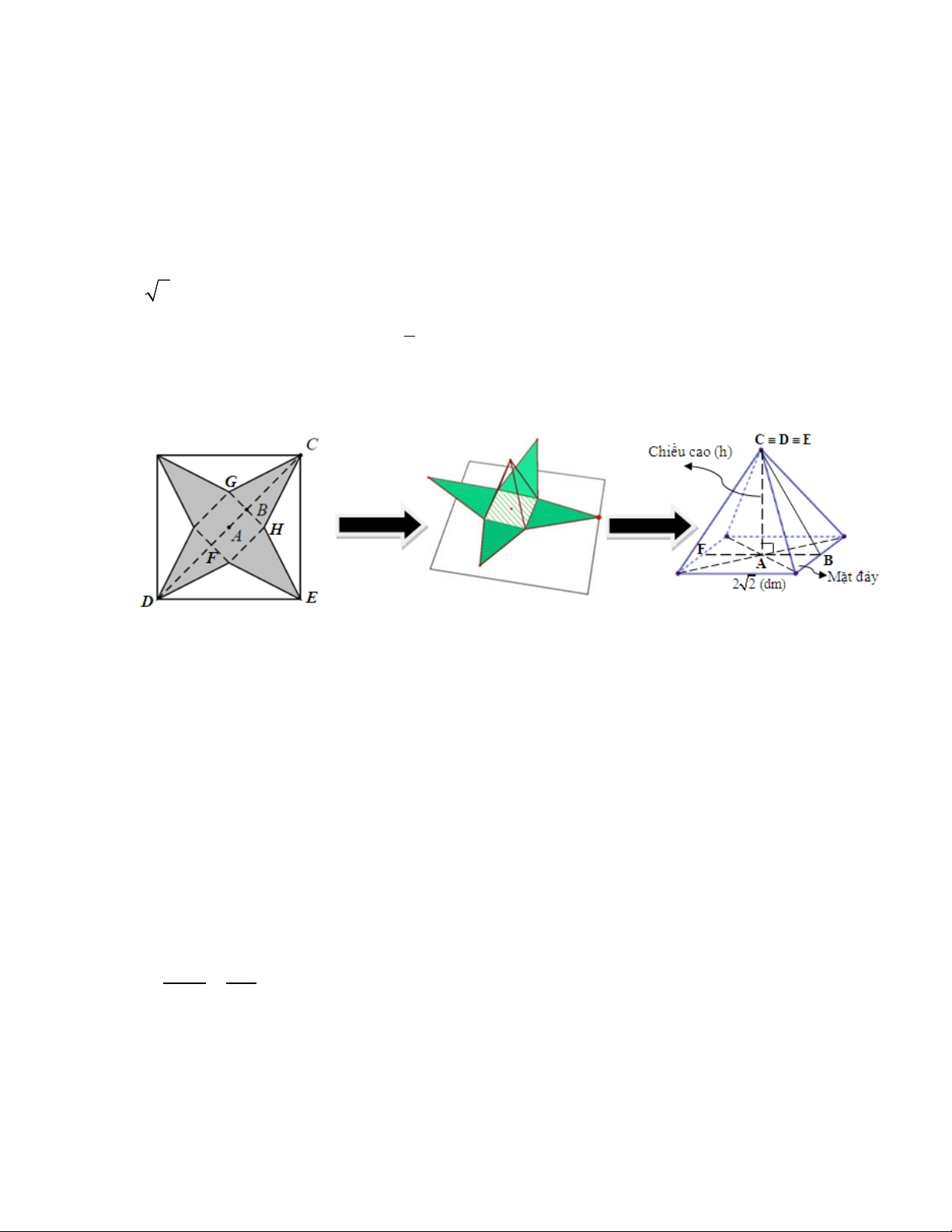
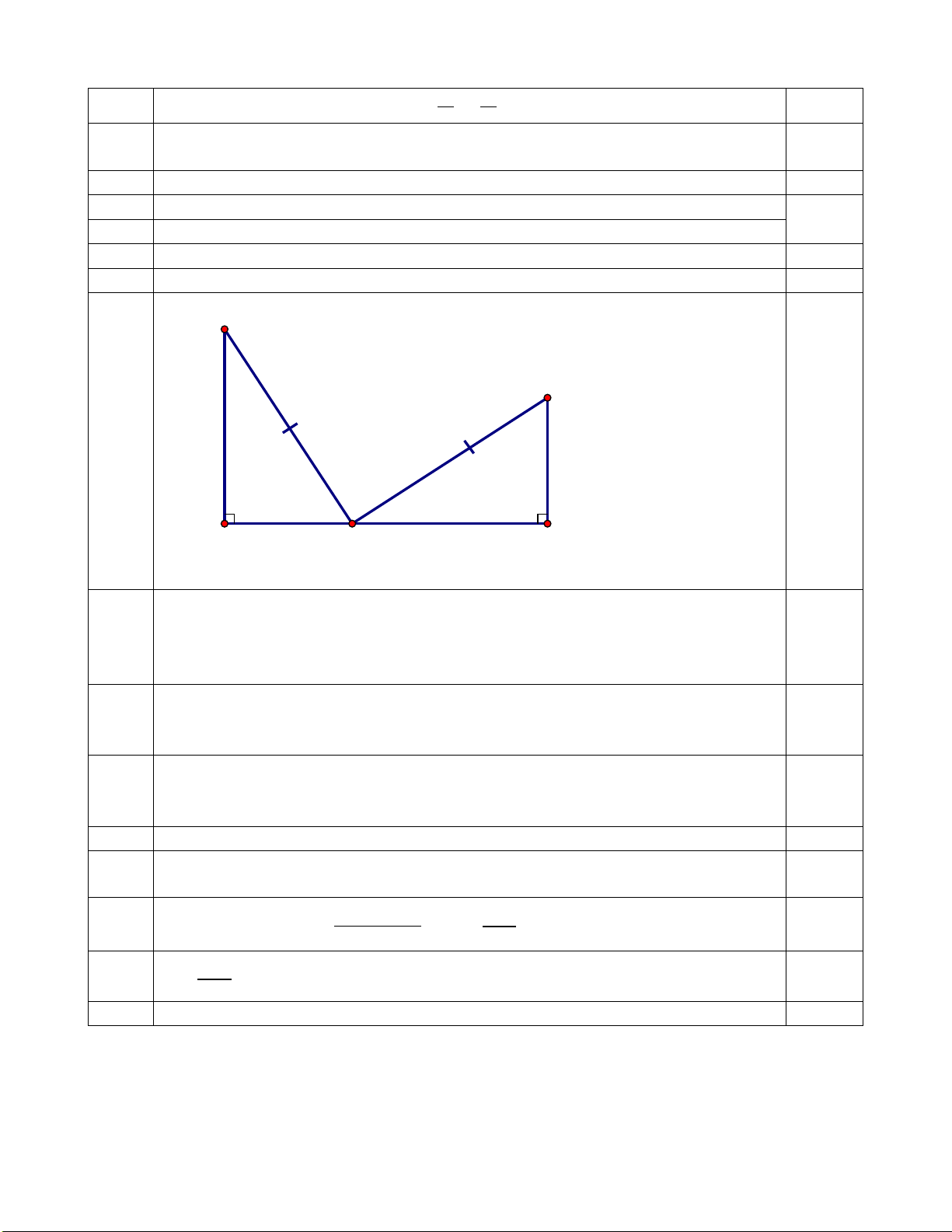
Bài 5. (1,0 điểm) Bạn An làm một mô hình kim tự tháp để giới thiệu về lịch sử Ai Cập cổ đại. Vì kích
thước giới hạn của khu trưng bày, An quyết định làm mô hình kim tự tháp từ một tấm bìa hình vuông
có cạnh là 5 dm. Nhờ sự giúp đỡ của thầy, An đã tạo một mô hình kim tự tháp bằng cách cắt bỏ bốn
tam giác cân bằng nhau có đáy là cạnh của hình vuông rồi gấp lên sau đó ghép lại để thành một hình
chóp tứ giác đều như hình vẽ. An đã cắt miếng bìa trên sao cho cạnh đáy của khối chóp tứ giác đều là
2 2 dm. Em hãy tính thể tích của khối chóp tứ giác đều đó (theo đơn vị dm3), biết thể tích của hình
chóp được tính theo công thức: 1
V = .S.h , trong đó S là diện tích mặt đáy, h là chiều cao hình chóp, 3
các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau,CB ⊥ GH và A là tâm hình vuông.
Bài 6. (1,0 điểm) Anh An là công nhân của khu chế xuất công nghiệp. Trong tháng 5 vừa qua, quản
lí lao động phân xưởng kiểm tra quẹt thẻ cho biết anh An đã làm tổng cộng 212 giờ, trong đó có giờ
làm theo định mức qui định và giờ làm thêm ngoài giờ. Trong định mức, mỗi giờ anh An được trả
công 38 000 đồng. Với mỗi giờ làm thêm, anh được trả 150% của tiền công làm một giờ trong định
mức. Trong tháng 5, lương anh An được lãnh tổng cộng là 8 436 000 đồng. Tính xem anh An đã làm
thêm bao nhiêu giờ ngoài định mức trong tháng 5.
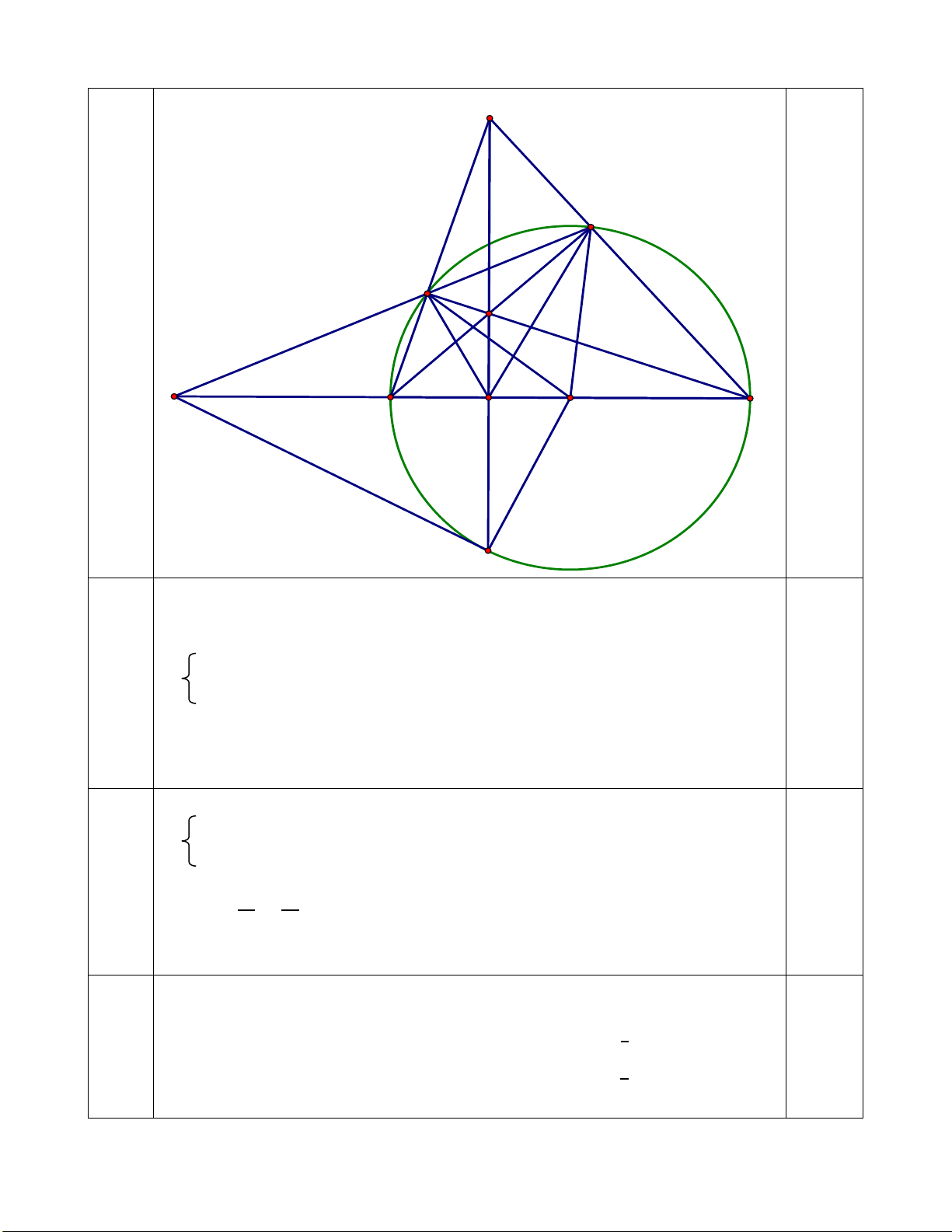
Bài 7. (3,0 điểm) Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn (O). Đường cao
AD của ΔABC cắt đường tròn (O) tại E (E khác A). Từ E vẽ EM vuông góc với đường thẳng AB tại
M. Qua điểm A vẽ tiếp tuyến xy với đường tròn (O); vẽ EK vuông góc với xy tại K (K thuộc xy).
a. Chứng minh tứ giác AKME nội tiếp và = MKE BCE .
b. Tia MD cắt AC tại N. Chứng minh tứ giác DNCE nội tiếp và EN.KM = ND.EK.
c. Đường thẳng KE cắt BC và AB lần lượt tại I và F. Chứng minh MN vuông góc KE và S EI END = . S EF EKM
------------ Hết ------------- 2 ĐÁP ÁN Bài Nội dung Điểm 1
a) Vẽ đồ thị (P). 0.5
b) Gọi M (x ; y là điểm thuộc (P). Theo đề, vì điểm M có tung độ bằng 4 0 0 ) lần hoành độ x = 0 0.5 2 2 0
y = 4x ⇔ x = 4x ⇔ x − 4x = 0 ⇔ 0 0 0 0 0 0 x = 4 0 0.5
Vậy điểm cần tìm là M (0;0) hoặc M (4;16) . 2 Cho phương trình: 2
3x − 6x − 2 = 0 có 2 nghiệm là x ;x . 0.25 1 2 a) Vì . a c = 3.( 2 − ) = 6
− < 0 nên phương trình có 2 nghiệm trái dấu.
b) Theo hệ thức Viéte ta có: 0.25 b
S x x 2 1 2 a c 2
P x .x 0.25 1 2 a 3 Ta có: 2 2 1x +1 2 2 x +1 2( 1x + 2 x ) − 4 1x 2 x + 1x + 2 x A = + = = – 19 0.25 2 x 1 x 1 x 2 x 3
a) Người thứ nhất có 6 cách chọn, người thứ hai có 5 cách chọn. 0.25
Số cách chọn ra 2 người là: 5.6 = 30 0.25
b) Người nam có 4 cách chọn, người nữ có 2 cách chọn. 0.5
Số cách chọn ra 1 nam, 1 nữ là: 4. 2 = 8 0.25
Xác suất là: (8 : 30).100 ≈ 26,7%. 0.25 4
a) 𝑇𝑇𝑁𝑁𝑁𝑁 = 𝐺𝐺𝐺𝐺𝑇𝑇 + 𝐻𝐻
⇒ 11 = 𝐺𝐺𝐺𝐺𝑇𝑇 − 5 (ngày 3/6)
⇒ 𝐺𝐺𝐺𝐺𝑇𝑇 = 16 𝑔𝑔𝑔𝑔ờ (ngày 3/6) 0.25
𝑇𝑇𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀 = 𝐺𝐺𝐺𝐺𝑇𝑇 + 𝐻𝐻 𝑇𝑇
𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀 = 16 + 3 (ngày 3/6) 𝑇𝑇
𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀 = 19 giờ (ngày 3/6) 3
Vậy lúc 11 giờ ngày 3/6 ở New York thì ở Moscow là 19 giờ ngày 3/6. 0.25
b) 𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑀𝑀 = 𝐺𝐺𝐺𝐺𝑇𝑇 + 𝐻𝐻
⇒ 14 𝑔𝑔𝑔𝑔ờ 30 𝑝𝑝ℎú𝑡𝑡 = 𝐺𝐺𝐺𝐺𝑇𝑇 + 7 (ngày 1/9)
⇒ 𝐺𝐺𝐺𝐺𝑇𝑇 = 7 𝑔𝑔𝑔𝑔ờ 30 𝑝𝑝ℎú𝑡𝑡 (ngày 1/9)
𝑇𝑇𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀 = 𝐺𝐺𝐺𝐺𝑇𝑇 + 𝐻𝐻 𝑇𝑇
𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀 = 7 𝑔𝑔𝑔𝑔ờ 30 𝑝𝑝ℎú𝑡𝑡 + 3 𝑔𝑔𝑔𝑔ờ (ngày 1/9) 𝑇𝑇 0.25
𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀 = 10 giờ 30 phút (ngày 1/9)
Vậy lúc 14 giờ 30 phút ngày 1/9 ở TPHCM thì ở Moscow là 10 giờ 30 phút ngày 1/9.
Mà Quỳnh đến sân bay quốc tế của Moscow lúc 21 giờ ngày 1/9.
Vậy chuyến bay kéo dài: 21 giờ – 10 giờ 30 phút = 10 giờ 30 phút. 0.25 5
Áp dụng định lí Pythagore vào tam giác CDE vuông cân tại E, ta có: CD = 5 2 (dm). 0.25 3 2
DF + FB + BC = CD ⇔ 2BC = CD − BF = 5 2 − 2 2 = 3 2 ⇒ BC = (dm) 2 0.25
(Vì BC = DF: tính chất hình chóp tứ giác đều)
Áp dụng định lí Pythagore, ta có: 2 2 2 2 2 2 2 2 2 3 2 2 2
CA + AB = BC ⇔ CA = BC − AB ⇔ h = − 2 2 10 ⇔ h = (dm) 0.25 2
Thể tích của mô hình kim tự tháp là: 1 √10 4√10 𝑆𝑆 = 0.25
3 . �2√2�2. 2 = 3 (𝑑𝑑𝑚𝑚3) 6
Gọi thời gian anh An làm theo giờ định mức là x (giờ) (x > 0).
Thời gian anh An làm ngoài giờ quy định là y (giờ) (y > 0).
Vì tổng thời gian trong tháng anh An làm là 212 giờ nên ta có: x + y = 212 (1) 0.25
Vì tổng số tiền trong tháng nhận được là 8 436 000 đồng nên ta có pt:
38000x 38000.150%y 8436000
⇔ 38x + 57y = 8436 (2) 0.25 x + y = 212 x = 192
Từ (1) và (2) ta có hệ phương trình: ⇔ (nhận) 38 x 57 y 8436 + = y = 20 0.25
Vậy anh An đã làm thêm 20 giờ ngoài giờ định mức. 0.25 4 7 y A K x N F O I B L D C M E
a. Chứng minh A, K, M, E cùng thuộc một đường tròn. 0.25
Vì AKME là tứ giác nội tiếp (cmt) nên 𝐺𝐺𝑀𝑀𝑀𝑀 � = 𝐺𝐺𝑀𝑀𝑀𝑀 � (cùng chắn cung ME 0.25
trong đường tròn ngoại tiếp AKME) Mà 𝐺𝐺𝑀𝑀𝑀𝑀 � = 𝐵𝐵𝐵𝐵𝑀𝑀
� (cùng chắn cung BE trong (O)). 0.25 Vậy 𝐺𝐺𝑀𝑀𝑀𝑀 � = 𝐵𝐵𝐵𝐵𝑀𝑀 �. 0.25
b. Chứng minh tứ giác DNCE nội tiếp và EN.KM = ND.EK.
* Chứng minh được tứ giác BDEM nội tiếp 0.25 ⇒ 𝐺𝐺𝐵𝐵𝑀𝑀 � = 𝐺𝐺𝑀𝑀𝑀𝑀
� (cùng chắn cung ME trong đường tròn ngoại tiếp BDEM) 𝐺𝐺𝐵𝐵𝑀𝑀 � = 𝑀𝑀𝐵𝐵𝑀𝑀
� (vì tứ giác ABEC nội tiếp) ⇒ 𝐺𝐺𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝐵𝐵𝑀𝑀 � 0.25
⇒ tứ giác DNCE nội tiếp. ⇒ 𝑀𝑀𝐷𝐷𝑀𝑀 � = 𝐵𝐵𝐵𝐵𝑀𝑀
� còn 𝐺𝐺𝑀𝑀𝑀𝑀 � = 𝐺𝐺𝑀𝑀𝑀𝑀 � (cmt) ⇒ 𝑀𝑀𝐷𝐷𝑀𝑀 � = 𝐺𝐺𝑀𝑀𝑀𝑀 � 0.25 Chứng minh được 0.25
∆END ~ ∆EKM (g,g) ⇒ EN.KM = ND.EK
c. Chứng minh MN vuông góc KE và S EI END = . S EF EKM
Gọi L là giao điểm của MN và KE.
Ta có: 𝐿𝐿𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝐵𝐵𝑀𝑀 � (DNCE nội tiếp) Mà 0.25 𝑀𝑀𝐵𝐵𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀
� nên 𝐿𝐿𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 �.
Ta có: 𝑀𝑀𝑀𝑀𝑀𝑀 � + 𝑀𝑀𝑀𝑀𝑀𝑀
� = 900 nên 𝐿𝐿𝑀𝑀𝑀𝑀 � + 𝑀𝑀𝑀𝑀𝑀𝑀
� = 900, tức là MN vuông góc KE. 0.25
Áp dụng hệ thức lượng vào tam giác vuông MEF và DEI ta có:
ME2 = EL. EF và DE2 = EL. EI ⇒ 2 DE EI = 2 ME EF 0.25 2 S DE EI
∆END ~ ∆EKM (cmt) ⇒ END = = 2 S ME EF 0.25 EKM
Lưu ý: Khi học sinh giải và trình bày cách khác thì giáo viên dựa trên thang điểm chung để chấm. 5
SỞ GIÁO DỤC VÀ ĐÀO TẠO TUYỂN SINH LỚP 10 THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2025 – 2026
TRƯỜNG TH, THCS VÀ THPT Môn: Toán EMASI NAM LONG
Thời gian làm bài: 120 phút
(không kể thời gian phát đề) ĐỀ THAM KHẢO
(Đề thi có 02 trang)
Bài 1. (1,5 điểm) Cho hàm số y = − x2. 4
a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm các điểm M thuộc đồ thị (P) sao cho tung độ bằng hai lần hoành độ.
Bài 2. (1,0 điểm) Cho phương trình x2 − 4x − 6 = 0.
a) Chứng minh phương trình trên có hai nghiệm phân biệt x1, x2.
b) Không giải phương trình, hãy tính giá trị của biểu thức x1x2 + x1x2. 4−x1 4−x2
Bài 3. (1,5 điểm) Lượng mưa trong một tuần tại Thành phố Hồ Chí Minh được đo mỗi
ngày. Bảng dưới đây thể hiện lượng mưa cao nhất và lượng mưa thấp nhất trong các ngày của tuần. Ngày
Lượng mưa cao nhất (𝐦𝐦𝐦𝐦) Lượng mưa thấp nhất (𝐦𝐦𝐦𝐦) Thứ Hai 25 12 Thứ Ba 32 18 Thứ Tư 40 19 Thứ Năm 37 22 Thứ Sáu 30 20 Thứ Bảy 33 15 Chủ nhật 28 16
a) Trong tuần này, hãy tính số ngày có tổng lượng mưa cao nhất và thấp nhất lớn hơn 50 mm.
b) Chọn ngẫu nhiên một ngày trong tuần, tính xác suất thực nghiệm của các biến cố sau:
A: “Ngày được chọn có lượng mưa cao nhất không vượt quá 30 mm”.
B: “Ngày được chọn có lượng mưa thấp nhất lớn hơn 15 mm”.
Bài 4. (1,0 điểm) Một sân bóng hình chữ nhật có chiều dài là x (đơn vị: mét, x > 0) và chiều
dài hơn chiều rộng là 3 m.
a) Viết biểu thức tính diện tích S của sân bóng theo x.
b) Nếu tăng chiều dài thêm 1 m và tăng chiều rộng thêm 3 m thì diện tích sân bóng tăng gấp
đôi. Tính chiều dài của sân bóng đó. Trang 1/2
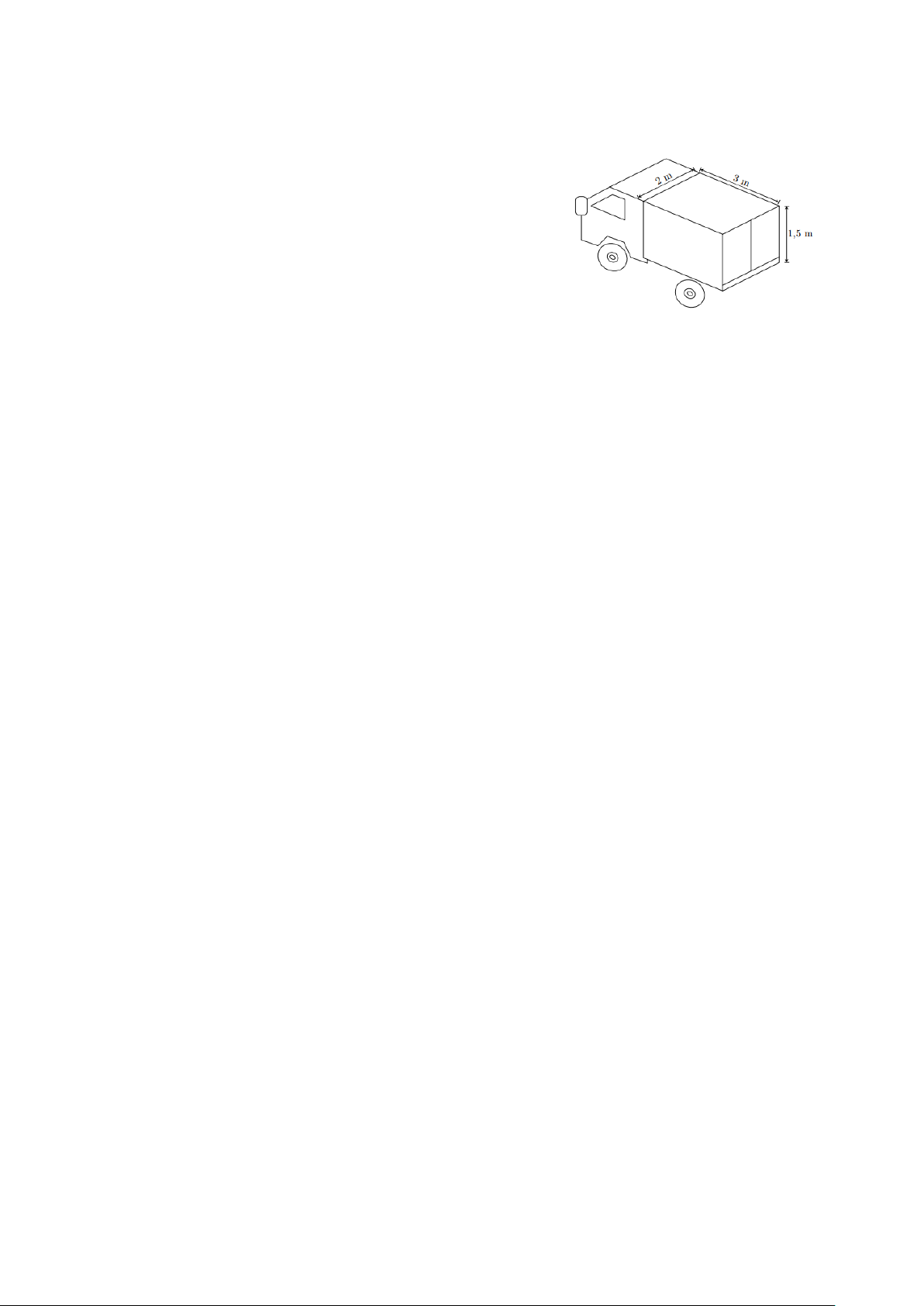
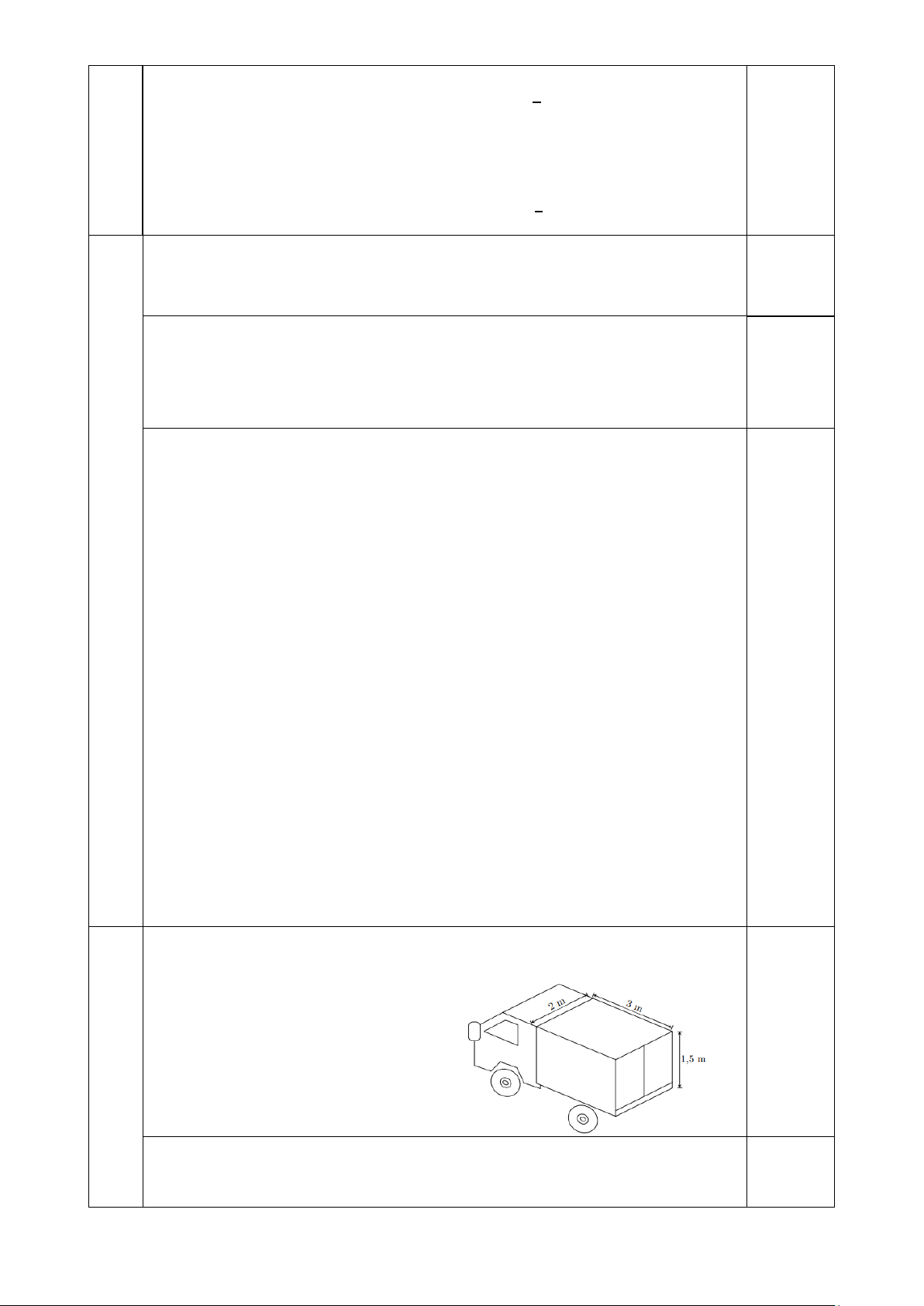
Bài 5. (1,0 điểm) Một xe tải chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên.
a) Hãy tính thể tích của thùng xe (độ dày của thùng xe xem như không đáng kể).
b) Người ta xếp vào thùng xe tải các thùng hàng loại A
có dạng hình lập phương độ dài cạnh 40 cm để vận
chuyển giao hàng. Hỏi mỗi lần vận chuyển xe có thể
chở được nhiều nhất bao nhiêu thùng hàng loại A?
Bài 6. (1,0 điểm) Một xí nghiệp dự tính chuyển hàng bằng hai xe tải và đang phân vân giữa
việc mua hẳn hai chiếc xe tải hoặc thuê hai xe tải. Nếu mua hai xe với giá mỗi xe là
200 000 000 đồng thì mỗi ngày xí nghiệp phải tốn 5 000 000 đồng cho tất cả tài xế và
nhiên liệu. Còn nếu thuê xe thì giá thuê một xe tải là 10 000 000 đồng/ngày (đã bao gồm
tiền công cho tài xế và nhiên liệu).
a) Trong trường hợp xí nghiệp quyết định mua và xe tải mới mua cần phải bảo dưỡng định
kì, xí nghiệp sẽ sử dụng kết hợp cả xe tải mua và xe tải thuê. Khi đó, tổng chi phí vận chuyển
cho một đợt chuyển hàng 300 ngày là 4 tỉ đồng (bao gồm cả tiền mua xe). Hãy tính số ngày
sử dụng xe tải mua và số ngày sử dụng xe tải thuê trong đợt chuyển hàng này.
b) Trong trường hợp xí nghiệp vẫn đang phân vân giữa việc mua xe và thuê xe thì sau bao
nhiêu ngày phương án mua xe sẽ tiết kiệm hơn phương án thuê xe?
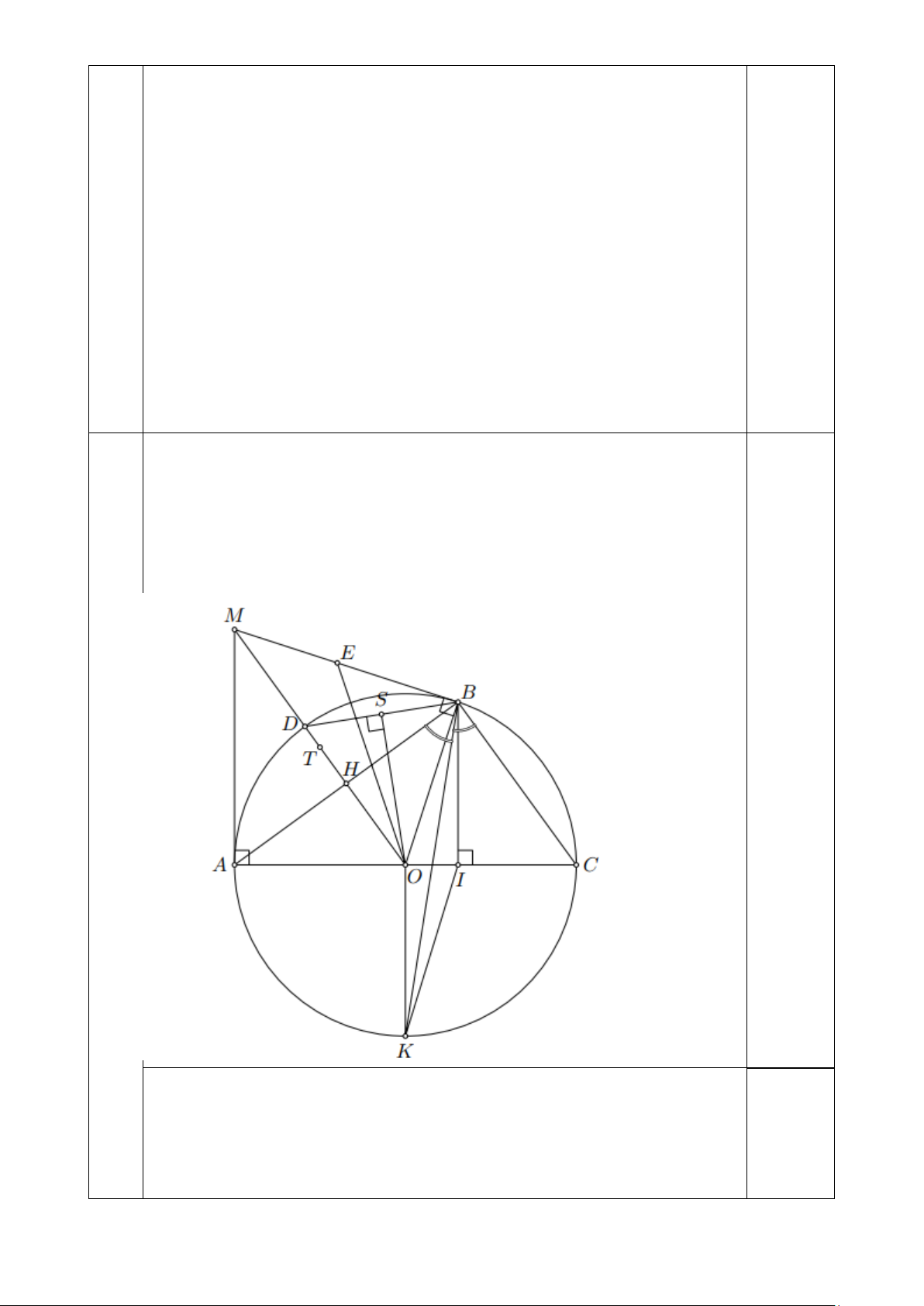
Bài 7. (3,0 điểm) Cho đường tròn (O; R) có đường kính AC và đường thẳng d là tiếp tuyến
của đường tròn (O) tại A. Trên đường thẳng d lấy điểm M khác A sao cho AM > AO. Từ điểm
M vẽ tiếp tuyến MB với đường tròn (O) (B là tiếp điểm, B khác A).
a) Chứng minh bốn điểm M, A, O, B cùng thuộc một đường tròn và OM ⊥ AB.
b) Gọi D là giao điểm của đoạn MO với đường tròn (O). Tia AD cắt đoạn thẳng MB tại E.
Chứng minh rằng EB2 = EA. ED.
c) Đường phân giác trong góc B của tam giác ABC cắt đường tròn (O; R) tại K (K khác B).
Kẻ BI ⊥ AC (I ∈ AC). Đặt BI = x, tính diện tích tam giác BIK theo R và x.
========== HẾT ========== Trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO TUYỂN SINH LỚP 10 THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2025 – 2026
TRƯỜNG TH, THCS VÀ THPT Môn: Toán EMASI NAM LONG
ĐÁP ÁN ĐỀ THI CHÍNH THỨC CÂU NỘI DUNG ĐIỂM 1,5 điểm
Cho hàm số 𝒚𝒚 = − 𝒙𝒙𝟐𝟐. 𝟒𝟒
a) Vẽ đồ thị (𝑷𝑷) của hàm số trên. 1,0 Bảng giá trị: 𝑥𝑥 −4 −2 0 2 4 𝑥𝑥2 −4 −1 0 −1 −4 𝑦𝑦 = − 4 Đồ thị: 1
b) Tìm các điểm 𝑴𝑴 thuộc đồ thị (𝑷𝑷) sao cho tung độ bằng hai lần hoành 0,5 độ. 𝑎𝑎2
𝑀𝑀(𝑎𝑎; 2𝑎𝑎) ∈ (𝑃𝑃) ⇒ 2𝑎𝑎 = − 4 𝑎𝑎2 + 8𝑎𝑎 = 0
𝑎𝑎(𝑎𝑎 + 8) = 0
𝑎𝑎 = 0 hoặc 𝑎𝑎 = −8
Vậy 𝑀𝑀(0; 0) hoặc 𝑀𝑀(−8; −16)
Cho phương trình 𝑥𝑥2 − 4𝑥𝑥 − 6 = 0. 1,0 điểm
2 a) Chứng minh phương trình trên có hai nghiệm phân biệt 𝒙𝒙𝟏𝟏,𝒙𝒙𝟐𝟐. Trang 1/7
Vì ∆′= (−4)2 − 4.1. (−6) = 40 > 0 nên phương trình trên có hai nghiệm 0,5
phân biệt 𝑥𝑥1, 𝑥𝑥2.
b) Không giải phương trình, hãy tính giá trị của biểu thức 𝒙𝒙𝟏𝟏𝒙𝒙𝟐𝟐 + 𝒙𝒙𝟏𝟏𝒙𝒙𝟐𝟐. 0,5 𝟒𝟒−𝒙𝒙𝟏𝟏 𝟒𝟒−𝒙𝒙𝟐𝟐
Áp dụng định lí Vi-ét ta có: �𝑥𝑥1 + 𝑥𝑥2 = 4 𝑥𝑥 1𝑥𝑥2 = −6 𝑥𝑥1𝑥𝑥2 𝑥𝑥1𝑥𝑥2 1 1
4 − 𝑥𝑥2 + 4 − 𝑥𝑥1 4 − 𝑥𝑥 + = 𝑥𝑥1𝑥𝑥2 � + � = 𝑥𝑥1𝑥𝑥2 1 4 − 𝑥𝑥2
4 − 𝑥𝑥1 4 − 𝑥𝑥2
(4 − 𝑥𝑥1)(4 − 𝑥𝑥2) 8 − (𝑥𝑥 8 − 4 = 𝑥𝑥 1 + 𝑥𝑥2) 1𝑥𝑥2 16 − 4(𝑥𝑥 = −6.
1 + 𝑥𝑥2) + 𝑥𝑥1𝑥𝑥2 16 − 4.4 + (−6) = 4
Lượng mưa trong một tuần tại Thành phố Hồ Chí Minh được đo mỗi
ngày. Biểu đồ cột kép dưới đây thể hiện lượng mưa cao nhất và lượng
mưa thấp nhất trong các ngày của tuần.
Lượng mưa cao nhất
Lượng mưa thấp nhất Ngày
(𝒎𝒎𝒎𝒎)
(𝒎𝒎𝒎𝒎) Thứ Hai 𝟐𝟐𝟐𝟐 𝟏𝟏𝟐𝟐 Thứ Ba 𝟑𝟑𝟐𝟐 𝟏𝟏𝟏𝟏 1,5 điểm Thứ Tư 𝟒𝟒𝟒𝟒 𝟏𝟏𝟏𝟏 Thứ Năm 𝟑𝟑𝟑𝟑 𝟐𝟐𝟐𝟐 3 Thứ Sáu 𝟑𝟑𝟒𝟒 𝟐𝟐𝟒𝟒 Thứ Bảy 𝟑𝟑𝟑𝟑 𝟏𝟏𝟐𝟐 Chủ nhật 𝟐𝟐𝟏𝟏 𝟏𝟏𝟏𝟏 0,5
a) Trong tuần này, hãy tính số ngày có tổng lượng mưa cao nhất và thấp
nhất lớn hơn 𝟐𝟐𝟒𝟒 𝐦𝐦𝐦𝐦.
Những ngày có tổng lượng mưa cao nhất và thấp nhất lớn hơn 50 𝑚𝑚𝑚𝑚 là:
Thứ Tư (40 + 19 = 59 𝑚𝑚𝑚𝑚), Thứ Năm (37 + 22 = 59 𝑚𝑚𝑚𝑚). 1,0
b) Chọn ngẫu nhiên một ngày trong tuần, tính xác suất thực nghiệm
của các biến cố sau:
A: “Ngày được chọn có lượng mưa cao nhất không vượt quá
𝟑𝟑𝟒𝟒 𝐦𝐦𝐦𝐦”.
B: “Ngày được chọn có lượng mưa thấp nhất lớn hơn 𝟏𝟏𝟐𝟐 𝐦𝐦𝐦𝐦”.
Số ngày có lượng mưa cao nhất không vượt quá 30 𝑚𝑚𝑚𝑚 là: 3 ngày Trang 2/7
Xác suất thực nghiệm của biến cố A là: 𝑃𝑃(𝐴𝐴) = 3 7
Số ngày có lượng mưa thấp nhất lớn hơn 15 𝑚𝑚𝑚𝑚 là: 5 ngày
Xác suất thực nghiệm của biến cố B là: 𝑃𝑃(𝐵𝐵) = 5 7
Một sân bóng hình chữ nhật có chiều dài là 𝒙𝒙 (đơn vị: mét, 𝒙𝒙 > 𝟒𝟒) và 1,0 điểm
chiều dài hơn chiều rộng là 𝟑𝟑 𝐦𝐦. 4 0,5
a) Viết biểu thức tính diện tích 𝑺𝑺 của sân bóng theo 𝒙𝒙.
Chiều rộng của sân bóng là: 𝑥𝑥 − 3 (𝑚𝑚)
Diện tích của sân bóng là: 𝑆𝑆 = 𝑥𝑥(𝑥𝑥 − 3) = 𝑥𝑥2 − 3𝑥𝑥 (𝑚𝑚2)
b) Sau đó người ta tăng chiều dài thêm 𝟏𝟏 m và tăng chiều rộng thêm 0,5
𝟑𝟑 𝐦𝐦 thì diện tích sân bóng tăng gấp đôi. Tính chiều dài của sân bóng đó?
Diện tích của hình chữ nhật sau khi tăng chiều dài thêm 1 m và tăng chiều rộng thêm 3 m là:
(𝑥𝑥 + 1)(𝑥𝑥 − 3 + 3) = (𝑥𝑥 + 1) ⋅ 𝑥𝑥 = 𝑥𝑥2 + 𝑥𝑥.
Theo bài ta có phương trình: 𝑥𝑥2 + 𝑥𝑥 = 2(𝑥𝑥2 − 3𝑥𝑥) 𝑥𝑥2 − 7𝑥𝑥 = 0 𝑥𝑥(𝑥𝑥 − 7) = 0 �𝑥𝑥 = 0
𝑥𝑥 = 7 ⇒ 𝑥𝑥 = 7 (vì 𝑥𝑥 > 0)
Vậy chiều dài của hình chữ nhật là 7 𝑚𝑚 .
Một xe tải chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước như hình bên. 1,0 điểm 5
a) Hãy tính thể tích của thùng xe (độ dày của thùng xe xem như 0,5 không đáng kể). Trang 3/7
Thể tích của thùng xe là: 2.3.1,5 = 9 (𝑚𝑚3)
b) Người ta xếp vào thùng xe tải các thùng hàng loại A có dạng hình lập
phương độ dài cạnh 𝟒𝟒𝟒𝟒 𝐜𝐜𝐦𝐦 để vận chuyển giao hàng. Hỏi mỗi lần vận 0,5
chuyển xe có thể chở được nhiều nhất bao nhiêu thùng hàng loại A?
Ta có: 40𝑐𝑐𝑚𝑚 = 0,4𝑚𝑚.
Số thùng hàng nhiều nhất có thể xếp được theo chiều cao của xe là 3 thùng vì 1,5: 0,4 = 3,75
Số thùng hàng nhiều nhất có thể xếp được theo chiều rộng của xe là 5 thùng vì 2: 0,4 = 5
Số thùng hàng nhiều nhất có thể xếp được theo chiều dài của xe là 7 thùng vì 3: 0,4 = 7,5
Vậy số thùng hàng nhiều nhất xe có thể chở được mỗi lần vận chuyển là: 3.5.7 = 105 thùng.
Một xí nghiệp dự tính chuyển hàng bằng hai xe tải và đang phân vân
giữa việc mua hẳn hai chiếc xe tải hoặc thuê hai xe tải. Nếu mua hai
xe với giá mỗi xe là 𝟐𝟐𝟒𝟒𝟒𝟒 𝟒𝟒𝟒𝟒𝟒𝟒 𝟒𝟒𝟒𝟒𝟒𝟒 đồng thì mỗi ngày xí nghiệp phải 1,0 điểm
tốn 𝟐𝟐 𝟒𝟒𝟒𝟒𝟒𝟒 𝟒𝟒𝟒𝟒𝟒𝟒 đồng cho tất cả tài xế và nhiên liệu. Còn nếu thuê xe
thì giá thuê một xe tải là 𝟏𝟏𝟒𝟒 𝟒𝟒𝟒𝟒𝟒𝟒 𝟒𝟒𝟒𝟒𝟒𝟒 đồng/ngày (đã bao gồm tiền
công cho tài xế và nhiên liệu). 0,5
a) Trong trường hợp xí nghiệp quyết định mua và xe tải mới mua
cần phải bảo dưỡng định kì, xí nghiệp sẽ sử dụng kết hợp cả xe tải mua
và xe tải thuê. Khi đó, tổng chi phí vận chuyển cho một đợt chuyển
6 hàng 𝟑𝟑𝟒𝟒𝟒𝟒 ngày là 𝟒𝟒 tỉ đồng (bao gồm cả tiền mua xe). Hãy tính số ngày
sử dụng xe tải mua và số ngày sử dụng xe tải thuê trong đợt chuyển hàng này.
Gọi số ngày sử dụng xe tải mua và sô ngày sử dụng xe tải thuê lần lượt là 𝑥𝑥
và 𝑦𝑦, đơn vị: ngày, điều kiện: 𝑥𝑥, 𝑦𝑦 ∈ ℕ∗ và 𝑥𝑥, 𝑦𝑦 < 300. Ta có hệ phương trình: � 𝑥𝑥 + 𝑦𝑦 = 300
2.200 + 2.5. 𝑥𝑥 + 2.10. 𝑦𝑦 = 4000 � 𝑥𝑥 + 𝑦𝑦 = 300
10𝑥𝑥 + 20𝑦𝑦 = 3600 �𝑥𝑥 = 240 𝑦𝑦 = 60
Vậy xí nghiệp sử dụng xe tải mua 240 ngày và xe tải thuê 60 ngày. Trang 4/7
b) Trong trường hợp xí nghiệp vẫn đang phân vân giữa việc mua xe và 0,5
thuê xe thì sau bao nhiêu ngày phương án mua xe sẽ tiết kiệm hơn phương án thuê xe?
Số tiền xí nghiệp phải trả để mua xe và chuyển hàng sau 𝑛𝑛 ngày là:
2.200 + 2.5𝑛𝑛 = 400 + 10𝑛𝑛 (triệu đồng)
Số tiền xí nghiệp phải trả khi thuê xe và chuyển hàng sau 𝑛𝑛 ngày là:
2.10. 𝑛𝑛 = 20𝑛𝑛 (triệu đồng)
Phương án mua xe sẽ tiết kiệm hơn phương án thuê xe khi:
400 + 10𝑛𝑛 < 20𝑛𝑛 10𝑛𝑛 > 400 𝑛𝑛 > 40
Vậy sau 40 ngày thì phương án mua xe sẽ tiết kiệm hơn.
Cho đường tròn (𝑶𝑶; 𝑹𝑹) có đường kính 𝑨𝑨𝑨𝑨 và đường thẳng 𝒅𝒅 là tiếp
tuyến của đường tròn (𝑶𝑶) tại 𝑨𝑨. Trên đường thẳng 𝒅𝒅 lấy điểm 𝑴𝑴 khác
𝑨𝑨 sao cho 𝑨𝑨𝑴𝑴 > 𝑨𝑨𝑶𝑶. Từ điểm 𝑴𝑴 vẽ tiếp tuyến 𝑴𝑴𝑴𝑴 với đường tròn (𝑶𝑶)
(𝑴𝑴 là tiếp điểm, 𝑴𝑴 khác 𝑨𝑨). 3,0 điểm 7 1,0
a) Chứng minh bốn điểm 𝑴𝑴, 𝑨𝑨, 𝑶𝑶, 𝑴𝑴 cùng thuộc một đường tròn và
𝑶𝑶𝑴𝑴 ⊥ 𝑨𝑨𝑴𝑴.
Do MA, MB là tiếp tuyến nên 𝑂𝑂𝐴𝐴𝑀𝑀 � = 𝑂𝑂𝐵𝐵𝑀𝑀 � = 90°. Trang 5/7
Gọi T là trung điểm của 𝑂𝑂𝑀𝑀.
Ta có Δ𝑂𝑂𝐴𝐴𝑀𝑀 vuông tại 𝐴𝐴 có 𝐴𝐴𝐴𝐴 là trung tuyến ứng với cạnh huyền.
Suy ra 𝐴𝐴𝑂𝑂 = 𝐴𝐴𝑀𝑀 = 𝐴𝐴𝐴𝐴 = 1 𝑂𝑂𝑀𝑀 (1) 2
Ta lại có Δ𝑂𝑂𝐵𝐵𝑀𝑀 vuông tại 𝐵𝐵 có 𝐵𝐵𝐴𝐴 là trung tuyến ứng với cạnh huyền.
Suy ra 𝐴𝐴𝑂𝑂 = 𝐴𝐴𝑀𝑀 = 𝐴𝐴𝐵𝐵 = 1 𝑂𝑂𝑀𝑀 (2) 2
Từ (1) và (2) suy ra 𝐴𝐴𝑂𝑂 = 𝐴𝐴𝑀𝑀 = 𝐴𝐴𝐴𝐴 = 𝐴𝐴𝐵𝐵.
Vậy 4 điểm 𝑀𝑀, 𝐴𝐴, 𝑂𝑂, 𝐵𝐵 cùng thuộc một đường tròn tâm 𝐴𝐴, đường kính 𝑀𝑀𝑂𝑂. �
𝑂𝑂𝐴𝐴 = 𝑂𝑂𝐵𝐵 ( bán kính)
𝑀𝑀𝐴𝐴 = 𝑀𝑀𝐵𝐵 ( tính chất hai tiếp tuyến cắt nhau)
Suy ra 𝑂𝑂𝑀𝑀 là đường trung trực của 𝐴𝐴𝐵𝐵.
Vậy 𝑂𝑂𝑀𝑀 ⊥ 𝐴𝐴𝐵𝐵. 1,0
b) Gọi 𝑫𝑫 là giao điểm của đoạn 𝑴𝑴𝑶𝑶 với đường tròn (𝑶𝑶). Tia 𝑨𝑨𝑫𝑫 cắt
đoạn thẳng 𝑴𝑴𝑴𝑴 tại 𝑬𝑬. Chứng minh rằng 𝑬𝑬𝑴𝑴𝟐𝟐 = 𝑬𝑬𝑨𝑨. 𝑬𝑬𝑫𝑫.
Vẽ 𝑂𝑂𝑆𝑆 ⊥ 𝐷𝐷𝐵𝐵 tại 𝑆𝑆.
Ta có 𝐷𝐷𝐵𝐵𝐷𝐷 � = 𝑆𝑆𝑂𝑂𝐵𝐵
� (cùng phụ 𝑂𝑂𝐵𝐵𝑆𝑆 �) (3)
Ta lại có Δ𝑂𝑂𝐷𝐷𝐵𝐵 cân tại 𝑂𝑂 (𝑂𝑂𝐵𝐵 = 𝑂𝑂𝐷𝐷) có 𝑂𝑂𝑆𝑆 là đường cao nên 𝑂𝑂𝑆𝑆 cũng là đường phân giác.
Suy ra 𝑆𝑆𝑂𝑂𝐵𝐵
� = 1 𝐷𝐷𝑂𝑂𝐵𝐵
� = 1 𝑠𝑠đ 𝐷𝐷𝐵𝐵 � (4) 2 2
Mặt khác, 𝐷𝐷𝐴𝐴𝐵𝐵
� = 1 𝑠𝑠đ 𝐷𝐷𝐵𝐵
� (góc nội tiếp chắn cung 𝐷𝐷𝐵𝐵 � ). 2
Từ (3), (4), (5) suy ra 𝐷𝐷𝐵𝐵𝐷𝐷 � = 𝐷𝐷𝐴𝐴𝐵𝐵 �.
Xét Δ𝐷𝐷𝐵𝐵𝐷𝐷 và Δ𝐷𝐷𝐴𝐴𝐵𝐵 có: �𝐵𝐵𝐷𝐷𝐴𝐴 � chung 𝐷𝐷𝐵𝐵𝐷𝐷 � = 𝐷𝐷𝐴𝐴𝐵𝐵 � (cmt)
Suy ra Δ𝐷𝐷𝐵𝐵𝐷𝐷~Δ𝐷𝐷𝐴𝐴𝐵𝐵 (g.g) Trang 6/7
Khi đó 𝐸𝐸𝐸𝐸 = 𝐸𝐸𝐸𝐸 𝐸𝐸𝐸𝐸 𝐸𝐸𝐸𝐸
Suy ra 𝐷𝐷𝐵𝐵2 = 𝐷𝐷𝐴𝐴. 𝐷𝐷𝐷𝐷. 1,0
c) Đường phân giác trong góc 𝑴𝑴 của tam giác 𝑨𝑨𝑴𝑴𝑨𝑨 cắt đường tròn
(𝑶𝑶; 𝑹𝑹) tại 𝑲𝑲 (𝑲𝑲 khác 𝑴𝑴 ). Kẻ 𝑴𝑴𝑩𝑩 ⊥ 𝑨𝑨𝑨𝑨 (𝑩𝑩 ∈ 𝑨𝑨𝑨𝑨) . Đặt 𝑴𝑴𝑩𝑩 = 𝒙𝒙 , tính diện
tích tam giác 𝑴𝑴𝑩𝑩𝑲𝑲 theo 𝑹𝑹 và 𝒙𝒙.
Ta có 𝐴𝐴𝐵𝐵𝐴𝐴
� = 90° (góc nội tiếp chắn nửa đường tròn).
Do BK là tia phân giác của 𝐴𝐴𝐵𝐵𝐴𝐴 � nên 𝐴𝐴𝐵𝐵𝐴𝐴 � = 𝐴𝐴𝐵𝐵𝐴𝐴
� = 1 𝐴𝐴𝐵𝐵𝐴𝐴 � = 45°. 2
Suy ra 𝑠𝑠đ 𝐴𝐴𝐴𝐴
� = 𝑠𝑠đ 𝐴𝐴𝐴𝐴 � = 90𝑜𝑜
Khi đó, 𝐴𝐴𝑂𝑂𝐴𝐴 � = 𝐴𝐴𝑂𝑂𝐴𝐴
� = 90° (hai góc ở tâm chắn hai cung bằng nhau)
Suy ra 𝑂𝑂𝐴𝐴 ⊥ 𝐴𝐴𝐴𝐴
Mà 𝐵𝐵𝐵𝐵 ⊥ 𝐴𝐴𝐴𝐴 (gt)
Suy ra 𝑂𝑂𝐴𝐴 ∥ 𝐵𝐵𝐵𝐵
Do đó, khoảng cách từ 𝑂𝑂 đến 𝐵𝐵𝐵𝐵 bằng khoảng cách 𝑑𝑑 từ 𝐴𝐴 đến 𝐵𝐵𝐵𝐵, nghĩa
là 𝑑𝑑 = 𝑂𝑂𝐵𝐵.
Suy ra: 𝑆𝑆ΔBIK = 𝑆𝑆Δ𝑂𝑂𝐸𝐸𝑂𝑂 (có cùng cạnh đáy 𝐵𝐵𝐵𝐵)
Xét Δ𝑂𝑂𝐵𝐵𝐵𝐵 vuông tại 𝐵𝐵 có: 𝑂𝑂𝐵𝐵2 = 𝑂𝑂𝐵𝐵2 − 𝐵𝐵𝐵𝐵2 = 𝑅𝑅2 − 𝑥𝑥2
Hay 𝑂𝑂𝐵𝐵 = √𝑅𝑅2 − 𝑥𝑥2. 1 1
𝑆𝑆Δ𝑂𝑂𝐸𝐸𝑂𝑂 = 2𝐵𝐵𝐵𝐵.𝑂𝑂𝐵𝐵 = 2𝑥𝑥�𝑅𝑅2 − 𝑥𝑥2
Vậy 𝑆𝑆ΔBIK = 𝑆𝑆Δ𝑂𝑂𝐸𝐸𝑂𝑂 = 1 𝑥𝑥√𝑅𝑅2 − 𝑥𝑥2. 2 Trang 7/7
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THAM KHẢO TUYỂN SINH 10 THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2025 – 2026
TRƯỜNG THCS VÀ THPT MÔN TOÁN LỚP 9 ĐỨC TRÍ
Thời gian làm bài: 120 phút
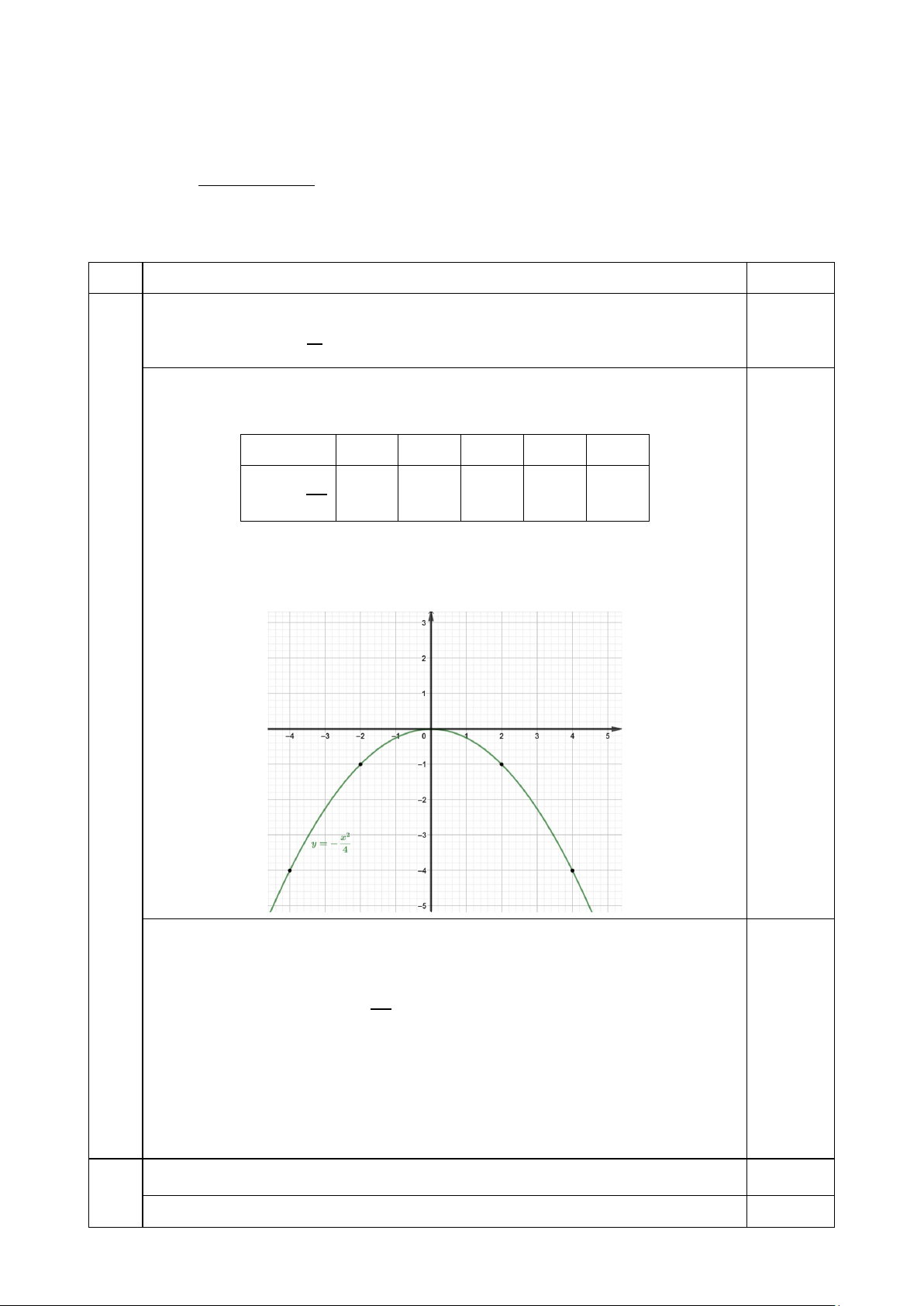
Câu 1 (1,5 điểm): Cho Parabol (𝑃𝑃): 𝑦𝑦 = 1 𝑥𝑥2. 4
a) Vẽ đồ thị hàm số trên.
b) Tìm trên (𝑃𝑃) các điểm 𝑀𝑀 có tung độ bằng 1.
Câu 2 (1 điểm): Cho phương trình 2𝑥𝑥2 − 𝑥𝑥 − 3 = 0. Không giải phương trình hãy:
a) Chứng tỏ phương trình luôn có 2 nghiệm phân biệt.
b) Với 𝑥𝑥1, 𝑥𝑥2 là hai nghiệm của phương trình trên, tính: 𝑥𝑥 𝑥𝑥 𝐴𝐴 = 1 2
𝑥𝑥2 − 1 + 𝑥𝑥1 − 1
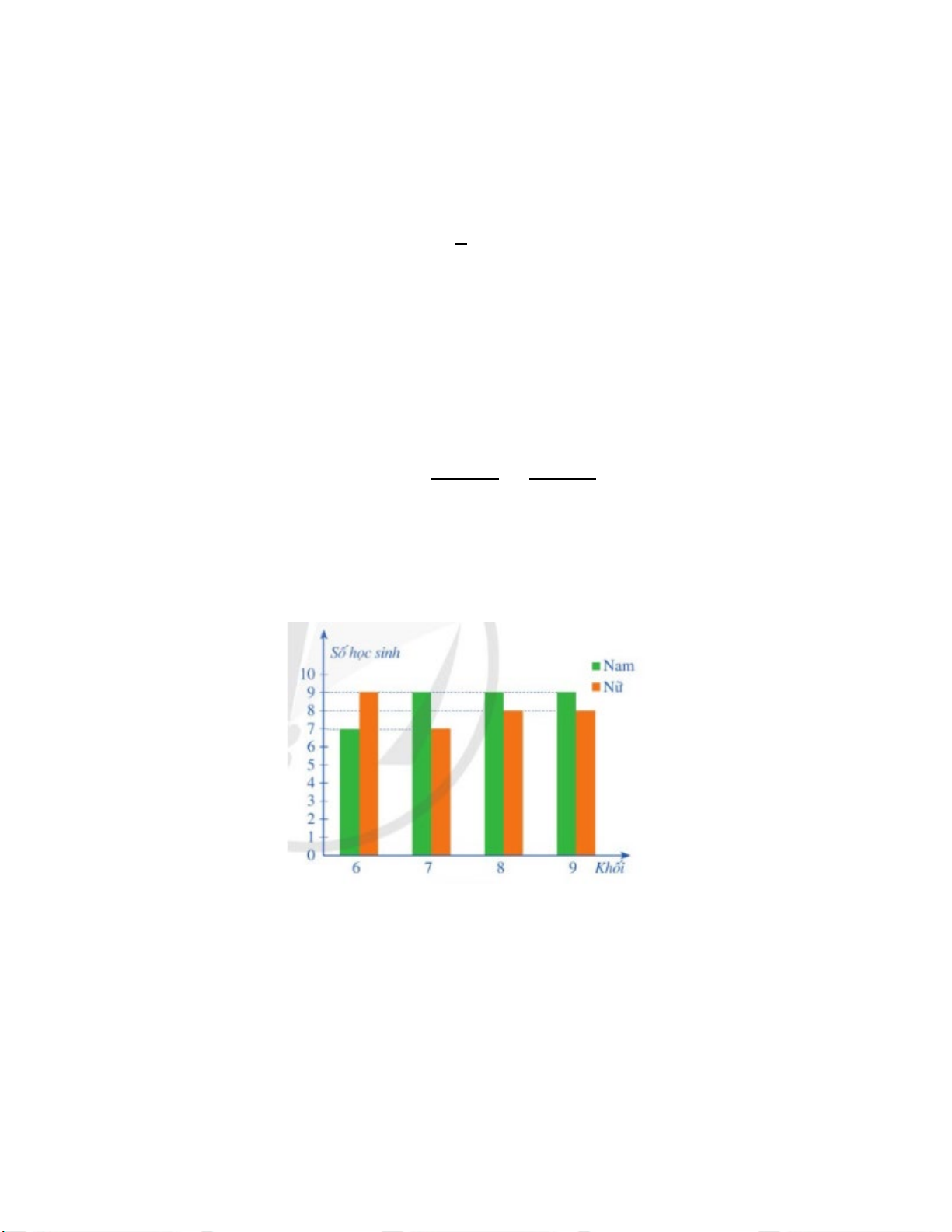
Câu 3 (1,5 điểm): Biểu đồ cột kép dưới đây biểu diễn số lượng học sinh tham gia giải thi đấu
thể thao của một trường trung học cơ sở.
a) Khối nào có tổng số học sinh tham gia nhiều nhất?
b) Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó, tính xác suất của các biến cố sau:
A: “Học sinh được chọn là nam”.
B: “Học sinh được chọn là nữ và không thuộc khối 9”.
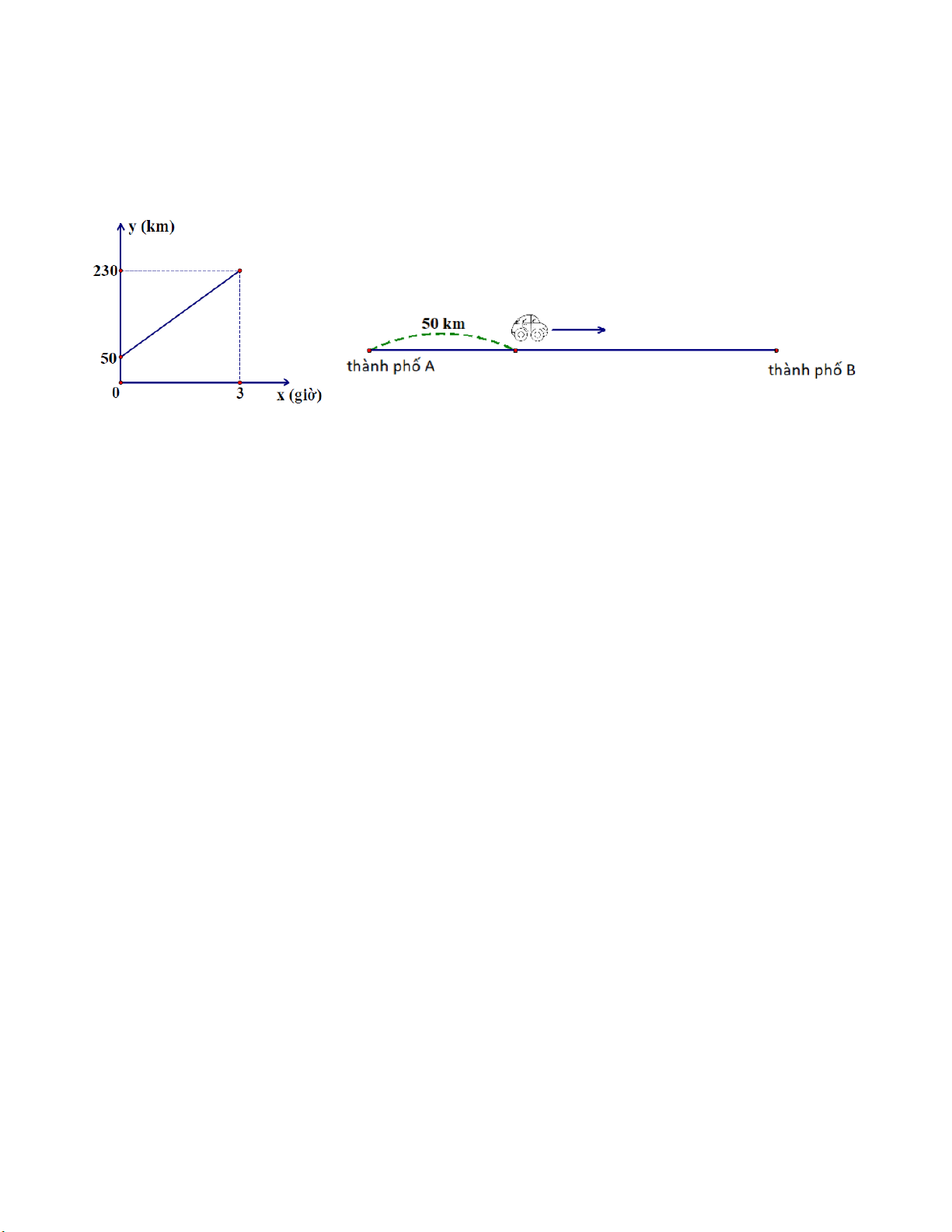
Câu 4 (1 điểm): Quãng đường từ thành phố A đến thành phố B là 350km. Lúc 6 giờ sáng, một
xe ô tô ở vị trí cách thành phố A 50km và khởi hành đi thành phố B (quan sát hình vẽ).
Gọi 𝑦𝑦 = 𝑎𝑎𝑥𝑥 + 𝑏𝑏 là hàm số biểu diễn độ dài quãng đường từ thành phố A đến vị trí của xe ô tô
sau 𝑥𝑥 giờ có đồ thị ở hình sau:
a) Tìm hệ số 𝑎𝑎 và 𝑏𝑏.
b) Xe ô tô đến thành phố B lúc mấy giờ?
Câu 5 (1 điểm): Hai chú chim bắt đầu bay cùng lúc từ đỉnh cột cờ Hà Nội và nóc di tích Đoan
Môn với quãng đường thẳng, dài như nhau. Chúng gặp nhau ở một điểm trên mặt đất, nằm giữa
hai công trình trên. Giả sử cột cờ Hà Nội cao 33m, di tích Đoan Môn cao 21m và hai nơi cách
nhau 300m. Hỏi điểm gặp nhau cách cột cờ Hà Nội bao nhiêu mét?
Câu 6 (1 điểm): Nón lá là biểu tượng cho sự dịu dàng, bình dị, thân thiện của người phụ nữ Việt
Nam từ bao đời nay. Để làm ra một chiếc nón lá, người thợ lấy từng chiếc lá, là (ủi) cho phẳng
rồi lấy kéo cắt chéo đầu lá trên, lấy kim xâu chúng lại với nhau một lượt sau đó xếp đều trên
khuôn nón. Mỗi chiếc nón có 16 vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn
thành những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất chỉ to bằng đồng xu. Đường
kính của vòng tròn lớn nhất của chiếc nón là 40cm; chiều cao của chiếc nón lá là 19cm. Hỏi cần
ít nhất bao nhiêu chiếc lá đã được làm phẳng để làm thành 1 chiếc nón lá, biết diện tích 1 chiếc
lá đã được làm phẳng là 72 cm2 và mỗi chiếc nón được phủ 2 lớp lá (giả sử phần chắp nối không
đáng kể). Biết công thức tính diện tích xung quanh hình nón là 𝑆𝑆𝑥𝑥𝑥𝑥 = 𝜋𝜋𝜋𝜋𝜋𝜋; với r là bán kính đáy
và 𝜋𝜋 là chiều dài đường sinh của hình nón.
Câu 7 (3 điểm): Cho ∆𝐴𝐴𝐴𝐴𝐴𝐴 nhọn, 𝐴𝐴𝐴𝐴 < 𝐴𝐴𝐴𝐴. Vẽ đường tròn (𝑂𝑂) đường kính 𝐴𝐴𝐴𝐴 cắt hai
cạnh 𝐴𝐴𝐴𝐴 và 𝐴𝐴𝐴𝐴 lần lượt tại 𝐸𝐸 và 𝐷𝐷, 𝐴𝐴𝐷𝐷 cắt 𝐴𝐴𝐸𝐸 tại 𝐻𝐻, 𝐴𝐴𝐻𝐻 cắt 𝐴𝐴𝐴𝐴 tại 𝐹𝐹.
a) Chứng minh: 𝐴𝐴𝐹𝐹 ⊥ 𝐴𝐴𝐴𝐴 tại 𝐹𝐹 và tứ giác 𝐴𝐴𝐸𝐸𝐻𝐻𝐹𝐹 nội tiếp.
b) Tia 𝐷𝐷𝐸𝐸 cắt đường thẳng 𝐴𝐴𝐴𝐴 tại 𝑆𝑆. Chứng minh: 𝑆𝑆𝐸𝐸. 𝑆𝑆𝐷𝐷 = 𝑆𝑆𝐴𝐴. 𝑆𝑆𝐴𝐴 và tứ giác 𝐴𝐴𝐸𝐸𝐹𝐹𝐴𝐴 nội tiếp.
c) Tia 𝐴𝐴𝐻𝐻 cắt (𝑂𝑂) tại 𝐾𝐾 (𝐹𝐹 nằm giữa 𝐴𝐴 và 𝐾𝐾). Chứng minh: 𝑆𝑆𝐾𝐾 là tiếp tuyến của (𝑂𝑂).
……………HẾT………….. HƯỚNG DẪN CHẤM CÂU NỘI DUNG ĐIỂM Câu 1 1,5đ a)
Lập đúng bảng giá trị 0,5 Vẽ đúng đồ thị 0,5 b)
Gọi 𝑀𝑀(𝑥𝑥; 1) ∈ (𝑃𝑃), khi đó: 1 4 𝑥𝑥2 = 1 0,25 ⇔ 𝑥𝑥2 = 4
⇔ 𝑥𝑥 = 2 hoặc 𝑥𝑥 = −2
Tọa độ điểm M là (2; 1) ℎ𝑜𝑜ặ𝑐𝑐 (−2; 1) 0,25 Câu 2 1đ a)
∆= 𝑏𝑏2 − 4𝑎𝑎𝑐𝑐 = (−1)2 − 4.2. (−3) = 25 > 0 nên phương trình luôn có 2 nghiệm phân biệt. 0,25 b)
Theo hệ thức Vi-ét, ta có: −𝑏𝑏 1 𝑥𝑥1 + 𝑥𝑥2 = � 𝑎𝑎 = 2 𝑐𝑐 −3 0,25
𝑥𝑥1. 𝑥𝑥2 = 𝑎𝑎 = 2 𝑥𝑥 𝑥𝑥 𝐴𝐴 = 1 2 𝑥𝑥 2 − 1 + 𝑥𝑥1 − 1 𝑥𝑥2 − 𝑥𝑥 2 − 𝑥𝑥 𝐴𝐴 = 1 1 + 𝑥𝑥2 2 0,25
𝑥𝑥1𝑥𝑥2 − 𝑥𝑥2 − 𝑥𝑥1 + 1 (𝑥𝑥
𝐴𝐴 = 1 + 𝑥𝑥2)2 − 2𝑥𝑥1𝑥𝑥2 − (𝑥𝑥1 + 𝑥𝑥2)
𝑥𝑥1𝑥𝑥2 − (𝑥𝑥2 + 𝑥𝑥1) + 1 −11 𝐴𝐴 = 0,25 4 Câu 3 1,5đ a) Từ biểu đồ ta có:
Tổng số HS khối 6: 7 + 9 = 16 HS
Tổng số HS khối 7: 9 + 7 = 16 HS
Tổng số HS khối 8: 9 + 8 = 17 HS 0,25x2
Tổng số HS khối 9: 9 + 8 = 17 HS
Khối 8 và 9 có tổng số học sinh tham gia nhiều nhất (9+8=17HS) b)
Không gian mẫu là 16 + 16 + 17 + 17 = 66 HS
Số kết quả thuận lợi của biến cố A là: 7 + 9 + 9 + 9 = 34HS 0,5
Xác suất của biến cố A là: P(A) = 34 = 17 66 33 0,5
Số kết quả thuận lợi của biến cố B là: 9 + 7 + 8 = 24HS
Xác suất của biến cố B là: P(B) = 24 = 4 66 11 Câu 4 1đ a)
Với 𝑥𝑥 = 0, 𝑦𝑦 = 50 ⇒ 𝑎𝑎. 0 + 𝑏𝑏 = 50 ⇒ 𝑏𝑏 = 50 0,25
Với 𝑥𝑥 = 3, 𝑦𝑦 = 230 ⇒ 𝑎𝑎. 3 + 50 = 230 ⇒ 𝑎𝑎 = 60 0,25
Vậy 𝑦𝑦 = 60𝑥𝑥 + 50 b)
Xe đến thành phố B thì 𝑦𝑦 = 350 ⇒ 60𝑥𝑥 + 50 = 350 ⇒ 𝑥𝑥 = 5 0,25
Vậy xe đến thành phố B lúc 6 + 5 = 11 (giờ) 0,25 Câu 5 A 1đ C 33m 21m D B E 300m
Áp dụng định lý Pytago vào tam giác ABD vuông tại D và tam giác BCE vuông tại E, ta có:
𝐴𝐴𝐴𝐴2 = 𝐴𝐴𝐷𝐷2 + 𝐷𝐷𝐴𝐴2 0,25
𝐴𝐴𝐴𝐴2 = 𝐴𝐴𝐸𝐸2 + 𝐸𝐸𝐴𝐴2
Gọi x là khoảng cách từ cột cờ Hà Nội đến vị trí gặp nhau, vì quãng đường
bay của 2 chú chim là như nhau nên ta có phương trình: 0,25
𝐴𝐴𝐷𝐷2 + 𝐷𝐷𝐴𝐴2 = 𝐴𝐴𝐸𝐸2 + 𝐸𝐸𝐴𝐴2
⇔ 332 + 𝑥𝑥2 = 212 + (300 − 𝑥𝑥)2 0,25 ⇔ 𝑥𝑥 = 148,92
Vậy điểm gặp nhau cách cột cờ Hà Nội 148,92m 0,25 Câu 6 1đ Diện tích xung quanh là:
𝑆𝑆𝑥𝑥𝑥𝑥 = 𝜋𝜋𝜋𝜋𝜋𝜋 = 𝜋𝜋. 20. √192 + 202 = 20√761𝜋𝜋 (𝑐𝑐𝑚𝑚2) 0,5 Số lá cần dùng là:
20√761𝜋𝜋: 72.2 ≈ 48,1 (chiếc lá) 0,25
Vậy cần dùng ít nhất 49 chiếc lá. 0,25 Câu 7 A D E H S B F O C K a)
+ Chứng minh H trực tâm ∆ABC ⇒ AH là đường cao ∆ABC ⇒ AH ⊥ BC 1đ tại F 0,5 Xét tứ giác BEHF có: 0
BEH = 90 (CE là đường cao) 0
BFH = 90 (AF là đường cao ) ⇒ BEH + 0 BFH =180
⇒ Tứ giác BEHF nội tiếp (Tứ giác có tổng hai góc đối bằng 1800) 0,5 b) Xét ∆ SEC và ∆ SBD 1đ 𝐸𝐸𝑆𝑆𝐴𝐴 � là góc chung 𝑆𝑆𝐷𝐷𝐴𝐴 � = 𝑆𝑆𝐴𝐴𝐸𝐸 � (cùng chắn cung EB ) ⇒ ∆ SEC ഗ ∆ SBD (g-g) 0,5
⇒ 𝑆𝑆𝑆𝑆 = 𝑆𝑆𝑆𝑆 𝑆𝑆𝑆𝑆 𝑆𝑆𝑆𝑆 ⇒ SE⋅SD = . SB SC 𝐴𝐴𝐹𝐹𝐴𝐴 � = 𝐴𝐴𝐸𝐸𝐴𝐴
� = 90° (tính chất đường cao)
Gọi M là trung điểm AC, tam giác AEC vuông tại E và tam giác AFC vuông
𝑀𝑀𝐴𝐴 = 𝑀𝑀𝐸𝐸 = 𝑀𝑀𝐴𝐴 = 1 𝐴𝐴𝐴𝐴
tại F có EM, FM là trung tuyến 0,5 ⇒ � 2
𝑀𝑀𝐴𝐴 = 𝑀𝑀𝐹𝐹 = 𝑀𝑀𝐴𝐴 = 1 𝐴𝐴𝐴𝐴 2
Suy ra A, E, F, C cùng thuộc đường tròn (M;MA) hay tứ giác AEFC nội tiếp c)
Tứ giác AEFC nội tiếp ⇒ 𝐴𝐴𝐸𝐸𝐹𝐹 � = 𝐹𝐹𝐴𝐴𝐴𝐴
� (cùng bù với góc 𝐴𝐴𝐸𝐸𝐹𝐹 �) 1đ ⇒ 𝐴𝐴𝐸𝐸𝐹𝐹 � = 𝑂𝑂𝐷𝐷𝐴𝐴 � (∆ODC cân tại O)
Tứ giác BEDC nội tiếp (O)⇒ 𝐸𝐸𝐴𝐴𝐹𝐹 � = 𝐸𝐸𝐷𝐷𝐴𝐴
� (cùng bù với góc 𝐸𝐸𝐷𝐷𝐴𝐴 �) Mà 𝐴𝐴𝐹𝐹𝐸𝐸 � + 𝐴𝐴𝐸𝐸𝐹𝐹 � + 𝐹𝐹𝐴𝐴𝐸𝐸
� = 180° (tổng 3 góc trong tam giác) ⇒ 𝐴𝐴𝐹𝐹𝐸𝐸 � + 𝑂𝑂𝐷𝐷𝐴𝐴 � + 𝐸𝐸𝐷𝐷𝐴𝐴 � = 180° 0,25
Lại có 𝐸𝐸𝐷𝐷𝑂𝑂 � + 𝑂𝑂𝐷𝐷𝐴𝐴 � + 𝐸𝐸𝐷𝐷𝐴𝐴 � = 180° ⇒ 𝐴𝐴𝐹𝐹𝐸𝐸 � = 𝐸𝐸𝐷𝐷𝑂𝑂
� mà 𝐴𝐴𝐹𝐹𝐸𝐸 � + 𝐸𝐸𝐹𝐹𝑂𝑂 � = 180° ⇒ 𝐸𝐸𝐹𝐹𝑂𝑂 � + 𝐸𝐸𝐷𝐷𝑂𝑂 � = 180°
tứ giác OFED nội tiếp (tổng 2 góc đối bằng 180°) Tứ giác OFED nội tiếp ⇒ OFD = OED 0,25 Mà OED =
ODE (∆ODE cân tại O) ⇒ OFD = ODE
Chứng minh ∆OFD ഗ ∆ODS (g-g) ⇒ OF OD 2 =
⇒ OD = OF.OS OD OS
Mà OK = OD ( bằng bán kính) 0,25 2 ⇒ = . ⇒ OK = OF OK OF OS OS OK
Chứng minh ∆OKS ഗ ∆OFK (c-g-c) ⇒ OKS = OFK Mà 0 OFK = 90 ⇒ 0 OKS = 90 Ta có: SK ⊥ OK ( 0 OKS = 90 ) K ∈ (O) 0,25
⇒ SK là tiếp tuyến của (O)