Đề thi chọn HSG Toán 9 THCS năm 2018 – 2019 sở GD và ĐT Thái Bình

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS NĂM HỌC 2018-2019 THÁI BÌNH
  Môn: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Câu 1. (3,0 điểm)  x + xy + x   xy + x x +  Cho biểu thức 1 1 P =  + +1 :1− −   xy 1 1   xy xy 1 xy 1 + − − +     với ;
x y ≥ 0 và xy ≠ 1. a. Rút gọn P .
b. Tính giá trị của biểu thức P khi 3 3
x = 4 − 2 6 + 4 + 2 6 và 2 y = x + 6 .
Câu 2. (3,0 điểm)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng (d): (m )
–1 x + y = 3m – 4
và (d’): x + (m )
–1 y = m . Tìm m để (d ) cắt (d’) tại điểm M sao cho  0 MOx = 30 .
Câu 3. (4,0 điểm) a. Giải phương trình: 2
3x +1 − 6 − x + 3x −14x − 8 = 0 3 2 2
x − 2x + 2x + 2y + x y − 4 = 0
b. Giải hệ phương trình:  2 x − xy − 
4x −1= 3x − y + 7
Câu 4. (2,0 điểm)
Chứng minh rằng nếu a, b, c là độ dài ba cạnh của một tam giác có chu vi bằng 3 thì 2 2 2
3a + 3b + 3c + 4abc ≥13 .
Câu 5. (3,0 điểm)
Cho tam giác ABC có ba góc nhọn, vẽ các đường cao BE và AD. Gọi H là trực tâm và G là trọng tâm tam giác ABC.
a. Chứng minh: nếu HG//BC thì tan . B tanC = 3.
b. Chứng minh: tan .Atan .
B tanC = tan A + tan B + tanC .
Câu 6. (3,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH, gọi I, J, K lần lượt là tâm các đường tròn
nội tiếp các tam giác ABC, ABH, ACH. Gọi giao điểm của các đường thẳng AJ, AK với
cạnh BC lần lượt là E và F.
a. Chứng minh: I là tâm đường tròn ngoại tiếp tam giác AEF.
b. Chứng minh: đường tròn ngoại tiếp tam giác IJK và đường tròn nội tiếp tam giác ABC có bán kính bằng nhau.
Câu 7. (2,0 điểm)
Tìm tất cả các bộ số nguyên dương ( ;
x y; z) sao cho x + y 2019 là số hữu tỉ và 2 2 2
x + y + z y + z 2019 là số nguyên tố.  HẾT 
Họ và tên thí sinh:................................................................... Số báo danh:..................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS NĂM HỌC 2018-2019 THÁI BÌNH
 
HƯỚNG DẪN CHẤM, ĐÁP ÁN VÀ BIỂU ĐIỂM MÔN TOÁN (Gồm 05 trang) Câu Ý Nội dung Điểm  x + xy + x   xy + x x +  Cho biểu thức 1 1 P =  + +1 :1− −      xy +1 1− xy xy −1 xy +    1 với ;
x y ≥ 0 và xy ≠ 1 a. Rút gọn P .
b. Tính giá trị của biểu thức P khi 3 3
x = 4 − 2 6 + 4 + 2 6 và 2 y = x + 6 .  x +1 xy + x   xy + x x +1  P =  + +1 :1− −   xy 1 1   xy xy 1 xy 1 + − − +     ( x + )
1 (1− xy ) + ( xy + x)( xy + ) 1 +1− xy = : 1− xy 0,5
xy −1− ( xy + x)( xy + )
1 − ( x + )1( xy − ) 1 xy −1 a.
( x + )1(1− xy)+( xy + x)( xy + )1+1− xy 1,5đ = 0,5
1− xy + ( xy + x)( xy + )1 + ( x + )1( xy − )1 1. 2( x + ) 1 1 = = 0,5 3,0đ 2( xy + x y ) xy Vậy với ;
x y ≥ 0 và xy ≠ 1 thì 1 P = . xy Ta có: x = ( − + + )3 3 3 3 4 2 6 4 2 6 0,5 = + (3 3 − + + )(3 3 8 3 4 2 6 4 2 6 4 − 2 6. 4 + 2 6 ) b. = 8 − 6x 1,5đ 3
⇒ x + x = ⇔ x( 2 6 8
x + 6) = 8 ⇔ xy = 8 thỏa mãn điều kiện xác định 0,5 Thay vào ta có 2 P = . Vậy 2 P = . 4 4 0,5
Cho hai đường thẳng (d): (m )
–1 x + y = 3m – 4 , (d’): x + (m )
–1 y = m . Tìm m để d cắt d’ tại điểm M sao cho  0 MOx = 30 .
Tọa độ giao điểm (nếu có) của (d) và (d’) là nghiệm của hệ phương trình: 2 (  m – )
1 x + y = 3m – 4 x = m −  (m − ) 1 y 3,0đ  ( *) 0,5 x +  ( ⇔  m – ) 1 y = m
m(m − 2) y = (m − 2)2 ( ) 1
Để (d) cắt (d’) ⇔ hệ (*) có nghiệm duy nhất m ≠ 0 ⇔ ( )
1 có nghiệm duy nhất ⇔  0,5 m ≠ 2 Câu Ý Nội dung Điểm  3m − 2 x = m ≠ 0  Với  m 
hệ phương trình có nghiệm duy nhất  m ≠ 2 m − 2  y =  m
Lúc đó  3m − 2 m − 2 M ;    0,5  m m  Từ giả thiết  0 MOx = 30 m − 2
⇒ nên M có hoành độ dương và  tan = m MOx 3m − 2 m 0,5 m − 2  0 m 1 m − 2 tan MOx = tan 30 =
⇒ 3m − 2 = ± 3 (m − 2) 3m 2 ⇔ = − 3 3m − 2 m 2 3 ⇔ m = ± thỏa mãn. 3 Vậy 2 3 2 3 m = ;m = − . 3 3 1,0 a. Giải phương trình: 2
3x +1 − 6 − x + 3x −14x − 8 = 0 3 2 2
x − 2x + 2x + 2y + x y − 4 = 0
b. Giải hệ phương trình:  2 x − xy − 
4x −1= 3x − y + 7 2
3x +1 − 6 − x + 3x −14x − 8 = 0 Điều kiện xác định 1 − ≤ x ≤ 6 (*) 3 Phương trình đã cho
⇔ ( x + − ) − ( − x − ) 2 3 1 4 6
1 + 3x −14x − 5 = 0 3x −15 5 − x 1,0 ⇔ −
+ (x − 5)(3x + ) 1 = 0 3x +1 + 4 6 − x +1 a.  3 1 
2,0đ ⇔ (x −5) + +  (3x + )1 = 0   3x +1 + 4 6 − x +1  x = 5 (t/m (*))  ⇔ 0,5  3 1 + + (3x + ) 1 = 0 ( ) 1  3.  3x +1 + 4 6 − x +1 4,0đ
VT của pt (1) luôn lớn hơn 0 với mọi x thỏa mãn(*) nên (1) vô nghiệm 0,5
Vậy tập nghiệm phương trình là S = { } 5 . 3 2 2
x − 2x + 2x + 2y + x y − 4 =  0 ( ) 1  b. 2
x − xy − 4x −1 = 3x − y + 7  ( 2)
2,0đ Điều kiện xác định 3x − y + 7 ≥ 0 2 Câu Ý Nội dung Điểm ( ) ⇔ ( 2 1
x + 2)(x + y − 2) = 0 0,5
⇔ x + y − = ⇔ y = − x ( 2 2 0 2
do x + 2 > 0∀x)
Thay y = 2 − x vào (2) ta được 2
x − x(2 − x) − 4x −1= 3x − (2 − x) + 7 2
⇔ 4x + 5 = 2x − 6x −1 2
⇔ 2 4x + 5 = 4x −12x − 2 2
⇔ (2x − 3) = 2 4x + 5 +11
Đặt 4x + 5 = 2t − 3. ( t − t x  )  = x + ( − = +   2t − 3) (2 3)2 2 2 4 5 2 3 4 5 Ta có = 4x + 5   ⇔  ⇔  ( t = x  2x − 3  )2 = 4t + 5 (  t − 
x)(t + x − 2) = 0  0,5
t = 2 − x 2  Trường hợp 1: x − 4x +1= 0
t = x ⇔ 4x + 5 = 2x − 3 ⇔  ⇔ x = 2 + 3 2x − 3 ≥ 0
⇒ y = − 3 thỏa mãn điều kiện xác định 0,5
Hệ có nghiệm ( ;x y) = (2 + 3;− 3) . 2  Trường hợp 2: x − 2x −1= 0
t = 4 − x ⇔ 4x + 5 =1− 2x ⇔  ⇔ x =1− 2 1  − 2x ≥ 0 0,5
⇒ y =1+ 2 thỏa mãn điều kiện xác định.
Hệ có nghiệm ( ;x y) = (1− 2;1+ 2).
Vậy hệ có nghiệm: ( ;x y) = (2 + 3;− 3);( ;x y) = (1− 2;1+ 2)
Chứng minh rằng nếu a, b, c là độ dài ba cạnh của một tam giác có chu vi bằng 3 thì 2 2 2
3a + 3b + 3c + 4abc ≥13 . Đặt 2 2 2
T = 3a + 3b + 3c + 4abc . Do vai trò của a, b, c bình đẳng nên không
giảm tổng quát ta có thể giả sử 0 < a ≤ b ≤ c .
Từ a + b + c = 3 và a + b > csuy ra 3 1≤ c < 2 0,5 2 2 2
T = 3(a + b ) + 3c + 4abc = 3(a + b)2 2 − 2  ab + 3c + 4   abc 2 4. = 3(3 − c) 2
+ 3c − 2ab(3 − 2c) 0,5 2,0đ 2 2 Do 3 – 2c > 0 và  a + b   3 − c  ab ≤ =  , suy ra 2   2      T ≥ ( − c)2 2 1 3 3
+ 3c − (a + b)2 (3 − 2c) 2 0,75 = ( 2 c − c + ) 2 1 3 6
9 + 3c − (3 − c)2 (3 − 2c) 2 3 3 2 27 = c − c + = c(c − )2 1 1 + (c − )2 1 +13 ≥13 2 2 2 3 Câu Ý Nội dung Điểm
Dấu bằng xảy ra khi a = b = c =1 0,25
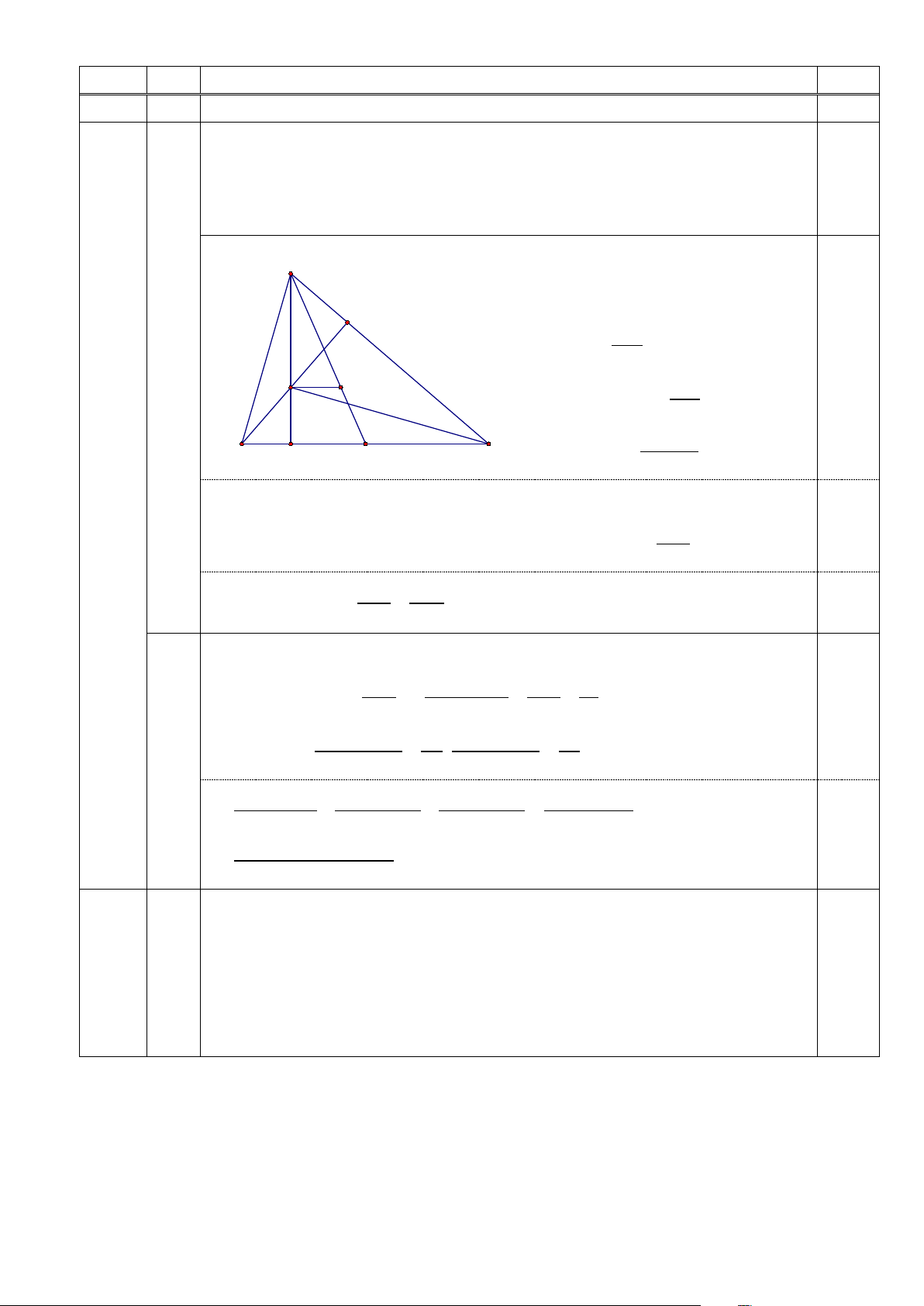
Cho tam giác ABC có ba góc nhọn. Vẽ đường cao BE và AD. Gọi H là
trực tâm và G là trọng tâm tam giác ABC.
a. Chứng minh: nếu HG//BC thì t . anB tanC = 3. b. Chứng minh: t . anAt .
anB tanC = tanA + tanB + tanC . A Gọi M là trung điểm BC E
Ta có tam giác ABD vuông tại D nên tanB = AD a. BD 1,5đ H G
Tương tự : tanC = AD CD B D M 2 C AD 0,5 ⇒ t . anB tanC = B . D CD Ta có  BHD =  EHA ⇒  HBD =  HAE AD
⇒ ∆BDH  ∆ADC ⇒ B . D CD = A . D DH ⇒ t . anB tanC = DH 0,5
Ta có HG//BC ⇒ AD = AM ⇒ t . anB tanC = 3 DH GM 0,5
Gọi S,S ,S ,S lần lượt là diện tích các tam giác ABC, HBC, HCA, HAB 1 2 3 Ta có t . anB tanC = AD 1 DH S1 ⇒ = = DH tan . B tanC AD S 1 S 1 2 5. b. Tương tự 3 ⇒ = , = S tanC.tan A S tan . A tan B S 1,0 3,0đ 1,5đ 1 1 1 S + S + S 1 2 3 ⇒ + + = =1 tan .
B tanC tanC.tan A tan . A tan B S
tan A + tan B + tan ⇒ C =1⇒ ĐPCM tan . A tan . B tanC 0,5
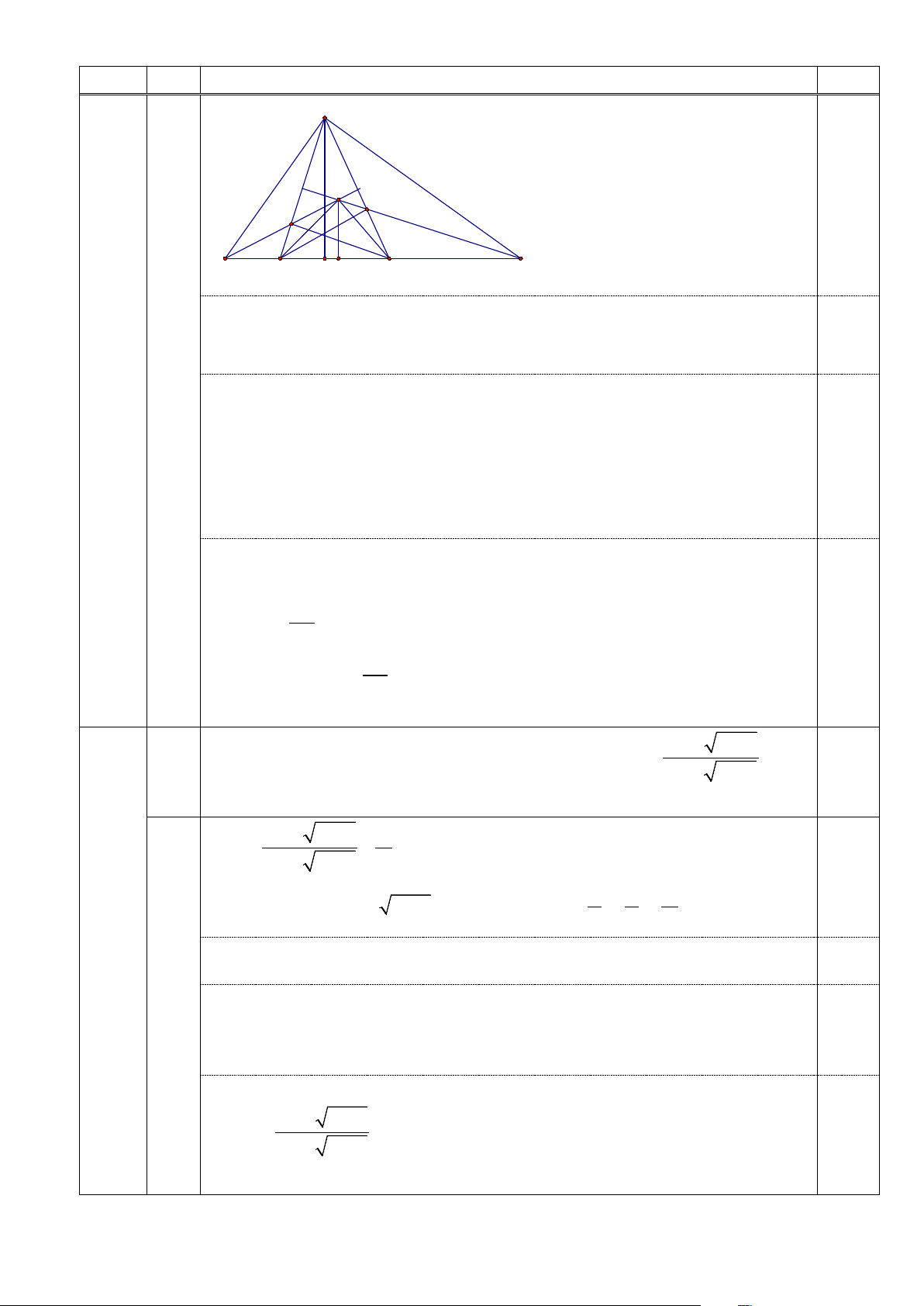
Cho tam giác ABC vuông tại A, đường cao AH, gọi I, J, K lần lượt là tâm
các đường tròn nội tiếp các tam giác ABC, ABH, ACH. Gọi giao điểm của
các đường thẳng AJ, AK với cạnh BC lần lượt là E và F.
a. Chứng minh: I là tâm đường tròn ngoại tiếp tam giác AEF.
b. Chứng minh: đường tròn ngoại tiếp tam giác IJK và đường tròn nội tiếp
tam giác ABC có bán kính bằng nhau. 4 Câu Ý Nội dung Điểm A 6. 3,0đ I K J B E H M F C a.  +  0 =  +  0 =  = 
AEC EAH 90 ,CAE EAB 90 ,EAH EAB ⇒  =  AEC CAE ⇒ AE ∆
C cân tại C⇒ CI là trung trực AE. 1,00
Tương tự BI là trung trực AF ⇒I là tâm đường tròn ngoại tiếp AE ∆ F .
b. Gọi M là hình chiếu vuông góc của I trên BC⇒ M là trung điểm EF và IM = r .
Tam giác ABF cân tại B, tam giác ACE cân tại C nên EF = AB + AC − BC. 1,0
Gọi r là bán kính đường tròn nội tiếp tam giác ABC, do tam giác ABC
vuông tại A ta chứng minh được AB + AC − BC = 2r ⇒ EF = 2r
A và E đối xứng nhau qua CI nên  =  KEC KAC mà  =  KAC KAH ,  +  0 KAH KFE = 90 ⇒  +  0 KEC KFE = 90 ⇒ KEF ∆ vuông tại K EF ⇒ MK = = r . 2 1,0 Tương tự EF ⇒ MJ = = r . 2
⇒ MJ = MI = MK = r ⇒ điều phải chứng minh. x + y
Tìm tất cả các bộ số nguyên dương ( ;x y; z) thỏa mãn 2019 là số y + z 2019 hữu tỉ và 2 2 2
x + y + z là số nguyên tố. 7.
x + y 2019 m * 2,0đ Ta có
= (m,n∈ ,(m,n) = ) 1 .
y + z 2019 n nx − my = 0 x y m
⇒ nx − my=(mz − ny) 2019 2 ⇒  ⇒ = = ⇒ xz = y . 0,5 mz − ny = 0 y z n 2 2 2
x + y + z = (x + z)2 2
− xz + y = (x + z)2 2 2
− y = (x + y + z)(x + z − y) 0,5
Vì x + y + z là số nguyên lớn hơn 1 và 2 2 2
x + y + z là số nguyên tố nên 2 2 2
x + y + z = x + y + z  0,5
x − y + z =1
Từ đó suy ra x = y = z =1. 0,5
Thử lại x + y 2019 =1 và 2 2 2
x + y + z = 3 thỏa mãn yêu cầu bài toán. y + z 2019 Kết luận (x;y;z) = (1;1; ) 1 . ______________ 5
Document Outline

• DeHSGlop9nam2018
• DapanHSGlop9nam2018