









Preview text:
UBND TỈNH BÌNH PHƯỚC
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2023-2024
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN
Thời gian làm bài: 90 phút
(40 câu trắc nghiệm – 02 câu tự luận) ĐỀ CHÍNH THỨC
(Đề thi gồm 04 trang) Mã đề thi 124
Họ và tên thí sinh: …………………………………… Số báo danh: ……………….
I. PHẦN TRẮC NGHIỆM: (8,0 ĐIỂM)
Câu 1: Trong không gian Oxyz , cho hai điểm A(1;0; 3 − ) và B(1;1; )
1 . Tọa độ của vectơ AB là A. (2;1; 2 − ). B. (0;1;4). C. 1 1; ; 1 − . D. (0; 1 − ; 4 − ). 2
Câu 2: Số phức liên hợp của số phức z =1− 2i là
A. z =1+ 2i . B. z = 1 − − 2i . C. z = 1 − + 2i .
D. z = 2 −i .
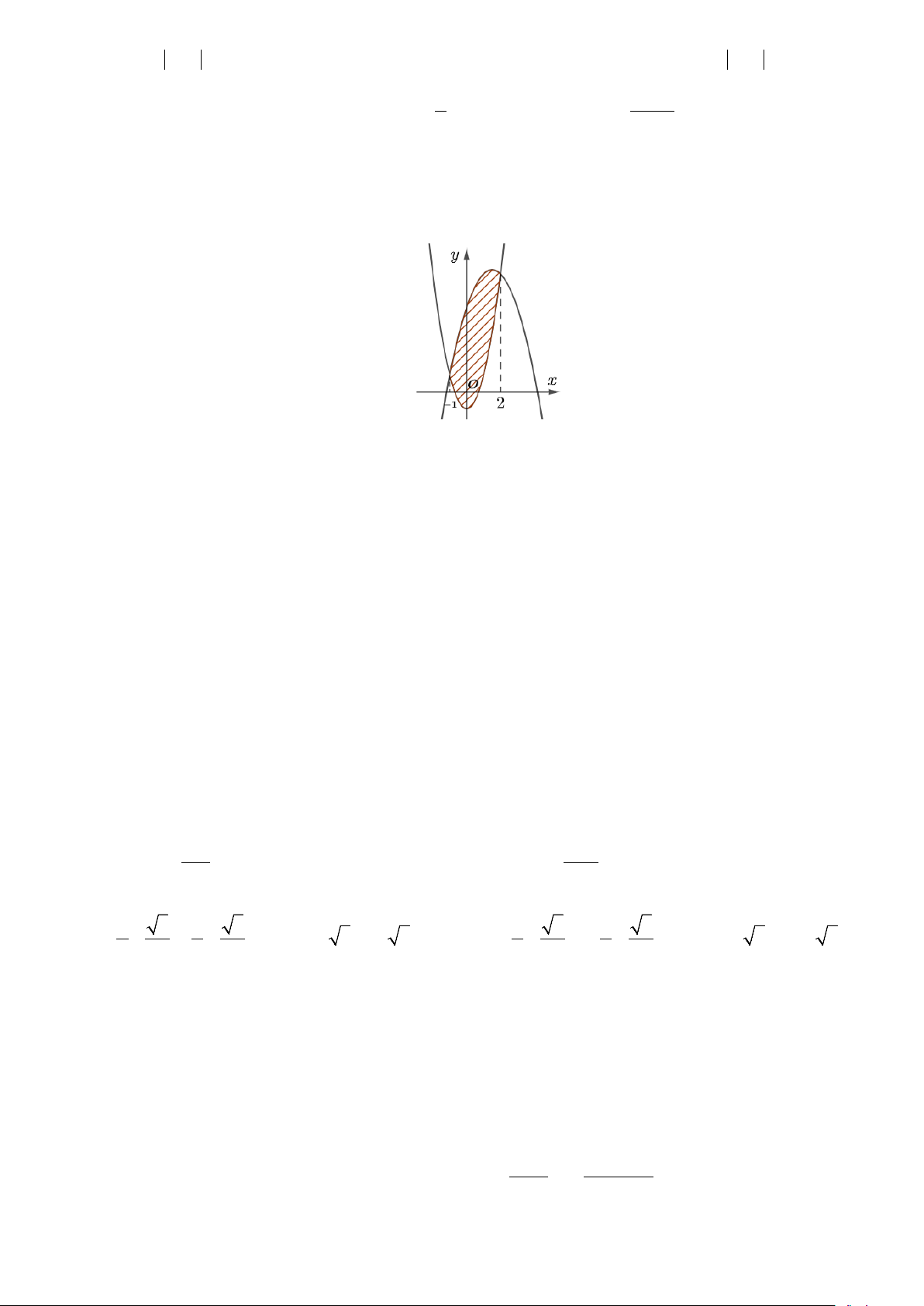
Câu 3: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x và trục hoành. Khẳng định nào đúng? 2 2 2 2
A. S = ∫( 2x −2x)dx . B. S = ∫( 2
2x − x )dx . C. S =π ∫( 2
2x − x )dx . D. S = ∫(x − 2x)2 2 dx . 0 0 0 0
Câu 4: Tìm số phức z biết 4z + 5z = 27 − 7i .
A. z = −3− 7i .
B. z = 3− 7i .
C. z = −3+ 7i .
D. z = 3+ 7i .
Câu 5: Trong không gian Oxyz , đường thẳng đi qua gốc tọa độ và điểm A(1;2;3) có phương trình là x = t A. 3x − − −
+ 2y + z − 6 = 0. B. x 1 y 2 z 3 = =
. C. y = 2t ,t ∈ .
D. x + 2y + 3z − 6 = 0. 3 2 1 z = 3t
Câu 6: Cho a,b∈ và thỏa mãn (a + bi)i − 2a =1+ 3i , với i là đơn vị ảo. Giá trị a −b bằng A. 4 − . B. 10 − . C. 10. D. 4 . 2 − 3 Câu 7: Nếu ( )d = 4 − ∫ f x x thì 1 f
∫ (x)dx bằng − 2 3 2 A. 1. − B. 2. C. 3. − D. 3. x = 1 − − 2t
Câu 8: Trong không gian Oxyz , cho hai đường thẳng x 1 : y z d
− = = và d :y = 2−t , t∈ . 2 ( ) 1 2 1 1 − z = 3+ t
Vị trí tương đối của d và d là 1 2 A. Cắt nhau. B. Trùng nhau. C. Song song. D. Chéo nhau.
Câu 9: Chọn khẳng định đúng?
A. sin xdx = −sin x +C ∫
. B. sin xdx = −cos x + C ∫
. C. sin xdx = sin x + C ∫ . D. sin = cos + ∫ xdx x C .
Câu 10: Biết F(x) là nguyên hàm của hàm số f (x) trên đoạn [a;b] . Chọn mệnh đề đúng. b b b b
A. f (x)dx = F(a) − F(b) ∫
.B. f (x)dx = F(b) − F(a) ∫
.C. f (x)dx = F(a).F(b) ∫
. D. f (x)dx = F(b) + F(a) ∫ . a a a a
Câu 11: Trong không gian Oxyz , cho mặt phẳng (P):x − 2y + z +3 = 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng (P). A. n = (2; 4; − 2 − ). B. n = (1; 2 − ; ) 1 . C. n = (1;1;3). D. n = (1; 2 − ;3).
Câu 12: Cho hàm số y = f (x) liên tục trên [ ;ab]. Khi đó diện tích S của hình phẳng giới hạn bởi đồ
thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a,x = b là
Trang 1/4 - Mã đề thi 124 b b b b
A. S =π f (x)dx ∫ . B. 2
S = π f (x)dx ∫ . C. 2
S = f (x)dx ∫ .
D. S = f (x)dx ∫ . a a a a
Câu 13: Cho hàm số f (x) xác định trên 1 2 \
và thỏa mãn f ′(x) =
, f (0) =1 và f ( ) 1 = 2 . Giá 2 2x −1
trị của biểu thức f (− ) 1 + f (3) bằng A. 2 + ln15. B. ln15. C. 4 + ln15. D. 3+ ln15.
Câu 14: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2 y = 2x −1 và 2
y = −x + 3x + 5 (miền gạch
sọc trong hình vẽ sau) được tính theo công thức nào sau đây? 2 2 2 2 A. ∫ ( 2 3
− x + 3x + 6)dx . B. ∫ ( 2x +3x + 4)dx . C. ∫ ( 2
3x − 3x − 6)dx. D. ∫ ( 2x +3x −4)dx. 1 − 1 − 1 − 1 −
Câu 15: Cho hai số phức z 3i và z 1i. Phần ảo của số phức z z bằng 1 2 1 2 A. 4 . B. 4i . C. 1 − . D. i − .
Câu 16: Cho hai số phức z = 3− 2i và z = 2 +i . Số phức z − z bằng 1 2 1 2 A. 1+ 3i . B. 1− 3i . C. 1 − − 3i . D. 1 − + 3i .
Câu 17: Trong không gian Oxyz , cho mặt phẳng (P):2x − y + z −3 = 0 . Điểm nào trong các điểm dưới đây thuộc (P) . A. M 0;1;2 . B. M 1;1;0 . C. M 1;0;1 . D. M 0;0; 3 − . 4 ( ) 1 ( ) 2 ( ) 3 ( )
Câu 18: Trong không gian Oxyz , cho hai điểm A(1;0;− ) 1 và B(1;2; )
1 . Phương trình mặt phẳng trung
trực của đoạn AB là
A. x + y − 2 = 0.
B. y + z −1= 0.
C. y + z − 2 = 0.
D. y + z +1= 0.
Câu 19: Số phức có phần thực bằng 3 và phần ảo bằng 4 là A. 4 −3i . B. 4 + 3i . C. 3− 4i . D. 3+ 4i .
Câu 20: Tìm nguyên hàm của hàm số ( ) 7x f x = . x x 1 + A. x 7 7 dx = + C ∫ . B. x x 1 7 dx 7 + = + C x 7 7 dx = + C x x dx = + C ln 7 ∫ . C. ∫ . D. 7 7 ln 7 x ∫ . +1
Câu 21: Phương trình 2z − z +1= 0 có hai nghiệm là A. 1 3 1 3 − i; +
.i B. 1− 3i; 1+ 3i . C. 1 3 1 3 − − i; − + .i D. 1
− − 3i; −1+ 3i . 2 2 2 2 2 2 2 2
Câu 22: Trong tập số phức, nghiệm có phần ảo dương của phương trình 2z + 4z +5 = 0 là A. z = 2 − − i .
B. z = 2 + 3i . C. z = 2 − + 2i . D. z = 2 − + i . 3 5 5
Câu 23: Cho f (x)dx = 2 − ∫
, f (x)dx = 3 − ∫
. Khi đó f (x)dx ∫ có giá trị là 1 3 1 A. 5. − B. 1. C. 5. D. 1. −
Câu 24: Khẳng định nào sau đây là sai? A. f
∫ (x)+ g(x) dx = f
∫ (x)dx+ g
∫ (x)dx. B. f
∫ (x)− g(x) dx = f
∫ (x)dx− g ∫ (x)dx . f (x) f (x)dx C. ∫ kf
∫ (x)dx = k f
∫ (x)dx , k ≠ 0. D. dx = ∫ . g(x) g(x).dx ∫
Trang 2/4 - Mã đề thi 124
Câu 25: Trong không gian Oxyz , tọa độ hình chiếu vuông góc của điểm M (1;2;3) lên mặt phẳng (Oxy) là A. (1;0;3). B. (0;0;3). C. (1;2;0). D. (1;0;0).
Câu 26: Trong không gian Oxyz , mặt cầu tâm I (1;0;0) và đi qua điểm M (2;1;0) có phương trình là A. (x + )2 2 2
1 + y + z = 2. B. (x + )2 2 2
1 + y + z = 2.C. (x − )2 2 2
1 + y + z = 2.D. (x − )2 2 2 1 + y + z = 2.
Câu 27: Trong không gian + +
Oxyz , cho đường thẳng x y 1 z 2 d : = =
. Vectơ nào dưới đây là một 1 1 − 2
vectơ chỉ phương của đường thẳng d . A. u = (0;1;2). B. u = (1; 1; − ) 1 . C. u = (1; 1; − 2). D. u = (0; 1 − ; 2 − ).
Câu 28: Cho hàm số f (x) 4
= 2x − 5x . Khẳng định nào dưới đây đúng? A. 1 1 ∫ f (x) 2 5
dx = x − x + C .
B. ∫ f (x) 2 5
dx = x − x + C . 2 5
C. ∫ f (x) 2 5
dx = x − 5x + C .
D. ∫ f (x) 5
dx = 2x − x + C .
Câu 29: Nếu u = u(x), v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [ ;ab]. Khẳng định nào sau đây là đúng ? b b b b b a b b
A. u.dv = u. b v − u.du ∫ ∫
. B. u.dv = u. b v − . v dv ∫ ∫
. C. u.dv = u.v |b − v du ∫ b u dv = u v − v du a . ∫ . D. . . . ∫ ∫ . a a a a a a a a b a a x = t
Câu 30: Trong không gian Oxyz , cho đường thẳng d :y =1−t ,(t ∈) . Hỏi điểm nào sau đây thuộc z =1+ t đường thẳng d . A. M 1;1;1 . B. M 1; 1; − 1 . C. M 0;1;1 . D. M 1;0; 1 − . 4 ( ) 1 ( ) 3 ( ) 2 ( )
Câu 31: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = −x + 2x − 2, trục hoành và các đường
thẳng x = 0, x = 3. A. 5. B. 3. C. 4 . D. 6 .
Câu 32: Trong không gian Oxyz , phương trình của mặt phẳng đi qua ba điểm A(1;0;0), B(0;2;0) , C (0;0;3) là A. x y z + + =1. B. x x y z
+ 2y + 3z +1 = 0. C. x + 2y + 3z =1. D. + + +1= 0. 1 2 3 1 2 3
Câu 33: Trong không gian Oxyz , mặt cầu có tâm I (1;1; )
1 và bán kính R = 5 có phương trình là
A. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 5.
B. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 25.
C. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 25.
D. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 5.
Câu 34: Trong không gian Oxyz , (P):2y + 2z −3 = 0 và mặt cầu (S) (x − )2 2 :
1 + y + (z − 2)2 = 4 . Có bao
nhiêu điểm M thuộc mặt phẳng (Oxy) với hoành độ nguyên dương sao cho từ M kẻ được ít nhất
một tiếp tuyến tới (S ) đồng thời vuông góc với (P) . A. 6. B. 1. C. 5. D. 2.
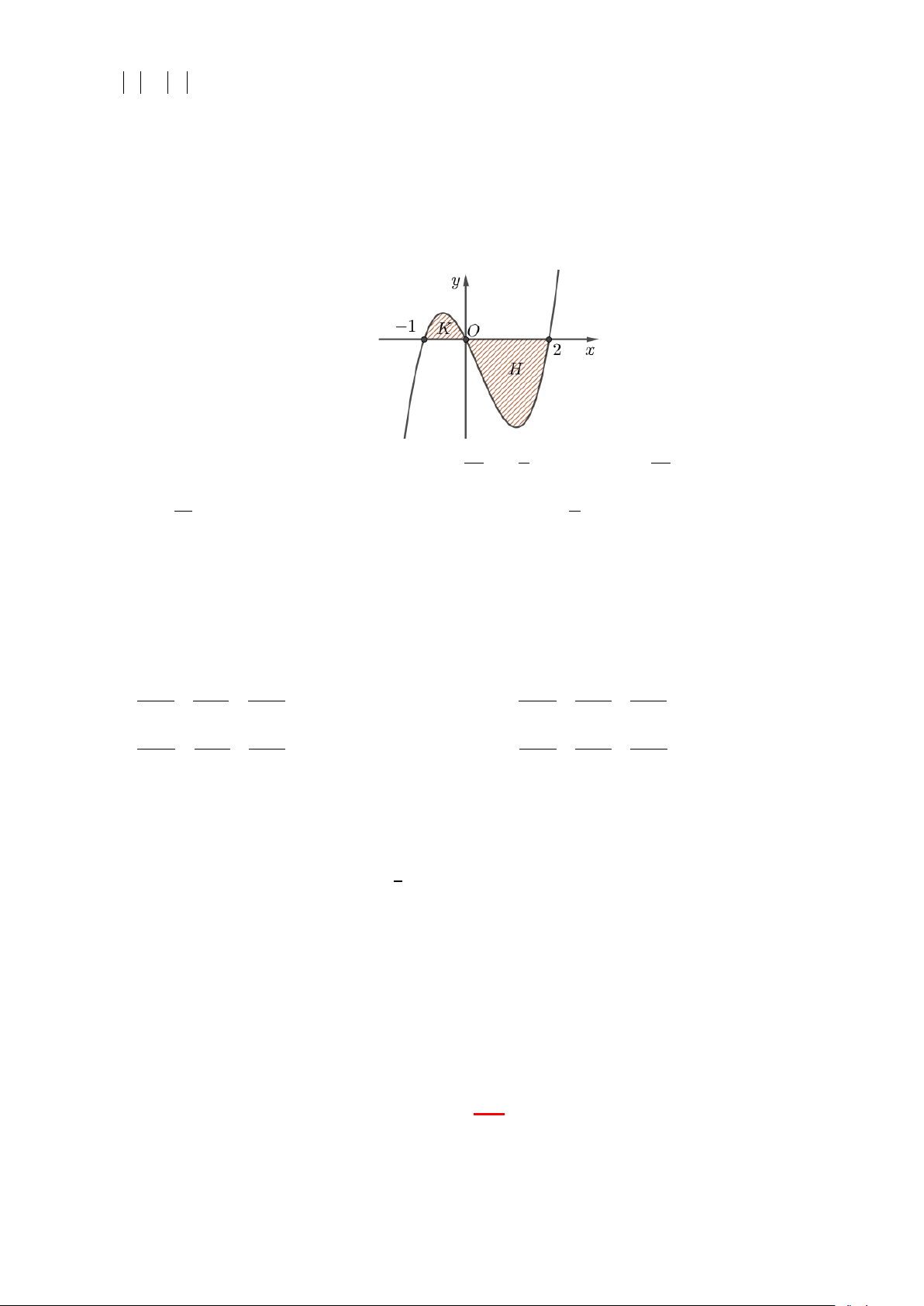
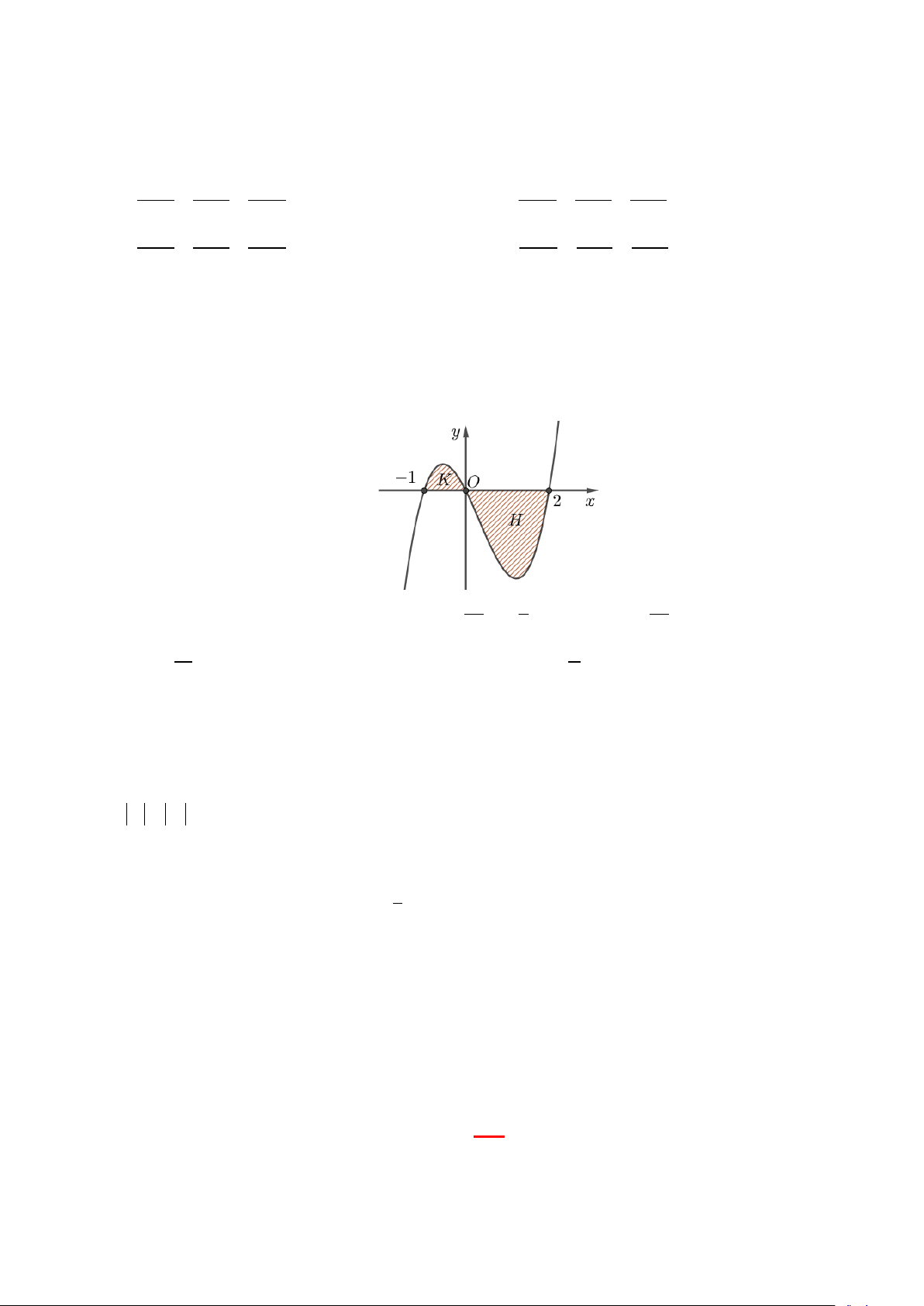
Câu 35: Cho hàm số f (x) liên tục trên . Đồ thị hàm số y = f ′(x) được cho như hình sau:
Trang 3/4 - Mã đề thi 124
Diện tích các hình phẳng (K ),(H ) lần lượt là 5 và 8 . Biết f (− ) 19 1 = , tính f (2) . 12 3 12 A. f ( ) 11 2 = . B. f ( ) 2 2 = − . C. f (2) = 0 . D. f (2) = 3. 6 3
Câu 36: Gọi z , z là hai nghiệm phức của phương trình 2 + + = . Tính giá trị của biểu thức 1 2 z 2z 10 0 2 2
A = z + z . 1 2 A. 20. B. 19. C. 17. D. 10.
Câu 37: Biết phương trình 2z + 2z + 26 = 0 có hai nghiệm phức z , z . Xét các khẳng định: 1 2 (1): z z = 26 1 2
(2): z là số phức liên hợp của z 1 2 (3): z + z = 2 − 1 2 (4): z > z 1 2
Hỏi có bao nhiêu khẳng định đúng? A. 2. B. 1. C. 4. D. 3. 9 3
Câu 38: Biết f (x) là hàm số liên tục trên và f
∫ (x)dx = 9 . Tính f (3x)dx ∫ . 0 0 3 3 3 3 A. f ∫ (3x)dx = 4. B. f ∫ (3x)dx =1. C. f ∫ (3x)dx = 2. D. f ∫ (3x)dx = 3. 0 0 0 0
Câu 39: Trong không gian Oxyz , cho mặt phẳng (P):x + y + z −6 = 0 và đường thẳng x = t
d :y =1−t ,(t ∈). Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông z =1+ 2t góc với d .
A. x − 2 y +1 z −5 − + + ∆ : = = .
B. x 3 y 1 z 2 ∆ : = = . 1 1 − 2 2 1 − 5
C. x − 2 y +1 z −5 − + + ∆ : = = .
D. x 3 y 1 z 2 ∆ : = = . 3 1 − 2 − 1 1 − 2
Câu 40: Trong không gian Oxyz , cho điểm M (1;2;3). Hỏi có bao nhiêu mặt phẳng đi qua M cắt các
tia Ox,Oy,Oz lần lượt tại ba điểm ,
A B,C (không trùng gốc tọa độ) sao cho OA = OB = OC . A. 1. B. 2. C. 4. D. 3.
II. PHẦN TỰ LUẬN: (2,0 ĐIỂM)
Câu 1: Tính modun của số phức z biết z = (4 + 3i).i
Câu 2: Trong không gian Oxyz , cho mặt phẳng (P): x + y + z −3 = 0 và đường thẳng x = t
d : y =1−t ,(t ∈) . z = t
a) Gọi A là giao điểm của đường thẳng d và mặt phẳng (P) . Tìm tọa độ điểm A .
b) Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông góc với d . Hết
Trang 4/4 - Mã đề thi 124
UBND TỈNH BÌNH PHƯỚC
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2023-2024
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN
Thời gian làm bài: 90 phút
(40 câu trắc nghiệm – 02 câu tự luận) ĐỀ CHÍNH THỨC
(Đề thi gồm 04 trang) Mã đề thi 235
Họ và tên thí sinh: …………………………………… Số báo danh: ……………….
I. PHẦN TRẮC NGHIỆM: (8,0 ĐIỂM)
Câu 1: Trong không gian Oxyz , đường thẳng đi qua gốc tọa độ và điểm A(1;2;3) có phương trình là x = t A. x − y − z −
y = 2t ,t ∈ . B. 1 2 3 = =
. C. 3x + 2y + z − 6 = 0. D. x + 2y + 3z − 6 = 0. 3 2 1 z = 3t x = t
Câu 2: Trong không gian Oxyz , cho đường thẳng d :y =1−t ,(t ∈) . Hỏi điểm nào sau đây thuộc z =1+ t đường thẳng d . A. M 1;1;1 . B. M 1;0; 1 − . C. M 1; 1; − 1 . D. M 0;1;1 . 1 ( ) 3 ( ) 4 ( ) 2 ( )
Câu 3: Cho hàm số y = f (x) liên tục trên [a;b] . Khi đó diện tích S của hình phẳng giới hạn bởi đồ thị
hàm số y = f (x) , trục hoành và hai đường thẳng x = a,x = b là b b b b
A. S = f (x)dx ∫ .
B. S =π f (x)dx ∫ . C. 2
S = f (x)dx ∫ . D. 2
S = π f (x)dx ∫ . a a a a
Câu 4: Trong không gian Oxyz , tọa độ hình chiếu vuông góc của điểm M (1;2;3) lên mặt phẳng (Oxy) là A. (1;0;0). B. (0;0;3). C. (1;2;0). D. (1;0;3).
Câu 5: Trong không gian Oxyz , mặt cầu có tâm I (1;0;0) và đi qua điểm M (2;1;0) có phương trình là A. (x + )2 2 2
1 + y + z = 2. B. (x + )2 2 2
1 + y + z = 2.C. (x − )2 2 2
1 + y + z = 2. D. (x − )2 2 2 1 + y + z = 2.
Câu 6: Trong tập số phức, nghiệm có phần ảo dương của phương trình 2z + 4z +5 = 0 là A. z = 2 − + i .
B. z = 2 + 3i . C. z = 2 − + 2i . D. z = 2 − − i .
Câu 7: Cho hàm số f (x) 4
= 2x − 5x . Khẳng định nào dưới đây đúng?
A. ∫ f (x) 2 5
dx = x − x + C .
B. ∫ f (x) 2 5
dx = x − 5x + C . C. 1 1 ∫ f (x) 5
dx = 2x − x + C .
D. ∫ f (x) 2 5
dx = x − x + C . 2 5
Câu 8: Trong không gian Oxyz , cho mặt phẳng (P):x − 2y + z +3 = 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng (P). A. n = (2; 4; − 2 − ). B. n = (1;1;3). C. n = (1; 2 − ; ) 1 . D. n = (1; 2 − ;3).
Câu 9: Tìm nguyên hàm của hàm số ( ) 7x f x = . x x 1 +
A. 7x = 7x dx ln 7 + C ∫ . B. x 7 7 dx = + C ∫ . C. x 7 7 dx = + C x x dx + = + C ln 7 ∫ . D. 1 7 7 ∫ . x +1
Câu 10: Tìm số phức z biết 4z + 5z = 27 − 7i .
A. z = −3− 7i .
B. z = 3+ 7i .
C. z = 3− 7i .
D. z = −3+ 7i .
Câu 11: Nếu u = u(x), v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [ ;ab] . Khẳng định nào sau đây là đúng ?
Trang 1/4 - Mã đề thi 235 b b b b b b b a
A. u.dv = u. b v − u.du ∫ ∫
. B. u.dv = u. b v − . v dv ∫ ∫
. C. u.dv = u. b v − . v du ∫ ∫
. D. u.dv = u.v |b − v du ∫ a . ∫ . a a a a a a a a a a b
Câu 12: Trong không gian Oxyz , cho mặt phẳng (P):2x − y + z −3 = 0 . Điểm nào trong các điểm dưới đây thuộc (P) . A. M 1;1;0 . B. M 0;0; 3 − . C. M 1;0;1 . D. M 0;1;2 . 3 ( ) 1 ( ) 4 ( ) 2 ( ) x = 1 − − 2t
Câu 13: Trong không gian Oxyz , cho hai đường thẳng x 1 : y z d
− = = và d :y = 2−t , t∈ . 2 ( ) 1 2 1 1 − z = 3+ t
Vị trí tương đối của d và d là 1 2 A. Song song. B. Cắt nhau. C. Chéo nhau. D. Trùng nhau.
Câu 14: Cho hai số phức z 3i và z 1i. Phần ảo của số phức z z bằng 1 2 1 2 A. i − . B. 1 − . C. 4 . D. 4i .
Câu 15: Số phức liên hợp của số phức z =1− 2i là A. z = 1 − + 2i .
B. z = 2 −i .
C. z =1+ 2i . D. z = 1 − − 2i .
Câu 16: Biết F(x) là nguyên hàm của hàm số f (x) trên đoạn [a;b]. Chọn mệnh đề đúng. b b b b
A. f (x)dx = F(a).F(b) ∫
. B. f (x)dx = F(a) − F(b) ∫
.C. f (x)dx = F(b) + F(a) ∫
. D. f (x)dx = F(b) − F(a) ∫ . a a a a 3 5 5
Câu 17: Cho f (x)dx = 2 − ∫
, f (x)dx = 3 − ∫
. Khi đó f (x)dx ∫ có giá trị là 1 3 1 A. 5. B. 5. − C. 1. − D. 1.
Câu 18: Trong không gian Oxyz , cho hai điểm A(1;0;− ) 1 và B(1;2; )
1 . Phương trình mặt phẳng trung
trực của đoạn AB là
A. y + z − 2 = 0.
B. x + y − 2 = 0.
C. y + z +1= 0.
D. y + z −1= 0. Câu 19: Cho hàm số 2
f (x) xác định trên 1 \
và thỏa mãn f ′(x) =
, f (0) =1 và f ( ) 1 = 2 . Giá 2 2x −1
trị của biểu thức f (− ) 1 + f (3) bằng A. 2 + ln15. B. 4 + ln15. C. ln15. D. 3+ ln15.
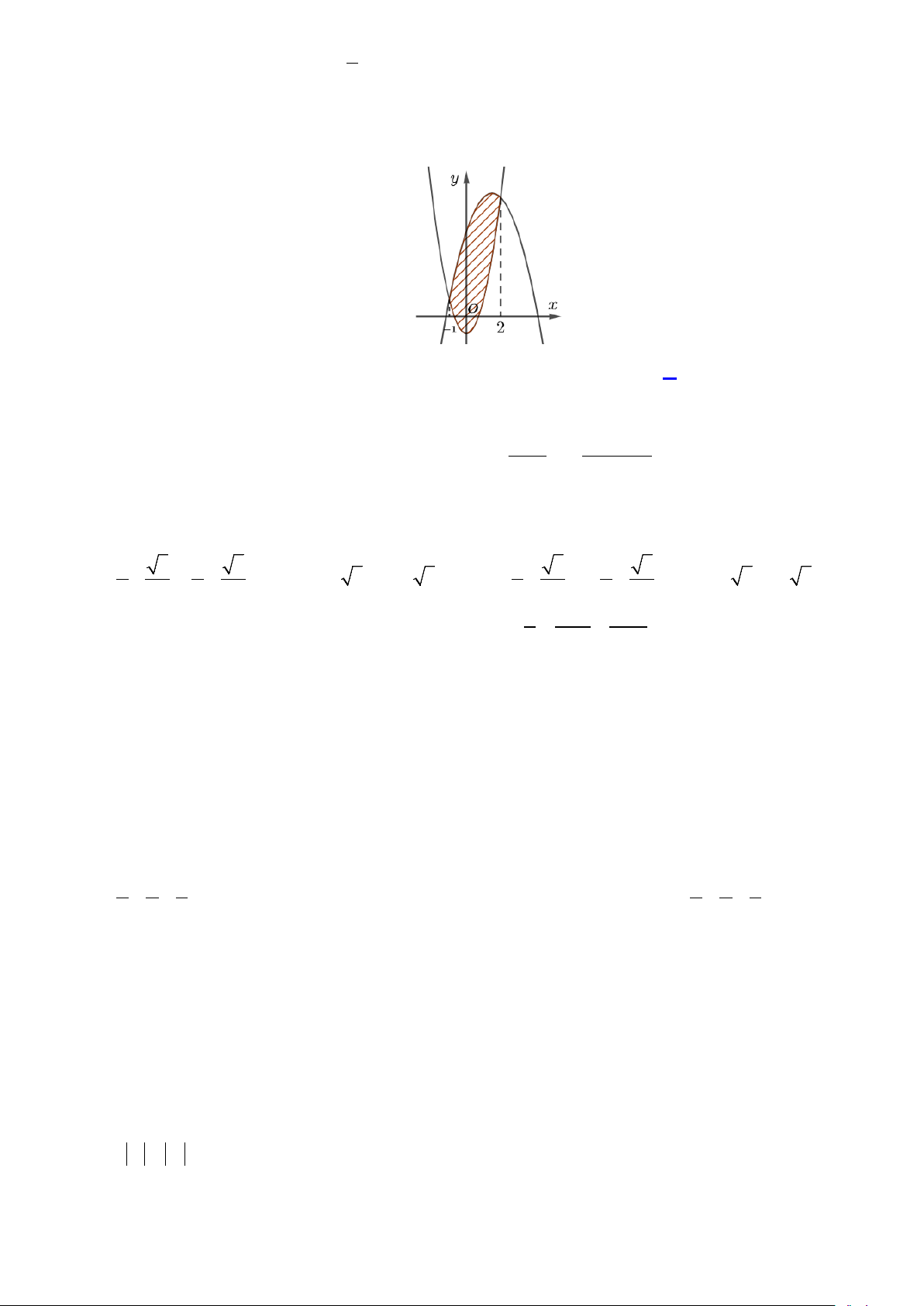
Câu 20: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x và trục hoành. Khẳng định nào đúng? 2 2 2 2
A. S = ∫(x −2x)2 2 dx . B. S = ∫( 2
2x − x )dx . C. S =π ∫( 2
2x − x )dx . D. S = ∫( 2x − 2x)dx . 0 0 0 0
Câu 21: Trong không gian Oxyz , mặt cầu có tâm I (1;1; )
1 và bán kính R = 5 có phương trình là
A. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 5.
B. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 25.
C. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 25.
D. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 5.
Câu 22: Trong không gian Oxyz , cho hai điểm A(1;0; 3 − ) và B(1;1; )
1 . Tọa độ của vectơ AB là A. 1 1; ; 1 − . B. (0;1;4). C. (2;1; 2 − ). D. (0; 1 − ; 4 − ). 2
Câu 23: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = −x + 2x − 2, trục hoành và các đường
thẳng x = 0, x = 3. A. 5. B. 3. C. 4 . D. 6 .
Câu 24: Số phức có phần thực bằng 3 và phần ảo bằng 4 là A. 3− 4i . B. 3+ 4i . C. 4 −3i . D. 4 + 3i .
Câu 25: Cho hai số phức z = 3− 2i và z = 2 + i . Số phức z − z bằng 1 2 1 2 A. 1 − + 3i . B. 1 − − 3i . C. 1+ 3i . D. 1− 3i .
Trang 2/4 - Mã đề thi 235 2 − 3 Câu 26: Nếu ( )d = 4 − ∫ f x x thì 1 f
∫ (x)dx bằng − 2 3 2 A. 3. B. 2. C. 1. − D. 3. −
Câu 27: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2 y = 2x −1 và 2
y = −x + 3x + 5 (miền gạch
sọc trong hình vẽ sau) được tính theo công thức nào sau đây? 2 2 2 2
A. ∫ ( 2x +3x−4)dx. B. ∫ ( 2x +3x+ 4)dx . C. ∫ ( 2
3x − 3x − 6)dx. D. ∫ ( 2 3
− x + 3x + 6)dx . 1 − 1 − 1 − 1 −
Câu 28: Khẳng định nào sau đây là sai? f (x) f (x)dx A. ∫ f
∫ (x)− g(x) dx = f
∫ (x)dx− g
∫ (x)dx . B. dx = ∫ . g(x) g(x).dx ∫ C. f
∫ (x)+ g(x) dx = f
∫ (x)dx+ g
∫ (x)dx. D. kf
∫ (x)dx = k f
∫ (x)dx , k ≠ 0.
Câu 29: Phương trình 2z − z +1= 0 có hai nghiệm là A. 1 3 1 3 − i; + .i B. 1
− − 3i; −1+ 3i . C. 1 3 1 3 − − i; − +
.i D. 1− 3i; 1+ 3i . 2 2 2 2 2 2 2 2
Câu 30: Trong không gian Oxyz , cho đường thẳng x y +1 z + 2 d : = =
. Vectơ nào dưới đây là một 1 1 − 2
vectơ chỉ phương của đường thẳng d . A. u = (1; 1; − 2). B. u = (0;1;2). C. u = (0; 1 − ; 2 − ). D. u = (1; 1; − ) 1 .
Câu 31: Chọn khẳng định đúng?
A. sin xdx = sin x + C ∫ . B. sin = cos + ∫ xdx
x C . C. sin xdx = −cos x + C ∫
. D. sin xdx = −sin x + C ∫ .
Câu 32: Cho a,b∈ và thỏa mãn (a + bi)i − 2a =1+3i , với i là đơn vị ảo. Giá trị a −b bằng A. 10. B. 4 − . C. 10 − . D. 4 .
Câu 33: Trong không gian Oxyz , phương trình mặt phẳng đi qua 3 điểm A(1;0;0), B(0;2;0) , C (0;0;3) là A. x y z + + =1.
B. x + 2y + 3z =1.
C. x + 2y + 3z +1= 0. D. x y z + + +1 = 0. 1 2 3 1 2 3 9 3
Câu 34: Biết f (x) là hàm số liên tục trên và f
∫ (x)dx = 9 . Tính f (3x)dx ∫ . 0 0 3 3 3 3 A. f ∫ (3x)dx = 2. B. f ∫ (3x)dx = 4. C. f ∫ (3x)dx = 3. D. f ∫ (3x)dx =1. 0 0 0 0
Câu 35: Biết phương trình 2z + 2z + 26 = 0 có hai nghiệm phức z , z . Xét các khẳng định: 1 2 (1): z z = 26 1 2
(2): z là số phức liên hợp của z 1 2 (3): z + z = 2 − 1 2 (4): z > z 1 2
Hỏi có bao nhiêu khẳng định đúng? A. 4. B. 3. C. 2. D. 1.
Trang 3/4 - Mã đề thi 235
Câu 36: Gọi z , z là hai nghiệm phức của phương trình 2z + 2z +10 = 0 . Tính giá trị của biểu thức 1 2 2 2
A = z + z . 1 2 A. 20. B. 10. C. 19. D. 17.
Câu 37: Trong không gian Oxyz , (P):2y + 2z −3 = 0 và mặt cầu (S) (x − )2 2 :
1 + y + (z − 2)2 = 4 . Có bao
nhiêu điểm M thuộc mặt phẳng (Oxy) với hoành độ nguyên dương sao cho từ M kẻ được ít nhất
một tiếp tuyến tới (S) đồng thời vuông góc với (P) . A. 2. B. 1. C. 6. D. 5.
Câu 38: Cho hàm số f (x) liên tục trên . Đồ thị hàm số y = f ′(x) được cho như hình sau:
Diện tích các hình phẳng (K ),(H ) lần lượt là 5 và 8 . Biết f (− ) 19 1 = , tính f (2) . 12 3 12 A. f ( ) 11 2 = . B. f (2) = 3. C. f ( ) 2 2 = − . D. f (2) = 0 . 6 3
Câu 39: Trong không gian Oxyz , cho mặt phẳng (P):x + y + z −6 = 0 và đường thẳng x = t
d :y =1−t ,(t ∈). Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông z =1+ 2t góc với d .
A. x −3 y +1 z + 2 − + − ∆ : = = .
B. x 2 y 1 z 5 ∆ : = = . 1 1 − 2 3 1 − 2 −
C. x − 2 y +1 z −5 − + + ∆ : = = .
D. x 3 y 1 z 2 ∆ : = = . 1 1 − 2 2 1 − 5
Câu 40: Trong không gian Oxyz , cho điểm M (1;2;3). Hỏi có bao nhiêu mặt phẳng đi qua M cắt các
tia Ox,Oy,Oz lần lượt tại ba điểm ,
A B,C (không trùng gốc tọa độ) sao cho OA = OB = OC . A. 4. B. 2. C. 3. D. 1.
II. PHẦN TỰ LUẬN: (2,0 ĐIỂM)
Câu 1: Tính modun của số phức z biết z = (4 +3i).i
Câu 2: Trong không gian Oxyz , cho mặt phẳng (P): x + y + z −3 = 0 và đường thẳng x = t
d : y =1−t ,(t ∈) . z = t
a) Gọi A là giao điểm của đường thẳng d và mặt phẳng (P) . Tìm tọa độ điểm A .
b) Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông góc với d . Hết
Trang 4/4 - Mã đề thi 235
UBND TỈNH BÌNH PHƯỚC
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2023-2024
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN
Thời gian làm bài: 90 phút
(40 câu trắc nghiệm – 02 câu tự luận) ĐỀ CHÍNH THỨC
(Đề thi gồm 04 trang) Mã đề thi 346
Họ và tên thí sinh: …………………………………… Số báo danh: ……………….
I. PHẦN TRẮC NGHIỆM: (8,0 ĐIỂM)
Câu 1: Trong không gian Oxyz , cho mặt phẳng (P):x − 2y + z +3 = 0. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng (P). A. n = (1; 2 − ; ) 1 . B. n = (1;1;3). C. n = (1; 2 − ;3). D. n = (2; 4; − 2 − ).
Câu 2: Số phức liên hợp của số phức z =1− 2i là A. z = 1 − + 2i .
B. z = 2 −i .
C. z =1+ 2i . D. z = 1 − − 2i .
Câu 3: Biết F(x) là nguyên hàm của hàm số f (x) trên đoạn [ ;ab]. Chọn mệnh đề đúng. b b b b
A. f (x)dx = F(a).F(b) ∫
. B. f (x)dx = F(a) − F(b) ∫
. C. f (x)dx = F(b) + F(a) ∫
. D. f (x)dx = F(b) − F(a) ∫ . a a a a
Câu 4: Trong không gian + +
Oxyz , cho đường thẳng x y 1 z 2 d : = =
. Vectơ nào dưới đây là một vectơ 1 1 − 2
chỉ phương của đường thẳng d . A. u = (0;1;2). B. u = (1; 1; − ) 1 . C. u = (1; 1; − 2). D. u = (0; 1 − ; 2 − ).
Câu 5: Trong không gian Oxyz , cho hai điểm A(1;0; 3 − ) và B(1;1; )
1 . Tọa độ của vectơ AB là A. (0;1;4). B. (0; 1 − ; 4 − ). C. (2;1; 2 − ). D. 1 1; ; 1 − . 2
Câu 6: Số phức có phần thực bằng 3 và phần ảo bằng 4 là A. 3− 4i . B. 3+ 4i . C. 4 −3i . D. 4 + 3i .
Câu 7: Cho hai số phức z = 3− 2i và z = 2 + i . Số phức z − z bằng 1 2 1 2 A. 1+ 3i . B. 1− 3i . C. 1 − − 3i . D. 1 − + 3i .
Câu 8: Trong không gian Oxyz , phương trình mặt phẳng đi qua ba điểm A(1;0;0), B(0;2;0) và C (0;0;3) là
A. x + 2y + 3z =1.
B. x + 2y + 3z +1= 0. C. x y z + + =1. D. x y z + + +1 = 0. 1 2 3 1 2 3
Câu 9: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = −x + 2x − 2, trục hoành và các đường
thẳng x = 0, x = 3. A. 5. B. 3. C. 6 . D. 4 .
Câu 10: Cho hai số phức z 3i và z 1i. Phần ảo của số phức z z bằng 1 2 1 2 A. 4i . B. 1 − . C. i − . D. 4 .
Câu 11: Tìm số phức z biết 4z + 5z = 27 − 7i .
A. z = −3− 7i .
B. z = −3+ 7i .
C. z = 3− 7i .
D. z = 3+ 7i .
Câu 12: Khẳng định nào sau đây là sai? A. f
∫ (x)+ g(x) dx = f
∫ (x)dx+ g
∫ (x)dx. B. kf
∫ (x)dx = k f
∫ (x)dx , k ≠ 0. f (x) f (x)dx C. ∫ dx = ∫ . D. f
∫ (x)− g(x) dx = f
∫ (x)dx− g ∫ (x)dx . g(x) g(x).dx ∫
Câu 13: Chọn khẳng định đúng?
A. sin xdx = −cos x +C ∫
. B. sin xdx = −sin x +C ∫
. C. sin xdx = sin x + C ∫ . D. sin = cos + ∫ xdx x C .
Trang 1/4 - Mã đề thi 346
Câu 14: Tìm nguyên hàm của hàm số ( ) 7x f x = . x x 1 + A. x x 1 7 dx 7 + = + C ∫ . B. x 7 7 dx = + C ∫ .
C. 7x = 7x dx ln 7 + C x 7 7 dx = + C ln 7 ∫ . D. ∫ . x +1
Câu 15: Trong không gian Oxyz , mặt cầu có tâm I (1;1; )
1 và bán kính R = 5 có phương trình là
A. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 5.
B. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 25.
C. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 25.
D. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 5.
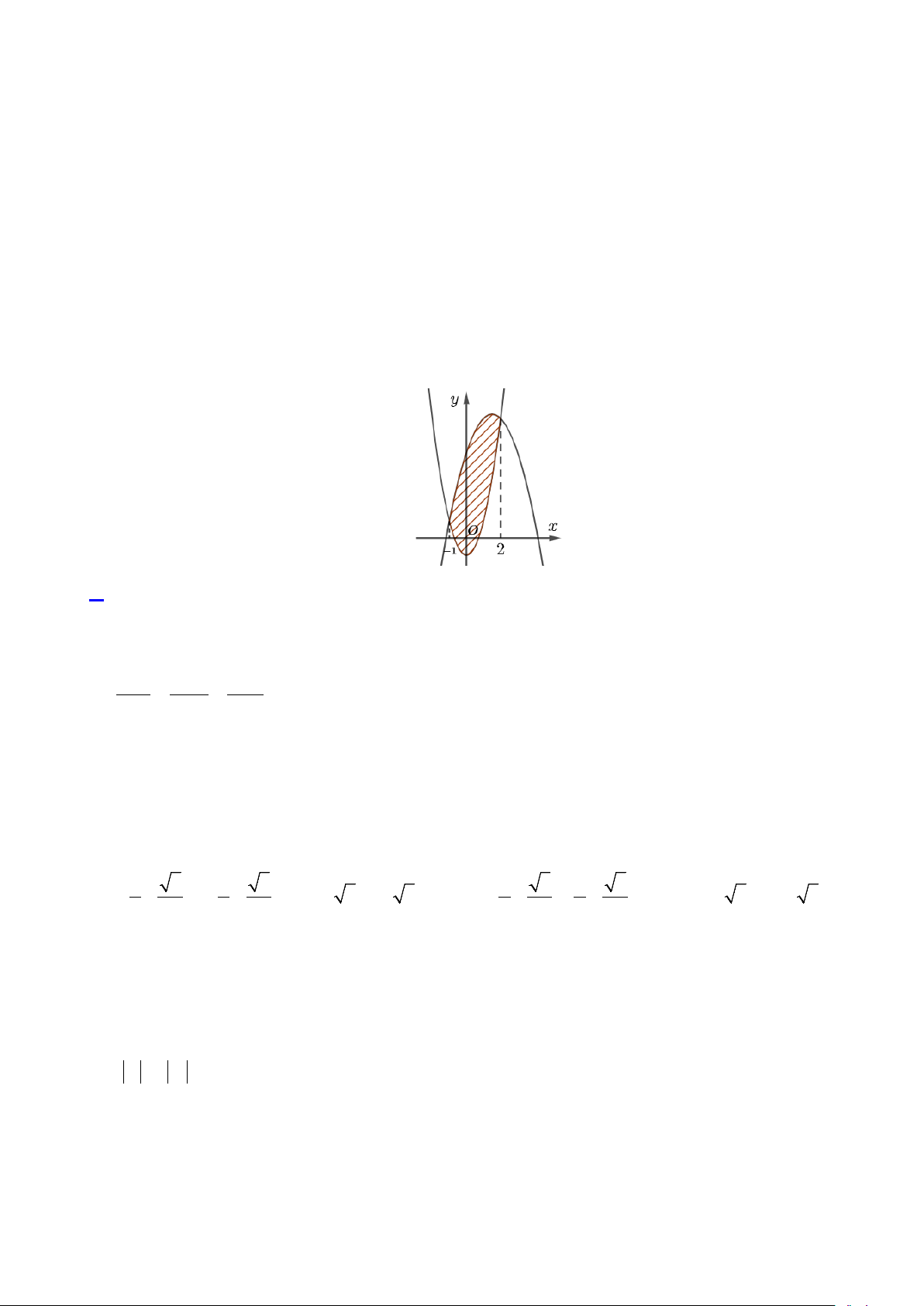
Câu 16: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x và trục hoành. Khẳng định nào đúng? 2 2 2 2
A. S = ∫( 2x −2x)dx . B. S =π ∫( 2
2x − x )dx .
C. S = ∫(x −2x)2 2 dx . D. S = ∫( 2
2x − x )dx . 0 0 0 0 2 − 3 Câu 17: Nếu ( )d = 4 − ∫ f x x thì 1 f
∫ (x)dx bằng − 2 3 2 A. 3. B. 2. C. 3. − D. 1. −
Câu 18: Cho hàm số f (x) 4
= 2x − 5x . Khẳng định nào dưới đây đúng?
A. ∫ f (x) 2 5
dx = x − 5x + C .
B. ∫ f (x) 5
dx = 2x − x + C . C. 1 1 ∫ f (x) 2 5
dx = x − x + C .
D. ∫ f (x) 2 5
dx = x − x + C . 2 5
Câu 19: Trong không gian Oxyz , mặt cầu có tâm I (1;0;0) và đi qua điểm M (2;1;0) có phương trình là A. (x − )2 2 2
1 + y + z = 2. B. (x − )2 2 2
1 + y + z = 2.C. (x + )2 2 2
1 + y + z = 2. D. (x + )2 2 2 1 + y + z = 2.
Câu 20: Nếu u = u(x), v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [ ;ab]. Khẳng định nào sau đây là đúng ? b b b b b a b b
A. u.dv = u. b v − . v dv ∫ ∫
. B. u.dv = u. b v − u.du ∫ ∫
. C. u.dv = u.v |b − v du ∫ b u dv = u v − v du a . ∫ . D. . . . ∫ ∫ . a a a a a a a a b a a
Câu 21: Trong không gian Oxyz , cho hai điểm A(1;0;− ) 1 và B(1;2; )
1 . Phương trình mặt phẳng trung
trực của đoạn AB là
A. y + z −1= 0.
B. y + z − 2 = 0.
C. x + y − 2 = 0.
D. y + z +1= 0.
Câu 22: Trong không gian Oxyz , cho mặt phẳng (P):2x − y + z −3 = 0 . Điểm nào trong các điểm dưới đây thuộc (P) . A. M 1;1;0 . B. M 1;0;1 . C. M 0;1;2 . D. M 0;0; 3 − . 4 ( ) 3 ( ) 1 ( ) 2 ( )
Câu 23: Cho hàm số y = f (x) liên tục trên [ ;ab]. Khi đó diện tích S của hình phẳng giới hạn bởi đồ
thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a,x = b là b b b b A. 2
S = f (x)dx ∫ . B. 2
S = π f (x)dx ∫ .
C. S =π f (x)dx ∫ .
D. S = f (x)dx ∫ . a a a a x = 1 − − 2t
Câu 24: Trong không gian Oxyz , cho hai đường thẳng x 1 : y z d
− = = và d :y = 2−t , t∈ . 2 ( ) 1 2 1 1 − z = 3+ t
Vị trí tương đối của d và d là 1 2 A. Song song. B. Chéo nhau. C. Trùng nhau. D. Cắt nhau.
Câu 25: Cho hàm số f (x) xác định trên 1 2 \
và thỏa mãn f ′(x) =
, f (0) =1 và f ( ) 1 = 2 . Giá 2 2x −1
trị của biểu thức f (− ) 1 + f (3) bằng A. 4 + ln15. B. ln15. C. 2 + ln15. D. 3+ ln15.
Trang 2/4 - Mã đề thi 346 x = t
Câu 26: Trong không gian Oxyz , cho đường thẳng d :y =1−t ,(t ∈) . Hỏi điểm nào sau đây thuộc z =1+ t đường thẳng d . A. M 0;1;1 . B. M 1;1;1 . C. M 1;0; 1 − . D. M 1; 1; − 1 . 3 ( ) 4 ( ) 2 ( ) 1 ( )
Câu 27: Trong không gian Oxyz , tọa độ hình chiếu vuông góc của điểm M (1;2;3) lên mặt phẳng (Oxy) là A. (0;0;3). B. (1;0;3). C. (1;0;0). D. (1;2;0). 3 5 5
Câu 28: Cho f (x)dx = 2 − ∫
, f (x)dx = 3 − ∫
. Khi đó f (x)dx ∫ có giá trị là 1 3 1 A. 5. − B. 1. C. 1. − D. 5.
Câu 29: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2 y = 2x −1 và 2
y = −x + 3x + 5 (miền gạch
sọc trong hình vẽ sau) được tính theo công thức nào sau đây? 2 2 2 2 A. ∫ ( 2 3
− x + 3x + 6)dx . B. ∫ ( 2x +3x − 4)dx. C. ∫ ( 2
3x − 3x − 6)dx. D. ∫ ( 2x +3x + 4)dx . 1 − 1 − 1 − 1 −
Câu 30: Trong không gian Oxyz , đường thẳng đi qua gốc tọa độ và điểm A(1;2;3) có phương trình là x = t
A. x −1 y − 2 z −3 = =
. B. x + 2y + 3z − 6 = 0. C. 3x + 2y + z − 6 = 0. D. y = 2t ,t ∈ . 3 2 1 z = 3t
Câu 31: Trong tập số phức, nghiệm có phần ảo dương của phương trình 2z + 4z +5 = 0 là A. z = 2 − + i .
B. z = 2 + 3i . C. z = 2 − − i . D. z = 2 − + 2i .
Câu 32: Cho a,b∈ và thỏa mãn (a + bi)i − 2a =1+ 3i , với i là đơn vị ảo. Giá trị a −b bằng A. 4 . B. 10. C. 4 − . D. 10 − .
Câu 33: Phương trình 2z − z +1= 0 có hai nghiệm là A. 1 3 1 3 − − i; − +
.iB. 1− 3i; 1+ 3i . C. 1 3 1 3 − i; + .i D. 1
− − 3i; −1+ 3i . 2 2 2 2 2 2 2 2 9 3
Câu 34: Biết f (x) là hàm số liên tục trên và f
∫ (x)dx = 9 . Tính f (3x)dx ∫ . 0 0 3 3 3 3 A. f ∫ (3x)dx = 3. B. f ∫ (3x)dx = 2. C. f ∫ (3x)dx = 4. D. f ∫ (3x)dx =1. 0 0 0 0
Câu 35: Gọi z , z là hai nghiệm phức của phương trình 2z + 2z +10 = 0 . Tính giá trị của biểu thức 1 2 2 2
A = z + z . 1 2 A. 10. B. 19. C. 20. D. 17.
Câu 36: Trong không gian Oxyz , cho điểm M (1;2;3). Hỏi có bao nhiêu mặt phẳng đi qua M cắt các
tia Ox,Oy,Oz lần lượt tại ba điểm ,
A B,C (không trùng gốc tọa độ) sao cho OA = OB = OC . A. 3. B. 1. C. 4. D. 2.
Trang 3/4 - Mã đề thi 346
Câu 37: Trong không gian Oxyz , cho mặt phẳng (P):x + y + z −6 = 0 và đường thẳng x = t
d :y =1−t ,(t ∈). Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông z =1+ 2t góc với d .
A. x −3 y +1 z + 2 − + − ∆ : = = .
B. x 2 y 1 z 5 ∆ : = = . 1 1 − 2 3 1 − 2 −
C. x −3 y +1 z + 2 − + − ∆ : = = .
D. x 2 y 1 z 5 ∆ : = = . 2 1 − 5 1 1 − 2
Câu 38: Trong không gian Oxyz , (P):2y + 2z −3 = 0 và mặt cầu (S) (x − )2 2 :
1 + y + (z − 2)2 = 4 . Có bao
nhiêu điểm M thuộc mặt phẳng (Oxy) với hoành độ nguyên dương sao cho từ M kẻ được ít nhất
một tiếp tuyến tới (S) đồng thời vuông góc với (P) . A. 1. B. 2. C. 5. D. 6.
Câu 39: Cho hàm số f (x) liên tục trên . Đồ thị hàm số y = f ′(x) được cho như hình sau:
Diện tích các hình phẳng (K ),(H ) lần lượt là 5 và 8 . Biết f (− ) 19 1 = , tính f (2) . 12 3 12 A. f ( ) 11 2 = . B. f (2) = 0 . C. f ( ) 2 2 = − . D. f (2) = 3. 6 3
Câu 40: Biết phương trình 2z + 2z + 26 = 0 có hai nghiệm phức z , z . Xét các khẳng định: 1 2 (1): z z = 26 1 2
(2): z là số phức liên hợp của z 1 2 (3): z + z = 2 − 1 2 (4): z > z 1 2
Hỏi có bao nhiêu khẳng định đúng? A. 2. B. 1. C. 4. D. 3.
II. PHẦN TỰ LUẬN: (2,0 ĐIỂM)
Câu 1: Tính modun của số phức z biết z = (4 + 3i).i
Câu 2: Trong không gian Oxyz , cho mặt phẳng (P): x + y + z −3 = 0 và đường thẳng x = t
d : y =1−t ,(t ∈) . z = t
a) Gọi A là giao điểm của đường thẳng d và mặt phẳng (P) . Tìm tọa độ điểm A .
b) Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông góc với d . Hết
Trang 4/4 - Mã đề thi 346
UBND TỈNH BÌNH PHƯỚC
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2023-2024
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN
Thời gian làm bài: 90 phút
(40 câu trắc nghiệm – 02 câu tự luận) ĐỀ CHÍNH THỨC
(Đề thi gồm 04 trang) Mã đề thi 457
Họ và tên thí sinh: …………………………………… Số báo danh: ……………….
I. PHẦN TRẮC NGHIỆM: (8,0 ĐIỂM)
Câu 1: Cho hai số phức z = 3− 2i và z = 2 + i . Số phức z − z bằng 1 2 1 2 A. 1− 3i . B. 1 − − 3i . C. 1 − + 3i . D. 1+ 3i .
Câu 2: Tìm số phức z biết 4z + 5z = 27 − 7i .
A. z = −3− 7i .
B. z = 3− 7i .
C. z = −3+ 7i .
D. z = 3+ 7i .
Câu 3: Cho hàm số y = f (x) liên tục trên [ ;ab] . Khi đó diện tích S của hình phẳng giới hạn bởi đồ
thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a,x = b là b b b b
A. S =π f (x)dx ∫ .
B. S = f (x)dx ∫ . C. 2
S = f (x)dx ∫ . D. 2
S = π f (x)dx ∫ . a a a a
Câu 4: Nếu u = u(x), v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a;b] . Khẳng định nào sau đây là đúng ? b a b b b b b b
A. u.dv = u.v |b − v du ∫ b u dv = u v − v du b u dv = u v − u du b u dv = u v − v dv a . ∫ . B. . . . ∫ ∫ . C. . . . ∫ ∫ . D. . . . ∫ ∫ . a a a a b a a a a a a
Câu 5: Phương trình 2z − z +1= 0 có hai nghiệm là A. 1
− − 3i; −1+ 3i . B. 1 3 1 3 − i; +
.i C. 1− 3i; 1+ 3i . D. 1 3 1 3 − − i; − + .i 2 2 2 2 2 2 2 2
Câu 6: Trong không gian Oxyz , phương trình mặt phẳng đi qua 3 điểm A(1;0;0), B(0;2;0) , C (0;0;3) là A. x y z + + +1 = 0.
B. x + 2y + 3z +1= 0. C. x y z + + = 1.
D. x + 2y + 3z =1. 1 2 3 1 2 3
Câu 7: Tìm nguyên hàm của hàm số ( ) 7x f x = . x x 1 + A. x 7 7 dx = + C ∫ . B. x x 1 7 dx 7 + = + C x 7 7 dx = + C x x dx = + C ln 7 ∫ . C. ∫ . D. 7 7 ln 7 ∫ . x +1
Câu 8: Trong tập số phức, nghiệm có phần ảo dương của phương trình 2z + 4z +5 = 0 là
A. z = 2 + 3i . B. z = 2 − + 2i . C. z = 2 − − i . D. z = 2 − + i .
Câu 9: Số phức liên hợp của số phức z =1− 2i là
A. z =1+ 2i . B. z = 1 − − 2i .
C. z = 2 −i . D. z = 1 − + 2i . x = 1 − − 2t
Câu 10: Trong không gian Oxyz , cho hai đường thẳng x 1 : y z d
− = = và d :y = 2−t , t∈ . 2 ( ) 1 2 1 1 − z = 3+ t
Vị trí tương đối của d và d là 1 2 A. Trùng nhau. B. Chéo nhau. C. Song song. D. Cắt nhau. 3 5 5
Câu 11: Cho f (x)dx = 2 − ∫
, f (x)dx = 3 − ∫
. Khi đó f (x)dx ∫ có giá trị là 1 3 1 A. 5. − B. 5. C. 1. − D. 1.
Câu 12: Trong không gian Oxyz , cho hai điểm A(1;0; 3 − ) và B(1;1; )
1 . Tọa độ của vectơ AB là A. 1 1; ; 1 − . B. (2;1; 2 − ). C. (0;1;4). D. (0; 1 − ; 4 − ). 2
Trang 1/4 - Mã đề thi 457
Câu 13: Khẳng định nào sau đây là sai? A. f
∫ (x)+ g(x) dx = f
∫ (x)dx+ g
∫ (x)dx. B. f
∫ (x)− g(x) dx = f
∫ (x)dx− g ∫ (x)dx . f (x) f (x)dx C. ∫ dx = ∫ . D. kf
∫ (x)dx = k f
∫ (x)dx , k ≠ 0. g(x) g(x).dx ∫
Câu 14: Chọn khẳng định đúng?
A. sin xdx = −sin x + C ∫
. B. sin xdx = −cos x +C ∫
. C. sin xdx = sin x + C ∫ . D. sin = cos + ∫ xdx x C .
Câu 15: Cho hai số phức z 3i và z 1i. Phần ảo của số phức z z bằng 1 2 1 2 A. 4i . B. i − . C. 1 − . D. 4 .
Câu 16: Cho a,b∈ và thỏa mãn (a +bi)i − 2a =1+3i , với i là đơn vị ảo. Giá trị a −b bằng A. 10. B. 10 − . C. 4 − . D. 4 .
Câu 17: Trong không gian Oxyz , đường thẳng đi qua gốc tọa độ và điểm A(1;2;3) có phương trình là x = t
A. x −1 y − 2 z −3 = =
. B. 3x + 2y + z − 6 = 0. C. y = 2t ,t ∈ .
D. x + 2y + 3z − 6 = 0. 3 2 1 z = 3t
Câu 18: Trong không gian Oxyz , tọa độ hình chiếu vuông góc của điểm M (1;2;3) lên mặt phẳng (Oxy) là A. (1;0;3). B. (1;2;0). C. (0;0;3). D. (1;0;0). x = t
Câu 19: Trong không gian Oxyz , cho đường thẳng d :y =1−t ,(t ∈) . Hỏi điểm nào sau đây thuộc z =1+ t đường thẳng d . A. M 1;0; 1 − . B. M 1;1;1 . C. M 1; 1; − 1 . D. M 0;1;1 . 1 ( ) 3 ( ) 2 ( ) 4 ( )
Câu 20: Trong không gian Oxyz , cho mặt phẳng (P):2x − y + z −3 = 0 . Điểm nào trong các điểm
dưới đây thuộc (P) . A. M 1;0;1 . B. M 0;1;2 . C. M 0;0; 3 − . D. M 1;1;0 . 2 ( ) 4 ( ) 3 ( ) 1 ( )
Câu 21: Biết F(x) là nguyên hàm của hàm số f (x) trên đoạn [ ;ab] . Chọn mệnh đề đúng. b b b b
A. f (x)dx = F(a) − F(b) ∫
.B. f (x)dx = F(a).F(b) ∫
. C. f (x)dx = F(b) + F(a) ∫
.D. f (x)dx = F(b) − F(a) ∫ . a a a a
Câu 22: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2 y = 2x −1 và 2
y = −x + 3x + 5 (miền
gạch sọc trong hình vẽ sau) được tính theo công thức nào sau đây? 2 2 2 2 A. ∫ ( 2 3
− x + 3x + 6)dx . B. ∫ ( 2
3x − 3x − 6)dx. C. ∫ ( 2x +3x − 4)dx. D. ∫ ( 2x +3x + 4)dx . 1 − 1 − 1 − 1 −
Câu 23: Cho hàm số f (x) 4
= 2x − 5x . Khẳng định nào dưới đây đúng?
Trang 2/4 - Mã đề thi 457
A. ∫ f (x) 1 2 1 5
dx = x − x + C .
B. ∫ f (x) 2 5
dx = x − x + C . 2 5
C. ∫ f (x) 5
dx = 2x − x + C .
D. ∫ f (x) 2 5
dx = x − 5x + C .
Câu 24: Trong không gian Oxyz , mặt cầu có tâm I (1;1; )
1 và bán kính R = 5 có phương trình là
A. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 25.
B. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 25.
C. (x − )2 + ( y − )2 + (z − )2 1 1 1 = 5.
D. (x + )2 + ( y + )2 + (z + )2 1 1 1 = 5.
Câu 25: Trong không gian Oxyz , cho hai điểm A(1;0;− ) 1 và B(1;2; )
1 . Phương trình mặt phẳng
trung trực của đoạn AB là
A. y + z −1= 0.
B. y + z +1= 0.
C. x + y − 2 = 0.
D. y + z − 2 = 0.
Câu 26: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x và trục hoành. Khẳng định nào đúng? 2 2 2 2 A. S = ∫( 2
2x − x )dx . B. S =π ∫( 2
2x − x )dx .
C. S = ∫( 2x −2x)dx .
D. S = ∫(x −2x)2 2 dx . 0 0 0 0
Câu 27: Số phức có phần thực bằng 3 và phần ảo bằng 4 là A. 4 + 3i . B. 4 −3i . C. 3− 4i . D. 3+ 4i .
Câu 28: Trong không gian + +
Oxyz , cho đường thẳng x y 1 z 2 d : = =
. Vectơ nào dưới đây là một 1 1 − 2
vectơ chỉ phương của đường thẳng d . A. u = (0;1;2). B. u = (0; 1 − ; 2 − ). C. u = (1; 1; − 2). D. u = (1; 1; − ) 1 .
Câu 29: Trong không gian Oxyz , mặt cầu có tâm I (1;0;0) và đi qua điểm M (2;1;0) có phương trình là A. (x + )2 2 2
1 + y + z = 2. B. (x − )2 2 2
1 + y + z = 2. C. (x − )2 2 2
1 + y + z = 2. D. (x + )2 2 2 1 + y + z = 2. 2 − 3 Câu 30: Nếu ( )d = 4 − ∫ f x x thì 1 f
∫ (x)dx bằng − 2 3 2 A. 3. − B. 3. C. 1. − D. 2.
Câu 31: Trong không gian Oxyz , cho mặt phẳng (P):x − 2y + z +3 = 0. Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng (P). A. n = (1; 2 − ; ) 1 . B. n = (1; 2 − ;3). C. n = (1;1;3). D. n = (2; 4; − 2 − ).
Câu 32: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = −x + 2x − 2, trục hoành và các
đường thẳng x = 0, x = 3. A. 4 . B. 6 . C. 3. D. 5.
Câu 33: Cho hàm số f (x) xác định trên 1 2 \
và thỏa mãn f ′(x) =
, f (0) =1 và f ( ) 1 = 2 2 2x −1
. Giá trị của biểu thức f (− ) 1 + f (3) bằng A. 4 + ln15. B. 2 + ln15. C. 3+ ln15. D. ln15.
Câu 34: Cho hàm số f (x) liên tục trên . Đồ thị hàm số y = f ′(x) được cho như hình sau:
Trang 3/4 - Mã đề thi 457
Diện tích các hình phẳng (K ),(H ) lần lượt là 5 và 8 . Biết f (− ) 19 1 = , tính f (2) . 12 3 12 A. f ( ) 11 2 = . B. f (2) = 0 . C. f ( ) 2 2 = − . D. f (2) = 3. 6 3
Câu 35: Gọi z , z là hai nghiệm phức của phương trình 2z + 2z +10 = 0 . Tính giá trị của biểu thức 1 2 2 2
A = z + z . 1 2 A. 17. B. 10. C. 19. D. 20.
Câu 36: Trong không gian Oxyz , cho điểm M (1;2;3). Hỏi có bao nhiêu mặt phẳng đi qua M cắt
các tia Ox,Oy,Oz lần lượt tại ba điểm ,
A B,C (không trùng gốc tọa độ) sao cho OA = OB = OC . A. 3. B. 1. C. 4. D. 2.
Câu 37: Trong không gian Oxyz , cho mặt phẳng (P):x + y + z −6 = 0 và đường thẳng x = t
d :y =1−t ,(t ∈). Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và z =1+ 2t vuông góc với d .
A. x −3 y +1 z + 2 − + + ∆ : = = .
B. x 3 y 1 z 2 ∆ : = = . 2 1 − 5 1 1 − 2
C. x − 2 y +1 z −5 − + − ∆ : = = .
D. x 2 y 1 z 5 ∆ : = = . 1 1 − 2 3 1 − 2 −
Câu 38: Trong không gian Oxyz , (P):2y + 2z −3 = 0 và mặt cầu (S) (x − )2 2 :
1 + y + (z − 2)2 = 4 . Có
bao nhiêu điểm M thuộc mặt phẳng (Oxy) với hoành độ nguyên dương sao cho từ M kẻ được
ít nhất một tiếp tuyến tới (S) đồng thời vuông góc với (P) . A. 2. B. 6. C. 1. D. 5.
Câu 39: Biết phương trình 2z + 2z + 26 = 0 có hai nghiệm phức z , z . Xét các khẳng định: 1 2 (1): z z = 26 1 2
(2): z là số phức liên hợp của z 1 2 (3): z + z = 2 − 1 2 (4): z > z 1 2
Hỏi có bao nhiêu khẳng định đúng? A. 1. B. 4. C. 3. D. 2. 9 3
Câu 40: Biết f (x) là hàm số liên tục trên và f
∫ (x)dx = 9 . Tính f (3x)dx ∫ . 0 0 3 3 3 3 A. f ∫ (3x)dx = 4. B. f ∫ (3x)dx = 3. C. f ∫ (3x)dx =1. D. f ∫ (3x)dx = 2. 0 0 0 0
II. PHẦN TỰ LUẬN: (2,0 ĐIỂM)
Câu 1: Tính modun của số phức z biết z = (4 +3i).i
Câu 2: Trong không gian Oxyz , cho mặt phẳng (P): x + y + z −3 = 0 và đường thẳng x = t
d : y =1−t ,(t ∈) . z = t
a) Gọi A là giao điểm của đường thẳng d và mặt phẳng (P) . Tìm tọa độ điểm A .
b) Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông góc với d . Hết
Trang 4/4 - Mã đề thi 457 UBND TỈNH BÌNH PHƯỚC
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 NĂM HỌC 2023-2024
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN LỚP 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) ĐỀ CHÍNH THỨC
I. BẢNG ĐÁP ÁN TRẮC NGHIỆM
Đề 124 Đề 235 Đề 346 Đề 457 1. B 1. A 1. A 1. A 2. A 2. D 2. C 2. D 3. B 3. A 3. D 3. B 4. D 4. C 4. C 4. B 5. C 5. D 5. A 5. B 6. C 6. A 6. B 6. C 7. B 7. A 7. B 7. A 8. C 8. C 8. C 8. D 9. B 9. B 9. C 9. A 10. B 10. B 10. D 10. C 11. B 11. C 11. D 11. A 12. D 12. C 12. C 12. C 13. D 13. A 13. A 13. C 14. A 14. C 14. B 14. B 15. A 15. C 15. B 15. D 16. B 16. D 16. D 16. A 17. C 17. B 17. B 17. C 18. B 18. D 18. C 18. B 19. D 19. D 19. B 19. D 20. A 20. B 20. D 20. A 21. A 21. C 21. A 21. D 22. D 22. B 22. B 22. A 23. A 23. D 23. D 23. B 24. D 24. B 24. A 24. B 25. C 25. D 25. D 25. A 26. C 26. B 26. A 26. A 27. C 27. D 27. D 27. D 28. A 28. B 28. A 28. C 29. D 29. A 29. A 29. C 30. C 30. A 30. D 30. D 31. D 31. C 31. A 31. A 32. A 32. A 32. B 32. B 33. B 33. A 33. C 33. C 34. C 34. C 34. A 34. C 35. B 35. B 35. C 35. D 36. A 36. A 36. B 36. B 37. D 37. D 37. B 37. D 38. D 38. C 38. C 38. D 39. C 39. B 39. C 39. C 40. A 40. D 40. D 40. B
II. HƯỚNG DẪN CHẤM TỰ LUẬN Câu Nội dung Điểm
Tính modun của số phức z biết z = (4 + 3i).i
Ta có z = (4 + 3i) 2 = + = − + 1 .i 4i 3i 3 4i 0,5 Suy ra z = 3 − − 4i 0,25 Do đó z = 3 − − 4i = 9 +16 = 5 0,25
Trong không gian Oxyz , cho mặt phẳng (P) : x + y + z −3 = 0 và đường thẳng x = t
d : y =1−t ,(t ∈) . 2 z = t
a) Gọi A là giao điểm của đường thẳng d và mặt phẳng (P) . Tìm tọa độ điểm A .
b) Viết phương trình đường thẳng ∆ nằm trong (P) , đồng thời ∆ cắt và vuông góc với d .
Tọa độ điểm A là nghiệm hệ: x = t x = t x = t x = 2 a) y = 1− t y = 1− t y = 1− t y = 1 − ⇔ ⇔ ⇔ ⇒ A(2, 1, − 2) . 0,5 z t z t z t = = = z = 2
x + y + z −3 = 0 t
+1−t +t −3 = 0 t = 2 t = 2
Mặt phẳng (P) có VTPT n = (1;1; ) ( )
1 , đường thẳng d có VTCP u = − . d (1; 1; )1 P 0,25
Đường thẳng ∆ qua A nhận u = n ,u = − làm một VTCP P d (2,0, 2) ( ) 0,125 b) x = 2 + 2t Đường thẳng : ∆ y = 1 − ,(t ∈). 0,125 z = 2− 2t Hết
Document Outline
- Mã đề 124
- Mã đề 235
- Mã đề 346
- Mã đề 457
- ĐÁP ÁN - HƯỚNG DẪN CHẤM




