Đề thi cuối kỳ Phương pháp tính | Đại học Bách Khoa Hà Nội

Đề thi cuối kỳ Phương pháp tính | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

66 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính (BK)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

6 trang 6 tháng trước

Tác giả:

Profile Thùy Dương
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH
Tg: 90 phú 81 t : 201Học kỳ Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy-
- Không sử dụng tài liệu.
Câu 1. Cho các mốc nội suy:
x
1.5
2
2.5
3
y
16.17
15.53
15.13
1. Tìm đa thức nội suy Lagrange.
2. Tính gần đúng giá trị hàm số tại
2.3.x =
Câu 2. Tìm hàm thực nghiệm
2
b
y ax
x
= +
biết bảng dữ liệu sau:
x
1.5
1.7
1.8
1.9
2.1
2.2
2.3
y
-1.375
-2.57
-3.19
-3.84
-5.18
-5.89
-6.63
Câu 3. Cho phương trình
3
3 25 0.x x+ − =
Tìm nghiệm của phương
trình bằng phương pháp chia đôi với sai số
2
10 .
−
Câu 4. Tính gần đúng
0.5
2
0
1
dx
x−
bằng phương pháp hình thang
với 3 chữ số đáng tin sau dấu phẩy.
Câu 5. Cho bài toán Cauchy
( )
( )
2 2
' 0.15 ; 1 2.y xy x y y= − =
Tính gần đúng
( ) ( )
1.1 ; 1.2y y
bằng phương pháp RK4 với
0.1.h =
Câu 6. Xây dựng công thức lặp tìm ma trận nghịch đảo của ma trận
chéo trội hàng cỡ n.
ĐỀ I
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH
Tg: 90 phút 81 Học kỳ: 201 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy-
- Không sử dụng tài liệu.
Câu 1. Cho các m ốc nội suy:
x
2
2.5
3
3.5
y
16.17
15.53
15.13
1. Tìm đa thức nội suy Lagrange.
2. Tính gần đúng giá trị hàm số tại
2.7.x =
Câu 2. Tìm hàm thực nghiệm
2
b
y ax
x
= +
biết bảng dữ liệu sau:
x
1.7
1.8
1.9
2.1
2.2
2.3
2.5
y
-1.51
-1.77
-2.02
-2.46
-2.68
-2.89
-3.26
Câu 3. Cho phương trình
3
17 25 0.x x+ − =
Tìm nghiệm của phương
trình bằng phương pháp chia đôi với sai số
2
10 .
−
Câu 4. Tính gần đúng
0.5
2
0
1
dx
x+
bằng phương pháp hình thang với
4 chữ số đáng tin sau dấu phẩy.
Câu 5. Cho bài toán Cauchy
( )
( )
2 2
' 1.5 ; 1 2.y x y x y y= − =
Tính gần đúng
( ) ( )
1.1 ; 1.2y y
pháp RK4 bằng phương với
0.1.h =
Câu 6. Xây dựng công thức lặp tìm ma trận nghịch đảo của ma trận
chéo trội hàng cỡ n.
ĐỀ II
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH
Tg: 90 phú 91 t : 201Học kỳ Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy-
- Không sử dụng tài liệu.
Câu 1. Cho phương trình
7
49 0.x − =
Tìm nghiệm của phương trình
bằng phương pháp ếp tuy ới ữ số đ ấu phti ến v 7 ch áng tin sau d ẩy.
Câu 2. Tìm hàm thực nghiệm
bx
y ae=
biết bảng dữ liệu sau:
x
1.5
1.7
1.8
1.9
2.1
2.2
2.3
2.4
2.6
y
-1.38
-2.57
-3.19
-3.84
-5.18
-5.89
-6.63
-7.75
-8.47
Câu 3. Cho các mốc nội suy:
x
1.5
2
2.5
3
3.5
y
15.93
16.17
16.53
17.05
17.86
3. Viết đa thức nội suy ến mốc cNewton ti ách đều dạng chính tắc
theo biến bit ết
1.5 0.5x t= +
.
4. Tính gần đúng
( )
2.8f
và
( )
' 2.8f
Câu 4. Tính gần đúng
2
2
1
x x
e dx
− +
bằng phương pháp ới Simpson v 10
đ đoạn chia và ánh giá sai số.
Câu 5. Cho bài toán Cauchy
( ) ( ) ( )
'' ' ; 1 1; ' 1 1.174y xy y y y y= − = =
Tính gần đúng
( )
1.1y
Euler c bằng phương pháp ải tiến với
0.1.h =
Câu 6. Viết s đồ khối ơ xác định dạng ch ắc củaính t đa thức tích
( ) ( )( )
( )
1 2
w ...
k
x x x x x x x= − − −
trong đó
1 2
, ,...,
k
x x x
là c sác ố
thực cho trước.
ĐỀ I
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH
Tg: 90 phút 91 Học kỳ: 201 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy-
- Không sử dụng tài liệu.
Câu 1. Cho phương trình
9
81 0x − =
. Tìm nghiệm của phương trình
bằng phương pháp ới 5 chữ số đ ấu phdây cung v áng tin sau d ẩy.
Câu 2. Tìm hàm thực nghiệm
b
y ax=
biết bảng dữ liệu sau:
x
1.7
1.8
1.9
2.1
2.2
2.3
2.5
2.6
2.8
y
-1.51
-1.77
-2.02
-2.46
-2.68
-2.89
-3.26
-3.93
-4.75
Câu 3. Cho các mốc nội suy:
x
1.5
2
2.5
3
3.5
y
15.93
16.17
16.53
17.05
17.86
1. Vi Newtonết đa thức nội suy lùi m ính tốc cách đều dạng ch ắc
theo biến t biết
3.5 0.5 .x t= +
2. Tính gần đúng
( )
2.8f
và
( )
' 2.8 .f
Câu 4. Tính gần đúng
2
3
2
2
x x
e dx
− +
bằng phương pháp ới Simpson v
10 ia v ánh gi . đoạn ch à đ á sai số
Câu 5. Cho bài toán Cauchy
( ) ( ) ( )
'' ' ; 1 1; ' 1 1.35y xy y y y y= − = =
Tính gần đúng
( )
1.1y
Euler c bằng phương pháp ải tiến với
0.1.h =
Câu 6. Viết s đồ khối ơ xác định dạng ch ắc củaính t đa thức tích
( ) ( )( )
( )
1 2
w ...
k
x x x x x x x= − − −
trong đó
1 2
, ,...,
k
x x x
là các số
thực cho trước.
ĐỀ II
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH
Tg: 90 phú 201 t : 20Học kỳ Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy-
- Không sử dụng tài liệu.
Câu 1. Tìm hàm thực nghiệm
2
y ax b= +
: biết bảng dữ liệu sau
x
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
y
1.23
1.16
1.12
1.08
0.83
0.65
0.51
0.23
-0.25
Câu 2. Cho các mốc nội suy:
x
1.5
1.8
2.2
2.4
2.7
y
15.93
16.17
16.53
17.05
17.86
5. Tính gần đúng
( )
1.95y
công th . theo ức nội suy Lagrange
6. Đưa đa thức
( )( )( )( )
1.5 1.8 2.2 2.4x x x x− − − −
về dạng chính tắc
bằng sơ đồ Hooner.
7. S ử dụng s đồ Hơ oocner trên xây dựng đa thức nội suy Newton
tiến xuất phát từ
0
1.5.x =
Câu 3. Giải h ệ phương trình
x Bx d= +
b áp l ằng phương ph ặp đơn với
ba l v ánh gi sai s cho x b ông thần lặp à đ á ố ấp x ứ 3ỉ th ằng c ức hậu
nghiệm bi ết
0
0.2 0.3 0.1 5.2 14
0.4 0.1 0.1 ; 4.7 ; 13 .
0.1 0.5 0.2 6.5 18
B d x
= = =
Câu 4. Cho bài toán Cauchy
( ) ( ) ( )
'' ' ; 1 1; ' 1 0.7.y xy y y y y= + = =
Tính gần đúng
( )
1.2y
Euler bằng phương pháp với
0.1.h =
Câu 5. Viết s đồ ơ tính gần đúng tích phân xác định
( )
b
a
f x dx
bằng
công th ình thang ãn sai sức h thoả m ố
cho tr , giá trước ị
( )
2
,
max "
a b
M f x=
đã biết.
ĐỀ I
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH
Tg: 90 phút 201 Học kỳ: 20 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy-
- Không sử dụng tài liệu.
Câu 1. Tìm hàm thực nghiệm
3
y ax b= +
biết bảng dữ liệu sau:
x
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
y
0.23
-0.61
-1.37
-2.46
-3.41
-4.89
-6.12
-7.68
-9.18
Câu 2. Cho các mốc nội suy:
x
1.5
1.8
2.2
2.4
2.7
y
15.93
16.17
16.53
17.05
17.86
3. Tính gần đúng
( )
2.35y
công th theo ức nội suy Lagrange
4. Đưa đa thức
( )( )( )( )
2.7 2.4 2.2 1.8x x x x− − − −
về dạng chính tắc
bằng sơ đồ Hooner.
5. S ử dụng s đồ ơ Hoocner trên xây dựng đa thức nội suy Newton
lùi xuất phát từ
4
2.7.x =
Câu 3. Giải h ệ phương trình
x Bx d= +
b áp l ằng phương ph ặp đơn với
ba l v ánh gi sai s cho x b ông thần lặp à đ á ố ấp x ứ 3ỉ th ằng c ức hậu
nghiệm bi ết
0
0.2 0.3 0.1 5.2 13.5
0.4 0.1 0.1 ; 4.7 ; 13.5 .
0.1 0.5 0.2 6.5 18.5
B d x
= = =
Câu 4. Cho bài toán Cauchy
( ) ( )
'' '; 1 1; ' 1 0.35.y xy y y y y= + = =
Tính gần đúng
( )
1.2y
Euler bằng phương pháp với
0.1.h =
Câu 5. Viết s đồ ơ tính gần đúng tích phân xác định
( )
b
a
f x dx
bằng
công th Simpson ãn sai sức thoả m ố
cho tr , giá trước ị
( )
( )
4
4
,
max
a b
M f x=
đã biết.
ĐỀ II
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH ĐỀ I
Tg: 90 phút Học kỳ: 20181 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy -
Không sử dụng tài liệu. -
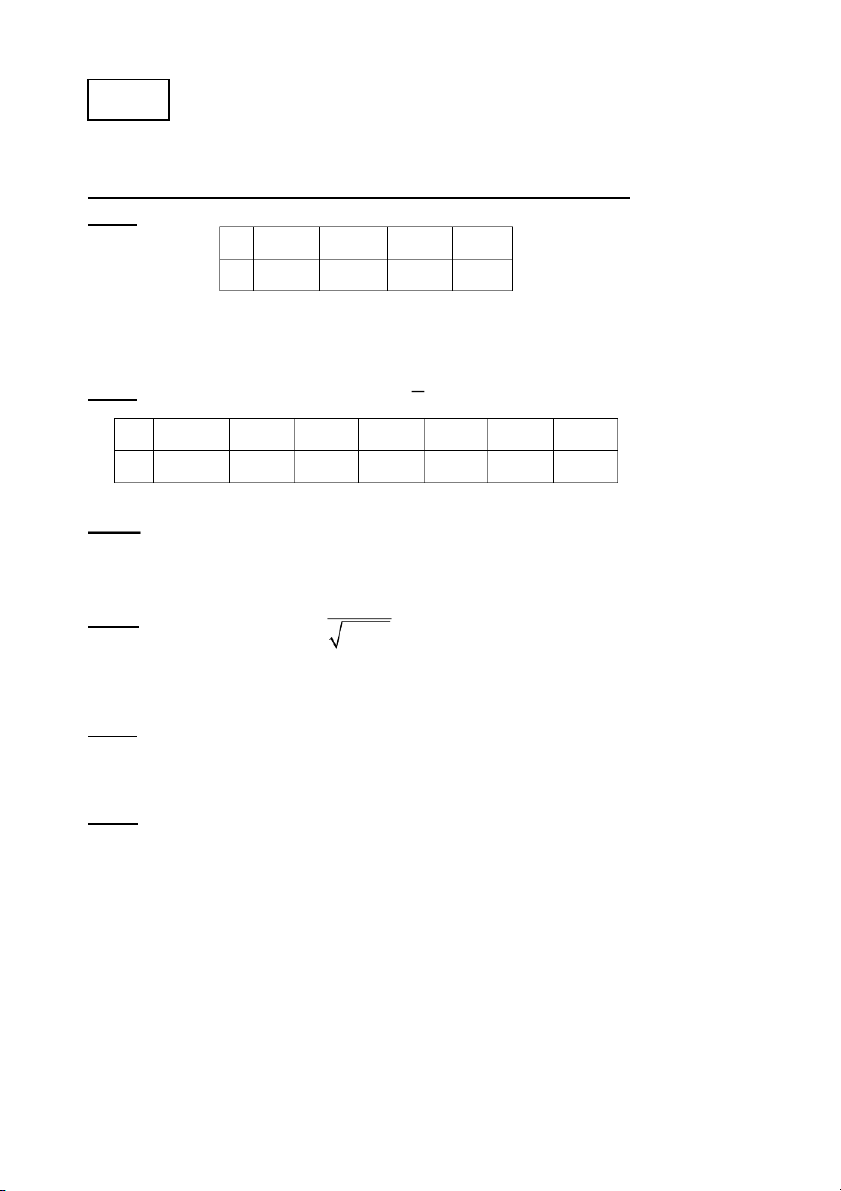
Câu 1. Cho các mốc nội suy: x 1.5 2 2.5 3
y 15.93 16.17 15.53 15.13
1. Tìm đa thức nội suy Lagrange.
2. Tính gần đúng giá trị hàm số tại x = 2.3.
Câu 2. Tìm hàm thực nghiệm 2 b y = ax +
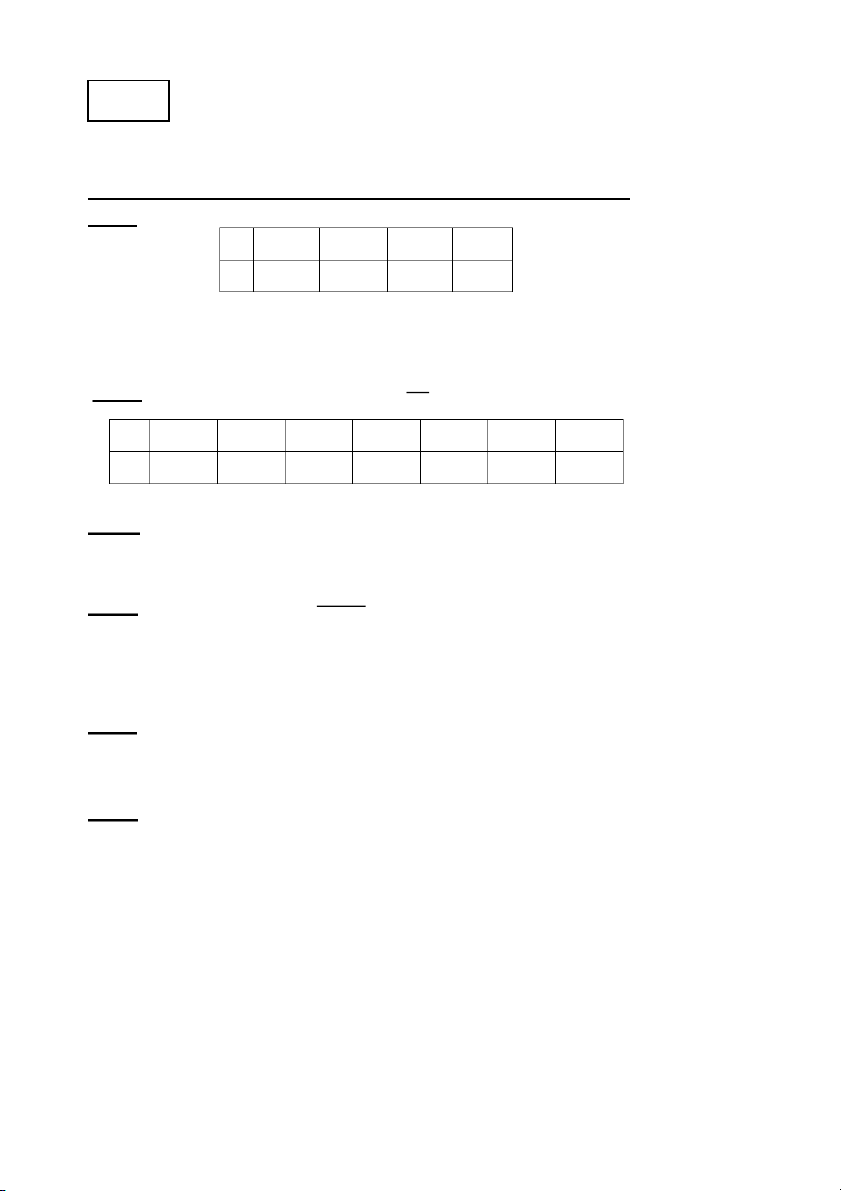
biết bảng dữ liệu sau: x x 1.5 1.7 1.8 1.9 2.1 2.2 2.3 y -1.375 -2.57 -3.19 -3.84 -5.18 -5.89 -6.63
Câu 3. Cho phương trình 3
x + 3x − 25 = 0. Tìm nghiệm của phương
trình bằng phương pháp chia đôi − với sai số 2 10 . 0.5 dx
Câu 4. Tính gần đúng
bằng phương pháp hình thang 2 − 0 1 x
với 3 chữ số đáng tin sau dấu phẩy. Câu 5. 2 2
Cho bài toán Cauchy y ' = 0.15xy( x − y ); y( ) 1 = 2.
Tính gần đúng y (1. )
1 ; y (1.2) bằng phương pháp RK4 với h = 0.1.
Câu 6. Xây dựng công thức lặp tìm ma trận nghịch đảo của ma trận chéo trội hàng cỡ n.
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH ĐỀ II
Tg: 90 phút Học kỳ: 20181 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy -
Không sử dụng tài liệu. -
Câu 1. Cho các mốc nội suy: x 2 2.5 3 3.5
y 15.93 16.17 15.53 15.13
1. Tìm đa thức nội suy Lagrange.
2. Tính gần đúng giá trị hàm số tại x = 2.7. b
Câu 2. Tìm hàm thực nghiệm y = ax +
biết bảng dữ liệu sau: 2 x x 1.7 1.8 1.9 2.1 2.2 2.3 2.5 y -1.51 -1.77 -2.02 -2.46 -2.68 -2.89 -3.26
Câu 3. Cho phương trình 3
x +17x − 25 = 0. Tìm nghiệm của phương
trình bằng phương pháp chia đôi với sai số −2 10 . 0.5 dx
Câu 4. Tính gần đúng
bằng phương pháp hình thang với 2 1 + x 0
4 chữ số đáng tin sau dấu phẩy. Câu 5. 2 2
Cho bài toán Cauchy y ' = 1.5x y (x − y); y( ) 1 = 2.
Tính gần đúng y (1. )
1 ; y (1.2) bằng phương pháp RK4 với h = 0.1.
Câu 6. Xây dựng công thức lặp tìm ma trận nghịch đảo của ma trận chéo trội hàng cỡ n.
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH ĐỀ I
Tg: 90 phút Học kỳ: 20191 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy -
Không sử dụng tài liệu. -
Câu 1. Cho phương trình 7
x − 49 = 0. Tìm nghiệm của phương trình
bằng phương pháp tiếp tuyến với 7 chữ số đáng tin sau dấu phẩy.
Câu 2. Tìm hàm thực nghiệm bx
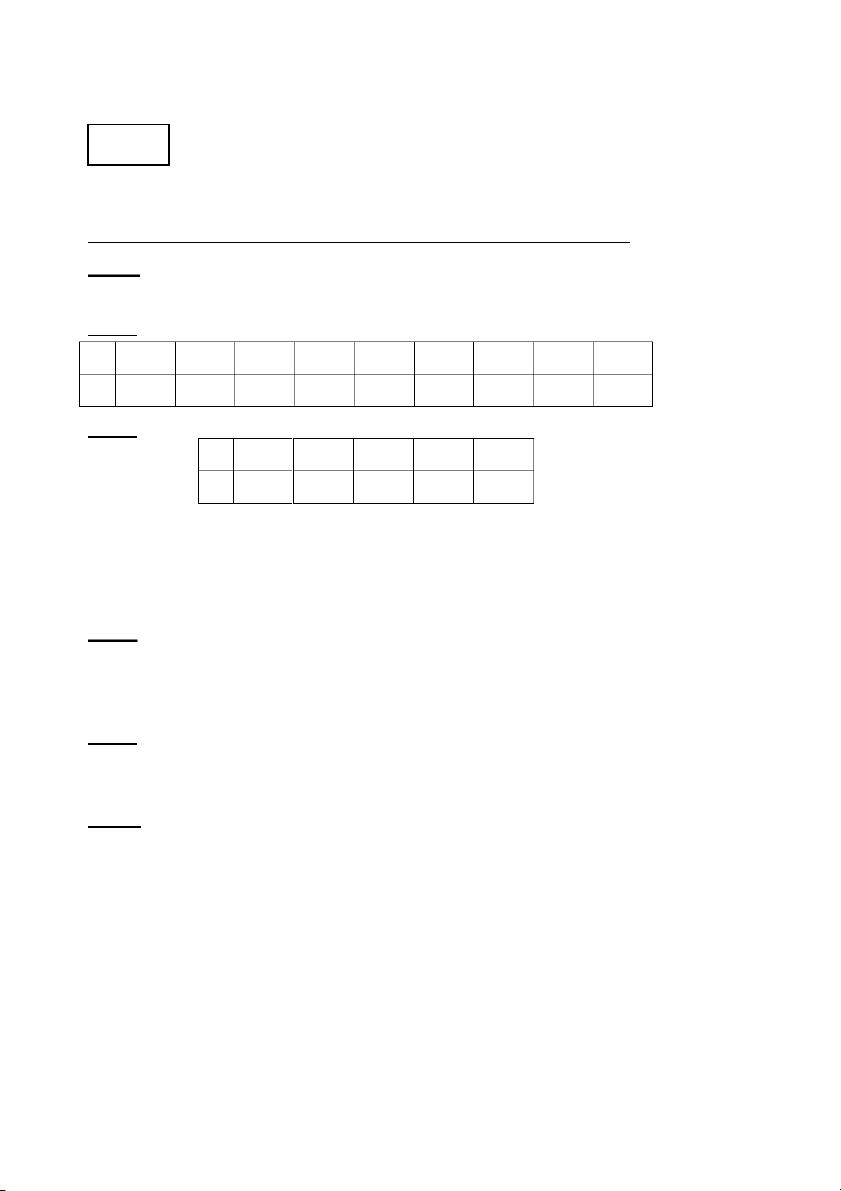
y = ae biết bảng dữ liệu sau: x 1.5 1.7 1.8 1.9 2.1 2.2 2.3 2.4 2.6
y -1.38 -2.57 -3.19 -3.84 -5.18 -5.89 -6.63 -7.75 -8.47
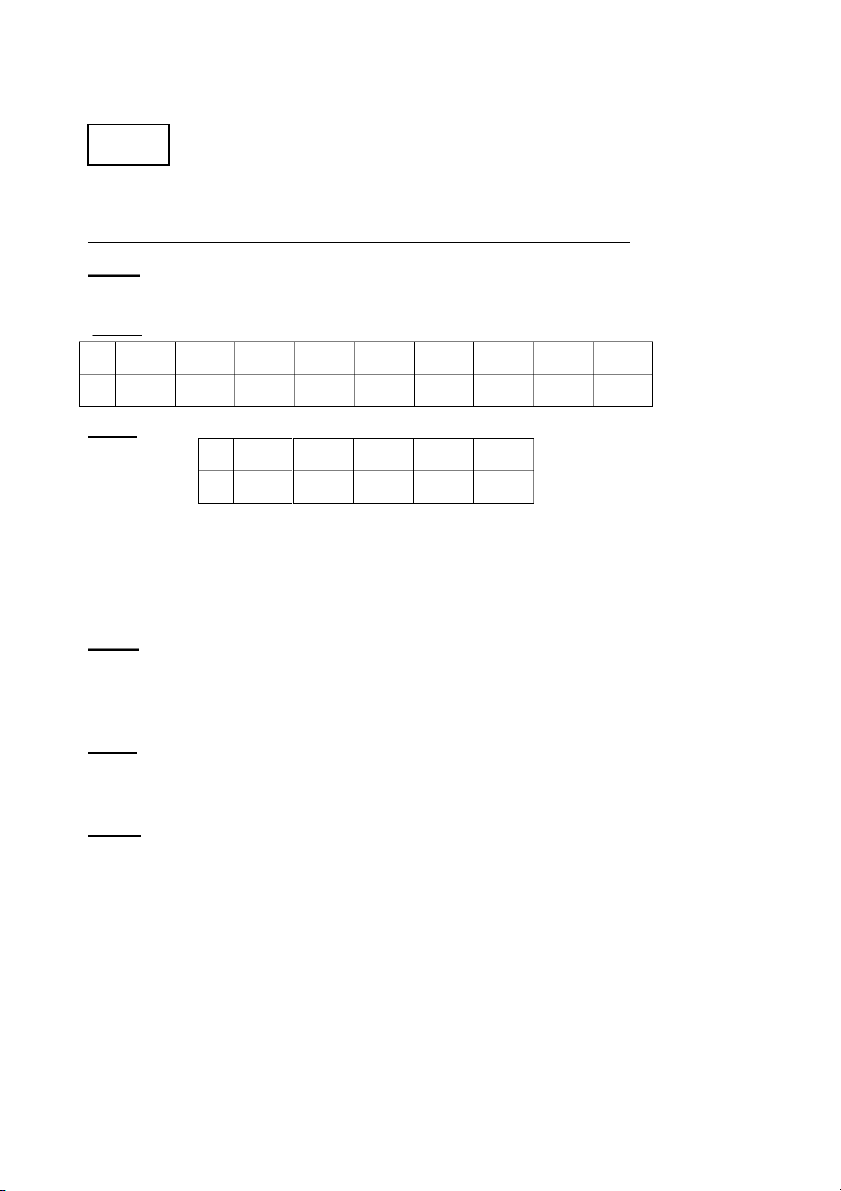
Câu 3. Cho các mốc nội suy: x 1.5 2 2.5 3 3.5
y 15.93 16.17 16.53 17.05 17.86
3. Viết đa thức nội suy Newton tiến mốc cách đều dạng chính tắc
theo biến t biết x =1.5 + 0.5t .
4. Tính gần đúng f ( 2.8) và f '(2.8) 2 2 − +
Câu 4. Tính gần đúng x x e dx
bằng phương pháp Simpson với 10 1
đoạn chia và đánh giá sai số.
Câu 5. Cho bài toán Cauchy y ' = xy ( y − y '); y (1) = 1; y '(1) = 1.174
Tính gần đúng y (1.1) bằng phương pháp Euler cải tiến với h = 0.1.
Câu 6. Viết sơ đồ khối xác định dạng chính tắc của đa thức tích w( )
x =( x − x
x − x ... x − x trong đó x x x là các số 1) ( 2 ) ( k ) 1, 2,..., k thực cho trước.
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH ĐỀ II
Tg: 90 phút Học kỳ: 20191 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy -
Không sử dụng tài liệu. -
Câu 1. Cho phương trình 9
x − 81= 0 . Tìm nghiệm của phương trình
bằng phương pháp dây cung với 5 chữ số đáng tin sau dấu phẩy.
Câu 2. Tìm hàm thực nghiệm b
y = ax biết bảng dữ liệu sau: x 1.7 1.8 1.9 2.1 2.2 2.3 2.5 2.6 2.8
y -1.51 -1.77 -2.02 -2.46 -2.68 -2.89 -3.26 -3.93 -4.75
Câu 3. Cho các mốc nội suy: x 1.5 2 2.5 3 3.5
y 15.93 16.17 16.53 17.05 17.86
1. Viết đa thức nội suy Newton lùi mốc cách đều dạng chính tắc
theo biến t biết x = 3.5 + 0.5t.
2. Tính gần đúng f ( 2.8) và f '(2.8). 3 2 − +
Câu 4. Tính gần đúng x 2 x e dx
bằng phương pháp Simpson với 2
10 đoạn chia và đánh giá sai số.
Câu 5. Cho bài toán Cauchy y ' = xy( y '− y); y( ) 1 = 1; y '( ) 1 = 1.35
Tính gần đúng y (1.1) bằng phương pháp Euler cải tiến với h = 0.1.
Câu 6. Viết sơ đồ khối xác định dạng chính tắc của đa thức tích w( )
x =( x − x
x − x ... x − x trong đó x x x là các số 1) ( 2 ) ( k ) 1, 2,..., k thực cho trước.
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH ĐỀ I
Tg: 90 phút Học kỳ: 20201 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy -
Không sử dụng tài liệu. -
Câu 1. Tìm hàm thực nghiệm 2
y = ax + b biết bảng dữ liệu sau: x 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
y 1.23 1.16 1.12 1.08 0.83 0.65 0.51 0.23 -0.25
Câu 2. Cho các mốc nội suy: x 1.5 1.8 2.2 2.4 2.7
y 15.93 16.17 16.53 17.05 17.86
5. Tính gần đúng y(1.9 ) 5 theo c
ông thức nội suy Lagrange.
6. Đưa đa thức (x −1.5 )(x −1.8)(x − 2.2 )(x − 2.4 )về dạng chính tắc bằng sơ đồ Hooner.
7. Sử dụng sơ đồ Hoocner trên xây dựng đa thức nội suy Newton
tiến xuất phát từ x = 1.5. 0
Câu 3. Giải hệ phương trình x = Bx + d bằng phương pháp lặp đơn vớ i
ba lần lặp và đánh giá sai số cho xấp xỉ t ứ h 3 bằng công thức hậu nghiệm biết 0.  2 0.3 0.1 5.  2  14         B = 0.4 0.1 0.1 ; d = 4.7 ; x = 13 . 0       0.  1 0.5 0.2  6.  5  18        
Câu 4. Cho bài toán Cauchy y ' =
xy (y + y ' ); y (1) =1; y ' (1) = 0.7.
Tính gần đúng y (1.2) bằng phương pháp Euler với h = 0.1. b
Câu 5. Viết sơ đồ tính gần đúng tích phân xác định f ( x) dx  bằng a
công thức hình thang thoả mãn sai số  cho trướ , c giá trị
M = max f " x đã biết. 2 ( )  ,ab
ĐỀ THI CUỐI KỲ MÔN PHƯƠNG PHÁP TÍNH ĐỀ II
Tg: 90 phút Học kỳ: 20201 Mã HP: MI2010
Lưu ý: Các kết quả tính đều lấy ít nhất 7 chữ số sau dấu phẩy -
Không sử dụng tài liệu. -
Câu 1. Tìm hàm thực nghiệm 3
y = ax + b biết bảng dữ liệu sau: x 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0
y 0.23 -0.61 -1.37 -2.46 -3.41 -4.89 -6.12 -7.68 -9.18
Câu 2. Cho các mốc nội suy: x 1.5 1.8 2.2 2.4 2.7
y 15.93 16.17 16.53 17.05 17.86
3. Tính gần đúng y( 2.3 ) 5 theo c
ông thức nội suy Lagrange
4. Đưa đa thức ( x − 2.7)( x − 2. ) 4 ( x − 2. ) 2 ( x −1. ) 8 về dạng chính tắc bằng sơ đồ Hooner.
5. Sử dụng sơ đồ Hoocner trên xây dựng đa thức nội suy Newton
lùi xuất phát từ x = 2.7. 4
Câu 3. Giải hệ phương trình x = Bx + d bằng phương pháp lặp đơn vớ i
ba lần lặp và đánh giá sai số cho xấp xỉ t ứ h 3 bằng công thức hậu nghiệm biết 0.  2 0.3 0.1 5.  2  13.  5       B = 0.4 0.1 0.1 ; d = 4.7 ; x = 13.5 . 0       0.  1 0.5 0.2  6.  5  18.  5       
Câu 4. Cho bài toán Cauchy y ' = xy y + y '; y (1) =1; y '(1) = 0.35.
Tính gần đúng y (1.2) bằng phương pháp Euler với h = 0.1. b
Câu 5. Viết sơ đồ tính gần đúng tích phân xác định f ( x) dx  bằng a
công thức Simpson thoả mãn sai số  cho trướ , c giá trị (4) M = max f x đã biết. 4 ( )  ,ab