TailieuVNU.com
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ
ĐỀ THI GIỮA KỲ MÔN HỌC GIẢI TÍCH 1 *****
(Học kỳ I năm học 2019-2020)
Thời gian làm bài 120 phút Mã số đề thi: 62
1.(1,0đ) Chứng minh rằng, hàm số y f (x)   x  x  k 2
1 là nghiệm của phương trình
1 x 2 'y' x 'y k y2  c x os 3 c x os   khi x 0
2.(2,0đ) Cho hàm số  f (x)   sin 2x
, tìm giá trị của tham số q để hàm số q khi x  0
này liên tục trên tập số thực R 2 x
3.(2,5đ) Cho hàm số f (x ) a , 
(với tham số a ≠ 0), chứng minh rằng f (n) , 0 ( ) 1  n ( n ) 1 x a e
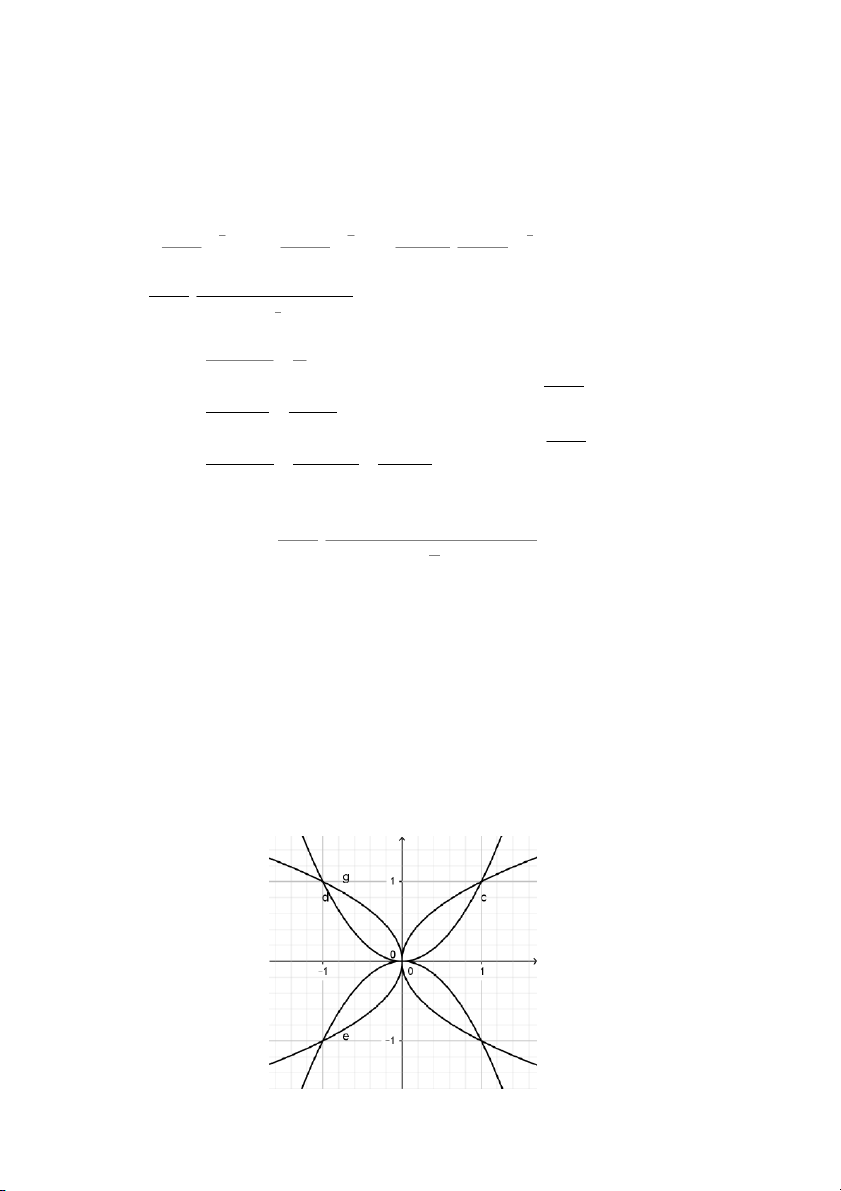
4.(2,5đ) Tính chu vi và diện tích của hình hoa 4 cánh được tạo bởi 4 đường parabol x   2 y  y   2 x  mx n
5.(2,0đ) Tính tích phânI   dx(p > 0) px e 0
================================
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ
ĐÁP ÁN ĐỀ THI GIẢI TÍCH 1 ***** -2020)
(Thi giữa kỳ, học kỳ I năm học 2019 Mã số đề thi: 62
1.(1,0đ) Ta có y f (x)   x  x  k 2 1 (1)  ' y  f '(x)   x x   ' k 2 1    2 k x  x  k 1 1 x  x ' 2 1         k 2 2 k 1   k 1 k x  x     2   x 2 1 1   
kx x2   x x 1 kx x 1 1 .   2 x2 1 x2 1 x 21 ky  (0,25đ) (2) x2  1 2    ky '  (ky)' x2  1 k  y x2   x 2 ' ky' x 1 k . y 1 2 x2 1 y'' [f '(x)]'      x2 1  2 2 x2   x 1 1 kxy ky' x2  1 x2 1  (0,25đ) (3) x2 1 ky kxy kxy k x2 1  k2y  x2  1 x2  1 x2  1
Thay (2) vào (3) ta được y''  (0,25đ) (4) x2 1 x 21
Thay (1), (2) và (4) vào biểu thức 1 x  2y'' x  y' ta được 1 TailieuVNU.com kxy k 2y   2 
1 x2y'' xy' 1 x 2 x 1 ky  x
k y2 (đpcm) (0,25đ) x2 1 x2 1  co x s 3 c x os   khi x 0 2.(2,0đ)  Hàm số f (x)   sin 2x
có D(f) = R (0,25đ) liên tục với x  R  \  0 q khi x  0
vì biểu thức tạo ra f(x) là các hàm số sơ cấp (0,25đ). Điểm gián đoạn của hàm số có thể có tại điểm x 0  (0,25đ).  c x os  3 t  3 c x os  2 t Đặt t 6 co x s   (0,25đ) và khi x 0  thì t 1  (0,25đ) co x s  6 t   2 sin  x  2 1 cos x  1 12 t c x os 3  c x os t 3  t 2 (t2  ) 1  (t3  ) 1 (t ) 1 (t ) 1  (t ) 1 (t2  t  ) 1     sin 2 x 1  t 12 t12  1 (t )
1 (t11  t10  ... t ) 1 (t  ) 1 (t2 )  t 2   (0,25đ) (t )
1 (t11  t10  ... t  ) 1 t11  t10  ... t 1 co x s 3  co x s  t2 12 1  lim  lim   (0,25đ) x 0  sin 2 x t 1
 t11  t10  ...  t 1 111 110 ... 11 12 1 1
Hàm số f(x) liên tục tại điểm x 0  li  m f (x) f    0   q  , do đó khi q   thì x 0  12 12
hàm số f(x) đang xét liên tục trên tập số thực R. (0,25đ) co x s 3  co x s * Có thể tìm lim
bằng cách sử dụng Quy tắc L’Hospitale: Biểu thức x0 sin 2x co x s 3  co x s 0 cần tìm giới hạn khi x 0
 có dạng vô định khi x 0  sin 2 x 0 1 sin x 1 sin x  .  co x s 3  co x s ( L) ( co x s 3  co x s )' 2 co x s 3 3 cos2 x  lim  lim  lim x 0  sin 2 x x 0  (sin2 x)' x 0  s 2 in c x o x s 1  1 1 1 1  1 1 1 1 1  1  1 1 1  lim  .  .    .  .        x 0  c 2 o x s  3 2  cos x co x s  1 . 2 3 3 2 3 2 2   1 1  2   3 2 12 x 2 x x     a ( u ) a , x e 3.  (2,5đ) 2 f ( ) a , x   x e a , đặt 
(0,25đ) và sử dụng công thức x 2 a e v(x)  x (n) f ( ) a , x n n (   n k) (k) C u ( ) a , x v .
(x) để tìm công thức đạo hàm bậc n của hàm số f(x) = n k0  u(0) (  ) a , x ( u ) a , x
u(x,a).v(x) với quy ước  (0,25đ) v(0) (x)  v(x) 1 Nếu đặt x     ( u ) a , x e  thì dễ thấy rằng x (k) k x e ( )  e   (0,25đ) a k x k x  1   ( ) 1   (k) a a  u ( ) a , x    e  e (0,25đ) k  a a 2 TailieuVNU.com  x 2 khi k  1 và vì v(x) = x2 (k )   v (x)  2 khi k  2 (0,25đ)  0 khi k  3 2 Do đó (n) f ( ) a , x  n (   n k) (k) n C u ( ) a , x v . (x)  k 0  C 0 u (n) ( ) a , x v . )0 ( (x) C1 un( )1 ( ) a , x v . )1 ( (x) C u2 ( n ( ) 2 ) a , x (0,25đ ) n n n v . (x)) 2 ( ( ) 1 n x  ( ) 1 n1 x  n ( n  ) 1 ( ) 1 n2 x   . 1 e x . 2 a  . n e a x 2 .  . e a2 . (0,25đ ) an a n1 2 an2 n 2 2 ( ) 1 x  x 2 na  n ( n  a ) 1  . (0,25đ ) (5) n x a a e  ! n ! n C0    1 n n ( ) 0 !. ! 0 ! n n    ( ) 1 n    1 ( ) 1   ( n ) 1  ! n ! n    1 ( ) 1 vì C1    n n và  (0,25đ)  n (  ) 1 !. ! 1 n (  ) 1 !  n ( ) 1 n  2 n ( ) 1 ( ) 1  ! n ! n      n ( n ) 1  (  2 ) 1 C2      n n (  ) 2 !. ! 2 n (  ) 2 ! 2 . 2
Thay x = 0 và a = -1 vào (5) ta được ( ) 1 n 02  . n . 0 . 2 ( ) 1  n ( n  ) 1 .( ) 1 2 f(n) , 0 (  ) 1  .  n ( n  ) 1 (0,25đ ) ( ) 1 n 0 e1 4.(2,5đ) (a ) Vẽ đồ thị y  2 x - Đồ thị của hai đường parabol 
giao nhau tại các điểm O(0,0); A(1,1) x  2 y x  2 y - Đồ thị của hai đường parabol 
giao nhau tại các điểm O(0,0); B(1,-1) y   2 x y   2 x
- Đồ thị của hai đường parabol 
giao nhau tại các điểm O(0,0); C(-1,-1) x   2 y x   2 y
- Đồ thị của hai đường parabol 
giao nhau tại các điểm O(0,0); C(-1,1) (0,25đ) y  2 x (0,25đ) 3 TailieuVNU.com (b) Tính chu vi
Do tính đối xứng của hình vẽ nên chu vi L của hình hoa bốn cánh này là L = 8L1 với L1 là độ dài
cung OA của đường parabol y = f 2 1(x) = x trên đoạn 0 x  1  .(0,25đ ) f (x)  2 b x  1
Theo công thức tính độ dài cung L 1 [ f (x )] dx 1   ' 2 1 với a 0 (0,25đ) a  b 1 ta có ' 2 ' 2 2 f (x) (x )'  x 2  1 [  f (x)]  1  x 4 1 1 1 1 1 1  L 1 [f (x)] dx 1 4x dx 2 x dx 1    ' 2 1    2   2  4 0 0 0 1 1  1 1  1   1 1  1   .
2 x x 2   ln x  x2    . 1 1  2
 ln1  1 2   2  4 4  4      4 4   0   4   1 1  1   . 5 1  5   1 2 2 1    . 0 0   l  n  0 0       l  n  1   0 ln 4 4  4  2 4  2               4 2    5  1  5 1  5 1 1 5 1  5 1      5 1  2    ln 1    ln    ln1   l  n     ln 2 4  2  4 2 2 4  2  2 2 4  1               2  5 ln 2 (  5)  5 ln 2 (  5)    L  8L  . 8   4 5 2ln 2 (  5)   (0,5đ) 2 4 1 2 4   1
*Ở trên ta đã dùng công thức tích phân x 2  d  x  
x x 2    ln x  x 2     C   2   (c) Tính diện tích
Do tính đối xứng của hình vẽ nên diện tích S của hình hoa bốn cánh này là S = 4S1 với S1 là diện
tích của cánh hoa nằm ở góc vuông thứ nhất của hệ tọa độ Oxy được tạo bởi cung OA của đường parabol y = f 2 1(x) = x trên đoạn 0 x  1
 và cung OA của đường parabol x = y2 hay y f
 (x)  x trên đoạn 0 x  1  .(0,25đ ) 2 f (x)  x2  1 b f (x)  x
Theo công thức tính diện tích hình phẳng S f (x) f (x) dx 2 (0,25đ) 1   2 1    với a 0 a   b 1 1  1  1 1 1 1 1  2 1   x x   S  f (x) f (x) dx x x dx x  x dx   1   2 1   2  2 2 2   1  2 1 0 0 0   1   2  0 1  2 x 3 x 3  2 1 1         3 3  3 3 3   0 1 4 Do đó S  S 4 . 4  (0,5đ) 1 3 3 4 TailieuVNU.com  mx b b n 1 5.(2,0đ) I   dx lim (m  px x e ) n dx   lim (m  px x e ( d ) n ) (0,25đ) px e b    p  b    0 0 0 1  b b  1  b b mx n  px  px      lim m (  x e ) n  lim e d m ( x px n) lim lim e d m ( x n) b  0 p b           px p b e b    0   0 0  1  mb n 0 . m  n b m 1 mb n n m px  b    lim    lim e dx   lim   px lim e ( d ) p  b  pb 0 . p e e P  b    pb pb 2 e p p b      0 0 b n 1 mb  n m b n 1 mb n m 1 px   lim  lim e   lim  lim p p b pb 2 pb 2 px  e p b 0 p p b e p b e 0 n 1 mbn m 1 1 n m 1 mb    n m 1   lim   lim      lim  lim (1,0đ) p p b pb 2 pb 0 . p 2 pb 2 pb  e p b  e e p  p p b e p b e 1 b Vì p > 0 nênlim  0 và pb
e   khi b   , do đó biểu thức cần tìm giới hạn có dạng  e pb b pb e  mb n (L) m ( b ) n ' m m 1 m vô định  lim  lim  lim  lim  0 .  0 (0,5đ)   epb b  e ( pb b )'  pepb b p  e pb b p  mx n n m 1 mb  n m 1 n m 1 m  1 m  I  dx    lim  lim pb   2  0 .  0 . 2   px 2 pb 2  n  e p p p b e p b  e p p p p 0  p p  (0,25đ) 5