Đề thi hết môn học kỳ II - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Đề thi hết môn học kỳ II - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 2 (MAT1042)

Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Thông tin:

1 trang 2 tháng trước

Tác giả:

Profile Mai Nguyệt
ĐẠI HỌC QUỐC GIA HÀ NỘI
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ
ĐỀ THI HẾT MÔN
HỌC K II C 2021 - 2022 Ỳ NĂM HỌ
Mã lớp h n: MAT1042 20, 21, 22, 23, 24, 25, 26, 27, 28 ọc phầ –
Tên học phần: i tích 2 Giả Thời gian làm bài: 120 phút
Đề thi số 1
Câu 1 (1.5đ). Xét tính liên tụ ủa hàm số sau c c trên
2
R
:
2 2 2 2
ln 2 2 khi , 0,0
,
0 khi , 0,0
x y x y x y
f x y
x y
.
Câu 2 (1.5đ). Tìm c c trự ị a hàm s địa phương củ ố
4 2
, 4 2z x y xy x y
.
Câu 3 (1.5đ). Tính tích phân sau b ng cách chuy n sang h ằ ể ệ toạ độ c ực:
2 2
4 1
0 0
2 1 2
x x
x x
I x y dydx x y dydx
.
Câu 4 (1.5đ). Tính tích phân
2 2
D
I x xy y dxdy
,
là mi n ph ng n b i ề ẳ được giới hạ ở
đường cong:
2 2
2x xy y
, s d n: ử ụng phép đổi biế
2 2
2 ; 2
3 3
v v
x u y u
.
Câu 5 i th t l y tích phân sau theo (1.0đ). Đổ ứ ự ấ
2 2 2
1 1 2
0
: , ,
y x y
dzdydx I f x y z dzdxdy
.
Câu 6 (1.5đ). Tính tích phân
2 2 3 2
3 2
I x y dx x xy xy dy
, với
C
là
đường cong kín gồm hai n ng tròn ửa đườ
2 2
4 , 1y x y x
và n th ng hai đoạ ẳ
,AB CD
,
trong đó
2,0 , 1,0 , 1,0 , 2,0A B C D
, chi u cề ủa
C
ngược chiều kim đồng hồ.
Câu 7 (1.5đ). Giải phương trình vi phân:
3 2 3 2
2 2 0 ; 0 1x xy dx y x y dy y
.
----------Hết----------
Chú ý: sinh viên không d ng tài liđược phép sử ụ ệu.
| 1/1
| | Tải xuống

Có thể bạn quan tâm:

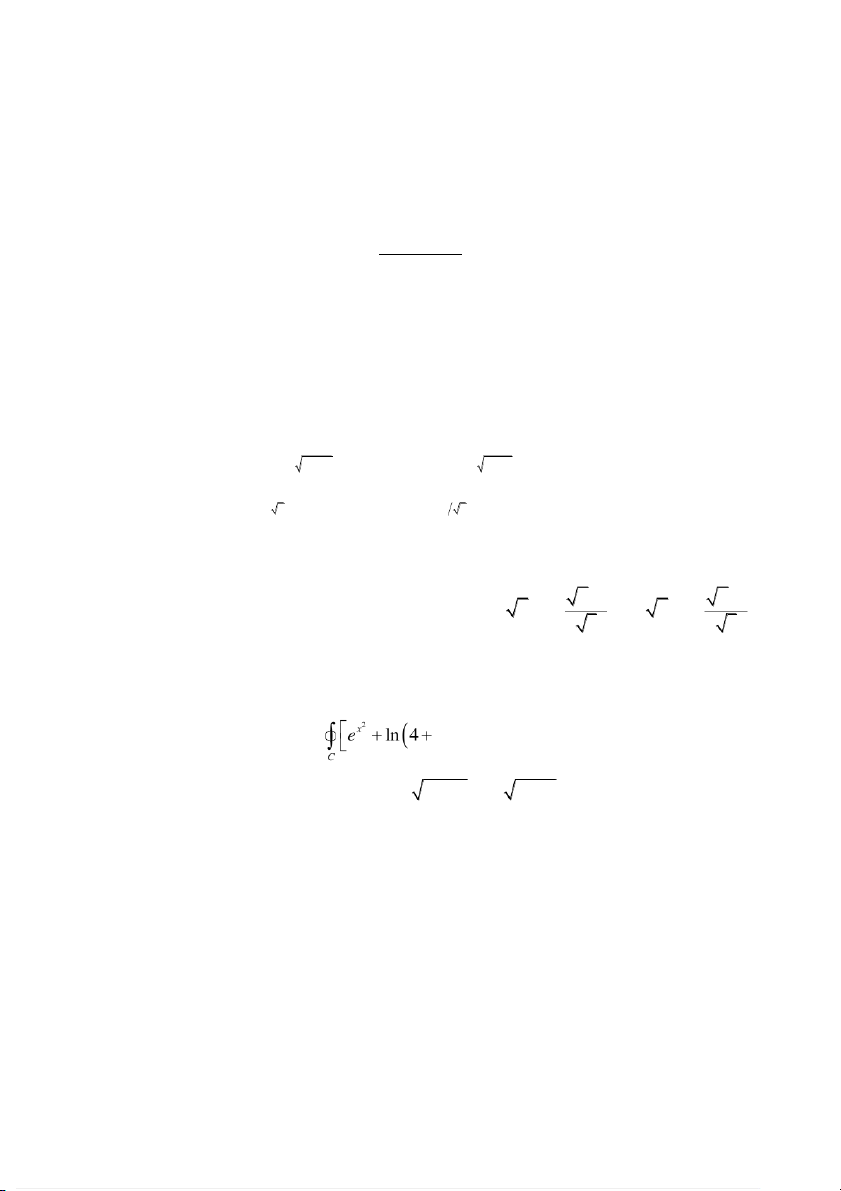
Preview text:

ĐẠI HỌC QUỐC GIA HÀ NỘI
ĐỀ THI HẾT MÔN
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ
HỌC KỲ II NĂM HỌC 2021 - 2022
Mã lớp học phần: MAT1042 – 20, 21, 22, 23, 24, 25, 26, 27, 28
Tên học phần: Giải tích 2
Thời gian làm bài: 120 phút
Đề thi số 1
Câu 1 (1.5đ). Xét tính liên tục của hàm số sau trên 2 R :  2 2
x y   2 2
ln 2x  2 y  khi  , x y   0,0
f x, y   . 0
khi  x, y  0,0 
Câu 2 (1.5đ). Tìm cực trị địa phương của hàm số zx y 4 2 ,
 4xy  2x y .
Câu 3 (1.5đ). Tính tích phân sau bằng cách chuyển sang hệ toạ độ cực: 2 2 0 4  x 0 1 x I
xydydx
xydydx     .  2 x 1 2 x
Câu 4 (1.5đ). Tính tích phân I   2 2
x xy y dxdy, D là miền phẳng được giới hạn bởi D   đườ v v ng cong: 2 2
x xy y  2 , sử dụng phép đổi biế 2 2 n: x  2  u  ; y  2  u  . 3 3 1 1 2
Câu 5 (1.0đ). Đổi thứ tự lấy tích phân sau theo dzdydx : I f
    ,x y,zdzdxdy. 2 2 2 0 y x y
Câu 6 (1.5đ). Tính tích phân 2 I x  2  y dx    3 2
x  3xy  2 xy dy , với C là
đường cong kín gồm hai nửa đường tròn 2 2 y
4  x , y  1 x và hai đoạn thẳng A , B CD, trong đó  A 2  ,  0 , B 1
 ,0,C1,0, D2, 
0 , chiều của C ngược chiều kim đồng hồ.
Câu 7 (1.5đ). Giải phương trình vi phân:  3 2
x xy dx   3 2 2
2y x ydy  0 ; y 0 1.
----------Hết----------
Chú ý: sinh viên không được phép sử dụng tài liệu.