SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI HỌC KÌ II NĂM HỌC 2013- 2014
TRƯỜNG THPT CHU VĂN AN
Môn: Toán Lớp 12 Nâng cao
Buổi thi: Chiều ngày 15/04/2014 ĐỀ THI SỐ 01
Thời gian làm bài: 120 phút, không kể thời gian giao đề
Đề thi gồm 01 trang ---------------------- 2x  4 Câ
u 1 (3,0 điểm). Cho hàm số y  x  (1) có đồ thị (C). 1
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
2. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng
d : 2x  y  3  0 .
Câu 2 (3,0 điểm). 2
1. Giải bất phương trình: 2 log (x  3)  4  log 4 2 x  . 1 
2. Tính tích phân: I 
(x  sin 2x) sin xdx  . 0 x 1  1  x 2
3. Giải phương trình: e
 2 x 1  e  x  x .
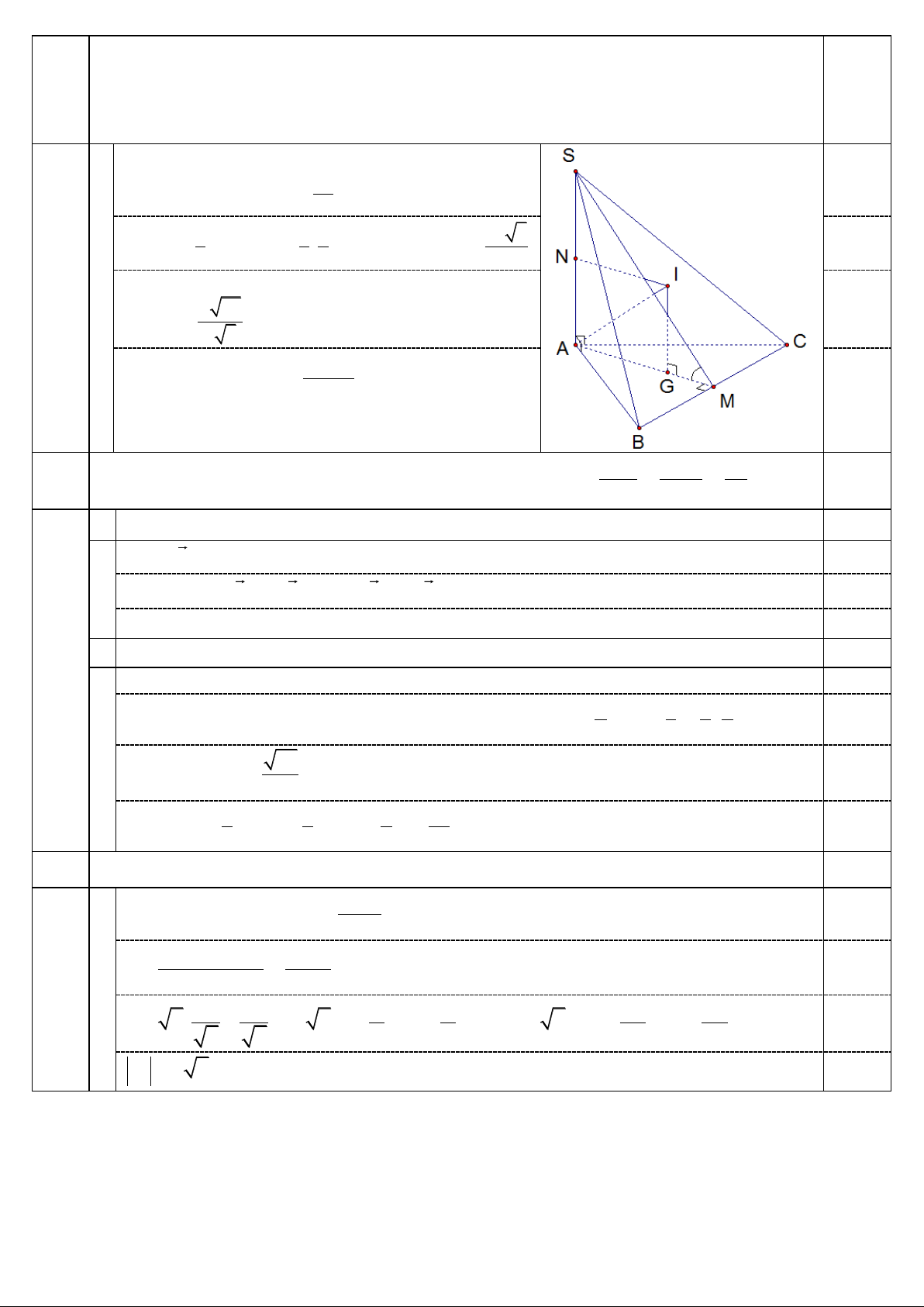
Câu 3 (1,0 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc
với mặt phẳng đáy. Mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 600. Tính thể tích khối chóp
S.ABC và diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
Câu 4 (2,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho điểm M (1; 2
 ;3) và đường thẳng d có x 1 y  2 z phương trình   2 1 1  .
1. Viết phương trình mặt phẳng (P) đi qua điểm M và vuông góc với d.
2. Viết phương trình mặt cầu (S) đi qua M và gốc tọa độ O và (S) có tâm thuộc d.
Câu 5 (1,0 điểm).
Cho số phức z thỏa mãn điều kiện (1 2i)z  i  3  0 .
Tìm môđun của số phức w = z7.
------------------ HẾT ------------------
Họ và tên học sinh: ...................................
......................................
Số báo danh : ......................................................................... 1 CÂU NỘI DUNG ĐIỂM x  1 Cho hàm số 2 4 y  (1) x 1
1 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1). 2,00  TXĐ: D = \{1}
 Giới hạn và tiệm cận: lim y  2; lim y   ;  lim y   x x 1  x 1 
 (C) nhận đường thẳng x = 1 là tiệm cận đứng và đường thẳng y = 2 là tiệm cận ngang. 1,00  2
Sự biến thiên: y '   0, x
  \{1} HSĐB trên từng khoảng xác định của nó. 2 (x 1)  Bảng biến thiên:  0,50
Hàm số không có cực trị.  Đồ thị: 0,50
2 Viết PTTT của (C) biết tiếp tuyến vuông góc với đường thẳng d : 2x  y  3  0 . 1,00
Hệ số góc của tiếp tuyến 1 k  0,25 2 1 2 1
x  3  M (3;1) Suy ra 0 y '(x )     0,50 0  2 2 (x 1) 2 x  1   M ( 1  ;3) 0  0
Phương trình hai tiếp tuyến: 1 1 1 7 y  x  ; y  x  0,25 2 2 2 2 2 2
1 Giải bất phương trình: 2 log (x  3)  4  log 4 2 x  1,00 1
ĐK: x > 3. BPT  log (x  3)(x 1)  5 0,50 2  2
x  2x  35  0  x  ( ;  5  ][7;+) 0,25
So sánh điều kiện: S  [7;+) 0,25 
2 Tính tích phân: I  (x  sin 2x) sin xdx  1,00 0   
I  (x  sin 2x) sin xdx  x sin xdx  sin 2x sin xdx    0,25 0 0 0     
I  x sin xdx   xd (cos x)  x cos x  cos xdx    sin x      1 0,25 0 0 0 0 0    3 sin x 2
I  sin 2x sin xdx  2 sin xd (sin x)  2  0   0,25 2 3 0 0 0
I  I  I   0,25 1 2
3 Giải phương trình: x 1  1  x 2 e
 2 x 1  e  x  x 1,00 ĐK: x 1  1  2 x 2
x ≥ 1; PT  e
 ( x 1 1)  e  x (1) 0,25
Chứng minh được hàm số 2 ( ) t
f t  e  t đồng biến trên [1;+) 0,25 2
(1)  f ( x 1 1)  f (x) 
x 1 1  x  x  3x  2  0  x  1; x  2 0,50 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt 3
phẳng đáy. Mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 600. Tính thể tích khối chóp 1,00
S.ABC và diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
Gọi M là trung điểm BC. Tính được 0 S  MA  60 3a 0,25
Suy ra SA = AMtan600 = 2 3 1 1 1 0 a 3    0,25 S V . S .SA . A . B AC.sin 60 . ABC ABC SA  3 3 2 8
Tìm được tâm I của mặt cầu ngoại tiếp. Tính được a 43 0,25 R  IA  4 3 2  Diện tích mặt cầu 43 a S  12 0,25 x 1 y  2 z 4
Trong không gian Oxyz, cho điểm M (1; 2
 ;3) và đường thẳng d:   2 1 1  .
1 Viết phương trình mặt phẳng (P) đi qua điểm M và vuông góc với d. 1,00 Ta có: u   d (2;1; 1) 0,25 Do (P)  d  n   
( P) // u d . Chọn n(P) ud (2;1; 1) 0,25 Do (P) qua M (1; 2
 ;3)  (P): 2(x 1) 1(y  2) 1(z  3)  0  2x  y  z  3  0 0,50
2 Viết phương trình mặt cầu (S) đi qua M và gốc tọa độ O và (S) có tâm thuộc d. 1,00
Gọi tâm của (S) là I (1 2t; 2   t; t  )d 0,25 2 1 8 2
(S) đi qua M và gốc tọa độ O  IO  IM  6t  4
  t    I( ; ; ) 0,25 3 3 3 3 69
Khi đó: R  IO  0,25 3 1 8 2 23 2 2 2
 (S) : (x  )  (y  )  (z  )  0,25 3 3 3 3 5
Cho số phức z thỏa mãn điều kiện (1 2i)z  i  3  0 . Tìm môđun của z7. 1,00 3  i
(1 2i)z  i  3  0  z  1 0,25 2i
(3  i)(1 2i) 5  5i z   1 i 0,25 5 5 1 1   7 7 7 7 z  2(  i)  2(cos
 isin )  z  ( 2) (cos  isin )  8(1 i) 0,25 2 2 4 4 4 4 7 z  8 2 0,25
----------------------------- HẾT ----------------------------- 3