SỞ GD & ĐT QUẢNG NGÃI
ĐỀ THI HỌC KỲ II- NĂM HỌC: 2011-2012
TRƯỜNG THPT NGUYỄN CÔNG PHƯƠNG Môn: TOÁN 12
Thời gian làm bài: 150 phút
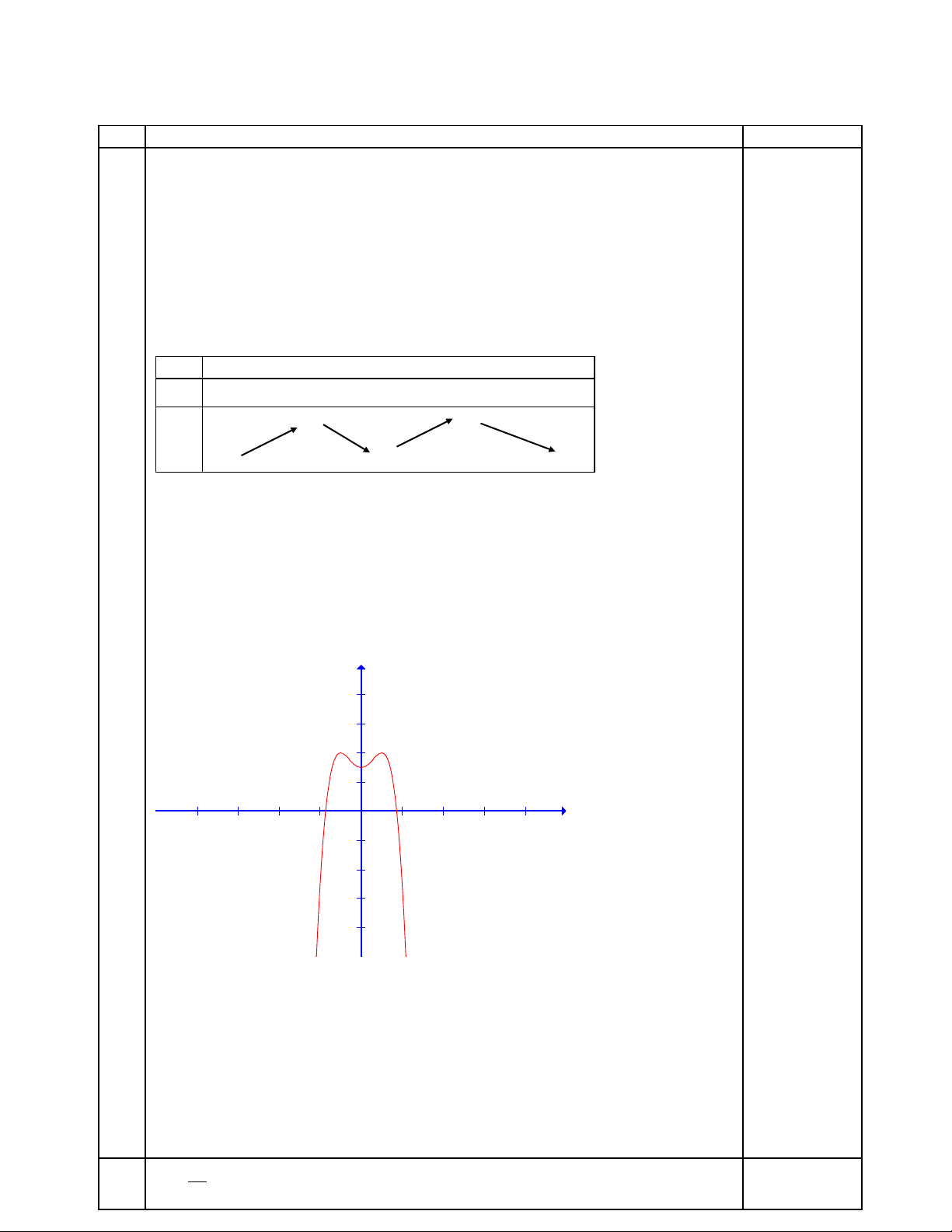
Câu 1(3 điểm): Cho hàm số y= 4 2
x  2x  3 có đồ thị (C)
a) Khảo sát sự biến thiên và vẽ đồ thị (C)
b) Dựa vào đồ thị (C), hãy tìm m để phương trình 4 2
x  2x  m  0 có 4 nghiệm phân biệt.
Câu 2( 1 điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 1 y  1 trên đoạn 0;  1 x e
Câu 3(1 điểm): Giải các phương trình sau: a) x 1 4  4 x  0 b) 2 log x  4  0 2 1 1
Câu 4(1 điểm): Tính các tích phân sau: 4
a) I  3x  2 dx b)  2x  3x J  2 x d 0 0
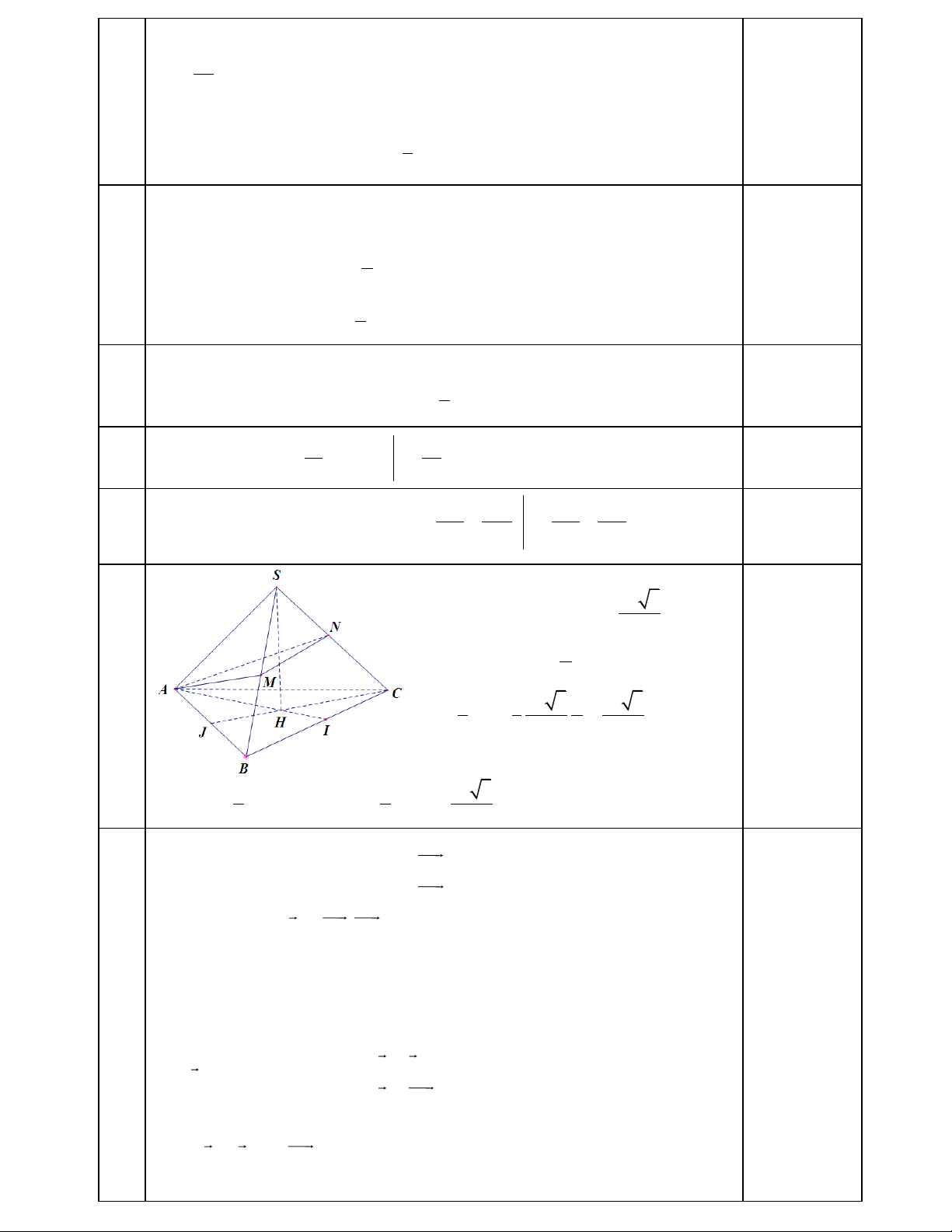
Câu 5(1điểm): Cho khối chóp tam giác đều S.ABC, đáy là tam giác đều ABC cạnh a và các mặt bên tạo với đáy một góc 0 60 .
a) Tính thể tích của khối chóp S.ABC theo a.
b) Gọi M, N lần lượt là trung điểm của SB, SC .Tính thể tích khối chóp A.BCNM .
Câu 6(2điểm): Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;2;-1), B(2;1;-1), C(-1;0;1),
D(-1;1;2) và mặt phẳng ( )
P : x  2y  2z 1  0 .
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện
b) Viết phương trình tham số của đường thẳng d qua A, song song với mặt phẳng (BCD) và vuông góc với đường thẳng CD.
Câu 7(1điểm): Tính mô 2
-đun của số phức w   z  2  4 z  i , trong đó số phức z  1 i .
----------------- Hết ----------------
SỞ GD & ĐT QUẢNG NGÃI
ĐỀ THI HỌC KỲ II- NĂM HỌC: 2011-2012
TRƯỜNG THPT NGUYỄN CÔNG PHƯƠNG Môn: TOÁN 12
Thời gian làm bài: 150 phút
Câu 1(3điểm): Cho hàm số y= 4 2
x  2x  3 có đồ thị (C)
a) Khảo sát sự biến thiên và vẽ đồ thị (C)
b) Dựa vào đồ thị (C), hãy tìm m để phương trình 4 2
x  2x  m  0 có 4 nghiệm phân biệt.
Câu 2(1điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 1 y  1 trên đoạn 0;  1 x e
Câu 3(1điểm): Giải các phương trình sau: a) x 1 4  4 x  0 b) 2 log x  4  0 2 1 1
Câu 4(1điểm): Tính các tích phân sau: a) I  3x  24 dx b)  2x  3x J  2 x d 0 0
Câu 5(1điểm): Cho khối chóp tam giác đều S.ABC, đáy là tam giác đều ABC cạnh a và các mặt bên tạo với đáy một góc 0 60 .
a) Tính thể tích của khối chóp S.ABC theo a.
b) Gọi M, N lần lượt là trung điểm của SB, SC .Tính thể tích khối chóp A.BCNM .
Câu 6(2điểm): Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;2;-1), B(2;1;-1), C(-1;0;1),
D(-1;1;2) và mặt phẳng ( )
P : x  2y  2z 1  0 .
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện
b) Viết phương trình tham số của đường thẳng d qua A, song song với mặt phẳng (BCD) và vuông góc với đường thẳng CD.
Câu 7(1điểm): Tính mô 2
-đun của số phức w   z  2  4 z  i , trong đó số phức z  1 i .
----------------- Hết ----------------
ĐÁP ÁN ĐỀ THI TOÁN 12 HỌC KỲ II-NĂM HỌC 2012 Bài ĐÁP ÁN ĐIỂM 1 a) TXĐ D= R 0,25đ , 3 y  4  x  4x  x  0 , 3 y  0  4
 x  4x  0   x  1  0,25đ lim y   0,25đ x Bảng biến thiên x -  -1 0 1 +  , y + 0 - 0 + 0 - 0,5đ y 4 4 -  3 - 
Điểm cực đại (-1;4) ;(1;4) Điểm cực tiểu (0;3)
Hàm số đồng biến trên (- ;-1);(0;1)
Hàm số nghịch biến trên (-1;0); (1;+  ) 0,25đ
Điểm đặc biệt (-2;5); (2;5) Đồ thị y 8 6 4 2 x -8 -6 -4 -2 2 4 6 8 -2 -4 -6 0,5đ -8 b) 4 2 4 2 4 2
x  2x  m  0  x  2x  m  0  x  2x  3  m  3 (1)
Số nghiệm của phương trình (1) là số giao điểm của 2 đồ thị 0,25đ y= 4 2
x  2x  3và y= m+3
Pt (1) có 4 nghiệm phân biệt khi và chỉ khi 0,25đ 3m  1 Vậy m0;  1 thoả đề bài 0,5đ 1 2 y  1 x e
Hàm số xác định và liên tục trên 0;  1 1  y '   0, x  0.25 x e
Hàm số nghịch biến trên 0;  1 0.25 M
   Miny  f   1 axy =f 0 2; 1  1 0.5 0; 1 0; 1 e x 1x 3a 4  4  0 0.25 Đặt  4x t , t  0 4 t  2  0 Phương trình trở thành: 2 t 
 0  t  4  0   t t  2   0 0.25 Với t = 2 x 1  4  2  x  2 3b x  4 log x  2 0.5 2 2  log x  4  0   2  1 log x  2    x  2  4 1 1 4a 0.5 I    4 1    5 33 3x 2 dx 3x 2   15 15 0 0 1 4b 1 x x    2x  3x 2 1
x=6x  2x J d   1 6 2 5 2 1 x d =      0.5 ln 6 ln 2 ln 6 ln 2   0 0 0 Câu 5 2 a 3
a) Diện tích đáy B  4 0.25 a h=SH=HI.tan600= 2 0.25 2 3 1 1 a 3 a a 3 V  Bh   3 3 4 2 24 0.5 3 1 3 a 3 b)V  V  V  V  SAMN 4 SABC ABCNM 4 SABC 32
Câu a. Viết phương trình mặt phẳng (BCD).Suy ra ABCD là một tứ diện 6 BC  ( 3  ; 1  ;2)
Mp(BCD) qua B và có cặp vtcp là BD  ( 3  ;0;3) 0.25
Mp (bcd) có vtpt n  [BC, B ] D =(-3;3;-3) 0.25
Phương trình mp (BCD) là: x-y+z=0
Thay tọa độ điểm A vào phương trình mp (BCD): 0.25
1-2-1=-2 (không thỏa) hay ABCD là 1 tứ diện 0.25
b. Viết phương trình đường thẳng d qua A,song song với mặt phẳng (BCD)
và vuông góc với đường thẳng CD. u   n   Gọi BCD
u là vtcp của d. Suy ra ( ) (1; 1;1)  0.5 u
  CD  (0;1;1)  x  1 2t  Chọn n  [n    ( BCD) , C ]
D =(-2;-1;1) .PTTS của d: y 2 t 0.5 z  1   t  Câu Mô 2
-đun của số phức w   z  2  4 z  i , trong đó z  1 i 7 0.5 2
w=(3+i)  4(1 2i)  8  6i  4  8i  4  2i z  16  4  20 0.5