Đề thi hk2 môn toán 12 có đáp án năm 2020 trường thpt thanh bình 1 tỉnh đồng tháp

Đề thi hk2 môn toán 12 có đáp án năm 2020 trường thpt thanh bình 1 tỉnh Đồng Tháp được soạn dưới dạng file PDF. Đề thi bao có 6 trang, bao gồm 50 câu hỏi. Đề thi có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mờicác bạn cùng đón xem ở dưới.

22 11 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang 1

ĐỀ 21

PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 120 phút

Câu 1. Lp 11A có

hc sinh nam và

hc sinh n. Có bao nhiêu cách chn mm

nam và

n?

. B.

. C.

. D.

500

Câu 2. Cho cp s cng

 

có s hu

2u 

, công sai

3d 

. S hng th

ca

 

bng

. B.

. C.

162

. D.

Câu 3. Din tích xung quanh ca hình tr  ng sinh



bng

4 rl



. B.

2 rl



. C.



. D.



Câu 4.Cho hàm s

 

có bng bi

Hàm s nghch bin trên kho

 

0;4

. B.

 

;1 

.C.

 

1;1

. D.

 

0;2

Câu 5. Cho hình hnh bng

và

chiu cao

. Th tích ca hình hng

. B.

. C.

. D.

Câu 6. 

2020 1

x



có nghim làA.

x 

. B.

2x 

. C.

x 

2x 

Câu 7. Nu

 

d5f x x 



và

   

2 d 13f x g x x







thì

 

dg x x



bngA.

3

. B.

1

. C.

Câu 8. Cho hàm s

 

y f x

có bng bi

Kh

A. Hàm s t cc tiu ti

4x 

B.m ci c th hàm s là

0x 

C. Giá tr cc tiu ca hàm s bng

D. m ci c th hàm s là

 

0; 3A 

Trang 2

Câu 9.  th ca hàm s 

21y x x  

. B.

21y x x  

21y x x  

. D.

21y x x   

Câu 10. Vi s th

tùy ý,

log a

bng

2 log a

.B.

log

a

. C.

2log a

. D.

log

Câu 11.H tt c các nguyên hàm ca hàm s

 

sin 6f x x x

là

cos 2x x C  

. B.

cos 2x x C

cos 18x x C  

. D.

cos 18x x C

Câu 12. Gi

là s phc liên hpca s phc

34zi  

. Tìm phn thc và phn o ca s phc

A.S phc

có phn thc bng

3

và phn o bng

B. S phc

có phn thc bng

và phn o bng

C. S phc

có phn thc bng

3

và phn o bng

4

D. S phc

có phn thc bng

và phn o bng

4

Câu 13. Trong không gian

Oxyz

, hình chiu vuông góc cm

 

1;2;3A

trên mt phng

 

Oyz

có ta

là

 

0;2;3

. B.

 

1;0;3

. C.

 

1;0;0

. D.

 

0;2;0

Câu 14. Trong không gian

Oxyz



 

2 2 2

: 2 4 6 0S x y z x y     

là

 

2;4;0

. B.

 

1;2;0

. C.

 

1;2;3

. D.

 

2;4;6

Câu 15. Trong không gian

Oxyz

, cho mt phng

 



2 3 1 0xz  



pháp tuyn ca

 



?A.

 

2;3; 1n 



. B.

 

2;3;0n 



. C.

 

2;0; 3n   



 

2;0; 3n 



Câu 16. Trong không gian

Oxyz

ng thng

d y t

















Trang 3

 

1;3;0M

. B.

 

1;3;3N

. C.

 

2; 1;0P 

. D.

 

2; 1;3Q 

Câu 17. Cho hình chóp

.S ABCD



ABD

u cnh

vuông góc vi mt ph

SA 

(minh

hng thng

và mt phng

 

ABCD

bng

45

. B.

30

. C.

60

. D.

90

Câu 18. Cho hàm s

 

y f x

, bng xét du ca

 





S m cc tiu ca hàm s A.

. B.

. C.

. D.

Câu 19. 

 

10 1f x x x  



 

3;2

A.

. B.

23

. C.

24

8

Câu 20. 

và



 

3 27

log loga a b





ab

. B.

ab

. C.

ab

. D.

ab

Câu 21. 

log log

9 18

x 

là

 

1;9

. B.







. C.



 



0;1 9; 

. D.





0; 9;



 







Câu 22. Cho mt cu

 

. Bit rng khi ct mt cu

 

bi mt mt phng cách tâm mt kho

dài là

c giao tuyng tròn

 

có chu vi là



. Din tích ca mt cu

 

bng

180



. B.

180 3



. C.



. D.



Câu 23. Cho hàm s bc ba

 

 th . S giá tr nguyên

ca tham s

 

 

1f x m

có

nghim phân bit là

. B.

. C.

. D.

Câu 24. 

cos











là

Trang 4

tan

e x C

. B.

tan

e x C

. C.

cos



. D.

cos



Câu 25. Tìm tnh ca hàm s

 

log 3xx





D  

. B.

 

0;3D 

. C.

 

3;D  

. D.

   

;0 3;D    

Câu 26. Cho kh ng

.ABCD A B C D

   

bình hành cnh

AB a

3AD a



120BAD 

và

2AB a





(minh h). Th tích ca kh

tr ng

. B.

. C.

. D.

Câu 27. Gi

và

lt là s ng tim cn ngang và s ng tim cng c th hàm s

 







. Kh

0k 

;

2l 

. B.

1k 

;

2l 

1k 

;

1l 

. D.

0k 

;

1l 

Câu 28. Cho hàm s

y ax bx c  

 

,,abc

 th 

 

0a 

0b 

0c 

. B.

0a 

0b 

0c 

0a 

0b 

0c 

. D.

0a 

0b 

0c 

Câu 29. Hãy tính din tích phm trong hình v 

. B.

. C.1. D.



Câu 30. Cho

42zi

. Hãy tìm phn o ca s phc

 

12z i z  

6i

. B.

2i

. C.

2

. D.

6

Câu 31.Cho s phc

 

,z x yi x y  

có phn thc khác 0. Bit s

phc

2w iz z

là s thun o. Tp hm biu din ca

là mt

ng th

 

0;1M

. B.

 

2; 1N 

. C.

 

1;3P

. D.

 

1;1Q

Trang 5

Câu 32.Trong không gian

Oxyz



 

2;1;2a 



 

1; 1;0b 



ng

 

.a b b

  

bng

3

. B.

1

. C.

5

. D.

Câu 33. Trong không gian

Oxyz

ng thng

2 2 1

x y z

  



và mt phng

 

:2 3 0P x y z   

. Gi

 

là mt cu có tâm

thuc



và tip xúc vi

 

tm

 

1; 1;0H 

a

 

là

     

2 2 2

3 2 1 36x y z     

. B.

     

2 2 2

3 2 1 36x y z     

     

2 2 2

3 2 1 6x y z     

. D.

     

2 2 2

3 2 1 6x y z     

Câu 34. Trong không gian

Oxyz

, mt phm

 

1;2;3M

và song song vi mt phng

 

: 2 3 0P x y z   



2 3 0x y z   

. B.

230x y z  

. C.

20x y z  

. D.

2 8 0x y z   

Câu 35. Trong không gian

Oxyz

ng thng

1 2 1

x y z







nh

ch 

 

1;2;1u 



. B.

 

2;4;2u 



. C.

 

2; 4;2u   



. D.

 

1;2;1u 



Câu 36. Gi

là tp hp các s t nhiên có

ch s khác nhau. Chn ngu nhiên mt s t tp

. Tìm

xác su s c chn có các ch s sp xp theo th t n và không cha hai ch s nguyên

nào liên tip nhau.

. B.

. C.

. D.

1512

Câu 37. Cho hình chóp

.S ABCD



ABCD

là hình thang vuông ti

và

3 , .AB a AD DC a  

Gi

m ca

, bit hai mt phng

 

SBI

và

 

SCI

cùng

vuông góc vt phng

 

SBC

to vt góc

60 .

Gi

m trên

sao cho

2AM a

, tính khong cách gia

và

. B.

. C.

. D.

Trang 6

Câu 38. Cho hàm s

 

có











và

 

sinf x x x





.Gi s rng

 

cos . d

x f x x







(vi

,,abc

là các s 

ti gi

abc

bngA.

. B.

. C.

. D.

Câu 39. Cho hàm s

 

1 2 3 1

()

   



   

(

0m 

và là tham s thc). Tp hp

 hàm s 

cho

nghch bin trên khong









có dng

  

 



; ; ;S a b c d     

, vi

, , ,a b c d

là các s

thc. Tính

P a b c d   

.A.

3

. B.

1

. C.

. D.

Câu 40. 



. Mt mt phnh ca hình nón và ct

hình nón theo thit din là tam giác vuông có din tích bng

. 

thit din 

30

. Th tích ca khc gii hn bng



. B.

10 2



. C.



. D.



Câu 41. Cho các s thc

,,abc

thuc khong

 

1; 

và tha mãn

log log .log 9log 4log

b b a a

b c c b



  





. Giá tr ca biu thc

log log

bc

bng:A.

.B.

.C.

.D.

Câu 42. Cho hàm s bc bn

 

y f x

 th  bên.Có bao nhiêu

giá tr nguyên ca tham s

thun

 

0;20

sao cho giá tr nh nht ca hàm

s

   

2 4 ( ) 3g x f x m f x    

n

 

2;2



. B.

. C.

. D.

Câu 43. 

 

3 3 3

log 4log 5 log 1x x m x   



là tham









27;

02m

. B.

02m

. C.

01m

. D.

01m

Câu 44. Cho hàm s

 

o hàmliên tctrên



tho mãn

     

f x f x x e



  

và

 

02f 

Tng tt c các nghim thc c

 

0fx

có giá tr làA.

2

. B.

. D.

1

Trang 7

Câu 45. Cho hàm s

 

y f x

liên tc trên



 th . Tng tt c giá tr

nguyên ca tham s

 

 

2 cosf f x m

có nghim













1

. B.

. C.

. D.

2

Câu 46. Cho hàm s c bc bn

 

y f x



3, 3, 5x x x   





 

3xx

g x f e m







A.

. B.

. C.

. D.

Câu 47. Có tt c bao nhiêu cp s

 

;ab

vi

,ab

là các s a mãn:

   

 

log 3 3 1 1a b a b a b ab a b        

.A.

. B.

. C.

. D.vô s.

Câu 48.Cho hàm s

 







 

2 2 4 4

1 2 , 0, 1

x x x x

x f x f x x

    



     







 

df x x





A.

.B.

.C.

.D.

Câu 49. Cho hình chóp

.S ABC



ABC

có

;2AB a AC a

và



135CAB 

, tam

giác

SAB

vuông ti

và tam giác

SAC

vuông ti

. Bit góc gia hai

mt phng

 

SAC

và

 

SAB

bng

30

. Tính th tích khi

chóp

.S ABC

.A.

.B.

. C.

.D.

Câu 50. Cho hàm s

 

y f x

và

 

0,f x x  

. Bit

hàm s

 

y f x





có bng bi và

1 137

2 16









Có bao nhiêu giá tr nguyên ca

 

2020; 2020m

 hàm s

   

x mx

g x e f x

  



ng bin trên









4040

. B.

4041

. C.

2019

. D.

2020

BẢNG ĐÁP ÁN

1

2

1

2

Trang 8

1.D

2.A

3.B

4.C

5.B

6.D

7.D

8.D

9.B

10.D

11.A

12.C

13.A

14.B

15.C

16.A

17.C

18.B

19.C

20.D

21.B

22.A

23.D

24.B

25.B

26.A

27.A

28.B

29.A

30.C

31.D

32.C

33.C

34.C

35.C

36.D

37.B

38.D

39.A

40.D

41.A

42.B

43.D

44.D

45.D

46.D

47.A

48.A

49.A

50.D

HƯỚNG DẦN GIẢI CHI TIẾT ĐÊ



Câu 1.Chọn D. chc mm mt nam và mt n ta thc hin liên tin:

Công đoạn 1: Chn

hc sinh nam t

hc sinh nam



có

cách chn.

Công đoạn 2: Chn

hc sinh n t

hc sinh na



có

cách chn.

Theo quy tc nhân ta có

20.25 500

cách chn.

Câu 2.Chọn A.S hng tng quát ca cp s cng có s hu

và công sai bng

là

 

u u n d  

Vy

4 2 4.3 14u u d    

Câu 3.Chọn B.Din tích xung quanh ca hình tr  ng sinh



là

S rl





Câu 4.Chọn C.Da vào bng bin thiên, hàm s nghch bin trên khong

 

1;1

Câu 5.Chọn B.Th tích ca hình h

. .3 3V B h a a a  

Câu 6.Chọn D.Ta có

4 8 4 8 0

2020 1 2020 2020 4 8 0 2



       

Vm

2x 

Câu 7.Chọn D.Ta có

   

2 d 13f x g x x







   

2. d d 13f x x g x x  



   

d 13 2. dg x x f x x  



 

d 13 2.5g x x  



 

d3g x x



Vy

 

d3g x x 



Câu 8.Chọn D.Da vào bng bin thiên ta thy m ci c th hàm s là

 

0; 3A 



chnD.

Trang 9

Câu 9.Chọn B

+) T  th hàm s trên, ta th th là dng ca hàm bc ba nên loA, C

+) T  th hàm s trên, ta thy gii hn ca hàm s khi

x  

là



nên h s ca

i

D

V

Câu 10.Chọn D.Vi

là s th

3 3 3

log log log

a a a

Câu 11.Chọn A.Ta có

 

2 2 3

d sin 6 d sin d 2 3 d cos 2f x x x x x x x x x x x C       

   

Câu 12.Chọn C.S phc

34zi  

có s phc liên hp là

34zi  

Vy s phc

có phn thc bng

3

và phn o bng

4

Câu 13.Chọn A.Theo lý thuyt ta có : hình chiu vuông góccm

 

;;M x y z

lên mt phng

 

Oyz

là

 

0; ;M y z



suy ra hình chiu vuông góc cm

 

1;2;3A

trên mt phng

 

Oyz

có tlà

 

0;2;3

Câu 14.Chọn B.Ta có

     

: 1 2 11S x y z    

nên t tâm mt cu là

 

1;2;0

Câu 15.Chọn C.Mt phng

0ax by cz d   

n dng

 

; ; , , 0n ka kb kc k k  





Suy ra

 



có mn là

 

2;0; 3n   



Câu 16.Chọn A.T ng thng

ta thng thm

 

1;3;0M

Câu 17.Chọn C.Do

 

SA ABCD

nên hình chiu ca

lên mt phng

 

ABCD

là

ng thng

và mt phng

 

ABCD

là góc



SOA

ABD

u cnh

nên

3 3 6

2 2 2

AO AB a  

SOA

vuông ti

có

SA 

AO 

nên

 

3 2 6

tan : 3 60

SA a a

SOA SOA

     

Vy góc ging thng

và mt phng

 

ABCD

bng

60

Trang 10

Câu 18.Chọn B. vào bng xét du ca

 



ta thy

 



i du t i các

m

1x 

và

1x 

nên hàm s m cc tiu.

Câu 19.Chọn C.

 

10 1f x x x  



 

3;2

Ta có

 

4 20f x x x





 

 

0 3;2

0 5 3;2 .

5 3;2

f x x



  





    



   





 

   

3 8; 5 24; 0 1; 2 23f f f f        

Vy giá tr nh nht ca hàm s n

 

3;2

bng

24

ti

5x 

Câu 20.Chọn D.Ta có

 

3 27

log loga a b

 

log log

a a b

 

3log loga a b

 

log loga a b

a a b

ab

Câu 21.Chọn B

 

log log

9 18 1

x 

u kin

0x 

 

log .log log

9 9 9

1 9 18

x x x

x 

 

log

9 18

x 

log

2 18

x

log

x

9 9 9

log .log log 9xx

 

log 1x

1 log 1x   

x  

(tha mãn).

Vy tp nghim ca b









Câu 22.Chọn A.Gi

là tâm mt cu

 

ng tròn

 

m thung tròn

 

ng tròn

 

là

r JA

3IJ 

ng tròn

 

là

2 12Pr





6r

Gi

là bán kính mt cu thì

35R r IJ  

Din tích mt cu

 

là

4 180SR





Vy

180S





Câu 23.Chọn D.+) Ta có

 

1f x m



   

1*f x m

Trang 11

+) S nghim c

 

bng s m c th hàm s

 

y f x

ng thng

1ym

+) T  th ng thng

1ym

c th hàm s

 

y f x

tm phân bit khi và ch

khi

1 1 3 0 4mm      

+) Vì

m

nên

 

1 ; 2 ;3m

Vy có 3 giá tr nguyên ca tham s

th bài.

Câu 24.Chọn B.Ta có

1 d d tan

cos cos

x x x

e x e x e x C





     







Câu 25.Chọn B.u kinh:

3 0 0 3x x x     

Vy tnh ca hàm s là

 

0;3D 

Câu 26.Chọn A.Din tích hình bình hành

ABCD

là



. .sin

ABCD

S AB AD BAD a

Tam giác

ABB



vuông ti

có

3BB AB AB a



  

Vy

3 3 3

. 3.

ABCD A B C D ABCD

V BB S a a a

   



  

Câu 27.Chọn A.Tnh





 

0;2 \ 1D 

+ Do tnh ca hàm s là





 

0;2 \ 1D 

nên không tn ti gii hn ca hàm s khi

x  

, do

 th hàm s không có tim cn ngang.

 

lim lim









  



;

 

lim lim







  



, suy ra

1x 

là tim cng

c th hàm s.

 

lim lim







  



, suy ra

0x 

là tim cng c th hàm s.

 th hàm s ng tim cng tim cng.

Vy

0k 

;

2l 

Câu 28.Chọn B

+ D th ta có

0a 

 th hàm s m cc tr suy ra

,ab

trái du, mà

0a 

suy ra

0b 

Trang 12

 th ct trc tung t âm, suy ra

0c 

Vy

0a 

0b 

0c 

Câu 29.Chọn A.Cách 1: Ta có

 

1 0, 1;1xx    

n tích phm là

1dxSx







 

1 dxx



















Cách 2: Công thc nhanh tính din tích

S Bh

Áp dng công thc vi

2B 

1h 

ta có:

2 2 4

.2.1

3 3 3

S Bh  

Câu 30.Chọn C.Ta có

 

12z i z  

3 4 4 2ii    

12i

.Vy phn o ca s phc

là

2

Câu 31.Chọn D.Ta có

 

, ; 0z x yi x y x   

Mt khác

     

 

2 2 2

2 2 2 2w iz z i x yi x yi x xy x y y i          

Vì

là s thun o nên

0x xy

 

0 kh«ngtháa m·n ®iÒu kiÖn

1 0 (tháam·n ®iÒu kiÖn)













Vy tp hm biu din s phc

ng th

10y 

(tr m

 

0;1M

ng thm

 

1;1Q

Câu 32.Chọn C.Ta có

 

3;2;2 . 5a b a b b      

    

Câu 33.Chọn C

Trang 13

ng thng

2 2 1

x y z

  



c vit li là

: 2 ,

y t t







  











Theo gi thit

I 



 

1 2 ;2 ;2I t t t  

Ta có

 

2 ;2 1; 2HI t t t   



Mt phng

 

có mn là

 

2; 1;1n 



Vì mt cu

 

tip xúc vi

 

tm

nên



và





Ta có



và



 khi

2 2 1 2

2 1 1

t t t  





2 1 2









   



 

1 3; 2;1tI    

Bán kính mt cu

 

là :

     

2 2 2

1 3 1 2 0 1 6R IH        

Vt cu

 

là :

     

2 2 2

3 2 1 6x y z     

Câu 34.Chọn C.Gi

 

là mt phm

 

1;2;3M

và song song vi mt phng

 

Vì

   

//QP

nên

 

nhn

 

1; 2;1

n 



ca mt phng

 



tuyn.

a mt phng

 

là:

     

1. 1 2. 2 1. 3 0 2 0x y z x y z         

Vt phng

 

: 2 0Q x y z  

Câu 35.Chọn C

ng thng

có m 

 

1;2; 1

u 



Mà

uu

 

suy ra

 

2; 4;2u   



là m ng thng

Câu 36.Chọn D.Xét phép thn ngu nhiên mt s t tp



S phn t ca không gian mu là:

 

9. 4536nA  

Gi

là bin c c chn có các ch s sp xp theo th t n và không cha hai ch s

nguyên nào liên ti

Gi s c chn là

abcd

+) Vì ch s sp xp theo th t n nên:

19a b c d    

Trang 14

+) Trong s c chn không cha hai ch s nguyên nào liên tip nhau nên:

1 1 2 3 6a b c d       

t:

aa

;

1bb

;

2cc

;

3dd



1 1 1 1

16a b c d    

S cách chn b bn s

 

1 1 1 1

;;;a b c d

là:

(cách)



có

cách chn

;

Mi cách chn

 

; ; ;a b c d

ch có mt cách sp xp tha mãn yêu cu bài toán nên to ra mt s. Suy ra:

 

15n A C

.Xác sut cn tìm là:

 

1512





Câu 37.

Chọn B+) Theo gi thit ta có

 

   

()

( ) ( )

ABCD

ABCD SI ABCD

SBI

SCI

SBI SCI







  











+) V

 



IK BC BC SIK SKI   

là góc gia mt phng

 

SBC

vi m



60SKI 

+) Vì

2 4 4

IDC IAB

S DI DC S



  

. Suy ra

 

BIC ABCD ICD IAB

S S S S a

  

  

+) Mt khác

 

5BC AB CD AD a   

và

IBC

S IK BC





Suy ra

IK 

+) Trong tam giác vuông

SIK

ta có

2a 15

.tan60

SI IK  

+) Vì

2AM a

nên

//BM a MD BC



   

 

, , ,d MD SC d MD SBC d D SBC

+) Gi

m ca

vi

, ta có

ED DC

ED AD ID

EA AB

    



 

d D SBC d I SBC

+) Gi

là hình chiu ca

lên

ta có

 

,d I SBC IH

Trong tam giác vuông

SIK

, ta có:

2 2 2 2 2 2

1 1 1 5 5 5 15

12 4 3 5

IH SI IK a a a

      

Vy

 

d MD SC 

Nhận xét:  tính và , ta có th 

Trang 15

1) Tính : Ta có

. .2 2

( , ) ( ; )

AI AM a a a

IK d I BC d A DM

    

2) Tính : Ta có



2 15

.sin .sin60

5 15

a a a

IH IK SKI    

Câu 38.Chọn D.Do

 

sinf x x x





nên

   

df x f x x







sin d dcosx x x x x   



cos cos dx x x x



cos sinx x x C   

Theo gi thit

2 1 2 1

f C C





     





.Suy ra

 

sin cos 1f x x x x  

   

 

2 2 2

0 0 0

cos . d cos sin cos 1 d sin cos cos cos dx f x x x x x x x x x x x x x

  

     

  

 

2 2 2

0 0 0

sin2 d 1 cos2 d cos d

x x x x x x x

  

   

  

1 1 1

cos2 sin d dsin 2

4 2 4

x x x x x x



    



2 2 2

1 1 1 3 1 7

1 sin2 sin2 d cos2

2 2 2

2 4 4 4 2 16 8 4 16

0 0 0

x x x x x



  



         



Vy

7, 4, 16abc  

. Suy ra

27abc  

Câu 39.Chọn A.u kinh:

2 3 0











    





t

2 3 0, ; 1

u x u x







        







, suy ra hàm s

23ux  

nghch bin trên

khong









.Vi

 

; 1 1; 2



   





Yêu cu bài toán tr thành tìm

 hàm s

 







ng bin trên khong

 

1; 2 .

Ta có

 

g u u















Trang 16

Hàm s

 

ng bin trên khong

 

1; 2

khi và ch khi

   

 

0, 1; 2

1; 2

g u u



  













 

1 1 0



  

























































































































































  







Vy

  

 



; 2 0; 1 2;S       

2; 0; 1; 2a b c d     



2 0 1 2 3P       

Câu 40.Chọn D

Mt phnh ca hình nón và ct hình nón theo thit din là tam giác vuông

SAB

Gi

SA l

ng sinh,

OA R

là bán kính và

SO h

ng cao c

Gi

m ca

và

là hình chiu ca

lên

Góc ging cao ca hình nón và mt phng thit din là

 









; 30SO SAB OSK  

SAB

vuông cân ti

nên

. 4 2 2

SAB

S SA l l    



. 2 4AB l   

ng trung tuyn

. .4 2

SI AB  

SOI

vuông ti



cos .cos30 2. 3 3

OSI SO SI h

       

Ta có:

   

2 2 3 5R l h    

Trang 17

Vy th tích ca khi nón là

1 1 5 3

.5. 3

3 3 3

V R h





  

Câu 41.Chọn A

Ta có:

log log .log 9log 4log

b b a a

b c c b



  





 

4log log . 2log log 9log 4log

a b b b a a

b c c b c b    

 

4log 2log log 9log 4log *

a b b a a

b c c c b    

t

log











(

,0xy

vì

, , 1abc

Ta có

log log .log

a a b

c b c xy

..Thay vào

 

c:

4 2 9 4x y y xy x   

 

4 8 2 4 0x xy xy y x y      

  

4 2 1 0x y x y    

 

4 0 ¹

x y lo i













Vy

log log log 2log 2 1

a b a b

b c b c x y     

Câu 42.Chọn B.Da vào hình v ta có:

 

2 ( ) 2, 2;2f x x     

 

 

2 4 0, 2;2f x x     

Vì

 

0;20m

nên

 

2 4 0f x m  

suy ra

   

 

2 4 2 4, 2;2f x m f x m x       

Ta có:

   

2 4 ( ) 3g x f x m f x    

   

2 4 3f x m f x    

 

1f x m  

 

2;2x  

+) Vi

0m 



   

1g x f x

 

2;2x  

 

* 

 

 

1 1 3, 2;2f x x      

 

 

0 1 3, 2;2f x x      

 

 

0 3, 2;2g x x     



 

 

2;2

0min g x





0m

không tha yêu cu bài toán.

+) Vi

 

1;20m

     

1 0 1f x m g x f x m       

T

 

ta có:

 

11f x m m   

 

 

2;2

1min g x m



  

Yêu cu bài toán:

 

 

2;2

1min g x





1 1 2mm   

 

2;20m

Vy có

giá tr nguyên ca tham s

tha yêu cu bài toán.

Trang 18

Câu 43.Chọn D.

logtx



27 3xt  



 

4 5 1 .t t m t   

 















0m 



4 5 0

, 5.





  













0m 

, ta có

4 5 0tt   

1 ( )

5 ( )

t loaïi

t thoûamaõn













0m 

thì

   

* 4 5 1t t m t    

   

2 2 2 2

1 2 4 5 0m t m t m      

. (**)



11mt   





1m

, ta có (**)

 

1 1 5 0t m t m



      



1 ( )

t loaïi





















5 0 1 1



       





0m 

suy

01m



01m



[27; )

Câu 44.Chọn D.Ta có

     

f x f x x e



  

   

. 2 1

f x f x e x





   





   

 

. . 2 1

f x e f x e x





   

 

. 2 1

f x e x





  

     

. 2 1 d .

f x e x x f x e x x C



      



(1).

 

02f 

nên t (1) ta có

2. 0 0 2e C C      



 

f x x x e  

 

0 2 . 0 2 0

f x x x e x x        













Vy tng tt c các nghim thc c

 

0fx

là

1 2 1  

Câu 45.Chọn Dt

costx

, do

;













nên suy ra





1;0 .t 

Trên khong

 

1;0

hàm s nghch bin nên suy ra

Vi





1;0t

thì

     

01f f t f  

hay

 

0 2.ft

Trang 19

t

 

2 cosu f x

thì

 





2 , 0;2 .u f t u

 thành:

Tìm

 

 

f u m

có nghim





0;2 .u 

 th ta thy rng vi





0;2u

thì

 





2;2 2 2.f u m     

Vì

 

2; 1;0;1 .mm    

Vy có 4 giá tr ca

Tng các giá tr ca

tha mãn yêu cu bài toán là

2

Câu 46.Chọn D.Ta có

 

3 2 3 2

2 3 3

3 6 .

x x x x

g x x x e f e m











 

3 2 3 2

2 3 3

0 3 6 . 0

x x x x

g x x x e f e m





    







   









 

3, 1

3, 2

5, 3













  













Hàm s

 

có

 tng s nghii l, khác

và

2

ca các



     

1 , 2 , 3

là

Xét hàm s

 

3xx

h x e





có

 

h x x x e







.Ta có

 





















Trường hợp 1:

Trang 20



3 3 51,6

1 3 4 3 57,6

m e m e



    





      



nguyên nên

 

52;53;54;55;56;57m

Trường hợp 2:



5 5 49,6

1 3 2 3

0 3 1 3 4

m e m e

m e m e m



    



         





    



Trường hợp 3:



3 1

3 0



  













4 5 49,6



    



    















Câu 47.Chọn A

Trang 21

Cách 1:Vi

,ab

là các s 

   

 

log 3 3 1 1a b a b a b ab a b        

 

3 3 2 2

log 3 3 3 1

a b ab a b a b ab ab a b

a b ab



          



     

 

3 3 3 3 2 2 2 2

log log 3 3 1a b a b a b ab a b ab



         



Xét hàm s:

 

logf t t t

trên

 

0;

 

' 1 0, 0

ln3

f t t

    

nên hàm s

 

ng bin trên

 

0;



 

tr thành :

     

3 3 2 2 3 3 2 2

33f a b f a b ab a b a b ab



        



 

a b ab

a b ab a b



  

      







,ab



 

vô nghim. Suy ra:

3ab

Mà

,ab

là các s 





















































Vy có hai cp s

 

;ab

tha mãn yêu cu bài toán.

Cách 2.Vi

,ab

là các s 

   

 

  

3 3 2 2 2 2

log 3 3 1 1

log 3 3 3 log 3 1

a b a b a b ab a b

a b a b

a b ab a b a b ab ab a b a b ab a b

        



               

ng hp 1:

2ab



 

1 log 4 3

ab  

loi do

,ab

ng hp 2:

3 log 0



   

và

 

3 0, , *a b ab a b a b      

nên

 

không xy ra.

ng hp 3:

3ab



 

tha mãn.

Trang 22

Mà

,ab

là các s 































Vy có hai cp s

 

;ab

tha mãn yêu cu bài toán.

Câu 48.Chọn A.T gi thit suy ra

 

2 2 2 4 4

x x x x

f x f

x x x

    



  





Ta có:

 

2 2 2

1 1 1

2 2 2 4 4

1 d . d d

x x x x

f x x f x x

x x x

    



  





  

   

2 2 2

1 1 1

2 2 2 2 4 4

1 d 1 d 1 d

f x x f x x

x x x x



     

         

     

     

  

   

f t t f t t x





       







   

d d 0f t t f t t



  



 

d0f t t







Vy

 

d0f x x







Cách trắc nghiệm.Ta có:

 

2 2 4 4

1 2 , 0, 1

x x x x

x f x f x x

    



     





 

2 2 4 4

1 2 , 0, 1

x x x x

x f x f x x

x x x

   



       





   

2 2 2 2

1 2 1 2 , 0, 1

x f x f x x x x



   

        

   

   

Chn

   

.d .d 0f x x f x x x x



   



Câu 49.Chọn A

Trang 23

Gi

là hình chiu vuông góc ca

xung mt phng

 

ABC

 

AB SB

AB SBD AB BD

AB SD





   







 

AC SA

AC SAD AC AD

AC SD





   







Tam giác

ABC

có



135 45CAB BAD    

Tam giác

ABD

vuông ti

có



45BAD 

suy ra tam giác

ABD

vuông cân và

2AD a

T 

ACD

vuông cân ti

A

t giác

ABDC

là hình thang vuông ti

và

Trong mt phng

 

SBD

, h

 

DH SB H SB

. D chng minh

 

DH SAB

Trong mt phng

 

SAD

, h

 

DK SA K SA

. D chng minh

 

DK SAC

Gi



là góc gia hai mt phng

 

SAB

và

 

SAC

ta có:

 



, 30DH DK HDK



   

do tam giác

DHK

vuông ti

t

SD x

 

0x 

.Tam giác

DHK

vuông ti

có



cos .

HD ax a x

HDK



  



2 2 2 2 2 2 2 2

6 2 2 6 6 8 4a x a x a x a x x a         



. . . .sin

S ABC

V SD AB AC BAC

.Vy th tích khi

.S ABC

bng

Câu 50.Chọn D

Ta có

       

4 5 4 5

2 4 . . .

x mx x mx

g x x m e f x e f x

     



   

       

2 4 . .

x mx

g x x m f x f x e

  



    





Trang 24

Yêu cu bài toán

 

0, 1;

g x x





    





và

 

0gx





ch xy ra ti mt s hu hm thuc









     

2 4 . 0, 1;

x m f x f x x





       





(vì

x mx

  



)

 

2 4 , 1;

x m x





       





, (vì

 

0,f x x  

)

 

4 2 , 1;

m x x





     





 

Xét

 

2 , 1;

h x x x





    





. Ta có

 

     

 

f x f x f x

 











Mà

 

, 1;











  













     

 

0, 1;

f x f x f x

 









    





T 

 

0, 1;

h x x





   





. Vy hàm s

 

ng bin trên









Bng bin thiên

Vu kin

 

1 1 225 225

4 4 2. 4

2 2 137 548

m h m m m







   



        

   



   





Li có

 

2020;2020

















 

1;2;3;...;2020m

Vy có

2020

giá tr nguyên ca

tha mãn yêu cu bài toán.

……….HẾT………

Trang 25

www.thuvienhoclieu.com

ĐỀ 22

PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 120 phút

Câu1.T mt nhóm gm

hc sinh nam và

hc sinh n, có bao nhiêu cách lp ra mt nhóm gm hai

hc sinh có c nam và n? A.

. B.

. C.

. D.

Câu2.Cho cp s nhân

 

vi

3u 

và

12u 

. Công bi

ca cp s ng

4q 

. B.

2q 

. C.

2q 

. D.

2q 

Câu 3.Cho khi nón có chiu cao bng

ng

. Th tích ca khng



. B.



. C.



. D.

2 a



Câu 4.Cho hàm s

 

y f x

có bng bi

Hàm s ch bin trên kho

( 3; 1)

. B.

( ;0)

. C.

( 2; 1)

. D.

( 3; 2) ( 2; 1)    

Câu5.

4,6,8



288

.B.

. C.

192

.D.

Câu6.Nghim c

 

log 1 3x 

là A.

4.x 

3.x 

6.x 

7.x 

Câu7.Cho

2 ( ) 2; ( ) 3.f x dx f x dx



Tính

( ) .I f x dx



4.x 

3.x 

6.x 

7.x 

Câu8.Cho hàm s

1y x x  

. M 

A.Hàm s có

m ci và

m cc tiu.B.Hàm s có

m cc tr.

C.Hàm s có

m cc tr.D.Hàm s có

m ci và

m cc tiu.

Câu 9. th hàm s i?

32y x x  

. B.

32y x x   

32y x x  

. D.

32y x x   

Câu 10.Vi

là s th

 

log a

bng

Trang 26

3log a

. B.

3 log a

. C.

log

. D.

log

Câu 11.H tt c các nguyên hàm ca hàm s

 

sin 8f x x x

cos 4x x C-+

cos 4x x C- - +

cos 4x x C++

cosxC-+

Câu12.

 

12zi

. B.

. C.

. D.

Câu 13.Trong không gian

Oxyz

, hình chiu vuông góc cm

 

3;5; 7M 

trên mt phng

 

Oyz

có t là

 

0;5; 7

. B.

 

3;0; 7

. C.

 

3;5;0

. D.

 

3;0;0

Câu 14.Trong không gian

Oxyz

, mt cu

2 2 2

( ) : 8 4 6 7 0S x y z x y z      

có tâm và bán

kính là:

 

4; 2; 3 ,I 

36R 

. B.

 

4; 2; 3 ,I 

6R 

. C.

 

4; 2; 3 ,I 

22R 

. D.

 

4; 2; 3 ,I 

6R 

Câu 15.Trong không gian vi h trc to 

Oxyz

, cho mt phng

 

: 3 2 6 0x y z



   

. Vecto nào

không phải là vecto pháp tuyn ca

 



?A.

 

1; 3; 2n   



. B.

 

1;3;2n 



. C.

 

1;3;2n 



. D.

 

2;6;4n 



Câu 16.Trong không gian

Oxyz

ng thm

 

1;2; 1A 

và

 

1;1;1B 

 

3;3; 3M 

. B.

 

3; 3; 3N 

. C.

 

3;3;3P 

. D.

 

3;3;3Q

Câu17.Cho hình chóp

.S ABC

có

 

SA ABC



2AC a

BC a

2SB a





 

SBC

.A.

45

. B.

60

. C.

30

90

Câu18.Cho hàm s

 

có

    

12f x x x x



  

. S m cc tr ca hàm s 

. B.

. C.

. D.

Trang 27

Câu19.

34y x x   

là bao nhiêu ? A.

. B.

. C.

. D.

Câu 20.Cho

là các s th tha mãn

log log 5ab

và

log log 4ab

. Giá tr

.ab

là:

. B.

256

. C.

144

. D.

324

Câu 21.Tp nghim ca b













là

;



 





. B.

 

1; 

. C.









. D.

 

; 1;



   





Câu 22.Choh

 hình



bng A.



. B.



. C.



. D.



Câu 23.Cho hàm s

 

y f x

 th 

S nghim c

   

2f x f x

là

A.2. B.3. C.4. D.5.

Câu 24.Tìm h tt các các nguyên hàm ca hàm s

 







trên khong

(1; ).

   

2 3ln 1 .x x C C    

   

2 3ln 1 .x x C C    

   

2 3ln 1 .x x C C    

   

2 3ln 1 .x x C C     

Câu25.Mi hàng tháng gi vào ngân hàng mt khong tin

theo hình thc lãi kép

vi lãi sut

0,6%

mi tháng. Bi tin là 10 tring. Hi s

tin

i hàng tháng là bao nhiêu? Cht)

A.643.000. B.535.000 C.613.000. D.635.000.

Câu26.Cho kh ng

.ABCD A B C D

   

nh

2AA a





góc gia



và mng

30

. Th tích ca kh ng:

.B.

23a

43a

. D.

Trang 28

Câu 27.Tng s tim cng và tim cn ngang c th hàm s







là:

. B.

. C.

. D.

Câu28.Cho hàm s

y x bx d  

 

,bd

 th i

 

0; 0bd

. B.

0; 0bd

0; 0bd

. D.

0; 0bd

Câu29. th

 

y f x

 n tích

ca hình phc gch chéo trong

i dây

bngA.

 

dS f x x







. B.

   

ddS f x x f x x







   

ddS f x x f x x



  



. D.

   

ddS f x x f x x







Câu30.Cho ba s phc

33zi

53zi

và

7zi

. S phc liên

hp ca s phc

1 2 3

w2z z iz  

bng:

8 16i

. B.

8 16i

. C.

8 16i

. D.

8 16i

Câu 31. Chos phc z tha mãn

(1 2 )(4 3 )z i i  

m biu din s phc z trên mt phng t là

A.

 

10;5 .Q

 

2;5 .M 

 

10; 5 .N 

 

2; 5 .P 

Câu32.Trong không gian

Oxyz



 

1;1;3a 



 

2;1;5b 



và

 

1; 3;2c 



. Tính tích vô

ng

 

.2a b c

  

bngA.

6

. B.

. C.

. D.

Câu 33.Trong không gian

Oxyz

m

 

1;3; 4A 

m

 

3; 1;0B 

. Mt cu

 

ng

kính

A.

     

2 2 2

2 1 2 3x y z     

. B.

     

2 2 2

2 1 2 9x y z     

     

2 2 2

2 1 2 9x y z     

. D.

     

2 2 2

2 1 2 3x y z     

Câu34.m

 

3;2; 2A 

 

1;0;1B

và

 

2; 1;3C 

. Vit ph

và

vuông góc

.A.

2 5 0x y z   

. B.

2 3 0x y z   

. C.

2 3 0x y z   

. D.

2 1 0x y z   

Trang 29

Câu35.Trong không gian

Oxyz

m

     

1;0;6 , 0;2; 1 , 2;4;3A B C



m ng thng cha trung tuyn

ca tam giác

ABC

 

2;3;7



. B.

 

0; 3;5



. C.

 

2;1;8



. D.

 

0;1; 4



Câu36.Cho

100

tm th  liên tip t

n

100

, Chn ngu nhiên

tm th. Xác su

Chc

tm th có tng các s ghi trên th là s chia ht cho

là

P 

. B.

P 

. C.

P 

. D.

P 

Câu 37.Cho hình chóp

.S ABCD

n

vuông góc mt ph

AD CD CB AB a   

3SA a

Khong cách ging thng

và

bng

. B.

Câu 38.

(x)f





, có

(0) 0f 

và

'(x)







0x 



(x) 2020f 

là A.

. B.

. C.

. D.

Câu39.Có bao nhiêu giá tr nguyên âm ca tham s

 hàm s







ng bin

 

0;1

. B.

. C.

. D.

Câu 40.Cho hình tr có thit dic là mt hình vuông có cnh bng

. Din tích xung quanh

ca hình tr làA.

16Sa





. B.

4Sa





. C.

24Sa





. D.

8Sa





Câu 41.Xét các s th

tha mãn

 

9 1

log log logx y x y  

. M 



;









. B.

;









. C.









. D.









Câu 42.Gi S tp hp giá tr thc ca tham s

sao cho giá tr nh nht ca hàm s

8y x x m   

n

 

1;3

bng 24. Tng các phn t ca S bng A.

7

. B.

4

. C.

Trang 30

Câu 43.

 

log 3 log 3 2 2 1 0x m x m m    

(

là tham s thc). Gi

là tp

hp tt c các s thc

m phân bit thun

 

1;3

. S phn t ca tp

là

. D.

Câu 44.Cho hàm s

()fx

liên tc trên



. Bit

23xx

là mt nguyên hàm ca hàm s

( ).5

h tt c các nguyên hàm ca hàm s

( ).5



là

 

2 1 ln5xC  

. B.

ln5 C

2 ln5

x x C



  





. D.

2 ln5

x x C



  





Câu 45.Cho hàm s

 

y f x

liên tc trên



 th .

Gi

là tp hp tt c các giá tr nguyên ca tham s

 

 

sin 3sin f x x m

có nghim thuc khong

 



. Tng các phn t ca

bng A.

9

. B.

10

. C.

6

. D.

5

Câu 46.

 

4 3 2

y f x ax bx cx dx e     





 

13y f x  

là

. B.

. C.

. D.

Câu47.Bit

1 2 1 2

, ( )x x x x

là hai nghim c

log 2 3





  





và

42x x a b  

, vi

,ab

là hai s nguyên



ab

9ab

. B.

12ab

. C.

7ab

. D.

14ab

Câu 48.Xét hàm s

 

liên tn

 

0;1

và thu kin

   

2 3 1 1f x f x x x   

Tính tích phân

 

dI f x x



. A.



Câu 49.









.S ABC



90SAB SCB  

, 









   

,SAB SCB









. 

















.S ABC

:

Trang 31

64 2

. B.

64 2

. C.

128 3

. D.

128 2

Câu 50.Cho hàm s

 

y f x

. Hàm s

 

'y f x

 th .

S m cc tr c th hàm s

 

   

4 3 3 2 2

y g x f x x x x       

là

. B.

. C.

. D.

BẢNG ĐÁP ÁN

1.A

2.D

3.B

4.C

5.C

6.D

7.A

8.A

9.A

10.C

11.B

12.D

13.A

14.B

15.C

16.A

17.B

18.D

19.A

20.D

21.C

22.C

23.D

24.D

25.D

26.C

27.C

28.C

29.D

30.D

31.C

32.D

33.B

34.C

35.B

36.B

37.D

38.D

39.C

40.A

41.B

42.A

43.C

44.C

45.B

46.A

47.D

48.B

49.D

50.A

HƯƠ



NG DÂ



N GIA



I CHI TIÊ



Câu1.Chọn A. lp ra mt nhóm gm hai hc sinh có c nam và n, ta thc hin liên tip

n

là Chn

hc sinh nam và Chn

hc sinh n, nên theo quy tc

. 35CC

Câu2.Chọn D.Ta có:

u u q q q

       

Câu 3.Chọn B.Th tích khi nón:

V a a



  

Câu 4.Chọn C.Da vào bng bin thiên ta thy hàm s ch bin

trên mi khong

 

3; 2

và

 

2; 1

Câu5.Chọn C.

4.6.8 192V ==

Câu6.Chọn D.u kin:

1 0 1.xx    

Vu kii:

 

log 1 3 1 2 1 8 7.x x x x         

Vy, m là

7.x 

Trang 32

Câu7.Chọn A.Ta có

2 ( ) 2 ( ) 1.f x dx f x dx  





5 2 5

1 1 2

( ) ( ) ( ) 1 3 4.I f x dx f x dx f x dx     

  

Vy,

( ) 4.I f x dx



Câu8.Chọn A.Tnh:

D  

Ta có

42y x x





;



















Gii hn

lim



 

Vy hàm s m cc tiu và mm ci.

Câu 9.Chọn A

*) Ta có

lim 0



   

, nên lo

 th, hàm s t cc tr ti

0x 

và

0x 

*) Xét hàm s

32y x x  

, ta có

' 3 6y x x

. Suy ra

' 0 3 6 0

y x x





    







Tc là hàm s

32y x x  

t cc tr ti

0x 

và

0x 

. Nên lo

Câu 10.Chọn C.

0a 

ta có

 

log log .

aa

Câu 11.Chọn B.Ta có

 

sin 8 cos 4x x dx x x C    



Câu12.ChọnD.Ta có

 

1 2 3 4z i i    

5z

.























1 1 1

5zz





















Trang 33

Câu 13.Chọn A.Hình chiu vuông góc cm

 

3;5; 7M 

trên mt phng

 

Oyz

có t là

 

0;5; 7

Câu 14.Chọn B

CÁCH 1:

 

2 2 2 2 2 2

8 4 6 7 0 2. 4 2.2 2.3 7 0.x y z x y z x y z x y z               

4, 2, 3, 7a b c d      

2 2 2

36.a b c d   

Vy

()S

có tâm

 

4; 2; 3 ,I 

bán kính

2 2 2

6.R a b c d    

CÁCH 2:

     

2 2 2

8 4 6 7 0 4 2 3 36.x y z x y z x y z             

Vy

()S

có tâm

 

4; 2; 3 ,I 

bán kính

6.R 

Câu 15.Chọn C.t phng

 

: 3 2 6 0x y z



   

Suy ra vecto pháp tuyn ca mt phng

 



là

 

1; 3; 2n 



Các vecto:

 

1;3;2n 



 

2;6;4n 



i vecto

 

1; 3; 2n 





tuyn ca mt phng

 



Câu 16.Chọn A.Ta có:

 

2; 1;2AB   



 cng thng

AB y t













  



là tham s thc.

Thay t m

 

3;3; 3M 

ng thng

, ta có:

3 1 2

3 2 1

3 1 2







    





   



m

 

3;3; 3M 

thung thng

Câu17.Chọn B.

AH SB

(

H SB



 

BC SA

BC SAB BC AH

BC AB





   









 

và

 



 

AH SBC



 









 



;;SA SBC SA SH ASH

Ta có

3AB AC BC a  

Trang 34

Trong vuông

SAB

ta có



sin

AB a

ASB

SB a

  



60ASB ASH  







 

SBC



60

Câu18.Chọn D.

 

0fx

















Ta có bng xét du sau:

D thy

 



i du khi qua

2x 

và

 



i du khi qua

1x 

nên hàm s m cc tr.

Câu19.Chọn A.u kin:

3 4 0 1 4x x x       

Tnh:

 

1;4

2 3 4







  



  

.Ta có:

   

1 0; ; 4 0

y y y



   





Vy giá tr ln nht ca hàm s

34y x x   

là

Câu 20.Chọn D.

log log 5

log log 4















log 2log 5

2log log 4













log 1

log 2



























. 324ab

Câu 21.Chọn C.

2 1 3 2 1 2

3 3 3 3 2 1

x x x







     





3 2 1 0 ;1

x x x





     





.Vy tp nghim ca BPT là









Câu 22.Chọn C.Gi s thit din qua trc ca hình nón là tam giác

OAB

ucó cnh

4OA OB AB= = =

 nh



4l OA OB  



r 

Vy din tích toàn phn ca hình nón là

.2.4 .2 12

S rl r

    

    

Trang 35

Câu 23.Chọn D.Ta có

       

 

2 2 0

f x f x f x f x





      









S nghim cu chính là s m c th hàm s

 

y f x

vng

thng

1y 

và

2y 

T  th  th ta thy:

 ng thng

1y 

c th hàm s

 

y f x

tm phân bit.

 ng thng

2y 

c th hàm s

 

y f x

tm phân bit.

Vy s nghim c

Câu 24.Chọn D.Ta có:

 

2 1 3

2 2 3ln 1

f x dx dx dx x x C





        







  

Vì xét trên khong

(1; )

nên

11xx  



   

2 3ln 1f x dx x x C    



Câu25.Chọn D. tin:

 

1T r T

 tin:

      

1 1 1T T T r r T r T      

Theo quy lu tin là

       

 

1 1 1 ... 1 1

T r T r r T r





        



Theo gi thit thì

10T 

và

0.006r 

suy ra

635.000T 

. Ta Chn D

Câu26.Chọn C.Vì

là hình chiu ca



trên mt phng

 

ABCD

nên



30B DB





là góc gia



và m



.cot30BD B B





23a

.Gi

O AC BD

Vì

ABCD

là hình thoi cnh

có

23BD a

2 2 2 2

2 2 2 4 3 2AC AO AB BO a a a      

. .2 .2 3 2 3

ABCD

S AC BD a a a   

. 2 .2 3 4 3

ABCD

V AA S a a a



   

Câu 27.Chọn C.

 

\ 2; 1D   

Có:

lim 2









nên

2y 

là tim cn ngang c th hàm s.

Có:

( 1) ( 1)

2 1 2 1

lim lim 3

3 2 2

x x x



   

  

  

  

( 1) ( 1)

2 1 2 1

lim lim 3

3 2 2

x x x



   

  

  

  

Trang 36

( 2) ( 2)

2 1 2 1

lim lim

3 2 2

x x x



   

  

  

  

( 2) ( 2)

2 1 2 1

lim lim

3 2 2

x x x



   

  

  

  

Suy ra

2x 

là tim cn ngang c th hàm s.

V th hàm s m cn ngang và 1 tim cng.

Câu28.Chọn C.D th ta th th hàm s

y x bx d  

ct trc tung t



0d 

, loi B, D

3 2 2

' 3 2y x bx d y x bx     

' 0 3 2 0

y x bx







    







Mà hàm s m cc tr không âm nên

b   

, loi A.

Câu29.Chọn D.Din tích cn tìm là

         

2 1 2 1 2

1 1 1 1 1

d d d d dS f x x f x x f x x f x x f x x

  

    

    

Câu30.Chọn D.Ta có:

     

1 2 3

w 2 2 8 16

3 3 5 3 7

z z iz i i

i i i

        

  

Vy s phc liên hp ca w là:

w 8 16i  

Câu 31. Chọn C.Ta có:

(1 2 )(4 3 ) 4 3i 8i 6i 10 5 10 5z i i i z i           

m biu din s phc z trên mt phng t m

(10; 5)N 

Câu32.Chọn D.Ta có:

 

2 2 2.1;1 2. 3 ;5 2.2 4;7;1bc        



nên

 

. 2 1. 4 1.7 3.1 6a b c     

  

Câu 33.Chọn B.Gi

m ca

 

2;1; 2I

;

 

1;2; 2IA   



   

1 2 2 3IA      

Mt cu

 

ng kính

nên có tâm là

 

2;1; 2I 

và bán kính

3R IA

t cu

 



     

2 2 2

2 1 2 9x y z     

Câu34.Chọn C.Gi

()



là mt phng cn tìm, ta có

(1; 1;2)n BC





  



,Vy

(1; 1;2)

( ) ( ):1( 3) 1( 2) 2( 2) 0 ( ): 2 3 0

(3;2; 2)

x y z x y z



  





           









Trang 37

Câu35.Chọn B.Gi

m ca

 

1;3;1BC M

Ta có

 

0;3; 5   

 

AM u

, vi

 

0; 3;5



n B

Câu36.Chọn B.S phn t ca không gian mu là

 

100

161700nC  

Gi

là bin cng các s ghi tên th là s chia ht cho



T

100

tm th có

tm th  chn và

tm th  l.

ng hp thun li ca bin c

là:

TH1: Chn

tm th  chn t

tm th  chn có:

TH2: Chn

tm th  chn và

tm th  l có:

50 50

.CC



 

3 1 2

50 50 50

. 80850n A C C C  

.Vy xác sut ca bin c

là

 

80850 1

161700 2

  



Câu 37.Chọn D.K

//DM BC

nên

 

//CB SDM

nên ta có

   

 

; ; ; ;d SD CB d CB SDM d B SDM d A SDM  

Vì ABCD là na lu nên

AC CB

Gi

H AC DM

, ta có:

AH DM

Mà

AH DM

SA DM











nên

 

DM SAH

K

AK SH

mà

AK DM

nên

 

AK SDM



   

 

;;d SD CB d A SDM AK

Ta xét tam giác

AMD

có

AM DM AD

nên tam giác

AMD

u cnh 2a.



AH a

.Xét tam giác SAH vuông ti A, ta có:

   

2 2 2 2

1 1 1 1 1 2

AK SA AH a

    

nên

AK a

.Vy

 

;

d SD CB 

Câu 38.Chọn D.Ta có:

'(x)dx 6 ( 1 1) 6 1 6

f dx x x dx x x dx xdx

      



    

Trang 38

2 2 2 2

3 1 ( 1) 6 2 1 3x d x xdx x x C       



.Vy

(x)f



(x) 2 1 3f x x C   

(0) 0f 

nên

2C 

vy

(x) 2 1 3 2f x x   

.Ta có

(x) 2020 2 1 3 2022 0f x x     



g(x) 2 1 3 2022xx   



(x)g















(0) 0g 

và

lim (x)



 

nên

(x) 0g 





(x) 0g 





Câu39.Chọn C.Tnh















 

2 12







. hàm s ng bin trên

 

0;1

thì

 



 



' 0, 0;1

2 12 0 6

6; 5 3;

  





   









  





        

   



  





  

   





















Vy các giá tr nguyên âm cn tìm ca

là

 

5; 3; 2; 1   

Câu 40.Chọn A.Hình tr có thit din qua trc là mt hình vuông có cnh bng













Din tích xung quanh hình tr:

2 2 .2 .4 16S rh a a a

  

  

Câu 41.Chọn B

t

 

log log logx y x y t   

















9 12 15

t t t

  

Chia hai v ca cho

c:

+ =1

   

   

   

Xét hàm s

 

   



   

   

có

 

3 3 4 4

ln + ln 0,

5 5 5 5

f t t

   



   

   

   



Suy ra hàm s

 

nghch bin trên



.Mt khác,

 

21f 

m duy nht

2t 

Trang 39

Vi

2t 

thì















9 9 1 2

0,5625 ;

12 16 2 3



    





Câu 42.Chọn A.t

 

8 1;3t x x x    

, ta có

 

' 4 16 4 4t x x x x     





  







BBT:

T BBT ta có

 

8 1;3t x x x    

 

9;16t  

Xét hàm s

 

9;16y t m t    

 

9;16

16; min 9max y m y m



    

Ta có

 

   

 

9;16 9;16

1;3

min min min 16; 9y t m m m



    

TH1:

 

9;16

min 16 24ym



  

16 24

9 24

  



   









TH2:

 

9;16

min 9 24ym



  

9 24

16 24

  



  









Vy

 

40;33S 

Câu 43.ChọnC.u kin:

0x 

PT:

 

log 3 log 3 2 2 1 0x m x m m    

log 3 log 2 1 0x m x m m     

log 1

log 2 1

  







  



Ta có

   

1;3 log 0;1xx  



 

0;1



0 1 1

0 2 1 1 0

1 2 1

   



   







      





    









Vy không có giá tr nào ca

tha mãn yêu cu bài toán.

Trang 40

Câu 44.Chọn C.

23xx

là mt nguyên hàm ca hàm s

( ).5

 

     

2 3 .5 2 2 .5

x x f x x f x f x





        

 

   

2.5 2 2 .5 .ln5

2 1 ln5

.5 2 1 ln5

f x f x x





















       











   

.5 2 1 ln5 2 ln5 .

f x dx x dx x x C





       











Câu 45.Chọn B.t

sintx

;

  



0; 0;1  xt



.Gi



ng

thm

 

1; 1

và song song vng thng

3yx

ng

thng





34yx

Gi



ng thm

 

0;1

và song song vng thng

3yx

ng thng





31yx



 

sin 3sin f x x m

có nghim thuc khong

 



khi và ch khi



 

3 f t t m

có nghim thuc na khong





0;1

41   m

Vy tng các phn t ca

là

       

4 3 2 1 0 10         

Câu 46.Chọn A.Xét

 

13g x f x  



D  

.Ta có:

 

   

1 3 1 3g x x f x





    

 

. 1 3





  



 







   

 

1 . 1 3h x x f x



   

 

1 3 0











  





1 3 2

1 3 0

1 3 1







   







  



  

































Trang 41





 





 

y g x

có



Câu47.Chọn Du kin:











Ta có:

log 2 3





  





 

log 1 2 1 logx x x x x      

   

log 1 1 logx x x x     

Xét hàm s

   

log 1 0, 0

.ln3

f t t t f t t



       

 thành

 

   

1 1 3 1 0

f x f x x x x x









         











Vy

4 2 9 5xx  



9, 5 14a b a b    

Câu 48.Chọn B.Do

   

2 3 1 1f x f x x x   

     

1 1 1

0 0 0

2 d 3 1 d 1 d 1

f x x f x x x x x    

  

1444442 444443 144442 44443

+ Xét

 

3 1 dI f x x



t

1 d dt x x t    

. Khi

0 1; 1 0x t x t     



 

3 d 3I f t t I



+ Xét

1dI x x x



t

1 1 d 2 dtt x x t x t       

Vi

0 1; 1 0x t x t     



 

2 2 4

1 2 d

5 3 15

I t t t t



     







Trang 42

Thay vào

 

1 : 2 3

15 15

I I I    

Câu 49.ChọnD.



 









 

ABC





:

90SAB 











 

.AB SAH AB AH  















BC CH







8AB BC AC  

, 









HAB HCBVV

, 30HA HC HBA HBC SA SC      













AC BH













 

.AC SHB AC SB  









AK SB

(

K SB

), 









 

.SB AKC SB KC  















   

,SAB SCB











90AKC 







90SAB SCB  

8AB BC AC  

SAB SCBVV

AK CK AKC  V



. 

8 4 2

AC AK KC    



SAB











2 2 2

1 1 1

8SA

AK AB SA

   







HAB





.tan 8.tan30

AH AB HBA   

8 6 1 1 8 6 8 3 128 2

. . . .

3 3 3 3 4 3

SABC ABC

SH SA AH V SH S       

Câu 50.Chọn A.Ta có

   

 

   

' 2 2 ' 4 3 6 2 2 2g x x f x x x x       

   

 

' 2 2 ' 4 3 4 1g x x f x x x x



      



;

 

   

' 4 3 2 4 3

f x x x x









     





Trang 43

T  th hàm s.Tng thng

2yx

c th

 

'y f x

ti bn

m phân bi

là

2; 0; 1; 2x x x x    

.Vy

4 3 2

4 3 0 3

4 3 1

4 3 2

x x x











   





     



  







  







Ta có BBT:

T  th hàm s m cc tr.

www.thuvienhoclieu.com

ĐỀ 23

PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 120 phút

Câu 1.T mt nhóm hc sinh gm

nam và

n, có bao nhiêu cách Chn ra hai hc sinh?

. B.

. C.

. D.

Câu 2.Cho cp s nhân

 

có các s hng tha mãn











. Tìm s hu

và công bi

ca cp s nhân. A.

2, 2uq

. B.

uq

. C.

up

3, 2uq

Câu 3.Mt hình tr có din tích xung quanh bng

4 a





 ng cao

ca hình tr A.

. B.

. C.

. D.

Câu 4.Cho hàm s

 

y f x

có bng bi

Trang 44

Hàm s ch bin trên kho

 

;2

. B.

 

;0

. C.

 

0;1

. D.

 

1; 

Câu 5.Tính th tích

ca kh ng có ding

và chiu cao

bng

32V 

. B.

96V 

. C.

68V 

. D.

64V 

Câu 6.Nghim c

log 3x

là A.

. B.

. C.

. D.

Câu 7.Nu

 

d9f x x 



và

 

d1



f x x

thì

 

df x x



bng A.

. B.

10

. C.

. D.

8

Câu 8.Cho hàm s

 

y f x

có bng bi

Giá tr ci ca hàm s ng A.

1

. B.

2

. C.

. D.

Câu 9. th ca hàm s ng cong trong hình bên?

2y x x

. B.

23y x x  

23y x x   

. D.

32y x x  

Câu 10.Vi

là s th

log







bng

3log 1a 

. B.

3log 1a 

. C.

 

3 log 1a 

. D.

3log

a 

-1

-3

-4

Câu 11.H nguyên hàm ca hàm s

 

sin 3f x x x

là

cos

x x C  

. B.

cos

x x C

. C.

cos 3x x C  

. D.

cos xC

Câu 12.Cho s phc

52zi

. Tính

.A.

5z 

. B.

3z 

. C.

7z 

. D.

29z 

Câu 13.Trong không gian

Oxyz

, hình chiu vuông góc cm

(1;2; 3)M 

lên mt phng

()Oyz

có

t là

 

1;0;0

( 1;2; 3)

(1; 2;3)

(0;2; 3)

Câu 14.Trong không gian

Oxyz

, cho mt cu

2 2 2

( ): 4 2 4 16 0S x y z x y z      

. Tìm tâm và

bán kính mt cu

()S

. A.

(2;1; 2), 5IR

.B.

(2;1; 2), 13IR

( 2; 1;2), 13IR  

. D.

( 2; 1;2), 5IR  

Câu 15.t ph

 

2;1; 1n 



n

2 1 0x y z   

2 1 0x y z   

4 2 1 0x y z   

2 1 0x y z    

Câu 16.Trong không gian

Oxyz

ng thng

1 2 1

x y z

  





(2;0; 2)P 

. B.

(1; 2; 1)Q 

. C.

( 1;3;2)N 

. D.

(1;2;1)M

Câu 17.Cho hình chóp

.S ABCD



ABCD

là hình vuông cnh

, cnh bên

vuông góc vi mt



2SA a

. Tìm s a góc ging thng

và mt phng

 

SAB

45

. B.

30

. C.

60

. D.

90

Trang 45

Câu 18.Cho hàm s

 

, bng xét du

 





S m cc tiu ca hàm s

 

là A.

. B.

. C.

. D.

Câu 19.Gi

lt là giá tr nh nht và giá tr ln nht ca hàm s



n

 

1;4

Giá tr ca

mM

bng A.

. B.

. C.

Câu 20.Cho

log 2

b 

vi

, 0ab

1a 

. Kh

 

log 3

ab 

. B.

 

log 4

ab 

. C.

 

log 4

b 

. D.

 

log 3

ab 

Câu 21.Tp nghim ca b

xx



là A.

 

0;6

. B.

 

;6

. C.

 

0;64

 

6;

Câu 22.ng 5. Bit rng khi ct hình nón cho bi mt phng qua trc,

thit dic là mu. Din tích toàn phn cng

50p

. B.

25p

. C.

75p

. D.

Câu 23.Cho hàm s

 

có bng bi

S nghim thc c

 

3 5 0fx

là A.

. B.

. C.

Câu 24.H tt c các nguyên hàm ca hàm s

 







trên khong

 

5; 

là

 

8ln 5x x C  

. B.

 

8ln 5x x C  

. C.

 





. D.

 





Câu 25. d báo dân s ca mt qui ta s dng công thc

S Ae

;



là dân s cy làm mc tính,

là s dân



là t l 

s  cc In--Nê-Xi-a là

272056300

i. Gi s

t l  i là

1.5%

, d báo dân s c

2035

i ?

345851300

. B.

445851300

. C.

395851300

. D.

545851300

Câu 26.Cho kh ng

.ABC A B C

  

u cnh bng

'2AB a

. Th tích ca kh ng

Trang 46

V 

. B.

V 

. C.

V 

. D.

Câu 27.Tng s tim cng và tim cn ngang c th hàm s

2019 2020







là

. B.

. C.

. D.

Câu 28.Cho hàm s bc ba

y ax bx cx d   

 

, , ,a b c d 

 th

hàm s . M 

0, 0, 0, 0a b c d   

. B.

0, 0, 0, 0a b c d   

0, 0, 0, 0a b c d   

. D.

0, 0, 0, 0a b c d   

Câu 29.Din tích hình phc gch chéo trong hình bên bng.

   

3 2 2

2 3 d 1 dx x x x x x x



     



   

3 2 2

2 3 d 1 dx x x x x x x



     



   

3 2 3 2

2 2 d 2 2 dx x x x x x x x



      



. D.

   

3 2 3 2

2 2 d 2 2 dx x x x x x x x



       



Câu 30.Cho hai s phc

43zi

và

12zi

. Phn thc ca s phc

bngA.

. B.

. C.

Câu 31.Trên mt phng tm biu din ca s phc















 

2;2D

. B.

 

1;3 3C

. C.

;







. D.

 

2; 2A 

Câu 32.Trong không gian

Oxyz



 

1; ;a m n



 

3; 2;2b 



tha mãn

. 17ab



và

 

, 60ab 



. Tính giá tr ca biu thc

S m n

. A.

. B.

. C.

Câu 33.Trong không gian

Oxyz

, cho mt cu

   

: 3 5S x y z   

. Mt cu

 

ct mt phng

 

: 2 2 3 0P x y z   

theo mng tròn có bán kính bng A.

. B.

. C.

Câu 34.Trong không gian

Oxyz

m

     

1;3;2 , 1;2;1 , 4;1;3A B C

. Mt phng

tâm

ca tam giác

ABC

và vuông góc vng thng



3 2 4 0x y z   

. B.

3 2 4 0x y z   

. C.

3 2 12 0x y z   

. D.

3 2 4 0x y z   

Câu 35.Trong không gian

,Oxyz

m

   

1;2;3 , 3;0;1 .AB



pháp tuyn ca mt phng trung trn

? A.

 

2;2;4n 



 

4;2; 2n 



. C.

 

2; 1;1n 



. D.

 

2; 1; 1n   



Trang 47

Câu 36.Chn ngu nhiên mt s t tp hp các s t nhiên chia ht cho 3 gm ba ch s. Xác su s

c Chn chia ht cho 5 bng A.

. C.

. D.

Câu 37.Cho hình chóp

.S ABCD



ABCD

là hình thoi tâm

. Bit

2 3 , 2AC a BD a

2SD a

và

vuông góc vi mt phng cách ging thng

và

bng

. B.

2 21

. C.

. D.

2 21

Câu 38.Cho hàm s

 

có

 

f 

và

 

ln 1.

f x x





vi

0x 



 

ln 1

xx



bng

 

ln2 ln 2 1



. B.

 

ln2 ln 2 1



. C.

 

ln2 ln 2 3



. D.

 

ln2 ln2 3



Câu 39.Cho hàm s

 

2 12







(

là tham s thc). Có bao nhiêu giá tr nguyên ca



hàm s ch bin trên khong

 

2;

? A.

. B.

. C.

. D.

Câu 40.Cho hình nón có góc  nh bng

120

. Mt mt phnh hình nón và ct hình nón theo

mt thit din là mt tam giác vuông có din tích bng

. Th tích ca khc gii hn bi hình

ng



. B.



. C.



. D.



Câu 41.Cho

,xy

là các s tha mãn

 

9 12 16

log log logx y x y  

và

x a b





, vi

,ab

là các s 

T a b

. B.

. C.

. D.

Câu 42.Gi

là tp hp tt c các giá tr thc ca tham s

sao cho giá tr ln nht ca hàm s

2y x x m  

n

 

0;2

bng

. Tng tt c các phn t ca

bngA.

. B.

. C.

2

Câu 43.

9 ( 5)3 3 6 0

mm    

(

là tham s thc). Tp hp tt c các giá tr

ca

 m phân bit thun

 

1;2

là A.

 

1;7

. B.





1;7





1;7

. D.

 

1;

Câu 44.Cho hàm s

 

liên tc trên



. Bit

2 cos sin 2020x x x

là mt nguyên hàm ca

 

. H tt c các nguyên hàm ca hàm s

 



là

2sin sin cos 2x x x x C  

2sin sin cos 2 2020x x x x C   

cos2 sin cos 2 2018x x x x C    

sin 2

cos2 2 2

x x C    

Câu 45.Cho hàm s

 

có bng bi nghim

thuc khong

 



c

Trang 48

 

3 2 2cos 4 0fx  

là . A.

. B.

. C.

Câu 46.Cho hàm s

 

o hàm liên tc trên



 th

 



cho  hình v i. Tìm s m cc tr ca hàm s

 

1y f x f x   

, bit rng

 

13f 

 

15f 

 

20 4 13f

và

   

0 21, 2 21ff

A.5. B.8. C.6. D.7.

Câu 47.Có bao nhiêu cp s thc

 

,xy

tha mãn



 

2 1 4

3 3 1

log 2 1 2

x x x x y

x x y

   

  





A. 4. B. 5. C. 6. D. 7.

Câu 48.Cho hàm s

 

liên tc trên

, và tha mãn

 

3 sin

2cos 1 cos 1 sin ,

2 cos

f x xf x x



     





. 

 

f x dx





bng

. B.

. C.

. D.

Câu 49.Cho hình chóp

.S ABC



ABC

là tam giác vuông cân ti



90SBA SCA

SA a

góc gia hai mt phng

   

,SAB SAC

bng

. Tính th tích khi chóp

.S ABC

theo

. B.

. C.

. D.

Câu 50.Cho hàm s

 

2f x x x

. Gi

 

là mt nguyên hàm ca hàm s

 

f f f x

. Hàm

s

   

3g x F x x

nghch bin trong kho

 

2 2;1 2

. B.

 

2;1 2

. C.

 

2 2;4

. D.

 

0;1 2

BẢNG ĐÁP ÁN

1.B

2.B

3.B

4.B

5.B

6.A

7.A

8.A

9.B

10.C

11.A

12.B

13.D

14.D

15.A

16.A

17.B

18.B

19.B

20.D

21.B

22.C

23.A

24.A

25.A

26.C

27.B

28.B

29.C

30.C

31.A

32.C

33.B

34.A

35.D

36.A

37.D

38.C

39.D

40.C

41.B

42.A

43.B

44.A

45.B

46.D

47.A

48.A

49.A

50.D

LỜI GIẢI CHI TIẾT

Câu 1.Chọn B.Mi cách Chn

hc sinh t

hc sinh là mt t hp chp

ca

hc sinh. Vy s

cách Chn là

91C 

cách.

Câu 2.Chọn B.Áp dng công thc

u q u





vi

2,nn

Ta có

1 1 1

. 33 (1 ) 33 (1)

66 (1 ) 66 (2)

u u q u q

u q u q u q q





   







  



   







Lc

(1 ) 66

(1 ) 33

u q q



  



. Thay

2q 

c

u 

Trang 49

Câu 3.Chọn B.Din tích xung quanh hình tr là

S 

2 Rh



.Theo  bài ta có

4 2 2a Rh h a



  

Câu 4.Chọn B.Da vào bng bin thiên ta thy hàm s ch bin trên các khong

 

;0

và

 

1; 

Câu 5.Chọn B.Áp dng công thc tính th tích kh c

8.12 96V 

Câu 6.Chọn A.u kin

0x



log 3 3 27xx   

Câu 7.Chọn A.Ta có

         

3 4 3 4 4

1 1 4 1 3

d d d d d 9 ( 1) 10f x x f x x f x x f x x f x x       

    

Câu 8.Chọn A.T bng bin thiên ta thy hàm s t ci ti

0x 

và giá tr ci ca hàm s là

CÐ

y 

. Vy ChA

Câu 9.Chọn B.D th ta thy:

 

03y 



loi A,D;

 

14y 



loi C, Chn B

Câu 10.Chọn C.Ta có

3 3 3

log log log 27









 

3log 3 3 log 1aa   

Câu 11.Chọn A.Ta có:

   

sin 3 cos

f x dx x x dx x x C     



Câu 12.Chọn B.Cách 1: Ta có:

 

5 2 5 2 9 3z i z      

Cách 2:Ta có:

 

5 2 9 3z     

Câu 13.Chọn D.Hình chiu vuông góc cm

(1;2; 3)M 

lên mt phng

()Oyz

m

(0;2; 3)M





Câu 14.Chọn D.Cách 1:

2 2 2 2 2 2

4 2 4 16 0 ( 2) ( 1) ( 2) 25x y z x y z x y z             

Tâm mt cu

()S

là

( 2; 1;2)I 

, bán kính

5R 

Cách 2:

2 2 2

4 2 4 16 0 2; 1; 2; 16x y z x y z a b c d              

Tâm và bán kính mt cu

()S

là

 

2 2 2

2; 1;2

4 1 4 16 5

R a b c d

  





        





Câu 15.Chọn A

T t phng

2 1 0x y z   

suy ra mt phng này có mn là

 

2;1; 1n 



Câu 16.Chọn A

Thay t mm

, , ,M N P Q

ng thng thng

m

(2;0; 2)P 

Câu 17.Chọn B.Ta có

 

CB SAB

SB

là hình chiu vuông góc ca

lên

 

SAB

Vy góc gia ng thng

và mt phng

 

SAB

là



CSB

Xét tam giác

CSB

vuông ti

có



tan

CB a

CSB

  

.Vy



CSB

30

Câu 18.Chọn B.T bng xét du, ta thy

 



i du t 

0x 

và

2x 

nên

hàm s

 

có

m cc tiu.

Câu 19.Chọn B.Hàm s nh và liên tn

 

1;4

Trang 50

Ta có:

1yx







   





 

3 1;4

0 1 0 9 0

3 1;4







        



  



Có

 

 

1; 4

1 10

3 6 min 6

f y m









   









và

 

1; 4

max 10yM

.Vy

16mM

Câu 20.Chọn D.Ta có

 

log log log 1 2log 1 2.2 5

a a a a

ab a b b      

nên

 

log 3

ab 

là



Câu 21.Chọn B.Ta có

2 2 2 6 6

x x x



     

.Vy tp nghim ca b

 

;6S  

Câu 22.Chọn C.a hình nón

5R 

và thit din ca hình nón b ct bi

mt phng qua tr ng sinh ca hình nón

2 10lR

50 25 75

S Rl R

    

     

Vy Chn C

Câu 23.Chọn A.Ta có

 

3 5 0fx

 

35fx

 

fx

. S nghim ca

 m c th

 

y f x

ng thng

y 

V

nghim thc phân bit.

Câu 24.Chọn A.Ta có:

 

3 5 8 8

d d d 1 d 8ln 5

5 5 5

f x x x x x x x C

x x x

  



       



  



   

 

8ln 5x x C   

Câu 25.Chọn A.Ta có

S Ae

thay s vi

272056300A

2035 2019 16n   

1.5%r 

c s dân ca In--Nê-Xi-

2035

;

16.1,5

272056300. 345851340,2145852Se

Vì kt qu 

345851300S 

Câu 26.Chọn C.Di

ABC





Tam giác

''AA B

vuông ti

nên ta có:

' ' ' ' . 3AA AB A B a  

Th  là:

. '. . 3

ABC

V B h AA S a



   

.Chọn đáp án C

Câu 27.Chọn B.Hàm s

2019 2020







u kinh là:

2019 2020 0









  





 

 

1 2;2 \ 1

2020

  





    











T u kinh suy ra không tn ti

lim



và

lim



 th hàm s không có tim cn

ngang.



Ta có

  

lim lim

1 2020







  



và

  

lim lim

1 2020







  



V th hàm s có 1 tim cng

1x 

Kt lun: Tng s tim cng và tim cn ngang c th hàm s là 1.

Trang 51

Câu 28.Chọn B.T  th ta có

lim 0



   

 th hàm s ct trc

t 

0d 

Gi

,xx

 m cc tr c th hàm s.



,xx

là nghim c

' 0 3 2 0y ax bx c    

.Suy ra

x x c

   

m un c th hàm s nm bên phi trc

Oy b



   

.Kt lun

0, 0, 0, 0a d b c   

Câu 29.Chọn C.Theo hình v ng cong:

23y x x x   

;

1y x x  

ct nhau tm

 lt là:

1x 

;

1x 

;

2x 

.Ta có din tích hình phng b gii hn bi 2 ng cong

trên là:

   

3 2 2

2 3 1x x x x x dx



     



 

2 2 dx x x x



  



   

3 2 3 2

2 2 d 2 2 dx x x x x x x x



      



   

3 2 3 2

2 2 d 2 2 dx x x x x x x x



      



Câu 30.Chọn C.Ta có

12zi

nên

12zi

. Suy ra







(4 3 )(1 2 )

(1 2 )(1 2 )







10 5



  

Vy phn thc ca s phc

bng

Câu 31.Chọn A.Ta có

1 3 3 9 3 3 4

1 3 3 1

i i i

i i i i

  

   

   

. Vm biu din ca

là

 

2;2D

Câu 32.Chọn C.Ta có

 

. 17

. . .cos , 2 17

.cos ,

17.

a b a b a b a

b a b

    



      

  

2 2 2 2

1 68 67m n m n      

Câu 33.Chọn B.Mt cu

   

: 3 5S x y z   

có tâm

 

0;0; 3I 

và bán kính

5R 

Ta có

 

2.0 0 2.3 3

4 1 4

d d I P

  

  



ng tròn giao tuyn gia mt cu

 

và mt phng

 

là

2.r R d  

Câu 34.Chọn A.Ta có t m

 

2;2;2G

và

 

3; 2;1AC 



Vì mt phng

 



cn tìm vuông góc vng thng

nên mt phng

 



có mn

là

 

3; 2;1n 



.Mt phng

 





 

2;2;2G

và nhn

 

3; 2;1n 



làm n, có



   

3 2 2 2 2 0 3 2 4 0x y z x y z          

Câu 35.Chọn D.

   

4; 2; 2 2 2; 1; 1 .AB      



Trang 52

Vy mn ca mt phng trung trn

là

 

2; 1; 1n   



Câu 36.Chọn A.+ S các s gm ba ch s và chia ht cho 3 là:

 

999 102

1 300 300.



    

+ S chia hng thi chia ht cho 5 khi và ch khi s t cho 15, có tt c các s

990 105

1 60





y. Vy xác su lc s chia ht cho 5 là

60 1

300 5

p 

Câu 37.Chọn D.+)Ta có

//AB CD

 

//AB SCD

   

 

, , , 2 ,d AB SD d AB SCD d A SCD d O SCD   

+)Do t giác

ABCD

là hình thoi tâm

nên

AC BD

và

AC BD

OC a OD a   

Tam giác

SOD

vuông ti

2 2 2 2

2SO SD OD a a a     

+)Xét t din

OSCD

có

,,OS OC OD

t vuông góc vi nhau ti

nên t din

OSCD

vuông ti



 

2 2 2 2 2 2 2

1 1 1 1 1 1 1 7

OS OC OD a a a a

d O SCD

      

 

d O SCD a

 

2 21

d AB SD a

Câu 38.Chọn C.Xét

 

.d ln 1. .d

f x x x x







t

ln 1xt

ln 1 .d .d

x t x t t

    

Suy ra:

 

ln 1

d . d

f x x t t t C C





    



.Vì vy:

 

ln 1

f x C





 

1 1 1

3 3 3

f C C     

. Suy ra:

 

ln 1





Vy

 

2 2 2 2

1 1 1 1

(ln 1)

ln 1 1

ln 1 (ln )

ln 1 3 ln 1

dx dx dx x d x

x x x x



   



   

1 1 1 1

ln ln ln 2 ln2

3 3 3 3

   

   

   

   

 

ln2 ln 2 3





Câu 39.Chọn D.Hàm s có tnh

 

\3Dm  

.Ta có

 

2 18









Hàm s nghch bin trên

 

2;



   

0 2;

f x khi x



    





  





2 18 0 3 1



     





















nhn giá tr nguyên nên

 

2; 1;1;2m  

.Vy có

giá tr nguyên ca

tha mãn bài toán.

Trang 53

Câu 40.Chọn C.Gnh ca hình nón là

t phnh ct hình

nón theo thit din là tam giác

SAB

và tam giác

SAB

vuông cân ti

.Ta có

. 6 2 3

SAB

S SA SB SA SA



    

Xét tam giác

OSA

vuông ti

, góc



60OSA 

nên

3, 3SO OA

Vu cao

3h SO



3R OA

Vy th tích ca khc gii hn b

.9. 3 3 3

V R h

  

  

Câu 41.Chọn B.t

 

9 12 16

log log logx y x y t   

. Suy ra

9 ; 12

















3 1 5

9 12 3 3 3 1 5

9 12 16 1 1 0

16 16 4 4 4 2

3 1 5

t t t t t

t t t

















         



           

         



         



















9 3 1 5

12 4 2





  





suy ra

1, 5ab

. Vy

1 5 26T a b    

Câu 42.Chọn A.Xét hàm s

 

2f x x x m  

là hàm s liên tn

 

0;2

Ta có:

 

22f x x





và

 

01f x x



  

     

0 ; 1 1; 2f m f m f m   

 

   

0;2

ax ax 1;m f x m m m  

   

 

 

0;2 0;2

ax ax ax 1 ; 3m y m f x m m m    

TH1:













Nu

3m 

thì

 

 

0;2

max ax 2;3 3ym

. Nu

3m 

thì

 

 

0;2

max ax 4;3 4ym

TH2:





  







Nu

4m 

thì

 

 

0;2

max ax 3;4 4ym

. Nu

2m 

thì

 

 

0;2

max ax 2;3 3ym

Vy có

giá tr ca tham s

tha mãn yêu cng là:

3 ( 2) 1  

Câu 43.Chọn B

 

    

9 ( 5)3 3 6 0 3 3 3 2 3 3 0 3 3 3 2 0 .

x x x x x x x

m m m m





                







3 3 1

x  

tha mãn

 

1;2x

.Mt khác:

   

1;2 3 3;9

x  

V m phân bit thun

 

1;2

khi và ch khi

3 2 9 1 7.mm     

Câu 44.Chọn A.Theo gi thit

     

2 cos sin 2020 e e 2 cos2

x x x f x f x x



     

Xét

 

I f x x







t

   

e d e d

u u x

v f x x v f x



















Trang 54

     

sin 2

e e d 2 cos2 2 cos2 d 2 cos2 2 1

I f x f x x x x x x x C           



sin 2

2 cos2 2 1 2sin sin cos 2

I x x C x x x x C         

Câu 45.Chọn B.Ta có

1 cos 1 0 2 2cos 4xx      

x

nên tbng bin thiên ca hàm s

 

ta suy ra

   

3 2 2cos 4 0 2 2cos

f x f x     

 

2 2cos 0;2

2 2cos 2;4

  







  





   

cos 1;0 1

cos 0;1 2





  



















P

 

có 1 nghim

thuc khong

 





P

 

có 1 nghim

thuc khong

 



Hai nghim

phân bit.Vy s nghim thuc khong

 



c

 

3 2 2cos 4 0fx  

là

nghim.

Câu 46.Chọn D.c tiên ta xét hàm s

   

 

1v x f x f x   

Ta có

 

1 1 2 1v f x f x f x x f x f x





  

         





 

( 1) 2 0

1 2 0

0 1 3 .

1 0 *

f x x

v f x x

f x f x

f x x





  



  





  









     





   







  



   



Ta tnh ti th hàm s

 



sang bên trái m th

ca hàm s

 

1y f x





và hàm s

2yx

c biu din trên h trc

t 



 

1 2 0f x x



  

có 3 nghim là

1, 0, 1x x x   

Xét hàm s

   

1g x f x x  

, có

   

12g x f x x



  

Kt hp vi gi thic

   

     

2 1 4 5 4 1

1 0 1 20

0 1 3

1 2 1 20

3 4 16 3;4

      





   









  



  



D th  ng bin thiên ca hàm

 



Trang 55

T bng bin thiên có th xét s a hàm

 

vi lng thng

1, 1, 3, 4y y y y    

, t 

 

có tt c 7 nghiy hàm s

 

có

tt c

m cc tr. Suy ra s m cc tr ca hàm s

 

1y f x f x   

chính bng

ln s

m cc tr a hàm s

 

cng vi

và bng

Câu 47.ChọnA.u kin:

3 3 1 0x x y   

. Ta có:

 

   

 

2 2 2 2

2 1 4 2 2 2 1 3 3 1

2 3 3 1 2 2 1

3 3 1

log 2 1 2 log 3 3 1 log 2 1 2 2

log 3 3 1 2 log 2 1 2 *

x x x x y x x x x y

x x y x x

x x y

x x y x x

        

    

  

          



        

Xét

 

log 2

f t t

là hàm s ng bin trên

 

0;



 

   

 

2 2 2 2 2

* 3 3 1 2 1 3 3 1 2 1 (2) 4 0 **f x x y f x x x x y x x x x y                 

u kin

 

c tha mãn do

 

Vì v tn ti

 

,xy

tha mãn yêu cu thì

 

có nghic

4 0 4yy   



 

1;2;3;4y

. Ta có 4 cp

 

,xy

tha mãn yêu cu bài toán.

Câu 48.Chọn A.

x

, ta có:

 

3 sin 4 cos

2cos 1 cos 1 sin 2 cos

2 cos 2 cos

f x xf x x



      



 

sin . 2cos 1 sin .cos . 1 sin 2 cos sinx f x x x f x x x     

 

π π π

2 2 2

0 0 0

sin . 2cos 1 d sin .cos . 1 sin d 2 cos .sin dx f x x x x f x x x x x     

  

 

+ Xét:

 

sin . 2cos 1 dI x f x x



t

2cos 1 d 2sin d sin d d

t x t x x x x t       

i cn:

01xt  

;

xt   

.Suy ra:

     

1 1 1

111

d d d

222

I f t t f t t f x x





   



+ Xét:

 

sin .cos . 1 sin dI x x f x x



.t

1 sin d 2sin .cos d sin .cos d d

t x t x x x x x x t       

i cn:

01xt  

;

xt  

.Suy ra:

     

0 1 1

1 0 0

111

d d d

222

I f t t f t t f x x   



Trang 56

+ Ta có:

 

ππ

2 cos .sin 2sin sin2 2cos cos2

x xdx x x dx x x

   

     

   

   



 

2 1 1

    

c:

   

1 1 3

222

f x x f x x







 

f x x







 

d3f x x



 



Câu 49.Chọn A

t

AB AC x

; gi

m BC

i A nên

2BC x



ABC

vuông cân ti

,SAB SAC

lt vuông ti

,BC

nên

SAB SAC  

u

k

 

BI SA I SA

thì

CI SA

t c

 

SA mp IBC

, góc gia hai mt phng

   

,SAB SAC

là góc gia hai

ng thng

,BI CI

TH 1 :



60 30BIC BIM  

.Do

IB IC

Tam giác

IBM

vuông ti

.2 2

2 sin30 2

x BM x

BM BI x x AB      

TH2:



120 60BIC BIM  

 c

sin60 3

BM x

BI 

;

IM 

SAB

vuông 

ng cao

nên

AB AI AS AI

  

AIB

vuông ti

nên

2 2 2 2 2

BI AB AI x a x

     

x x a

a x x

    

IM BC  

 

. . .

1 1 1 1 2 6 3

. . . . . . .

3 3 2 6 6 3 54

S ABC S IBC A IBC IBC

a a a

V V V S SI IA IM BC SA a



       

Câu 50.Chọn D.Ta có

   

 

3g x f f f x





c ht ta tìm các nghim c

 

30f f f x 

t

 

a f f x

 thành:

 

3 2 3 0

f a a a





     







Vi

3a 

: Suy ra

 

3f f x 

t

 

b f x

 

3 2 3 2 3 0

f b b b b b









          











Vi

1a 

Suy ra

 

1f f x 

t

 

b f x

     

 

1 2 1 1 0 1 0f b b b b f x            

.Vc:

   

 

   

2 2 2

3 3 1 1 2 3 2 1 2 1g x f f f x f x f x f x x x x x x x



            

Trang 57

 

0 1 2

g x x









   







Bng xét du

 



Da vào bng xét du, ta có hàm s

 

nghch bin trên

 

1;3

Cách 2:Ta có

   

 

3g x f f f x





   

 

03g x f f f x



  

 ra ta có

   

2 1,f x x x f x x      

và

 

3 1 3f x x    

Vy

 

3 1 3 1 3 1 3f f f x f f x f x x            

Bên c

 



c nên

 

0gx





ti hu hm.

Vy

 

nghch bin trên

 

1;3

www.thuvienhoclieu.com

ĐỀ 24

PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 120 phút

Câu 1.Bn Vy có

cây vit chì,

cây vit bi xanh và

cây vi trong hp bút,các cây vit phân

bi bn Vy Chn ra mt cây vit? A.

. B.

. C.

Câu 2.Cho cp s nhân

 

vi

2u 

và

64u 

. S hu ca cp s ng

2

. B.

1

. C.

. D.

Câu 3.Din tích xung quanh ca hình tr ng cao



bng



. B.

2 rh



. C.



. D.

4 rh



Câu 4.Cho hàm s

 

y f x

 th .Chn khnh sai trong các khnh



A.Hàm s nghch bin trên khong

 

2;

.B.Hàm s nghch bin trên khong

 

;0

C.Hàm s ng bin trên khong

 

0;1

.D.Hàm s ng bin trên khong

 

0;3

Câu 5.Cho kh u có tt c các cnh bng a. Th tích khng tr tam giác

ng A.

. B.

. C.

. D.

1

Trang 58

Câu 6.Nghim c

 

log 2x 1 3

x 

. B.

4x 

. C.

x 

. D.

3x 

Câu 7.Nu

 

dx 2fx 



và

 

dx 1fx 



thì

 

4. dxfx



bng A.

3

. B.

. C.

. D.

Câu 8.Cho hàm s

 

y f x

có bng bi

Tng giá tr cc tiu và giá tr ci ca hàm s ng

.B.

. C.

.D.

2

Câu 9. th ca hàm s ng cong trong hình bên?







. B.







. C.

2y x x

. D.

3y x x  

Câu 10.Vi

là s th

   

2 2020

log log 100aa

bng

2 2022log a

. B.

2 log 2020logaa

2 2020log 2logaa

. D.

2 2020log log

aa

Câu 11.H tt c các nguyên hàm ca hàm s

 

sinx 4f x x

là

cos 4x x C

. B.

cos 2x x C  

. C.

cos x x C  

. D.

cos 2x x C

Câu 12.a s phc

32i

bng A.

. B.

. C.

. D.

Câu 13.Trong không gian vi h t

Oxyz

i xng ca

 

1; 2; 3M

qua trc

có t là

 

1; 2; 3

. B.

 

1; 0 0

. C.

 

0; 2; 3

. D.

 

1; 2; 3  

Câu 14.Trong không gian vi h t

Oxyz

, cho mt cu

 

2 2 2

: 2 2 4 2 0S x y z x y z      

Tính bán kính

ca mt cu.A.

22r 

. B.

26r 

. C.

4r 

2r 

Trang 59

Câu 15.Trong không gian

Oxyz

, cho mt phng

 

1 2 2

x y z



  



không là

n ca

 



? A.

 

1;2; 2n 



. B.

 

2;1; 1n 



. C.

1; ;











 

2; 1;1n   



Câu 16.Trong không gian vi h t

Oxyz

ng thng

1 3 2

x y z





i

ng thng

?A.

 

1; 3;2u   



. B.

 

1;3;2u 



. C.

 

1; 3; 2u   



 

1;3; 2u   



Câu 17.Cho hình chóp

.S ABCD

nh

vuông góc vi mt ph

2.SA a

Góc ging thng

và mt phng

 

SAB

bng A.

45

. B.

30

60

. D.

90

Câu 18.Cho hàm s

 

, bng xét du ca

 





S m cc tr ca hàm s A.

. B.

. C.

. D.

Câu 19.Gi

,Mm

lt là giá tr ln nht và giá tr nh nht ca hàm s

32y x x  

n

 

1;1

. Tính

Mm

.A.

. B.

. C.2. D.3.

Câu 20.

,,a b x



1 1 1

2 2 2

log log log

x a b





x a b

x a b

. C.

x a b





x a b





Câu 21.Tp nghim ca b

2 1 2 6

x x x  

   



   

   

là

 

; 1 ;



   





. B.





; 1 ;



   







.C.









. D.









Trang 60

Câu 22.Ct mt khi tr bi mt mt phng qua trc thit din là hình ch nht

ABCD

có

và

thua khi tr. Bit

6AD 

và góc

CAD

bng

60 .

Th tích ca khi tr là

126



. B.



. C.

162



. D.

112



Câu 23.Cho hàm s

 

y f x

 th 

S nghim thc c

 

3 2020 0fx

là

. B.

. C.

. D.

Câu 24.H tt c nguyên hàm ca hàm s

 

()







trên khong

( ; )



là:

 

ln 2 3

4 4(2 3)

   



. B.

 

ln 3 2

4 4(2 3)

   



 

ln 3 2

2 2(2 3)

  



. D.

 

ln 3 2

2 2(2 3)

  



Câu 25. d báo dân s ca mt qui ta s dng công thc

S Ae



là dân s

cy làm mc tính,

là dân s sau



là t l  t r

dân s Vit Nam là khong 78.685.800 i. Gi s t l  i là 1,7%, c

 vi t l  c ta  mc 120 trii. A. 2022.

B.2026. C. 2025. D. 2021.

Câu 26.Cho kh ng

  

ABC ABC



ABC

là tam giác vuông cân ti

và

2AC a

'AC

to vt góc

. Tính th tích

ca kh 



. B.



. C.



. D.



Câu 27.Tng s tim cng và tim cn ngang c th hàm s







làA.

. B.

. C.

. D.

Câu 28.Cho hàm s

y ax bx cx d   

 th 

, , , a b c d

có bao nhiêu giá tr âm?

. B.

. C.

. D.

Câu 29.  th hàm s

 

y f x

 n

 

2;2

   i. Bit

   

f x dx f x dx







2

Trang 61

và

 

f x dx







. Tính din tích hình phng gch chéo

. C.

. D.

Câu 30.

,zz



4 5 0zz  



zz



. B.

. C.

. D.

Câu 31.Trong mt phng

Oxy

m

 m cn thng

biu din s

phc.A.

2 i

. B.

i

. C.

i

. D.

12i

Câu 32.Trong không gian

Oxyz

   

 

2;1;5a 



 

1;1;4b 



và

 

;2;5cx



. Tìm

tha mãn

 

. 90  

   

a a b c

5x

. B.

5x

. C.

0x

. D.

1x

Câu 33.Trong không gian

Oxyz

, cho mt cu

 

   m

 

6;0;0I 

   m

 

0;0;8M

a

 

là

 

6 100x y z   

.B.

 

6 10x y z   

.C.

 

6 100x y z   

. D.

 

6 10x y z   

Câu 34.Trong không gian vi h trc

Oxyz

, cho

 

1;0; 3A 

 

3;2;1B

. Mt phng trung trc ca n

thng



2 1 0x y z   

. B.

2 1 0x y z   

. C.

2 1 0x y z   

. D.

2 1 0x y z   

Câu 35.Trong không gian

,Oxyz

ng thng song song vi hai mt phng

 

:3 3 0P x y  

 

:2 3 0Q x y z   

có m 

( )

1;3;1u =

. B.

( )

1; 3; 1u = - -

. C.

( )

1; 3;1u = - -

. D.

( )

1; 3;1u =-

Câu 36. t   t n 6 và 5 viên bi vàng

 t n 5. Chn ngu nhiên 4 viên bi. Tính xác su c Ch 3 màu,

có c s chia ht cho 3 và s không chia ht cho 3? A.

362

7752

. B.

323

. C.

969

586

1615

Trang 62

Câu 37.Cho hình chóp

.S ABCD

 n

2AB a

AD DC CB a  

vuông góc v

3SA a

. Khong cách ging thng

và

bng

. B.

. C.

. D.

Câu 38.Cho hàm s

()fx

có

(0)

f 

và

'( ) ,

()

f x x R



  





( )df x x



bng?

e 

. B.

e 

. C.

e 

. D.

ln( 1)

e 

Câu 39.Cho hàm s

24x







. Có bao nhiêu giá tr  hàm s ch bin trên

khong

(0;1)

. B.

. C.

. D.

Câu 40. 



, bán kính,

3cmR 



120









SAB







SAB

A.

3 3 cm

. B.

6 3 cm

. C.

6 cm

. D.

3 cm

Câu 41.Cho các s th

tha mãn

 

4 6 9

log log log 4 5 1x y x y   

. Tính



. B.



. C.



. D.



Câu 42.Cho hàm s

()y f x

liên t th 

Gi

là tng các giá tr nguyên ca tham s

sao cho giá tr ln nht ca hàm s

( ) | ( ) |g x f x m

n

[ 1;3]

nh c bng

2 505

2019

. B.

2018

. C.

1

. D.

Câu 43.

     

1 log 2 4 5 log 4 4 0

m x m m

      



(

là tham s thc). Tp hp tt c các giá tr ca

 

nghim thun







là A.











. B.

;









. C.









. D.







Trang 63

Câu 44.Cho

là s th  t rng

 

là mt nguyên hàm ca hàm s

   

e ln

f x ax









tha mãn









và

 

2020

2020 eF 

. M 

2020









. B.

2020











. C.





1;2020a

. D.





2020;a 

Câu 45.Cho hàm s

()fx

 th 

S nghim thun

[0;3 ]



c

2 (cos ) 1 0fx

là:

. B.

. C.

. D.

Câu 46.Cho hàm s bc bn

 

y f x

 th  bên.

S m cc tr ca hàm s

 

34g x f x x  

là

A.5. B.3. C.7. D.11.

Câu 47.Có bao nhiêu cp s nguyên

( )

;xy

tha mãn

0 2020x££

và

 

log 4 4 1 2

x x y    

? A.

. B.

. C.

2020

. D.

Câu 48.Cho hàm s

()y f x

liên tc trên

 

0;

tha mãn

     

2 2 4 2 4 2

2 1 2 1 4 8 2 4f x x f x x x x x       

. Tính tích phân

 

f x dx



. B.

. C.

. D.

Câu 49.Cho hình chóp

.S ABC



ABC

là tam giác vuông cân ti

3BA BC a

. Khong

cách t

n mt phng

 

SBC

bng

và



90SAB SCB



. Tính th tích

kh

. B.

. C.

. D.

Câu 50. Cho hàm s

 

. Hàm s

 

'y f x

 th 

Hàm s

   

   

g x f x x

nghch bin trên kho  i

Trang 64



 

1;2

 

2;0

. C.

 

0;4

. D.

 

1;5

BẢNG ĐÁP ÁN

LỜI GIẢI CHI TIẾT

Câu 1.Chọn B

S cách Chn mt cây vit t

cây vit chì,

cây vit bi xanh và

cây vi là

3 8 2 13  

cách.

Câu 2.Chọn B.Ta có

.u u q

   

.S hu ca cp s ng

  

Câu 3.Chọn B.S dng công thc tính din tích xung quanh ca hình tr ta có:

S rl rh





Câu 4.Chọn D.Vì trên khong

 

2;3

hàm s nghch bin.

Câu 5.Chọn A.Kh  ng có cnh bên bu cnh





a 3 a 3

V a.

Câu 6.Chọn A.Ta có

 

log 2x 1 3 2x 1 2 x

      

Câu 7.Chọn B.Ta có:

     

3 2 3

1 1 2

dx dx dxf x f x f x

  

3 3 2

2 1 1

( ) ( ) ( ) 1 ( 2) 1f x dx f x dx f x dx       

  

Trang 65

Vy:

 

4. dx 4 ( ) 4f x f x dx



Câu 8.Chọn D.Da vào bng bin thiên ta thy: giá tr cc tiu ca hàm s 

4y 

ti

3x 

và giá tr ci ca hàm s 

2y 

ti

0x 

. Vy tng ca giá tr ci và giá tr cc tiu

bng

( 4) 2 2   

Câu 9.Chọn A. th hàm s th  th hàm b th hàm trùng



 th ta thy hàm s ng bin trên mi khong

 

;1

và

 

1; 

Xét hàm s







vi tnh

 

\1D  

Ta có

 

y x D



   



suy ra hàm s ng bin trên mi khong

 

;1

và

 

1; 

Xét hàm s







vi tnh

 

\1D  

Ta có

 

y x D



    



suy ra hàm s nghch bin trên mi khong

 

;1

và

 

1; 

Câu 10.Chọn C.Ta có:

     

2 2020 2020

log log 100 2log log100 loga a a a   

2log 2 2020logaa  

Câu 11.Chọn B.Ta có:

 

sinx 4 cos 2x dx x x C    



Câu 12.Chọn A.Ta có:

 

3 2 3 2 13i    

Câu 13.Chọn A.Gi

là hình chiu vuông góc ca

lên

nên

 

1;0;0H



i xng vi

qua

suy ra

m ca



Ta có:

M H M

x x x

y y y

x x x



  





   





   



. Vy

 

1; 2; 3M





Câu 14.Chọn A.Mt cu

 

có tâm

 

1;1;2I

và bán kính

 

2 2 2

1 1 2 2r     

22

Câu 15.Chọn A.Mt phng

 

1 2 2

x y z



  



n là

1; ;













C 

Trang 66

2nn

 

B 

2nn

 

D 

Câu 16.ChọnA.T c cng thng

suy ra vtcp

     

1;3; 2 1 . 1; 3;2v u v       

  

a

Câu 17.Chọn B .Ta có

 

SA ABCD

SA BC

BC ABCD

















Mt khác do

ABCD

là hình vuông nên

BC AB

y

 

BC SA

BC SAB

BC AB













Suy ra

 



,,SC SAB SC SB BSC

Trong

SBC

có

 

tan 30

BC BC a

BSC BSC

AB SA

      



Câu 18.Chọn B.Hàm s m cc tr lt là

1x 

2x 

3x 

không phm cc tr vì hàm s nh ti

3x 

Câu 19.Chọn B.Ta có:

 

0 1;1

' 3 6 ; ' 0

2 1;1

y x x y



  

   



  



(0) 2, (1) 0, ( 1) 2y y y    

.

2, 2Mm  

.Vy

0Mm

Câu 20.Chọn D.Ta có

2 2 2

3 3 3

1 1 1

5 5 5

1 1 1 1 1 1

2 2 2 2 2 2

log log log log log log

x a b a b a b x a b

  



      





Câu 21.Chọn C.Ta có:

2 1 2 6

x x x  

   



   

   

2 1 2 6x x x   

2 3 5 0xx   

x   

Vy tp nghim ca b

2 1 2 6

x x x  

   



   

   

là











Trang 67

Câu 22.Chọn C

Ta có xét tam giác

ACD

có:



tan

DAC





.tanDC AD DAC

6.tan60

63

Vì

ng kính ca khi tr nên suy ra bán kính khi tr là

R DC

33



dii tr là





 









Suy ra th tích khi tr là

.V h S

6.27





162





Câu 23.Chọn D.Ta có

   

3 2020 0

2020

fxfx  

S nghim ci s m c th hàm s

 

y f x

ng thng

2020

y 

2020



nên t  th  th hàm s

 

y f x

ng thng

2020

y 

ct nhau ti 1

m. Vm thc.

Câu 24.Chọn B.Ta có:

 

(2 3)

( )dx dx

  







 

1 1 1 1

dx+ dx

2 2 3 2







ln 2 3

4 4(2 3)

    



 

ln 3 2

4 4(2 3)

    



Câu 25.Chọn B.Áp dng công thc

S Ae

, gi n là s  n thm dân s

Vit mc 120 trii.Dân s Vii thi nên ta có

.1.7%

78.685.800. 120.000.000 24.8

S e n   

Vy 2026 thì dân s Vit Nam s  mc 120 trii.

Câu 26.Chọn C.Do

ABC

là tam giác vuông cân ti

và

2AC a

nên

BA BC a

'AC

to vt góc

30

nên



( ',( )) ( ', ) 30



   AC ABC AC AC C AC

Suy ra

' .tan30 2.

   CC AC a a

kh ng

  

ABC A BC

là

1 6 6

2 3 6



V a a a

Trang 68

Câu 27.Chọn C.



  

3; \ 1;2D   

- Ta có:

lim lim 0

 







ng thng

0y 

là tim cn ngang c th hàm s.

- Li có:

  

 

1 1 1 1

3 2 1 1 1

lim lim lim lim

3 2 4

1 2 3 2 2 3 2

x x x x

x x x x x

   

   

  

    



      

  

 

1 1 1 1

3 2 1 1 1

lim lim lim lim

3 2 4

1 2 3 2 2 3 2

x x x x

x x x x x

   

   

  

    



      

  

 

2 2 2 2

3 2 1 1

lim lim lim lim

1 2 3 2 2 3 2

x x x x

x x x x x

   

   

  

    



      

ng thng

2x 

là tim cng c th hàm s.

V th hàm s ng tim cn.

Câu 28.Chọn B. th ta th th hàm s

y ax bx cx d   

giao vi trc

ti

m

 

0;Dd

ni trc

nên

0d 

, và hình dng c th hàm s ng vi

ng hp

0a 

Hàm s t cc tiu ti

0x 

t ci ti

0x 

và

0xx

là hai nghim ca



3 2 0ax bx c  



S x x

P x x c









  





















mà

0a 

nên:











Vy có

giá tr âm trong các giá tr

là











Câu 29.Chọn D.D th, ta có din tích hình phng bng

       

2 1 1 2

2 2 1 1

22 76 22

15 15 15

f x dx f x dx f x dx f x dx



  

       

   

Câu 30.Chọn A.Vì

,zz



4 5 0zz  

nên ta có:













 

1 2 1 2 1 2

2 16 10 6z z z z z z      

Trang 69

Câu 31.Chọn C.Ta có:

   

2;1 , 1;3AB

m

là









biu din s phc là

zi  

Câu 32.Chọn A .Ta có:

 

3 ;4;14   

  

a b c x

.Suy ra

 

. 2 3 4.1 14.5 2 80       

   

a a b c x x

Theo gi thit

 

. 90 2 80 90 5       

   

a a b c x x

.Vy

5x

tha mãn yêu c bài.

Câu 33.Chọn A.Bán kính mt cu là

10R IM

.Va mt cu

 

là:

 

6 100x y z   

Câu 34.Chọn D.m cn thng

là

 

2;1; 1I 

. Mt phng trung trn thng

cha

n là

 

2;2;4AB 



, nên 

     

2 2 2 1 4 1 0x y z     

2 1 0x y z    

Câu 35.Chọn D.

 

và

 

ln là

 

3;1;0

n 



và

 

2;1;1

n 



ng th bài cho song song vi hai mt phng

 

:3 3 0P x y  

 

:2 3 0Q x y z   

 

   

 

1; 3;1

nn  



Câu 36.Chọn D.Ta có

 

nC

Xét cách Ch 3 màu.

2 1 1 1 2 1 1 1 2

9 6 5 9 6 5 9 6 5

.C .C .C .C .C .C 2295C C C  

Xét cách Ch 3 màu và mi s chia ht cho 3.

2 1 1 1 2 1

3 2 1 3 2 1

. . . . 9C C C C C C

Xét cách Ch 3 màu và mi s không chia ht cho 3:

2 1 1 1 2 1 1 1 2

6 4 4 6 4 4 6 4 4

. . . . . . 528C C C C C C C C C  

Suy ra s cách Ch 3 màu và có c s chia ht cho 3 và không chia ht cho 3 là:

2295 9 528 1758  

Xác sut cn tìm:

1758 586

1615



Câu 37.Chọn D

Trang 70

Gi

m ca

, ta có

BC DE

. Suy ra

 

BC SDE

   

 

, , , ,d BC SD d BC SDE d B SDE d A SDE   

.H

   

AF DE F DE DE SAF   

H

 

AH SF H SF

. Suy ra

 

AH SDE

 

,d A SDE AH

Ta có:

ADE

u cnh

, suy ra

AF 

.Trong

2 2 2 2 2 2

1 1 1 1 4 5

3 3 3

SAF

AH SA AF a a a

     

Suy ra

3 15

AH AH

.Vy

   

 

d BC SD d A SDE AH  

Câu 38.Chọn ATa có:

2 2 2 2 2 2

2.0 2

2 2 d( 1) 1

( ) d d

( ) ( 1) ( 1) 1

1 1 1

(0) 1 ( )

2 1 2 1

x x x x x

f x x x C

e e e e e

f C C f x





     

   

        



  



1 1 1

2 2 2

0 0 0

1 d ( 1) 1 1

( )d d ln

1 2 1 2 2

e x e e

f x x x



   



  

Câu 39.Chọn C.Tnh ca hàm s

( ; ) ( ; )D m m    

.Ta có:

()







Hàm s nghch bin trên

(0;1)

' 0 (0;1)yx   

2 4 0 1

(0;1) 2 0





   





  









   













y

1m 

tha mãn yêu cu bài toán.

Trang 71

Câu 40. Chọn A.

120











SAB







120





nên



60OSC 

Xét tam giác vuông

SOC

ta có



tan

OSC





tan

OSC



tan60





3

Xét tam giác vuông

SOA

ta có

SA SO OA

23

Do tam giác

SAB



 

2 3 .sin60

SAB





33

 

Câu 41.Chọn D.t

 

4 6 9

log log log 4 5 1t x y x y    

. Suy ra

4 5 9 9.9















  



Vì

 

9 .4 6

t t t



nên ta có

 

9.9.4 9. 6

t t t



. Hay là

    

2 2 2

4 5 9 4 5 9 0 4 9 0 4 9

x y x y x xy y x y x y x y



             



.Vy



Câu 42.Chọn A.Xét hàm s

()u f x m

n

[ 1;3]

có

[ 1;3]

max (1) (1) 2u u f m m



    

và

[ 1;3]

min (0) (0) 1u u f m m



    

Suy ra giá tr ln nht ca hàm s

| ( ) |y f x m

n

[ 1;3]

là

max{| 2|,| -1|}mm



[ 1;3]

max ( ) max{ | 2|, | -1|}g x m m





. Suy ra, hàm s  ln nht nh c

bng

2 505

khi và ch khi

| 2| | -1| 2020 (1)

| 1| | 2| 2020 (2)

  





   



Ta có+)

| 2| | 1|

(1) 2019

| 1| 2020

2019 2021



  







      









  



| 1| | 2 |

(2) 2018

| 2| 2020

2022 2018



  







     









  



T ng hp trên suy ra

2019 2018m  

Trang 72

Vì vy, tng các giá tr nguyên tha mãn bài toán là

2019T 

Câu 43.Chọn C.u kin:

2.x 

Ta có:

     

1 log 2 4 5 log 4 4 0

m x m m

      



       

4 1 log 2 4 5 log 2 4 4 0m x m x m        

       

1 log 2 5 log 2 1 0m x m x m        

t

 

log 2tx

 thành:

     

1 5 1 0 *m t m t m     

Vi

;4 ,









ta có:

 

1;1 .t 

 







 

1;1t 

Xét hàm s

 







. Ta có:

 

 

' 0, 1;1

f t t



    



Suy ra:

     

 

1 1 , 1;1f f t f t     

hay

 

 

3 , 1;1

f t t     

m

thun









 

có nghim

thun

 

1;1

m   

Câu 44.Chọn A.

   

e ln d e ln d d

I ax x ax x x



   





  

 Tính

 

e ln d

ax x



t

 

d e d

u ax























   

e ln d e ln d

ax x ax x C

   



 c:

   

e ln

F x ax C

Ta có:

 

2020

2020 e





















 

2020 2020

e .ln1 0

e ln .2020 e















 

ln .2020 1















2020

Þ a 

 Vy

2020









Câu 45.Chọn A.t

costx

vi

[0;3 ] t [ 1;1]



   x

;

Trang 73



2 (cos ) 1 0fx

tr thành

(t) (1)

(t) (2)

















  th hàm s

()fx

ta thy:

( 1;0)

(1) ( )

( 1;0)

  







  



Vi

( 1;0) cos    t t x t

có 3 nghim thuc

[0;3 ]



Vi

( 1;0) cos    t t x t

có 3 nghim thuc

[0;3 ]



(0;1)

(2) ( )

(0;1)













Vi

(0;1) cos   t t x t

có 3 nghim thuc

[0;3 ]



Vi

(0;1) cos   t t x t

có 3 nghim thuc

[0;3 ]



Các nghim trên không có nghim nào trùng nhau

Vm thuc

[0;3 ]



Câu 46.Chọn C.Tnh ca hàm s là

D  

.Ta có

 

   

2 3 2

3 6 3 4g x x x f x x



   

;

 

3 6 0

0 2

3 4 0

g x x

f x x













   





  







  





Mt khác, t  th hàm s ta thy

   

0 0;4

f x x b









   









 

1 3 4 3

x x a

x x b

x x c



  



   



  



Xét hàm s

34u x x  

36u x x



















T 

Vi

0a 



 

có mt nghim duy nht nh 

1

Vi

 

0;4b



 

có ba nghim lt thuc các

Bng bin thiên

Trang 74

khong

     

1;0 ; 0;2 ; 2;3

Vi

4c 



 

có mt nghim duy nht l

Vy

 

0gx





có 7 nghi m cc tr.

Câu 47.Chọn B.t

( )

log 4 4 4 4 2 2 1

x t x x

+ = Û + = Û = -

T u kin

0 2020 0 2 1 2020 1 1 1 log 2021

£ £ Þ £ - £ Û £ - £ +

Theo gi thit ta có:

( )

1 2 1 2 *

- + = + +

.Xét hàm s

( )

f u u

vi

1 1 log 2021u£ £ +

Có

( ) [ ]

' 1 2 .ln2 0, 1;1 log 2021

f u u

= + > " Î +

nên hàm

( )

ng bin

[ ]

1;1 log 2021+

Da vào

( ) ( ) ( )

* 1 1 1 1f t f y t yÞ - = + Û - = +

Mt khác

2 2 2

1 1 1 log 2021 1 1 1 log 2021 0 log 2021 10,98t y y£ - £ + Þ £ + £ + Þ £ £ »

Vì

{ }

0;1;2;3;4;5;6;7;8;9;10yyÎ Þ Î¢

.Vy có 11 cp s nguyên tha mãn ycbt.

Câu 48.Chọn A.Ta có

       

2 3 4 2 4 2

4 2 4 4 2 1 4 8 2 4 .4xf x x x f x x x x x x       

       

1 1 1

2 3 4 2 4 2

0 0 0

4 2 4 4 2 1 4 8 2 4 .4xf x dx x x f x x dx x x x xdx        

  

     

1 4 4

0 1 0

64 32

f t dt f u du f x dx    

  

Vi

2 4 2

; 2 1.t x u x x   

Câu 49.Chọn D. Gi s

 

SD ABC

. Ta chng minh:

ABCD

là hình vuông.

Ta có:

 

AB SD

AB SDA AB DA

AB SA





   









90 .BAD



Ta có:

 

BC SD

BC SDC BC DC

BC SC





   









90BCD



T giác

ABCD

có:



90DAB ABC BCD  



ABCD

là hình ch nht.

Trang 75

Mà

BA BC

ABCD

là hình vuông cnh

Vì

   

 

/ / / / , , 2AD BC AD SBC d D SBC d A SBC a   

K

DH SC

ti

Ta có:

 

BC SDC BC DH  

Mà

DH SC

 

DH SBC

 

,2d D SBC DH a  

Xét tam giác

SDC

vuông ti

có:

2 2 2

1 1 1

DH SD DC



6SD a

 

1 1 6

. . . . 6

3 3 2 2

S ABC ABC

V S SD a   

Câu 50.Chọn A.Ta có

   

' ' 1 3   g x f x x

     

' 1 1 2 1 2      f x x x



 

'0gx

     

' 1 1 2 1 2 (1)       f x x x

t

1tx

. BPT

 

tr thành

   

' 2 2 2   f t t t



 

'y f t

và

22   y t t

ta có nghim ca BPT là

03t

0 1 3   x

12   x

Suy ra hàm s

   

   

g x f x x

nghch bin trên

 

1;2

A.

www.thuvienhoclieu.com

ĐỀ 25

PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 120 phút

Câu1.Lp

11A

có 29 hc sinh n và 14 hc sinh nam, giáo viên gi

hc sinh lên lau bng. Hi

có bao nhiêu cách cách Chn?

. B.

. C.

. D.

Trang 76

Câu2.Cho cp s cng

()

vi

1, 3uu  

. Công sai ca cp s cng bng

bao nhiêu?A.

2

. B.

4S 

. C.

4

. D.

Câu 3. Tính th tích

ca khi tr u bng 2.





.B.





.C.

16V





. D.

12V





Câu4.Cho hàm s

 

y f x

 th  bên.

Hàm s ch bin trên khong

 

0;2

. B.

 

2;0

. C.

 

3; 1

. D.

 

2;3

Câu5.Cho khi hp ch nh dài chiu rng, chiu dài, chiu cao ln

t là

3 ;4 ;5a a a

. Th tích ca khi hp ch nhng

12a

. B.

60a

. C.

12a

. D.

60a

Câu6.Tp nghim c

 

log 2 2 1xx  

là

 

0;2

. B.

 

2

. C.

 

1

. D.

 

2;0

Câu 7.H tt c các nguyên hàm ca hàm s

 

2020x

f x e

là

2020

C

. B.

2020

2020.

eC

2020x

eC

. D.

2019

2020.

eC

Câu 8.Cho hàm s

( ) , 0f x ax bx cx d a    

 th  

Giá tr ci ca hàm s làA.

. B.

. C.

. D.

Câu9.











. B.







.C.







. D.







Câu10.



log a



2 log a

. B.

log

a

. C.

2log a

. D.

log

Câu11.Nu

 

ld n xC

f x x   



thì

 

là

 

lnf xCx x  

. B.

 

lnx x C

fx    

 

lnf C

x x   

.D.

 





Câu12.Cho hai s thc

tho 

2 3 4x i yi  

 ca

và

là:

3x 

2y 

. B.

3xi

y 

. C.

3x 

y 

. D.

3x 

y 

Câu 13.Trong không gian Oxyz, hình chiu vuông góc cm

 

3;1; 4M 

lên trc

là

 

3;0;0M

. B.

 

3;0; 4M 

. C.

 

0;1;0M

. D.

 

0;0; 4M 

Câu 14.Trong không gian Oxyz, cho 

2 2 2

( ): 4 2 4 16 0S x y z x y z      

. 

Trang 77

tâm



 

. A.

( 2; 1;2)I 

. B.

( 2; 1;2)I 

. C.

(4;2; 4)I 

. D.

(2;1; 2)I 

Câu 15.Trong không gian

Oxyz



 

: 2 4 31 0x y z



   





 



?A.

 

1;2;4n



 

1;2; 4n 



. C.

 

1;2; 4n 



. D.

 

1; 2; 4n   



Câu 16.Trong không gian

Oxyz



1 2 1

1 3 3

x y z

  







 

1; ;M a b





ab



13

. C.

9

. D.

7

Câu17.Cho hình chóp

.S ABCD



ABCD

là hình ch nht vi

2AB a

AD a

. Bit

vuông góc vi mt ph

15SA a

. Góc ging thng



 

ABCD



. B.

. C.

. D.

Câu18.Cho hàm s

 

y f x

liên tc trên



và có bng xét d

A.

. B.

. C.

. D.

Câu19.Hàm s

62y x x  

có giá tr cc tiu bng

30

. B.

. C.

. D.

Câu20.Cho

log 3

b 

vi

là các s th

khác

. Tính giá tr biu thc

log log

T b b

.A.

. B.

. D.

Câu 21.Tp nghim ca b

 

log 2 1 log 1xx  

có cha bao nhiêu giá tr

nguyên thun

 

2020;2020

? A.

. B.

. C.

4040

2020

Câu 22.Cho khi nón có th tích là

. Bit rng khi ct khi mt mt phng qua

trc, thit dic là mu có din tích bng

. Giá tr ca

bng



. B.



. C.



. D.



Câu23.Cho hàm s

 

y f x

 th . S nghim c

trình

 

sin 1 1fx

thun

 

0;3



là A.

. B.

. C.

. D.

Câu24.H tt c các nguyên hàm ca

 

2 ln 1









là

 

ln 1



. B.

 

ln 1





 

ln 1





. D.

 

ln 1



  

Câu25.Mi tháng ông A gi tit kim ngân hàng

1500000

ng vi lãi sut kép

0,6%

trên

tháng. Sau mi lãi sut kép thành

0,8%

trên tháng. Sau ba

i ngân hàng, ông A rút toàn b s tin c gc và lãi. S tin ông A nhc là:

Trang 78

62791439,15

ng. B.

57662945,82

ng. C.

60435853,82

ng. D.

93973001,03

ng.

Câu26.Cho hình chóp t giác

.S ABCD



ABCD

hình vuông vi

AB a

. Bit

,,SD AD DC

t vuông góc nhau và góc gia hai mt phng

 

SAC

và

 

ABCD

là



Khong cách t

ti mt phng

 

SBC

là: A.

. B.

. C.

. D.

Câu 27.Tng s tim cng tim cn ngang c th hàm s

2019 2020

3 2 1

  





là

. B.

. C.

. D.

Câu 28. ng cong trong hình v  th ca hàm s nào trong bn

hàm s 

43y x x  

. B.

43y x x  

43y x x  

. D.

43y x x   

Câu 29.Cho hàm s

 

y f x

 th n tích hình phng gii hn b

th hàm s

 

y f x

và trc

là

S 

   

ddf x x f x x





. B.

 

dS f x x







   

ddS f x x f x x







.D.

   

ddS f x x f x x







. Câu

30.Cho s phc

32zi

. Tìm phn o ca s phc liên hp ca

 

w2iz

1

. B.

. C.

. D.

Câu31.Cho s phc

23zi

u din cho s

phc

 

2.w i z

 

1; 8M 

. B.

 

1; 8N 

. C.

 

1;8P 

. D.

 

1;8Q

Câu32.Trong không gian

Oxyz

, cho

2 3 4a i j k  

   

 

1;0; 2A 

và

 

2; 1;1B 

. ng

.a AB

 

bng

. B.

. C.

. D.

Câu 33.Trong không gian

Oxyz

m

 

4; 2;3A 

 

2;6;9B

t cu có

ng kính

là:

     

2 2 2

3 2 6 26x y z     

. B.

     

2 2 2

3 2 6 26x y z     

     

2 2 2

3 2 6 26x y z     

. D.

     

2 2 2

3 2 6 26x y z     

Câu 34.m

 

2;3;4A

và hai mt phng

 

:2 3 1 0P x y z   

 

: 2 3 10 0Q x y z   

ng thng



song song vi c

 

và

 

là

2 3 4

11 5 7

x y z  





. B.

2 3 4

11 5 7

x y z  





. C.

2 3 4

11 5 7

x y z  





. D.

2 3 4

11 5 7

x y z  



Trang 79

Câu 35.Trong không gian

Oxyz

 ng thng

m

 

1; 2; 3M 

và

 

5; 4;7N 

 

3; 3;2u 



. B.

 

2; 1;5u 



. C.

 

3; 1;2u 



. D.

 

4; 6;4u   



Câu 36.





 A.

176400

151200

201600

Câu 37. nht

3,AB a AD a

. SA vuông góc vi mt ph

2SA a

. Gi M là

m thun thng DC sao cho

3DC DM

. Khong cách gia hai

ng BM và SD bng

. B.

. C.

. D.

Câu 38.

 

có

 

30f 

và

   

, 2;

f x x



   





 

f x dx ae b







 

,ab

. Tích

.ab



2.

24.

24.

Câu39.Tìm s giá tr nguyên ca tham s

 hàm s







nghch bin trên khong

 

2;5

. B.

. C.

. D.

Câu40.nh

, tâm c

ng

. Mt phng

()P

nh hình nón và c dài bng

. Bit rng khong

cách t

n

()P

bng

. Tính th tích khi nón gii hn bi hình nón trên.

50 3



. B.

50 3



. C.

100 3



. D.

100 3



Câu41.Cho

0a 

0b 

tha mãn

 

16 9 12

log 3 2 log loga b a b  

. Giá tr ca

3 2 3

a ab b

a a b b





bng



. B.

. C.



. D.



Câu 42.Có bao nhiêu giá tr  ln nht ca hàm s

 

3 2 3 2

3 2 9 1f x x m x m m    

n

 

0;3

bng 30?A.

. B.

. C.

. D.Vô s.

Câu 43.

4 2 2 4 0

mm   

, (

là tham s thc). Tp hp tt c các giá tr

ca

 m phân bit thun

 

1;1

là









. B.









. C.











. D.











Trang 80

Câu44.Cho hàm s

()fx

liên tc trên



.Bit

là mt nguyên hàm ca hàm s

 

, h

tt c nguyên hàm ca hàm s

 



là

( 3)e

xC

. B.

(3 2 )



. C.

( 1)e

xC

. D.

( 1)e

xC

Câu 45.Cho hàm s

 

có bng bi

S nghim thun

;











c

 

2 2cos 9 0fx

là

.B.

. C.

. D.

Câu 46. Cho hàm s

 

y f x

o hàm trên



và có bng xét du co hàm

 

'fx



Hi hàm s

 

2g x f x x

m cực

tiểu ?

. B.

. C.

. D.

Câu 47.Có tt c bao nhiêu giá tr nguyên ca tham s

 

 

log 2 2 3 1

m x m x    

có nghim thuc

 

0;2

? A.

. B.

. D.

Câu48.Cho hàm s

 

o hàm liên tc trên



sao cho

     

  

1 1 ,

f x y f x f y e e     

,xy

và

 

02f





. Tính

 

.f x dx



Ie

. B.

Ie  

. C.

Ie  

. D.

Ie

Câu49.Cho khi chóp

.S ABC



ABC

là tam giác có



4 , 5 , 60AB a AC a BAC  



90SBA SCA

, góc gia

 

SAB

và

 

SAC

bng

. Th tích ca khng:

20 39

. B.

10 13

. C.

20 13

. D.

10 39

Câu50.Cho hàm s

 

. Hàm s

 

y f x





 th .

Hàm s

   

g x f x  

nghch bin trong khoi



 

3; .

 

; 2 . 

 

2;1 .

 

1;3 .

………HẾT……

BẢNG ĐÁP ÁN

1.D

2.C

3.A

4.D

5.B

6.D

7.A

8.A

9.C

10.D

11.D

12.C

13.C

14.D

15.C

16.C

17.C

18.D

19.A

20.C

Trang 81

21.B

22.B

23.D

24.A

25.D

26.D

27.B

28.C

29.D

30.A

31.D

32.C

33.B

34.D

35.B

36.D

37.B

38.D

39.A

40.D

41.C

42.B

43.D

44.D

45.B

46.A

47.C

48.D

49.D

50.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu1.Chọn D.Tng s hc sinh ca lp

11A

là:

29 14 43

S cách Chn mt hc sinh trong lp là:

Câu2.Chọn C.Gi

là công sai ca cp s cTa có:

3 1 4d u u      

Câu 3. Chọn A.Th tích ca khi tr

 

. 2 .2 8V r h

  

  

Câu4.Chọn D.D th ta có hàm s nghch bin trên các khong

 

1;1

và

 

2;3 .

Câu5.Chọn B.Th tích ca khi hp ch nht là:

3 .4 .5 60V a a a a

Câu6.Chọn D.Ta có

 

2 2 2

log 2 2 1 2 2 2 2 0

x x x x x x





          







Vy tp nghim c

 

2;0S 

Câu 7.Chọn A.Ta có

2020

e x C



Câu 8.Chọn A.D th ta thy giá tr ci ca hàm s là 5.

Câu9.Chọn C.D th hàm s  th hàm s có mng tim cng

1x 

nên

loi A,B.

 th là mng v bên phi nên hàm s nghch bin trên mi khong ca tp







nên Chn C

Câu10.Chọn D.Ta có:

2 2 2

log log log

a a a

Câu11.Chọn D.Ta có

1 1 1 1

x x x x







     





, suy ra

 





là hàm s cn tìm.

Câu12.Chọn C.T

2 3 4x i yi  





























.Vy

3x 

y 

Câu 13.Chọn C.Hình chiu vuông góc cm

 

3;1; 4M 

lên trc

là

 

0;1;0M

Câu 14.Chọn D.Vit lt cu

 

có dng

     

2 2 2

2 1 2 9x y z     

Suy ra mt cu

 

có tâm là

(2;1; 2)I 

Câu 15.Chọn C.Mt vecto pháp tuyn ca mt phng

 



là

 

1;2; 4n 



Câu 16.Chọn C.m

 

1; ;M a b

thung thng

nên t m

th

ng thng

1 1 2 1

4; 5 9

1 3 3

a b a b

  

          



Trang 82

Câu17.Chọn C

Vì

 

SA ABCD

nên

là hình chiu ca

lên 

 

ABCD

ng thng



 

ABCD



và





SCA

Ta có:

 

2 2 2 2

2 5 5AC AB BC a a a a     

Xét tam giác

SAC

vuông ti

 

tan 3 60

SA a

SCA SCA

    

Vy góc ging thng



 

ABCD



Câu18.Chọn D.T bng bin thiên suy ra

 



i du khi

qua

1x 

và

4x 

nên hàm s

 

y f x

có

m cc tr.

Câu19.Chọn A.Ta có:

3 12y x x





. Xét

0 3 12 0

4 30

y x x

  





    



   



BBT:Vy giá tr cc tiu

y 

Câu20.Chọn C.Ta có:

log log

T b b

log log

bb

3log 2log 5log 5.3 15

a a a

b b b    

Câu 21.Chọn Bu kin:

1x 

i bpt

 

   

2 2 2

1 1 1 1

2 2 2 2

log 2 1 2log 1 log 2 1 log 1 2 1 1x x x x x x          

2 0 0 2x x x     

. Suy ra có 3 giá tr nguyên th bài.

Câu 22.Chọn B.Gi s thit din qua trc là tam giác

SAB

Ta có

SAB

S AB



   

Kh

r OA  

ng cao là

h SO  

.Vy th tích ca kh

1 1 3

.1 . 3

3 3 3

V r h





  

Câu23.Chọn D.

 

sin 1 1fx

t

sin 1tx

   

0;3 0;2xt



  

D thng thng

1y 

ct

 

y f t

vi

 

0;2t 

ti

1, 2tt

Vi

1 sin 1 1 sin 0 ( )t x x x k k



        

. Do

 

0;3x





, nên nhn

0,1,2,3.k 

m

0, , 2 , 3x x x x

  

   

Vi

2 sin 1 2 sin 1 2 ( )

t x x x k k



         

. Do

 

0;3x





, nên nhn

0,1.k 

m





V

 

sin 1 1fx

có 6 nghim thun

 

0;3



Trang 83

Câu24.Chọn A.t

 

ln 1 d d

t x t x

   



. Thay vào I c:

 

ln 1

I t t C C



    



Câu25.Chọn D.Gi

là s tin ông A gi vào ngân hàng hàng tháng.

u tháng

, ông A có

ng.

Cui tháng

, ông A có

 

0,6% 1 0,6% 1,006a a a a   

u tháng

, ông A có

 

1,006 1 1,006a a a  

Cui tháng

, ông A có

 

1 1,006 .1,006 1,006 1,006aa  

u tháng

, ông A có

   

1,006 1,006 1 1,006 1,006a a a    

Cui tháng

, ông A có

   

2 2 3

1 1,006 1,006 .1,006 1,006 1,006 1,006aa    

, cui tháng

, ông A có

 

2 20

1,006 1

1,006 1,006 ... 1,006 .1,006.

1,006 1



   



S tin ông A nhc sau mu mi tháng gi vào ngân hàng

1500000

là:

1,006 1

1500000.1,006. 31963799,34

1,006 1







ng.

i lãi sut thành

0,8%

trên tháng, s tic sau

tháng

nu mi tháng gi vào ngân hàng

1500000

là:

1,008 1

1500000.1,008. 25699146,48

1,008 1







ng.

Tng s tic sau



 

31963799,34 25699146,48 31963799,34. 1 0,008 93973001,03   

ng.

Câu26.Chọn D. Gi

O AC BD

.Ta có

 

SD AD

SD ABCD

SD DC













;

 

AC BD

AC SBD

SD AC













SO AC

Di

ABCD

là:

ABCD

S AB a

   

 



 



SAC ABCD AC

SO AC SAC ABCD SO BD SOD

BD AC







   











45SOD



Xét

SDO

vuông ti cân ti

2 2 2

DB AD AB a

SD DO



   

 

AD BC

AD SBC

BC SBC

















nên

 

,,d A SBC d D SBC

 

DC CB

BC SDC

SD BC













và

   

SBC SDC

V

DH SC

ti

Ta có

   

     

SBC SDC

SBC SDC SC DH SBC

DH SC







   









nên

 

,,d A SBC d D SBC DH

Trang 84

Xét

SDC

vuông ti

2 2 2 2 2

1 1 1 1 1 3

DH SD DC a a

    







Vy

DH 

Câu 27.Chọn B.Ta có

2019 2020 1

lim lim

3 2 1 3

 

  

  



Suy ra 



y 

  

 

1 1 1 1

1 2020 2020

2019 2020 2021

lim lim lim lim

3 2 1 4

3 1 3

x x x x

x x x

   

    

  

    



   

  

   

   

  

 

1 1 1 1

3 3 3 3

1 2020 2020

2019 2020

lim lim lim lim

3 2 1

3 1 3

x x x x

x x x

   

       

       

       

       

    

  

    



   

  

   

   



 

x 



Câu 28.Chọn C.Ta có

lim



 



loiD. Vì 

cc tr nên

trái du



loiB.

 





Câu 29.Chọn D.T hình v ta có:

       

0 2 0 2

1 0 1 0

d d d d .S f x x f x x f x x f x x



   

   

Câu 30.Chọn A.Ta có

    

w 2 2 3 2 8i z i i i      

8wi  

Vy s phc liên hp ca

có phn o bng

1

Câu31.Chọn D.

23zi

23zi  

 

2.w i z

  

2 2 3ii  

18i

Vm biu din s phc

là

 

1;8Q

Câu32.Chọn C.Ta có

 

2; 3;4a 



;

 

1; 1;3AB 



.Vy

   

. 2.1 3 . 1 4.3 17a AB      

 

Câu 33.Chọn B.Mt cng kính

nên tâm

m

Suy ra

 

3;2;6I

.Mt khác bán kính

R AB

 

2 8 6 26

    

Vt cu cn tìm là:

     

2 2 2

3 2 6 26x y z     

Câu 34.Chọn D.Ta có

 

:2 3 1 0P x y z   

có mn là

 

2; 3; 1

n   



 

: 2 3 10 0Q x y z   

có mn là

 

1;2; 3

n 



ng thng

có m 



ng thng

song song vi

 

và

 

nên

   

 

, 11;5;7

u n n



  



  

Mng thng



 

2;3;4A

 

 

11;5;7

u 





trình chính tc ca

là

2 3 4

11 5 7

x y z  



Câu 35.Chọn B.Ta có:

 

4; 2;10MN 



là m ng th

m

,MN

Trang 85

Vì

 

2; 1;5u 



và

 

4; 2;10MN 







là m ng

thm

,MN

Câu 36.Chọn D

Ta có:

( ) 9 .n 

TH1: Xếp bất kỳ.

2 2 4

8 6 7

. .A 352.800CC 

TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán



7. .AC

cách.



7. .AC

cách.



nhóm Y

+ Xp X, Y và 4 s còn li có:

.6!C

Vy s cách xp không tha mãn yêu cu là:

2 4 4

6 7 7

2.7. .A .6! 151200CC

Vy

201600

( ) 352.800 151.200 201.600 ( )

n A p A    

Chn D

Câu 37.Chọn B.Gn thng AB sao cho AB

 giác DMBN là hình bình hành nên suy ra

BM // DN. Suy ra

 

//BM SDN

.Vy

   

 

, , ,d BM SD d BM SDN d B SDN

 

d A SDN

Trong mp k AE vuông góc DN ti E. Ta suy ra

 

DN SAE

Trong tam giác SAE, t A k ng thng AH vuông góc vi

SE ti H.

Có:

   

 

AH DN

AH SDN d A SDN AH

AH SE





   







2 2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 1 3

4 4 2AH SA AE SA AD AN a a a a

        

AH

.Vy

 

d BM SD 

Câu 38.Chọn D

Cách 1. Ta có:

 

f x dx dx I

  









2t x dt dx   

2( 2) 4

2ln

I dt t C



   





31xt  

nên có

 

1 0 4fC  



31xt  

;

2x e t e   



 

2ln 4 4 6.

f x dx t dt e





    







Suy ra

4; 6.ab  

Cách 2.

 

   

2 2 4

2 2 1

4 4 2

f x dx dx dx dx

x x x



   

  



   

2ln 2

   



Trang 86

 

3 0 4fC  

. Vy

 

2ln 2 4

f x x

   



 

2ln 2 4 4 6

f x dx x dx e





     









. Suy ra

4; 6.ab  

Câu39.Chọn A.Tnh:













.Ta có

 

18 36

mx m





  



YCBT

 

36 0

2;5



















  

























  







  























46m  

Vy có hai giá tr nguyên ca tham s

tha mãn.

Câu40.Chọn D.Gi s thit din to bi

 

và hình nón là tam giác

SAB

.Gi

n



5r OA

6AB 

4OM OA AM   

Gi

là hình chiu vuông góc ca

lên

. Suy ra

vuông

góc vi

()P

nên

23OH 

Ta có:

2 2 2

1 1 1

OH OM OS



1 1 1 1

12 16 48OS

   

43SO

Th tích khi nón

1 1 100 3

. . .5 .4 3

3 3 3

V r h





  

Câu41.Chọn C.t

 

16 9 12

log 3 2 log logt a b a b   

3 2 16

















3.9 2.12 16

t t t

  

3 2. 1

16 4

   

  

   

   

 



































Vy

3 2 3

a ab b

a a b b

   



   



   





   



   

   



Câu 42.Chọn B.Xét hàm s

 

3 2 3 2

3 2 9 1g x x m x m m    

nh và liên tn

 

0;3

Ta có:

 

33g x x m





;

 

x m ktm















 

0 2 9 1g m m  

;

 

3 2 28gm

;

 

91g m m

Vì

     

0 0 ; 3 ;gg g m

và

   

00g m g m  

Suy ra

 

 

   

 

3 2 3

0;3

0 ; 3 2 9 1; 2 28Maxf x Max g g Max m m m    

TH 1:

3 2 3

3 2 9 1 2 28m m m m     

Giá tr ln nht ca hàm s

 

3 2 3 2

3 2 9 1f x x m x m m    

n

 

0;3

bng 30

Trang 87

2 9 1 30mm   

 

1,548m ktm

TH 2:

3 2 3

3 2 9 1 2 28m m m m     

Giá tr ln nht ca hàm s

 

3 2 3 2

3 2 9 1f x x m x m m    

n

 

0;3

bng 30

2 28 30m  

 

1m tm

Vy có 1 giá tr ca

tha mãn yêu cu bài toán.

Câu 43.Chọn D.

i

2 2 2 4 0

mm   

.t

t 

, vì

 

1;1 ;2



   





Yêu cu bài toán tr thành tìm

 

 

2 4 0 1t mt m   

có hai nghim phân

bit thun







.

 

  

2 2 0t t m    









  



Yêu cu bài toán

2 2 4;



        







Câu44.Chọn D.Ta có

   

e d e e (1 )e ( )

x x x x

f x x x C f x x f x



      





e e (1 ) 2

( ) ( )e (2 )e

f x f x x

  



    

Tính

   

e d 2 e d

f x x x x







t

2 d d

d e d e

u x u x

v x v

  











 

e d (2 )e e d (2 )e e ( 1)e

x x x x x x

f x x x x x C x C



          



Câu 45.Chọn B.t

2costx

 

2;2t

thì

 

2 2cos 9 0fx

tr thành

     

2 9 0 1

f t f t   

Nhn xét: S nghim c

 

s m c th:

   

:C y f t

ng thng

 

dy

Bng bin thiên hàm s

 

y f t

n

 

2;2

Da vào bng bin thiên, s nghim

 

2;2t 

ca

 

là 2 nghim phân bit

   

2;0 , 0;2tt  

 th hàm s

cosyx

trên

;











Trang 88

Vi

     

2;0 2cos 2;0 cos 1;0

t x t x         

D th hàm s

cosyx

trên

;











ta th

 

cos 1;0

x   

có

3 nghim phân bit:

1 2 3

2 2 2

x x x

  



        

 

có 3 nghim

;











Vi

     

0;2 2cos 0;2 cos 0;1

t x t x      

D th hàm s

cosyx

trên

;











ta th

 

cos 0;1

x 

có 2 nghim phân bit



    

Vy s nghim thun

;











c

 

2 2cos 9 0fx

là

2 3 5

Câu 46. Chọn A.Ta có

'( ) (2 2) '( 2 )g x x f x x  

2 2 0

2 2 0 2 2

'( ) 0

'( 2 ) 0 2 1

x x x

f x x x x









    







   



   











  



12x 

là nghim kép nên ta có bng bin thiên sau

Da vào bng bii chiu vn A

Câu 47.Chọn C.u kin:

0mx

Ta có:

 

log 2 2 3 1

m x m x    

 

log 2 2 2 2 2

m x m x x     

 

log 2 2 2 2 log 2 2

m x m x     

 

Xét hàm s

 

logf t t t

trên

 

0;

. Ta có:

 

1 0, 0

.ln 2

f t t



    

Suy ra hàm s

 

liên tng bin trên

 

0;



 

2 2 2 2 2 2 2 2 2

x x x

f m x f m x m x        

t

 

g x x

. Vì

 

 

' 2 .ln2 2 0, 0;2

g x x    

nên ta có BBT:



1 2 8 4

mm    

.Vì

m

 

1;2;3;4m

Vy có

giá tr

cn tìm.

Trang 89

Câu48.Chọn D.Ta có

     

  

1 1 ,

f x y f x f y e e     

,xy

Lo hàm hai v ca theo bin xc

   

 

f x y f x e e



   

Thay

0x 

c

   

0 1 1.

f y f e e



    



 

f y dy e dy f y e y C



     



Thay

0x 

và

0y 

c

     

0 2 0 0 0.f f f  

T và, suy ra

1.C 



 

f y e y  

Vy

   

 

1 1 1

0 0 0

f x dx f y dy e y dy e     

  

Câu49.Chọn D.Ta có



2 . .cosBC AB AC AB AC BAC  

   

4 5 2.4 .5 .cos60 21a a a a a   

T 

ABC

là tam giác nhn và có bán kính

ng tròn ngoi tip là



2sin60

2sin

BC a

BAC

  

Gi

là hình chiu ca

trên mt phng

 

ABC



 

SH AB

AB SHB AB HB

SB AB





   









AC HC

T 

ABHC

là t giác ni ting kính

2 2 7HA R a

Gi

,IK

lt là hình chiu ca

,BH

trên

và



 

HK SAC

Gi

m ca

và

. Ta có



.tan 4 .tan60 4 3BE BA BAC a a  

Li có

 

2 7 4 2 3BH AH AB a a a    

 

2 7 5 3CH AH AC a a a    

.Suy ra

4 3 2 3 2 3HE BE BH a a a    

t

0SH x

, ta có

2 2 2 2

12SB SH BH x a   

 

2 2 2 2

. 12 .4

SB AB x a a

d B SA BI

SB AB x a



   



 

2 2 2 2

. . 3

; , 2. 2 2

BE SH CH x a

d B SAC d H SAC HK

SH CH x a

   



Gi góc gia

 

SAB

và

 

SAC

là



.Ta có

 

2 2 2 2

3 28

sin

2 3 . 12

d B SAC

x x a

d B SA

x a x a









Vì





nên

2 2 2 2 2 2

2 2 2 2

3 28 3

28 3 . 12

2 3 . 12

x x a

x x a x a x a

x a x a



     



    

2 2 2 2 2 2 2 2 2

28 3 12 13 36

x x a x a x a x a x        





1 1 1 1 1 6 10 39

. . . . . .sin . . 4 .5 .sin60 .

3 3 2 3 2 13

S ABC ABC

V S SH AB AC BAC SH a a   

Trang 90

Câu50.Chọn A.Xét

   

g x f x



   

Ta có

     

0 3 0 3

g x f x f x

  

         

t

   

 

   

3 1 2 .

t x f t f t





       

Trên cùng h trc t

,Oxy

v  th hàm s

 

y f t





ng

thng





 .D th, ta thy

 

0 3 0 3

3 6 3 3 6 3 0

t x x

   

  





   

  

       

  

Vy

 









  



nên

 

nghch bin trong

 

3;

www.thuvienhoclieu.com

ĐỀ 26

PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 120 phút

Câu1.T mt nhóm hc sinh gm 5 nam và 6 n, có bao nhiêu cách Chn ra mm mt

nam và mt n? A.11. B.6. C.5.

D.30.

Câu2.Cho cp s cng

 

vi

2u 

và

4u 

. Công sai ca cp s cng

A.6. B. 3. C.2. D.

2

Câu 3.Din tích xung quanh ca hình tr  ng cao



bng

4 rh



. B.



. C.

2 rh



. D.



Câu 4.Cho hàm s

()fx

có bng bi

Hàm s nghch bin trên kho

 

3;5

.B.

 

0;

. C.

 

;2

.D.

 

0;2

Câu5.Cho khi lnh bng

. Th tích khi lp

ng.

. B.

. C.

. D.

Trang 91

Câu 6.Nghim c

 

log 3 8 2x 

là A.



. B.

. C.

4

Câu 7. Nu

( ) 3f x dx 



và

( ) 1f x dx 



thì

()f x dx



bngA.

2.

4.

Câu 8.Cho hàm s

()y f x

có bng bi

Giá tr ci ca hàm s cho bng

4.

Câu9.  th ca hàm s 

34y x x  

. B.

34y x x  

34y x x   

. D.

34y x x   

Câu10. Vi

là s th

 

log 9a

bng?

4log a

. B.

9log a

. C.

2(1 log )a

. D.

6log a

Câu 11. H tt c các nguyên hàm ca hàm s

( ) sin 2 2f x x

là

2cos2 2x x C

. B.

2cos2 2x x C  

cos2 2

x x C

. D.

cos2 2

x x C  

Câu 12. a s phc

i

bng A.

1

. B.

. C.

. D.

Câu 13.Trong không gian

Oxyz

, hình chiu vuông góc cm

 

1; 3;4M 

trên mt phng

 

Oyz

có

t là

 

1; 3;0

. B.

 

0; 3;4

. C.

 

1;0;0

. D.

 

0;0;1

Câu 14.Trong không gian

Oxyz

, cho mt cu

       

2 2 2

: 2 1 3 25S x y z     

. Tâm ca

 

có

t là

 

2; 1;3

. B.

 

2,1, 3

. C.

 

1;2; 3

. D.

 

2;1;3

Câu15. Trong không gian

Oxyz

, cho mt phng

 

:5 4 3 0x y z



   

t

n ca

 



? A.

 

5; 1;3n 



. B.

 

1; 4;3n   



. C.

 

4; 1;5n   



. D.

 

5; 1; 4n   



Trang 92

Câu16. Trong không gian

Oxyz

ng thng

2 1 1

3 4 2

x y z

  



 

4;9;3P

. B.

 

2; 1;1Q 

. C.

 

3;4;2N

. D.

 

4;7;2M

Câu17.Cho hình chóp

.S ABCD

 nht có

,2AB a BC a

vuông góc vi

mt ph

3SA a

. Góc ging thng

và mt phng

 

ABCD

bng:

45

. B.

30

. C.

60

. D.

90

Câu 18.Cho hàm s

 

, bng xét du ca

 





S m cc tr ca hàm s làA.

. B.

. C.

. D.

Câu19.

và





32y x x  



 

0;2



Mm



. B.

. C.

. D.

Câu 20.Cho hai s th

,ab

và

1a 

. Trong các khnhnào đúng?

 

log log

ab b

. B.

 

2018

2018log 1 log

ab b

 

2018

log 2018 log

a b b

 

2018

log 2018 1 log

a b b

Câu 21.Tp nghim ca b

xx









là

( ;1).

( 3; ). 

( 3;1).

( ; 3) (1; ).   

Câu 22.Cho hình tr có thit din qua trc là mt hình vuông và din tích toàn phn bng

64 a



. Tính

a hình tr.A.

r 

. B.

r 

. C.

4ra

. D.

2ra

Câu 23.Cho hàm 

 

có    sau



 

10fx

là A.2. B.1. C.4. D.3.

Câu 24.   các nguyên hàm  hàm 

 







trên 

 

;1

là

 

3ln 1

x x C   

. B.

 

3ln 1

x x C   

 

3ln 1

x x C   

. D.

 

3ln 1

x x C   

Trang 93

Câu 25. d báo dân s ca mt qui ta s dng công thc

S Ae

;



là dân s cy làm mc tính,

là dân s sau



là t l

  s  ca mc là

96.208.984

i. Và nu t l  i là

0,9

n

 báo dân s ci?

2038

. B.

2040

. C.

2039

. D.

2041

Câu 26. Cho 

.ABCD A B C D

   



3AC a





và

2AA a







. B.

53a

. C.

. D.

Câu 27.Tng s ng tim cng và tim cn ngang c th hàm s

2 3 1xx







là

. B.

. C.

. D.

Câu 28.Cho hàm s

 

4,y a x x b a b   

 th 

M ?

0; 0ab

. B.

0; 0ab

0; 0ab

. D.

0; 0ab

Câu 29.Din tích phn hình phc gch i bng

 

2 2 4 dx x x



  



. B.

 

2 2 4 dx x x



  



 

2 2 4 dx x x







. D.

 

2 2 4 dx x x







Câu 30. Cho hai s phc

3 2 , 1 4z i z i    

. Phn o ca s phc

zz

bng A.

6

. B.

6i

. C.

. D.

Câu 31.Trên mt phng t m biu din s phc

  

1 3 2z i i  



 

5; 5 .P 

 

5;5 .Q 

 

5;5 .N

 

1; 5 .M 

Trang 94

Câu32.Trong không gian

Oxyz



 

1;0;3a 



và

3; ; 5











ng

 

.2a a b

  

bng

26.

26.

25.

25.

Câu33.Trong không gian

Oxyz

, vit cu

 

m

 

0;0; 3I 

c ct

bi mt phng

 

:2 2 3 0x y z



   

theo giao tuyng tròn

 

có bán kính bng 4.

 

3 25x y z   

. B.

 

35x y z   

.C.

 

3 25x y z   

. D.

 

35x y z   

Câu34.Trong không gian

Oxyz

, mt phm

 

1;1; 1M 

và song song vi mt phng

 

:2 2 0x y z



  



2 2 3 0x y z   

. B.

20x y z  

. C.

2 2 3 0x y z   

. D.

2 2 0x y z   

Câu35.m

   

1; 2;3 , 3;4;5AB

. T

m cn

là:

 

1; 2;1

. B.

 

1;1;4

. C.

 

2;0;1

. D.

 

1;1;0

Câu36.Mt hp cha 15 cái th  t n 15, rút ngu nhiên ba cái th. Xác su c

ba cái th có tng các s ghi trên ba th là s l bng:

. B.

. C.

. D.

Câu 37.Cho hình chóp

.S ABC

u cnh

. Hình chiu vuông góc ca

trên mt

phng

 

ABC

m

ca cnh

. Góc ging thng

và mt phng

 

ABC

bng

30

. Tính khong cách ging thng

và

2 21

. B.

. C.

. D.

Câu 38.Cho hàm s

 

có

 

1fe

và

 

f x e







0x



 

ln3

xf x dx



bng

2 e

. B.

3 e

. C.

3 e

. D.

2 e

Câu39.Cho hàm s

 







(

là tham s thc). Có bao nhiêu giá tr nguyên ca



hàm s ch bin trên khong

 

0;

Trang 95

. B.

. C.

. D.

Câu40.Cho hình nón có chiu cao bng

. Mt mt phnh ca hình nón và ct hình nón theo

mt thit diu, góc gia mt phng và ma hình nón bng

. Th tích ca khi

c gii hn bng



. B.



. C.



. D.

168



Câu 41.Cho hai s 

,ab

tha mãn

 

4 10 25

log 2 3 log loga b a b  

. Tính giá tr ca biu thc

3 2 3

a ab b







.C.

. D

Câu 42.Có tt c bao nhiêu giá tr nguyên ca

 giá tr ln nht ca hàm s

 

3 2 2 2

13y x x m x m m      

n

 

1;2

t quá

. B. . C.

. D.Vô s.

Câu 43.

   

log 9 5 log 3 10 0x m x m    

. S giá tr nguyên ca tham s 

m phân bit thuc

 

1;81

là A.

. B.

. C.

Câu44.Cho hàm s

()fx

liên tc trên



. Bit

cos x

là mt nguyên hàm ca hàm s

( )e

, h tt

c các

nguyên hàm ca hàm s

 

là

sin 2 2cosx x C

. B.

sin 2 2cosx x C

.C.

sin 2 2cosx x C  

. D.

sin 2 2cosx x C  

Câu45. Cho hàm s có bng bi

S nghin

 

2 ;2





c

 

4 cos 5 0fx

là

Câu46. Cho hàm s bc bn

 

y f x

 th  m cc tr ca hàm s

 

25g x f x x  

là

11.

Câu 47. Cho các s

0; 0xy

tha mãn

log 3 2 4

xy x y



   



. Giá tr

ln nht ca

bng

khi

   

; ; .x y x y

Tính

.xy

Trang 96

 

3 11 2



 

3 11 2



65 10 22



65 10 22



Câu 48.Cho hàm s

 







   

,f x f x x x   

. Tính

 

I f x dx





I 

I 

I 

Câu49.Cho hình chóp

.S ABCD



ABCD

là hình bình hành

22AD AB a



60BAD 

. Bit

hình chiu ca

lên mt phng

 

ABCD

m

ca

và góc gia hai mt phng

 

SAB

và

 

SAD

là

. Tính

.S ABCD

. B.

. C.

. D.

Câu50.Cho hàm s

 

. Hàm s

 

y f x





 th 

Hàm s

   

2 2 3 2

g x f x x x     

ng bin trên kho

 

;1 

. B.

 

1;4

. C.

 

4;

. D.

 

2;3

ĐÁP ÁN

Trang 97

10C

11D

12D

13B

14B

15D

16A

17C

18A

19A

20C

21D

22A

23C

24A

25B

26A

27D

28D

29B

30A

31A

32B

33A

34C

35B

36B

37A

38B

39D

40A

41A

42A

43C

44D

45D

46C

47D

48A

49D

50C

LỜI GIẢI CHI TIẾT

Câu1.Chọn D.S cách Chn mi nam: 5 cách.

S cách Chn mi n: 6 cách.Áp dng quy tc nhân, s cách Chn là: 30 cách.

Câu2.Chọn B.

u u d d



    

Câu 3.Chọn C.Din tích xung quanh ca hình tr là

S rh





Câu 4.Chọn D

Quan sát bng bin thiên ta thy

 

'0fx

trên khong

 

0;2



 

nghch bin trên

khong

 

0;2

Câu5.Chọn D.Th tích khi l

4 64Va  

Câu 6.Chọn D.

;



 





;

   

log 3 8 2 3 8 2 4x x x tm      

Vy

4x 

là nghim c

Câu 7.Chọn B.Ta có:

5 5 3

3 1 1

( ) ( ) ( ) 3 1 4.f x dx f x dx f x dx      

  

Câu 8.Chọn A. vào bng bic giá tr ci ca hàm s bng

Câu9.Chọn A

Câu10. Chọn C.Vì

là s th

 

3 3 3

log 9 2log 3 2(1 log )a a a  

Câu 11.Chọn D.Ta có

 

sin 2 2 sin 2 2 cos2 2

x dx xdx dx x x C      

  

Câu 12.Chọn D.Ta có

 

0 1 1i    

Câu 13.Chọn B.Hình chiu vuông góc cm

 

1; 3;4M 

trên mt phng

 

Oyz

có t là

 

0; 3;4

Trang 98

Câu 14.Chọn B.Gi

là tâm mt cu

   

2;1; 3SI

Câu15.Chọn D.Vì các h s c

;;x y z

t phng

 

:5 4 3 0x y z



   

là mt

t cn ca

 



n ca

 



là:

 

5; 1; 4n   



Câu16.Chọn A.Thay t m

 

4;9;3P

ng thng

2 1 1

3 4 2

x y z

  



c:

4 2 9 1 3 1

3 4 2

  

  

. Vm

thung thng

Câu17.Chọn C.Áp dnh lí Pytago ta có:

3AC AB BC a  

Ta có

 

SA ABCD

AC

là hình chiu vuông góc ca

trên

 

ABCD

 



,,SC ABCD SC AC SCA  

Xét

SAC



tan 3

SA a

SCA

  



60SCA  

Vy

 

, 60SC ABCD 

Câu 18.Chọn A.Da vào bng bin thiên ta có:Hàm s

 

m cc tr ti

2, 1, 2, 3x x x x     

Câu19.Chọn A.Ta có

 

1 0;2

' 3 3 0

1 0;2



  

   











     

 

max 0 ; 1 ; 2 max 2;0;4 4M y y y  

     

 

min 0 ; 1 ; 2 min 2;0;4 0m y y y  

.Vy

4Mm

Câu 20.Chọn C.Kim tra t

 

2018 2018

log log log 2018 log

a a a a

a b a b b   

Câu 21.Chọn D.Ta có

   

2 2 3

1 1 1 1

2 3 ; 3 1;

2 8 2 2

x x x x

x x x



     

           

     

     

Câu 22.Chọn A.Gi

.Do thit din qua trc là hình

vuông nên hình tr có chiu cao là

2hr

.Din tích toàn phn bng

64 a



Trang 99

2 2 64r rh a

  

  

2 2 2

2. 4 64r r a

  

  

6 64

r a r



   

Câu 23.Chọn C.Ta có

 





  









T  th ta thy ng thng

1y 

ct  th hàm s

 

ti 1 m và

ng thng

1y 

ct  th hàm s

 

ti 3 m phân bit.Nên

 trình có 4 nghim phân bit.

Câu 24.Chọn A.

 

;1 1 0xx     

Nên

   

2 2 2

d d 1 d 3ln 1 3ln 1

1 1 2 2

x x x

f x x x x x x x C x x C





             







  

Câu 25.Chọn B.Áp dng công thc

ln ln :

nr nr

S S S

S Ae e nr n r

A A A

   

      

   

   

vi:

116224393S 

96208984A 

0,9r 

%..Suy ra:

116224393

ln :0,9% 21

96208984









V

2019 21 2040

thì d báo dân s ci.

Câu 26. Chọn A.Gi c

. Ta có:

2 2 2 2 2 2 2 2 2

AC AB AD AA a x x a x



        



. .2 5

ABCD

V S AA x a a



  

Câu 27.Chọn D.Tnh

 

\ 0;1D  

Ta có:

2 3 1

lim lim 2

 







 th hàm s có 1 tim cn ngang là

2.y 

Xét

  

 

1 1 1

1 2 1

2 3 1

lim lim lim 1

x x x

x x x x

  





  



Và

0 0 0 0

2 3 1 2 3 1

lim lim ; lim lim

x x x x

   

   

   

     



 th hàm s có 1 tim cn

ng là

0.x 

Câu 28.Chọn D.D nhn thy

0a 

 th ct trc tung t 

0b 

Trang 100

Câu 29.ChọnB. m

2 2 2

3 3 1 2 2 4 0

x x x x x x





           







Din tích hình phng cn tìm là

   

2 2 2

3 3 1 d 2 2 4 dS x x x x x x x x





          





Câu 30.Chọn A.Ta có

   

3 2 1 4 2 6z z i i i        

.Phn o ca s phc

zz

bng

6

Câu 31.Chọn A.Ta có

  

1 3 2 2 6 3 5 5z i i i i i i        

.Vm biu din ca s phc

là

 

5; 5 .P 

Câu32.Chọn B.Ta có

   

 

   

2 6;1; 10 2 5;1; 7 . 2 1 .5 0.1 3. 7 26.b a b a a b              

     

Câu33.Chọn A.Gi

lt là bán kính ca mt cu

 

ng tròn

 

Ta có

 

2 2 2

2.0 0 2. 3 3

2 1 2



   







 

2 2 2 2

, 3 4 5R d I r



    

Va

 

là

 

3 25x y z   

Câu34.Chọn C.Gi

 



là mt phng cn tìm.

Mt phng

 

:2 2 0x y z



  

có mn là

 

2;2;1n







Vì

   



nên

 



nhn

 

2;2;1n







n.

Vy

 





     

2 1 2 1 1 0x y z     

hay

2 2 3 0x y z   

Câu35.Chọn B.m cn AB



















   



















Câu36.Chọn B.

455C 



56C 



. 168CC

S c ba cái th có tng các s ghi trên ba th là s l là:

56 168 224

Trang 101

c ba cái th có tng các s ghi trên ba th là s

l là:

224 32

455 65

P 

Câu 37.Chọn A.Trong mt phng

 

ABC

dng

//Ax BC

.Gi

là hình chiu ca cm

trên

và

là hình chiu ca

trên

.Suy ra

HD AD

và

HE SD

Ta có

 

AD HD

AD SHD

AD SH













mà

 

HE SHD AD HE  

T và suy ra

 

HE SAD

.Do

//BC Ax

mà

   

//Ax SAD BC SAD

   

 

, , , 2 , 2 2.

SH DH

d BC SA d BC SAD d B SAD d H SAD HE

SH DH

     



Xét

SHC

vuông ti

có

3CH a

và



30SCH 

nên

.tan30 3.

SH CH a a   

Xét tam giác

ADH

vuông ti

có

AH a

và



60HAD HBC  

nên

.sin60

DH AH  

Vy

 

2 21

, 2.

d BC SA





Câu 38.Chọn B.Ta có

 

2 2 2

1 1. ( ) . ( ) .

x x x x x x

x e x e e x x e e e

f x e dx dx dx dx C

x x x x x







  

     





   

Vì

   

f e e C e C f x

       

.Vy

 

ln3 ln3

ln3

xf x dx e dx e e   



Câu39.Chọn D.Tnh:

 

\2Dm

.Ta có:

 

2 2 4

f x f x







  



 hàm s ch bin trên khong

 

0;

Trang 102

 

2 2 4 0

















  









   



  

















Câu40.Chọn A.Gi

nh ca hình nón. Mt mt phnh ca hình nón và

ct hình nón theo mt thit diu

SAB

. Gi



6SO

.Gi

m



, 60AB OH AB SH AB SHO    

T gi thit ta có:

sin



, do

ABC

u

SH SA  

Nên

64 36 2 7OA SA SO    

.Vy

. . . . .28.6 56

V OA SO

  

  

Câu 41.Chọn A.t

 

4 10 25

log 2 3 log loga b a b t   

2 3 4

















2.10 3.25 4

t t t

  

2. 3 0

   

   

   

   

1 ( )

































Ta có









và

3 2 3

27 3 1 25

27 3 1 29

a ab b







   



   

   









Câu 42.Chọn A.Xét hàm s

 

3 2 2 2

13f x x x m x m m      

n

 

1;2

Ta có

 

 

' 2 2 2 2

3 2 1 2 1 0, 1;2f x x x m x x m x           

Suy ra hàm s

 

ng bin

 

1;2



 

   

 

   

1;2

min 1 4

max 2 3 11

f x f m

f x f m m



    







   







   

 

1;2 1;2

max maxy f x





 

max 4 ; 3 11m m m    

15

4 15

3 11 15

   







  





19 11

15 4 15

3 4 0

15 3 11 15

3 26 0

  



   





   



    





  



19 11

  









  





. Vi

m

 

1;0;1m  

Câu 43.Chọn C.Ta có:

   

log 9 5 log 3 10 0x m x m    

t

logtx

vì

   

1;81 0;4xt  

Trang 103

 thành:

 

1 3 6 0t m t m    













ycbt

0 2 4 2 6

2 3 5

    







  



. Vy có 4 s nguyên m tho ycbt.

Câu44.Chọn D.Vì

cos x

là mt nguyên hàm ca hàm s

 

f x e

nên:

 

cos ' 2cos .sin sin2

f x e x x x x     

Tính

 

I f x e dx



t

   

u e du e dx

dv f x dx v f x

















   

2 2 2

.e 2 sin2 2cos

I f x f x e dx x x C      



Câu45.Chọn D.T

     

4 cos 5 0 cos 1

f x f x    

t

costx

vi

 

2 ;2x





thì

 

1;1t 

     

ft  

Xét hàm s

 

 

cos ; 2 ;2h x x x



  

ta có BBT:

Vi

1t 

thì PT có

nghim.

Vi

11t  

thì PT có

nghim

Vi

1t 

thì PT có

nghim

Xét

   

ft

vi

 

1;1t 

Nhìn vào BBT PT

   

ft

có hai nghim

 

1 1 0

2 2 0

1 0 4

0 1 4

t x x n

    





   





Vy tt c có

nghim

Câu46.Chọn C.

 

   

4 2 3 4 2

2 5 4 4 2 5 0g x f x x g x x x f x x



        

Trang 104

 

4 1 0

4 4 0

2 5 0

f x x

















  





  





  

2 5 0 4 1

2 5 4 5 2

2 5 5 3

x x x x

















    



    



   



Xét

   

 

4 2 3 2

2 5 4 4 4 1f x x x f x x x x x



       

;

 

0 4 1 0 1

f x x x x









      







Da vào bng bin thiên ta thy.PT có vô nghim, PT có 4

nghim, PT có 2 nghim

Nên PT

 

0gx





có

nghit, suy ra

Hàm s

 

25g x f x x  

m cc tr.

Ta có BBT:

Câu 47. Chọn D.

 

log 3 2 4 1 .

xy x y



   





0; 0xy

, u kinh ca

 

là:

1.xy 

Ta có:

log 3 2 4

xy x y



   



   

log 1 log 1 2 1 (3 3 ) ( 2 )xy y xy x y         

     

log 3 3 (3 3 ) log 1 2 ( 2 ) *xy xy y x y       



 

logf t t t

trên

 

0;

, có

 

1 0, 0.

.ln3

f t t



    



 



 

0; .

     

* 3 3 2 3 3 2 2 2PT f xy f x y xy x y xy        

Suy ra:

2 11 2 11

3 2 2 3 0

xy xy xy

   

     

Trang 105

 

13 2 22

max xy





khi

26 4 22

13 2 22

26 4 22





































26 4 22

65 10 22

26 4 22













  















65 10 22





Câu 48.Chọn A.

 

0 0 0

2 2 1

  







  





T gt:

   

,f x f x x x   



         

. . . ,f x f x f x f x x f x x

  

   

         

. . .f x f x f x f x dx x f x dx

  



  





   

2 2 2

0 0 0

f x f x

x f x f x dx   





   





I

Câu49.Chọn D.Gi

m ca



ng trung

bình ca

ABCD

//IJ AB

và

IJ a

T giác

ABIJ

có

AB BI IJ AJ  

ABIJ

là hình thoi.

Xét hai tam giác vuông

SIB

và

SIJ

có

chung và

BI IJ a

suy ra

SIB SIJ  

nên

SB SJ

Xét

SBA

và

SJA

có:

SB SJ

AB AJ

và

chung suy ra

SBA SJA  

K

 

BH SA H SA

, d thy

JH SA

và

BH HJ

Ta có:

   

 



   

 



, , 60

120

SAB SAD SA

BHJ

SA BH SAB BH HJ SAB SAD

BHJ

SA JH SAD











     

















 

SA BH

SA BHJ SA HK

SA HJ





   







Trang 106

Tam giác

BAJ

có

BA AJ a

và



60BAJ 



BAJ

u

BJ a

















Gi s



60BHJ 



HK AK

nên



120BHJ 



tan

KJ a

KHJ

  

HA AK HK   

Ta có

. 2 . 6

AH HK AI HK AK HK a

AHK AIS SI

AI SI AH AH

       



1 1 2

. . .sin .

3 3 4

S ABCD ABCD

V S SI AB AD BAD SI  

Câu50.Chọn C.Ta có:

   

2 4 3g x f x x x



     

       

0 2 4 3 2 2 1g x f x x x f x x

  

          

t

2tx



 

1f t t





S nghim c

 

1f t t





chính là s m c th hàm s

 

y f t





 th hàm s

1yt

D th ta thy

 

f t t







  









   

2 2 4

2 2 1

2 0 2

f x x

   





     



  



Ta có bng xét du :

Da vào bng xét du ta thy hàm s ng bin trên

 

4;

Bấm Tải xuống để xem toàn bộ.

| 1/106

| | Tải xuống

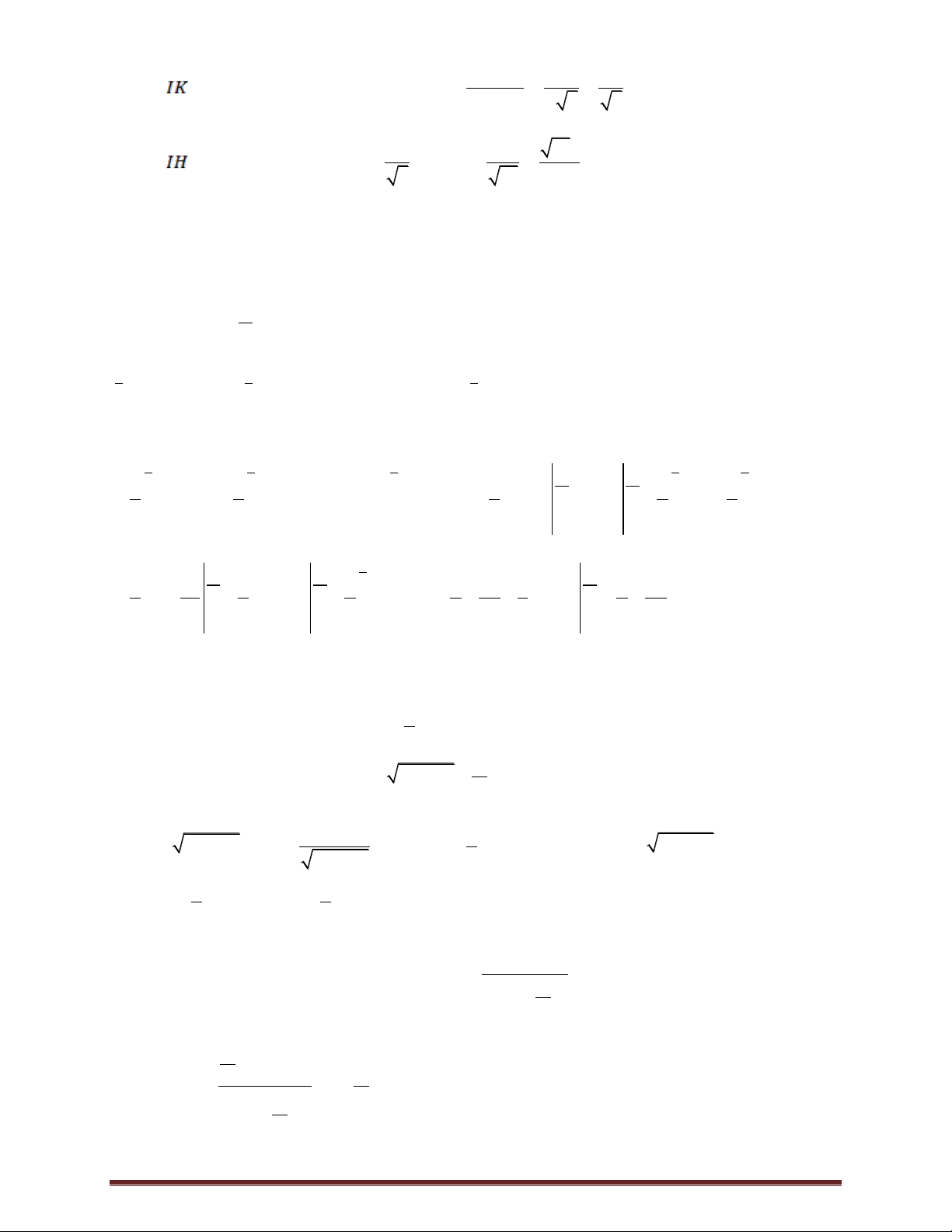
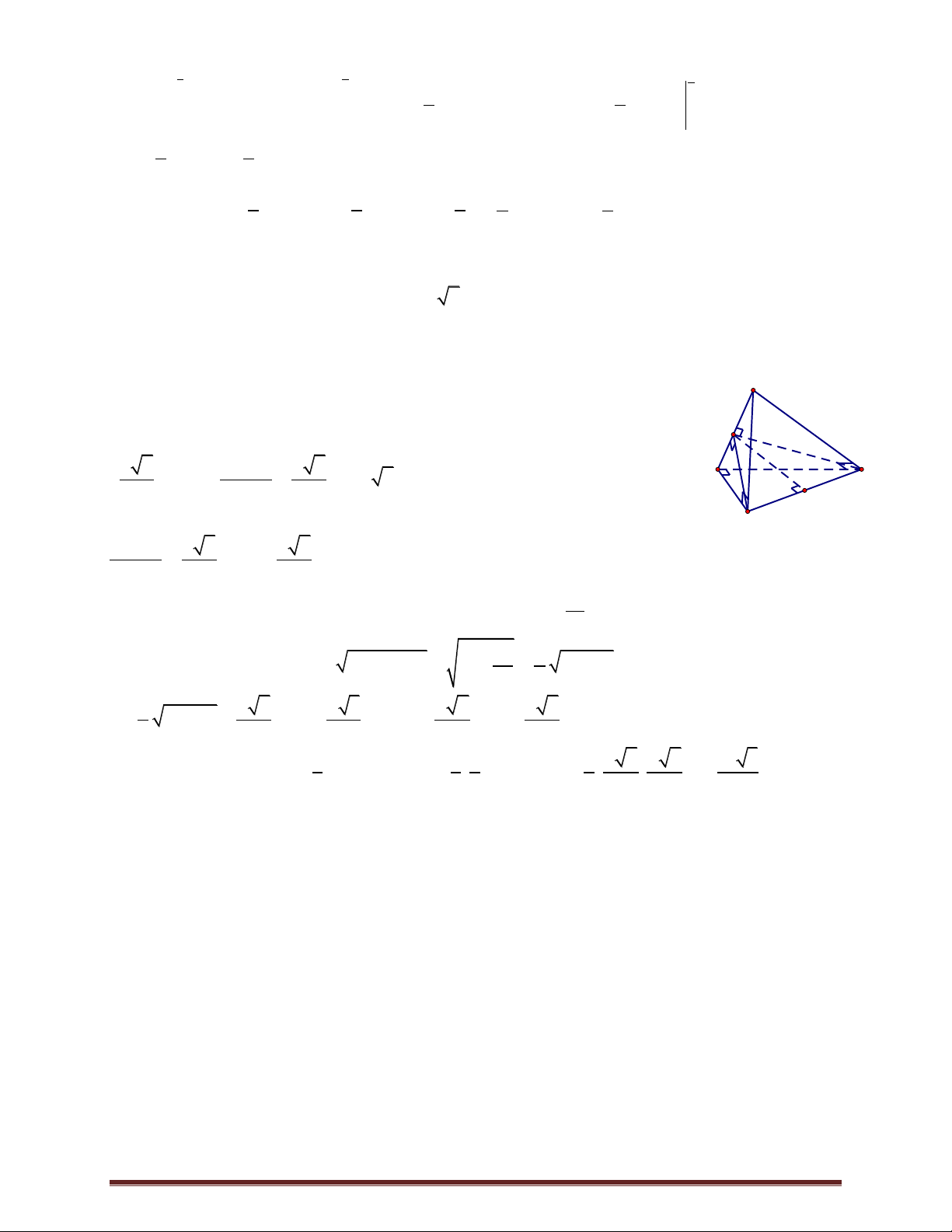
Preview text:

ĐỀ 21
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2 MÔN TOÁN Thời gian: 120 phút
Câu 1. Lớp 11A có 20 học sinh nam và 25 học sinh nữ. Có bao nhiêu cách chọn một đôi song ca gồm 1 nam và 1 nữ? A. 45 . B. 2 C . C. 2 A . D. 500 . 45 45
Câu 2. Cho cấp số cộng u
có số hạng đầu u  2 , công sai d  3. Số hạng thứ 5 của u bằng n  n  1 A.14 . B.10 . C.162 . D. 30 .
Câu 3. Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng 1
A. 4 rl .
B. 2 rl .
C.  rl . D.  rl . 3
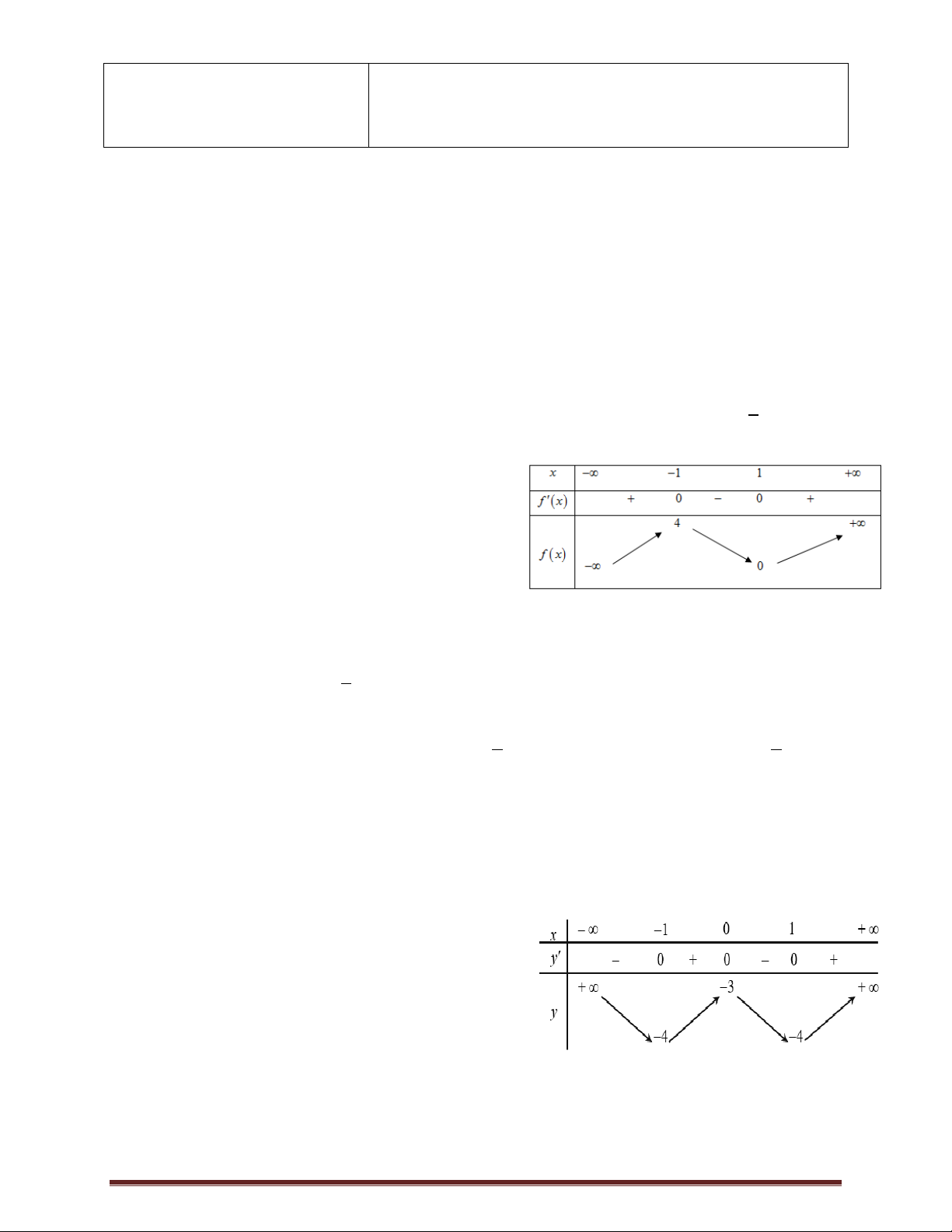
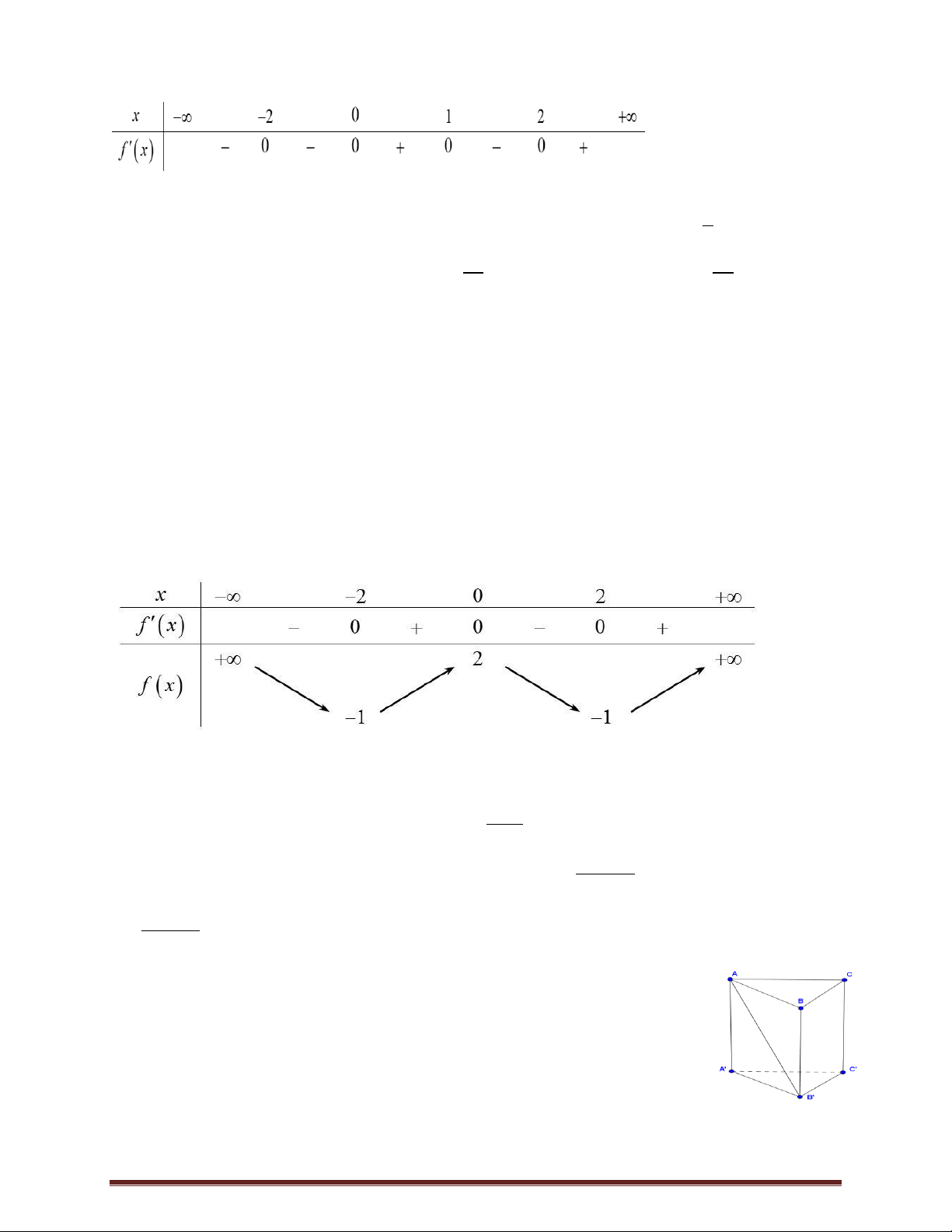
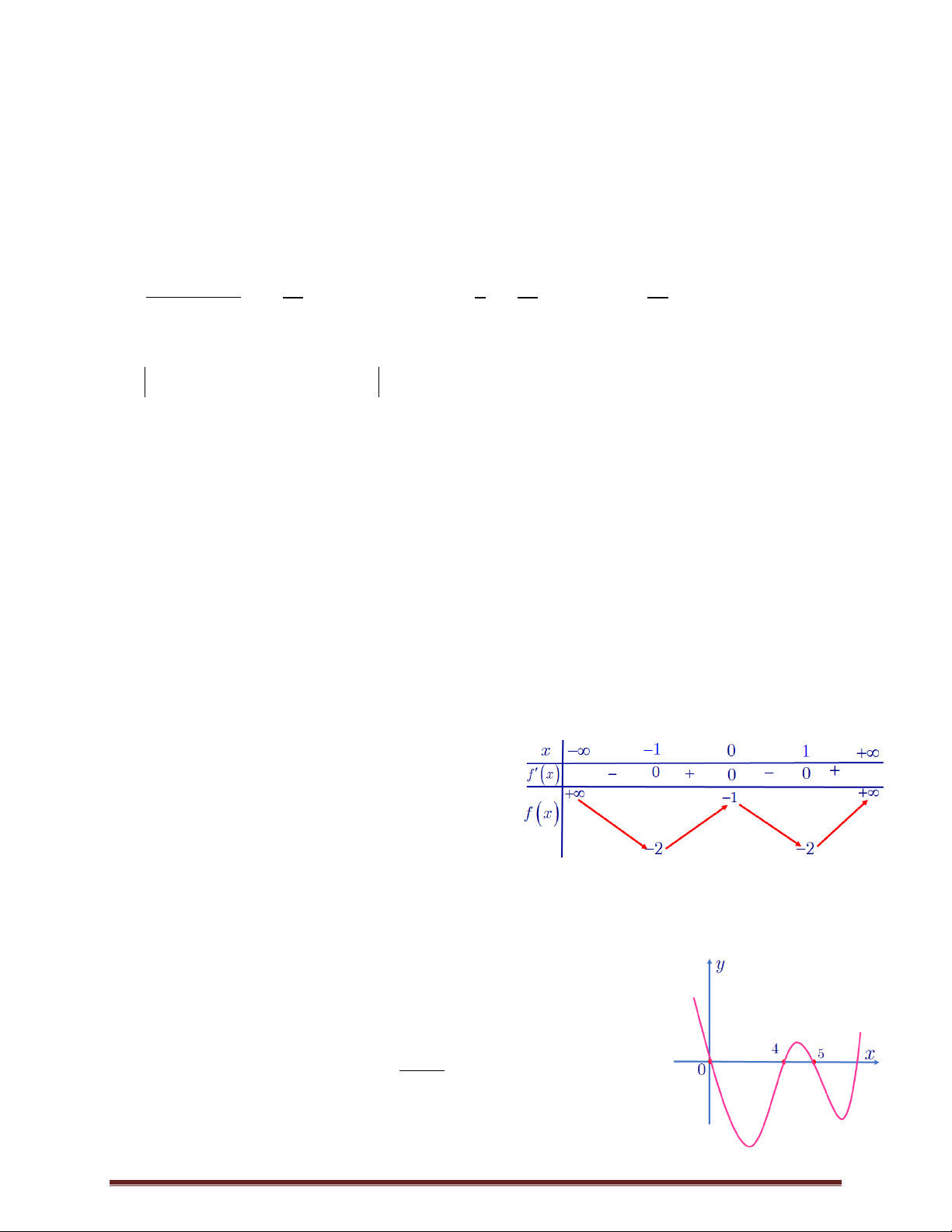
Câu 4.Cho hàm số f  x có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng nào dưới đây?
A. 0; 4 . B.  ;    1 .C.  1   ;1 . D. 0; 2 .
Câu 5. Cho hình hộp có đáy là hình vuông cạnh bằng a và
chiều cao 3a . Thể tích của hình hộp đã cho bằng 1 A. 3 a . B. 3 3a . C. 3 9a . D. 3 a . 3 7 9
Câu 6. Phương trình 4 x8 2020
 1 có nghiệm làA. x  . B. x  2
 . C. x  . 4 4 D. x  2 . 2 2 2 Câu 7. Nếu f
 xdx 5 và 2f
 x gxdx 13 
thì g  x dx  bằngA. 3  . B. 1. C. 1. 1 1 1 D. 3 .
Câu 8. Cho hàm số y  f  x có bảng biến thiên như sau:
Khẳng định nào sau đây đúng
A. Hàm số đạt cực tiểu tại x  4  .
B.Điểm cực đại của đồ thị hàm số là x  0 .
C. Giá trị cực tiểu của hàm số bằng 1.
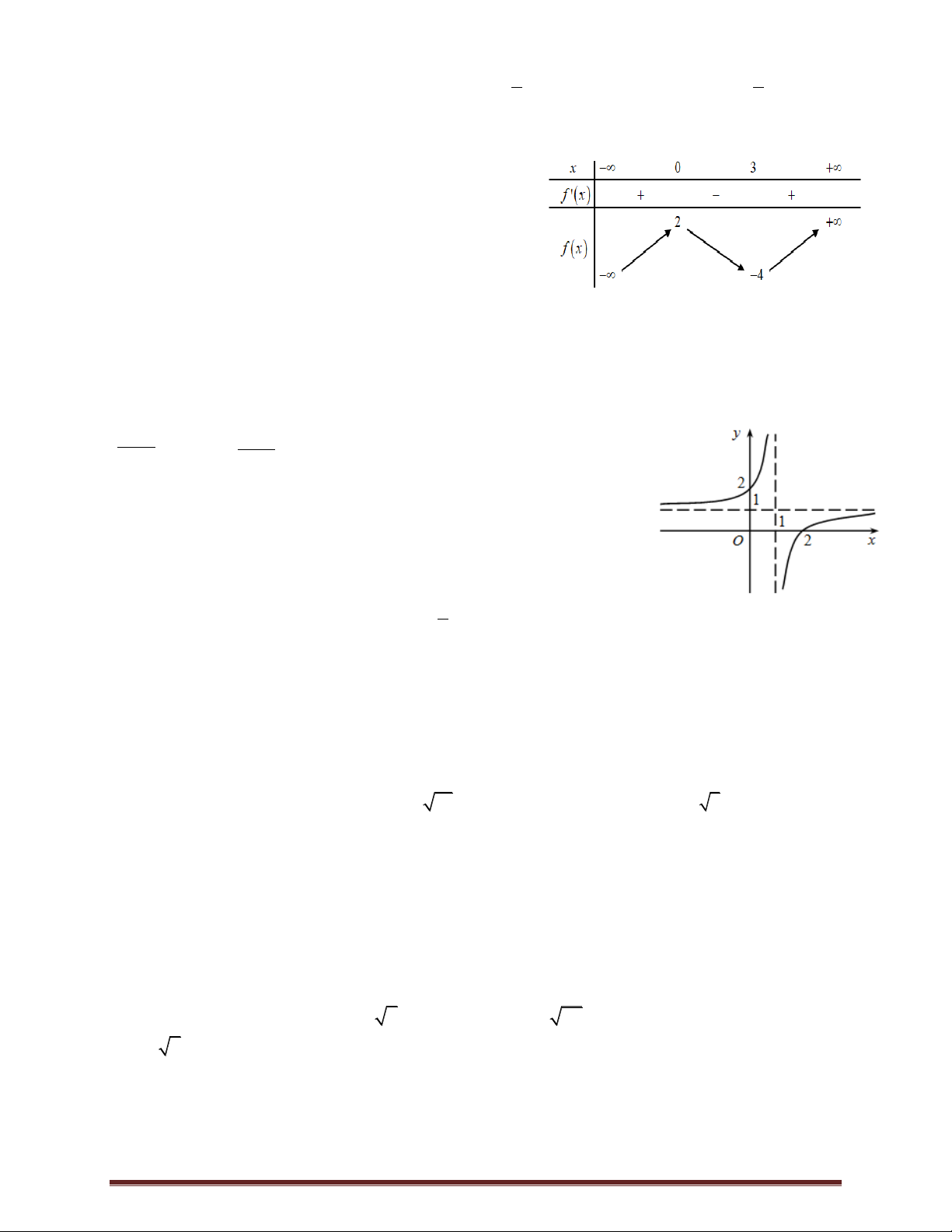
D. Điểm cực đại của đồ thị hàm số là A0 ;  3 . Trang 1
Câu 9. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới đây? A. 2
y  x  2x 1. B. 3
y  x  2x 1 . C. 4 2
y  x  2x 1. D. 3
y  x  2x 1 .
Câu 10. Với số thực dương a tùy ý, log a bằng 3 1 1
A. 2  log a .B.
 log a . C. 2log a . D. log a . 3 3 2 3 3 2
Câu 11.Họ tất cả các nguyên hàm của hàm số f  x 2
 sin x  6x là A. 3
 cos x  2x  C . B. 3
cos x  2x  C . C. 3
 cos x 18x  C . D. 3
cos x 18x  C .
Câu 12. Gọi z là số phức liên hợpcủa số phức z  3
  4i . Tìm phần thực và phần ảo của số phức z .
A.Số phức z có phần thực bằng 3
 và phần ảo bằng 4 .
B. Số phức z có phần thực bằng 3 và phần ảo bằng 4 .
C. Số phức z có phần thực bằng 3  và phần ảo bằng 4  .
D. Số phức z có phần thực bằng 3 và phần ảo bằng 4  .
Câu 13. Trong không gian Oxyz , hình chiếu vuông góc của điểm A1; 2;3 trên mặt phẳng Oyz  có tọa độlà
A. 0; 2;3 .
B. 1;0;3 .
C. 1;0;0 .
D. 0; 2;0 .
Câu 14. Trong không gian Oxyz , tọa độ tâm của mặt cầu S  2 2 2
: x  y  z  2x  4y  6  0 là
A. 2; 4;0 .
B. 1; 2;0 .
C. 1; 2;3 . D. 2; 4;6 .
Câu 15. Trong không gian Oxyz , cho mặt phẳng   : 2x  3z 1 0 . Vectơ nào dưới đây là một vectơ   
pháp tuyến của   ?A. n  2;3;  
1 . B. n  2;3; 0 . C. n  2;0;  3 . 
D. n  2;0;  3 . x 1 2t 
Câu 16. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :  y  3  t ? z  3t  Trang 2
A. M 1;3;0 . B. N 1;3;3 . C. P 2; 1;0 . D. Q 2; 1;3 .
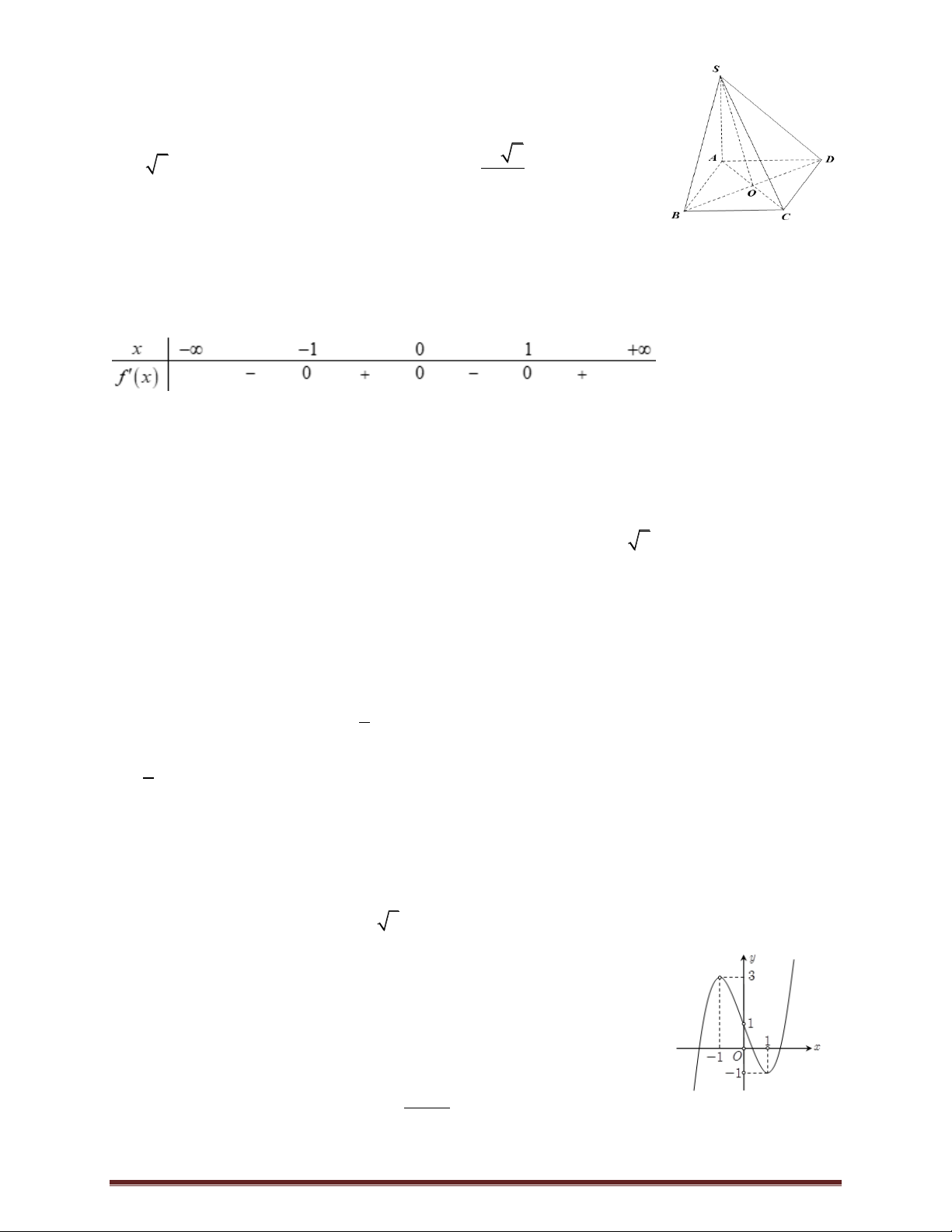
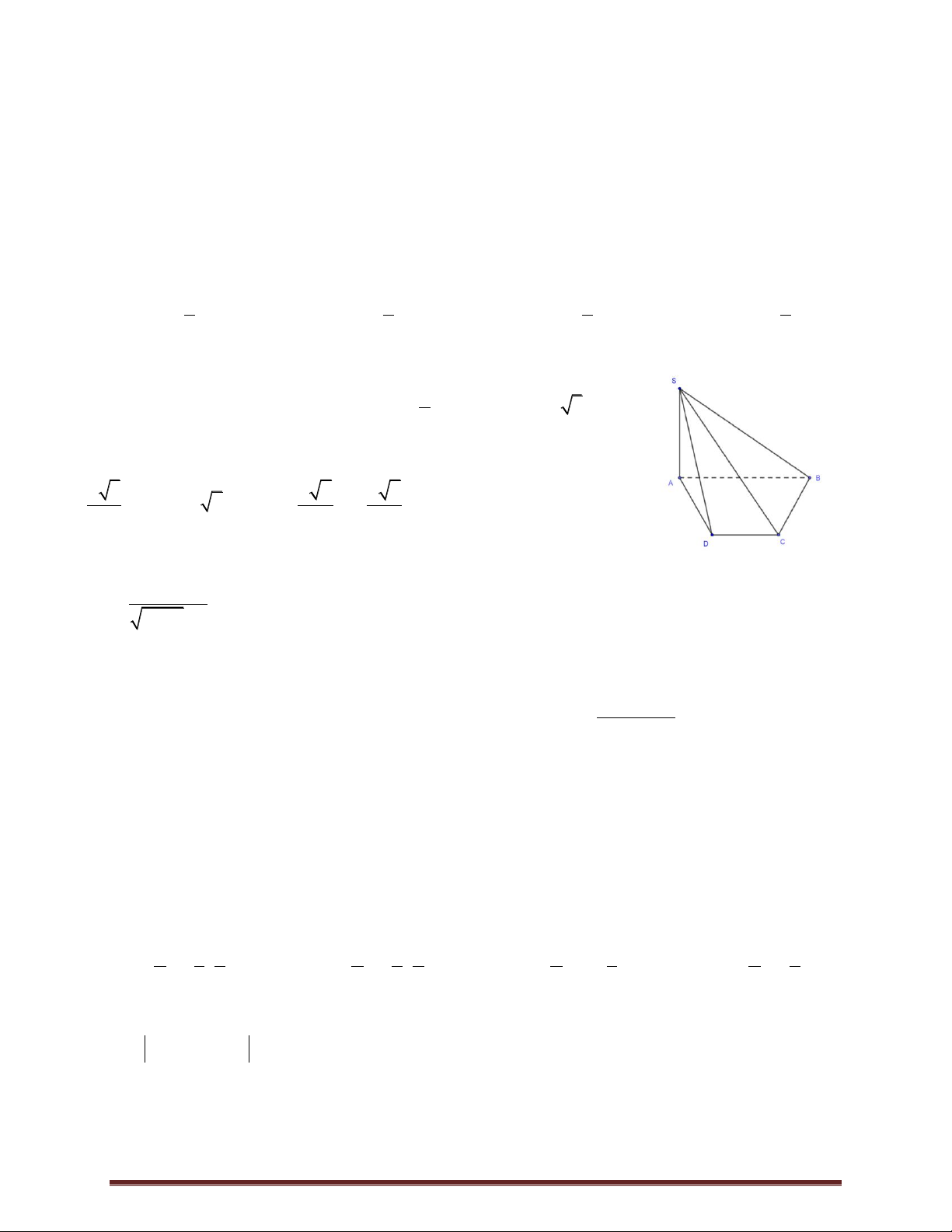
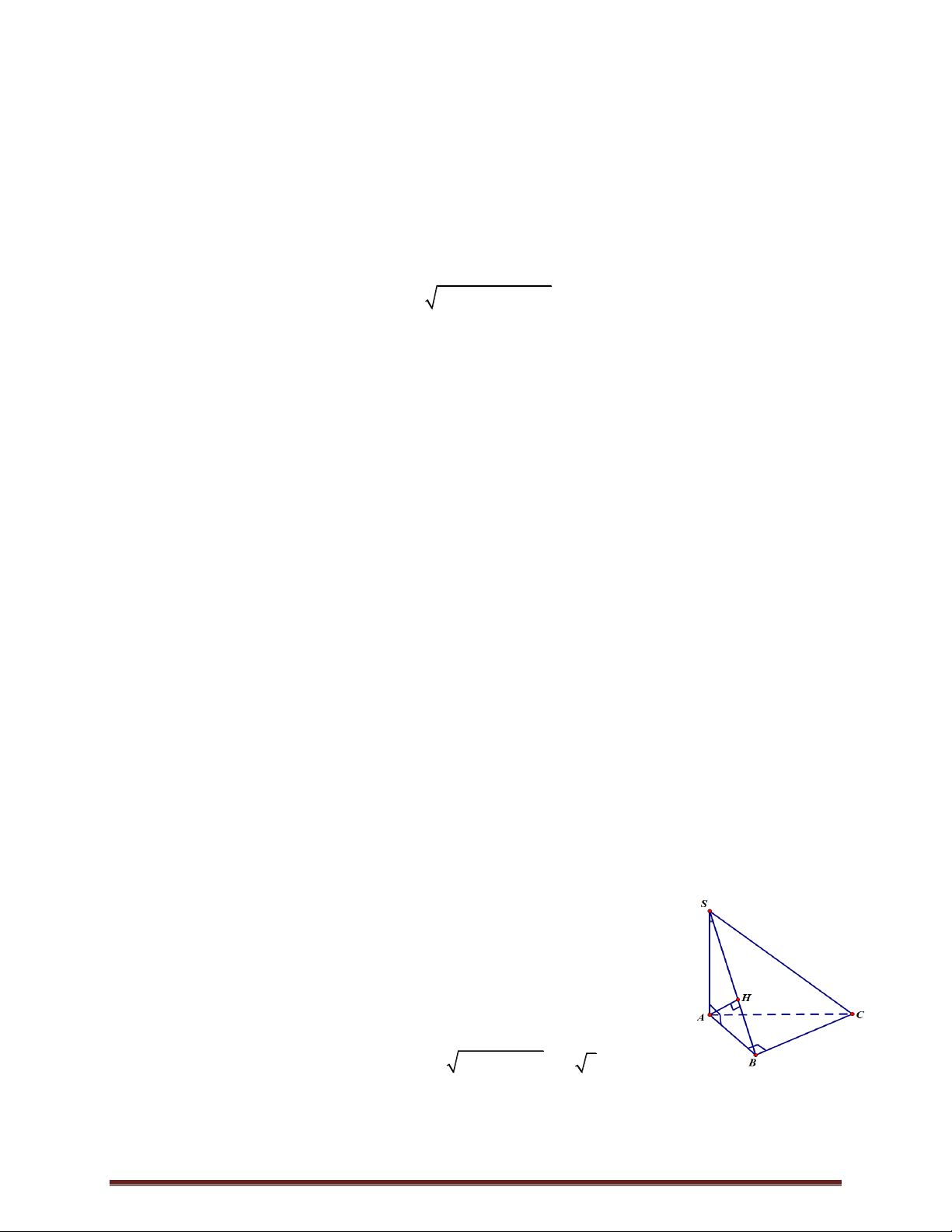
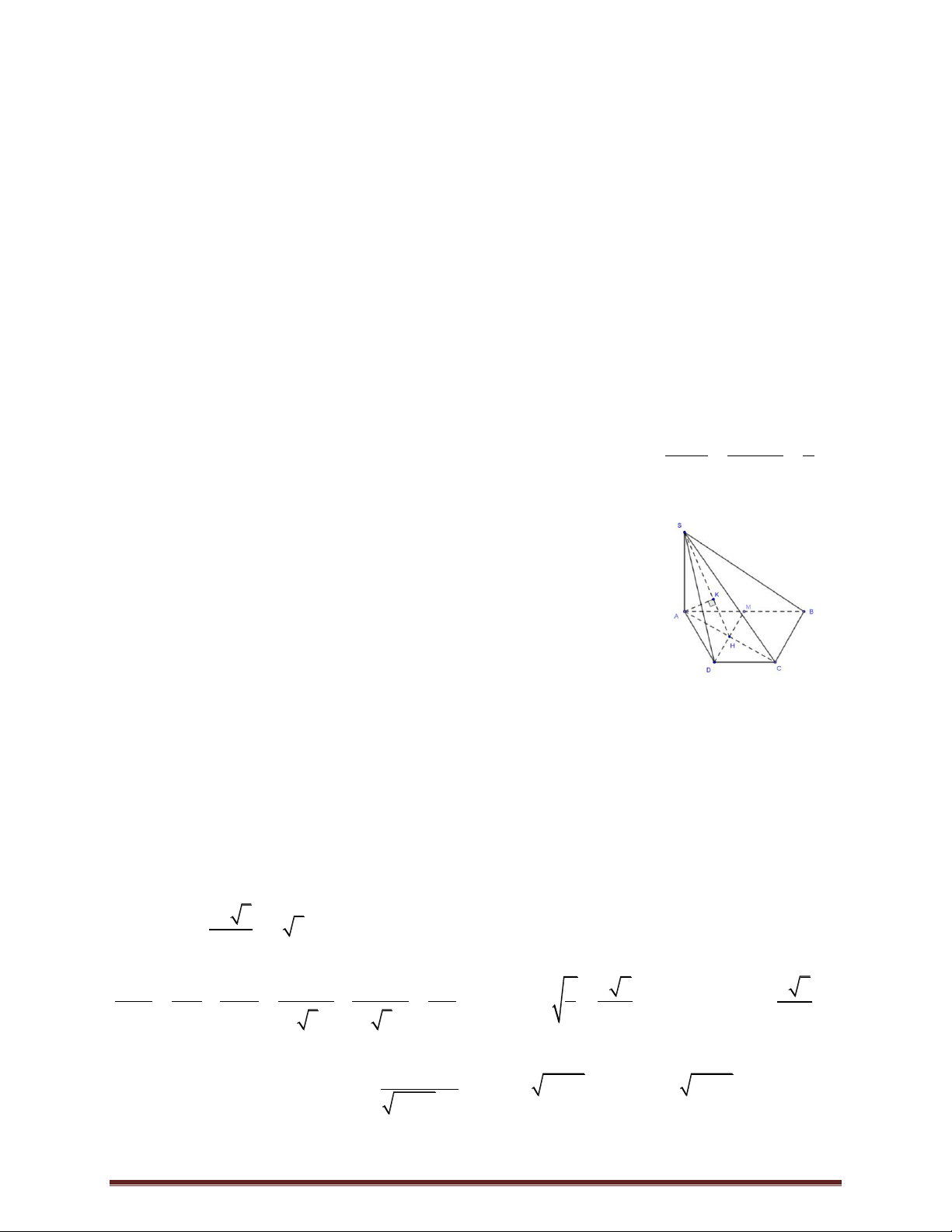
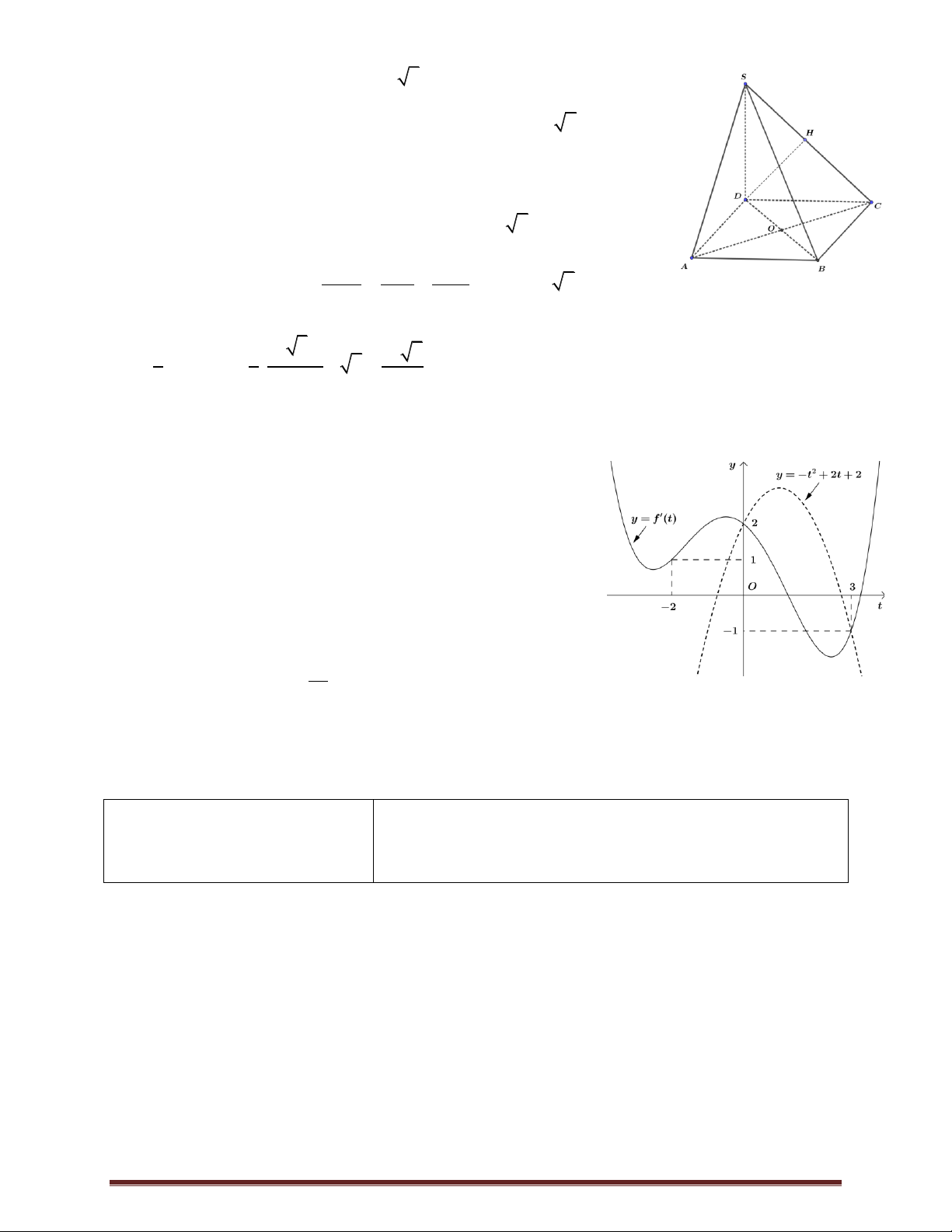
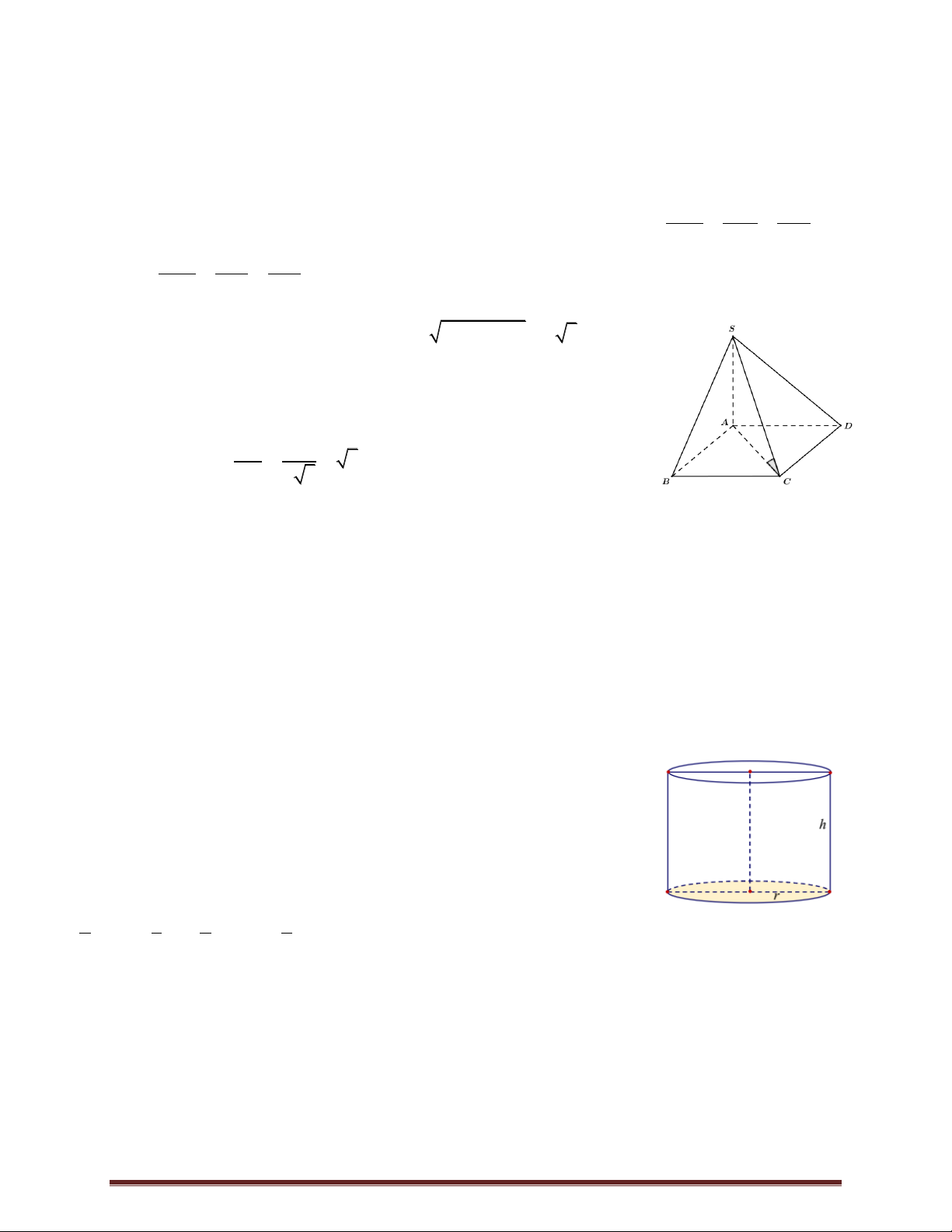
Câu 17. Cho hình chóp S.ABCD có đáy là hình hình thoi tâm O , ABD  3a 2
đều cạnh a 2 , SA vuông góc với mặt phẳng đáy và SA  (minh 2
họa như hình bên).Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng
A. 45 . B. 30 . C. 60 . D. 90 .
Câu 18. Cho hàm số y  f  x , bảng xét dấu của f  x như sau
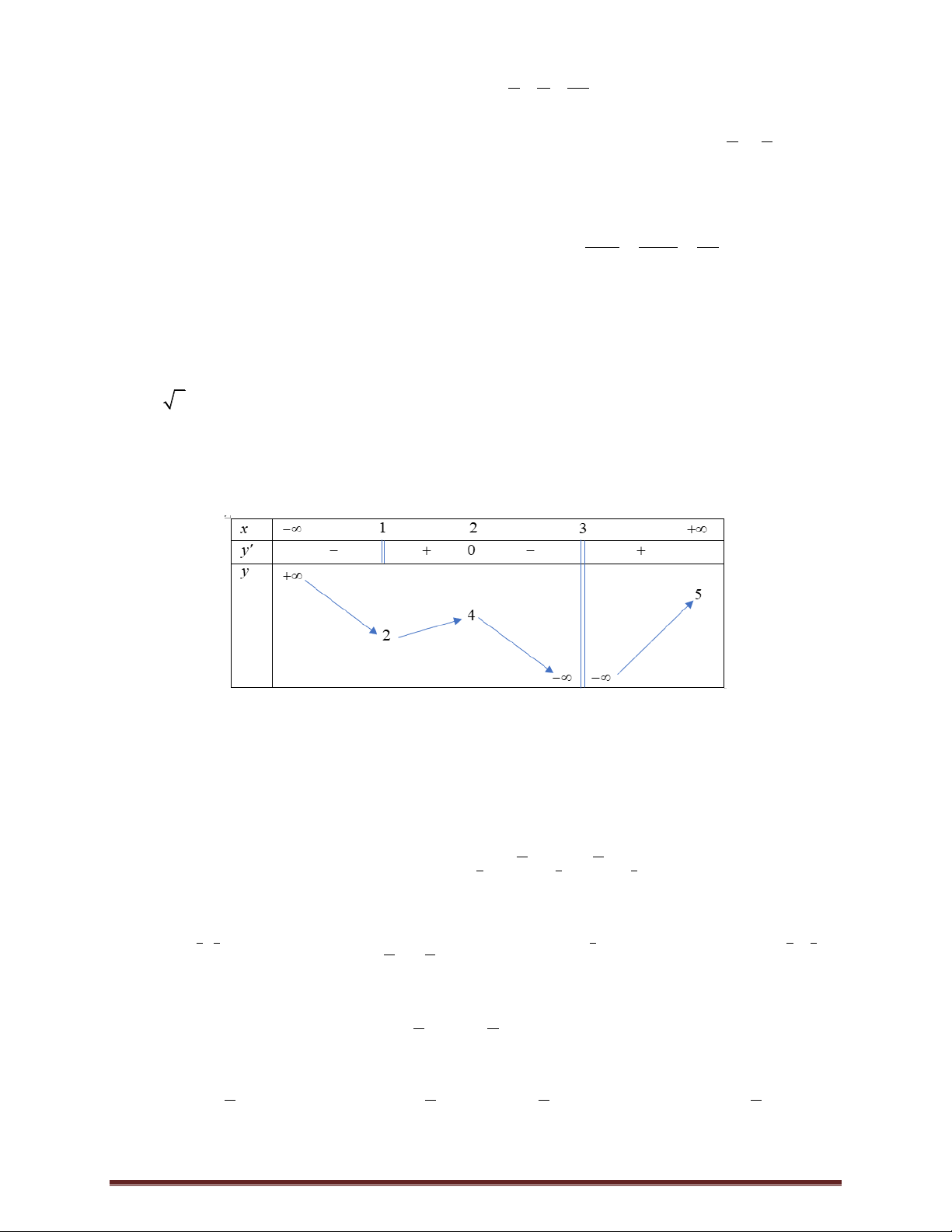
Số điểm cực tiểu của hàm số đã cho làA. 0 . B. 2 . C.1. D. 3 .
Câu 19. Giá trị nhỏ nhất của hàm số f  x 4 2
 x 10x 1trên đoạn  3
 ;2 bằngA.1. B. 23  . C. 24 . D. 8  .
Câu 20. Xét tất cả các số thực dương a và b thỏa mãn log a  log  2 a
b . Mệnh đề nào dưới đây 3 27  đúng? A. 2
a  b . B. 3
a  b .
C. a  b . D. 2 a  b . 2 log x log x
Câu 21. Tập nghiệm của bất phương trình 9 9 9  x  18 là 1  A. 1;9 . B. ;9   . C. 0;  1 9;  . D. 9   1 0; 9;    .  9
Câu 22. Cho mặt cầu  S  . Biết rằng khi cắt mặt cầu  S  bởi một mặt phẳng cách tâm một khoảng có độ
dài là 3 thì được giao tuyến là đường tròn T  có chu vi là 12 . Diện tích của mặt cầu  S  bằng A.180 . B.180 3 . C. 90 . D. 45 .
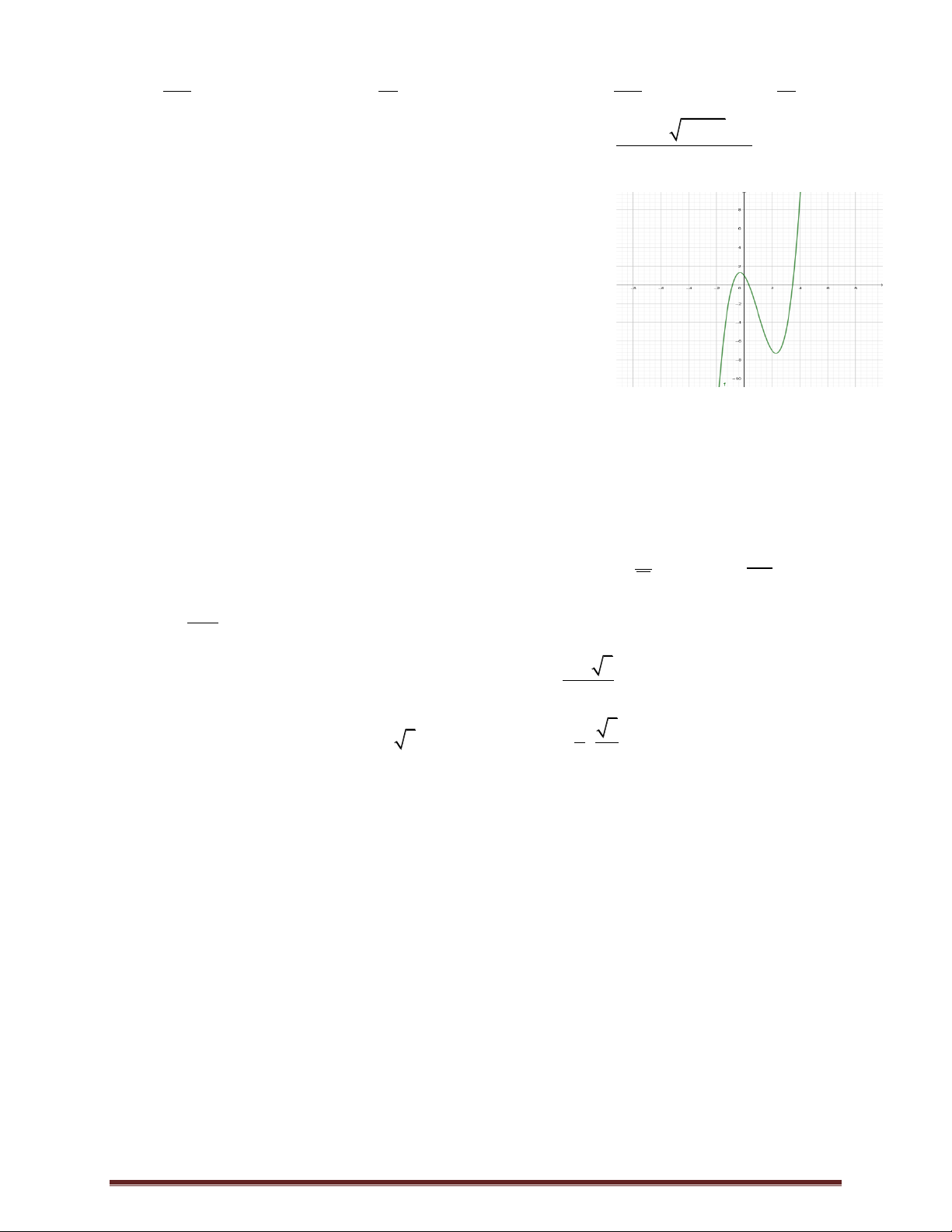
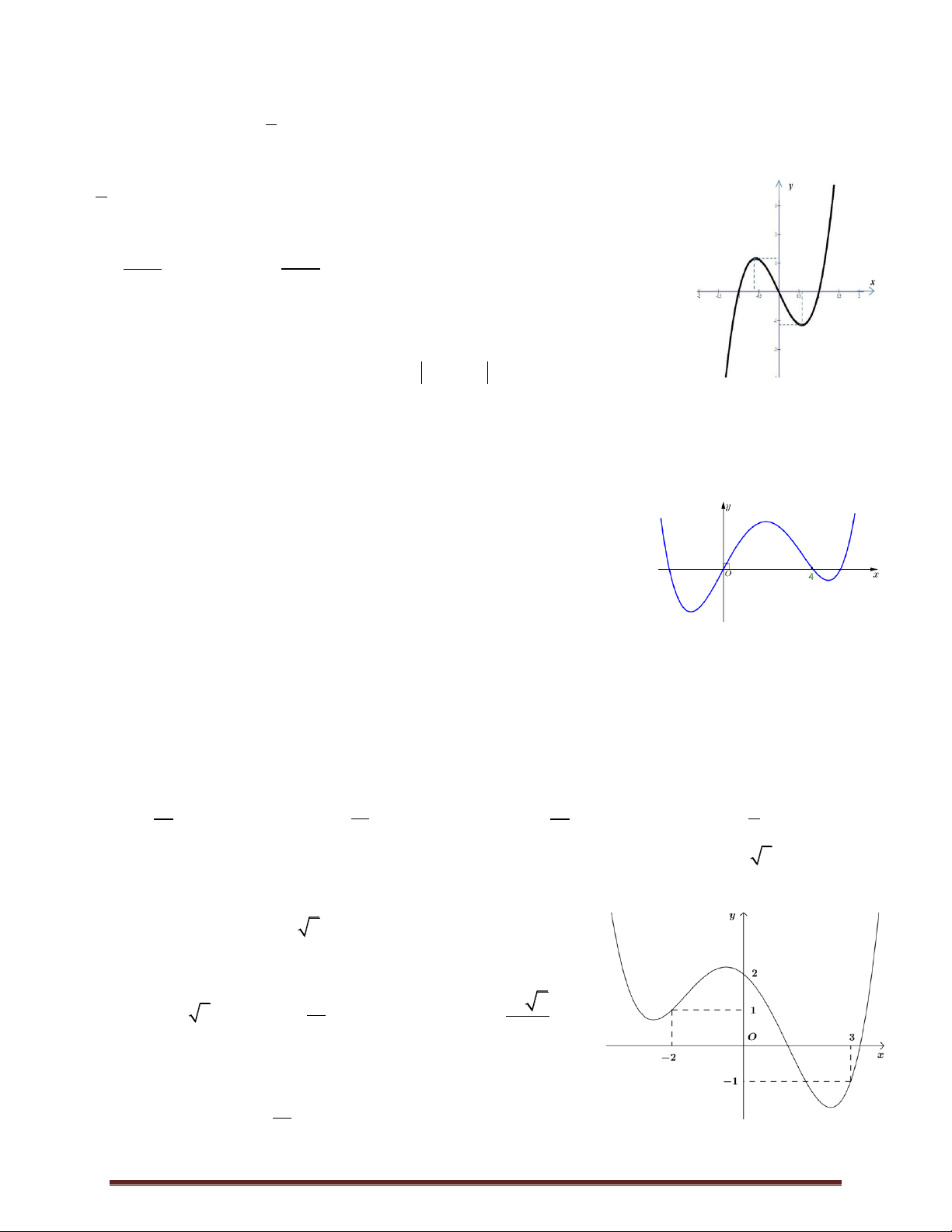
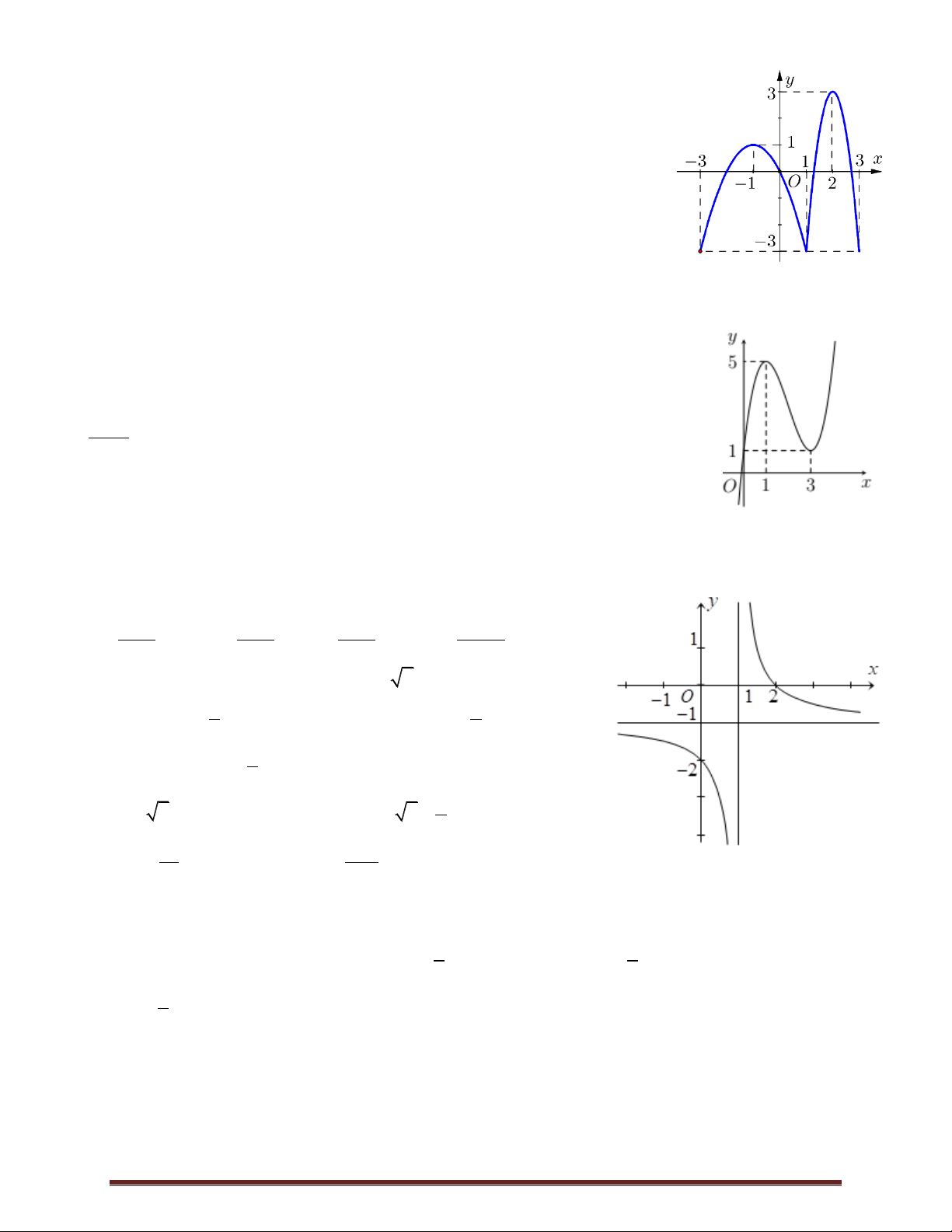
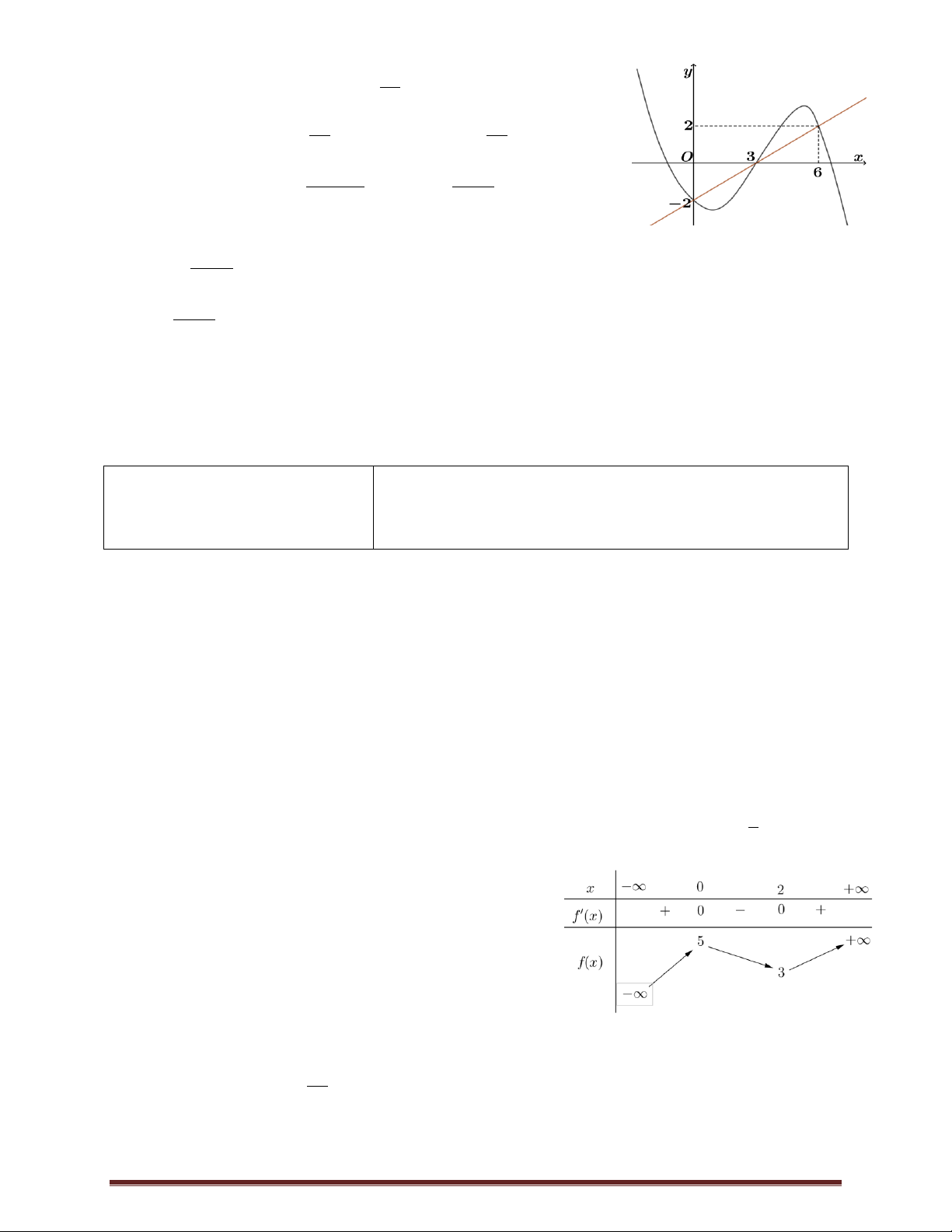
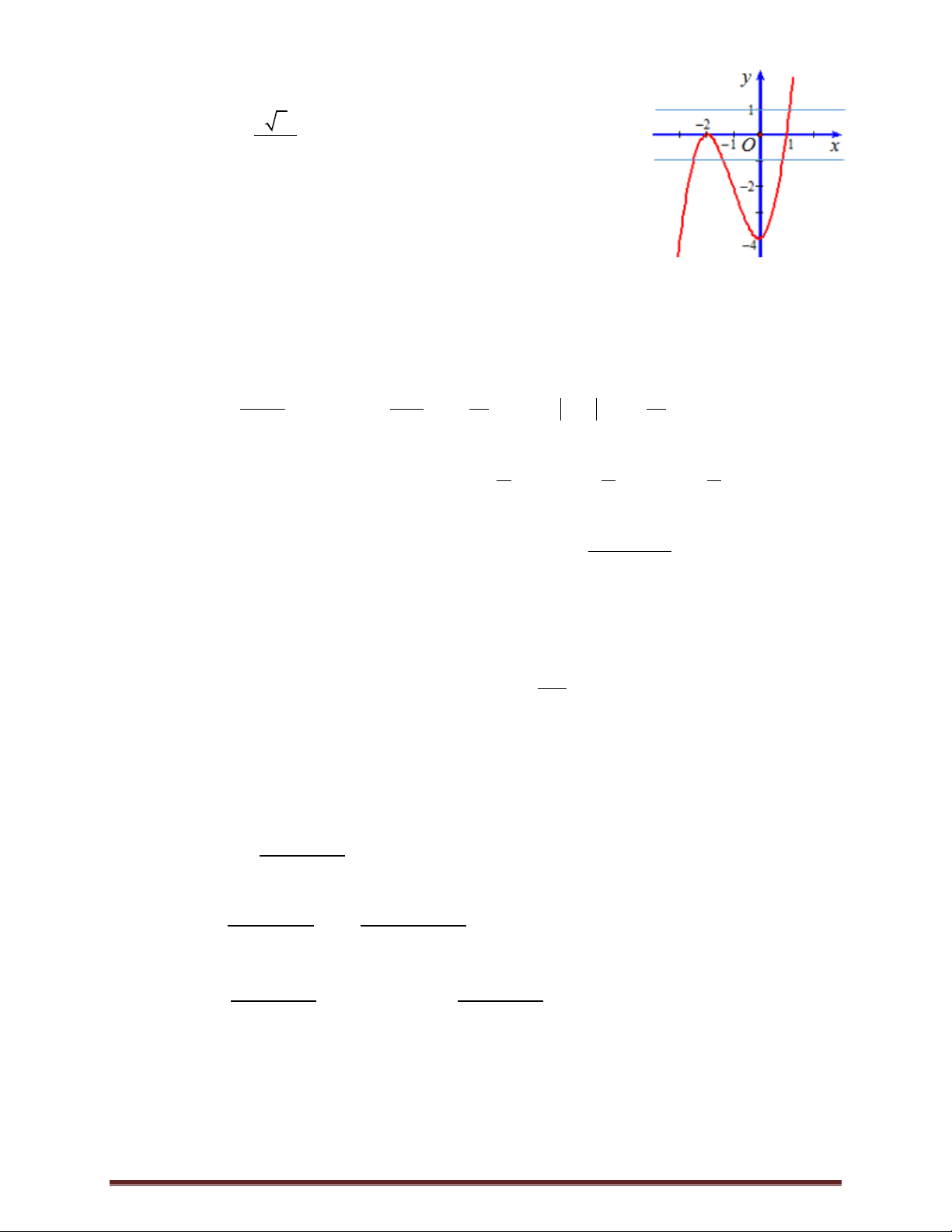
Câu 23. Cho hàm số bậc ba f  x có đồ thị như hình vẽ. Số giá trị nguyên
của tham số m để phương trình f  x 1  m có 3 nghiệm phân biệt là A. 4 .
B. 5 . C. 2 . D. 3 . x  e 
Câu 24. Họ nguyên hàm của hàm số x y  e 1  là 2  cos x  Trang 3 x 1 A. x
e  tan x  C . B. x
e  tan x  C . C. e   C . D. cos x x 1 e   C . cos x  2
log  x 3x
Câu 25. Tìm tập xác định của hàm số y  e .
A. D   .
B. D  0;  3 .
C. D  3;  . D. D   ;  03;
Câu 26. Cho khối lăng trụ đứng ABC . D A B  C  D
  , có đáy là hình bình hành cạnh AB  a , AD  a 3 
, BAD  120 và AB  2a (minh họa như hình dưới đây). Thể tích của khối lăng trụ đã cho bằng 3 3 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 2 4 6
Câu 27. Gọi k và l lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số 2  x y  
. Khẳng định nào sau đây đúng x   1 x
A. k  0 ; l  2.
B. k 1; l  2.
C. k 1; l 1.
D. k  0 ; l 1. Câu 28. Cho hàm số 4 2
y  ax  bx  c , a, ,
b c    có đồ thị như hình vẽ
dưới đây. Mệnh đề nào sau đây đúng?
A. a  0 , b  0 , c  0 .
B. a  0 , b  0 , c  0 .
C. a  0 , b  0 , c  0 .
D. a  0 , b  0 , c  0 .
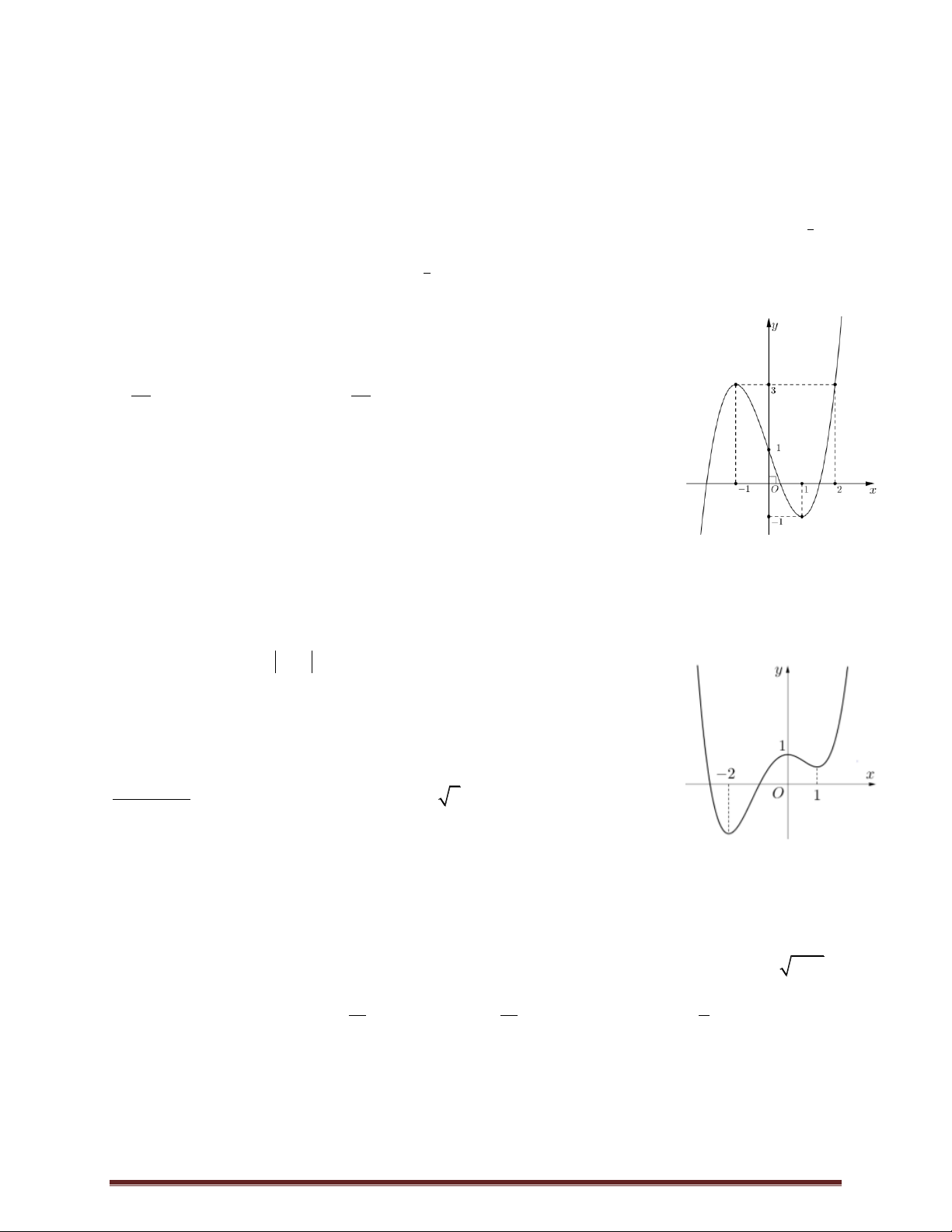
Câu 29. Hãy tính diện tích phần tô đậm trong hình vẽ dưới đây. 4 3  A. . B. . C.1. D. . 3 4 2
Câu 30. Cho z  4  2i . Hãy tìm phần ảo của số phức z  1 2i  z . 2  2 1 1 A. 6  i . B. 2  i . C. 2  . D. 6  .
Câu 31.Cho số phức z  x  yi  x, y    có phần thực khác 0. Biết số phức 2
w  iz  2z là số thuần ảo. Tập hợp các điểm biểu diễn của z là một
đường thẳng đi qua điểm nào dưới đây? A. M 0 
;1 . B. N 2;  1 .
C. P 1;3 . D. Q 1  ;1 . Trang 4 
Câu 32.Trong không gian Oxyz , cho các vectơ a  2;1; 2 ,     b  1; 1
 ;0 . Tích vô hướng a b.b bằng A. 3  . B. 1. C. 5  . D.12 . x 1 y z  2
Câu 33. Trong không gian Oxyz , cho đường thẳng  :   2  và mặt phẳng 2 1
P:2x  y  z 3  0 . Gọi Slà mặt cầu có tâm I thuộc  và tiếp xúc với P tại điểm H 1; 1
 ;0 . Phương trình của S  là 2 2 2 2 2 2
A.  x  3   y  2   z   1  36 .
B.  x  3   y  2   z   1  36. 2 2 2 2 2 2 C.  x   3
  y  2  z   1  6 . D.  x   3
  y  2  z   1  6 .
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;2;3 và song song với mặt phẳng
P: x 2y  z 3  0 có phương trình là
A. x  2 y  z  3  0 .
B. x  2 y  3z  0 .
C. x  2 y  z  0 . D.
x  2 y  z  8  0 . x  2 y z 1
Câu 35. Trong không gian Oxyz , đường thẳng d :   1 2 1
 nhận vectơ nào sau đây làm vectơ chỉ phương?   
A. u  1; 2;1 .
B. u  2; 4; 2 .
C. u  2; 4; 2 . D. 3   2   1    u  1  ;2;1 . 4  
Câu 36. Gọi S là tập hợp các số tự nhiên có 4 chữ số khác nhau. Chọn ngẫu nhiên một số từ tập S . Tìm
xác suất để số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không chứa hai chữ số nguyên nào liên tiếp nhau. 1 2 5 5 A. . B. . C. . D. . 36 3 63 1512
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D ,
AB  3a, AD  DC  .
a Gọi I là trung điểm của AD , biết hai mặt phẳng  SBI  và SCI  cùng
vuông góc với đáy và mặt phẳng SBC  tạo với đáy một góc 0
60 . Gọi M điểm trên AB sao cho
AM  2a , tính khoảng cách giữa MD và SC . a 17 a 15 a 6 a 3 A. . B. . C. . D. . 5 10 19 15 Trang 5     2 a 
Câu 38. Cho hàm số f  x có f  2  
và f  x  x sin x .Giả sử rằng cos . x f  x 2 dx     2  b c 0 a
(với a, b, c là các số nguyên dương,
tối giản). Khi đó a  b  c bằngA. 23. B. 5 . C. 20 . D. 27 . b m  1 2  x  3 1
Câu 39. Cho hàm số f (x) 
( m  0 và là tham số thực). Tập hợp m để hàm số đã 2  2
 x  3  m cho  1 
nghịch biến trên khoảng  ; 1 
 có dạng S   ;  a ;
b cd;   , với a, b, c, d là các số  2 
thực. Tính P  a  b  c  d .A. 3  .
B. 1. C. 0 . D. 2 .
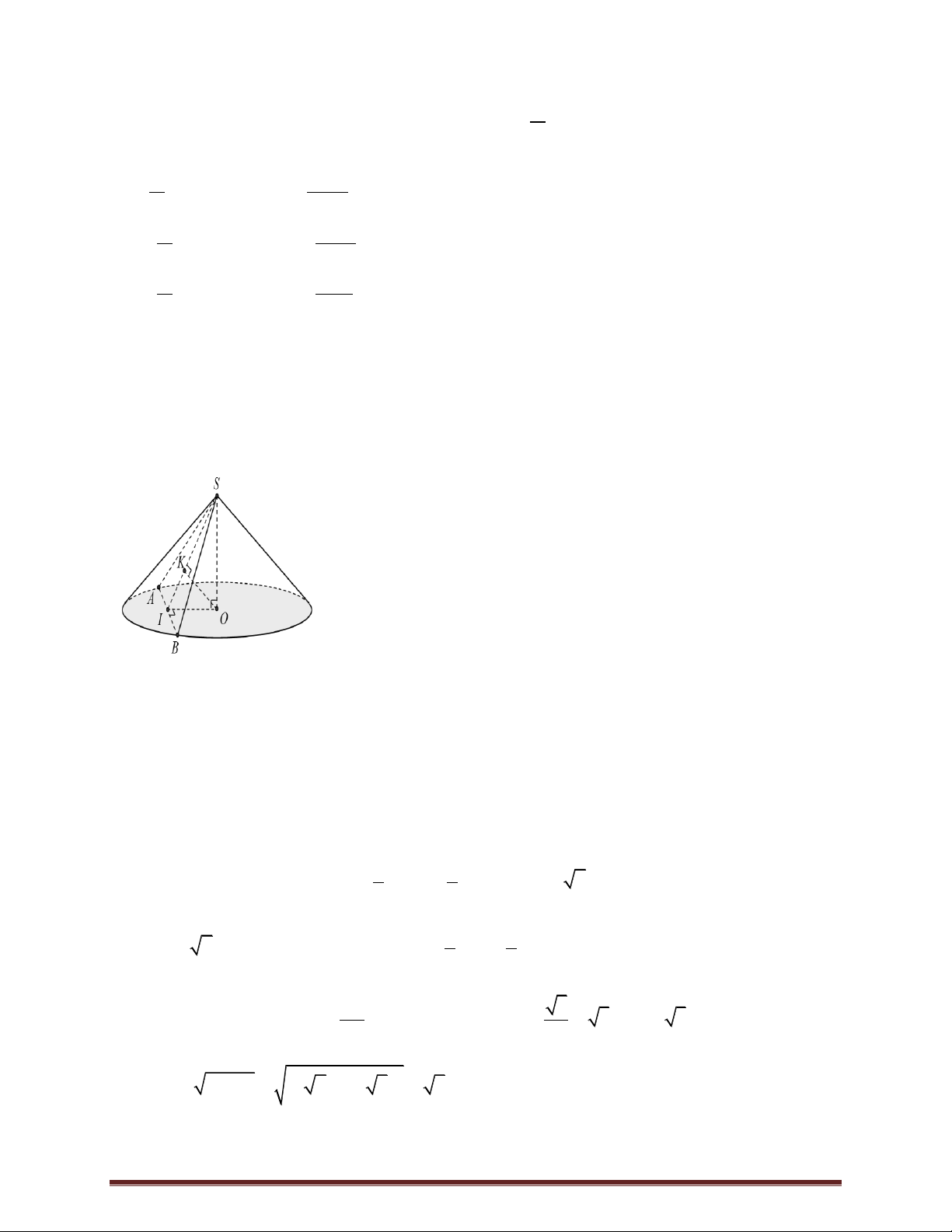
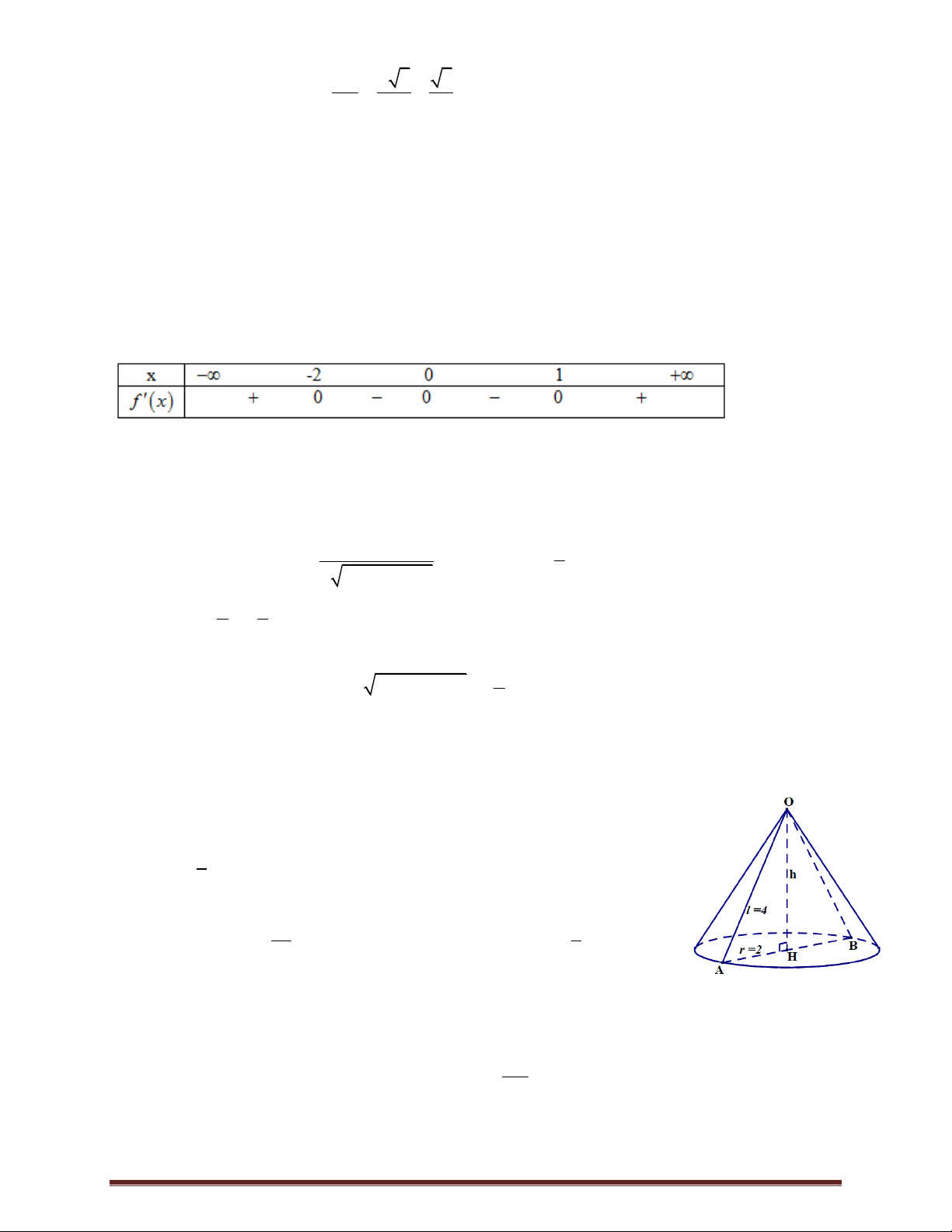
Câu 40. Cho hình nón đỉnh S có đáy là hình tròn tâm O . Một mặt phẳng qua đỉnh của hình nón và cắt
hình nón theo thiết diện là tam giác vuông có diện tích bằng 4 . Góc giữa đường cao của hình nónvà mặt
phẳng thiết diện bằng 30 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng 10 2 8 3 5 3 A. 5 . B. . C. . D. . 3 3 3
Câu 41. Cho các số thực a, b, c thuộc khoảng 1;  và thỏa mãn 2  c  2 1 log b  log . c log 
  9log c  4log b . Giá trị của biểu thức 2
log b  log c bằng:A.1.B. b b a a a  b  a b 2 .C. 2 .D. 3 .
Câu 42. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ bên.Có bao nhiêu
giá trị nguyên của tham số m thuộc đoạn 0; 20 sao cho giá trị nhỏ nhất của hàm
số g  x  2 f  x  m  4  f (x)  3 trên đoạn  2  ;2 không bé hơn 1?
A.18 . B.19 . C. 20 . D. 21 .
Câu 43. Cho phương trình 2
log x  4 log x  5  m log x 1 với m là tham 3 3  3 
số thực. Tìm tất cả các giá trị của m để phương trình có nghiệm thuộc 27; .
A. 0  m  2 . B. 0  m  2 .
C. 0  m 1.
D. 0  m 1.
Câu 44. Cho hàm số f  x có đạo hàmliên tụctrên  thoả mãn       2   1 x f x f x x e và f 0  2  .
Tổng tất cả các nghiệm thực của phương trình f  x  0 có giá trị làA. 2  . B. 2 . C.1. D. 1. Trang 6 y
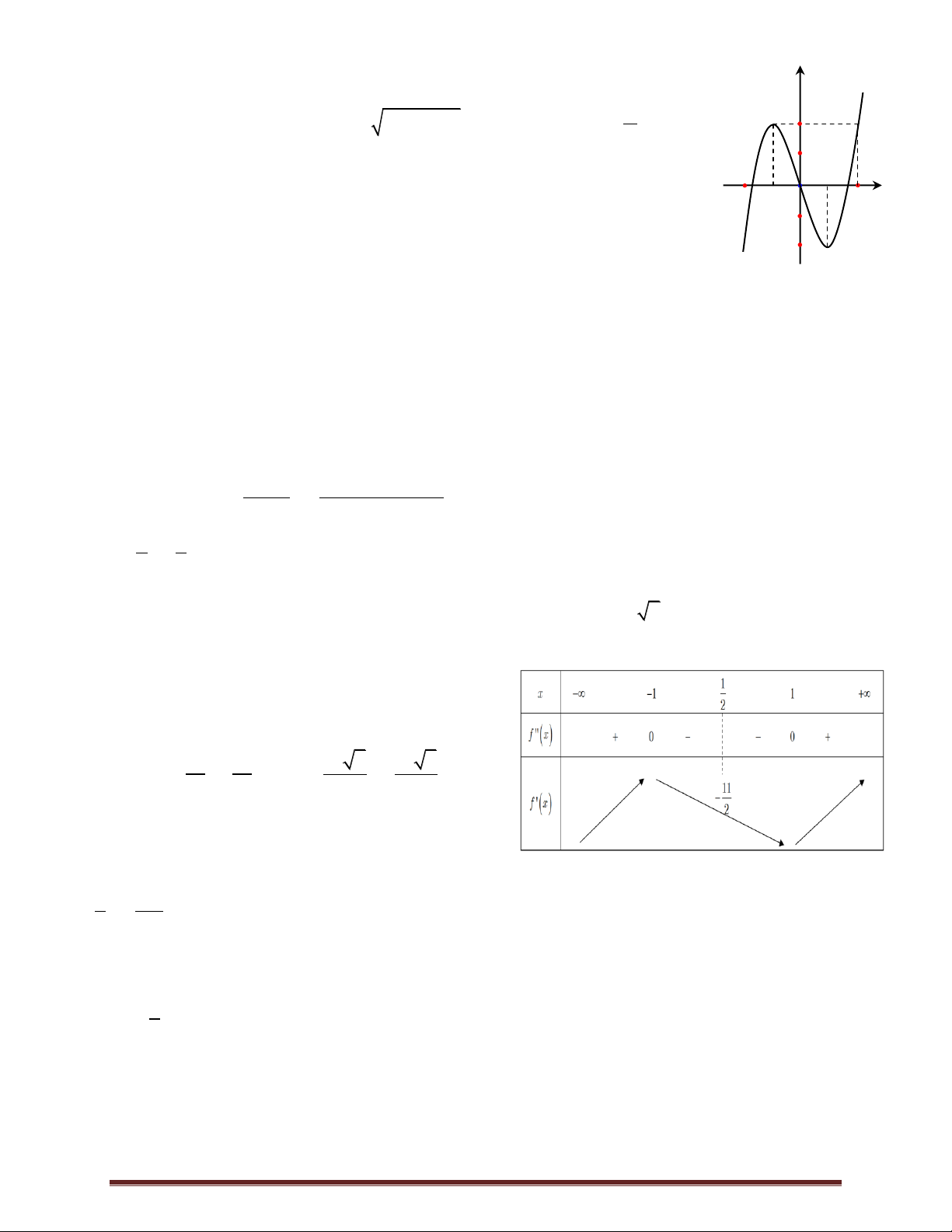
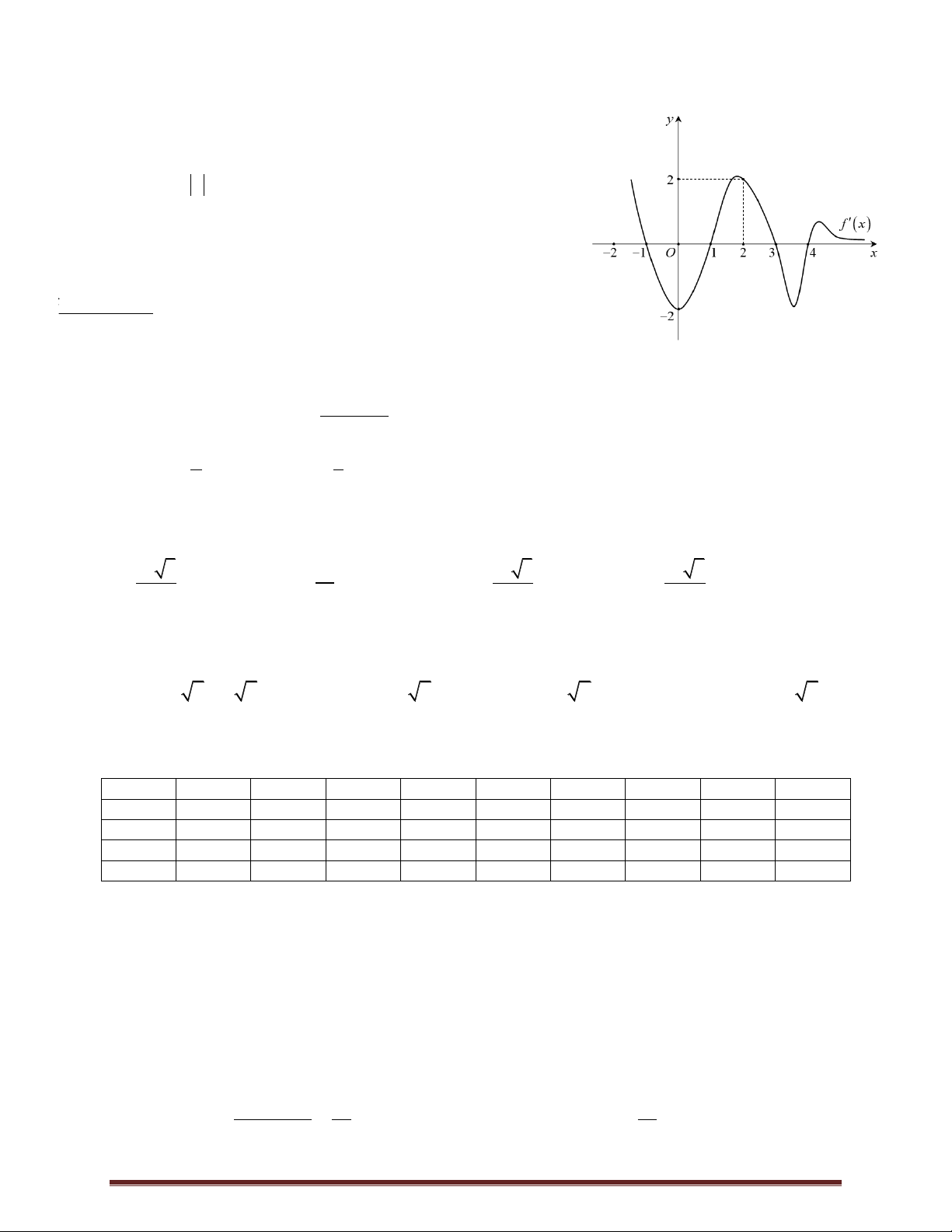
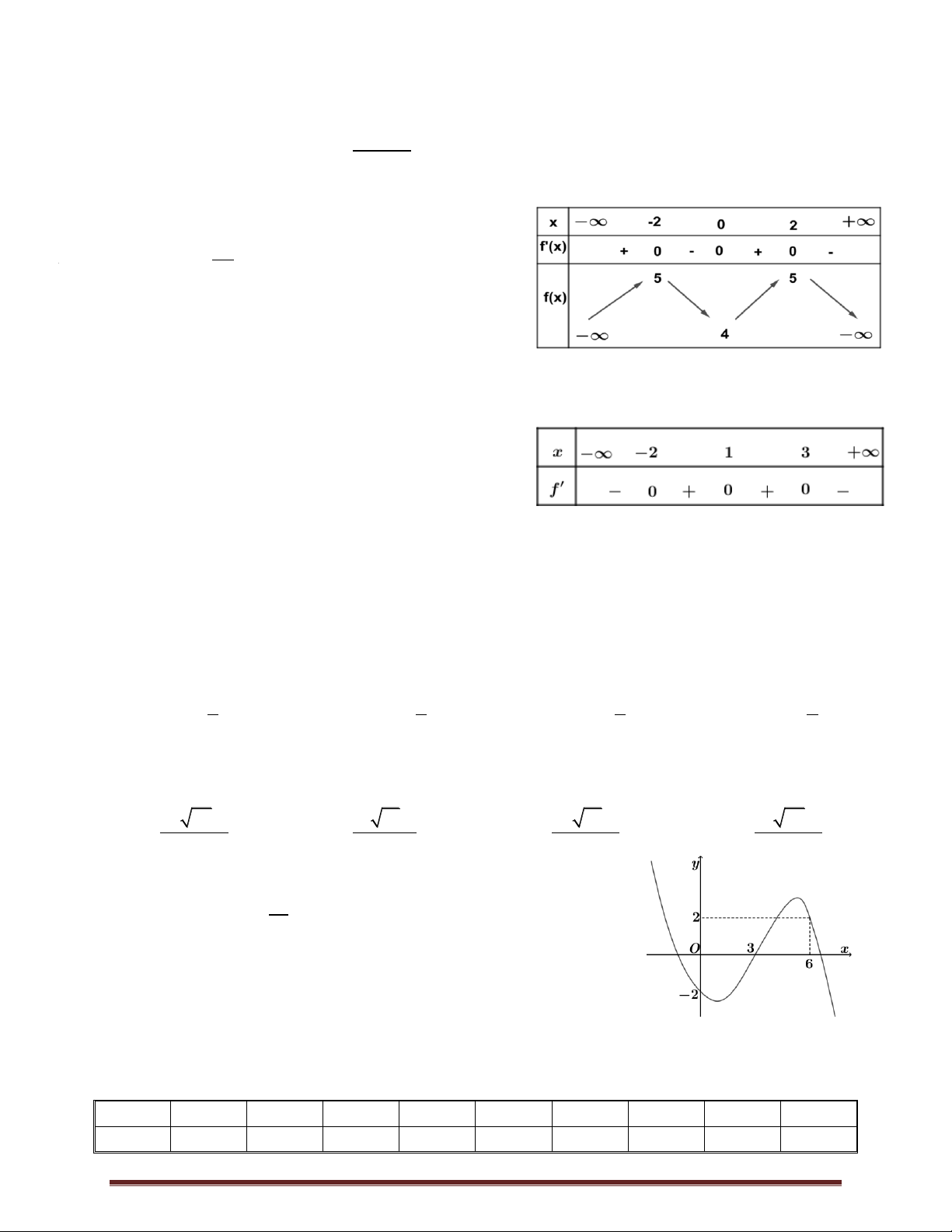
Câu 45. Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ. Tổng tất cả giá trị  
nguyên của tham số m để phương trình f  2 f cos x   m có nghiệm x  ; . 2    2  1 x
A. 1. B. 0 . C.1. D. 2  . 2 1 1  O 2 1 
Câu 46. Cho hàm số đa thức bậc bốn y  f  x , biết hàm số có ba điểm cực trị 2 x  3
 , x  3, x  5 . Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số     3 2 x 3x g x f e
 m có đúng 7 điểm cực trị A.3. B.4 . C.5. D.6
Câu 47. Có tất cả bao nhiêu cặp số a;b với a, b là các số nguyên dương thỏa mãn:
log a  b  a  b3  3 2 2 a  b
 3ab a  b 1 1.A. 2 . B.3 . C.1. D.vô số. 3   
Câu 48.Cho hàm số f  x liên tục trên  thỏa mãn 1 
 x   x  x  x  x f 1 x 4 3 2 2 4 4 2  2 f  , x   0, x  1   . Khi đó f
 xdx có giá trị làA.0.B.1  x  x 1  1 3 .C. .D. . 2 2 
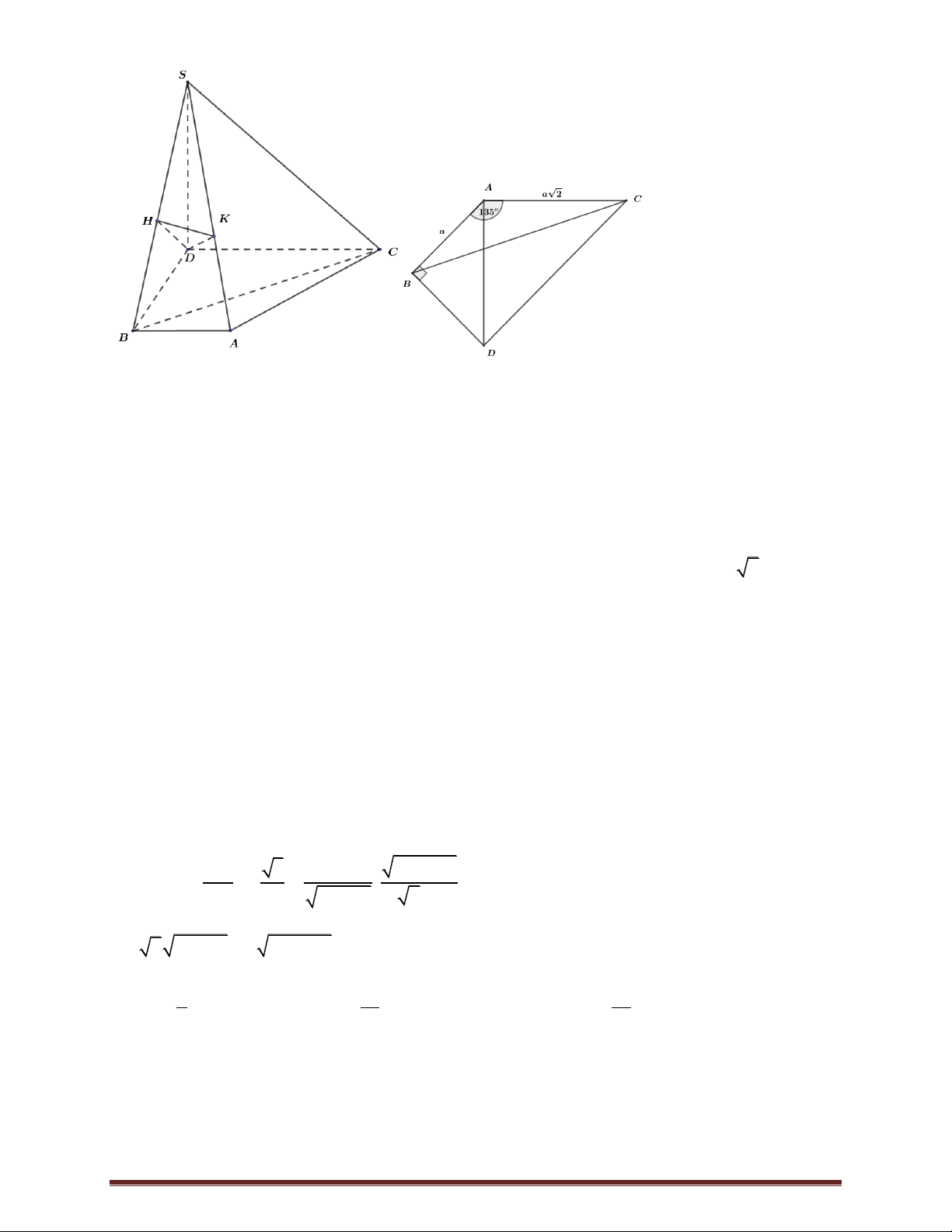
Câu 49. Cho hình chóp S.ABC , đáy là tam giác ABC có AB  ;
a AC  a 2 và CAB  135 , tam giác SAB
vuông tại B và tam giác SAC vuông tại A . Biết góc giữa hai
mặt phẳng SAC  và  SAB bằng 30 . Tính thể tích khối 3 a 3 a 3 a 6 3 a 6
chóp S.ABC .A. .B. . C. .D. . 6 3 3 6
Câu 50. Cho hàm số y  f  x và f  x  0, x   . Biết
hàm số y  f  x có bảng biến thiên như hình vẽ và  1  137 f    .  2  16 2   
Có bao nhiêu giá trị nguyên của m  2  020; 202 
0 để hàm số g  x x 4mx 5  e
. f  x đồng biến trên  1  1  ;  .  2  A. 4040 . B. 4041. C. 2019 . D. 2020 . BẢNG ĐÁP ÁN Trang 7 1.D 2.A 3.B 4.C 5.B 6.D 7.D 8.D 9.B 10.D 11.A 12.C 13.A 14.B 15.C 16.A 17.C 18.B 19.C 20.D 21.B 22.A 23.D 24.B 25.B 26.A 27.A 28.B 29.A 30.C 31.D 32.C 33.C 34.C 35.C 36.D 37.B 38.D 39.A 40.D 41.A 42.B 43.D 44.D 45.D 46.D 47.A 48.A 49.A 50.D
HƯỚNG DẦN GIẢI CHI TIẾT ĐỀ
Câu 1.Chọn D.Để chọn được một đôi song ca gồm một nam và một nữ ta thực hiện liên tiếp 2 công đoạn:
Công đoạn 1: Chọn 1 học sinh nam từ 20 học sinh nam  có 20 cách chọn.
Công đoạn 2: Chọn 1 học sinh nữ từ 25 học sinh nữa  có 25 cách chọn.
Theo quy tắc nhân ta có 20.25  500 cách chọn.
Câu 2.Chọn A.Số hạng tổng quát của cấp số cộng có số hạng đầu u và công sai bằng d là 1
u  u  n 1 d . n 1  
Vậy u  u  4d  2  4.3  14 . 5 1
Câu 3.Chọn B.Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r là S  2rl . xq
Câu 4.Chọn C.Dựa vào bảng biến thiên, hàm số nghịch biến trên khoảng 1;  1 .
Câu 5.Chọn B.Thể tích của hình hộp đã cho là 2 3 V  .
B h  a .3a  3a .   Câu 6.Chọn D.Ta có 4 x 8 4 x 8 0 2020  1  2020
 2020  4x  8  0  x  2 .
Vậy phương trình đã cho có nghiệm x  2 . 2 2 2
Câu 7.Chọn D.Ta có 2 f
 x gxdx 13   2. f
 xdx g
 xdx 13 1 1 1 2 2 2 2  g
 xdx 132. f
 xdx  g
 xdx 132.5  g
 xdx 3. 1 1 1 1 2 Vậy g
 xdx  3. 1
Câu 8.Chọn D.Dựa vào bảng biến thiên ta thấy điểm cực đại của đồ thị hàm số là A0 ;  3 do đó chọnD. Trang 8 Câu 9.Chọn B
+) Từ đồ thị hàm số trên, ta thấy đồ thị là dạng của hàm bậc ba nên loại đáp án A, C
+) Từ đồ thị hàm số trên, ta thấy giới hạn của hàm số khi x   là  nên hệ số của 3 x dương, loại đáp án D Vậy B là đáp án đúng. 1 1
Câu 10.Chọn D.Với a là số thực dương tùy ý, ta có 2 log a  log a  log a . 3 3 3 2
Câu 11.Chọn A.Ta có f
 x x   2 x  x  2 3 d sin 6 dx  sin d
x x  2 3x dx   cos x  2x  C   .
Câu 12.Chọn C.Số phức z  3
  4i có số phức liên hợp là z  3   4i .
Vậy số phức z có phần thực bằng 3  và phần ảo bằng 4  .
Câu 13.Chọn A.Theo lý thuyết ta có : hình chiếu vuông góccủa điểm M  ;
x y; z  lên mặt phẳng Oyz là M 0; ;
y z  suy ra hình chiếu vuông góc của điểm A1;2;3 trên mặt phẳng Oyz có tọa độlà 0;2;3 . 2 2
Câu 14.Chọn B.Ta có S   x     y   2 : 1 2
 z 11 nên tọa độ tâm mặt cầu là 1;2;0 .
Câu 15.Chọn C.Mặt phẳng ax  by  cz  d  0 có các vectơ pháp tuyến dạng
n  ka;kb;kc,k ,k  0. 
Suy ra   có một vectơ pháp tuyến là n   2  ;0; 3 .
Câu 16.Chọn A.Từ phương trình đường thẳng d ta thấy đường thẳng đi qua điểm M 1;3;0  .
Câu 17.Chọn C.Do SA   ABCD nên hình chiếu của SO lên mặt phẳng
ABCD là AO. Khi đó góc giữa đường thẳng SO và mặt phẳng ABCD  là góc SOA . 3 3 a 6 ABD 
đều cạnh a 2 nên AO  AB  a 2.  . 2 2 2 3a 2 a 6 S
 OA vuông tại A có SA  , AO  nên 2 2  SA 3a 2 a 6  tan SOA   :
 3  SOA  60 . OA 2 2
Vậy góc giữa đường thẳng SO và mặt phẳng  ABCD bằng 60 . Trang 9
Câu 18.Chọn B.Căn cứ vào bảng xét dấu của f  x ta thấy f  x đổi dấu từ âm sang dương tại các điểm x  1 
và x 1 nên hàm số đã cho có 2 điểm cực tiểu.
Câu 19.Chọn C.Hàm số f  x 4 2
 x 10x 1 xác định trên  3  ;2. x  0  3  ;2 
Ta có f  x 3
 4x  20x . f x  0  x  5  3  ;2 .  x   5    3  ;2 f   3  8
 ; f  5  2
 4; f 0 1; f 2  2  3.
Vậy giá trị nhỏ nhất của hàm số trên đoạn  3
 ;2 bằng 24 tại x   5 . 1
Câu 20.Chọn D.Ta có log a  log  2 a b  log a  log  2 a
b  3log a  log  2 a b 3 3  3 3  3 27  3 3  log a  log  2 a b 3 2
 a  a b  a  b 2  a  b . 3 3  2 log x log x Câu 21.Chọn B 9 9 9  x  18   1 . log x Điề x x x x log x log x
u kiện x  0 .   log .log log 9 9 9 1  9  x  18   log  9 9 9 9  x  18 9  2x 18 log9 x  x  9  log .
x log x  log 9  log x 1  1   log x  1 1 
 x  9 (thỏa mãn). 9 2 9 9 9 9 9 1 
Vậy tập nghiệm của bất phương trình đã cho là S  ;9   . 9 
Câu 22.Chọn A.Gọi I là tâm mặt cầu  S  , J là tâm đường tròn T  , A
là điểm thuộc đường tròn T  I
Có bán kính đường tròn T  là r  JA, IJ  3.Có chu vi đường tròn T 
là P  2 r 12  r  6 . J A
Gọi R là bán kính mặt cầu thì 2 2
R  r  IJ  3 5 .
Diện tích mặt cầu  S  là 2
S  4 R  180 . Vậy S 180 .
Câu 23.Chọn D.+) Ta có f  x 1  m  f  x  m 1  * . Trang 10
+) Số nghiệm của phương trình * bằng số giao điểm của đồ thị hàm số y  f  x và đường thẳng y  m 1 .
+) Từ đồ thị ta có, đường thẳng y  m 1 cắt đồ thị hàm số y  f  x tại 3 điểm phân biệt khi và chỉ khi 1
  m1 3  0  m  4 .
+) Vì m nên m 1 ; 2 ;  3 .
Vậy có 3 giá trị nguyên của tham số m thỏa mãn đề bài. x  e    x x 1
Câu 24.Chọn B.Ta có e  1 dx  e  d x
x  e  tan x  C   . 2 2  cos x   cos x 
Câu 25.Chọn B.+ Điều kiện xác định: 2
x  3x  0  0  x  3 .
Vậy tập xác định của hàm số là D  0;3 .  3
Câu 26.Chọn A.Diện tích hình bình hành ABCD là 2 S  . AB . AD sin BAD  a . ABCD 2
Tam giác ABB vuông tại B có 2 2 BB 
AB  AB  a 3 . 3 3 3 Vậy 2 3 V         BB .S a 3. a a . ABCD. A B C D ABCD 2 2
Câu 27.Chọn A.Tập xác định D  0; 2 \   1 .
+ Do tập xác định của hàm số là D  0; 2 \  
1 nên không tồn tại giới hạn của hàm số khi x   , do
đó đồ thị hàm số không có tiệm cận ngang. 2  x 2  x
+ lim f  x  lim
  ; lim f x  lim
  , suy ra x 1 là tiệm cận đứng    x 1  x 1    x   1 x x 1  x 1   x   1 x của đồ thị hàm số. 2  x
+ lim f  x  lim
  , suy ra x  0 là tiệm cận đứng của đồ thị hàm số.   x0
x0  x   1 x
Do đó đồ thị hàm số không có đường tiệm cận ngang và có hai đường tiệm cận đứng.
Vậy k  0 ; l  2. Câu 28.Chọn B
+ Dựa vào hình dáng đồ thị ta có a  0 .
+ Đồ thị hàm số có ba điểm cực trị suy ra a, b trái dấu, mà a  0 suy ra b  0 . Trang 11
+ Đồ thị cắt trục tung tại điểm có tung độ âm, suy ra c  0 .
Vậy a  0 , b  0 , c  0 .
Câu 29.Chọn A.Cách 1: Ta có 2 x 1  0, x   1   ;1 . 1 1
Do đó diện tích phần tô đậm là 2 S  x 1dx     2 1 x dx 1 1 1 3  x   4  x    .  3  3 1  2
Cách 2: Công thức nhanh tính diện tích S  Bh 3 2 2 4
Áp dụng công thức với B  2 , h 1 ta có: S  Bh  .2.1  . 3 3 3
Câu 30.Chọn C.Ta có z  1 2i2  z  3
  4i  4 2i 1 2i .Vậy phần ảo của số phức z là 2  . 2 1 2
Câu 31.Chọn D.Ta có z  x  yi  ,
x y   ; x  0 2 Mặt khác 2
w  iz  z  i  x  yi   x  yi   x  xy   2 2 2 2 2
x  y  2 y i .
x  0 kh«ngtháa m·n ®iÒu kiÖn 
Vì w là số thuần ảo nên x  xy  0   .
y 1 0 (tháa m·n ®iÒu kiÖn)
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình y 1  0 (trừ điểm M 0  ;1
), do đó đường thẳng này đi qua điểm Q 1  ;1 .     
Câu 32.Chọn C.Ta có a  b   3
 ;2;2  ab.b  5  . Câu 33.Chọn C Trang 12 x 1 2t x 1 y z  2 
Phương trình đường thẳng  :  
được viết lại là  :  y  2t , t  . 2  2 1  z  2t 
Theo giả thiết I    I 1 2t ; 2t ; 2  t    . 
Ta có HI  2t; 2t 1;t  2 . 
Mặt phẳng  P có một vectơ pháp tuyến là n  2; 1   ;1 .  
Vì mặt cầu  S  tiếp xúc với  P tại điểm H nên HI và n cùng phương.   2t 2t 1 t  2
 t  2t 1
Ta có HI và n cùng phương khi và chỉ khi     2 1  1 2t 1  t   2  t  1   I 3; 2  ;  1 . 2 2 2
Bán kính mặt cầu  S  là : R  IH  1 3  1 2  0 1  6 . 2 2 2
Vậy phương trình mặt cầu  S  là :  x   3
  y  2 z   1  6 .
Câu 34.Chọn C.Gọi Q là mặt phẳng đi qua điểm M 1;2;3 và song song với mặt phẳng  P . 
Vì Q //  P nên Q nhận vectơ pháp tuyến n  1; 2  ;   
1 của mặt phẳng  P làm vectơ pháp P tuyến.
Phương trình của mặt phẳng Q là:1. x  
1  2. y  2 1. z  3  0  x  2y  z  0 .
Vậy phương trình mặt phẳng Q : x  2y  z  0 . Câu 35.Chọn C 
+) Đường thẳng d có một vectơ chỉ phương là u  1;2;  1 . d    Mà u  2
 u suy ra u  2;4;2 cũnglà một vectơ chỉ phương của đường thẳng d . 3   3 d
Câu 36.Chọn D.Xét phép thử: “ Chọn ngẫu nhiên một số từ tập S ”.
Số phần tử của không gian mẫu là: n  3  9.A  4536 . 9
Gọi A là biến cố: “ Số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không chứa hai chữ số
nguyên nào liên tiếp nhau”.
Gọi số được chọn là abcd .
+) Vì chữ số sắp xếp theo thứ tự tăng dần nên: 1 a  b  c  d  9 . Trang 13
+) Trong số được chọn không chứa hai chữ số nguyên nào liên tiếp nhau nên:
1 a  b 1 c  2  d 3  6 .
Đặt: a  a ; b  b 1; c  c  2 ; d  d  3 . 1 1 1 1
Khi đó: 1  a  b  c  d  6 . 1 1 1 1
Số cách chọn bộ bốn số a ;b ;c ; d là: 4 C (cách)  có 4
C cách chọn a ; b ; c ; d . 1 1 1 1  6 6 Mỗi cách chọn  ; a ; b ;
c d  chỉ có một cách sắp xếp thỏa mãn yêu cầu bài toán nên tạo ra một số. Suy ra: n A 5 n  A 4
 C 15 .Xác suất cần tìm là: P A     6 n  1512 Câu 37. S A 2a M a B I H D C K E
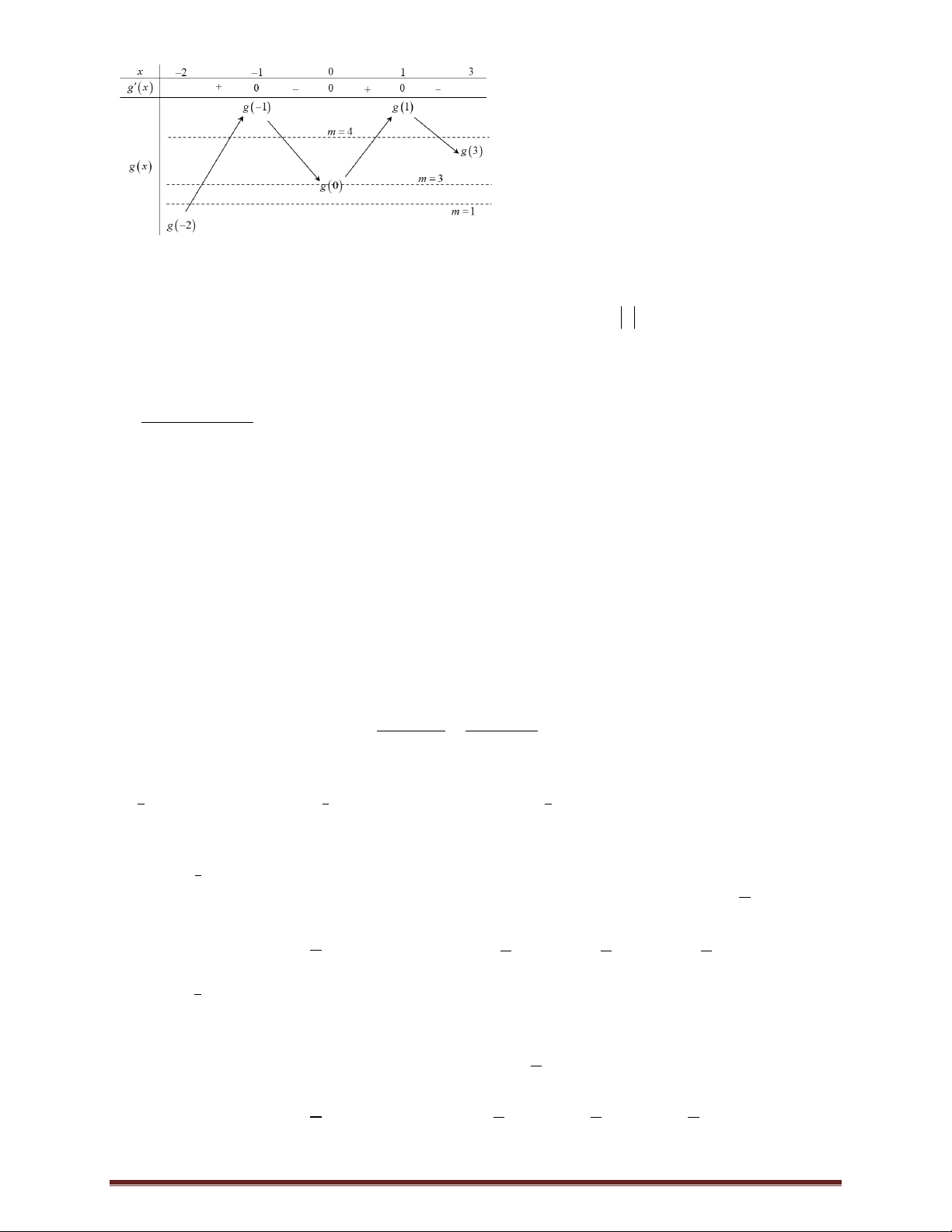
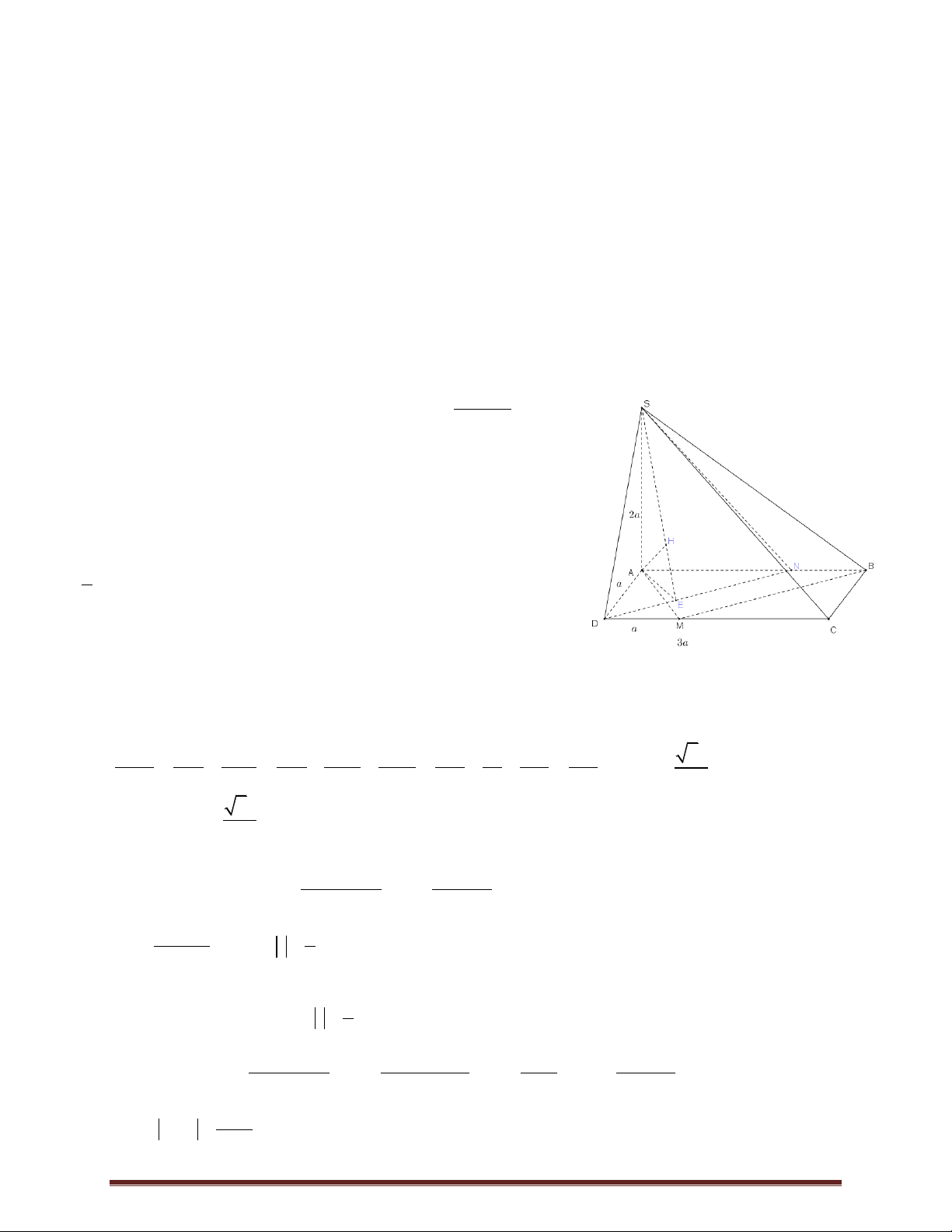
SBI  (ABCD) 
Chọn B+) Theo giả thiết ta có 
 SCI   (ABCD)  SI  (ABCD) SI  
SBI SCI  +) Vẽ       IK BC BC
SIK  SKI là góc giữa mặt phẳng SBC  với mặt đáy nên  SKI  60 . 2 2 1 a 3a +) Vì S  DI.DC  , S  . Suy ra S  S S  S  a . B  IC ABCD  ICD I  AB  2 - I  DC  2 4 IAB 4 1 2a 5 +) Mặt khác BC   AB CD2 2
 AD  a 5 và S
 IK.BC. Suy ra IK  I  BC 2 5 2a 15
+) Trong tam giác vuông SIK ta có SI  IK.tan 60  . 5
+) Vì AM  2a nên BM  a  MD // BC , do đó d MD , SC   d MD ,SBC   d D ,SBC . ED DC 1 1
+) Gọi E là giao điểm của AD với BC , ta có 
  ED  AD  ID . EA AB 3 2 1
Do đó d D ,SBC   d I ,SBC  . 2
+) Gọi H là hình chiếu của I lên SK ta có d  I , SBC  IH . 1 1 1 5 5 5 a 15
Trong tam giác vuông SIK , ta có:       IH  . 2 2 2 2 2 2 IH SI IK 12a 4a 3a 5 a
Vậy d MD SC  15 ,  . 10
Nhận xét: Để tính và , ta có thể làm như sau: Trang 14 AI.AM .2 a a 2a 1) Tính
: Ta có IK  d (I , BC)  d ( ; A DM )    . DM a 5 5 a a a 2) Tính : Ta có  2 15
IH  IK.sin SKI  .sin 60   . 5 15 15
Câu 38.Chọn D.Do f  x  x sin x nên f  x  f 
 xdx  xsin d x x   d x cos x   
xcos x  cos d x x 
 xcos x sin x C .    Theo giả thiết f
 2 1 C  2  C  1  
.Suy ra f  x  sin x  x cos x 1.  2     2 cos . x f  x 2 dx  cos x 
sin x  xcos x   2 1 dx   2
sin x cos x  x cos x  cos xdx 0 0 0        2 2 1 1 2 2  1 1 1 sin 2 d x x  x   1cos2x 2 dx  cos d x x 
  cos 2x 2  sin x 2  d x x  d x sin 2x   2 2 4 2 4 0 0 0 0 0 0 0     2 2 2 2 1 x 1 1 3  1 7   1 2  x sin 2x 2  sin 2 d x x    cos 2x 2    . 2 4 4 4 2 16 8 4 16 0 0 0 0
Vậy a  7, b  4, c  16 . Suy ra a  b  c  27 .  3 x   2
Câu 39.Chọn A.Điều kiện xác định:  . 2  2  x  3   0  m 1   1  Đặt u  2
 x  3  u   0, x    ; 1 
 , suy ra hàm số u  2
 x  3 nghịch biến trên 2  x  3  2   1   1  khoảng  ; 1 
 .Với x  ; 1  u    1; 2 .  2   2  m  u 
Yêu cầu bài toán trở thành tìm m để hàm số g u   1 1 
đồng biến trên khoảng 1; 2. 2 u   m 2 m  11 2 m
Ta có gu   , u  . 2  2  m u      m  Trang 15
gu  0, u  1; 2 
Hàm số g u đồng biến trên khoảng 1; 2 khi và chỉ khi  2  1; 2 m  2  m  2   m   1 1  0   0  m 0   m  m 0  m  m  2   m  2   2 m  2         m 2 1     0   m  2    0  m 1  . m  m   m  2   m  0 m  2  2       m 1    2  m 1   0      m   m 0 m 1  Vậy S   ;   2 0; 
1  2;     a  2; b  0; c  1; d  2 . Do đó P  2  012  3  . Câu 40.Chọn D
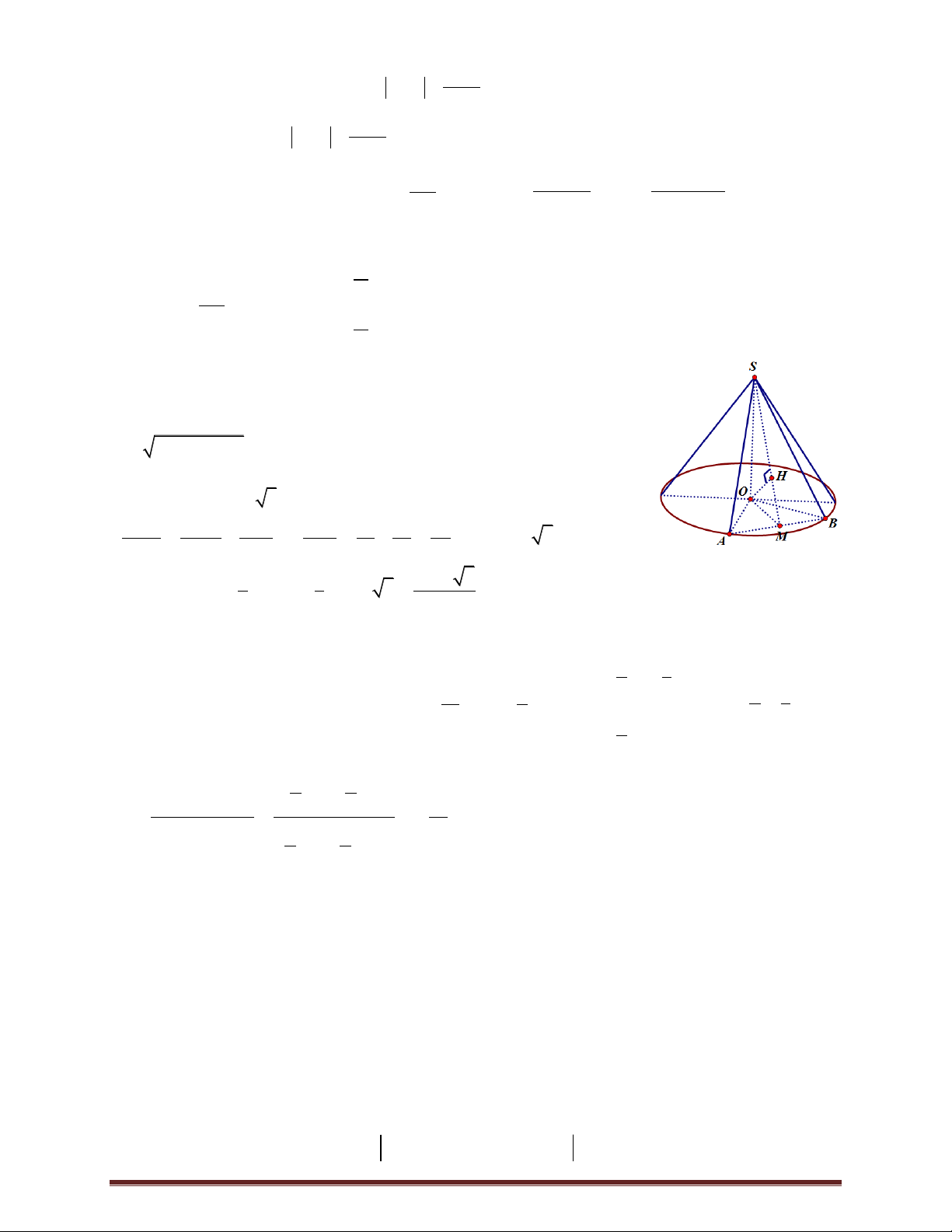
Mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông SAB .
Gọi SA  l là đường sinh, OA  R là bán kính và SO  h là đường cao của hình nón đã cho.
Gọi I là trung điểm của AB và K là hình chiếu của O lên SI . 
Góc giữa đường cao của hình nón và mặt phẳng thiết diện là  SO SAB   ;  OSK  30 . 1 1 S
 AB vuông cân tại S nên 2 2 S
 .SA  l  4  l  2 2 .  SAB 2 2  1 1
AB  l. 2  4  Đường trung tuyến SI  .AB  .4  2 . 2 2 SO S
 OI vuông tại O :  3 cos OSI 
 SO  SI.cos30  2.  3  h  3 . SI 2 2 2 Ta có: 2 2
R  l  h  2 2   3  5 . Trang 16 1 1 5 3
Vậy thể tích của khối nón là 2
V   R h  .5. 3  . 3 3 3 Câu 41.Chọn A 2  c  Ta có: 2 log b  log . c log 
  9log c  4log b b b a a a  b  2  4log b  log .
c 2log c  log b  9log c  4log b a b b b a a log b  x 2 2
 4log b  2log c  log c  9log c  4log b * .Đặ a t 
( x, y  0 vì a, , b c  1 ). a b b a a  log c  y  b Ta có log c  log .
b log c  xy ..Thay vào * ta được: 2 2
4x  2 y  y  9xy  4x a a b
4x  y  0  ¹ lo i 2 2
 4x  xy 8xy  2y 4x  y  0  4x  yx  2y   1  0   . x  2y 1 Vậy 2
log b  log c  log b 2log c  x 2 y 1  . a b a b
Câu 42.Chọn B.Dựa vào hình vẽ ta có: 2
  f (x)  2, x   2  ;2 * .
 2 f x  4  0, x   2  ;2.
Vì m 0; 20 nên 2 f  x  m  4  0
suy ra 2 f  x  m  4  2 f  x  m  4, x   2  ;  2 .
Ta có: g  x  2 f  x  m  4  f (x)  3  2 f  x  m  4  f  x  3  f  x  m 1 , x   2  ;2 .
+) Với m  0  g  x  f  x 1 , x   2  ;2.   *  1
  f x 1 3, x   2
 ;2. 0  f x 1  3, x   2  ;2
 0  g x  3, x   2  ;2.
 min g x  0  m  0 không thỏa yêu cầu bài toán.  2  ;2
+) Với m 1; 20  f  x  m 1  0  g  x  f  x  m 1.
Từ * ta có: f  x  m 1  m 1  min g  x  m 1.  2  ;2
Yêu cầu bài toán: min g  x  1  m 11  m  2  m 2; 20 .  2  ;2
Vậy có 19 giá trị nguyên của tham số m thỏa yêu cầu bài toán. Trang 17
Câu 43.Chọn D.Đặt t  log x , với x  27  t  3 . 3 t   1  Phương trình trở thành 2
t  4t  5  m t  
1 . * Điều kiện xác định:  . t   5 2     +) Với t 4t 5 0
m  0 thì phương trình vô nghiệm, do  , t   5. t  1 0 t    loaïi
+) Với m  0, ta có 2
t  4t  5  0  1 ( ) .  t
  5 (thoûa maõ ) n
+) Với m  0 thì    t  t   m t  2 2 2 * 4 5 1   2
 m  2t  2 m   2 1 2
4 t  5  m  0 . (**)
Nếu m 1 t  1  không thỏa mãn. t  1  (loaïi) Nếu 
m  1, ta có (**)  t    2   m  2 1 1
t  m  5  0    2 m  5  . t  2  1 m 2 2 m  5 6m
Do đó, phương trình đã cho có nghiệm   5   0  1
  m  1, kết hợp m  0 suy 2 2 1 m 1 m ra 0  m 1.
Vậy với 0  m 1 thì phương trình đã cho có nghiệm thuộc [27;  ) . 
Câu 44.Chọn D.Ta có
      2   1 x f x f x x e   
     . x f x f x e  2x 1 
  . x   .   x f x e f x
e   2x 1    .   x
f x e   2x 1
 f x x e
  x  x  f x x 2 . 2 1 d .e
 x  x  C (1). Do f 0  2  nên từ (1) ta có 0 2 2.
 e  0  0  C  C  2  . x 
Khi đó     2   2. x f x x x
e . f  x    2
x  x   x 2 0
2 .e  0  x  x  2  1 0   . x  2 
Vậy tổng tất cả các nghiệm thực của phương trình f  x  0 là 1 2  1  .  
Câu 45.Chọn D+) Đặt t  cos x , do x  ; 
 nên suy ra t  1  ;0.  2  Trên khoảng  1
 ;0 hàm số nghịch biến nên suy ra Với t   1
 ;0 thì f 0  f t  f  
1 hay 0  f t   2. Trang 18
+) Đặt u  2 f cos x thì u  2 f t ,u 0;2. Khi đó bài toán trở thành:
Tìm m để phương trình f u  m có nghiệm u 0;2.
Quan sát đồ thị ta thấy rằng với u 0;2 thì f u 2  ;2  2   m  2.
Vì m    m  2  ; 1  ;0; 
1 . Vậy có 4 giá trị của m.
Tổng các giá trị của m thỏa mãn yêu cầu bài toán là 2  . 3 2 3 2  
Câu 46.Chọn D.Ta có     2 
 x 3x  x 3 3 6 . x g x x x e f e  m   x  0 x  0   x  2   x  2          3 2  x  x  3 2 2 3 x 3 3 2 0 3 6 . x g x x x e f e  m  3 2 0 x 3x   e  m  3 x 3x   e  m  3 ,  1 .  3 2  x 3x 3 2 e  m  3 x 3x  e  m  3 , 2 3 2  x 3x e  m  5 3 2 x 3x e  m  5  , 3
Hàm số g  x có 7 điểm cực trị khi và chỉ khi tổng số nghiệm đơn và bội lẻ, khác 0 và 2  của các phương trình   1 ,2,3 là 5 .  x  Xét hàm số   3 2 x 3x h x e   có     3 2 2 3 3 6 x x h x x x e   
.Ta có h x 0  0   . x  2  Bảng biến thiên:
Khi đó có 3 trường hợp sau: Trường hợp 1: Trang 19 4 4
m  3  e
m  e  3  51,6 Khi đó:   
Do m nguyên nên m 52;53;54;55;56;5  7 . 4 4
 1 m  3  e
 4  m  e  3  57,6 Trường hợp 2: 4 4 m  5  e
m  e  5  49,6   Khi đó: 4 4 1
  m  3  e   2
  m  e  3  m .   0  m  3  1 3  m  4   Trường hợp 3: 4
 1 m  5  e 4  4
  m  e  5  49,6  
Khi đó: m  3  1  m  2  m .   m  3  0  m  3 
Vậy có 6 giá trị nguyên của tham số m thỏa yêu cầu bài toán. Câu 47.Chọn A Trang 20
Cách 1:Với a, b là các số nguyên dương, ta có:
log a  b  a  b3  3 2 2 a  b
 3ab a  b 1 1 3    3 3 a  b 3 3  log
 a  b  3aba  b  3 2 2
a  b  ab  3ab a  b 1 3 2 2    a  b  ab  log  3 3 a  b  3 3
 a  b  log 3   2 2
a  b  ab  3   2 2
a  b  ab 1 3 3   
Xét hàm số: f t   log t  t trên 0;  . 3 f t  1 '  1  0, t
  0 nên hàm số f t đồng biến trên 0;. t ln 3
Khi đó, phương trình  
1 trở thành : f  3 3
a  b   f   2 2
a  b  ab 3 3
  a b    2 2 3
3 a  b  ab     
 a  b  ab 2 2 a b ab 0 * 2 2
a b 3    0  
a  b  3  0 Do * ,
a b   nên phương trình * vô nghiệm. Suy ra: a  b  3. 0  a  3 a  2   0  b  3 b  1
Mà a, b là các số nguyên dương nên   a  b  3   a 1  * a,b  b   2
Vậy có hai cặp số a;b thỏa mãn yêu cầu bài toán.
Cách 2.Với a, b là các số nguyên dương, ta có:
log a  b  a  b3  3 2 2 a  b
 3ab a  b 1 1 3    a  b a  b 3 3  log
 a  b  3aba  b  3 2 2
a  b  ab  3aba  b  log  2 2
a  b  ab 3  a  b 1 3 3    3 3 2
Trường hợp 1: a  b  2 . Khi đó:   1  log
 4  3ab loại do * a, b   . 3 3 a  b
Trường hợp 2: a  b  3  log  0 và  2 2
a  b  ab3 a  b  0, a  ,b * 3 3 nên   1 không xảy ra.
Trường hợp 3: a  b  3, khi đó   1 thỏa mãn. Trang 21 a  2 b  1
Mà a, b là các số nguyên dương nên  . a 1   b   2
Vậy có hai cặp số a;b thỏa mãn yêu cầu bài toán. 2
 2x  2  x  x  4x  4
Câu 48.Chọn A.Từ giả thiết suy ra f 1 x 4 3  f    2 3 x  x  x 2 2 2 4 3  2x  2  2
x  x  4x  4 Ta có: f
 1 xdx f . dx  dx     2 3  x  x x 1 1 1 2 2 2           f
   x   x 2x 2 2x 2 4 4 1 d 1  f d  x 1  dx        2 3
 x   x   x x  1 1 1 1  1 0 1 1     x 
  f t dt  f  t 2 4 2 2 dt     x     f
 tdt  f
 tdt  0  f
 tdt  0. 2  2 x x 1  0 0 1  0 1 1 Vậy f
 xdx  0. 1 
 2x  2  x  x  4x  4
Cách trắc nghiệm.Ta có: x f 1 x 4 3 2  2 f  , x   0, x  1    x  x  
 x   x  x x  x f 1 x 4 3 2 2 4 4 2  2 f   , x   0, x  1    x  x x  2x  2   2x  2  2
 x f 1 x 2  2 f  x   1 x 2 , x   0, x 1    x   x  1 1
Chọn f  x  x  f
 x.dx  .xdx  0  . 1  1  Câu 49.Chọn A Trang 22
Gọi D là hình chiếu vuông góc của S xuống mặt phẳng  ABC  . AB  SB AC  SA 
 AB  SBD  AB  BD 
 AC  SAD  AC  AD . AB  SD AC  SD  
Tam giác ABC có CAB  135  BAD  45 . 
Tam giác ABD vuông tại B có BAD  45 suy ra tam giác ABD vuông cân và AD  a 2 .
Từ đó có tam giác ACD vuông cân tại A  tứ giác ABDC là hình thang vuông tại B và D .
Trong mặt phẳng SBD , hạ DH  SB  H  SB . Dễ chứng minh DH  SAB .
Trong mặt phẳng SAD , hạ DK  SA  K  SA . Dễ chứng minh DK  SAC  .  
Gọi  là góc giữa hai mặt phẳng  SAB và SAC  ta có:    DH , DK   HDK  30 do tam giác
DHK vuông tại H .
Đặt SD  x ,  x  0 .Tam giác DHK vuông tại H có 2 2  HD 3 ax 2a  x cos HDK    . 2 2 DK 2 a  x 2.ax 2 2 2 2 2 2 2 2
 6 a  x  2 2a  x  6a  6x  8a  4x  x  a . 3 1 3  a a V  . . SD A . B AC.sin BAC 
.Vậy thể tích khối S.ABC bằng . S . ABC 6 6 6 Câu 50.Chọn D 2 2      
Ta có g x   x  m x 4mx 5 e f  x x 4mx 5 2 4 . .  e . f  x
           2 4 5 2 4 . . x mx g x x m f x f x e      . Trang 23  
Yêu cầu bài toán  g x 1  0, x   1  ; 
 và g x  0 chỉ xảy ra tại một số hữu hạn điểm thuộc  2   1  1  ;  .  2       2
x  m f  x  f  x 1 2 4 .  0, x   1  ;   (vì x 4mx 5 e    0)  2  f  x  1  f  x   1  2
 x  4m      
 , (vì f  x  0, x
  )  4m  2x  , x   1  ;  
f  x , x 1;  2  f  x  2  * . 2 f  x  1 
f  x . f x   f  x    Xét h  x    2x     
 . Ta có h x        2  .
f  x , x 1;  2  2 f  x  2 f   x  0  1 
f   x. f  x   f    x  1  Mà         0, x   1  ;   .  f   x , x 1;  0  2  2 f  x  2     1 
Từ đó suy ra h x 1  0, x   1  ; 
 . Vậy hàm số h x đồng biến trên 1  ;  .  2   2  Bảng biến thiên  1  f    1   1   2  225 225
Vậy điều kiện *  4m  h  4m  2.   4m   m      .  2   2   1  137 548 f    2  m   Lại có 
 m1;2;3;...;202  0 . m   2  020;2020
Vậy có 2020 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
……….HẾT……… Trang 24 www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 22 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2 Thời gian: 120 phút
Câu1.Từ một nhóm gồm 5 học sinh nam và 7 học sinh nữ, có bao nhiêu cách lập ra một nhóm gồm hai
học sinh có cả nam và nữ? A. 35 . B. 70 . C.12 . D. 20 .
Câu2.Cho cấp số nhân u
với u  3 và u  12 . Công bội q của cấp số nhân đã cho bằng n  1 3
A. q  4 .
B. q  2 .
C. q  2 . D. q  2 .
Câu 3.Cho khối nón có chiều cao bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 4 a 3 2 a 3  a A. . B. . C. . D. 3 2 a . 3 3 3
Câu 4.Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (3; 1) . B. ( ;  0) . C. (2; 1  ). D. ( 3  ; 2)   ( 2  ; 1  ) .
Câu5.Cho khối hộp chữ nhật có độ dài ba kích thước lần lượt là
4, 6, 8 . Thể tích khối hộp chữ nhật đã cho bằng
A. 288 .B. 64 . C.192 .D. 96 .
Câu6.Nghiệm của phương trình log
x 1  3 là A. x  4.
B. x  3. C. 2  
x  6. D. x  7. 2 5 5
Câu7.Cho 2 f (x)dx  2;
f (x)dx  3.   Tính I  f (x)d . x 
A. x  4. B. x  3. C. x  6. 1 2 1 D. x  7. Câu8.Cho hàm số 4 2
y  x  x 1. Mệnh đề nào dưới đây đúng?
A.Hàm số có 1 điểm cực đại và 2 điểm cực tiểu.B.Hàm số có 1 điểm cực trị.
C.Hàm số có 2 điểm cực trị.D.Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
Câu 9.Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? A. 3 2
y  x  3x  2 . B. 3 2
y  x  3x  2 . 3 2
C. y  x  3x  2 . D. 3 2
y  x  3x  2 .
Câu 10.Với a là số thực dương tùy ý, log  3 a bằng 4  Trang 25 3 2
A. 3 log a . B. 3  log a . C. log a . D. log a . 2 4 2 2 2 3
Câu 11.Họ tất cả các nguyên hàm của hàm số f  x  sin x  8x A. 2
cos x - 4x + C B. 2
- cos x - 4x + C C. 2
cos x + 4x + C D. - cos x + C
Câu12.Tính môđun số phức nghịch đảo của số phức z    i2 1 2 . 1 1 1 A. . B. 5 . C. . D. . 5 25 5
Câu 13.Trong không gian Oxyz , hình chiếu vuông góc của điểm M  3  ;5; 7
  trên mặt phẳng Oyz có tọa độ là A. 0;5; 7   . B.  3  ;0;7. C.  3  ;5;0 . D.  3  ;0;0.
Câu 14.Trong không gian Oxyz , mặt cầu 2 2 2
(S) : x  y  z  8x  4 y  6z  7  0 có tâm và bán kính là: A. I  4
 ; 2; 3, R  36. B. I  4  ; 2; 
3 , R  6 . C. I 4;  2; 3, R  22 . D.
I 4;  2; 3, R  6 .
Câu 15.Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng   : x  3y  2z  6  0 . Vecto nào   
không phải là vecto pháp tuyến của   ?A. n  1;  3;  2 . B. n  1  ;3;2 . C. n  1;3; 2 2   1    . D. n  2  ;6;4 . 3  
Câu 16.Trong không gian Oxyz , điểm nào sau đây thuộc đường thẳng đi qua hai điểm A1;2; 1   và B  1  ;1;  1 ?
A. M 3;3;  3 .
B. N 3;  3;  3 . C. P  3  ;3;3 .
D. Q 3;3;3 .
Câu17.Cho hình chóp S.ABC có SA   ABC  và đáy là tam giác vuông tại B , AC  2a , BC  a ,
SB  2a . Tính góc giữa SA và mặt phẳng SBC  .A. 45. B. 60 . C. 30 . D. 90 .
Câu18.Cho hàm số f  x có f  x  x  x   x  5 2 1
2 . Số điểm cực trị của hàm số đã cho là A. 4 . B.1. C. 3 . D. 2 . Trang 26 5 2
Câu19.Giá trị lớn nhất của hàm số 2 y 
x  3x  4 là bao nhiêu ? A. . B. . C. 2 5 3 . D.0 . 2
Câu 20.Cho a , b là các số thực dương thỏa mãn 2
log a  log b  5 và 2
log a  log b  4 . Giá trị 4 9 4 9 . a b là: A. 48 . B. 256 . C.144 . D. 324 . 2 3   x 1  x
Câu 21.Tập nghiệm của bất phương trình 2 1  3   là  3   1   1  A.  ;     .
B. 1;  . C.  ;1   . D.  3   3   1   ;   1;    .  3 
Câu 22.Chohình nón có thiết diện qua trục là tam giác đều có cạnh bằng 4 . Diện tích toàn phần của hình nón đã cho
bằng A. 3 .
B. 8 . C.12 . D. 9 .
Câu 23.Cho hàm số y  f  x có đồ thị như hình vẽ
Số nghiệm của phương trình 2
f  x  f  x  2 là
A.2. B.3. C.4. D.5. x 
Câu 24.Tìm họ tất các các nguyên hàm của hàm số f  x 2 1  1 trên khoảng x (1; ). A. 2
 x 3ln 1 x C C  . B. 2
 x  3lnx  
1  C C  . C. 2
 x  3ln 1 x C C  . D. 2
 x 3ln x  
1  C C   .
Câu25.Một người hàng tháng gửi vào ngân hàng một khoảng tiền T theo hình thức lãi kép A' D'
với lãi suất 0, 6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số
tiền T người đó gửi hàng tháng là bao nhiêu? Chọn đáp án gần đúng nhất) B' C'
A.643.000. B.535.000 C.613.000. D.635.000. A D
Câu26.Cho khối lăng trụ đứng ABC . D A B  C  D
  có đáy là hình thoi cạnh 2a , AA  2a , B C góc giữa B D
 và mặt đáy bằng 30. Thể tích của khối lăng trụ đã cho bằng: 3 2a 3 3 4a 3 A. .B. 3 2 3a C. 3 4 3a . D. . 3 3 Trang 27 2 2x  x 1
Câu 27.Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  2 x  3x  là: 2 y
A. 0 . B.1. C. 2 . D. 3 . Câu28.Cho hàm số 3 2
y  x  bx  d  ,
b d    có đồ thị như hình dưới O x
đây.Mệnh đề nào dưới đây đúng?
A. b  0; d  0 . B. b  0; d  0 .
C. b  0; d  0 .
D. b  0; d  0 .
Câu29.Cho đồ thị y  f  x như hình vẽ sau đây. Diện tích S của hình phẳng được gạch chéo trong hình dưới dây 2 1 2 bằngA. S  f
 xdx . B.S  f
 xdx f  xdx. 1  1  1 1 2 1 2 C. S   f
 xdx f
 xdx . D.S  f
 xdx f  xdx. 1  1 1  1
Câu30.Cho ba số phức z  3  3i , z  5  3i và z  7  i . Số phức liên 1 2 3
hợp của số phức w  z  2z  iz bằng: 1 2 3 A. 8
 16i . B.816i .
C. 8 16i . D. 8  16i .
Câu 31. Chosố phức z thỏa mãn z  (1 2i)(4  3i) . Điểm biểu diễn số phức z trên mặt phẳng tọa độ là
điểm nào dưới đây? A. Q 10;5. B. M  2  ;5. C. N 10; 5  . D. P  2  ; 5  .   
Câu32.Trong không gian Oxyz , cho các vectơ a  1;1;3 , b   2
 ;1;5 và c  1; 3  ;2 . Tính tích vô    hướng .
a b  2c bằngA. 6
 . B. 22 . C.10 . D. 6 .
Câu 33.Trong không gian Oxyz , cho hai điểm A1;3; 4
  và điểm B3; 1
 ;0 . Mặt cầu S  có đường 2 2 2
kính AB có phương trình là A.  x  2   y   1
 z  2  3 . B.
x  2  y  2 z  2 2 1 2  9 . 2 2 2 2 2 2
C.  x  2   y   1
 z  2  9 .
D.  x  2   y   1
 z  2  3.
Câu34.Cho ba điểm A3;2; 2   , B1;0  ;1 và C 2; 1
 ;3. Viết phương trình mặt phẳng đi qua A và
vuông góc BC .A. x  y  2z  5  0 . B. x  y  2z  3  0 . C. x  y  2z  3  0 . D.
x  y  2z 1  0 . Trang 28
Câu35.Trong không gian Oxyz , cho ba điểm A1;0;6 , B 0;2; 1
 , C 2;4;3  . Vectơ nào dưới đây là
một vectơ chỉ phương của đường thẳng chứa trung tuyến AM của tam giác ABC ?   
A. u  2;3; 7 .
B. u  0; 3; 5 .
C. u  2;1;8 . D. 3   2   1    u  0;1; 4  . 4  
Câu36.Cho 100 tấm thẻ được đánh số liên tiếp từ 1 đến 100 , Chọn ngẫu nhiên 3 tấm thẻ. Xác suất để
Chọn được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 2 là 5 1 5 3 A. P  . B. P  . C. P  . D. P  . 6 2 7 4
Câu 37.Cho hình chóp S.ABCD , có đáy là hình thang có đáy lớn AB , 1
SA vuông góc mặt phẳng đáy, AD  CD  CB 
AB  2a , SA  a 3 . 2
Khoảng cách giữa hai đường thẳng SD và CB bằng a 3 a 2 a 6 A.
. B. a 6 C. D. . 2 3 2
Câu 38.Cho hàm số f (x) xác định và liên tục trên  , có f (0)  0 và 3 6x f '(x) 
với mọi x  0 . Số nghiệm của phương trình 2 x 1 1
f (x)  2020 là A. 0 . B.1. C. 4 . D. 2 . 4x  m
Câu39.Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y  đồng biến 0;  1 . 2x  m  3 A.1. B. 5 . C. 4 . D. 3 .
Câu 40.Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a . Diện tích xung quanh của hình trụ làA. 2
S  16 a . B. 2
S  4 a . C. 2
S  24 a . D. 2 S  8 a .
Câu 41.Xét các số thực dương x , y thỏa mãn log x  log y  log
x  y . Mệnh đề nào dưới đây 9 2 1   15 đúng? x  1 1  x  1 2  x  1  x  2  A.  ;   . B.  ;   . C.  0;   . D.  ;1   . y  3 2  y  2 3  y  3  y  3 
Câu 42.Gọi S tập hợp giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số 4 2
y  x  8x  m trên đoạn 1;3 bằng 24. Tổng các phần tử của S bằng A. 7  . B. 4  . C. 4 . D. 7 . Trang 29
Câu 43.Cho phương trình 2
log x  3m log 3x 2
 2m  2m 1  0 ( m là tham số thực). Gọi S là tập 3 3
hợp tất cả các số thực m mà phương trình có hai nghiệm phân biệt thuộc đoạn 1; 
3 . Số phần tử của tập S là A. 2 B.1 C. 0 . D. 3 . x
Câu 44.Cho hàm số f ( x) liên tục trên  . Biết 2
x  2x  3 là một nguyên hàm của hàm số 2 f (x).5 , x
họ tất cả các nguyên hàm của hàm số 2 f (  x).5 là
A. 2   x  
1 ln 5  C . B. ln 5  C . 2  x  2  x  C. 2x  
 xln5 C . D. 2x    xln5 C .  2   2 
Câu 45.Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
f sin x  3sin x  m có nghiệm thuộc khoảng 0;  . Tổng các phần tử của S bằng A. 9  . B. 10  . C. 6  . D. 5  . Câu 46.Cho hàm số    4 3 2 y
f x  ax  bx  cx  dx  e có đồ thị như hình vẽ
Số cực trị của hàm số y  f  x 1  3 là A. 7 . B. 5 . C. 6 . D. 3 .
Câu47.Biết x , x (x  x ) là hai nghiệm của phương trình 1 2 1 2 2
 x  2x 1 2 log 
  x  2  3x và 4x  2x  a  b , với a,b là hai số nguyên 3  3x  1 2
dương. Tính a  b
A. a  b  9. B. a  b  12. C. a  b  7 .
D. a  b  14.
Câu 48.Xét hàm số f  x liên tục trên đoạn 0 
;1 và thỏa mãn điều kiện 2 f  x  3 f 1 x  x 1 x . 1 4 4 2 Tính tích phân I  f
 xdx . A. B.  C.  15 15 5 0 D. 1 · ·
Câu 49.Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 8 , SAB  SCB  90 , hai mă ̣t phẳng
SAB,SCB vuông góc với nhau. Thể tích của khối chóp S.ABC là: Trang 30 64 2 128 3 128 2 A. . B. 64 2 . C. . D. . 3 3 3
Câu 50.Cho hàm số y  f  x . Hàm số y  f ' x có đồ thị như hình vẽ.
Số điểm cực trị của đồ thị hàm số
y  g  x  f  x  x     x  2 1 4 3 3 2  x  24 2 là 2
A. 6 . B. 7 . C. 8 . D. 9 . BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.C 5.C 6.D 7.A 8.A 9.A 10.C 11.B 12.D 13.A 14.B 15.C 16.A 17.B 18.D 19.A 20.D 21.C 22.C 23.D 24.D 25.D 26.C 27.C 28.C 29.D 30.D 31.C 32.D 33.B 34.C 35.B 36.B 37.D 38.D 39.C 40.A 41.B 42.A 43.C 44.C 45.B 46.A 47.D 48.B 49.D 50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu1.Chọn A.Để lập ra một nhóm gồm hai học sinh có cả nam và nữ, ta thực hiện liên tiếp 2 công đoạn
là Chọn 1 học sinh nam và Chọn 1 học sinh nữ, nên theo quy tắc nhân ta được 1 1
C .C  35 . 5 7 u 12 Câu2.Chọn D.Ta có: 2 2 3
u  u q  q  
 4  q  2 . 3 1 u 3 1 2a 3 1 2 a
Câu 3.Chọn B.Thể tích khối nón: 2 V   a .2a  . 3 3 a
Câu 4.Chọn C.Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên mỗi khoảng  3  ; 2   và  2  ;  1 .
Câu5.Chọn C.Áp dụng công thức tính thể tích khối hộp chữ nhật: V = 4.6.8 = 192 .
Câu6.Chọn D.Điều kiện: x 1  0  x  1  .
Với điều kiện đó, phương trình đã cho tương đương với: log  x   3
1  3  x 1  2  x 1  8  x  7. 2
Vậy, phương trình đã cho có nghiệm là x  7. Trang 31 2 2
Câu7.Chọn A.Ta có 2 f (x)dx  2 
f (x)dx  1.   1 1 5 2 5 5
Khi đó, I  f (x)dx  f (x)dx  f (x)dx 1 3  4.    Vậy, I 
f (x)dx  4.  1 1 2 1
Câu8.Chọn A.Tập xác định: D   . x  0  Ta có 3
y  4x  2x ; y  0  2  . x    2
Giới hạn lim y   . x 2 2 x   0  2 2 y  0  0  0   1  y 0 0
Vậy hàm số có hai điểm cực tiểu và một điểm cực đại. Câu 9.Chọn A
*) Ta có lim y    a  0 , nên loại đáp án B và đáp án x D.
*) Nhìn vào đồ thị, hàm số đạt cực trị tại x  0 và x  0 . 1 2 x  0 *) Xét hàm số 3 2
y  x  3x  2 , ta có 2
y '  3x  6x . Suy ra 2
y '  0  3x  6x  0   . x  2  3 2
Tức là hàm số y  x  3x  2 đạt cực trị tại x  0 và x  0 . Nên loại đáp án 1 2 C. 3
Câu 10.Chọn C.Với a  0 ta có log  3 a  log . a 4  2 2
Câu 11.Chọn B.Ta có  x  x 2 sin 8
dx   cos x  4x  C
Câu12.ChọnD.Ta có z    i2 1 2  3
  4i  z  5 .Vâ ̣y môđun số phức nghi ̣ch đảo của z là 1 1 1   . z z 5 Trang 32
Câu 13.Chọn A.Hình chiếu vuông góc của điểm M  3  ;5; 7
  trên mặt phẳng Oyz có tọa độ là 0;5; 7   . Câu 14.Chọn B 2 2 2 2 2 2
CÁCH 1: x  y  z  8x  4 y  6z  7  0  x  y  z  2. 4
  x  2.2y  2.3z 7  0. a  4
 , b  2, c  3, d  7   2 2 2
a  b  c  d  36. 2 2 2
Vậy (S ) có tâm I  4
 ; 2; 3, bán kính R  a b  c  d  6. 2 2 2 CÁCH 2: 2 2 2
x  y  z  8x  4y  6z  7  0   x  4   y  2   z  3  36.
Vậy (S ) có tâm I  4
 ; 2; 3, bán kính R  6.
Câu 15.Chọn C.Phương trình mặt phẳng   : x  3y  2z  6  0 
Suy ra vecto pháp tuyến của mặt phẳng   là n 1;  3;  2 .    Các vecto: n  1  ;3;2 , n  2
 ;6;4 cùng phương với vecto n1;3; 2 nên cũng là vecto pháp 3   1  
tuyến của mặt phẳng   . 
Câu 16.Chọn A.Ta có: AB   2  ;1;2 . x 1 2t 
Phương trình tham số của đường thẳng AB : y  2  t , t là tham số thực. z  1   2t  3  1 2t 
Thay tọa độ điểm M 3;3; 3 vào phương trình đường thẳng AB , ta có: 3   2  t  t  1  .  3   1   2t 
Do đó điểm M 3;3; 3 thuộc đường thẳng AB .
Câu17.Chọn B.Kẻ AH  SB ( H  SB ). Theo giả thiết ta có BC  SA 
 BC SAB BC  AH . Từ  
1 và 2  AH SBC . BC  AB Do đó 
SA SBC   SA SH   ; ;  ASH Ta có 2 2
AB  AC  BC  a 3 . Trang 33 AB a Trong vuông S  AB ta có  3 3 sin ASB    SB 2a 2  
 ASB  ASH  60 . Vậy góc giữa SA và mặt phẳng SBCbằng 60.  x  0 
Câu18.Chọn D.Xét phương trình f  x  0  x  1  x  2   Ta có bảng xét dấu sau:
Dễ thấy f  x đổi dấu khi qua x  2
 và f x đổi dấu khi qua x 1nên hàm số có 2 điểm cực trị.
Câu19.Chọn A.Điều kiện: 2
x  3x  4  0  1  x  4 . 2  x  3 3 Tập xác định:  1  ;4. y 
. y  0  x  .Ta có: 2
2 x  3x  4 2   y   3 5 1  0; y  ; y   4  0.  2  2 5
Vậy giá trị lớn nhất của hàm số 2 y 
x  3x  4 là . 2 2
log a  log b  5
log a  2log b  5 log a 1 a  4 4 9 4 9
Câu 20.Chọn D.Ta có hệ:    4     . 2
log a  log b  4 
2 log a  log b  4  log b  2  b   81 4 9 4 9 9 Vậy . a b  324 . 2 3  x 2  1    Câu 21.Chọn C. 2 x 1 3x 2 x 1 2  3  3  3
 3x  2x 1    3   1    1  2
 3x  2x 1 0  x ;1 
.Vậy tập nghiệm của BPT là T   ;1  .  3   3 
Câu 22.Chọn C.Giả sử thiết diện qua trục của hình nón là tam giác OAB đềucó cạnh
OA = OB = A B = 4 như hình vẽ trên. Khi đó hình nón có đỉnh O , AB
độ dài đường sinh là l  OA  OB  4 , bán kính đáy r   2 . 2
Vậy diện tích toàn phần của hình nón là 2 2
S  rl   r  .2.4   .2  12 . tp Trang 34
 f x  1 
Câu 23.Chọn D.Ta có 2
f  x  f  x 2
 2  f x  f x  2  0    f   x  2
Số nghiệm của phương trình ban đầu chính là số giao điểm của đồ thị hàm số y  f  x với các đường
thẳng y  1 và y  2 .
Từ đồ thị đồ thị ta thấy:
– Đường thẳng y  1 cắt đồ thị hàm số y  f  x tại hai điểm phân biệt.
– Đường thẳng y  2 cắt đồ thị hàm số y  f  x tại ba điểm phân biệt.
Vậy số nghiệm của phương trình đã cho là 5 . x   
Câu 24.Chọn D.Ta có: f  x 2 1 3 dx  dx  2   dx  2
 x  3ln 1 x  C    1 x  1 x 
Vì xét trên khoảng (1; ) nên 1 x  x 1.Do đó: f
 xdx  2
 x 3ln x   1  C
Câu25.Chọn D.Sau 1 tháng người đó có số tiền: T  1 r T 1  
Sau 2 tháng người đó có số tiền: T  T T 1 r  1 rT  1 r2 T 2 1
Theo quy luật đó sau 15 tháng người đó có số tiền là  
T    rT     r     r    T   r  1 r15 14 1 1 1 1 ... 1 1 15   r
Theo giả thiết thì T  10 và r  0.006 suy ra T  635.000 . Ta Chọn D 10 
Câu26.Chọn C.Vì BD là hình chiếu của B D
 trên mặt phẳng  ABCD nên B DB   30 là góc giữa B D
 và mặt đáy  BD  B . B
 cot30  2a 3 .Gọi O  AC BD .
Vì ABCD là hình thoi cạnh 2a có BD  2a 3 2 2 2 2
 AC  2AO  2 AB  BO  2 4a 3a  2a 1 1 2  S
 AC.BD  .2 .2 a a 3  2a 3 2 3
V  AA .S  2 . a 2a 3  4a 3 ABCD 2 2 ABCD
Câu 27.Chọn C.TXĐ: D   \  2  ;  1 . 2 2x  x 1 Có: lim  2
y  là tiệm cận ngang của đồ thị hàm số. 2
x x  3x  nên 2 2 2 2x  x 1 2x 1 2 2x  x 1 2x 1 Có: lim  lim  3  lim  lim  3   2   2  x( 1  )   x( 1  ) x 3x 2 x  . 2 x( 1  )   x( 1  ) x 3x 2 x  . 2 Trang 35 2 2x  x 1 2x 1 2 2x  x 1 2x 1 lim  lim   lim  lim    2   2  x( 2  )   x( 2  ) x 3x 2 x  . 2 x( 2  )   x( 2  ) x 3x 2 x  . 2 Suy ra x  2
 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 1 tiệm cận ngang và 1 tiệm cận đứng.
Câu28.Chọn C.Dựa vào đồ thị ta thấy đồ thị hàm số 3 2
y  x  bx  d cắt trục tung tại điểm có tung độ
dương nên d  0 , loại B, D x  0 3 2 2
y  x  bx  d  y '  3x  2bx  . 2
y '  0  3x  2bx  0  2b  . x    3 2b
Mà hàm số có hai điểm cực trị không âm nên 
 0  b  0 , loại A. 3
Câu29.Chọn D.Diện tích cần tìm là 2 1 2 1 2 S  f
 x dx  f
 x dx f
 x dx  f
 xdx f
 xdx . 1  1  1 1  1
Câu30.Chọn D.Ta có: w  z  2z  iz  3  3i  25  3i  i 7  i  8  16i 1 2 3
Vậy số phức liên hợp của w là: w  8  16i
Câu 31. Chọn C.Ta có: 2
z  (1 2i)(4  3i)  4  3i 8i 6i  10  5i  z  10  5i .
Do đó điểm biểu diễn số phức z trên mặt phẳng tọa độ là điểm N (10; 5  ) .  
Câu32.Chọn D.Ta có: b  2c   2   2.1;1 2. 3  ;52.2   4  ;7;  1 nên    .
a b  2c 1. 4
  1.73.1 6. 
Câu 33.Chọn B.Gọi I là trung điểm của AB  I 2;1; 2
 ; IA   1  ;2; 2    IA   2 2 1  2   2  2  3
Mặt cầu  S  có đường kính AB nên có tâm là I 2;1; 2
  và bán kính R  IA  3. Do đó, Mặt cầu  2 2 2
S  có phương trình là:  x  2   y   1
 z  2  9 .
Câu34.Chọn C.Gọi ( ) là mặt phẳng cần tìm, ta có  
n  BC  (1; 1  ;2)  ,Vậy n (1; 1  ;2)  ( )   () :1( x 3) 1
 ( y 2) 2( z 2) 0 ( )
 : x y 2 z 3 0  ( A 3; 2; 2  ) Trang 36
Câu35.Chọn B.Gọi M là trung điểm của BC  M 1;3;  1 .    Ta có AM  0;3; 5
   u , với u  0;3;5 . Do đó Chọn B 2   2
Câu36.Chọn B.Số phần tử của không gian mẫu là n  3
 C 161700. 100
Gọi A là biến cố: “ tổng các số ghi tên thẻ là số chia hết cho 2 ”.
Từ 100 tấm thẻ có 50 tấm thẻ đánh số chẵn và 50 tấm thẻ đánh số lẻ.
Trường hợp thuận lợi của biến cố A là:
TH1: Chọn 3 tấm thẻ đánh số chẵn từ 50 tấm thẻ đánh số chẵn có: 3 C 50
TH2: Chọn 1 tấm thẻ đánh số chẵn và 2 tấm thẻ đánh số lẻ có: 1 2 C .C 50 50 n A 80850 1
Do đó: n A 3 1 2
 C  C .C  80850 .Vậy xác suất của biến cố A là P A      . 50 50 50 n  161700 2
Câu 37.Chọn D.Kẻ DM / /BC nên CB / / SDM  nên ta có d S ;
D CB  d C ;
B SDM   d  ;
B SDM   d  ;
A SDM  .
Vì ABCD là nửa lục giác đều nên AC  CB.
Gọi H  AC  DM , ta có: AH  DM .  AH  DM Mà 
nên DM  SAH  . SA  DM
Kẻ AK  SH mà AK  DM nên AK  SDM  . Do đó d S ;
D CB  d  ;
A SDM   AK .
Ta xét tam giác AMD có AM  DM  AD nên tam giác AMD là tam giác đều cạnh 2a. 2a 3 Do đó AH 
 a 3 .Xét tam giác SAH vuông tại A, ta có: 2 1 1 1 1 1 2      3 a 6 a nên AK  a 
.Vậy d SD CB  6 ;  . 2 2 2 AK SA AH  2  2 2 3 3 3 a a a 2 2 2 3 6x
Câu 38.Chọn D.Ta có: 2 2 f '(x) dx 
dx  6x( x 1 1)dx  6x x 1dx  6xdx      2 x 1 1 Trang 37 3 3 2 2 2 2
 3 x 1d(x 1)  6xdx  2 x 1  3x  C  
.Vậy f (x) có dạng 2 2
f (x)  2 x 1  3x  C 3
Do f (0)  0 nên C  2  vậy 2 2
f (x)  2 x 1  3x  2 .Ta có 3 2 2
f (x)  2020  2 x 1  3x  2022  0 3 Đặt 2 2
g(x)  2 x 1  3x  2022 thì dễ thấy g (x) là hàm số chẵn, xác định liên tục trên  , đồng biến trên     
 đồng thời có g (0) 0 và lim g(x) nên g(x)
0 có đúng 1 nghiệm dương. x
Do đó phương trình g(x)  0 có đúng 2 nghiệm trên  .  m  3 2m  12
Câu39.Chọn C.Tập xác định D   \   , khi đó y ' 
.Để hàm số đồng biến trên  2 
2x  m  3 0; 1 thì y '  0, x   0  ;1  2m 12  0 m  6   m  3    1     m  5   m  5   m   6  ; 5   3  ;. 2    m  3  m  3  m  3    0   2
Vậy các giá trị nguyên âm cần tìm của m là  5  ; 3  ; 2  ;  1
Câu 40.Chọn A.Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 4a h  4a   r  2a
Diện tích xung quanh hình trụ: 2 S  2rh  2.2 .
a 4a  16 a . xq Câu 41.Chọn B x  9t 
Đặt log x  log y  log
x  y  t   y  12t 9t 12t 15t    . 9 12   15
x  y  15t  t t  3   4 
Chia hai vế của cho 15t ta được: + =1     .  5   5  t t     t t    
Xét hàm số f t  3 4  +
    có f t 3 3 4 4  ln + ln  0, t        .  5   5   5  5  5  5
Suy ra hàm số f t  nghịch biến trên  .Mặt khác, f 2  1 nên phương trình có nghiệm duy nhất t  2. Trang 38 2 x  9 2 x 9 9  1 2  Với t  2 thì      0,5625 ;   . 2  2 y  12 y 12 16  2 3 
Câu 42.Chọn A.Đặt 4 2
t  x  8x x  1;  3 , ta có 3 t   x 
x   x  2 ' 4 16 4 x  4 x  0  t '  0   . x  2  BBT: Từ BBT ta có 4 2
t  x  8x x  1;  3  t  9  ;16.
Xét hàm số y  t  m t   9
 ;16  max y  m16; min y  m9  9  ;1  6  9  ;1  6
Ta có min y  min t  m  min  m 16; m  9  .    9  ;1  6  9  ;1  6 1;3  m 16  24 
TH1: min y  m 16  24    m  40  .  9  ;16  m  9  24   m  9  24 
TH2: min y  m  9  24    m  33.  9  ;16  m 16  24  Vậy S   4  0;3  3 .
Câu 43.ChọnC.Điều kiện: x  0 . PT: 2
log x  3m log 3x 2
 2m  2m 1  0 2 2
 log x 3mlog x  2m  m 1 0 . 3 3 3 3
log x  m 1 3   log x  2  m 1  3 Ta có x 1; 
3  log x  0;1 .Vậy để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 0  ;1 3    2   m  1
0  m 1  1    1 khi và chỉ khi 0  2
 m 1 1  0  m  . 2  
m 1  2m 1  m  2 
Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán. Trang 39 x Câu 44.Chọn C. 2
x  2x  3 là một nguyên hàm của hàm số 2 f (x).5   x x  2x  2 2
x  2x  3  f  x 2
.5  2x  2  f  x 2
.5  f  x  x 2 5 x  1 x  2
 2.5  2x  2 2    .5 .ln 5 x       f x 2x 2 2 2  x  1 ln 5       f  x   x  x x   2 .5 2 1 ln 5 2   x     2 2  5  2 5 5    x    f 
 x dx     x  2 x 2 .5 2
1 ln 5 dx 2x   
 x ln5 C.  2 
Câu 45.Chọn B.Đặt t  sin x ; x 0;   t 0;  1 .Gọi  là đường 1 thẳng đi qua điểm 1; 1
 và song song với đường thẳng y  3x . Đường
thẳng  có phương trình y  3x  4 . 1
Gọi  là đường thẳng đi qua điểm 0; 
1 và song song với đường thẳng 2
y  3x . Đường thẳng  có phương trình y  3x 1 .Do đó, phương trình 2
f sin x  3sin x  m có nghiệm thuộc khoảng 0;  khi và chỉ khi
phương trình f t  3t  m có nghiệm thuộc nửa khoảng 0;  1  4   m 1.
Vậy tổng các phần tử của S là  4     3     2      1  0  1  0 .
Câu 46.Chọn A.Xét g  x  f  x 1  3 x 1 1 Tập xác định 
D   .Ta có: g x   x 1  3 f  x 1  3 
. f  x 1  3  h  x x 1 x  1
với h x   x  
1 . f  x 1  3 x  1     x  1 x 0         x 2 x 1  3  2   h  x x 1 0  0      x  2  f 
  x 1 3  0 x 1  3  0  x  4   x 1  3 1   x  3 x  5   Trang 40
 Bảng xét dấu gx
Vậy hàm số y  g  x có 7 cực trị. x  0
Câu47.Chọn DĐiều kiện:   x  1 2
 x  2x 1 Ta có: 2 log 
  x  2  3x  log x 1  x  2x 1 log x  x 3  2 2 3  3x  3  1 log  x  2 1   x  2 1
 log x  x Xét hàm số f t  log t  t  f  t  1  0, t   0 3   3 3 t.ln 3  3  5  x  Phương trình trở 2
thành f  x  
1   f x  x   1 2 2 2 1
 x  x  3x 1  0    3  5 x  2  2
Vậy 4x  2x  9  5 . Khi đó a  9, b  5  a  b  14 1 2 1 1 1
Câu 48.Chọn B.Do 2 f  x  3 f 1 x  x 1 x  2 f
 xdx 3f
 1 xdx  x 1 xdx    1 . 0 0 0 1444442 444443 144442 44443 1 I I2 1
+ Xét I  3 f 1 x dx 
:Đặt t 1 x  dx  d
 t . Khi x  0  t 1; x 1 t  0 . 1   0 1
Khi đó I  3 f t dt  3I  . 1   0 1 + Xét I 
x 1 xdx  . Đặt 2
t  1 x  x  1 t  dx  2  d t t . 2 0 0 0 5 3  2t 2t  4
Với x  0  t  1; x  1  t  0 .Khi đó I   2 1 t t 2  t dt      . 2     5 3  15 1 1 Trang 41 Thay vào   4 4
1 : 2I  3I   I   . S 15 15
Câu 49.ChọnD.Gọi H là chân đường cao hạ từ S xuống mă ̣t phẳng  ABC  . Theo giả thiết ·
: SAB  90 ta chứng minh đươ ̣c AB  SAH   AB  AH. H K C
Chứng minh tương tự ta được BC  CH . M
Theo giả thiết AB  BC  AC  8, ta chứng minh được H V AB  H V CB A · ·
 HA  HC, HBA  HBC  30  SA  SC và HB đi qua trung điểm của AC B
 AC  BH tại M. Ta chứng minh được AC  SHB  AC  S . B
Từ A hạ AK  SB ( K SB ), ta chứng minh được SB   AKC  SB  KC.
Theo giả thiết hai mă ̣t phẳng SAB,SCB vuông góc với nhau · AKC  90 . Theo giả thiết · ·
SAB  SCB  90 , AB  BC  AC  8  S V AB  S V CB  8
AK  CK  A
V KC là tam giác vuông cân tại K . Mà AC  8  AK  KC   4 2 . 2
Áp dụng hệ thức lượng vào tam giác 1 1 1
SAB vuông ta ̣i A ta có:    SA  8 . 2 2 2 AK AB SA
Trong tam giác vuông HAB · 8
ta có: AH  A .
B tan HBA  8. tan 30  3 2 8 6 1 1 8 6 8 3 128 2 2 2
 SH  SA  AH  V  SH.S  . .  . 3 SABC 3 ABC 3 3 4 3
Câu 50.Chọn A.Ta có g  x   x   f  x  x     x     x  3 2 ' 2 2 ' 4 3 6 2 2 2 x  2
g  x   x    f   2 x  x   2 ' 2 2 ' 4
3  x  4x 1 ; g 'x  0   f '   2
x  4x  3  2   2
x  4x  3 Trang 42
Từ đồ thị hàm số.Ta có đường thẳng y  2  x cắt đồ thị y  f ' x tại bốn
điểm phân biệt có hoành độ x  2 x  2   2
x  4x  3  2   x 1   2 là x  2
 ; x  0; x  1; x  2 .Vậy  x  4x  3  0  x  3   2
x  4x  3  1 x  2  2   2
x  4x  3  2  x  2  3 Ta có BBT:
Từ BBT suy ra đồ thị hàm số có 6 điểm cực trị. www.thuvienhoclieu.com
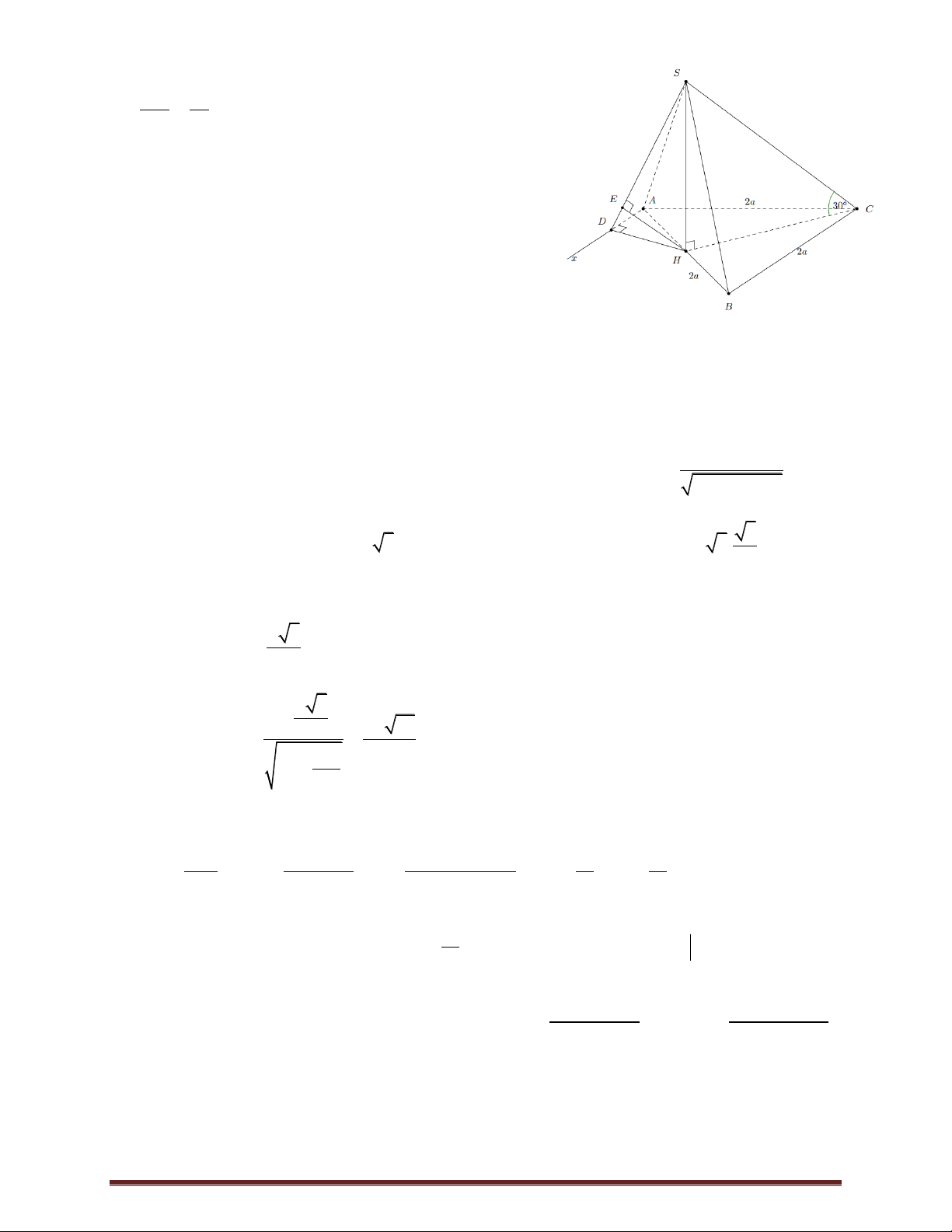
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 23 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2 Thời gian: 120 phút
Câu 1.Từ một nhóm học sinh gồm 5 nam và 9 nữ, có bao nhiêu cách Chọn ra hai học sinh? A. 45 . B. 91. C.14 . D. 9 . u   u  33 1 5
Câu 2.Cho cấp số nhân u
có các số hạng thỏa mãn 
. Tìm số hạng đầu u và công bội n  u  u  66  1 2 6 33 33
q của cấp số nhân. A. u  2, q  2 . B. u 
, q  2 . C. u  , p  2 . 1 1 17 1 17
D. u  3, q  2 . 1
Câu 3.Một hình trụ có diện tích xung quanh bằng 2
4 a và bán kính đáy là a . Tính độ dài đường cao
của hình trụ đó. A. 4a . B. 2a . C. 3a . D. a .
Câu 4.Cho hàm số y  f  x có bảng biến thiên như sau Trang 43
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  ;  2 . B.  ;  0 . C. 0;  1 . D.  1  ;.
Câu 5.Tính thể tích V của khối lăng trụ đứng có diện tích đáy bằng 8 và chiều cao h bằng 12 .
A.V  32 .
B.V  96 .
C.V  68 . D.V  64 . 1 1
Câu 6.Nghiệm của phương trình log x  3 là A. 27 . B. . C. 9 . D. . 3 27 27 4 3 f
 xdx 9 f  x 4 dx  Câu 7.Nếu 1 và  d  1   f x x thì 1 bằng A.10 . B. 10  . C. 3 8 . D. 8  .
Câu 8.Cho hàm số y  f  x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 1. B. 2
 . C.0 . D.1.
Câu 9.Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? y A. 4 2
y  x  2x . B. 4 2
y  x  2x  3 . -1 O 1 x C. 4 2
y  x  2x  3 . D. 3 2
y  x  3x  2 3  a  -3
Câu 10.Với a là số thực dương tùy ý, log   bằng 3  27  -4 1
A. 3log a 1 . B. 3log a 1 . C. 3log a 1 . D. 3log a  . 3  3 3 3 3
Câu 11.Họ nguyên hàm của hàm số f  x  sin x  3x là 3 3 A. 2
 cos x  x  C . B. 2 cos x 
x  C . C. 2
 cos x  3x  C .
D. cos x  C . 2 2
Câu 12.Cho số phức z 
5  2i . Tính z .A. z  5 . B. z  3 . C. z  7 . D. z  29 .
Câu 13.Trong không gian Oxyz , hình chiếu vuông góc của điềm M (1; 2; 3
 ) lên mặt phẳng (Oyz) có tọa độ là A. 1;0;0
B. (1; 2 ; 3) C. (1; 2  ;3) D. (0; 2; 3  )
Câu 14.Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x  y  z  4x  2 y  4z 16  0 . Tìm tâm và
bán kính mặt cầu (S ) . A. I (2;1; 2), 
R  5 .B. I (2;1; 2),  R  13 C. I ( 2  ; 1
 ;2), R 13 . D. I( 2  ; 1  ;2), R  5 . 
Câu 15.Phương trình mặt phẳng nào sau đây nhận véc tơ n  2;1;   1 làm véc tơ pháp tuyến
A. 2x  y  z 1  0
B. 2x  y  z 1  0
C. 4x  2 y  z 1  0 D.
2x  y  z 1  0 x 1 y  2 z 1
Câu 16.Trong không gian Oxyz , điểm nào sau đây thuộc đường thẳng d :   1 2 1 A. P(2; 0; 2)  .
B. Q(1; 2; 1) .
C. N (1;3; 2) . D. M (1; 2;1) .
Câu 17.Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
đáyvà SA  a 2 . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng SAB A. 45 . B. 30 . C. 60 . D. 90 . Trang 44
Câu 18.Cho hàm số f  x , bảng xét dấu f  x như sau:
Số điểm cực tiểu của hàm số f  x là A.1. B. 2 . C. 3 . D. 4 . 9
Câu 19.Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  x  trên đoạn 1; 4 . x 65 49
Giá trị của m  M bằng A. . B.16 . C. . 4 4 D.10 .
Câu 20.Cho log b  2 với a, b  0 , a  1. Khẳng định nào sau đây là sai? a
A. log ab  3 . B. a b  . C. b  . D. a  2 log  4 a  2 log  4 a  2 log ab   3 . a
Câu 21.Tập nghiệm của bất phương trình 2x x6 2
 2 là A.0;6 . B.  ;  6 . C. 0;64 . D. 6;  .
Câu 22.Cho hình nón có bán kính đáy bằng 5. Biết rằng khi cắt hình nón cho bởi mặt phảng qua trục,
thiết diện thu được là một tam giác đều. Diện tích toàn phần của hình nón đã cho bằng A. 50p . B. 25p . C. 75p . D. 5p .
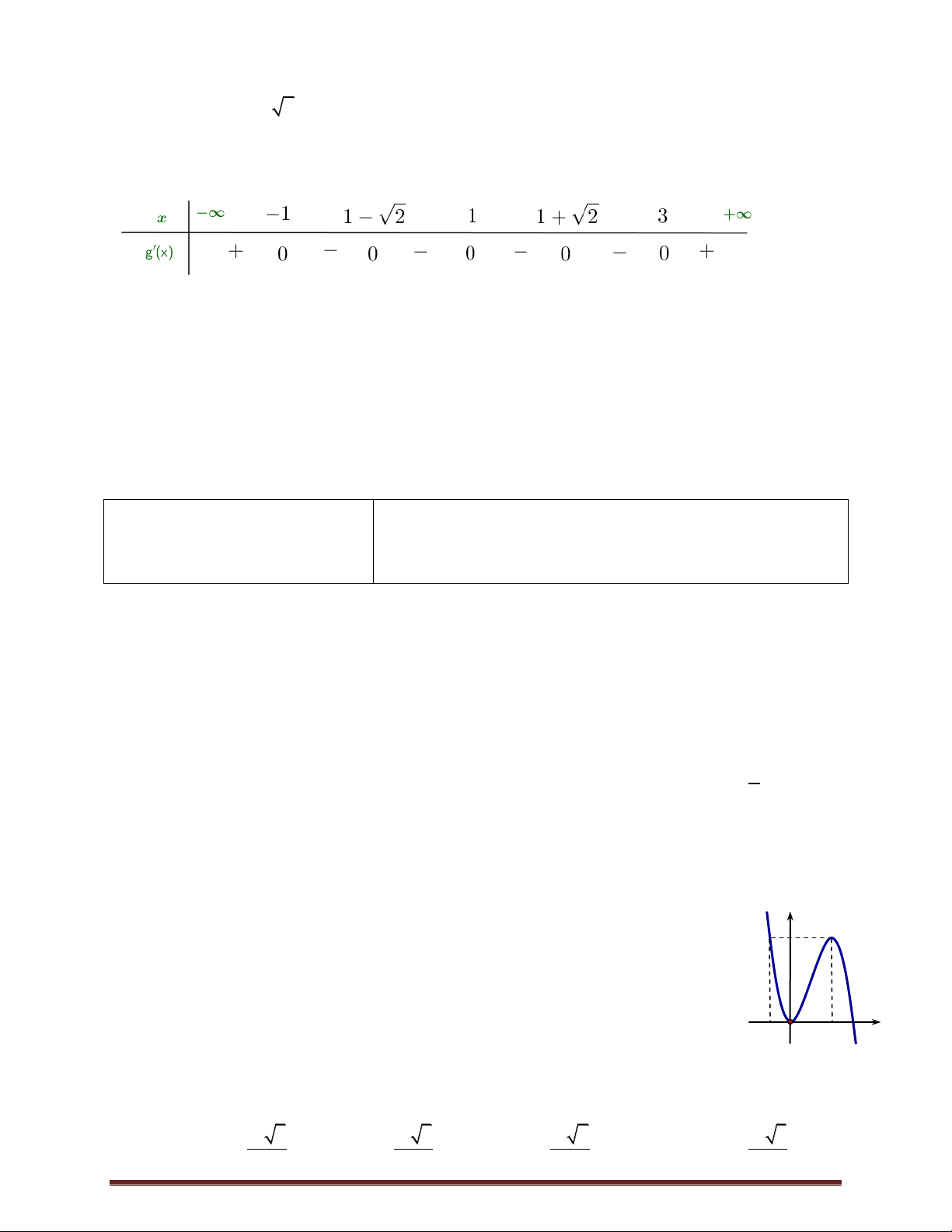
Câu 23.Cho hàm số f  x có bảng biến thiên như sau:
Số nghiệm thực của phương trình 3 f  x  5  0 là A. 4 . B. 2 . C. 0 . D. 3 . x 
Câu 24.Họ tất cả các nguyên hàm của hàm số f  x 3  5;   là
x  trên khoảng   5 8
A. x  8ln  x  5  C .
B. x  8 ln  x  5  C . C. x    C . D. x  52 8 x    C . x  52
Câu 25.Để dự báo dân số của một quốc gia, người ta sử dụng công thức  . nr S A e ;
trong đó A là dân số của năm lấy làm mốc tính, S là số dân n năm, r là tỉ lệ tăng dân
số hàng năm. Năm 2019 dân số của nước In-Đô-Nê-Xi-a là 272056300 người. Giả sử
tỉ lệ tăng dân số hàng năm không đổi là 1.5% , dự báo dân số của nước này vào năm
2035 là bao nhiêu người ?
A. 345851300. B. 445851300 . C. 395851300. D. 545851300.
Câu 26.Cho khối lăng trụ đứng AB . C A B  C
  có đáy là tam giác đều cạnh bằng a ,
AB '  2a . Thể tích của khối lăng trụ đã cho bằng Trang 45 2 3a 2 a 3 3a 3 a A.V  . B.V  . C.V  . D. . 4 12 4 12 2 x  4  x
Câu 27.Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  2 x  2019x  là 2020 A. 2 . B.1. C. 0 . D. 3 .
Câu 28.Cho hàm số bậc ba 3 2
y  ax  bx  cx  d  , a , b ,
c d    có đồ thị
hàm số như hình vẽ. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0, d  0 . B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 . D. a  0, b  0, c  0, d  0 .
Câu 29.Diện tích hình phẳng được gạch chéo trong hình bên bằng. 1 2 A.  3 2
x  x  2x  3dx   2 x  x    1dx . 1  1 1 2 B.  3 2
x  x  2x  3dx   2 x  x    1dx. 1  1 1 2 C.   3 2
x  2x  x  2dx   3 2
x  2x  x  2dx . D. 1  1 2
x 2x  x2 2 3 2 dx    3 2
x  2x  x  2dx . 1  1  z - 2
Câu 30.Cho hai số phức z  4  3i và z  1 2i . Phần thực của số phức 1 bằngA.1. B. . C. 2 . 1 2 z 5 2 - 11 D. . 5 3 1 i 3 
Câu 31.Trên mặt phẳng tọa độ, điểm biểu diễn của số phức z    
 là điểm nào dưới đây? 1 i    1 3 
A. D 2; 2 .
B. C 1;3 3 . C. B  ;    . D. A2; 2   . 2 2      
Câu 32.Trong không gian Oxyz , cho hai véctơ a  1; ;
m n , b  3; 2  ;2 thỏa mãn . a b  17 và  ,
a b  60 . Tính giá trị của biểu thức 2 2
S  m  n . A.16 . B.17 . C. 67 . D. 33 .
Câu 33.Trong không gian Oxyz , cho mặt cầu S  x  y   z  2 2 2 : 3
 5 . Mặt cầu S  cắt mặt phẳng
P: 2x  y  2z 3  0 theo một đường tròn có bán kính bằng A.4 . B.2 . C.1. D. 3 .
Câu 34.Trong không gian Oxyz , cho ba điểm A1;3;2 , B 1;2;1 , C 4;1;3  . Mặt phẳng đi qua trọng
tâm G của tam giác ABC và vuông góc với đường thẳng AC có phương trình là
A. 3x  2 y  z  4  0 .
B. 3x  2 y  z  4  0 .
C. 3x  2 y  z 12  0 . D.
3x  2 y  z  4  0 .
Câu 35.Trong không gian Oxyz, cho hai điểm A 1
 ;2;3, B3;0;1. Vectơ nào dưới đây là một vectơ  
pháp tuyến của mặt phẳng trung trực đoạn AB ? A. n  2; 2; 4 B. n  4; 2; 2 . C. 2   1     n  2; 1
 ;1 . D. n  2; 1  ; 1  . 4   3   Trang 46
Câu 36.Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên chia hết cho 3 gồm ba chữ số. Xác suất để số 1 1 đượ 1 1
c Chọn chia hết cho 5 bằng A. . B. . C. . D. . 5 15 3 6
Câu 37.Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết AC  2 3 , a BD  2a,
SD  2a và SO vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AB và SD bằng 21 2 21 21 2 21 A. a . B. a . C. a . D. a . 3 3 7 7 ln x
Câu 38.Cho hàm số f  x có f   1 1 
và f  x 2  ln x 1.
với x  0 . Khi đó 3 x 2 f  x dx  bằng 2 1 x ln x 1  3 ln 2 ln 2   1 2 ln 2ln 2   1 ln 2ln 2 3 A. . B. . C. . D. 3 3 9 ln 2 ln 2  3 9 2x  12
Câu 39.Cho hàm số f  x  2
x  m  ( m là tham số thực). Có bao nhiêu giá trị nguyên của m để 3
hàm số đã cho nghịch biến trên khoảng 2;   ? A.1. B. 2 . C. 3 . D. 4 .
Câu 40.Cho hình nón có góc ở đỉnh bằng 0
120 . Một mặt phẳng qua đỉnh hình nón và cắt hình nón theo
một thiết diện là một tam giác vuông có diện tích bằng 6 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng A. 9 3 . B. 27 . C. 3 3 . D. 9 . x a  b
Câu 41.Cho x, y là các số thực dương thỏa mãn log x  log y  log x  y và  , với 9 12 16   y 2
a , b là các số nguyên dương. Tính 2
T  a  b A. 25. B. 26 . C. 24 . D. 23 .
Câu 42.Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
y  x  2x  m trên đoạn 0;2 bằng 3 . Tổng tất cả các phần tử của S bằngA.1. B. 3 . C. 4 . D. 2  . x x
Câu 43.Cho phương trình 9  (m  5)3  3m  6  0 ( m là tham số thực). Tập hợp tất cả các giá trị
của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 1; 2 là A. 1;7 . B. 1;7 . C. 1;7 . D. 1;  .
Câu 44.Cho hàm số f  x liên tục trên  . Biết 2x  cos xsin x  2020 là một nguyên hàm của
ex f  x . Họ tất cả các nguyên hàm của hàm số ex f  x là A. 2
2 sin x  sin x cos x  2x  C . B. 2
2 sin x  sin x cos x  2x  2020  C .
C. cos 2x  sin x cos x  2x  2018  C . sin 2x
D.  cos 2x 
 2x  2  C . 2
Câu 45.Cho hàm số f  x có bảng biến thiên như sau .Số nghiệm
thuộc khoảng 0;  của phương trình Trang 47
3 f 2  2cos x  4  0 là . A.1. B. 2 . C. 4 . D. 0 .
Câu 46.Cho hàm số f  x có đạo hàm liên tục trên  và đồ thị f  x
cho ở hình vẽ dưới. Tìm số điểm cực trị của hàm số y  f  2
x  f  x  
1 , biết rằng f   1  3 , f   1  5 ,
20  f 4  13 và f 0  21, f 2  21.
A.5. B.8. C.6. D.7.
Câu 47.Có bao nhiêu cặp số thực  x, y thỏa mãn y nguyên dương và 2    2 3x 3x y 1 2 x  x 1 log  2   2 x 4 1 2 x y 2  2x  x  ? 1 A. 4.
B. 5. C. 6. D. 7.
Câu 48.Cho hàm số f  x liên tục trên R , và thỏa mãn 0   x
f 2 cos x  
1  cos xf 1 sin x 2 3 sin 2  , x
   . Khi đó f
 xdx bằng 2  cos x 1  3 5 A. 3 . B. . C. . D. 5 . 2 2  
Câu 49.Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A . 0
SBA  SCA  90 , SA  a ,
góc giữa hai mặt phẳng SAB, SAC  bằng 0
60 . Tính thể tích khối chóp S.ABC theo a . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 54 6 27 81
Câu 50.Cho hàm số f  x 2
 x  2x . Gọi F x là một nguyên hàm của hàm số f  f  f x. Hàm
số g  x  F  x  3x nghịch biến trong khoảng nào sau đây? A.  2  2;1 2 . B.  2  ;1 2. C. 2 2;4. D. 0;1 2 . BẢNG ĐÁP ÁN 1.B 2.B 3.B 4.B 5.B 6.A 7.A 8.A 9.B 10.C 11.A 12.B 13.D 14.D 15.A 16.A 17.B 18.B 19.B 20.D 21.B 22.C 23.A 24.A 25.A 26.C 27.B 28.B 29.C 30.C 31.A 32.C 33.B 34.A 35.D 36.A 37.D 38.C 39.D 40.C 41.B 42.A 43.B 44.A 45.B 46.D 47.A 48.A 49.A 50.D
LỜI GIẢI CHI TIẾT
Câu 1.Chọn B.Mỗi cách Chọn học sinh từ 14 học sinh là một tổ hợp chập 2 của 14 học sinh. Vậy số 2 cách Chọn là 2
C  91 cách. 14 
Câu 2.Chọn B.Áp dụng công thức n 1 u  q
.u với n  2, n   . n 1 4 4 u   u  33 u
  u .q  33 u
 (1 q )  33 (1) 1 5 Ta có 1 1 1      5 4 u  u  66         2 6 u q u q 66 u q(1 q ) 66 (2) 1 1  1 4 u q(1 q ) 66 33 Lấy chia ta được 1   q  2 q  vào ta được u  . 4 1 u (1 . Thay 2 q ) 33 17 1 Trang 48
Câu 3.Chọn B.Diện tích xung quanh hình trụ là S
 2Rh .Theo đề bài ta có xq 2
4 a  2 Rh  h  2a .
Câu 4.Chọn B.Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên các khoảng  ;  0 và 1;.
Câu 5.Chọn B.Áp dụng công thức tính thể tích khối lăng trụ ta được V  8.12  96.
Câu 6.Chọn A.Điều kiện x  0 . Khi đó 3
log x  3  x  3  27 . 3 3 4 3 4 4 Câu 7.Chọn A.Ta có f
 xdx  f
 xdx f
 xdx  f
 xdx f
 xdx  9( 1  ) 10 . 1 1 4 1 3
Câu 8.Chọn A.Từ bảng biến thiên ta thấy hàm số đạt cực đại tại x  0 và giá trị cực đại của hàm số là y  1
 . Vậy Chọn đáp án A CÐ
Câu 9.Chọn B.Dựa vào đồ thị ta thấy: y 0  3
 loại A,D; y   1  4
 loại C, Chọn B 3  a 
Câu 10.Chọn C.Ta có 3 log 
  log a  log 27  3log a  3  3 log a 1 . 3  3  3 3 3  27  3
Câu 11.Chọn A.Ta có: f
 xdx  sin x 3x 2
dx   cos x 
x  C . 2
Câu 12.Chọn B.Cách 1: Ta có: z 
 i  z   2 2 5 2 5  2  9  3 . 2 2
Cách 2:Ta có: z = z 
 5  2  9 3.
Câu 13.Chọn D.Hình chiếu vuông góc của điềm M (1; 2; 3
 ) lên mặt phẳng (Oyz) là điểm M (  0;2; 3  ) .
Câu 14.Chọn D.Cách 1: 2 2 2 2 2 2
x  y  z  4x  2y  4z 16  0  (x  2)  ( y 1)  (z  2)  25
Tâm mặt cầu (S ) là I (2 ; 1; 2) , bán kính R  5 . Cách 2: 2 2 2
x  y  z  4x  2 y  4z 16  0  a  2  ;b  1
 ;c  2;d  1  6 I   2  ; 1  ;2
Tâm và bán kính mặt cầu (S ) là  2 2 2
R  a  b  c  d  4 1 4 16  5 Câu 15.Chọn A
Từ phương trình mặt phẳng 2x  y  z 1  0 suy ra mặt phẳng này có một véc tơ pháp tuyến là  n  2;1;   1 . Câu 16.Chọn A
Thay tọa độ mỗi điểm M , N , P,Q vào phương trình đường thẳng, ta có đường thẳng d đi qua điểm P(2;0; 2)  .
Câu 17.Chọn B.Ta có CB  SAB  SB là hình chiếu vuông góc của SC lên  SAB . 
Vậy góc giữa đường thẳng SC và mặt phẳng  SAB là CSB .  CB a 1 
Xét tam giác CSB vuông tại B có tan CSB   
.Vậy CSB  30. SB a 3 3
Câu 18.Chọn B.Từ bảng xét dấu, ta thấy f  x đổi dấu từ âm sang dương khi qua x  0 và x  2 nên
hàm số f  x có 2 điểm cực tiểu.
Câu 19.Chọn B.Hàm số xác định và liên tục trên đoạn 1; 4 . Trang 49   9  9 9  x  3 1;4 2  
Ta có: y  x  1  
.  y  0  1
 0  x  9  0   . 2  x  x 2 x x  3    1;4   f   1  10 
Có  f 3  6  min y  6  m và max y 10  M .Vậy m  M 16 . 1; 4  1; 4  f   25 4   4
Câu 20.Chọn D.Ta có  2 ab  2 log
 log a  log b 1 2log b 1 2.2  5 nên ab  là a  2 log  3 a a a a đáp án sai. 
Câu 21.Chọn B.Ta có 2x x 6 2  2
 2x  x  6  x  6 .Vậy tập nghiệm của bất phương trình là S   ;  6 .
Câu 22.Chọn C.Do bán kính đáy của hình nón R  5 và thiết diện của hình nón bị cắt bởi
mặt phẳng qua trục tam giác đều nên độ dài đường sinh của hình nón l  2R 10 2
 S   Rl  R  50  25  75 Vậy Chọn C tp
Câu 23.Chọn A.Ta có 3 f  x  5  0  3 f  x  5  f  x 5  . Số nghiệm của 3 phương trình là số 5
giao điểm của đồ thị y  f  x và đường thẳng y  . 3
Vậy phương trình có 4 nghiệm thực phân biệt. x  x    
Câu 24.Chọn A.Ta có: f  x 3 5 8 8 dx  dx  dx  1
dx  x  8ln x  5  C     x  5 x  5  x  5 
 x 8ln x 5 C .
Câu 25.Chọn A.Ta có  . nr S
A e thay số với A  272056300 , n  2035 2019 16 , r 1.5% .
Ta được số dân của In-Đô-Nê-Xi-a vào năm 2035 ; 16.1,5
S  272056300.e  345851340,2145852
Vì kết quả làm tròn đến hàng trăm nên S  345851300 . 2 3.a
Câu 26.Chọn C.Diện tích đáy là: S  . ABC  4
Tam giác AA ' B ' vuông tại A ' nên ta có: 2 2 AA' 
AB '  A' B '  . a 3 . 2 3 a 3 3a
Thể tích lăng trụ là: V  .
B h  AA'.S  .a 3  .Chọn đáp án C ABC  4 4 2 x  4  x
Câu 27.Chọn B.Hàm số y  2 x  2019x 
có điều kiện xác định là: 2020  2   x  2 2 4  x  0    x 1  x  2  ;2\  1 . 2
x  2019x  2020  0 x  2020  
 Từ điều kiện xác định suy ra không tồn tại lim y và lim y , do đó đồ thị hàm số không có tiệm cận x x ngang. 2   2    x 4 x x 4 x Ta có lim y  lim   lim y  lim       x 1  x 1 
x  1x  và 2020 x 1  x 1   x   1  x  . 2020
Vậy đồ thị hàm số có 1 tiệm cận đứng x 1 .
Kết luận: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 1. Trang 50
Câu 28.Chọn B.Từ đồ thị ta có lim y    a  0 . x
Đồ thị hàm số cắt trục Oy tại điểm có tung độ dương nên d  0 .
Gọi x , x là hoành độ hai điểm cực trị của đồ thị hàm số. 1 2 c
Khi đó x , x là nghiệm của phương trinh 2
y '  0  3ax  2bx  c  0 .Suy ra x x   0  c  0 . 1 2 1 2 3a b
Điểm uốn của đồ thị hàm số nằm bên phải trục Oy 
 0  b  0.Kết luận 3a
a  0, d  0, b  0, c  0 .
Câu 29.Chọn C.Theo hình vẽ 2 đường cong: 3 2
y  x  x  2x  3 ; 2
y  x  x 1 cắt nhau tại các điểm
có hoành độ lầnlượt là: x  1
 ; x 1; x  2 .Ta có diện tích hình phẳng bị giới hạn bởi 2 đường cong trên là: 2  2 3 2
x  x  2x  3   2 x  x   1dx =   3 2
x  2x  x  2 dx 1  1  1
 x 2x  x2 2 3 2 dx    3 2
x  2x  x  2 dx = 1  1 1
x 2x  x2 2 3 2 dx   3 2
x  2x  x  2dx . 1  1 z 4  3i
(4  3i)(1 2i)
Câu 30.Chọn C.Ta có z  1 2i nên z  1 2i . Suy ra 1   2 2 z 1 2i
(1 2i)(1 2i) 2 10  5i   2  i . 5 z
Vậy phần thực của số phức 1 bằng 2 . z2 2 3
1 3i 3  9i  3 3i 4
Câu 31.Chọn A.Ta có z  
 2  2i . Vậy điểm biểu diễn của z là D2;2 2 3
1 3i  3i  i 1 i .          . a b 17
Câu 32.Chọn C.Ta có .
a b  a . b .cos a,b  a       b a b 2 17 1 .cos , 17. 2 2 2 2 2
 1 m  n  68  m  n  67 .
Câu 33.Chọn B.Mặt cầu S  x  y   z  2 2 2 : 3
 5 có tâm I 0;0;3 và bán kính R  5 .   
Ta có d  d  I  P 2.0 0 2.3 3 ,  1. 4 1 4
Khi đó bán kính của đường tròn giao tuyến giữa mặt cầu S  và mặt phẳng P là 2 2 r  R  d  2. 
Câu 34.Chọn A.Ta có tọa độ điểm G 2;2;2  và AC  3; 2;  1 .
Vì mặt phẳng   cần tìm vuông góc với đường thẳng AC nên mặt phẳng   có một véctơ pháp tuyến   là n  3; 2  
;1 .Mặt phẳng   đi qua G 2; 2; 2 và nhận n  3; 2  
;1 làm véctơ pháp tuyến, có phương trình
3 x  2  2 y  2  z  2  0  3x  2y  z  4  0 . 
Câu 35.Chọn D. AB  4; 2  ; 2    22; 1  ;  1 . Trang 51 
Vậy một vectơ pháp tuyến của mặt phẳng trung trực đoạn AB là n  2; 1  ; 1  . 4   999 102
Câu 36.Chọn A.+ Số các số gồm ba chữ số và chia hết cho 3 là:
1  300  n  300. 3
+ Số chia hết cho 3 và đồng thời chia hết cho 5 khi và chỉ khi số đó chia hết cho 15, có tất cả các số 990 105  60 1
1  60 như vậy. Vậy xác suất để lấy được số chia hết cho 5 là p   . 15 300 5
Câu 37.Chọn D.+)Ta có AB // CD  AB // SCD S  d  A ,
B SD  d  AB,SCD  d  ,
A SCD  2d  ,
O SCD .
+)Do tứ giác ABCD là hình thoi tâm O nên AC  BD và AC BD OC   3a,OD   a . A D 2 2
Tam giác SOD vuông tại O 2 2 2 2
 SO  SD  OD  2a  a  a. O B
+)Xét tứ diện OSCD có OS, OC, OD đôi một vuông góc với nhau tại O C
nên tứ diện OSCD vuông tại O . Do đó: 1 1 1 1 1 1 1 7        2 d  , O SCD 2 2 2 2 2 2 2 OS OC OD a 3a a 3a
 d O SCD 21 , 
a  d  AB SD 2 21 ,  a . 7 7 lnx Câu 38.Chọn C.Xét f   x 2 .dx  ln x 1. .dx  .Đặt 2 ln x 1  t x lnx 2 2
 ln x  t 1
.dx  t.dt . x  x ln x 3 2 t 3 2 3 ln 1 1 Suy ra: f 
 xdx  t.tdt  C   C 
.Vì vậy: f  x   C . 3 3 3  x 3 2 ln 1 Do f   1 1 1 1 
  C   C  0 . Suy ra: f x  . 3 3 3 3 2 f  x 2 2 3 2 2 2 (ln x 1) ln x 1 1 Vậy dx  dx  dx      2 ln x   1 d (ln x) 2 2   3x 3 1 x ln x 1 1 3x ln x 1 1 1 2  2 ln 2 ln 2  3 1  1  1  1  3 3  ln x  ln x  ln 2  ln 2      . 3  3  3  3  9 1 2  2 2m 18
Câu 39.Chọn D.Hàm số có tập xác định D   \ m  
3 .Ta có f  x   .
x  m  32 2
 f x  0 khi x 2; 
Hàm số nghịch biến trên 2;     2 m  3  2 2 2m 18  0  3   m  1      . 2 m  1 1   m  3
Do m nhận giá trị nguyên nên m  2  ;1;1; 
2 .Vậy có 4 giá trị nguyên của m thỏa mãn bài toán. Trang 52
Câu 40.Chọn C.Gọi đỉnh của hình nón là S , O là tâm đáy. Mặt phẳng qua đỉnh cắt hình
nón theo thiết diện là tam giác SAB và tam giác SAB vuông cân tại S .Ta có 1 1 2 S  . SA SB 
SA  6  SA  2 3 . S  AB 2 2 
Xét tam giác OSA vuông tại O , góc 0
OSA  60 nên SO  3, OA  3.
Vậy hình nón đã cho có:+ Chiều cao h  SO 
3 .+ Bán kính đáy R  OA  3.
Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho là 1 1 2 V 
 R h  .9. 3  3 3 . 3 3
x  9t ; y 12t
Câu 41.Chọn B.+) Đặt log x  log y  log
x  y  t . Suy ra  . 9 12 16  
x  y 16t +) Do đó: t  3  1   5   t t 2t t   t               t t t 9 12 3 3 4 2 3 1 5 9 12  16   1   1 0              16  16   4   4  t       4  2 3 1 5      4  2 t x 9t  3  1   5 +) Khi đó     
suy ra a  1, b  5 . Vậy 2 2
T  a  b  1 5  26 . y 12t  4  2
Câu 42.Chọn A.Xét hàm số f  x 2
 x  2x  m là hàm số liên tục trên đoạn0;2 .
Ta có: f  x  2x  2 và f  x  0  x  1. f 0  m; f  
1  m 1; f 2  m .  a
m x f  x  a
m xm 1;  m .  a m x y  a
m x f  x  max m 1 ; m   3. 0;2 0;2 0;2 m  3
TH1: m  3   . m  3 
Nếu m  3 thì max y  a m x2;  3  3 . Nếu m  3  thì max y  a m x4;  3  4 . 0;2 0;2 m  4
TH2: m 1  3   . m  2 
Nếu m  4 thì max y  a m x3;  4  4 . Nếu m  2  thì max y  a m x2;  3  3 . 0;2 0;2
Vậy có 2 giá trị của tham số m thỏa mãn yêu cầu bài toán. Khi đó tổng là: 3  ( 2)   1 . Câu 43.Chọn B    m   m       x x x x x
 m   x      x   x  m  3 3 9 ( 5)3 3 6 0 3 3 3 2 3 3 0 3 3 3 2  0   .
3x  m  2
3x  3  x  1 thỏa mãn x 1;2 .Mặt khác: 1;2 3x x   3;9 .
Vậy để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 1; 2 khi và chỉ khi
3  m  2  9 1 m  7. 
Câu 44.Chọn A.Theo giả thiết 2  cos sin  202 
0  ex    ex x x x f x
f  x  2 cos 2x .   ex d  ex u u dx Xét  ex I f  
xdx.Đặt    . dv  f  
xdx v  f  x Trang 53 x x I  f  x x  f
 x x   x    x sin 2 e e d 2 cos 2 2 cos 2
dx  2  cos 2x  2x  1 C . 2 sin 2x 2
I  2  cos 2x  2x 
1 C  2sin x  sin x cos x  2x  C . 2
Câu 45.Chọn B.Ta có 1
  cos x 10  2 2cos x  4, x
  nên từbảng biến thiên của hàm số
2  2cos x  a 0;2
f  x ta suy ra f  
x    f   x 4 3 2 2 cos 4 0 2 2 cos    3
2  2cos x  b  2;4  a  2 cos x   1  ;0   1  2   . b  2 cos x  0  ;1 2  2  Phương trình   1 có 1 nghiệm 1
x thuộc khoảng 0;  .
 Phương trình 2 có 1 nghiệm x2 thuộc khoảng 0;  . Hai nghiệm 1
x , x2 phân biệt.Vậy số nghiệm thuộc khoảng 0;  của phương trình
3 f 2  2cos x  4  0 là 2 nghiệm.
Câu 46.Chọn D.Trước tiên ta xét hàm số v  x  f  2
x  f x   1  . 
Ta có v   f   2
x  f x     f x   x f    2 1 1 2
x  f x   1  .
 f (x 1)  2x  0  2    
 f x   f  x  1 x 1 1  2x  0 
Xét phương trình v  0         f    f  x  2 1 x 3 . 2
x  f x   1   0 *
 f x   2 1  x  4 
 f x   2 1  x  1  
Ta tịnh tiến đồ thị hàm số f  x sang bên trái một đơn vị, khi đó đồ thị
của hàm số y  f  x  
1 và hàm số y  2x được biểu diễn trên hệ trục tọa độ như sau.
Như vậy phương trình f  x  
1  2x  0 có 3 nghiệm là
x  1, x  0, x  1.
Xét hàm số g  x  f  x   2
1  x , có g x  f  x   1  2x . g  2
   f   1  4  5  4  1  g  
1  f 0 1  20 
Kết hợp với giả thiết, ta được g 0  f   1  3 .
g 1  f 21 20 
g 3  f 416  3;4
Dựa vào đồ thị ở trên, khi đó ta có bảng biến thiên của hàm g  x như sau. Trang 54
Từ bảng biến thiên có thể xét sự tương giao của hàm g  x với lần lượt các đường thẳng y  1
 , y 1, y  3, y  4 , từ đó suy ra phương trình * có tất cả 7 nghiệm, như vậy hàm số vx có
tất cả 9 điểm cực trị. Suy ra số điểm cực trị của hàm số y  f  2
x  f  x  
1  chính bằng 2 lần số
điểm cực trị dương của hàm số v  x cộng với 1 và bằng 7 .
Câu 47.ChọnA.Điều kiện: 2
3x  3x  y 1  0 . Ta có: 2    2 3x 3x y 1 2 x x 1 log  2   2 x 4 1 2
x y   log 2
3x  3x  y   1  log  2 2x  x   2 2 2 x x 1 
3x 3x y 1 1  2  2  2 2x  x 1  log 2
3x  3x  y   2
3x 3x y 1 1  2   log 2 2x  x   2 2 x x 1 1  2  * Xét    log  2t f t t
là hàm số đồng biến trên 0;  . Do đó:
   f  2x  x y   f  2x  x  2 2 2 * 3 3 1 2
1  3x  3x  y 1  2x  x 1
(2)  x  4x  y  0 ** Điều kiện  
1 luôn được thỏa mãn do 2 .
Vì vậy để tồn tại  x, y thỏa mãn yêu cầu thì ** có nghiệm. Khi đó ta được 4  y  0  y  4 .
Do y nguyên dương nên y 1;2;3; 
4 . Ta có 4 cặp  x, y thỏa mãn yêu cầu bài toán. Câu 48.Chọn A. x   , ta có:   x  x
f 2 cos x  
1  cos xf 1 sin x 2 2 3 sin 4 cos 2    2  cos x 2  cos x 2  cos x  x f  x    x x f  2 sin . 2cos 1 sin .cos .
1 sin x  2  cos xsin x π π π 2  sin . x f  2cos x   2 1 dx  sin . x cos . x f  1sin x 2 2
dx  2 cos x.sin d x x .   1 0 0 0 π 2 1 + Xét: I   sin .
x f 2 cos x 1 dx .Đặt t  2 cos x 1  dt  2 sin xdx  sin xdx   dt . 1   0 2 π 1  1 1 1 1 1
Đổi cận: x  0  t 1; x 
 t  1.Suy ra: I   f t dt  f t dt  f x dx    . 1       2 2 2 2 1 1  1  π 2 + Xét: I   sin . x cos . x f  2
1 sin x dx .Đặt 1  0 1 2
t  1 sin x  dt  2 sin x.cos xdx  sin x.cos xdx   dt . 2 π 0 1 1 1 1 1
Đổi cận: x  0  t 1; x 
 t  0 .Suy ra: I   f t dt  f t dt  f x dx    . 2       2 2 2 2 1 0 0 Trang 55 π π π 2 2 2  1   1 
+ Ta có: 2  cos x.sin xdx  2sin x  sin 2x dx  2
 cos x  cos 2x      2   4  0 0 0 1      3 2 1 1  4 2 1 1 1 1 3 0 1 3 0 Thay vào, ta được:
f  x dx 
f  x dx     f
 xdx   f
 xdx 3. 2 2 2 2 2 1  0 1  1  Câu 49.Chọn A
 Đặt AB  AC  x ; gọi M là trung điểm BC
 Tam giác ABC vuông cân tại A nên BC  x 2 .  Do ABC 
vuông cân tại A , SAB  , SAC 
lần lượt vuông tại B, C nên S  AB  S  AC . Do đó nếu
kẻ BI  SA I  SA thì CI  SA,
từ đó ta được SA  mp  IBC  , góc giữa hai mặt phẳng SAB, SAC  là góc giữa hai S
đường thẳng BI ,CI .   0  I TH 1 : 0
BIC  60  BIM  30 .Do IB  IC  Tam giác IBM vuông tại M , x 2 BM x 2 C A BM   BI  
.2  x 2  x  AB . 0 2 sin 30 2 M   0  TH2: 0
BIC  120  BIM  60 . Tương tự trên ta tính được B BM x 6 x 6 BI   ; IM  . 0 sin 60 3 6 2 x o S
 AB vuông ở B đường cao BI nên 2
AB  AI.AS  AI  . a 4 x x o A
 IB vuông tại I nên 2 2 2 2 2 BI  AB  AI  x   a  x . 2 a a x x 6 a 3 a a 2 2  a  x   x  2 6  IM  ; BC  . a 3 3 6 3 1 a a a V V V  S SI  IA  IM BC SA  a  . S ABC S IBC A IBC I  BC   3 1 1 1 2 6 3 . . . . . . . . . . 3 3 2 6 6 3 54
Câu 50.Chọn D.Ta có g x  f  f  f x 3.
Trước hết ta tìm các nghiệm của phương trình f  f  f x 3  0 . a  3
Đặt a  f  f  x , phương trình trở thành: f a 2
 3  a  2a 3  0   a  1 
Với a  3: Suy ra f  f  x  3. b  3
 f x  3
Ta đặt b  f  x  f b 2 2
 3  b  2b  3  b  2b  3  0     b  1   f   x  1  Với a  1
 Suy ra f  f x  1
 . Ta cũng đặt b  f  x .
 f b    b  b    b  2 2 1 2 1 1
 0   f x  2 1  0 .Vậy ta được:
g x  f  f  f  x    f  x   f  x   f  x  2   2
x  x   2
x  x   2 3 3 1 1 2 3 2
1 x  2x  2 1 Trang 56 x  1  
g x  0  x  1 2  x  3 
Bảng xét dấu g x
Dựa vào bảng xét dấu, ta có hàm số g  x nghịch biến trên 1;3 .
Cách 2:Ta có g x  f  f  f x 3. g x  0  f  f  f x  3.
Theo đề ra ta có f  x 2
 x  2x  f x  1  , x
  và f x  3  1   x  3 .
Vậy f  f  f x  3  1
  f  f x 3 1 f x 3 1 x  3
Bên cạnh đó g x là hàm đa thức nên g x  0 tại hữu hạn điểm.
Vậy g  x nghịch biến trên 1;3 . www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 24 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2 Thời gian: 120 phút
Câu 1.Bạn Vy có 3 cây viết chì, 8 cây viết bi xanh và 2 cây viết bi đỏ trong hộp bút,các cây viết phân
biệt. Có bao nhiêu cách để bạn Vy Chọn ra một cây viết? A.10 . B.13 . C.11. D. 48 .
Câu 2.Cho cấp số nhân u
với u  2 và u  64
 . Số hạng đầu của cấp số nhân đã cho bằng n  2 7 1 A. 2  . B. 1. C.1. D. . 2
Câu 3.Diện tích xung quanh của hình trụ có đường cao h và bán kính đáy r bằng
A.  rh .
B. 2 rh . C. 2  r h . D. 4 rh .
Câu 4.Cho hàm số y  f  x có đồ thị như hình vẽ.Chọn khẳng định sai trong các khẳng định y 4 sau đây?
A.Hàm số nghịch biến trên khoảng 2;  .B.Hàm số nghịch biến trên khoảng  ;0  . 1 O x 2 3
C.Hàm số đồng biến trên khoảng 0; 
1 .D.Hàm số đồng biến trên khoảng 0;3 .
Câu 5.Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Thể tích khối lăng trụ tam giác 3 a 3 3 a 3 3 a 2 3 a 3
đều đã cho bằng A. . B. . C. . D. . 4 2 4 3 Trang 57 9 7
Câu 6.Nghiệm của phương trình log
2x 1  3A. x  .
B. x  4 . C. x  . D. 2   2 2 x  3. 2 3 3 Câu 7.Nếu
f  xdx  2   và
f  x dx  1   thì 4. f  x  dx 1 1 2 bằng A. 3
 . B. 4 . C.1. D. 3 .
Câu 8.Cho hàm số y  f  x có bảng biến thiên như sau:
Tổng giá trị cực tiểu và giá trị cực đại của hàm số đã cho bằng
A. 2 .B. 3 . C. 0 .D. 2  .
Câu 9.Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? x  2 2  x A. y  y  . C. 4 2
y  x  2x . D. 3 2
y  x  3x . x  . B. 1 x 1
Câu 10.Với a là số thực dương tùy ý, log  2 a   log 2020 100a bằng 2 
A. 2  2022 log a . B. 2  log a  2020 log a . 2 2 1 C.  
2  2020 log a  2 log a . D. 2 2020 log a log a . 2 2 2
Câu 11.Họ tất cả các nguyên hàm của hàm số f  x  s inx  4x là A. 2
cos x  4x  C . B. 2
cos x  2x  C . C. 2
 cos x  x  C . D. 2
cos x  2x  C . 
Câu 12.Môđun của số phức 3
2i bằng A. 13 . B.13 . C. 5 . D. 5 .
Câu 13.Trong không gian với hệ tọa độ Oxyz , điểm đối xứng của M 1; 2; 3 qua trục Ox có tọa độ là
A. 1;  2;  3 .
B. 1; 0 0 .
C. 0; 2; 3 . D.  1  ;  2; 3 .
Câu 14.Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  2 y  4z  2  0 .
Tính bán kính r của mặt cầu.A. r  2 2 . B. r  26 .
C. r  4 . D. r  2 . Trang 58 x y z
Câu 15.Trong không gian Oxyz , cho mặt phẳng   :  
 1. Vectơ nào dưới đây không là 1 2 2      1 1 
vectơ pháp tuyến của   ? A. n  1;2; 2
 . B. n  2;1;1 . C. n  1; ; . 2   1   3    2 2  
D. n  2; 1;1 . 4   x 1 y  2 z
Câu 16.Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   , vectơ nào dưới 1 3 2   
đây là vtcp của đường thẳng d ?A. u   1  ; 3  ;2 .
B. u  1;3; 2 . C. u  1; 3  ; 2   .  D. u   1  ;3; 2   .
Câu 17.Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và
SA  a 2. Góc giữa đường thẳng SC và mặt phẳng  SAB bằng A. 45. B. 30 .
C. 60 . D. 90 . f  x f  x Câu 18.Cho hàm số , bảng xét dấu của như sau:
Số điểm cực trị của hàm số đã cho là A. 0 .
B. 2 . C.1. D. 3 .
Câu 19.Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y  x  3x  2 trên đoạn  1  ; 
1 . Tính M  m.A.1. B. 0 . C.2. D.3. 2 1
Câu 20.Cho các số thực dương a, ,
b x thoả mãn log x 
log a  log b . Mệnh đề nào dưới đây 1 1 1 3 5 2 2 2 đúng ? 2 1 2 1 2 2 1  A. 3 5 x  a b 5 . B. x  a  b . C. 3 x a b  3 5  . D. x a b . 3 5 2 2 x 1  2 x  x6  1   1 
Câu 21.Tập nghiệm của bất phương trình      là  2   2       5   5  A.    5 ; 1  ;  
 . B.   5 ; 1  ;   .C. 1  ; . D. 1  ;  .    2  2   2   2  Trang 59
Câu 22.Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB
và CD thuộc hai đáy của khối trụ. Biết AD  6 và góc CAD bằng 60 .
 Thể tích của khối trụ là
A.126 . B. 24 . C.162 . D.112 . y 2
Câu 23.Cho hàm số y  f  x có đồ thị như sau
Số nghiệm thực của phương trình 3 f  x  2020  0 là 2  O 1 x
A. 2 . B. 0 . C. 3 . D.1. 2  2  x 3
Câu 24.Họ tất cả nguyên hàm của hàm số f (x)    trên khoảng ( ; ) là: 2x  32 2 1 1 1 1 A.  ln 2x  3   C  ln 3  2x   C 4 4(2x  . B.   3) 4 4(2x  . 3) 1 1 1 1 C. ln 3  2x   C ln 3  2x   C 2 2(2x  . D.   3) 2 2 2(2x  . 3)
Câu 25.Để dự báo dân số của một quốc gia, người ta sử dụng công thức nr
S  Ae ; trong đó A là dân số
của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Biết rằng năm 2001,
dân số Việt Nam là khoảng 78.685.800 người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là 1,7%, cứ
tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người. A. 2022. B.2026. C. 2025. D. 2021.
Câu 26.Cho khối lăng trụ đứng AB . C  A  B 
C có đáy ABC là tam giác vuông cân tại B và AC  a 2 ,
AC ' tạo với đáy một góc 0
30 . Tính thể tích V của khối lăng trụ đã cho. 3 6 3 3 6 3 A.  a V . B.  a V . C.  a V . D.  a V . 3 6 6 3 x  3  2
Câu 27.Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  2 x  3x  2
làA. 0 . B.1. C. 2 . D. 3 . 3 2
Câu 28.Cho hàm số y  ax  bx  cx  d có đồ thị như hình bên. Trong các giá trị
a, b, c, d có bao nhiêu giá trị âm?
A.1. B. 2 . C. 4 . D. 3 .
Câu 29.Cho đồ thị hàm số
y  f  x trên đoạn  2
 ;2 như hình vẽ dưới. Biết 1  2 
f  x dx  f  x 22 dx    15 2  1 Trang 60 1 76 và
f  x dx  
. Tính diện tích hình phẳng gạch chéo 15 1  98 32 18 A. B. . C. . D. 8 . 15 15 5
Câu 30.Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 1 2 2 2 z  z bằng 1 2
A. 6 . B.16 . C. 26 . D. 8 .
Câu 31.Trong mặt phẳng Oxy , cho các điểm A , B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số 1 1
phức.A. 2  i . B. 2  i . C.   2i . D. 1   2i . 2 2  
Câu 32.Trong không gian Oxyz , cho các vectơ a  2;1;5 , b  1;1; 4 và      c   ;
x 2;5 . Tìm x thỏa mãn .
a a  b  c  90.
A. x  5. B. x  5  .
C. x  0 . D. x 1 .
Câu 33.Trong không gian Oxyz , cho mặt cầu  S  có tâm là điểm I  6
 ;0;0 và đi qua điểm
M 0;0;8 . Phương trình của S  là
A.  x  2 2 2 6
 y  z 100 .B.x  2 2 2 6
 y  z 10 .C. x  2 2 2 6
 y  z 100 . D. x  2 2 2 6
 y  z 10.
Câu 34.Trong không gian với hệ trục Oxyz , cho A1; 0; 3 , B 3; 2; 
1 . Mặt phẳng trung trực của đoạn
thẳng AB có phương trình là
A. 2x  y  z 1  0 .
B. x  y  2z 1  0 .
C. 2x  y  z 1  0 . D.
x  y  2z 1  0 .
Câu 35.Trong không gian Oxyz, đường thẳng song song với hai mặt phẳng  P : 3x  y  3  0 ,
Q:2x  y  z 3  0 có một véc tơ chỉ phương là r r r
A. u = 1;3;1 .
B. u = 1;- 3;- 1 .
C. u = - 1;- 3;1 . D. 3 ( ) 2 ( ) 1 ( ) ru = 1;- 3;1 . 4 ( )
Câu 36.Có 9 viên bi xanh được đánh số từ 1 đến 9; 6 viên bi đỏ được đánh số từ 1 đến 6 và 5 viên bi vàng
được đánh số từ 1 đến 5. Chọn ngẫu nhiên 4 viên bi. Tính xác suất để 4 viên bi được Chọn có đủ 3 màu, 362 17 11
có cả số chia hết cho 3 và số không chia hết cho 3? A. . B. . C. . 7752 323 969 586 D. . 1615 Trang 61
Câu 37.Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB  2a , AD  DC  CB  a , SA
vuông góc với đáy và SA 
3a . Khoảng cách giữa hai đường thẳng BC và SD bằng a 3 a 3 a 15 A. . B. a . C. . D. . 5 2 5 1 1 2
Câu 38.Cho hàm số f ( x) có f (0)  và f '( x)  , x
  R . Khi đó f (x)dx  bằng? 2 x x 2 (e  e ) 0 2 1 e  1 2 1 e  1 2 1 e  1 1 A. ln . B. ln . C. ln . D. 2 ln(e  1) 2 2 2 2 2 4 2 . 2x  4
Câu 39.Cho hàm số y 
. Có bao nhiêu giá trị m nguyên âm để hàm số đã cho nghịch biến trên x  m khoảng (0 ;1) . A. 0 . B. 2 . C.1. D. 3 .
Câu 40. Cho hình nón đỉnh S , đáy là hình tròn tâm O , bán kính, R  3cm , góc ở đỉnh hình nón là
  120. Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB , trong đó A , B thuộc
đường tròn đáy. Diện tích tam giác SAB bằngA. 2 3 3 cm . B. 2 6 3 cm . C. 2 6 cm . D. 2 3 cm . x
Câu 41.Cho các số thực dương x , y thỏa mãn log x  log y  log
4x  5y 1. Tính . 4 6 9   y x 4 x 2 x 3 x 9 A.  . B.  . C.  . D.  . y 9 y 3 y 2 y 4
Câu 42.Cho hàm số y  f (x) liên tục và có đồ thị như hình vẽ
Gọi S là tổng các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số
g(x)  | f (x)  m | trên đoạn [ 1; 3] nhỏ hơn hoặc bằng 2 505 . A. 2019  . B. 2018 .
C. 1. D. 0 . 2 1 2
Câu 43.Cho phương trình m   1 log x  2  4 m 5 log  4m  4  0 1     1 x 2 2 2
( m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có 5   7   7   7   7  nghiệm thuộc đoạn , 4   là A. 3;   . B. ;   . C. 3;  . D. 1;   .     2   3   3   3   3  Trang 62
Câu 44.Cho a là số thực dương. Biết rằng F  x là một nguyên hàm của hàm số     x f x  ax 1 e ln    thỏa mãn  x   1  F  0   và F   2020 2020  e
. Mệnh đề nào sau đây đúng?  a   1   1  A. a  ;1 
 . B. a  0; 
. C. a 1;2020 .
D. a 2020; .   2020   2020
Câu 45.Cho hàm số f (x) có đồ thị như sau:
Số nghiệm thuộc đoạn [0 ; 3 ] của phương trình 2 f (cos x) 1  0 là:
A.12 . B. 6 . C.10 . D. 8
Câu 46.Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số g  x  f  3 2
x  3x  4 là
A.5. B.3. C.7. D.11.
Câu 47.Có bao nhiêu cặp số nguyên ( ;
x y) thỏa mãn 0 £ x £ 2020 và log 4  4   1 2y x x y
? A.10 . B.11. C. 2020 . D. 4 . 2  
Câu 48.Cho hàm số y  f (x) liên tục trên 0;  4 thỏa mãn f  2 x    2
x   f  4 2 x  x   4 2 2 1 2
1  4x  8x  2x  4 . Tính tích phân f  x dx  0 32 13 23 2 A. . B. . C. . D. . 3 3 3 3
Câu 49.Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , BA  BC  a 3 . Khoảng cách từ A
đến mặt phẳng SBC bằng a 2 và  
SAB  SCB  90 . Tính thể tích khối chóp đã cho. 3 a 3 a 6 A. 3 a . B. 3 a 6 . C. . D. . 2 2
Câu 50. Cho hàm số f  x . Hàm số y  f ' x có đồ thị như hình bên. x
Hàm số g  x  f  x   3 1 
 3x nghịch biến trên khoảng nào dưới 3 Trang 63 đây? A.  1  ;2 . B. 2  ;0 . C. 0; 4 . D. 1;5 . BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B B B D A A B D A C B A A A A A B B B D C C D B B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C C B D A C A A D D D D A C A D A C A A C B A D A
LỜI GIẢI CHI TIẾT Câu 1.Chọn B
Số cách Chọn một cây viết từ 3 cây viết chì, 8 cây viết bi xanh và 2 cây viết bi đỏ là 3  8  2 13 cách. 5 u
Câu 2.Chọn B.Ta có u  u .q 7  q 
 2.Số hạng đầu của cấp số nhân đã cho bằng 7 2 5 u2 u2 u   1  . 1 q
Câu 3.Chọn B.Sử dụng công thức tính diện tích xung quanh của hình trụ ta có: S
 2rl  2rh . xq
Câu 4.Chọn D.Vì trên khoảng 2;3 hàm số nghịch biến.
Câu 5.Chọn A.Khối lăng trụ tam giác đều là lăng trụ đứng có cạnh bên bằng a, đáy là tam giác đều cạnh a. 2 3 a 3 a 3 Khi đó V  a.  . 4 4 9
Câu 6.Chọn A.Ta có log 2x 1 3
 3  2x 1  2  x  2 2 3 2 3 Câu 7.Chọn B.Ta có: f
 xdx  f
 xdx f  xdx 1 1 2 3 3 2
 f (x)dx  f (x)dx  f (x)dx  1  ( 2  ) 1    2 1 1 Trang 64 3 3 Vậy: 4. f
 xdx  4 f (x)dx  4  2 2
Câu 8.Chọn D.Dựa vào bảng biến thiên ta thấy: giá trị cực tiểu của hàm số đã cho là y  4 tại x  3.
và giá trị cực đại của hàm số đã cho là y  2 tại x  0 . Vậy tổng của giá trị cực đại và giá trị cực tiểu bằng ( 4)   2  2 
Câu 9.Chọn A.Dựa vào đồ thị hàm số thấy đây không thể là đồ thị hàm bậc 3 và đồ thị hàm trùng
phương nên loại đáp án C vàD.
Dựa vào đồ thị ta thấy hàm số đồng biến trên mỗi khoảng   ;1  và 1; x  2 Xét hàm số y  D   \ 1 . x  với tập xác định   1 1 Ta có y     
suy ra hàm số đồng biến trên mỗi khoảng   ;1  và 1; . x   0, x D 2 1 2  x Xét hàm số y  D   \ 1 . x  với tập xác định   1 1 Ta có y      
suy ra hàm số nghịch biến trên mỗi khoảng   ;1  và 1; . x   0, x D 2 1
Câu 10.Chọn C.Ta có: log  2 a   log 2020 100a
  2log alog100log 2020 a 2 2 
 2log a  2  2020log a . 2
Câu 11.Chọn B.Ta có:   x 2 s inx 4
dx   cos x  2x  C .
Câu 12.Chọn A.Ta có:  i    2 2 3 2 3 2  13 .
Câu 13.Chọn A.Gọi H là hình chiếu vuông góc của M lên Ox nên H 1;0;0 .
M  là điểm đối xứng với M qua Ox suy ra H là trung điểm của MM  . x     2x x 1 M H M  Ta có:  y        2 y y 2 . Vậy M 1; 2; 3 . M H M x       2x x 3 M H M
Câu 14.Chọn A.Mặt cầu  S  có tâm I 1;1;2 và bán kính 2 2 2
r  1  1  2   2    2 2 . x y z   1 1 
Câu 15.Chọn A.Mặt phẳng   :    1 n  1; ;    suy ra đáp án 1 2 2 
có vectơ pháp tuyến là 3  2 2  C đúng Trang 65    
+ n  2n nên đáp án B đúng + n  2
 n nên đáp án D đúng 2 3 4 3
Câu 16.ChọnA.Từ phương trình chính tắc của đường thẳng d suy ra vtcp    v  1;3; 2
   u    1 .v   1  ; 3
 ;2 cũng là 1 VTCP của d . SA   ABCD
Câu 17.Chọn B .Ta có  .    
  SA  BC BC ABCD
Mặt khác do ABCD là hình vuông nên BC  AB. S BC  SA Như vậy 
 BC  SAB . BC  AB a 2 D a A
Suy ra SC SAB  SC SB  , ,  BSC . B C  BC BC a 1  Trong S
 BC có tan BSC      BSC  30. 2 2 SB AB  SA a 3 3
Câu 18.Chọn B.Hàm số có hai điểm cực trị lần lượt là x 1 , x  2 .
x  3 không phải điểm cực trị vì hàm số không xác định tại x  3. x  0 1  ;1 2  
Câu 19.Chọn B.Ta có: y '  3x  6 ; x y '  0   . x  2  1    ;1
y(0)  2, y(1)  0, y( 1  )  2
 .Do đó M  2, m  2 .Vậy M  m  0. Câu 20.Chọn D.Ta có 2 2 2 1 1 1 2 1      3 3 3 5 5 5 log x  log a 
log b  log a  log b
 log a b   x  a b . 1 1 1 1 1 1 3 5   2 2 2 2 2 2 2 2 x 1  2 x  x6  1   1 
Câu 21.Chọn C.Ta có:       2
2x 1  2x  x  6 2
 2x  3x  5  0  2   2  5
 1  x  . 2 2 2 x 1  2 x  x6  1   1   5 
Vậy tập nghiệm của bất phương trình      là 1  ; . Đáp ánC.    2   2   2  Trang 66 Câu 22.Chọn C D C  DC
Ta có xét tam giác ACD có: tan DAC    DC  A . D tan DAC 0  6.tan 60 AD  6 3 600 A B 1
Vì DC là đường kính của khối trụ nên suy ra bán kính khối trụ là R  DC  3 3 2
 diện tích đáy khối trụ là 2
S   R    2 3 3  27
Suy ra thể tích khối trụ là V  .
h S  6.27 162 . 2020
Câu 23.Chọn D.Ta có 3 f  x  2020  0  f  x  . 3
Số nghiệm của phương trình trùng với số giao điểm của đồ thị hàm số y  f  x và đường thẳng 2020 y  . 3 2020 2020 Do
 2 nên từ đồ thị ta có đồ thị hàm số y  f x và đường thẳng y  cắt nhau tại 1 3 3
điểm. Vậy phương trình có 1 nghiệm thực. 1 1  (2x  3)  1 1 1 1
Câu 24.Chọn B.Ta có: 2 2 f (x)dx       dx+ dx   2x  3 dx 2 2 2x  3 2 2x  32 1 1   1 1 ln 2x  3 
 C   ln 3 2x   C 4 4(2x  3) 4 4(2x  . 3)
Câu 25.Chọn B.Áp dụng công thức nr
S  Ae , gọi n là số năm tính từ năm 2001 đến thời điểm dân số
Việt Nam đạt mức 120 triệu người.Dân số Việt Nam năm tại thời điểm đó là 120 triệu người nên ta có n.1.7%
S  78.685.800.e
 120.000.000  n  24.8
Vậy 2026 thì dân số Việt Nam sẽ ở mức 120 triệu người.
Câu 26.Chọn C.Do ABC là tam giác vuông cân tại B và AC  a 2 nên BA  BC  a 
Do AC ' tạo với đáy một góc 30 nên ( AC ', ( ABC))  ( AC ', AC)  CAC  30 3 6
Suy ra CC '  A .
C tan 30  a 2.  a 3 3 3 1 6 6
Vậy thể tích của khối lăng trụ đứng AB . C  A  B C là  . .  a V a a a . 2 3 6 Trang 67
Câu 27.Chọn C.TXĐ: D   3  ; \1;  2 x  3  2 - Ta có: lim y  lim
 0 Nên đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số. 2 x
x x  3x  2 x  3  2 x 1 1 1
- Lại có: lim y  lim  lim  lim     2   x 1  x 1    x 1 x 3x 2  x  
1  x  2 x  3  2 x 1 
x  2 x  3  2 4 x  3  2 x  1 1 1 lim y  lim  lim  lim     2   x 1  x 1    x 1 x 3x 2  x  
1  x  2 x  3  2 x 1 
x  2 x  3  2 4 x  3  2 x 1 1 lim y  lim  lim  lim     2   x 2 x 2   x 2 x 3x 2 x  
1  x  2 x  3  2 x2  x  2 x  3  2
Nên đường thẳng x  2 là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 28.Chọn B.Qua đồ thị ta thấy: đồ thị hàm số 3 2
y  ax  bx  cx  d giao với trục Oy tại
điểm D 0;d  nằm phía dưới trục Ox nên d  0 , và hình dạng của đồ thị hàm số ứng với
trường hợp a  0 .
Hàm số đạt cực tiểu tại x  0 , đạt cực đại tại x  0 và x  x  0 . x , x là hai nghiệm của 1 2 1 2 1 2 phương trình 2
3ax  2bx  c  0 .  2  b  0
S  x  x  0  b   0 Khi đó: 1 2 3a    mà a  0 nên:  . P  x x  0 c  c  0 1 2   0 3a a  0
Vậy có 2 giá trị âm trong các giá trị a , b , c , d là  . d  0
Câu 29.Chọn D.Dựa vào đồ thị, ta có diện tích hình phẳng bằng 2 1  1 2 f
 xdx   f
 xdx f
 xdx f  x 22 76 22 dx     8 . 15 15 15 2  2  1  1 z  z  4 Câu 30.Chọn A. 1 2
Vì z , z là nghiệm của phương trình 2
z  4z  5  0 nên ta có:  1 2 z .z  5  1 2
Khi đó: z  z   z  z 2 2 2
 2z z 16 10  6. 1 2 1 2 1 2 Trang 68  1 
Câu 31.Chọn C.Ta có: A 2  
;1 , B 1;3 .Trung điểm AB là I  ;2 
 biểu diễn số phức là  2  1 z    2i . 2       
Câu 32.Chọn A .Ta có: a  b  c  3  ; x 4;14 .Suy ra .
a a  b  c  23 x  4.114.5  2x 80 .     Theo giả thiết .
a a  b  c  90  2x 80  90  x  5.Vậy x  5 thỏa mãn yêu cầu đề bài.
Câu 33.Chọn A.Bán kính mặt cầu là R  IM 10 .Vậy phương trình của mặt cầu  S  là: x  2 2 2 6
 y  z 100
Câu 34.Chọn D.Trung điểm của đoạn thẳng AB là I  2;1;  
1 . Mặt phẳng trung trực đoạn thẳng AB 
chứa I và có vectơ pháp tuyến là AB   2; 2; 4 , nên có phương trình
2 x  2  2 y   1  4 z  
1  0  x  y  2z 1  0 .  
Câu 35.Chọn D.  P và Q lần lượt có véc tơ pháp tuyến là n  3;1;0 và n  Q 2;1; 1 P     
Vì đường thẳng đề bài cho song song với hai mặt phẳng P :3x  y 3  0 , Q : 2x  y  z  3  0  
nên có véc tơ chỉ phương là n
 n  1;3;      1 . P Q
Câu 36.Chọn D.Ta có n 4  C . 20
Xét cách Chọn 4 viên bi đủ 3 màu. 2 1 1 1 2 1 1 1 2
C .C .C  C .C .C  C .C .C  2295 . 9 6 5 9 6 5 9 6 5
Xét cách Chọn 4 viên bi đủ 3 màu và mọi số chia hết cho 3. 2 1 1 1 2 1
C .C .C  C .C .C  9 . 3 2 1 3 2 1
Xét cách Chọn 4 viên bi đủ 3 màu và mọi số không chia hết cho 3: 2 1 1 1 2 1 1 1 2
C .C .C  C .C .C  C .C .C  528 . 6 4 4 6 4 4 6 4 4
Suy ra số cách Chọn 4 viên bi đủ 3 màu và có cả số chia hết cho 3 và không chia hết cho 3 là: 2295  9  528  1758 . 1758 586
Xác suất cần tìm: P   . 4 C 1615 20 Câu 37.Chọn D Trang 69
Gọi E là trung điểm của AB , ta có BC  DE . Suy ra BC SDE  .
 d BC,SD  d BC,SDE  d B,SDE  d  ,
A SDE  .Hạ
AF  DE F  DE  DE  SAF  .
Hạ AH  SF  H  SF  . Suy ra AH  SDE  .  d  ,
A SDE  AH . a 3 1 1 1 1 4 5 Ta có: A
 DE đều cạnh a , suy ra AF  .Trong SAF  :      . 2 2 2 2 2 2 2 AH SA AF 3a 3a 3a 2 3a a 15 a Suy ra 2 AH   AH 
.Vậy d  BC SD  d  A SDE 15 , ,  AH  . 5 5 5 2 x 2 2 2e d( x e  1) 1 f (x)  dx  dx     C    x  x 2 2 x 2 2 x 2 2 (e  e ) (e  1) (e  1) x e  1 Câu 38.Chọn ATa có: 2 1 1 1 x e f (0)   
 C   C  1  f (x)  2.0 2 2 e  1 2 x e  1 1 1 2 x 1 2 x 2   Khi đó: e 1 dx(e 1) 1 e 1
 f (x)dx  dx   ln    2 x 2 e  1 2 x e  1 2 2 0 0 0 2  m  4
Câu 39.Chọn C.Tập xác định của hàm số D  ( ; m)  (m;  ) .Ta có: y '  2 (x  . m) m  2   2  m  4  0  m 1
Hàm số nghịch biến trên (0 ;1)  y '  0 x  (0;1)  
 m 1   . m(0;1)   2   m  0 m  0 Như vậy m  1
 thỏa mãn yêu cầu bài toán. Trang 70
Câu 40. Chọn A.Theo đề bài ta có góc ở đỉnh hình nón là   120 và khi cắt hình nón S
bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Do góc ở đỉnh hình nón là   120  nên OSC  60 . B D C OC OC O
Xét tam giác vuông SOC ta có  tan OSC   SO  3   3 . A SO  tan OSC tan 60
Xét tam giác vuông SOA ta có 2 2
SA  SO  OA  2 3 .
Do tam giác SAB đều nên S    3 3  2 cm  . SA  B  2 1 2 3 .sin 60 2 x  4t 
Câu 41.Chọn D.Đặt t  log x  log y  log
4x  5y 1. Suy ra  y  6t . 4 6 9    t 1
4x  5 y  9   9.9t  Vì t t  t  2 9 .4 6 nên ta có t t  t  2 9.9 .4 9. 6 . Hay là  x 4x  5y  9 2 2 2
x  9 y  4x  5xy  9 y  0   x  y4x  9 y  0  4x  9 y   .Vậy  y 4 0 x 9  . y 4
Câu 42.Chọn A.Xét hàm số u  f (x)  m trên đoạn [ 1; 3] có
max u  u(1)  f (1)  m  m  2 và min u  u(0)  f (0)  m  m 1 [ 1  ;3] [ 1  ;3]
Suy ra giá trị lớn nhất của hàm số y |
 f (x)  m | trên đoạn [ 1;3] là max{| m  2 |,| m -1|}
Do đó max g(x)  max{ | m  2 |, | m -1|}. Suy ra, hàm số đã cho có giá trị lớn nhất nhỏ hơn hoặc [ 1  ;3] |
 m  2 || m -1| 2020 (1)
bằng 2 505 khi và chỉ khi  |
 m 1|| m  2 | 2020 (2)  1 |
 m  2 || m 1| m   1 Ta có+) (1)     2  2  019 m  |  m 1| 2020 2  2  019 m 2021  1 |
 m 1|| m  2 | m   1 +) (2)     2    m 2018 |  m  2 | 2020 2  2  022 m 2018
Từ hai trường hợp trên suy ra 2
 019  m  2018 . Trang 71
Vì vậy, tổng các giá trị nguyên thỏa mãn bài toán là T  2019  .
Câu 43.Chọn C.Điều kiện: x  2. 2 1 2 Ta có: m   1 log x  2  4 m 5 log  4m  4  0 1     1 x 2 2 2  4m   2 1 log
x  2  4 m  5 log
x  2  4m  4  0 2     2    m   2 1 log
x  2  m  5 log
x  2  m 1  0 2     2  
Đặt t  log x  2 , ta có phương trình trở thành: m   2
1 t  m  5t  m 1  0   * 2   5  t  5t 1 Với x  ; 4 ,   ta có: t  1   ;1 . * 2  m  t  1  ;1 . 2  2 t  t  ,   1 t  5t 1 2 4  t  4
Xét hàm số f t  2  f ' t   0, t   1  ;1 2   2 t  t  . Ta có:   1
 2t t  1 7 Suy ra: f  
1  f t   f   1 , t   1  ; 
1 hay 3  f t   , t  1;  1 3  
Do đó:Phương trình đã cho có nghiệ 5 m x thuộc đoạn , 4 
  * có nghiệm t thuộc đoạn  1  ;1  2  7  3  m  . 3   x 1 x ex
Câu 44.Chọn A. I  e ln
  ax dx  e ln   axdx  dx   x  x  u   ax 1 ln du  dx x
 Tính ex ln axdx  :Đặt    x x     x ax x  ax e e ln d e ln  dx  C 
dv  exdx  x v  ex
 Thay vào, ta được:    ex F x
ln ax  C .   1  1  F  0      
ea .ln1 C  0 C 0  e Ta có:   a  Û  Û  Þ a  .  ln   . a 2020 2020   e ln   .2 a 020 2020   1 2020 F  2020 2020  e C e  1   Vậy a  ;1   .  2020 
Câu 45.Chọn A.Đặt t  cos x với x [0;3 ]  t [1;1] ; Trang 72  1 f (t)  (1)  Phương trình 2
2 f (cos x) 1  0 trở thành  1   f (t)  (2)  2
Căn cứ đồ thị hàm số f (x) ta thấy:
t  t ( 1  ;0) 1 + (1)  (t  t )  1 2 t  t  ( 1  ;0)  2
Với t  t  ( 1
 ;0)  cos x  t có 3 nghiệm thuộc [0;3 ] 1 1
Với t  t  ( 1
 ;0)  cos x  t có 3 nghiệm thuộc [0;3 ] 2 2
t  t (0;1) 3 + (2)  (t  t )  3 4
t  t  (0;1)  4
Với t  t  (0;1)  cos x  t có 3 nghiệm thuộc [0 ; 3 ] 3 3
Với t  t  (0;1)  cos x  t có 3 nghiệm thuộc [0 ; 3 ] 4 4
Các nghiệm trên không có nghiệm nào trùng nhau
Vậy phương trình đã cho có 12 nghiệm thuộc [0 ; 3 ]
Câu 46.Chọn C.Tập xác định của hàm số là D   .Ta có g x   2
x  x f  3 2 3 6
x  3x  4 ; x  0 2     g x 3x 6x 0  0       f    x 2 3 2
x  3x  4  0  f    3 2
x  x     1 3 4 0 x  a  0 3 2
x  3x  4  a 2  
Mặt khác, từ đồ thị hàm số ta thấy f   x  0  x  b  0; 4 3 2  Do đó  
1  x  3x  4  b  3   x  c  4 3 2
x  3x  4  c 4  x  0 Xét hàm số 3 2
u  x  3x  4 , 2
u  3x  6x , u  0   x  2 Từ đó ta có Bảng biến thiên
Với a  0 , phương trình  2 có một nghiệm duy nhất nhỏ hơn 1
Với b 0; 4 , phương trình 3 có ba nghiệm lần lượt thuộc các Trang 73 khoảng  1  ;0;0;2;2;3
Với c  4 , phương trình  4 có một nghiệm duy nhất lớn hơn 3
Vậy g x  0 có 7 nghiệm đơn nên hàm số có 7 điểm cực trị.
Câu 47.Chọn B.Đặt log (4x + ) t t- 2
4 = t Û 4x + 4 = 2 Û x = 2 - 1. 2 Từ điều kiện t- 2
0 £ x £ 2020 Þ 0 £ 2
- 1£ 2020 Û 1£ t - 1£ 1+ log 2021. 2 Theo giả thiết ta có: t- 2 - 1+ 2 = + 1+ 2y t y ( ) * .Xét hàm số ( ) 1 2u f u u - = + với 1£ u £ 1+ log 2021. 2 Có f '(u) u- 1
= 1+ 2 .ln 2 > 0, " u Î [1;1+ log 2021 nên hàm f (u) đồng biến trên đoạn 2 ] [1;1+ log 2021 . 2 ] Dựa vào ( ) * Þ f (t - ) 1 = f (y + )
1 Û t - 1= y + 1.
Mặt khác 1£ t - 1£ 1+ log 2021Þ 1£ y + 1£ 1+ log 2021Þ 0 £ y £ log 2021 » 10, 98 . 2 2 2
Vì y Î ¢ Þ y Î {0;1; 2;3; 4;5;6;7;8;9;1 }
0 .Vậy có 11 cặp số nguyên thỏa mãn ycbt.
Câu 48.Chọn A.Ta có xf  2 x    3
x  x f  4 2
x  x     4 2 4 2 4 4 2 1
4x  8x  2x  4.4x 1  4xf  x  1 dx  2
 4x 4x f x 2x   1 2 3 4 2 1 dx   4 2
4x  8x  2x  4.4xdx 0 0 0 1 4 4 
f t  dt  f u 64 du   f x 32 2 2 dx     3 3 0 1 0 Với 2 4 2
t  x ;u  x  2x  1.
Câu 49.Chọn D. Giả sử SD   ABC  . Ta chứng minh: ABCD là hình vuông. AB  SD Ta có:
  AB  SDA  AB  DA   BAD  90 . AB  SA  BC  SD Ta có:
  BC  SDC  BC  DC   BCD  90 . BC  SC 
Tứ giác ABCD có:   
DAB  ABC  BCD  90  ABCD là hình chữ nhật. Trang 74
Mà BA  BC  ABCD là hình vuông cạnh a 3 .
Vì AD / / BC  AD / /  SBC   d  D,SBC   d  ,
A SBC   a 2 .
Kẻ DH  SC tại H.Ta có: BC  SDC   BC  DH .
Mà DH  SC  DH  SBC  .  d  D,SBC   DH  a 2 . 1 1 1
Xét tam giác SDC vuông tại D có:  
 SD  a 6 . 2 2 2 DH SD DC a 3 1 1 2 3 a 6 V  .S .SD  . .a 6  . S.ABC 3 ABC 3 2 2 2
Câu 50.Chọn A.Ta có g  x  f  x   2 ' '
1  x  3  f ' x   1   x   1  2 x   1  2 . Khi đó 2
g ' x  0  f ' x   1   x   1  2 x   1  2 (1)
Đặt t  x 1. BPT  
1 trở thành f t  2 '
 t  2t  2 2
Xét tương giao của ĐTHS y  f 't  và 2
y  t  2t  2
ta có nghiệm của BPT là 0  t  3  0  x 1 3  1   x  2 . x
Suy ra hàm số g  x  f  x   3 1 
 3x nghịch biến trên  1  ;2 . 3
Do đó ta Chọn đáp án A. www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 25 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2 Thời gian: 120 phút
Câu1.Lớp 11A có 29 học sinh nữ và 14 học sinh nam, giáo viên gọi 1 học sinh lên lau bảng. Hỏi
có bao nhiêu cách cách Chọn? A. 29 . B.14 . C.1. D. 43. Trang 75
Câu2.Cho cấp số cộng (u ) với u  1, u  3
 . Công sai của cấp số cộng bằng n 1 2 bao nhiêu?A. 2  . B. S  4 . C. 4  . D. 2 .
Câu 3. Tính thể tích V của khối trụ có bán kính đáy và chiều cao đều bằng 2.
A. V  8 .B. V  4 .C. V 16 .
D. V 12 .
Câu4.Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng A 0; 2 . B.  2  ;0 . C.  3  ;  1 . D. 2;3 .
Câu5.Cho khối hộp chữ nhật có độ dài chiều rộng, chiều dài, chiều cao lần
lượt là 3a; 4a;5a . Thể tích của khối hộp chữ nhật đã cho bằng A. 2 12a . B. 3 60a . C. 3 12a .
D. 60a .
Câu6.Tập nghiệm của phương trình log  2
x  2x  2  1 là 2  A.0;  2 . B.  2  . C.  1  . D.  2  ;  0 .
Câu 7.Họ tất cả các nguyên hàm của hàm số   2020x f x  e là 2020 x e A.  C . B. 2020 2020. x e  C . 2020 C. 2020x e  C . D. 2019 2020. x e  C . Câu 8.Cho hàm số 3 2
f (x)  ax  bx  cx  d, a  0 có đồ thị như hình vẽ dưới đây.
Giá trị cực đại của hàm số làA. 5 .
B.1. C. 3 . D. 0 .
Câu9.Đồ thị dưới đây là đồ thị của 1 trong 4 đồ thị của hàm số ở các phương án A, B, C, D dưới đây.
Hãy Chọn phương án đúng. x  2 2  x 2  x x  2 A. y  . B. y  .C. y  . D. y  . x 1 x 1 x 1 x 1
Câu10.Với a là số thực dương tùy ý, log a bằng: 2 1 1
A. 2  log a . B.
 log a . C. 2log a . D. log a . 2 2 2 2 2 2 Câu11.Nếu f  x 1 dx 
 ln x  C thì f  x là x
A. f  x  x  ln x  C . B. f  x 1
  x   ln x  C . x 1 x 1
C. f  x  
 ln x  C .D. f x  . 2 x 2 x
Câu12.Cho hai số thực x , y thoả mãn phương trình x  2i  3  4 yi . Khi đó giá trị của x và y là: 1 1
A. x  3, y  2 .
B. x  3i , y  .
C. x  3, y  . D. x  3, 2 2 1 y   . 2
Câu 13.Trong không gian Oxyz, hình chiếu vuông góc của điểm M 3;1; 4
  lên trục Oy là
A. M 3;0;0 . B. M 3;0; 4  . C. M 0;1; 0 . D. 3   2   1   M 0;0; 4  . 4  
Câu 14.Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x  y  z  4x  2 y  4z 16  0 . Tìm tọa độ Trang 76
tâm I của mặt cầu  S  . A. I (2; 1  ;2) .
B. I (2; 1; 2) . C. I (4; 2; 4)
 . D. I (2;1; 2) .
Câu 15.Trong không gian Oxyz , cho mặt phẳng   : x  2y  4z  31  0 . Vectơ nào dưới đây là   
một vectơ pháp tuyến của   ?A. n1;2;4 B. n1;2;4. C. n1;2;4 . D. n 1  ; 2  ; 4   . x  y  z 
Câu 16.Trong không gian Oxyz , cho đường thẳng 1 2 1 d :   . 1  3 3 Một điểm M 1; ;
a b thuộc đường thẳng d . Khi đó a  b bằng A. 13  B. 9 . C. 9  . D. 7  .
Câu17.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a , AD  a . Biết SA
vuông góc với mặt phẳng đáy và SA  a 15 . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 .
Câu18.Cho hàm số y  f  x liên tục trên  và có bảng xét dấu như sau
Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C.1. D. 2 . Câu19.Hàm số 3 2
y  x  6x  2 có giá trị cực tiểu bằng A. 30  . B. 2 . C. 0 . D. 4 .
Câu20.Cho log b  3 với a , b là các số thực dương và 1 khác 1. Tính giá trị biểu thức a 9
T  log b  log
b .A. 5 . B. 3 C. 15 . D.10 . 3 a a
Câu 21.Tập nghiệm của bất phương trình log  2 2x 1  log
x 1 có chứa bao nhiêu giá trị 1  1   2 2 nguyên thuộc đoạn  2  020;2020? A.1.
B. 3 . C. 4040 . D. 2020 .
Câu 22.Cho khối nón có thể tích là V . Biết rằng khi cắt khối nón đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một tam giác đều có diện tích bằng 3 . Giá trị của V bằng  3 A.  3 . B. . C. 2 . D. 4 . 3
Câu23.Cho hàm số y  f  x có đồ thị như hình vẽ. Số nghiệm của phương
trình f sin x  
1  1 thuộc đoạn  0;3  là A. 8 . B. 5 . C. 3 . D. 6 . 2x ln  2 x   1
Câu24.Họ tất cả các nguyên hàm của I  dx  là 2 x 1 2  2 ln x   1 2  2 ln x   1 A.  C . B.
 x  C . 2 2 2  2 ln x   1 2  2 ln x   1 C.   C . D.   x  C . 2 2
Câu25.Mỗi tháng ông A gửi tiết kiệm ngân hàng 1500000 đồng với lãi suất kép 0, 6% trên
tháng. Sau một năm tám tháng, ngân hàng thay đổi lãi suất kép thành 0,8% trên tháng. Sau ba
năm gửi ngân hàng, ông A rút toàn bộ số tiền cả gốc và lãi. Số tiền ông A nhận được là: Trang 77
A. 62791439,15 đồng.
B. 57662945,82 đồng.
C. 60435853,82 đồng. D. 93973001, 03 đồng.
Câu26.Cho hình chóp tứ giác S.ABCD có đáy ABCD hình vuông với AB  a . Biết
SD, AD, DC đôi một vuông góc nhau và góc giữa hai mặt phẳng SAC  và  ABCD là 45 . a 2
Khoảng cách từ A tới mặt phẳng SBC  là: A. a . B. . C. a 2 2 a 3 . D. . 3
Câu 27.Tổng số tiệm cận đứng tiệm cận ngang của đồ thị hàm số 2
x  2019x  2020 y  là 2 3x  2x 1
A. 3 . B. 2 . C.1. D. 0 .
Câu 28. Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong bốn hàm số dưới đây? A. 4 2
y  x  4x  3 . B. 4 2
y  x  4x  3 . C. 4 2
y  x  4x  3 . D. 4 2
y  x  4x  3 .
Câu 29.Cho hàm số y  f  x có đồ thị như hình dưới đây. Diện tích hình phẳng giới hạn bởi đồ
thị hàm số y  f  x và trục Ox là 2 0 2 A. S  f
 xdx f
 xdx . B. S   f
 xdx. 0 1  1  0 2 0 2 C. S  f
 xdx f
 xdx.D. S  f
 xdx f
 xdx . Câu 1  0 1  0
30.Cho số phức z  3 2i . Tìm phần ảo của số phức liên hợp của
w  2  i z A. 1. B. 5 .
C.1. D. i .
Câu31.Cho số phức z  2  3i . Điểm nào sau đây biểu diễn cho số
phức w  2  i.z A. M  1  ; 8
  . B. N 1; 8
  . C. P 1  ;8 .
D. Q 1;8 .    
Câu32.Trong không gian Oxyz , cho a  2i  3 j  4k , A1;0; 2   và B2; 1   ;1 . Tích vô hướng   . a AB bằng A.15 . B.16 . C. 17 . D.18 .
Câu 33.Trong không gian Oxyz , cho điểm A4;  2;3 , B 2;6;9 . Phương trình mặt cầu có
đường kính AB là: 2 2 2 2 2 2 A.  x   3
  y  2  z  6  26 .
B.  x  3   y  2   z  6  26. 2 2 2 2 2 2
C.  x  3   y  2   z  6  26 .
D.  x  3   y  2   z  6  26 .
Câu 34.Cho điểm A2;3; 4 và hai mặt phẳng  P : 2x  3y  z 1  0 , Q : x  2y  3z 10  0 .
Phương trình đường thẳng d đi qua A song song với cả P và Q là x  2 y  3 z  4 x  2 y  3 z  4 x  2 y  3 z  4 A.   . B.   . C.   . D. 11  5  7 11 5  7 11 5 7  x  2 y  3 z  4   . 11 5 7 Trang 78
Câu 35.Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
đi qua hai điểm M 1; 2  ; 3   và N 5; 4  ;7 ?    A. u  3; 3  ;2 .
B. u  2; 1;5 . C. u  3; 1  ;2 . D. 1   3   4    u  4; 6; 4 . 2  
Câu 36.Gọi X là tập hợp tất cả các số tự nhiên có 8 chữ số được lập từ các chữ số 1, 2, 3, 4, 5, 6,
7, 8, 9. Lấy ngẫu nhiên một số trong tập hợp X. Gọi A là biến cố lấy được số có đúng hai chữ số
1, có đúng hai chữ số 2, bốn chữ số còn lại đôi một khác nhau, đồng thời các chữ số giống nhau
không đứng liền kề nhau. Xác suất của biến cố A bằng 176400 151200 A. . B. . 8 9 8 9 5 201600 C. . D. . 9 8 9
Câu 37.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
AB  3a, AD  a . SA vuông góc với mặt phẳng đáy, SA  2a . Gọi M là
điểm thuộc đoạn thẳng DC sao cho DC  3DM . Khoảng cách giữa hai đường BM và SD bằng 2a a 6 a 6 a A. . B. . C. . D. . 3 6 3 3
Câu 38.Cho hàm số f  x có f 3  0 và   2x f x  , x   2; . 2   x  4x  4 e2 Khi đó f 
xdx  ae b a,b . Tích .abbằng 3 A. 2.  B. 24. C. 8. D. 24.  mx 18
Câu39.Tìm số giá trị nguyên của tham số m để hàm số y 
nghịch biến trên khoảng 2x  m  2  ;5. A. 2 . B.1. C.11. D.10 .
Câu40.Cho hình nón đỉnh S , tâm của đáy là O và bán kính đường tròn đáy bằng 5 . Mặt phẳng
(P) qua đỉnh hình nón và cắt đường tròn đáy theo dây cung có độ dài bằng 6 . Biết rằng khoảng
cách từ O đến (P) bằng 2 3 . Tính thể tích khối nón giới hạn bởi hình nón trên. 50 3 100 3 A. 50 3 . B. . C.100 3 . D. . 3 3 3 2 3
a  ab  b
Câu41.Cho a  0 , b  0 thỏa mãn log
3a  2b  log a  log b . Giá trị của 16   9 12 3 2 3 a  a b  3b bằng 19 1 7 1 A.  . B. . C.  . D.  . 83 3 17 5
Câu 42.Có bao nhiêu giá trị m dương sao cho giá trị lớn nhất của hàm số f  x 3 2 3 2
 x 3m x  2m  9m 1 trên đoạn 0; 
3 bằng 30?A. 0 . B. 1. C. 2 . D.Vô số.
Câu 43.Cho phương trình 4x  2x m
 2m  4  0 , ( m là tham số thực). Tập hợp tất cả các giá trị
của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn  1  ;  1 là  5   5   5   5  A. 4;     . B. 4;   . C. 4;     . D. 4;    .     2   2   2   2  Trang 79
Câu44.Cho hàm số f (x) liên tục trên  .Biết ex x
là một nguyên hàm của hàm số   2ex f x , họ
tất cả nguyên hàm của hàm số   2 e x f x là (3  2x) A. (  3) ex x  C . B.
ex  C . C. ( 1) ex x  C . D. 4 ( 1) ex x  C .
Câu 45.Cho hàm số f  x có bảng biến thiên như sau:  3  Số nghiệm thuộc đoạn   ;   của phương trình  2 
2 f 2cos x  9  0 là
A. 2 .B. 5 . C. 3 . D. 6 .
Câu 46. Cho hàm số y  f  x có đạo hàm trên  và có bảng xét dấu của đạo hàm f ' x như sau :
Hỏi hàm số g  x  f  2
x  2x có bao nhiêu điểm cực tiểu ?
A.1. B. 2 . C. 3 . D. 4 .
Câu 47.Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình log   2  2x m x m
 3x 1 có nghiệm thuộc 0;2 ? A. 6 . B. 5 . 2  
C. 4 . D. 3 .
Câu48.Cho hàm số f  x có đạo hàm liên tục trên  sao cho 1
        x  1 y f x y f x f y e e  
1 , x, y   và f 0  2 . Tính f  x d . x  0 1 1 3 3
A. I  e  .
B. I  e  .
C. I  e  .
D. I  e  . 2 2 2 2
Câu49.Cho khối chóp S.ABC , đáy ABC là tam giác có  0
AB  4a, AC  5a, BAC  60 ,   0
SBA  SCA  90 , góc giữa  SAB và SAC  bằng 0
60 . Thể tích của khối chóp đã cho bằng: 3 20 39a 3 10 13a 3 20 13a 3 10 39a A. . B. . C. . D. . 13 13 13 13
Câu50.Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình vẽ. x
Hàm số g  x  f   x 2 3 
nghịch biến trong khoảng nào dưới 3 đây?
A. 3;  . B. ;  2. C.  2   ;1 . D. 1;3. ………HẾT…… BẢNG ĐÁP ÁN 1.D 2.C 3.A 4.D 5.B 6.D 7.A 8.A 9.C 10.D 11.D 12.C 13.C 14.D 15.C 16.C 17.C 18.D 19.A 20.C Trang 80 21.B 22.B 23.D 24.A 25.D 26.D 27.B 28.C 29.D 30.A 31.D 32.C 33.B 34.D 35.B 36.D 37.B 38.D 39.A 40.D 41.C 42.B 43.D 44.D 45.B 46.A 47.C 48.D 49.D 50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu1.Chọn D.Tổng số học sinh của lớp 11A là: 29 14  43 .
Số cách Chọn một học sinh trong lớp là: 43
Câu2.Chọn C.Gọi d là công sai của cấp số cộng đã cho.Ta có: d  u  u  3  1  4  2 1
Câu 3. Chọn A.Thể tích của khối trụ V   r h    2 2 . 2 .2  8 .
Câu4.Chọn D.Dựa vào đồ thị ta có hàm số nghịch biến trên các khoảng  1   ;1 và 2;3.
Câu5.Chọn B.Thể tích của khối hộp chữ nhật là: 3 V  3 .4 a .5
a a  60a . x  2 
Câu6.Chọn D.Ta có log  2
x  2x  2 2 2
1 x  2x  2  2  x  2x  0  . 2  x  0
Vậy tập nghiệm của phương trình đã cho là S   2  ;  0 . 2020 x e Câu 7.Chọn A.Ta có 2020 x e dx   C  . 2020
Câu 8.Chọn A.Dựa vào đồ thị ta thấy giá trị cực đại của hàm số là 5.
Câu9.Chọn C.Dựa vào đồ thị hàm số ta có đồ thị hàm số có một đường tiệm cận đứng x 1 nên loại A,B.
Vì đồ thị là một đường đi xuống về bên phải nên hàm số nghịch biến trên mỗi khoảng của tập
xác định do đó y  0 nên Chọn C 1 1
Câu10.Chọn D.Ta có: 2 log a  log a  log a . 2 2 2 2   1  1 1 x 1 x 1 Câu11.Chọn D.Ta có
 ln x  C      
, suy ra f  x 
là hàm số cần tìm. 2 2  x  x x x 2 x    x 3 x   1
Câu12.Chọn C.Từ x  2i  3  3 4 yi    
1 .Vậy x  3, y  . 2  4y y   3  2
Câu 13.Chọn C.Hình chiếu vuông góc của điểm M 3;1; 4
  lên trục Oy là M 0;1;0 . 3   2 2 2
Câu 14.Chọn D.Viết lại phương trình mặt cầu  S  có dạng  x  2   y  
1   z  2  9 .
Suy ra mặt cầu  S  có tâm là I (2;1; 2) . 
Câu 15.Chọn C.Một vecto pháp tuyến của mặt phẳng   là n 1; 2; 4  2  
Câu 16.Chọn C.Điểm M 1; ;
a b thuộc đường thẳng d nên tọa độ điểm M thỏa mãn phương    trình đườ 1 1 a 2 b 1 ng thẳng d  
 a  4;b  5  a  b  9 1  3 3 Trang 81 Câu17.Chọn C S
Vì SA   ABCD nên AC là hình chiếu của SC lên mặt phẳng  ABCD .
Ta suy ra góc giữa đường thẳng SC và mặt phẳng  ABCD bằng góc giữa
SC và AC . Đó là góc  SCA . 2a A B Ta có: AC 
AB  BC   a2 2 2 2 2 2
 a  5a  a 5 . a SA a 15 D C
Xét tam giác SAC vuông tại A :   0 tan SCA    3  SCA  60 . AC a 5
Vậy góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 0 60 .
Câu18.Chọn D.Từ bảng biến thiên suy ra f  x đổi dấu khi qua x  1
 và x  4 nên hàm số y  f x có hai điểm cực trị.
Câu19.Chọn A.Ta có: 2
y  3x 12x . Xét
x  0  y  2 2
y  0  3x 12x  0   .
x  4  y  3  0
BBT:Vậy giá trị cực tiểu y  30  . CT 9
Câu20.Chọn C.Ta có: 9
T  log b  log b  log b  log b 3 a a 1 3 a 2 a
 3log b  2log b  5log b  5.3 15 . a a a
Câu 21.Chọn B.Điều kiện: x  1
 . Khi đó bpt đã cho tương đương với bpt log 2x  
1  2 log  x   1  log 2x  
1  log  x  2 1
 2x 1 x  2 2 2 2 1 1 1 1 1 2 2 2 2 2
 x  2x  0  0  x  2 . Suy ra có 3 giá trị nguyên thỏa đề bài.
Câu 22.Chọn B.Giả sử thiết diện qua trục là tam giác SAB . 2 AB 3 Ta có S 
 3  AB  2 . S  AB 4 AB
Khối nón có bán kính đáy là r  OA   1 và đường cao là 2 AB 3 1 1  3 h  SO 
 3 .Vậy thể tích của khối nón đã cho là 2 2
V   r h  .1 . 3  . 2 3 3 3
Câu23.Chọn D.Xét phương trình f sin x  
1  1. Đặt t  sin x 1, x  0;3   t 0;2 .
Dựa theo đồ thị, đường thẳng y  1 cắt y  f t  với t 0; 2 tại t  1, t  2 .
Với t  1  sin x 1  1  sin x  0  x  k (k   ) . Do x  0;3  , nên nhận k  0,1, 2,3.
Phương trình có 4 nghiệm x  0, x   , x  2 , x  3 . 
Với t  2  sin x 1  2  sin x  1  x 
 k2 (k  ) . Do x 0;3  , nên nhận k  0,1. 2   Phương trình có 2 nghiệ 5 m x  , x  . 2 2
Vậy phương trình f sin x  
1  1 có 6 nghiệm thuộc đoạn  0;3  . Trang 82 2x
Câu24.Chọn A.Đặt t  ln  2 x   1  dt 
dx . Thay vào I ta được: 2 x 1 2  2 2 ln x t   1 I  d t t   C   C  . 2 2
Câu25.Chọn D.Gọi a là số tiền ông A gửi vào ngân hàng hàng tháng.
Đầu tháng 1, ông A có a đồng.
Cuối tháng 1, ông A có a  0, 6%a  a 1 0,6% 1,006a
Đầu tháng 2 , ông A có a 1,006a  a11,006
Cuối tháng 2 , ông A có a     a 2 1 1, 006 .1, 006 1, 006 1, 006 
Đầu tháng 3 , ông A có a 2  a  a 2 1, 006 1, 006 11, 006 1, 006 
Cuối tháng 3 , ông A có a  2     a 2 3 1 1, 006 1, 006 .1, 006
1, 006 1, 006 1, 006   Tương tự 1, 006 1
, cuối tháng 20 , ông A có a 1,006 1,006  ...1,006  20 2 20  . a 1, 006. 1,006 1
Số tiền ông A nhận được sau một năm tám tháng nếu mỗi tháng gửi vào ngân hàng 1500000 là: 20 1, 006 1 1500000.1, 006.  31963799,34 đồng. 1, 006 1
Sau khi ngân hàng thay đổi lãi suất thành 0,8% trên tháng, số tiền ông A thu được sau 16 tháng 16 1, 008 1
nếu mỗi tháng gửi vào ngân hàng 1500000 là: 1500000.1, 008.  25699146,48 1, 008  đồng. 1
Tổng số tiền ông A thu được sau 3 năm là:     16
31963799,34 25699146, 48 31963799,34. 1 0, 008  93973001,03 đồng.
Câu26.Chọn D. Gọi O  AC  BD .Ta có SD  AD AC  BD
  SD   ABCD ;
  AC  SBD  SO  AC . SD  DC SD  AC 
Diện tích đáy ABCD là: 2 2 S  AB  a ABCD
SAC ABCD  AC SO  AC    
SAC   ABCD   SO BD  , ,  SOD   SOD  45 .  BD  AC  Xét S
 DO vuông tại cân tại D : 2 2 DB AD  AB a 2 SD  DO    . 2 2 2 AD  BC     nên d  ,
A SBC   d D,SBC  .
BC  SBC  AD SBC   DC  CB
  BC  SDC và SBC  SDC Vẽ DH  SC tại H . SD  BC 
SBC  SDC  
Ta có SBC   SDC   SC   DH  SBC  nên d  ,
A SBC  d  ,
D SBC   DH  DH  SC  Trang 83 1 1 1 1 1 3 a 3 Xét S
 DC vuông tại D :      Vậy DH  . 2 2 2 2 2 2 DH SD DC  2  a a a 3   2   2    Câu 27.Chọn B. x 2019x 2020 1 Ta có lim y  lim   . 2 x x 3x  2x 1 3
Suy ra đồ thị hàm số có 1 đường tiệm cận ngang là 1 y   . 3 2
x  2019x  2020 x   1  x  2020 x  2020 2021 lim y  lim  lim  lim   . 2 x 1  x 1  x 1 3x  2x 1        x   x 1 1 1 4 3 1 x  3 x       3   3  2
x  2019x  2020 x   1  x  2020 x  2020 lim y  lim  lim  lim   . 2             3x 2x 1  1  1 1 1  1    x  x  x  3 x   1 1 x  x          3 x       3  3   3   3  3    3 
Đồ thị hàm số có 1 đường tiệm cận đứng 1
x   .Vậy đồ thị hàm số có 2 đường tiệm cận. 3
Câu 28.Chọn C.Ta có lim y    loạiD. Vì hàm số có 3 cực trị nên a , b trái dấu  x loạiB.
Đồ thị cắt trục tung tại điểm có tung độ dương  loại A. 0 2 0 2
Câu 29.Chọn D.Từ hình vẽ ta có: S  f
 x dx  f
 x dx  f
 xdx  f
 xdx. 1  0 1  0
Câu 30.Chọn A.Ta có w  2  i z  2  i3  2i  8  i  w  8  i
Vậy số phức liên hợp của w có phần ảo bằng 1.
Câu31.Chọn D. z  2  3i  z  2  3i w  2  i.z  2  i2  3i 18i
Vậy điểm biểu diễn số phức w là Q 1;8 .    
Câu32.Chọn C.Ta có a  2; 3; 4 ; AB  1; 1  ;3 .Vậy . a AB  2.1   3  .  1  4.3 17 .
Câu 33.Chọn B.Mặt cầu có đường kính AB nên tâm I là trung điểm AB . 1 1
Suy ra I 3; 2;6 .Mặt khác bán kính R  AB  22 2 2  8  6  26 . 2 2 2 2 2
Vậy phương trình mặt cầu cần tìm là:  x  3   y  2   z  6  26. 
Câu 34.Chọn D.Ta có  P : 2x  3y  z 1  0 có một véctơ pháp tuyến là n  2; 3  ;    1 . P  
Q : x  2y  3z 10  0 có một véctơ pháp tuyến là n  1;2; 3  . Q    
Đường thẳng d có một véctơ chỉ phương là u . d   
Do đường thẳng d song song với P và Q nên  u  n ,n   11;5;7 . d P Q        
Mặt khác đường thẳng d đi qua A2;3; 4 và có véctơ chỉ phương u  11;5;7 nên phương d  x  2 y  3 z  4
trình chính tắc của d là   . 11 5 7 
Câu 35.Chọn B.Ta có: MN  4; 2
 ;10 là một vectơ chỉ phương của đường thẳng đi qua hai
điểm M , N . Trang 84   
Vì u  2; 1;5 và MN  4; 2
 ;10 cùng phương nên u là một vectơ chỉ phương của đường 3   3
thẳng qua hai điểm M , N . Câu 36.Chọn D n   .Ta có: 8 ( ) 9 .
TH1: Xếp bất kỳ.Xếp hai chữ số 1, hai chữ số 2 bất kỳ và 4 chữ số còn lại: Có 2 2 4
C .C .A  352.800 . 8 6 7
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: 2 4 7.C .A cách. 6 7
Xếp hai chữ số 2 đứng liền nhau: 2 4 7.C .A cách. 6 7
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1 đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: 4 C .6! 7
Vậy số cách xếp không thỏa mãn yêu cầu là: 2 4 4
2.7.C .A  C .6! 151200 6 7 7 201600 Vậy n( )
A  352.800 151.200  201.600  p( ) A  , 8 9 Chọn D
Câu 37.Chọn B.Gọi N là điểm trên đoạn thẳng AB sao cho AB
= 3BN. Khi đó có tứ giác DMBN là hình bình hành nên suy ra
BM // DN. Suy ra BM / / SDN  .Vậy
d  BM , SD  d BM ,SDN   d B,SDN  1  d  ,
A SDN  2
Trong mp kẻ AE vuông góc DN tại E. Ta suy ra DN  SAE .
Trong tam giác SAE, từ A kẻ đường thẳng AH vuông góc với SE tại H. AH  DN  Có:
  AH  SDN   d  ,
A SDN   AH AH  SE  1 1 1 1 1 1 1 1 1 3          6a  AH  .Vậy 2 2 2 2 2 2 2 2 2 2 AH SA AE SA AD AN 4a a 4a 2a 3  SD  6a d BM ,  . 6 Câu 38.Chọn D 2x 2x
Cách 1. Ta có: f  x  dx  dx  I  
.Đặt t  x  2  dt  dx 2 x  4x  4 x 22 2(t  2) 4 I 
dt  2 ln t   C 
.Với x  3  t 1nên có f   1  0  C  4 2 t t
Đổi cận: x  3  t 1; x  e  2  t  e    Vậy e 2 f  x e 4 dx  2 ln t 
 4 dt  4e  6.   
Suy ra a  4; b  6. 3 1  t  2x 2 x  2  4 2 1
Cách 2. f  x    dx  dx  dx  4 dx     2 x  4x  4 x 22 x  2 x 22 4  2ln x  2   C x  2 Trang 85
f 3  0  C  4. Vậy f  x 4  2ln x  2   4 x  2 e2    f  x e 2 4 dx  2 ln x  2 
 4 dx  4e  6   
. Suy ra a  4; b  6. 3 3  x  2  m 2 mx 18 m  36
Câu39.Chọn A.Tập xác định: D   \   .Ta có y   y  .  2  2x  m 2x  m2  6   m  6  2     m  36  0 6 m 6   m    5  YCBT     m   m  10   4  m  6 .  2   2  ;5     2 m       m 4 2    2
Vậy có hai giá trị nguyên của tham số m thỏa mãn.
Câu40.Chọn D.Giả sử thiết diện tạo bởi  P và hình nón là tam giác
SAB .Gọi M là trung đoạn AB , khi đó r  OA  5, AB  6 2 2
 OM  OA  AM  4 .
Gọi H là hình chiếu vuông góc của O lên SM . Suy ra OH vuông
góc với (P) nên OH  2 3 . 1 1 1 1 1 1 1 Ta có:        SO  4 3 . 2 2 2 OH OM OS 2 OS 12 16 48 1 1 100 3 Thể tích khối nón 2 2
V  .r .h  .5 .4 3  . 3 3 3
Câu41.Chọn C.Đặt t  log
3a  2b  log a  log b 16   9 12 t   3
 a  2b 16t 3 1    t t         4  3 a 1 a  9t 3.9t 2.12t 16t    9 3  3  2. 1        .  16   4   t  3  b 3 b  12t    1    vn  4  3  a   a   1     3 2 3
a  ab  b  b   b  7 Vậy    . 3 2 3 3 2
a  a b  3b  a   a    17 3      b   b 
Câu 42.Chọn B.Xét hàm số g  x 3 2 3 2
 x  3m x  2m  9m 1 xác định và liên tục trên đoạn 0; 3 x  m
Ta có: g x 2 2
 3x 3m ; gx  0   x  m  ktm g   3 2
0  2m  9m 1; g   3
3  2m  28 ; g m 2  9m 1
Vì 0  g 0; g 3;g m và g m  g 0 m   0
Suy ra Maxf  x  Maxg 0; g 3  Max 3 2 3
2m  9m 1; 2m  2  8 0;  3 TH 1: 3 2 3
m  3  2m  9m 1  2m  28
Giá trị lớn nhất của hàm số f  x 3 2 3 2
 x 3m x  2m  9m 1 trên đoạn 0;  3 bằng 30 Trang 86 3 2
 2m  9m 1  30  m 1,548 ktm TH 2: 3 2 3
m  3  2m  9m 1  2m  28
Giá trị lớn nhất của hàm số f  x 3 2 3 2
 x  3m x  2m  9m 1 trên đoạn 0;  3 bằng 30 3
 2m  28  30  m 1tm.
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán. Câu 43.Chọn D.
Phương trình đã cho tương đương với 2 2 x  2x m
 2m  4  0 .Đặt 2x t  , vì   x   1 1;1  t  ; 2   2 
Yêu cầu bài toán trở thành tìm m để phương trình 2
t  mt  2m  4  0  1 có hai nghiệm phân 1  t   biệt thuộc đoạn ; 2 
 .Phương trình  
1  t  2t  m  2  2 0    2  t   m  2 1  5  Yêu cầu bài toán 
 m  2  2  m 4  ;   2  2   x x x x x 1 Câu44.Chọn D.Ta có f  x 2
e dx  x e  C  f  x 2 e
 (1 x)e  f (x)   . ex x x    Lúc đó e e (1 x) 2 x 2 f (  x)  
 f (x)e x  (2  x)ex 2 e x ex u   2  x du  dx Tính   2 e xd  2    ex f x x x dx .Đặt   
dv  exdx v  ex  
   2exd  (2 )ex  exd  (2 )ex ex   ( 1)ex f x x x x x C x  C  .
Câu 45.Chọn B.Đặt t  2cos x , t  2
 ;2 thì 2 f 2cos x 9  0 trở thành
f t     f t  9 2 9 0    1 . 2
Nhận xét: Số nghiệm của phương trình là  
1 số giao điểm của hai đồ thị: C  : y  f t và đường thẳng d  9 : y  . 2
Bảng biến thiên hàm số y  f t  trên đoạn  2  ;2 :
Dựa vào bảng biến thiên, số nghiệm t  2
 ;2 của 2 là 2 nghiệm phân biệt t  2  ;0 , t  0;2 . 1   2    3 
Ta có đồ thị hàm số y  cos x trên   ;   :  2  Trang 87  t Với t   2
 ;0  2cos x  t  2  ;0 1  cos x   1;  0 . 1 1   2  3  t
Dựa vào đồ thị hàm số y  cos x trên   ;   ta thấy phương trình 1 cos x  1;0 có  2  2   3  3  3 nghiệm phân biệt:    x   
 x    x  T   1 có 3 nghiệm x    ; . 1 2 3   2 2 2  2   t
Với t  0; 2  2 cos x  t  0; 2 2
 cos x   0;1 . 2 2   2  3  t
Dựa vào đồ thị hàm số y  cos x trên   ;   ta thấy phương trình 2 cos x  0;  1 có 2 nghiệm phân biệt  2  2  
  x  0  x  . 4 5 2 2  3 
Vậy số nghiệm thuộc đoạn   ; 
 của phương trình 2 f 2cos x  9  0 là 23  5.  2 
Câu 46. Chọn A.Ta có 2
g '(x)  (2x  2) f '(x  2x) 2x  2  0 x  1   2 2x  2  0 x  2x  2   x  1 2 
g '(x)  0     2  2
 f '(x  2x)  0 x  2x  1 x  1    2
x  2x  3 x  3
Do x  1 2 là nghiệm kép nên ta có bảng biến thiên sau
Dựa vào bảng biến thiên và đối chiếu với các đáp án, ta Chọn A
Câu 47.Chọn C.Điều kiện: m  x  0 Ta có: log   2  2x m x m
 3x 1  log 2  2  2  2  2x m x m x  x 2   2  
 log 2  2  2  2  log 2x  2x m x m x * . 2   2
Xét hàm số f t   log t  t trên 0;  . Ta có: f t  1  1  0, t   0 . 2 t.ln 2
Suy ra hàm số f t  liên tục và đồng biến trên 0;  .
Do đó *  2  2   2x   2  2  2x  2  2x f m x f m x m  2x . Đặt    2x g x
 2x . Vì '   2 .x g x ln 2  2  0, x
 0;2 nên ta có BBT: Do đó ycbt 1 1  2m  8 
 m  4 .Vì m m1;2;3; 
4 Vậy có 4 giá trị m cần tìm. 2 Trang 88 Câu48.Chọn D.Ta có
        x  1 y f x y f x f y e e  
1 , x, y   .
Lấy đạo hàm hai vế của theo biến x, ta được       x   y f x y f x e e   1 .
Thay x  0 vào, ta được    0 y  1 y f y f e  e 1. Do đó 
     y  1    y f y dy e dy
f y  e  y  C.
Thay x  0 và y  0 vào, ta được f 0  2 f 0  f 0  0.
Từ và, suy ra C  1.  Khi đó   y
f y  e  y 1. Vậy 1 1 1
         y f x dx f y dy e  y   3
1 dy  e  . 2 0 0 0 Câu49.Chọn D.Ta có 2 2  BC  AB  AC  2 .
AB AC.cos BAC . S
  a2   a2 0 4 5  2.4 .5 a .
a cos 60  a 21 E
Từ đó suy ra tam giác ABC là tam giác nhọn và có bán kính K I C đườ BC a 21
ng tròn ngoại tiếp là R    .  a 7 0 5a 2sin BAC 2sin 60
Gọi H là hình chiếu của S trên mặt phẳng  ABC  . H 60o A O SH  AB 4a Khi đó ta có 
 AB  SHB  AB  HB. B SB  AB
Tương tự AC  HC .
Từ đó suy ra ABHC là tứ giác nội tiếp đường tròn đường kính HA  2R  2 7a .
Gọi I , K lần lượt là hình chiếu của B, H trên SA và SC . Khi đó HK  SAC  .
Gọi E là giao điểm của BH và AC . Ta có  0 BE  B .
A tan BAC  4 .
a tan 60  4 3a . 2 2 Lại có 2 2 BH 
AH  AB  2 7a  4a  2 3a . CH 
AH  AC  
a2   a2 2 2 2 7 5
 a 3 .Suy ra HE  BE  BH  4 3a  2 3a  2 3a .
Đặt SH  x  0 , ta có 2 2 2 2
SB  SH  BH  x 12a    SA 2 2 S . B AB x 12a .4a d B,  BI   . 2 2 2 2 SB  AB x  28a
d B SAC BE 
d H SAC  SH.CH . x a 3 ; ,  2.HK  2  2 2 2 2 2 HE SH  CH x  3a d  , B SAC 2 2 3x x 28a
Gọi góc giữa SAB và SAC  là  .Ta có sin   
d  B, SA 2 2 2 2
2 x  3a . x 12a 2 2 3x x  28a 3 Vì 0   60 nên 2 2 2 2 2 2 
 x x  28a  x  3a . x 12a 2 2 2 2   2 2 x 3a . x 12a 6a 2  x  2 2
x  28a    2 2
x  3a  2 2 x 12a  2 2
 13x  36a  x  13 3 Khi đó 1 1 1  1 1 6a 10 39a 0 V  .S .SH  . .A . B A . C sin BA . C SH  . 4 . a 5 . a sin 60 .  . S.ABC 3 ABC 3 2 3 2 13 13 Trang 89 x
Câu50.Chọn A.Xét g x   f   x 2 3  . 3 2x 2x
Ta có g x  0   f 3  x 
 0  f 3 x   3 3 2 3  t  Đặ 2t 6
t t  3  x   
1  f t     
 f t  2. 3 3
Trên cùng hệ trục tọa độ Oxy, vẽ đồ thị hàm số y  f t  và đường 2t  6 thẳng y 
như hình vẽ .Dựa vào đồ thị, ta thấy 3         f t  2t 6 t 0 3 x 0 x 3     .    3 3   t  6 3   3 x  6  3   x  0 x  Vậy   3 1  
nên g  x nghịch biến trong 3;    3   x  0 www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 26 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH HỌA LẦN 2 Thời gian: 120 phút
Câu1.Từ một nhóm học sinh gồm 5 nam và 6 nữ, có bao nhiêu cách Chọn ra một đôi song ca gồm một
nam và một nữ? A.11. B.6. C.5. D.30.
Câu2.Cho cấp số cộng u với u  2
 và u  4 . Công sai của cấp số cộng đã cho bằng n  1 3 A.6. B. 3. C.2. D. 2  .
Câu 3.Diện tích xung quanh của hình trụ có độ dài đường cao h và bán kính đáy r bằng 1
A. 4 rh .
B. rh .
C. 2 rh . D.  rh . 3
Câu 4.Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. 3;5 .B. 0;  . C.  ;
 2 .D.0;2 .
Câu5.Cho khối lập phương có cạnh bằng 4 . Thể tích khối lập phương đã cho bằng. 64
A.16 . B. 96 . C. . D. 64 . 3 Trang 90 4
Câu 6.Nghiệm của phương trình log
3x  8  2 là A. . B.12 . C. 4  . 2   3 D. 4 . 5 3 5 Câu 7. Nếu
f (x)dx  3   và
f (x)dx  1  thì f (x)dx  bằngA. 1 1 3 2.  B. 4.
 C. 4. D. 2.
Câu 8.Cho hàm số y  f (x) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A. 2.B. 3. C. 0. D. 4. 
Câu9. Đường cong bên dưới là đồ thị của hàm số nào dưới đây? A. 3 2
y  x  3x  4 . B. 3 2
y  x  3x  4 . C. 3 2
y  x  3x  4 . D. 3 2
y  x  3x  4 .
Câu10. Với a là số thực dương tùy ý, log  2 9a bằng? 3 
A. 4 log a . B. 2 9log a .
C. 2(1 log a) . D. 6 log a . 3 3 3 3
Câu 11. Họ tất cả các nguyên hàm của hàm số f (x)  sin 2x  2 là
A. 2cos 2x  2x  C . B. 2
 cos2x 2x C . 1 1 C.
cos 2x  2x  C . D. 
cos 2x  2x  C . 2 2
Câu 12. Môđun của số phức i bằng A. 1. B. 0 . C. i . D.1.
Câu 13.Trong không gian Oxyz , hình chiếu vuông góc của điểm M 1; 3
 ;4 trên mặt phẳng Oyz có tọa độ là A. 1; 3  ;0. B. 0; 3  ;4 .
C. 1;0;0 . D. 0;0  ;1 . 2 2 2
Câu 14.Trong không gian Oxyz , cho mặt cầu S  :  x  2   y  
1   z  3  25 . Tâm của  S  có tọa độ là A.  2  ; 1  ;3 . B. 2,1,   3 . C.  1  ;2; 3   . D.  2  ;1;3 .
Câu15. Trong không gian Oxyz , cho mặt phẳng   : 5x  y  4z  3  0 . Vectơ nào dưới đây là một  
vectơ pháp tuyến của   ? A. n  5; 1  ;3 .
B. n  1; 4  ;3 . C. 3   1    
n  4; 1;5 . D. n  5; 1  ; 4  . 2   4   Trang 91 x  2 y 1 z 1
Câu16. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :   ? 3 4 2
A. P 4;9;3 . B. Q 2; 1  ;  1 .
C. N 3; 4; 2 .
D. M 4;7; 2 .
Câu17.Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB  ,
a BC  a 2 , SA vuông góc với
mặt phẳng đáy và SA  3a . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng: A. 45 . B. 30 . C. 60 . D. 90 .
Câu 18.Cho hàm số f  x , bảng xét dấu của f   x như sau:
Số điểm cực trị của hàm số làA. 4 . B. 3 . C.1. D. 2 .
Câu19.Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y  x  3x  2 trên đoạn 0;2 . Khi đó tổng M  m bằng. A. 4 . B. 16 . C. 2 . D. 6 .
Câu 20.Cho hai số thực dương a, b và a  1. Trong các khẳng định dưới đây, khẳng địnhnào đúng? A. ab 1 log   log b . B. ab   b a   2018 2018log 1 log . 2 a a a C.  2018 log a
b  2018  log b 2018 log a
b  2018 1 log b a a . D. a    a  . 2 x 2 x  1  1
Câu 21.Tập nghiệm của bất phương trình    là  2  8 A. ( ;  1). B. ( 3  ;). C. (3;1). D. ( ;  3  )  (1;).
Câu 22.Cho hình trụ có thiết diện qua trục là một hình vuông và diện tích toàn phần bằng 2 64 a . Tính 4 6a 8 6a
bán kính đáy của hình trụ.A. r  . B. r 
. C. r  4a .
D. r  2a . 3 3
Câu 23.Cho hàm số f  x có đồ thị như sau
Số nghiệm thực của phương trình 2
f  x 1  0 là A.2. B.1. C.4. D.3. x 
Câu 24.Họ tất cả các nguyên hàm của hàm số f  x 2 2
 x trên khoảng   ;1  là 1 2 x 2 x A.
 x  3ln 1 x  C . B.
 x  3ln x   1  C . 2 2 2 x 2 x C.
 x  3ln x   1  C . D.
 x  3ln 1 x  C . 2 2 Trang 92
Câu 25.Để dự báo dân số của một quốc gia người ta sử dụng công thức nr S  Ae ;
trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ
tăng dân số hàng năm. Giả sử năm 2019, dân số của một đất nước là
96.208.984 người. Và nếu tỉ lệ tăng dân số hàng năm không đổi là 0, 9 %, thì đến
năm bao nhiêu dự báo dân số của nước đó là 116.224.393 người? A. 2038 . B. 2040 . C. 2039 . D. 2041 .
Câu 26. Cho khối lăng trụ đứng ABC . D A B  C  D
  có đáy là hình vuông. AC  3a
và AA  2a .Thể tích của khối lăng trụ đã cho bằng 3 5a 3 5 3a A. 3 5a . B. 3 5 3a . C. . D. . 3 3 2 2x  3x 1
Câu 27.Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  2 x  là x A. 3 . B.1. C. 0 . D. 2 . y Câu 28.Cho hàm số 3
y  a x  4x  b a,b    có đồ thị như hình bên. x O
Mệnh đề nào sau đây đúng ?
A. a  0;b  0 .
B. a  0; b  0 .
C. a  0;b  0 .
D. a  0;b  0 .
Câu 29.Diện tích phần hình phẳng được gạch ngang trong hình dưới bằng 1 1 A.   2 2
 x  2x  4dx. B.   2 2
 x  2x  4dx. 2  2  1 1 C.   2
2x  2x  4dx . D.   2
2x  2x  4dx . 2  2 
Câu 30. Cho hai số phức z  3
  2i, z 1 4i . Phần ảo của số phức z  z 1 2 1 2 bằng A. 6  . B. 6
 i . C.6 . D.6i .
Câu 31.Trên mặt phẳng tọa độ điểm biểu diễn số phức z  1 3i2  i là điểm nào dưới đây?
A. P 5;  5. B. Q  5  ;5.
C. N 5;5. D. M  1  ;5. Trang 93    1 
Câu32.Trong không gian Oxyz , cho các véctơ a  1; 0;3 và b  3; ;  5   . Tích vô hướng  2     .
a a  2b bằng A. 26. B. 26.  C. 25. D. 25. 
Câu33.Trong không gian Oxyz , viết phương trình mặt cầu  S  có tâm là điểm I 0;0; 3   và được cắt
bởi mặt phẳng   : 2x  y  2z  3  0 theo giao tuyến là đường tròn C  có bán kính bằng 4.
A. x  y   z  2 2 2 3
 25. B. x  y  z  2 2 2 3
 5 .C. x  y  z  2 2 2 3  25 . D.
x  y   z  2 2 2 3  5 .
Câu34.Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;1; 1
  và song song với mặt phẳng
 :2x  2y  z  0 có phương trình là
A. 2x  2 y  z  3  0 .
B. x  2 y  z  0 .
C. 2x  2 y  z  3  0 . D.
x  2 y  z  2  0 .
Câu35.Cho điểm A1; 2  ;3, B 3
 ;4;5  . Tọa độ I trung điểm của đoạn AB là: A. 1; 2   ;1 . B.  1  ;1;4 . C. 2;0  ;1 . D.  1  ;1;0 .
Câu36.Một hộp chứa 15 cái thẻ được đánh số từ 1 đến 15, rút ngẫu nhiên ba cái thẻ. Xác suất để rút được
ba cái thẻ có tổng các số ghi trên ba thẻ là số lẻ bằng: 8 32 16 24 A. . B. . C. . D. . 65 65 65 65
Câu 37.Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a . Hình chiếu vuông góc của S trên mặt
phẳng  ABC  là trung điểm H của cạnh AB . Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng
30 . Tính khoảng cách giữa hai đường thẳng BC và SA . 2a 21 a 21 2a 7 a 7 A. . B. . C. . D. . 7 7 7 7 x 1 ln 3
Câu 38.Cho hàm số f  x có f  
1  e và f  x x  e , x
  0. Khi đó xf  xdx  bằng 2 x 1
A. 2  e .
B. 3  e .
C. 3  e . D. 2  e . m  x 
Câu39.Cho hàm số f  x   1 4  x 
( m là tham số thực). Có bao nhiêu giá trị nguyên của m để 2m
hàm số đã cho nghịch biến trên khoảng 0;  ? Trang 94
A. 4 . B. 3 .
C. 2 . D.1.
Câu40.Cho hình nón có chiều cao bằng 6 . Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo
một thiết diện là tam giác đều, góc giữa mặt phẳng và mặt đáy của hình nón bằng 0 60 . Thể tích của khối
nón được giới hạn bởi hình nón đã cho bằng A. 56 .
B. 28 . C. 84 . D.168 .
Câu 41.Cho hai số dương a, b thỏa mãn log
2a  3b  log a  log b . Tính giá trị của biểu thức 4   10 25 3 2 3
a  ab  b 25 5 25 25 P  B. .C. . D . 3 2 3 a  ab  A. b 29 6 27 28
Câu 42.Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số 3 2
y  x  x   2 m   2
1 x  m  m  3 trên đoạn  1
 ;2 không vượt quá 15? A. 3 . B. . C. 5 . D.Vô số.
Câu 43.Cho phương trình 2 log
9x  m  5 log x  3m 10  0 . Số giá trị nguyên của tham số m để 3     3
phương trình đã cho có hai nghiệm phân biệt thuộc 1;8  1 là A. 2 . B. 3 . C. 4 . D. 5 .
Câu44.Cho hàm số f ( x) liên tục trên  . Biết 2
cos x là một nguyên hàm của hàm số 2 ( ) e x f x , họ tất cả các nguyên hàm của hàm số   2 ' e x f x là A. 2
sin 2x  2 cos x  C . B. 2
sin 2x  2 cos x  C .C. 2
sin 2x  2cos x  C . D. 2
sin 2x  2cos x  C .
Câu45. Cho hàm số có bảng biến thiên như sau: Số nghiệm đoạn  2
 ;2 của phương trình
4 f cos x  5  0 là A. 4. B. 6. C. 3. D. 8.
Câu46. Cho hàm số bậc bốn y  f  x có đồ thị như hình bên. Số điểm cực trị của hàm số
g  x  f  4 2
x  2x  5 là A. 5. B. 3. C. 9. D.11. 1 xy
Câu 47. Cho các số x  0; y  0 thỏa mãn log
 3xy  x  2y  4 3 1 . Giá trị 2 y
lớn nhất của xy bằng M khi  ;
x y   x ; y . Tính 2 2
x  y . 0 0  0 0 Trang 95 3 11  2 3 11  2 65 10 22 65 10 22 A. . B. . C. . D. . 6 6 18 18 2
Câu 48.Cho hàm số f  x liên tục trên  và thỏa mãn 3
f  x  f  x  , x x
  . Tính I  f  xdx 0 ta được 5 5 5 5 A. I  . B. I   . C. I   . D. I  . 4 8 4 8 
Câu49.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành AD  2AB  2a , 0 BAD  60 . Biết
hình chiếu của S lên mặt phẳng  ABCD là trung điểm I của BC và góc giữa hai mặt phẳng  SAB và SAD là 0 60 . Tính V ? S . ABCD 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 3 6 8 4
Câu50.Cho hàm số f  x . Hàm số y  f  x có đồ thị như hình vẽ x
Hàm số g  x  f   x 3 2 2 
 2x  3x  2 đồng biến trên khoảng nào dưới đây? 3 A.  ;   
1 . B. 1; 4 .
C. 4;  . D. 2;3 . ĐÁP ÁN Trang 96 1D 2B 3C 4D 5D 6D 7B 8A 9A 10C 11D 12D 13B 14B 15D 16A 17C 18A 19A 20C 21D 22A 23C 24A 25B 26A 27D 28D 29B 30A 31A 32B 33A 34C 35B 36B 37A 38B 39D 40A 41A 42A 43C 44D 45D 46C 47D 48A 49D 50C
LỜI GIẢI CHI TIẾT
Câu1.Chọn D.Số cách Chọn một người nam: 5 cách.
Số cách Chọn một người nữ: 6 cách.Áp dụng quy tắc nhân, số cách Chọn là: 30 cách. u  u Câu2.Chọn B. 3 1
u  u  2d  d   3 . 3 1 2
Câu 3.Chọn C.Diện tích xung quanh của hình trụ là S  2rh . xq Câu 4.Chọn D
Quan sát bảng biến thiên ta thấy f ' x  0 trên khoảng 0; 2 , do đó hàm số f  x nghịch biến trên khoảng 0; 2 .
Câu5.Chọn D.Thể tích khối lập phương đã cho là 3 3
V  a  4  64  8 
Câu 6.Chọn D.TXĐ: D  ;  
 ; log 3x 8 2
 2  3x 8  2  x  4 tm 2    3 
Vậy x  4 là nghiệm của phương trình. 5 5 3 Câu 7.Chọn B.Ta có:
f (x)dx 
f (x)dx 
f (x)dx  3  1  4  .    3 1 1
Câu 8.Chọn A.Căn cứ vào bảng biến thiên ta được giá trị cực đại của hàm số bằng 2. Câu9.Chọn A
Câu10. Chọn C.Vì a là số thực dươg nên ta có: log  2 9a
 2log 3a  2(1 log a) 3  3   3
Câu 11.Chọn D.Ta có  x   1 sin 2
2 dx  sin 2xdx  2 dx  
cos 2x  2x  C   . 2
Câu 12.Chọn D.Ta có i    2 2 0 1  1.
Câu 13.Chọn B.Hình chiếu vuông góc của điểm M 1; 3
 ;4trên mặt phẳng Oyz có tọa độ là 0; 3  ;4 . Trang 97
Câu 14.Chọn B.Gọi I là tâm mặt cầu S   I 2;1; 3  .
Câu15.Chọn D.Vì các hệ số trước ; x ;
y z trong phương trình mặt phẳng   : 5x  y  4z  3  0 là một 
tọa độ của vectơ pháp tuyến của   . Do đó, một vectơ pháp tuyến của   là: n  5; 1; 4 . 2   x  2 y 1 z 1
Câu16.Chọn A.Thay tọa độ điểm P 4;9;3 vào phương trình đường thẳng d :   ta 3 4 2 4  2 9 1 3 1 được:  
 2 . Vậy điểm P thuộc đường thẳng d . 3 4 2
Câu17.Chọn C.Áp dụng định lí Pytago ta có: 2 2 AC 
AB  BC  a 3
Ta có SA   ABCD  AC là hình chiếu vuông góc của SC trên
ABCD  SC ABCD  SC AC  , ,  SCA  SA 3a  Xét S
 AC : tan SCA  
 3  SCA  60 Vậy AC a 3
SC,ABCD  60
Câu 18.Chọn A.Dựa vào bảng biến thiên ta có:Hàm số f  x có 4 điểm cực trị tại x  2  , x  1
 , x  2, x  3 x  1  0;2 Câu19.Chọn A.Ta có 2
y '  3x  3  0   x 1  0;2
Khi đó: M  maxy0; y  
1 ; y 2  max2;0;  4  4
m  miny 0; y  
1 ; y 2  min2;0; 
4  0 .Vậy M  m  4
Câu 20.Chọn C.Kiểm tra từng đáp án ta thấy đáp án C đúng vì  2018 a b 2018 log  log a
 log b  2018  log b a a a a
Câu 21.Chọn D.Ta có 2 2 x 2 x x 2 x 3  1  1  1   1  2   
 x  2x  3  x  ;  31;         2  8  2   2 
Câu 22.Chọn A.Gọi r là bán kính đáy hình trụ.Do thiết diện qua trục là hình
vuông nên hình trụ có chiều cao là h  2r .Diện tích toàn phần bằng 2 64 a Trang 98 2 2
 2 r  2 rh  64 a 2 2 2
 2. r  4 r  64 a 4 6a 2 2
 6r  64a  r  . 3
 f x 1 Câu 23.Chọn C.Ta có 2
f  x 1  0   .  f   x  1 
Từ đồ thị ta thấy đường thẳng y  1 cắt đồ thị hàm số f  x tại 1 điểm và
đường thẳng y  1 cắt đồ thị hàm số f  x tại 3 điểm phân biệt.Nên
phương trình có 4 nghiệm phân biệt.
Câu 24.Chọn A.Ta thấy x   ;  
1  x 1  0 2 2 2 x  2  3  x x Nên f
 xdx  dx  x 1 dx 
 x  3ln x 1  C   x  3ln   
1 xC x 1  x 1  2 2 S  S   S 
Câu 25.Chọn B.Áp dụng công thức nr nr
S  Ae  e   nr  ln  n  ln : r     A  A   A  116224393 
với: S  116 224 393 , A  96 208 984 , r  0, 9 %..Suy ra: n  ln : 0,9%  21    96208984 
Vậy đến năm: 2019  21  2040 thì dự báo dân số của nước đó là 116.224.393 người.
Câu 26. Chọn A.Gọi cạnh đáy là x . Ta có: 2 5a 2 2 2 2 2 2 2 2 2
AC  AB  AD  AA  9a  x  x  4a  x  . 2
Thể tích của khối lăng trụ đã cho là: 2 3 V  S
.AA  x .2a  5a . ABCD
Câu 27.Chọn D.Tập xác định D   \ 0;  1 2 2x  3x 1 Ta có: lim y  lim
 2 , nên đồ thị hàm số có 1 tiệm cận ngang là y  2. 2 x x x  x 2 2x  3x 1 x   1 2x   1 Xét lim y  lim  lim 1 2 x 1  x 1  x 1 x  x  x  x   1 2 2 2x  3x 1 2x  3x 1 Và lim y  lim   ;  lim y  lim
  , nên đồ thị hàm số có 1 tiệm cận   2   2 x0 x0  x0 x0 x x x  x đứng là x  0.
Câu 28.Chọn D.Dễ nhận thấy a  0 và đồ thị cắt trục tung tại tung độ dương nên b  0 . Trang 99
Câu 29.ChọnB.Phương trình hoành độ giao điểm x  2  2 2 2
x  x  3  x  3x 1 2
 x  2x  4  0   x 1 1 1
Diện tích hình phằng cần tìm là 2 S 
x  x  3  
 2x 3x 1dx     2 2
 x  2x  4dx . 2  2 
Câu 30.Chọn A.Ta có z  z  3
  2i  1 4i  2
  6i .Phần ảo của số phức z  z bằng 6  . 1 2     1 2
Câu 31.Chọn A.Ta có z    i  i 2 1 3 2
 2  i  6i 3i  5 5i .Vậy điềm biểu diễn của số phức z
là P 5;  5. Câu32.Chọn B.Ta có       2b  6;1; 1
 0  a  2b  5;1; 7    .
a a  2b    1 .5  0.1 3. 7    2  6.
Câu33.Chọn A.Gọi R , r lần lượt là bán kính của mặt cầu  S  và đường tròn C  . 2.0  0  2. 3   3
Ta có d  I,      3.Khi đó 2
R  d I   2 2 2 ,
 r  3  4  5. 2 2 2 2 1  2
Vậy phương trình của  S  là x  y   z  2 2 2 3  25.
Câu34.Chọn C.Gọi   là mặt phẳng cần tìm. 
Mặt phẳng   : 2x  2 y  z  0 có một vectơ pháp tuyến là n   2;2  ;1 . 
Vì   / /   nên   nhận n   2;2  ;1 làm vectơ pháp tuyến.
Vậy   có phương trình là 2 x   1  2 y   1   z  
1  0 hay 2x  2 y  z  3  0 .  x  x A B x   I 2  x  1  I  y  y 
Câu35.Chọn B.Ta có: I là trung điểm của đoạn AB A B  y   y 1 I 2 I  z  4  I  z  z A B z   I  2
Câu36.Chọn B.Số cách rút ba thẻ bất kì trong số15 thẻ là: 3 C  455 . 15
Số cách rút ba thẻ mang số lẻ trong 8 thẻ lẻ là: 3 C  56 . 8
Số cách rút ba thẻ trong đó có hai thẻ mang số chẵn và một thẻ mang số lẻ là: 2 1 C .C  168 7 8
Số cách rút được ba cái thẻ có tổng các số ghi trên ba thẻ là số lẻ là: 56 168  224 . Trang 100
Vậy xác suất rút được ba cái thẻ có tổng các số ghi trên ba thẻ là số 224 32 lẻ là: P   . 455 65
Câu 37.Chọn A.Trong mặt phẳng  ABC  dựng Ax / /BC .Gọi D
là hình chiếu của của điểm H trên Ax và E là hình chiếu của H
trên SD .Suy ra HD  AD và HE  SD AD  HD Ta có 
 AD  SHD mà AD  SH
HE  SHD  AD  HE
Từ và suy ra HE  SAD .Do BC / / Ax mà
Ax  SAD  BC / / SAD  
SA  d BC SAD  d B SAD  d H SAD SH.DH d BC, , , 2 ,  2HE  2. 2 2 SH  DH  3 Xét S
 HC vuông tại H có CH  a 3 và SCH  30 nên SH  CH.tan30  a 3.  a . 3   Xét tam giác A
 DH vuông tại D có AH  a và HAD  HBC  60 nên a 3
DH  AH.sin 60  . 2 a 3 . a 2a 21
Vậy d  BC SA 2 ,  2.  . 2 7 3a 2 a  4
Câu 38.Chọn B.Ta có         f  x x 1 x e x 1. x e ( x
e ) .x (x) . x x x e e e x  e dx  dx  dx    
  dx  C 2 2 2 x x x  x  x x e ln3 ln3 ln3 Vì f  
1  e  e  C  e  C  0  f  x  .Vậy    x x xf x dx  e dx  e  3 e  . x 1 1 1 2 m 1 x  4 2m  2m  4
Câu39.Chọn D.Tập xác định: D   \  2  
m .Ta có: f  x   
 f x  . x  2m x  2m2
Để hàm số đã cho nghịch biến trên khoảng 0; Trang 101  2  m  0  m  0   S  m 0       0  m 1.  f    x 2  0
2m  2m  4  0  2   m 1 m Do   m  0. B 0   m 1 H O
Câu40.Chọn A.Gọi S là đỉnh của hình nón. Một mặt phẳng đi qua đỉnh của hình nón và A
cắt hình nón theo một thiết diện là tam giác đều SAB . Gọi O là tâm đường tròn đáy  SO  6 
.Gọi H là trung điểm 0
AB  OH  AB, SH  AB  SHO  60 . SO SA 3
Từ giả thiết ta có: SH   4 3 , do ABC  đều SH   SA  8. 0 sin60 2 1 1 Nên 2 2
OA  SA  SO  64  36  2 7 .Vậy 2 V 
. .OA .SO  . .28.6  56 . 3 3
Câu 41.Chọn A.Đặt log
2a  3b  log a  log b  t 4   10 25 t   
2a  3b  4t 2     1 (l) 2t t         5   2 2 a  10t 2.10t 3.25t 4t      2.  3  0        5   5   t  2  b  25t    3    5  3  a  a   t 1   a  2  3 2 3
a  ab  b  b  b 27  3 1 25 Ta có   3   và P     . b  5  3 2 3 3
a  ab  b  a  a 27  3 1 29  1    b  b
Câu 42.Chọn A.Xét hàm số f  x 3 2
 x  x   2 m   2
1 x  m  m  3 trên đoạn  1  ;2. 2 Ta có ' f  x 2
 x  x   2 m   2
 x  x   2 3 2 1 2 1  m  0, x   1  ;2
min f x  f   1  m  4  1;2
Suy ra hàm số f  x đồng biến trên đoạn  1  ;2     . max f 
x  f 2 2
 3m  m 11   1;2  m  4 15 
Khi đó max y  max f  x   2
max m  4 ; 3m  m 11 15    1  ;2  1  ;2 2
3m  m 11  15   19   m  11   1  9  m 11 15   m  4  15   2   3
 m  m  4  0   4
. Với m  m  1  ;0;  1 2  15
  3m  m 11 15  1   m   2
3m  m  26  0   3
Câu 43.Chọn C.Ta có: 2 log
9x  m  5 log x  3m 10  0 .Đặt t  log x vì 3     3 3 x 1;8  1  t 0;4. Trang 102 t  
Khi đó phương trình đã cho trở thành: 2
t  m  
1 t  3m  6  3 0   . t   m  2 0   m  2  4 2  m  6 ycbt    
. Vậy có 4 số nguyên m thoả ycbt. m  2  3 m  5 Câu44.Chọn D.Vì 2
cos x là một nguyên hàm của hàm số   2x f x e nên:    2x f x e   2 cos x'  2  cos .
x sin x  sin 2x . 2 x 2     2 x u e du e dx Tính     2 ' x I f x e dx .Đặt    . dv  f ' 
xdx v  f  x
 I  f x 2x f  x 2x 2 .e 2
e dx  sin 2x  2cos x  C . 5
Câu45.Chọn D.Từ 4 f cos x  5  0  f cos x     1 4 5
Đặt t  cos x với x  2
 ;2  thì t  1  ;  1  
1  f t    2 4
Xét hàm số h  x  cos x ; x  2  ;2  ta có BBT: Với t  1  thì PT có 2 nghiệm. Với 1
  t 1thì PT có 4 nghiệm
Với t 1thì PT có 3 nghiệm 5
Xét f t    2 với t  1  ;  1 4 3
t  x 1 x  0  4n 1  1  0
Nhìn vào BBT PT f t    2 có hai nghiệm  2
t  x 0  x  1  4n  2  2  0
Vậy tất cả có 8 nghiệm
Câu46.Chọn C. g  x  f  4 2
x  x    g x   3
x  x f  4 2 2 5 4 4
x  2x  5  0 Trang 103 x  0 x  1   3
4x  4x  0
4x 2x   1  0 x 1        4 2 f 
x  2x  5  x 0  x  4 1  1  1     4 2
x  2x  5  0  f    4 2
x  2x  5  0  4 2
x  2x  5  x 4  x  5 2 2  2     4 2
x  2x  5  x x  5 3  3  3   Xét f  x 4 2
 x  x   f x 3
 x  x  x 2 2 5 4 4 4 x   1 ; x  0 
f  x  0  4x  2 x   1  0  x  1   x 1 
Dựa vào bảng biến thiên ta thấy.PT có vô nghiệm, PT có 4 Ta có BBT: nghiệm, PT có 2 nghiệm
Nên PT g x  0 có 9 nghiệm đơn phân biệt, suy ra
Hàm số g  x  f  4 2
x  2x  5 có 9 điểm cực trị. 1 xy
Câu 47. Chọn D.Xét phương trình: log
 3xy  x  2y  4 1 . 3   1 2 y
Với x  0; y  0 , điều kiện xác định của   1 là: xy  1. 1 xy Ta có: log
 3xy  x  2y  4  log 1 xy  log 1 2y 1 (3 3xy)  (x  2y) 3   3   3 1 2y
 log 33xy  (3 3xy)  log 1 2y  (x  2y) * 3   3    
Xét hàm số f t t  log t trên 0;  , có f t 1 1  0, t   0. 3 t.ln 3
Suy ra hàm số f t  đồng biến trên 0; .
PT *  f 3  3xy  f  x  2 y  3  3xy  x  2 y  2 2xy .  2  11  2  11
Suy ra: 3xy  2 2xy  3  0   xy  . 3 3 Trang 104  26  4 22 x  2y    x   3
max  xy 13 2 22  khi  13  2 22   . 9 xy   26  4 22  9 y   6  26  4 22 x  0  3 65 10 22 65 10 22 Do đó 2 2   x  y  . Vậy 2 2 x  y  . 0 0 18 0 0  26  4 22 18 y   0  6 x  0  f  0  0
Câu 48.Chọn A.Với  x  2  f  2 1 Từ gt: 3
f  x  f  x  , x x    3
f  x. f  x  f  x. f  x  .
x f  x, x   2 2 4 f  x 2 2 f  x 2 2 2 3   f
 x.f x f x.f xdx  .xf   xdx      .
x f  x  f  xdx 4 0 2 0 0 0 0 0  1 1   5 I  2      I  .  4 2  4
Câu49.Chọn D.Gọi J là trung điểm của AD  IJ là đường trung
bình của ABCD  IJ //AB và IJ  a .
Tứ giác ABIJ có AB  BI  IJ  AJ  ABIJ là hình thoi.
Xét hai tam giác vuông S  IB và S
 IJ có SI chung và BI  IJ  a, suy ra S  IB  S
 IJ nên SB  SJ . Xét S  BA và S
 JA có: SB  SJ , AB  AJ và SA chung suy ra S  BA  S  JA. Kẻ BH  S
A H  SA , dễ thấy JH  SA và BH  HJ . 
 SAB SAD  SA   0   BHJ  60
Ta có: SA  BH  SAB
 BH, HJ   SAB,SAD 0  60   .     SA  JH   SAD 0 BHJ 120 SA  BH Do 
 SA  BHJ   SA  HK . SA  HJ Trang 105 BJ  a   Tam giác BAJ 
có BA  AJ  a và 0
BAJ  60  BAJ  đều   a 3 . AK   2  a  KJ a 3 Giả sử 0 BHJ  60  3 HK   AK nên 0
BHJ  120  HK   2  tan KHJ 6 a 6 2 2
 HA  AK  HK  . 3 AH HK AI.HK 2AK.HK a 6 Ta có A  HK  A  IS    SI    . AI SI AH AH 4 3 1 1  a 2 V  S .SI  A . B A . D sin BA . D SI  . S.ABCD 3 ABCD 3 4
Câu50.Chọn C.Ta có: g x   f   x 2 2
 x  4x  3
g x   f   x  x  x   f   x    x2 2 0 2 4 3 2 2 1
Đặt t  2  x . Xét phương trình f t 2  t 1
Số nghiệm của phương trình f t  2
 t 1 chính là số giao điểm của đồ thị hàm số
y  f t  và đồ thị hàm số 2 y  t 1 t   2 
Dựa vào đồ thị ta thấy f t  2  t 1  t   0   x   x 
Khi đó f   x    x2 2 2 4 2 2 1    2  x  0 x  2 Ta có bảng xét dấu :
Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên 4;  . Trang 106

Đề thi hk2 môn toán 12 có đáp án năm 2020 trường thpt thanh bình 1 tỉnh đồng tháp

Thông tin :

Tài liệu liên quan:

Đề kiểm tra cuối kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Vĩnh Long

Đề kiểm tra học kỳ 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Bình Dương

Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Quảng Nam

Đề cuối kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Đắk Lắk

Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị