Đề Thi HK2 Môn Toán 12 Có Lời Giải Chi Tiết Năm 2022-Đề 5

Đề thi HK2 môn Toán 12 năm 2022 được biên soạn dưới dạng file PDF gồm 24 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 5
ĐỀ ÔN THI HỌC KỲ II – NĂM HỌC 2021-2022
Môn: Toán lớp 12
Câu 1: Trong không gian
Oxyz
cho
3;4; 5a 
,
1;1; 2b
thì tọa độ của
34n a b
là:
A.
13;8; 7
. B.
5;8; 7
. C.
. D.
13;8; 23
.
Câu 2: Cho số phức
2 14zi
. Phần thực và phần ảo của số phức lần lượt là:
A.
2; 14i
. B.
2; 14
. C.
14 ;2i
. D.
14; 2
.
Câu 3: Trong hệ tọa độ
Oxyz
cho phương trình mặt phẳng
:3 2 7 10 0x y z
thì một véc-tơ
pháp tuyến có tọa độ là:
A.
3; 2; 7
. B.
3;2;7
. C.
3; 2;7
. D.
3; 2; 7
.
Câu 4: Giải phương trình
2
10 29 0zz
trong tập số phức
ta được tập nghiệm là:
A.
52Si
. B.
52Si
. C.
5 2 ;5 2S i i
. D.
S 
.
Câu 5: Trong hệ tọa độ
Oxyz
, phương trình mặt phẳng
đi qua điểm
1; 2;3A
và nhận
2;4; 5n 
làm vectơ pháp tuyến là
A.
2 4 5 21 0x y z
. B.
2 4 5 5 0x y z
.
C.
2 4 5 21 0x y z
. D.
2 4 5 21 0x y z
.
Câu 6: Trong không gian
Oxyz
, tìm tọa độ tâm
I
của mặt cầu
S
có phương trình
2 2 2
3 1 5 36x y z
là
A.
3;1; 5I
. B.
3;1;6I
. C.
3; 1;5I 
. D.
3;1;5I
.
Câu 7: Cho
tanF x x C
là họ nguyên hàm của hàm số
fx
. Khẳng định đúng là
A.
cotf x x
. B.
2
1
cos
fx
x
. C.
2
1
sin
fx
x
. D.
2
1 cosf x x
.
Câu 8: Số phức
z a bi
có modun là
A.
22
z a b
. B.
22
z a b
. C.
22
z a b
. D.
z a b
.
Câu 9: Cho số phức
2
13
z
i
. Số phức liên hợp của
z
là:
A.
13
22
i
. B.
13i
. C.
13i
. D.
13
22
i
.
Câu 10: Cho hai số phức
12
,z m ni z p qi
. Tổng của
12
zz
là số phức:
A.
z m p n q
. B.
z m p n q i
.
C.
z m p n q i
. D.
z m q n p i
.
Câu 11: Mệnh đề nào sau đây đúng?
A.
d d d
b c c
a a b
f x x f x x f x x
.
B.
d
b
a
f x x F a F b
(
Fx
là một nguyên hàm của
fx
).
Trang2
C.
d0
a
a
f x x
.
D.
d d 0
ba
ab
f x x f x x

.
Câu 12: Trong không gian
Oxyz
, tìm bán kính
R
của mặt cầu
S
có phương trình
22
2
6 3 128x y z
là
A.
2
128 .R
B.
128.R
C.
2 8.R
D.
8 2.R
Câu 13: Cho hàm số
2
2.f x x
Họ nguyên hàm của hàm số là
A.
2.F x x C
B.
3
1
2.
3
F x x x C
C.
3
1
.
3
F x x C
D.
2 2 .F x x C
Câu 14:
Tích phân
2
5
1
I x dx
có giá trị là
A.
32
.
3
B.
16
.
3
C.
21
.
2
D.
19
.
3
Câu 15: Biểu thức
V
để tính thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi đồ thị
hàm số
sinyx
và các đường thẳng
0,
3
xx

, trục hoành, quay quanh trục
Ox
là
A.
3
2
0
sinV xdx
. B.
3
0
sinV x dx
. C.
3
2
0
sinV xdx
. D.
3
0
sinV x dx
.
Câu 16: Trong không gian
Oxyz
cho hai điểm
1;2;3A
,
0;1;1B
, độ dài đoạn
AB
bằng
A.
6
. B.
8
. C.
12
. D.
10
.
Câu 17: Trong không gian
Oxyz
cho đường thẳng
d
đi qua
2;3; 5A 
và có véc tơ chỉ phương
3; 5; 2a 
thì phương trình tham số của đường thẳng
d
là
A.
23
35
52
xt
yt
zt

. B.
32
53
25
xt
yt
zt

. C.
23
35
52
xt
yt
zt



. D.
32
53
25
xt
yt
zt
.
Câu 18: Trong không gian
Oxyz
cho đường
12
:3
28
xt
d y t
zt



. Đường thẳng
d
vuông góc với đường thẳng
nào sau đây?
A.
1
34
: 5 2
2 16
xt
d y t
zt
. B.
2
32
: 5 3
25
xt
d y t
zt

. C.
3
25
: 3 2
5
xt
d y t
zt

. D.
4
1
1
:3
2
24
xt
d y t
zt



.
Câu 19: Tìm căn bậc hai của số thực âm
64
trên tập số phức
.
A.
8;8
. B.
8i
. C.
8 ;8ii
. D.
8
.
Trang3
Câu 20: Dạng
z a bi
của số phức
1
32
z
i
là số phức nào dưới đây?
A.
32
13 13
i
. B.
32
13 13
i
. C.
32
13 13
i
. D.
32
13 13
i
.
Câu 21: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
2
2022yx
và hai đường thẳng
3, 4xx
với trục hoành được tính bởi biểu thức:
A.
4
2
3
2022 .

S x dx
B.
4
2
3
2022 .

S x dx
C.
4
2
2
3
2022 .

S x dx
D.
3
2
4
2022 .

S x dx
Câu 22:
Số phức
z a bi
. Khi đó
zz
là số phức:
A.
2.bi
B.
2 2 .a bi
C.
2a
. D.
2b
.
Câu 23: Cho
5
21A x dx
. Đặt
21tx
. Khẳng định đúng là:
A.
5
1
.
2
A t dx
B.
5
2.A t dx
C.
5
1
1.
2
A t dx
D.
5
A t dx
Câu 24: Trong hệ trục tọa độ
,Oxyz
cho mặt phẳng
( )
:3 2 7 10 0α x y z- + - =
. Mặt phẳng
( )
α
song
song với mặt phẳng nào có phương trình sau?
A.
3 2 7 3 0x y z
. B.
3 2 7 5 0x y z
.
C.
3 2 7 0x y z
. D.
3 2 7 3 0x y z
.
Câu 25: Cho các số phức
12
3 , 4z bi z c i
. Phần thực và phần ảo của số phức
12
z z z=-
lần
lượt là
A.
7; bc
. B.
3 ; 4cb
. C.
3 ; 4cb
. D.
3 ; 4cb
.
Câu 26: Cho số phức
z
thỏa mãn
2016
1
1
i
z
i



. Viết
z
dưới dạng
,,z a bi a b= + Î ¡
. Khi đó tổng
ab
có giá trị bằng bao nhiêu?
A.
2
. B.
0
. C.
1
. D.
1
.
Câu 27: Cho số phức
12
,z a bi z c di
. Khi đó
,MN
lần lượt là hai điểm biểu diễn cho các số
phức
12
,zz
. Khi đó độ dài véctơ
MN
là
A.
22
MN c a d b
. B.
22
MN b a d c
.
C.
22
MN c a d b
. D.
22
MN c a d b
.
Câu 28: Cho hai đường thẳng
12
: 2 3
34
xt
d y t
zt



và
3 4 '
': 5 6 '
7 8 '
xt
d y t
zt



Trong các mệnh đề sau, mệnh đề nào đúng?
A.
'dd
. B.
'dd
. C.
/ / 'dd
. D.
d
và
'd
chéo nhau.
Câu 29: Cho
4
0
d 16f x x
. Tính
2
0
2dI f x x
.
A.
32I
. B.
4I
. C.
16I
. D.
8I
.
Trang4
Câu 30: Trong hệ tọa độ
Oxyz
khoảng cách từ điểm
1; 2;3A
đến mặt phẳng
: 2 2 10 0x y z
bằng
A.
1
3
. B.
1
3
. C.
7
3
. D.
1
3
.
Câu 31: Phần gạch chéo trong hình bên dưới là hình phẳng giới hạn bởi đồ thị của hàm số
2
( ) ( 1)( 2)f x x x
với trục hoành. Hãy tính diện tích
S
đó
A.
15
2
. B.
27
4
. C.
27
4
. D.
15
2
.
Câu 32: Cho 3 điểm
2;0;0M
,
0; 3;0N
,
0;0;4P
. Nếu
MNPQ
là hình bình hành thì tọa độ của
điểm
Q
là
A.
3;4;2
. B.
2;3;4
. C.
2; 3; 4
. D.
2;3; 4
.
Câu 33: Tọa độ giao điểm của hai đường thẳng
32
: 2 3
64
xt
d y t
zt

và
5
: 1 4
20
xt
d y t
zt



là
A.
0; 3;2
. B.
7; 8; 2
. C.
3;7;18
. D.
8; 13;23
.
Câu 34: Gọi
n
là số nghiệm của phương trình
52
0z az bz c
(
,,abc
là các số thực) trong tập số
phức
. Tìm giá trị của số
n
.
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 35: Trong không gian
Oxyz
, viết phương trình mặt cầu
S
có tâm
4;0; 2I
và bán kính
9R
.
A.
( ) ( ) ( )
22
2
: 4 2 81S x y z- + + + =
. B.
( ) ( ) ( )
22
2
: 4 2 9S x y z- + + + =
.
C.
( ) ( ) ( )
22
2
: 4 2 9S x y z+ + + - =
. D.
( ) ( ) ( )
22
2
: 4 2 81S x y z+ + + - =
.
Câu 36: Hình chiếu của điểm
( )
2; 3;5A -
lên đường thẳng
32
: 2 3
1
xt
d y t
zt
ì
= - +
ï
ï
ï
ï
= - +
í
ï
ï
=+
ï
ï
î
có tọa độ là
A.
31 5 25
;;
14 14 14
æö
÷
ç
-
÷
ç
÷
ç
èø
. B.
10 5 25
;;
7 14 14
æö
÷
ç
--
÷
ç
÷
ç
èø
. C.
10 5 25
;;
7 14 14
æö
÷
ç
--
÷
ç
÷
ç
èø
. D.
10 5 25
;;
7 14 14
æö
÷
ç
-
÷
ç
÷
ç
èø
.
Câu 37: Trong hệ tọa độ
Oxyz
mặt phẳng
đi qua điểm
3; 1; 5M 
và vuông góc với hai mặt
phẳng
:3 2 2 7 0P x y z
và
:5 4 3 1 0Q x y z
có phương trình là
A.
30x y z
. B.
2 2 15 0x y z
.
C.
2 2 15 0x y z
. D.
2 2 16 0x y z
.
Trang5
Câu 38: Trong không gian với hệ tọa độ
Oxyz
, cho tứ diện
ABCD
, biết
2;3;1 , 4;1; 2AB
,
6;3;7C
,
5; 4; 8D
. Độ dài đường cao
DH
của tứ diện
ABCD
bằng:
A.
15
7
. B.
5
7
. C.
45
21
. D.
45
7
.
Câu 39: Cho số phức
z
thỏa mãn
3 8 7zi
và số phức
43wi
. Gọi
M
là giá trị lớn nhất của
biểu thức
P z w
. Chọn khẳng định đúng trong các khẳng định sau.
A.
20;21M
. B.
21;22M
. C.
18;19M
. D.
19;20M
.
Câu 40: Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
3 31f x x
và
7 35
11 11
g x x
với trục
Ox
và đường thẳng
9x 
.
A.
8125
198
S
. B.
1029
22
S
. C.
647
18
S
. D.
1797
50
S
.
Câu 41: Trong không gian
Oxyz
, cho mặt cầu
S
có phương trình là
2 2 2
2 2 2 8 4 12 6 0x y z x y z
và mặt phẳng
: 3 2 5 0x y z
. Gọi
I
là tâm mặt
cầu
S
,
I
là điểm đối xứng của
I
qua mặt phẳng
. Tính độ dài đoạn
II
.
A.
6 14
7
II
. B.
3 14
7
II
. C.
17II
. D.
2 17II
.
Câu 42: Biết tích phân
5
1
d
ln3 ln5
31
x
I a b
xx
,ab
. Khi đó
ab
có giá trị là
A.
4
. B.
1
. C.
5
. D.
0
.
Câu 43: Số phức
1
;
1 ( 2 )
m
zm
m m i


. Môđun lớn nhất của số phức
z
là
A.
12
2
. B.
3
. C.
1
. D.
21
2
.
Câu 44: Tính
2
1
56
dx
xx
kết quả đúng là.
A.
ln 2 ln 3x x C
. B.
1
(ln 3 ln 2 )
2
x x C
.
C.
ln 3 ln 2x x C
. D.
ln( 2 . 3)x x C
.
Câu 45: Biết
2
cos
d.
13
x
x
xm
p
p
-
-
=
+
ò
Tính giá trị của
2
cos
d.
13
x
x
Ix
p
p-
=
+
ò
A.
m
. B.
4
m
. C.
m
. D.
4
m
.
Câu 46: Trong hệ tọa độ Oxyz một mặt phẳng
( )
a
đi qua điểm
( )
1;2;3M
và cắt ba tia Ox, Oy, Oz lần
lượt tại các điểm A, B, C sao cho thể tích tứ diện OABC nhỏ nhất, có phương trình là
A.
6 3 2 18 0x y z
. B.
3 2 2 13 0x y z
.
C.
3 6 18 0x y z
. D.
2 3 6 26 0x y z
.
Trang6
Câu 47: Trong mặt phẳng toạ độ
Oxyz
, đường thẳng
đi qua điểm
4; 2;4A 
, đường thẳng
cắt
và vuông góc với đường thẳng
32
:
1
14
xt
d
yt
zt

thì phương trình đường thẳng
là
A.
4 2 4
3 2 1
x y z

. B.
4 2 4
3 2 1
x y z


.
C.
4 2 4
3 2 1
x y z

. D.
4 2 4
3 2 1
x y z

.
Câu 48: Số các giá trị
m
nguyên để có đúng hai số phức
z
thỏa
3 3 4z m i
và
1 1 2z i z i
là
A.
9
. B.
8
. C.
11
. D.
6
.
Câu 49: Cho
ln2F x x
là một nguyên hàm của
2
x
fx
. Tính
' .lnf x xdx
. Kết quả đúng là
A.
3
' .ln ln
3
x
f x xdx x x C
. B.
3
3
' .ln ln
3
x
f x xdx x x C
.
C.
3
' .ln
3
x
f x xdx C
. D.
3
2
' .ln ln
2
x
f x xdx x x C
.
Câu 50: Các bồn chứa xăng vận chuyển trên xe cơ giới thường có dạng hình trụ nằm ngang với đáy là
một hình elip mà không phải hình tròn. Việc chế tạo theo hình elip có nhiều ưu điểm như: làm
cho trọng tâm xe thấp, độ dao động của chất lỏng bên trong bồn sẽ thấp …. Giả sử một bồn chở
xăng có đáy là đường elip có phương trình
22
1
94
xy

và chiều dài của bồn là
10m
. Sau khi
bơm xăng cho một trạm xăng thì phần xăng còn lại cách đỉnh của elip
1m
(Tham khảo hình
vẽ). Tính gần đúng lượng xăng còn lại trong bồn xăng (Làm tròn đến hàng đơn vị theo lít và giả
sửa các vật liệu chế tạo nên bồn xăng có độ dài không đáng kể).
A.
151 646
lít. B.
151 645
lít. C.
151 644
lít. D.
151 647
lít.
BẢNG ĐÁP ÁN
1.A
2.B
3.C
4.C
5.C
6.A
7.B
8.A
9.A
10.B
11.D
12.D
13.B
14.C
15.C
16.A
17.A
18.C
19.C
20.A
21.A
22.A
23.A
24.A
25.C
26.D
27.D
28.B
29.D
30.D
31.B
32.B
33.C
34.C
35.A
36.D
37.B
38.D
39.A
40.C
41.A
42.B
43.A
44.C
45.C
46.A
47.A
48.A
49.B
50.C
ĐÁP ÁN CHI TIẾT
Câu 1. Trong không gian
Oxyz
cho
3;4; 5a 
,
1;1; 2b
thì tọa độ của
34n a b
là:
Trang7
A.
13;8; 7
. B.
5;8; 7
. C.
13;16; 7
. D.
13;8; 23
.
Lời giải
Chọn A
3;4; 5 3 9;12; 15aa

.
1;1; 2 4 4; 4;8bb

.
3 4 13;8; 7n a b
.
Câu 2. Cho số phức
2 14zi
. Phần thực và phần ảo của số phức lần lượt là:
A.
2; 14i
. B.
2; 14
. C.
14 ;2i
. D.
14; 2
.
Lời giải
Chọn B
Câu 3. Trong hệ tọa độ
Oxyz
cho phương trình mặt phẳng
:3 2 7 10 0x y z
thì một véc-tơ
pháp tuyến có tọa độ là:
A.
3; 2; 7
. B.
3;2;7
. C.
3; 2;7
. D.
3; 2; 7
.
Lời giải
Chọn C
Câu 4. Giải phương trình
2
10 29 0zz
trong tập số phức
ta được tập nghiệm là:
A.
52Si
. B.
52Si
. C.
5 2 ;5 2S i i
. D.
S 
.
Lời giải
Chọn C
2
10 29 0zz
.
2
25 29 4 4 2ii
.
Phương trình có nghiệm:
52
52
b
xi
a
b
xi
a


Vậy tập nghiệm của phương trình là:
5 2 ;5 2S i i
.
Câu 5. Trong hệ tọa độ
Oxyz
, phương trình mặt phẳng
đi qua điểm
1; 2;3A
và nhận
2;4; 5n 
làm vectơ pháp tuyến là
A.
2 4 5 21 0x y z
. B.
2 4 5 5 0x y z
.
C.
2 4 5 21 0x y z
. D.
2 4 5 21 0x y z
.
Lời giải
Chọn C
Phương trình mặt phẳng
đi qua điểm
1; 2;3A
và nhận
2;4; 5n 
làm vectơ pháp
tuyến là
2 1 4 2 5 3 0 2 4 5 21 0x y z x y z
.
Câu 6. Trong không gian
Oxyz
, tìm tọa độ tâm
I
của mặt cầu
S
có phương trình
2 2 2
3 1 5 36x y z
là
A.
3;1; 5I
. B.
3;1;6I
. C.
3; 1;5I 
. D.
3;1;5I
.
Trang8
Lời giải
Chọn A
Câu 7. Cho
tanF x x C
là họ nguyên hàm của hàm số
fx
. Khẳng định đúng là
A.
cotf x x
. B.
2
1
cos
fx
x
. C.
2
1
sin
fx
x
. D.
2
1 cosf x x
.
Lời giải
Chọn B
Áp dụng bảng nguyên hàm cơ bản
2
1
d tan
cos
x x C
x

.
Câu 8. Số phức
z a bi
có modun là
A.
22
z a b
. B.
22
z a b
. C.
22
z a b
. D.
z a b
.
Lời giải
Chọn A
Câu 9. Cho số phức
2
13
z
i
. Số phức liên hợp của
z
là:
A.
13
22
i
. B.
13i
. C.
13i
. D.
13
22
i
.
Lời giải
Chọn A
Ta có
2 1 3
22
13
zi
i
nên
13
22
zi
.
Câu 10. Cho hai số phức
12
,z m ni z p qi
. Tổng của
12
zz
là số phức:
A.
z m p n q
. B.
z m p n q i
.
C.
z m p n q i
. D.
z m q n p i
.
Lời giải
Chọn B
12
z z z m p n q i
.
Câu 11. Mệnh đề nào sau đây đúng?
A.
d d d
b c c
a a b
f x x f x x f x x
.
B.
d
b
a
f x x F a F b
(
Fx
là một nguyên hàm của
fx
).
C.
d0
a
a
f x x
.
D.
d d 0
ba
ab
f x x f x x

.
Lời giải
Chọn D
d d d 0
b a a
a b a
f x x f x x f x x
là đúng.
Trang9
d d d
b c c
a a b
f x x f x x f x x
d d d
c c b
a b a
f x x f x x f x x
là sai .
d
b
a
f x x F a F b
là sai vì
d
b
a
f x x F b F a
.
d0
a
a
f x x
là sai vì
d2
a
a
a
a
x x a

.
Câu 12. Trong không gian
Oxyz
, tìm bán kính
R
của mặt cầu
S
có phương trình
22
2
6 3 128x y z
là
A.
2
128 .R
B.
128.R
C.
2 8.R
D.
8 2.R
Lời giải
Chọn D
Mặt cầu
S
có bán kính
8 2.R
Câu 13. Cho hàm số
2
2.f x x
Họ nguyên hàm của hàm số là
A.
2.F x x C
B.
3
1
2.
3
F x x x C
C.
3
1
.
3
F x x C
D.
2 2 .F x x C
Lời giải
Chọn B
Họ nguyên hàm của hàm số
2
2f x x
là
3
1
2.
3
F x x x C
Câu 14. Tích phân
2
5
1
I x dx
có giá trị là
A.
32
.
3
B.
16
.
3
C.
21
.
2
D.
19
.
3
Lời giải
Chọn C
Ta có
2
2
66
5
1
1
2 1 21
.
6 6 6 2
x
I x dx
Câu 15. Biểu thức
V
để tính thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi đồ thị
hàm số
sinyx
và các đường thẳng
0,
3
xx

, trục hoành, quay quanh trục
Ox
là
A.
3
2
0
sinV xdx
. B.
3
0
sinV x dx
.C.
3
2
0
sinV xdx
. D.
3
0
sinV x dx
.
Lời giải
Chọn C
Trang10
Ta có thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi đồ thị hàm số
sinyx
và các đường thẳng
0,
3
xx

, trục hoành, quay quanh trục
Ox
là
3
2
0
sinV xdx
.
Câu 16. Trong không gian
Oxyz
cho hai điểm
1;2;3A
,
0;1;1B
, độ dài đoạn
AB
bằng
A.
6
. B.
8
. C.
12
. D.
10
.
Lời giải
Chọn A
Ta có
1; 1; 2AB 
22
2
1 1 2 6AB AB
.
Câu 17. Trong không gian
Oxyz
cho đường thẳng
d
đi qua
2;3; 5A 
và có véc tơ chỉ phương
3; 5; 2a 
thì phương trình tham số của đường thẳng
d
là
A.
23
35
52
xt
yt
zt

. B.
32
53
25
xt
yt
zt

. C.
23
35
52
xt
yt
zt



. D.
32
53
25
xt
yt
zt
.
Lời giải
Chọn A
Ta có phương trình tham số của đường thẳng
d
đi qua
2;3; 5A 
và có véc tơ chỉ phương
3; 5; 2a 
là
23
35
52
xt
yt
zt

.
Câu 18. Trong không gian
Oxyz
cho đường
12
:3
28
xt
d y t
zt



. Đường thẳng
d
vuông góc với
đường thẳng nào sau đây?
A.
1
34
: 5 2
2 16
xt
d y t
zt
. B.
2
32
: 5 3
25
xt
d y t
zt

. C.
3
25
: 3 2
5
xt
d y t
zt

. D.
4
1
1
:3
2
24
xt
d y t
zt



.
Lời giải
Chọn C
Đường thẳng
d
cóvéctơ chỉ phương
2;1;8u 
.
Đường thẳng
3
25
: 3 2
5
xt
d y t
zt

cóvéctơ chỉ phương
3
5;2;1u
.
Ta có
33
. 2.5 1.2 8.1 0u u d d
.
Câu 19. Tìm căn bậc hai của số thực âm
64
trên tập số phức
.
Trang11
A.
8;8
. B.
8i
. C.
8 ;8ii
. D.
8
.
Lời giải
Chọn C
Ta có
2
64 64i
có hai căn bậc hai là
8i
và
8i
.
Câu 20. Dạng
z a bi
của số phức
1
32
z
i
là số phức nào dưới đây?
A.
32
13 13
i
. B.
32
13 13
i
. C.
32
13 13
i
. D.
32
13 13
i
.
Lời giải
Chọn A
Ta có
22
1 3 2 3 2 3 2
3 2 3 2 3 2 3 2 13 13
ii
zi
i i i

.
Câu 21.Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
2
2022yx
và hai đường thẳng
3, 4xx
với trục hoành được tính bởi biểu thức:
A.
4
2
3
2022 .

S x dx
B.
4
2
3
2022 .

S x dx
C.
4
2
2
3
2022 .

S x dx
D.
3
2
4
2022 .

S x dx
Lời giải
Chọn A
Diện tích hình phẳng cần tìm là:
4
2
3
2022 .

S x dx
Câu 22. Số phức
z a bi
. Khi đó
zz
là số phức:
A.
2.bi
B.
2 2 .a bi
C.
2a
. D.
2b
.
Lời giải
Chọn A
Ta có
2z z a bi a bi bi
.
Câu 23. Cho
5
21A x dx
. Đặt
21tx
. Khẳng định đúng là:
A.
5
1
.
2
A t dx
B.
5
2.A t dx
C.
5
1
1.
2
A t dx
D.
5
A t dx
Lời giải
Chọn A
Ta có
55
1 1 1
2 1 2 .
2 2 2
t x dt dx dx dt A t dt t dt




Câu 24. Trong hệ trục tọa độ
,Oxyz
cho mặt phẳng
( )
:3 2 7 10 0α x y z- + - =
. Mặt phẳng
( )
α
song
song với mặt phẳng nào có phương trình sau?
A.
3 2 7 3 0x y z
. B.
3 2 7 5 0x y z
.
C.
3 2 7 0x y z
. D.
3 2 7 3 0x y z
.
Lời giải
Trang12
Chọn A
Ta thấy:
3 2 7 10
3 2 7 3


nên mặt phẳng
song song với mặt phẳng có phương trình
3 2 7 3 0x y z
.
Câu 25. Cho các số phức
12
3 , 4z bi z c i
. Phần thực và phần ảo của số phức
12
z z z=-
lần
lượt là
A.
7; bc
. B.
3 ; 4cb
. C.
3 ; 4cb
. D.
3 ; 4cb
.
Lời giải
Chọn C
Ta có:
( ) ( ) ( ) ( )
12
3 4 3 4z z z bi c i c b i= - = + - - = - + +
.
Do đó, phần
thực và phần ảo của số phức
z
lần lượt là:
3 ; 4cb
.
Câu 26. Cho số phức
z
thỏa mãn
2016
1
1
i
z
i



. Viết
z
dưới dạng
,,z a bi a b= + Î ¡
. Khi đó tổng
ab
có giá trị bằng bao nhiêu?
A.
2
. B.
0
. C.
1
. D.
1
.
Lời giải
Chọn D
Ta có:
1008
2
2016 1008 1008
2016
1008
2016 1008 1008
1008 1008
2
1
1 2 2 .
1
1
1 2 .
12
1
i
i i i
i
z
ii
ii
i







.
Suy ra:
1
1
0
a
ab
b
.
Câu 27. Cho số phức
12
,z a bi z c di
. Khi đó
,MN
lần lượt là hai điểm biểu diễn cho các số
phức
12
,zz
. Khi đó độ dài véctơ
MN
là
A.
22
MN c a d b
. B.
22
MN b a d c
.
C.
22
MN c a d b
. D.
22
MN c a d b
.
Lời giải
Chọn D
; , ;M a b N c d
.
22
MN c a d b
.
Câu 28. Cho hai đường thẳng
12
: 2 3
34
xt
d y t
zt



và
3 4 '
': 5 6 '
7 8 '
xt
d y t
zt



Trong các mệnh đề sau, mệnh đề nào đúng?
A.
'dd
. B.
'dd
. C.
/ / 'dd
. D.
d
và
'd
chéo nhau.
Lời giải
Chọn B
Trang13
Véctơ chỉ phương của
d
là:
2;3;4u
.
Véctơ chỉ phương của
'd
là:
' 4;6;8u

.
Ta có
'2uu
, suy ra hai đường thẳng
d
và
'd
song song hoặc trùng nhau.
Chọn điểm
1;2;3Ad
, thay tọa độ điểm
A
vào phương trình đường thẳng
'd
ta được hệ
1 3 4 '
1
2 5 6 ' '
2
3 7 8 '
t
tt
t


. Suy ra điểm
A
thuộc đường thẳng
'd
.
Vậy
'dd
.
Câu 29. Cho
4
0
d 16f x x
. Tính
2
0
2dI f x x
.
A.
32I
. B.
4I
. C.
16I
. D.
8I
.
Lời giải
Chọn D
Đặt
2tx
,
d 2dtx
.
Đổi cận:
44
00
d1
d8
22
t
I f t f x x

.
Câu 30. Trong hệ tọa độ
Oxyz
khoảng cách từ điểm
1; 2;3A
đến mặt phẳng
: 2 2 10 0x y z
bằng
A.
1
3
. B.
1
3
. C.
7
3
. D.
1
3
.
Lời giải
Chọn D
Khoảng cách từ điểm
1; 2;3A
đến mặt phẳng
: 2 2 10 0x y z
là:
1 4 6 10
1
;
3
1 4 4
dA


.
Câu 31. Phần gạch chéo trong hình bên dưới là hình phẳng giới hạn bởi đồ thị của hàm số
2
( ) ( 1)( 2)f x x x
với trục hoành. Hãy tính diện tích
S
đó
Trang14
A.
15
2
. B.
27
4
. C.
27
4
. D.
15
2
.
Lời giải
Chọn B
Dựa vào hình vẽ
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
2
( ) ( 1)( 2)f x x x
với trục hoành là
2
2
1
1 2 .dS x x x
2
32
1
3 4 dx x x
2
4
3
1
27
4
44
x
xx



.
Câu 32. Cho 3 điểm
2;0;0M
,
0; 3;0N
,
0;0;4P
. Nếu
MNPQ
là hình bình hành thì tọa độ của
điểm
Q
là
A.
3;4;2
. B.
2;3;4
. C.
2; 3; 4
. D.
2;3; 4
.
Lời giải
Chọn B
Ta có:
0;3;4NP
;
2; ;
Q Q Q
MQ x y z
MNPQ
là hình bình hành khi
MQ NP
2
3
4
Q
Q
Q
x
y
z

.
Vậy tọa độ của điểm
2;3;4Q
.
Câu 33. Tọa độ giao điểm của hai đường thẳng
32
: 2 3
64
xt
d y t
zt

và
5
: 1 4
20
xt
d y t
zt



là
A.
0; 3;2
. B.
7; 8; 2
. C.
3;7;18
. D.
8; 13;23
.
Lời giải
Chọn C
Giao điểm của
d
và
d
là nghiệm của hệ:
3 2 5
3
2 3 1 4
2
6 4 20
tt
t
tt
t
tt


.
Do đó giao điểm
d
và
d
là
3;7;18M
.
Trang15
Câu 34. Gọi
n
là số nghiệm của phương trình
52
0z az bz c
(
,,abc
là các số thực) trong tập số
phức
. Tìm giá trị của số
n
.
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn C
Trên tập số phức, phương trình bậc
n
có
n
nghiệm. Do đó phương trình trên có 5 nghiệm.
Câu 35. Trong không gian
Oxyz
, viết phương trình mặt cầu
S
có tâm
4;0; 2I
và bán kính
9R
.
A.
( ) ( ) ( )
22
2
: 4 2 81S x y z- + + + =
. B.
( ) ( ) ( )
22
2
: 4 2 9S x y z- + + + =
.
C.
( ) ( ) ( )
22
2
: 4 2 9S x y z+ + + - =
. D.
( ) ( ) ( )
22
2
: 4 2 81S x y z+ + + - =
.
Lời giải
Chọn A
Nhớ: Phương trình mặt cầu tâm
;;I a b c
, bán kính là
R
có phương trình là:
2 2 2
2
x a y b z c R
.
Áp dụng với mặt cầu
S
có tâm
4;0; 2I
và bán kính
9R
có phương trình là:
( ) ( ) ( )
22
2
: 4 2 81S x y z- + + + =
.
Câu 36. Hình chiếu của điểm
( )
2; 3;5A -
lên đường thẳng
32
: 2 3
1
xt
d y t
zt
ì
= - +
ï
ï
ï
ï
= - +
í
ï
ï
=+
ï
ï
î
có tọa độ là
A.
31 5 25
;;
14 14 14
æö
÷
ç
-
÷
ç
÷
ç
èø
. B.
10 5 25
;;
7 14 14
æö
÷
ç
--
÷
ç
÷
ç
èø
. C.
10 5 25
;;
7 14 14
æö
÷
ç
--
÷
ç
÷
ç
èø
. D.
10 5 25
;;
7 14 14
æö
÷
ç
-
÷
ç
÷
ç
èø
.
Lời giải
Chọn D
Gọi
H
là hình chiếu của điểm
A
lên đường thẳng
d
.
Ta có:
3 2 ; 2 3 ;1H d H t t t
;
2 5;3 1; 4AH t t t
.
Ta có:
2;3;1n
là một vecto chỉ phương của đường thẳng
d
.
Suy ra
11
. 0 2 2 5 3 3 1 1 4 0
14
AH n t t t t
.
Suy ra
10 5 25
;;
7 14 14
H



.
Câu 37. Trong hệ tọa độ
Oxyz
mặt phẳng
đi qua điểm
3; 1; 5M 
và vuông góc với hai mặt
phẳng
:3 2 2 7 0P x y z
và
:5 4 3 1 0Q x y z
có phương trình là
A.
30x y z
. B.
2 2 15 0x y z
.
C.
2 2 15 0x y z
. D.
2 2 16 0x y z
.
Lời giải
Trang16
Chọn B
Ta có:
( )
3; 2;2n=-
r
là một vecto pháp tuyến của mặt phẳng
P
.
( )
5; 4;3u =-
r
là một vecto pháp tuyến của mặt phẳng
Q
.
Mặt phẳng
vuông góc với hai mặt phẳng
P
và
Q
nên
có một vecto pháp tuyến là
, 2;1; 2v n u


. Do đó phương trình của
là
2 2 15 0x y z
.
Câu 38.Trong không gian với hệ tọa độ
Oxyz
, cho tứ diện
ABCD
, biết
2;3;1 , 4;1; 2AB
,
6;3;7C
,
5; 4; 8D
. Độ dài đường cao
DH
của tứ diện
ABCD
bằng:
A.
15
7
. B.
5
7
. C.
45
21
. D.
45
7
.
Lời giải
Chọn D
Ta có:
( ) ( ) ( )
2; 2; 3 , 4;0;6 , 7; 7; 9AB AC AD= - - = = - - -
uuur uuur uuur
.
, 12; 24;8AB AC


;
, . 180AB AC AD


;
22
2
, 12 24 8 28AB AC


.
Suy ra:
1
, . 30
6
ABCD
V AB AC AD



;
1
, 14
2
ABC
S AB AC



.
Suy ra độ dài đường cao
DH
của tứ diện
ABCD
bằng
3
45
7
ABCD
ABC
V
S
.
Câu 39. Cho số phức
z
thỏa mãn
3 8 7zi
và số phức
43wi
. Gọi
M
là giá trị lớn nhất của
biểu thức
P z w
. Chọn khẳng định đúng trong các khẳng định sau.
A.
20;21M
. B.
21;22M
. C.
18;19M
. D.
19;20M
.
Lơ
i gia
i
Chọn A
Gọi số phức
. ; ,z x y i x y
.
Theo đề ra, ta có:
3 8 7 3 8 7 3 8 7z i x yi i x y i
2 2 2 2
3 8 7 3 8 49x y x y
.
Do đó, tập hợp các số phức thỏa mãn
3 8 7zi
là một đường tròn
C
có tâm
3; 8I
và bán kính
7r
.
Lại có
22
4 3 4 3 4 3P z w x yi i x y i x y
.
Theo đề,
M
là giá trị lớn nhất của biểu thức
P z w
điều đó có nghĩa là ta tìm số phức
z
thuộc đường tròn
C
có tâm
3; 8I
và bán kính
7r
sao cho khoảng cách đến điểm
4;3w
là lớn nhất.
Trang17
Dựa vào đồ thị, ta thấy số phức
z
thỏa yêu cầu bài toán có điểm biểu diễn là giao điểm của
đường thẳng
d
và đường tròn
C
.
Đường thẳng
d
đi qua hai là điểm
4;3W
và
3; 8I
nên có phương trình là
37
8 11
xt
yt

, với
t
.
Ta có tọa độ của
A
và
B
thỏa hệ phương trình
2 2 2 2
49 170
30
170
3 7 3 7 3 7
77 170
8 11 8 11 8 11 8
170
49 121 49
7 170
3 8 49
7 170
170
170
x
x t x t x t
y t y t y t y
tt
xy
t
t



hay
49 170
30
170
77 170
8
170
7 170
170
x
y
t

.
Dựa vào hình vẽ, ta thấy điểm
B
có hoành độ dương và tung độ âm nên ta nhận
49 170
3
170
77 170
8
170
x
y

.
22
22
49 170 77 170
4 3 3 4 8 3 20,0384
170 170
P x y
.
Trang18
Câu 40. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
3 31f x x
và
7 35
11 11
g x x
với trục
Ox
và đường thẳng
9x 
.
A.
8125
198
S
. B.
1029
22
S
. C.
647
18
S
. D.
1797
50
S
.
Lơ
i gia
i
Chọn C
Theo đề bài ta có:
Hoành độ giao điểm của
3 31f x x
và trục
Ox
là
31
3
x 
.
Hoành độ giao điểm của
7 35
11 11
g x x
và trục
Ox
là
5x 
.
Hoành độ giao điểm của
3 31f x x
và
7 35
11 11
g x x
thỏa phương trình
7 35
3 31 6
11 11
x x x
.
Ta có hình vẽ của đồ thị các hàm số như sau:
Dựa vào hình vẽ, ta có
12
S S S
.
5
5
1
9
9
3 112
3 31d 3 31 3 31
29
S x x x x
.
6
6
2
2
5
5
7 35 3 7 35 47
3 31 d 3 31 3 31
11 11 2 22 11 2
S x x x x x x x
.
Suy ra
12
647
18
S S S
.
Câu 41. Trong không gian
Oxyz
, cho mặt cầu
S
có phương trình là
2 2 2
2 2 2 8 4 12 6 0x y z x y z
và mặt phẳng
: 3 2 5 0x y z
. Gọi
I
là tâm mặt
cầu
S
,
I
là điểm đối xứng của
I
qua mặt phẳng
. Tính độ dài đoạn
II
.
A.
6 14
7
II
. B.
3 14
7
II
. C.
17II
. D.
2 17II
.
Lời giải
Chọn A
Trang19
Ta có
2 2 2 2 2 2
2 2 2 8 4 12 6 0 4 2 6 3 0x y z x y z x y z x y z
2, 1, 3, 3a b c d
. Do đó mặt cầu
S
có tâm
2; 1; 3I 
.
Gọi
H
là hình chiếu vuông góc của
I
trên
.
I
là điểm đối xứng của
I
qua
là mặt phẳng trung trực của đoạn
II
.
Suy ra
II
2
22
2 3 6 5
6 14
2 2 , 2.
7
1 3 2
IH d I
.
Câu 42. Biết tích phân
5
1
d
ln3 ln5
31
x
I a b
xx
,ab
. Khi đó
ab
có giá trị là
A.
4
. B.
1
. C.
5
. D.
0
.
Lời giải
Chọn B
Đặt
2
2
21
3 1 3 1 d d ,
33
t
t x t x t t x x
Đổi cận
12xt
,
54xt
Khi đó:
44
4
2
2
22
1 2 1 1
. d d ln 1 ln 1
1
3 1 1
.
3
I t t t t t
t
tt
t





ln3 ln5 ln1 ln3 2ln3 ln5
2, 1 1a b a b
.
Câu 43. Số phức
1
;
1 ( 2 )
m
zm
m m i


. Môđun lớn nhất của số phức
z
là
A.
12
2
. B.
3
. C.
1
. D.
21
2
.
Lời giải
Chọn A
Ta có
2
2
22
2
22
1 1 1 1
1
1 2 1
12
1 2 1
m m m m
m
z
m m i m
m mi
m m m

.
Trang20
Xét hàm số
2
22
1
21
11
m
mm
gm
mm



với
m
.
Có
32
2
22
31
2 1 1
m m m
gm
m m m
.
gm
không xác định khi
1m
.
0 1 2g m m
.
BBT
m

12
1
12

gm
0
0
gm
12
2
0
0
21
2
0
Từ bảng biến thiênsuy ra môđun lớn nhất của số phức
z
là
12
2
.
Câu 44. Tính
2
1
56
dx
xx
kết quả đúng là .
A.
ln 2 ln 3x x C
. B.
1
(ln 3 ln 2 )
2
x x C
.
C.
ln 3 ln 2x x C
. D.
ln( 2 . 3)x x C
.
Lời giải
Chọn C
Ta có
2
1 1 1 1
ln 3 ln 2
5 6 2 3 3 2
dx dx dx x x C
x x x x x x



.
Câu 45. Biết
2
cos
d.
13
x
x
xm
p
p
-
-
=
+
ò
Tính giá trị của
2
cos
d.
13
x
x
Ix
p
p-
=
+
ò
A.
m
. B.
4
m
. C.
m
. D.
4
m
.
Lời giải
Chọn C
Đặt
ddx t x t
Khi đó
2
cos
d
13
x
x
x
p
p
-
-
=
+
ò
( )
2
22
cos
cos cos
d d d
1 3 1 3 1 3
t t x
t
tx
t m t x I
p p p
p p p
-
--
-
- Þ = = =
+ + +
ò ò ò
Mặt khác
22
cos 3 cos
d d .
1 3 1 3
x
xx
xx
m x x
pp
pp
-
--
==
++
òò
Suy ra
( )
( )
2
22
2
1 3 cos
cos 3 cos 1
2 d d d cos d 1 cos2 d
1 3 1 3 1 3 2
x
x
x x x
x
xx
m x x x x x x x
p p p p p
p p p p p- - - - -
+
= + = = = +
+ + +
ò ò ò ò ò
Trang21
1 sin2
2 2 2
x
xm
p
p
p
p
æö
÷
ç
= + = Þ =
÷
ç
÷
ç
èø
-
Vậy
2
cos
d
1 3 2
x
x
I x m
p
p
p
p
-
= = = -
+
ò
. Chọn C
Câu 46. Trong hệ tọa độ Oxyz một mặt phẳng
( )
a
đi qua điểm
( )
1;2;3M
và cắt ba tia Ox, Oy, Oz lần
lượt tại các điểm A, B, C sao cho thể tích tứ diện OABC nhỏ nhất, có phương trình là
A.
6 3 2 18 0x y z
. B.
3 2 2 13 0x y z
.
C.
3 6 18 0x y z
. D.
2 3 6 26 0x y z
.
Lời giải
Chọn A
Gọi
( ) ( ) ( )
;0;0 , 0; ;0 , 0;0; ,A a B b C c
với
, , 0.abc>
Phương trình mặt phẳng
( )
a
là
1
x y z
a b c
+ + =
.
( )
a
đi qua điểm
( )
1 2 3
1;2;3 1M
abc
Þ + + =
.
Thể tích khối tứ diện
OABC
là :
1
6
OABC
V abc
Áp dụng bất đẳng thức Cauchy ta có :
3
1 2 3 1 2 3
3 . .
a b c a b c

Hay
3
6 162
1 3 1
abc abc
Suy ra :
1
162 27
6
abc abc
27
OABC
V
.
Vậy thể tích khối tứ diện
OABC
nhỏ nhất khi
3
1 2 3 1
6
3
9
a
b
abc
c
ì
=
ï
ï
ï
ï
= = = Û =
í
ï
ï
=
ï
ï
î
Phương trình của mặt phẳng
( )
a
là
1 6 3 2 18 0.
3 6 9
x y z
x y z+ + = Û + + - =
Câu 47. Trong mặt phẳng toạ độ
Oxyz
, đường thẳng
đi qua điểm
4; 2;4A 
, đường thẳng
cắt
và vuông góc với đường thẳng
32
:
1
14
xt
d
yt
zt

thì phương trình đường thẳng
là
A.
4 2 4
3 2 1
x y z

. B.
4 2 4
3 2 1
x y z


.
C.
4 2 4
3 2 1
x y z

. D.
4 2 4
3 2 1
x y z

.
Lời giải
Chọn A
Gọi
P
là mặt phẳng đi qua
4; 2;4A 
và vuông góc với đường thẳng
d
.
Trang22
Khi đó
2; 1;4
d
P
nu
.
Phương trình mặt phẳng
P
là
2 4 2 4 4 0x y z
2 4 10 0x y z
.
Gọi
B d P
thì toạ độ điểm
B
thoả mãn hệ phương trình
32
1
14
2 4 10 0
xt
yt
zt
x y z

1
1
0
3
t
x
y
z

1;0;3B
.
Đường thẳng
cần tìm là đường thẳng đi qua hai điểm
,AB
.
Ta có
3;2; 1u AB
. Phương trình đường thẳng
là
4 2 4
3 2 1
x y z

.
Câu 48. Số các giá trị
m
nguyên để có đúng hai số phức
z
thỏa
3 3 4z m i
và
1 1 2z i z i
là
A.
9
. B.
8
. C.
11
. D.
6
.
Lời giải
Chọn A
Giả sử
,z x yi x y
.
Ta có
3 3 4z m i
22
3 3 4 3 3 16x m y i x m y
Tập hợp các điểm biểu diễn số phức
z
là đường tròn
C
có tâm
3; 3Im
, bán kính
4R
Ta lại có
1 1 2z i z i
1 1 2x yi i x yi i
1 1 1 2x y i x y i
2 2 2 2
1 1 1 2x y x y
2 2 2 2 4 5x y x y
4 2 3 0xy
.
Tập hợp các điểm biểu diễn số phức
z
là đường thẳng
:d
4 2 3 0xy
.
Để có đúng hai số phức
z
thỏa mãn yêu cầu bài toán thì đường thẳng
d
phải cắt
C
tại hai
điểm phân biệt.
Trang23
ycbt
,Id
dR
22
4 3 2. 3 3
4
42
m

4 3 8 5m
8 5 3 8 5 3
8 5 4 3 8 5
44
mm
Mà
m
nên
5; 4; 3;...;1;2;3m
.
Có tất cả 9 giá trị
m
nguyên.
Câu 49. Cho
ln2F x x
là một nguyên hàm của
2
x
fx
. Tính
' .lnf x xdx
. Kết quả đúng là
A.
3
' .ln ln
3
x
f x xdx x x C
. B.
3
3
' .ln ln
3
x
f x xdx x x C
.
C.
3
' .ln
3
x
f x xdx C
. D.
3
2
' .ln ln
2
x
f x xdx x x C
.
Lời giải
Chọn B
Do
ln2F x x
là một nguyên hàm của
2
x
fx
nên:
2
ln 2
x
x dx
fx

22
1
ln 2
xx
x
f x x f x


3
f x x
.
Xét
' .lnI f x xdx
.
Đặt
ln
'
dx
ux
du
x
dv f x dx
v f x


.
Khi đó:
' .ln ln .
fx
I f x xdx x f x dx
x

3
3 2 3
ln ln
3
x
x x x dx x x C
.
Câu 50. Các bồn chứa xăng vận chuyển trên xe cơ giới thường có dạng hình trụ nằm ngang với đáy là
một hình elip mà không phải hình tròn. Việc chế tạo theo hình elip có nhiều ưu điểm như: làm
cho trọng tâm xe thấp, độ dao động của chất lỏng bên trong bồn sẽ thấp …. Giả sử một bồn chở
xăng có đáy là đường elip có phương trình
22
1
94
xy

và chiều dài của bồn là
10m
. Sau khi
bơm xăng cho một trạm xăng thì phần xăng còn lại cách đỉnh của elip
1m
(Tham khảo hình
vẽ). Tính gần đúng lượng xăng còn lại trong bồn xăng (Làm tròn đến hàng đơn vị theo lít và giả
sửa các vật liệu chế tạo nên bồn xăng có độ dài không đáng kể).
Trang24
A.
151 646
lít. B.
151 645
lít. C.
151 644
lít. D.
151 647
lít.
Lời giải
Chọn C
Từ phương trình elip
22
1
94
xy

ta có
3
2
a
b
.
Diện tích đáy của bồn hình elip:
6
E
S ab


.
Đặt hệ trục tọa độ như hình vẽ.
Ta có:
12M
S S S
là phần diện tích đáy có xăng bị mất đi.
Gọi
,MN
là giao điểm của elip và đường thẳng
1y
.
Khi đó:
2
33
1 3 3
2
1 ;1
9 4 2
33
2
x
x
N
x





.
Phần diện tích
1
S
được giới hạn bởi đường elip
22
1
94
xy

, đường thẳng
1y
và hai đường
0x
,
33
2
x
.
Do đó:
33
2
2
1
0
2 1 1
9
x
S dx




. Mà
33
2
2
12
0
2 2 1 1
9
M
x
S S S dx




.
Nên diện tích phần đáy còn xăng là:
M
E
S S S
.
Vậy thể tích phần xăng còn lại là:
33
2
3
2
0
. 10. 6 2 2 1 1 151,644
9
x
V S h dx m








151 644
lít.
HẾT
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 5
ĐỀ ÔN THI HỌC KỲ II – NĂM HỌC 2021-2022 Môn: Toán lớp 12      Câu 1:
Trong không gian Oxyz cho a  3; 4; 5 , b  1;1; 2 thì tọa độ của n  3a  4b là: A. 13;8; 7   . B. 5;8; 7   . C. 13;16; 7  . D.  1  3;8; 2  3 . Câu 2:
Cho số phức z  2 14i . Phần thực và phần ảo của số phức lần lượt là: A. 2; 14  i . B. 2; 14 . C. 14i; 2 . D. 14; 2  . Câu 3:
Trong hệ tọa độ Oxyz cho phương trình mặt phẳng   : 3x  2y  7z 10  0 thì một véc-tơ
pháp tuyến có tọa độ là: A.  3  ; 2  ; 7  . B.  3  ;2;7 . C. 3; 2  ;7. D. 3; 2  ; 7   . Câu 4: Giải phương trình 2
z 10z  29  0 trong tập số phức  ta được tập nghiệm là:
A. S  5  2  i .
B. S  5  2  i .
C. S  5  2 ; i 5  2 
i . D. S   . Câu 5:
Trong hệ tọa độ Oxyz , phương trình mặt phẳng   đi qua điểm A1; 2  ;3 và nhận
n  2;4;5 làm vectơ pháp tuyến là
A. 2x  4 y  5z  21  0 . B. 2x  4 y  5z  5  0 .
C. 2x  4 y  5z  21  0 . D. 2
x  4y  5z  21  0 . Câu 6:
Trong không gian Oxyz , tìm tọa độ tâm I của mặt cầu  S  có phương trình
x  2  y  2 z  2 3 1 5  36 là A. I 3;1; 5  .
B. I 3;1;6 . C. I  3  ; 1  ;5 .
D. I 3;1;5 . Câu 7:
Cho F x  tan x C là họ nguyên hàm của hàm số f x . Khẳng định đúng là 1 1
A. f x  cot x .
B. f x  .
C. f x  .
D. f x 2 1 cos x . 2 cos x 2 sin x Câu 8:
Số phức z a bi có modun là A. 2 2 z a b . B. 2 2
z a b . C. 2 2
z a b .
D. z a b . 2 Câu 9: Cho số phức z
. Số phức liên hợp của z là: 1 i 3 1 3 1 3 A. i . B. 1 i 3 . C. 1 i 3 . D. i . 2 2 2 2
Câu 10: Cho hai số phức z m ni, z p qi . Tổng của z z là số phức: 1 2 1 2
A. z  m p  n q . B. z  m p  n qi .
C. z  m p  n qi .
D. z  m q  n pi .
Câu 11: Mệnh đề nào sau đây đúng? b c c A. f
 xdxf
 xdx f  xdx . a a b b B. f
 xdx F aF b (F x là một nguyên hàm của f x). a Trang1 a C. f
 xdx  0. a b a D. f
 xdxf
 xdx  0. a b
Câu 12: Trong không gian Oxyz , tìm bán kính R của mặt cầu S  có phương trình
x   y  2   z  2 2 6 3 128 là A. 2 R  128 . B. R 128. C. R  2 8. D. R  8 2.
Câu 13: Cho hàm số f x 2
x  2. Họ nguyên hàm của hàm số là 1
A. F x  2x C.
B. F x 3
x  2x C. 3 1
C. F x 3  x C.
D. F x  2x  2  C. 3 2 5 
Câu 14: Tích phân I x dx  có giá trị là 1 32 16 21 19 A. . B. . C. . D. . 3 3 2 3
Câu 15: Biểu thức V để tính thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi đồ thị 
hàm số y  sin x và các đường thẳng x  0, x
, trục hoành, quay quanh trục Ox là 3     3 3 3 3 A. 2 V  sin xdx. B. V  sin x dx  . C. 2
V   sin xdx  .
D. V   sin x dx  . 0 0 0 0
Câu 16: Trong không gian Oxyz cho hai điểm A 1
 ;2;3, B0;1 
;1 , độ dài đoạn AB bằng A. 6 . B. 8 . C. 12 . D. 10 .
Câu 17: Trong không gian Oxyz cho đường thẳng d đi qua A 2
 ;3;5 và có véc tơ chỉ phương
a3;5;2 thì phương trình tham số của đường thẳng d là x  2   3tx  3 2t
x  2  3tx  3   2t    
A. y  3  5t . B. y  5   3t .
C. y  3  5t . D. y  5   3t .     z  5   2tz  2   5tz  5  2tz  2   5t  x 1 2t
Câu 18: Trong không gian Oxyz cho đường d : y  3  t . Đường thẳng d vuông góc với đường thẳng z  28t  nào sau đây?     x 1 t x  3   4t
x  3  2tx  2   5t     1
A. d : y  5   2t .
B. d :  y  5
  3t . C. d : y  3 2t . D. d :y  3 t . 1 4  2  3  2  z  2  16tz  2   5tz  5   t
z  2  4t
Câu 19: Tìm căn bậc hai của số thực âm 64
 trên tập số phức  . A. 8  ;8 . B. 8i .
C. 8i;8i . D. 8 . Trang2 1
Câu 20: Dạng z a bi của số phức z  3 là số phức nào dưới đây? 2i 3 2 3 2 3 2 3 2 A. i . B.   i . C. i . D.   i . 13 13 13 13 13 13 13 13
Câu 21: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2022 và hai đường thẳng
x  3, x  4 với trục hoành được tính bởi biểu thức: 4 4 A. 2 S x  2022d .  x
B. S    2 x  2022d . x 3  3  4 3  2
C. S    2
x  2022 d . x D. 2 S x  2022d .  x 3  4
Câu 22: Số phức z a bi . Khi đó z z là số phức: A. 2 . bi
B. 2a  2b . i C. 2a . D. 2b .
Câu 23: Cho A   x   5 2
1 dx . Đặt t  2x 1. Khẳng định đúng là: 1 1 A. 5 A t . dxB. 5 A  2 t d . xC. A  t   5 1 d . x D. 5 A t dx  2 2
Câu 24: Trong hệ trục tọa độ Oxyz, cho mặt phẳng (α): 3x - 2 y + 7z - 10 = 0 . Mặt phẳng (α) song
song với mặt phẳng nào có phương trình sau? A. 3
x  2y  7z  3  0 . B. 3x  2y  7z  5  0 . C. 3
x  2y  7z  0 . D. 3x  2y  7z  3  0 .
Câu 25: Cho các số phức z  3  bi, z c  4i . Phần thực và phần ảo của số phức z = z - z lần 1 2 1 2 lượt là
A. 7; b c . B. 3  ; c b  4 . C. 3  ; c b  4 . D. 3  ; c b  4 . 2016 1 i
Câu 26: Cho số phức z thỏa mãn z   
. Viết z dưới dạng z = a + bi, a, b Î ¡ . Khi đó tổng 1 i
a b có giá trị bằng bao nhiêu? A. 2 . B. 0 . C. 1. D. 1.
Câu 27: Cho số phức z a bi, z c di . Khi đó M , N lần lượt là hai điểm biểu diễn cho các số 1 2 
phức z , z . Khi đó độ dài véctơ MN là 1 2   2 2 2 2
A. MN  c a  d b .
B. MN  b a  d c .   2 2 2 2
C. MN  c a  d b .
D. MN  c a  d b . x 1 2t
x  3 4t '  
Câu 28: Cho hai đường thẳng d :  y  2  3t và d ' :  y  5  6t '   z  3  4tz  7  8t ' 
Trong các mệnh đề sau, mệnh đề nào đúng?
A. d d ' .
B. d d ' .
C. d / /d ' .
D. d và d ' chéo nhau. 4 2 Câu 29: Cho f
 xdx 16. Tính I f
 2xdx . 0 0 A. I  32 . B. I  4 . C. I  16 . D. I  8 . Trang3
Câu 30: Trong hệ tọa độ
Oxyz khoảng cách từ điểm A1; 2
 ;3 đến mặt phẳng
:x 2y  2z 10  0 bằng 1 1 7 1 A.  . B. . C. . D. . 3 3 3 3
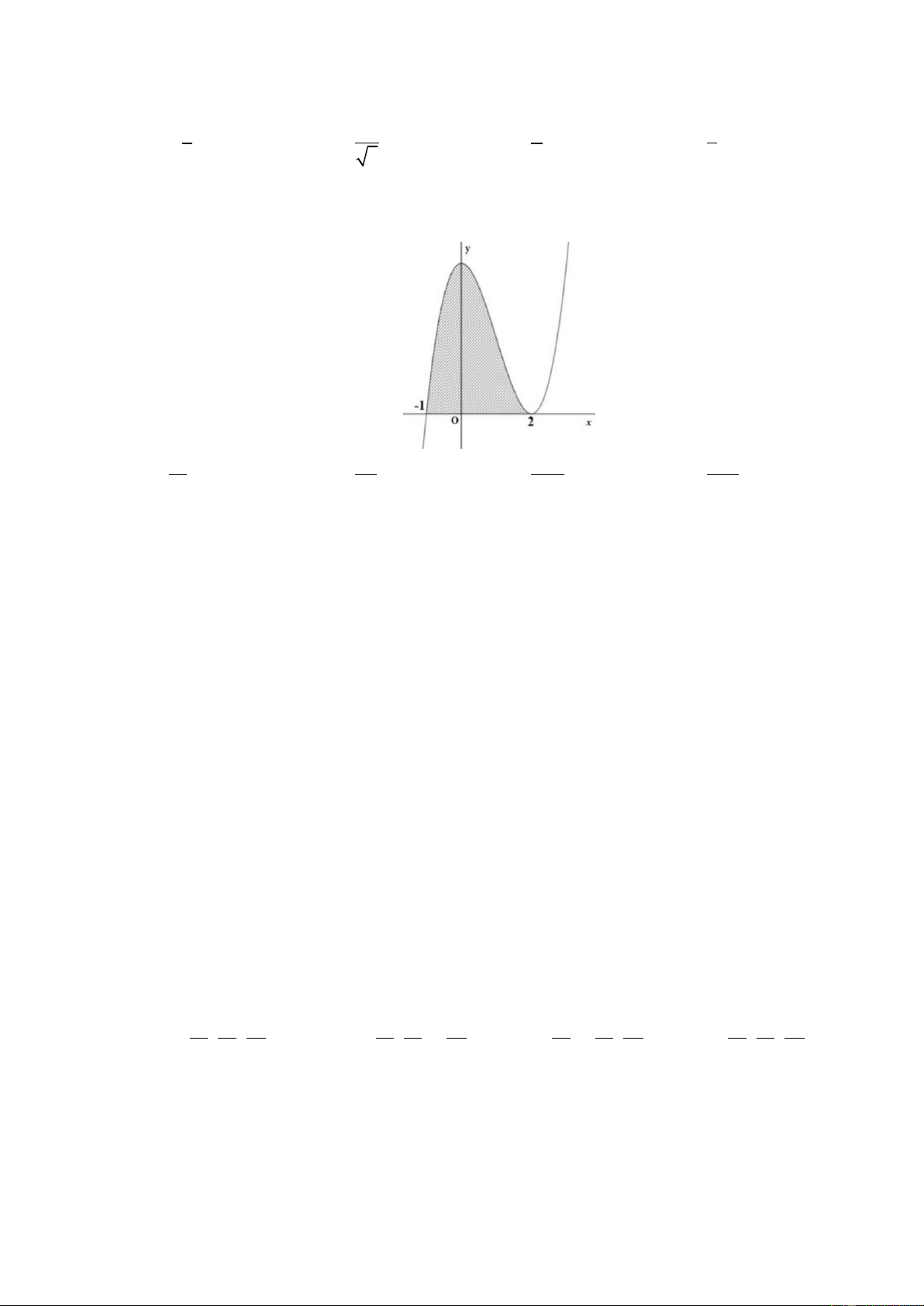
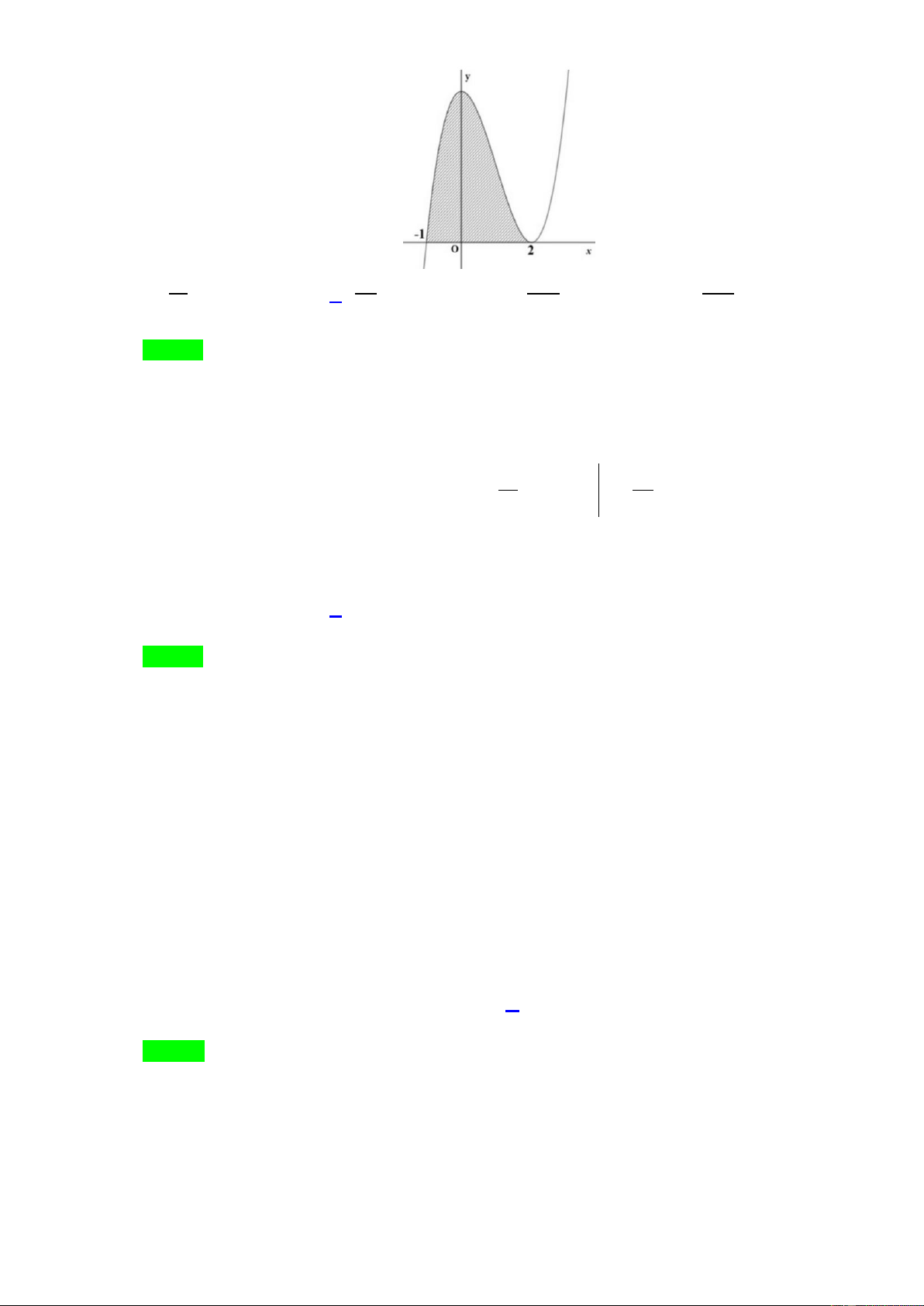
Câu 31: Phần gạch chéo trong hình bên dưới là hình phẳng giới hạn bởi đồ thị của hàm số 2
f (x)  (x 1)(x  2) với trục hoành. Hãy tính diện tích S đó 15 27 27 15 A. . B. . C. . D. . 2 4 4 2
Câu 32: Cho 3 điểm M 2;0;0 , N 0; 3
 ;0 , P0;0;4 . Nếu MNPQ là hình bình hành thì tọa độ của điểm Q là A. 3; 4; 2 . B. 2;3; 4 . C.  2  ; 3  ; 4   . D. 2;3; 4  . x  3   2t
x  5  t  
Câu 33: Tọa độ giao điểm của hai đường thẳng d :  y  2
  3t và d: y  1   4t là   z  6  4t
z  20  t  A. 0; 3  ;2 . B.  7  ; 8  ; 2   . C. 3;7;18 . D. 8; 1  3;23.
Câu 34: Gọi n là số nghiệm của phương trình 5 2
z az bz c  0 ( a , b , c là các số thực) trong tập số
phức  . Tìm giá trị của số n . A. 2 . B. 3 . C. 5 . D. 4 .
Câu 35: Trong không gian Oxyz , viết phương trình mặt cầu S  có tâm I 4;0; 2
  và bán kính R  9. 2 2 2 2
A. (S) (x - ) 2 : 4 + y + (z + ) 2 = 81.
B. (S) (x - ) 2 : 4 + y + (z + ) 2 = 9 . 2 2 2 2
C. (S) (x + ) 2 : 4 + y + (z - ) 2 = 9 .
D. (S) (x + ) 2 : 4 + y + (z - ) 2 = 81. ìï x = - 3+ 2t ïï
Câu 36: Hình chiếu của điểm A(2;- 3; )
5 lên đường thẳng d :í y = - 2 + 3t ï có tọa độ là ïï z = 1+ t ïî æ 31 5 25ö æ 10 5 25ö æ 10 5 25ö æ 10 5 25ö A. ç- ; ; ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç . B. - ; ;- ç ÷. C. - ;- ; ç ÷. D. - ; ; ç ÷. è 14 14 14÷ø çè 7 14 14÷ø çè 7 14 14 ÷ ø çè 7 14 14÷ø
Câu 37: Trong hệ tọa độ Oxyz mặt phẳng   đi qua điểm M 3; 1  ; 5
  và vuông góc với hai mặt
phẳng  P : 3x  2y  2z  7  0 và Q : 5x  4y  3z 1  0 có phương trình là
A. x y z  3  0 .
B. 2x y  2z 15  0 .
C. 2x y  2z 15  0 . D. 2x y  2z 16  0 . Trang4
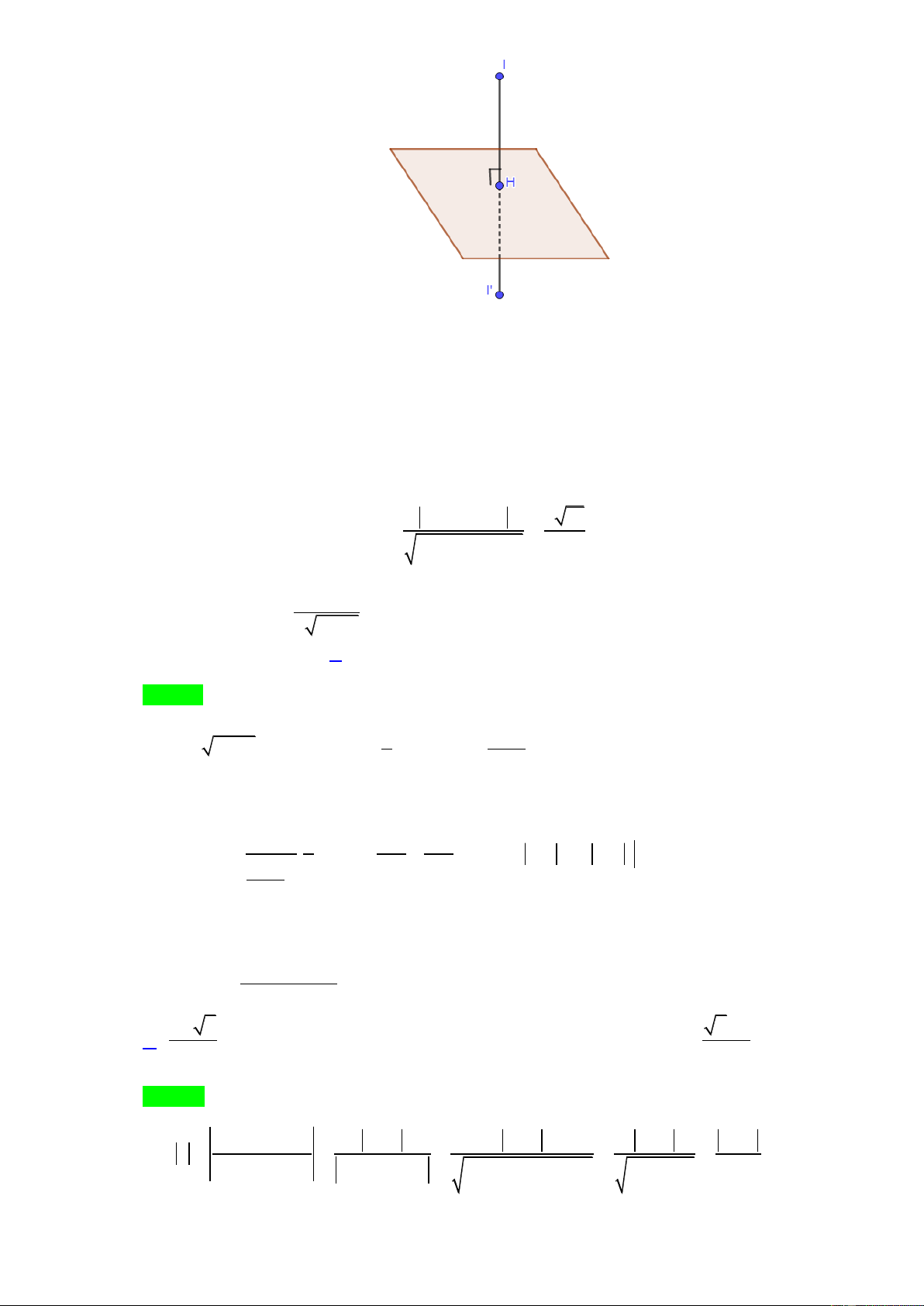
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD , biết A2;3;  1 , B 4;1; 2   , C 6;3; 7 , D  5  ; 4  ; 8
  . Độ dài đường cao DH của tứ diện ABCD bằng: 15 5 45 45 A. . B. . C. . D. . 7 7 21 7
Câu 39: Cho số phức z thỏa mãn z  3  8i  7 và số phức w  4
 3i . Gọi M là giá trị lớn nhất của
biểu thức P z w . Chọn khẳng định đúng trong các khẳng định sau.
A. M 20; 2  1 .
B. M 21; 22 .
C. M 18;19 .
D. M 19;20 .
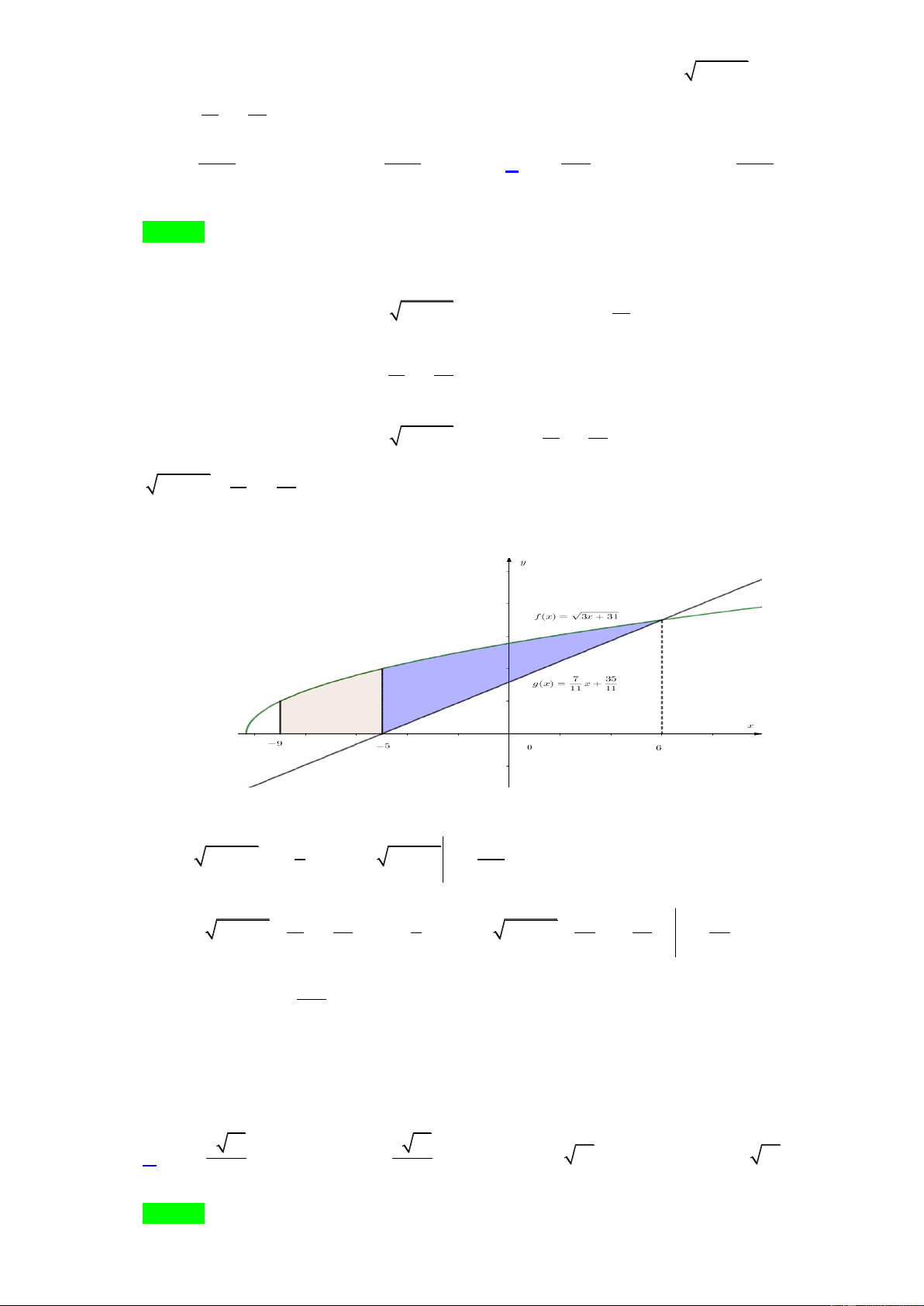
Câu 40: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số f x  3x  31 và g x 7 35  x
với trục Ox và đường thẳng x  9  . 11 11 8125 1029 647 1797 A. S  . B. S  . C. S  . D. S  . 198 22 18 50 Câu 41: Trong không gian Oxyz , cho mặt cầu
S có phương trình là 2 2 2
2x  2 y  2z  8x  4 y 12z  6  0 và mặt phẳng   : x  3y  2z  5  0 . Gọi I là tâm mặt
cầu S  , I  là điểm đối xứng của I qua mặt phẳng   . Tính độ dài đoạn II . 6 14 3 14 A. II   . B. II   .
C. II   17 .
D. II   2 17 . 7 7 5 dx
Câu 42: Biết tích phân I   aln3 bln5 
a,b . Khi đó a b có giá trị là x 3x 1 1 A. 4 . B. 1. C. 5 . D. 0 . 1 m
Câu 43: Số phức z
; m   . Môđun lớn nhất của số phức z là
1 m(m  2i) 1 2 2 1 A. . B. 3 . C. 1. D. . 2 2 1 Câu 44: Tính dx  kết quả đúng là. 2 x  5x  6 1
A. ln x  2  ln x  3  C . B.
(ln x  3  ln x  2 )  C . 2
C. ln x  3  ln x  2  C .
D. ln( x  2 . x  3 )  C . p 2 p cos x 2 cos x Câu 45: Biết dx = . m ò
Tính giá trị của I = d . x ò 1+ 3- x 1+ 3x - p - p   A.   m . B. m . C.   m . D. m . 4 4
Câu 46: Trong hệ tọa độ Oxyz một mặt phẳng (a ) đi qua điểm M (1; 2; )
3 và cắt ba tia Ox, Oy, Oz lần
lượt tại các điểm A, B, C sao cho thể tích tứ diện OABC nhỏ nhất, có phương trình là
A. 6x  3y  2z 18  0 . B. 3x  2 y  2z 13  0 .
C. 3x  6 y z 18  0 . D. 2x  3y  6z  26  0 . Trang5
Câu 47: Trong mặt phẳng toạ độ Oxyz , đường thẳng  đi qua điểm A 4  ; 2
 ;4, đường thẳng  cắt x  3   2t
và vuông góc với đường thẳng d :  y  1 t thì phương trình đường thẳng  là  z  1   4t x  4 y  2 z  4 x  4 y  2 z  4 A.     3 2 1  . B. 3 2 1  . x  4 y  2 z  4 x  4 y  2 z  4 C.      . 3 2  . D. 1 3 2 1
Câu 48: Số các giá trị m nguyên để có đúng hai số phức z thỏa z  m  3  3i  4 và
z 1 i z 1 2i là A. 9 . B. 8 . C. 11. D. 6 . 2 x
Câu 49: Cho F x  ln 2x là một nguyên hàm của . Tính
f ' x.ln xdx  . Kết quả đúng là f xx x A. f  x 3 '
.ln xdx x ln x   C . B. f  x 3 3 '
.ln xdx x ln x   C . 3 3 x x C. f  x 3 ' .ln xdx   C . D. f  x 3 2 '
.ln xdx x ln x   C . 3 2
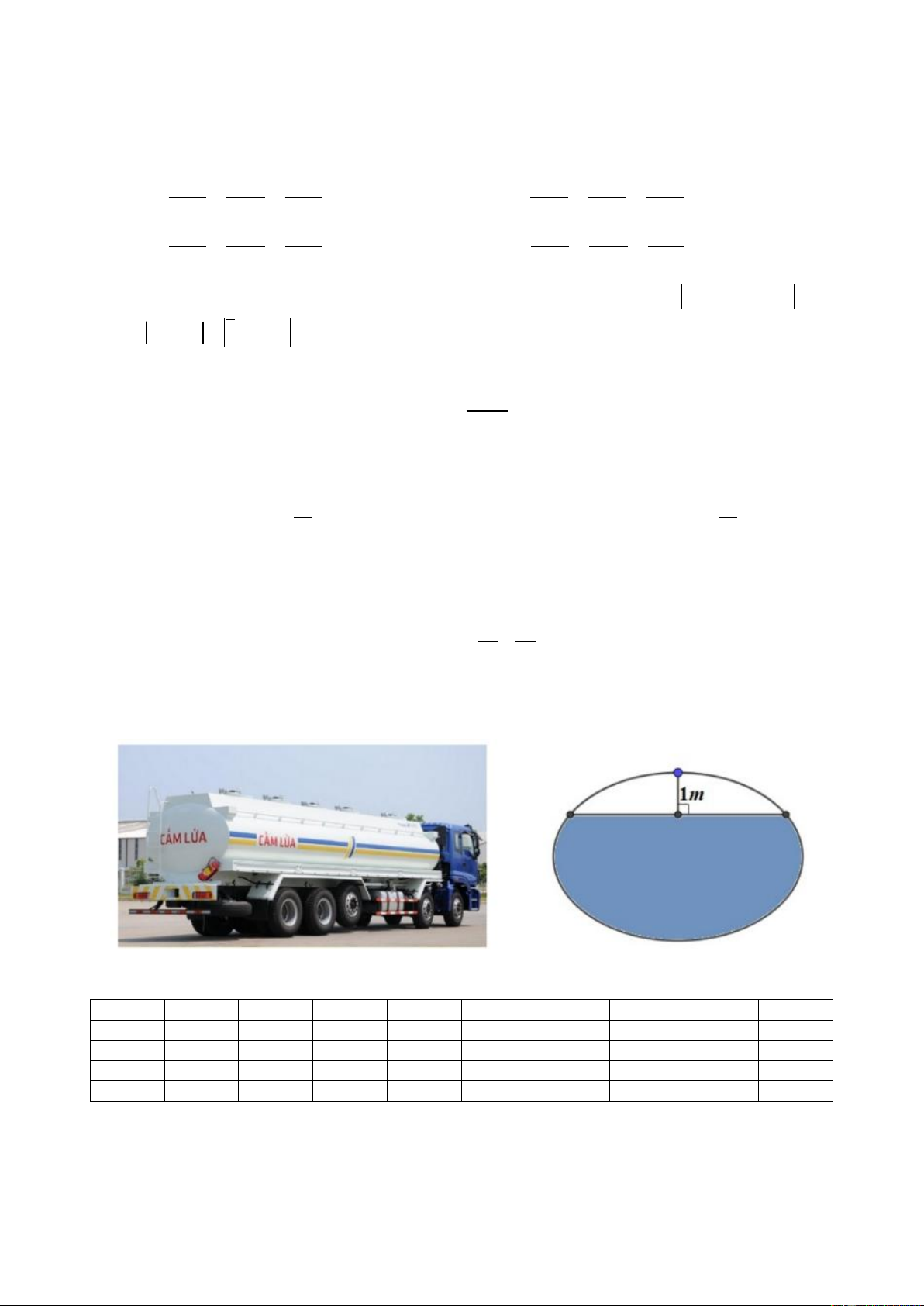
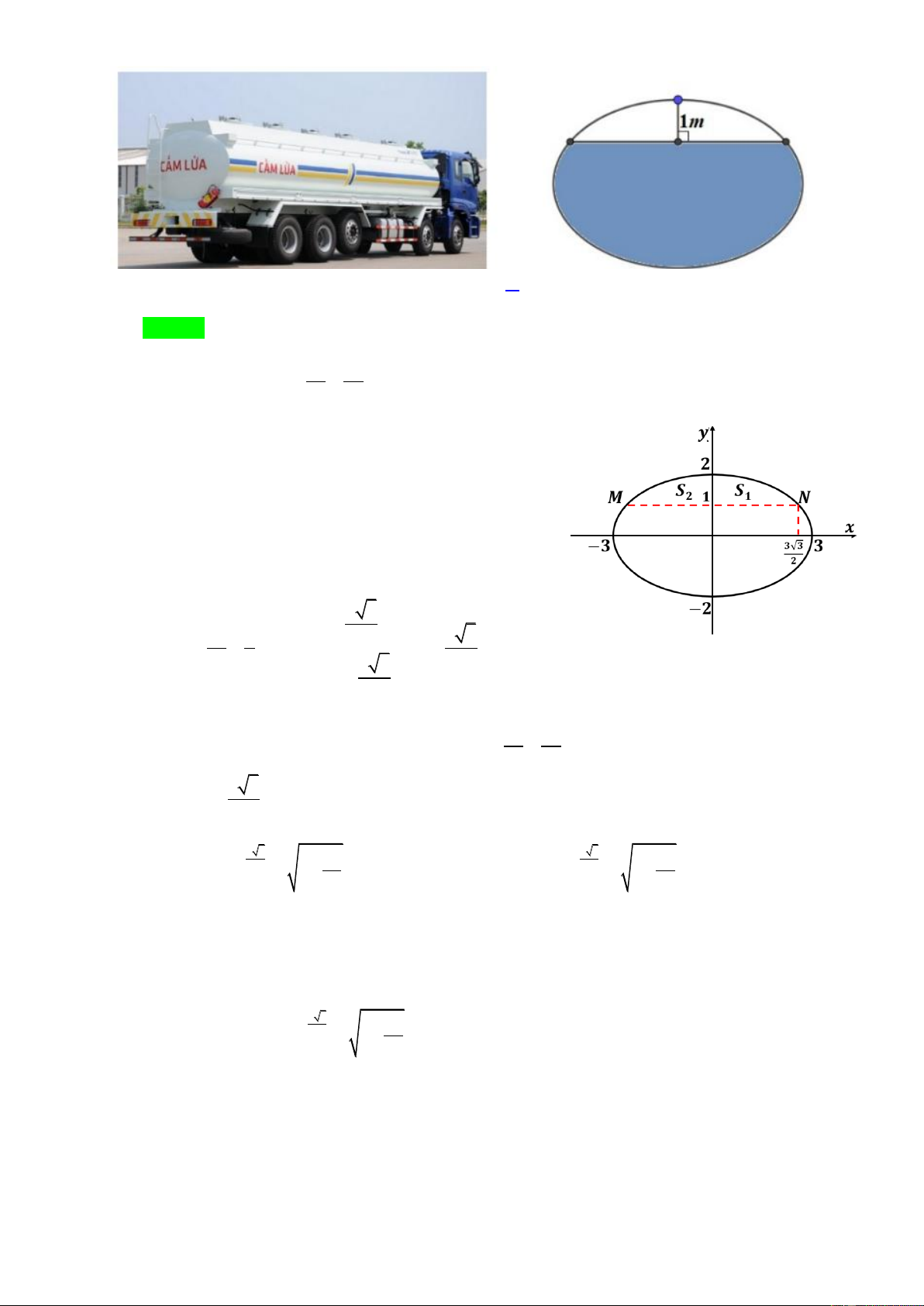
Câu 50: Các bồn chứa xăng vận chuyển trên xe cơ giới thường có dạng hình trụ nằm ngang với đáy là
một hình elip mà không phải hình tròn. Việc chế tạo theo hình elip có nhiều ưu điểm như: làm
cho trọng tâm xe thấp, độ dao động của chất lỏng bên trong bồn sẽ thấp …. Giả sử một bồn chở 2 2
xăng có đáy là đường elip có phương trình x y
 1 và chiều dài của bồn là 10m. Sau khi 9 4
bơm xăng cho một trạm xăng thì phần xăng còn lại cách đỉnh của elip 1m (Tham khảo hình
vẽ). Tính gần đúng lượng xăng còn lại trong bồn xăng (Làm tròn đến hàng đơn vị theo lít và giả
sửa các vật liệu chế tạo nên bồn xăng có độ dài không đáng kể). A. 151 646 lít. B. 151 645 lít. C. 151 644 lít. D. 151 647 lít. BẢNG ĐÁP ÁN 1.A 2.B 3.C 4.C 5.C 6.A 7.B 8.A 9.A 10.B 11.D 12.D 13.B 14.C 15.C 16.A 17.A 18.C 19.C 20.A 21.A 22.A 23.A 24.A 25.C 26.D 27.D 28.B 29.D 30.D 31.B 32.B 33.C 34.C 35.A 36.D 37.B 38.D 39.A 40.C 41.A 42.B 43.A 44.C 45.C 46.A 47.A 48.A 49.B 50.C ĐÁP ÁN CHI TIẾT      Câu 1.
Trong không gian Oxyz cho a  3; 4; 5 , b  1;1; 2 thì tọa độ của n  3a  4b là: Trang6 A. 13;8; 7   . B. 5;8; 7   . C. 13;16; 7  . D.  1  3;8; 2  3 . Lời giải Chọn A   a  3; 4; 5
   3a  9;12; 15   .   b  1;1; 2
   4b  4;4;8.   
n  3a  4b  13;8; 7  . Câu 2.
Cho số phức z  2 14i . Phần thực và phần ảo của số phức lần lượt là: A. 2; 14  i . B. 2; 14 . C.14i; 2 . D.14; 2  . Lời giải Chọn B Câu 3.
Trong hệ tọa độ Oxyz cho phương trình mặt phẳng   :3x  2y  7z 10  0 thì một véc-tơ
pháp tuyến có tọa độ là: A.  3  ; 2  ; 7  . B.  3  ;2;7 . C. 3; 2  ;7. D. 3; 2  ; 7   . Lời giải Chọn C Câu 4. Giải phương trình 2
z 10z  29  0 trong tập số phức  ta được tập nghiệm là:
A. S  5  2  i .
B. S  5  2  i .
C. S  5  2 ; i 5  2 
i . D. S   . Lời giải Chọn C 2
z 10z  29  0 . 2    25 29  4
  4i    2i .
 Phương trình có nghiệm:  b     x   5  2i a   b     x   5  2ia
Vậy tập nghiệm của phương trình là: S  5  2 ;i5  2  i . Câu 5.
Trong hệ tọa độ Oxyz , phương trình mặt phẳng   đi qua điểm A1; 2  ;3 và nhận
n  2;4;5 làm vectơ pháp tuyến là
A. 2x  4 y  5z  21  0 .
B. 2x  4 y  5z  5  0 .
C. 2x  4 y  5z  21  0 . D. 2
x  4y  5z  21  0 . Lời giải Chọn C
Phương trình mặt phẳng   đi qua điểm A1; 2
 ;3 và nhận n  2;4;5 làm vectơ pháp
tuyến là 2 x  
1  4 y  2  5 z  3  0  2x  4y  5z  21  0 . Câu 6.
Trong không gian Oxyz , tìm tọa độ tâm I của mặt cầu  S  có phương trình
x  2  y  2 z  2 3 1 5  36 là A. I 3;1; 5  .
B. I 3;1;6 . C. I  3  ; 1  ;5 .
D. I 3;1;5 . Trang7 Lời giải Chọn A Câu 7.
Cho F x  tan x C là họ nguyên hàm của hàm số f x . Khẳng định đúng là 1 1
A. f x  cot x .
B. f x  .
C. f x  .
D. f x 2 1 cos x . 2 cos x 2 sin x Lời giải Chọn B 1
Áp dụng bảng nguyên hàm cơ bản
dx  tan x C  . 2 cos x Câu 8.
Số phức z a bi có modun là A. 2 2 z a b . B. 2 2
z a b . C. 2 2
z a b .
D. z a b . Lời giải Chọn A Câu 9. Cho số phức 2 z
. Số phức liên hợp của z là: 1 i 3 1 3 1 3 A. i . B. 1 i 3 . C.1 i 3 . D.i . 2 2 2 2 Lời giải Chọn A 2 1 3 1 3 Ta có z    i nên z   i . 1 i 3 2 2 2 2
Câu 10. Cho hai số phức z m ni, z p qi . Tổng của z z là số phức: 1 2 1 2
A. z  m p  n q .
B. z  m p  n qi .
C. z  m p  n qi .
D. z  m q  n pi . Lời giải Chọn B
z z z m p n q i . 1 2    
Câu 11. Mệnh đề nào sau đây đúng? b c c A. f
 xdxf
 xdx f  xdx . a a b b B. f
 xdx F aF b (F x là một nguyên hàm của f x). a a C. f
 xdx  0. a b a D. f
 xdxf
 xdx  0. a b Lời giải Chọn D b a a f
 xdxf
 xdx f
 xdx  0 là đúng. a b a Trang8 b c c c c b
f xdx f xdx f xdx     f
 xdx f
 xdxf
 xdx là sai . a a b a b a b b f
 xdx F aF b là sai vì f
 xdx F bF a . a a a a f
 xdx  0 là sai vì d a x x  2a   . aaa
Câu 12. Trong không gian Oxyz , tìm bán kính R của mặt cầu S  có phương trình
x   y  2   z  2 2 6 3 128 là A. 2 R  128 . B. R 128. C. R  2 8. D. R  8 2. Lời giải Chọn D
Mặt cầu S  có bán kính R  8 2.
Câu 13. Cho hàm số f x 2
x  2. Họ nguyên hàm của hàm số là 1
A. F x  2x C.
B. F x 3
x  2x C. 3 1
C. F x 3  x C.
D. F x  2x  2  C. 3 Lời giải Chọn B 1
Họ nguyên hàm của hàm số f x 2
x  2 là F x 3
x  2x C. 3 2 Câu 14. Tích phân 5 I x dx  có giá trị là 1 32 16 21 19 A. . B. . C. . D. . 3 3 2 3 Lời giải Chọn C 2 2 6 6 x 2 1 21 Ta có 5 I x dx     .  6 6 6 2 1 1
Câu 15. Biểu thức V để tính thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi đồ thị 
hàm số y  sin x và các đường thẳng x  0, x
, trục hoành, quay quanh trục Ox là 3     3 3 3 3 A. 2 V  sin xdx. B. V  sin x dx  .C. 2
V   sin xdx  .
D. V   sin x dx  . 0 0 0 0 Lời giải Chọn C Trang9
Ta có thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi đồ thị hàm số   3
y  sin x và các đường thẳng x  0, x
, trục hoành, quay quanh trục Ox là 2
V   sin xdx  . 3 0
Câu 16. Trong không gian Oxyz cho hai điểm A 1
 ;2;3, B0;1 
;1 , độ dài đoạn AB bằng A. 6 . B. 8 . C. 12 . D. 10 . Lời giải Chọn A   2 2
Ta có AB 1; 1;  2 2
AB AB  1    1   2    6 .
Câu 17. Trong không gian Oxyz cho đường thẳng d đi qua A 2
 ;3;5 và có véc tơ chỉ phương
a3;5;2 thì phương trình tham số của đường thẳng d là x  2   3tx  3 2t
x  2  3tx  3   2t    
A. y  3  5t . B. y  5   3t .
C. y  3  5t . D. y  5   3t .     z  5   2tz  2   5tz  5  2tz  2   5tLời giải Chọn A
Ta có phương trình tham số của đường thẳng d đi qua A 2
 ;3;5 và có véc tơ chỉ phương      x 2 3t
a 3;  5;  2 là y  3 5t  . z  5   2t  x 1 2tCâu 18.
Trong không gian Oxyz cho đường d : y  3  t . Đường thẳng d vuông góc với z  28t
đường thẳng nào sau đây?     x 1 t x  3   4t
x  3  2tx  2   5t     1
A. d : y  5   2t .
B. d :  y  5
  3t . C. d : y  3 2t .
D. d : y  3  t . 1 4  2  3  2  z  2  16tz  2   5tz  5   t
z  2  4tLời giải Chọn C
Đường thẳng d cóvéctơ chỉ phương u   2  ;1;8 . x  2   5t  
Đường thẳng d :y  3 2t cóvéctơ chỉ phương u  5;2;1 . 3   3 z  5   t   
Ta có u .u  2
 .5 1.2 8.1  0  d d . 3 3
Câu 19. Tìm căn bậc hai của số thực âm 64
 trên tập số phức  . Trang10 A. 8  ;8 . B. 8i .
C. 8i;8i . D. 8 . Lời giải Chọn C Ta có 2
64  64i có hai căn bậc hai là 8i và 8  i . 1
Câu 20. Dạng z a bi của số phức z  3 là số phức nào dưới đây? 2i 3 2 3 2 3 2 3 2 A. i . B.   i . C.i . D.   i . 13 13 13 13 13 13 13 13 Lời giải Chọn A 1 3  2i 3  2i 3 2 Ta có z      i 3  2i
3 2i32i 2 2 3  . 2 13 13
Câu 21.Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2022 và hai đường thẳng
x  3, x  4 với trục hoành được tính bởi biểu thức: 4 4 A. 2 S x  2022d .  x
B. S    2 x  2022d . x 3  3  4 3  2
C. S    2
x  2022 d . x D. 2 S x  2022d .  x 3  4 Lời giải Chọn A 4
Diện tích hình phẳng cần tìm là: 2 S x  2022d .  x 3 
Câu 22. Số phức z a bi . Khi đó z z là số phức: A. 2 . bi
B. 2a  2b . i C. 2a . D. 2b . Lời giải Chọn A
Ta có z z a bi  a bi  2bi .
Câu 23. Cho A   x   5 2
1 dx . Đặt t  2x 1. Khẳng định đúng là: 1 1 A. 5 A t . dxB. 5 A  2 t d . xC. A  t   5 1 d . x D. 5 A t dx  2 2 Lời giải Chọn A 1  1  1 Ta có 5 5
t  2x 1 dt  2dx dx
dt A t dt t dt.     2  2  2
Câu 24. Trong hệ trục tọa độ Oxyz, cho mặt phẳng (α): 3x - 2 y + 7z - 10 = 0 . Mặt phẳng (α) song
song với mặt phẳng nào có phương trình sau? A. 3
x  2y  7z  3  0 .
B. 3x  2 y  7z  5  0 . C. 3
x  2y  7z  0 .
D. 3x  2 y  7z  3  0 . Lời giải Trang11 Chọn A 3 2  7 10  Ta thấy:     
song song với mặt phẳng có phương trình 3 2 7  nên mặt phẳng   3 3
x  2y  7z  3  0 .
Câu 25. Cho các số phức z  3  bi, z c  4i . Phần thực và phần ảo của số phức z = z - z lần 1 2 1 2 lượt là
A. 7; b c . B. 3  ; c b  4 . C. 3  ; c b  4 . D. 3  ; c b  4 . Lời giải Chọn C
Ta có: z = z - z = 3+ bi - c - 4i = 3- c + b + 4 i 1 2 ( ) ( ) ( ) ( ) .
Do đó, phần thực và phần ảo của số phức z lần lượt là: 3  ; c b  4 . 2016 1 i
Câu 26. Cho số phức z thỏa mãn z   
. Viết z dưới dạng z = a + bi, a,b Î ¡ . Khi đó tổng 1 i
a b có giá trị bằng bao nhiêu? A. 2 . B. 0 . C. 1. D.1. Lời giải Chọn D 1008 2016    1 i     1 1 i i 2 2016    2  i1008  2  1008 1008 .i Ta có: z          . 1 i  1i 1 2016    1008  2 1 i i 1008 1008 1008 2 2 .i   a 1 Suy ra: 
a b 1. b   0
Câu 27. Cho số phức z a bi, z c di . Khi đó M , N lần lượt là hai điểm biểu diễn cho các số 1 2 
phức z , z . Khi đó độ dài véctơ MN là 1 2   2 2 2 2
A. MN  c a  d b .
B. MN  b a  d c .   2 2 2 2
C. MN  c a  d b .
D. MN  c a  d b . Lời giải Chọn D M  ; a b, N  ; c d  .
    2   2 MN c a d b . x 1 2t
x  3 4t '  
Câu 28. Cho hai đường thẳng d :  y  2  3t và d ' :  y  5  6t '   z  3  4tz  7  8t ' 
Trong các mệnh đề sau, mệnh đề nào đúng?
A. d d ' .
B. d d ' .
C. d / /d ' .
D. d và d ' chéo nhau. Lời giải Chọn B Trang12
Véctơ chỉ phương của d là: u  2;3;4 . 
Véctơ chỉ phương của d ' là: u '  4;6;8 .  
Ta có u '  2u , suy ra hai đường thẳng d và d ' song song hoặc trùng nhau.
Chọn điểm A1; 2;3  d , thay tọa độ điểm A vào phương trình đường thẳng d ' ta được hệ 1   3 4t '  1
2  5  6t '  t '   . Suy ra điểm A thuộc đường thẳng d '. 2 3  7 8t ' 
Vậy d d ' . 4 2 Câu 29. Cho f
 xdx 16. Tính I f
 2xdx . 0 0 A. I  32 . B. I  4 . C. I  16 . D. I  8 . Lời giải Chọn D
Đặt t  2x , dt  2dx . Đổi cận: 4 4 I f  tdt 1  f
 xdx 8. 2 2 0 0
Câu 30. Trong hệ tọa độ Oxyz khoảng cách từ điểm A1; 2
 ;3 đến mặt phẳng
:x 2y  2z 10  0 bằng 1 1 7 1 A.  . B. . C. . D. . 3 3 3 3 Lời giải Chọn D
Khoảng cách từ điểm A1; 2
 ;3 đến mặt phẳng   :x  2y  2z 10  0 là:   
d A   1 4 6 10 1 ;   . 1 4  4 3
Câu 31. Phần gạch chéo trong hình bên dưới là hình phẳng giới hạn bởi đồ thị của hàm số 2
f (x)  (x 1)(x  2) với trục hoành. Hãy tính diện tích S đó Trang13 15 27 27 15 A. . B. . C. . D. . 2 4 4 2 Lời giải Chọn B Dựa vào hình vẽ
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 2
f (x)  (x 1)(x  2) với trục hoành là 2 2 2 4  x  27
S   x  
1  x  22 .dx    3 2
x  3x  4dx 3
   x  4x  .  4  4 1  1  1 
Câu 32. Cho 3 điểm M 2;0;0 , N 0; 3
 ;0 , P0;0;4 . Nếu MNPQ là hình bình hành thì tọa độ của điểm Q là A. 3; 4; 2 . B. 2;3; 4 . C.  2  ; 3  ; 4   . D. 2;3; 4  . Lời giải Chọn B  
Ta có: NP  0;3; 4 ; MQ   x  2; y ; z Q Q Q  x  2   Q
MNPQ là hình bình hành khi MQ NP   y  3. Qz  4  Q
Vậy tọa độ của điểm Q 2;3; 4 . x  3   2t
x  5  t  
Câu 33. Tọa độ giao điểm của hai đường thẳng d :  y  2
  3t và d: y  1   4t là   z  6  4t
z  20  t  A. 0; 3  ;2 . B.  7  ; 8  ; 2   . C. 3;7;18 . D. 8; 1  3;23. Lời giải Chọn C  3
  2t  5  t  t   3
Giao điểm của d và d là nghiệm của hệ:  2   3t  1   4t   . t    2 
6  4t  20  t 
Do đó giao điểm d và d là M 3;7;18 . Trang14
Câu 34. Gọi n là số nghiệm của phương trình 5 2
z az bz c  0 ( a , b , c là các số thực) trong tập số
phức  . Tìm giá trị của số n . A. 2 . B. 3 . C. 5 . D. 4 . Lời giải Chọn C
Trên tập số phức, phương trình bậc n có n nghiệm. Do đó phương trình trên có 5 nghiệm.
Câu 35. Trong không gian Oxyz , viết phương trình mặt cầu S  có tâm I 4;0; 2
  và bán kính R  9. 2 2 2 2
A. (S) (x - ) 2 : 4 + y + (z + ) 2 = 81.
B. (S) (x - ) 2 : 4 + y + (z + ) 2 = 9 . 2 2 2 2
C.(S) (x + ) 2 : 4 + y + (z - ) 2 = 9 .
D.(S) (x + ) 2 : 4 + y + (z - ) 2 = 81. Lời giải Chọn A
Nhớ: Phương trình mặt cầu tâm I a ;b;c, bán kính là R có phương trình là:
  2   2   2 2 x a y b z cR .
Áp dụng với mặt cầu S  có tâm I 4;0; 2
  và bán kính R  9 có phương trình là:
(S) (x - )2 + y + (z + )2 2 : 4 2 = 81. ìï x = - 3+ 2t ïï
Câu 36. Hình chiếu của điểm A(2;- 3; )
5 lên đường thẳng d :í y = - 2 + 3t ï có tọa độ là ïï z = 1+ t ïî æ 31 5 25ö æ 10 5 25ö æ 10 5 25ö æ 10 5 25ö A. ç- ; ; ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç . B. - ; ;- ç ÷. C. - ;- ; ç ÷. D. - ; ; ç ÷. è 14 14 14÷ø çè 7 14 14÷ø çè 7 14 14 ÷ ø çè 7 14 14÷ø Lời giải Chọn D
Gọi H là hình chiếu của điểm A lên đường thẳng d . 
Ta có: H d H  3   2t; 2
  3t;1 t; AH  2t  5;3t 1;t  4 . 
Ta có: n  2;3; 
1 là một vecto chỉ phương của đường thẳng d .   Suy ra AH n
  t     t    t   11 . 0 2 2 5 3 3 1 1 4  0  t  . 14  10 5 25  Suy ra H  ; ;   .  7 14 14 
Câu 37. Trong hệ tọa độ Oxyz mặt phẳng   đi qua điểm M 3; 1  ; 5
  và vuông góc với hai mặt
phẳng P :3x  2y  2z  7  0 và Q :5x  4y  3z 1  0 có phương trình là
A. x y z  3  0 . B. 2x y  2z 15  0 .
C. 2x y  2z 15  0 .
D. 2x y  2z 16  0 . Lời giải Trang15 Chọn B r Ta có: n = (3;- 2; )
2 là một vecto pháp tuyến của mặt phẳng  P . r u = (5;- 4; )
3 là một vecto pháp tuyến của mặt phẳng Q .
Mặt phẳng   vuông góc với hai mặt phẳng  P và Q nên   có một vecto pháp tuyến là    v   , n u  2;1; 2    
. Do đó phương trình của   là 2x y  2z 15  0 .
Câu 38.Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD , biết A2;3;  1 , B 4;1; 2
  , C 6;3;7 , D  5  ; 4  ; 8
  . Độ dài đường cao DH của tứ diện ABCD bằng: 15 5 45 45 A. . B. . C. . D. . 7 7 21 7 Lời giải Chọn D uuur uuur uuur Ta có: AB = (2;- 2;- ) 3 , AC = (4;0; ) 6 , AD = (- 7;- 7;- ) 9 .  
      2 2 A , B AC   1  2; 2  4;8 2   ;  A ,
B AC.AD  180  
;  AB, AC    1  2   2  4 8  28   .
1    1   Suy ra: V
  AB, AC.AD  30 ; S
  AB, AC  14 . ABCD     6 ABC 2 Suy ra độ 3V 45
dài đường cao DH của tứ diện ABCD bằng ABCD  . S 7 ABC
Câu 39. Cho số phức z thỏa mãn z  3  8i  7 và số phức w  4
 3i . Gọi M là giá trị lớn nhất của
biểu thức P z w . Chọn khẳng định đúng trong các khẳng định sau.
A. M 20; 2  1 .
B. M 21; 22 .
C. M 18;19 .
D. M 19;20 . Lời giải Chọn A
Gọi số phức z x  .
y i ; x , y   .
Theo đề ra, ta có: z  3 8i  7  x yi  3 8i  7  x 3   y 8i  7
  x  2   y  2    x  2   y  2 3 8 7 3 8  49 .
Do đó, tập hợp các số phức thỏa mãn z  3  8i  7 là một đường tròn C có tâm I 3;8
và bán kính r  7 .
Lại có P z w x yi   i   x     y  i   x  2   y  2 4 3 4 3 4 3 .
Theo đề, M là giá trị lớn nhất của biểu thức P z w điều đó có nghĩa là ta tìm số phức z
thuộc đường tròn C có tâm I 3;8 và bán kính r  7 sao cho khoảng cách đến điểm w 4  ;3 là lớn nhất. Trang16
Dựa vào đồ thị, ta thấy số phức z thỏa yêu cầu bài toán có điểm biểu diễn là giao điểm của
đường thẳng d và đường tròn C .
Đường thẳng d đi qua hai là điểm W  4
 ;3 và I 3;8 nên có phương trình là x  3 7t  , với t  . y  8  11t
Ta có tọa độ của A và B thỏa hệ phương trình  49 170  x  3   0 170   x  3  7t x  3  7t x  3  7t         77 170 y  8  11t
 y  811t
 y  811t  y  8 hay       x  3   170 2   y  82 2 2  49
49t 121t  49 7 170 t     7 170  170 t    170   49 170 x  3   0 170   77 170 y  8   . 170   7 170 t     170 
Dựa vào hình vẽ, ta thấy điểm B có hoành độ dương và tung độ âm nên ta nhận  49 170 x  3   170  .  77 170 y  8   170 2 2    
P  x  2   y  2 49 170 77 170 4 3  3  4   8    3  20,0384     . 170 170     Trang17
Câu 40. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
f x  3x  31 và g x 7 35  x
với trục Ox và đường thẳng x  9  . 11 11 8125 1029 647 1797 A. S  . B. S  . C. S  . D. S  . 198 22 18 50 Lời giải Chọn C Theo đề bài ta có: 31
Hoành độ giao điểm của f x  3x  31 và trục Ox là x   . 3
Hoành độ giao điểm của g x 7 35  x
và trục Ox là x  5  . 11 11
Hoành độ giao điểm của f x  3x  31 và g x 7 35  x  thỏa phương trình 11 11 7 35 3x  31  x   x  6 . 11 11
Ta có hình vẽ của đồ thị các hàm số như sau:
Dựa vào hình vẽ, ta có S S S . 1 2 5  5  3 112 S  3x  31dx  3x  31 3x  31   . 1   2 9 9  9  6 6  7 35   3  S  3x  31  x  dx      3x  3  7 35 47 2 1 3x  31  x x  . 2   11 11   2 22 11  2 5  5  647
Suy ra S S S  . 1 2 18
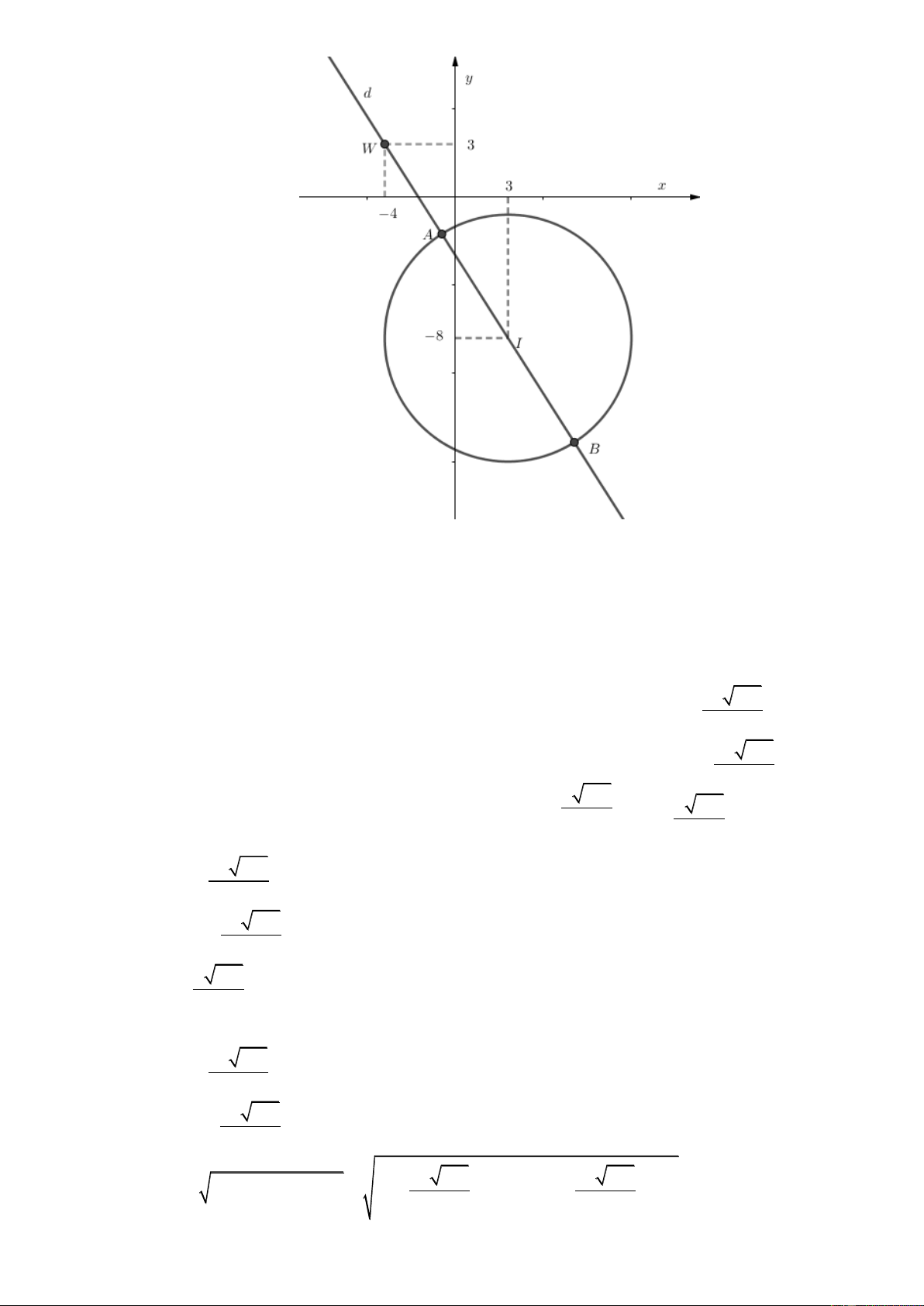
Câu 41. Trong không gian Oxyz , cho mặt cầu S  có phương trình là 2 2 2
2x  2 y  2z  8x  4 y 12z  6  0 và mặt phẳng   : x  3y  2z  5  0 . Gọi I là tâm mặt
cầu S  , I là điểm đối xứng của I qua mặt phẳng   . Tính độ dài đoạn II . 6 14 3 14 A. II   . B. II   .
C. II   17 .
D. II   2 17 . 7 7 Lời giải Chọn A Trang18 Ta có 2 2 2 2 2 2
2x  2 y  2z  8x  4 y 12z  6  0  x y z  4x  2 y  6z  3  0
a  2,b  1
 ,c  3, d  3. Do đó mặt cầu S  có tâm I 2; 1  ; 3   .
Gọi H là hình chiếu vuông góc của I trên   .
I  là điểm đối xứng của I qua      là mặt phẳng trung trực của đoạn II . 2  3  6  5 6 14
Suy ra II   2IH  2d I,   2.  .   2 2 2 7 1 3  2 5 dx
Câu 42. Biết tích phân I   aln3 bln5 
a,b . Khi đó a b có giá trị là x 3x 1 1 A. 4 . B. 1. C. 5 . D. 0 . Lời giải Chọn B 2 2 t 1 Đặt 2
t  3x 1  t  3x 1 
tdt  dx, x  3 3
Đổi cận x 1 t  2, x  5  t  4 4 4   Khi đó: 1 2 1 1 I  . d t t   dt    
ln t 1 ln t 14 2 2 t 1 3
t 1 t 1 2 2 .t 3
 ln3ln5ln1ln3  2ln3ln5  a  2,b  1 a b  1.  m Câu 43. Số phức 1 z
; m   . Môđun lớn nhất của số phức z là
1 m(m  2i) 1 2 2 1 A. . B. 3 . C.1. D. . 2 2 Lời giải Chọn A 1 m 1 m 1 m 1 m 1 m Ta có z      .
1 m m  2i 2 1 m  2mim
1 m 2  2m m   2 2 2 2 2 1 1 Trang19 1 m m  2m 1
Xét hàm số g m 2   2 2 m 1 m  với m . 1 3 2
m  3m m 1
Có gm  .
m  2m 1m  2 2 2 1
gm không xác định khi m 1.
gm  0  m  1 2 . BBT m   1 2 1 1 2
gm  0   0  g m 1 2 2 1 2 2 0 0 0 1 2
Từ bảng biến thiênsuy ra môđun lớn nhất của số phức z là . 2 1 Câu 44. Tính dx  kết quả đúng là . 2 x  5x  6 1
A. ln x  2  ln x  3  C . B.
(ln x  3  ln x  2 )  C . 2
C. ln x  3  ln x  2  C .
D. ln( x  2 . x  3 )  C . Lời giải Chọn C 1 1  1 1  Ta có dx dx  
dx  ln x  3  ln x  2  C     . 2   x  5x  6
x 2x 3
x 3 x  2  p 2 p cos x 2 cos x Câu 45. Biết dx = . m ò
Tính giá trị của I = d . x ò 1+ 3- x 1+ 3x - p - p   A.   m . B. m . C.  m . D.m . 4 4 Lời giải Chọn C Đặt x t   dx  d  t p 2 - p p p cos x 2 2 2 cos - t cos t cos x Khi đó dx = ò ( ) - dt Þ m = dt = dx = I ò ò ò 1+ 3- x 1+ 3t 1+ 3t 1+ 3x - p p - p - p p 2 p x 2 cos x 3 cos x Mặt khác m = dx = d . x ò ò 1+ 3- x 1+ 3x - p - p Suy ra p p p (1+ 3x x ) 2 2 2 cos p p cos 3 cos x x x 1 2 2m = dx + dx = dx = cos d x x = (1+ cos 2x)dx ò ò ò ò ò 1+ 3x 1+ 3x 1+ 3x 2 - p - p - p - p - p Trang20 1 æ sin 2xö p p = x ç ÷ + ç ÷ = p Þ m = 2 ç è 2 ÷ ø- p 2 p 2 cos x p Vậy I = dx = = p - m ò . Chọn C 1+ 3x 2 - p
Câu 46. Trong hệ tọa độ Oxyz một mặt phẳng (a ) đi qua điểm M (1; 2; )
3 và cắt ba tia Ox, Oy, Oz lần
lượt tại các điểm A, B, C sao cho thể tích tứ diện OABC nhỏ nhất, có phương trình là
A. 6x  3y  2z 18  0 .
B. 3x  2 y  2z 13  0 .
C. 3x  6 y z 18  0 .
D. 2x  3y  6z  26  0 . Lời giải Chọn A Gọi A( ; a 0; ) 0 , B(0; ; b )
0 ,C(0;0;c), với a,b, c > 0. x y z
Phương trình mặt phẳng (a ) là + + = 1. a b c 1 2 3
(a ) đi qua điểm M (1; 2; ) 3 Þ + + = 1. a b c
Thể tích khối tứ diện 1 OABC là : Vabc OABC 6 1 2 3 1 2 3
Áp dụng bất đẳng thức Cauchy ta có : 3    3 . . a b c a b c 6 162 Hay 3 1  3  1 abc abc 1
Suy ra : abc  162  abc  27  V  27 . 6 OABC ìï a = 3 ï
Vậy thể tích khối tứ diện 1 2 3 1 ï OABC nhỏ nhất khi = = = Û í b = 6 a b c 3 ïïï c= 9 ïî x y z
Phương trình của mặt phẳng (a ) là + +
= 1 Û 6x + 3y + 2z - 18 = 0. 3 6 9
Câu 47. Trong mặt phẳng toạ độ Oxyz , đường thẳng  đi qua điểm A 4  ; 2
 ;4, đường thẳng  cắt x  3   2t
và vuông góc với đường thẳng d :  y 1 t thì phương trình đường thẳng  là  z  1   4t x  4 y  2 z  4 x  4 y  2 z  4 A.     3 2 1  . B. 3 2 1  . x  4 y  2 z  4 x  4 y  2 z  4 C.      . 3 2 1  . D. 3 2 1 Lời giải Chọn A
Gọi  P là mặt phẳng đi qua A 4  ; 2
 ;4 và vuông góc với đường thẳng d . Trang21  
Khi đó n u   . P 2; 1;4 d   
Phương trình mặt phẳng P là 2x  4   y  2  4z  4  0  2x y  4z 10  0 .
Gọi B d   P thì toạ độ điểm B thoả mãn hệ phương trình  x  3   2tt  1    y  1 tx  1     B 1  ;0;3 . z  1   4ty  0 
2x y  4z 10  0  z  3
Đường thẳng  cần tìm là đường thẳng đi qua hai điểm , A B .   x  4 y  2 z  4
Ta có u AB      3;2; 
1 . Phương trình đường thẳng  là 3 2 1  .
Câu 48. Số các giá trị m nguyên để có đúng hai số phức z thỏa z  m  3  3i  4 và
z 1 i z 1 2i là A. 9 . B. 8 . C.11. D. 6 . Lời giải Chọn A
Giả sử z x yi x, y    . 2 2
Ta có z  m  3  3i  4  x m  3   y  3i  4   x m  3   y  3  16
Tập hợp các điểm biểu diễn số phức z là đường tròn C có tâm I m  3; 3
  , bán kính R  4 Ta lại có
z 1 i z 1 2i
x yi 1 i x yi 1 2i
x 1  y  
1 i x 1 2  yi
 x  2   y  2  x  2   y  2 1 1 1 2
 2x  2y  2  2
x  4y  5
 4x  2y  3  0 .
Tập hợp các điểm biểu diễn số phức z là đường thẳng d : 4x  2 y  3  0 .
Để có đúng hai số phức z thỏa mãn yêu cầu bài toán thì đường thẳng d phải cắt C tại hai điểm phân biệt. Trang22
4 m  3  2. 3    3 ycbt d      R   4 4m 3 8 5 I ,d  2 2 4  2 8  5 3 8 5  3  8
 5  4m  3  8 5   m  4 4
Mà m nên m  5  ; 4  ; 3  ;...;1;2;  3 .
Có tất cả 9 giá trị m nguyên. 2 x
Câu 49. Cho F x  ln 2x là một nguyên hàm của . Tính
f ' x.ln xdx  . Kết quả đúng là f xx x A. f  x 3 '
.ln xdx x ln x   C . B. f  x 3 3 '
.ln xdx x ln x   C . 3 3 x x C. f  x 3 ' .ln xdx   C . D. f  x 3 2 '
.ln xdx x ln x   C . 3 2 Lời giải Chọn B 2 x
Do F x  ln 2x là một nguyên hàm của nên: f x  2 2  x 1 x x 2 x ln 2    dx   ln  2x        3 f x x . f x f xx f x Xét I f '
 x.ln xdx.  dx u   ln x  du  Đặt    x . dv f ' 
xdx v f  xf x 3 Khi đó: x I f
 xxdx x f x   ' .ln ln .  dx  3 2 3
x ln x x dx x ln x   C  . x 3
Câu 50. Các bồn chứa xăng vận chuyển trên xe cơ giới thường có dạng hình trụ nằm ngang với đáy là
một hình elip mà không phải hình tròn. Việc chế tạo theo hình elip có nhiều ưu điểm như: làm
cho trọng tâm xe thấp, độ dao động của chất lỏng bên trong bồn sẽ thấp …. Giả sử một bồn chở 2 2
xăng có đáy là đường elip có phương trình x y
 1 và chiều dài của bồn là 10m. Sau khi 9 4
bơm xăng cho một trạm xăng thì phần xăng còn lại cách đỉnh của elip 1m (Tham khảo hình
vẽ). Tính gần đúng lượng xăng còn lại trong bồn xăng (Làm tròn đến hàng đơn vị theo lít và giả
sửa các vật liệu chế tạo nên bồn xăng có độ dài không đáng kể). Trang23 A. 151 646 lít. B.151 645 lít. C.151 644 lít. D.151 647 lít. Lời giải Chọn C 2 2 x ya  3 Từ phương trình elip   1 ta có  . 9 4 b   2
Diện tích đáy của bồn hình elip: S       ab 6 . E
Đặt hệ trục tọa độ như hình vẽ. Ta có: S
S S là phần diện tích đáy có xăng bị mất đi. M 1 2
Gọi M , N là giao điểm của elip và đường thẳng y  1.  3 3 x  2   Khi đó: x 1 2 3 3   1    N  ;1   . 9 4  2 3 3   x    2 2 2 x y
Phần diện tích S được giới hạn bởi đường elip 
 1, đường thẳng y 1 và hai đường 1 9 4 3 3 x  0 , x  . 2 3 3 2   3 3 2   Do đó: x x 2 S   2 1 1 dx  . Mà 2
S S S  2  2 1 1dx  . 1 1 2 M 0  9      0 9  
Nên diện tích phần đáy còn xăng là: S S  S . E M
Vậy thể tích phần xăng còn lại là:  3 3 2    x
V S.h  10.6  2  2 1 1dx 151,644   3 2
m   151 644 lít. 0  9        HẾTTrang24