SỞ GD & ĐT THÁI NGUYÊN ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2015 – 2016
TRƯỜNG THPT MÔN: TOÁN – LỚP 12 LƯƠNG NGỌC QUYẾN
Thời gian làm bài 90 phút (không kể thời gian phát đề) 
Câu 1 (2,5 điểm). Cho hàm số: 2x 1 y  x 1 
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b) Tìm tọa độ giao điểm của đồ thị (C) và đường thẳng d: y = x + 1. Viết phương trình tiếp
tuyến của đồ thị (C) tại các giao điểm đó.
Câu 2 (1,0 điểm). Giải bất phương trình: log x  2log (4 x) 1. 3 9
Câu 3 (3,0 điểm).
a) Tính môđun của số phức z biết: z  4i  2  2z .  2
b) Tính tích phân: I  xsin 2xdx  . 0
c) Cho các số thực không âm a, b, c thỏa mãn điều kiện: a + b + c = 3. Tìm giá trị nhỏ a b c
nhất của biểu thức: A    . 4 4 4 b 16 c 16 a 16
Câu 4 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a. Hình chiếu
vuông góc của đỉnh S lên mặt đáy là điểm I thuộc cạnh AB sao cho BI=2AI và SI  3a 3 .
Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AD, SC theo a.
Câu 5 (2,0 điểm). Trong không gian tọa độ Oxyz, cho hai đường thẳng
x  2 t  x  4 y 1 z  5  d         1: và d2: y 3 3t (t ) 3 1 2 z t 
a) Chứng minh hai đường thẳng d1 và d2 chéo nhau.
b) Viết phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng d1, d2.
---------------------- Hết ---------------------
Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………………… Số báo danh:……………, Phòng thi:……….
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II, NĂM HỌC 2015 - 2016 MÔN TOÁN LỚP 12 CÂU ĐÁP ÁN ĐIỂM  Cho hàm số: 2x 1 y  Câu 1 x 1  a) 1,5
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) 1,0
b) Tìm tọa độ giao điểm của đồ thị (C) và đường thẳng d: y = x
+ 1. Viết phương trình tiếp tuyến tại các giao điểm đó. a) 1,5
a) TXĐ: D   \   1 0,25
* Giới hạn và tiệm cận: lim y  2 => Tiệm cận ngang: y=2 x lim y  ;
 lim y      Tiệm cận đứng x =1 0,5 x 1  x 1  1
* Chiều biến thiên: y '    0, x 1 2 (x 1)
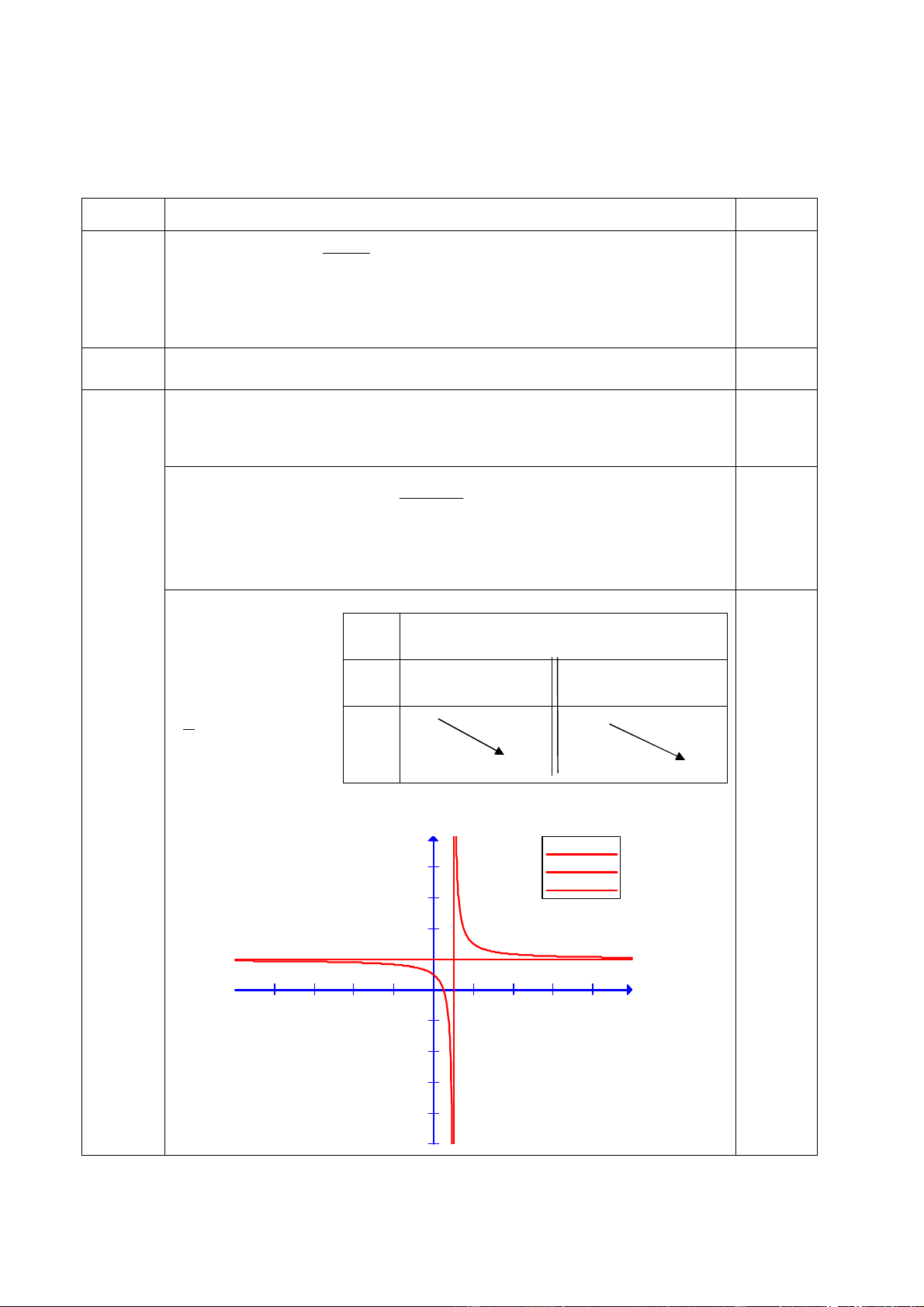
hàm số nghịch biến trên mỗi khoảng ( ;1  ), (1; )  và không 0,25 có cực trị. * Bảng biến thiên: x  1 +  * Đồ thị cắt trục Ox tại điểm y’ - -  0,25 1    ; 0      y 2 + 2 và cắt Oy tại điểm (0;1). -  2 y f(x)=(2x-1)/(x-1) f(x)=2 8 x(t )=1 , y(t )=t 6 4 0,25 2 x -8 -6 -4 -2 2 4 6 8 -2 -4 -6 -8 2 b) 1,0
b) Phương trình hoành độ giao điểm của d và (C) là: 2x 1 2        2x 1 x 1 x 0  x 1     x 1 x 1 x  2   0,5
Đường thẳng d cắt đồ thị (C) tại hai điểm M(0;1) và N(2;3)
Phương trình tiếp tuyến tại M(0;1): y= - x +1
Phương trình tiếp tuyến tại N(2;3): y= - x +5 0,5
Vậy: có hai tiếp tuyến cần tìm là y = - x + 1 và y = - x + 5
Câu 2 Giải bất phương trình:
log x  2log (4  x) 1 (1) 3 9 1,0  x  0  ĐK:  x  4  0,25
Ta có: (1)  log x(4 x) 1 3 0,25 x  3 2 0,25
 x 4x  3 0   x 1  0,25
Vậy: bất phương trình đã cho có tập nghiệm: T  (0;1)  (3;4)
Câu 3 a) Tính môđun của số phức z biết: z  4i  2  2z .  2 3,0đ
b) Tính tích phân:  ( x I
e  xsin 2x)dx  . 0
c) Xét các số thực không âm a, b, c thỏa mãn điều kiện: a + b +
c = 3. Tìm giá trị nhỏ nhất của biểu thức: a b c A    . 4 4 4 b 16 c 16 a 16 a) Đặt z=x+yi ( ;
x y  )  z  x  yi . a) 1,5
Ta được: x  ( y  4)i  2  2x  2 yi 0,5  2
x  22x x        3  y  4  2 y   y  4  0,5 2 2
 z   4i  z  37 0,5 3 3 3  b)1,0 du  dx u   x    Đặt   1 d
 v  sin 2xdx  v   cos2x   0,25 2   2 0,25 2 1 1
 I   x o c s2x  o c s2xdx  2 2 0 0  2  1 0,25 Suy ra I=  sin 2x 4 4 0  I  0,25 4 Ta có 4 2
b 16  8b . Suy ra c)0,5 4 4 2 a a b a b a b  (1 )  (1 )  (1 ) 4 4 2 16  b 16 b 16 16 8b 16 8 2 b b c 2 c c a Tương tự:  (1 ) ;  (1 ) 4 16  c 16 8 4 16  a 16 8 3 1 0,25 Suy ra: 2 2 2 A  
(ab  bc  ca ) (1) 16 128
Không mất tính tổng quát ta giả sử b nằm giữa a và c, khi đó ta có:
a(b  a)(b  c)  0 2 2 2 2 2
ab  bc  ca  b(a  c)  b(3  b) hay Xét hàm số 2
f (b)  b(3 b) ; 0  b  3ta được
f (b)  f (1)  4 (2) 5
Từ (1) và (2) ta có A  . 32
Dấu đẳng thức xảy ra khi a=0; b=1; c=2. 0,25 5 Vậy: minA= . 32
Câu 4 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a.
Hình chiếu vuông góc của S lên mặt đáy là điểm I thuộc cạnh AB 1,5
sao cho BI=2AI và SI  3a 3 . Tính thể tích khối chóp S.ABCD
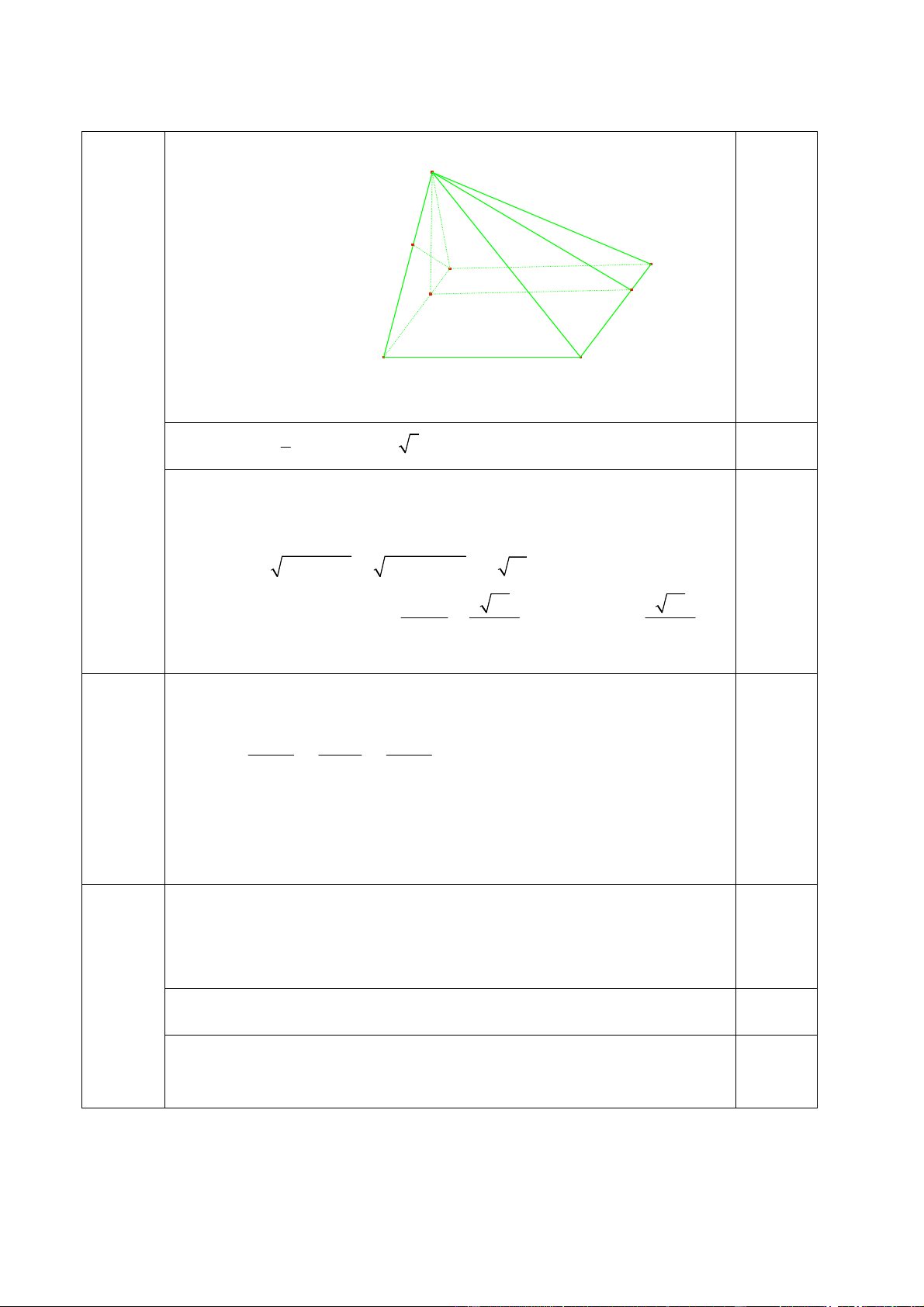
và khoảng cách giữa hai đường thẳng AD, SC theo a. 4 a) S Ta có 2 S  9a . ABCD K A D 0,5 H I B C 1 0,5 Vậy 3 V  .S .SI  9a 3 (đvtt). S . ABCD 3 ABCD
b) Ta có AD / /(SBC)  d(A ;
D SC)  d (A ;
D (SBC))  d( ; A (SBC))
Trong mp(SAB) kẻ AK  SB  AK  (SBC)  d( A ; D SC)  AK 0,25 Ta có 2 2 2 2 SB 
SI  IB  27a  4a  a 31 A . B SI 9 93a 9 93a
Từ SB.AK=AB.SI  AK  
 d (AD;SC)  SB 31 31 0,25
Học sinh có thể giải bằng cách tọa độ hóa bài toán.
Trong không gian tọa độ Oxyz, cho hai đường thẳng    Câu 5 x 2 t  x  4 y 1 z  5  2,0 đ d         1: và d2: y 3 3t (t ) 3 1 2 z t 
a) Chứng minh d1 và d2 chéo nhau.
b) Viết phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với
cả hai đường thẳng d1 và d2.
a) d1 đi qua điểm M(4;1;-5) và có véc tơ chỉ phương a)  u  (3; 1  ; 2  ) 1,5 0,5 
d2 đi qua điểm N(2;-3;0) và có véc tơ chỉ phương v  (1;3;1)    [u, v]  (5; 5  ;10) , MN  ( 2  ; 4  ;5) 0,5   
 [u,v].MN  80  0 0,5 Do đó d1 và d2 chéo nhau. 5
b) Mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng
d1, d2 là mặt cầu nhận đoạn vuông góc chung của hai đường b) 0,5
thẳng đó làm đường kính.
Gọi AB là đoạn vuông góc chung của d1 và d2 với A  d  (
A 4  3t;1t; 5
 2t) và B  d  B(2 ; s 3  3 ; s s) 1 2 
 AB  (23t  s;4 t 3s;5 2t  s) 0,25   AB  d   A . B u  0 7
 t  s  6 t  1 ( A 1; 2;3) mà 1              AB  d     2
 t 11s  9
s 1 B(3;0;1) 2 A . B v 0   
Do đó phương trình mặt cầu cần tìm là: 0,25 2 2 2
(x  2)  ( y 1)  (z 1)  6
(Lưu ý: Học sinh giải theo cách khác đúng vẫn cho điểm) 6