Tr-êng THPT TrÇn Quang Kh¶i §Ò thi häc kú II LíP 12 N¨m 2015 - 2016 M¤N TO¸N. Thêi gian lµm bµi 90 phót
Họ và tên: ………………………………. SBD:………………….. 2x 1
Câu 1 (1,5 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số y  x .  3
Câu 2 (2,0 điểm). Giải các phương trình: a) 5.25x 26.5x   5  0
b) log x log 4x  5. 4 2  
Câu 3 (1,0 điểm). Số phức z thỏa mãn z  3z  8  4i . Tìm mô đun của số phức   z 10 . e  ln x 
Câu 4 (1,5 điểm). Tính tích phân: I  x  dx    x  1
Câu 5 (1,5 điểm). Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  y  z  3  0 và x y 1 z 1 đường thẳng d :   P 1
. Tìm tọa độ giao điểm A của d với ( ) và lập phương trình tham  1 1
số của đường thẳng  đi qua điểm A , vuông góc với đường thẳng d và nằm trong mặt phẳng (P) .
Câu 6 (1,5 điểm). Hình chóp S.ABCD có ABCD là hình chữ nhật với AB  a . SA  (ABCD) ,
SC tạo với mp(ABCD) góc 0
45 và SC  2a 2 . Tính V
và khoảng cách từ trọng tâm G của tam S . ABCD
giác ABC đến mp SCD theo a . 3 3 8
 x  y  2x  y  0 
Câu 7 (1,0 điểm). Giải hệ phương trình:  2
 2y 1  4x 1 1  …HÕt…
Gi¸m thÞ kh«ng gi¶i thÝch g× thªm !
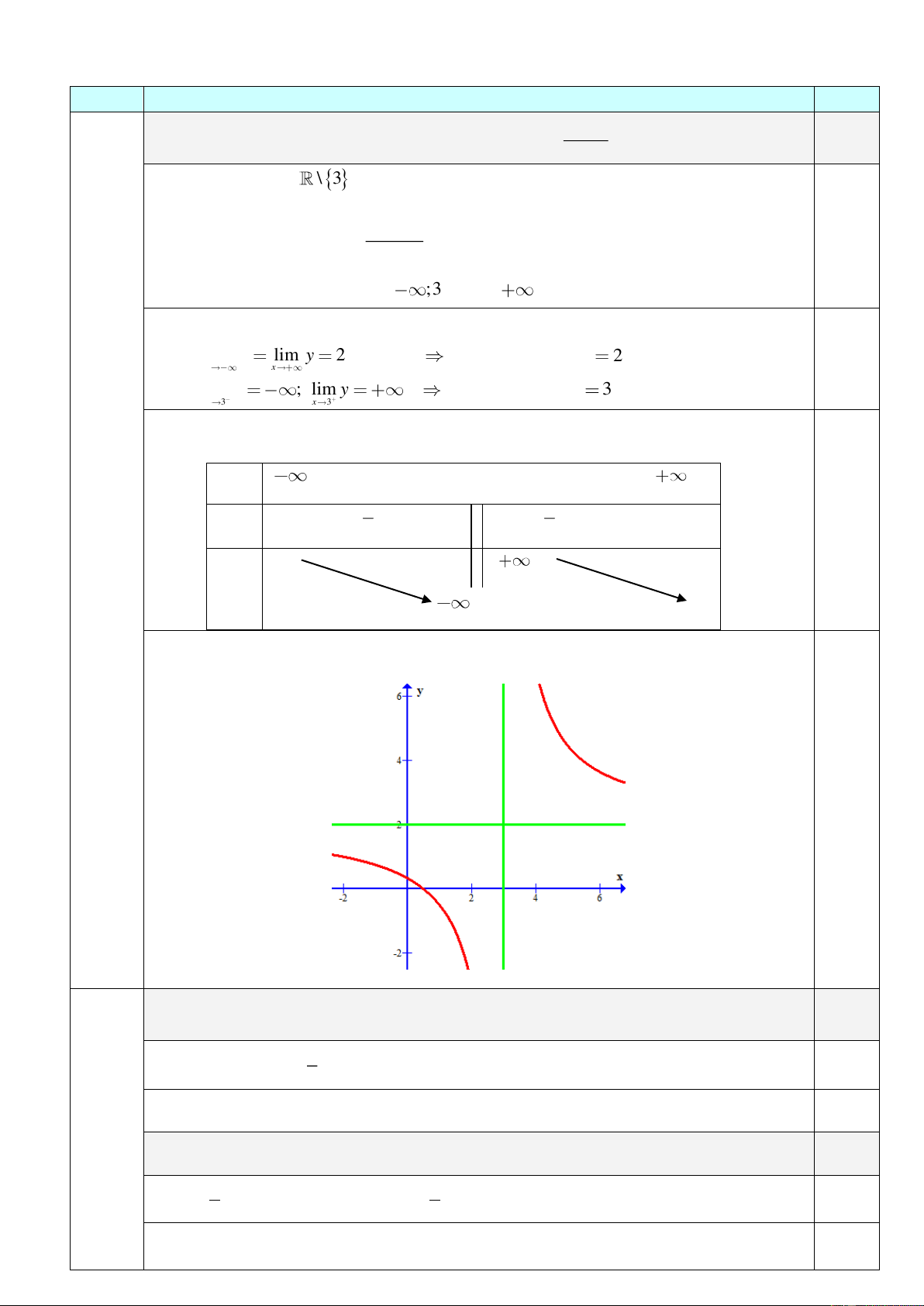
®¸p ¸n §Ò thi M¤N TO¸N.kú II LíP 12 Câu Đáp án Điểm 2x 1 1,5
Khảo sát sự biện thiên và vẽ đồ thị của hàm số y  x .  3 1
Tập xác định: D  \   3 Sự biến thiên: 5 
ￚ Chiều biến thiên: y '      ; y ' 0, x 3 . x  32 0,5
Hàm số nghịch biến trên ;3 và 3;
. Hàm số không có cực trị.
ￚ Giới hạn: lim y
lim y 2 tiệm cận ngang: y 2 x x 0,25 lim y ; lim y tiệm cận đúng: x 3 x 3 x 3
ￚ Bảng biến thiên: x 3 y' y 0,25 2 2
Đồ thị: Đồ thị nhận giao điểm I 3;2 của hai tiệm cận làm tâm đối xứng. 0,5
Giải các phương trình: a) 5.25x 26.5x   5  0   1 b) log x log 4x  5. 2,0 4 2   2 0,5 a)   x x 1 1  5  5;5  5  x  1
 . Vậy: S    1 . 0,5 b) Điều kiện: x > 0. 1 3 0,5
2  log x log x  log 4  5  log x  3 2 2 2 2 2 2
 log x  2  x  4 (t/m) 0,5 2
Vậy phương trình có 1 nghiệm là: x = 4.
Số phức z thỏa mãn z  3z  8  4i . Tìm mô đun của số phức   z 10 . 1,0
* Gọi z  a  bi ( , a b  ) 3 4a  8 a  2
* Từ giả thiết ta có: 4a  2bi  8  4i    
 z  2  2i 0,5      2b 4 b 2
* Số phức   z 10  2  2i 10  8   2i 0,25 2 2   ( 8  )  2  2 17 0,25 e  ln x  1,5
Tính tích phân: I  x  dx    x  4 1 e e ln x 0,25 I  xdx  dx   x 1 1 e e 2 2 x e 1 0,5 I  xdx    1 2 2 1 1 e e e 2 ln x ln x 1 0,5 I 
dx  ln xd (ln x)     2 x 2 2 1 1 1 2 e 0,25 Vậy: I  2 x y 1 z 1
Cho mặt phẳng (P) : x  y  z  3  0 và đường thẳng d :   1 . Tìm tọa độ  1 1 1,5 5
giao điểm A của d với (P) và lập phương trình tham số của đường thẳng  đi qua
điểm A , vuông góc với đường thẳng d và nằm trong mặt phẳng (P) . Gọi A  ;
t 1 ;t1 t  d P  t  3 . 0,5
Vậy: A 3;4;2 0,25
(P) có VTPT là n  1;1;1 (P)  ;
d có VTCP là u   1  ;1;  1
u  n ;u   0;2;2 d . Suy ra VTCP của  là (P) d     . 0,5
Vậy phương trình tham số của  là x  3; y  4  ; t z  2   t 0,25
Hình chóp S.ABCD có ABCD là hình chữ nhật với AB  a . SA  (ABCD) , SC tạo với mp(ABCD) góc 0
45 và SC  2a 2 . Tính V
và khoảng cách từ trọng 1,5 6 S . ABCD
tâm G của tam giác ABC đến mp SCD theo a . S , H A D G B C
Do SA  (ABCD) nên SC  ABCD 0 ,
 SCA  45 0,5
Ta có SA  AC  2a . 2 2 BC 
AC  AB  a 3 , 2 S  A . B BC  a 3 ABCD 3 a 2 3 0,25 Từ đó: V  . 3 GD 2 0,25
* G là trọng tâm tam giác ABC nên  2  d( , G (SC ) D )  .d( , B (SC ) D ) BD 3 3
+ Gọi H là hình chiếu của A lên SD thì AH  SCD .
Vì AB / /mp(SCD) nên d  B,SCD  d  ,
A SCD =AH 1 1 1 1 1 a 0,5 + Trong S  AD có     2 21  AH  2 2 2 2 2 AH AS AD 4a 3a 7 2 4a 21  d( , G (SC ) D )  .d( , B (SC ) D ) = . 3 21 3 3 8
 x  y  2x  y  0  1,00 7
Giải hệ phương trình:  2
 2y 1  4x 1 1 
Điều kiện: x  ;  1
 / 21/ 2;; y 1/ 2 0.25
Ta có:    x  x  y  y   x3 3 3 3 1 8 2 2
 2x  y  y Xét hàm số:   3
f t  t  t với t  R và ' f t  2  3t 1  0, t   R Suy ra:   3
f t  t  t đồng biến trên khoảng  ;   0,5 3 Ta có:  x 3 2
 2x  y  y  f 2x  f  y  2x  y Khi đó:   2
2  4x 1  4x 1  1  x 1/ 2 2
Do : 4x 1  4x 1  1, x  1/ 2 0,25
Nên PT  x 1/ 2  1  Vậy: S   ;1     2 