TRƯỜNG THPT LÊ QUẢNG CHÍ
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC KỲ II Tổ : Toán - Tin Môn : Toán 11
Thời gian làm bài : 90 phút Mã đề thi 01
(Không kể thời gian phát đề)
(Gồm 12 câu hỏi trắc nghiệm và 03 câu hỏi tự luận)
Phần I: Trắc nghiệm khách quan (Mỗi câu hỏi sau chỉ có một phương án đúng trong bốn phương án
A, B, C, D. Hãy chọn phương án đúng và ghi phương án đúng vào tờ giấy thi.) 1
Câu 1: Đạo hàm của hàm số y  tại điểm x  2  là x 1 1 1 1
A. y '2   .
B. y '2  .
C. y '2   .
D. y '2  . 4 4 2 2 Câu 2: Tính lim  3
2x  3x bằng x 1  A. -1. B. -5. C. 1. D. 5. 1
Câu 3: Hàm số có đạo hàm bằng 2x  là 2 x 3 x 1 3 x  5x 1 2 1 A. y  . B. y  C. y  2  . D. y  2  . x x 3 x 2 x
Câu 4: Cho c là hằng số, k là số nguyên dương. Chọn khẳng định sai, trong các khẳng định sau c A. lim  0.
B. lim c   . C. lim c  . c
D. lim x  x . k 0 x x x xx xx 0 0 Câu 5: Hàm số 4
y  x có đạo hàm trên  ;   là A. 3 y '  4x . B. 3 y '  3x . C. 4 y '  4x . D. 4 y '  3x .
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy.
Tìm khẳng định sai.
A. SA  AB .
B. CD  SD .
C. AD  SC .
D. SA  AD .
Câu 7: Chọn khẳng định đúng trong các khẳng định sau A. 3 lim x   . B. 4 lim x   .  C.  4 lim  x    .  D. 3 lim x   .  x x x x  3  x neáu x  3  Câu 8: Cho hàm số
f  x   x 1  2
m neáu x  3. 
Hàm số đã cho liên tục tại x  3 khi m bằng: A. 1. B. 4 . C. 1. D. 4 .
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA vuông góc với mặt phẳng
đáy. Tìm khẳng định đúng.
A. AB  SBC  .
B. AC  SBC  .
C. SC   SAB .
D. BC  SAB . Câu 10: Cho hàm số 2
y  cos x . Khi đó, với mọi x   thì A. 2
y '   sin x .
B. y '  2 cos x .
C. y '  2sin . x cos x .
D. y '  2sin . x cos x .
Câu 11: Cho các mệnh đề sau:
(I) Nếu lim f  x  L  0 và lim g  x   thì lim f  x g  x   . x x  x x  x x  0 0 0
(II) Nếu lim f  x  L  0 và lim g  x   thì lim f  x g  x   . x x  x x  x x  0 0 0 f  x
(III) Nếu lim f  x  L và lim g  x   thì lim  0 . x x  x x   0 0 x 0 x g  x f  x
(IV) Nếu lim f  x  L  0 và lim g  x  0 thì lim   . x x  x x   0 0 x 0 x g  x Số mệnh đề đúng là: A. 3. B. 2. C. 4. D. 1.
Câu 12: Tìm mệnh đề sai trong các mệnh đề sau: A. Hàm số n
y  x (n  , n  2) có đạo hàm trên  và 1 ' n y nx   .
B. Hàm số hằng y  c có đạo hàm trên  và y '  0 . 1
C. Hàm số y 
x có đạo hàm trên khoảng (0; ) và y '  . x
D. Hàm số y  x có đạo hàm trên  và y '  1 . Phần II: Tự luận 2016x 1 3  x
Câu 13: Tính các giới hạn sau: a) lim . b) lim . x x  3 2 x3 x  9 Câu 14: Cho hàm số 4 2
y  x  3x  2 có đồ thị C  .
a) Giải phương trình y ' x  0 .
b) Viết phương trình tiếp tuyến của đồ thị C  tại điểm có hoành độ bằng 1. 5
c) Chứng minh rằng đường thẳng d  : y  x  cắt đồ thị C  tại bốn điểm phân biệt. 2
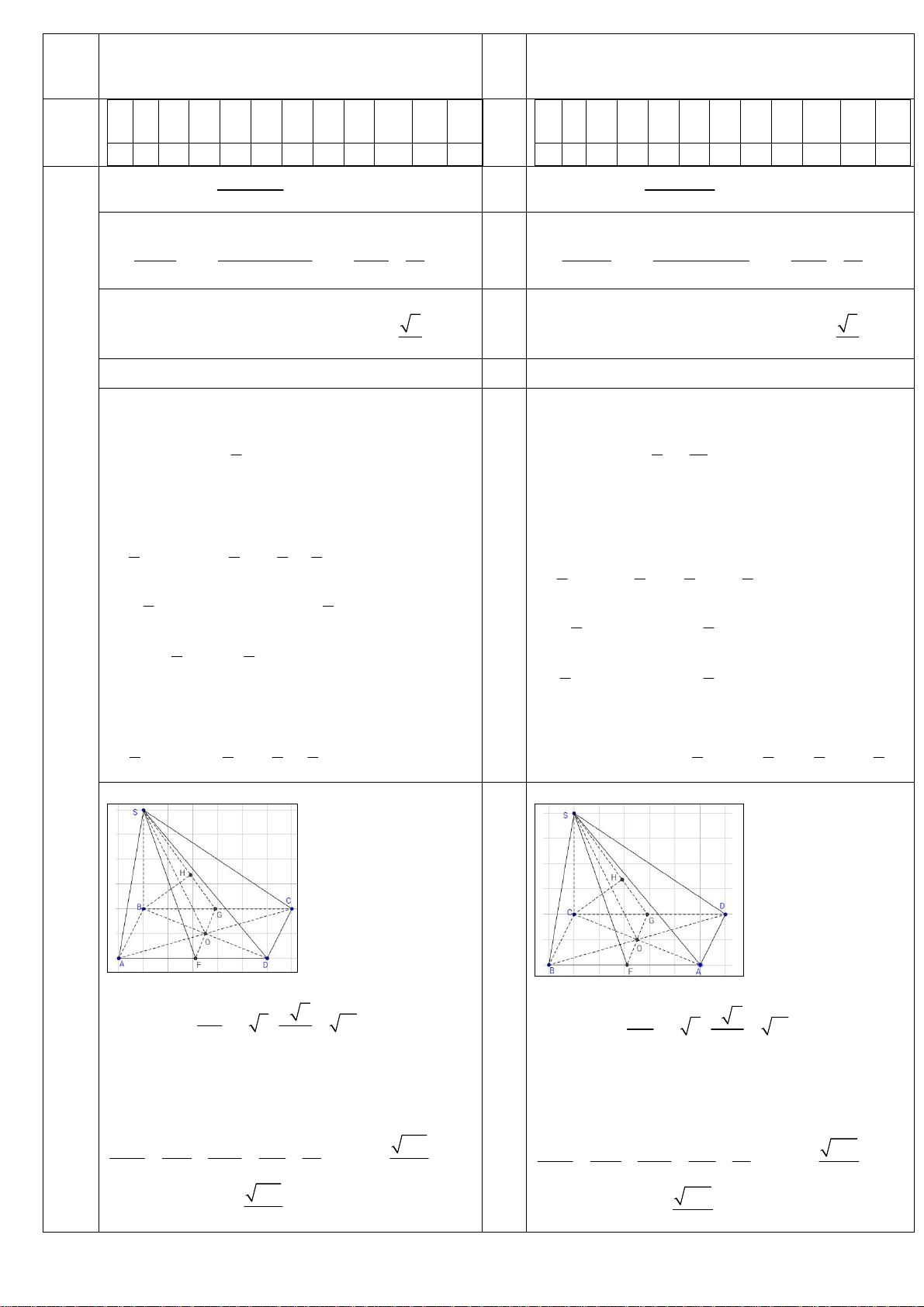
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SB vuông góc với mặt phẳng
 ABCD và SB  a 5 . Gọi O là giao điểm của AC, BD .
a) Chứng minh rằng AC vuông góc với mặt phẳng  SBD .
b) Xác định và tính góc giữa đường thẳng SO và  ABCD .
c) Tính khoảng cách giữa hai đường thẳng SO và CD . HẾT.
TRƯỜNG THPT LÊ QUẢNG CHÍ
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC KỲ II Tổ : Toán - Tin Môn : Toán 11
Thời gian làm bài : 90 phút Mã đề thi 02
(Không kể thời gian phát đề)
(Gồm 12 câu hỏi trắc nghiệm và 03 câu hỏi tự luận)
Phần I: Trắc nghiệm khách quan ( Mỗi câu hỏi sau chỉ có một phương án đúng trong bốn phương án
A, B, C, D. Hãy chọn phương án đúng và ghi phương án đúng vào tờ giấy thi. ) Câu 1: Tính lim  3
4x  2x bằng: x1 A. 2. B. -6. C. -2. D. 6.
Câu 2: Cho các mệnh đề sau:
(I) Nếu lim f  x  L  0 và lim g  x   thì lim f  x g  x   . x x  x x  x x  0 0 0
(II) Nếu lim f  x  L  0 và lim g  x   thì lim f  x g  x   . x x  x x  x x  0 0 0 f  x
(III) Nếu lim f  x  L và lim g  x   thì lim  0 . x x  x x   0 0 x 0 x g  x f  x
(IV) Nếu lim f  x  L  0 và lim g  x  0 thì lim   . x x  x x   0 0 x 0 x g  x Số mệnh đề đúng là A. 3. B. 2. C. 1. D. 4.
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy.
Tìm khẳng định sai.
A. SA  BC .
B. CD  SD .
C. DC  SB .
D. SA  AD Câu 4: Hàm số 3
y  x có đạo hàm trên  ;   là: A. 2 y '  3x . B. 3 y '  3x . C. 2 y '  2x . D. 2
y '  x . Câu 5: Cho hàm số 2
y  sin x . Khi đó, với mọi x   thì
A. y '  2sin . x cos x .
B. y '  2sin . x cos x .
C. y '  2 sin x . D. 2 y '  cos x . 1
Câu 6: Đạo hàm của hàm số y  tại điểm x  3  là x 1 1 1 1
A. y '3  . B. y ' 3     . C. y ' 3     .
D. y '3  . 9 9 3 3
Câu 7: Cho c là hằng số, k là số nguyên dương. Chọn khẳng định sai, trong các khẳng định sau: c A. lim c  . c
B. lim c   .
C. lim x  x . D. lim  0. 0 xx x xx k x 0 0 x
Câu 8: Chọn khẳng định đúng trong các khẳng định sau: A.  4 lim  x    .  B. 4 lim x   .  C. 3 lim x   . D. 3 lim x   .  x x x x  4  x neáu x  4  Câu 9: Cho hàm số
f  x   x  5  3
m neáu x  4. 
Hàm số đã cho liên tục tại x  4 khi m bằng: A. 1. B. 6 . C. 1. D. 6  . 1
Câu 10: Hàm số có đạo hàm bằng 2x  là 2 x 3 x  5x  2 3 x 1 2 3 x  5x 1 A. y  B. y  . C. y  2  . D. y  . x x 3 x x
Câu 11: Tìm mệnh đề sai trong các mệnh đề sau: A. Hàm số n
y  x (n  , n  2) có đạo hàm trên  và 1 ' n y x   .
B. Hàm số hằng y  c có đạo hàm trên  và y '  0 .
C. Hàm số y  x có đạo hàm trên  và y '  1 . 1
D. Hàm số y 
x có đạo hàm trên khoảng (0; ) và y '  . 2 x
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , SA vuông góc với mặt phẳng đáy. Tìm khẳng định đúng.
A. AB  SBC  .
B. AC  SBC 
C. BC  SAB .
D. BC  SAC  . Phần II: Tự luận 2017x  2 4  x
Câu 13: Tính các giới hạn sau: a) lim . b) lim . x x  2016 2 x4 x 16 Câu 14: Cho hàm số 4 2
y  2x  3x  3 có đồ thị C  .
a) Giải phương trình y ' x  0 .
b) Viết phương trình tiếp tuyến của đồ thị C  tại điểm có hoành độ bằng 1. 1 17
c) Chứng minh rằng đường thẳng d  : y  x 
cắt đồ thị C  tại bốn điểm phân biệt. 2 5
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh x , SC vuông góc với mặt phẳng
 ABCD và SC  x 7 . Gọi O là giao điểm của AC, BD .
a) Chứng minh rằng BD vuông góc với mặt phẳng  SAC  .
b) Xác định và tính góc giữa đường thẳng SO và  ABCD .
c) Tính khoảng cách giữa hai đường thẳng SO và AD . HẾT. PH ĐỀ SỐ 1 ĐI ĐỀ SỐ 2 ẦN Ể M I-TN 1 2 3 4 5 6 7 8 9 10 1 1 3,0 1 2 3 4 5 6 7 8 9 10 1 1 1 2 1 2 A C B C A C A D D D B C C A C A B B B C D D A D 2016x 1 2017 x  2 Câu 13a) lim  2016 . Câu 13a) lim  2017. x x  3 0,5 x x  2016 Câu 13b) Câu 13b) II- 3  x  x  3 1  1  4  x  x  4 1  1  TL lim  lim  lim  . lim  lim  lim  . 2 1.0 x3 x 3 x  9
  x  3 x  3 x3 x  3 6 2 x4 x4 x 16
 x  4 x  4 x4 x  4 8 Câu 14a) Câu 14a) 6 1,5 3 y  x 3 '
 4x  6x ; y ' x  0  x  0; x   . y  x 3 '  8
 x  6x ; y ' x  0  x  0; x   . 2 2
Câu 14b) y   1  4  ; y '  1  2   y  2  x  2.
1,0 Câu 14b) y   1  2; y '  1  2   y  2  x  4. Câu 14*c) Câu 14*c) +) Xét: +) Xét: 5 1 17 4 2 4 2
x  3x  2  x 
 2x  6x  2x  1  0. 4 2 4 2
2x  3x  3  x 
 20x  30x  5x  4  0. 2 2 5
+) Đặt: f  x 4 2
 2x  6x  2x  1  0.
+) Hàm số y  f  x liên tục trên các đoạn
+) Đặt: f  x 4 2  2
 0x  30x  5x  4  0.
+) Hàm số y  f  x liên tục trên các đoạn  3   1   1   3   ; 1  , 1; , 0; , ; 2 và 2           2   2   2   3   1   1   3   ; 1   ,  ;0 , ;1 , 1;       và  3   1   2   2   2   2  f  . f     1  0; f   1 . f   0;    2   2  0,5  3   1  f  . f     1  0; f  . f   0  0;  1   3   2   2  f 0. f  0; f . f     2  0.  2   2   1   3  f f     1  0; f   1 . f  0.  
+) Do đó, phương trình f  x  0 có bốn nghiệm  2   2  thuộc các khoảng
+) Do đó, phương trình f  x  0 có bốn nghiệm  3   1   1   3   3   1   1   3   ; 1 , 1;  , 0; , ; 2 .        
thuộc các khoảng  ;1 ,  ;0 , ;1 , 1; .          2   2   2   2   2   2   2   2  Câu 15 Câu 15 BD  AC  AC  BD 
a) BD  SC  
a) AC  SB 1,0 
 BD  SAC .
 AC   SBD.
Câu 15b) + Góc cần tìm:  SOB .
Câu 15b) + Góc cần tìm:  SOC . SB a +  2 tan SOB   a 5 :  10. SC x +  2 tan SOC   x 7 :  14. OB 2 OC 2 Câu 15c*) Câu 15c*) 0,5 d  S ;
O CD  d C ;
D SGF   d C;SFG d  S ;
O AD  d  A ;
D  SGF   d  ; A SFG  d  ;
B  SFG  BH
 d C;SFG  CH 1 1 1 1 4 105 203      BH  . a 1 1 1 1 4 2 2 2 2 2      CH  . x BH SB BG 5a a 21 2 2 2 2 2 CH SC CG 7x x 29 105 Vậy: d S ; O CD  . a 1,0 203 Vậy: d S ; O AD  . x 21 29