Đề thi HK2 Toán 12 năm 2020 – 2021 trường Năng khiếu TDTT Bình Chánh – TP HCM

sOiIAoD

VA DAO TiO TP HO CHI M[NI-I

T

TR

FoE CHINH THIJ'C

ANG KHIEU TDTT H.BC

luEM TRA HQC Kill— NAM HQC 2020 — 2021

MON TOAN HQC — KHOI 12

Thô'i gian lam bài : 90 phüt

TIU

C iO TIÔN

NA KTl11it

B1N

HAI11

MADE

121

TU H

NAN K

Phãn I. TRAC NGHIEM:

(32 cliii, 08

diem; môi câu 0,25 diem)

Câu 1:

x = 2 + 7t

Trong không gian Oxyz, cho duing thang

(s): y = —

1 + t (t

E

I).

z

= 6— 8t

Mt vectx chi phtrcmg

cüa

(is)

là:

A.

ii = (7,0,

—8)

B.

ii

= (2, —1,6)

C.

11 =

(2,1,6)

Câu 2:

Clio s phtrc

z

= 2 + 1. Tich cüa

z

và 51 bang:

A. z.51=5+l0i

B. z.51=-5-1Oi

C.

z.51=5—lOi

Cãu 3:

Cho

so

plirc

z

= —6 + 81. Modul cia

z

là:

A.

Izi

=

10

B.

IzI

=

C.

zl = 8

Cãu4:

Nghim cCa phuong trinh

z

— 41 = 9 là:

A. z=9-41

B.

z=9+41

C.

z=-9+41

Câu 5: Giá trj

cüa

tIch phán f

1

2

(3

+

4x)dx

là:

A.1

B. 2

C. 3

1).

u

= (7,1, —8)

D.

z.51=-5+101

D.

IzI

=

6

D.

z-9-41

D.

4

Câu6: Trong không gian Oxyz, cho mt phng

(P): x

— 3y + 5z + 2 = 0. Mt vectc pháp tuyn

cüa

ciia (P) là:

A.

if

=

(1,

—3,5)

B.

ff

=

(0,

—3,2)

C.

ff

=

(1,

—3,2)

D.

ff

=

(1,3,5)

Câu 7: Trong không gian Oxyz, cho mt cu

(S): (x — 2)

2

+ y

2

+

(z

+

3)2

100. Ban kInh

cüa

(S)

là:

A. R=10

B. R=100

C. R=5

D. R=20

Câu8: Cho

hai

s phác

z

1

= 3 +

t và

z2

= 1

—

1. Hiu cUa

hai

s6

ph(rc nay là:

A.

z

1

—z

2

=2-21

B.

z

1

—z

2

=2+2i

C.

z1

—z

2

=2

D.

z

1

—z

2

=4

Can

9: Cho

hal s phüc

z

1

= 4 —

I

và

z

2

= 3 + 21. Tng cüa hal s ph(ic nà là:

A.

z1

-l-z

2

=7—i

B.

z

1

+z

7

=1

-31

C.

z

1

+z

2

=7+i

D.

z

1

+z

2

=

-1-31

Can 10: Cho s

phcrc

z

= 1 + 41. SE,

phüc lien hp

cüa

z

là:

A.

=-1+4i B.

=-1-4i

C. =1+4i

D. =1-4i

1/4Mädê 121

Câu 11:

((C):y

= f(x)

Cho hinh phng

(H):

(a <b).

Quay hinh

(H)

quanh tri,ic

Ox

&rçic khM Iron xoay

(T).

Cong th(rc tInh th

tIch cüa

(T)

là:

A.

V=

ff(x)dx

B.

V=Jf

2

(

x

)d

x

C.

V=flfx)dx

D.

V=ff

2

(

x

)d

x

Cãu 12:

Cho s

phirc

z

= 7 — 31. Phn thi,rc cia

z

là:

A.

a=-3

B.

a=-31

C.

a=7

D.

a=31

Cãu 13:

Trong khOng

gian Oxyz, cho mt phng

(P): x

— y —

3z + 9

= 0. T9a d

mt diem thuc

(P)

là:

A.

A(0,0,2)

B.

B(0,0,3)

C.

C(1,0,0)

D.

D(-2,0,0)

Câu 14:

Cho s

phirc

z

thda

— 2 = 121. Khi dO,

z

— 1 bang:

A.

—1 — 121

B.

1

+

121

C.

1

— 121

D.

—1 + 121

Câu 15: Cho

so

phirc

z

thOa

Izi

= 8.

l'p

hçip

các dim biu din cho

z

là:

A.

Dumg trOn

(C)

có tam 0(0,0), ban kmnh

R

= 8

B.

DuOng trOn

(C)

có tam 0(0,0), ban kInh

R

= 4

C.

£hr&ng trOn

(C)

CO tam 0(0,0), bàn kInh

R

= 16

D.

Du&ng trOn

(C)

cO tam 0(0,0), ban kmnh

R

= 2

Câu 16: Trong không gian

Oxyz, cho dim

A(1,2,0)

và mt phng

(P):

2x + y —

2z +

5 =

0. Khoãng oách tr

A

dn

(P)

bang:

A.1

B. 2

C. 3

D. 4

Câu

17: Cho s phác

2

= 3 + 4i. S6 phixc nghjch

dâo càa

z

là:

A.

B.

__

z

25 25

z

25 25

1 3 4

C.

D.

Câu 18:

Cho tIch phOn

I

f

3

1

(

x

2

+

4)

5

xdx.

Khi dat t =

x

2

+

4 thi:

A.

xdx=dt

B.

xdx=—dt

C.

xcix

=

cit

D.

xcix

=

2dt

Cau 19: Cho hInh phAng

(H):

f

(

C

)

:

i f(x)

=

x

2

Quay hinh

(H)

quanh tric

Ox

&rçic khi trOn xoay

(T).

Cong thtrc tInh th tIch cUa

(T)

là:

2/4Mäd 121

C.

x+1

y+2

z-3

D.

(A'):

3

—2

2

(Af):C1=1=Z1

—3

—2

2

3/4MAd 121

A.

V= flx

2

_41dx

B.

V=

f(

x

2_4)2d

x

-2

C.

V=rr

f

(

x

2

-4)dx

D.

V=f(

x

2_4)

2

d

x

Câu 20:

Cho s

phirc

z

thóa

= 3

+ 21.

S

di cüa

s6

phrc

z

là:

A. -z=3-21

B. -z=3+21

C. -z=-3+21

D. -z=-3-2i

2

Cãu 21: Biêt

f'

-dx

= +

n In

2,

vo'i

m,n là cac s6

nguyen. TInh rn +

n?

0 x+1

A.

S=4

B. S=1

C. S=-5

D. S=-1

Câu 22: Cho s ph(rc

z

= x +

yUx,y

E

R) thöa man (1 + 2i) +

z

= 3 - 41.

TInh giá trj cüa biu thirc S = 3x -

2y.

A. S = -12

B. S = -10

C. S = -11

D. S = -13

Câu 23:

Phucmg trInh bc hai

z

2

+

mz

+

n

= 0 nhân hai

s6

phirc 2 - 31 và 2 + 31 là nghim. Hói giá tn cUa m?

A.4

B. 13

C. 3

D.

-4

Câu 24:

Co bao nhiêu

s6

ph(rc thoã

Izi

= '/

và

(z

+ 2i)( -2) là s thu.n áo?

A. 2

B. 1

C. 4

D. 0

Câu 5: Cho s6 phic z thoã man

Iz

+ I +

ii

I

- 2i. TIm giá trj nhô nh.t cüa tzl?

A._

B.

C.

I

D.

Câu 26: Trong không gian Oxyz, tim tt cá các giá trj cüa tham s m d dtring th&ng

d:

= =

song song

vimtphâng(P):2x+y-m

2

z+m=0

A. m=2hoäcm=-2

B. in=2

C.

m

= -2

D. Khong có giá tr nào clia m

Câu 27:

TInh tng S cüa các phn thrc c1ia tt

câ các

so

phirc z thoã diu kin =

-

sJz

2

A. S=0

B.

3

Câu 28: Tinh giá trj cüa

I

= (1 + i)

2018

A.

I

= 2

1009

B.

I

= 2

2018

C.

s=V

D.

C.

I

= 2'°°i

D.

I

= 2

2018

1

Câu29:

x=2+t

Trong khong gian

Oxyz,

cho &rng th&ng (A): y = 1

(t E fl)

và

mt phng

z

= 1 + 4t

(P): x + y

-

z

- 2 = 0. Phucmg trinh duing th&ng (A') d6i thng vói du'&ng thng (A) qua mp

(P)

là:

A.

(A

!

)

,xlYZ

3

B. (/)x+1Y+1z±1

3

-2 -2

3

2

4

C)fl

:

'I

D.

lOir(cm

3

)

6

cm

Câu 30:

Trong không gian Oxyz, cho mt cu don vj (S). Phuong trInh các mt phng song song vài Ox,vuông

góc

voi

(Oxz)

va

tip xác v&i (S) là:

A. (P):x+2=Ovà(Q):x-2=O

B.

(P):x+2=Ovà(Q):x-2=0

C. (P):y+1=Ovà(Q):y-1=O

D.

(P):z+1=Ova(Q):z-1=0

Câu 31: Mt chic

ly (nhwhlnh vêbên cgnh) có

dumg kInh cüa ming lylà 4cm và chiu cao là 6cm.

Bit thit din cüa ly và mt phng qua tri,ic có vin AIB là môt phn

ctia parabol. Th tIch cCia ly là:

A. 6ir(crn

3

)

B. l2ir(cm

3

)

C.

81r(cm

3

)

Can 32: Cho X là $p hop tt cà cac s phtrc

z

có phn thi,rc và phn áo không vuqt

qua

4, dng thai tng cüa

phn thijc vói phn áo không nhO han 6. GQi

m

là modul nhô nht cüa các s phuic trong X và

M

là

modul lan nht ciia các

s6

ph(rc trong X. Giá trj

m + M

bang:

A. 9'/

•

B.

7V

C. 3f

D.

Phãn II.

TU

LUAN: (02 câu, 02 dkm)

Cãu 1: (1,0

diem)

Trong tp

s6

phüc C:

a) Cho

s6

z

= 9 — 21. TInh hiu cUa phan thirc vth pMn áo cüa z;

b)Chos6z=x+yi cOx,y E Rvàx— 1+yi = 2i.TInhI.iI.

Cáu

2:

(1,0 dim)

Trong không gian Oxyz:

a) Cho diiông thng (iX) qua dim

A

(2, — 1,0) và có vec to chi phrang ii = (1,0, —3).

Vit phrang trinh tham s cüa

(Lx);

x=3t

b)TImgiaodiemlcUadu?xngthang(d): y=0 vàmtphäng(P):x+y—z-6 = 0.

z=0

...Hêt...

Ho ten HS

S báo

danh

Lóp

4/4Mãd 121

SC GIAO DI)C VA DAO

T4O

TP HO CHI MINH

TRNGT NANG KHIEU TDTT H.BC

E

CHINH THU'C

KIEM TRA HOC

K II— NAM

HQC

2020 —2021

MON TOAN HOC—KilO! 12

ThOi gian

lam

bai: 90 phüt

MADE 122

Phãn

I.

TRAC NGHIEM:

(32 câu, 08 diem; môi

call

0,25 diem)

Cãu 1:

Clio hInli pliang

(H):

(C):y = f(x)

Ox

(a < b). Quay

hInh

(H)

quanh tn,ic

Ox

ducvc khOi trôn xoay

x=a

(T).

Cong thc tInh th tIch

ctia (T)

là:

A.

V= ff(x)dx

B.

V=Jf

2

(

x

)d

x

C.

v=flfxldx

D.

V=ff

2

(

x

)d

x

Cãu 2: Cho

so

phüc

z

= 2 + 1. TIch

c"ia z

và 51 bang:

A. z.51=5+lOi

B. z.51=5-101

C. z.51=-5+l0i

D. z.51-5—lOi

Câu3:

x=2+7t

Trong khOng gian Oxyz, cho duàng thang (A): y = —1 +

t (t E ll).

z

= 6— 8t

Môt vecto clii phuoiig cüa (A) là:

A.

i = (2, —1,6)

B.

u

= (

7,1, —8)

C.

Z = (

2,1,6)

D. ii = (

7,0, —8)

Câu 4:

Cho

so

phirc

z

= 1 + 41. SO phüc

lien

hcp

cüaz

là:

A. =-1-4t B. =1+4i

C. =-1+4i

D. =1-4i

Câu 5:

Cho s phc

z

=

7 —

31. Plin thiic cüa

z

là:

A. a=-31

B. a=7

C. a=-3

D. a=3i

Câu 6:

Cho hai

s6

phüc

z1

= 4 —

i

và

z

2

= 3 +

21. Tang cüa hai s plirc

nay

là:

A.

z

1

+z

2

=7—i

B.

z

1

+z2=

-1-3i

C.

z

1

+z

2

=7+i

D.

z

1

+z

2

=1-31

Câu

7: Nghirn c6a phuang trInli

z

—

41 = 9

là:

A. z=9-41

B.

z=-9+41

C. z=-9-41

D. z=9+41

Câu 8:

Cho s phrc

z

= —6 +

81.

Modul ci1a

z

là:

A.

IzI

= 10

B.

Iz!

= viii

C.

IzI

= 8

D.

IzI

=

6

Câu 9:

Giá trj cüa tIch phãn

1'2(

+ 4x)dx

là:

A.1

B. 2

C. 3

D. 4

Cãu 10:

Trong khong gian Oxyz, cho mat phang

(P): x

— 3y + 5z + 2 = 0.

1/4 Ma d 122

MOt vect pháp tuyn cüa ct'ia (P) là:

A.

T = (0, —3,2)

B.

= (

1,3,5)

C. 1

(1, —3,5)

D.

= (1,

—3,2)

Câu 11:

Trong không

gian

Oxyz, cho

that

ciu (S): (x —

2)2 + y

2

+ (z + 3)2 =

100. Bàn kInh cia (S) là:

A.

R=10

B.

R=100

C. R=5

D.

R=20

Can

12: Cho

hal s phrc

z1

= 3 +

i

và

2

= 1 — i.

Hiu

cüa hai

s6

ph(rc nay là:

A.

z

1

—z

2

=2+21

B.

z

1

—z

2

=2-21

C.

z

1

—z

2

=2

D.

z

1

—z

2

=4

Càu 13: Cho s

phüc

z

thOa

IzI

= 8. Tp

hcip các dim biu din cho

z

là:

A.

Di.r?rng trOn

(C)

có tam 0(0,0), ban kInh

R = 16

B.

Dtthng trôn

(C)

có tam 0(0,0), ban kInh

R = 4

C.

Dtrng trOn

(C)

có tam

0(0,0),

ban kInh

R = 8

D.

Dithng trOn

(C)

cO tam 0(0,0), ban kInh

R = 2

Can

14:

Cho tIch phân

I

=

f

3

1

(x

2

+ 4)

5

xdx.

Khi dt

t =

x

2

+ 4

thI:

A.

xdx = —dt

B.

xcix

=

2dt

C. xdx=dt

1

D.

xdx=—dt

Câu 15:

Cho s phirc

z

= 3 +

41.

S phirc nghjch dào ciiia

z

là:

A. 1_ 3

4.

B. 1

3 4

C. 13

4

•

D. 1

3 4

.

Can

16:

Cho

s6

ph(rc

z

thOa — 2 =

121.

Khi do,

z

— 1 bng:

A. —1 + 12i

B. 1 —

121

C. 1 + 121

D. —1 — 12i

Cáu 17:

Cho s phtc

z

thOa =

3 +

21. S di cüa s phüc

z

là:

A.

—z=3+21

B. —z=-3-21

C. —z=3-21

D.

—z=-3+21

Câu 18:

Cho hInh phng

(H):

1(C): ' = f(x) =

x

2

— •

Quay hmnh

(H)

quanh tic

Ox

ducc khi trOn xoay

(.Ox

(T).

Cong thrc tInh th tIch cCia

(T)

là:

A.

V=f(

x

2

_4)

2

d

x

B.

V=f(

x

2

_4)

2

d

x

C.

v=fIx

2

_41d

x

P.

V=T

f(x

2

— 4)x

Câu 19: Trong không gian

Oxyz, cho

nit

pling

(P): x

— y —

3z + 9

= 0. Tça dO mt dim thuOc

(P)

là;

A.

B(0,0,3)

B.

A(0,O,2)

C. C(1,0,0)

D.

D(-2,0,0)

Cau

20:

Trong không

gian

Oxyz, cho diôm

A(1,2,O)

Va mat

phang

(P):

2x + y —

2z +

5 = 0. Khoáng cacti

tü

A

dn

(P)

bang:

2/4Mäd 122

A.1

B.

3

C.

2

D.

4

Cãu 21: PhtrcingtrInh bc haiz

2

+

mz + n

=

0 nhnhai

s6

ph(rc 2 — 3i và 2

+ 3i là iigliim.

HOi giá frj cüa m?

A.-4

B. 4

C. 3

D. 13

Cãu 22: Bit

f1

dx = — + n In

2,

vol

m, n

là các s nguyen. TInh

m +

n?

Ox+1

m

A. S=-5

B. S=1

C. S=-1

D. S=4

Câu 23: Tinh giá tn cOa

I

= (1 +

i

)

2018

A.

I

= 2

2018

i

B.

I

= 2

201

8

C.

I

= 2

1009

D.

I

= 2'

°°9

L

Câu 24: TInh tang

S

cOa các phn thuc cUa tt cã các sé ph(ic

z

thoã diu kin

=

A. S=/

B.

3

C. S=O

2

D.

Câu 25:

Cho

s6

phüc

z

=

x + yi(x,y

e

R)

thöa

mAn (1

+

2i) +

z

= 3 —

4i.

TInh giá trj cüa biu thrc S = 3x — 2y.

A. S=-12

B. S=-11

C. S=-13

D. S=-10

Câu 26: Trong không gian Oxyz, tim tt cà cac giá trj cña tham

s6

m d du&ng thing

d.

= =

sor

ong

song vri

mt

phâng

(P):

2x + y —

m

2

z

+ m

= 0

TAL/UNa

A.

Không có giá frj

nào

ca m

B.

m

=

2

C.

tie.

-

h. iIIJI' Ill

-

15.

III.

-

—

. — —

. —

LU TDTT

Câu27: Cóbaonhiêus phácthoaIzI

=

'

I

vA (z +

2i)(

—

2)Iàsthunâo?

*

B. 2

C. 4

D. 0

CAu 28: Cho s phüc zthoâmän

Iz

+ I + i = — 211. Tim giátrj nhOnhtcüa

Izi?

A.

B._!

C.!

D.

_i

2

CAu29:

x=2+t

Trong khong gian

Oxyz,

cho duOng thing (h): y = 1

(t

E

IR)

và mt phAng

z

= 1 + 4t

(P): x

+ y

—

z

— 2 = 0. Phixcng trInh dithng thâng

(ia')

di xfrng vói &rmg th&ng

()

qua mp

(P)

là:

A.

:

X+t

=

Y

+t

B.

(E)X+lY+2Z3

3

2

3

—2

2

C.

(L

f

):

Xl

=

Y

2

=

Z+3

D.

(f).X1=1=z1

3 —2 —2

—3 —2 2

Câu 30: Trong không gian Oxyz, cho mt cu dcm

vj (S).

Phucvng trinh các mt ph&ng song song vài

Ox,

vuông

góc vâi

(Oxz)

và tip xic vâi (S) là:

A.

(P):x+20va(Q):x-20

B.

(P):x+2=Ova(Q):x-20

C. (P):y+1=0và(Q):y-10

D. (P):z+1=Ovà(Q):z-10

3/4Mãdê 122

Câu 31:

MOt

chic

ly (nhw hmnh ye ben canh) có

dtr&ng kInh cüa ming ly là 4cm và

chiu cao là 6cm. Bitt thit din cüa ly và

mat

ph&ng qua tri,jc có vin AIB

là mt phAn cüa parabol. Th tIch ctia ly là:

A. 6ir(cm

3

)

B.

l2ir(cm

3

)

C. 8ir(cm

3

)

D. lOir(cm

3

)

Câu 32:

Cho X là tp hqp tt câ các s ph(rc

z

có phn th,rc và phAn ào không vuçlt qua 4, dng thri tng cüa

phn thirc vài phn ão không nhö hcm 6. Goi

m

là modul nhô nht cüa các s phüc trong X và

M

là

modul Ian nht cüa các

s6

phic trong X. Giá trj

m + M

bang:

A. 9V

B.

7

\

I

C. 3/

D. 5/

Phân II. TI) LUN:

(02 câu, 02 dim)

Câu 1: (1,0 dim)

Trong tp

s6

phirc C:

a) Cho

s6

z

=

—

7 +

41. TInh hiu cüa phn áo vài ph.n thc cüa z;

b)Chosiz=x+yt cóx,yERvà3x+yi =4LTInhI+iI.

Câu 2: (1,0 dim)

Trong không gian Oxyz:

a)

Cho dträng th.ng

(is)

qua dim

ACt,

—2,0) vã Co vec to chi phi.rong

i1

= (3,0, —1).

Vit phtrong trinh tham s cüa (is);

x=0

b)

Tim giao dim

I

cña rmg thang

(d):

y = 2t và

mat

phäng

(P): x

+ y +

z

— 4 = 0.

z=0

...Hét...

Ho

ten HS

So bao

danh

LOp

4/4 M d 122

TR1I

N

- TBLJKC

BO

NNG KH'EU TTT

NH fAAHi/.,

*

sO

GIAo

DVC

VA

DAO TAO TP HO cHi MIINH

IRIS IeT NANG KrnEU TDTT H.BC

FoE

CHINH THC

JuEM TRA HQC Kill

—

NAM HQC 2020 —2021

MON TOAN I1QC — KIIOI 12

Thôi gian lam bãi: 90 phñt

MA BE 123

Phân I.

TRAC NGHIEM:

(32

câu, 08 diem;

môi câu

0,25 diCni)

Cãul:

x=2+7t

Trong không

gian Oxyz, cho &rông thAng

(a):

= -

1 + t

(t E

ll).

z

6— 8t

Mt vect

chi phixcmg cüa (IX) là:

A.

Z = (2,1,6)

B.

i

(2, —1,6)

C.

7

= (7,0, —8)

D.

u

= (7,1,-8)

Câu 2:

Cho hai

s6

phrc

z

1

4

—

i va

z

2

= 3 + 2i.

Tng

cia hai s

ph6

,

c nay là:

A.

z

1

+z

2

=1

-31

B.

z

1

+z

2

=-1-3i

C

z

1

+z

2

=7—i

D.

z

1

+z

2

=7+i

-'

Câu3:

Trong không gian Oxyz,

cho mat cAu (S): (x — 2)

2

+ y

2

+

(z

+ 3)2 = 100. Bàn kInli cfia (S) là:

A.

R

=

5

B.

R

= 20

C.

R = 100

1).

R = 10

Cãu 4:

Cho

s6

phc

z

= —6 + 8i.

Modul cia

z

là:

A.

jzl = 10

B.

IzI

=

6

C.

IzI

=

D.

Iz!

=

8

Câu 5:

Cho s

phrc

z

= 2 +

1. Tich cUa

z

và

Si

bang:

A.

z.51=-5—lOi

B.

z.5i=5—l0i

C.

z.5i=5+lOi

D.

z.5i=-5+lOi

Câu 6:

Trong không gian Oxyz,

cho mt phng

(P): x

— 3y +

5z +

2 =

0. Mt vectci pháp tuyn cCia cüa (P) là:

A.

ff

=

(1,3,5)

B.

= (1, —3,2)

C.

=

(0, —3,2)

D.

ff

= (1,

—3,5)

Câu

7:

Cho

so

ph'rc

z

= 7 — 3i. PhAn tic cüa

z

là:

A.

a=-3

B.

a=-3i

C.

a=7

D.

a=31

Câu8:

Chohais6ph6cz

1

=

3+ivàz

2

=

1—i.HiucüahaisOphCrcnàylà:

A.

z

1

—z

2

=2-2i

B.

z

1

—z

2

=2

C.

z

1

—z

2

=2+21

D.

z

1

—z

2

=4

Câu

9:

((C):y

=

fx)

Cho hinh ph&ng

(H):

Ox

(a < b).

Quay hinh

(H)

quanh

tric

Ox

&rçc

khi

trOn xoay

(T).

Cong thfrc tInh th tIch cia

(T)

là:

A. V=Jf

2

(

x

)d

x

B.

v=flf(x)Idx

c.

v=

ff(x)dx

D. v=Jf

2

(

x

)d

x

1/4Mãdê 123

Cãu 10: Cho s phcrc

z

= 1 + 41.

S6

phc lien hp ciia

z

là:

A.

=1-4i

B. =-1+4i

C. =1+4i

D.

=-1-4i

Câu 11:

Giá trj cia tIch phân 1

1

2

(3 +

4x)dx là:

A.2

B. 3

C. I

D. 4

Câu 12:

Nghim cia phtrng trinh

z

— 41 = 9 là:

A. z=9-4i

B.

z=-9-41

C.

z=9+4i

D.

z=-9+41

Câu 13:

Cho s phirc

z

= 3 +

41. S

phCrc nghjch dáo cia

z

là:

A.

1 3 4

13 4

—+i

B.

C.

3

4

.

D.

z

25 25

Câu 14: Cho s phic

z

thOa

IzI

8. Tp hcip các dim biu din cho

z

là:

A.

Di.r?ng trôn

(C)

có

tam 0(0,0), ban kInh

R = 8

B.

Di.thng trOn

(C)

có

tam 0(0,0), ban kInh

R = 2

C.

Dithng trOn

(C)

có

tam

0(0,0),

ban kInh

R = 4

D.

Du&ng trOn

(C)

có tam 0(0,0), ban kinh

R = 16

Câu 15: Trong không gian Oxyz, cho mt phng

(P): x

— y —

3z + 9

= 0. TQa d mt dim thuc

(P)

là:

A.

D(-2,0,0)

B.

A(0,0,2)

C. B(0,0,3)

D. C(1,0,0)

Cãu 16:

Cho tIch phân

I

= f

3

1

(

x

2

+

4)

5

xdx.

Khi dat

t =

x

2

+ 4

thi:

A.

xdx =

dt

B.

xcix =

—

dt

C. xdx =

cit

D.

xdx

=

2dt

Câu 17:

Cho s phüc

z

thia — 2 = 121. Khi do,

z

— 1 bng:

A.

—1+121

B. 1+121

C. —1-121

D. 1-121

C1Iu 18:

Cho hInh phang

(H):f' = f(x)

=

x

2

— Quay hInh

(H)

quanh triic

Ox

ducxc khM trOn xoay

(T).

'

Ox

Cong thfrc tInh th tIch cia

(T)

là:

A.

V=

f(

x

2

_4)

2

d

x

B.

v

=

f(x2

—4)2dx

-2

C.

V=fj

x

2

_4ld

x

D.

V=ir

f

(

x

2

—

4)dx

Câu 19:

Cho

s6

phi'rc

z

thOa

= 3 + 21.

s6

dM cia s phüc

z

là:

A.

—z=3-2i

B.

—z=-3+21

C.

—z=-3-21

D.

—z=3+2i

Can 20:

Trong không gian Oxyz, cho dim

A(1,2,0)

và mt

phAng

(P):

2x + y —

2z +

5 = 0. Khoàng each tü

A

dn

(P)

bang:

A.3

B. 4

C. 1

D. 2

Can 21:

Cho s phüc

z

= x +

yi(x,y

E

ll) thia man (1 + 2i) +

z

= 3 —

41.

Tinh giá tn cia biu thirc S = 3x — 2y.

2/4Mâd 123

'I

A. S = —12.

B. S = —11.

C. S = —13.

Can

22: Bi& f

1

_!d

x

=

+

n In

2,

vol

in, n là cac s nguyen. TInh

m + n?

0 x+1

m

A.

S=-5.

B. S=1.

C. 5=—i.

Câu 23: Cho s phüc z thoà mn

Iz

+ I +

ii = I

— 211. Tim giá trj nhô ithãt ciia

IzI?

D.

5=—b.

D. S=4.

A..

B.

c.

D.

—.

2

Cãu 24: Phisong trinh bc liai

z

2

+ rnz + n

=

0 nhn hai

s phüc 2 — 31 và 2 + 31 là nghim. HOi giá

tn cia m?

A. 13.

B. 4.

C.

3.

Câu25: TInhgiatrjcüal

=

(1+

)2018

A.

I =

2

2018

1.

B.

I =

2

1009

1

.

C.

I

=

2'°°'.

Can

26:

Co

bao

nhiêu

s6

phfrc thoá zl

= '/

và

(z +

21)( — 2) Ia

SO

thuAn ào?

B.

0.

C.

2.

B.

C. S=0.

Trong không gian

Oxyz, tim

tht

cã các giá fri cüa tham

so

m dê du?ng thing

d:

=

z-1

1

2

11 g song

A.4.

Câu 27: Tinh thng S ciXa các phn thc cüa

tht cã cac

s6

ph(rc z thoã diu kiin

=

A. S=.

Câu28:

D.

—4.

D.

I =

2

2018

.

D.

1.

D.

A.

-

C.

Câu29:

vài mAt phAng

(P):

2x + y —

m

2

z + m =

0

m =

—2.

B.

m=2.

m =

2 hoc

m

= —2.

D. Không cO giá trj nao cüa m.

MOt chik

ly (nhw hmnh

ye

ben cgnh)

co

dung kInh cüa ming ly là 4cm và

chiu cao là 6cm. Bitt thit din cUa ly và mt phng qua tric có

viM

AIB là

mt phM cüa parabol. Th tIch cia ly là:

cn:

C.

8rr(crn

3

)

M

D. l0ir(cm

3

)

A.

6ir(cm

3

)

B.

l2ir(cm

3

)

Câu 30: Trong không gian Oxyz, cho mt cAu dan vi (S).

Phuong tnlnh cac mt phâng song song vâi

Ox,

vuOng

B.

(P):x+2=ova(Q):x-2=0

D.

(P):x+20và(Q):x-20

A.

C.

Câu 31:

góc vâi

(Oxz)

va

tip xüc vài

(5)

là:

(P):z+1=

0và(Q):z— 1=0

(P):y+

1=0 và (Q):y— 1=0

(x =

2

+t

Trong không gian

Oxyz,

cho du?ing thang (A): y

=

1

(t

E

ll) và mt phang

(.z =

1 + 4t

(P): x + y

—

z

— 2

=

0. Phtrcmg trinh dtring thing (A')

di xtrng v&i durng thAng (A) qua mp

(P)

là:

A. (A):X+l=Y+2=Z3

3

—2

2

x+1 y+1 z+1

B. (A'):

=

2 —

2

C. (A'):

x-1 y+l z-1

D.

(A):Xl=Y2=Z+3

3

—2

—3

—2

2

3/4Mäd 123

Câu

32: Cho X là tp hcp tht cá các s6 phic

z

có phn thirc và phAn âo không vtrçit qua 4, d6ng thii tng eüa

phn

thLrc

voi plin áo khong nhô lioii 6. Goi

m

là modul nhó nht eüa các s phtc trong

X và M

là

modul lan

nht cüa các

s6 phic trong X. Giá trj

m

+ M

bAng:

A.

B. 7/

C. 3/

D. 5f

Phân II. TI)' LUAN:

(02 câu, 02 1k4n)

Can 1: (1,0

diem) Trong tp s phic C:

a) Cho s

z

=

9

— 2i. TInh hiu cüa phn th%rc vài phAn áo cUa z;

b)Chosz=x+yi cóx,yE lRvàx-1+yi = 2i.TinhI.iI.

Can

2:

(1,0 dim)

Trong không gian Oxyz:

a)

Cho duing th.ng

()

qua dim

A(2,

—1,0) và có vec tci chi phi.rcrng

ff

= (1,0, —3).

Vit phrcnig trInh tharn s cüa

(is);

x=3t

b)

TIm giao diem

i

cUa throng thang

(d):

y = 0 vàmt phang

(P):

x + y —

z

— 6 = 0.

z=0

.Hêt...

HQtênHS

Sôbáodanh

LOp

4/4 Mâd 123

sO

GIAO DIJC VA DAO TO TP HO CHI MINH

TRifI'

':

NANG KHIEU TDTT H.BC

E

CHiNH TH1

TRW'

(TJ6 it

TH

KIEM TRA HQC Kill

—

NAM HQC 2020 —2021

MON TOAN HQC — KIIOI 12

Thvi gian

lam

bài: 90 phñt

MADE 124

Phn I. TRAC NGHIM:

(32 câu, 08 diem

;

nii câu

0,25 diem,)

Câu 1: Nghim

cüa phi.rong trinh

z

— 41 = 9 là:

A.

z=9+41

B.

z=-9+41

C.

z=-9-41

ft

z=9-41

Cãu 2: Trong không gian Oxyz,

cho

mt phng

(P): x

— 3y

+

5z +

2 = 0. Mt vecta pháp tuyn cüa cüa

(P) là:

A.

if

= (1,3,5)

B. ii = (1,

—3,5)

C.

ff = (0, —3,2)

D.

ii = (1, —3,2)

Câu 3: Trong không gian

Oxyz, cho mt cu (S): (x — 2)

2

+

y

2

+ (z +

3)2 =

100. Ban kInh cUa

(S) là:

A.

R=5

B.

R=20

C. R=100

D.

R=10

Câu 4: Cho hai s phác

z1

= 3

+ I

vã

z

2

= 1 — 1.

Hiu cüa hal s

phlrc nay là:

A.

z

1

—z

2

=2+21

B.

z

1

—z

2

=2-21

C.

z

1

—z

2

=2

D.

z

1

—z

2

=4

Câu5:

x=2+7t

Trong không gian Oxyz, cho

&ràrng th&ng

(a): = -

1 +

t (t E

R).

z = 6-8t

-

,'

T1t

Mt vect chi phucing

cüa

(i')

là:

A.

ii =

(7,0,

—8)

B.

u

= (7,1,

—8)

C.

Câu 6: Giá trj cila tIch phãn

f

1

2

(3

+

4x)dx

là:

A.2

B.1

C.

Câu

7: Cho s ph(rc

z

= 1 + 41. S ph(rc lien hcip cüa

z

là:

A.

=1+4i

B.

=-1-4i C.

Clu 8: Cho s phic

z

= —6 + 81. Modul cUa

z

là:

A.

jzj

= 6

B.

IzI

=

C.

Câu 9: Cho

s6

ph&c

z

2 + 1. TIch cüa

z

và 51 bang:

A. z.51=-5+101 B.

z.51=5—lOt

C.

if

=

(2, —1,6)

D.

ii = (2,1,6)

D.

3

=-1+4i

D.

=1-4i

IzI = 10

IJ.

zl

=

8

z.51=-5-101

D.

z.51=5+lUi

Câu 10:

(C):y

= f(x)

Cho hinh phâng

(H):

a

(a <b).

Quay hinh

(H)

quanh tri,ic

Ox

ducrc khi trôn xoay

(T).

Cong thirc tInh th tIch cüa

(T)

là:

A.

V=flf(x)Idx

B.

v=f[

2

(

x

)d

x

1/4 Ma dé 124

C.

v=f[

2

(

x

)d

x

D.

V=

[f(x)dx

Câu

11:

Cho s

phrc

z

=

7

-

3i. Phin tlii,rc ella

z

là:

A.

a=

-

3

B.

a=31

C.

a=7

D.

a=-31

Câu 12:

Cho hai s phüc

z

1

4

-

I và

z

2

=

3 + 21. Tng

elm

hai s phüc nay là:

A.

z

1

+z

2

=1

-

31

B.

z

1

+z

2

=—l-31

C.

z

1

+z

2

=7—i

D.

z

1

+z

2

=7+j

Câu 13:

Cho

s

pliitc

z

thba jzl

=

8. Tp

hqp các dim biu din clio

z

là:

A.

DLr&ng trôn

(C)

có tam 0(0,0), ban

kInh

R

=

16

B.

DuOng trOn

(C)

cO tam 0(0,0), ban kInh

R

=

8

C.

DuingtrOn

(C)

cOtâm

0(0,0),

báii

kInh

R

=

4

D.

Dtr&ngtrOn

(C)

cótâm 0(0,0), bàn kmnh

R

=

2

Cãu 14:

Cho

s

phüc

z

thOa

-

2

=

121. Khi do,

z

-

1 bAng:

A.

—1

+

121

B.

1

+

121

C.

1

-

121

D.

—1

-

121

C1Iu 15:

Cho hInh phAng

(H):

{g):

'

=

f(x)

=

x

2

-

Quay hinh

(H)

quanh trc

Ox

ducic

khi

trOn xoay

(T).

Cong thlrc tInh th tIch cüa

(T)

là:

A.

V=lrf(x

2

_4)dx

B.

V=f(x

2

_4)

2

dx

C.

V=f(x

2

_4)

2

dx

D.

V=11x2_41dx

Càu 16:

Cho so

plilic

z

=

3 + 4i.

S

phic nghjch dão clia

z

là:

1

3

4

1

3

4

A.

—=----j

z

25

B.

_=__+_i

z

25

1

3

4

1

3

4

C

.

D.

-=------

z

25

z

25

Cáu 17:

Cho tIch phân

I

=

f31(x2

+

4)

5

xdx.

Khi dt t

=

x

2

+ 4 thi:

A.

xdx

=

-

dt

B.

xdx

=

—dt

C.

xdx

=

dt

D.

xdx

=

2dt

Cãu 18:

Trong

khOng gian Oxyz, cho

mat

phâng

(P):x

-

y

-

3z + 9

0.

Ta

dO mOt

dim

thuOc

(P)

là:

A.

D(-2,0,0)

B.

C(1,0,0)

C.

A(0,0,2)

D.

B(0,0,3)

Cãu 19:

Trong khong gian Oxyz, cho dim

A(1,2,0)

và

mat phng

(P):

2x + y

-

2z + S

=

0.

Khoãng

cachtlrAdn(P)bâng:

A.1

B.4

C.

3

D.

2

Câu 20:

Cho s6 phüc

z

thOa

=

3

~

21. S

di elm

s phüc

z

là:

2/4

Ma d 124

A. —z=3-2i

B. —z=-3-2i

C. -z=-3+2i

D. —

z=3+21

Câu 21:

Tmnh

giá

trj cüa

I

=

(1 +

i)

2018

A.

I

=

2

1009

.

B. /

=

2

2018

i.

C.

I

=

D.

I

=

2

1009

i.

Câu 22: Co bao nhiêu

s

phrc thoâ

Izi

=

\/

vã

(z

+ 2i)(

-

2) là

s

thun ào?

A. 4.

B. 0.

C. 2.

D. 1.

Câu 23: Trong không gian Oxyz, tim

tht

cã các giá trj cüa thain

s

m d

dtrng

thâng ci:

= =

song

song vi mt

phng

(P):

2x +

y

-

m

2

z + m

=

0

A. m=2.

B. m=

-

2.

C.

772

=

2 hoic

in

=

—

2,

D.

Không có giá trj nào cüa m.

Câu 24:

Cho

sé phrc

z

=

x

+

yi(x, y

E

IR) thOa

man (1 + 2i) +

z

=

3

-

4i.

TInh giá

trj cüa biu thrc

S

=

3x

-

2y.

A.

S

=

—

13.

B.

S

=

—12.

C.

S

=

—

ii.

D.

S

=

—

10.

Câu 25: Cho so

phrc z thoá mAn

Iz

+

I +

ii

=

-

2i.

TIm giá trj nhô nhAt cüa

Izi?

A.

.

B.

C.

_!•

D.

-~&

2

Cãu 26:

Phu'ong trInh bc hai

z2

+

mz

+

n

0

nhãn hal

s phüc 2

-

31 và 2 + 31 là nghim.

HOi giá tn

cüam?

-

A.

—4.

B. 13.

C. 3.

D.

4.

•.

Câu

27: Bit

J

---

dx

=

—i

+

ii

in

2, voi

ni, n

là cac sO nguyen.

TInh

m

+

n?

A. S=4.

B. S=1.

C. 5=—i.

D. S=-5.

Câu 28: TInh tOng S cüa các phn

thirc cüa tht

cà cac sO phirc z thoâ diu kin

=

A.

5=--.

B. S=.

C. S=v.

0. S0.

3

Cãu 29: Trong

không gian

Oxyz, cho mt cAu dcm vi

(5).

Phuong trinh

các

rntt phang song song vói

Ox,

vuông góc vâi

(Oxz)

và tip xüc vâi (S) là:

A. (P):y+1=Ovà(Q):y-1=0

B.

(P):x+2=ovà(Q):x-20

C.

(P):z+1=0và(Q):z-1=0

D.

(P):x+2=ovà(Q):x-2=0

Câu 30: Cho X là tp

hçip

tht

câ các sO phüc

z

cO phAn thrc và phAn âo không vuçlt qua 4, dng thai tOng

cüa phAn thrc vài phAn ào không nhO hon 6. GQi

m

là modul nhO nht cüa các

sO phirc

trong X và

M

là

modul

lan

nht cüa cac sO phIrc trong X. Giá

trj

m + M

b&ng:

A.

9'J

B. 7V

C. 3

-

I'

D. 5V

Câu

31: Mt chik

ly

'nhw hInh

ye

ben canh) CO

dtr?mg kInh ct:ia rniéng ly là 4cm

và chiu cao là 6cm. Bit thiOt din cüa ly và mt phng qua tn,ic có

viàn

AIB

là mt phn cüa parabol.

ThO tIch cüa ly là:

3/4 Ma dê 124

A.

l2it(cm

3

)

B.

6ir(cm

3

)

C.

8rr(cm

3

)

D.

lOir(crn

3

)

Cáu 32:

=

2

+t

Trong không gian

Oxyz,

cho thr?ing thing (s):

y =

1

(t

E

)

và mt phng

=

1 + 4t

A.

(P): x +

y —

z

— 2

= 0. Phuong trInh dung thng (s') d6i

xüng

vâi du&ng thng () qua mp

(P)

là:

x +

1 —

y

+ 2_

z

—3

(a'):

3

— —2 —

2

x+1

y+l

z+1

B.

(s'):

3

2 2

C.

x-1

1

L'

y+l

z-1

\

—3

—2

2

x-1

y-2

z+3

D.

(a'):

—2

Phân II. TT

LUN:

(02 câu, 02

dilm)

Câu 1: (1,0 dim)

Trong tp

s6

phirc C:

a)

Cho

S6

Z

=

—

7 +

41. Tinh hiu cüa ph.n àø vâi phAn thc cüa

z;

b)

Cho

s6

z

= x +

yi Co

x,y E R và 3x + yi = 4i. 11th

[

+ i.

Câu 2: (1,0 dim)

Trong không gian Oxyz:

a)

Cho dumg th.ng (LX) qua dim

A(1,

—2,0) và có vec tci chi phucing

ii

= (3,0, —1). Vit phircrng

trInh tham

s6

cUa

(s);

x=O

b)

TIm giao diem

i

cüa diRmg thang

(d):

y = 2t và m.t phang

(P): x +

y +

z

— 4 0.

z=0

...Hêt...

fly ten HS

So báo

danh

LOp

4/4 Ma

d 124

81N

SO GIAO

DLJC

VA DAO T4O TP. HCM

TRI1NtTI1PTNANG

KHIEU TDTT H.BC

/.7

TflUONG

DAP AN BE KIEM TRA HOC KIll

\

HANS

1IU 1DT1/

MON:

TOAN

12- NAM

HQC:

2020 — 2021

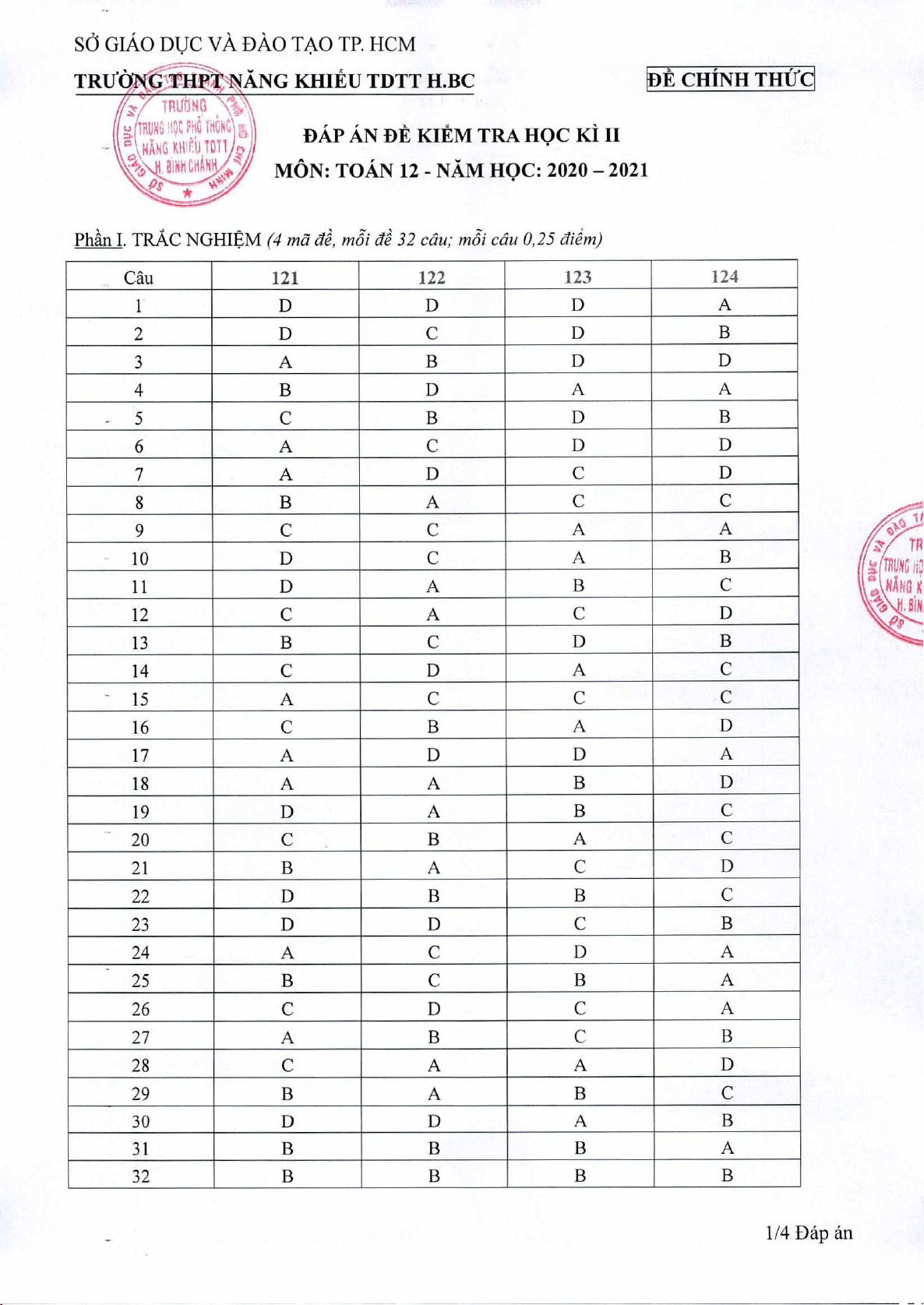
Phn I.

TRAC NGHIM

(4 ma d, m3'i d 32 cáu, mi cáu 0,25 diem,)

Câu

121

122

123

124

1

D

A

2

D

C

D

B

3

A

B

D

4

B

D

A

-5

C

B

D

B

6

A

C

D

7

A

D

C

D

8

B

A

C

9

C

A

10

D

C

A

B

11

D

A

B

C

12

C

A

C

D

13

B

C

D

B

14

C

D

A

C

-

15

A

C

16

C

B

A

D

17

A

D

A

18

A

B

D

19

D

A

B

C

20

C

B

A

C

21

B

A

C

D

22

D

B

C

23

D

C

B

24

A

C

D

A

25

B

C

B

A

26

C

D

C

A

27

A

B

C

B

28

C

A

D

29

B

A

B

C

30

D

A

B

31

B

A

32

B

BE

CHINH THUC

1/4Dápán

Phn II. TIJ LUAN (4

ma d, mi d 2 cóu; ini cau 1,0 dim,.)

Màd 121

Câu

Dáp an

Dim

(1,0dhm)

a) (ho séJ z

9 — 21. Tin/i

/i&u

cüaphân t/nrc vflp/iân âo cüa z.

0,5

Có:

fL

9

2

0,25

b)C/ios1z=x+yi cox,yEI1vax-1+yi=2LTinhI.iI.

0,5

Cóx_1+Yi=2i[

z=

1+2i

0,25

Nén I.ij = 1(1 — 2i)il = "/

0,25

2

(1,0dkm)

a)

(ho du'&ng tlzáng () qua them A(2, —1,0) và cO vec to c/il p/i u'o'ng

= (1, 0, —3). Vk4plzwong trinh t/iam

so

cüa

(is);

0,5

x =

x0 + u

1

t

Co (ix):

y =

Yo +

u2t (t

E ll).

z

=

z

0

+ u3t

0,25

Hay

(a):

x=2+t

y

= —

1 .

z=-3t

0,25

x3t

b)

Tim giao diem I cüa dithng 1/lang (d): y = 0 và m1p/iáng

z=0

(P):x+y—z-6

=

0.

0,5

Thay

x,y,z tr

pt

(d)

vào pt

(P):

3t + 0-0-6 = 0

t = 2

0,25

Thay t = 2 vão pt

(d):

x=6

y

= 0

1(6,0,0)

z=0

0,25

Ma d 122

Cãu

Dáp an

Dim

1

(7,0dkm)

a)

C/,o s

z = —7 + 41.

Tin/i

/iiu

cüa p/thu

ão váipIin thy'c

cüa

z;

0,5

Có: {

=

0,25

b—a=4—(-7)=11

0,25

b)

C'/,osz

=

x +yi cóx,y

E IRvà 3x+yi = 4i. Tin/i

+ fl.

0,5

Có3x+yi=4i[

z=4i

0,25

Nén

I+

Il = 1-41 +

Il

3

0,25

2/4 Dáp

an

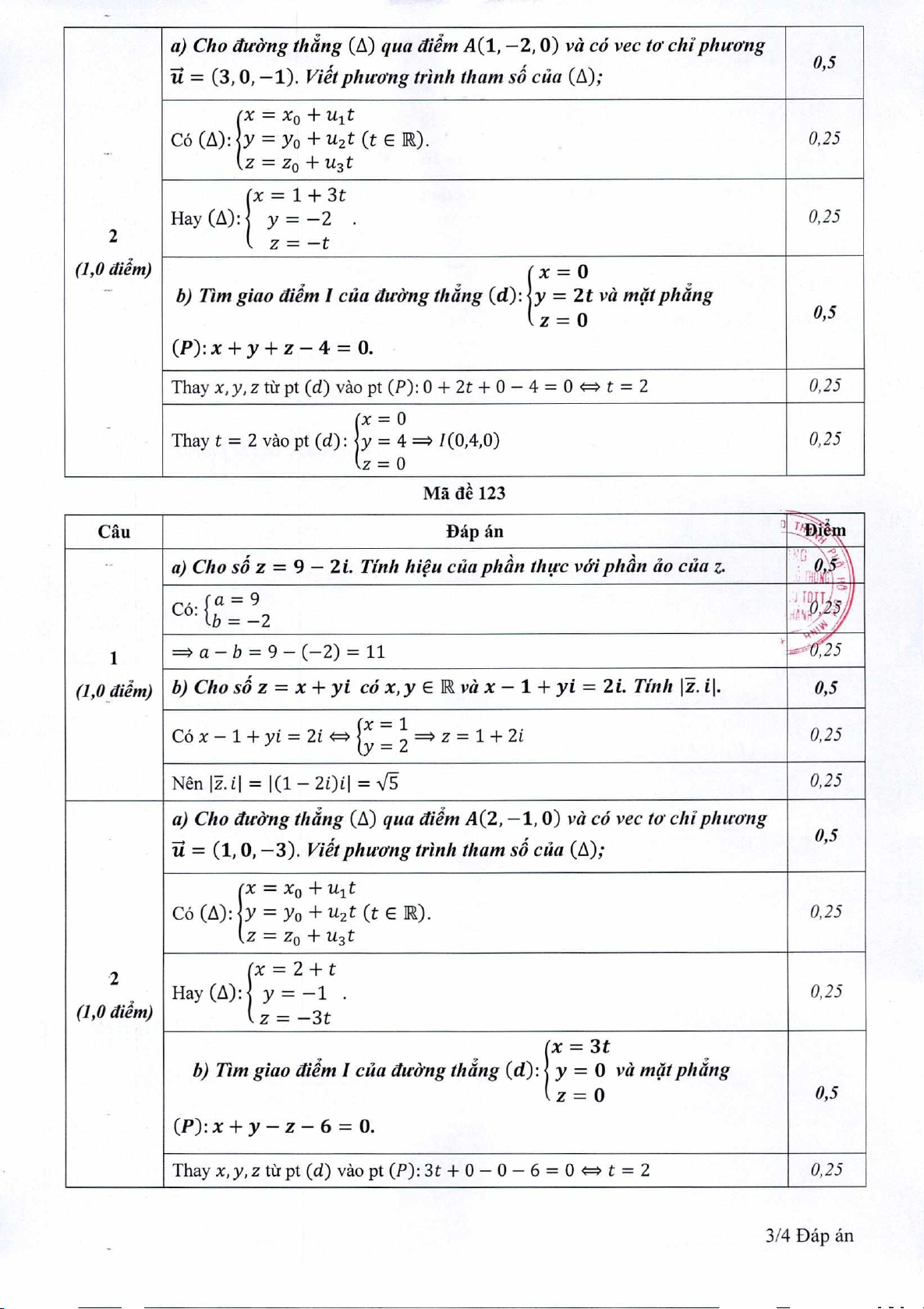
2

(1,0diEm)

a) Cho du*ng thing

(Lx)

qua dim A(1, —2,0) và

có

vec to ciii p/i wong

=

(3, 0, —1). VIut p/i uung trinh tham

so cüa

Co (a):

x =

x

0

+

u

1

t

y = Yo +

U

2

t (t

E IR).

z = z

0

+ u

3

t

0,25

x

= 1 +

3t

Hay

(ii):

y

= —2

.

z=

-

t

0,25

x=0

b) Tim giao diem I cüa dithng t/ung (d):

y =

2t và mtphàng

z=0

(P):x+y+z-4=

0.

0,5

Thay

x, y, z

t1r

pt

(d)

vào pt

(P):

0

+

2t + 0

—

4

= 0

t

= 2

0,25

Thayt=2vàopt(d):

x=0

y=4=i(O,4,O)

z=O

0,25

MA d 123

Câu

Dápán

(1,0dilm)

a)

Cho

so z

= 9

—

2i Tinh h,êu cüap/lân thur voiphân ao cüa z

Có:

[b=-2

=

'a

—

b

=9—

(

-2

)

=11

b)

Chosz

= x

+yi

cóx,y

E

IPvàx

—

1+ yi = 2i.

TIn/i

Iz.il.

0,5

lx=1

.

COX_l+Yl

=2=

ty2

Zl

+

2l

-

0,2

NenI.iI = I(1-2i)il =/

0,25

2

(1,0diêm)

a) Cho dithng tInng

()

qua dilm A(2, —1, 0) và

có vec to chIp/iuo'ng

=

(1, 0,

—3). Viltp/iu'o'ng trinh tham st cüa

(is);

Co

(Lx):

x =

x

0

+

u

1

t

3' = Yo

+ U

2

t (t E

ilk).

z = z

0

+ u

3

t

0,25

Hay

(ia):

x=2+t

= —1

.

= —

3t

0,25

x=3t

b) Tim giao diem I cüa du?rng t/làng (d):

y =

0 và intp/thng

z=0

(P):x+y—z-6=0.

0,5

Thay

x,y,z tl'lpt

(d)

vào

pt (P):

3t + 0-0-6 = 0

t

= 2

0,25

3/4 Dáp an

x=6

Thayt=2vàopt(d): y=O=I(6,O,O)

zO

Ma d 124

Câu

Báp

an

Diem

(1,0

diem)

a)

Cizo s z

=

—

7 +

4i. T:'nh /

,

u cdap/in do vóip/in t/,rc cda z;

0,5

Có: [

=

0,25

='b—a=4—(-7)=11

0,25

b)

C/jo

s z = x +

yi có

x, y E

và 3x

+

yi

=

4i. TInh

+ ii.

0,5

(x=O

Co

3x

+yL

=4

=t4=z=

4

L

0,25

NênI+i=I

-

4i+iI=3

0,25

2

('1,0

diem)

a) C/jo dud'ng t/zng (A) qua dkm A(1, —2, 0) vd có vec to' c/li p/i wo'ng

=

(3, 0, —1). Villphu'o'iig trInhi 1/jam st cda (A);

Có(A):

x =

x

0

+

u

1

t

y=y

0

+u

2

t(tEIR).

z

=

z

0

+

u

3

t

0,25

Hay (A):

x

= 1 + 3t

y = —2

0,25

b) Tim giao diem I cda dithng tiubig (d):

(P):x+y+z-4=0.

x

= 0

y =

2t vd m1p/iáng

z=0

0,5

Thay

x, y, z tü pt (d)

vào pt

(P):

0 + 2t + 0 —

4

= 0

t

2

0,25

Thayt=2vâopt(d):

x=0

y=4==J(O,4,O)

z=0

0,25

4/4 Dáp an

Đề thi HK2 Toán 12 năm 2020 – 2021 trường Năng khiếu TDTT Bình Chánh – TP HCM

Thông tin :

Tài liệu liên quan:

Đề kiểm tra cuối kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Vĩnh Long

Đề kiểm tra học kỳ 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Bình Dương

Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Quảng Nam

Đề cuối kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Đắk Lắk

Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị