Đề thi HK2 Toán 12 năm học 2016 – 2017 sở GD và ĐT Đồng Nai

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

37 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 1 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA HỌC KÌ II LỚP 12
ĐỒNG NAI Năm học: 2016 – 2017
Môn: Toán
ĐỀ CHÍNH THỨC Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Mã đề 01 (50 câu trắc nghiệm)
Câu 1. Tìm nguyên hàm của hàm số
sin3f x x
.
A.
1
f x dx cos3x C
3
. B.
1
cos3
3
f x dx x C

.
C.
3.cos3f x dx x
. D.
3cos3f x dx x C
.
Câu 2. Tìm nguyên hàm của hàm số
3
45
gx
x
.
A.
3
ln 4 5
5
f x dx x C
. B.
3
ln 4 5
5
f x dx x C
.
C.
. D.
3.ln 4 5g x dx x C
.
Câu 3. Cho hàm số
8
h x 19 12x
. Tìm
f x dx
.
A.
7
8. 19 12h x dx x C
B.
7
96. 19 12h x dx x C
C.
9
1
. 19 12
96
h x dx x C
D.
9
1
. 12 19
108
h x dx x C
Câu 4. Tìm nguyên hàm của hàm số
8 9 .7
x
f x x
A.
18
8 9 .7 .7
ln7 ln7
xx
f x dx x C
. B.
18
8 9 .7 .7
ln7 ln7
xx
f x dx x
.
C.
7 .ln7. 8 9 8ln7
x
f x dx x C
. D.
18
.7 . 8 9
ln7 ln7
x
f x dx x C



.
Câu 5. Tìm một nguyên hàm
Fx
của hàm số
f x 48x 7 .lnx
biết
F 1 0
.
A.
xx
22
F x 24.x 7 ln x 12 7x 5
B.
xx
22
F x 24.x 7 ln x 12 7x 17
C.
xx
22
F x 24.x 7 ln x 12 7x 5
D.
xx
22
F x 24.x 7 ln x 12 7x 5
Câu 6. Tính
a
x
0
I 25 dx
theo số thực
a
.
A.
a
1
I . 25 1
ln25
B.
a
25
I . 25 1
a1
C.
a1
I a.25
D.
a
I 25 1 ln 25
Câu 7. Cho
π
a 0;
2
. Tính
x
a
2
0
29
J dx
cos
theo
a
.
A.
1
J tana
29
. B.
J 29 tana
C.
J 29tana
D.
J 29cota
Câu 8. Cho số thực
m1
. Tính
m
3
1
1
K 2 dx
x
theo
m
.
A.
3
2
4m 1 3
K
2
2.m
B.
4
3
K3
m
C.
2
2
K 2m
m
D.
3
2
4m 1 3
K
2
2.m
Câu 9. Để tính
π
d
0
H xsin12x x
bằng phương pháp tích phân từng phần ta đặt
ux
và
ddv sin12x x
. Tìm
du
và tính
H
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 2 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
A.
du1
và
π
H
12
. B.
du dx
và
π
H
12
.
C.
d
2
1
ux
2
và
π
H
12
. D.
du dx
và
π
H
12
.
Câu 10. Để tính
1
x
0
M x 1 .2 dx
bằng phương pháp tích phân từng phần ta đặt
u x 1
và
x
dv 2 dx
. Tìm
du
và tính
M
.
A.
du1
và
2
M 3.ln2 ln2
. B.
d
2
1
u x x
2
và
2
31
M
ln 2
ln 2
.
C.
du dx
và
2
31
M
ln 2
ln 2
. D.
du dx
và
2
31
M
ln2
ln2
.
Câu 11. Cho
π
e
2
cos25x
0
m.e n
e .sin25x dx
25
. Với
m
và
n
là số nguyên. Tính
k m n
.
A.
k0
. B.
k2
C.
k1
D.
k1
Câu 12. Cho
1
2
0
m. 29 n
28x 1.xdx
84
. Với
m
và
n
là số nguyên. Tính
k m n
.
A.
k 30
. B.
k2
C.
k 28
D.
k0
Câu 13. Tính diện tích
S
của hình phẳng giới hạn bởi đồ t hị hàm số
y lnx
, trục hoành và hai
đường thẳng
x 1
,
x 25
.
A.
S 25.ln25 24
. B.
S 50.ln5 24
. C.
S 25.ln24 1
. D.
S 25.ln26 1
Câu 14. Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
xy cos
, trục hoành và hai đường
thẳng
πx 0,x 2
. Tính thể tích
V
của khối tròn xoay sinh bởi
H
quay quanh trục
hoành.
A.
2
2V
. B.
2
V
. C.
2
4
V

. D.
V
.
Câu 15. Trên mặt phẳng tọa độ cho điểm
6;7M
là điểm biểu diễn số phức z. tìm a là phần
thực và b là phần ảo của số phức
z
.
A.
6, 7ab
. B.
7, 6ab
. C.
6, 7a b i
. D.
7, 6a b i
.
Câu 16. Tìm số phức liên hợp của số phức
2 3 7 8 .z i i
A.
10 37zi
. B.
38 37zi
. C.
10 37zi
. D.
38 37zi
.
Câu 17. Tìm modun của số phức z thỏa
1 3 . 7 5i z i
.
A.
185
25
z
B.
290
5
z
C.
185
4
z
D.
185
5
z
Câu 18. Tìm nghịch đảo
1
z
của số phức
2
( 1 4 )zi
A.
1 15 8
289 289
i
z

B.
1 15 8
289 289
i
z

C.
1 15 8
289 289
i
z

D.
1 15 8
289 289
i
z

Câu 19. Cho z1 là nghiệm phức có phần ảo âm của phương trình
2
8 20 0zz
, gọi
1
M
là
điểm biểu diện số phức
1
z
trên mặt phẳng tọa độ. Tìm
1
M
.
A.
1
( 4; 2)M 
B.
1
(8; 4)M
C.
1
( 8; 4)M 
D.
1
(4; 2)M
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 3 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Câu 20. Trong không gian với hệ tọa độ
Oxyz
cho điểm
5;0;5I
là trung điểm của đoạn
MN
,
biết
1; 4;7M
. Tìm tọa độ
N
.
A.
N( 10;4;3)
B.
N( 2; 2;6)
C.
N( 11; 4;3)
D.
N( 11;4;3)
Câu 21. Trong không gian với hệ tọa độ
Oxyz
cho 3 điểm
(0;1;2)M
,
N(7;3;2)
,
(3;5;0)P
, Tìm tọa
độ điểm Q thỏa
MN QP
A.
(12;5;2)Q
B.
( 12;5;2)Q
C.
( 12; 5;2)Q 
D.
( 2; 1;2)Q 
Câu 22. Trong không gian với hệ tọa độ
Oxyz
cho 3 điểm
( 3;1; 6)M 
, và
(3;5;0)N
. Viết phương
trình mặt cầu
S
đường kính
MN
.
A.
22
2
3 3 22x y z
B.
22
2
3 3 22x y z
C.
22
2
3 3 22x y z
D.
22
2
3 3 22x y z
Câu 23. Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu (S) có phương trình
là
2 2 2
4 10 20 0x y z x y
. Tìm tọa độ tâm và bán kính R của mặt cầu (S).
A.
2; 5;0 ; 3IR
B.
2;5;0 ; 3IR
.
C.
2;5; 10 ; 129IR
D.
4;10;0 ; 4 6IR
Câu 24. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
P
đi qua 3 điểm
(0; 2;3)E
;
(0; 3;1)F
(1; 4;2)G
. Viết phương trình mặt phẳng
P
A.
:3 2 1 0P x y z
B.
:3 2 1 0P x y z
.
C.
:3 2 7 0P y y z
D.
:3 2 7 0P x y z
Câu 25. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
P
đi qua ba điểm
(0;0;3)H
,
(0; 1;0)K
,
(9;0;0)L
. Viết phương trình mặt phẳng
P
.
A.
:1
9 1 3
x y z
P
B.
:0
9 1 3
x y z
P
C.
y
xz
P : 1
3 1 9
. D.
y
xz
P : 0
3 1 9
.
Câu 26. Trong không gian với hệ trục tọa độ
Oxyz
cho ba mặt phẳng
P , Q , R
tương ứng có
phương trình là
z2x 6y 4 8 0
,
z5x 15y 10 20 0
,
z6x 18y 12 24 0
.
Chọn mệnh đề đúng trong bốn mệnh đề sau:
A.
//PQ
. B.
P
cắt
Q
. C.
Q
cắt
R
. D.
//RP
.
Câu 27. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
xz2y 4 1 0
và điểm
M 1;0; 2
. Tính khoảng cách
d
1
từ điểm
M
đến mặt
phẳng
P
và tính khoảng cách
d
2
từ điểm
M
đến mặt phẳng
Oxy
.
A.
d
1
10
21
và
d
2
1
. B.
d
1
10 21
21
và
d
2
3
.
C.
d
1
10
20
và
d
2
2
. D.
d
1
10. 21
21
và
d
2
2
.
Câu 28. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
z2x 2y 3 0
. Viết phương trình của mặt phẳng
Q
đi qua hai điểm
H 1;0;0
và
K 0; 2;0
biết
Q
vuông góc với
P
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 4 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
A.
zQ : 6x 3y 4 6 0
. B.
zQ : 2x y 2 2 0
.
C.
Q : 2x y 2z 2 0
. D.
zQ : 2x y 2 2 0
.
Câu 29. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
z2x y 5 6 0
. Viết phương trình của đường thẳng
d
đi qua điểm
M 1; 2;7
biết
d
vuông góc với
P
.
A.
y2
x 1 z 7
d:
2 1 5
. B.
y1
x 2 z 5
d:
1 2 7
.
C.
y2
x 1 z 7
d:
2 1 5
. D.
y2
x 1 z 7
d:
2 1 5
.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
viết phương trình của đường thẳng
d
đi
qua hai điểm
E 9; 8;8
và
F 10;6;8
.
A.
x 9 19t
d : y 8 14t t
z 8 t
. B.
x 9 19t
d : y 8 14t t
z0
.
C.
x 10 19t
d : y 6 14t t
z 8 t
. D.
x 10 19t
d : y 6 14t t
z8
.
Câu 31. Trong không gian với hệ trục tọa độ
Oxyz
cho hai đường thẳng
p
và
q
thương ứng
có phương tình là
y1
x z 6
1 2 4
và
x 1 t
y 6 7t t
z 2 4t
. Chọn mệnh đề đúng trong
bốn mệnh đề sau:
A.
//pq
. B.
p
cắt
q
. C.
p
trùng với
q
. D.
p
chéo
q
.
Câu 32. Trong không gian với hệ trục tọa độ
Oxyz
cho đường thẳng
d
có phương trình là
y3
x 3 z
1 6 2
. Viết phương trình của đường thẳng đi qua điểm
M 6; 7;0
biết
song song với
d
.
A.
y7
x 6 z
:
1 6 2
. B.
y7
x 6 z
:
1 6 2
.
C.
y6
x 1 z 2
:
1 6 2
. D.
y7
x 6 z
:
1 6 2
.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
cho đường thẳng
d
và mặt phẳng
P
tương ứng có phương trình là
y1
x 3 z 2
2 1 1
và
z3x y 5 5 0
, gọi mặt
phẳng
Q
là mặt phẳng
zOx
. Chọn mệnh đề đúng trong bốn mệnh đề sau
A.
//dP
và
d
cắt
Q
. B.
dP
và
d
cắt
Q
.
C.
d
cắt
P
và
d
cắt
Q
. D.
//dP
và
//dQ
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 5 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Câu 34. Trong không gian với hệ trục tọa độ
Oxyz
cho đường thẳng
d
có phương trình là
y2
x z 1
8 3 5
. Viết phương trình của mặt phẳng
P
vuông góc với đường thẳng
d
và biết mặt phẳng
P
đi qua điểm
M 0; 8;1
.
A.
zP :8x 3y 5 19 0
. B.
P :8x 3y 5z 27 0
.
C.
P :8x 3y 5z 19 0
. D.
P : 8x 3y 5z 19 0
.
Câu 35. Tìm tập nghiệm
S
của bất phương trình
x 3 x
4 2 0
.
A.
S 0;
. B.
S 3;
. C.
S 6;
. D.
S
.
Câu 36. Tìm tập nghiệm
S
của bất phương trình
39
log x 6log x 8
.
A.
S 0;6
. B.
S ;6
. C.
S ;9
. D.
S 0;9
.
Câu 37. Trong mặt phẳng hệ trục tọa độ
Oxy
tập hợp
T
các điểm biểu diễn của các số phức
z
thỏa
z 10
và phần ảo của
z
bằng 6.
A.
T
là đường tròn tậm
O
bán kính
R 10
. B.
T 8;6 , 8;6
.
C.
T
là đường tròn tậm
O
bán kính
R 6
. D.
T 6;8 , 6; 8
.
Câu 38. Tìm các số phức
z
thỏa
2iz 3z 1 4i
.
A.
z 1 2i
. B.
z 1 2i
. C.
z 1 2i
. D.
z 1 2i
.
Câu 39. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
2x 2y z 16 0
. Viết phương trình của mặt cầu
S
có tâm
I 3;1;0
biết
S
tiếp
xúc với mặt phẳng
P
.
A.
22
2
S : x 3 y 1 z 16
. B.
22
2
S : x 3 y 1 z 4
.
C.
22
2
S : x 3 y 1 z 16
. D.
22
2
S : x 3 y 1 z 16
.
Câu 40. Trong không gian với hệ trục tọa độ
Oxyz
cho hai mặt phẳng
P
và
Q
tương ứng có
phương trình là
z3x 6y 12 3 0
và
z2x my 8 2 0
, với
m
là tham số thực.
Tìm
m
để mặt phẳng
P
song song ới mặt phẳng
Q
và khi đó tính khoảng cách
d
giữa hai mặt phẳng
P
và
Q
.
A.
m4
và
d
2
21
. B.
m4
và
d
1
21
.
C.
m2
và
d
2
21
. D.
m4
và
d
2
21
.
Câu 41. Trong không gian với hệ trục toạ độ
Oxyz
, cho mặt phẳng
P
và đườngthẳng
tương ứng có phương trình là
3 1 0x y z
và
22
21
x y z
m


, với
m
là tham số
thực khác
0
. Tìm
m
để đường thẳng
song song với mặt phẳng
P
và khi đó tính
khoảng cách giữa đườngthẳng
và mặt phẳng
P
A.
2m
và
3
11
d
. B.
1m
và
3
11
d
.
C.
1m
và
4
11
d
. D.
1m
và
3
11
d
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 6 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Câu 42. Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
ln 2 2y x x
trên đoạn
1
1;
2



.
A.
ln2M
và
1
2
m
. B.
ln2M
và
1 ln4m
.
A.
1
2
M
và
1 ln4m
. D.
ln2M
và
1 ln4m
.
Câu 43. Tìm tập nghiệm
S
của bất phương trình
2
25 25
log 3.log 2 0xx
.
A.
;25 625;S  
. B.
0;25 625;S 
.
C.
0;25 625;S 
. D.
625;S 
.
Câu 44. Tìm tập nghiệm
S
của bất phương trình
9 4.3 3 0
xx
.
A.
0;1S
. B.
1;3S
. C.
;1S 
. D.
0;1S
.
Câu 45. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
2
31yx
và đồ thị hàm số
31yx
.
A.
1
2
S
. B.
2S
. C.
1
6
S
. D.
1
3
S
.
Câu 46. Cho hàm số
32
2 1 2y x m x x
, với
m
là tham số thực. Tìm tập hợp
M
của các
tham số thực
m
sao cho hàm số đã cho đạt cực tiểu tại điểm
1x
.
A.
M 
. B.
3M
. C.
3M 
. D.
6M 
.
Câu 47. Cho hình tứ diện
EFGH
có
EF
vuông góc với
EG
,
EG
vuông góc với
EH
,
EH
vuông
góc với
EF
; biết
6EF a
,
8EG a
,
12EH a
, với
0,aa
. Gọi
I
,
J
tương ứng là
trung điểm của hai cạnh
FG
,
FH
. Tính khoảng cách
d
từ điểm
F
đến mặt phẳng
EIJ
theo
a
A.
12 29.
29
a
d
. B.
6 29.
29
a
d
. C.
24 29.
29
a
d
. D.
8 29.
29
a
d
.
Câu 48. Một lọ trống miệng đựng nước là hình trụ tròn xoay có chiều
cao bằng
1,6 dm
; đường kính đáy bằng
1 dm
; đáy (dưới) của
lọ phẳng với bề dày không đổi bằng
0,2 dm
; thành lọ với bề
dày không đổi bằng
0,2 dm
; thiết diện qua trục của lọ như
hình vẽ; đổ vào lọ
2,5 dl
nước (trước đó trong lọ không có
nước hoặc vật khác). Tính gần đúng khoảng cách
k
từ mặt
nước trong lọ khi nước lặng yên đến mép trên của lọ (quy
tròn số đến hàng phần trăm, nghĩa là làm tròn số đến hai chữ
số sau dấu phảy)
A.
0,52k dm
. B.
1,18k dm
. C.
0,53k dm
. D.
0,51k dm
.
Câu 49. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
P
và đường thẳng
d
tương ứng có phương trình là
2 3 3 0x y z
và
122
2 1 1
x y z


. Biết đường
thẳng
d
cắt mặt phẳng
P
tại điểm
M
. Gọi
N
là điểm thuộc
d
sao cho
3MN
,
gọi
K
là hình chiếu vuông góc của điểm
N
trên mặt phẳng
P
. Tính độ dài đoạn
MK
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 7 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
A.
7
105
MK
. B.
7
4 21
MK
. C.
4 21
7
MK
. D.
105
7
MK
.
Câu 50. Cho hình hộp
.MNPQ M N P Q
có các cạnh đều bằng
2a
, với
0;aa
. Biết
60QMN 
,
120M MQ M MN

. Tính thể tích
V
của khối hộp
.MNPQ M N P Q
theo
a
.
A.
3
8.Va
. B.
3
2.Va
. C.
3
2 2.Va
. D.
3
4 2.Va
.
----------HẾT----------
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
A
D
D
C
A
C
D
D
C
A
C
B
B
A
A
D
A
D
D
C
B
B
C
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
D
B
C
D
B
A
A
C
C
D
B
A
C
D
B
B
C
A
A
C
C
A
D
D
HƯỚNG DẪN GIẢI
Câu 1. Tìm nguyên hàm của hàm số
sin3f x x
.
A.
1
f x dx cos3x C
3
. B.
1
cos3
3
f x dx x C

.
C.
3.cos3f x dx x
. D.
3cos3f x dx x C
.
Hướng dẫn giải
Chọn B
1
d sin3 d cos3
3
f x x x x x C

Câu 2. Tìm nguyên hàm của hàm số
3
45
gx
x
.
A.
3
ln 4 5
5
f x dx x C
. B.
3
ln 4 5
5
f x dx x C
.
C.
3.ln 4 5g x dx x C
. D.
3.ln 4 5g x dx x C
.
Hướng dẫn giải
Chọn A
33
d d ln 4 5
4 5 5
f x x x x C
x

Câu 3. Cho hàm số
8
19 12h x x
. Tìm
f x dx
.
A.
7
8. 19 12h x dx x C
B.
7
96. 19 12h x dx x C
C.
9
1
. 19 12
96
h x dx x C
D.
9
1
. 12 19
108
h x dx x C
Hướng dẫn giải
Chọn D
9
8 8 9
12 9
11
d 19 12 d 12 9 d 12 9
12 9 108
x
f x x x x x x C x C
Câu 4. Tìm nguyên hàm của hàm số
8 9 .7
x
f x x
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 8 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
A.
18
8 9 .7 .7
ln7 ln7
xx
f x dx x C
. B.
18
8 9 .7 .7
ln7 ln7
xx
f x dx x
.
C.
7 .ln7. 8 9 8ln7
x
f x dx x C
. D.
18
.7 . 8 9
ln7 ln7
x
f x dx x C



.
Hướng dẫn giải
Chọn D
Xét
d 8 9 .7 d .
x
f x x x x

Đặt
d 8d
89
,
7
d 7 d
ln7
x
x
ux
ux
vx
v


. Ta có
2
(8 9).7 8.7 (8 9).7 8.7 7 8
d d 8 9
ln7 ln7 ln7 ln7 ln7
ln 7
x x x x x
xx
f x x x C x C





Câu 5. Tìm một nguyên hàm
Fx
của hàm số
48 7 .lnf x x x
biết
10F
.
A.
22
24. 7x ln 12x 7 5F x x x x
B.
22
24. 7x ln 12x 7 17F x x x x
C.
22
24. 7x ln 12x 7 5F x x x x
D.
22
24. 7x ln 12x 7 5F x x x x
Hướng dẫn giải
Chọn C
Xét
d 48 7 .ln .df x x x x x

Đặt
2
1
ln
dd
,
d 48 7 d
24 7
ux
ux
x
v x x
v x x




()Fx
là một nguyên hàm của
()fx
nên
2 2 2
( ) d 24 7 ln 24 7 d 24 7 ln 12 7F x f x x x x x x x x x x x x C

Do
10F
nên
5 0 5.CC
Do đó
22
( ) 24 7 ln 12 7 5F x x x x x x
Câu 6. Tính
0
25
a
x
I dx
theo số thực
a
.
A.
1
. 25 1
ln25
a
I 
B.
25
. 25 1
1
a
I
a

C.
1
.25
a
Ia
D.
25 1 ln 25
a
I 
Hướng dẫn giải
Chọn A
Ta có
0
0
25 25 1
25
ln25 ln25
a
a
xa
x
I dx



Câu 7. Cho
0;
2
a



. Tính
2
0
29
cosx
a
J dx
theo
a
.
A.
1
tan
29
Ja
. B.
29tanJa
C.
29tanJa
D.
29cotJa
Hướng dẫn giải
Chọn C
Ta có
22
0
00
29 29
29tan 29tan
cos
cosx
aa
a
J dx dx x a
x

Câu 8. Cho số thực
1m
. Tính
3
1
1
2
m
K dx
x




theo
m
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 9 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
A.
3
2
4 1 3
2
2.
m
K
m

B.
4
3
3K
m

C.
2
2
2Km
m

D.
3
2
4 1 3
2
2.
m
K
m

Hướng dẫn giải
Chọn D
Ta có
23
3
3 2 2
11
1
1 1 3 4 1 3
2 2 2 2
2 2 2
22
m
mm
xm
K dx x dx x m
x m m







Câu 9. Để tính
0
sin12 dH x x x
bằng phương pháp tích phân từng phần ta đặt
ux
và
d sin12 dv x x
. Tìm
du
và tính
H
.
A.
d1u
và
12
H
. B.
du dx
và
12
H
.
C.
2
1
d
2
ux
và
12
H
. D.
du dx
và
12
H
.
Hướng dẫn giải
Chọn D
Với
0
sin12 dH x x x
và phép đặt
d 1d
1
d sin12 d
cos12
12
ux
ux
v x x
vx


. Ta có
00
0
cos12 1 1
cos12 d sin12
12 12 12 144 12
xx
H x x x


Câu 10. Để tính
1
0
1 .2
x
M x dx
bằng phương pháp tích phân từng phần ta đặt
1ux
và
2
x
dv dx
. Tìm
du
và tính
M
.
A.
d1u
và
2
3.ln2 ln2M 
. B.
2
1
d
2
u x x
và
2
31
ln2
ln2
M 
.
C.
ddux
và
2
31
ln2
ln2
M 
. D.
du dx
và
2
31
ln2
ln2
M 
.
Hướng dẫn giải
Chọn C
Với
1
0
1 .2
x
M x dx
và phép đặt
d 1d
1
2
d 2 d
ln 2
x
x
ux
ux
vx
v


. Ta có
11
1
22
0
00
( 1).2 2 3 2 3 1
d
ln2 ln2 ln 2 ln2
ln 2 ln 2
x x x
x
Mx
Câu 11. Cho
π
e
2
cos25x
0
m.e n
e .sin25x dx
25
. Với
m
và
n
là số nguyên. Tính
k m n
.
A.
k0
. B.
k2
C.
k1
D.
k1
Hướng dẫn giải
Chọn A
ππ
π
2
cos25x cos25x cos25x
0
00
1 1 1 1 e 1
I e .sin25x dx e d cos25x e e
25 25 25 e 25e
.
Vậy
1; 1 0m n k
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 10 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Câu 12. Cho
1
2
0
m. 29 n
28x 1.xdx
84
. Với
m
và
n
là số nguyên. Tính
k m n
.
A.
k 30
. B.
k2
C.
k 28
D.
k0
Hướng dẫn giải
Chọn C
1
2
0
I 28x 1.xdx
Đặt
2 2 2
28 1 28 1 .d 28 .dt x t x t t x x
Đổi cận:
01xt
;
1 29xt
.
29
29
3
2
1
1
1 1 29 29 1
.
28 28 3 84
t
I t dt
.
Vậy
29; 1 28m n k
.
Câu 13. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
y lnx
, trục hoành và hai
đường thẳng
x 1
,
x 25
.
A.
S 25.ln25 24
. B.
S 50.ln5 24
. C.
S 25.ln24 1
. D.
S 25.ln26 1
Hướng dẫn giải
Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số
y lnx
và trục hoành là:
ln 0 1xx
.
Diện tích hình phẳng cần tính là
25 25
11
ln lnS x dx xdx

.
Đặt
1
lnux
du dx
x
dv dx
vx

25
25
25
1
1
1
ln ln 25 ln 25 25 1 50 ln 5 24S x x dx x x x
.
Câu 14. Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
xy cos
, trục hoành và hai đường
thẳng
πx 0,x 2
. Tính thể tích
V
của khối tròn xoay sinh bởi
H
quay quanh trục
hoành.
A.
2
2V
. B.
2
V
. C.
2
4
V

. D.
V
.
Hướng dẫn giải
Chọn B
Theo công thức tinh thể tích khói tròn xoay, ta có:
2
22
00
0
1 cos2 1
cos d d sin 2
2 2 2
Ox
x
V x x x x x





.
Câu 15. Trên mặt phẳng tọa độ cho điểm
6;7M
là điểm biểu diễn số phức z. Tìm a là phần
thực và b là phần ảo của số phức
z
.
A.
6, 7 ab
. B.
7, 6ab
. C.
6, 7a b i
. D.
7, 6a b i
.
Hướng dẫn giải
Chọn A
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 11 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Điểm
6;7M
là điểm biểu diễn số phức z nên ta có
67zi
.
Vì vậy phần thực của
z
là
6a 
và phần ảo của
z
là
7b
.
Câu 16. Tìm số phức liên hợp của số phức
2 3 7 8 .z i i
A.
10 37zi
. B.
38 37zi
. C.
10 37zi
. D.
38 37zi
.
Hướng dẫn giải
Chọn A.
Bấm máy tính ta được
10 37zi
. Suy ra
10 37 .zi
Câu 17. Tìm modun của số phức z thỏa
1 3 . 7 5i z i
.
A.
185
25
z
B.
290
5
z
C.
185
4
z
D.
185
5
z
Hướng dẫn giải
Chọn D.
7 5 4 13
1 3 . 7 5
1 3 5 5
i
i z i z i
i

. Từ đây, suy ra
4 13 185
.
5 5 5
zi
Câu 18. Tìm nghịch đảo
1
z
của số phức
2
( 1 4 )zi
A.
1 15 8
289 289
i
z

B.
1 15 8
289 289
i
z

C.
1 15 8
289 289
i
z

D.
1 15 8
289 289
i
z

Hướng dẫn giải
Chọn A.
2
1 1 15 8
15 8
15 8 289 2
4)
8
1
9
( ii
zi
zi


.
Câu 19. Cho
1
z
là nghiệm phức có phần ảo âm của phương trình
2
8 20 0zz
, gọi
1
M
là
điểm biểu diện số phức
1
z
trên mặt phẳng tọa độ. Tìm
1
M
.
A.
1
( 4; 2)M 
B.
1
(8; 4)M
C.
1
( 8; 4)M 
D.
1
(4; 2)M
Hướng dẫn giải
Chọn D.
Giải phương trình
2
8 20 0zz
, ta được
42zi
,
42zi
1
z
có phần ảo âm nên ta chọn
1
42zi
. Điểm biểu diễn số phức
1
z
là
1
4; 2 .M
Câu 20. Trong không gian với hệ tọa độ
Oxyz
cho điểm
5;0;5I
là trung điểm của đoạn
MN
,
biết
1; 4;7M
. Tìm tọa độ
N
.
A.
N( 10;4;3)
B.
N( 2; 2;6)
C.
N( 11; 4;3)
D.
N( 11;4;3)
Hướng dẫn giải
Chọn D.
Áp dụng công thức trung điểm, ta có
2 2 11
2 2 4 11;4;3 .
2 2 3
M N I N I M
M N I N I M
M N I N I M
x x x x x x
y y y y y y N
z z z z z z





Câu 21. Trong không gian với hệ tọa độ
Oxyz
cho 3 điểm
(0;1;2)M
,
N(7;3;2)
,
( 5; 3;2)P 
, Tìm
tọa độ điểm Q thỏa
MN QP
A.
(12;5;2)Q
B.
( 12;5;2)Q
C.
( 12; 5;2)Q 
D.
( 2; 1;2)Q 
Hướng dẫn giải
Gọi
;;Q x y z
là điểm cần tìm.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 12 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Ta có:
7;2;0MN
;
5 ; 3 ;2QP x y z
Vì
7 5 12
2 3 5 12; 5;2
0 2 2
xx
MN QP y y Q
zz




.
Chọn C.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
cho 3 điểm
( 3;1; 6)M 
, và
(3;5;0)N
. Viết phương
trình mặt cầu
S
đường kính
MN
.
A.
22
2
3 3 22x y z
B.
22
2
3 3 22x y z
C.
22
2
3 3 22x y z
D.
22
2
3 3 22x y z
Hướng dẫn giải
Vì mặt cầu
S
đường kính
MN
nên tâm mặt cầu
S
là trung điểm
0;3; 3I
của đoạn
MN
và bán kính mặt cầu
S
là
2 2 2
11
6 4 6 22
22
R MN
.
Vậy phương trình mặt cầu
S
là
22
2
3 3 22x y z
.
Chọn B.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu
S
có phương trình
là
2 2 2
4 10 20 0x y z x y
. Tìm tọa độ tâm và bán kính R của mặt cầu (S).
A.
2; 5;0 ; 3IR
B.
2;5;0 ; 3IR
.
C.
2;5; 10 ; 129IR
D.
4;10;0 ; 4 6IR
Hướng dẫn giải
Mặt cầu
S
có tâm
4 10 0
; ; 2;5;0
222
II
; bán kính
2
2
2 5 0 20 3R
Chọn đáp án B.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
P
đi qua 3 điểm
(0; 2;3)E
;
(0; 3;1)F
(1; 4;2)G
. Viết phương trình mặt phẳng
P
A.
:3 2 1 0P x y z
B.
:3 2 1 0P x y z
.
C.
:3 2 7 0P y y z
D.
:3 2 7 0P x y z
Hướng dẫn giải
Ta có:
0; 1; 2 ; 1; 2; 1EF EG
.
Vì mặt phẳng
P
đi qua 3 điểm
(0; 2;3)E
;
(0; 3;1)F
(1; 4;2)G
nên có véctơ pháp tuyến
là:
, 3; 2;1n EF EG
. Vậy phương trình mặt phẳng
P
là
3 2 2 3 0 3 2 7 0 3 2 7 0x y z x y z x y z
.
Chọn đáp án C.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
P
đi qua ba điểm
(0;0;3)H
,
(0; 1;0)K
,
(9;0;0)L
. Viết phương trình mặt phẳng
P
.
A.
:1
9 1 3
x y z
P
B.
:0
9 1 3
x y z
P
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 13 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
C.
y
xz
P : 1
3 1 9
. D.
y
xz
P : 0
3 1 9
.
Hướng dẫn giải
Vì mặt phẳng
P
đi qua ba điểm
(9;0;0)L Ox
,
(0; 1;0)K Oy
,
(0;0;3)H Oz
nên
phương trình mặt phẳng
P
là:
1
9 1 3
x y z
( Phương trình theo đoạn chắn)
Chọn đáp án A.
Câu 26. Trong không gian với hệ trục tọa độ
Oxyz
cho ba mặt phẳng
P , Q , R
tương ứng có
phương trình là
z2x 6y 4 8 0
,
z5x 15y 10 20 0
,
z6x 18y 12 24 0
.
Chọn mệnh đề đúng trong bốn mệnh đề sau:
A.
//PQ
. B.
P
cắt
Q
. C.
Q
cắt
R
. D.
//RP
.
Hướng dẫn giải
Ta có:
P :2x 6y 4z 8 0
có vtpt là:
2;6; 4 2 1;3; 2
P
n
.
zQ : 5x 15y 10 20 0
có vtpt là
5;15; 10 5 1;3; 2
Q
n
.
zR : 6x 18y 12 24 0
có vtpt là
6;18; 12 6 1;3; 2
R
n
.
Ta thấy :
PQ
đáp án A, B sai.
Và
Q
song song
R
đáp án C sai.
Và
//RP
( Vì ta thấy:
6 18 12 24
2 6 4 8
). Chọn đáp án D.
Câu 27. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
xz2y 4 1 0
và điểm
M 1;0; 2
. Tính khoảng cách
d
1
từ điểm
M
đến mặt
phẳng
P
và tính khoảng cách
d
2
từ điểm
M
đến mặt phẳng
Oxy
.
A.
d
1
10
21
và
d
2
1
. B.
d
1
10 21
21
và
d
2
3
.
C.
d
1
10
20
và
d
2
2
. D.
d
1
10. 21
21
và
d
2
2
.
Hướng dẫn giải
Ta có:
1
2
22
1 2. 0 4 2 1
10 21
;
21
1 2 4
d d M P
.
Mặt phẳng
2
2
2
: 0 ; 2
1
Oxy z d d M Oxy
. Chọn đáp án D.
Câu 28. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
z2x 2y 3 0
. Viết phương trình của mặt phẳng
Q
đi qua hai điểm
H 1;0;0
và
K 0; 2;0
biết
Q
vuông góc với
P
.
A.
zQ : 6x 3y 4 6 0
. B.
zQ : 2x y 2 2 0
.
C.
Q : 2x y 2z 2 0
. D.
zQ : 2x y 2 2 0
.
Hướng dẫn giải
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 14 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Ta có:
1;2;0KH
và vtpt của
P
là:
2; 2; 3
P
n
.
Vì mặt phẳng
Q
đi qua hai điểm
H 1;0;0
,
K 0; 2;0
và vuông góc với
P
nên véctơ
pháp tuyến của
Q
là:
, 6;3; 6 3 2; 1;2
QP
n KH n
.
Vậy
:2 1 2 0 2 2 2 0Q x y z x y z
. Chọn đáp án B.
Câu 29. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
z2x y 5 6 0
. Viết phương trình của đường thẳng
d
đi qua điểm
M 1; 2;7
biết
d
vuông góc với
P
.
A.
y2
x 1 z 7
d:
2 1 5
. B.
y1
x 2 z 5
d:
1 2 7
.
C.
y2
x 1 z 7
d:
2 1 5
. D.
y2
x 1 z 7
d:
2 1 5
.
Hướng dẫn giải
Ta có vtpt của
P
là:
2;1; 5
P
n
.
Vì đường thẳng
d
vuông góc với
P
nên vtcp của
d
là:
2;1; 5
P
n
.
Suy ra phương trình đường thẳng
d
là:
y2
x 1 z 7
2 1 5
. Chọn đáp án C.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
viết phương trình của đường thẳng
d
đi
qua hai điểm
E 9; 8;8
và
F 10;6;8
.
A.
x 9 19t
d : y 8 14t t
z 8 t
. B.
x 9 19t
d : y 8 14t t
z0
.
C.
x 10 19t
d : y 6 14t t
z 8 t
. D.
x 10 19t
d : y 6 14t t
z8
.
Hướng dẫn giải
Vì
d
đi qua hai điểm
E 9; 8;8
và
F 10;6;8
nên véctơ chỉ phương của
d
là:
19; 14;0FE
. Vậy phương trình tham số của
d
là:
x 10 19t
d : y 6 14t t
z8
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 15 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Câu 31. Trong không gian với hệ trục tọa độ
Oxyz
cho hai đường thẳng
p
và
q
tương ứng
có phương tình là
y1
x z 6
1 2 4
và
x 1 t
y 6 7t t
z 2 4t
. Chọn mệnh đề đúng trong
bốn mệnh đề sau:
A.
//pq
. B.
p
cắt
q
. C.
p
trùng với
q
. D.
p
chéo
q
.
Hướng dẫn giải
Ta có:
xt
y1
x z 6
p : y 1 2t t
1 2 4
z 6 4t
.
Cho
t 1 t t 1
1 2t 6 7t t 0
6 4t 2 4t
6 4t 2 4t OK
.
Chọn B.
Câu 32. Trong không gian với hệ trục tọa độ
Oxyz
cho đường thẳng
d
có phương trình là
y3
x 3 z
1 6 2
. Viết phương trình của đường thẳng đi qua điểm
M 6; 7;0
biết
song song với
d
.
A.
y7
x 6 z
:
1 6 2
. B.
y7
x 6 z
:
1 6 2
.
C.
y6
x 1 z 2
:
1 6 2
. D.
y7
x 6 z
:
1 6 2
.
Hướng dẫn giải
Đường thẳng
d
có véctơ chỉ phương là:
d
u 1; 6; 2
Vì song song với
d
nên
u 1; 6; 2
.
Phương trình đường thẳng là
y7
x 6 z
:
1 6 2
.
Chọn A.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
cho đường thẳng
d
và mặt phẳng
P
tương ứng có phương trình là
y1
x 3 z 2
2 1 1
và
z3x y 5 5 0
, gọi mặt
phẳng
Q
là mặt phẳng
zOx
. Chọn mệnh đề đúng trong bốn mệnh đề sau
A.
//dP
và
d
cắt
Q
. B.
dP
và
d
cắt
Q
.
C.
d
cắt
P
và
d
cắt
Q
. D.
//dP
và
//dQ
.
Hướng dẫn giải
Ta có:
Đường thẳng
d
qua điểm
M 3; 1; 2
và có véctơ chỉ phương
d
u 2; 1;1
.
Mặt phẳng
P
có véctơ pháp tuyến
1
n 3;1; 5
.
Mặt phẳng
Q
có phương trình là
y0
và có véctơ pháp tuyến là
2
n 0;1;0
.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 16 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Vì
d1
d2
u .n 2.3 1.1 1. 5 0
u .n 2.0 1.1 1.0 1
Và thế điểm
M 3; 1; 2
vào
P
,
Q
đều không
thỏa. Suy ra
//dP
và
d
cắt
Q
.
Chọn A.
Câu 34. Trong không gian với hệ trục tọa độ
Oxyz
cho đường thẳng
d
có phương trình là
y2
x z 1
8 3 5
. Viết phương trình của mặt phẳng
P
vuông góc với đường thẳng
d
và biết mặt phẳng
P
đi qua điểm
M 0; 8;1
.
A.
zP : 8x 3y 5 19 0
. B.
P :8x 3y 5z 27 0
.
C.
P :8x 3y 5z 19 0
. D.
P : 8x 3y 5z 19 0
.
Hướng dẫn giải
Véctơ chỉ phương của đường thẳng
d
là
d
u 8;3; 5
.
Vì mặt phẳng
P
vuông góc với đường thẳng
d
nên véctơ pháp tuyết của
P
là
d
n u 8;3; 5
.
Phương trình mặt phẳng
P
:
z8 x 0 3 y 8 5 z 1 0 8x 3y 5 19 0
.
Chọn C.
Câu 35. Tìm tập nghiệm
S
của bất phương trình
x 3 x
4 2 0
.
A.
S 0;
. B.
S 3;
. C.
S 6;
. D.
S
.
Hướng dẫn giải
Ta có
2
x 3 x x x x
1
4 2 0 64. 2 2 0 2 x 6
64
.
Chọn C.
Câu 36. Tìm tập nghiệm
S
của bất phương trình
39
log x 6log x 8
.
A.
S 0;6
. B.
S ;6
. C.
S ;9
. D.
S 0;9
.
Hướng dẫn:
2
39
3
3 3 3 3
3
log x 6log x 8
x0
x 0 x 0 x 0
x0
log x 6log x 8
log x 3log x 8 4log x 8 log x 2
x9
Vậy chọn đáp án D
Câu 37. Trong mặt phẳng hệ trục tọa độ
Oxy
tập hợp
T
các điểm biểu diễn của các số phức
z
thỏa
z 10
và phần ảo của
z
bằng 6.
A.
T
là đường tròn tậm
O
bán kính
R 10
. B.
T 8;6 , 8;6
.
C.
T
là đường tròn tậm
O
bán kính
R 6
. D.
T 6;8 , 6; 8
.
Hướng dẫn:
Gọi
2
z x yi(x,y ,i 1)
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 17 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Ta có:
2
22
x8
x
z 10
x
64
y 10
y6
y6
y6
y6
Vậy chọn đáp án B
Câu 38. Tìm các số phức
z
thỏa
2iz 3z 1 4i
.
A.
z 1 2i
. B.
z 1 2i
. C.
z 1 2i
. D.
z 1 2i
.
Hướng dẫn:
Gọi
2
z x yi(x,y ,i 1) zx yi
Ta có:
2iz 3z 1 4i 2i(x yi) 3(x yi) 1 4i
3x 2y (2x 3y)i 1 4i
3x 2y 1 x 1
2x 3y 4 y 2
Vậy chọn đáp án A.
Câu 39. Trong không gian với hệ trục tọa độ
Oxyz
cho mặt phẳng
P
có phương trình là
2x 2y z 16 0
. Viết phương trình của mặt cầu
S
có tâm
I 3;1;0
biết
S
tiếp
xúc với mặt phẳng
P
.
A.
22
2
S : x 3 y 1 z 16
. B.
22
2
S : x 3 y 1 z 4
.
C.
22
2
S : x 3 y 1 z 16
. D.
22
2
S : x 3 y 1 z 16
.
Hướng dẫn:
Vì
S
tiếp xúc với
P
nên
S
có bán kính
2
22
2. 3 2.1 0 16
,4
2 2 1
R d I P
.
Phương trình mặt cầu
22
2
: 3 1 16S x y z
.
Vậy chọn đáp án C.
Câu 40. Trong không gian với hệ trục tọa độ
Oxyz
cho hai mặt phẳng
P
và
Q
tương ứng có
phương trình là
z3x 6y 12 3 0
và
z2x my 8 2 0
, với
m
là tham số thực.
Tìm
m
để mặt phẳng
P
song song ới mặt phẳng
Q
và khi đó tính khoảng cách
d
giữa hai mặt phẳng
P
và
Q
.
A.
m4
và
d
2
21
. B.
m4
và
d
1
21
.
C.
m2
và
d
2
21
. D.
m4
và
d
2
21
.
Hướng dẫn:
Mặt phẳng
P
và
Q
có vectơ pháp tuyến lần lượt là
1
3; 6;12n 
và
2
2; ;8nm
.
Để
PQ€
thì
1
n
cùng phương
2
n
, tức là
12
0,k n kn
3 .2
3
6.
2
4
12 .8
k
k
km
m
k



.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 18 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Chọn
1;0;0
o
MP
. Khi đó:
0
2
22
2.1 4.0 8.0 2
2
,;
21
2 4 8
d P Q d M Q
.
Vậy chọn đáp án D.
Câu 41. Trong không gian với hệ trục toạ độ
Oxyz
, cho mặt phẳng
P
và đườngthẳng
tương ứng có phương trình là
3 1 0x y z
và
22
21
x y z
m


, với
m
là tham số
thực khác
0
. Tìm
m
để đường thẳng
song song với mặt phẳng
P
và khi đó tính
khoảng cách giữa đườngthẳng
và mặt phẳng
P
A.
2m
và
3
11
d
. B.
1m
và
3
11
d
.
C.
1m
và
4
11
d
. D.
1m
và
3
11
d
.
Hướng dẫn giải
Chọn B.
Ta có
ó VTCP 2;1; ; 0; 2; 2c u m quaM
Mặt phẳng
ó 1; 3;1P c VTPT n 
Để
.0
/ / ì 1
un
P th m
MP
3
( ; )
11
dP
Câu 42. Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
ln 2 2y x x
trên đoạn
1
1;
2



.
A.
ln2M
và
1
2
m
. B.
ln2M
và
1 ln4m
.
A.
1
2
M
và
1 ln4m
. D.
ln2M
và
1 ln4m 
.
Hướng dẫn giải
Chọn B.
Ta có
1
ê 1; ó ' ' 0 0
21
x
Tr n tac y y x
x



11
( 1) 1 ln4; 0 ln2;
22
f f f



Vậy ta có
ln2M
và
1 ln4m
Câu 43. Tìm tập nghiệm
S
của bất phương trình
2
25 25
log 3.log 2 0xx
.
A.
;25 625;S 
. B.
0;25 625;S 
.
C.
0;25 625;S 
. D.
625;S 
.
Hướng dẫn giải
Chọn C.
Điều kiện:
0x
25
logtx
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 19 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Bất phương trình trở thành:
25
2
25
log 2
2 625
3 2 0
1 log 1 25
x
tx
tt
t x x




Kết hợp điều kiện ta có nghiệm của bất phương trình là:
0;25 625;S 
Câu 44. Tìm tập nghiệm
S
của bất phương trình
9 4.3 3 0
xx
.
A.
0;1S
. B.
1;3S
. C.
;1S 
. D.
0;1S
.
Hướng dẫn giải
Chọn A.
Đặt
30
x
tt
Bất phương trình trở thành:
2
4 3 0 1 3 1 3 3 0 1
x
t t t x
Kết hợp điều kiện ta có nghiệm của bất phương trình là:
0;1S
Câu 45. Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
2
31yx
và đồ thị hàm số
31yx
.
A.
1
2
S
. B.
2S
. C.
1
6
S
. D.
1
3
S
.
Hướng dẫn giải
Chọn A.
Phương trình hoành độ giao điểm là:
2
0
3x 1 3x 1
1
x
x
Ta có:
11
22
00
1
3x 1 (3x 1) x= 3x 3x x
2
S d d

Câu 46. Cho hàm số
32
2 1 2y x m x x
, với
m
là tham số thực. Tìm tập hợp
M
của các
tham số thực
m
sao cho hàm số đã cho đạt cực tiểu tại điểm
1x
.
A.
M 
. B.
3M
. C.
3M 
. D.
6M 
.
Hướng dẫn giải.
Chọn C.
Ta có:
2
6 2 1 2,y x m x
12 2 1 .y x m

Hàm số đã cho đạt cực tiểu tại điểm
1x
khi
1 0 6 2 1 2 0 3.y m m
Với
3m 
ta có
1 12 2 3 1 12 0y

suy ra hàm số đã cho đạt cực tiểu tại điểm
1x
.
Vậy
3m 
là giá trị cần tìm.
Câu 47. Cho hình tứ diện
EFGH
có
EF
vuông góc với
EG
,
EG
vuông góc với
EH
,
EH
vuông
góc với
EF
; biết
6EF a
,
8EG a
,
12EH a
, với
0,aa
. Gọi
I
,
J
tương ứng là
trung điểm của hai cạnh
FG
,
FH
. Tính khoảng cách
d
từ điểm
F
đến mặt phẳng
EIJ
theo
a
A.
12 29.
29
a
d
. B.
6 29.
29
a
d
. C.
24 29.
29
a
d
. D.
8 29.
29
a
d
.
Hướng dẫn giải.
Chọn C.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 20 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
z
y
x
8a
12a
6a
K
J
I
E
F
H
G
M
N
Cách 1: Vì
EF
vuông góc với
EG
,
EG
vuông góc với
EH
nên
()EG EFH
. Gọi K là
trung điểm của
EF
suy ra
()IK EFH
. Gọi
, MN
lần lượt là hình chiếu của
K
trên
EJ
và
IM
ta có
,d K EIJ KN
. Ta có:
, 2 , 2d F EIJ d K EIJ KN
Trong tam giác
EKJ
vuông tại
K
và tam giác
IKM
vuông tại
K
ta có:
2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 1 29 12 29
29
9 16 36 144
KN a
KN KM KI KJ KE KI a a a a
. Vậy
24 29.
.
29
a
d
Cách 2: Vì
EF
vuông góc với
EG
,
EG
vuông góc với
EH
nên
()EG EFH
. Gọi
K
là
trung điểm của
EF
suy ra
()IK EFH
. Chọn hệ trục tọa độ
Oxyz
như hình vẽ ta có:
0;0;0 , 0;0;4 , 3 ;0;0 , 0;6 ;0K I a E a J a
Phương trình mặt phẳng
: 1 4 2 3 12 0
3 6 4
x y z
EIJ x y z a
a a a
12 24 24 29
, 2 , 2
29
4 9 16 29
a a a
d F EIJ d K EIJ

.
Câu 48. Một lọ trống miệng đựng nước là hình trụ tròn xoay có chiều
cao bằng
1,6 dm
; đường kính đáy bằng
1 dm
; đáy (dưới) của
lọ phẳng với bề dày không đổi bằng
0,2 dm
; thành lọ với bề
dày không đổi bằng
0,2 dm
; thiết diện qua trục của lọ như
hình vẽ; đổ vào lọ
2,5 dl
nước (trước đó trong lọ không có
nước hoặc vật khác). Tính gần đúng khoảng cách
k
từ mặt
nước trong lọ khi nước lặng yên đến mép trên của lọ (quy
tròn số đến hàng phần trăm, nghĩa là làm tròn số đến hai chữ
số sau dấu phảy)
A.
0,52k dm
. B.
1,18k dm
. C.
0,53k dm
. D.
0,51k dm
.
Hướng dẫn giải.
Chọn A.
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 21 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Thể tích nước có thể chứa của lọ:
2
3
0,3 .1,4 3,96d 3,96 .V m l
Thể tích nước đổ vào trong lọ là:
2,5 0,25V dl l

Phần thể tích không nước là
0,396 0,25 0,146V V V l
Vậy độ cao của phần không chứa nước là
22
0,146
0,52d
. 0,3 . 0,3
V
hm


Câu 49. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
P
và đường thẳng
d
tương ứng có phương trình là
2 3 3 0x y z
và
122
2 1 1
x y z


. Biết đường
thẳng
d
cắt mặt phẳng
P
tại điểm
M
. Gọi
N
là điểm thuộc
d
sao cho
3MN
,
gọi
K
là hình chiếu vuông góc của điểm
N
trên mặt phẳng
P
. Tính độ dài đoạn
MK
.
A.
7
105
MK
. B.
7
4 21
MK
. C.
4 21
7
MK
. D.
105
7
MK
.
Hướng dẫn giải
Chọn D.
P
d
α
M
N
K
P
có vec tơ pháp tuyến
2; 1;3n 
,
d
có vec tơ chỉ phương
2;1; 1u
.
Gọi
là góc giữa
P
và
d
. Ta có:
. 8 4 5
sin cos
14. 6 21 21
.
nu
nu

.
0.2 dm
0.2 dm
1.6 dm
1 dm
Lời giải: Tập thể giáo viên ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Trang 22 Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Tam giác MNK vuông tại K nên
5 5 105
cos .3 .
7
21 21
MK
MK
MN
Câu 50. Cho hình hộp
.MNPQ M N P Q
có các cạnh đều bằng
2a
, với
0;aa
. Biết
60QMN 
,
120M MQ M MN

. Tính thể tích
V
của khối hộp
.MNPQ M N P Q
theo
a
.
A.
3
8.Va
. B.
3
2.Va
. C.
3
2 2.Va
. D.
3
4 2.Va
.
Hướng dẫn giải
Chọn D
P
P'
N'
Q
M
M'
Q'
N
N
M'
Q
M
O
Do hình chóp
.M NQM
có 3 cạnh bên cùng bằng
2a
nên chân đường cao của hình chóp
.M NQM
là tâm
O
của đường tròn ngoại tiếp mặt đáy
NQM
.
Như thế
..
6. 2 .
MNPQ M N P Q M NQM NQM
V V S OM
Từ giả thiết ta có
MNQ
đều, suy ra
2NQ a
.
Dùng định lý côsin cho
M MN
và
M MQ
ta tính được
23M N M Q a
.
Dùng Hêrông cho
NQM
ta tính được
2
1 1.
NPM
Sa
Từ đó bán kính đường tròn ngoại tiếp
NQM
là
. . 6
4
11
NQM
NQ QM NM a
ON
S
Xét tam giác
,OMN
ta có
22
2 22
11
a
OM MN ON
Vậy
23
.
2 22
2. 11. 4 2
11
MNPQ M N P Q
a
V a a
.
----------HẾT----------
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KÌ II LỚP 12 ĐỒNG NAI Năm học: 2016 – 2017 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Mã đề 01
(50 câu trắc nghiệm)
Câu 1. Tìm nguyên hàm của hàm số f x  sin3x . 1  A. f x dx cos 3x C. B. f  x 1 dx  cos 3x C . 3 3 C. f
 xdx 3.cos3x . D. f
 xdx  3
 cos3x C .
Câu 2. Tìm nguyên hàm của hàm số g x 3  4 . 5xA. f  x 3 dx
ln 4  5x C . B. f  x 3 dx
ln 4  5x C . 5 5 C. g
 xdx 3.ln 4 5x C . D. g
 xdx 3.ln45xC . Câu 3. 8 Cho hàm số h x 19 12x . Tìm f x dx . A. h
 xdx    x7 8. 19 12  C B. h
 xdx     x7 96. 19 12  C 1  1 C. h
 xdx  .1912x9 C D. h
 xdx  .12x199 C 96 108
Câu 4. Tìm nguyên hàm của hàm số    8 9.7x f x x 1 1 x 8 x 8 A.     8 9.7  .7x f x dx xC . B.     8 9.7  .7x f x dx x . ln 7 ln 7 ln 7 ln 7  
C.     7 .x f x dx
ln 7.8x  9 8ln 7  C . D. f  x 1 x 8 dx  .7 . 8x  9   C   . ln 7  ln 7 
Câu 5. Tìm một nguyên hàm F x của hàm số f x 48x 7 .ln x biết F 1 0 . A. 2 x x2 F x 24.x 7 ln x 12 7x 5 B. 2 x x2 F x 24.x 7 ln x 12 7x 17 C. 2 x x2 F x 24.x 7 ln x 12 7x 5 D. 2 x x2 F x 24.x 7 ln x 12 7x 5 a Câu 6. Tính x I 25 dx theo số thực a . 0 1 25 A. a I . 25 1 B. a I . 25 1 C. a 1 I a.25 D. a I 25 1 ln 25 ln 25 a 1 a Câu 7. π 29 Cho a 0; . Tính J dx theo a . 2 2 0 cos x 1 A. J tan a . B. J 29 tan a C. J 29 tan a D. J 29 cot a 29 m Câu 8. 1
Cho số thực m 1. Tính K 2 dx theo m . 3 x 1 3 4m 1 3 3 2 3 4m 1 3 A. K B. K 3 C. K 2m D. K 2 2.m 2 4 m 2 m 2 2.m 2 π Câu 9. Để tính H
x sin 12xdx bằng phương pháp tích phân từng phần ta đặt u x và 0 dv sin12 d
x x . Tìm du và tính H . Trang 1
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI π π A. du 1 và H . B. du dx và H . 12 12 1 π π C. d 2 u x và H . D. du dx và H . 2 12 12 1 Câu 10. Để tính x M x
1 .2 dx bằng phương pháp tích phân từng phần ta đặt u x 1 và 0 x dv
2 dx . Tìm du và tính M . 2 1 3 1 A. du 1 và M 3.ln 2 ln 2 . B. d 2 u x x và M . 2 2 ln 2 ln 2 3 1 3 1 C. du dx và M . D. du dx và M . 2 ln 2 2 ln 2 ln 2 ln 2 π 2 Câu 11. m.e n Cho cos 25x e .sin 25x dx
. Với m và n là số nguyên. Tính k m n. 25e 0 A. k 0 . B. k 2 C. k 1 D. k 1 1 Câu 12. m. 29 n Cho 2 28x 1.xdx
. Với m và n là số nguyên. Tính k m n. 84 0 A. k 30 . B. k 2 C. k 28 D. k 0
Câu 13. Tính diện tích S của hình phẳng giới hạn bởi đồ t hị hàm số y lnx , trục hoành và hai đường thẳng x 1, x 25 . A. S 25.ln 25 24 . B. S 50.ln5 24 . C. S 25.ln24 1. D. S 25.ln26 1
Câu 14. Cho hình phẳng H giới hạn bởi đồ thị hàm số y cosx , trục hoành và hai đường thẳng x 0,x
2π . Tính thể tích V của khối tròn xoay sinh bởi H quay quanh trục hoành.  A. 2 V  2 . B. 2 V   . C. 2 V    . D. V   . 4
Câu 15. Trên mặt phẳng tọa độ cho điểm M  6
 ;7là điểm biểu diễn số phức z. tìm a là phần
thực và b là phần ảo của số phức z . A. a  6  ,b  7 .
B. a  7,b  6  . C. a  6  ,b  7i .
D. a  7,b  6  i .
Câu 16. Tìm số phức liên hợp của số phức z   2
  3i7 8i.
A. z 10  37i . B. z  3  837i . C. z  1  037i .
D. z  38  37i .
Câu 17. Tìm modun của số phức z thỏa 1
  3i.z  7 5i . 185 290 185 185 A. z  B. z  C. z  D. z  25 5 4 5 Câu 18. 1
Tìm nghịch đảo của số phức 2 z  ( 1   4i) z 1 15 8i 1 15 8i 1 15 8i 1 15 8i A.   B.   C.   D.   z 289 289 z 289 289 z 289 289 z 289 289
Câu 19. Cho z1 là nghiệm phức có phần ảo âm của phương trình 2
z  8z  20  0 , gọi M là 1
điểm biểu diện số phức z trên mặt phẳng tọa độ. Tìm M . 1 1 A. M ( 4  ; 2  ) B. M (8; 4)  C. M ( 8  ; 4  ) D. M (4; 2  ) 1 1 1 1 Trang 2
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Câu 20. Trong không gian với hệ tọa độ Oxyz cho điểm I  5
 ;0;5 là trung điểm của đoạn MN , biết M 1; 4
 ;7 . Tìm tọa độ N . A. N( 10  ;4;3) B. N( 2  ; 2  ;6) C. N( 11  ; 4  ;3) D. N(11; 4;3)
Câu 21. Trong không gian với hệ tọa độ Oxyz cho 3 điểm M (0;1;2) , N(7;3;2) , P(3;5;0) , Tìm tọa độ điểm Q thỏa MN QP A. Q(12;5; 2) B. Q(12;5; 2) C. Q( 1  2; 5  ;2) D. Q( 2  ; 1  ;2)
Câu 22. Trong không gian với hệ tọa độ Oxyz cho 3 điểm M ( 3  ;1; 6
 ) , và N(3;5;0) . Viết phương
trình mặt cầu S  đường kính MN . 2 2 2 2 A. 2 x y 3 z 3 22 B. 2 x y 3 z 3 22 2 2 2 2 C. 2 x y 3 z 3 22 D. 2 x y 3 z 3 22
Câu 23. Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) có phương trình là 2 2 2
x y z  4x 10 y  20  0 . Tìm tọa độ tâm và bán kính R của mặt cầu (S). A. I 2; 5;0 ; R 3 B. I 2;5;0 ; R 3 . C. I 2;5; 10 ; R 129 D. I 4;10;0 ; R 4 6
Câu 24. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P đi qua 3 điểm
E(0; 2;3) ; F (0; 3;1) G(1; 4; 2) . Viết phương trình mặt phẳng  P
A. P : 3x  2y z 1  0
B. P : 3x  2y z 1  0 .
C. P : 3y  2y z  7  0
D. P : 3x  2y z  7  0
Câu 25. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P đi qua ba điểm
H (0; 0;3) , K (0; 1; 0) , L(9; 0; 0) . Viết phương trình mặt phẳng  P . x y z x y z A.  P :    1 P    9 1  B.   : 0 3 9 1  3 x y z x y z C. P : 1. D. P : 0 . 3 1 9 3 1 9
Câu 26. Trong không gian với hệ trục tọa độ Oxyz cho ba mặt phẳng P , Q , R tương ứng có
phương trình là 2x 6y 4z 8 0 , 5x 15y 10z 20 0 , 6x 18y 12z 24 0 .
Chọn mệnh đề đúng trong bốn mệnh đề sau: A. P // Q . B. P cắt Q . C. Q cắt R . D. R // P .
Câu 27. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là x 2y 4z 1
0 và điểm M 1; 0; 2 . Tính khoảng cách d từ điểm M đến mặt 1
phẳng P và tính khoảng cách d từ điểm M đến mặt phẳng Oxy . 2 10 10 21 A. d và d 1 . B. d và d 3 . 1 2 1 2 21 21 10 10. 21 C. d và d 2 . D. d và d 2 . 1 2 1 2 20 21
Câu 28. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là 2x 2y 3z
0 . Viết phương trình của mặt phẳng Q đi qua hai điểm H 1; 0; 0 và
K 0; 2; 0 biết Q vuông góc với P . Trang 3
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI A. Q : 6x 3y 4z 6 0 . B. Q : 2x y 2z 2 0 . C. Q : 2x y 2z 2 0 . D. Q : 2x y 2z 2 0 .
Câu 29. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là 2x y 5z 6
0 . Viết phương trình của đường thẳng d đi qua điểm M 1; 2;7
biết d vuông góc với P . x 1 y 2 z 7 x 2 y 1 z 5 A. d : . B. d : . 2 1 5 1 2 7 x 1 y 2 z 7 x 1 y 2 z 7 C. d : . D. d : . 2 1 5 2 1 5
Câu 30. Trong không gian với hệ trục tọa độ Oxyz viết phương trình của đường thẳng d đi
qua hai điểm E 9; 8; 8 và F 10; 6; 8 . x 9 19t x 9 19t A. d : y 8 14t t . B. d : y 8 14t t . z 8 t z 0 x 10 19t x 10 19t C. d : y 6 14t t . D. d : y 6 14t t . z 8 t z 8
Câu 31. Trong không gian với hệ trục tọa độ Oxyz cho hai đường thẳng p và q thương ứng x 1 t x y 1 z 6 có phương tình là và y 6 7t t
. Chọn mệnh đề đúng trong 1 2 4 z 2 4t bốn mệnh đề sau: A. p // q . B. p cắt q .
C. p trùng với q . D. p chéo q .
Câu 32. Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình là x 3 y 3
z . Viết phương trình của đường thẳng
đi qua điểm M 6; 7; 0 biết 1 6 2 song song với d . x 6 y 7 z x 6 y 7 z A. : . B. : . 1 6 2 1 6 2 x 1 y 6 z 2 x 6 y 7 z C. : . D. : . 1 6 2 1 6 2
Câu 33. Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d và mặt phẳng P x 3 y 1 z 2
tương ứng có phương trình là và 3x y 5z 5 0 , gọi mặt 2 1 1 phẳng Q là mặt phẳng z
Ox . Chọn mệnh đề đúng trong bốn mệnh đề sau
A. d // P và d cắt Q . B. d P và d cắt Q . C. d cắt P và d cắt Q .
D. d // P và d // Q . Trang 4
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Câu 34. Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình là x y 2
z 1 . Viết phương trình của mặt phẳng P vuông góc với đường thẳng 8 3 5
d và biết mặt phẳng P đi qua điểm M 0; 8;1 . A. P : 8x 3y 5z 19 0 . B. P : 8x 3y 5z 27 0 . C. P : 8x 3y 5z 19 0 . D. P : 8x 3y 5z 19 0 .
Câu 35. Tìm tập nghiệm S của bất phương trình x 3 x 4 2 0 . A. S 0; . B. S 3; . C. S 6; . D. S .
Câu 36. Tìm tập nghiệm S của bất phương trình log x 6 log x 8 . 3 9 A. S 0; 6 . B. S ; 6 . C. S ; 9 . D. S 0; 9 .
Câu 37. Trong mặt phẳng hệ trục tọa độ Oxy tập hợp T các điểm biểu diễn của các số phức z thỏa z
10 và phần ảo của z bằng 6.
A. T là đường tròn tậm O bán kính R 10. B. T 8; 6 , 8; 6 .
C. T là đường tròn tậm O bán kính R 6 . D. T 6; 8 , 6; 8 .
Câu 38. Tìm các số phức z thỏa 2iz 3z 1 4i . A. z 1 2i . B. z 1 2i . C. z 1 2i . D. z 1 2i .
Câu 39. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là 2x 2y z 16
0 . Viết phương trình của mặt cầu S có tâm I 3;1; 0 biết S tiếp xúc với mặt phẳng P . 2 2 2 2 A. 2 S : x 3 y 1 z 16 . B. 2 S : x 3 y 1 z 4 . 2 2 2 2 C. 2 S : x 3 y 1 z 16 . D. 2 S : x 3 y 1 z 16 .
Câu 40. Trong không gian với hệ trục tọa độ Oxyz cho hai mặt phẳng P và Q tương ứng có
phương trình là 3x 6y 12z 3 0 và 2x my 8z 2
0 , với m là tham số thực.
Tìm m để mặt phẳng P song song ới mặt phẳng Q và khi đó tính khoảng cách d
giữa hai mặt phẳng P và Q . 2 1 A. m 4 và d . B. m 4 và d . 21 21 2 2 C. m 2 và d . D. m 4 và d . 21 21
Câu 41. Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng P và đườngthẳng  x y  2 z  2
tương ứng có phương trình là x  3y z 1  0 và  
, với m là tham số 2 1 m
thực khác 0 . Tìm m để đường thẳng  song song với mặt phẳng P và khi đó tính
khoảng cách giữa đườngthẳng  và mặt phẳng P 3 3
A. m  2 và d  .
B. m 1 và d  . 11 11 4 3
C. m 1 và d  . D. m  1  và d  . 11 11 Trang 5
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Câu 42. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y x  ln 2  2x trên đoạn  1  1;   .  2  1
A. M  ln 2 và m  .
B. M  ln 2 và m  1   ln 4. 2 1 A. M  và m  1   ln 4.
D. M  ln 2 và m 1 ln 4 . 2
Câu 43. Tìm tập nghiệm S của bất phương trình log x2 3.log x  2  0. 25 25
A. S   ;  2  5 625; .
B. S  0;2  5 625; .
C. S  0;2  5 625; .
D. S  625; .
Câu 44. Tìm tập nghiệm S của bất phương trình 9x 4.3x   3  0 .
A. S  0;  1 .
B. S  1;  3 .
C. S    ;1 .
D. S  0;  1 .
Câu 45. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x 1 và đồ thị hàm số
y  3x 1. 1 1 1 A. S  . B. S  2 . C. S  . D. S  . 2 6 3 Câu 46. Cho hàm số 3
y x  m   2 2
1 x  2x , với m là tham số thực. Tìm tập hợp M của các
tham số thực m sao cho hàm số đã cho đạt cực tiểu tại điểm x 1. A. M   . B. M    3 .
C. M    3 .
D. M    6 .
Câu 47. Cho hình tứ diện EFGH có EF vuông góc với EG , EG vuông góc với EH , EH vuông
góc với EF ; biết EF  6a, EG  8a, EH 12a , với a  0, a
. Gọi I , J tương ứng là
trung điểm của hai cạnh FG , FH . Tính khoảng cách d từ điểm F đến mặt phẳng
EIJ  theo a 12 29.a 6 29.a 24 29.a 8 29.a A. d  . B. d  . C. d  . D. d  . 29 29 29 29
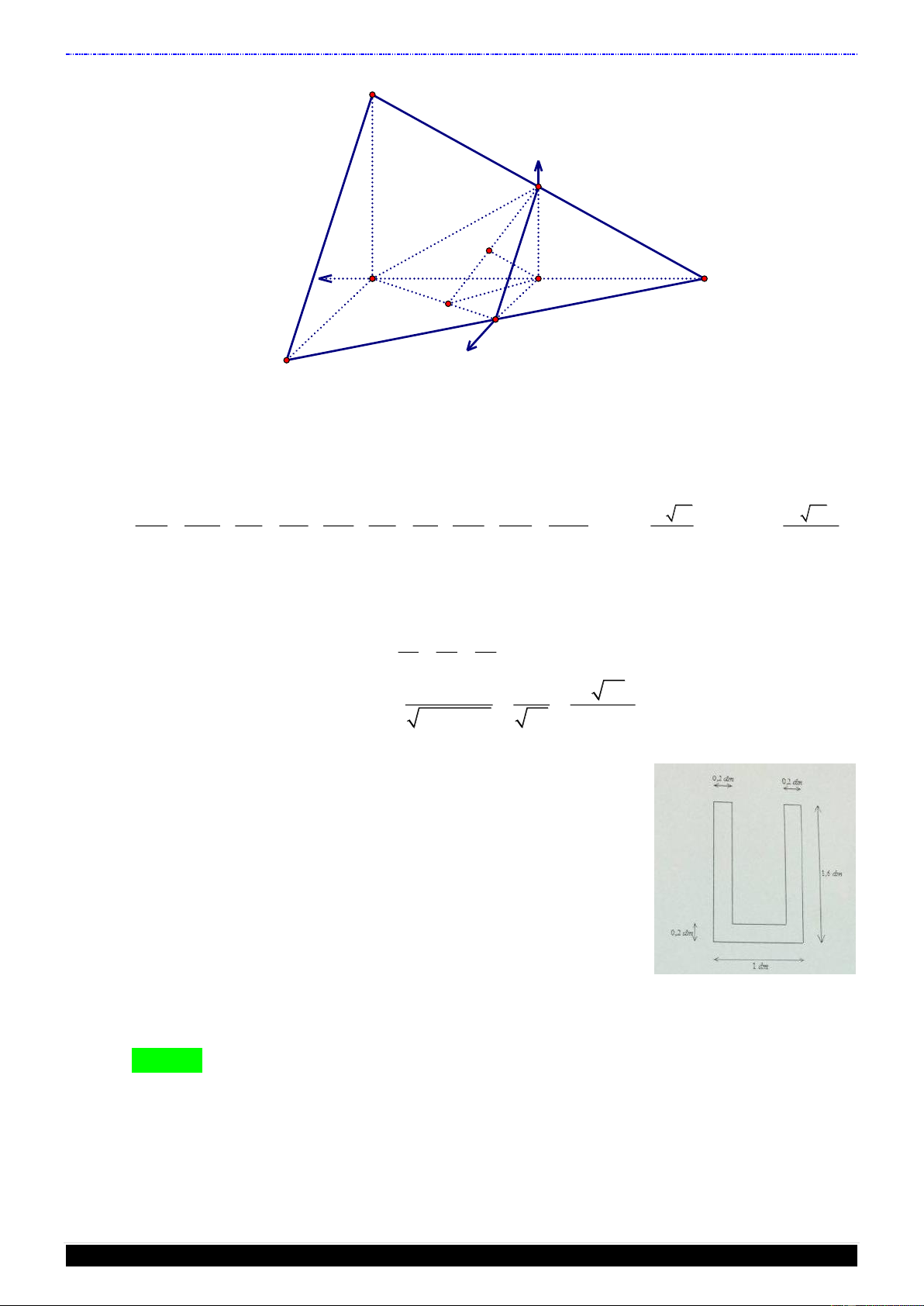
Câu 48. Một lọ trống miệng đựng nước là hình trụ tròn xoay có chiều
cao bằng 1, 6 dm ; đường kính đáy bằng 1 dm ; đáy (dưới) của
lọ phẳng với bề dày không đổi bằng 0,2 dm ; thành lọ với bề
dày không đổi bằng 0,2 dm ; thiết diện qua trục của lọ như
hình vẽ; đổ vào lọ 2,5 dl nước (trước đó trong lọ không có
nước hoặc vật khác). Tính gần đúng khoảng cách k từ mặt
nước trong lọ khi nước lặng yên đến mép trên của lọ (quy
tròn số đến hàng phần trăm, nghĩa là làm tròn số đến hai chữ số sau dấu phảy)
A. k  0,52dm.
B. k  1,18dm .
C. k  0,53dm . D. k  0,5  1 dm .
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P và đường thẳng d x 1 y  2 z  2
tương ứng có phương trình là 2x y  3z  3  0 và   2  1 1  . Biết đường
thẳng d  cắt mặt phẳng P tại điểm M . Gọi N là điểm thuộc d  sao cho MN  3,
gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng P . Tính độ dài đoạn MK . Trang 6
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 7 7 4 21 105 A. MK  . B. MK  . C. MK  . D. MK  . 105 4 21 7 7
Câu 50. Cho hình hộp M . NPQ M NPQ
  có các cạnh đều bằng 2a , với a  0;a  . Biết
QMN  60 , M MQ M M
N 120 . Tính thể tích V của khối hộp M . NPQ M NPQ   theo a . A. 3 V  8.a . B. 3 V  2.a . C. 3 V  2 2.a . D. 3 V  4 2.a .
----------HẾT---------- ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A D D C A C D D C A C B B A A D A D D C B B C A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D D B C D B A A C C D B A C D B B C A A C C A D D HƯỚNG DẪN GIẢI
Câu 1. Tìm nguyên hàm của hàm số f x  sin3x . 1  A. f x dx cos 3x C. B. f  x 1 dx  cos 3x C . 3 3 C. f
 xdx 3.cos3x . D. f
 xdx  3
 cos3x C . Hướng dẫn giải Chọn B f  x 1
dx  sin 3x dx   cos 3x C  3
Câu 2. Tìm nguyên hàm của hàm số g x 3  4 . 5x A. f  x 3
dx   ln 4  5x C . B. f  x 3 dx
ln 4  5x C . 5 5 C. g
 xdx 3.ln 4 5x C . D. g
 xdx 3.ln45xC . Hướng dẫn giải Chọn A f  x 3 3 dx
dx   ln 4  5x C  4  5x 5
Câu 3. Cho hàm số hx    x8 19 12
. Tìm f xdx  . A. h
 xdx    x7 8. 19 12  C B. h
 xdx     x7 96. 19 12  C 1  1 C. h
 xdx  .1912x9 C D. h
 xdx
.12x 199  C 96 108 Hướng dẫn giải Chọn D 9  f
 xx    x8 x   x  8 1 12x 9 1 d 19 12 d 12 9 dx   C
12x 99 C 12 9 108
Câu 4. Tìm nguyên hàm của hàm số    8  9.7x f x x Trang 7
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 1 x 8 1 x 8 A.     8 9.7  .7x f x dx xC . B.     8 9.7  .7x f x dx x . ln 7 ln 7 ln 7 ln 7  
C.     7 .x f x dx
ln 7.8x  9 8ln 7  C . D. f  x 1 x 8 dx  .7 . 8x  9   C   . ln 7  ln 7  Hướng dẫn giải Chọn D du  8dx u   8x  9 
Xét   d  8 9.7x f x x x d . x Đặt  ,  . Ta có x 7x
dv  7 dx v   ln 7     f  x (8 9).7x 8.7x (8 9).7x 8.7x 7x x x 8 dx   dx    C   8x  9    C 2 ln 7 ln 7 ln 7 ln 7 ln 7  ln 7 
Câu 5. Tìm một nguyên hàm F x của hàm số f x  48x  7.ln x biết F   1  0 .
A. F x   2 x   2 24.
7x ln x 12x  7x  5
B. F x   2 x   2 24.
7x ln x 12x  7x 17
C. F x   2 x   2 24.
7x ln x 12x  7x  5
D. F x   2 x   2 24.
7x ln x 12x  7x  5 Hướng dẫn giải Chọn C  1 u   ln x  du  dx Xét f
 xdx  48x7.ln .xdx Đặt    v    x   , x d 48 7 dx  2
v  24x  7x
F (x) là một nguyên hàm của f (x) nên F x f
 xx   2x xx   x   x   2x x 2 ( ) d 24 7 ln 24 7 d 24 7
ln x 12x  7x C Do F   1  0 nên 5
 C  0  C  5. Do đó F x   2 x x 2 ( ) 24 7
ln x 12x  7x  5 a
Câu 6. Tính  25x I dx  theo số thực a . 0 1 25 A.  .25a I    1 B.  .25a I   1  D. 25a I    1 ln 25 ln 25 a C. 1 .25a I a 1 Hướng dẫn giải Chọn A a a  25x  25a x 1
Ta có I  25 dx      ln 25 ln 25   0 0   a Câu 7.  29 Cho a  0;   . Tính J dx  theo a .  2  cosx2 0 1 A. J  tan a . B. J  2  9tan a
C. J  29tan a
D. J  29cot a 29 Hướng dẫn giải Chọn C a a 29 29 a Ta có J dx dx   29tan x    a cos x  29 tan 2 2 0 cos x 0 0 m   Câu 8. 1
Cho số thực m 1. Tính K   2 dx   theo m . 3  x  1 Trang 8
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 3 4m 1 3 3 2 3 4m 1 3 A. K   B. K  3 
C. K  2m D. K   2 2.m 2 4 m 2 m 2 2.m 2 Hướng dẫn giải Chọn D m m m   1     x 1 3 4m 1 3 Ta có K   2 dx    x  2 2 3 3 dx  
 2x   2m     3 2 2  x  2  2m 2 2m 2   1 1 1 
Câu 9. Để tính H xsin12 d x x
bằng phương pháp tích phân từng phần ta đặt u x và 0 dv  sin12 d
x x . Tìm du và tính H .  
A. du 1 và H  .
B. du dx và H  . 12 12 1     C. 2 du x và H
. D. du dx và H  . 2 12 12 Hướng dẫn giải Chọn D  du 1dx u   x
Với H x sin12 d x x  và phép đặt    1 . Ta có
dv  sin12xdx v   cos12x 0  12     x cos12x  1   1   H    cos12 d x x    sin12x         12  12 12 144  12 0 0 0 1 Câu 10. Để tính      1 .2x M x
dx bằng phương pháp tích phân từng phần ta đặt u x 1 và 0  2x dv
dx . Tìm du và tính M . 1 3 1
A. du 1 và M   2 3.ln 2 ln 2 . B. 2 du
x x và M   . 2 ln 2 ln22 3 1 3 1
C. du  dx và M   .
D. du dx và M   . ln 2 ln22 ln 2 ln22 Hướng dẫn giải Chọn C du  1dx 1 u x 1  Với      1 .2x M x
dx và phép đặt    . Ta có x 2x dv  2 dxv  0  ln 2 1 1 x 1  ( 1).2  2x 3  2x x  3 1 M     dx        2 2 ln 2 ln 2 ln 2 ln 2 ln 2 ln 2     0 0 0 π 2 Câu 11. m.e n Cho cos 25x e .sin 25x dx
. Với m và n là số nguyên. Tính k m n. 25e 0 A. k 0 . B. k 2 C. k 1 D. k 1 Hướng dẫn giải Chọn A π π π 2 cos 25x 1 cos 25x 1 cos25x 1 1 e 1 I e .sin 25x dx e d cos 25x e e . 0 25 25 25 e 25e 0 0 Vậy m  1
 ;n  1 k  0. Trang 9
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 1 Câu 12. m. 29 n Cho 2 28x 1.xdx
. Với m và n là số nguyên. Tính k m n. 84 0 A. k 30 . B. k 2 C. k 28 D. k 0 Hướng dẫn giải Chọn C 1 2 I 28x 1.xdx 0 Đặt 2 2 2
t  28x  1  t  28x  1  t.dt  28x.dx
Đổi cận: x  0  t  1 ; x  1  t  29 . 29 29 3 1 1 t 29 29 1 2 I t dt  .   . 28 28 3 84 1 1
Vậy m  29;n  1   k  28.
Câu 13. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y lnx , trục hoành và hai đường thẳng x 1, x 25 . A. S 25.ln 25 24 . B. S 50.ln5 24 . C. S 25.ln24 1. D. S 25.ln26 1 Hướng dẫn giải Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số y lnx và trục hoành là:
ln x  0  x  1 . 25 25
Diện tích hình phẳng cần tính là S  ln x dx  ln xdx   . 1 1  1 u  ln xdu dx Đặt    xdv dx v x 25 25
S x ln xdx  
x ln x x 25  25ln25251  50ln524. 1 1 1
Câu 14. Cho hình phẳng H giới hạn bởi đồ thị hàm số y cosx , trục hoành và hai đường thẳng x 0,x
2π . Tính thể tích V của khối tròn xoay sinh bởi H quay quanh trục hoành.  A. 2 V  2 . B. 2 V   . C. 2 V    . D. V   . 4 Hướng dẫn giải Chọn B
Theo công thức tinh thể tích khói tròn xoay, ta có: 2   1 cos2x   1  2 2 V   cos d x x   dx x  sin 2x     . Ox   2 2  2  0 0 0
Câu 15. Trên mặt phẳng tọa độ cho điểm M  6
 ;7 là điểm biểu diễn số phức z. Tìm a là phần
thực và b là phần ảo của số phức z . A. a  6  ,b  7 .
B. a  7,b  6  . C. a  6  ,b  7i .
D. a  7,b  6  i . Hướng dẫn giải Chọn A Trang 10
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI Điểm M  6
 ;7 là điểm biểu diễn số phức z nên ta có z  6   7i .
Vì vậy phần thực của z là a  6
 và phần ảo của z là b  7 .
Câu 16. Tìm số phức liên hợp của số phức z   2
  3i7 8i.
A. z 10  37i . B. z  3  837i . C. z  1  037i .
D. z  38  37i . Hướng dẫn giải Chọn A.
Bấm máy tính ta được z 10 37i . Suy ra z 10  37 . i
Câu 17. Tìm modun của số phức z thỏa 1
  3i.z  7 5i . 185 290 185 185 A. z  B. z  C. z  D. z  25 5 4 5 Hướng dẫn giải Chọn D.     4 13 185 i 7 5i 4 13
1 3 .z  7  5i z    i z   i  . 1   . Từ đây, suy ra 3i 5 5 5 5 5 Câu 18. 1
Tìm nghịch đảo của số phức 2 z  ( 1   4i) z 1 15 8i 1 15 8i 1 15 8i 1 15 8i A.   B.   C.   D.   z 289 289 z 289 289 z 289 289 z 289 289 Hướng dẫn giải Chọn A. 1 1 15 8 2 z  ( 1   4i)  1  5 8i      i . z 1  5 8i 289 289
Câu 19. Cho z là nghiệm phức có phần ảo âm của phương trình 2
z  8z  20  0 , gọi M là 1 1
điểm biểu diện số phức z trên mặt phẳng tọa độ. Tìm M . 1 1 A. M ( 4  ; 2  ) B. M (8; 4)  C. M ( 8  ; 4  ) D. M (4; 2  ) 1 1 1 1 Hướng dẫn giải Chọn D. Giải phương trình 2
z  8z  20  0 , ta được z  4  2i , z  4  2i
z có phần ảo âm nên ta chọn z  4  2i . Điểm biểu diễn số phức z là M 4; 2  . 1   1 1 1
Câu 20. Trong không gian với hệ tọa độ Oxyz cho điểm I  5
 ;0;5 là trung điểm của đoạn MN , biết M 1; 4
 ;7 . Tìm tọa độ N . A. N( 10  ;4;3) B. N( 2  ; 2  ;6) C. N( 11  ; 4  ;3) D. N(11; 4;3) Hướng dẫn giải Chọn D.
Áp dụng công thức trung điểm, ta có
x x  2x
x  2x x  11 M N I N I M  
y y  2y  y  2y y  4  N M N I N I M  11;4;3.  
z z  2z
z  2z z  3  M N IN I M
Câu 21. Trong không gian với hệ tọa độ Oxyz cho 3 điểm M (0;1;2) , N(7;3;2) , P(5;3;2), Tìm
tọa độ điểm Q thỏa MN QP A. Q(12;5; 2) B. Q(12;5; 2) C. Q( 1  2; 5  ;2) D. Q( 2  ; 1  ;2) Hướng dẫn giải Gọi Q ; x ;
y z là điểm cần tìm. Trang 11
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Ta có: MN  7; 2;0 ; QP   5   ; x 3
  y;2  z 7  5   xx  12   
Vì MN QP  2  3  y   y  5  Q 12;5;2 .   0  2  z z  2   Chọn C.
Câu 22. Trong không gian với hệ tọa độ Oxyz cho 3 điểm M ( 3  ;1; 6
 ) , và N(3;5;0) . Viết phương
trình mặt cầu S  đường kính MN . 2 2 2 2 A. 2 x y 3 z 3 22 B. 2 x y 3 z 3 22 2 2 2 2 C. 2 x y 3 z 3 22 D. 2 x y 3 z 3 22 Hướng dẫn giải
Vì mặt cầu S  đường kính MN nên tâm mặt cầu S  là trung điểm I 0;3; 3 của đoạn 1 1
MN và bán kính mặt cầu S là 2 2 2 R MN 6 4 6 22 2 2 . 2 2
Vậy phương trình mặt cầu S  là 2 x y 3 z 3 22 . Chọn B.
Câu 23. Trong không gian với hệ tọa độ Oxyz cho mặt cầu S có phương trình là 2 2 2
x y z  4x 10 y  20  0 . Tìm tọa độ tâm và bán kính R của mặt cầu (S). A. I 2; 5;0 ; R 3 B. I 2;5;0 ; R 3 . C. I 2;5; 10 ; R 129 D. I 4;10;0 ; R 4 6 Hướng dẫn giải 4 10 0 2
Mặt cầu S có tâm I ; ; I 2;5;0 2 R 2 5 0 20 3 2 2 2 ; bán kính Chọn đáp án B.
Câu 24. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P đi qua 3 điểm
E(0; 2;3) ; F (0; 3;1) G(1; 4; 2) . Viết phương trình mặt phẳng  P
A. P : 3x  2y z 1  0
B. P : 3x  2y z 1  0 .
C. P : 3y  2y z  7  0
D. P : 3x  2y z  7  0 Hướng dẫn giải Ta có: EF 0; 1; 2 ; EG 1; 2; 1 .
Vì mặt phẳng P đi qua 3 điểm E(0; 2
 ;3) ; F(0;3;1) G(1;4;2) nên có véctơ pháp tuyến là: n EF,EG
3; 2;1 . Vậy phương trình mặt phẳngP là 3x 2 y 2 z 3 0 3x 2y z 7 0 3x 2y z 7 0 . Chọn đáp án C.
Câu 25. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P đi qua ba điểm
H (0; 0;3) , K (0; 1; 0) , L(9; 0; 0) . Viết phương trình mặt phẳng  P . x y z x y z A.  P :    1 P    9 1  B.   : 0 3 9 1  3 Trang 12
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI x y z x y z C. P : 1. D. P : 0 . 3 1 9 3 1 9 Hướng dẫn giải
Vì mặt phẳng P đi qua ba điểm L(9;0;0) Ox , K (0; 1
 ;0) Oy , H (0;0;3)Oz nên x y z
phương trình mặt phẳng P là: 
  1 ( Phương trình theo đoạn chắn) 9 1  3 Chọn đáp án A.
Câu 26. Trong không gian với hệ trục tọa độ Oxyz cho ba mặt phẳng P , Q , R tương ứng có
phương trình là 2x 6y 4z 8 0 , 5x 15y 10z 20 0 , 6x 18y 12z 24 0 .
Chọn mệnh đề đúng trong bốn mệnh đề sau: A. P // Q . B. P cắt Q . C. Q cắt R . D. R // P . Hướng dẫn giải Ta có: P :2x 6y 4z 8 0 có vtpt là: n 2;6; 4 2 1;3; 2 P . Q : 5x 15y 10z 20 0 có vtpt là n 5;15; 10 5 1;3; 2 Q . R : 6x 18y 12z 24 0 có vtpt là n 6;18; 12 6 1;3; 2 R . Ta thấy : P Q
đáp án A, B sai. Và Q song song R
đáp án C sai. 6 18 12 24
Và R // P ( Vì ta thấy: 2 6 4
8 ). Chọn đáp án D.
Câu 27. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là x 2y 4z 1
0 và điểm M 1; 0; 2 . Tính khoảng cách d từ điểm M đến mặt 1
phẳng P và tính khoảng cách d từ điểm M đến mặt phẳng Oxy . 2 10 10 21 A. d và d 1 . B. d và d 3 . 1 2 1 2 21 21 10 10. 21 C. d và d 2 . D. d và d 2 . 1 2 1 2 20 21 Hướng dẫn giải 1 2.0 4 2 1 10 21 Ta có: d d M; P 1 . 2 2 2 21 1 2 4 2
Mặt phẳng Oxy : z 0 d d M; Oxy 2 2 . Chọn đáp án D. 2 1
Câu 28. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là 2x 2y 3z
0 . Viết phương trình của mặt phẳng Q đi qua hai điểm H 1; 0; 0 và
K 0; 2; 0 biết Q vuông góc với P . A. Q : 6x 3y 4z 6 0 . B. Q : 2x y 2z 2 0 . C. Q : 2x y 2z 2 0 . D. Q : 2x y 2z 2 0 . Hướng dẫn giải Trang 13
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI Ta có: KH
1;2;0 và vtpt của P là: n 2; 2; 3 P .
Vì mặt phẳng Q đi qua hai điểm H 1; 0; 0 , K 0; 2; 0 và vuông góc với P nên véctơ
pháp tuyến của Q là: n KH,n 6;3; 6 3 2; 1;2 Q P . Vậy Q : 2 x 1 y 2z 0
2x y 2z 2 0 . Chọn đáp án B.
Câu 29. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là 2x y 5z 6
0 . Viết phương trình của đường thẳng d đi qua điểm M 1; 2;7
biết d vuông góc với P . x 1 y 2 z 7 x 2 y 1 z 5 A. d : . B. d : . 2 1 5 1 2 7 x 1 y 2 z 7 x 1 y 2 z 7 C. d : . D. d : . 2 1 5 2 1 5 Hướng dẫn giải
Ta có vtpt của P là: n 2;1; 5 P .
Vì đường thẳng d vuông góc với P nên vtcp của d là: n 2;1; 5 P . x 1 y 2 z 7
Suy ra phương trình đường thẳng d là: . Chọn đáp án C. 2 1 5
Câu 30. Trong không gian với hệ trục tọa độ Oxyz viết phương trình của đường thẳng d đi
qua hai điểm E 9; 8; 8 và F 10; 6; 8 . x 9 19t x 9 19t A. d : y 8 14t t . B. d : y 8 14t t . z 8 t z 0 x 10 19t x 10 19t C. d : y 6 14t t . D. d : y 6 14t t . z 8 t z 8 Hướng dẫn giải
Vì d đi qua hai điểm E 9; 8; 8 và F
10; 6; 8 nên véctơ chỉ phương của d là: x 10 19t FE
19; 14;0 . Vậy phương trình tham số của d là: d : y 6 14t t z 8 Trang 14
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Câu 31. Trong không gian với hệ trục tọa độ Oxyz cho hai đường thẳng p và q tương ứng x 1 t x y 1 z 6 có phương tình là và y 6 7t t
. Chọn mệnh đề đúng trong 1 2 4 z 2 4t bốn mệnh đề sau: A. p // q . B. p cắt q .
C. p trùng với q . D. p chéo q . Hướng dẫn giải x t x y 1 z 6 Ta có: p : y 1 2t t . 1 2 4 z 6 4t t 1 t t 1 Cho 1 2t 6 7t t 0 . 6 4t 2 4t 6 4t 2 4t OK Chọn B.
Câu 32. Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình là x 3 y 3
z . Viết phương trình của đường thẳng
đi qua điểm M 6; 7; 0 biết 1 6 2 song song với d . x 6 y 7 z x 6 y 7 z A. : . B. : . 1 6 2 1 6 2 x 1 y 6 z 2 x 6 y 7 z C. : . D. : . 1 6 2 1 6 2 Hướng dẫn giải
Đường thẳng d có véctơ chỉ phương là: u 1; 6; 2 d Vì song song với d nên u 1; 6; 2 . x 6 y 7 z
Phương trình đường thẳng là : . 1 6 2 Chọn A.
Câu 33. Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d và mặt phẳng P x 3 y 1 z 2
tương ứng có phương trình là và 3x y 5z 5 0 , gọi mặt 2 1 1 phẳng Q là mặt phẳng z
Ox . Chọn mệnh đề đúng trong bốn mệnh đề sau
A. d // P và d cắt Q . B. d P và d cắt Q . C. d cắt P và d cắt Q .
D. d // P và d // Q . Hướng dẫn giải Ta có:
Đường thẳng d qua điểm M 3; 1; 2 và có véctơ chỉ phương u 2; 1;1 . d
Mặt phẳng P có véctơ pháp tuyến n 3;1; 5 . 1
Mặt phẳng Q có phương trình là y
0 và có véctơ pháp tuyến là n 0;1; 0 . 2 Trang 15
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI u .n 2.3 1.1 1. 5 0 Vì d 1
Và thế điểm M 3; 1; 2 vào P , Q đều không u .n 2.0 1.1 1.0 1 d 2
thỏa. Suy ra d // P và d cắt Q . Chọn A.
Câu 34. Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình là x y 2
z 1 . Viết phương trình của mặt phẳng P vuông góc với đường thẳng 8 3 5
d và biết mặt phẳng P đi qua điểm M 0; 8;1 . A. P : 8x 3y 5z 19 0 . B. P : 8x 3y 5z 27 0 . C. P : 8x 3y 5z 19 0 . D. P : 8x 3y 5z 19 0 . Hướng dẫn giải
Véctơ chỉ phương của đường thẳng d là u 8; 3; 5 . d
Vì mặt phẳng P vuông góc với đường thẳng d nên véctơ pháp tuyết của P là n u 8; 3; 5 . d Phương trình mặt phẳng P : 8 x 0 3 y 8 5 z 1 0 8x 3y z 5 19 0. Chọn C.
Câu 35. Tìm tập nghiệm S của bất phương trình x 3 x 4 2 0 . A. S 0; . B. S 3; . C. S 6; . D. S . Hướng dẫn giải 2 Ta có x 3 x x x x 1 4 2 0 64. 2 2 0 2 x 6 . 64 Chọn C.
Câu 36. Tìm tập nghiệm S của bất phương trình log x 6 log x 8 . 3 9 A. S 0; 6 . B. S ; 6 . C. S ; 9 . D. S 0; 9 . Hướng dẫn: log x 6 log x 8 3 9 x 0 x 0 x 0 x 0 x 0 log x 6 log x 8 3 2 log x 3log x 8 4 log x 8 log x 2 x 9 3 3 3 3 3 Vậy chọn đáp án D
Câu 37. Trong mặt phẳng hệ trục tọa độ Oxy tập hợp T các điểm biểu diễn của các số phức z thỏa z
10 và phần ảo của z bằng 6.
A. T là đường tròn tậm O bán kính R 10. B. T 8; 6 , 8; 6 .
C. T là đường tròn tậm O bán kính R 6 . D. T 6; 8 , 6; 8 . Hướng dẫn: Gọi 2 z x yi(x, y ,i 1) Trang 16
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 2 2 2 z 10 x y 10 x 64 x 8 Ta có: y 6 y 6 y 6 y 6 Vậy chọn đáp án B
Câu 38. Tìm các số phức z thỏa 2iz 3z 1 4i . A. z 1 2i . B. z 1 2i . C. z 1 2i . D. z 1 2i . Hướng dẫn: Gọi 2 z x yi(x, y ,i 1) zx yi Ta có: 2iz 3z 1 4i 2i(x yi) 3(x yi) 1 4i 3x 2y (2x 3y)i 1 4i 3x 2y 1 x 1 2x 3y 4 y 2 Vậy chọn đáp án A.
Câu 39. Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P có phương trình là 2x 2y z 16
0 . Viết phương trình của mặt cầu S có tâm I 3;1; 0 biết S tiếp xúc với mặt phẳng P . 2 2 2 2 A. 2 S : x 3 y 1 z 16 . B. 2 S : x 3 y 1 z 4 . 2 2 2 2 C. 2 S : x 3 y 1 z 16 . D. 2 S : x 3 y 1 z 16 . Hướng dẫn: 2. 3   2.1 0 16
Vì S  tiếp xúc với P nên S  có bán kính R d I, P     4 . 2  2   2 2 2 1 Phương trình mặ 2 2
t cầu S   x     y   2 : 3 1  z  16 . Vậy chọn đáp án C.
Câu 40. Trong không gian với hệ trục tọa độ Oxyz cho hai mặt phẳng P và Q tương ứng có
phương trình là 3x 6y 12z 3 0 và 2x my 8z 2
0 , với m là tham số thực.
Tìm m để mặt phẳng P song song ới mặt phẳng Q và khi đó tính khoảng cách d
giữa hai mặt phẳng P và Q . 2 1 A. m 4 và d . B. m 4 và d . 21 21 2 2 C. m 2 và d . D. m 4 và d . 21 21 Hướng dẫn:
Mặt phẳng P và Q có vectơ pháp tuyến lần lượt là    1
n  3; 6;12 và n2 2; ; m 8 . 3   k.2  3  k
Để P€ Q thì      6
  k.m  1
n cùng phương n2 , tức là k 0, 1 n k n2  2 .     m  4 12 k.8 Trang 17
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 2.1 4.0  8.0  2 2
Chọn M 1;0;0  P . Khi đó: d P,Q  d M ; Q   . 0   o      2 2 2 21 2 4  8
Vậy chọn đáp án D.
Câu 41. Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng P và đườngthẳng  x y  2 z  2
tương ứng có phương trình là x  3y z 1  0 và  
, với m là tham số 2 1 m
thực khác 0 . Tìm m để đường thẳng  song song với mặt phẳng P và khi đó tính
khoảng cách giữa đườngthẳng  và mặt phẳng P 3 3
A. m  2 và d  .
B. m 1 và d  . 11 11 4 3
C. m 1 và d  . D. m  1  và d  . 11 11 Hướng dẫn giải Chọn B. Ta có  ó c
VTCP u  2;1;m;qua M 0; 2  ; 2  
Mặt phẳng  P ó c VTPT n  1; 3  ;  1 u  .n  0 Để   / /  P ì th    M   Pm 1 d   P 3 ( ; )  11
Câu 42. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y x  ln 2  2x trên đoạn  1  1;   .  2  1
A. M  ln 2 và m  .
B. M  ln 2 và m  1   ln 4. 2 1 A. M  và m  1   ln 4.
D. M  ln 2 và m 1 ln 4 . 2 Hướng dẫn giải Chọn B.  1  x
Ta có Trên 1; ta ó c y ' 
y '  0  x  0    2  1 x   f     f   1 1 ( 1) 1 ln 4; 0  ln 2; f     2  2
Vậy ta có M  ln 2 và m  1   ln 4
Câu 43. Tìm tập nghiệm S của bất phương trình log x2 3.log x  2  0. 25 25
A. S   ;  2  5 625; .
B. S  0;2  5 625; .
C. S  0;2  5 625; .
D. S  625; . Hướng dẫn giải Chọn C.
Điều kiện: x  0 t  log x 25 Trang 18
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI t  2 log x  2 x  625
Bất phương trình trở thành: 2 25
t  3t  2  0       t 1 log x  1  x  25 25
Kết hợp điều kiện ta có nghiệm của bất phương trình là: S  0;2  5 625;
Câu 44. Tìm tập nghiệm S của bất phương trình 9x 4.3x   3  0 .
A. S  0;  1 .
B. S  1;  3 .
C. S    ;1 .
D. S  0;  1 . Hướng dẫn giải Chọn A. Đặt  3x tt  0
Bất phương trình trở thành: 2  4  3  0  1   3  1  3x t t t  3  0  x 1
Kết hợp điều kiện ta có nghiệm của bất phương trình là: S  0;  1
Câu 45. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y  3x 1 và đồ thị hàm số
y  3x 1. 1 1 1 A. S  . B. S  2 . C. S  . D. S  . 2 6 3 Hướng dẫn giải Chọn A. x  0
Phương trình hoành độ giao điểm là: 2 3x 1  3x 1   x 1 1 1 1 Ta có: 2 2 S  3x 1 (3x 1) x d = 3x  3x x d    2 0 0 Câu 46. Cho hàm số 3
y x  m   2 2
1 x  2x , với m là tham số thực. Tìm tập hợp M của các
tham số thực m sao cho hàm số đã cho đạt cực tiểu tại điểm x 1. A. M   . B. M    3 .
C. M    3 .
D. M    6 . Hướng dẫn giải. Chọn C. Ta có: 2
y  6x  2m  
1 x  2, y  12x  2m   1 .
Hàm số đã cho đạt cực tiểu tại điểm x 1khi y 
1  0  6  2m  
1  2  0  m  3  . Với m  3  ta có y   1  12  2 3    1  1
 2  0 suy ra hàm số đã cho đạt cực tiểu tại điểm x 1. Vậy m  3
 là giá trị cần tìm.
Câu 47. Cho hình tứ diện EFGH có EF vuông góc với EG , EG vuông góc với EH , EH vuông
góc với EF ; biết EF  6a, EG  8a, EH 12a , với a  0, a
. Gọi I , J tương ứng là
trung điểm của hai cạnh FG , FH . Tính khoảng cách d từ điểm F đến mặt phẳng
EIJ  theo a 12 29.a 6 29.a 24 29.a 8 29.a A. d  . B. d  . C. d  . D. d  . 29 29 29 29 Hướng dẫn giải. Chọn C. Trang 19
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI G z 8a I N x E 6a F K 12a M J y H
Cách 1: Vì EF vuông góc với EG , EG vuông góc với EH nên EG  (EFH ) . Gọi K là
trung điểm của EF suy ra IK  (EFH ) . Gọi M , N lần lượt là hình chiếu của K trên EJ
và IM ta có d K,EIJ   KN . Ta có: d  F,EIJ   2d K,EIJ   2KN
Trong tam giác EKJ vuông tại K và tam giác IKM vuông tại K ta có: 1 1 1 1 1 1 1 1 1 29 12 29           a KN a . Vậy 24 29. d  . 2 2 2 2 2 2 2 2 2 2 KN KM KI KJ KE KI 9a 16a 36a 144a 29 29
Cách 2: Vì EF vuông góc với EG , EG vuông góc với EH nên EG  (EFH ) . Gọi K là
trung điểm của EF suy ra IK  (EFH ) . Chọn hệ trục tọa độ Oxyz như hình vẽ ta có:
K 0;0;0, I 0;0;4a, E 3 ;
a 0;0, J 0;6 ; a 0 x y z
Phương trình mặt phẳng  EIJ  :  
 1  4x  2y  3z 12a  0 3a 6a 4a
  EIJ   d K EIJ  12a 24a 24 29a d F , 2 ,  2   . 4  9 16 29 29
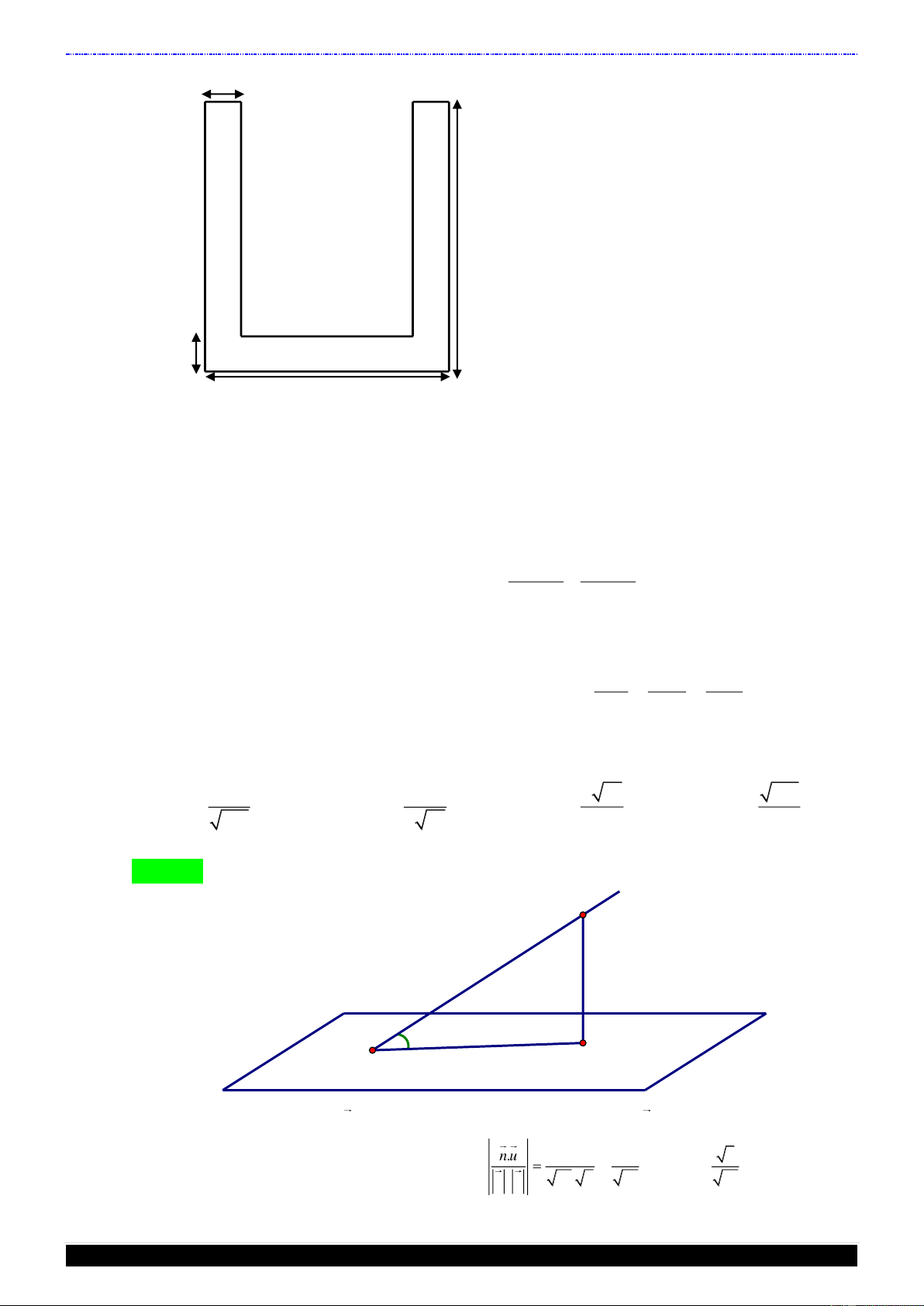
Câu 48. Một lọ trống miệng đựng nước là hình trụ tròn xoay có chiều
cao bằng 1, 6 dm ; đường kính đáy bằng 1 dm ; đáy (dưới) của
lọ phẳng với bề dày không đổi bằng 0,2 dm ; thành lọ với bề
dày không đổi bằng 0,2 dm ; thiết diện qua trục của lọ như
hình vẽ; đổ vào lọ 2,5 dl nước (trước đó trong lọ không có
nước hoặc vật khác). Tính gần đúng khoảng cách k từ mặt
nước trong lọ khi nước lặng yên đến mép trên của lọ (quy
tròn số đến hàng phần trăm, nghĩa là làm tròn số đến hai chữ số sau dấu phảy)
A. k  0,52dm.
B. k  1,18dm .
C. k  0,53dm . D. k  0,5  1 dm . Hướng dẫn giải. Chọn A. Trang 20
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI 0.2 dm 1.6 dm 0.2 dm 1 dm
Thể tích nước có thể chứa của lọ: V    2 3
0,3 .1, 4  3,96dm  3,96 . l
Thể tích nước đổ vào trong lọ là: V  2,5dl  0,25l
Phần thể tích không nước là V
 V V  0,3960,25  0,146l
Vậy độ cao của phần không chứa nước là V 0,146 h    m .0,3 0, 52d 2 .0,32
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P và đường thẳng d x 1 y  2 z  2
tương ứng có phương trình là 2x y  3z  3  0 và   2  1 1  . Biết đường
thẳng d  cắt mặt phẳng P tại điểm M . Gọi N là điểm thuộc d  sao cho MN  3,
gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng P . Tính độ dài đoạn MK . 7 7 4 21 105 A. MK  . B. MK  . C. MK  . D. MK  . 105 4 21 7 7 Hướng dẫn giải Chọn D. N d α K M P
P có vec tơ pháp tuyến n  2; 1
 ;3 , d  có vec tơ chỉ phương u   2  ;1;  1 . . n u 8 4 5
Gọi  là góc giữa P và d  . Ta có: sin     cos  . n . u 14. 6 21 21 Trang 21
Nguyễn Văn Huy - Biên Hòa, Đồng Nai
Lời giải: Tập thể giáo viên
ĐỀ THI HỌC KỲ 2 – TOÁN 12 SỞ GD&ĐT ĐỒNG NAI
Tam giác MNK vuông tại K nên 5 MK 5 105 cos    MK  .3  . 21 MN 21 7
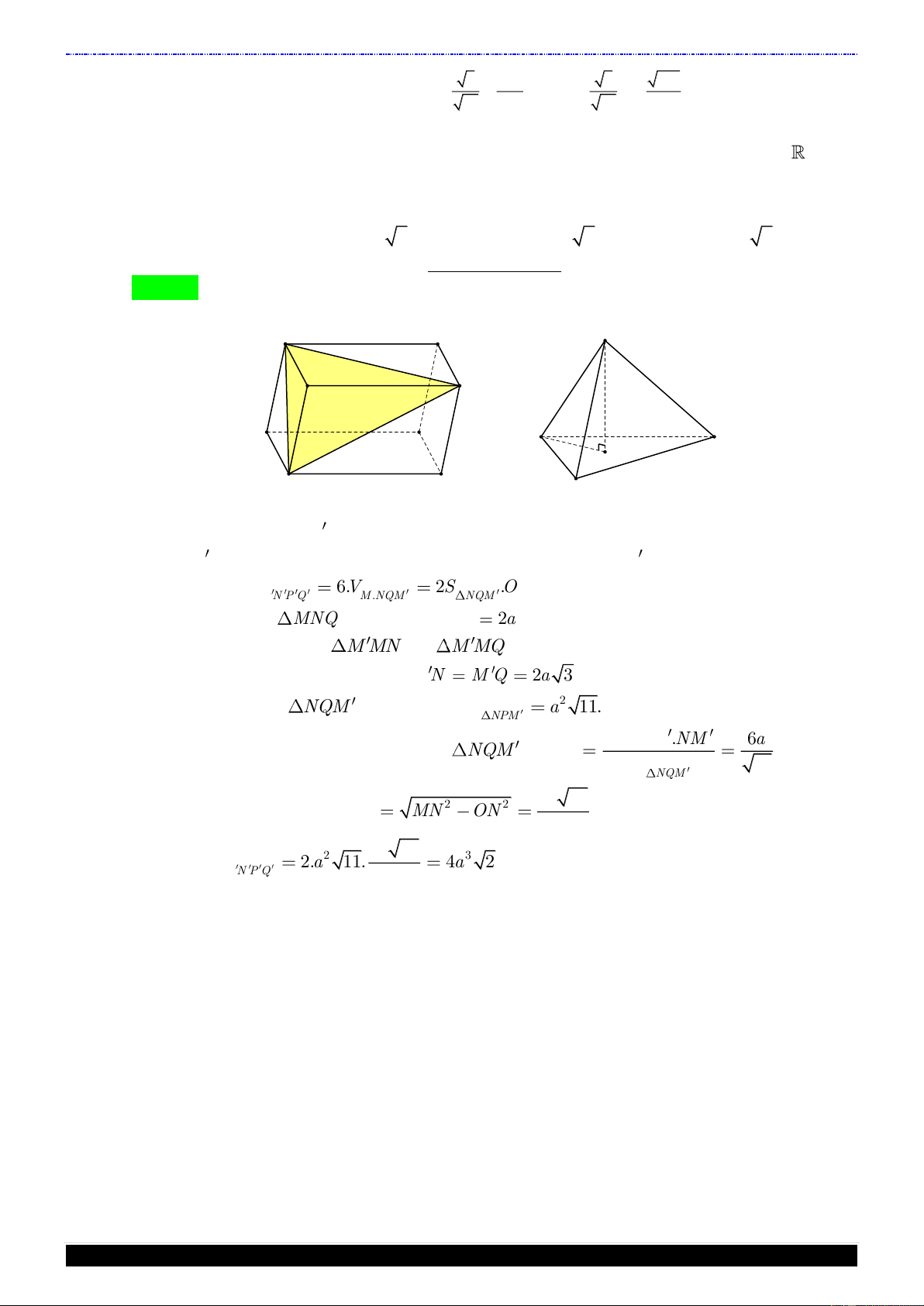
Câu 50. Cho hình hộp M . NPQ M NPQ
  có các cạnh đều bằng 2a , với a  0;a  . Biết
QMN  60 , M MQ M M
N 120 . Tính thể tích V của khối hộp M . NPQ M NPQ   theo a . A. 3 V  8.a . B. 3 V  2.a . C. 3 V  2 2.a . D. 3 V  4 2.a . Hướng dẫn giải Chọn D N P M M Q P' N' N M' O M' Q' Q
Do hình chóp M.NQM có 3 cạnh bên cùng bằng 2a nên chân đường cao của hình chóp
M.NQM là tâm O của đường tròn ngoại tiếp mặt đáy NQM . Như thế V 6.V 2S .OM MNPQ.M N P Q M .NQM NQM
Từ giả thiết ta có MNQ đều, suy ra NQ 2a .
Dùng định lý côsin cho M MN và M MQ ta tính được M N M Q 2a 3 .
Dùng Hêrông cho NQM ta tính được 2 S a 11. NPM NQ.QM .NM 6a
Từ đó bán kính đường tròn ngoại tiếp NQM là ON 4S 11 NQM a
Xét tam giác OMN, ta có 2 2 2 22 OM MN ON 11 2a 22 Vậy 2 3 V 2.a 11. 4a 2 . MNPQ.M N P Q 11
----------HẾT---------- Trang 22
Nguyễn Văn Huy - Biên Hòa, Đồng Nai