Đề thi HK2 Toán 12 năm học 2016 – 2017 sở GD và ĐT Lâm Đồng

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/6 – Mã đề 155

SƠ
GIA
O DU
C VA
ĐA
O TA
O
LÂM ĐÔ
NG
KIÊM TRA CHÂ
T LƯƠ
NG HO
C KI
II
Năm ho
c 2016 - 2017

ĐÊ
CHI
NH THƯ
C
(
Đê
co
6
tran
g
)
MÔN: TOA
N – Lơ
p 12 THPT
Thơ
i
g
ian la
m ba
i: 90
p
hu
t

Mã đề: 155
Câu 1.
Cho số thực
a
thỏa ma
n
01.a
Phát biểu nào sau đây
đúng
?
A.
.
xx
adx a C

B.
22
ln .
xx
adx a a C

C.
ln .
xx
adx a a C

D.
.
ln
x
x
a
adx C
a

Câu 2.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho mă
t câu

22 2
: 3 1 2 25.Sx y z
Tı
m tọa độ tâm
I
và bán kính
của mặt cầu
S
.
A.
3; 1; 2 ; 5IR
.
B.
3;1; 2 ; 5IR
.
C.
3;1; 2 ; 25IR
.
D.
3; 1; 2 ; 25IR
.
Câu 3.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho hai vectơ

0; 1; 0 , 3 ;1; 0ab

. Tı
nh góc
giữa hai vectơ
a
va
.b
A.
,30.
o
ab

B.
,60.
o
ab

C.
, 120 .
o
ab

D.
,90.
o
ab

Câu 4.
Trong không gian vơ
i hê
tọa độ
,Oxyz
tı
m tọa độ của vectơ
u
biê
t
2ui k

.
A.
(0;1; 2).u 
B.
(1; 0; 2).u 
C.
(1; 2; 0).u 
D.
(1; 0; 2).u
Câu 5.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho ba vectơ
(1; 0; 2)a 
,
(1;1;2)b 
và
(3; 1;1).c 
Tı
nh
,.ab c



.
A.
,. 5ab c



.
B.
,. 6ab c



.
C.
,. 7ab c




.
D.
,. 7ab c



.
Câu 6.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho mă
t phă
ng
():5 3 2 7 0Pxyz
.
Trong ca
c vectơ sau, vectơ na
o la
vectơ pha
p tuyê
n cu
a
()?
P
A.
(5;2;1)n
.
B.
(5;3;2)n
.
C.
(5; 3;2)n 
.
D.
(5; 3;1)n 
.
Câu 7.
Cho hàm số
()yfx
liên tu
c trên đoa
n

;ab
, hình thang cong
()
H
giới hạn bởi đồ thị
hàm số
()yfx
trục
Ox
và hai đường thẳng
,
x
ax b
. Khô
i tro
n xoay ta
o tha
nh khi
()
H
quay xung quanh trục
Ox
co
thê
tı
ch
V
đươ
c tı
nh bơ
i công thư
c
A.
() .
b
a
Vfxdx
B.
2
() .
b
a
Vfxdx
C.
2
().
b
a
Vfxdx
D.
() .
b
a
Vfxdx
Câu 8.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho hai điê
m
(2;3;1), (3;1;5).MN
Tìm tọa độ vectơ
.
M
N

A.
1; 2; 4 .MN 

B.
1; 2; 4 .MN 

C.
1; 2; 4 .MN 

D.

6;3;5 .MN

Câu 9.
Cho
,
f
g
là hai ha
m sô
liên tu
c trên đoa
n

2;5 ,
biết

5
2
3fxdx
và

5
2
9
g
tdt
.
Tı
nh
 
5
2
.
A
fx gx dx


A.
3.A
B.
12.A
C.
6.A
D.
8.A
Trang 2/6 – Mã đề 155
Câu 10.
Tı
nh
2
1
.Ixdx
A.
3
.
2
I
B.
3.I 
C.
1.I
D.
3.I
Câu 11.
Trong không gian vơ
i hê
tọa độ
,Oxyz
viê
t phương trình tham số của đường thẳng
()
đi qua điểm
(2;0; 1)M
và có vectơ chỉ phương

4; 6; 2a 
.
A.
42
(): 6.
2
xt
y
zt



B.
24
(): 6 .
12
xt
yt
zt



C.
42
(): 6 3.
2
xt
yt
zt



D.
24
(): 6 .
12
xt
yt
zt



Câu 12.
Cho hàm số
()yfx
co
đồ thị như hı
nh vẽ dươ
i đây. Diện tích hình phẳng (phần tô
ma
u trong hình vẽ) đươ
c tı
nh bơ
i công thư
c na
o?
A.
0
0
() () .
b
a
S f xdx f xdx


B.
0
2().
b
Sfxdx

C.
0
0
() () .
b
a
S f xdx f xdx


D.
() .
b
a
Sfxdx
Câu 13.
Tìm phần thực và phần ảo của số phức

14 3zi
.
A.
Phần thực bằng
11
và phần ảo bằng
(4).i
B.
Phần thực bằng
13
và phần ảo bằng
4
.
C.
Phần thực bằng
11
và phần ảo bằng
4.i
D.
Phần thực bằng
11
và phần ảo bằng
4
.
Câu 14.
Tính

sin 1 .Ixdx
A.
cos 1 .IxC
B.
cos .IxxC
C.
cos .IxC
D.
cos .IxxC
Câu 15.
Tính
53 (74).ii
A.
2.i
B.
27.i
C.
12 .i
D.
12 7 .i
Câu 16.
Nê
u hàm số
()Fx
là mô
t nguyên hàm của hàm số
()fx
thı
A.
'( ) ( ).fx Fx
B.
'( ) ( ).Fx fx
C.
() ().Fx f x
D.
() () .Fx f x C
Câu 17.
Nếu
()Fx
là nguyên hàm của hàm số
()fx
trên đoa
n

,ab
thì

b
a
fxdx
bă
ng
A.

() ().
b
a
fxdx Fb Fa
B.

() ().
b
a
fxdx Fa Fb

C.

() ().
b
a
fxdx Fa Fb
D.

().
b
a
fxdx Fb a
Câu 18.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho điê
m
(2;6; 3)I
va
ca
c mă
t phă
ng

:20,x


:60,y


:30.z

Tı
m khă
ng đi
nh
sai
.
A.

đi qua
.I
B.

.

C.

song song vơ
i
.Oz
D.

song song vơ
i

.xOz
Câu 19.
Tı
m số phức liên hợp của số phức
zabi
(
,ab R
).
A.
.abi
B.
.abi
C.
.abi
D.
.abi
Câu 20.
Go
i
12
,zz
lâ
n lươ
t la
hai nghiê
m cu
a phương trı
nh
2
250.zz
Tı
nh
12
.Fz z
A.
2.F
B.
10.F
C.
10.F
D.
25.F
x
y
b
a
O
Trang 3/6 – Mã đề 155
Câu 21.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho ba điểm
1; 3; 2 , 0; 1; 3 , ; ; 8
A
BCmn
(vơ
i
m, n la
tham sô
). Tìm tâ
t cả các giá trị của m, n để ba điểm
,,
A
BC
thẳng hàng.
A.
3; 11.mn
B.
1; 5.mn 
C.
1; 5 .mn
D.
1; 5.mn
Câu 22.
Tı
nh diện tích hình phẳng được giới hạn bởi đô
thi
ha
m sô
2
3yx x
và đường
thẳng
21.yx
A.
19
.
6
S
B.
47
.
6
S
C.
1
.
6
S
D.
11
.
6
S
Câu 23.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho hai mă
t phă
ng

:50 Pxyz
va
:2 2 2 3 0.Qxyz
Khă
ng đi
nh na
o sau đây đu
ng?
A.

P
song song vơ
i
.Q
B.
P
vuông góc vơ
i
.Q

C.
P
cắt
.Q

D.
P
trùng với
.Q
Câu 24.
Tı
nh thê
tı
ch
V
cu
a khôi tro
n xoay ta
o tha
nh khi quay hı
nh phă
ng giơ
i ha
n bơ
i ca
c
đươ
ng
tan , 0, 0,
4
yxyxx

xung quanh tru
c
.Ox
A.
ln 2.V
B.
ln 2.V
C.
ln 2
.
4
V
D.
2
.
4
V
Câu 25.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho hai đường thẳng
115
():
231
xyz

và
121
():
322
x
yz
d


. Mệnh đề nào sau đây
đúng
?
A.
()
và
()d
tru
ng nhau.
B.
()
và
()d
chéo nhau.
C.
()
và
()d
cắt nhau.
D.
()
và
()d
song song.
Câu 26.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho mặt phẳng
:2260Px y z
và điểm
1; 2; 1 .M
Khoảng cách từ điểm
M
đến mặt phẳng
()
P
là
A.
11
.
3
B.
11
.
9
C.
5
.
3
D.
13
.
3
Câu 27.
Tı
m nguyên hàm của ha
m sô
() 2cos2.
f
xx
A.
() sin2 C.fxdx x
B.
() 2sin2 C.fxdx x

C.
() 2sin2 C.fxdx x
D.
() sin2 C.fxdx x
Câu 28.
Trong ca
c khă
ng đi
nh sau, khă
ng đi
nh na
o
sai
?
A.
Co
vô sô
sô
phư
c bă
ng sô
phư
c liên hơ
p cu
a no
.
B.
Nê
u sô
phư
c
z
cu
ng la
sô
thư
c thı
gia
tri
tuyê
t đô
i cu
a
z
cu
ng la
môđun cu
a
.z
C.
Sô
phư
c
10 2zi
co
phâ
n a
o bă
ng
2.
D.
Sô
phư
c
37ze
co
phâ
n thư
c la
3.
Câu 29.
Trong không gian vơ
i hê
tọa độ
,Oxyz
viê
t phương trình mặt phẳng
()
P
đi qua điểm
1; 2; 1M
và nhận vectơ
2;3;5n
làm vectơ pháp tuyến.
A.
():2 3 5 2 0.Pxyz
B.
():2 3 5 1 0.Pxyz

C.
():2 3 5 3 0.Pxyz
D.
():2 3 5 2 0.Pxyz
Trang 4/6 – Mã đề 155
Câu 30.
Khă
ng đi
nh na
o sau đây
đu
ng
?
A.
44
00
tan .
x
dx tdt



B.
33
00
sin cos .
x
dx xdx


C.

55
22
22
11.
x
dx t dt

D.
22
2
11
.
xt
edx edt

Câu 31.
Cho hı
nh phă
ng
()
H
giới hạn bởi ca
c đươ
ng thă
ng
2, 0, 0, 2yx y x x
. Tı
nh thể
tích
V
khô
i tro
n xoay khi hình phẳng
()
H
quay quanh trục
.Ox
A.
2.V
B.
8
.
3
V
C.
8
.
3
V
D.
2.V
Câu 32.
Trong ca
c khă
ng đi
nh sau, khă
ng đi
nh na
o
sai
?
A.
1
cos3 sin 3 .
3
x
dx x C
B.
1
.
1
x
x
e
edx C
x

C.
1
ln1.
1
dx x C
x

D.
1
.
1
e
e
x
x
dx C
e

Câu 33.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho ba điê
m
(1;2;1),A (4;2;2),B 
(1;1;2).C 
Viê
t phương trı
nh tô
ng qua
t cu
a mă
t phă
ng
().
A
BC
A.
(): 20ABC x y z
.
B.
(): 20ABC x y z
.
C.
(): 70ABC x y z
.
D.
(): 0ABC x y z
.
Câu 34.
Trên mă
t phă
ng phư
c,
go
i
(1; 2)M
la
điê
m biểu diễn của số phức
.z
Tìm số phức liên
hơ
p cu
a
.z
A.
12.i
B.
2.i
C.
2.i
D.
12.i
Câu 35.
Tı
m nguyên ha
m
()Fx
của hàm số
1
() , 1
1
f
xx
x

biê
t
21F
.
A.
() ln 1 .Fx x C
B.
() ln 1 1.Fx x
C.
() ln 1 1.Fx x
D.
() ln 1.Fx x
Câu 36.
Trong mă
t phă
ng phư
c, xác định tập hợp các điểm biểu diễn số phức
z
sao cho
1
zi
là số thuần ảo.
A.
Trục tung, bỏ điểm co
tọa đô
0;1 .

B.
Trục tung.
C.
Đường thẳng
1y
, bỏ điểm co
tọa đô
0;1 .

D.
Đường thẳng
1y
.
Câu 37.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho đường thẳng
(): 8 4
32
xt
d
y
t
zt


và mặt phẳng
(): 7 0Pxyz
. Viê
t phương trình đường thẳng
(')d
là hình chiếu vuông góc của đường
thẳng
()d
lên mặt phẳng
().
P
A.
14
('): 125.
5
x
t
d
y
t
zt



B.
48
( ') : 10 10 .
12
x
t
d
y
t
zt



C.
38
('): 110.
12
x
t
d
y
t
zt



D.
4
('): 85.
3
xt
d
y
t
zt


Câu 38.
Cho số phức
z
thỏa mãn:
32 41 2iz i iz
. Tı
nh môđun của
.z
A.
210.z
B.
45.z
C.
22.z
D.
10.z
Trang 5/6 – Mã đề 155
Câu 39.
Trong không gian vơ
i hê
tọa độ
,Oxyz
viết phương trình mặt cầu
()S
có tâm
I
thuộc
trục
Oz
và đi qua hai điểm
2; 1; 4A
,
0; 2; 1B
.
A.
2
22
8269
():
525
Sx y z




.
B.
2
22
8269
():
55
Sx y z




.
C.
2
22
8269
():
525
Sx y z




.
D.
2
22
8269
():
525
Sx y z




.
Câu 40.
Trong không gian với hệ trục tọa độ
,Oxyz
cho đường thẳng
64
(): 2
12
x
t
d
y
t
zt



va
điê
m
(1;1;1).A
Tı
m toa
đô
điê
m
'
A
đô
i xư
ng vơ
i điểm
A
qua đường thẳng
().d
A.
'( 3;17;1).A
B.
'( 1;9;1).A
C.
'(3; 7;1).A
D.
'(5; 15;1).A
Câu 41.
Go
i
12
,zz
lâ
n lươ
t la
hai nghiê
m cu
a phương trı
nh
2
2100,zz
trong đó
1
z
co
phâ
n
a
o dương. Go
i
,,
M
NP
lâ
n lươ
t la
điê
m biê
u diê
n cu
a
12
,zz
va
sô
phư
c
kxyi
trên mă
t
phă
ng phư
c. Tı
m sô
phư
c
k
đê
tư
gia
c
OMNP
la
hı
nh bı
nh ha
nh (
O
la
gô
c tọa đô
cu
a mă
t
phă
ng phư
c).
A.
6.ki
B.
6.ki
C.
2.k 
D.
2.k
Câu 42.
Cho ha
m sô
()
f
x
liên tu
c trên
R
va
3
1
() 5.fxdx
Tı
nh
2
1
(2 1) .Ifxdx
A.
15
.
2
I
B.
5
.
2
I
C.
7
.
2
I
D.
9
.
2
I
Câu 43.
Cho hình phẳng
()
H
giới hạn bởi ca
c đươ
ng
2
2, 0yxxy
. Khi
()
H
quay xung
quanh trục
Ox
thu được khô
i tro
n xoay co
thê
tı
ch
1
a
V
b




, vơ
i
a
b
la
phân sô
tô
i gia
n.
Khi đo
.ab
bă
ng bao nhiêu?
A.
.3.ab
B.
. 12.ab
C.
. 24.ab
D.
. 15.ab
Câu 44.
Cho
2
1
ln
e
Ixxdxaeb
. Tı
nh giá trị biểu thức
.
A
ab
A.
0.A
B.
1
.
2
A
C.
.
A
e
D.
1
.
2
Ae
Câu 45.
Trong không gian vơ
i hê
tọa độ
,Oxyz
cho mặt cầu
222
(): 2 4 6 11 0Sx y z x y z
và mặt phẳng
:2 2 17 0.xyz

Viê
t phương trình mặt phẳng
()
song song với
()
và cắt
()S
theo giao tuyến là đường tròn có chu vi bằng
6.
A.
:2 2 – –7 0.xyz

B.
: 2 2 – 17 0.xyz


C.
:2 2 – 7 0.xyz

D.
:2 2 – 17 0.xyz

Câu 46.
Trong mặt phẳng phức, cho số phức
z
thỏa mãn
34 2z+i=
và
21w= z+i
. Tập hợp
điểm biểu diễn số phức
w
là đường tròn co
tâm
,I
bán kính
.R
Tı
m toa
đô
tâm
I
va
ba
n
kı
nh
.R
A.
57 4.
I
;,R=
B.
45 4.
I
;,R=
C.

34 2.
I
;,R=
D.
79 4.
I
;,R=
Trang 6/6 – Mã đề 155
Câu 47.
Trong không gian với hệ toạ độ
,Oxyz
cho 3 điểm
(1;2; 1), (2;1;1), (0;1;2)ABC
. Lập
phương trình đường thẳng
()
đi qua trực tâm của tam giác
ABC
và vuông góc với mặt
phẳng
().ABC
A.
1
2
5
(): 11.
2
4
5
xt
yt
zt



B.
71
35
8
(): 1.
3
52
35
xt
yt
zt



C.
11
4
(): 5.
3
2
2
3
xt
yt
zt



D.
22
8
(): 10.
3
4
2
3
xt
yt
zt



Câu 48.
Đê
đa
m ba
o an toa
n giao thông, khi dư
ng đe
n đo
ca
c xe ô tô pha
i ca
ch nhau tô
i thiê
u
1. m
Mô
t ô tô A đang cha
y vơ
i vâ
n tô
c
12 / sm
thı
gă
p ô tô B đang dư
ng đe
n đo
nên ô tô A
pha
i ha
m phanh va
chuyê
n đô
ng châ
m dâ
n đê
u vơ
i vâ
n tô
c đươ
c biê
u thi
bơ
i công thư
c

12 3 ( / ).
A
vt tms
Đê
đa
m ba
o an toa
n thı
ô tô A pha
i ha
m phanh khi ca
ch ô tô B mô
t
khoa
ng ı
t nhâ
t la
bao nhiêu me
t?
A.
23.
B.
24.
C.
25.
D.
22.
Câu 49.
Cho parabol như hı
nh ve
. Ha
y tı
nh diê
n tı
ch giơ
i ha
n bơ
i parabol va
tru
c hoa
nh.
A.
16.S
B.
28
.
3
S
C.
16
.
3
S
D.
32
.
3
S
Câu 50.
Trong không gian với hệ tọa độ
,Oxyz
cho ca
c điê
m
(6;0;6),A
(8;4;2),B 
(0;0;6),C
(1;1; 5).D
Go
i
(;;)M abc
thuô
c đươ
ng thă
ng
CD
sao cho diê
n tı
ch tam gia
c
MAB
nho
nhâ
t.
Tı
nh
3.Tab c
A.
16.T
B.
12.T 
C.
12.T
D.
8.T
……………… HẾT……………….
Họ và tên thí sinh:…………………………...SBD:…………………………………………
Chữ kí GT1: …………………………………Chữ kí GT2:…………………………………
y
x
4
2
-2
O 1
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA HỌC KÌ II - Năm học: 2016 – 2017
LÂM ĐÔ
NG Môn: Toán 12
ĐỀ CHÍNH THỨC Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Mã đề 155 (50 câu trắc nghiệm)
Câu 1. Cho số thực
0 1.
a
Phát biểu nào sau đây đúng?
A.
d .
x x
a x a C
B.
2 2
d ln .
x x
a x a a C
C.
d ln .
x x
a x a a C
D.
d .
ln
x
x
a
a x C
a
Hướng dẫn giải.
Chọn D.
Sử dụng trực tiếp bản nguyên hàm của hàm số cơ bản ta có d
ln
x
x
a
a x C
a
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
2 2 2
:( 3) ( 1) ( 2) 25.
S x y z
Tìm
tâm và bán kính
R
của mặt cầu
S
.
A.
(3; 1;2 5
),I R
. B.
( 3;1;
2), 5
I R
.
C.
( 3;1; 2
), 25
I R
. D.
(3; 1;2
), 25
I R
.
Hướng dẫn giải.
Chọn B.
Phương trình mặt cầu :
2 2 2 2
( ) ( ) ( )
x a y b z c R
có tâm
( ; ; ), bán kính .
I a b c R
Vậy suy
ra tâm và bán kính của mặt cầu là:
( 3;1; 2), 5.
I R
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho hai véc tơ
0;1;0 ;
a
3;1;0 .
b
Tìm góc giữa
hai véc tơ
a
va
.
b
A.
0
; 30
a b
. B.
0
; 60
a b
. C.
0
; 90
a b
. D.
0
; 120
a b
.
Hướng dẫn giải.
Chọn B.
Ta có
.
1
os ;
2
.
a b
c a b
a b
Suy ra
0
; 60
a b
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ của véc tơ
u
biết
2 .
u i k
A.
0;1; 2 .
u
B.
1;0; 2 .
u
C.
1; 2;0 .
u
D.
1;0;2 .
u
Hướng dẫn giải.
Chọn B.
Ta có
1;0;0 ; 0;0;1 2 0;0;2 2 1;0; 2 .
i k k u i k
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 2
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho ba véc tơ
1;0; 2 ; 1;1;2 ; 3; 1;1
a b c
.
Tính
;
a b c
?
A.
; 5.
a b c
B.
; 6.
a b c
C.
; 7.
a b c
D.
; 7.
a b c
Hướng dẫn giải.
Chọn D.
Ta có
0 2 2 1 1 0
; ; ; 2;0;1 ; 2.3 0. 1 1.1 7.
1 2 2 1 1 1
a b a b c
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:5x 3 2z 7 0
P y
. Trong các véc
tơ sau, vectơ nào là véctơ pháp tuyến của
P
?
A.
5;2;1
n
. B.
5;3;2
n
. C.
5; 3;2
n
. D.
5; 3;1
n
.
Hướng dẫn giải.
Chọn C.
Câu ly
thuyết nhâ
n biêt.
Câu 7. Cho hàm số
y f x
liên tục trên
;
a b
, hình thang cong
H
giới hạn bởi đồ thị hàm số
y f x
, trục
Ox
và hai đường thẳng
;
x a x b
. Khối tròn xoay tại thành khi
H
quay
quanh trục
Ox
có thể tích
V
được tính bởi công thức
A.
b
a
V f x dx
. B.
2
b
a
V f x dx
. C.
2
b
a
V f x dx
. D.
b
a
V f x dx
.
Hướng dẫn giải.
Chọn B.
Câu ly
thuyết nhâ
n biêt.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2;3;1 , 3;1;5
M N
. Tìm tọa độ của vectơ
MN
A.
1; 2; 4
MN
. B.
1; 2; 4
MN
. C.
1; 2;4
MN
. D.
6;3;5
MN
.
Hướng dẫn giải.
Chọn C.
Tọa độ của vectơ bằng tọa độ điểm ngọn trừ tọa độ điểm gôc.
3 2;1 3;5 1 1
;
; 4
2
MN
.
Câu 9. Cho
,
f g
là hai hàm số liên tục trên
2;5
, biết
5
2
3
f x dx
và
5
2
9
g t dt
. Tính
5
2
A f x g x dx
.
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 3
A.
3
A
. B.
12
A
. C.
6
A
. D.
8
A
.
Hướng dẫn giải.
Chọn B.
5 5 5 5 5
2 2 2 2 2
3 9 12
A f x g x dx f x dx g x dx f x dx g t dt
.
Câu 10. Tính
2
1
I xdx
A.
3
2
I
. B.
3
I
. C.
1
I
. D.
3
I
.
Hướng dẫn giải.
Chọn A.
2
2
2
1
1
1 3
2
2 2 2
x
I xdx
.
Câu 11. Trong không gian với hệ toạ độ
Oxyz
, viết phương trình tham số của đường thẳng
đi qua
điểm
2;0; 1
M
và có vectơ chỉ phương
4; 6;2
a
.
A.
4 2
: 6
2
x t
y
z t
. B.
2 4
: 6
1 2
x t
y t
z t
. C.
4 2
: 6 3
2
x t
y t
z t
. D.
2 4
: 6
1 2
x t
y t
z t
.
Hướng dẫn giải.
Chọn D.
Phương trình tham số của đường thẳng
đi qua điểm
2;0; 1
M
và có vectơ chỉ phương
4; 6;2
a
là
2 4
: 6
1 2
x t
y t
z t
.
Câu 12. Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây. Diện tích hình phẳng (phần tô màu trong
hình vẽ) được tính bởi công thức nào?
A.
0
0
d d
b
a
S f x x f x x
. B.
0
2 d
b
S f x x
.
C.
0
0
d d
b
a
S f x x f x x
. D.
0
d
b
S f x x
.
Hướng dẫn giải
Chọn C.
Vì trong đoạn
;0
a
thì
0
f x
, còn trong đoạn
0; b
thì
0
f x
nên ta tính theo công
thức
0
0
d d
b
a
S f x x f x x
.
Câu 13. Tìm phần thực và phần ảo của số phức
1 4 3
z i
.
x
y
b
O
a
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 4
A. Phần thực bằng
11
và phần ảo bằng
4
i
. B. Phần thực bằng 13 và phần ảo bằng
4
.
C. Phần thực bằng
11
và phần ảo bằng
4
i
. D. Phần thực bằng
11
và phần ảo bằng
4
.
Hướng dẫn giải.
Chọn D.
Có
1 4 3 1 4 12 11 4
z i i i
. Vậy phần thực bằng
11
và phần ảo bằng
4
.
Câu 14. Tính
sin 1 d
I x x
.
A. cos 1
I x C
. B. cos
I x x C
. C. cos
I x C
. D. cos
I x x C
.
Hướng dẫn giải.
Chọn B.
Có
sin 1 d cos
I x x x x C
Câu 15. Tính
5 3 7 4
i i
.
A.
2
i
. B.
2 7
i
. C.
12
i
. D.
12 7
i
Hướng dẫn giải
Chọn B.
Có
5 3 7 4 5 3 7 4 2 7
i i i i i
.
Câu 16. Nếu hàm số
F x
là một nguyên hàm của hàm số
f x
thì
A.
f x F x
. B.
F x f x
.
C.
F x f x
. D.
F x f x C
.
Hướng dẫn giải.
Chọn B.
Câu 17. Nếu
F x
là nguyên hàm của hàm số
f x
trên đoạn [a,b] thì
( )
b
a
f x dx
bằng
A.
( ) ( ) ( )
b
a
f x dx F b F a
. B.
( ) ( ) ( )
b
a
f x dx F b F a
.
C.
( ) ( ) ( )
b
a
f x dx F b F a
. D.
( ) ( )
b
a
f x dx F b a
.
Hướng dẫn giải.
Chọn A.
Câu 18. Trong không gian với hệ tọa độ
Oxyz
cho điểm
2;6; 3
I
và các mặt phẳng
: 2 0
x
; 6 0
y
;
: 3 0
z
. Tìm khẳng định sai.
A.
đi qua
I
. B.
. C.
/ /
Oz
. D.
song song
xoz
.
Hướng dẫn giải.
Chọn C.
+ Thay tọa độ T vào đáp án A thấy A đúng.
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 5
+
có ve
c tơ pháp tuyến (1;0;0);
có ve
c tơ pháp tuyến (0;1;0) tích vô hướng bằng 0 nên
hai mặt này vuông góc.
+
có ve
c tơ pháp tuyến (0;0;1);
Oz
có VTCP (0;0;1) nên
Oz
vuông với
dẫn đến C sai.
+
có ve
c tơ pháp tuyến (0;1;0);
xoz
có VTPT (0;1;0) nên hai mặt này song song .
Câu 19. Tìm số phức liên hợp của số phức
, , .
z a bi a b R
A.
a bi
. B.
a bi
. C.
a bi
. D.
a bi
.
Hướng dẫn giải.
Chọn B.
.
z a bi z a bi
.
Câu 20. Gọi
1 2
,
z z
lần lượt là hai nghiệm của phương trình
2
2 5 0.
z z
Tính
1 2
.
F z z
A.
2
F
. B.
10
F
. C.
10
F
. D.
2 5
F
.
Hướng dẫn giải.
Chọn D.
1
2
2
1 2
2 5 0
1 2
z i
z z
z i
1 2
5 5 2 5.
F z z
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
1;3; 2 , 0; 1;3 , ; ;8
A B C m n
, (với
,
m n
là tham số). Tìm tất cả các giá trị của
,
m n
để ba điểm
, ,
A B C
thẳng hàng.
A.
3; 11
m n
. B.
1; 5
m n
. C.
1; 5
m n
. D.
1; 5
m n
.
Hướng dẫn giải.
Chọn B.
Ta có:
1; 4;5
AB

và
1; 3;10
AC m n
Ba điểm
, ,
A B C
thẳng hàng
AB
và
AC
cùng phương
1 3 10
1 4 5
m n
1 2 1
3 8 5
m m
n n
.
Câu 22. Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
2
3
y x x
và đường thẳng
2 1
y x
.
A.
19
6
S
. B.
47
6
S
. C.
1
6
S
. D.
11
6
S
.
Hướng dẫn giải.
Chọn C.
Ta có phương trình :
2 2
1
3 2 1 3 2 0
2
x
x x x x x
x
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 6
Vậy diện tích hình phẳng được giới hạn bởi đồ thị hàm số
2
3
y x x
và đường thẳng
2 1
y x
là
2
2 2
3 2
2 3
1 1
1
3 1
3 2 .d 3 2 .d 2
3 2 6
x x
S x x x x x x x
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
: 5 0
P x y z
và
: 2 2 2 3 0
Q x y z
. Khẳng định nào sau đây đúng ?
A.
P
song song với
Q
. B.
P
vuông góc với
Q
.
C.
P
cắt
Q
. D.
P
trùng với
Q
.
Hướng dẫn giải.
Chọn A.
Ta có:
P
có vtpt
1;1; 1
P
n
và
Q
có vtpt
2;2; 2
Q
n
Ta thấy 2.
Q P
n n
hai vtpt
1;1; 1
P
n
,
2;2; 2
Q
n
cùng phương và
0;0;5
M P
nhưng
M Q
. Vậy
P
song song với
Q
.
Câu 24. Tính thể tích
V
của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
tan , 0, 0,
4
y x y x x
xung quanh trục
Ox
.
A.
ln 2
V
. B.
ln 2
V . C.
ln 2
4
V
. D.
2
4
V
.
Hướng dẫn giải.
Chọn A.
Thể tích
V
của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
tan , 0, 0,
4
y x y x x
xung quanh trục
Ox
là:
4 4 4
2
4
0
0 0 0
1 2
tan .d tan .d .d cos ln cos ln ln 2
cos 2
V x x x x x x
x
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho hai đường thẳng
1 1 5
:
2 3 1
x y z
và
1 2 1
:
3 2 2
x y z
d
. Mệnh đề nào sau đây là mệnh đề đúng?
A.
và
d
trùng nhau. B.
và
d
chéo nhau.
C.
và
d
cắt nhau. D.
và
d
song song.
Hướng dẫn giải.
Chọn B.
Đường thẳng
có vtcp
2;3;1
u
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 7
Đường thẳng
d
có vtcp
3;2;2
v
.
Ta thấy :
2;3;1
u
và
3;2;2
v
không cùng phương, do đó : loại đáp án A, D.
PTTS của đường thẳng
1 2
: 1 3
5
x t
y t
z t
và
1 3
: 2 2
1 2
x t
d y t
z t
.
Xét hệ phương trình :
3
5
1 2 1 3
2
1 3 2 2
5
5 1 2
3 2
5 1 2
5 5
t
t t
t t t
t t
hệ vô nghiệm.
Vậy
và
d
chéo nhau.
Câu 26. Trong không gian
Oxyz
, cho mặt phẳng
: 2 2 6 0
P x y z
và điểm
1;2; 1
M
. Khoảng
cách từ điểm
M
đến mặt phẳng
P
là
A.
11
.
3
B.
11
.
9
C.
5
.
3
D.
13
.
3
Hướng dẫn giải.
Chọn A.
Áp dụng công thức tính khoảng cách từ 1 điểm đến mặt phẳng, ta có:
2
2
1 2.2 2. 1 6
2 2 6
11
, .
3 3
1 2 2
M M M
x y z
d M P
Câu 27. Tìm nguyên hàm của hàm số
2cos2
f x x
A.
d sin 2 .
f x x x C
B.
d 2sin 2 .
f x x x C
C.
d 2sin 2 .
f x x x C
D.
d sin 2 .
f x x x C
Hướng dẫn giải.
Chọn D.
1
2cos 2 2. sin 2 sin 2 .
2
f x dx xdx x C x C
Câu 28. Trong các khẳng định sau, khẳng định nào sai ?
A. Có vô số số phức bằng số phức liên hợp của nó.
B. Nếu số phức
z
là số thực thì giá trị tuyệt đối của
z
cũng là mô đun của
.
z
C. Số phức
10 2
z i
có phần ảo bằng 2.
D. Số phức
3 7
z e
có phần thực là 3.
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 8
Hướng dẫn giải.
Chọn D.
Nếu số phức có dạng
,z a bi a b
thì phần thực là
a
, phần ảo là
b
.
Suy ra, số phức
3 7
z e
có phần thực là
3 7
e
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng
P
đi qua điểm
1;2; 1
M
và nhận
2;3;5
n
làm véc tơ pháp tuyến.
A.
: 2 3 5 2 0.
P x y z
B.
: 2 3 5 1 0.
P x y z
C.
: 2 3 5 3 0.
P x y z
D.
: 2 3 5 2 0.
P x y z
Hướng dẫn giải.
Chọn C.
Phương trình mặt phẳng
P
là:
2 1 3 2 5 1 0 2 3 5 3 0.
x y z x y z
Câu 30. Khẳng định nào sau đây là khẳng định đúng ?
A.
4 4
0 0
tan d d .
x x t t
B.
3 3
0 0
sin d cos d
x x x x
.
C.
5 5
2 2
2 2
1 d 1 d
x x t t
. D.
2 2
2
1 1
d d
x t
e x e t
.
Hướng dẫn giải.
Chọn C.
Câu 31. Cho hình phẳng
H
giới hạn bởi các đường thẳng
2
y x
,
0
y
,
0
x
,
2
x
. Tính thể tích
V
khối tròn xoay khi hình phẳng
H
quay quanh trục
Ox
.
A.
2 .
V
B.
8
.
3
V
C.
8
.
3
V
D.
2.
V
Hướng dẫn giải.
Chọn B.
2
2
2 3
0
0
1 8
2 . 2 .
3 3
V x dx x
Câu 32. Trong các khẳng định sau, khẳng định nào sai ?
A.
1
cos 3 d sin 3 .
3
x x x C
B.
1
d .
1
x
x
e
e x C
x
C.
1
d ln 1 .
1
x x C
x
D.
1
d .
1
e
e
x
x x C
e
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 9
Hướng dẫn giải.
Chọn B.
Công thức đúng là
d
x x
e x e C
nên B sai.
Câu 33. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
1;2;1
A
,
4;2; 2
B
,
1; 1; 2
C
.
Viết phương trình tổng quát của mặt phẳng
.
ABC
A.
2 0.
x y z
B.
2 0.
x y z
C.
7 0.
x y z
D.
0.
x y z
Hướng dẫn giải.
Chọn D.
3;0; 3 , 0; 3 3
AB AC
, 9; 9;9
AB AC
cùng phương với
1;1; 1
n
.
Mặt phẳng
ABC
qua điểm
1;2;1
A
và nhận
1;1; 1
n
có phương trình là:
1 1 1 2 1 1 0 0.
x y z x y z
Câu 34. Trên mặt phẳng phức, gọi
1;2
M
là điểm biểu diễn số phức
.
z
Tìm số phức liên hợp của
.
z
A.
1 2 .
i
B.
2 .
i
C.
2 .
i
D.
1 2 .
i
Hướng dẫn giải.
Chọn A.
Điểm biểu diễn của
z
là
1;2
M
, suy ra
1 2 1 2 .
z i z i
Câu 35. Tìm nguyên hàm
F x
của hàm số
1
1
f x
x
trên
1;

, biết
2 1.
F
A.
ln 1 .
F x x C
B.
ln 1 1.
F x x
C.
ln 1 1.
F x x
D.
ln 1 .
F x x
Hướng dẫn giải.
Chọn B.
1
ln 1 .
1
F x f x dx dx x C
x
2 1 ln1 1 1.
F C C
Vậy
ln 1 1.
F x x
Câu 36. Trong mặt phẳng phức, xác định tập hợp điểm biểu diễn số phức
z
sao cho
1
z i
là số thuần ảo.
A. Trục tung, bỏ điểm có tọa độ
0;1 .
B. Trục tung.
C. Đường thẳng
1
y
, bỏ điểm
0;1 .
D. Đường thẳng
1.
y
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 10
Hướng dẫn giải.
Chọn A.
Gọi
,z x yi x y
. Với
0
1
x
z i
y
Ta có:
2
2
1
1 1
1
x y i
z i x yi i
x y
1
z i
thuần ảo
2
2
0 0.
1
x
x
x y
Vậy, tập hợp điểm biểu diễn
z
là trục tung và bỏ điểm
0;1 .
Câu 37. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
: 8 4
3 2
x t
d y t
z t
và mặt phẳng
: 7 0
P x y z
. Viết phương trình đường thẳng
d
là hình chiếu vuông góc của
d
lên mặt
phẳng
P
A.
1 4
: 12 5 .
5
x t
d y t
z t
B.
4 8
: 10 10 .
1 2
x t
d y t
z t
C.
3 8
: 1 10 .
1 2
x t
d y t
z t
D.
4
: 8 5 .
3
x t
d y t
z t
Hướng dẫn giải.
Chọn B.
d
qua
0;8;3
A
và có véc tơ chỉ phương
1;4;2
u
P
có véc tơ pháp tuyến
1;1;1
n
Gọi
Q
là mặt phẳng chứa
d
và vuông với
P
, suy ra
d P Q
.
Pháp tuyến của
Q
là
, 2;1; 3
m u n
Véc tơ chỉ phương của
d
là
, 4; 5;1
v m n
Phương trình
Q
qua
A
và có véc tơ pháp tuyến
m
là:
2 3 1 0
x y z
Xét hệ
2 3 1 0
7 0
x y z
x y z
. Ta chọn được
4, 10, 1
x y z
thỏa mãn hệ này.
Suy ra, phương trình
d
qua
4;10;1
M
và có véc tơ chỉ phương
v
là
d
d'
u
n
Q
P
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 11
4 4
: 10 5
1 1
x t
d y t
z t
hay
4 8
: 10 10 .
1 2
x t
d y t
z t
Câu 38. Cho số phức
z
thỏa mãn
3 2 4 1 2
i z i i z
. Tính mô đun của
.
z
A.
2 10.
z B.
4 5.
z C.
2 2.
z D.
10.
z
Hướng dẫn giải.
Chọn D.
Gọi
,z a bi a b
. Suy ra:
3 2 4 1 2
i a bi i i a bi
3 3 2 2 4 4 2 2
a bi ai b i a bi ai b
3 2 4 4 2 3 2 2
a b a b i a b a b i
3 2 4 2 4 3
4 2 3 2 3 5 4 1
a b a b a b a
a b a b a b b
Suy ra
2 2
10.
z a b
Câu 39. Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt cầu
S
có tâm
I
thuộc trục
Oz
và đi qua hai điểm
2; 1;4 , 0;2; 1 .
A B
A.
2
2 2
8 269
.
5 25
x y z
B.
2
2 2
8 269
.
5 5
x y z
C.
2
2 2
8 269
.
5 25
x y z
D.
2
2 2
8 269
.
5 25
x y z
Hướng dẫn giải.
Chọn D.
Gọi tâm
0;0;
I m Oz
. Ta có
2 2
2 2
8
5 4 4 1 .
5
IA IB IA IB m m m
Suy ra, tâm
8
0;0;
5
I
.
Bán kính
2
269
5 4 .
5
R IA m
Phương trình mặt cầu
2
2 2
8 269
: .
5 25
S x y z
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 12
Câu 40. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
6 4
: 2
1 2
x t
d y t
z t
và điểm
1;1;1
A
. Tìm
tọa độ điểm
A
đối xứng với
A
qua
.
d
A.
3;17;1 .
A
B.
1;9;1 .
A
C.
3; 7;1 .
A
D.
5; 15;1 .
A
Hướng dẫn giải.
Chọn C.
4; 1;2
u
là véc tơ chỉ phương của
.
d
Gọi
6 4 ; 2 ; 1 2
H t t t
là hình chiếu vuông góc của
A
trên
d
.
Suy ra
. 0 5 4 . 4 3 . 1 2 2 .2 0 21 21 0 1.
AH u t t t t t
Với
1 2; 3;1
t H
H
là trung điểm của
AA
, suy ra
2 3
2 7 3; 7;1 .
2 1
A H A
A H A
A H A
x x x
y y y A
z z z
Câu 41. Gọi
1 2
,
z z
lần lượt là hai nghiệm của phương trình
2
2 10 0,
z z
trong đó
1
z
có phần ảo dương.
Gọi
, ,
M N P
lần lượt là điểm biểu diễn của
1 2
,
z z
và số phức
k x yi
trên mặt phẳng phức.
Tìm số phức
k
để tứ giác
OMNP
là hình bình hành
(
O
là gốc toạ độ của mặt phẳng phức)
A.
6
k i
. B.
6
k i
. C.
2
k
. D.
2
k
.
Hướng dẫn giải.
Chọn A.
Phương trình
2
2 10 0
z z
có 2 nghiệm phức là
1 2
1 3 , 1 3
z i z i
.
Từ đó
1;3 , 1; 3 , ;
M N P x y
.
Ta có
OMNP
là hình bình hành
0
6
6
x
OP MN k i
y

.
Câu 42. Cho hàm số
f x
liên tục trên
sao cho
3
1
d 5.
f x x
Tính
2
1
2 1 d .
I f x x
A.
15
2
I
. B.
5
2
I
. C.
7
2
I
. D.
9
2
I
.
Hướng dẫn giải.
Chọn B.
2 2 3
1 1 1
1 1 5
2 1 d 2 1 d 2 1 d 2 1
2 2 2
I f x x f x x f t t t x
d
u
H
A'
A
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 13
Câu 43. Cho hình phẳng
H
giới hạn bởi các đường
2
2 , 0.
y x x y
Khi quay
H
xung quanh trục
Ox
ta thư được khối tròn xoay có thể tích
1 ,
a
V
b
với
a
b
là phân số tối giản. Khi đó
ab
bằng bao nhiêu?
A.
3
ab
. B.
12
ab
. C.
24
ab
. D.
15
ab
.
Hướng dẫn giải.
Chọn D.
Phương trình hoành độ:
2
2 0 0 2
x x x x
Thể tích khối tròn xoay (nêu trong đề):
2
2
2
0
16 1
2 d 1
15 15
V x x x
Từ đó
1, 15 15
a b ab
.
Câu 44. Cho
2
1
ln d .
e
I x x x ae b
Tính giá trị biểu thức
.
A a b
A.
0
A
. B.
1
2
A
. C.
A e
. D.
1
2
A e
.
Hướng dẫn giải.
Chọn A.
2 2 2 2 2 2
1 1 1
1 1
.ln 1 1
ln d ln .d d
2 2 2 2 4 4 4
e e
e e e
x x x x e x e
I x x x x x
x
Từ đó
1 1
, 0
4 4
a b a b
.
Câu 45. Trong không gian với hệ toạ độ
,
Oxyz
cho mặt cầu
2 2 2
: 2 4 6 11 0
S x y z x y z
và
mặt phẳng
: 2 2 17 0.
x y z
Viết phương trình mặt phẳng
song song với
và
cắt
S
theo giao tuyến là đường tròn có chu vi bằng
6 .
A.
: 2 2 7 0
x y z
. B.
: 2 2 17 0
x y z
.
C.
: 2 2 7 0
x y z
. D.
: 2 2 17 0
x y z
.
Hướng dẫn giải.
Chọn A.
Do
//
nên
: 2 2 0 17
x y z D D
Mặt cầu
S
có tâm
1; 2;3 ,
I
bán kính
2 2 2
1 ( 2) 3 ( 11) 5
R
Đường tròn giao tuyến của
S
và
có bán kính
6
3
2
r
Như thế khoảng cách từ tâm
I
đến
là
2 2
,( ) 4
d I R r
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 14
2 2 2
2.1 2( 2) 3 5
4 4 7 do 17
3
2 2 ( 1)
D D
D D
Như vậy
: 2 2 7 0
x y z
Câu 46. Trong mặt phẳng phức, cho số phức
z
thỏa mãn
3 4 2
z i
và
2 1
w z i
. Tập hợp điểm
biểu diễn số phức
w
là đường tròn có tâm
I
, bán kính
R
. Tìm tọa độ tâm
I
và bán kính
R
.
A.
5; 7 , 4
I R
. B.
4;5 , 4
I R
. C.
3; 4 , 2
I R
. D.
7; 9 , 4
I R
.
Hướng dẫn giải.
Chọn A.
Đặt
w x yi
với
,x y
Ta có
1 1 5 7
2 1 3 4 3 4 3 4
2 2 2
w i w i w i
w z i z i z i z i
Vậy
5 7 5 7
3 4 2 5 7 4 5 7 4
2 2
w i w i
z i w i x y i
Tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
5; 7 , 4
I R
.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
1;2; 1
A
,
2;1;1
B
,
0;1;2
C
. Lập phương
trình đường thẳng
đi qua trực tâm của tam giác
ABC
và vuông góc với mặt phẳng
ABC
.
A.
1
2
5
: 1 1
2
4
5
x t
y t
z t
. B.
7 1
3 5
8
: 1
3
5 2
3 5
x t
y t
z t
. C.
1 1
4
: 5
3
2
2
3
x t
y t
z t
. D.
2 2
8
: 10
3
4
2
3
x t
y t
z t
.
Hướng dẫn giải.
Chọn B.
Ta có
1; 1;2 , 1; 1;3 , 1; 5; 2 1;5;2
AB AC u AB AC

Gọi
P
là mặt phẳng đi qua
C
và vuông góc với
AB
. Khi đó
P
có phương trình tổng quát
là:
1 0 1 1 2 2 0 2 3 0
x y z x y z
Gọi
Q
là mặt phẳng đi qua
B
và vuông góc với
AC
. Khi đó
Q
có phương trình tổng quát
là:
1 2 1 1 3 1 0 3 0
x y z x y z
Đường thẳng
P Q
Ta thấy véctơ chỉ phương của
chính là
u
nhận thấy hai đáp án B và C có véctơ chỉ phương
cùng phương
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyê
n Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đô
ng Page 15
Điểm
7 8 5
; ;
3 3 3
P
và
Q
còn điểm
4 2
1; ;
3 3
không thuộc mặt phẳng nào.
Nên đáp án B là đáp án cần tìm.
Câu 48. Để đảm bảo an toàn giao thông, khi dừng đèn đỏ các xe ô tô phải cách nhau tối thiểu
1m
. Một ô
tô
A
đang chạy với vận tốc
12 /m s
thì gặp ô tô
B
đang dừng đèn đỏ nên ô tô
A
phải hãm phanh
và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức
12 3 /
A
v t t m s
. Để
đảm bảo an toàn thì ô tô
A
phải hãm phanh cách ô tô
B
một khoảng ít nhất là bao nhiêu mét?
A.
23
. B.
24
. C.
25
. D.
22
.
Hướng dẫn giải.
Chọn C.
Khi ô tô A dừng hẳn thì
0V
suy ra:
v
(
t
)
0
12
3
t
0
t
4
Quảng đường ô tô A đi được từ lúc hãm phanh đến lúc dừng hẳn:
S (12 3t)dt
0
4
24
Để có khoảng cách an toàn thì cần quảng đường ít nhất là:
25 m
(cô
ng thêm 1 me
t khoảng cách
tôi thiê
u giư
a 2 xe).
Câu 49. Cho Parabol như hình ve
. Hãy tính diện tích giới hạn bởi Parabol và trục hoành.
A.
16S
. B.
28
3
S
. C.
16
3
S
. D.
32
3
S
.
Hướng dẫn giải.
Chọn D.
Từ hình vẽ ta dễ dàng tìm được phương trình của Parabol là
2
4y x
Diện tích hình cần tìm la
2
2
2
32
4 d
3
S x x
Sa
n Phâ
m Cu
a Tâ
p Thê Gia
o Viên Toa
n ABC…
Nhâ
n go
p y
: Nguyên Cho
e – Trươ
ng THPT Lê Quy
Đôn – Đa
Te
h – Lâm Đông Page 16
Câu 50. Trong không gian với hệ tọa độ
Oxyz
cho các điểm
6;0;6
A
,
8; 4; 2
B
,
0;0;6
C
,
1;1;5
D
. Gọi
; ;
M a b c
thuộc đường thẳng
CD
sao cho diện tích tam giác
MAB
nhỏ nhất. Tính
3
T a b c
A.
16
T
. B.
12
T
. C.
12
T
. D.
8
T
.
Hướng dẫn giải.
Chọn C.
Ta có
1;1; 1
CD
, phương trình tham số của đường thẳng
:
6
x t
CD y t
z t
Tọa độ
; ; ; ;6
M a b c t t t
6; ; ; 2; 4; 8 , 12 ;48 6 ;6 24 6 2 ;8 ; 4
AM t t t AB AB AM t t t t t t
Ta có
2 2
2 2
1
, 3 4 8 6 3 6 24 80
2
ABM
S AB AM t t t t t
 
Dễ dàng thấy được diện tích tam giác nhỏ nhất bằng
56
tại
2
t
Vậy
2; 6 4
a b t c t
Nên
3 12
T a b c
.
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DU ̣C VÀ ĐÀO TẠO
KIÊM TRA CHẤT LƯỢNG HỌC KÌ II LÂM ĐỒNG
Năm ho ̣c 2016 - 2017
ĐỀ CHÍNH THỨC
MÔN: TOÁN – Lớp 12 THPT (Đề có 6 trang)
Thời gian làm bài: 90 phút Mã đề: 155
Câu 1. Cho số thực a thỏa mãn 0  a 1. Phát biểu nào sau đây đúng? A. x x
a dx a C.  B. 2 x 2 x
a dx a ln a C.  x a C. x x
a dx a ln a C.  D. x a dx   C.  ln a
Câu 2. Trong không gian với hê ̣ tọa độ Oxyz, cho mă ̣t cầu S  x  2   y  2  z  2 : 3 1 2  25.
Tı̀m tọa độ tâm I và bán kính R của mặt cầu S . A. I 3; 1  ;2;R  5 . B. I  3;  1; 2  ;R  5. C. I  3;  1; 2  ;R  25 . D. I 3; 1  ;2;R  25.  
Câu 3. Trong không gian với hê ̣ tọa độ Oxyz, cho hai vectơ a  0;1;0,b   3;1;0 . Tı́nh góc  
giữa hai vectơ a và . b         A.  ,  30o a b  .
B.  ,  60 .o a b
C.  ,  120 .o a b
D.  ,  90 .o a b     
Câu 4. Trong không gian với hê ̣ tọa độ Oxyz, tı̀m tọa độ của vectơ u biết u i  2k .     A. u  (0;1; 2  ). B. u  (1;0; 2  ). C. u  (1; 2  ;0).
D. u  (1;0;2).  
Câu 5. Trong không gian với hê ̣ tọa độ Oxyz, cho ba vectơ a  (1;0; 2  ) , b  ( 1  ;1;2) và     c  (3; 1
 ;1).Tı́nh a,b.c   .            
A.a,b.c  5   .
B.a,b.c  6   .
C.a,b.c  7   .
D.a,b.c  7   .
Câu 6. Trong không gian với hê ̣ tọa độ Oxyz, cho mă ̣t phẳng (P) :5x 3y  2z  7  0 .
Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của (P)?    
A. n  (5;2;1) .
B. n  (5;3;2) . C. n  (5; 3  ;2) . D. n  (5; 3  ;1) .
Câu 7. Cho hàm số y f (x) liên tu ̣c trên đoa ̣n  ;
a b , hình thang cong (H) giới hạn bởi đồ thị
hàm số y f (x) trục Ox và hai đường thẳng x a, x b . Khối tròn xoay ta ̣o thành khi (H)
quay xung quanh trục Ox có thể tı́ch V được tı́nh bởi công thức b b b b
A. V f (x)d . xB. 2
V   f (x)d . xC. 2
V   f (x )d . x
D. V   f (x)d . xa a a a
Câu 8. Trong không gian với hê ̣ tọa độ Oxyz, cho hai điểm M (2;3;1), N(3;1;5). Tìm tọa độ vectơ  MN.     A. MN   1;  2; 4  . B. MN   1;  2; 4
 . C. MN  1; 2  ;4.
D. MN  6;3;5. 5 5
Câu 9. Cho f , g là hai hàm số liên tu ̣c trên đoa ̣n 2;  5 , biết f
 xdx  3 và g
 tdt  9 . 2 2 5
Tı́nh A   f
 x gxd .x  2 A. A  3. B. A 12. C. A  6.
D. A  8.
Trang 1/6 – Mã đề 155 2
Câu 10. Tı́nh I xd .x  1 3 A. I  . B. I  3.  C. I 1. D. I  3. 2
Câu 11. Trong không gian với hê ̣ tọa độ Oxyz, viết phương trình tham số của đường thẳng () 
đi qua điểm M (2;0;1) và có vectơ chỉ phương a  4; 6;2 .
x  4  2tx  2   4t
x  4  2t
x  2  4t    
A. () :  y  6  .
B. () :  y  6
t . C. () : y  6
  3t . D. () :  y  6  t .  z  2t     z  1 2tz  2  tz  1   2t
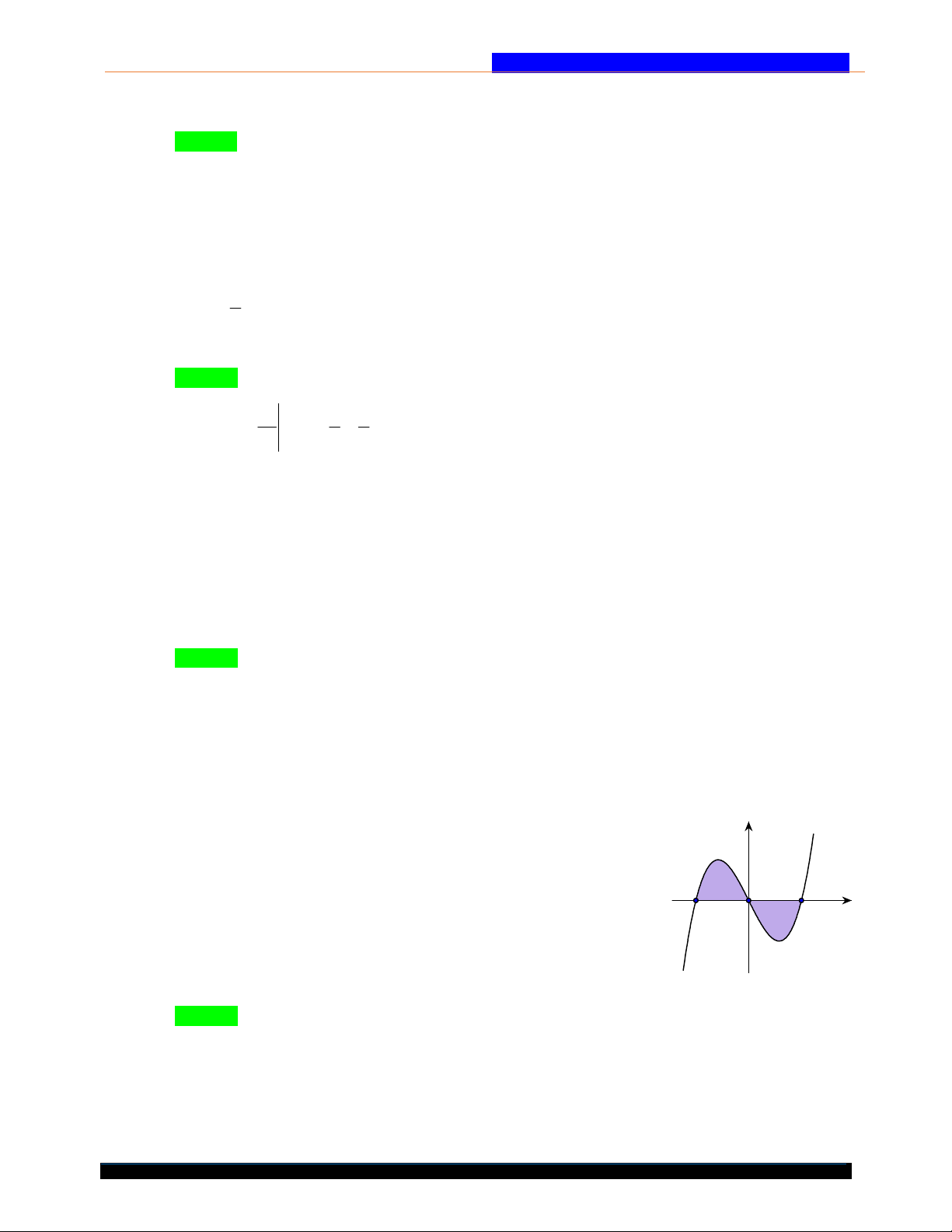
Câu 12. Cho hàm số y f (x) có đồ thị như hı̀nh vẽ dưới đây. Diện tích hình phẳng (phần tô
màu trong hình vẽ) được tı́nh bởi công thức nào? y 0 b b
A. S f (x)dx f (x)d . x  
B. S  2 f (x)d . xx a O b a 0 0 0 b b
C. S f (x)dx f (x)d . x  
D. S f (x)d . xa 0 a
Câu 13. Tìm phần thực và phần ảo của số phức z 1 4i  3 .
A. Phần thực bằng 11  và phần ảo bằng ( 4
 ) .iB. Phần thực bằng 13 và phần ảo bằng 4  .
C. Phần thực bằng 11
 và phần ảo bằng 4 .i D. Phần thực bằng 11
 và phần ảo bằng 4 .
Câu 14. Tính I  sin x    1 d . x
A. I  cos x 1 C.
B. I  cos x x  .
C C. I  cos x  . C
D. I  cos x x C.
Câu 15. Tính 5  3i  (7  4i). A. 2   .i B. 2   7 .i C. 12  .i D. 12  7 .i
Câu 16. Nếu hàm số F(x) là mô ̣t nguyên hàm của hàm số f (x) thı̀
A. f '(x)  F(x).
B. F '(x)  f (x).
C. F(x)  f (x).
D. F(x)  f (x)  C. b
Câu 17. Nếu F(x) là nguyên hàm của hàm số f (x) trên đoa ̣n a,b thì f xdx  bằng a b b A. f
 xdx F(b) F(a). B. f
 xdx F(a) F(b). a a b b C. f
 xdx F(a) F(b). D. f
 xdx F(b a). a a
Câu 18. Trong không gian với hê ̣ tọa độ Oxyz, cho điểm I(2;6; 3
 ) và các mă ̣t phẳng
: x 2  0,  : y 6  0,  : z 3  0. Tı̀m khẳng đi ̣nh sai.
A.   đi qua I.
B.     .
C.   song song với . Oz
D.   song song với xOz.
Câu 19. Tı̀m số phức liên hợp của số phức z a bi ( a,bR ).
A. a b .i
B. a b .i
C.a b .i
D.a b .i
Câu 20. Go ̣i z , z
F z z . 1
2 lần lươ ̣t là hai nghiê ̣m của phương trı̀nh 2
z  2z  5  0. Tı́nh 1 2 A. F  2. B. F 10. C. F  10. D. F  2 5.
Trang 2/6 – Mã đề 155
Câu 21. Trong không gian với hê ̣ tọa độ Oxyz, cho ba điểm A1;3; 2  , B0; 1  ;3,C  ; m ; n 8 (với
m, n là tham số). Tìm tất cả các giá trị của m, n để ba điểm ,
A B,C thẳng hàng.
A. m  3;n 11. B. m  1;  n  5. C. m  1  ;n  5.
D. m  1;n  5.
Câu 22. Tı́nh diện tích hình phẳng được giới hạn bởi đồ thi ̣ hàm số 2
y x x  3 và đường
thẳng y  2x 1. 19 47 1 11 A. S  . B. S  . C. S  . D. S  . 6 6 6 6
Câu 23. Trong không gian với hê ̣ tọa độ Oxyz, cho hai mă ̣t phẳng P: x y z 5  0 và
Q:2x  2y 2z 3  0. Khẳng đi ̣nh nào sau đây đúng?
A.P song song với Q.
B.P vuông góc với Q.
C.P cắt Q.
D.P trùng với Q.
Câu 24. Tı́nh thể tı́ch V của khối tròn xoay ta ̣o thành khi quay hı̀nh phẳng giới ha ̣n bởi các 
đường y  tan x, y  0, x  0, x  xung quanh tru ̣c . Ox 4  2 
A. V   ln 2. B. V  ln 2. C. ln 2 V  . D. V  . 4 4 x 1 y 1 z  5
Câu 25. Trong không gian với hê ̣ tọa độ Oxyz, cho hai đường thẳng () :   và 2 3 1 x 1 y  2 z 1 (d ) :  
. Mệnh đề nào sau đây đúng? 3 2 2
A. () và (d) trùng nhau.
B. () và (d) chéo nhau.
C. () và (d) cắt nhau.
D. () và (d) song song.
Câu 26. Trong không gian với hê ̣ tọa độ Oxyz, cho mặt phẳng P: x  2y  2z 6  0 và điểm M 1;2; 
1 . Khoảng cách từ điểm M đến mặt phẳng (P) là 11 11 5 13 A. . B. . C. . D. . 3 9 3 3
Câu 27. Tı̀m nguyên hàm của hàm số f (x)  2cos2 .x
A. f (x)dx  sin 2x  C. 
B. f (x)dx  2sin 2x  C. 
C. f (x)dx  2sin 2x  C. 
D. f (x)dx  sin 2x  C. 
Câu 28. Trong các khẳng đi ̣nh sau, khẳng đi ̣nh nào sai?
A. Có vô số số phức bằng số phức liên hợp của nó.
B. Nếu số phức z cũng là số thực thı̀ giá tri ̣ tuyê ̣t đối của z cũng là môđun của z.
C. Số phức z  10  2i có phần ảo bằng 2.
D. Số phức z  3 7e có phần thực là 3.
Câu 29. Trong không gian với hê ̣ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm  M 1;2; 
1 và nhận vectơ n  2;3;5 làm vectơ pháp tuyến.
A. (P) : 2x  3y  5z  2  0.
B. (P) : 2x  3y  5z 1  0.
C. (P) : 2x  3y  5z  3  0.
D. (P) : 2x  3y  5z  2  0.
Trang 3/6 – Mã đề 155
Câu 30. Khẳng đi ̣nh nào sau đây đúng?     4 4 3 3
A. tan xdx tdt.  
B. sin xdx  cos . xdx   0 0 0 0 5 5 2 2 C.  2 x  
1 dx   2t    1dt. D. 2x t e dx e dt.   2 2 1 1
Câu 31. Cho hı̀nh phẳng (H) giới hạn bởi các đường thẳng y x  2, y  0, x  0, x  2. Tı́nh thể
tích V khối tròn xoay khi hình phẳng (H) quay quanh trục . Ox 8 8 A. V  2. B. V  . C. V  . D. V  2. 3 3
Câu 32. Trong các khẳng đi ̣nh sau, khẳng đi ̣nh nào sai? 1 x 1 
A. cos3xdx  sin 3x C.  e B. x e dx   C.  3 x 1 1 e 1  C.
dx  ln x 1  C.  x D. e x dx   C.  x 1 e 1
Câu 33. Trong không gian với hê ̣ tọa độ Oxyz, cho ba điểm ( A 1  ;2;1), B( 4  ;2; 2  ), C( 1  ; 1  ; 2  ).
Viết phương trı̀nh tổng quát của mă ̣t phẳng (ABC).
A. (ABC) : x y z  2  0 .
B. (ABC) : x y z  2  0 .
C. (ABC) : x y z  7  0 .
D. (ABC) : x y z  0 .
Câu 34. Trên mă ̣t phẳng phức, go ̣i M (1;2) là điểm biểu diễn của số phức z. Tìm số phức liên hơ ̣p của z. A. 1 2 .i B. 2  .i C. 2  .i D. 1   2 .i 1
Câu 35. Tı̀m nguyên hàm F(x) của hàm số f (x)  , x
  1 biết F 2 1. x 1
A. F(x)  ln x 1  C. B. F(x)  ln x 1 1. C. F(x)  ln x  
1 1. D. F(x)  ln x 1. 1
Câu 36. Trong mă ̣t phẳng phức, xác định tập hợp các điểm biểu diễn số phức z sao cho z i là số thuần ảo.
A. Trục tung, bỏ điểm có tọa đô ̣ 0;  1 . B. Trục tung.
C. Đường thẳng y  1, bỏ điểm có tọa đô ̣ 0; 
1 . D. Đường thẳng y  1. x t
Câu 37. Trong không gian với hê ̣ tọa độ Oxyz, cho đường thẳng (d) : y  8 4t và mặt phẳng z  3 2t
(P) : x y z  7  0 . Viết phương trình đường thẳng (d ') là hình chiếu vuông góc của đường
thẳng (d) lên mặt phẳng (P). x 1 4t  x  4   8t  x  3 8t  x  4t
A. (d ') : y 12  5t.
B. (d ') : y 10 10t. C. (d ') : y 110t. D. (d ') : y  8  5t. z  5  t  z 1 2t  z 1 2t  z  3  t
Câu 38. Cho số phức z thỏa mãn: 3 2iz  41i  2  iz . Tı́nh môđun của .z A. z  2 10. B. z  4 5. C. z  2 2. D. z  10.
Trang 4/6 – Mã đề 155
Câu 39. Trong không gian với hê ̣ tọa độ Oxyz, viết phương trình mặt cầu (S) có tâm I thuộc
trục Oz và đi qua hai điểm A2; 1
 ;4 , B0;2;  1 . 2 2 A.  8  269  8  269 2 2
(S) : x y z     . B. 2 2
(S) : x y z     .  5  25  5  5 2 2 C.  8  269  8  269 2 2
(S) : x y z     . D. 2 2
(S) : x y z     .  5  25  5  25
x  6  4t
Câu 40. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng (d) : y  2
  t và điểm z  1   2t  (
A 1;1;1). Tı̀m toa ̣ đô ̣ điểm A' đối xứng với điểm A qua đường thẳng (d). A. A'( 3  ;17;1). B. A'( 1  ;9;1).
C. A'(3;7;1).
D. A'(5;15;1).
Câu 41. Go ̣i z , z    z 1
2 lần lươ ̣t là hai nghiê ̣m của phương trı̀nh 2 z
2z 10 0, trong đó 1 có phần
ảo dương. Go ̣i M , N, P lần lượt là điểm biểu diễn của z , z   1 2 và số phức k x yi trên mă ̣t
phẳng phức. Tı̀m số phức k để tứ giác OMNPlà hı̀nh bı̀nh hành (O là gốc tọa đô ̣ của mă ̣t phẳng phức). A. k  6  .i
B. k  6 .i C. k  2.  D. k  2. 3 2
Câu 42. Cho hàm số f (x) liên tu ̣c trên R và f (x)dx  5. 
Tı́nh I f (2x 1)d .x  1 1 15 5 7 9 A. I  . B. I  . C. I  . D. I  . 2 2 2 2
Câu 43. Cho hình phẳng (H) giới hạn bởi các đường 2
y  2x x , y  0 . Khi (H ) quay xung a a
quanh trục Ox thu được khối tròn xoay có thể tı́ch V     1   , vơ la  b  ́ i ̀ phân số tối giản. b Khi đó .
a b bằng bao nhiêu? A. . a b  3. B. . a b 12. C. . a b  24. D. . a b 15. e Câu 44. Cho 2
I x ln xdx ae b
. Tı́nh giá trị biểu thức A a  .b 1 1 1
A. A  0. B. A  . C. A   . e
D. A  e  . 2 2
Câu 45. Trong không gian với hê ̣ tọa độ Oxyz, cho mặt cầu 2 2 2
(S) : x y z  2x  4y  6z 11  0
và mặt phẳng   : 2x  2y z 17  0. Viết phương trình mặt phẳng ( ) song song với ()
và cắt (S) theo giao tuyến là đường tròn có chu vi bằng 6.
A.   : 2x  2y – z – 7  0.
B.   : 2x  2y – z 17  0.
C.   : 2x  2y – z  7  0.
D.   : 2x  2y – z 17  0.
Câu 46. Trong mặt phẳng phức, cho số phức z thỏa mãn z  3+4i = 2 và w= 2z+i 1. Tập hợp
điểm biểu diễn số phức w là đường tròn có tâm I, bán kính .
R Tı̀m toa ̣ đô ̣ tâm I và bán kı́nh . R
A. I 5; 7   ,R = 4.
B. I 4; 5
  ,R = 4. C. I 3; 4   ,R= 2.
D. I 7; 9   ,R = 4.
Trang 5/6 – Mã đề 155
Câu 47. Trong không gian với hệ toạ độ Oxyz, cho 3 điểm ( A 1;2; 1
 ), B(2;1;1),C(0;1;2) . Lập
phương trình đường thẳng () đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC).  7 1  1 x   t   x  2  t   3 5  x 11t
x  2  2t 5      8  4  8
A. () : y 11t .
B. () : y  1t . C. () :y   5t.
D. () :y  10t.  3 3 3 2    z  4  t  5 2  2  4  5 z   tz   2t z   2t  3 5  3  3
Câu 48. Để đảm bảo an toàn giao thông, khi dừng đèn đỏ các xe ô tô phải cách nhau tối thiểu 1 .
m Mô ̣t ô tô A đang cha ̣y với vâ ̣n tốc 12m / s thı̀ gă ̣p ô tô B đang dừng đèn đỏ nên ô tô A
phải hãm phanh và chuyển đô ̣ng châ ̣m dần đều với vâ ̣n tốc được biểu thi ̣ bởi công thức
v t 12 3t(m / s). A
Để đảm bảo an toàn thı̀ ô tô A phải hãm phanh khi cách ô tô B mô ̣t
khoảng ı́t nhất là bao nhiêu mét? A. 23. B. 24. C. 25. D. 22.
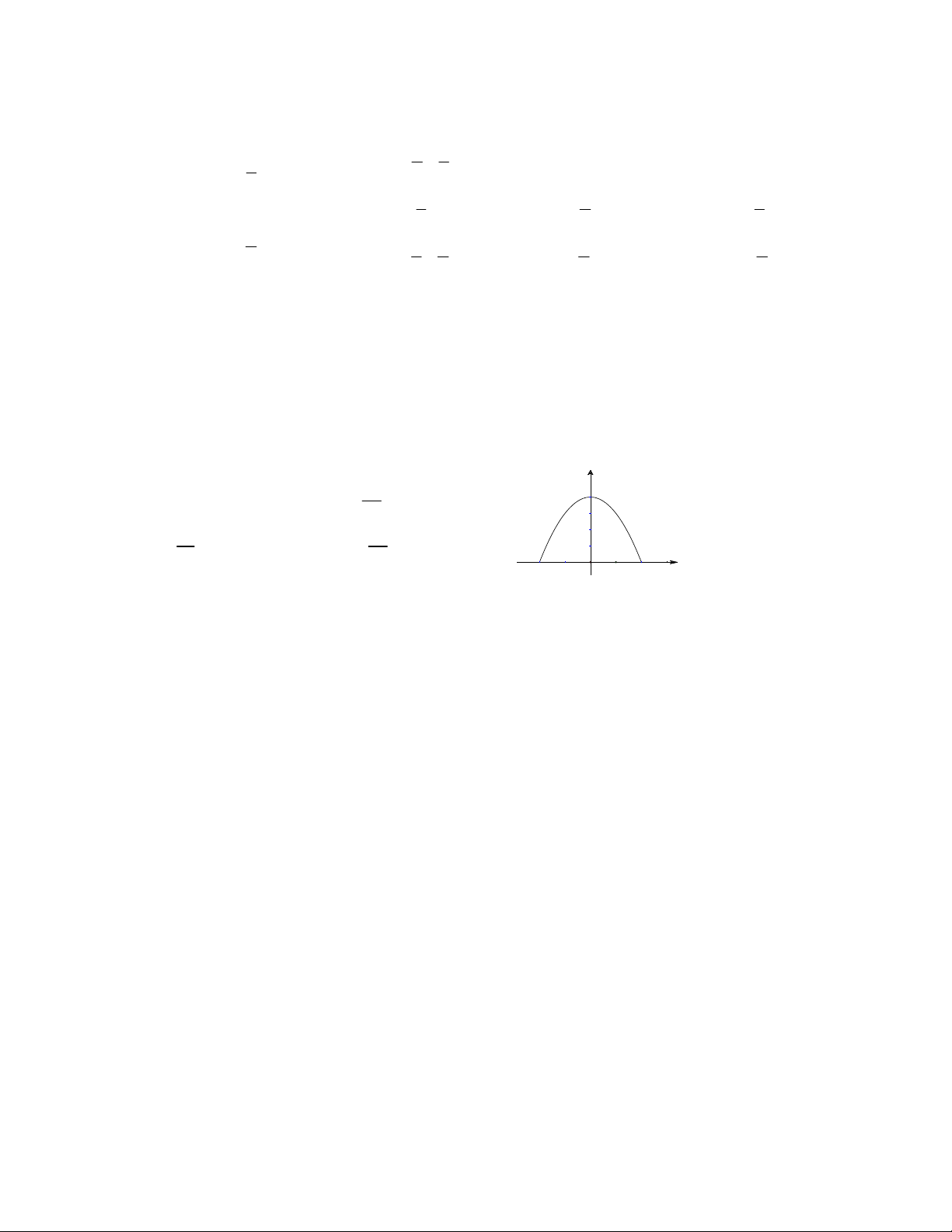
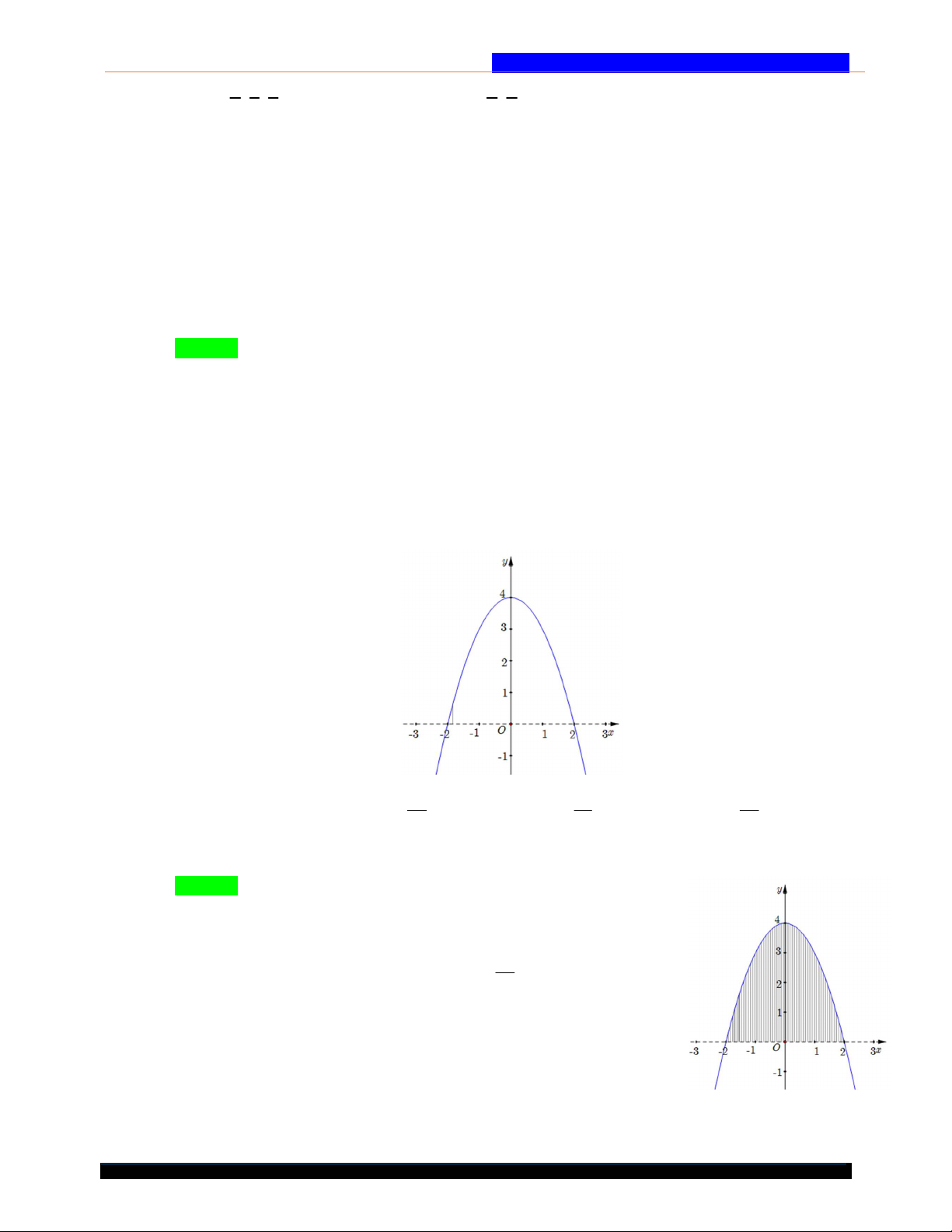
Câu 49. Cho parabol như hı̀nh vẽ. Hãy tı́nh diê ̣n tı́ch giới ha ̣n bởi parabol và tru ̣c hoành. y 28 A. S 16. B. S  . 4 3 16 32 C. S  . D. S  . 3 3 x -2 O 1 2
Câu 50. Trong không gian với hệ tọa độ Oxyz, cho các điểm ( A 6;0;6), B(8; 4  ;2), C(0;0;6),
D(1;1;5). Go ̣i M ( ; a ;
b c) thuô ̣c đường thẳng CD sao cho diê ̣n tı́ch tam giác MAB nhỏ nhất.
Tı́nh T a b 3 .c A. T 16. B. T  12  . C. T 12. D.T  8.
……………… HẾT……………….
Họ và tên thí sinh:…………………………...SBD:…………………………………………
Chữ kí GT1: …………………………………Chữ kí GT2:…………………………………
Trang 6/6 – Mã đề 155
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KÌ II - Năm học: 2016 – 2017 LÂM ĐỒNG Môn: Toán 12 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Mã đề 155 (50 câu trắc nghiệm)
Câu 1. Cho số thực 0  a  1. Phát biểu nào sau đây đúng? A. xd x a x  a  C.  B. 2 x 2 d x a x  a ln a  C.  x a C. xd x a x  a ln a  C.  D. x a dx   C.  ln a Hướng dẫn giải. Chọn D. x a
Sử dụng trực tiếp bản nguyên hàm của hàm số cơ bản ta có x a dx   C  . ln a
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  2 2 2
: (x  3)  (y 1)  (z  2)  25. Tìm
tâm và bán kính R của mặt cầu S  . A. I (3; 1;2), R  5 .
B. I (3;1; 2), R  5 .
C. I (3;1; 2), R  25 . D. I (3; 1;2), R  25 . Hướng dẫn giải. Chọn B. Phương trình mặt cầu : 2 2 2 2
(x  a)  ( y  b)  (z  c)  R có tâm I (a; ; b c), bán kính R. Vậy suy
ra tâm và bán kính của mặt cầu là: I (3;1; 2), R  5.  
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho hai véc tơ a  0;1;0; b   3;1;0.Tìm góc giữa   hai véc tơ a và . b         A. a b 0 ;  30 . B. a b 0 ;  60 . C. a b 0 ;  90 . D. a b 0 ;  120 . Hướng dẫn giải. Chọn B.     a b   Ta có c a b . 1 os ;
    Suy ra a b 0 ;  60 . a . b 2    
Câu 4. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ của véc tơ u biết u  i  2k.     A. u  0;1; 2  . B. u  1;0;2. C. u  1; 2  ;0. D. u  1;0;2. Hướng dẫn giải. Chọn B.      
Ta có i  1;0;0;k  0;0; 
1  2k  0;0;2  u  i  2k  1;0;2.
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 1
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…   
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho ba véc tơ a  1;0; 2
 ;b  1;1;2;c  3;1;  1 .    Tính a;b c   ?             A. a;b c  5.   B. a;b c  6.   C. a;b c  7  .   D. a;b c  7.   Hướng dẫn giải. Chọn D.    0 2 2 1 1 0     Ta có  ; a b   ; ;   2;0;  1   ;
a b c  2.3  0.  1 1.1  7.   1 2 2 1 1 1      
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : 5x  3y  2z  7  0 . Trong các véc
tơ sau, vectơ nào là véctơ pháp tuyến của P ?     A. n  5;2;  1 . B. n  5;3;2 . C. n  5; 3  ;2. D. n  5; 3  ;  1 . Hướng dẫn giải. Chọn C.
Câu lý thuyết nhâ ̣n biết.
Câu 7. Cho hàm số y  f  x liên tục trên  ;
a b , hình thang cong H  giới hạn bởi đồ thị hàm số
y  f x , trục Ox và hai đường thẳng x  a; x  b . Khối tròn xoay tại thành khi H  quay
quanh trục Ox có thể tích V được tính bởi công thức b b b b A. V  f  x dx. B. 2 V   f  xdx. C. V  f   2xdx. D. V  f  xdx. a a a a Hướng dẫn giải. Chọn B.
Câu lý thuyết nhâ ̣n biết.
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M 2;3; 
1 , N 3;1;5 . Tìm tọa độ của vectơ  MN     A. MN   1
 ; 2;4 . B. MN   1
 ; 2;4 . C. MN  1; 2
 ;4. D. MN  6;3;5 . Hướng dẫn giải. Chọn C.
Tọa độ của vectơ bằng tọa độ điểm ngọn trừ tọa độ điểm gốc. 
MN  3 2;1  3;5   1  1;  ; 2 4. 5 5
Câu 9. Cho f , g là hai hàm số liên tục trên 2;5, biết f  xdx  3 và g  tdt  9. Tính 2 2 5 A   f
 x gxdx  . 2
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 2
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… A. A  3. B. A  12 . C. A  6 . D. A  8 . Hướng dẫn giải. Chọn B. 5 5 5 5 5 A   f
 x gxdx  f   xdx  g  xdx  f  xdx  g
 tdt  39 12. 2 2 2 2 2 2 Câu 10. Tính I  xdx  1 3 A. I  . B. I  3  . C. I  1. D. I  3 . 2 Hướng dẫn giải. Chọn A. 2 2 2 x 1 3 I  xdx   2    . 2 2 2 1 1
Câu 11. Trong không gian với hệ toạ độ Oxyz , viết phương trình tham số của đường thẳng  đi qua  điểm M 2;0;  
1 và có vectơ chỉ phương a  4; 6  ;2. x  4  2t x  2  4t x  4  2t x  2  4t     A.  : y  6 . B.  : y  6t . C.  : y  6
  3t . D.  : y  6  t . z  2 t     z  1 2t  z  2  t  z  1 2t  Hướng dẫn giải. Chọn D.
Phương trình tham số của đường thẳng  đi qua điểm M 2;0;  
1 và có vectơ chỉ phương  x  2  4t  a  4; 6
 ;2 là : y  6  t . z  1 2t 
Câu 12. Cho hàm số y  f  x có đồ thị như hình vẽ dưới đây. Diện tích hình phẳng (phần tô màu trong
hình vẽ) được tính bởi công thức nào? y 0 b b A. S  f  xdx f  xdx. B. S  2 f  xdx . a O b x a 0 0 0 b b C. S  f  xdx  f  xdx. D. S  f  xdx. a 0 0 Hướng dẫn giải Chọn C.
Vì trong đoạn a;0 thì f  x  0 , còn trong đoạn 0;b thì f  x  0 nên ta tính theo công 0 b thức S  f  xdx  f  xdx. a 0
Câu 13. Tìm phần thực và phần ảo của số phức z  1 4i  3 .
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 3
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…
A. Phần thực bằng 11 và phần ảo bằng 4i . B. Phần thực bằng 13 và phần ảo bằng 4 .
C. Phần thực bằng 11 và phần ảo bằng 4i .
D. Phần thực bằng 11 và phần ảo bằng 4 . Hướng dẫn giải. Chọn D.
Có z  1 4i  3  1 4i 12  11 4i . Vậy phần thực bằng 11 và phần ảo bằng 4 .
Câu 14. Tính I  sin x    1 dx .
A. I   cos x 1 C . B. I   cos x  x  C . C. I  cos x  C . D. I  cos x  x  C . Hướng dẫn giải. Chọn B. Có I  sin x  
1 dx   cos x  x  C
Câu 15. Tính 5  3i  7  4i . A. 2  i . B. 2   7i . C. 12  i . D. 12  7i Hướng dẫn giải Chọn B.
Có 5  3i  7  4i  5  3i  7  4i  2  7i .
Câu 16. Nếu hàm số F  x là một nguyên hàm của hàm số f  x thì
A. f  x  F  x .
B. F  x  f  x .
C. F  x  f  x .
D. F x  f  x  C . Hướng dẫn giải. Chọn B. b
Câu 17. Nếu F  x là nguyên hàm của hàm số f  x trên đoạn [a,b] thì f (x)dx  bằng a b b A. f (x)dx  F(b)  F(a)  . B. f (x)dx  F(b)  F (a)  . a a b b C. f (x)dx  F(b)  F(a)  . D. f (x)dx  F(b  a)  . a a Hướng dẫn giải. Chọn A.
Câu 18. Trong không gian với hệ tọa độ Oxyz cho điểm I 2;6; 3
  và các mặt phẳng  : x  2  0
 ; y  6  0;  : z  3  0. Tìm khẳng định sai. A.   đi qua I .
B.      .
C.   / /Oz . D.   song song  xoz . Hướng dẫn giải. Chọn C.
+ Thay tọa độ T vào đáp án A thấy A đúng.
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 4
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…
+   có véc tơ pháp tuyến (1;0;0);   có véc tơ pháp tuyến (0;1;0) tích vô hướng bằng 0 nên hai mặt này vuông góc.
+   có véc tơ pháp tuyến (0;0;1); Oz có VTCP (0;0;1) nên Oz vuông với   dẫn đến C sai.
+   có véc tơ pháp tuyến (0;1;0);  xoz có VTPT (0;1;0) nên hai mặt này song song .
Câu 19. Tìm số phức liên hợp của số phức z  a  bi, a,b  R. A. a  bi . B. a  bi . C. a  bi . D. a  bi . Hướng dẫn giải. Chọn B.
z  a  bi  z  a  b .i .
Câu 20. Gọi z , z lần lượt là hai nghiệm của phương trình 2
z  2z  5  0. Tính F  z  z . 1 2 1 2 A. F  2 . B. F  10 . C. F  10 . D. F  2 5 . Hướng dẫn giải. Chọn D.  z  1 2i 2 1 z  2z  5  0  
 F  z  z  5  5  2 5. z  1 2i  1 2 2
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;3; 2  , B0; 1  ;3,C  ; m ; n 8 , (với m, n
là tham số). Tìm tất cả các giá trị của m, n để ba điểm , A B,C thẳng hàng. A. m  3; n  11. B. m  1; n  5 . C. m  1; n  5 . D. m  1; n  5 . Hướng dẫn giải. Chọn B.  
Ta có: AB  1;4;5 và AC  m 1;n  3;10   m 1 n  3 10 Ba điểm ,
A B,C thẳng hàng  AB và AC cùng phương    1 4 5 m 1  2  m  1     . n  3  8  n  5 
Câu 22. Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số 2
y  x  x  3 và đường thẳng y  2x 1. 19 47 1 11 A. S  . B. S  . C. S  . D. S  . 6 6 6 6 Hướng dẫn giải. Chọn C. x  1 Ta có phương trình : 2 2
x  x  3  2x 1  x  3x  2  0   x  2
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 5
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…
Vậy diện tích hình phẳng được giới hạn bởi đồ thị hàm số 2
y  x  x  3 và đường thẳng 2 2 2 3 2  x 3x  1 y  2x 1 là 2
S  x  3x  2 .dx   
 3x 3x 2.dx     2x   .  3 2  6 1 1 1
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng P : x  y  z  5  0 và
Q:2x  2y 2z 3 0. Khẳng định nào sau đây đúng ?
A. P song song với Q .
B. P vuông góc với Q . C. P cắt Q .
D. P trùng với Q . Hướng dẫn giải. Chọn A.  
Ta có: P có vtpt n  1;1; 
1 và Q có vtpt n  2;2;2 Q  P    
Ta thấy n  2.n  hai vtpt n 
 , n  2;2;2 cùng phương và M 0;0;5P Q  P 1;1; 1 Q P
nhưng M Q . Vậy P song song với Q .
Câu 24. Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 
y  tan x, y  0, x  0, x  xung quanh trục Ox . 4  ln 2 2  A. V   ln 2 . B. V  ln 2 . C. V  . D. V  . 4 4 Hướng dẫn giải. Chọn A.
Thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 
y  tan x, y  0, x  0, x  xung quanh trục Ox là: 4    4  V    tan x  4 4 2 1 .dx   tan . x dx    .d   cos x    ln  cos x 2 4    ln   ln 2  . 0 cos x 2 0 0 0 x  y  z 
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng  1 1 5 :   và 2 3 1     d  x 1 y 2 z 1 :  
. Mệnh đề nào sau đây là mệnh đề đúng? 3 2 2
A.  và d  trùng nhau.
B.  và d  chéo nhau.
C.  và d  cắt nhau.
D.  và d  song song. Hướng dẫn giải. Chọn B. 
Đường thẳng  có vtcp u  2;3;  1
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 6
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… 
Đường thẳng d  có vtcp v  3;2;2 .   Ta thấy : u  2;3; 
1 và v  3;2;2 không cùng phương, do đó : loại đáp án A, D. x  1 2t x 1 3t  
PTTS của đường thẳng  : y  1
  3t và d  : y  2   2t . z  5t   z  1   2t   3 t    5 1   2t  1 3t    2
Xét hệ phương trình : 1 3t  2  2t  t      hệ vô nghiệm. 5 5  t  1 2t     3  2  5   1 2      5  5 
Vậy  và d  chéo nhau.
Câu 26. Trong không gian Oxyz , cho mặt phẳng P : x  2y  2z  6  0 và điểm M 1;2;  1 . Khoảng
cách từ điểm M đến mặt phẳng P là 11 11 5 13 A. . B. . C. . D. . 3 9 3 3 Hướng dẫn giải. Chọn A.
Áp dụng công thức tính khoảng cách từ 1 điểm đến mặt phẳng, ta có:        d M P x 2 y 2z 6 1 2.2 2. M M M  1 6 11 ,    .   2 2 3 3 1 2  2
Câu 27. Tìm nguyên hàm của hàm số f  x  2cos 2x A. f
 xdx  sin2x C. B. f
 xdx  2sin2x C. C. f
 xdx  2sin 2x C. D. f  xdx  sin2x C. Hướng dẫn giải. Chọn D. f  x 1
dx  2 cos 2xdx  2. sin 2x  C  sin 2x  C.  2
Câu 28. Trong các khẳng định sau, khẳng định nào sai ?
A. Có vô số số phức bằng số phức liên hợp của nó.
B. Nếu số phức z là số thực thì giá trị tuyệt đối của z cũng là mô đun của z.
C. Số phức z  10  2i có phần ảo bằng 2.
D. Số phức z  3  7e có phần thực là 3.
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 7
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… Hướng dẫn giải. Chọn D.
Nếu số phức có dạng z  a  bi a,b thì phần thực là a, phần ảo là b .
Suy ra, số phức z  3  7e có phần thực là 3 7e .
Câu 29. Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng P đi qua điểm M 1;2;  1 
và nhận n  2;3;5 làm véc tơ pháp tuyến.
A. P : 2x  3y  5z  2  0.
B. P : 2x  3y  5z 1  0.
C. P : 2x  3y  5z  3  0.
D. P : 2x  3y  5z  2  0. Hướng dẫn giải. Chọn C.
Phương trình mặt phẳng P là: 2 x  
1  3 y  2  5z  
1  0  2x  3y  5z  3  0.
Câu 30. Khẳng định nào sau đây là khẳng định đúng ?     4 4 3 3 A. tan d x x  tdt.   B. sin d x x  cos d x x   . 0 0 0 0 5 5 2 2 C.  2 x   1 dx   2t    1dt . D. 2 xd t e x  e dt   . 2 2 1 1 Hướng dẫn giải. Chọn C.
Câu 31. Cho hình phẳng H  giới hạn bởi các đường thẳng y  x  2 , y  0, x  0 , x  2 . Tính thể tích
V khối tròn xoay khi hình phẳng H  quay quanh trục Ox . 8 8 A. V  2. B. V  . C. V  . D. V  2. 3 3 Hướng dẫn giải. Chọn B. 2 2  V   x  2 1 dx   x  3 8 2 . 2  . 3 3 0 0
Câu 32. Trong các khẳng định sau, khẳng định nào sai ? 1 x 1 e  A. cos 3 d x x  sin 3x  C.  B. x e dx   C.  3 x 1 1 e 1 x  C. dx  ln x 1  C.  D. e x dx   C.  x 1 e 1
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 8
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… Hướng dẫn giải. Chọn B. Công thức đúng là xd x e x  e  C  nên B sai.
Câu 33. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A 1  ;2;  1 , B  4  ;2; 2  , C  1  ; 1  ; 2   .
Viết phương trình tổng quát của mặt phẳng  ABC.
A. x  y  z  2  0.
B. x  y  z  2  0. C. x  y  z  7  0. D. x  y  z  0. Hướng dẫn giải. Chọn D.   AB   3  ;0;3, AC  0; 3   3   
AB, AC  9;9;9  
cùng phương với n  1;1;  1 . 
Mặt phẳng  ABC qua điểm A 1  ;2; 
1 và nhận n  1;1;  1 có phương trình là: 1 x   1   1 y  2 1z  
1  0  x  y  z  0.
Câu 34. Trên mặt phẳng phức, gọi M 1;2 là điểm biểu diễn số phức z. Tìm số phức liên hợp của z. A. 1 2 .i B. 2  .i C. 2  .i D. 1   2 .i Hướng dẫn giải. Chọn A.
Điểm biểu diễn của z là M 1;2 , suy ra z  1 2i  z 1 2 .i
Câu 35. Tìm nguyên hàm F  x của hàm số f  x 1 
trên 1; , biết F 2 1. x 1
A. F  x  ln x 1  C. B. F  x  ln x 1 1. C. F  x  ln  x  
1 1. D. F x  ln x 1 . Hướng dẫn giải. Chọn B. F  x  f  x 1 dx  dx  ln x 1  C.  x 1
F 2 1 ln1 C 1  C  1.
Vậy F  x  ln x 1 1. 1
Câu 36. Trong mặt phẳng phức, xác định tập hợp điểm biểu diễn số phức z sao cho là số thuần ảo. z  i
A. Trục tung, bỏ điểm có tọa độ 0;  1 . B. Trục tung.
C. Đường thẳng y  1, bỏ điểm 0;  1 .
D. Đường thẳng y  1.
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 9
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… Hướng dẫn giải. Chọn A. x  0
Gọi z  x  yi  x, y  . Với z  i   y  1 1 1 x   y   1 i Ta có:   z  i x  yi  i x   y  2 2 1 1 x thuần ảo   0  x  0. z  i x   y  2 2 1
Vậy, tập hợp điểm biểu diễn z là trục tung và bỏ điểm 0;  1 . x  t 
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : y  8  4t và mặt phẳng z  3 2t 
P: x y  z 7  0 . Viết phương trình đường thẳng d là hình chiếu vuông góc của d lên mặt phẳng P x  1 4t x  4   8t x  3 8t x  4t    
A. d : y  12  5t .
B. d : y  10 10t. C. d : y  110t . D. d : y  8  5t . z  5t     z  1 2t  z  1 2t  z  3  t  Hướng dẫn giải. Chọn B. 
d qua A0;8;3 và có véc tơ chỉ phương u  1;4;2 u Q  
P có véc tơ pháp tuyến n  1;1;  1 d n
Gọi Q là mặt phẳng chứa d và vuông với P , suy ra P d' d  P Q.   
Pháp tuyến của Q là m  u,n  2;1; 3       
Véc tơ chỉ phương của d là v   , m n  4;5;  1   
Phương trình Q qua A và có véc tơ pháp tuyến m là: 2x  y  3z 1  0 2x  y  3z 1  0 Xét hệ 
. Ta chọn được x  4, y  10, z  1 thỏa mãn hệ này. x  y  z  7  0 
Suy ra, phương trình d qua M  4  ;10; 
1 và có véc tơ chỉ phương v là
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 10
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… x  4  4t x  4  8t  
d : y  10 5t hay d: y 10 10t. z 11t   z  1 2t 
Câu 38. Cho số phức z thỏa mãn 3  2i z  41i  2  i z . Tính mô đun của . z A. z  2 10. B. z  4 5. C. z  2 2. D. z  10. Hướng dẫn giải. Chọn D.
Gọi z  a  bi a,b . Suy ra:
3 2ia bi 41i  2ia bi
 3a  3bi  2ai  2b  4  4i  2a  2bi  ai  b
 3a  2b  4  4  2a 3bi  2a b  a  2bi 3
 a  2b  4  2a  b a  b  4 a  3      
4  2a  3b  a  2b  3  a  5b  4 b   1 Suy ra 2 2 z  a  b  10.
Câu 39. Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt cầu S  có tâm I thuộc trục Oz
và đi qua hai điểm A2; 1  ;4, B0;2;  1 . 2  8  269 2  8  269 A. 2 2 x  y  z   .   B. 2 2 x  y  z   .    5  25  5  5 2  8  269 2  8  269 C. 2 2 x  y  z   .   D. 2 2 x  y  z   .    5  25  5  25 Hướng dẫn giải. Chọn D.
Gọi tâm I 0;0;mOz . Ta có  8 
IA  IB  IA  IB  5  4  m2  4  1 m2 8 2 2
 m  . Suy ra, tâm I 0;0;   . 5  5  Bán kính R  IA     m2 269 5 4  . 5 2  8  269
Phương trình mặt cầu S  2 2 : x  y  z   .    5  25
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 11
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… x  6  4t 
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : y  2
  t và điểm A1;1;  1 . Tìm z  1 2t 
tọa độ điểm A đối xứng với A qua d. A. A 3  ;17;  1 . B. A 1  ;9;  1 . C. A3; 7  ;  1 . D. A5; 1  5;  1 . Hướng dẫn giải. A Chọn C. u  d u   4
 ;1;2 là véc tơ chỉ phương của d. H Gọi H 6  4t; 2   t; 1
  2t là hình chiếu vuông góc của A trên d . A'  
Suy ra AH.u  0  5  4t. 4     3   t .  1   2
  2t.2  0  21t  21 0  t 1. Với t  1 H 2; 3  ;  1 x  2x  x  3 A H A 
H là trung điểm của AA , suy ra y         2 y y 7 A A H A 3; 7; 1. z      2z z 1 A H A
Câu 41. Gọi z , z lần lượt là hai nghiệm của phương trình 2
z  2z 10  0, trong đó z có phần ảo dương. 1 2 1
Gọi M , N , P lần lượt là điểm biểu diễn của z , z và số phức k  x  yi trên mặt phẳng phức. 1 2
Tìm số phức k để tứ giác OMNP là hình bình hành (O là gốc toạ độ của mặt phẳng phức) A. k  6  i . B. k  6i . C. k  2  . D. k  2 . Hướng dẫn giải. Chọn A. Phương trình 2
z  2z 10  0 có 2 nghiệm phức là z  1 3 ,i z  1 3i . 1 2
Từ đó M 1;3, N 1; 3  , P ; x y .   x  0
Ta có OMNP là hình bình hành  OP  MN    k  6  i .  y  6 3 2
Câu 42. Cho hàm số f  x liên tục trên  sao cho f
 xdx  5. Tính I  f 2x   1 d . x 1 1 15 5 7 9 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 Hướng dẫn giải. Chọn B. 2 2 3 I  f  x   1 x 
f  x    x   1  f t 5 2 1 d 2 1 d 2 1 dt  t  2x     1 2 2 2 1 1 1
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 12
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…
Câu 43. Cho hình phẳng H  giới hạn bởi các đường 2
y  2x  x , y  0. Khi quay H  xung quanh trục a a
Ox ta thư được khối tròn xoay có thể tích V     1 , 
 với là phân số tối giản. Khi đó ab  b  b bằng bao nhiêu? A. ab  3. B. ab  12 . C. ab  24 . D. ab  15. Hướng dẫn giải. Chọn D. Phương trình hoành độ: 2
2x  x  0  x  0  x  2 2 2 16 1
Thể tích khối tròn xoay (nêu trong đề): V   2 2x x  dx         1   15 15  0
Từ đó a  1, b  15  ab  15 . e Câu 44. Cho 2 I  x ln d x x  ae  . b 
Tính giá trị biểu thức A  a  . b 1 1 1 A. A  0 . B. A  . C. A  e . D. A  e  . 2 2 Hướng dẫn giải. Chọn A. e e e e 2 2 e 2 2 2 2  x   x .ln x  x 1 e  x  e 1 I  x ln d x x  ln . x d          dx         2   2  2 x 2  4  4 4 1 1 1 1 1 1 1
Từ đó a  , b   a  b  0 . 4 4
Câu 45. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu S  2 2 2
: x  y  z  2x  4y  6z 11  0 và
mặt phẳng   : 2x  2y  z 17  0. Viết phương trình mặt phẳng   song song với   và
cắt S  theo giao tuyến là đường tròn có chu vi bằng 6.
A.   : 2x  2y  z  7  0 .
B.   : 2x  2y  z 17  0 .
C.   : 2x  2y  z  7  0 .
D.   : 2x  2y  z 17  0 . Hướng dẫn giải. Chọn A.
Do   //   nên   : 2x  2y  z  D  0 D  17
Mặt cầu S  có tâm I 1; 2  ;3, bán kính 2 2 2
R  1  (2)  3  (11)  5 6
Đường tròn giao tuyến của S  và   có bán kính r   3 2
Như thế khoảng cách từ tâm I đến   là d I   2 2 ,( )  R  r  4
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 13
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC… 2.1 2( 2  )  3  D D  5   4 
 4  D  7 do D  17 2 2 2 2  2  (1) 3
Như vậy   : 2x  2y  z  7  0
Câu 46. Trong mặt phẳng phức, cho số phức z thỏa mãn z  3 4i  2 và w  2z  i 1. Tập hợp điểm
biểu diễn số phức w là đường tròn có tâm I , bán kính R . Tìm tọa độ tâm I và bán kính R . A. I 5; 7  , R  4. B. I 4;5, R  4 . C. I 3; 4
 , R  2 . D. I 7; 9  , R  4 . Hướng dẫn giải. Chọn A.
Đặt w  x  yi với x, y   w 1 i w 1 i w  5  7i Ta có w  2z  i 1   z 
 3  4i  z  3  4i   z  3  4i 2 2 2 w  5  7i w  5  7i Vậy  z  3  4i 
 2  w  5  7i  4  x  5   y  7i  4 2 2
Tập hợp điểm biểu diễn số phức w là đường tròn tâm I 5; 7  , R  4.
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;2;  1 , B2;1; 
1 , C 0;1;2 . Lập phương
trình đường thẳng  đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng  ABC .  7 1  1 x   t   x  2  t   3 5 x 11t x  2  2t 5      8  4  8
A.  : y 11t .
B.  : y  1t . C.  : y   5t . D.  : y  10t .  3 3 3 2    z  4  t  5 2  2  4  5 z   t  z   2t z   2t  3 5  3  3 Hướng dẫn giải. Chọn B.     
Ta có AB  1;1;2, AC  1;1;3  u  AB, AC   1  ; 5
 ;2  1;5;2  
Gọi P là mặt phẳng đi qua C và vuông góc với AB . Khi đó P có phương trình tổng quát
là: 1 x  0 1 y  
1  2 z  2  0  x  y  2z  3  0
Gọi Q là mặt phẳng đi qua B và vuông góc với AC . Khi đó Q có phương trình tổng quát là: 1
  x  2 1 y   1  3 z  
1  0  x  y  3z  0
Đường thẳng   P Q 
Ta thấy véctơ chỉ phương của  chính là u nhận thấy hai đáp án B và C có véctơ chỉ phương cùng phương
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 14
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…  7 8 5   4 2  Điểm ; ;  
 P và Q còn điểm 1; ; 
 không thuộc mặt phẳng nào.  3 3 3   3 3 
Nên đáp án B là đáp án cần tìm.
Câu 48. Để đảm bảo an toàn giao thông, khi dừng đèn đỏ các xe ô tô phải cách nhau tối thiểu 1m. Một ô
tô A đang chạy với vận tốc 12m / s thì gặp ô tô B đang dừng đèn đỏ nên ô tô A phải hãm phanh
và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức v t 12  3t m / s . Để A 
đảm bảo an toàn thì ô tô A phải hãm phanh cách ô tô B một khoảng ít nhất là bao nhiêu mét? A. 23. B. 24 . C. 25 . D. 22 . Hướng dẫn giải. Chọn C.
Khi ô tô A dừng hẳn thì V  0 suy ra: v(t)  0 123t  0 t  4 4
Quảng đường ô tô A đi được từ lúc hãm phanh đến lúc dừng hẳn: S   (12 3t)dt  24 0
Để có khoảng cách an toàn thì cần quảng đường ít nhất là: 25 m (cô ̣ng thêm 1 mét khoảng cách
tối thiểu giữa 2 xe).
Câu 49. Cho Parabol như hình vẽ. Hãy tính diện tích giới hạn bởi Parabol và trục hoành. 28 16 32 A. S 16 . B. S  . C. S  . D. S  . 3 3 3 Hướng dẫn giải. Chọn D.
Từ hình vẽ ta dễ dàng tìm được phương trình của Parabol là 2 y  x  4 2 32
Diện tích hình cần tìm là S   2 x  4dx   3 2
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 15
Sản Phẩm Của Tập Thê Giáo Viên Toán ABC…
Câu 50. Trong không gian với hệ tọa độ Oxyz cho các điểm A6;0;6 , B8; 4  ; 2
 , C 0;0;6 , D1;1;5 . Gọi M  ; a ;
b c thuộc đường thẳng CD sao cho diện tích tam giác MAB nhỏ nhất. Tính T  a  b  3c A. T  16 . B. T  1  2 . C. T  12 . D. T  8 . Hướng dẫn giải. Chọn C.  x  t  Ta có CD  1;1; 
1 , phương trình tham số của đường thẳng CD : y  t z  6t  Tọa độ M  ; a ; b c  t;t;6 t    
 AM  t  6;t;t; AB  2;4; 8
   AB, AM   12t;48  6t;6t  24  62t;8  t;t  4   1   Ta có S
 AB, AM   3 4t  t  t   t  t  ABM 8 2  62 2 2 3 6 24 80 2
Dễ dàng thấy được diện tích tam giác nhỏ nhất bằng 56 tại t  2
Vậy a  b  t  2;c  6  t  4
Nên T  a  b  3c  12 .
Nhâ ̣n góp ý : Nguyễn Chòe – Trường THPT Lê Quý Đôn – Đa ̣ Tẻh – Lâm Đồng Page 16
Document Outline

  • de-155
  • [toanmath.com] - Đề thi HK2 Toán 12 năm học 2016 - 2017 sở GD và ĐT Lâm Đồng