Đề thi HK2 Toán 12 năm học 2016 – 2017 sở GD và ĐT Quảng Nam

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

75 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/3 – Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 2. Tìm
sin 2
xdx
.
A.
sin 2 2cos2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos2
xdx x C
.
Câu 3. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Câu 4. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 5. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 6. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 7. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 8. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 9. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Mã đề 101
Trang 2/3 – Mã đề 101
Câu 10. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 11. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 12. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 13. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 14. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 15. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 16. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 17. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 18. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 19. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 20. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 21. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Trang 3/3 – Mã đề 101
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) :( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) :( 1) ( 2) ( 1) 7
S x y z
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
0; 1;3
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
--------------- HẾT ---------------
Trang 4/3 – Mã đề 101
Trang 1/3 – Mã đề 102
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Câu 2. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Câu 3. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 4. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 5. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 6. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 7. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 8. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Mã đề 102
Trang 2/3 – Mã đề 102
Câu 9. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 10. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 11. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 12. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 13. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 14. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 15. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 16. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 17. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 18. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 19. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 20. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 21. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Trang 3/3 – Mã đề 102
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 103
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 2. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 3. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 4. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 5. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 6. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 7. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 8. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Mã đề 103
Trang 2/3 – Mã đề 103
Câu 9. Biết
3
1
1
ln5 ln3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 10. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 11. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 12. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Câu 13. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 14. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 15. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 16. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 17. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 18. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 19. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 20. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 21. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Trang 3/3 – Mã đề 103
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 104
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 2. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 3. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 4. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 5. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 6. Tìm
sin 2
xdx
.
A.
sin 2 2cos 2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos2
xdx x C
.
Câu 7. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Câu 8. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 9. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 10. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Câu 11. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Mã đề 104
Trang 2/3 – Mã đề 104
Câu 12. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 13. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 14. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 15. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 16. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 17. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 18. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 19. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 20. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 22. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
Trang 3/3 – Mã đề 104
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
0; 1;3
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 2. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 3. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 4. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm. Tìm
số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 5. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 6. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 7. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 8. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 9. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 10. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 11. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Câu 12. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Mã đề 105
Trang 2/3 – Mã đề 105
Câu 13. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 14. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 15. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 16. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 17. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 18. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 19. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 20. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 21. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Trang 3/3 – Mã đề 105
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 106
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 2. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 3. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 4. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 5. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 6. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 7. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 8. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 9. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 10. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 11. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 12. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Mã đề 106
Trang 2/3 – Mã đề 106
Câu 13. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 14. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 15. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Câu 16. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 17. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 18. Biết
3
1
1
ln5 ln3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 19. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 20. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Trang 3/3 – Mã đề 106
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) :( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) :( 1) ( 2) ( 1) 25
S x y z
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 28. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 107
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 2. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 3. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 4. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 5. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 6. Tìm
sin 2
xdx
.
A.
sin 2 2cos 2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos2
xdx x C
.
Câu 7. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 8. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 9. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 10. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Mã đề 107
Trang 2/3 – Mã đề 107
Câu 11. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 12. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 13. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 14. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 15. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 16. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Câu 17. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 18. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 19. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 20. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
Trang 3/3 – Mã đề 107
Câu 23. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
0; 1;3
A
và đường thẳng
1 1
:
2 1 1
x y z
d
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 108
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 2. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 3. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 4. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 5. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 6. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm. Tìm
số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 7. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 8. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 9. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Câu 10. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 11. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 12. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Mã đề 108
Trang 2/3 – Mã đề 108
Câu 13. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 14. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 15. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 16. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 17. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 18. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 19. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 20. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Trang 3/3 – Mã đề 108
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 24. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 5.
A.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 109
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 2. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 3. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 4. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 5. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 6. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 7. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 8. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 9. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 10. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 11. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 12. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Mã đề 109
Trang 2/3 – Mã đề 109
Câu 13. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Câu 14. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 15. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 16. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 17. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 18. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 19. Biết
3
1
1
ln5 ln 3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 20. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Trang 3/3 – Mã đề 109
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 29. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
--------------- HẾT ---------------
Trang 1/3 – Mã đề 110
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 2. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 3. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 4. Tìm
sin 2
xdx
.
A.
sin 2 2cos 2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos 2
xdx x C
.
Câu 5. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 6. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 7. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Câu 8. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 9. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 10. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 11. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Mã đề 110
Trang 2/3 – Mã đề 110
Câu 12. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 13. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 14. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 15. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 16. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 17. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 18. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 19. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 20. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 23. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Trang 3/3 – Mã đề 110
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
0; 1;3
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) :( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) :( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 111
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 2. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 3. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 4. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 5. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 6. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 7. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Câu 8. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 9. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 10. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 11. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Mã đề 111
Trang 2/3 – Mã đề 111
Câu 12. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 13. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 14. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 15. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 16. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 17. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 18. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 19. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 20. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Trang 3/3 – Mã đề 111
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 5.
A.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 29. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 112
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 2. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 3. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 4. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 5. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 6. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 7. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 8. Biết
3
1
1
ln5 ln 3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 9. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 10. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 11. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Mã đề 112
Trang 2/3 – Mã đề 112
Câu 12. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 13. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 14. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 15. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 16. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 17. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 18. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 19. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 20. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Trang 3/3 – Mã đề 112
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 31. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 113
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Câu 2. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 3. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 4. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 5. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 6. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 7. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 8. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 9. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 10. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 11. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Mã đề 113
Trang 2/3 – Mã đề 113
Câu 12. Tìm
sin 2
xdx
.
A.
sin 2 2cos2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos 2
xdx x C
.
Câu 13. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 14. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 15. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Câu 16. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 17. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 18. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 19. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 20. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Trang 3/3 – Mã đề 113
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
Câu 28. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
0; 1;3
A
và đường thẳng
1 1
:
2 1 1
x y z
d
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 114
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 2. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 3. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 4. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 5. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm. Tìm
số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 6. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 7. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 8. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 9. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 10. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 11. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Mã đề 114
Trang 2/3 – Mã đề 114
Câu 12. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 13. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 14. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 16. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 17. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 18. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 19. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Câu 20. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 5.
A.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 22. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Trang 3/3 – Mã đề 114
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 31. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 115
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 2. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Mã đề 115
Trang 2/3 – Mã đề 115
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ) : 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 13. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 14. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 15. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 16. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 17. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 18. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 19. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 20. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 21. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 22. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 23. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Trang 3/3 – Mã đề 115
Câu 24. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 25. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 26. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 27. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 28. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 29. Biết
3
1
1
ln5 ln 3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 30. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 31. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 32. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 116
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 2. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 3. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Câu 4. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 5. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 6. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 7. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 8. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 9. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 10. Tìm
sin 2
xdx
.
A.
sin 2 2cos 2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos2
xdx x C
.
Câu 11. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Mã đề 116
Trang 2/3 – Mã đề 116
Câu 12. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 13. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 14. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 16. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 17. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 18. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 19. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 20. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 22. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Trang 3/3 – Mã đề 116
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
Câu 25. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 26. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 30. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
0; 1;3
A
và đường thẳng
1 1
:
2 1 1
x y z
d
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 3 0
P x y z
. B.
( ) : 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 117
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới đây
là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo của
góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1; 2;1
I
.
Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn có bán kính
bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Mã đề 117
Trang 2/3 – Mã đề 117
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 13. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Câu 14. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Câu 15. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 16. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 17. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 18. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 19. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Trang 3/3 – Mã đề 117
Câu 20. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 21. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 22. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 23. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 24. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 25. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 26. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 27. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 28. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 29. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 30. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 31. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 32. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 118
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) :( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) :( 1) ( 2) ( 1) 25
S x y z
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 9. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Mã đề 118
Trang 2/3 – Mã đề 118
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 13. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 14. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 15. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 16. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 17. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 18. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 19. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 20. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 21. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 22. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 23. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Trang 3/3 – Mã đề 118
Câu 24. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 25. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 26. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 27. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Câu 28. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 29. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 30. Biết
3
1
1
ln5 ln3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 31. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 32. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 119
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 2. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới đây
là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo của
góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1; 2;1
I
.
Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn có bán kính
bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
Mã đề 119
Trang 2/3 – Mã đề 119
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
0; 1;3
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
Câu 13. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 14. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 15. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 16. Tìm
sin 2
xdx
.
A.
sin 2 2cos2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos 2
xdx x C
.
Câu 17. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Câu 18. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 19. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 20. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 21. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Trang 3/3 – Mã đề 119
Câu 22. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 23. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 24. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 25. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Câu 26. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 27. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
Câu 28. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 29. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 30. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 31. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 32. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 120
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1; 2;1
I
.
Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn có bán kính
bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 4. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới đây
là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo của
góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Mã đề 120
Trang 2/3 – Mã đề 120
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 13. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 14. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 16. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 17. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 18. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Câu 19. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Câu 20. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Câu 21. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Trang 3/3 – Mã đề 120
Câu 22. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 23. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 24. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 25. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 26. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 27. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 28. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 29. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
Câu 30. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 31. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 32. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 121
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) :( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
.
Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 9. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Mã đề 121
Trang 2/3 – Mã đề 121
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 13. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 14. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 15. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 16. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 17. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 18. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 19. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 20. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 21. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 22. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 23. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Trang 3/3 – Mã đề 121
Câu 24. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 25. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Câu 26. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 27. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 28. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 29. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 30. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 31. Biết
3
1
1
ln5 ln3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 32. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 122
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục Oz.
A.
2;0;0
. B.
0; 1;0
. C.
2; 1;0
. D.
0;0;3
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
(2;1; 1)
b
. Tính
.a b
.
A.
. 1
a b
. B.
. 2
a b
. C.
. (2; 1; 2)
a b
. D.
. 1
a b
.
Câu 3. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3;0; 2
M
. D.
1
; 1;2
2
M
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới đây
là vectơ chỉ phương của đường thẳng d ?
A.
1
(1; 2;0)
u
. B.
2
(2;1; 1)
u
. C.
3
( 2;1; 1)
u
. D.
4
( 2; 1;1)
u
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Ox
?
A.
1 0.
y z
B.
1 0.
x
C.
0.
x
D.
1 0.
x
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;1)
N
. C.
( 1;3;0)
P
. D.
(1;2; 1)
Q
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(2; 4;3)
u
. B.
2
(2;4;3)
u
. C.
3
(2;4; 3)
u
. D.
4
(2; 4; 3)
u
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oxy
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(3; 1;0)
n
. B.
2
(3;1;0)
n
. C.
3
(1;3;0)
n
. D.
4
(1; 3;0)
n
.
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
0; 1;3
A
.
Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ): 3 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ) : 2 3 6 0
P x y z
. D.
( ) : 3 6 0
P x y z
.
Mã đề 122
Trang 2/3 – Mã đề 122
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d chứa trong (P). B. d song song với (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 11. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
(1; 1;0)
b
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 90
a b
. D.
0
, 135
a b
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ): 2 2 2 0
P x y z
và điểm
1; 2;1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn
có bán kính bằng 4.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 7
S x y z
.
Câu 13. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 14. Tính môđun của số phức
3z i
.
A.
2
z
. B.
2
z
. C.
4
z
. D.
3
z
.
Câu 15. Cho
2
1
( ) 2
f x dx
,
3
1
( ) 3
f x dx
. Tính
3
2
( )I f x dx
.
A.
1I
. B.
1I
. C.
5
I
. D.
5
I
.
Câu 16. Cho
2
1
( ) 2
f x dx
,
2
1
2 ( ) ( ) 3
f x g x dx
. Tính
2
1
( )I g x dx
.
A.
7
I
. B.
1I
. C.
5
I
. D.
1I
.
Câu 17. Tìm
2
x
e dx
.
A.
2 2
1
2
x x
e dx e C
. B.
2 2x x
e dx e C
. C.
2 2
2
x x
e dx e C
. D.
2
2
x x
e dx e C
.
Câu 18. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(1) 3
F
.
A.
( ) 2
F x x
. B.
( ) 2 1F x x
. C.
1 5
( )
2 2
F x x
. D.
( ) 2 1F x x
.
Câu 19. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo dương.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 20. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 9 5z i z i
. Tính
a b
.
A.
1a b
. B.
1
a b
. C.
4
a b
. D.
5
a b
.
Câu 21. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
2 0
x y
. B.
4 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 22. Cho tích phân
4
0
2 1
x
I dx
x
. Đặt
2 1t x
. Mệnh đề nào sau đây đúng ?
A.
3
2
1
(2 2)I t dt
. B.
3
2
1
1
( 1)
2
I t dt
. C.
3
2
1
( 1)I t dt
. D.
3
2
1
1
( 1)
2
I t dt
.
Trang 3/3 – Mã đề 122
Câu 23. Biết
4
2
1
ln5 ln3 ( , )
2 1
dx m n m n R
x
. Tính
P m n
.
A.
3
2
P
. B.
3
2
P
. C.
1P
. D.
1P
.
Câu 24. Tìm
sin 2
xdx
.
A.
sin 2 2cos2
xdx x C
. B.
1
sin 2 cos 2
2
xdx x C
.
C.
1
sin 2 cos2
. D.
sin 2 cos 2
xdx x C
.
Câu 25. Tìm nguyên hàm của hàm số
2
( )
4
x
f x
x
.
A.
2 2
1
( )
2( 4)
f x dx C
x
. B.
2
( ) ln 4
f x dx x C
.
C.
1 2
( ) ln
4 2
x
f x dx C
x
. D.
2
1
( ) ln 4
2
f x dx x C
.
Câu 26. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 27. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực không dương. B.
1.
z
C. Phần thực của
z
là số âm. D.
z
là số thuần ảo.
Câu 28. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
4
5
x y
. B.
9
5
x y
. C.
9
5
x y
. D.
1
5
x y
.
Câu 29. Tìm
2
x
xe dx
.
A.
2 2 2
x x x
. B.
2 2 2
x x x
xe dx xe e C
.
C.
2
2
x x
xe dx x e C
. D.
2 2
x x x
xe dx xe e C
.
Câu 30. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;2
,
(0) 5
f
,
(2) 2
f
. Tính
2
0
'( )I f x dx
.
A.
3
I
. B.
3
I
. C.
2I
. D.
7
I
.
Câu 31. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 1
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
Câu 32. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
32
3
V
. C.
8
3
V
. D.
16
3
V
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 123
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 1;2
a
và
( 2;1;1)
b
. Tính
.a b
.
A.
. ( 2; 1;2)
a b
. B.
. 6
a b
. C.
. 1
a b
. D.
. 1
a b
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oy
?
A.
0.
y
B.
1 0.
y
C.
1 0.
y
D.
1 0.
x z
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
: 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(2; 1;3)
N
. C.
( 1;3;4)
P
. D.
( 3;4; 5)
Q
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2;1;2)
a
và
( 1;1;0)
b
. Tính số đo của
góc giữa hai vectơ
a
và
b
.
A.
0
, 30
a b
. B.
0
, 45
a b
. C.
0
, 60
a b
. D.
0
, 135
a b
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
1 3 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Oy
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
2;0;3
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1; 2;1
I
.
Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường tròn có bán kính
bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) :( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) :( 1) ( 2) ( 1) 25
S x y z
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(6; 4; 1)
u
. B.
2
(6;4; 1)
u
. C.
3
(6; 4;1)
u
. D.
4
(6;4;1)
u
.
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Oyz
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(0;2; 3)
n
. B.
2
(0;2;3)
n
. C.
3
(0;3; 2)
n
. D.
4
(0;3;2)
n
.
Mã đề 123
Trang 2/3 – Mã đề 123
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
2; 1;0
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 2 0
P x y z
.
C.
( ): 2 5 1 0
P x y z
. D.
( ) : 3 1 0
P x y z
.
Câu 11. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2
OA i j k
và
3OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
1
;1; 2
2
M
. B.
3
;0; 1
2
M
. C.
3
;0;1
2
M
. D.
1;2; 4
M
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2
:
2 1 1
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
(2;1; 1)
u
. B.
2
( 2;1;1)
u
. C.
3
(2; 1;1)
u
. D.
4
(1; 2;0)
u
.
Câu 13. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 5 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 4w i
. B.
2 4w i
. C.
2 4w i
. D.
2 4w i
.
Câu 14. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 8 2z i z i
. Tính
a b
.
A.
4
a b
. B.
4
a b
. C.
2
a b
. D.
2
a b
.
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
2 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
3 0
x y
. B.
3 0
x y
. C.
0
x y
. D.
0
x y
.
Câu 16. Cho số phức
z
thỏa mãn
0
z z
. Mệnh đề nào sau đây đúng ?
A.
z
là số thực dương. B.
1.
z
C. Phần thực của
z
không âm. D.
z
là số thuần ảo.
Câu 17. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun nhỏ nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Câu 18. Tìm
3
x
e dx
.
A.
3 3
3
x x
e dx e C
. B.
3 3x x
e dx e C
. C.
3 3
1
3
x x
e dx e C
. D.
3 2
3
x x
e dx e C
.
Câu 19. Tìm
s 2
co xdx
.
A.
1
s 2 sin 2
2
co xdx x C
. B.
1
s 2 sin 2
2
co xdx x C
.
C.
s 2 2sin 2
co xdx x C
. D.
s 2 2sin 2
co xdx x C
.
Câu 20. Tìm số phức liên hợp của số phức
3 2z i
.
A.
3 2z i
. B.
3 2z i
. C.
3 2z i
. D.
2 3z i
.
Câu 21. Cho số phức
z
thỏa mãn
(1 2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
(2;1)
M
. B.
(1; 2)
N
. C.
( 2;1)
P
. D.
(1;2)
Q
.
Câu 22. Cho tích phân
2
3 2
1
5
I x x dx
. Đặt
2
5
t x
. Mệnh đề nào sau đây đúng ?
A.
2
3
1
5
I t t dt
. B.
2
3
1
(5 )I t t dt
. C.
2
2 4
1
(5 )I t t dt
. D.
2
4 2
1
5
I t t dt
.
Trang 3/3 – Mã đề 123
Câu 23. Tính môđun của số phức
2 2z i
.
A.
1 2 2
z
. B.
9
z
. C.
7
z
. D.
3
z
.
Câu 24. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(4) 1
F
.
A.
1 3
( )
4
2
F x
x
. B.
( ) 1F x x
. C.
( ) 2 3
F x x
. D.
( ) 2 3
F x x
.
Câu 25. Cho
4 4
1 1
( ) 2, 2 ( ) ( ) 5
f x dx g x f x dx
. Tính
4
1
( )I g x dx
.
A.
3
2
I
. B.
3
2
I
. C.
7
2
I
. D.
7
2
I
.
Câu 26. Tìm nguyên hàm của hàm số
2
( )
9
x
f x
x
.
A.
2
2 2
9
( )
( 9)
x
f x dx C
x
. B.
2
1
( ) ln 9
2
f x dx x C
.
C.
1 3
( ) ln
6 3
x
f x dx C
x
. D.
2
( ) ln 9
f x dx x C
.
Câu 27. Tìm
4
x
xe dx
.
A.
4 4
x x x
xe dx xe e C
. B.
4 4 4
x x x
xe dx xe e C
.
C.
2
4 2
x x
xe dx x e C
. D.
4 4 4
x x x
.
Câu 28. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 29. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
6
,
6
f
và
6
0
'( )
3
f x dx
. Tính
0
f
.
A.
2
0
3
f
. B.
2
0
3
f
. C.
0
3
f
. D.
0
3
f
.
Câu 30. Biết
2
1
1
ln 7 ln 2 ( , )
3 1
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
2
3
P
. C.
1P
. D.
1P
.
Câu 31. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 4
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
16
S
. B.
14
S
. C.
12
S
. D.
8
S
.
Câu 32. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
32
3
V
. B.
16
3
V
. C.
10
3
V
. D.
8
3
V
.
--------------- HẾT ---------------
Trang 1/3 – Mã đề 124
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
ĐỀ CHÍNH THỨC
(Đề có 03 trang)
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề
Họ và tên học sinh: ……………………………..……………….
Lớp: …………
Câu 1. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
1;1;2
M
. Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm
M
và vuông góc với trục
Oz
?
A.
2 0.
z
B.
2 0.
z
C.
0.
z
D.
0.
x y
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
1; 2;2
a
và
(2;1; 2)
b
. Tính
.a b
.
A.
. (2; 2; 4)
a b
. B.
. 4
a b
. C.
. 4
a b
. D.
. 9
a b
.
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )P
đi qua hai điểm
A 1; 2;2
,
B 2;1;0
và vuông góc với mặt phẳng
Ozx
. Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
( )P
?
A.
1
(1; 1; 1)
n
. B.
2
(0;2;3)
n
. C.
3
(2;0; 1)
n
. D.
4
(2;0;1)
n
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
a (2;2;0)
và
b ( 1;0;1)
. Tính số đo
của góc giữa hai vectơ
a
và
b
.
A.
0
a , b 30
. B.
0
a , b 60
. C.
0
a , b 120
. D.
0
a , b 150
.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 1
:
6 3 3
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y z
. Mệnh đề nào sau đây đúng ?
A. d song song với (P). B. d chứa trong (P).
C. d vuông góc với (P). D. d cắt (P) và không vuông góc với (P).
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, tìm tọa độ hình chiếu vuông góc điểm
2; 1;3
M
trên
trục
Ox
.
A.
2;0;0
. B.
0; 1;0
. C.
0;0;3
. D.
0; 1;3
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
2
: 3 2
1 3
x t
d y t
z t
. Điểm nào sau đây thuộc
đường thẳng d ?
A.
(3;1; 2)
M
. B.
(1;1;4)
N
. C.
(0;7;5)
P
. D.
( 1;9; 8)
Q
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 3 0
P x y z
và hai điểm
(1;0;1)
A
,
( 1;2; 3)
B
. Gọi
là đường thẳng nằm trong mặt phẳng
( )P
sao cho mọi điểm thuộc
đều
có khoảng cách đến
A
và đến
B
bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng
?
A.
1
(3; 5; 4)
u
. B.
2
(3;5; 4)
u
. C.
3
(3; 5;4)
u
. D.
4
(3;5;4)
u
.
Câu 9. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 2 0
P x y z
và điểm
1;2; 1
I
. Viết phương trình mặt cầu
( )S
có tâm
I
và cắt mặt phẳng
( )P
theo giao tuyến là đường
tròn có bán kính bằng 5.
A.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
. B.
2 2 2
( ) : ( 1) ( 2) ( 1) 34
S x y z
.
C.
2 2 2
( ) : ( 1) ( 2) ( 1) 16
S x y z
. D.
2 2 2
( ) : ( 1) ( 2) ( 1) 25
S x y z
.
Mã đề 124
Trang 2/3 – Mã đề 124
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 1
:
2 1 1
x y z
d
và điểm
1; 2;1
A
. Viết phương trình mặt phẳng
( )P
đi qua điểm
A
và chứa đường thẳng
d
.
A.
( ) : 2 5 0
P x y z
. B.
( ): 4 2 5 0
P x y z
.
C.
( ) : 2 5 7 0
P x y z
. D.
( ) : 2 0
P x y z
.
Câu 11. Trong không gian với hệ tọa độ
( ; , , )O i j k
, cho hai điểm A, B thỏa mãn
2 3OA i j k
và
4 3
OB i j k
. Tìm tọa độ trung điểm
M
của đoạn thẳng
AB
.
A.
3;1;1
M
. B.
3; 1; 1
M
. C.
2;4; 4
M
. D.
1;2; 2
M
.
Câu 12. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 4
:
2 1 3
x y z
d
. Vectơ nào dưới
đây là vectơ chỉ phương của đường thẳng d ?
A.
1
( 2;1; 3)
u
. B.
2
( 2; 1;3)
u
. C.
3
(2; 1; 3)
u
. D.
4
(1; 2;4)
u
.
Câu 13. Tìm số phức liên hợp của số phức
3 2z i
.
A.
2 3z i
. B.
3 2z i
. C.
3 2z i
. D.
3 2z i
.
Câu 14. Cho số phức
( , )z a bi a b R
thỏa mãn
2 1 7z i z i
. Tính
a b
.
A.
1
a b
. B.
1a b
. C.
5
a b
. D.
5
a b
.
Câu 15. Tìm
4
x
e dx
.
A.
4 4
4
x x
e dx e C
. B.
4 3
4
x x
e dx e C
. C.
4 4
1
4
x x
e dx e C
. D.
4 4x x
e dx e C
.
Câu 16. Cho số phức
z
thỏa mãn
(2 )z i i
. Điểm nào sau đây là điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ ?
A.
( 1;2)
M
. B.
(1;2)
N
. C.
( 2;1)
P
. D.
(2;1)
Q
.
Câu 17. Cho số phức
z
thỏa mãn
z z
. Mệnh đề nào sau đây đúng ?
A. Phần thực của
z
không âm. B.
z
là số thuần ảo.
C.
z
là số thực dương. D.
1.
z
Câu 18. Tìm
2
1
os
dx
c x
.
A.
2
1
t anx
os
dx C
c x
. B.
2
1
t anx
os
dx C
c x
.
C.
2
1
t x
os
dx co C
c x
. D.
2
1
t x
os
dx co C
c x
.
Câu 19. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
3 1 2z i z i
là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A.
8 6 5 0
x y
. B.
8 2 5 0
x y
. C.
8 2 5 0
x y
. D.
8 6 5 0
x y
.
Câu 20. Biết
3
1
1
ln5 ln3 ( , )
2 3
dx m n m n R
x
. Tính
P m n
.
A.
0
P
. B.
1P
. C.
3
2
P
. D.
3
2
P
.
Câu 21. Cho
2 5
1 1
( ) 3, ( ) 2
f x dx f x dx
. Tính
5
2
( )I f x dx
.
A.
5
I
. B.
5
I
. C.
1I
. D.
1I
.
Câu 22. Cho số phức
,
z x yi x y R
thỏa mãn
3 4 4
z i
và
z
có môđun lớn nhất. Tính
x y
.
A.
9
5
x y
. B.
9
5
x y
. C.
1
5
x y
. D.
1
5
x y
.
Trang 3/3 – Mã đề 124
Câu 23. Cho
4 4
1 1
( ) 3, ( ) 2 ( ) 7
f x dx f x g x dx
. Tính
4
1
( )I g x dx
.
A.
2I
. B.
2I
. C.
5
I
. D.
5
I
.
Câu 24. Gọi
( )H
là hình phẳng giới hạn bởi đồ thị hàm số
y x
, trục hoành và đường thẳng
2y x
. Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành .
A.
10
3
V
. B.
8
3
V
. C.
16
3
V
. D.
32
3
V
.
Câu 25. Tìm nguyên hàm của hàm số
2
( )
16
x
f x
x
.
A.
2
2 2
16
( )
( 16)
x
f x dx C
x
. B.
2
1
( ) ln 16
2
f x dx x C
.
C.
1 4
( ) ln
8 4
x
f x dx C
x
. D.
2
( ) ln 16
f x dx x C
.
Câu 26. Tính môđun của số phức
2 2z i
.
A.
0
z
. B.
8
z
. C.
4
z
. D.
2 2
z
.
Câu 27. Cho hàm số
( )f x
có đạo hàm liên tục trên đoạn
0;
,
0 1
f
và
0
'( ) 9
f x dx
. Tính
f
.
A.
10
f
. B.
10
f
. C.
8
f
. D.
8
f
.
Câu 28. Tìm
3
x
xe dx
.
A.
3 3
x x x
xe dx xe e C
. B.
3 3 3
x x x
xe dx xe e C
.
C.
2
3
3
2
x x
xe dx x e C
. D.
3 3 3
x x x
xe dx xe e C
.
Câu 29. Tìm nguyên hàm
( )F x
của hàm số
1
( )f x
x
, biết
(9) 0
F
.
A.
( ) 2 6
F x x
. B.
( ) 2 6
F x x
. C.
( ) 3F x x
. D.
1 1
( )
6
2
F x
x
.
Câu 30. Gọi
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2 10 0
z z
, trong đó
1
z
có phần ảo âm.
Tìm số phức
1 2 2
( )w z z z
.
A.
2 6w i
. B.
2 6w i
. C.
2 6w i
. D.
2 6w i
.
Câu 31. Cho tích phân
2
3 2
0
4
I x x dx
. Đặt
2
4
t x
. Mệnh đề nào sau đây đúng ?
A.
2
2 4
0
(4 )I t t dt
. B.
2
3
0
(4 )I t t dt
. C.
2
3
0
4
I t t dt
. D.
2
4 2
0
4
I t t dt
.
Câu 32. Tính diện tích
S
của hình phẳng giới hạn bởi parabol
2
( ) : 3 2
P y x
, trục hoành, trục tung và
đường thẳng
2
x
.
A.
8
S
. B.
10
S
. C.
12
S
. D.
14
S
.
--------------- HẾT ---------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Câu
Mã đề
101
Mã đề
102
Mã đề
103
Mã đề
104
Mã đề
105
Mã đề
106
Mã đề
107
Mã đề
108
Mã đề
109
Mã đề
110
Mã đề
111
Mã đề
112
1
A C C
C A B C A A A C B
2
C B A
B D D D D B C A D
3
B D A
A C D B A D A D C
4
D B B
C D A A D C C A A
5
A D D
A A B A C A C D A
6
C A B
C B B C D D B B A
7
D C C
A A C A A B A B C
8
B B A
D C A C B B B C D
9
A D D
B C B B B C D D B
10
D C A
B D C A C A B B C
11
B A C
B C C D D B B C C
12
D B C
D B A D C C C B B
13
C A B
A A A B C C D C B
14
B D D
C D B D B B D D D
15
A C A
D B C C A D A A A
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
ĐÁP ÁN
QUẢNG NAM
15
A C A
D B C C A D A A A
16
C D B
B D D B D A A A D
17
B A D
D B A D B A C D A
18
D B C
C D D B D A D B B
19
A C A
D C A A C D B D A
20
C D B
A B C C B C D C C
21
B A D
A A A B A B A C B
22
D B A
B B D B D D A B B
23
A C B
D C B B B C B A D
24
C A C
A B C D A A D A C
25
B C B
D C B A C D C A C
26
C D D
C A D C B C D B A
27
D B C
B C A A C B C D D
28
A A C
C D D C C D B B A
29
A B D
D B C D B D A A B
30
B A B
A A B A A C D C D
31
A C D
B B D A A A A C D
32
D B A
A A C D B B B B C
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Câu
Mã đề
113
Mã đề
114
Mã đề
115
Mã đề
116
Mã đề
117
Mã đề
118
Mã đề
119
Mã đề
120
Mã đề
121
Mã đề
122
Mã đề
123
Mã đề
124
1
B A B A A B A B B D C B
2
D D D C B A B C D A C B
3
B B A A C B D A C B D D
4
C C C B A D C A A C B C
5
D D D C C C B A D B A C
6
A A D B D B C C C C B A
7
C A C A B A D D B D A D
8
B D C C A D A B D A B A
9
A C B A A D B A D A B B
10
A A B C B C A B C A C D
11
C B D B C C A B A D A D
12
C D A D B D D C B B A C
13
A D D A C B C D A C D B
14
B C C C B D D A B B A D
15
A B B D D D A B D C B C
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017
Môn: TOÁN – Lớp 12
ĐÁP ÁN
QUẢNG NAM
15
A B B D D D A B D C B C
16
D C D D B A C C C D C A
17
D D A B D C B D A A D A
18
B B B D A C C C D B C A
19
D C B B C B B B B C B C
20
C B C D B B D C B B A D
21
D A A A D C A D C D C B
22
A C A B C A D C A D C B
23
A B B D A B A B B A D C
24
A C C D B A B D C C D C
25
D B A C A A D A C D C B
26
B A A A D B B B B A B D
27
B A B B C C D D D A D A
28
B B D C D D C A A C A D
29
C D D D A A B B A A B A
30
A B A A B D A A A B D B
31
C A C B C A A D D B A A
32
D C C A D C C C C D B C
| 1/75
| | Tải xuống

Có thể bạn quan tâm:

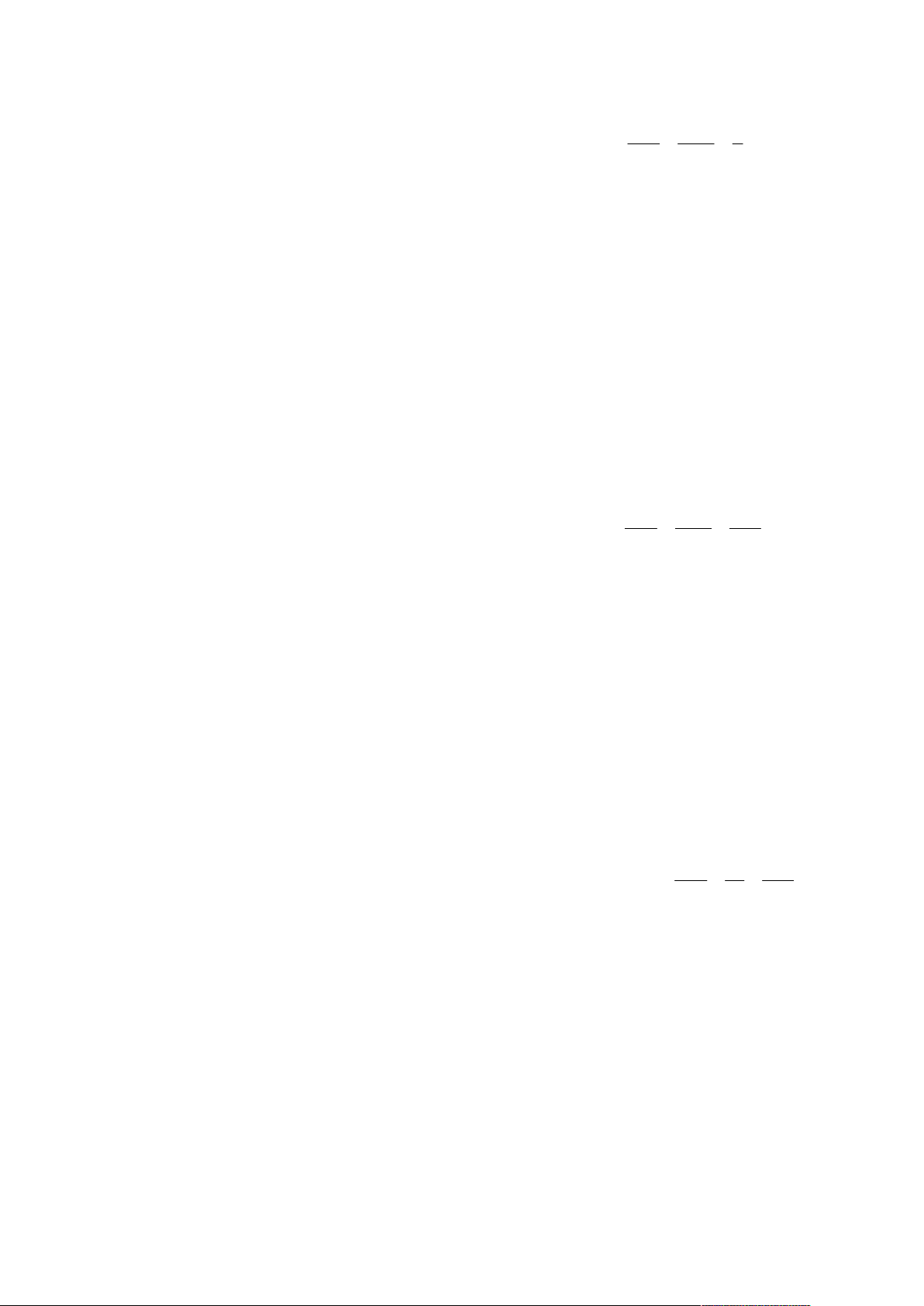
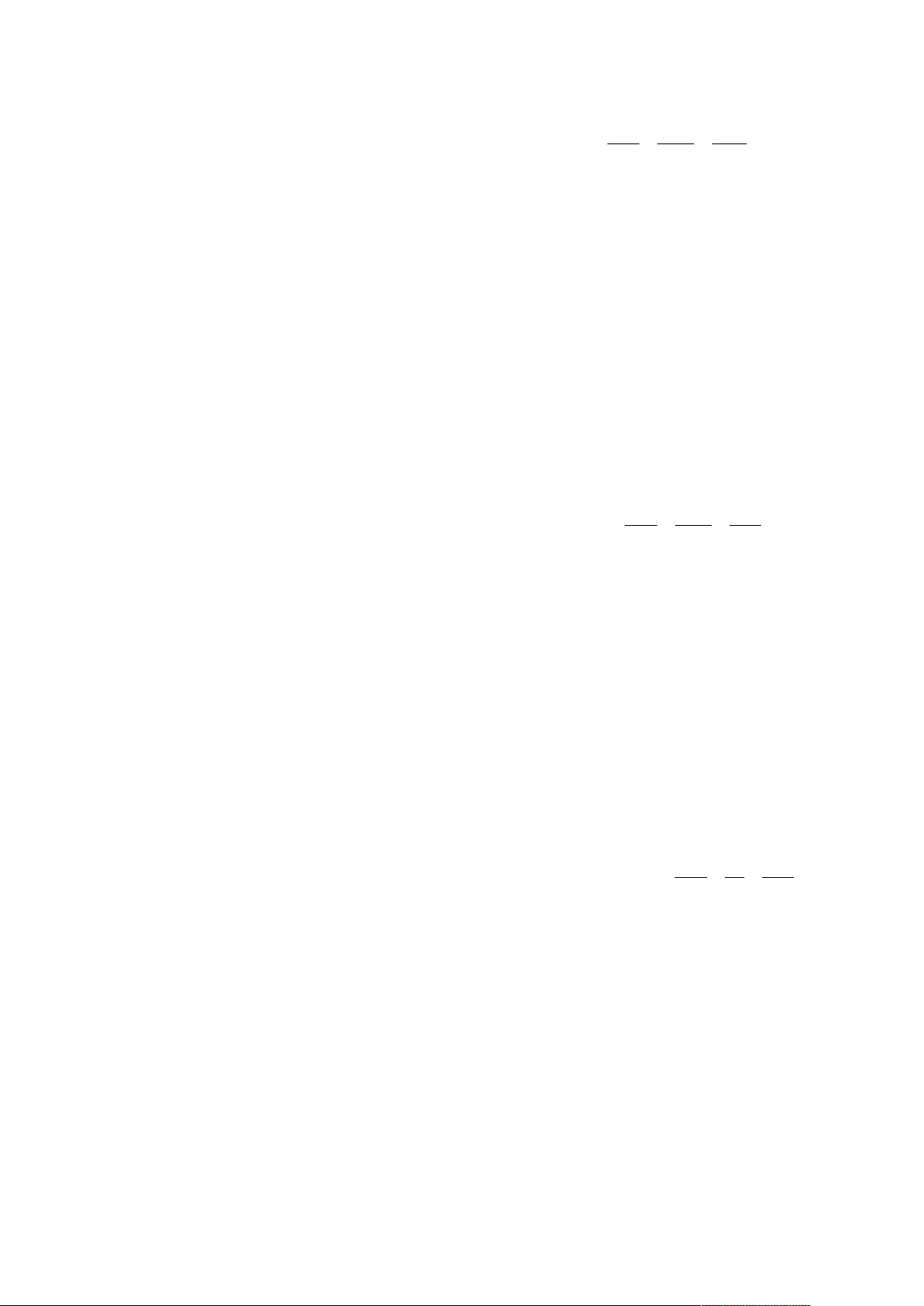
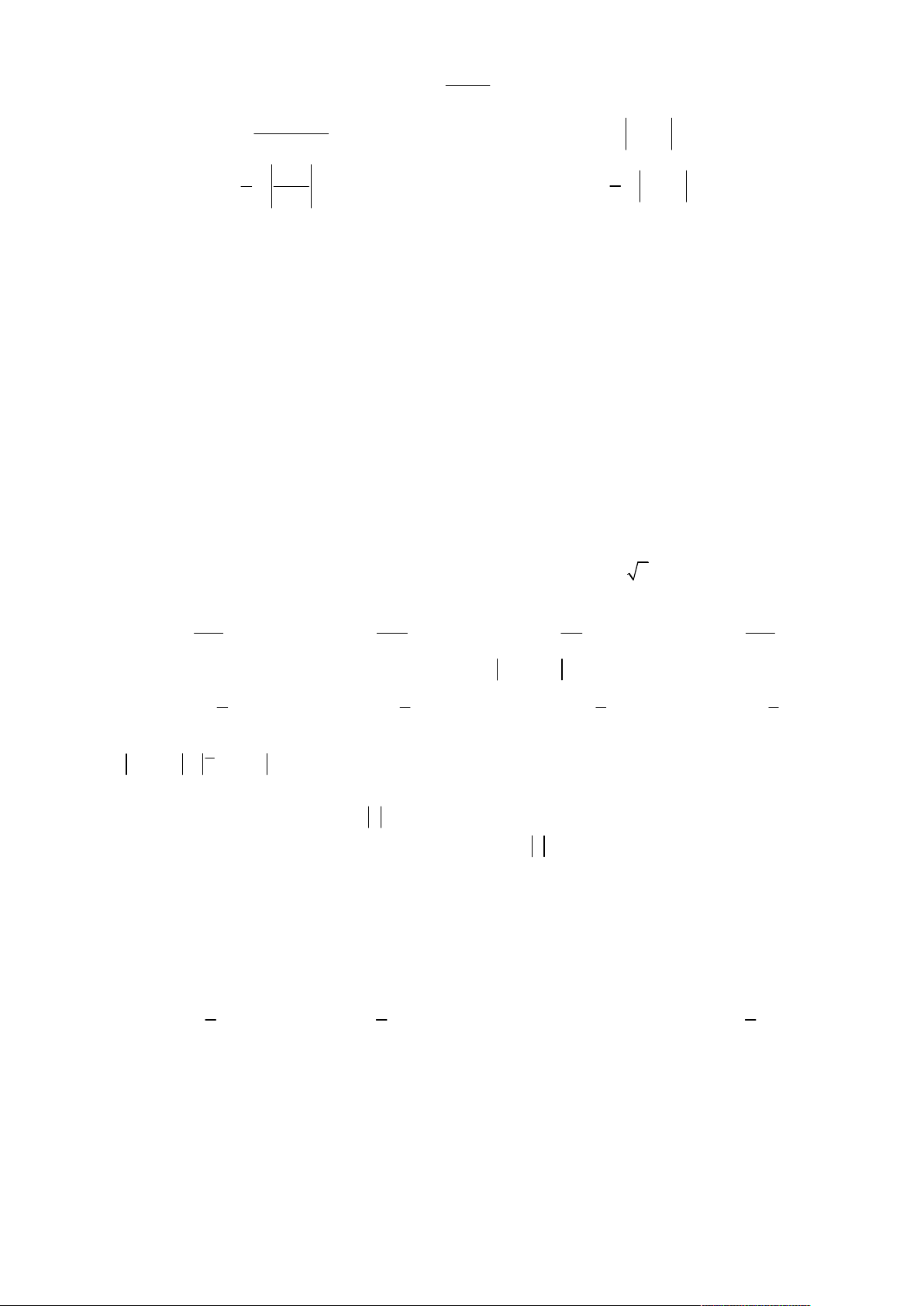
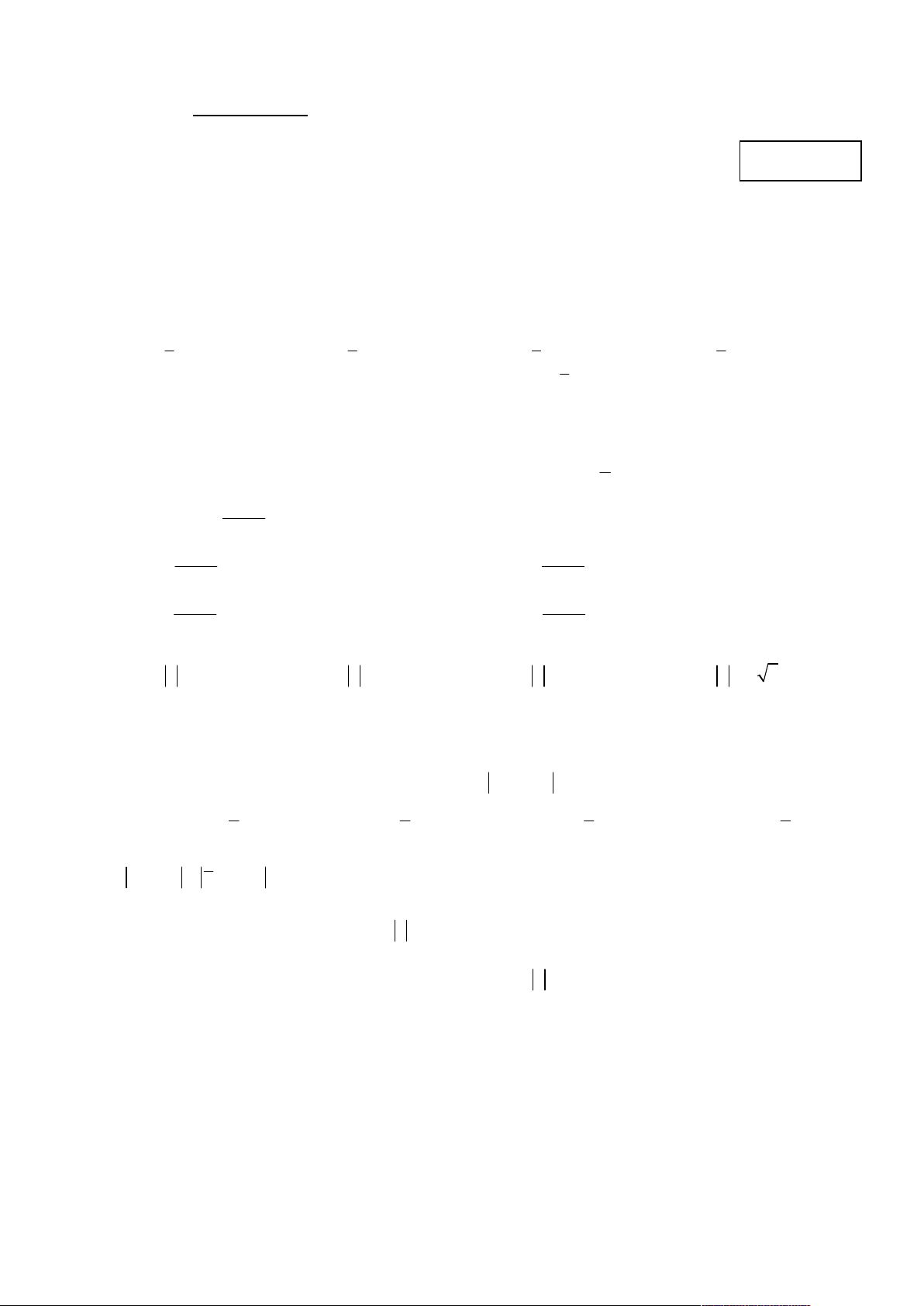
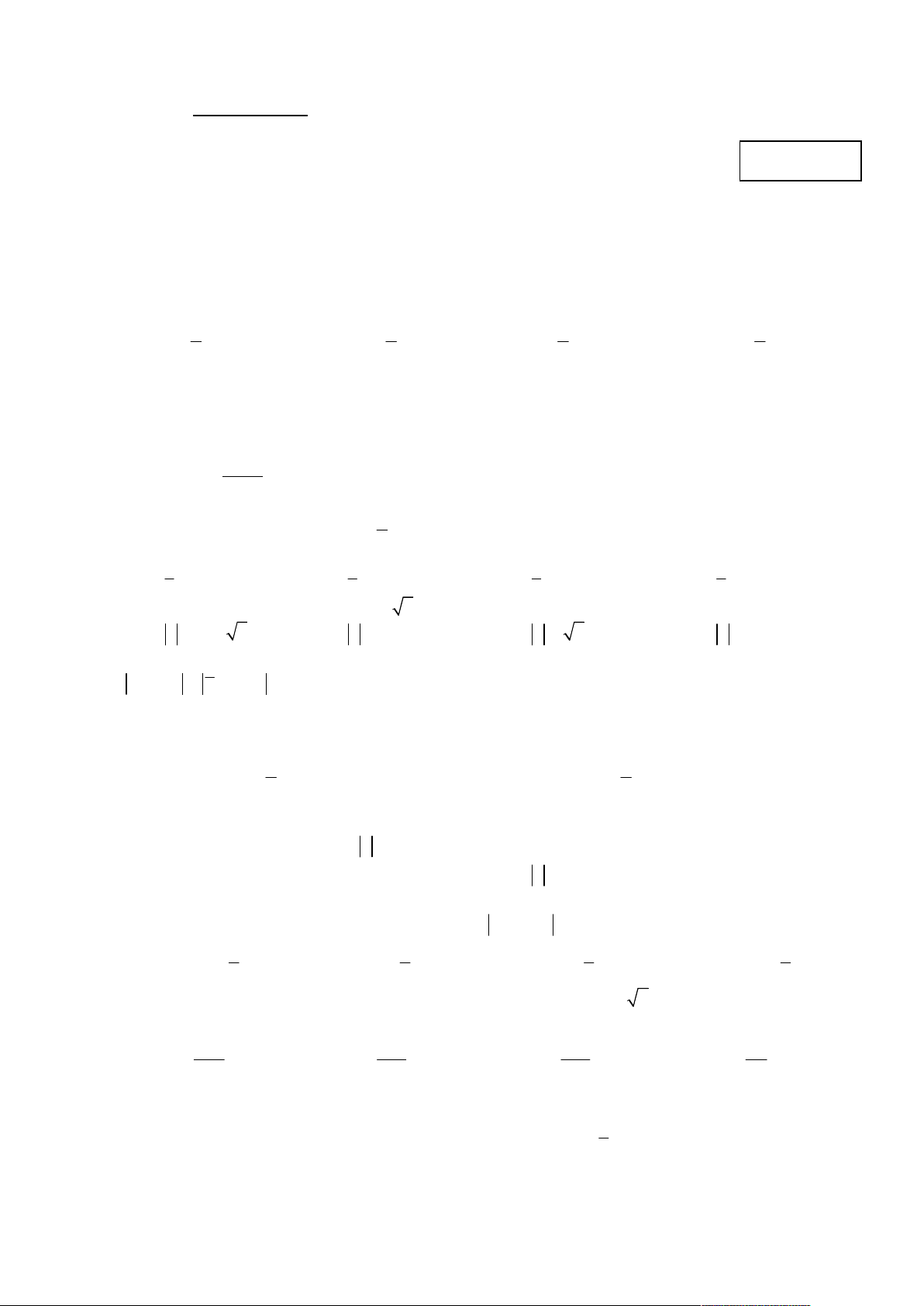
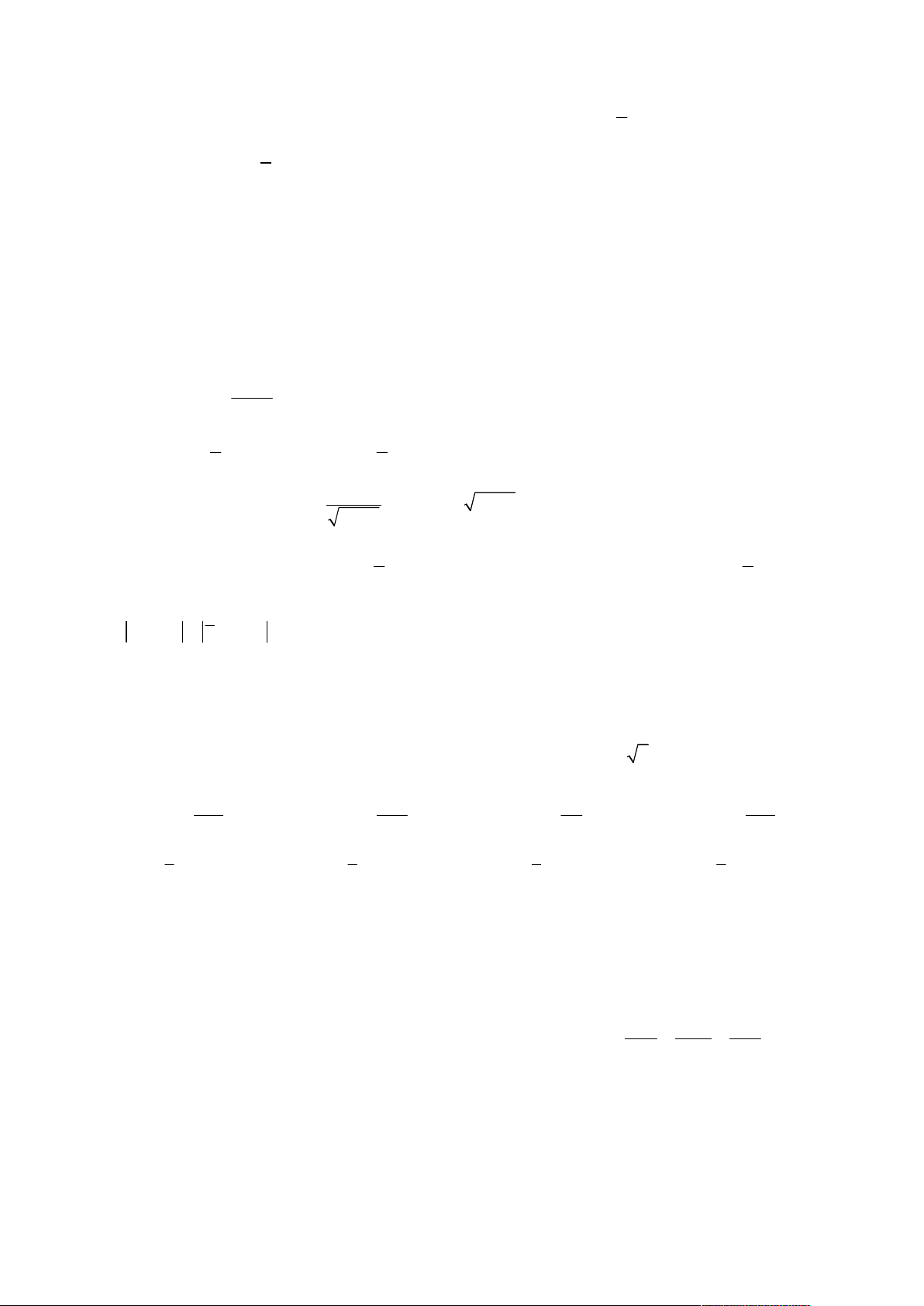
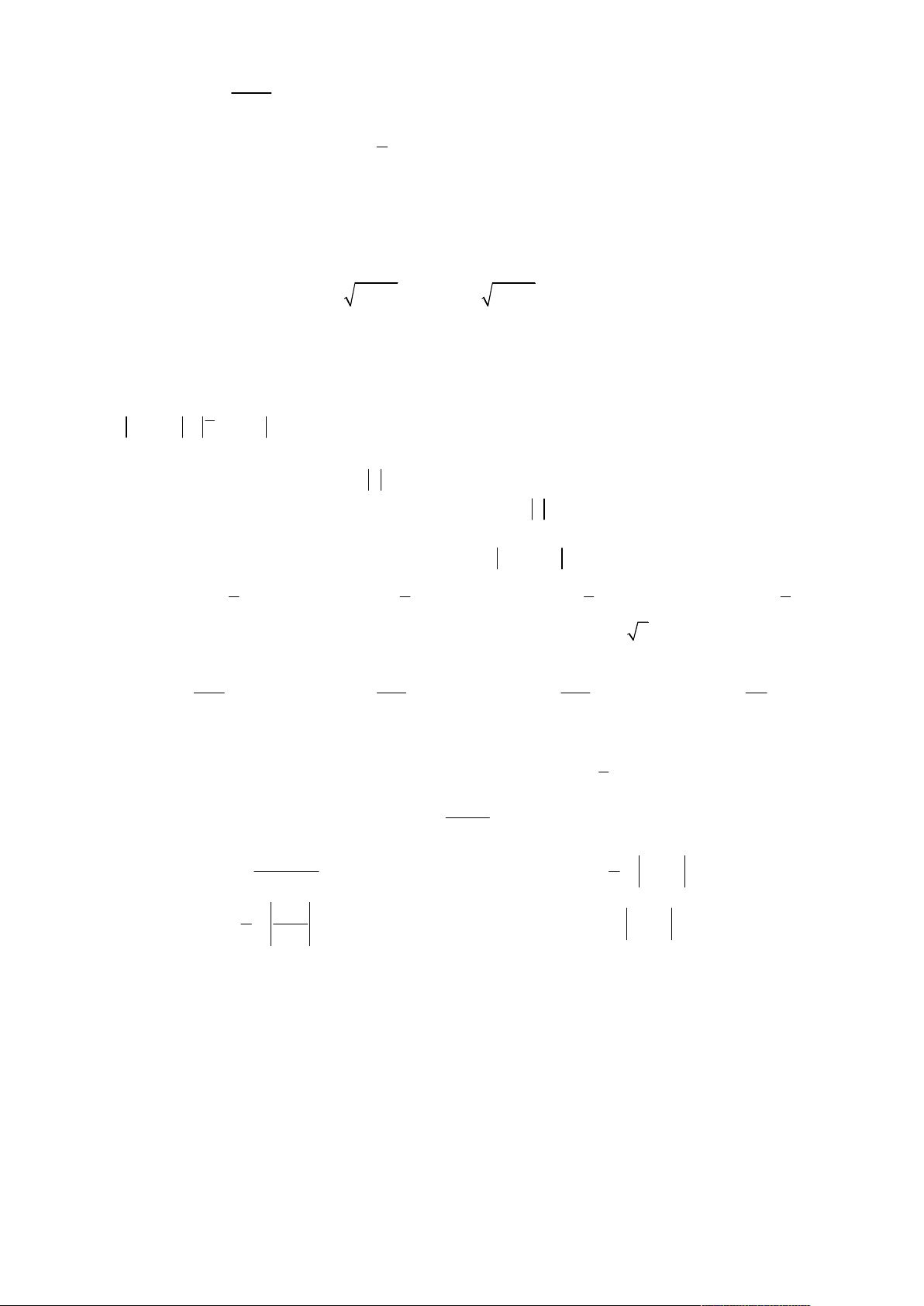
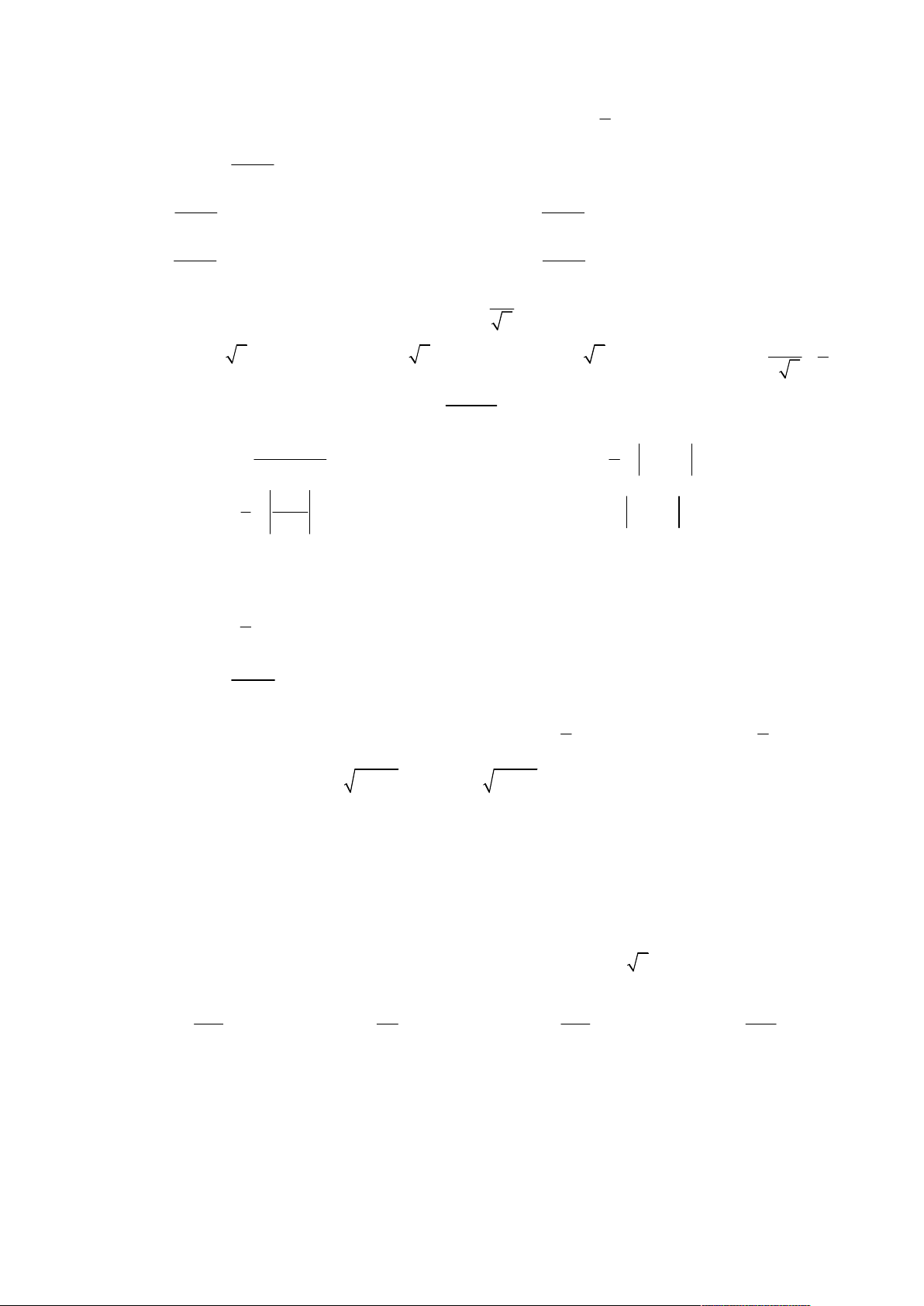
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 101
Họ và tên học sinh: ……………………………..………………. Lớp: ………… Câu 1. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 2. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 1
Câu 3. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 x
Câu 4. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2 Câu 5. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2 3 3 Câu 6. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 7. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1. 2
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 . 4 1 Câu 9. Biết
dx m ln 5  n ln 3 (m, n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 Trang 1/3 – Mã đề 101 4 x
Câu 10. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 11. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 12. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 13. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i .
Câu 14. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 .
Câu 15. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 16. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 17. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 .
Câu 18. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 .
Câu 19. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.
Câu 20. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5       
Câu 21. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2   . D. M ; 1; 2   .  2   2   2 
Câu 22. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1;0 . D. 0;0;3 .    
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 . Trang 2/3 – Mã đề 101 x 1 y  2 z
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) .
B. u2  (2;1; 1) . C. 3 u  (2;1; 1) .
D. u4  (2; 1;1) .
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho điểm M  1
 ;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0. x  1 2t
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .  
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2  ; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 . x 1 y z 1
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A0; 1
 ;3 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2; 4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2;  4;  3) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 101 Trang 4/3 – Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 102
Họ và tên học sinh: ……………………………..………………. Lớp: ………… Câu 1. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3
Câu 2. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  . 1
Câu 3. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 x
Câu 4. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 5. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 5 5 Câu 6. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 7. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2  6       
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3 Trang 1/3 – Mã đề 102 2 1 Câu 9. Biết
dx m ln 7  n ln 2 (m, n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3 2 Câu 10. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1
Câu 11. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 .
Câu 12. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 13. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 14. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .
Câu 15. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 16. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 17. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 18. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 19. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 20. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5       
Câu 21. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   . D. M  1  ; 2; 4   .  2   2   2 
Câu 22. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 . Trang 2/3 – Mã đề 102    
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 . x 1 y  2 z
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  (2;1;1) . C. 3 u  (2; 1;1) .
D. u4  (1;  2;0) .
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0. x  1 2t
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .  
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1  ;1; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y z 1
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) .
B. u2  (6; 4; 1) . C. 3 u  (6;  4;1) . D. u4  (6; 4;1) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 102
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 103
Họ và tên học sinh: ……………………………..………………. Lớp: ………… Câu 1. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4 1 Câu 2. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x 1
Câu 3. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 x
Câu 4. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4 Câu 5. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 2 5 5 Câu 6. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 7. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 . 
Câu 8. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 .
B. f    10 .
C. f    8 .
D. f    8 . Trang 1/3 – Mã đề 103 3 1 Câu 9. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 2 Câu 10. Cho tích phân 3 2 I x 4  x dx  . Đặt 2
t  4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0
Câu 11. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 12. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 13. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 14. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 .
Câu 15. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) . Câu 16. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i .
Câu 17. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 .
Câu 18. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 .
Câu 19. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1.
Câu 20. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5       
Câu 21. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 .
Câu 22. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 . Trang 2/3 – Mã đề 103    
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 . x 1 y  2 z  4
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) .
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0. x  2  t
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) .  
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  (1; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 . x 1 y  2 z 1
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6  3 3
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y z 1
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 103
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 104
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i .
Câu 2. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 .
Câu 3. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 4. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i . Câu 5. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 6. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 4 1 Câu 7. Biết
dx m ln 5  n ln 3 (m, n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 4 x
Câu 8. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 9. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 . 1
Câu 10. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2
Câu 11. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 . Trang 1/3 – Mã đề 104 x
Câu 12. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2 Câu 13. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2 3 3 Câu 14. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 15. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1. 2
Câu 16. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 .
Câu 17. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 18. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5
Câu 19. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 .
Câu 20. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.    
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 .       
Câu 22. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2 . D. M ; 1; 2   .  2   2   2 
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2;4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2; 4; 3) . Trang 2/3 – Mã đề 104 x 1 y  2 z 1
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 25. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1;0 . D. 0;0;3 . x 1 y  2 z
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) . B. u2  (2;1;1) . C. 3 u  ( 2  ;1; 1) . D. u4  ( 2  ; 1;1) .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0. x  1 2t
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .  
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) .
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 . x 1 y z 1
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A0; 1
 ;3 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 104
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 105
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 2. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .
Câu 3. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 4. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm. Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 5. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 6. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 . 2 5 5 Câu 7. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 8. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2
Câu 9. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 10. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 Câu 11. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3
Câu 12. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  . Trang 1/3 – Mã đề 105
Câu 13. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 . 1
Câu 14. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 x
Câu 15. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 16. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  .  6       
Câu 17. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3 2 1 Câu 18. Biết
dx m ln 7  n ln 2 (m, n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3 2 Câu 19. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1
Câu 20. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3       
Câu 21. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   . D. M  1  ; 2; 4   .  2   2   2 
Câu 22. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 . Trang 2/3 – Mã đề 105 x 1 y z 1
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) .
B. u2  (6; 4; 1) . C. 3 u  (6;  4;1) . D. u4  (6; 4;1) .    
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 . x 1 y  2 z
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  (2;1;1) . C. 3 u  (2; 1;1) .
D. u4  (1;  2;0) .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0. x  1 2t
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .  
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1  ;1; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2  ; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 106
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 2. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 .
Câu 3. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 .
Câu 4. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) . Câu 5. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i .
Câu 6. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
Câu 7. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 .
Câu 8. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1. 2 5 5 Câu 9. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 10. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 . Câu 11. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4 1 Câu 12. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x Trang 1/3 – Mã đề 106 1
Câu 13. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 x
Câu 14. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4
Câu 15. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Câu 16. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 
Câu 17. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 .
B. f    10 .
C. f    8 .
D. f    8 . 3 1 Câu 18. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 2 Câu 19. Cho tích phân 3 2 I x 4  x dx  . Đặt 2
t  4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0
Câu 20. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 21. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 .
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) .    
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 . Trang 2/3 – Mã đề 106 x 1 y  2 z 1
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6  3 3
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y z 1
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) .       
Câu 28. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 . x 1 y  2 z  4
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0. x  2  t
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) .  
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  (1; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 106
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 107
Họ và tên học sinh: ……………………………..………………. Lớp: ………… 2 3 3 Câu 1. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 2. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1.
Câu 3. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 .
Câu 4. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 5. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 6. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 Câu 7. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . Câu 8. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i . 2
Câu 9. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 . 4 1 Câu 10. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 Trang 1/3 – Mã đề 107 4 x
Câu 11. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 12. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 .
Câu 13. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 14. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 15. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i . 1
Câu 16. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 x
Câu 17. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2
Câu 18. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 .
Câu 19. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.
Câu 20. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0.
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 . Trang 2/3 – Mã đề 107       
Câu 23. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2 . D. M ; 1; 2   .  2   2   2 
Câu 24. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1  ; 0 . D. 0;0;3 .    
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 . x 1 y  2 z
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) . B. u2  (2;1;1) . C. 3 u  ( 2  ;1; 1) . D. u4  ( 2  ; 1;1) .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho điểm A0; 1
 ;3 và đường thẳng x 1 y z 1 d :  
. Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d . 2 1  1
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 . x  1 2t
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .  
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2; 4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2;  4;  3) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 107
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 108
Họ và tên học sinh: ……………………………..………………. Lớp: ………… 2 5 5 Câu 1. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 2 1 Câu 2. Biết
dx m ln 7  n ln 2 (m, n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3
Câu 3. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 4. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .
Câu 5. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 6. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm. Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 7. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 8. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 9. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  .
Câu 10. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 11. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 Câu 12. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3 Trang 1/3 – Mã đề 108 4 4 4 Câu 13. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2  6       
Câu 14. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3
Câu 15. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 . 1
Câu 16. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 x
Câu 17. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 18. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 Câu 19. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1
Câu 20. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 x 1 y  2 z
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  ( 2  ;1;1) . C. 3 u  (2; 1  ;1) .
D. u4  (1; 2;0) . x  1 2t
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) . Trang 2/3 – Mã đề 108
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) . B. u2  (6;4;1) . C. 3 u  (6;  4;1) . D. u4  (6;4;1) .       
Câu 24. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   .
D. M 1; 2;4 .  2   2   2     
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 .
Câu 26. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 . x 1 y z 1
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho điểm M  1
 ;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0.  
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1  ;1; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 5. A. 2 2 2
(S) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y  2 z 1
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2  ; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 108
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 109
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) .
Câu 2. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 3. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 . Câu 4. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4 1 Câu 5. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x
Câu 6. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 . Câu 7. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i .
Câu 8. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
Câu 9. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 .
Câu 10. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1. 2 5 5 Câu 11. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 12. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 . Trang 1/3 – Mã đề 109
Câu 13. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 x
Câu 14. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4 Câu 15. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 1
Câu 16. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 2 Câu 17. Cho tích phân 3 2 I x 4  x dx  . Đặt 2 t
4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0 
Câu 18. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 .
B. f    10 .
C. f    8 .
D. f    8 . 3 1 Câu 19. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2
Câu 20. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .    
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 .
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2  ; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) .  
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  (1; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 . Trang 2/3 – Mã đề 109
Câu 24. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 . x  2  t
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) . x 1 y  2 z 1
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6  3 3
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y z 1
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2  ; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .       
Câu 29. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 . x 1 y  2 z  4
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) .
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0.
--------------- HẾT --------------- Trang 3/3 – Mã đề 109
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 110
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 2. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i . Câu 3. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 4. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2
Câu 5. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i .
Câu 6. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 . 4 1 Câu 7. Biết
dx m ln 5  n ln 3 (m, n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2
Câu 8. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 . 4 x
Câu 9. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 10. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 . 1
Câu 11. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 Trang 1/3 – Mã đề 110
Câu 12. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5 x
Câu 13. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2
Câu 14. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 .
Câu 15. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo. Câu 16. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2 3 3 Câu 17. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 18. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1. 2
Câu 19. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 .
Câu 20. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 x 1 y  2 z 1
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).    
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 .       
Câu 23. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2 . D. M ; 1; 2   .  2   2   2  Trang 2/3 – Mã đề 110
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2;4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2; 4; 3) . x  1 2t
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .
Câu 26. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1  ; 0 . D. 0;0;3 . x 1 y  2 z
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) .
B. u2  (2;1; 1) . C. 3 u  (2;1; 1) .
D. u4  (2; 1;1) .
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0. x 1 y z 1
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A0; 1
 ;3 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 .  
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 .
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 110
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 111
Họ và tên học sinh: ……………………………..………………. Lớp: ………… 4 4 4 Câu 1. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2 2 5 5 Câu 2. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 2 1 Câu 3. Biết
dx m ln 7  n ln 2 ( , m n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3
Câu 4. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 5. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .
Câu 6. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 7. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  .
Câu 8. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 9. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
Câu 10. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Câu 11. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3 Trang 1/3 – Mã đề 111  6       
Câu 12. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3
Câu 13. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 14. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 15. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 16. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 . 1
Câu 17. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 x
Câu 18. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 19. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 Câu 20. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1    
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 .
Câu 22. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 . x 1 y  2 z
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  ( 2  ;1;1) . C. 3 u  (2; 1  ;1) .
D. u4  (1; 2;0) . Trang 2/3 – Mã đề 111
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 5. A. 2 2 2
(S) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y  2 z 1
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) . x  1 2t
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) . B. u2  (6;4;1) . C. 3 u  (6;  4;1) . D. u4  (6;4;1) .       
Câu 29. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   .
D. M 1; 2;4 .  2   2   2  x 1 y z 1
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0.  
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1  ;1; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 111
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 112
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 2. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 . Câu 3. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4
Câu 4. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) .
Câu 5. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1. 1 Câu 6. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x
Câu 7. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 . 3 1 Câu 8. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 2 5 5 Câu 9. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 10. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 .
Câu 11. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Trang 1/3 – Mã đề 112
Câu 12. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 x
Câu 13. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4
Câu 14. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 . 
Câu 15. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 . B. f    1  0 .
C. f    8 . D. f    8  . Câu 16. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 1
Câu 17. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 Câu 18. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i . 2 Câu 19. Cho tích phân 3 2 I x 4  x dx  . Đặt 2
t  4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0
Câu 20. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0.    
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 .
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) . Trang 2/3 – Mã đề 112  
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  (1; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 . x 1 y  2 z 1
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6  3 3
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 26. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 . x  2  t
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) .
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) .
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y z 1
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .       
Câu 31. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 . x 1 y  2 z  4
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 112
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 113
Họ và tên học sinh: ……………………………..………………. Lớp: ………… 1
Câu 1. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 x
Câu 2. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2
Câu 3. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 . 2 3 3 Câu 4. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 5. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1.
Câu 6. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.
Câu 7. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5
Câu 8. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 .
Câu 9. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 10. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 11. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i . Trang 1/3 – Mã đề 113 Câu 12. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 Câu 13. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2
Câu 14. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 . 4 1 Câu 15. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 4 x
Câu 16. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 17. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 .
Câu 18. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 19. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 20. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i .
Câu 21. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1  ; 0 . D. 0;0;3 .    
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 . x 1 y  2 z 1
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P). Trang 2/3 – Mã đề 113
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) .
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2;4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2; 4; 3) .
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0.
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 .       
Câu 28. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2   . D. M ; 1; 2   .  2   2   2  x 1 y  2 z
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) .
B. u2  (2;1; 1) . C. 3 u  (2;1; 1) .
D. u4  (2; 1;1) .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho điểm A0; 1
 ;3 và đường thẳng x 1 y z 1 d :  
. Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d . 2 1  1
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 . x  1 2t
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .  
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 113
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 114
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 2. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .  6       
Câu 3. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3
Câu 4. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 5. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm. Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 6. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 7. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 . 1
Câu 8. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 4 4 4 Câu 9. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2 2 5 5 Câu 10. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1.
Câu 11. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  . Trang 1/3 – Mã đề 114 2 1 Câu 12. Biết
dx m ln 7  n ln 2 (m, n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3 Câu 13. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 Câu 14. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 16. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 17. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
Câu 18. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Câu 19. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3 x
Câu 20. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 5. A. 2 2 2
(S) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 .
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0. Trang 2/3 – Mã đề 114  
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1  ;1; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 .    
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 .
Câu 25. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 . x 1 y  2 z
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  (2;1;1) . C. 3 u  (2; 1;1) .
D. u4  (1;  2;0) . x 1 y  2 z 1
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) . x  1 2t
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) .
B. u2  (6; 4; 1) . C. 3 u  (6;  4;1) . D. u4  (6; 4;1) .       
Câu 31. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   .
D. M 1; 2;4 .  2   2   2  x 1 y z 1
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 114
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 115
Họ và tên học sinh: ……………………………..………………. Lớp: …………    
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 .       
Câu 2. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 .
Câu 3. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 . x 1 y  2 z  4
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) . x  2  t
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) .  
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  ( 1  ; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 . x 1 y  2 z 1
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6 3 3 
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . Trang 1/3 – Mã đề 115
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0. x 1 y z 1
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5;4) .
Câu 13. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 .
Câu 14. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 .
Câu 15. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 16. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 .
Câu 17. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) . Câu 18. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i . 2 5 5 Câu 19. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 20. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 . 
Câu 21. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 .
B. f    10 .
C. f    8 .
D. f    8 .
Câu 22. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1.
Câu 23. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 Trang 2/3 – Mã đề 115 Câu 24. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4 1 Câu 25. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x 1
Câu 26. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 x
Câu 27. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4 Câu 28. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 3 1 Câu 29. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 2 Câu 30. Cho tích phân 3 2 I x 4  x dx  . Đặt 2 t
4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0
Câu 31. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 32. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
--------------- HẾT --------------- Trang 3/3 – Mã đề 115
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 116
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) .
Câu 2. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i . 4 1 Câu 3. Biết
dx m ln 5  n ln 3 (m, n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2
Câu 4. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 . Câu 5. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 6. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 .
Câu 7. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.
Câu 8. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5 Câu 9. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 10. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 1
Câu 11. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 Trang 1/3 – Mã đề 116 x
Câu 12. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2 Câu 13. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2 3 3 Câu 14. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 .
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 . 2 2 2 Câu 16. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1. 2
Câu 17. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 . 4 x
Câu 18. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 19. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 20. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3    
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 .       
Câu 22. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2 . D. M ; 1; 2   .  2   2   2 
Câu 23. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1;0 . D. 0;0;3 . Trang 2/3 – Mã đề 116
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2;4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2; 4; 3) . x 1 y  2 z
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) .
B. u2  (2;1; 1) . C. 3 u  (2;1; 1) .
D. u4  (2; 1;1) .
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0. x  1 2t
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z 1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .  
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho điểm A0; 1
 ;3 và đường thẳng x 1 y z 1 d :  
. Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d . 2 1  1
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 116
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 117
Họ và tên học sinh: ……………………………..………………. Lớp: …………       
Câu 1. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   .
D. M 1; 2;4 .  2   2   2 
Câu 2. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 .    
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 . x 1 y  2 z
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới đây 2 1  1
là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  ( 2  ;1;1) . C. 3 u  (2; 1  ;1) .
D. u4  (1; 2;0) .
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0. x  1 2t
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z  1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .  
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1
 ;1; 0) . Tính số đo của  
góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ;  1 .
Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . Trang 1/3 – Mã đề 117
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) . x 1 y z 1
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) .
B. u2  (6; 4; 1) . C. 3 u  (6;  4;1) . D. u4  (6; 4;1) . Câu 13. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3
Câu 14. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  . 1
Câu 15. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 x
Câu 16. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 17. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 5 5 Câu 18. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. 4 4 4 Câu 19. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2 Trang 2/3 – Mã đề 117  6       
Câu 20. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3 2 1 Câu 21. Biết
dx m ln 7  n ln 2 ( , m n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3 2 Câu 22. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1
Câu 23. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 .
Câu 24. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 25. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 26. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .
Câu 27. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . Câu 28. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 29. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 30. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 31. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 32. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
--------------- HẾT --------------- Trang 3/3 – Mã đề 117
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 118
Họ và tên học sinh: ……………………………..………………. Lớp: …………    
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 .
Câu 2. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 .
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0.
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) . x 1 y  2 z 1
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6 3 3 
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 .
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) . x  2  t
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) .       
Câu 9. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 . Trang 1/3 – Mã đề 118  
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  (1; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 . x 1 y  2 z  4
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) . x 1 y z 1
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .
Câu 13. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 14. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 .
Câu 15. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 .
Câu 16. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) . 4 4 4 Câu 17. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 . Câu 18. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4 Câu 19. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i .
Câu 20. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
Câu 21. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 .
Câu 22. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1. 2 5 5 Câu 23. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. Trang 2/3 – Mã đề 118 1 Câu 24. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x 1
Câu 25. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 x
Câu 26. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4
Câu 27. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Câu 28. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 
Câu 29. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 . B. f    1  0 .
C. f    8 . D. f    8  . 3 1 Câu 30. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 2 Câu 31. Cho tích phân 3 2 I x 4  x dx  . Đặt 2
t  4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0
Câu 32. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 118
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 119
Họ và tên học sinh: ……………………………..………………. Lớp: …………    
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 .       
Câu 2. Trong không gian với hệ tọa độ ( ;
O i , j , k ) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2 . D. M ; 1; 2   .  2   2   2 
Câu 3. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1;0 . D. 0;0;3 . x 1 y  2 z
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới đây 2 1  1
là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) .
B. u2  (2;1; 1) . C. 3 u  (2;1; 1) .
D. u4  (2; 1;1) .
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0. x  1 2t
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z  1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .  
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1; 0) . Tính số đo của  
góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ;  1 .
Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 . Trang 1/3 – Mã đề 119
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) . x 1 y z 1
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A0; 1
 ;3 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 .
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2; 4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2;  4;  3) . 2 3 3 Câu 13. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 14. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1. Câu 15. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 Câu 16. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 1
Câu 17. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 Câu 18. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 19. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 .
Câu 20. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 . 4 1 Câu 21. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 Trang 2/3 – Mã đề 119 x
Câu 22. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2 Câu 23. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2
Câu 24. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 . 4 x
Câu 25. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1
Câu 26. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 27. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 28. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i .
Câu 29. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 .
Câu 30. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) .
Câu 31. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.
Câu 32. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5
--------------- HẾT --------------- Trang 3/3 – Mã đề 119
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 120
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 .    
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 .
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ;  1 .
Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 .       
Câu 4. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   .
D. M 1; 2;4 .  2   2   2  x 1 y  2 z
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới đây 2 1  1
là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  (2;1;1) . C. 3 u  (2; 1;1) .
D. u4  (1;  2;0) .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0. x  1 2t
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z  1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .  
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1
 ;1; 0) . Tính số đo của  
góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P). Trang 1/3 – Mã đề 120
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) .
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) . B. u2  (6;4;1) . C. 3 u  (6;  4;1) . D. u4  (6;4;1) . x 1 y z 1
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 . Câu 13. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 14. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 16. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 17. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 Câu 18. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3
Câu 19. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  . 2 Câu 20. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1 1
Câu 21. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 Trang 2/3 – Mã đề 120 4 4 4 Câu 22. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2 x
Câu 23. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 24. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 5 5 Câu 25. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1.  6       
Câu 26. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3 2 1 Câu 27. Biết
dx m ln 7  n ln 2 (m, n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3
Câu 28. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 .
Câu 29. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 30. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 31. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 .
Câu 32. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) .
--------------- HẾT --------------- Trang 3/3 – Mã đề 120
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 121
Họ và tên học sinh: ……………………………..………………. Lớp: …………    
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 .
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) .  
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  ( 1  ; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 .
Câu 4. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 . x  2  t
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) . x 1 y  2 z 1
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6 3 3 
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . x 1 y z 1
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  
và điểm A1; 2;  1 . 2 1  1
Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .       
Câu 9. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 . Trang 1/3 – Mã đề 121 x 1 y  2 z  4
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1
u  (2;1;  3) . B. u2  (2; 1  ;3) . C. 3 u  (2; 1; 3  ) .
D. u4  (1;  2;4) .
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) .
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là
phương trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0.
Câu 13. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) .
Câu 14. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 15. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 . Câu 16. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4 1 Câu 17. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x
Câu 18. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 . Câu 19. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i .
Câu 20. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5
Câu 21. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 .
Câu 22. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1. 2 5 5 Câu 23. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1. Trang 2/3 – Mã đề 121 4 4 4 Câu 24. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 .
Câu 25. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 x
Câu 26. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4 Câu 27. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 1
Câu 28. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 2 Câu 29. Cho tích phân 3 2 I x 4  x dx  . Đặt 2
t  4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0 
Câu 30. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 . B. f    1  0 .
C. f    8 . D. f    8  . 3 1 Câu 31. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2
Câu 32. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 121
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 122
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oz. A. 2;0;0 . B. 0; 1  ; 0 . C. 2; 1;0 . D. 0;0;3 .    
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1; 1
 ) . Tính a . b .         A. a . b  1  .
B. a . b  2 .
C. a . b  (2; 1  ; 2  ) .
D. a . b  1 .       
Câu 3. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   1  A. M  ;1; 2    . B. M ; 0; 1   . C. M 3;0; 2 . D. M ; 1; 2   .  2   2   2  x 1 y  2 z
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới đây 2 1  1
là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (1; 2; 0) .
B. u2  (2;1; 1) . C. 3 u  (2;1; 1) .
D. u4  (2; 1;1) .
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Ox ?
A. y z 1  0. B. x 1  0. C. x  0. D. x 1  0. x  1 2t
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z  1 t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;1) . C. P( 1  ;3; 0) . D. Q(1; 2; 1  ) .
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1 u  (2;  4;3) . B. u2  (2; 4;3) . C. 3 u  (2; 4;  3) .
D. u4  (2;  4;  3) .
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2  ; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oxy . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (3; 1; 0) . B. 2 n  (3;1; 0) . C. 3 n  (1;3; 0) . D. 4 n  (1;  3; 0) . x 1 y z 1
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm A0; 1  ;3 . 2 1  1
Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : x  3y z  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  3y z  6  0 .
D. (P) : x  3y z  6  0 . Trang 1/3 – Mã đề 122 x 1 y  2 z 1
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d chứa trong (P).
B. d song song với (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).  
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  (1; 1  ; 0) . Tính số đo  
của góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  90 . D. a b 0 ,  135 .
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ; 
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn
có bán kính bằng 4. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  7 .
Câu 13. Tìm số phức liên hợp của số phức z  3   2i .
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  2   3i .
Câu 14. Tính môđun của số phức z  3  i . A. z  2 . B. z  2 . C. z  4 . D. z  3 . 2 3 3 Câu 15. Cho
f (x)dx  2  ,
f (x)dx  3  . Tính I f (x)dx  . 1 1 2 A. I  1. B. I  1. C. I  5 . D. I  5 . 2 2 2 Câu 16. Cho
f (x)dx  2 
, 2 f (x)  g(x)dx  3 
. Tính I g(x)dx  . 1 1 1 A. I  7 . B. I  1. C. I  5 . D. I  1. Câu 17. Tìm 2x e dx  . x 1 A. 2 2x e dx eC  . B. 2x 2x e dx eC  . C. 2x 2  2 x e dx eC  . D. 2x  2 x e dx e C  . 2 1
Câu 18. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (1)  3 . x 1 5 A. F (x)  x  2 .
B. F (x)  2 x 1. C. F (x)  x  .
D. F (x)  2 x 1. 2 2 Câu 19. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo dương.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 20. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  9  5i . Tính a b .
A. a b  1. B. a b  1  .
C. a b  4 .
D. a b  5 .
Câu 21. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x y  2  0 .
B. x y  4  0 .
C. x y  0 .
D. x y  0 . 4 x
Câu 22. Cho tích phân I dx
. Đặt t  2x 1 . Mệnh đề nào sau đây đúng ? 2x 1 0 3 3 3 3 1 1 A. 2
I  (2t  2)dt  . B. 2 I  (t 1)dt  . C. 2
I  (t 1)dt  . D. 2 I  (t 1)dt  . 2 2 1 1 1 1 Trang 2/3 – Mã đề 122 4 1 Câu 23. Biết
dx m ln 5  n ln 3 (m, n R) 
. Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 Câu 24. Tìm sin 2xdx  . 1
A. sin 2xdx  2 cos 2x C  . B. sin 2xdx  cos 2x C  . 2 1
C. sin 2xdx   cos 2x C  .
D. sin 2xdx   cos 2x C  . 2 x
Câu 25. Tìm nguyên hàm của hàm số f (x)  . 2 x  4 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  4  C 2 2  . 2(x  4) 1 x  2 1 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  4  C  . 4 x  2 2
Câu 26. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) .
Câu 27. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực không dương. B. z  1.
C. Phần thực của z là số âm.
D. z là số thuần ảo.
Câu 28. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 4 9 9 1 A. x y  . B. x y  .
C. x y   . D. x y  . 5 5 5 5 Câu 29. Tìm 2 x xe dx  . A. 2 x  2 x  2 x xe dx xe e C  . B. 2 x  2 x  2 x xe dx xe e C  . C. 2 2 x x
xe dx x e C  . D. 2 x  2 x x xe dx
xe e C  . 2
Câu 30. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;2 , f (0)  5 , f (2)  2 . Tính I f '(x)dx  . 0 A. I  3 . B. I  3  . C. I  2 . D. I  7 .
Câu 31. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x 1, trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
Câu 32. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 32 8 16 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
--------------- HẾT --------------- Trang 3/3 – Mã đề 122
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 123
Họ và tên học sinh: ……………………………..………………. Lớp: …………    
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 1; 2 và b  (2;1;1) . Tính a . b .        
A. a . b  (2; 1  ; 2) .
B. a . b  6 . C. a . b  1  .
D. a . b  1 .
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Oy ? A. y  0. B. y 1  0. C. y 1  0.
D. x z 1  0. x  1 2t
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  2  t . Điểm nào sau đây thuộc z  1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (2; 1  ;3) . C. P( 1  ;3; 4) . D. Q( 3  ; 4; 5) .  
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  ( 2
 ;1; 2) và b  ( 1
 ;1; 0) . Tính số đo của  
góc giữa hai vectơ a và b .         A. a b 0 ,  30 . B. a b 0 ,  45 . C. a b 0 ,  60 . D. a b 0 ,  135 . x 1 y  2 z 1
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 1 3 1
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 6. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Oy . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 2;0;3 .
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I 1; 2  ;  1 .
Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 .
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (6;  4; 1) .
B. u2  (6; 4; 1) . C. 3 u  (6;  4;1) . D. u4  (6; 4;1) .
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2  ; 2 ,
B2;1;0 và vuông góc với mặt phẳng Oyz . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1 n  (0; 2;  3) . B. 2 n  (0; 2;3) . C. 3 n  (0;3;  2) . D. 4 n  (0;3; 2) . Trang 1/3 – Mã đề 123 x 1 y z 1
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A2; 1
 ; 0 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  2  0 .
C. (P) : 2x  5 y z 1  0 .
D. (P) : x  3y z 1  0 .       
Câu 11. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2
i j k và    
OB i j  3k . Tìm tọa độ trung điểm M của đoạn thẳng AB .  1   3   3  A. M  ;1; 2    . B. M ; 0; 1   . C. M  ; 0;1   . D. M  1  ; 2; 4   .  2   2   2  x 1 y  2 z
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1  1
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  (2;1; 1) . B. u2  ( 2  ;1;1) . C. 3 u  (2; 1  ;1) .
D. u4  (1; 2;0) . Câu 13. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z  5  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 . A. w  2   4i . B. w  2   4i .
C. w  2  4i .
D. w  2  4i .
Câu 14. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  8  2i . Tính a b .
A. a b  4 . B. a b  4  .
C. a b  2 . D. a b  2  .
Câu 15. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  2  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. x  3y  0 .
B. x  3y  0 .
C. x y  0 .
D. x y  0 .
Câu 16. Cho số phức z thỏa mãn z z  0 . Mệnh đề nào sau đây đúng ?
A. z là số thực dương. B. z  1.
C. Phần thực của z không âm.
D. z là số thuần ảo.
Câu 17. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun nhỏ nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 Câu 18. Tìm 3x e dx  . x 1 A. 3x 3  3 x e dx eC  . B. 3x 3x e dx eC  . C. 3 3x e dx eC  . D. 3x 2  3 x e dx eC  . 3
Câu 19. Tìm co s 2xdx  . 1 1
A. co s 2xdx   sin 2x C  . B. co s 2xdx  sin 2x C  . 2 2
C. co s 2xdx  2 sin 2x C  .
D. co s 2xdx  2 sin 2x C  .
Câu 20. Tìm số phức liên hợp của số phức z  3  2i .
A. z  3  2i . B. z  3   2i . C. z  3   2i .
D. z  2  3i .
Câu 21. Cho số phức z thỏa mãn z i(1 2i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M (2;1) . B. N (1; 2) . C. P(2;1) . D. Q(1; 2) . 2 Câu 22. Cho tích phân 3 2 I x 5  x dx  . Đặt 2
t  5  x . Mệnh đề nào sau đây đúng ? 1 2 2 2 2 A. I   3
t  5t dt . B. 3
I  (5t t ) dt  . C. 2 4
I  (5t t ) dt  . D. I   4 2
t  5t dt . 1 1 1 1 Trang 2/3 – Mã đề 123
Câu 23. Tính môđun của số phức z  2 2  i . A. z  1 2 2 . B. z  9 . C. z  7 . D. z  3 . 1
Câu 24. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (4)  1. x 1 3 A. F (x)   . B. F (x)  x 1 .
C. F (x)  2 x  3 .
D. F (x)  2 x  3 . 2 x 4 4 4 4 Câu 25. Cho
f (x)dx  2, 2g(x)  f (x)dx  5  
. Tính I g(x)dx  . 1 1 1 3 3 7 7 A. I  . B. I   . C. I  . D. I   . 2 2 2 2 x
Câu 26. Tìm nguyên hàm của hàm số f (x)  . 2 x  9 2 x  9 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x  9  C 2 2  . (x  9) 2 1 x  3 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x  9  C  . 6 x  3 Câu 27. Tìm 4 x xe dx  . A. 4 x  4 x x xe dx
xe e C  . B. 4 x  4 x  4 x xe dx xe e C  . C. x 2 4  2 x xe dx x e C  . D. 4 x  4 x  4 x xe dx xe e C  . 2 5 5 Câu 28. Cho
f (x)dx  3,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1.  6       
Câu 29. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f     và
f '(x) dx   . Tính f 0 . 6     6  3 0 2 2   A. f 0   . B. f 0  . C. f 0   . D. f 0  . 3 3 3 3 2 1 Câu 30. Biết
dx m ln 7  n ln 2 (m, n R) 
. Tính P m n . 3x 1 1 2 A. P  0 . B. P  . C. P  1  . D. P  1 . 3
Câu 31. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  4 , trục hoành, trục tung và
đường thẳng x  2 . A. S  16 . B. S  14 . C. S  12 . D. S  8 .
Câu 32. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 32 16 10 8 A. V  . B. V  . C. V  . D. V  . 3 3 3 3
--------------- HẾT --------------- Trang 3/3 – Mã đề 123
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12
Thời gian: 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 124
Họ và tên học sinh: ……………………………..………………. Lớp: …………
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;1; 2 . Phương trình nào sau đây là phương
trình mặt phẳng đi qua điểm M và vuông góc với trục Oz ? A. z  2  0. B. z  2  0. C. z  0.
D. x y  0.    
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  1; 2
 ; 2 và b  (2;1; 2
 ) . Tính a . b .        
A. a . b  (2; 2  ; 4) . B. a . b  4  .
C. a . b  4 .
D. a . b  9 .
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua hai điểm A 1; 2; 2 ,
B2;1;0 và vuông góc với mặt phẳng Ozx . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P) ?     A. 1
n  (1; 1; 1) . B. 2 n  (0; 2;3) . C. 3 n  (2; 0; 1) . D. 4 n  (2; 0;1) .  
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a  (2; 2; 0) và b  ( 1  ; 0;1) . Tính số đo  
của góc giữa hai vectơ a và b .         A.   0 a , b  30 . B.   0 a , b  60 . C.   0 a , b  120 . D.   0 a , b  150 . x 1 y  2 z 1
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt phẳng 6 3 3 
(P) : 2x y z  3  0 . Mệnh đề nào sau đây đúng ?
A. d song song với (P).
B. d chứa trong (P).
C. d vuông góc với (P).
D. d cắt (P) và không vuông góc với (P).
Câu 6. Trong không gian với hệ tọa độ Oxyz , tìm tọa độ hình chiếu vuông góc điểm M 2; 1  ;3 trên trục Ox . A. 2;0;0 . B. 0; 1  ; 0 . C. 0;0;3 . D. 0; 1;3 . x  2  t
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :  y  3  2t . Điểm nào sau đây thuộc z 1 3t  đường thẳng d ? A. M (3;1; 2  ) . B. N (1;1; 4) . C. P(0; 7 ;5) . D. Q( 1  ;9;  8) .
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x  2 y z  3  0 và hai điểm (
A 1;0;1) , B(1; 2;  3) . Gọi  là đường thẳng nằm trong mặt phẳng (P) sao cho mọi điểm thuộc  đều
có khoảng cách đến A và đến B bằng nhau. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng  ?     A. 1
u  (3;  5;  4) .
B. u2  (3;5; 4) . C. 3 u  (3;  5; 4) . D. u4  (3;5; 4) .
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x  2 y  2z  2  0 và điểm I  1  ; 2;  
1 . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường
tròn có bán kính bằng 5. A. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . B. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  34 . C. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  16 . D. 2 2 2
(S ) : (x 1)  ( y  2)  (z 1)  25 . Trang 1/3 – Mã đề 124 x 1 y z 1
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1  1 A1; 2; 
1 . Viết phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d .
A. (P) : 2x y z  5  0 .
B. (P) : x  4 y  2z  5  0 .
C. (P) : 2x  5 y z  7  0 .
D. (P) : x y z  2  0 .       
Câu 11. Trong không gian với hệ tọa độ ( ;
O i , j , k) , cho hai điểm A, B thỏa mãn OA  2 i j  3k và    
OB  4 i  3 j k . Tìm tọa độ trung điểm M của đoạn thẳng AB . A. M 3;1;  1 . B. M  3  ; 1;   1 .
C. M 2; 4;  4 .
D. M 1;2;  2 . x 1 y  2 z  4
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào dưới 2 1 3
đây là vectơ chỉ phương của đường thẳng d ?     A. 1 u  ( 2  ;1;  3) . B. u2  ( 2  ; 1  ;3) . C. 3 u  (2; 1  ; 3  ) .
D. u4  (1; 2;4) .
Câu 13. Tìm số phức liên hợp của số phức z  3  2i .
A. z  2  3i .
B. z  3  2i . C. z  3   2i . D. z  3   2i .
Câu 14. Cho số phức z a bi (a, b R) thỏa mãn 2z  1 iz  7  i . Tính a b .
A. a b  1  .
B. a b  1. C. a b  5  .
D. a b  5 . Câu 15. Tìm 4x e dx  . x 1 A. 4x 4  4 x e dx eC  . B. 4x 3  4 x e dx eC  . C. 4 4x e dx eC  . D. 4x 4x e dx eC  . 4
Câu 16. Cho số phức z thỏa mãn z i(2  i) . Điểm nào sau đây là điểm biểu diễn số phức z trên mặt phẳng tọa độ ? A. M ( 1  ; 2) . B. N (1; 2) . C. P(2;1) . D. Q(2;1) .
Câu 17. Cho số phức z thỏa mãn z z . Mệnh đề nào sau đây đúng ?
A. Phần thực của z không âm.
B. z là số thuần ảo.
C. z là số thực dương. D. z  1. 1 Câu 18. Tìm dx  . 2 o c s x 1 1 A.
dx  t anx  C  . B.
dx   t anx  C 2  . o c s x 2 o c s x 1 1 C.
dx co t x  C  . D.
dx  co t x  C 2  . cos x 2 cos x
Câu 19. Biết rằng trong mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z  3  i z 1 2i là một đường thẳng. Hãy xác định phương trình của đường thẳng đó ?
A. 8x  6 y  5  0 .
B. 8x  2 y  5  0 .
C. 8x  2 y  5  0 .
D. 8x  6 y  5  0 . 3 1 Câu 20. Biết
dx m ln 5  n ln 3 ( , m n R) 
. Tính P m n . 2x  3 1 3 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 2 5 5 Câu 21. Cho
f (x)dx  3  ,
f (x)dx  2   . Tính I f (x)dx  . 1  1  2 A. I  5  . B. I  5 . C. I  1. D. I  1.
Câu 22. Cho số phức z x yi x, y R thỏa mãn z  3  4i  4 và z có môđun lớn nhất. Tính x y . 9 9 1 1
A. x y   . B. x y  . C. x y  .
D. x y   . 5 5 5 5 Trang 2/3 – Mã đề 124 4 4 4 Câu 23. Cho
f (x)dx  3,  f (x)  2g(x)dx  7  
. Tính I g(x)dx  . 1 1 1 A. I  2  . B. I  2 . C. I  5  . D. I  5 .
Câu 24. Gọi (H ) là hình phẳng giới hạn bởi đồ thị hàm số y
x , trục hoành và đường thẳng
y x  2 . Tính thể tích V của khối tròn xoay tạo bởi khi quay hình phẳng (H) xung quanh trục hoành . 10 8 16 32 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 x
Câu 25. Tìm nguyên hàm của hàm số f (x)  . 2 x 16 2 x 16 1 A.
f (x)dx    C  . B. 2
f (x)dx  ln x 16  C 2 2  . (x 16) 2 1 x  4 C.
f (x)dx  ln  C  . D. 2
f (x)dx  ln x 16  C  . 8 x  4
Câu 26. Tính môđun của số phức z  2  2i . A. z  0 . B. z  8 . C. z  4 . D. z  2 2 . 
Câu 27. Cho hàm số f (x) có đạo hàm liên tục trên đoạn 0;  , f 0  1 và f '(x) dx  9  . Tính f   . 0
A. f    10 .
B. f    10 .
C. f    8 .
D. f    8 . Câu 28. Tìm 3 x xe dx  . A. 3 x  3 x x xe dx
xe e C  . B. 3 x  3 x  3 x xe dx xe e C  . x 3 C. 2 3 x xe dx x e C  . D. 3 x  3 x  3 x xe dx xe e C  . 2 1
Câu 29. Tìm nguyên hàm F (x) của hàm số f (x)  , biết F (9)  0 . x 1 1
A. F (x)  2 x  6 .
B. F (x)  2 x  6 . C. F (x)  x  3. D. F (x)   . 2 x 6 Câu 30. Gọi 1
z và z2 là 2 nghiệm phức của phương trình 2
z  2z 10  0 , trong đó 1
z có phần ảo âm.
Tìm số phức w  ( 1
z z2)z2 .
A. w  2  6i .
B. w  2  6i . C. w  2   6i . D. w  2   6i . 2 Câu 31. Cho tích phân 3 2 I x 4  x dx  . Đặt 2 t
4  x . Mệnh đề nào sau đây đúng ? 0 2 2 2 2 A. 2 4
I  (4t t ) dt  . B. 3
I  (4t t ) dt  . C. I   3
t  4t dt . D. I   4 2
t  4t dt . 0 0 0 0
Câu 32. Tính diện tích S của hình phẳng giới hạn bởi parabol 2
(P) : y  3x  2 , trục hoành, trục tung và
đường thẳng x  2 . A. S  8 . B. S  10 . C. S  12 . D. S  14 .
--------------- HẾT --------------- Trang 3/3 – Mã đề 124
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12 ĐÁP ÁN
Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Câu 101 102 103 104 105 106 107 108 109 110 111 112 1 A C C C A B C A A A C B 2 C B A B D D D D B C A D 3 B D A A C D B A D A D C 4 D B B C D A A D C C A A 5 A D D A A B A C A C D A 6 C A B C B B C D D B B A 7 D C C A A C A A B A B C 8 B B A D C A C B B B C D 9 A D D B C B B B C D D B 10 D C A B D C A C A B B C 11 B A C B C C D D B B C C 12 D B C D B A D C C C B B 13 C A B A A A B C C D C B 14 B D D C D B D B B D D D 15 1 A C A D B C C A D A A A 16 C D B B D D B D A A A D 17 B A D D B A D B A C D A 18 D B C C D D B D A D B B 19 A C A D C A A C D B D A 20 C D B A B C C B C D C C 21 B A D A A A B A B A C B 22 D B A B B D B D D A B B 23 A C B D C B B B C B A D 24 C A C A B C D A A D A C 25 B C B D C B A C D C A C 26 C D D C A D C B C D B A 27 D B C B C A A C B C D D 28 A A C C D D C C D B B A 29 A B D D B C D B D A A B 30 B A B A A B A A C D C D 31 A C D B B D A A A A C D 32 D B A A A C D B B B B C
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2016-2017 QUẢNG NAM Môn: TOÁN – Lớp 12 ĐÁP ÁN
Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Mã đề Câu 113 114 115 116 117 118 119 120 121 122 123 124 1 B A B A A B A B B D C B 2 D D D C B A B C D A C B 3 B B A A C B D A C B D D 4 C C C B A D C A A C B C 5 D D D C C C B A D B A C 6 A A D B D B C C C C B A 7 C A C A B A D D B D A D 8 B D C C A D A B D A B A 9 A C B A A D B A D A B B 10 A A B C B C A B C A C D 11 C B D B C C A B A D A D 12 C D A D B D D C B B A C 13 A D D A C B C D A C D B 14 B C C C B D D A B B A D 15 1 A B B D D D A B D C B C 16 D C D D B A C C C D C A 17 D D A B D C B D A A D A 18 B B B D A C C C D B C A 19 D C B B C B B B B C B C 20 C B C D B B D C B B A D 21 D A A A D C A D C D C B 22 A C A B C A D C A D C B 23 A B B D A B A B B A D C 24 A C C D B A B D C C D C 25 D B A C A A D A C D C B 26 B A A A D B B B B A B D 27 B A B B C C D D D A D A 28 B B D C D D C A A C A D 29 C D D D A A B B A A B A 30 A B A A B D A A A B D B 31 C A C B C A A D D B A A 32 D C C A D C C C C D B C
Document Outline

  • 101
    • Họ và tên học sinh: ……………………………..……………….
  • 102
    • Họ và tên học sinh: ……………………………..……………….
  • 103
    • Họ và tên học sinh: ……………………………..……………….
  • 104
    • Họ và tên học sinh: ……………………………..……………….
  • 105
    • Họ và tên học sinh: ……………………………..……………….
  • 106
    • Họ và tên học sinh: ……………………………..……………….
  • 107
    • Họ và tên học sinh: ……………………………..……………….
  • 108
    • Họ và tên học sinh: ……………………………..……………….
  • 109
    • Họ và tên học sinh: ……………………………..……………….
  • 110
    • Họ và tên học sinh: ……………………………..……………….
  • 111
    • Họ và tên học sinh: ……………………………..……………….
  • 112
    • Họ và tên học sinh: ……………………………..……………….
  • 113
    • Họ và tên học sinh: ……………………………..……………….
  • 114
    • Họ và tên học sinh: ……………………………..……………….
  • 115
    • Họ và tên học sinh: ……………………………..……………….
  • 116
    • Họ và tên học sinh: ……………………………..……………….
  • 117
    • Họ và tên học sinh: ……………………………..……………….
  • 118
    • Họ và tên học sinh: ……………………………..……………….
  • 119
    • Họ và tên học sinh: ……………………………..……………….
  • 120
    • Họ và tên học sinh: ……………………………..……………….
  • 121
    • Họ và tên học sinh: ……………………………..……………….
  • 122
    • Họ và tên học sinh: ……………………………..……………….
  • 123
    • Họ và tên học sinh: ……………………………..……………….
  • 124
    • Họ và tên học sinh: ……………………………..……………….
  • Dap an DeKTraHK2_Toan12_1617